 曲线饱和模型,相比基于瞬态场路耦合的有限元模型[14-15],其精度远远不够。
曲线饱和模型,相比基于瞬态场路耦合的有限元模型[14-15],其精度远远不够。摘要 利用变压器T形模型,推导换流变压器直流偏磁对换相角影响的理论计算公式。利用电磁场有限元仿真软件,配合外电路开关控制,搭建考虑实际换流变压器电感变化的逆变器换相模型。通过给换流变压器中性点施加不同流向、不同大小的直流电流,模拟地磁暴侵害换流变压器的影响。通过对一个周期内六次换相角大小变化的分析,得到彼此之间的联系以及各自随触发超前角,直流方向、大小的变化关系。通过对直流电压、交流电流波形进行傅里叶分解,发现磁暴期间交流电流出现非特征谐波,且高频分量增幅更大,直流电压谐波次数由六的倍数变为三的倍数。结合偏磁时的换相角理论计算公式和励磁电流波形,解释了换相角以及谐波的变化原因,也验证了模型和结论的正确性。
关键词:地磁暴 直流偏磁 换流变压器 换相角 谐波分析
太阳活动引起的地磁场剧烈变化称为磁暴。时变磁场在地面感应出的电场通过输电线、中性点接地变压器和大地构成的回路产生地磁感应电流(Geomagnetically Induction Current, GIC)。与直流接地极产生的直流不同,GIC具有周期性,其频率成分一般为0.000 1~0.01Hz[1],也就是说在一次磁暴期间,既有流进变压器中性点的直流,也有流出的。另外在数值上,GIC的数值一般较大,2004年我国在500kV电网测到过最大值为75.5A(变压器中性点)的GIC[2],随着电网的发展,导线电阻的减小,该值会越来越大[3]。
直流侵害变压器次生的谐波、温升、无功损耗和振动、噪声增大等有害的干扰,国内外已有大量的研究[4-7]。然而其大都是研究交流变压器本身或者换流变压器(下文简称换流变)的空载情况,没有考虑换流变压器所处的实际工况以及对系统的影响。正常工作时,由于换流变压器二次侧接换流阀,其存在换相这一特殊的工况,而换相角(换流变压器二次电流由额定值减小到零所对应的电角度)是衡量系统工作状态的一个重要指标,与换流变压器的电感参数有关。换相角过大会导致换相失败,过小会使逆变器吸收更多的无功功率,降低直流传输效率[8]。文献[9-10]通过在PSCAD中搭建高压直流系统仿真模型,研究了换流变压器直流偏磁对换相失败的影响,认为直流偏磁导致励磁电感的非线性,造成换相电压的畸变,增大了换相角。文献[11]直接从谐波的幅值、频率、相位这三个方面定量分析了其对于换相失败的影响。文献[12-13]利用调制波理论,证明了换流变压器直流偏磁产生的2次谐波,会对系统的稳定性产生不利的影响。但上述研究所用到的换流变压器模型不是漏电感模型,就是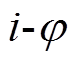 曲线饱和模型,相比基于瞬态场路耦合的有限元模型[14-15],其精度远远不够。
曲线饱和模型,相比基于瞬态场路耦合的有限元模型[14-15],其精度远远不够。
因此,本文通过搭建基于有限元的换相模型,着重研究换流变压器直流偏磁状态下换相角数值大小及其变化规律。首先通过换相角的计算原理,推导了在直流偏磁状态下换相角的表达式,从而证明了换相角与换流变压器所遭受的直流侵害大小有关。接着在磁场有限元软件中,搭建了考虑换流变压器电感变化的逆变器换相模型,计算得出了GIC侵害下的换相角数值。运用计算得出的换相期间的励磁电流波形和换相角的理论计算公式,阐明了换流变压器直流偏磁时换相角随触发超前角、直流大小和方向之间的具体变化规律以及不同桥臂之间换相角的大小关系。最后分析由于换相角变化引发的直流电压、交流电流谐波含量的改变对直流系统以及换流变压器的影响。得到的规律和结论可为预防地磁暴侵害直流工程提供依据。
高压直流输电的基本模块是三相全波桥式电路,其逆变侧的六脉波换流桥等效电路如图1所示[16]。
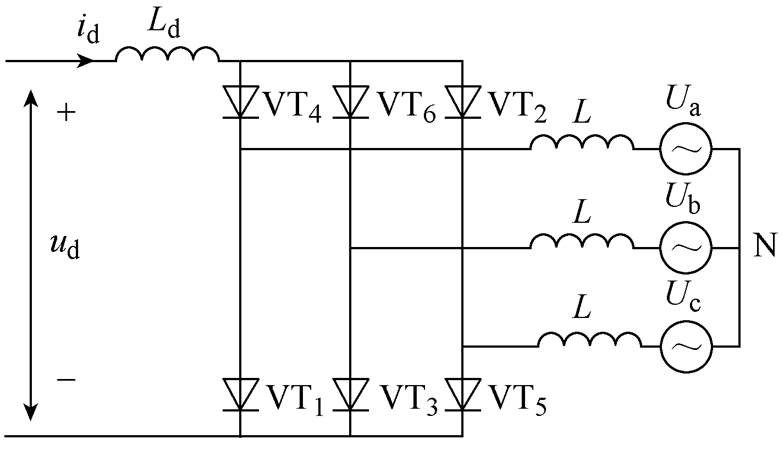
图1 六脉波换流桥等效电路
Fig.1 Equivalent circuit of six-pulse converter bridge
图1中,Ld为平波电抗器;ud为直流电压;Ua、Ub、Uc分别为三相母线电压。晶闸管VT2、VT4、VT6位于上桥臂,其彼此之间的换相过程对应的换相角称为上桥臂换相角;同理,晶闸管VT1、VT3、VT5之间的换相过程对应的换相角称为下桥臂换相角。直流电流id从一个晶闸管所在的支路转移到另一个晶闸管所在的支路的过程称为换相。由阀4向阀6换相过程的等效电路如图2所示。
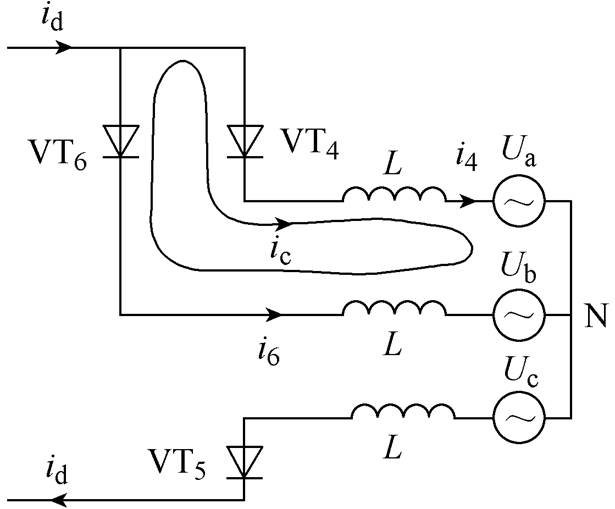
图2 换相过程等效电路
Fig.2 Equivalent circuit of commutation process
如图2所示,换相过程可表示为
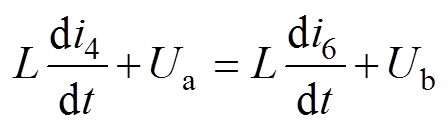 (1)
(1)式中,i4、i6分别为流过晶闸管VT4和VT6的电流;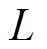 为换流变压器漏电感。因为直流侧都装有一个较大的平波电抗器,因此直流电流
为换流变压器漏电感。因为直流侧都装有一个较大的平波电抗器,因此直流电流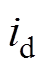 可认为不变,即
可认为不变,即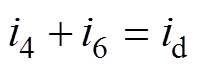 ,式(1)可表示为
,式(1)可表示为
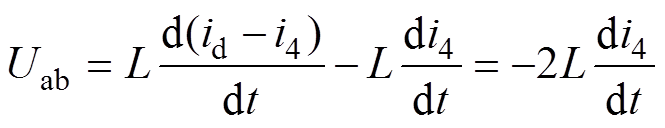 (2)
(2)
对式(2)两端进行关于时间的定积分,积分下限为换相开始时刻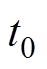 ,上限为换相结束时刻
,上限为换相结束时刻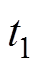 ,因为换相期间
,因为换相期间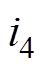 从
从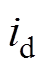 减小到零,因此可得
减小到零,因此可得
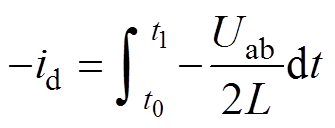 (3)
(3)因为假设交流母线电压不含谐波,所以
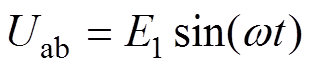 (4)
(4)
式中,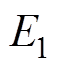 为交流系统基波线电压,将式(4)代入到式(3)化简得
为交流系统基波线电压,将式(4)代入到式(3)化简得
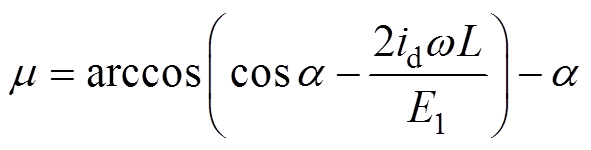 (5)
(5)式中,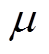 为换相角;
为换相角;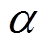 为触发延迟角,其与触发超前角
为触发延迟角,其与触发超前角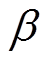 的关系为
的关系为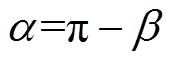 。对于具体的换流变压器,其漏电感是确定的,因此由式(5)可知,针对一个特定的逆变站,换相角与换流变压器的运行状态无关。
。对于具体的换流变压器,其漏电感是确定的,因此由式(5)可知,针对一个特定的逆变站,换相角与换流变压器的运行状态无关。
当忽略交流系统中的线路电感时,换相电感就是换流变压器的等效电感。换流变压器一次回路电压方程(忽略漏磁通)为
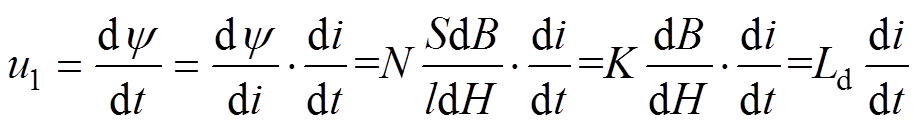 (6)
(6)式中,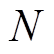 为一次绕组匝数;
为一次绕组匝数;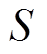 为铁心截面积;
为铁心截面积;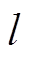 为主磁路长度;
为主磁路长度;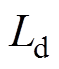 为励磁电感;K=NS/l。由式(6)可知,励磁电感与
为励磁电感;K=NS/l。由式(6)可知,励磁电感与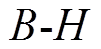 曲线的斜率呈正相关。正常工作时,换流变压器工作在磁化曲线的拐点附近,其斜率很大,因此励磁电感远大于漏电感,其模型可用恒定不变的漏电感表示,换相过程等效电路如图2所示。但当直流侵入时,铁心严重饱和,励磁电感迅速减小,因此必须考虑励磁支路的影响,此时阀4向阀6换相模型如图3所示。图中,换流变压器用由一次、二次侧漏电感和励磁支路组成的T形模型表示。
曲线的斜率呈正相关。正常工作时,换流变压器工作在磁化曲线的拐点附近,其斜率很大,因此励磁电感远大于漏电感,其模型可用恒定不变的漏电感表示,换相过程等效电路如图2所示。但当直流侵入时,铁心严重饱和,励磁电感迅速减小,因此必须考虑励磁支路的影响,此时阀4向阀6换相模型如图3所示。图中,换流变压器用由一次、二次侧漏电感和励磁支路组成的T形模型表示。
此时换相过程可表示为
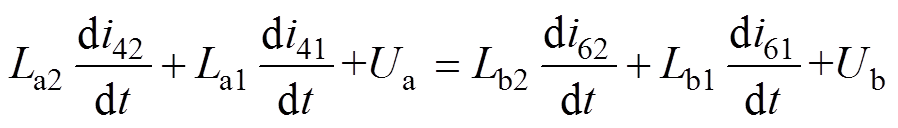 (7)
(7)将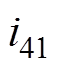 用
用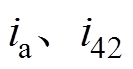 表示,
表示,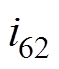 用
用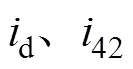 表示,
表示,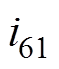 用
用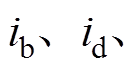
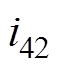 表示。其中,
表示。其中,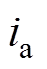 为A相换流变压器的励磁电流,
为A相换流变压器的励磁电流,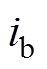 为B相换流变压器的励磁电流。假设在偏磁前后,换流变压器一次、二次侧漏电感恒定不变,则总的漏电感恒定不变,即
为B相换流变压器的励磁电流。假设在偏磁前后,换流变压器一次、二次侧漏电感恒定不变,则总的漏电感恒定不变,即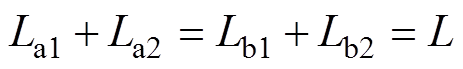 。经过化简,式(7)可表示为
。经过化简,式(7)可表示为
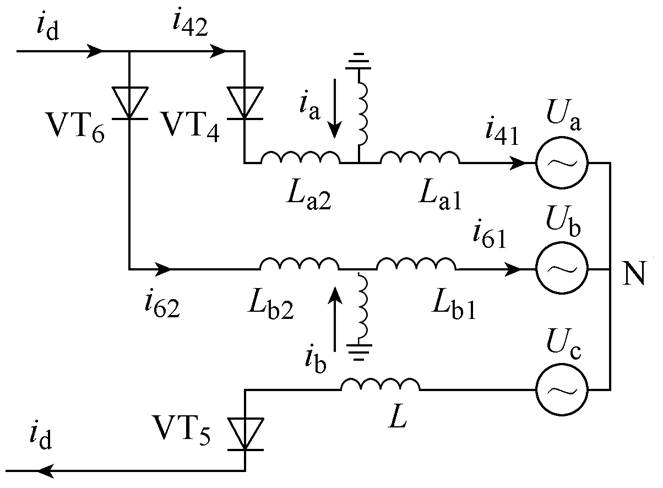
图3 饱和换相过程等效电路
Fig.3 Equivalent circuit of commutation process under saturation
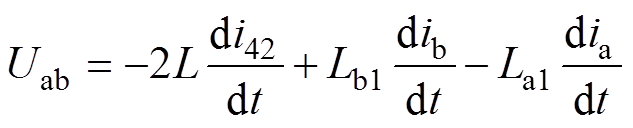 (8)
(8)式(8)与式(2)相比多了A、B相励磁电流对时间导数这两项,因为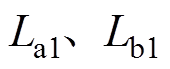 为常数,与式(2)一样,再对式(8)两端作定积分,可得
为常数,与式(2)一样,再对式(8)两端作定积分,可得
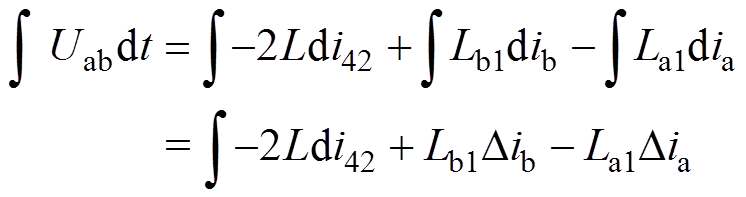 (9)
(9)
式中,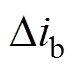 为换相结束和起始时刻B相励磁电流差值;
为换相结束和起始时刻B相励磁电流差值;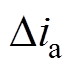 同理。与第1节一样,进一步推导可得换相角的表达式为
同理。与第1节一样,进一步推导可得换相角的表达式为
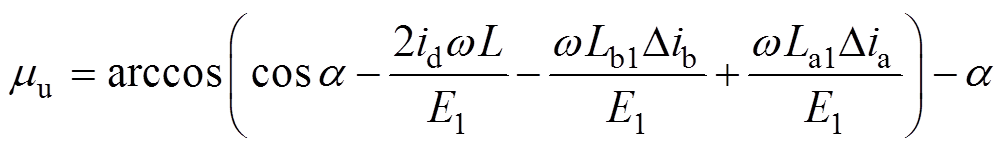 (10)
(10)因为处于同一桥臂的换相角表达式一样,因此上桥臂换相角可表示为
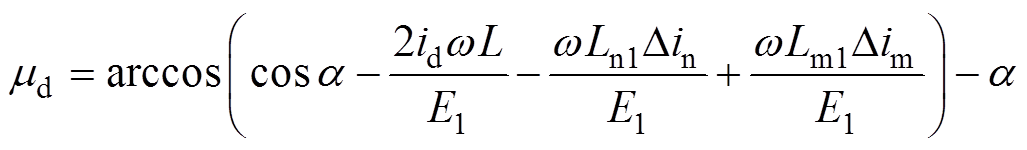 (11)
(11)
式中,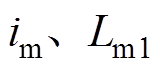 分别为参与换相的两相中电流由
分别为参与换相的两相中电流由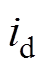 减小到零的那相的励磁电流和一次侧漏电感;
减小到零的那相的励磁电流和一次侧漏电感;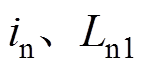 分别为参与换相的两相中电流由零增大到
分别为参与换相的两相中电流由零增大到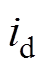 的那相的励磁电流、一次侧漏电感。
的那相的励磁电流、一次侧漏电感。
同理,下桥臂换相角可表示为
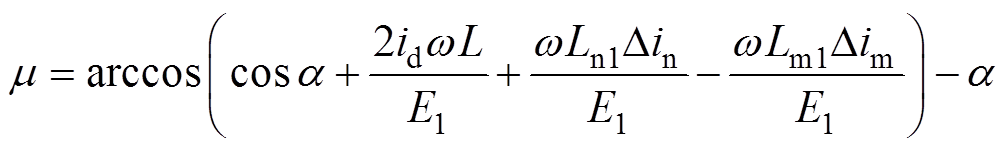 (12)
(12)由式(12)可知,当换流变压器处于直流偏磁状态时,换相角的大小与换相结束和起始时刻的励磁电流差值有关,也就是和换流变压器的工作状态有关。
在通用有限元仿真软件中分别搭建A相和B相两台变压器八分之一磁场模型,利用场路耦合的方法实现两台变压器的电气连接,通过电路模型中的开关控制,模拟换相过程。八分之一磁场模型和换相电路模型如图4所示(由于A、B相换流变压器结构一样,所以图4a只画出一相),图中, 分别为A、B相换流变压器绕组电阻。
分别为A、B相换流变压器绕组电阻。
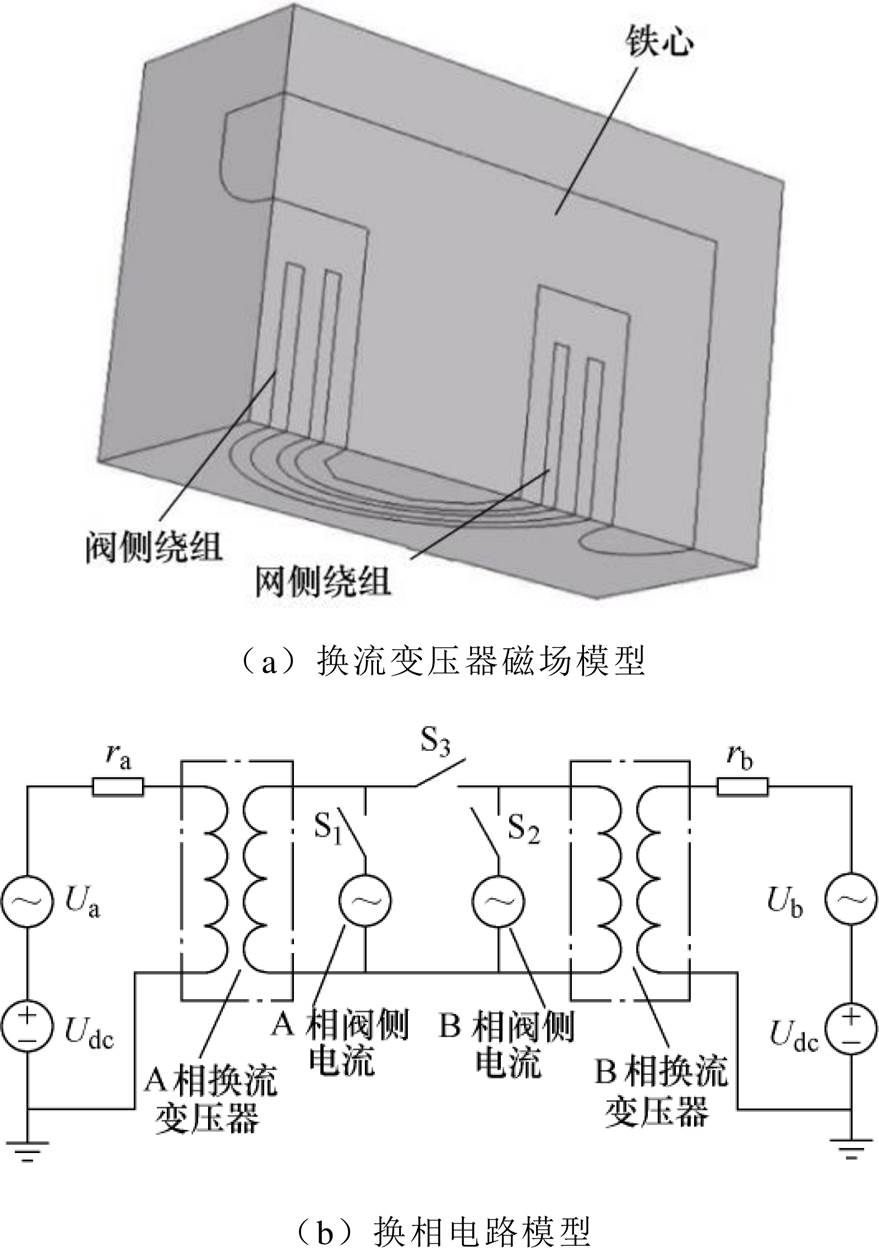
图4 换相模型
Fig.4 Commutation model
如图4b所示,在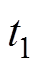 时刻之前(
时刻之前(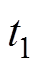 由触发超前角
由触发超前角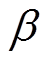 确定),开关S1闭合,S2闭合,S3打开。此时A、B相换流变压器阀侧分别流过额定负载电流,两者相位差120°(负载电流利用调制波理论推导计算得 出[17]),此时模拟的是换相开始之前变压器的运行状态:两者独立运行,无电气连接。在
确定),开关S1闭合,S2闭合,S3打开。此时A、B相换流变压器阀侧分别流过额定负载电流,两者相位差120°(负载电流利用调制波理论推导计算得 出[17]),此时模拟的是换相开始之前变压器的运行状态:两者独立运行,无电气连接。在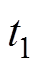 时刻,S1打开,S2打开,S3闭合表示晶闸管
时刻,S1打开,S2打开,S3闭合表示晶闸管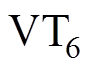 导通。此时,电路等效为图2,表示换相过程。当A相阀侧绕组电流降到零时,即
导通。此时,电路等效为图2,表示换相过程。当A相阀侧绕组电流降到零时,即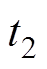 时刻,结束仿真,
时刻,结束仿真,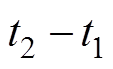 就是对应的换相时间。
就是对应的换相时间。
上述为换相模型的全部建立流程,但在实际操作中必须要解决一个问题才能实现计算:由于特高压变压器线圈的电感远大于其电阻,所以电路时间常数很大,这会导致在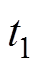 时刻之前,直流偏磁下的换流变压器达到稳定状态所需的时间过长,从而无法完成计算。如果直接像文献[18-19]一样,在电路中串联一个大电阻,那么在
时刻之前,直流偏磁下的换流变压器达到稳定状态所需的时间过长,从而无法完成计算。如果直接像文献[18-19]一样,在电路中串联一个大电阻,那么在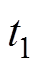 之后即换相时,该电阻会影响换相角的计算精度。因此在进行换相仿真之前,需要先分别计算出A、B两相换流变压器在换相开始之前的运行状态,此时可以用串联大电阻的方法加快仿真速度。在完成计算后,分别取其空间三维矢量磁位分布值作为初值,代入到换相模型里的A、B相换流变压器中。这样在仿真开始时,A、B相换流变压器即可达到偏磁时的稳定状态,同时换相电路中也不用串联大电阻。
之后即换相时,该电阻会影响换相角的计算精度。因此在进行换相仿真之前,需要先分别计算出A、B两相换流变压器在换相开始之前的运行状态,此时可以用串联大电阻的方法加快仿真速度。在完成计算后,分别取其空间三维矢量磁位分布值作为初值,代入到换相模型里的A、B相换流变压器中。这样在仿真开始时,A、B相换流变压器即可达到偏磁时的稳定状态,同时换相电路中也不用串联大电阻。
特高压换流变压器的具体参数见表1。由于换流变压器需要实现有载调压,因此其绕组的分接头有很多,所以表中换流变压器的网侧额定电压不是唯一的且跨度较大,但是为了研究方便,本文不考虑换流变压器有载调压的影响。
表1 换流变压器参数
Tab.1 Converter transformer parameters
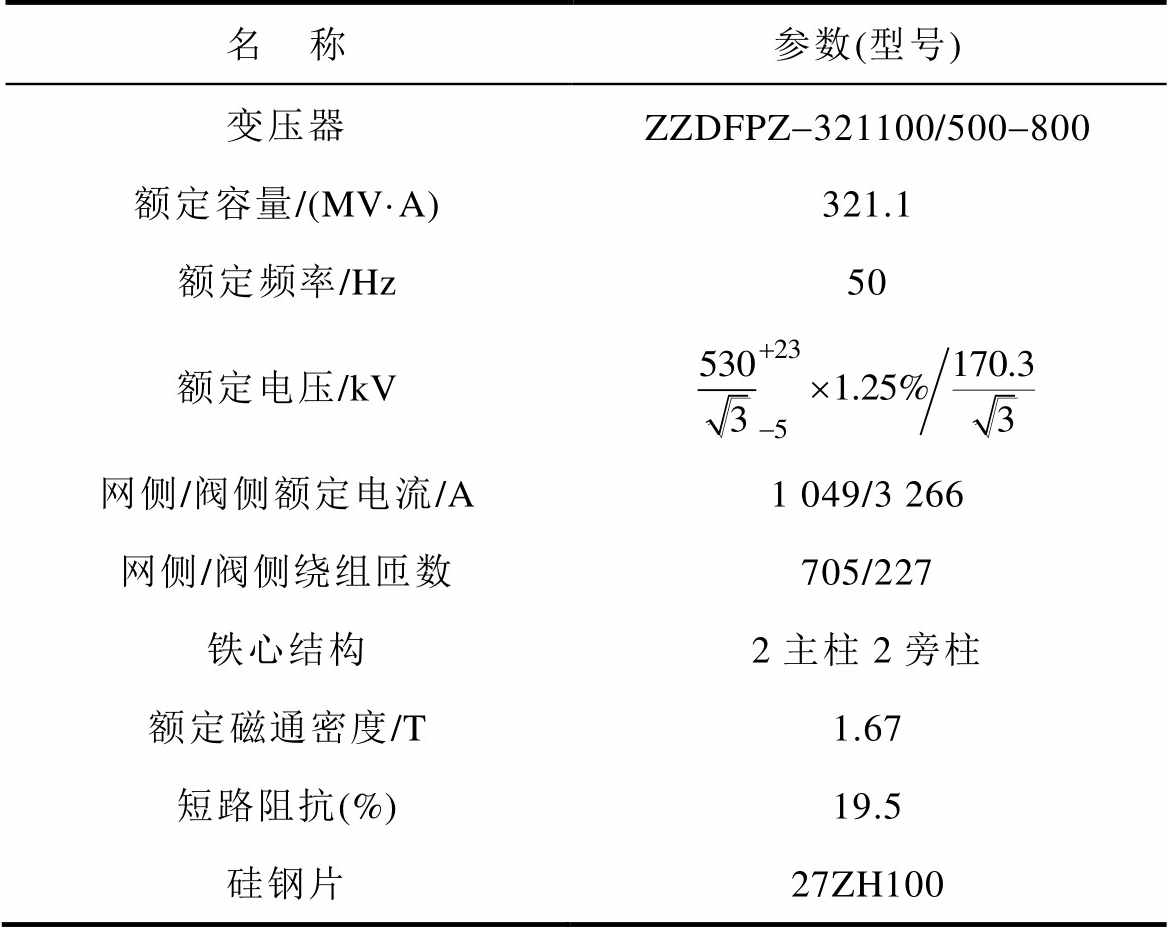
名 称参数(型号) 变压器ZZDFPZ-321100/500-800 额定容量/(MV·A)321.1 额定频率/Hz50 额定电压/kV 网侧/阀侧额定电流/A1 049/3 266 网侧/阀侧绕组匝数705/227 铁心结构2主柱2旁柱 额定磁通密度/T1.67 短路阻抗(%)19.5 硅钢片27ZH100
本文仿真计算如下六种情况:阀1向阀3(1-3)、阀2向阀4(2-4)、阀3向阀5(3-5)、阀4向阀6(4-6)、阀5向阀1(5-1)、阀6向阀2(6-2)换相。
由引言可知,GIC具有正负方向、幅值较大这两个特点,因此仿真时通入的直流电流设置为±100A、±70A、±50A、±30A、±10A以及正常工况下的0A(正负表示是直流的流向,流入换流变压器中性点为正,流出为负)。高压直流输电系统逆变器正常工作时,触发超前角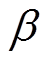 为30°~40°,因此角度设置为40°、35°、32°,直流电流设置为3 000A。
为30°~40°,因此角度设置为40°、35°、32°,直流电流设置为3 000A。
4.1.1 阀4向阀6换相
图5为直流电流为100A,触发超前角为32°时的仿真波形,其与理论计算的换相波形一致[16]:A、B相换相电流为正余弦波形。另外换流变压器正常工作时,利用式(5)计算得到的换相角与仿真计算的值接近,具体数值见表2。这表明本文使用有限元结合外电路的仿真方法的正确性。
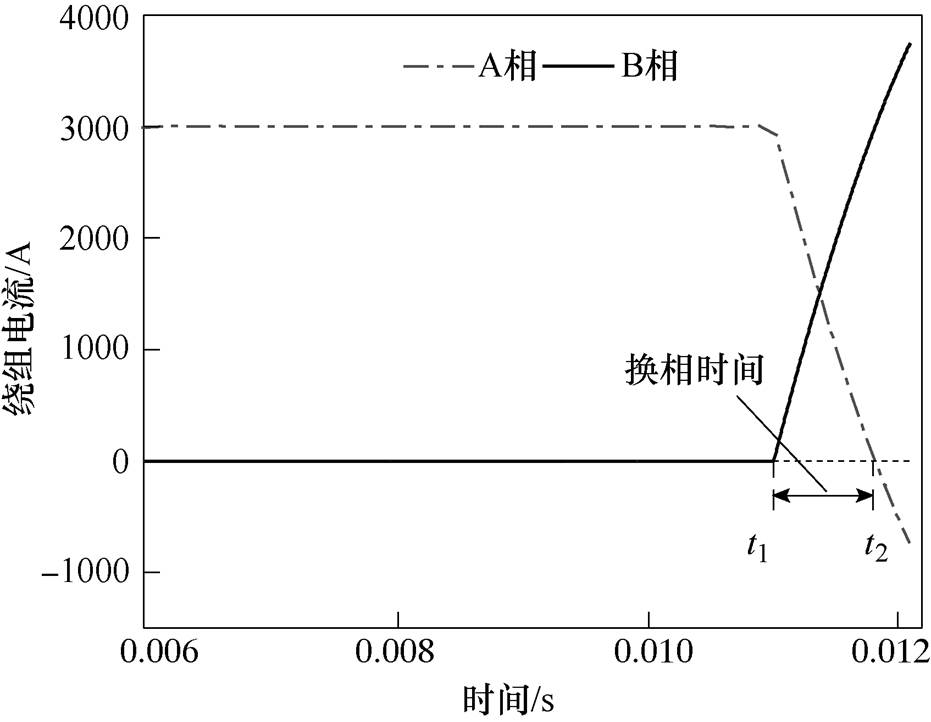
图5 正方向100A换相波形(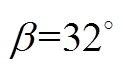 )
)
Fig.5 Positive direction 100A commutation waveforms (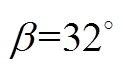 )
)
表2 换相角仿真数值(4-6)
Tab.2 Simulation value of commutation angle (4-6)
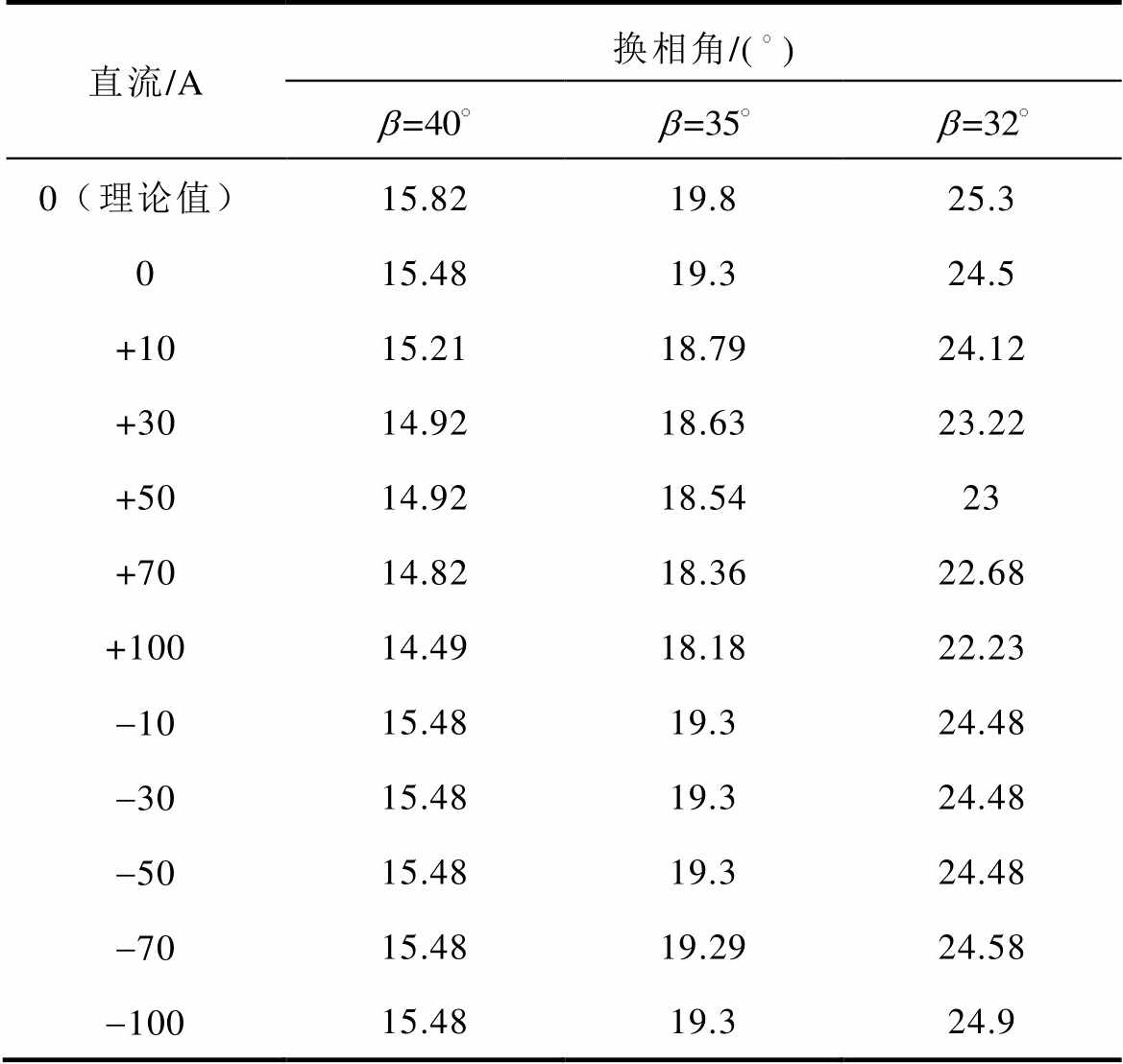
直流/A换相角/() 0(理论值)15.8219.825.3 015.4819.324.5 +1015.2118.7924.12 +3014.9218.6323.22 +5014.9218.5423 +7014.8218.3622.68 +10014.4918.1822.23 -1015.4819.324.48 -3015.4819.324.48 -5015.4819.324.48 -7015.4819.2924.58 -10015.4819.324.9
由表2可见,直流电流的方向不同,触发超前角大小不同,对于换相角的影响也不同。对于正方向的直流电流,随着直流电流的增大,换相角逐渐减小,且触发超前角越小换相角减小的越大,最大减幅为2.27°。而对于负方向的直流电流,当触发超前角大于35°时,换相角恒定不变,当触发超前角小于35°且直流电流大于50A时,换相角随着直流电流的增大而增大,但变化较小,最大增幅仅 为0.4°。
4.1.2 六次换相之间换相角的关系
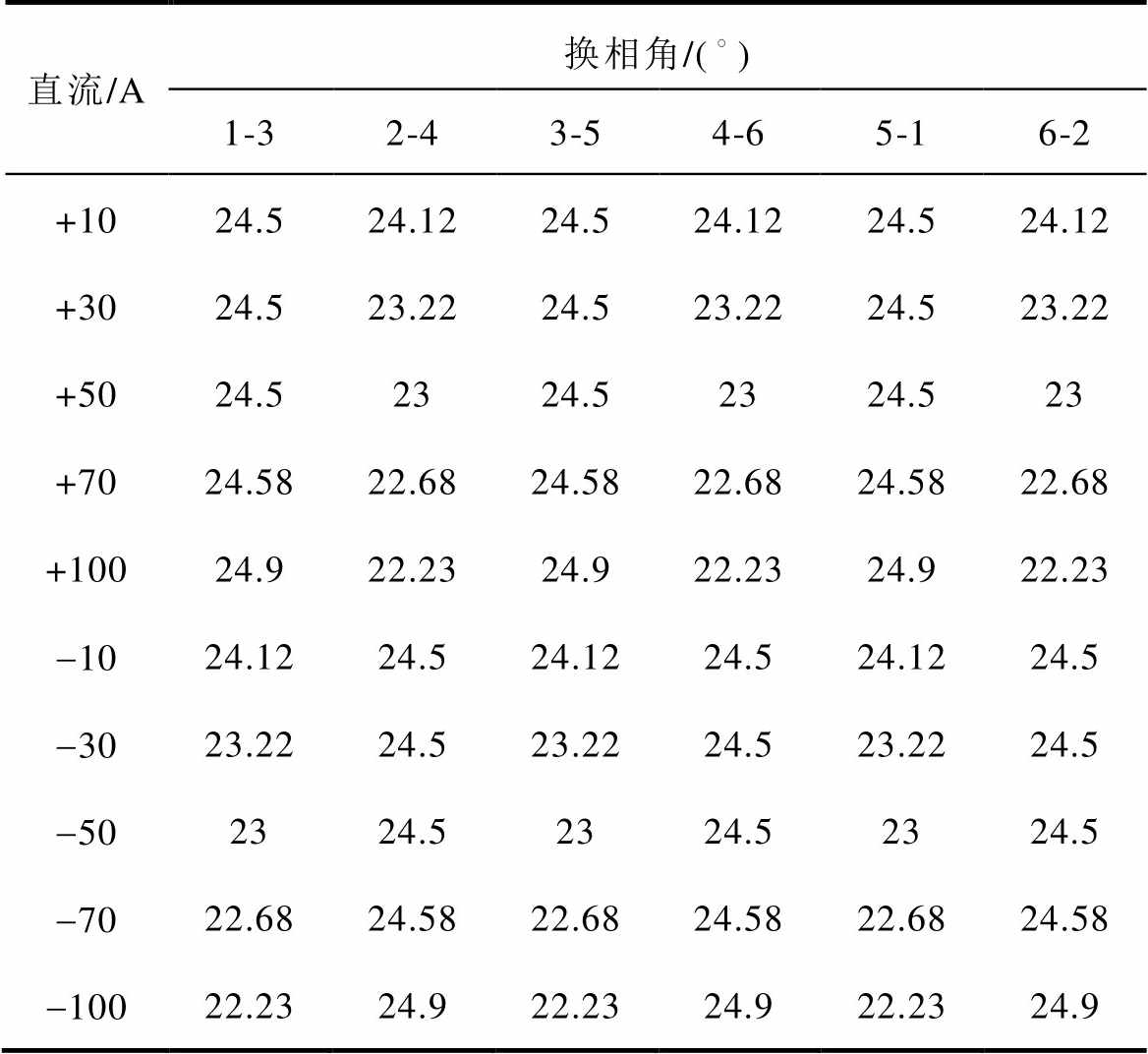
表3为在触发超前角为32°时,一个周期内六次换相对应的换相角大小。由表3可知,4-6、2-4、6-2(上桥臂换相)换相角大小完全一样,1-3、3-5、5-1(下桥臂换相)完全一样。上桥臂换相中正、负方向直流电流对应的换相角为下桥臂换相中的负、正方向电流对应的换相角。因此,4.1.1节的结论可以扩展为:当换相发生在上桥臂时,对于正方向的直流电流,随着直流电流的增大,换相角逐渐减小,且触发超前角越小换相角减小得越大,而对于负方向的直流电流,当触发超前角较大时,换相角恒定不变,当触发超前角较小且直流较大时,换相角随着直流电流的增大而增大。当换相发生在下桥臂时正负方向直流的结论与上桥臂相反。触发延迟角为35°和40°时,结论一样。
表3 换相角仿真数值(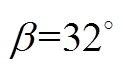 )
)
Tab.3 Simulation valueofcommutationangle (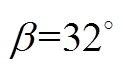 )
)
直流/A换相角/() 1-32-43-54-65-16-2 +1024.524.1224.524.1224.524.12 +3024.523.2224.523.2224.523.22 +5024.52324.52324.523 +7024.5822.6824.5822.6824.5822.68 +10024.922.2324.922.2324.922.23 -1024.1224.524.1224.524.1224.5 -3023.2224.523.2224.523.2224.5 -502324.52324.52324.5 -7022.6824.5822.6824.5822.6824.58 -10022.2324.922.2324.922.2324.9
4.2.1 阀4向阀6换相结果分析
由式(10)可知,直流偏磁时换相角的变化,取决于参与换相的两相换流变压器的励磁电流的差值的正负和大小,因此只需要分析换相期间换流变压器的励磁电流波形就可以解释换流角的变化原因。
不同触发超前角下正负100A换相电压和励磁电流如图6所示。由图6可知(图中100A-A表示A相通入100A直流,100A-B表示B相通入100A直流,换相电压缩小了500倍,励磁电流为归算到阀侧的电流),当直流流向为正时,随着触发超前角的增大,换相角度不断减小,换相区间的对称轴逐渐往左平移,所以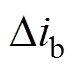 (负值)逐渐减小,此时A相励磁电流处于负半轴,由于正向直流的影响其数值很小,可忽略。因此触发超前角越小,相同直流电流下,换相角减小的数值越大。另外,随着直流电流数值的减小,励磁电流幅值减小,励磁电流的差值也就减小,因此直流越大换相角减小得越多。
(负值)逐渐减小,此时A相励磁电流处于负半轴,由于正向直流的影响其数值很小,可忽略。因此触发超前角越小,相同直流电流下,换相角减小的数值越大。另外,随着直流电流数值的减小,励磁电流幅值减小,励磁电流的差值也就减小,因此直流越大换相角减小得越多。
当直流电流流向为负时,由图6可知,只有当触发超前角为32°时即换相角较大时,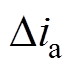 (负值)才足够引起换相的变化。而此时B相励磁电流很小,所以忽略其影响,因此若触发超前角较大,换相角恒定不变,当触发超前角较小且直流较大时,换相角随着直流电流的增大而增大,且其变化不大。
(负值)才足够引起换相的变化。而此时B相励磁电流很小,所以忽略其影响,因此若触发超前角较大,换相角恒定不变,当触发超前角较小且直流较大时,换相角随着直流电流的增大而增大,且其变化不大。
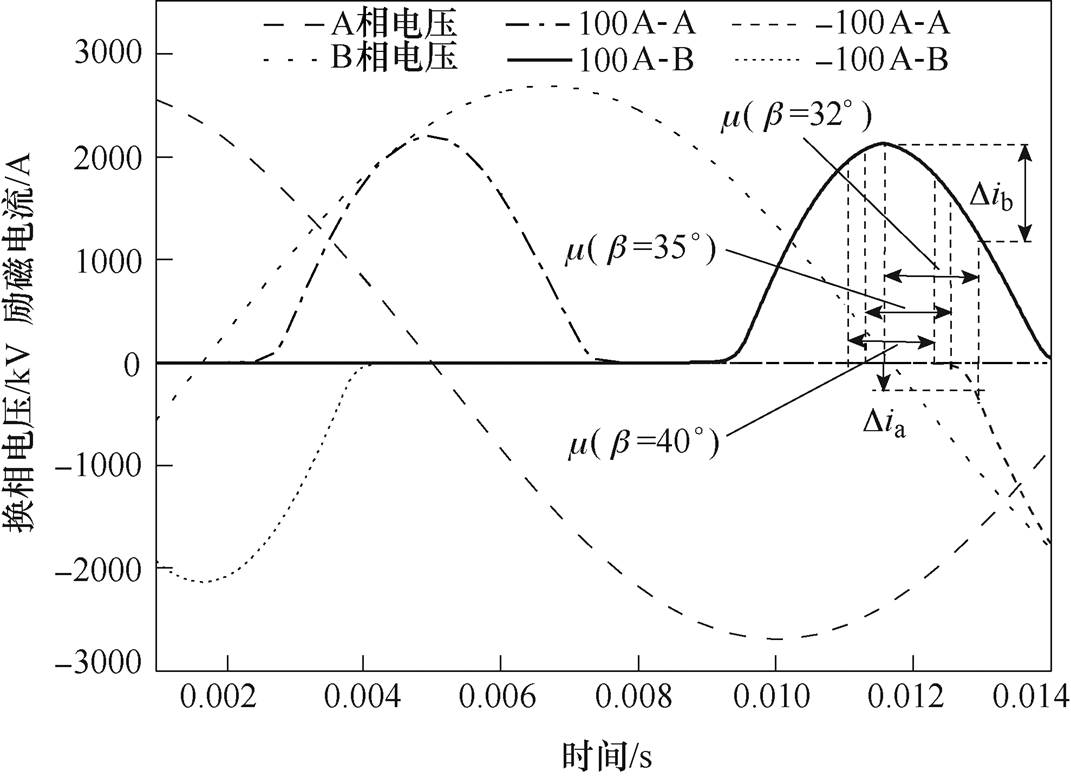
图6 不同触发超前角下正负100A换相电压和励磁电流(4-6)
Fig.6 The positive and negative 100A phase-changing voltage and excitation current under different trigger lead angle (4-6)
4.2.2 六次换相之间换相角的关系结果分析
换相电压-励磁电流如图7所示。由图7可知,因为A、B、C三相的励磁电流波形相同,相位互差120°,而处于同一桥臂的换相之间正好也差120°,因此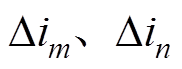 分别相等,所以换相角变化相同。而将图7反过来看,上、下桥臂正好颠倒,因此
分别相等,所以换相角变化相同。而将图7反过来看,上、下桥臂正好颠倒,因此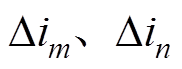 互为相反数,再由式(11)和式(12)可知,此时换相角变化相同。因此,在正、负方向直流作用下,上桥臂换相的换相角等于负、正方向直流作用下,下桥臂换相的换相角。
互为相反数,再由式(11)和式(12)可知,此时换相角变化相同。因此,在正、负方向直流作用下,上桥臂换相的换相角等于负、正方向直流作用下,下桥臂换相的换相角。
根据表2求取的各个情况下的换相角以及一个周期内六次换相角之间的关系,结合直流电流和交流母线电压,即可求得交流电流和直流电压,并分析其谐波含量,根据国标要求,只需分析前49次谐波。
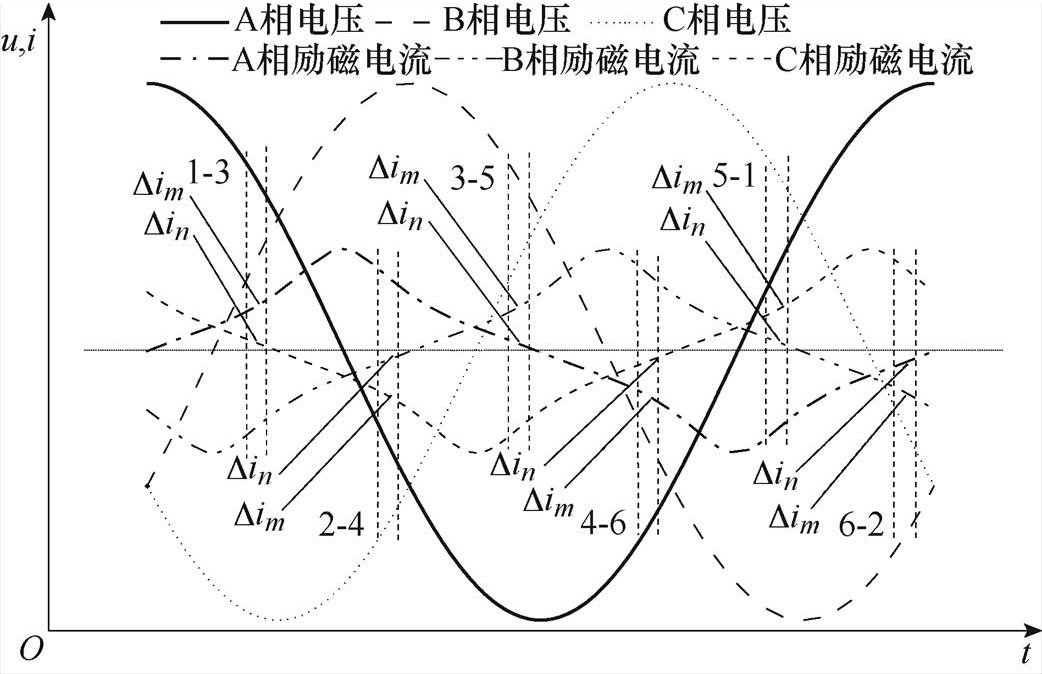
图7 换相电压-励磁电流
Fig.7 Commutation voltage-exciting current
由4.2.2节的分析可知,直流电流方向的改变,只是将交流电流波形翻转后平移180°,因此电流谐波含量的有效值与直流电流方向无关。谐波含量的变化,是由于上、下桥臂换相角变化,且其变化角度不一致,导致正、负半波不对称造成的,因此取换相角变化最大的情况分析:触发超前角32°、直流100A。
交流电流谐波含量如图8所示。由图8可知,交流电流中正常存在的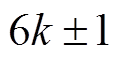 次特征谐波,在加直流前后数值基本不变,但出现大量非特征谐波,且随着频率的增大,其幅值与相邻的特征谐波相比增幅变大。因此应重点关注交流电流中高频谐波的危害,如换流变压器的负载损耗。
次特征谐波,在加直流前后数值基本不变,但出现大量非特征谐波,且随着频率的增大,其幅值与相邻的特征谐波相比增幅变大。因此应重点关注交流电流中高频谐波的危害,如换流变压器的负载损耗。
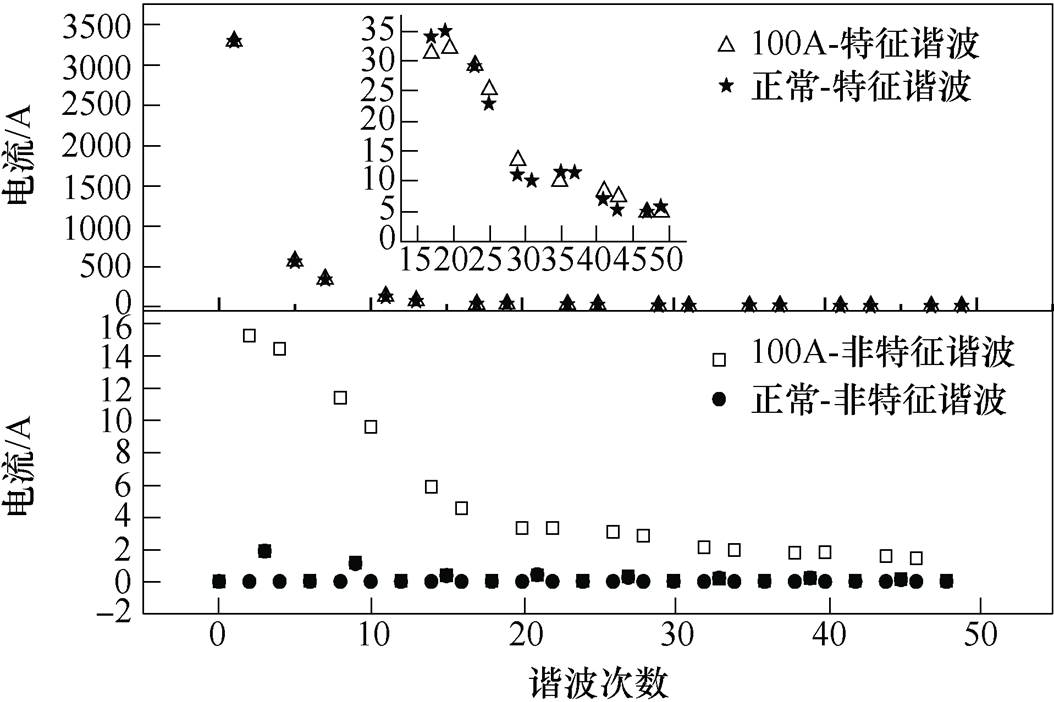
图8 交流电流谐波含量
Fig.8 AC current harmonic content
直流电压谐波含量如图9所示。由图9可知,由于直流的加入,直流电压中的6k次特征谐波的有效值基本不变,3k次非特征谐波由0增加到2 000左右的数量级,其余非特征谐波还是几乎为0。这是因为正常时一个周期内直流电压脉动6次,其6次波形完全一样,直流的加入使得上、下桥臂换相角不一致,因此其脉动3次的波形完全一样。另外虽然单次换相角变化不大,但由于一个周期内波形脉动6次,叠加起来就造成3k次非特征谐波的大量增加。
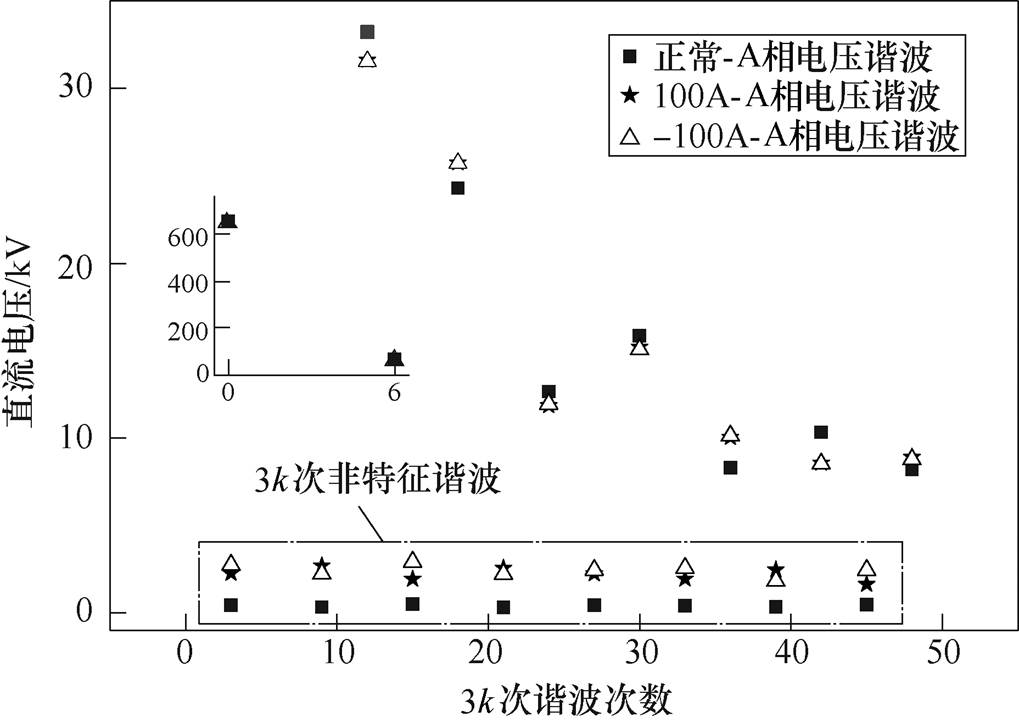
图9 直流电压谐波含量
Fig.9 DC voltage harmonic content
由于直流正负方向的不同,直流电压的波形不一致,且无法通过基本变化转换,因此其非特征谐波含量不同,由图9可知,负方向直流造成的谐波有效值整体更大,但与正方向直流的数值差别不大。
由上述分析可知,当发生磁暴时,应重点关注直流线路的高频3k次非特征谐波对附近通信设备的影响。
通过模拟地磁暴期间,直流输电逆变侧换相角、交流电流和直流电压的谐波含量变化,得到如下结论:
1)一个周期六次换相中,处于同一桥臂(上,下)的三次换相所对应的换相角相等,且上桥臂换相中加正、负方向直流电流的换相角为下桥臂换相中加负、正方向电流的换相角。
2)当换相发生在上桥臂时,对于正方向的直流电流,随着直流电流的增大,换相角逐渐减小,且触发超前角越小换相角减小得越多,而对于负方向的直流电流,当触发超前角大于35°时,换相角恒定不变,当触发超前角小于35°且直流大于50A时,换相角随着直流电流的增大而增大,但其变化很小,即最大增幅仅为0.4°。当换相发生在下桥臂正负方向直流的结论与上桥臂相反。因此在磁暴期间更应关注逆变侧触发超前角在30°~35°之间的直流输电工程。
3)加入直流后,交流电流出现非特征谐波,且随着频率的增大,其幅值与相邻的特征谐波相比增幅变大。在磁暴期间,应注意换流变压器负载损耗的增大。
4)直流电压谐波次数由6k次变为3k次,且负方向直流造成的非特征谐波的有效值比正方向直流大。在磁暴期间,因关注直流线路的高频3k次谐波对附近通信设备的影响,尤其是负方向直流时刻。
参考文献
[1] Albertson V D, Thorson J M, Miske S A, et al. The effects of geomagnetic storms on electric power system[J]. IEEE Transactions on Power Apparatus and System, 1974, 93(4): 1031-1044.
[2] 刘连光. 灾害空间天气对我国电网安全的影响及风险[J]. 中国工程科学, 2010, 12(9): 29-33.
Liu Lianguang. Influence and hazard of disastrous space weather on power grid in China[J]. Engineering Sciences, 2010, 12(9): 29-33.
[3] 刘连光, 王开让, 郭世晓, 等. 双电压等级电网GIC的相互作用特征[J]. 中国科学: 技术科学, 2015, 45(12): 1311-1320.
Liu Lianguang, Wang Kairang, Guo Shixiao, et al. Characteristics of GIC interaction in a dual-voltage- level power network[J]. Scientia Sinica Techological Sciences, 2015, 45(12): 1311-1320.
[4] Marti L, Rezaei-Zare A, Narang A. Simulation of transformer hot-spot heating due to geomagnetically induced currents[J]. IEEE Transactions on Power Delivery, 2013, 28(1): 320-327.
[5] Rezaei-Zare A. Reactive power loss versus GIC characteristic of single-phase transformers[J]. IEEE Transactions on Power Delivery, 2015, 30(3): 1639- 1640.
[6] 潘超, 王格万, 蔡国伟, 等. 交直流混杂模式下变压器励磁电流谐波与箱体损耗映射研究[J]. 电工技术学报, 2019, 34(13): 2830-2838.
Pan Chao, Wang Gewan, Cai Guowei, et al. Study on the mapping of transformer excitation current harmonics and enclosure loss in AC-DC hybrid mode[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(13): 2830-2838.
[7] 张鹏宁, 李琳, 程志光, 等. 并联电抗器与变压器模型铁心振动仿真与试验对比[J]. 电工技术学报, 2018, 33(22): 5273-5281.
Zhang Pengning, Li Lin, Cheng Zhiguang, et al. Vibration simulation and test comparison of model cores of shunt reactor and transformer[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(22): 5273-5281.
[8] 韩明晓, 文俊, 徐永海. 高压直流输电原理与运行[M]. 北京: 机械工业出版社, 2012.
[9] 肖楚鹏, 金祖洋, 邱泽晶, 等. 直流偏磁对换相失败的影响机理及定量分析方法[J]. 科学技术与工程, 2016, 16(36): 30-35.
Xiao Chupeng, Jin Zuyang, Qiu Zejing, et al. The influence mechanism and quantitative analysis method of DC bias on the failure of commutation[J]. Science Technology and Engineering, 2016, 16(36): 30-35.
[10] 黄敏, 郭倩雯, 童重立, 等. 直流偏磁增大换相失败风险的机理分析及仿真[J]. 华中科技大学学报:自然科学版, 2014, 42(9): 102-106.
Huang Min, Guo Qianwen, Tong Zhongli, et al. Mechanism analysis and simulation of DC bias to increase the risk of commutation failure[J]. Journal of Huazhong University of Science and Technology: Natural Science Edition, 2014, 42(9): 102-106.
[11] 王峰, 刘天琪, 周胜军, 等. 谐波对HVDC系统换相失败的影响机理及定量分析方法[J]. 中国电机工程学报, 2015, 35(19): 4888-4894.
Wang Feng, Liu Tianqi, Zhou Shengjun, et al. The influence mechanism and quantitative analysis method of harmonic on HVDC system[J]. Proceedings of the CSEE, 2015, 35(19): 4888-4894.
[12] Burton R S, Fuchshuber C F, Woodford D A, et al. Prediction of core saturation instability at an HVDC converter[J]. IEEE Transactions on Power Delivery, 1996, 11(4): 1961-1969.
[13] 余瑜, 刘开培, 陈俊, 等. 基于调制理论的高压直流输电系统混合谐振型谐波不稳定判据[J]. 高电压技术, 2014, 40(5): 1582-1589.
Yu Yu, Liu Kaipei, Chen Jun, et al. The harmonic instability criterion of HVDC system based on modulation theory[J]. High Voltage Engineering, 2014, 40(5): 1582-1589.
[14] 潘超, 王泽忠, 李海龙, 等. 基于瞬态场路耦合模型的变压器直流偏磁计算[J]. 电工技术学报, 2013, 28(5): 174-181.
Pan Chao, Wang Zezhong, Li Hailong, et al. DC bias calculation of transformer based on transient field coupling model[J]. Transactions of China Electro- technical Society, 2013, 28(5): 174-181.
[15] 潘超, 米俭, 王格万, 等. 基于场路耦合的变压器绕组匝间短路电磁谐响应分析方法[J]. 电工技术学报, 2019, 34(4): 673-682.
Pan Chao, Mi Jian, Wang Gewan, et al. An electro- magnetic harmonic response analysis method based on field-circuit coupling of transformer winding[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 673-682.
[16] 李兴源. 高压直流输电系统[M]. 北京: 科学出版社, 2010.
[17] Hu Lihua, Yacamini R. Harmonic transfer through converters and HVDC links[J]. IEEE Transactions on Power Electronics, 1992, 7(3): 514-525.
[18] 王泽忠, 谭瑞娟, 李书连, 等. 基于动态电感-励磁电流曲线的特高压变压器空载直流偏磁计算[J]. 电工技术学报, 2017, 32(10): 154-161.
Wang Zezhong, Tan Ruijuan, Li Shulian, et al. Calculation of no-load DC bias of UHV Transformer based on dynamic inductance-excitation current curve[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 154-161.
[19] 王泽忠, 谭瑞娟, 臧英, 等. 基于串联电阻的特高压变压器空载直流偏磁计算[J]. 电工技术学报, 2017, 32(8): 129-137.
Wang Zezhong, Tan Ruijuan, Zang Ying, et al. Calculation of no-load DC bias of UHV transformer based on series resistance[J]. Transactions of China Electrotechnical Society, 2017, 32(8): 129-137.
Mechanism Analysis of Geomagnetic Storm on Commutation Angle and Harmonic of Invert Side of HVDC Transmission
Abstract Based on the T model of transformer, the theoretical formula for calculating the effect of DC bias on commutation angle of converter transformer is derived. Using finite element simulation software of electromagnetic field and external circuit switch control, the inverter commutation model considering the actual transformer inductance change is established. The influence of geomagnetic storm on the converter transformer is simulated by applying direct current of different magnitude and direction to the neutral point of converter transformer. By analyzing the commutation angle change of six times in a period, the relationship between each other and the relations of the changes with DC direction, magnitude and the trigger leading angle are obtained. By Fourier decomposition of the DC voltage and AC current waveform, it is found that the non-characteristic harmonics appear in the AC current during the magnetic storm, the high-frequency component increases more greatly, and the DC voltage harmonic number changes from multiples of six to multiples of three. The reason of commutation angle and harmonic change is explained by combining the theoretical formula of commutation angle and excitation current waveform, and the model is verified.
keywords:Geomagnetic storm, DC bias, converter transformer, commutation angle, harmonic analysis
中图分类号:TM422; TM74
DOI: 10.19595/j.cnki.1000-6753.tces.190880
国家重点研发计划专项资助项目(2016YFC0800100)。
收稿日期2019-07-15
改稿日期 2019-08-27
黄天超 男,1993年生,博士研究生,研究方向为换流变压器直流偏磁、电磁场数值计算等。E-mail: 17717016682@163.com(通信作者)
王泽忠 男,1960年生,教授,博士生导师,研究方向为电磁场分析计算、电力系统电磁兼容和电磁测量等。E-mail: wzzh@ncepu.edu.cn
(编辑 赵 鹏)