图1 波纹护套高压电缆结构
Fig.1 Structure of HV cable with helical corrugated aluminum sheath
摘要 高压电缆线芯导体和金属护层互感是计算护层感应电压、环流和损耗的基础，是电缆线路设计和规划的重要参数。为提高感应参数的计算精度，该文采用毕奥-萨伐尔定律求解高压电缆线芯电流的磁感应强度，利用高斯定理求解波纹护套截面的磁通量，建立环形纹和螺纹护套的参数方程，确定以相距为护套厚度的内外曲面作为磁通量面积分的边界，推导出线芯与波纹护套的互感和等效直径方法误差的解析公式。以400mm2、800mm2、1 200mm2截面110kV高压电缆几何参数为算例计算，互感随护套厚度和压纹深度的增大而增大，随几何平均半径的增大而减小。解析解与数值解一致，等效半径方法计算得到的近似解比解析解小0.2%～0.3%。整数倍节距长电缆线路，环形纹和螺纹护套电缆互感相等，平滑护套电缆互感大于波纹护套。
关键词：高压电缆 波纹金属护套 互感 感应电动势 护层电流
高压电缆因不占用地上空间、可靠性高等原因被广泛应用于城市输配电网，110kV和220kV高压电缆已逐渐取代架空线成为中国大城市和特大城市电网主干[1]。20世纪初，电缆已被用作信号和电力传输，常用的电缆是小截面的平滑金属和金属丝护套电缆。随着负荷的不断增长，电缆截面也随之增大。超过400mm2截面的平滑护套高压电缆在敷设时弯曲困难[2]。1950年，波纹铅护套电缆被发明，解决了平滑护套电缆敷设的问题，而后广泛应用于电力工业[3]。波纹金属护套交联聚乙烯（Cross- Linked Polyethylene, XLPE）高压电缆结构如图1所示。相对于铅护套，铝护套原料成本较低，抗压和拉伸性能较好，且质量较轻，便于敷设安装[4-5]。现阶段，陆地用波纹金属护套高压电缆以铝护套为主。
图1 波纹护套高压电缆结构
Fig.1 Structure of HV cable with helical corrugated aluminum sheath
高压电缆导体和金属护层互感是计算护层感应电压[6-7]、环流[8]和损耗[9]的基础，是电缆线路设计和规划的重要参数[10]。1928年，A. Arnold建立了等效直径方法计算电缆护层损耗的理论模型[11]。之后，IEC 60287[12]、IEEE 575[5]和多导体传输线理 论[13-14]采纳电缆金属护层等效直径方法计算电缆导体和金属护套互感，具有计算简单的优点。用等效直径方法计算电缆互感的理论本质是将磁力线与护套交链的区域等效为空心圆柱体[15]。对于平滑结构金属护套，如铅护套海底电缆、钢丝屏蔽陆地电缆，等效直径方法求得的近似解和解析解相同[16]。但是，波纹结构改变了磁通与护层交链的区域，等效直径方法是否适用于波纹金属护套高压电缆需要电磁理论的证明。
对于波纹管状结构如高压电缆、信号电缆、水管、热交换管引起的非线性物理现象，已有学者进行了研究。文献[17]分析了波纹结构对高压电缆护层与外半导电层间热阻的影响，依据傅里叶传热定律建立了波纹结构间隙的二维传热模型，研究发现，护层与外半导电层间的气隙会显著提升波纹结构附近热阻。但是，热流量为径矢量，磁感应强度为轴矢量，与护套的相互作用机理不同。文献[18]在二维笛卡尔和柱面坐标系下研究了波纹同轴电缆的阻抗和导纳，用数值方法求解电报方程，证明了波纹深度会对脉冲信号传输产生影响。但其理论实质是求解同轴电缆自感，即电报方程的感抗分量。文献[19]分析了波纹水管水压和阻力的影响。文献[20]分析了波纹热交换的热交换速率及热阻。上述文献使用的几何模型没有给出波纹结构参数方程。
本文的主要目的有：①建立环形纹和螺纹结构波纹铝护套的几何模型，求出高压电缆线芯与波纹护套互感解析解，分析波纹参数对常用高压电缆互感的影响；②与等效直径方法求出的近似解对比，确定等效方法对波纹护套是否适用。
本节首先介绍等效直径理论的高压电缆线芯和互感的解析模型；然后建立环形纹和螺纹两种典型压纹护套的参数方程；最后依据毕奥-萨伐尔定律、高斯定理和法拉第电磁感应定律推导出两种压纹波纹护套的互感解析公式。
IEC 60287定义的铝护套平均直径ds为
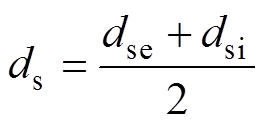（1）式中，dse为波纹护套的外径；dsi为波纹护套的内径。计算护套的互感，需要确定积分的上下限，即需要考虑护套的厚度d。为方便对比，本文采用几何平均半径（等效半径）计算电缆互感，得到的近似解和等效直径方法一致。设等效半径r=0.5ds，那么护层可以等效为内半径为r-0.5d，外半径为r+0.5d的空心圆柱体。电缆护层为两个同心圆柱面所夹的区域，柱面坐标系下的参数方程为
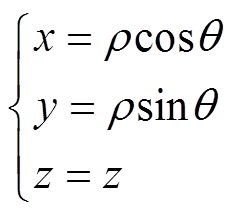（2）
式中，柱面半径r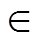
[r-0.5d, r+0.5d]，r为护套等效半径，d为护套厚度；
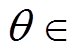[0, 2p
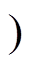；z方向为电缆 轴向。
依据毕奥-萨伐尔定律，线芯电流I在距离导线r 处产生的磁感应强度矢量B为
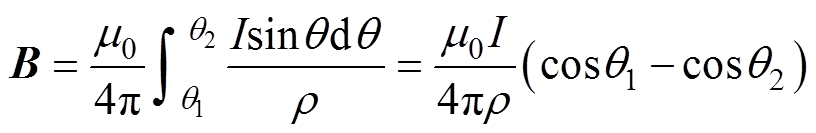（3）式中，q1和q2分别为定长直导线首末两端与r 处连线和电流元的夹角。当线芯足够长时，q1=0，q2≈p。式（3）可化为
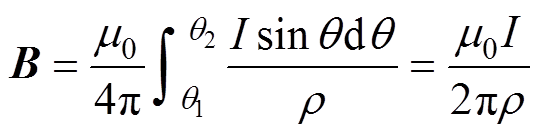（4）
依据高斯定理，穿过护套的磁通量F 等于线芯电流产生的磁感应强度矢量B对护套截面S的面积分[21]，有
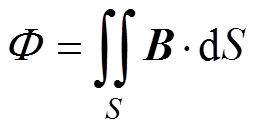（5）长度为l的高压电缆线芯对护层的互感M可以依据法拉第电磁感应定律求得
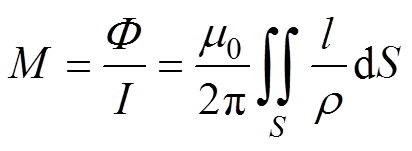（6）
对于等效直径方法，等效半径r不随长度l变化。高压电缆线芯对护层的互感Mer可以表示为
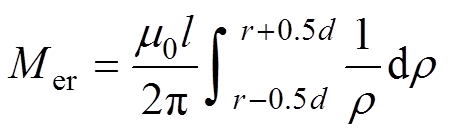（7）求解积分得
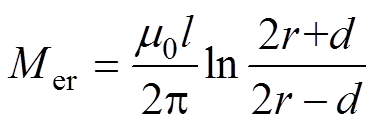（8）
目前，波纹铝护套的制作工艺有挤出、氩弧焊、压纹三种[22]。铝护套的压纹形状主要有螺纹形、环纹形和平滑形三种，其中螺纹形最为常见[5]。螺纹形铝护套的内外表面是由曲线（压辊或压轮）作螺旋运动形成的曲纹螺旋面[23]，护套厚度保持不变。螺纹形电缆沿轴线方向做匀速运动，压辊或压轮持续挤压成型。环形纹电缆运动节距距离，压辊或压轮挤压一次。平滑铝护套电缆的护层不需要挤压，可用同轴圆柱体等效。
对于波纹（螺纹和环形纹）金属护套高压电缆，磁力线与护层交链的截面几何形状与平滑护套不同。采用式（6）计算波纹金属护套电缆互感时，需要考虑护层波纹的几何形状才能确定积分边界条件，求解互感解析解。本小节建立了环形和螺旋形波纹护套的参数方程作为式（6）的边界条件，推导出环形纹和螺纹护套电缆互感的解析解。因螺纹形电缆线芯与护层的互感需要借用环形纹的互感表示，下面先介绍环形波纹护套电缆的参数方程。
对环形波纹护套在xyz直角坐标系下建模，护套在yOz平面的投影如图2所示。曲线1为区域1与正弦曲线交界的曲线，曲线2为区域2与正弦曲线交界的曲线。曲线1、2分别对内半径为r-0.5d-0.5dc，外半径为r+0.5d+0.5dc的空心圆柱体作挤压或切割运动，r为护套的等效半径，dc为压纹深度，p为节距。
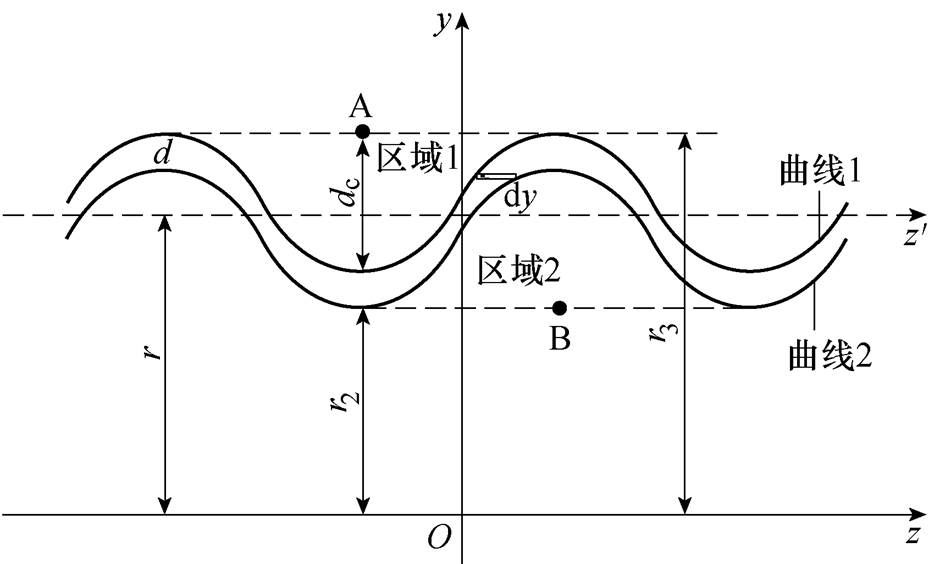
图2 环形纹护套在yOz平面的投影
Fig.2 The projection of annular corrugated sheath on yOz
曲线1、2在yOz平面的参数方程为
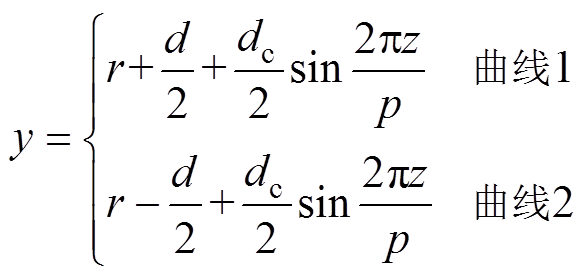（9）设电流I的方向沿z轴正方向，可以将式（6）对面积的积分简化为yOz平面的积分求磁感应线交链面积。设dy为沿y轴方向积分面微元，dz沿z轴方向的积分面微元，那么曲线1、2在一个正弦周期内，z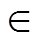[0, p]所围成的区域的互感Map为
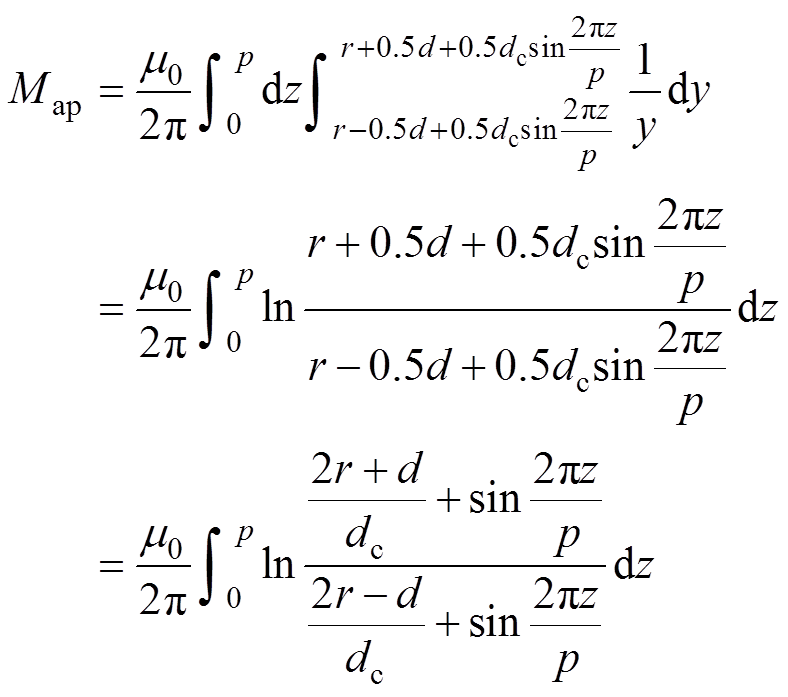（10）
令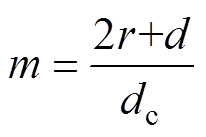
，
，
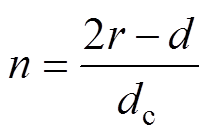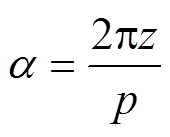，式（10）可以化简为
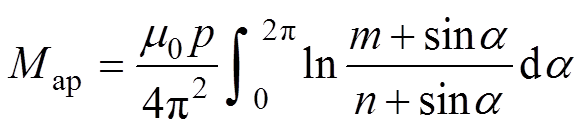（11）式中，a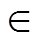[0, 2p]。形如ln(m+sina )函数的不定积分在实数域无法得到初等函数表示的解析解，附录给出了复数域的不定积分解析解。但是，可以先计算节距长度高压电缆线芯与护套的互感值，整数倍的节距长度环形纹护套电缆线路采用累加方式得到长度为l的电缆线路互感Ma为
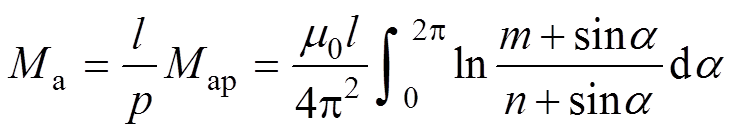（12）
由式（12）可见，Ma中p参数被约去，环形纹电缆互感不受节距影响。实际应用中高压电缆的长度（一般大于500m）远大于节距（20～30mm），采用式（12）计算较为准确。如果需要计算非整数倍节距长度的短电缆线路互感，可使用附录内的解析解。
螺纹护套的三维模型如图3所示，在yOz面上的投影如图4所示。环形护套截面沿z轴对称，即在柱面坐标系下沿任意极角径向切割电缆护套，护套截面均相等。但螺纹护套不同，如图4所示，若上半部分（曲线1和2围成的区域）护套截面为两条正弦曲线包围的区域，则下半部分（曲线3和4围成的区域）为两条余弦曲线包围的区域。曲线3、4在yOz平面的参数方程为
图3 螺纹护套的三维模型
Fig.3 3D model of helical corrugated sheath
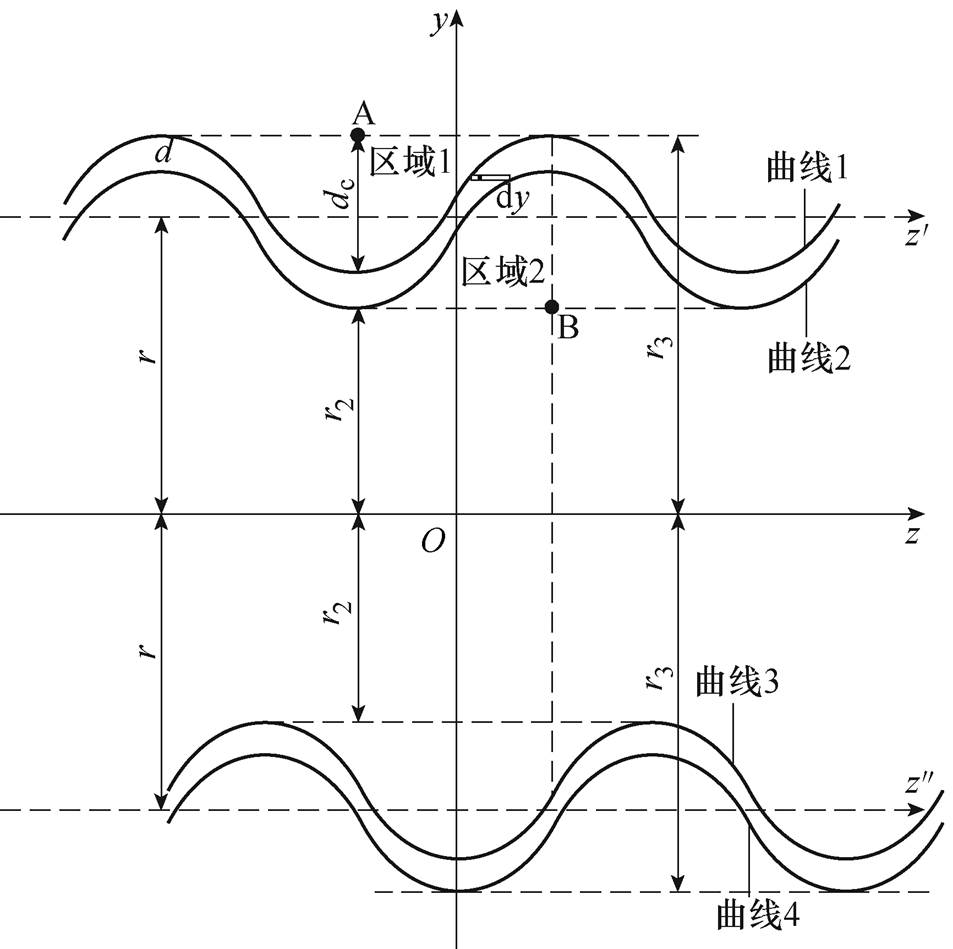
图4 螺纹护套在yOz平面的投影
Fig.4 The projection of helical corrugated sheath on yOz
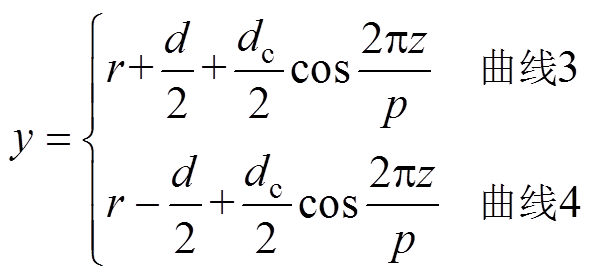（13）求解螺纹护套电缆线芯与护层互感的方法和环形纹一致，仅需要改变边界条件。式（6）中与螺纹护层交链区域的磁通为上半部分和下半部分的平均值。因此，单位节距长度p的螺纹护套电缆线芯与护层互感Mhp为
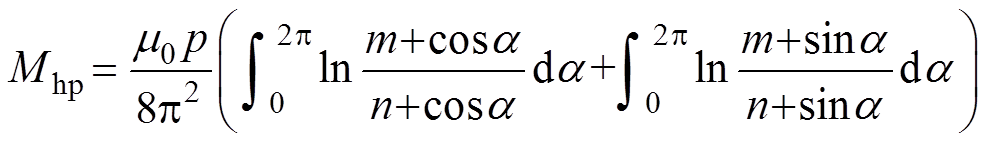（14）
对于2p 周期整数倍积分，有
=
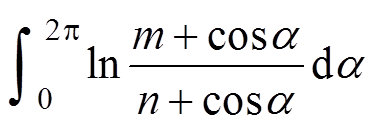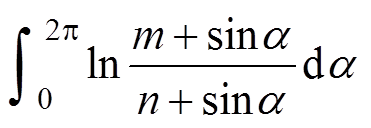（15）因此，整数倍节距长度的螺纹护套电缆线芯与护层互感Mh为
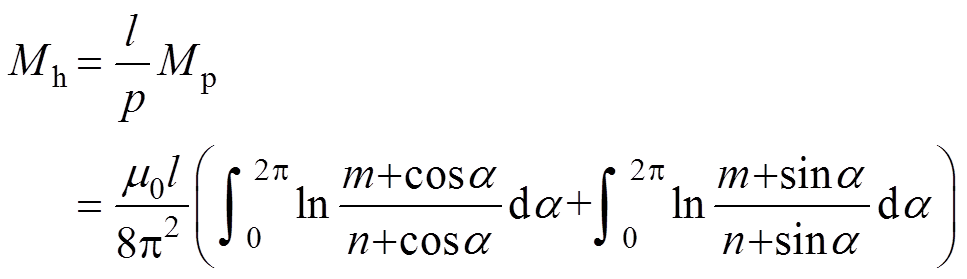
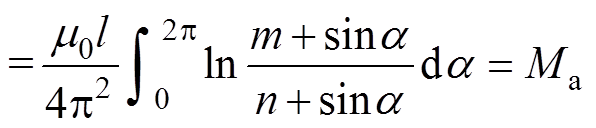（16）因此，Mh=Ma，整数倍节距的螺纹与环形纹高压电缆线芯与护层的互感相等。由式（16）可见，Mh中p参数被约去，螺纹电缆互感不受节距影响。
式（16）和式（8）相减可得等效直径方法计算波纹护套高压电缆线芯与护层互感的误差d 为
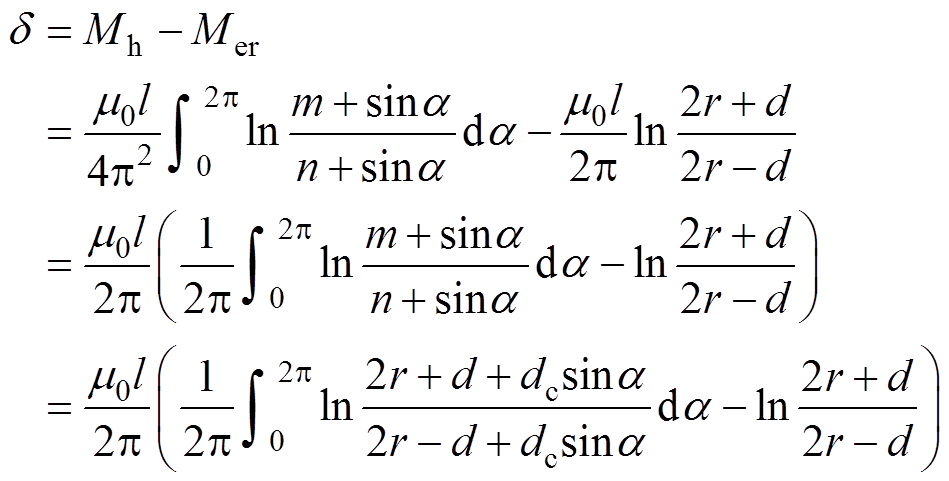（17）由式（17）可见，误差来源于dcsina 项，即压纹的形状。如果dcsina 项接近于0，那么误差d 也接近于0。
本节先采用不同截面的螺纹和环形波纹铝护套110kV电缆作为算例，考虑电缆生产过程中的误差，分析护套厚度、压纹深度、等效半径对互感的影响。然后，对比解析解、数值解和近似解的精度。最后，对比螺纹、环形纹和平滑金属护套电缆的互感。
附表1中110kV 400mm2和800mm2电缆波纹铝护套厚度d标称值为2.0mm，在实际制造过程中，最薄点和最厚点的厚度分别为1.6mm和2.2mm；1 200mm2电缆的护套厚度d标称值为2.3mm，最薄点和最厚点的厚度分别为1.9mm和2.5mm。因不同截面电缆的护套厚度不同，为控制单一变量，引入参数Dd为护套厚度增量计算，取Dd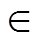[-0.4, 0.2]mm，对于400mm2和800mm2截面电缆，d+Dd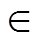[1.6, 2.2]mm；对于1 200mm2截面电缆，d+Dd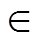[1.9, 2.5]mm。代入式（16）计算可得如图5所示的护套厚度随线芯与护层互感M的变化趋势。由图5可见，M随护套实际厚度的增大线性增大。
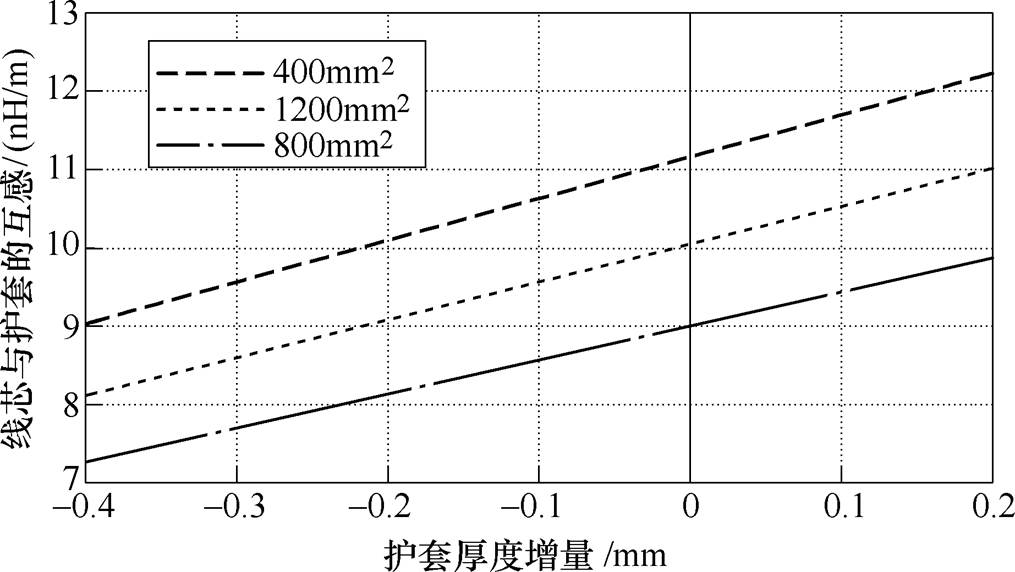
图5 护套厚度对波纹金属护套电缆互感的影响
Fig.5 The changes in M with sheath thickness
IEEE 575并未规定压纹深度dc的取值及误差范围，取dc[4.5, 5.5]mm，代入式（16）计算可得如图6所示的压纹深度对M的影响变化趋势。由式（16）可以推算，M随压纹深度的增大而增大。其原因在于，压纹越深，如图4所示的波纹正弦曲线高度越大，而磁通交链面积不变。但是，增大的趋势微弱，可以忽略。交链区域的磁感应强度B在压纹深度dc的微小变化区域内的改变可以忽略。
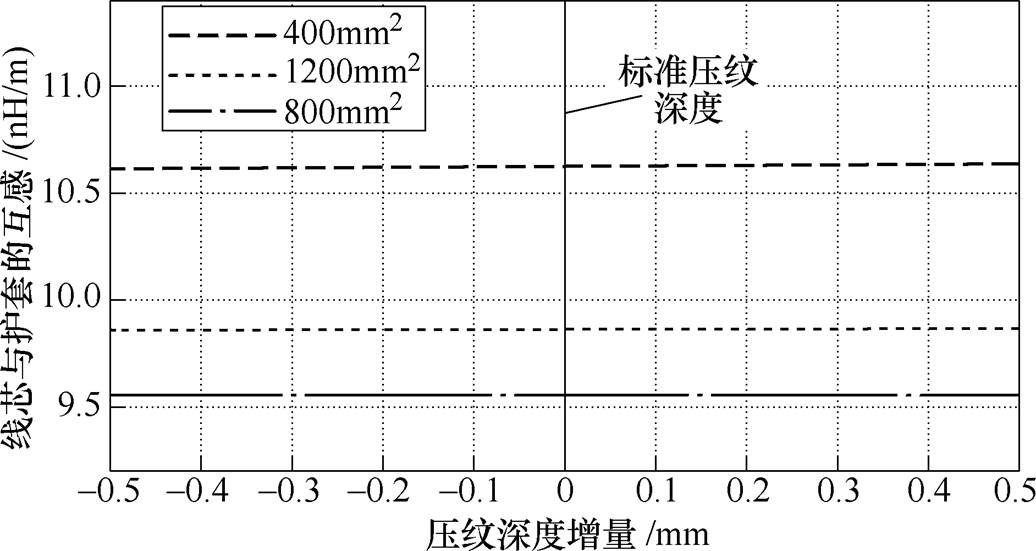
图6 压纹深度对波纹金属护套电缆互感的影响
Fig.6 The changes in M with embossing depth
为控制单一变量，以附表1所示的110kV 400mm2电缆为算例，设几何平均半径r的增量为Dr。取Dr [0, 20]mm，代入式（16）计算可得如图7所示的几何平均半径r对波纹金属护套电缆互感的影响。由图7可见，M随r的增大而减小。
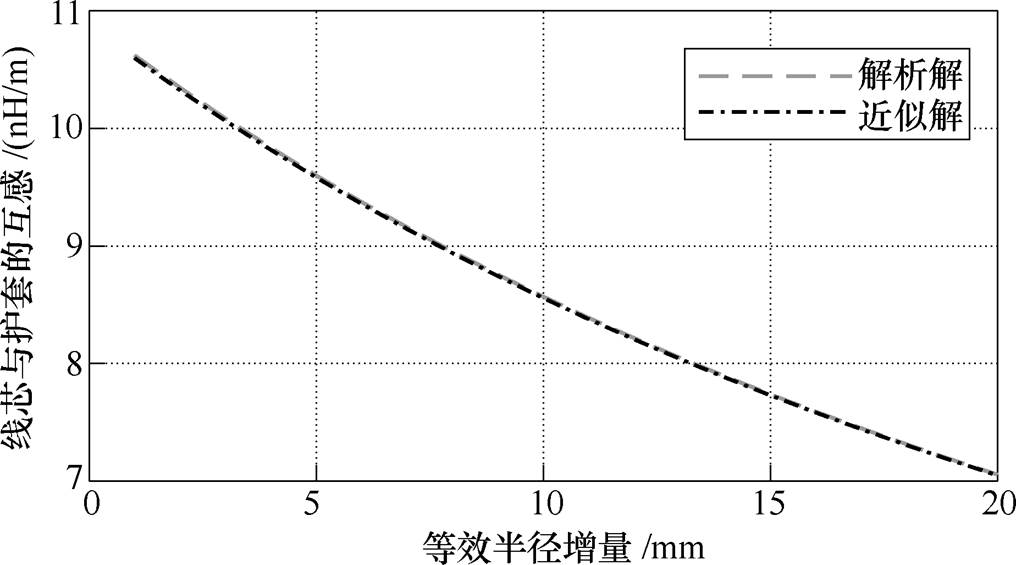
图7 几何平均半径对波纹金属护套电缆互感的影响
Fig.7 The changes in M with geometric mean radius
采用附表1中的110kV高压电缆结构参数计算，可以得到的解析解、数值解和近似解对比见表1。数值解采用高斯赛德积分法求解式（16）。波纹金属护套高压XLPE电缆线芯与护层互感解析解、数值解和近似解的对比如图8所示，对于400mm2、800mm2、1 200mm2截面的110kV波纹金属护套高压电缆，线芯与护层互感的解析解与数值解接近，误差在千分之一以内，误差源自数值积分算法，可以忽略。400mm2、800mm2和1 200mm2电缆近似解和解析解的误差分别为0.23%、0.24%和0.22%，说明采用等效直径方法相较于本文提出的解析方法计算得到的高压电缆线芯与护层的互感偏小。
然而，解析解和近似解随截面下降呈现波动趋势。原因是，实际生产的电缆结构及波纹参数随截面的增大呈现阶梯式增长，式（16）中的r、d和dc共同影响互感值，由附表1可见，400mm2、800mm2电缆的护套厚度为2mm，1 200mm2截面电缆的护套厚度为2.3mm，大截面电缆护套厚度的增加会改变解析解和近似解减小的趋势。
表1 110kV波纹铝护套截面高压电缆线芯护套互感的解析解、数值解和近似解对比
Tab.1 Analytical, numerical and approximate solutions of mutual inductance between conductor and metallic sheath of single conductor 110kV XLPE cable
截面/mm2解析解/ (nH/m)数值解/ (nH/m)近似解/ (nH/m)误差(%) 40010.62210.62210.5990.23 8009.5619.5619.5370.24 1 2009.8649.8649.8420.22
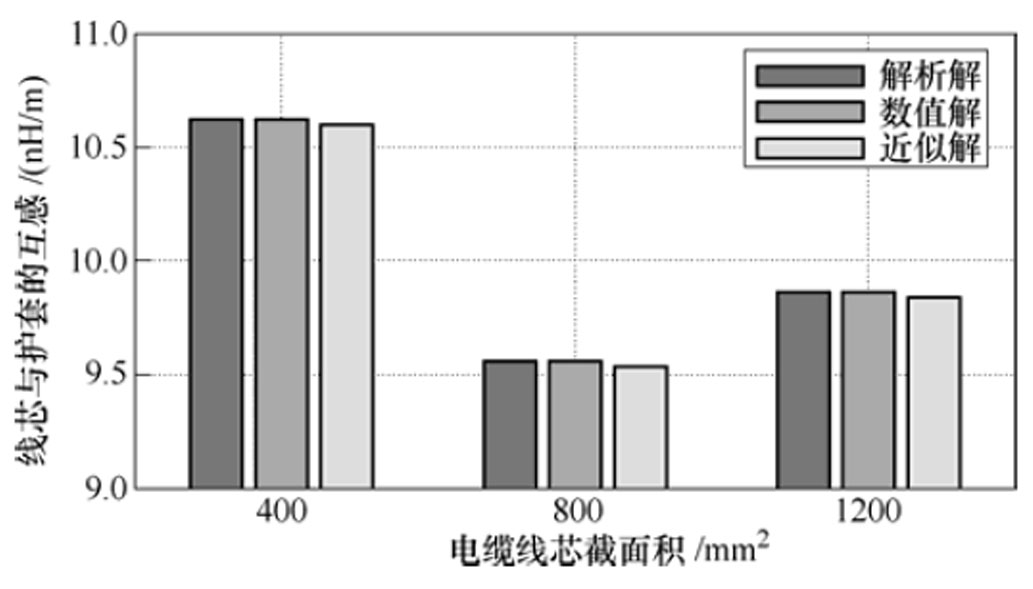
图8 波纹金属护套高压XLPE电缆线芯与护层互感解析解、数值解和近似解的对比
Fig.8 Analytical, numerical and approximate solutions of mutual inductance between conductor and metallic sheath of single conductor HV XLPE cable
平滑护套的内半径和波纹护套相同，为r2，外半径使用内半径与厚度之和r2+d计算。计算结果见表2，平滑护套高压电缆线芯与护套互感大于螺纹护套电缆。平滑护套的等效半径小于波纹护套，等效半径对互感的影响起主要作用，波纹形状的影响起次要作用。
表2 三种金属护套电缆互感对比
Tab.2 Mutual inductance of HV cables with three kinds of metallic sheath
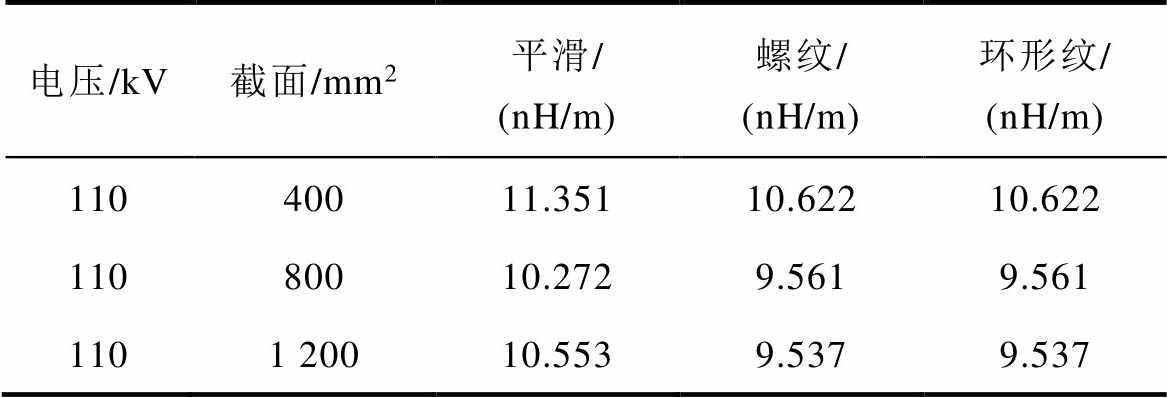
电压/kV截面/mm2平滑/ (nH/m)螺纹/ (nH/m)环形纹/ (nH/m) 11040011.35110.62210.622 11080010.2729.5619.561 1101 20010.5539.5379.537
实际系统中，电缆线芯与波纹铝护套的互感测量困难，原因是，长电缆线路护层感应电流的测量主要依靠接地电流测量反推，但地网和大地的阻抗难以获取精确值[24-25]。
本文所提出的电缆导体和护层的互感不同于同轴电缆自感，如果用于波纹铝护套电缆电抗的计算，需要将式（6）中的截面积S替换为导体至护套内侧线的截面。本文所提出的电缆线芯与波纹铝护套的互感模型目前仅适用于传输工频电流的高压电缆，对于有类似波纹屏蔽层结构的通信电缆可能需要考虑趋肤效应和临近效应的影响[26-27]。
本文提出了高压电缆波纹金属护套的几何参数方程，根据麦克斯韦电磁理论推导出了线芯与护套互感及等效直径方法误差的解析解，从理论上确定了等效直径方法的适用范围。以110kV高压电缆结构参数为算例，分析了护套厚度、压纹深度和几何平均半径对互感的影响。对比了解析解、数值解和近似解精度，IEC 60287与IEEE 575采纳的等效直径方法得到近似解与解析解误差在0.2%～0.3%之间。本模型有助于提升多导体传输线理论的互感，IEC 60287的金属屏蔽层损耗比率及护层感应电动势的计算精度。基于理论推导和计算的结果，结论如下：
1）波纹金属护套高压电缆导体与护套的互感随护套厚度、压纹深度的增大而增大，随截面的阶梯上升而波动下降。
2）互感的解析解与数值解一致；等效直径方法的误差在0.2%～0.3%之间，误差很小。
3）螺纹和环形纹电缆互感小于平滑护套电缆互感；对于整数倍节距长电缆线路，螺纹和环形纹电缆的互感相等。
1. 仿真参数
r1为线芯导体半径，r2为护层内半径，r3为护层外半径。结构参数来自电缆厂依据文献[28]实际生产的参数。
附表1 110kV高压电缆结构参数
App.Tab.1 Geometrical parameter of 110kV cable （单位: mm）
截面/mm2ddcpr1r2r3 4002.005.0025.0011.8034.2541.25 8002.006.0025.0017.0037.9545.95 1 2002.306.3030.0021.5042.4551.05
2. 复数域的解析解
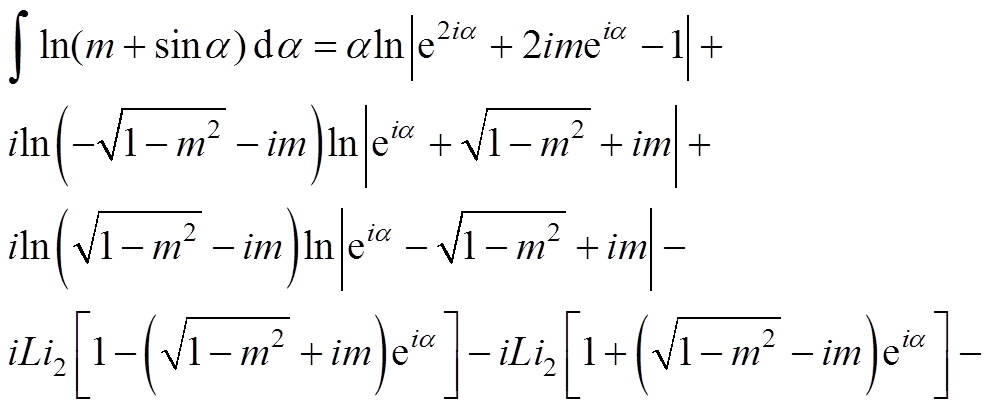
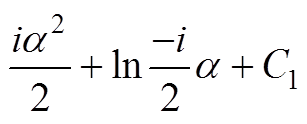（A1）
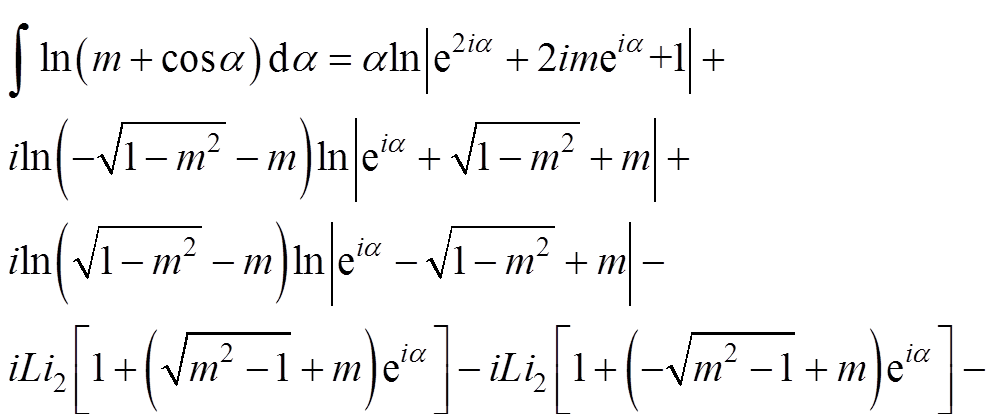
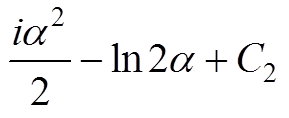（A2）
式中，C1、C2为常数。
参考文献
[1] Zhou Chengke, Yi Huajie, Dong Xiang. Review of recent research towards power cable life cycle management[J]. High Voltage, 2017, 2(3): 179-187.
[2] Andresen K, Dias F, Kenney N D. Corrugated metallic cable sheath[J]. IEEE Transactions on Power Apparatus and Systems, 1958, 77(3): 169-177.
[3] Nelson R A, Daly J M. Corrugated metallic sheathed cable-design and applications[J]. IEEE Transactions on Industry Applications, 1975, 11(2): 196-203.
[4] Krishnasamy S. Fatigue resistance of large-size helically corrugated aluminum sheathed cables[J]. IEEE Transactions on Power Apparatus and Systems, 1980, 99(6): 2265-2271.
[5] IEEE 575-2014 IEEE guide for the application of sheath-bonding methods for single-conductor cables and the calculation of induced voltages and currents in cable sheaths[S]. The Institute of Electrical and Electronics Engineers, New York, USA, 2014.
[6] Shaban M, Salam M A, Ang S P, et al. Induced sheath voltage in power cables: a review[J]. Renewable and Sustainable Energy Review, 2016, 62: 1236-1251.
[7] 王雄伟, 张哲, 尹项根, 等. 多回单芯电力电缆并联运行护套感应电压的计算与分析[J]. 电力系统保护与控制, 2015, 43(22): 77-84.
Wang Xiongwei, Zhang Zhe, Yin Xianggen et al. Calculation and analysis of sheath induced voltage for multi-circuit single-core power cable lines in parallel[J]. Power System Protection and Control, 2015, 43(22): 77-84.
[8] 张嘉乐, 吴耀辉. 多回输电线路下单芯电力电缆护套感应电压和环流计算分析[J]. 电气技术, 2016, 17(8): 50-54.
Zhang Jiale, Wu Yaohui. Calculation analysis of induced voltage and circulating current in sheath of single-core power cable applied under transmission lines[J]. Electrical Engineering, 2016, 17(8): 50-54.
[9] 周伟, 方进, 刘勃, 等. 管内电缆导体传输交流损耗的理论计算和实验[J]. 电工技术学报, 2017, 32(23): 220-226.
Zhou Wei, Fang Jin, Liu Bo, et al. Theoretical and experi- mental study on transport current loss for cable- in-conduit conductor[J]. Transactions of China Elec- trotechnical Society 2017, 32(23): 220-226.
[10] Wang Hang, Zhou Wenjun, Qian Kejun, et al. Modelling of ampacity and temperature of MV cables in presence of harmonic currents due to EVs charging in electrical distribution networks[J]. International Journal of Electrical Power and Energy Systems, 2019, 112: 127-136.
[11] Arnold A. The theory of sheath losses in single- conductor lead-covered cables[J]. Journal of the Institution of Electrical Engineers, 1929, 67(384): 69-89.
[12] IEC 60287-2006 Calculation of the continuous current rating of cables[S]. International Electro- technical Commission, Geneva, Switzerland, 2006.
[13] 张刚, 王立欣, 刘超. 一种求解屏蔽电缆场线耦合问题的混合方法[J]. 电工技术学报, 2010, 25(5): 9-13.
Zhang Gang, Wang Lixin, Liu Chao. A hybrid method for solving field-line coupling problem of shielded cables[J]. Transactions of China Electrotechnical Society, 2010, 25(5): 9-13.
[14] Paul C R. Analysis of multi-conductor transmission lines[M]. 2nd ed. John Wiley & Sons, 2008.
[15] 焦重庆, 汪贝, 李昱蓉, 等. 一种用于传输线的缩尺等效方法[J].电工技术学报, 2018, 33(9): 229- 235.
Jiao Chongqing, Wang Bei, Li Yurong, et al. A scaling method for equivalent modelling of trans- mission lines[J]. Transactions of China Electro- technical Society, 2018, 33(9): 229-235.
[16] 吕安强, 寇欣, 尹成群, 等. 三芯海底电缆中复合光纤与导体温度关系建模[J]. 电工技术学报, 2016, 31(18): 59-65.
Lü Anqiang, Kou Xin, Yin Chengqun, et al. Modeling of temperature relation between optical fiber and conductor in 3-core submarine power cable[J]. Transactions of China Electrotechnical Society, 2016, 31(18): 59-65.
[17] Brakelmann H, Honerla J, Rasquin W. Thermal resistances of cables with corrugated sheaths[J]. European Transactions on Electrical Power, 1991, 1(6): 341-346.
[18] Li Jichun, Machorro E A, Shields S. Numerical study of signal propagation in corrugated coaxial cables[J]. Journal of Computational and Applied Mathematics, 2017, 309: 230-243.
[19] Córcoles-Tendero J I, Belmonte J F, Molina A E, et al. Numerical simulation of the heat transfer process in a corrugated tube[J]. International Journal of Thermal Sciences, 2018, 126: 125-136.
[20] Wu Shuanying, Chen Sujun, Li Yourong, et al. Numerical investigation of turbulent flow, heat transfer and entropy generation in a helical coiled tube with larger curvature ratio[J]. Heat and Mass Transfer, 2009, 45(5): 569-578.
[21] 麦克斯韦. 电磁通论[M]. 北京: 北京大学出版社, 2010.
[22] 赖建华. 高压电力电缆皱纹铝护套的挤制[J]. 电线电缆, 2012, 5(1): 15-19.
Lai Jianhua. Conform of corrugated aluminum Sheath for high voltage power cables[J]. Electric Cable and Wire, 2012, 5(1): 15-19.
[23] 叶玉驹, 焦永和, 张彤. 机械制图手册[M]. 4版. 北京: 机械工业出版社, 2008.
[24] 李露露, 雍静, 曾礼强, 等. 基于系统电力扰动的交叉互联电缆绝缘整体老化在线监测[J]. 电工技术学报, 2018, 33(14): 3396-3405.
Li Lulu, Yong Jing, Zeng Liqiang, et al. On-line monitoring of insulation overall aging for cross- bonded cables based on system power disturbances[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3396-3405.
[25] 邓丰, 李欣然, 曾祥君. 基于全波形信息的混联线路单端行波定位方法[J]. 电工技术学报, 2018, 33(15): 3471-3485.
Deng Feng, Li Xinran, Zeng Xiangjun. Single-ended traveling-wave-based fault location algorithm for hybrid transmission line based on the full-waveform[J]. Transactions of China Electrotechnical Society, 2018，33(15): 3471-3485.
[26] 高欣欣, 王世山, 娄千层, 等. 基于“一致性”原则的“场-多导体”传输线辐射敏感度测试的等效理论及实现[J]. 电工技术学报, 2018, 33(7): 1588-1598.
Gao Xinxin, Wang Shishan, Lou Qianceng, et al. Equivalent theory and its realization of the radiated immunity test with incident field excitation coupling to multi-conductor transmission lines based on the consistency[J]. Transactions of China Electro technical Society, 2018, 33(7): 1588-1598.
[27] 赵洪山, 张伟韬, 王艳. 基于改进模态分解的中压地埋电缆载波通信信道特性分析[J]. 电力系统自动化, 2019, 43(18): 177-184.
Zhao Hongshan, Zhang Weitao, Wang Yan. Modified mode decomposition based channel characteristic analysis of power line carrier communication of medium-voltage underground cables[J]. Automation of Electric Power Systems, 2019, 43(18): 177-184.
[28] GB/T 11017.2—2014 额定电压110kV(Um=126kV)交联聚乙烯绝缘电力电缆及其附件 第2部分: 电缆[S]. 北京: 中国标准出版社, 2014.
Analytical Solution of the Mutual Inductance of a HV Single Conductor Cable with Corrugated Metallic Sheath
Abstract In this paper, the analytical solution of the mutual inductance between the centre conductor and the sheath of HV single conductor cable with corrugated metallic sheath is deduced based on the Maxwell equations. The parametric equation of the helical and annular corrugated sheath cable is proposed as the limits of surface integral of the magnetic flux within the sheath. The mutual inductances of 110kV cables with 400mm2, 800mm2, 1 200mm2 cross-section are analyzed. The results show that the mutual inductance increases with the increase of the sheath thickness and embossing depth, and decreases with the increase of the geometric mean distance between conductor and sheath. The analytical solution is consistent with the numerical solution. Besides, the approximate solution of mutual inductance calculated by the geometric mean distance is 0.2～0.3% smaller than that of the analytical solution. For a long cable with multiple pitches, the mutual inductance of HV cable with helical and annular corrugated sheath is identical, whilst smaller than that with smooth sheath.
keywords：High voltage cable, corrugated metallic sheath, mutual inductance, induced electro- motive force, sheath current
中图分类号：TM274
DOI: 10.19595/j.cnki.1000-6753.tces.190928
国家电网江苏省电力公司科技资助项目（J2018071）。
收稿日期 2019-07-22
改稿日期 2019-11-07
王 航 男，1989年生，博士，研究方向为电力电缆状态检测与新能源并网。E-mail: wanghang@whu.edu.cn
周文俊 男，1959年生，博士，教授，博士生导师，研究方向为高电压与绝缘技术。E-mail: wjzhou@whu.edu.cn（通信作者）
（编辑 崔文静）