0 引言
当前，化石能源短缺、环境污染严重以及全球气候变化等问题引发世界范围的新能源革命，促使我国电力系统电源和负荷结构均发生了深刻变革[1-5]。
风力发电作为一种典型的可再生能源发电，具有清洁环保、资源丰富、能量密度大、转换效率高等特点，受到了各国的重视。世界许多国家都加快了发展风力发电的步伐。目前，我国风电装机容量已跃居世界第一位。
大规模风电场接入电网对电力系统稳定性具有重大影响[6-9]。不同于传统发电机，大规模风电场包含成百上千台风电机组。针对每台风电机组详细建模是不现实的，建立合理的风电场动态等值模型对于电力系统稳定性分析、控制算法设计、网络规划和继电保护设计等具有十分重要的意义。
目前风电场等值模型的建立根据等值机数量可分为单机等值法[10-11]与多机等值法[12-15]。根据建模数据来源可分为基于风电场内部物理参数的聚合法和基于实测数据的参数辨识法。多机等值法的思想在于根据风电机组的特征参数（如位置、风速、转差、定子电压、实时功率等）将风电机组采用聚类算法分组，然后将每组内的众多风电机组采用聚合算法得到一台等值机。然而，不同于传统发电机，绝大部分风电机组特征参数通常是未知的，且特征参数动态变化，导致所构建的等值机数量与参数是变化的，因此，难于长期使用。而且聚类算法计算量较大，使得该方法难于实际应用。单机等值法着眼于整个风电场的动态响应特性，忽略了风电机组复杂的位置分布、运行状态差异与电气相互作用，将整个风电场等值为一台发电机，大幅降低了等值过程的计算量与电力系统仿真时间。
由于配电网故障率较高且运行工况复杂多变，发电机转子旋转速度较高，风电场长期运行后，风机参数可能与铭牌标称值偏差较大。传统的基于风电场详细物理参数的聚合方法不能有效解决上述参数变化问题。基于实测数据的风电场等值建模方法能够弥补此不足，受到了众多专家与学者的关注。文献[16]分析了风电场实测曲线与等值模型仿真曲线存在差异的原因。文献[17]对比分析了单机与多机等值模型对风电场扰动后动态响应曲线的描述能力，指出单机等值模型能够有效描述风电场。文献[18]以发电机功角为广域信号分析了恒速异步风机的参数轨迹灵敏度，以功角拟合误差最小为目标函数，采用遗传算法进行参数辨识。文献[19]指出，由于恒速异步风机在暂态过程中需要吸收大量无功，其接入位置对等值配网阻抗具有重要影响。文献[20]采用混合动态仿真简化风电场外部系统，并采用粒子群梯度搜索算法辨识风电场等值模型参数。文献[21]采用改进的遗传算法辨识双馈风电场等值模型参数。文献[22]根据双馈风电机组的位置分布进行分组聚合，采用振荡模式分析以验证等值模型的有效性。文献[23]构建了双馈风电场的线性差分方程等值模型，并采用特征根分析验证模型的有效性。文献[24]分析了双馈风电场等值模型的鲁棒性。当前针对永磁直驱风电场等值模型参数辨识的文献报导较少。
目前风电场等值模型及其对电力系统暂态稳定的影响以及配电网广义综合负荷等值模型方面的研究一般采用忽略感应电动机定子非基波分量的机电暂态模型，而且忽略网侧变流器的动态过程。此类简化方法对于大多数暂态仿真与稳定性研究是有效的，但是仍存在一些问题，必须采用风电机组的详细模型，例如风电机组的次同步振荡、控制器的设计、电磁谐振以及过电压抑制问题等。
本文在分析永磁直驱风电机组结构、控制系统、功率特性的基础上，基于实测数据构建了永磁直驱风电场的详细动态等值模型与初始化方法。仿真算例表明，所提出的参数辨识方法能够提高全局寻优能力。
1 永磁直驱风机的模型与初始化
永磁直驱风机的模型如图1所示，主要由风力机、永磁同步发电机、背靠背变流器、直流电容、Crowbar、耦合与滤波电感以及控制系统等组成。控制系统包括桨距角控制、机侧换流器控制（Machine Side Converter Control, MSC）与网侧换流器控制（Grid Side Converter Control, GSC）。MSC与桨距角控制配合，当风速小于额定风速时实现最大功率点追踪，当风速大于额定风速时输出额定功率，而且MSC能够调节永磁同步发电机的无功输出。GSC调节直流电容器的电压及整个风机输出的无功。Crowbar的作用在于保护换流器与直流电容器免于系统故障导致的过电压与过电流而损坏。
图1 永磁直驱风机的模型
Fig.1 Model of PMSG wind turbine
永磁同步发电机稳态等效电路与相量图如图 2所示。
假设稳态时，永磁直驱风机并网点电压为V0(pu)，注入系统的有功功率为 P0(pu)，无功功率为Q0(pu)，则注入系统的电流的二次方为
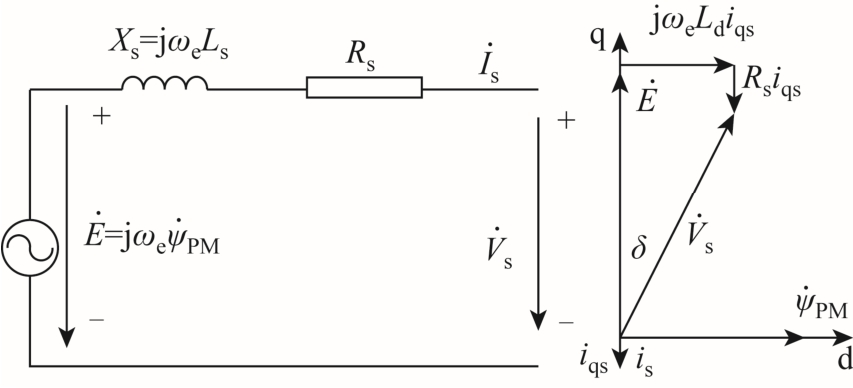
图2 永磁同步发电机稳态等效电路和相量图
Fig.2 Steady state equivalent circuit and phasor diagram of PMSG
耦合与滤波电感上的有功损耗为
式中， gR滤波电感的电阻。
永磁同步发电机定子损耗为
式中， sR为永磁同步发电机定子电阻； qsi为永磁同步发电机定子q轴电流。
永磁同步发电机发出的电磁功率为
式中，PMψ、E分别为永磁同步发电机的磁链和电动势；eω为永磁同步发电机转子的电角速度。
根据功率守恒可以得到
将式（1）~式（4）代入式（5）可得
由于采用最优转矩控制，电磁转矩控制指令为
式中， optk 为最优转矩-转速系数，需根据永磁直驱风机功率-转速曲线确定。
永磁同步发电机电磁转矩的标幺值为
稳态时，电磁转矩等于控制指令控制，即
将式（7）、式（8）代入式（9）可得
将式（10）代入式（6）可以得到关于eω的一元四次方程式（11）。
求解式（11）时可首先忽略 sR，得到
采用式（13）进行开立方计算后得到e0ω。
然后针对式（11），以e0ω作为预估值，在此预估值附近采用牛顿-拉夫逊法迭代求解得到eω的稳态值。最后将eω代入式（10）得到qsi的稳态值。
2 参数的轨迹灵敏度
永磁直驱风机风电场等值模型参数数量众多，对系统动态特性影响程度各不相同。如果针对所有参数进行辨识势必耗费大量计算时间，而且辨识结果会出现较大分散性，难以应用，故只针对关键参数进行辨识。在暂态过程中，桨距角控制一般来不及动作，故其参数不参与辨识。由于直流电容器、滤波电感、等值配网阻抗为静止元件，其参数时变性较小，可根据铭牌数据或技术手册固定为聚合值，不参与参数辨识，具体聚合方法参见文献[24]。
永磁同步发电机属于旋转元件，长期运行后，其定子电阻、电抗与磁链可能与铭牌数据差异较大，应作为候选辨识参数。惯性时间常数虽然时变性较小，但是铭牌与技术手册上一般不包含此数据，故作为候选辨识参数。各厂家一般将控制器参数视作商业机密，因此控制器参数亦应作为候选辨识参数。候选辨识参数中的低灵敏度参数一般难以精确辨识，可固定为典型值。因此需要针对候选参数进行灵敏度分析，只辨识其中的高灵敏度参数。灵敏度分析与参数辨识的关系在于前者为后者指引了方向，即应辨识哪些参数。如果不进行灵敏度分析而辨识所有候选参数，将导致辨识结果出现极大的分散性，而且降低程序收敛速度，增加参数辨识的时间。
本文采用文献[21]轨迹灵敏度以及平均轨迹灵敏度的定义方法。风电场的非线性模型可表示为
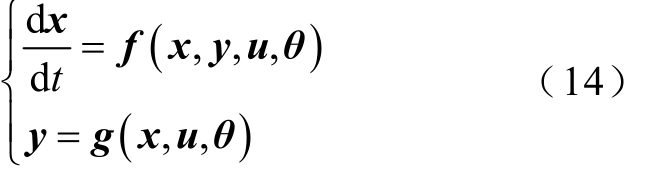
式中，x代表状态变量，如定、转子磁链与转子转速等；u代表输入变量，如风速、公共并网点电压等；y代表输出变量，如输出有功、无功功率等；θ代表参数，如等值配网阻抗、定、转子阻抗、励磁电抗。参数的轨迹灵敏度反映了当参数变化时，输出变量的变化大小。在某个运行状态下，输出 y j(t)相对于参数θi的轨迹灵敏度定义为
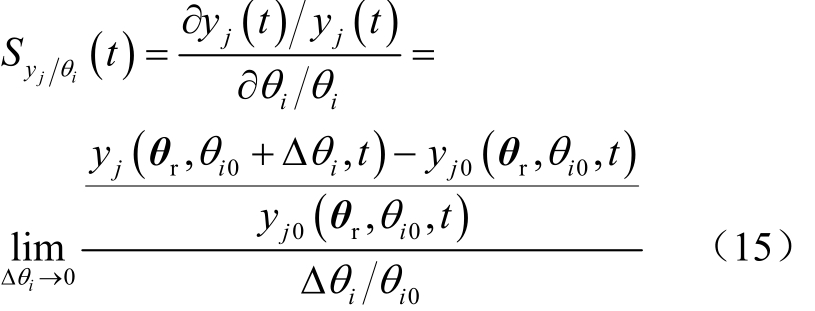
式中，0jy为当参数iθ值为0iθ时的模型输出；iθΔ为iθ的变化量；rθ为模型中除了iθ的其他参数。
为定量研究参数总的灵敏度，定义平均灵敏度为
式中，t1、t2分别为扰动发生前、后的某一时刻，可根据输出曲线情况合理选取。在实际中，根据式（14）~式（16）解析求取参数的轨迹灵敏度及其平均值较为困难。可采用仿真软件求取数值解。算法如下：
1）首先构建仿真算例，将风电场等值模型候选辨识参数设置为铭牌或技术手册上的值，若铭牌与技术手册上查不到该候选辨识参数的值则设置为典型值。
2）然后进行潮流计算，设置短路故障，进行暂态分析计算，记录等值模型输出的有功功率、无功功率曲线 P 0( t)、 Q 0( t)。
3）将风电场等值模型第 k个候选辨识参数在步骤1）中设置值的基础上增加5%，重复步骤2）得到等值模型输出的有功功率、无功功率曲线Pk( t)、 Q k( t)。
4）计算第k个候选辨识参数的有功、无功轨迹灵敏度分别为
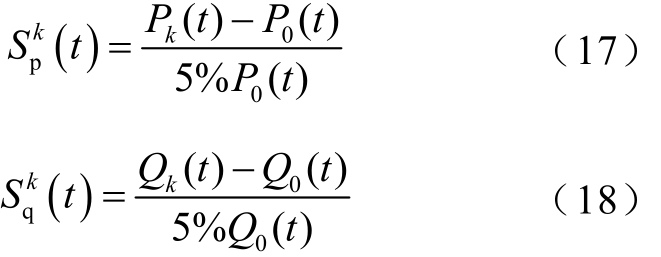
5）计算第k个候选辨识参数的有功、无功功率平均轨迹灵敏度分别为
6）重复步骤2）~步骤5）计算所有候选辨识参数的轨迹灵敏度与平均轨迹灵敏度。
采用如图3所示的仿真系统研究等值模型候选参数的轨迹灵敏度。575V母线处接入1台永磁直驱风机，额定有功功率为1.5MW，额定功率因数为1.0。物理与控制系统参数分别见表 1和表 2，永磁同步发电机为隐极机。假设母线 B0处安装了相量测量（Phasor Measurement Unit, PMU）。在线路L1的中点设置三相短路，过渡电阻 8Ω，持续时间 4个周波，仿真时间为 0.2s。B0处电压跌落深度为约为30%。
图3 仿真系统
Fig.3 Simulation system
表1 1.5MW永磁直驱风机物理参数
Tab.1 Physical parameters of 1.5MW PMSG
参 数 数 值 参 数 数 值定子电阻(pu) 0.027 2 T2额定容量/(MV·A) 2定子电抗(pu) 0.513 1 T2电阻(pu) 0.001 5永磁体磁链(pu) 1.188 4 T2漏抗(pu) 0.041 5惯性时间常数/s 1.439 3 额定功率因数 1.0 MSC容量(pu) 1.0 GSC容量(pu) 1.2直流母线电压/V 115 0 滤波器电阻(pu) 0.03直流电容/F 0.01 滤波器电抗(pu) 0.3
表2 1.5MW永磁直驱风机控制器参数
Tab.2 1.5MW PMSG controller parameters
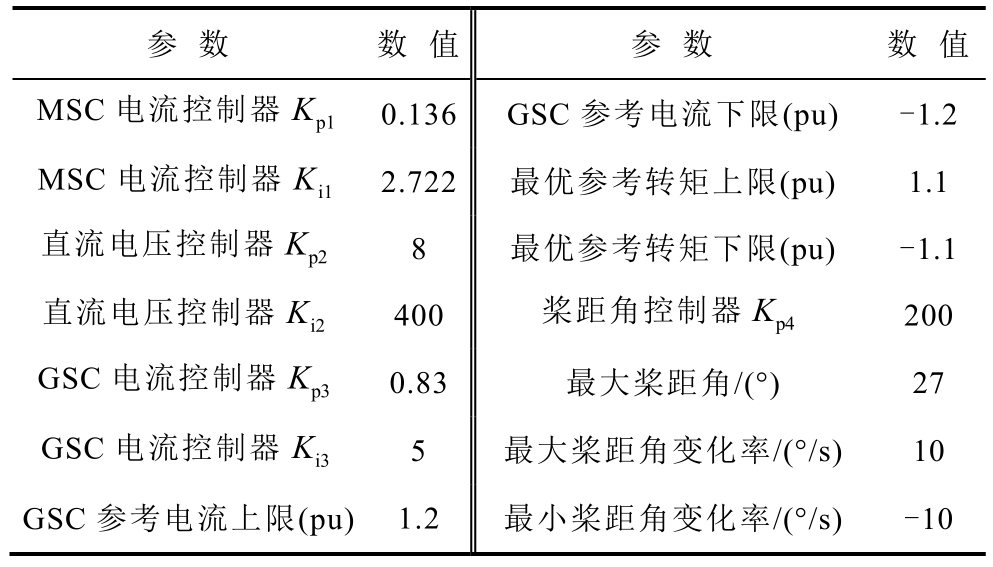
参 数 数 值 参 数 数 值MSC电流控制器 p1K 0.136 GSC参考电流下限(pu) -1.2 MSC电流控制器 i1K 2.722 最优参考转矩上限(pu) 1.1直流电压控制器 p2K 8 最优参考转矩下限(pu) -1.1直流电压控制器 i2K 400 桨距角控制器 p4K 200 GSC电流控制器 p3K 0.83 最大桨距角/(°) 27 GSC电流控制器 i3K 5 最大桨距角变化率/(°/s) 10 GSC参考电流上限(pu) 1.2 最小桨距角变化率/(°/s) -10
依次将候选辨识参数根据表1、表2中数值增加5%，各候选辨识参数的平均轨迹灵敏度见表3。从表 3可以看出，定子电抗、惯性时间常数 jT、MSC电流控制器比例与积分放大倍数的灵敏度均为0，难以辨识。铭牌或技术手册上一般给出了定子电抗 dL、 qL的值，因此，可将定子电抗 dL、 qL固定为铭牌值或技术手册上的值，将惯性时间常数 jT、MSC电流控制器比例与积分放大倍数固定为典型值。
表3 时变参数的平均轨迹灵敏度-电压跌落约30%
Tab.3 Average trajectory sensitivity of parameters when voltage dips about 30%
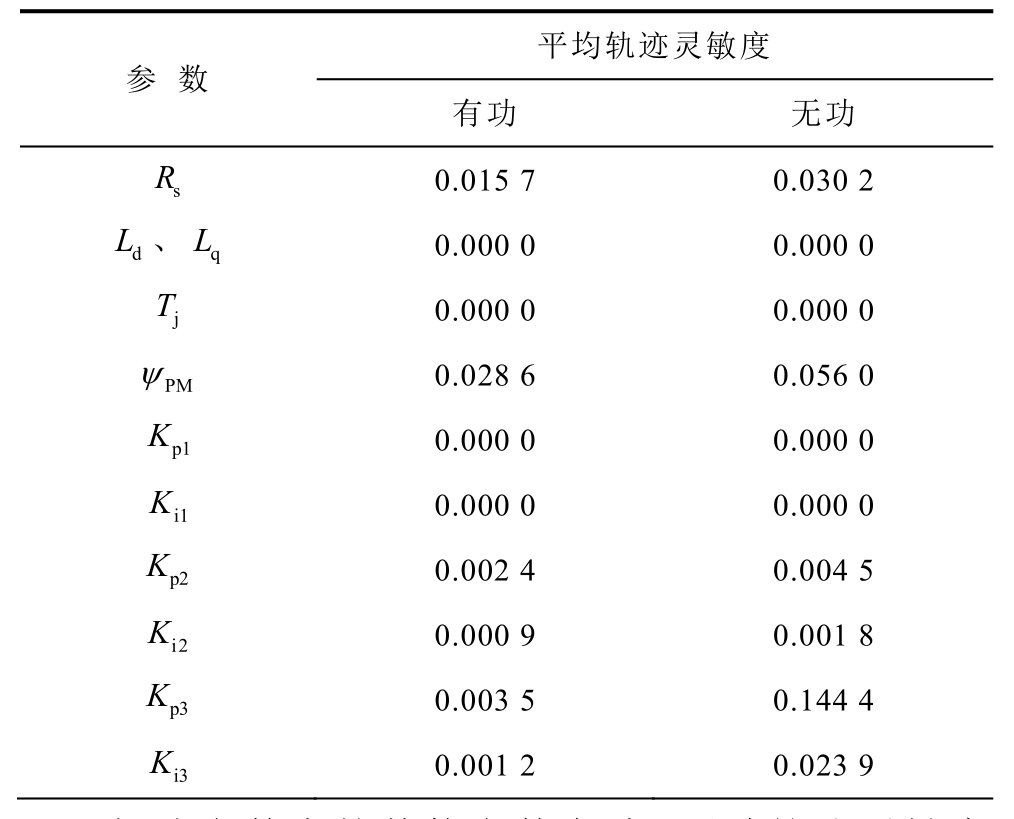
平均轨迹灵敏度参 数有功 无功R 0.015 7 0.030 2 s L、 qL 0.000 0 0.000 0 d T 0.000 0 0.000 0 j ψ 0.028 6 0.056 0 PM K 0.000 0 0.000 0 p1 K 0.000 0 0.000 0 i1 K 0.002 4 0.004 5 p2 K 0.000 9 0.001 8 i2 K 0.003 5 0.144 4 p3 K 0.001 2 0.023 9 i3
候选参数中的其他参数有功、无功轨迹灵敏度分别如图4和图5所示。图4a、图5a分别为同步发电机定子电阻sR与永磁体磁链PMψ的有功、无功轨迹灵敏度。图4b、图5b分别为直流电压控制器比例与积分放大倍数 p2K 、 i2K以及GSC电流控制器积分放大倍数 i3K 的有功、无功轨迹灵敏度。图4c、图5c分别为GSC电流控制器比例放大倍数K p3 的有功、无功轨迹灵敏度。从图4、图 5中可看出，在控制系统的四个参数中， K p 3的有功、无功轨迹灵敏度波动幅度均最大，K p2 、K i3 次之，K i2最小。
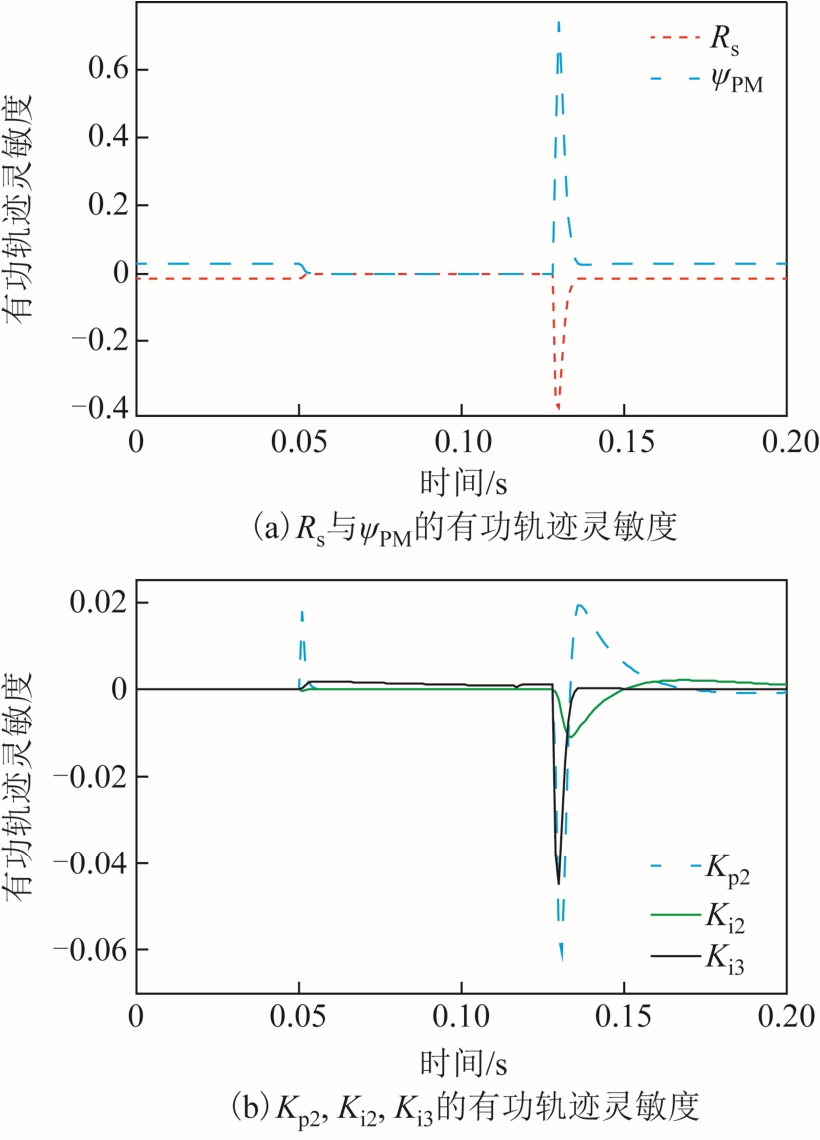
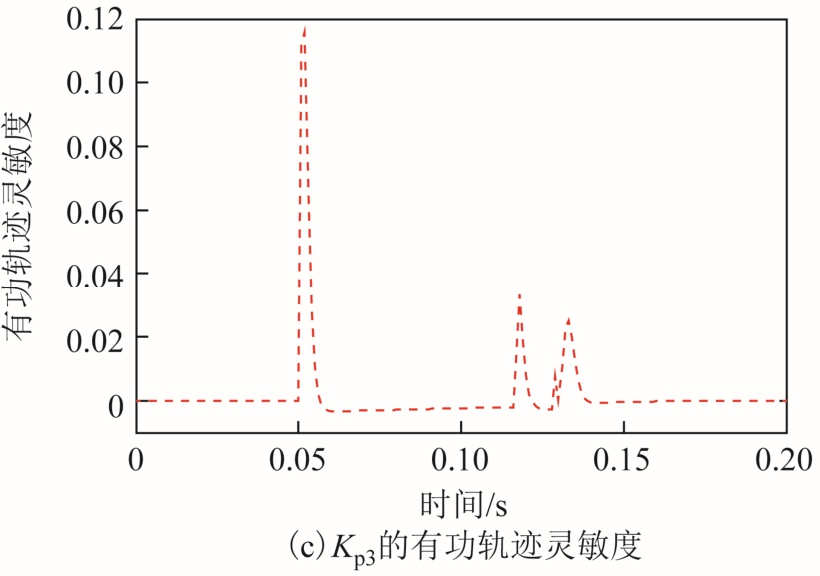
图4 有功轨迹灵敏度
Fig.4 Active power trajectory sensitivity
图5 无功轨迹灵敏度
Fig.5 Reactive power trajectory sensitivity
从图 4a、图 5a可看出，定子电阻 sR有功（无功）轨迹灵敏度为负值时，永磁体磁链PMψ有功（无功）轨迹灵敏度为正值，而且当 sR有功（无功）轨迹灵敏度处于波谷时，永磁体磁链PMψ有功（无功）轨迹灵敏度处于波峰。因此定子电阻 sR与永磁体磁链PMψ有功、无功轨迹灵敏度相位相反。这是由于电阻是能量耗散元件，而永磁体是能量转换的枢纽元件，特性不同。由于电阻与磁链有功、无功轨迹灵敏度相位均相反，增加一个参数的值与减小另一个参数的值可导致相同的有功、无功曲线变化。故难以将两个参数同时精确辨识出来。本文进一步深入研究发现，当电阻与磁链同时参与参数辨识时，二者的辨识结果分散性均很大，且均偏离其真实值较远，即存在参数不可辨识问题。因此可行方案是将定子电阻固定为铭牌上的值，不参与辨识。
设置过渡电阻为1Ω，此时B0母线电压跌落深度大约为80%。各候选辨识参数的平均轨迹灵敏度见表 4。可以看出，定子电抗、惯性时间常数 jT、MSC电流控制器比例与积分放大倍数的灵敏度仍为0。sR、PMψ、p2K、i2K、p3K、i3K平均轨迹灵敏度均大幅下降，这是因为GSC控制系统电流限幅环节起到了限幅作用。
表4 时变参数的平均轨迹灵敏度-电压跌落约80%
Tab.4 Average trajectory sensitivity of parameters when voltage dips about 80%
平均轨迹灵敏度参 数有功 无功R 0.004 7 0.017 7 s L、 qL 0.000 0 0.000 0 d T 0.000 0 0.000 0 j ψ 0.007 1 0.015 0 PM K 0.000 0 0.000 0 p1 K 0.000 0 0.000 0 i1 K 3.15×10-5 0.000 36 p2 K 2.47×10-5 2.76×10-5 i2 K 0.002 4 0.065 0 p3 K 0.000 53 0.009 2 i3
3 永磁直驱风电场等值模型参数辨识
3.1 参数辨识的模型
参数辨识是一个优化过程，目标函数为在模型结构、状态变量与待辨识参数约束条件下调整风电场等值模型参数估计的输出与实际输出二次方和最小，如式（21）所示。
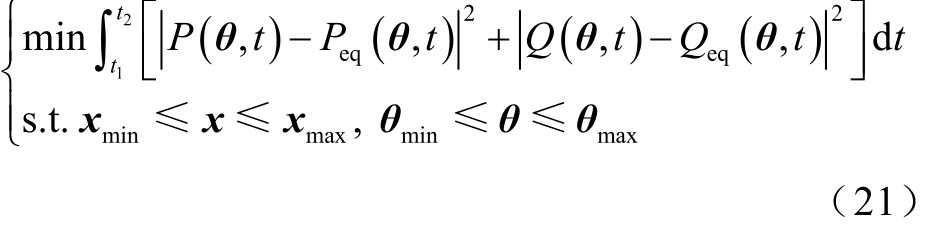
式中， P (θ ,t)、Q(θ,t)分别为电压扰动下风电场公共并网点 PMU有功、无功数据样本； P eq(θ ,t)、Qeq (θ ,t)分别为风电场等值模型在相同电压扰动下有功、无功功率输出数据；x为状态变量； x m in、x m ax分别为 x的上、下限；θ为优化的关键参数；θmin、θmax分别为θ的上、下限，以确保优化结果的合理性。
由于等值模型参数众多，为减小参数辨识过程中的计算量，只针对对系统动态特性具有较大影响的关键参数与时变参数进行辨识。本文只辨识永磁体磁链ψPM、GSC控制器比例与积分放大倍数Kp2、K i2 、 K p3 、 K i3共五个参数，其他参数固定为聚合值或典型值。
3.2 参数辨识算法
遗传算法（Genetic Algorithm, GA）和粒子群优化（Particle Swarm Optimization, PSO）都是十分受欢迎的算法，然而两种算法的缺点也是十分明显的。例如，由于GA交叉与变异操作是随机的，因而收敛速度慢。PSO全局搜索能力弱，易于陷入局部最优点导致早熟。为了克服上述问题，专家与学者们提出了多种结合GA和PSO的混合算法。文献[25]提出了一种采用单一模范与级联结构的基因学习粒子群（Genetic Learning PSO, GLPSO）混合算法。在GLPSO中，基因操作产生的最优个体提供给粒子群学习以更新速度和位置，粒子群在觅食过程中积累的经验 gbest，pbest作为遗传物质提供给 GA算法进行基因操作，如此循环，反复迭代，直至满足结束条件。由于级联结构能够产生正反馈机制，故极大地提高了收敛速度，达到“1+1＞2”的效果。然而，该方法中，交叉概率 cP与变异概率 mP、惯性权重系数ω和加速因子c均为常数。针对此不足，本文在文献[25]所提出的GLPSO基础上，通过动态调整cP、 mP、ω、c，对GA和PSO进行改进。改进后的GA和PSO分别称为IGA与IPSO。改进的GLPSO算法流程如图6所示。
1）首先初始化所有优化参数，如种群规模、最大迭代次数、IPSO和 IGA中的系数以及每个粒子的速度和位置等。
2）在基因操作过程中，若增加交叉概率值 cP，则能够扩大搜索空间；若减小 cP，则能够保证在最优解附近搜索的连续性。因此本文自适应动态调整cP 为[21]。
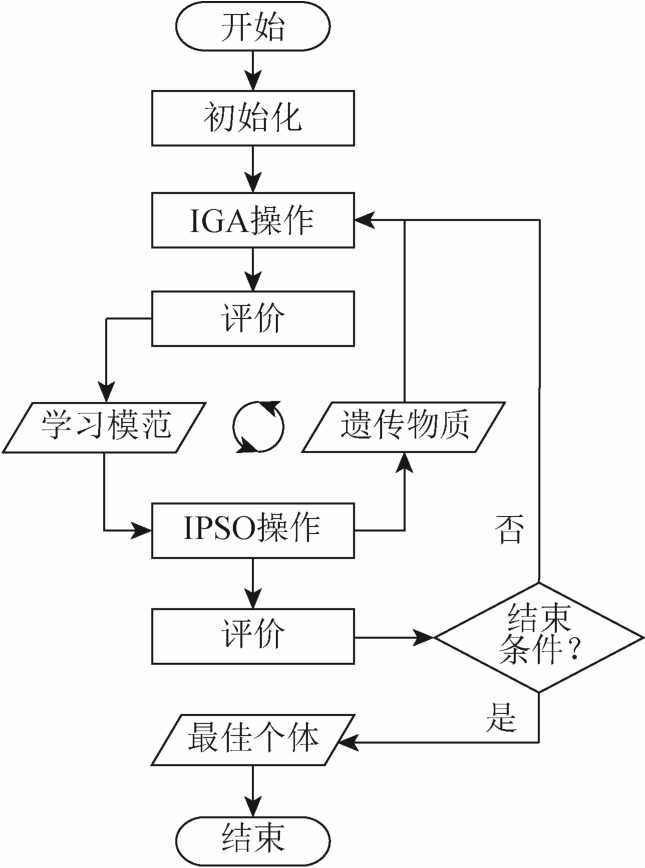
图6 改进GLPSO算法的流程
Fig.6 Flow chart of improved GLPSO algorithm
式中，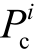 
为第i次迭代过程中，交叉概率设置值；Pc0为初始的交叉概率设置值，本文设置为0.9；N为最大迭代次数。
变异操作的目的是产生新的个体，扩大搜索范围。增加变异概率值可以避免陷入局部最优解，同时也会破坏最优解空间。变异概率值 Pm的设置范围一般为0.001~0.1。本文自适应动态调整 P m为[21]
式中，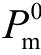
设置为0.1；τ为决定是否将第i次迭代过程中的变异概率 
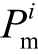设置为初始值的标记符。若最优目标函数值的改善幅度连续10代小于1%，则τ设置为1，即若连续10代不能够找到更优解，则扩大搜索空间。
3）将参数向量传递至等值模型，计算目标函数值，保存最优目标函数值与对应的参数向量。
4）IGA操作与目标函数值计算完成后，执行IPSO算法。惯性权重系数ω、加速度系数c动态调整为
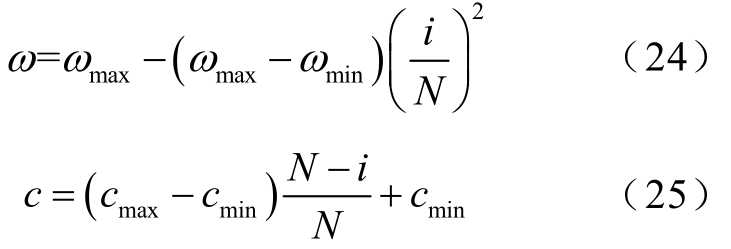
本文将ωmax、ωmin分别设置为0.9和0.4；cmax、cm in分别设置为0.5和0.25。
5）再次将参数向量传递至等值模型，计算目标函数值，保存最优目标函数值和对应的参数向量。若满足结束条件，则终止程序，输出最优解；否则，转至步骤2）。
4 仿真算例
4.1 仿真条件
为验证所提出的风电场等值模型的鲁棒性与适应性，基于Matlab构建了文献[24]中所示的WECC标准仿真系统详细模型。风电场包含20台永磁直驱风机，每台永磁直驱风机经额定容量为 2MV·A的升压变压器接入 35kV中压配电网。每台风机的参数以及升压变压器的阻抗参数与表1与2相同。当全部风机在线时，选取系统基准容量 S B =Seq=30MV· A。230kV输电网采用恒定电压源表示。设置线路 L1中点经 8Ω过渡电阻发生三相短路故障，故障持续时间为4个周波，仿真时间为0.2s。设置种群个体规模为 50，迭代次数为15代。参数辨识区间见表5。
表5 参数辨识区间
Tab.5 Identification intervals of parameters
ψ (pu) p2K i2K p3K i3K PM[0.594,2.377] [1.6,40] [80,200 0] [0.166,4.15] [1,25]
4.2 仿真结果
4.2.1 算法的收敛速度比较
计及尾流效应，设置各风机风速见表 6，采用改进的GLPSO、GA与PSO算法进行参数辨识，每步迭代的最优个体目标函数值比较结果如图 7所示。可以看出，改进的 GLPSO全局寻优能力远优于GA与PSO。
表6 计及尾流效应的各风机风速
Tab.6 Wind speed of PMSG considering wake effect
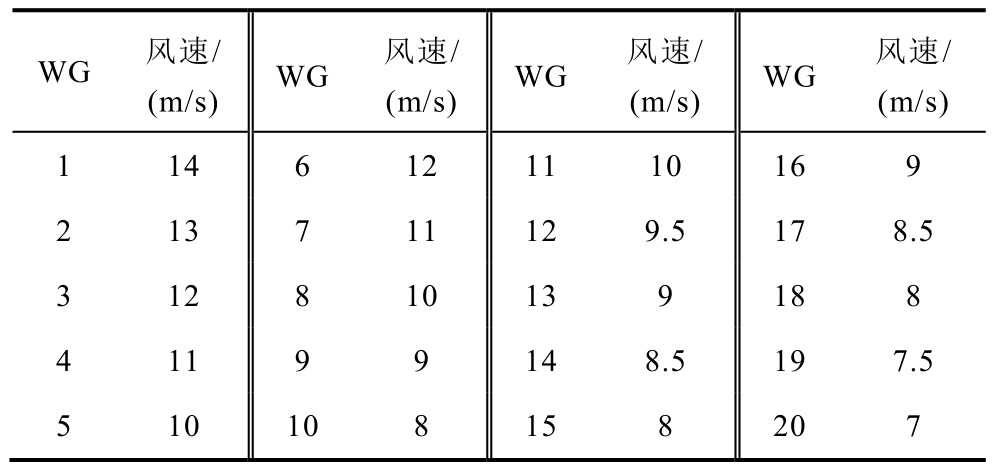
WG 风速/(m/s) WG 风速/(m/s) WG 风速/(m/s) WG 风速/(m/s)1 14 6 12 11 10 16 9 2 13 7 11 12 9.5 17 8.5 3 12 8 10 13 9 18 8 4 11 9 9 14 8.5 19 7.5 5 10 10 8 15 8 20 7
4.2.2 鲁棒性与适应性分析
1）等值模型参数辨识结果的稳定性分析
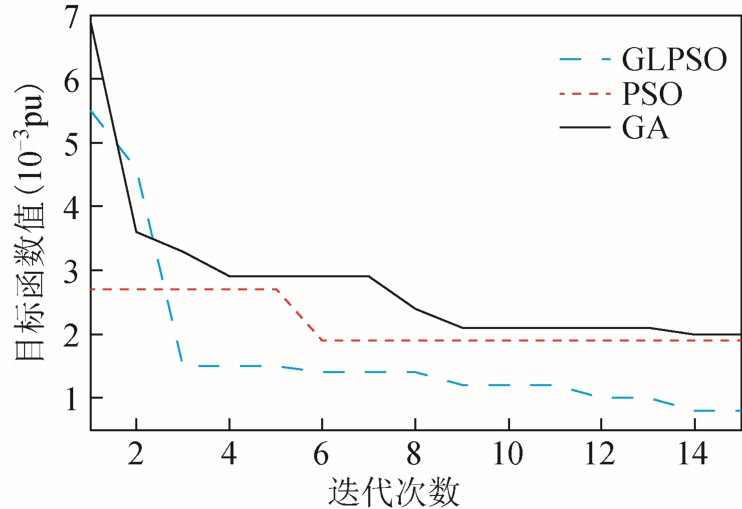
图7 三种算法寻优能力比较
Fig.7 Comparisons of three algorithms
表7 风电场100%风机在线时的参数辨识结果
Tab.7 Parameter identification results 100% on-line
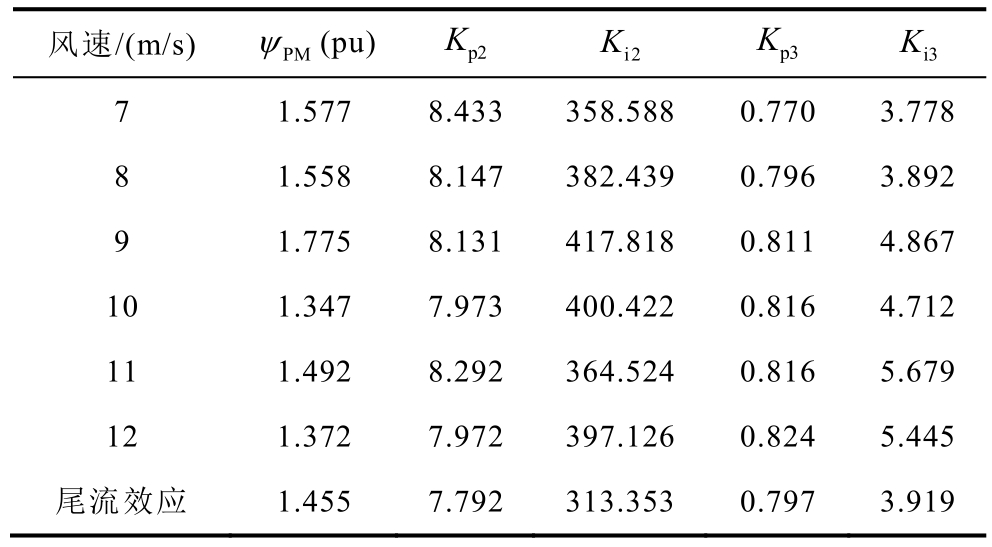
风速/(m/s)PMψ(pu)p2K i2K p3K i3K 7 1.577 8.433 358.588 0.770 3.778 8 1.558 8.147 382.439 0.796 3.892 9 1.775 8.131 417.818 0.811 4.867 10 1.347 7.973 400.422 0.816 4.712 11 1.492 8.292 364.524 0.816 5.679 12 1.372 7.972 397.126 0.824 5.445尾流效应 1.455 7.792 313.353 0.797 3.919
多种风速与计及尾流效应场景下的等值模型参数辨识结果见表 7。可以看出， K p2 、 K p3 分散性较小，其他参数具有一定的分散性。
在实际运行中，部分风机可能由于检修或风速小于切入风速而处于离线状态。假设风机 5、9、13、17（见文献[24]中图5）处于离线状态，此时，系统基准容量选取为 S B =Seq =30×0.8MV·A。风电场80%风机在线时的参数辨识结果见表8。可以看出， K p2 、 K p 3分散性仍较小，其他参数具有一定的分散性。
表8 风电场80%风机在线时的参数辨识结果
Tab.8 Parameter identification results 80% on-line
风速/(m/s)PMψ(pu)p2K i2K p3K i3K 7 1.556 8.638 257.237 0.759 4.335 8 1.563 8.369 355.734 0.786 3.568 9 1.792 8.321 395.770 0.789 3.865 10 1.760 8.278 352.339 0.802 4.569 11 1.593 8.225 432.273 0.816 5.542 12 1.588 8.140 400.245 0.829 4.916尾流效应 1.485 7.800 295.827 0.826 3.577
计及尾流效应的各风机风速见表 6，类似于文献[24]，本文通过设置各风机风速不同来考虑尾流效应。风电场参数辨识结果见表7和表8，考虑尾流效应后，由于各风机的运行状态差异较大，参数辨识结果的精度略低于不考虑尾流效应的参数辨识结果，但仍然是令人满意的。
2）等值模型的描述能力验证
将参数辨识结果以及风电场公共并网点PMU记录的电压扰动数据样本（包括电压幅值与相角）传递给等值模型，进行解微分方程与功率等计算，得到模型输出的有功、无功功率曲线。此模型输出有功、无功功率曲线与PMU记录的风电场在相同电压扰动下有功、无功功率曲线进行对比。分别观察有功、无功功率曲线拟合效果校验模型的描述能力。各风机风速均为 8m/s、9m/s、10m/s、11m/s以及当各风机风速均为 9m/s且有 20%风机处于离线状态时的有功、无功功率拟合曲线如图8所示。可以看出，拟合效果较好。因此，等值模型的描述能力较好。
图8 等值模型的描述能力验证
Fig.8 Descriptive capability of equivalent model
3）等值模型的泛化能力验证
采用吻合度指标定义拟合精度[24]，针对9m/s的数据样本辨识得到的等值模型参数拟合7m/s、12m/s和计及尾流效应的数据样本以及相应20%风机离线时的数据样本，拟合曲线如图9所示，可以看出拟合效果较好。多种场景下，有功、无功功率的吻合度指标见表9。可以看出，吻合较好。因此，等值模型的泛化能力较好。
图9 等值模型的泛化能力验证
Fig.9 Generalization ability of equivalent model
表9 等值模型的拟合曲线吻合度比较结果
Tab.9 Comparisons of fitting curves of equivalent model
参数数值（%）风速有功 无功7m/s 99.99 99.75 100%在线12m/s 99.99 99.98尾流效应 99.94 99.95 7m/s 99.99 99.59 80%在线12m/s 99.99 99.98尾流效应 99.93 99.94
4）风机风速未知情形
假设风电场未安装任何测风设备，由于在暂态过程中各风机的机械输入转矩可近似认为不变，因此可假定等值机输入机械转矩恒定不变，固定为稳态潮流计算值。应用此方法针对尾流效应情形的参数辨识结果见表10。可以看出，参数辨识结果与表7、表8是一致的。
表10 风电场风机风速未知时的参数辨识结果
Tab.10 Identification results if wind speed is unknown
ψ (pu) p2K i2K p3K i3K PM 1.552 7.841 279.277 0.824 3.913
值得指出的是，表7、表8与表10中的辨识结果PMψ与真实值1.188 4(pu)偏差较大。当设置三相短路过渡电阻为1Ω时，可精确辨识出PMψ与p3K，尽管其他参数仍存在分散性。多次辨识结果PMψ与真实值的1.188 4(pu)偏差均小于5%。
由于电力系统的暂态过程时间很短，一般在10s以内。永磁直驱风电场的动态特性取决于GSC换流器的动态特性与调节速度，一般在ms级。从图8与图9可以看出，永磁直驱风电场暂态过程时间很短，远小于0.2s。在这么短的时间内，可以认为风速是恒定的。由于本文采用的是基于实测数据的参数辨识方法，对于风速随机性，具有很好的鲁棒性与适应性。
5 结论
本文构建了永磁直驱风电场的详细动态等值模型与初始化方法。分析了模型参数的轨迹灵敏度，发现定子电抗、惯性时间常数、MSC电流控制器比例与积分放大倍数灵敏度极小，而且定子电抗与永磁体磁链轨迹灵敏度相位相反，存在参数不可辨识问题。提出了针对时变且高灵敏度参数以及高灵敏度控制器参数采用改进的 GLPSO混合算法进行参数辨识，其他参数固定为聚合值或典型值的策略，能够提高程序的收敛速度和全局寻优能力，降低参数辨识结果的分散性。
[1] Zhang Jian, Cui Mingjian, He Yigang, et al. Primal dual interior point dynamic programming for coordinated charging of EVs[J]. Journal of Modern Power Systems and Clean Energy, 2017, 5(6): 1004-1015.
[2] 苗磊, 张勇军, 童朝南, 等. 基于模型预测直接转矩控制的永磁同步发电机效率优化研究[J]. 电工技术学报, 2018, 33(15): 3535-3546.Miao Lei, Zhang Yongjun, Tong Zhaonan, et al.Efficiency optimization of permanent magnet synchronous generators based on model predictive direct torque control[J]. Transactions of China Electro technical Society, 2018, 33(15): 3535-3546.
[3] Zhang Jian, Cui Mingjian, Fang Hualiang, et al. Two novel load balancing platforms using common DC buses[J]. IEEE Transactions on Sustainable Energy,2018, 9(3): 1099-1107.
[4] 关中杰, 鲁效平, 李钢强, 等. 基于风速模型的风电机组动态转矩前馈控制技术[J]. 电工技术学报,2018, 32(22): 5338-5345.Guan Zhongjie, Lu Xiaoping, Li Gangqiang, et al.Dynamic torque feed forward control technology of wind turbine based on wind speed model[J].Transactions of China Electrotechnical Society, 2018,32(22): 5338-5345.
[5] 苏田宇, 杜文娟, 王海风. 多直驱永磁同步发电机并联风电场次同步阻尼控制器降阶设计方法[J].电工技术学报, 2019, 34(1): 116-127.Su Tianyu, Du Wenjuan, Wang Haifeng. A reduced order design method for sub-synchronous damping controller of multi-PMSGs parallel wind farm[J].Transactions of China Electrotechnical Society, 2019,34(1): 116-127.
[6] 任必兴, 杜文娟, 王海风. 静止同步补偿器与直驱永磁风机的次同步控制交互研究[J]. 电工技术学报, 2018, 33(24): 5884-5896.Ren Bixing, Du Wenjuan, Wang Haifeng. Analysis on sub-synchronous control interaction between static synchronous compensator and permanent magnet synchronous generator[J]. Transactions of China Electrotechnical Society, 2018, 33 (24): 5884-5896.
[7] 唐飞, 刘扬, 施浩波, 等. 一种考虑风电场并网的大电网快速主动解列策略[J]. 电工技术学报, 2018,33(24): 5884-5896.Tang Fei, Liu Yang, Shi Haobo, et al. A fast active islanding strategy for large power grid considering wind farm integration[J]. Transactions of China Electro technical Society, 2018, 33(24): 5884-5896.
[8] Ruan Jiayang, Lu Zongxiang, Qiao Ying, et al.Transient stability of wind turbine adopting a generic model of DFIG and singularity-induced instability of generators/ units with power-electronic interface[J].IEEE Transactions on Energy Conversion, 2015, 30(3):1069-1080.
[9] Kunjumuhammed L, Pal B, Gupta R, et al. Stability analysis of a PMSG-based large offshore wind farm connected to a VSC-HVDC[J]. IEEE Transactions on Energy Conversion, 2017, 32(3): 1166-1176.
[10] Marandi V, Pak L, Dinavahi V. Real-time simulation of grid-connected wind farms using physical aggregation[J].IEEE Transactions on Industrial Electronics, 2010,57(9): 3010-3021.
[11] Fernandeza L, Juradob F, Saenz J. Aggregated dynamic model for wind farms with doubly fed induction generator wind turbines[J]. Renewable Energy, 2008(33): 129-140.
[12] Li Weixing, Chao Pupu, Liang Xiaodong, et al. A practical equivalent method for DFIG wind farms[J].IEEE Transactions on Sustainable Energy, 2018, 9 (2):610-620.
[13] Ali M, Ilie I, Milanovic J, et al. Wind farm model aggregation using probabilistic clustering[J]. IEEE Transactions on Power Systems, 2013, 28(1): 309-316.
[14] Zou Jianxiao, Peng Chao, Xu Hongbing, et al. A fuzzy clustering algorithm-based dynamic equivalent modeling method for wind farm with DFIG[J]. IEEE Transactions on Energy Conversion, 2015, 530(4):1329-1337.
[15] Wang Peng, Zhang Zhenyuan, Huang Qi, et al.Improved wind farm aggregated modeling method for large-scale power system stability studies[J]. IEEE Transactions on Power Systems, 2018, 33(6): 6332-6342.
[16] Zhang Yingchen, Muljadi E, Kosterev D, et al. Wind power plant model validation using synchrophasor measurements at the point of interconnection[J]. IEEE Transactions on Sustainable Energy, 2015, 6(3): 984-991.
[17] Brochu J, Larose C, Gagnon R. Validation of singleand multiple-machine equivalents for modeling wind power plants[J]. IEEE Transactions on Energy Conversion, 2011, 26(2): 532-541.
[18] Lin Jin, Cheng Lin. Model parameters identification method for wind farms based on wide-area trajectory sensitivities[J]. International Journal of Emerging Electric Power Systems, 2010, 11(5): 2.
[19] 张剑, 孙元章. 含分布式电源的广义负荷建模研究[J].电网技术, 2011, 35(8): 41-46.Zhang Jian, Sun Yuanzhang. Generalized load modeling considering wind generators connected to distribution network[J]. Power System Technology,2011, 35(8): 41-46.
[20] Cheng Xueyang, Lee W, Sahni M, et al. Dynamic equivalent model development to improve the operation efficiency of wind farm[J]. IEEE Transactions on Industry Applications, 2016, 52(4): 2759-2767.
[21] Wang Yinfeng, Lu Chao, Zhu Lipeng, et al.Comprehensive modeling and parameter identification of wind farms based on wide-area measurement systems[J]. Journal of Modern Power Systems and Clean Energy, 2016, 4(3): 383-393.
[22] Kunjumuhammed L, Pal B, Oates C, et al. The adequacy of the present practice in dynamic aggregated modeling of wind farm systems[J]. IEEE Transactions on Sustainable Energy, 2017, 8(1): 23- 32.
[23] Kim D, Sharkawi M. Dynamic equivalent model of wind power plant using parameter identification[J]. IEEE Transactions on Energy Conversion, 2016, 31(1): 37-45.
[24] Zhou Yuhao, Zhao Long, Lee W. Robustness analysis of dynamic equivalent model of DFIG wind farm for stability study[J]. IEEE Transactions on Industry Applications, 2018, 54(6): 5682-5690.
[25] Gong Yuejiao, Li Jingjing, Zhou Yicong, et al.Genetic learning particle swarm optimization[J]. IEEE Transactions on Cybernetics, 2016, 46(10): 2277-2289.