0 引言
近年来，随着我国电网建设速度加快，电力系统规模不断扩大，电网的短路电流水平不断升高，已逐渐逼近甚至超过断路器的允许开断容量[1-2]，特别是京津冀等负荷密集区的短路电流问题日趋严重[3]，严重威胁电力系统的安全稳定运行[4]。如何有效地限制电网的短路电流水平已成为电网规划和运行中不可忽视的问题。相较于其他措施[5-6]，输电网结构优化（Optimal Transmission Switching, OTS）无需加装设备，通过断开部分线路即可降低电网的短路电流水平[7]，在限制短路电流问题上具有很大的优势。随着电力改革和电力市场化的不断推进[8-9]，充分利用电网已有资源，灵活控制网络拓扑结构，通过网络结构优化的方法来限制短路电流，也势必成为一种趋势。实际电网运行过程中，已有调度员根据人工经验选择开断部分线路，以降低短路电流水平的实例，但难以保证电网运行的安全性和经济性以及N-1安全要求[10]。因此，迫切需要提出能够考虑短路电流约束的最优线路开断模型，辅助调度人员制定线路开断计划。
输电网结构优化通过改变部分线路的运行状态能够消除电网的薄弱环节，提升电网运行的安全性、经济性和鲁棒性。目前减轻线路过载[11]、消除电压越限[12]、降低系统网损[13]和发电成本[14-16]方面已开展广泛的研究，但通过输电网结构优化限制短路电流的相关研究尚处于初步阶段。文献[17-18]提出了不同的灵敏度指标，并通过指标的计算排序依次开断单一线路。文献[19-20]建立了限制短路电流的网架结构优化模型，分别利用智能算法或基于灵敏度的启发式方法对模型进行求解。这些方法虽均能够给出相对较优的开断线路组合，但缺乏对线路开断与短路电流之间内在关系的探讨与研究，灵敏度法忽视了不同线路之间的耦合因素，而智能算法模型的收敛性差。
部分学者为了避免建模过程中短路电流约束的非线性问题以及节点导纳矩阵求逆困难的问题，从不同角度对节点阻抗矩阵进行近似线性化或隐式表达。文献[21]利用矩阵分解补偿求逆法巧妙地推导出节点阻抗矩阵与线路运行状态的近似线性关系，根据节点自阻抗与短路电流的对应关系，实现了短路电流约束的近似线性化，并建立了相应的最优线路开断模型。文献[22]考虑了机组组合对短路电流的影响，推导并建立了对节点阻抗矩阵的隐式约束，避免了矩阵求逆出现的非线性问题，提出了计及短路电流约束的UC-TS优化模型，利用Benders分解法对模型进行迭代求解。但目前对短路电流约束显式线性表达的研究尚未见报道。
基于此，根据节点自阻抗的物理意义，本文提出通过构造与原电网相似拓扑、不同参数的节点自阻抗定义电路，使得线路开断的同时作用于原电网和构造的“伴随网络”，实现短路电流约束的显式线性建模。进一步地，以最小化综合开断代价和发电成本为优化目标，建立以线路开断方式消除短路电流越限的混合整数线性规划模型（Mixed-Integer Linear Programming, MILP）。此外，通过确定问题节点集和有效开断线路集，降低了决策空间规模；并采用N-1静态安全约束追加迭代策略，提高了模型的求解效率。最后，通过IEEE 30节点系统和IEEE 118节点系统算例结果证明了本文所提模型和求解算法的有效性。
1 短路电流约束的线性解析化建模
在实际工程应用中，短路电流计算时通常采用近似计算方法，将电网近似看作纯感性网络，节点短路电流的标幺值约等于该节点自阻抗的倒数[23]。
式中，If为节点f短路电流的标幺值；Zff为节点f的自阻抗。
根据支路追加法[23]可知，断开线路相当于在原网络中减少连支，即原网络中的任一节点的自阻抗将增大或者保持不变[24]。因此开断线路能够有效地降低系统中短路电流水平。但若不经处理，直接将式（1）建模为短路电流约束，则这是一个典型的非线性约束，对于模型的求解不利。针对这一问题，本文基于节点自阻抗物理意义将短路电流约束解析化建模为一组线性约束。
1.1 节点自阻抗的物理意义
根据电网分析理论中的回路电流方程可知，节点阻抗矩阵Z与节点电压向量V、电流向量I的关系为[23]
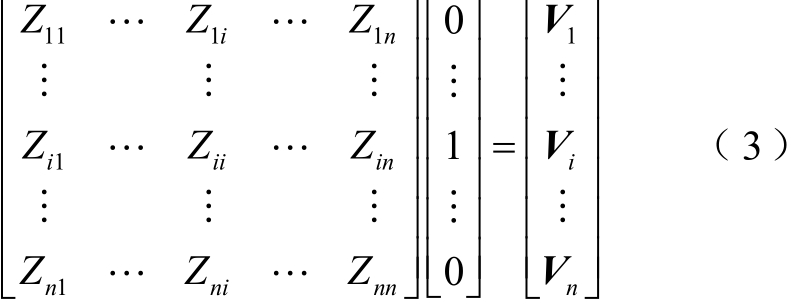
即将式（2）展开，当Ii=1且ji∀≠、Ij=0时，Vi=Zii，Vj=Zij，如式（3）所示。
由式（3）得到节点自阻抗和互阻抗的物理意义[23]：当节点i注入单位电流源，其余节点所接电流源均置零时，节点i的电压数值为Zii，节点j的电压数值为Zij，如图1所示。
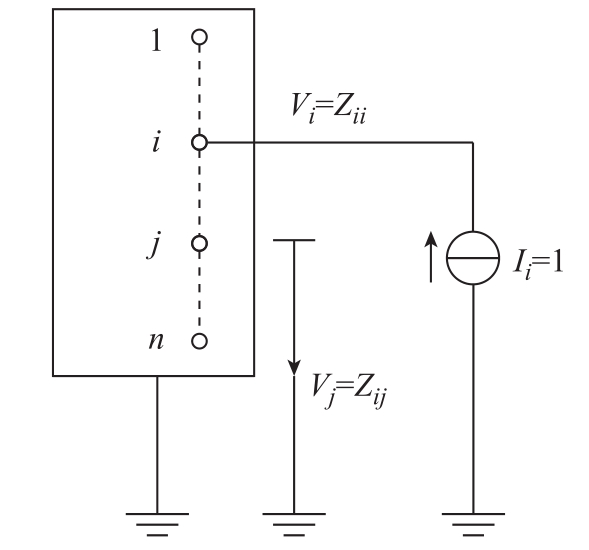
图1 自阻抗和互阻抗的物理意义
Fig.1 Physical meaning of self-impedance and mutual impedance
1.2 基于节点自阻抗物理意义的短路电流约束的建模
1.2.1 单一节点短路电流约束的建模
本节结合一个简单的电网示例，说明基于节点自阻抗物理意义的短路电流约束的建模方法。设该电网包含4台机组、8个节点、11条线路，其结构示意图如图2所示。
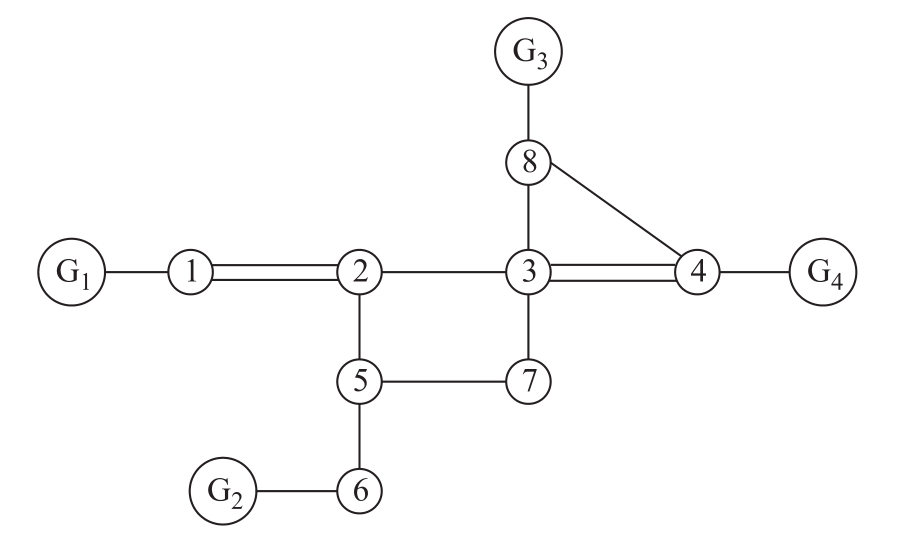
图2 电网示例结构示意图
Fig.2 Structure diagram of grid example
以分析节点4的短路电流值为例，构造原电网相应的“伴随网络”（拓扑相似但参数不同）。将机组、线路和变压器等效为支路，采用电抗近似代表线路或变压器支路阻抗，机组则以暂态电抗大小的接地支路表示；在节点4处注入单位电流源；并将节点集合从N扩展到考虑大地的N0，得到如图3所示的纯感性的原网络等效电路。
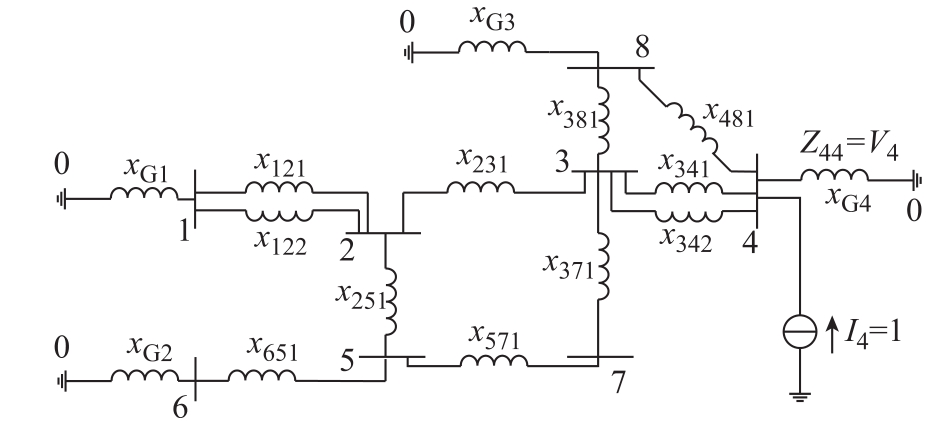
图3 电网示例等效电路
Fig.3 Equivalent map of grid example
结合图1所示的节点自阻抗和互阻抗的物理意义可知，在图3中节点4的电压值即为此网络下节点4的自阻抗，即Z44＝V4。
因此，针对任意电网中某节点 f的短路电流问题，根据节点自阻抗的物理意义，向节点 f注入单位电流源，其余节点所接电流源均置零，构建一个与原网络同型的等效电路，节点 f的电压值即为自阻抗Zff的值。采用0-1的二元决策变量 zijc来描述线路的运行状态。其中，i、j分别表示线路的首、末节点，c表示回线编号。zijc＝0表示该线路i-j-c断开；反之，zijc＝1表示该线路 i-j-c运行。则节点 f的短路电流约束建模为
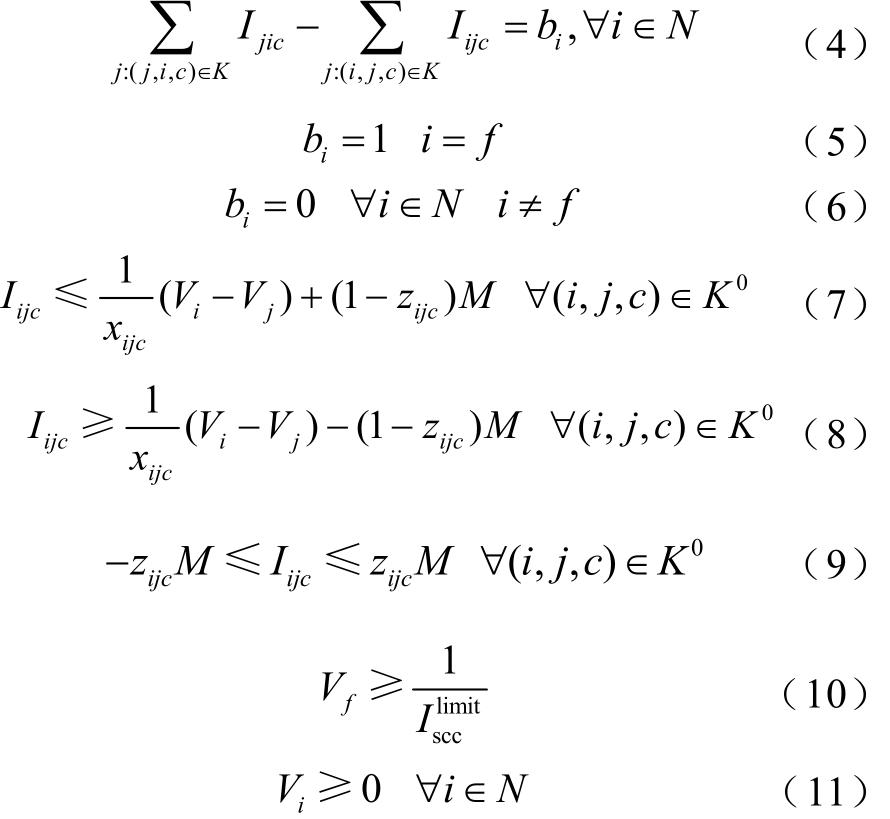
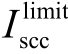M N K 0 K
式（4）为各节点的基尔霍夫电流定律；式（5）保证仅节点f有单位电流源；式（6）保证除了节点f和大地节点外的其他节点的电流的流入和流出量平衡；式（7）和式（8）为各线路的欧姆定律，由大M法变换而来，当 zijc＝1时，线路电流为首末节点的电压差与线路电抗的比值；式（9）保证当zijc＝0时，线路电流恒为零；式（10）保证节点 f的短路电流不超过限值；式（11）保证各节点电压非负。
1.2.2 多节点短路电流约束的建模
由于系统运行中可能出现多个节点短路电流越限问题，因此进一步研究将单一节点的短路电流约束推广为全网中多个节点的短路电流约束。本文将考虑短路电流问题的节点称为问题节点，其节点编号集合记为NS，则对每个问题节点均单独建立如式（4）～式（11）的一套约束，即集合NS中每个节点对应一个与原网络对应的等效电路。
设f为NS中的某个节点，则式（4）～式（11）可相应修改为
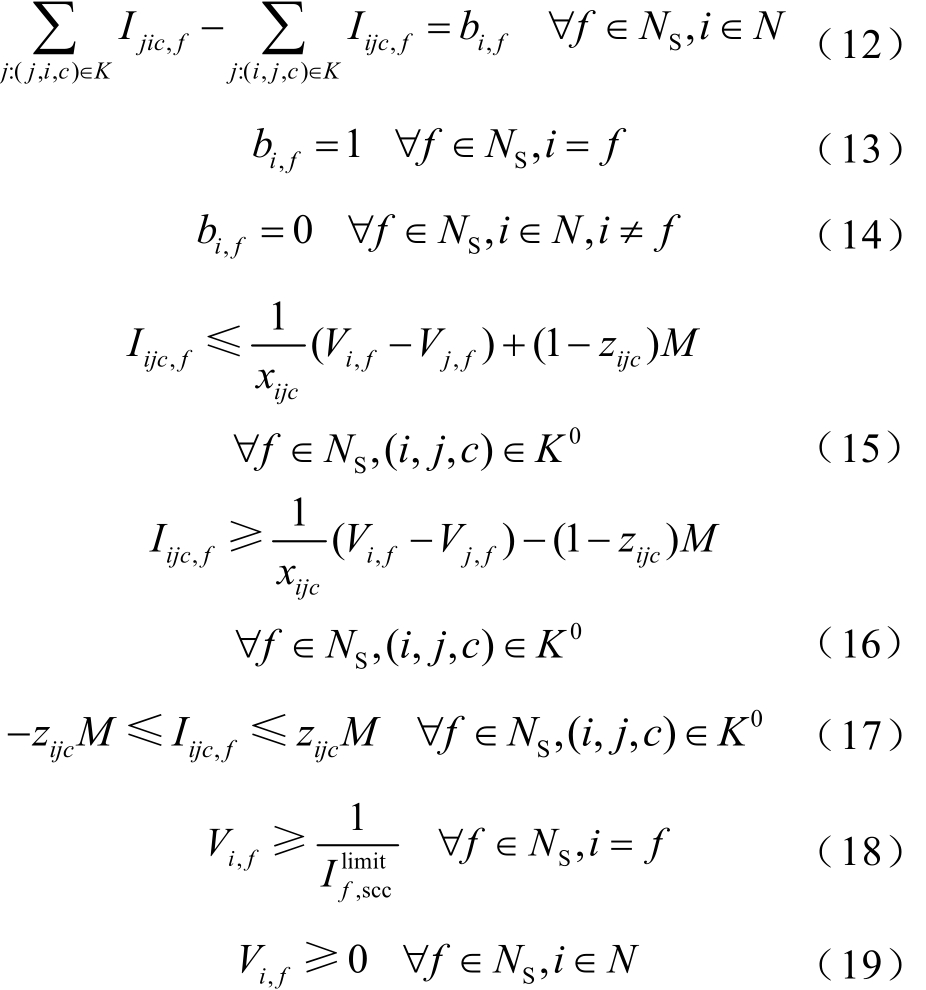
式中，Iijc,f和bi,f分别为基于节点f的等效电路中流经线路i-j-c的电流和节点i的注入电流；Vi,f、Vj,f分别为基于节点f的等效电路中的节点i、j的电压；f为问题节点编号。
不难看出，若集合NS中只存在节点f，即NS＝f时，式（12）～式（19）即退化为式（4）～式（11）。因此，式（12）～式（19）共同构成了一组基于节点自阻抗物理意义的短路电流线性约束，实现了对于节点集 NS内多个节点短路电流约束的显式线性表达。
2 网络结构优化问题的数学模型
2.1 目标函数
本文建立的网络结构优化模型的目标函数分为两部分：第一部分是开断线路的操作成本，以期待尽可能少的开断线路；第二部分是运行时的发电成本。
式中，Pg为发电机 g的有功出力；ck为任意单条线路的开断成本，cg为机组 g单位时间内的发电成本。
2.2 约束条件
在确定网络结构优化问题的线路开断方案时，要综合考虑潮流约束、连通性约束、短路电流约束以及N-1安全约束等。
2.2.1 潮流约束
式中，Pijc为线路i-j-c上的有功潮流值；Pdi为节点i所接的有功负荷量；θij为节点i和节点j的电压相位差；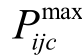
为线路传输功率的限值； 
、
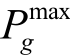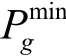分别为发电机组g有功出力的上、下限值；Gi为节点i上所接机组集合；G为所有机组集合。
式（21）保证系统中各节点上的有功平衡。式（22）和式（23）为由大 M法变换后的线路直流潮流约束，当zijc＝1时，线路i-j-c上的有功潮流为节点i、j的相位差与线路电抗的比值。式（24）为线路功率传输限值约束，在防止线路过载的同时也保证当线路被切除时，即 zijc＝0，该条线路上的潮流Pijc恒为零。式（25）和式（26）分别为发电机出力上、下限和母线电压相位差上、下限约束。
2.2.2 系统连通性约束
经过开断部分线路后，系统中可能出现孤岛，因此模型中必须引入相关的防孤岛约束，即需保证系统是连通的。本文引入网络流理论[25]来构建系统连通性约束：将系统视为一个单源多汇网络，取系统中任一发电机节点为源点，其余发电机节点为汇点，剩余节点为中间点，保证各汇点的流量需求与系统中的流量平衡。
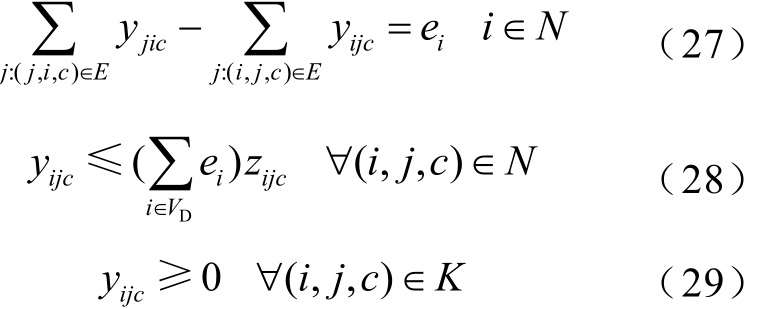
式中，yijc为系统中节点i流向节点j的线路c上的流量；ei为各点的流量需求，在本文中并无实际物理意义。当节点 i为汇点时，ei＝1；当节点 i为中间点时，ei＝0；当节点 i为唯一源点时，ei为所有汇点流量需求和的相反数；E为网络流理论中所构建的边集；VD为汇点集合。
式（27）给出了系统内各点流量的流入量和流出量之间的关系，保证了系统整体的流量平衡，即源点提供的流量最终均被各汇点所消耗；式（28）保证任一线路上的流量不得超过源点所提供的流量；式（29）表示任一线路流量非负，且与式（28）共同保证网络流只能在存在的线路上流动，即当该条线路被切除时，zijc＝0，此时线路上的流量yijc恒为零。式（27）～式（29）能保证所有发电机节点的连通性，而式（21）～式（26）保障的是所有负荷节点的供电，即保障了“源”与“荷”节点集合的连通，故二者共同保证了系统中任意节点均是连通的。
2.2.3 N-1安全约束
网络结构优化方案需满足基本的静态安全约束[26-27]。记不满足N-1校验的线路编号集合为KN，集合KN中的任一条线路t的N-1安全约束，实际上是该条线路退出运行时，系统在N-1工况下的潮流约束。若采用直流潮流表征潮流约束，则N-1安全约束为
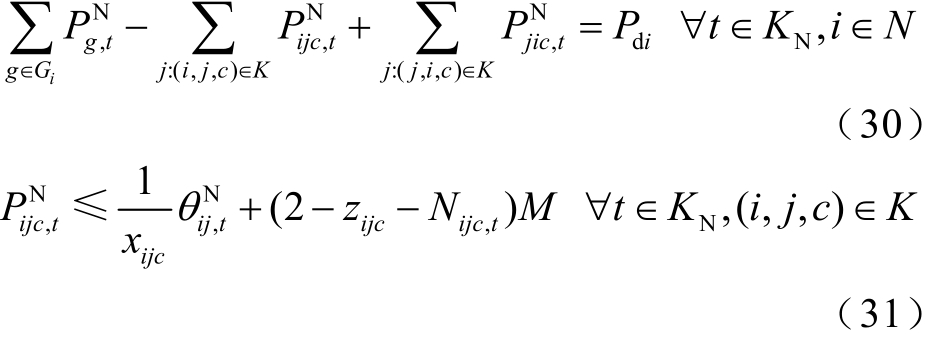
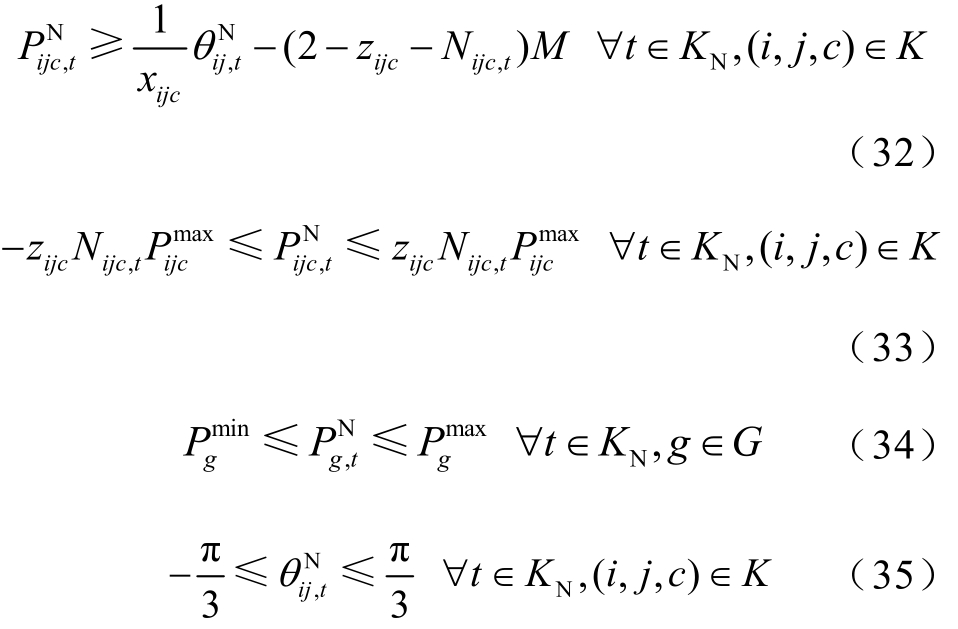
式中，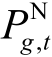 
、 
、
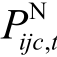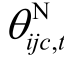分别为当线路t退出运行时，发电机g的有功出力、线路i-j-c上的有功潮流值和节点 i、j之间的相位差；t为线路编号；Nijc,t为常量，当线路i-j-c的编号恰好为t时取0，表示此时考虑该线路的N-1工况，否则取1。式（30）保证了N-1工况下各节点的有功平衡；式（31）～式（33）为N-1工况下的线路潮流约束，当且仅当zijc＝Nijc,t＝1时，即该条线路正在运行，且考虑其他线路的 N-1工况，该条线路上的潮流等于首末节点相位差与线路电抗的比值；式（34）和式（35）分别为N-1工况下的发电机出力及节点相位差上、下限约束；式（30）～式（35）共同防止了系统在任意N-1工况下出现线路潮流过载，即保证系统满足N-1安全性的要求。
综上所述，限制短路电流的网络结构优化模型为
由式（36）可知，作为网架调整方案的关键表征，线路开断决策变量zijc贯穿所建模型中的目标函数和各主要约束集。不同的是，在潮流约束和 N-1安全约束集中，zijc表征线路开断；而短路电流约束和连通约束中，zijc表征的分别是“伴随”等效电路中支路和网络流中边的开断。
3 限制短路电流的OTS模型的求解
3.1 模型预处理
本文建立的限制短路电流的 OTS模型是一个典型的 MILP模型。随着系统规模的增大及系统中短路电流越限节点数目的增多，决策空间将剧烈增长。求解模型时需要大量的计算资源和较长的计算时间，不利于在大规模电力系统中的应用。因此有必要对模型预处理，缩小决策空间以提高模型的求解效率。
3.1.1 问题节点集NS的确定
对电网中任意节点而言，切除部分线路，短路电流显然只能是减小或保持不变。由于本文所提模型对问题节点集NS中每一个节点均建立一套约束，若问题节点集中节点过多，则将产生大量无意义的短路电流约束。实际电网运行时，几乎不存在电网整体短路电流均越限的情况，因此预先计算各节点的短路电流值，对节点进行筛选，将需要关注短路电流的问题节点挑选出来，能够缩小问题节点集NS的规模，从而大大减少模型中的约束条件数量，有效地提高模型求解的计算效率。
3.1.2 有效开断线路集的确定
通过合理缩小开断线路集合，可以有效地提高OTS模型的计算速度[28]。原网架中通常存在部分辐射型线路，开断后会产生两个孤立系统。即使存在连通性约束保证开断线路后系统不产生孤岛，但这些线路所构成的开断组合仍会占用大量求解空间，大大降低模型的求解效率。实际上，基于电网 N-1安全性的要求，任意节点度小于3的带负荷节点所连线路均不应被开断。
除去电网中的不可开断线路，网架中还往往存在与问题节点间电气距离很远的某些节点，切除这部分节点间的线路，对限制问题节点短路电流水平的贡献很小，则该部分线路可视为低效开断线路。出于模型求解效率和工程实用性的考虑，在模型优化求解过程中忽略低效开断线路是合理且可以接受的。其中，根据叠加原理可知，电力系统节点i、j之间的电气距离可定义为两点之间等值阻抗Zij,equ，即[29]
式中，Zij为系统节点阻抗矩阵第i行第j列元素。
同时，定义节点 i与所有问题节点的电气耦合程度 Di为
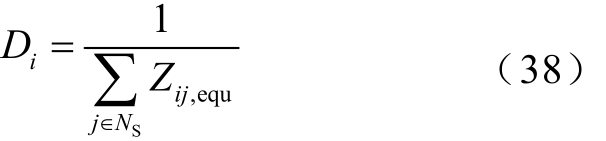
式（38）可以定量描述系统中任一节点与所有问题节点间电气耦合程度的强弱。Di值越小，表明节点 i与所有问题节点的电气耦合作用越弱。通过计算任一节点与问题节点间的电气距离及电气耦合程度，并依据电气耦合程度进行从小到大排序，筛选出前m个节点，则该m个节点间所连线路均视为低效开断线路。
因此，对于所有线路集合K而言，存在子集K*为允许开断线路集，同时存在子集K#为有效开断线路集，且满足K#⊆K*⊆K，如图4所示。
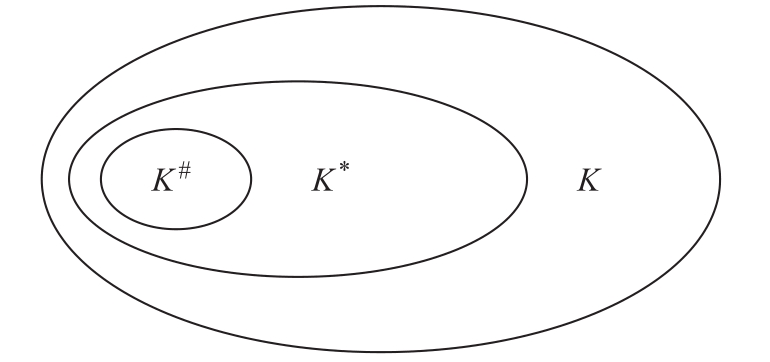
图4 不同的线路开断集合
Fig.4 Different sets of switching branches
3.2 求解算法
本文具体计算流程如图5所示。
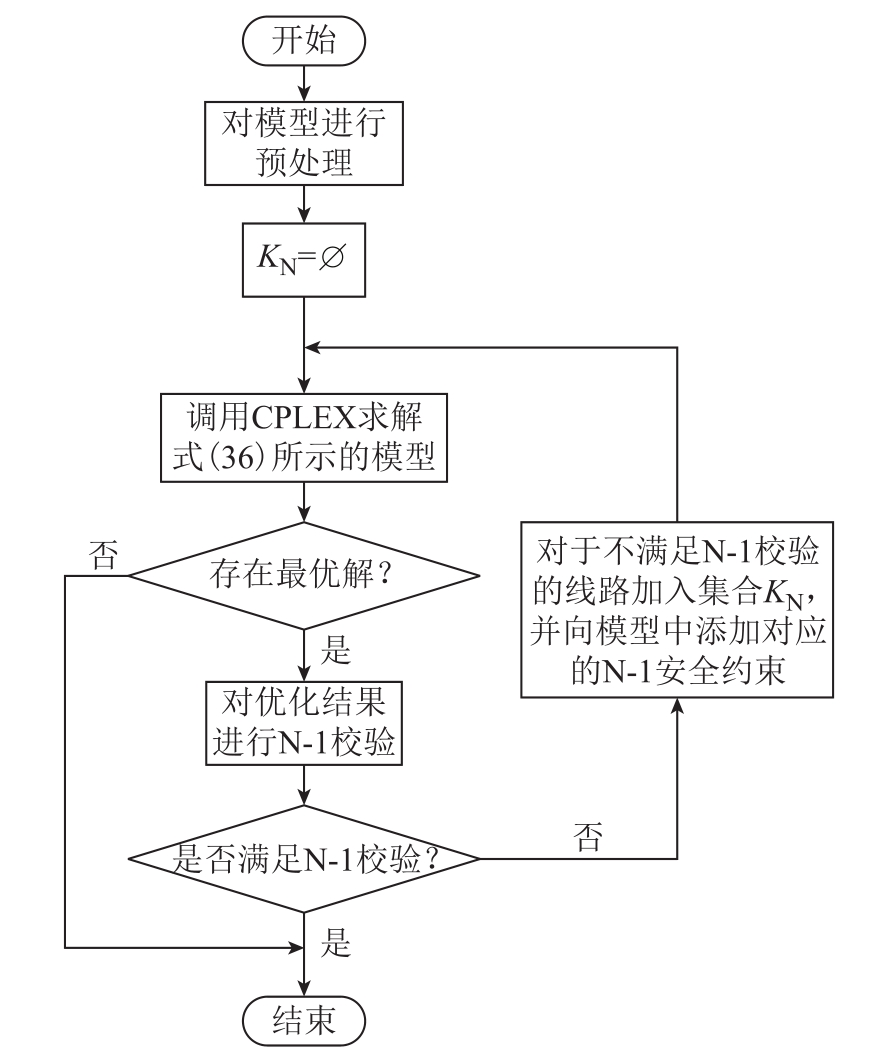
图5 求解算法流程
Fig.5 Flow chart of solving algorithm
由于网络结构优化方案需满足基本的静态安全约束，但直接向模型中添加所有线路的N-1安全约束将大大降低模型的计算速度，模型的求解时间难以满足工程需求。因此，本文采用首先不向模型中加入任何N-1安全约束，并对优化方案中不满足N-1校验的线路添加对应线路的N-1约束的方法[21]，反复进行迭代求解，直至获得一个既能够起到短路电流限制作用，又满足 N-1安全性的网架优化方案。
4 算例分析
本文采用修改的IEEE 30节点系统和IEEE 118节点系统为算例，验证所提模型和方法的有效性和求解效率。模型预处理在Matlab平台进行，而具体优化模型搭建在 GAMS平台，工程 MIP求解器设定为 CPLEX。计算平台为 PC，配置为 Intel（R）Core（TM）i5-4590 CPU，安装内存为8 GB。同时，虽然模型对节点设置不同短路电流耐受水平具有通用性，但为了便于展示，算例部分假定各节点具有相等的短路电流限值。
4.1 算例一
首先采用修改的IEEE 30节点系统[21]进行测试，系统结构如图 6所示。该系统包含 30个节点，42条线路，6台机组。假定各节点短路电流限值均为12kA。发电机的发电成本设置在 0.217~5.882$/(MW·h)，线路的开断成本设置为10$/条。由于系统规模较小，无需考虑有效开断线路集合的影响。模型简单预处理后，短路电流越限的问题节点为节点2、6和22。
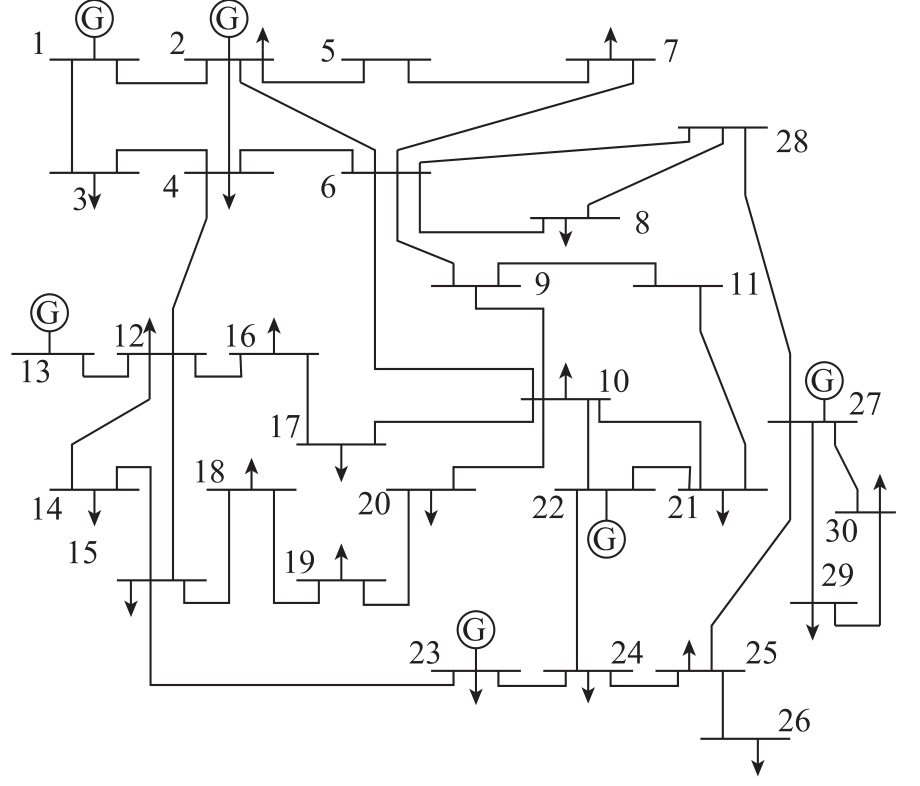
图6 修改的IEEE 30节点系统图
Fig.6 Diagram of the modified IEEE 30-bus system
在针对N-1安全性要求进行三次迭代之后，最终得到断开两条线路（2-6-1和 4-6-1）的最优开断线路组合，成功地将各节点的短路电流限制到12kA以下。线路开断前后节点的短路电流水平如图7所示。由图7可知，通过本文方法开断小部分线路，就能够有效降低节点短路电流水平，且不会使任何节点的短路电流升高，并且在图7中最下方的两条实线和虚线完全重合，表明本文所提方法与经典的节点导纳矩阵求逆法的计算结果相同，证明了本文模型和算法的准确性。这主要是由于本文提出的短路电流约束显式线性映射并无化简过程，因此优化过程中没有引入额外的计算误差。
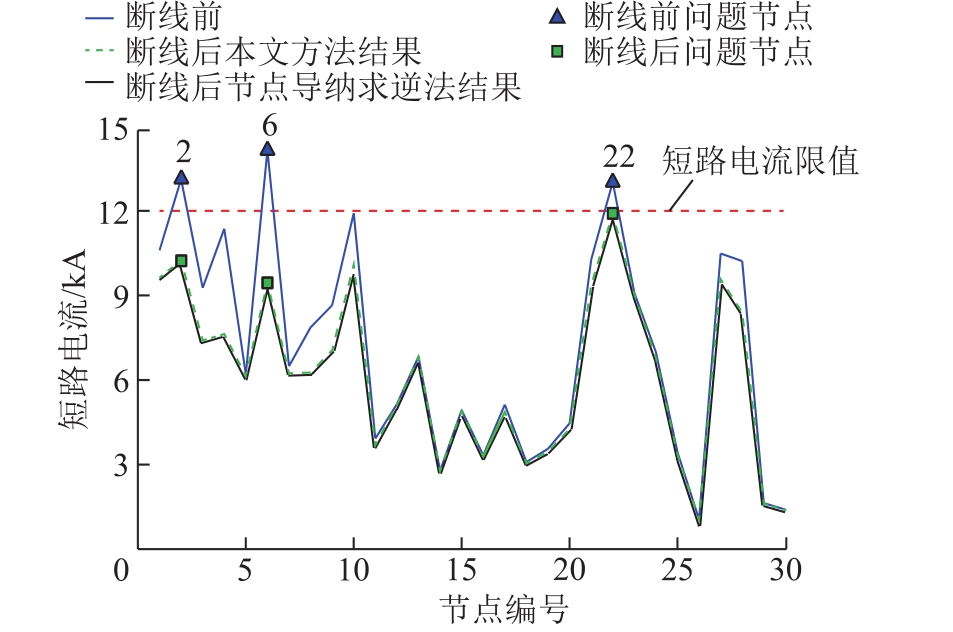
图7 修改的IEEE 30节点系统的短路电流水平
Fig.7 SCC magnitude of the modified IEEE 30-bus system
通常，发电机出口短路会产生很大的短路电流，但观察图7发现，节点13虽为发电机节点，但其短路电流水平远远低于其他发电机节点，甚至低于部分非发电机节点；而节点6为非发电机节点，但其短路电流水平在开断线路前为该系统中的最大值。基于通过开断部分线路，减小节点与发电机组之间的电气联系，从而降低某些节点的短路电流水平的思路，本文进一步基于式（37）通过电气距离[29]对节点6和节点13进行分析，见表1、表2。
表1 线路开断前发电机节点之间的电气距离
Tab.1 Electrical distance between generator nodes before switching lines
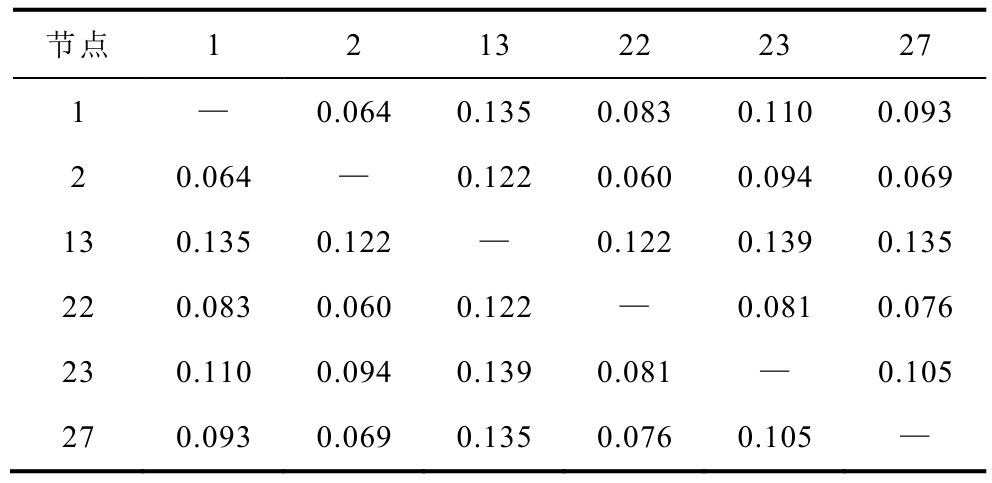
节点 1 2 13 22 23 27 1 — 0.064 0.135 0.083 0.110 0.093 2 0.064 — 0.122 0.060 0.094 0.069 13 0.135 0.122 — 0.122 0.139 0.135 22 0.083 0.060 0.122 — 0.081 0.076 23 0.110 0.094 0.139 0.081 — 0.105 27 0.093 0.069 0.135 0.076 0.105 —
表2 节点6与各发电机节点间的电气距离
Tab.2 Electrical distance between node 6 and each generator node
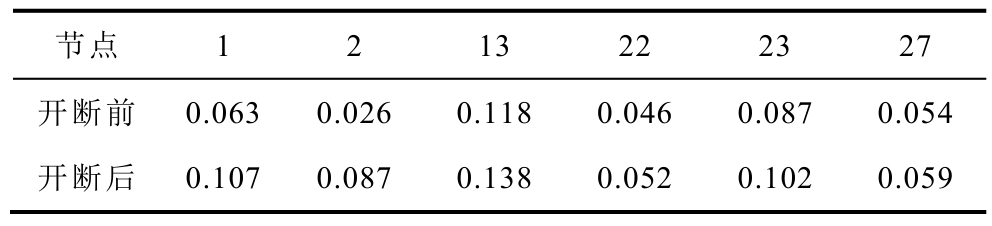
节点 1 2 13 22 23 27开断前 0.063 0.026 0.118 0.046 0.087 0.054开断后 0.107 0.087 0.138 0.052 0.102 0.059
由表1可知，相较于其他发电机节点而言，节点13与其他发电机节点间的电气距离均很远，导致该节点的短路电流水平主要源于该节点所接发电机组的贡献；当节点13短路时，由于电气距离很远，其他发电机节点流入节点 13的短路电流很小。因此，节点的短路电流水平主要与其和各发电机节点间的电气距离有关，并不是所有发电机节点的短路电流水平一定都处于系统中的较高水平。
同时，表2表明开断线路前节点6与各发电机节点间的电气距离值均相对较小。当节点6短路时，各发电机组均会产生很大的短路电流汇集到节点 6，因此该节点的短路电流水平很高，且从系统结构图分析，开断线路前节点6所连线路有7条，与各节点联系紧密，属于系统中最重要的节点之一。而通过开断线路，减小了节点6与各发电机组间的电气联系，从而有效地降低了节点6的短路电流水平。
此外，在模型的三次迭代求解过程中，第一次迭代后，发现线路9-11-1和11-21-1的开断不满足N-1要求，故向模型中添加如式（30）～式（35）的线路9-11-1、11-21-1的N-1安全约束；第二次迭代后，发现线路6-9-1和28-27-1的开断不满足N-1要求，故继续向模型中添加如式（30）～式（35）的线路6-9-1、28-27-1的N-1安全约束，最终得到满足N-1要求的优化结果。具体计算结果见表3。
表3 修改的IEEE 30节点系统模型的迭代过程
Tab.3 Iteration process of the model in the modified IEEE 30-bus system
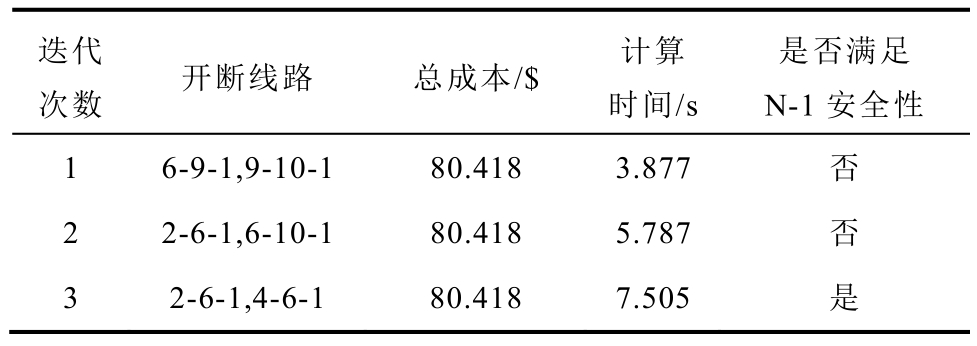
迭代次数 开断线路 总成本/$ 计算时间/s是否满足N-1安全性1 6-9-1,9-10-1 80.418 3.877 否2 2-6-1,6-10-1 80.418 5.787 否3 2-6-1,4-6-1 80.418 7.505 是
算例一的规模相对较小，通过迭代得到最优解的时间也较短。若系统规模扩大，随之而来的计算代价将无法估量，因此有必要对模型进行预处理。
4.2 算例二
为进一步证明本文方法的有效性以及说明模型预处理的作用，采用修改的IEEE 118节点系统[21,30]进行测试。修改的IEEE 118系统包含118个节点，185条线路，19台机组。假定各节点短路电流承受水平均为 24kA。发电机的发电成本设置在 0.19~10$/(MW·h)，线路的开断成本仍设置为10$/条。
模型求解前对模型进行预处理。其中，短路电流越限的问题节点为节点49、65、66和68，不可开断线路共65条，低效开断线路共36条。将余下的84条线路作为有效开断线路集，并对模型进行优化求解。
由图8可知，若对开断线路总数不加限制，则可通过一次迭代就得到满足N-1要求的断开两条线（38-65-1和65-66-1）的最优断线组合，成功地将各节点的短路电流限制到 24kA以下。同时，为进一步说明本文方法的准确性，将本文方法与经典的节点导纳矩阵求逆法的短路电流计算结果进行对比，见表 4。由于篇幅限制，本文简单取各短路电流越限节点为对象。
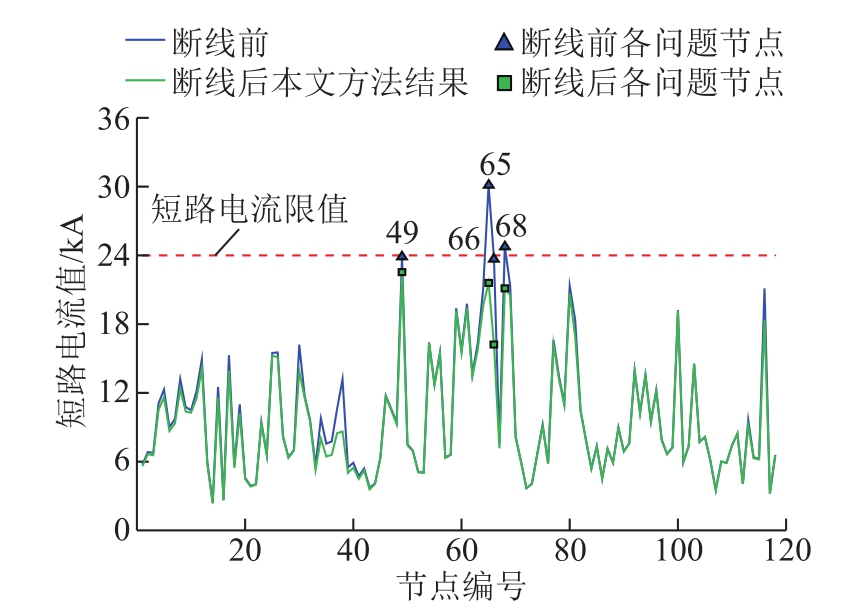
图8 修改的IEEE 118节点系统的短路电流水平
Fig.8 Short circuit current magnitude of the modified IEEE 118-bus system
表4 本文方法与求逆法的计算结果对比
Tab.4 Comparison of calculation results between the method in this paper and the inversion method（单位：kA）
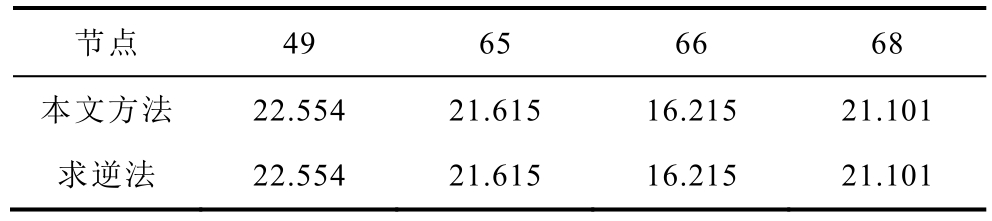
节点 49 65 66 68本文方法 22.554 21.615 16.215 21.101求逆法 22.554 21.615 16.215 21.101
表4进一步表明，相较于近似线性化的方法[21]，本文方法与经典的节点导纳矩阵求逆法给出的结果一致，即所提出的显式线性映射是严格的，并未引入误差。
此外，通过设置不同的断线总数，还可以得到满足N-1要求的不同的断线组合。对断线数设置为2、3、4的模型求解结果进行比较，具体计算结果见表5。由表5可知，38-65-1和65-66-1的开断线路组合是本算例中较优的优化结果，在开断成本、迭代次数、计算时间以及对短路电流的限制上均有明显的优势。随着迭代次数的增多，模型的求解速度也将大幅降低。
表5 修改的IEEE 118节点系统不同断线数的计算结果
Tab.5 Calculation results of different switching lines number in the modified IEEE 118-bus system
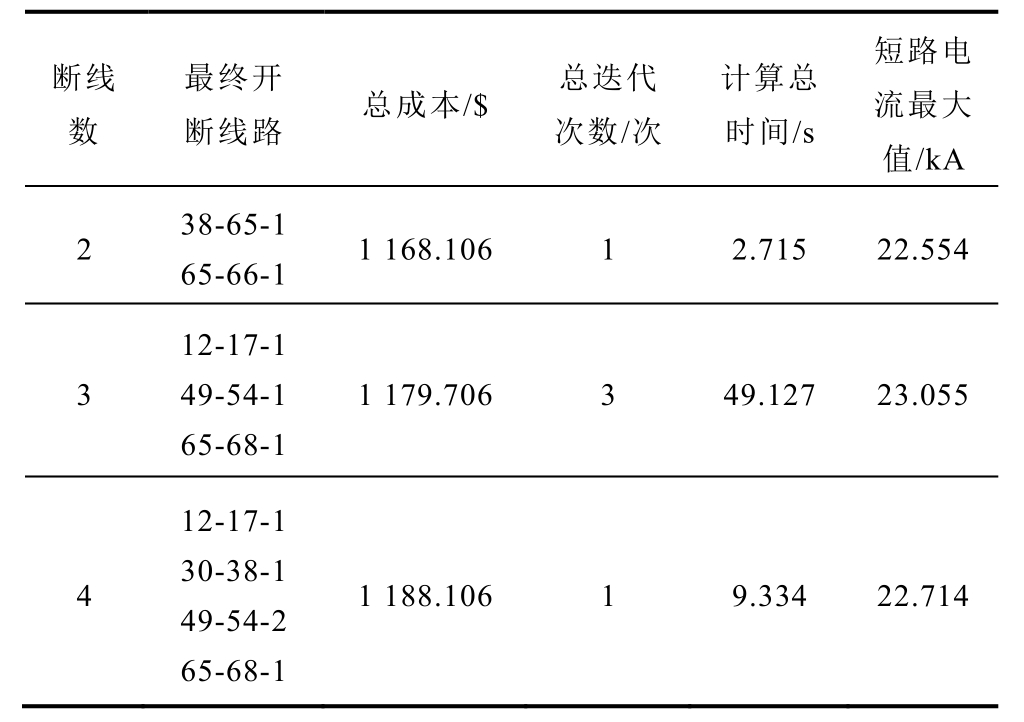
断线数最终开断线路 总成本/$ 总迭代次数/次计算总时间/s短路电流最大值/kA 2 38-65-1 65-66-1 1 168.106 1 2.715 22.554 3 12-17-1 49-54-1 65-68-1 1 179.706 3 49.127 23.055 4 12-17-1 30-38-1 49-54-2 65-68-1 1 188.106 1 9.334 22.714
为说明本文预处理的作用，取断线数设置为4，对模型分别进行预处理和不进行预处理，比较模型的求解速率和优化结果见表 6。由表6可知，模型预处理通过缩小决策空间，能够明显减少求解时的迭代次数以及每次迭代的计算效率，大大减少计算时间，且不牺牲计算结果的最优性。
表6 模型预处理的计算结果比较
Tab.6 Comparison of calculation results with model preprocessing
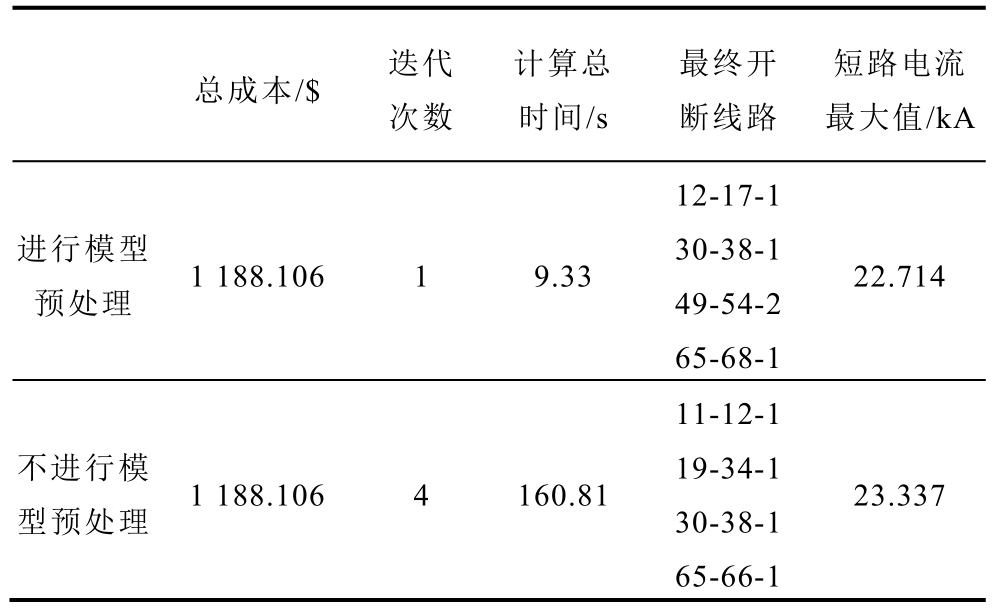
总成本/$ 迭代次数计算总时间/s最终开断线路短路电流最大值/kA进行模型预处理 1 188.106 1 9.33 12-17-1 30-38-1 49-54-2 65-68-1 22.714不进行模型预处理 1 188.106 4 160.81 11-12-1 19-34-1 30-38-1 65-66-1 23.337
由表 5、表 6的计算结果可见，采用本文方法后能在有效时间内对模型进行求解，证明了本文求解策略对较大规模系统的有效性，且能在较少迭代次数中消除短路电流越限，具有工程应用价值。本文从原理上对线路开断与短路电流约束的关系进行推导，且未做近似，可以证明其高计算精度。此外，相较于现有方法[21-22]，本文方法可在相当的计算时间内给出最优方案；而且基于提出的短路电流约束显式线性建模思路，本文方法具有灵活性等方面的优势。
5 结论
本文基于节点自阻抗的物理意义，提出通过构造与原电网相似拓扑、不同参数的“伴随网络”，实现线路开断与短路电流约束之间显式线性关系表达的新思路，避免了线性化过程带来的误差问题以及非线性约束求解困难的问题。此外，针对建立的模型因约束和变量数量增加而带来的求解困难问题，从不同方面提出约束集削减策略及方法，有效降低了求解规模，提高了模型的求解效率。
算例结果表明，本文方法对于一定规模的电力系统的求解速度满足工程要求，在牺牲了一定快速性的同时提高了算法的准确性。同时，由于所提出的短路电流的线性建模方法中，线路开断决策变量显性贯穿各类约束集，且有效避免了节点导纳矩阵求逆的过程，不仅适用于正常的网架完整情况，也为研究系统网架拓扑不完整，特别是节点数不确定场景下的短路容量约束提供了可能。因此，下一步工作内容是探索本文提出的短路电流约束建模方法在电网特殊工况中的应用。
[1] 陈庆国, 诸葛祥丽, 刘贺千, 等. 采用纳米改性纸板的换流变压器出线装置电场分布[J]. 电机与控制学报, 2016, 20(1): 29-34.Chen Qingguo, Zhuge Xiangli, Liu Heqian, et al.Electric field distribution of converter transformer barrier system using nano modified pressboard[J].Electric Machines and Control, 2016, 20(1): 29-34.
[2] 刘凯, 陈红坤, 林军, 等. 故障限流器在电力系统中应用研究现状[J]. 电力系统保护与控制, 2010,38(7): 147-151.Liu Kai, Chen Hongkun, Lin Jun, et al. Study situation of applications of fault current limiter in power system[J]. Power System Protection and Control, 2010,38(7): 147-151.
[3] 艾琳, 冯艳虹, 陈为化, 等. 特高压接入京津冀北500kV电网短路电流问题及限流措施研究[J]. 电力系统保护与控制, 2017, 45(9): 133-137.Ai Lin, Feng Yanhong, Chen Weihua, et al. Research on short-circuit current problem and limiting measures caused by UHV substation connecting to 500 kV network in Beijing-Tianjin area and Northern Hebei[J].Power System Protection and Control, 2017, 45(9):133-137.
[4] 兰生, 胡忠平, 廖福旺, 等. 短路电动力对变压器低压绕组辐向稳定性的研究[J]. 电机与控制学报,2018, 22(5): 19-24.Lan Sheng, Hu Zhongping, Liao Fuwang, et al. Radial stability of transformer low voltage windings under sudden short-circuit[J]. Electric Machines and Control,2018, 22(5): 19-24.
[5] 张立晖, 石晶, 严思念, 等. 磁通约束型超导限流开关系统应用[J]. 电工技术学报, 2018, 33(22):5292-5299.Zhang Lihui, Shi Jing, Yan Sinian, et al. System application of flux-coupling superconducting fault current limiting switch[J]. Transactions of China Electrotechnical Society, 2018, 33(22): 5292-5299.
[6] 刘海波, 王浩, 刘树枫, 等. 节能型故障限流器的应用研究[J]. 电气技术, 2018, 19(7): 33-38.Liu Haibo, Wang Hao, Liu Shufeng, et al. Application research of an energy saving fault current limiter[J].Electrical Engineering, 2018, 19(7): 33-38.
[7] 韩戈, 韩柳, 吴琳. 各种限制电网短路电流措施的应用与发展[J]. 电力系统保护与控制, 2010, 38(1):141-144.Han Ge, Han Liu, Wu Lin. Application and development of methods on limiting power grid’s short-circuit current[J]. Power System Protection and Control, 2010, 38(1): 141-144.
[8] 王毅, 张宁, 康重庆, 等. 电力用户行为模型:基本概念与研究框架[J]. 电工技术学报, 2019, 34(10):2056-2068.Wang Yi, Zhang Ning, Kang Chongqing, et al.Electrical consumer behavior model: basic concept and research framework[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2056-2068.
[9] 贾雨龙, 米增强, 余洋, 等. 计及不确定性的柔性负荷聚合商随机-鲁棒投标决策模型[J]. 电工技术学报, 2019, 34(19): 4096-4107.Jia Yulong, Mi Zengqiang, Yu Yang, et al. Stochasticrobust decision-making model for flexible load aggregator considering uncertainties[J]. Transactions of China Electrotechnical Society, 2019, 34(19):4096-4107.
[10] 杨知方, 钟海旺, 夏清, 等. 输电网结构优化问题研究综述和展望[J]. 中国电机工程学报, 2016,36(2): 426-434.Yang Zhifang, Zhong Haiwang, Xia Qing, et al.Review and prospect of transmission topology optimization[J]. Proceedings of the CSEE, 2016, 36(2):426-434.
[11] Mazi A, Wollenberg B, Hesse M. Corrective control of power system flows by line and bus-bar switching[J]. IEEE Transactions on Power Systems,1986, 1(3): 258-264.
[12] Shao W, Vittal V. Corrective switching algorithm for relieving overloads and voltage violations[J]. IEEE Transactions on Power Systems, 2005, 20(4): 1877-1885.
[13] Bacher R, Glavitsch H. Loss reduction by network switching[J]. IEEE Transactions on Power Systems,1988, 3(2): 447-454.
[14] Fisher E B, O'neill R P, Ferris M C. Optimal transmission switching[J]. IEEE Transactions on Power Systems, 2008, 23(3): 1346-1355.
[15] Khodaei A, Shahidehpour M. Transmission switching in security-constrained unit commitment[J]. IEEE Transactions on Power Systems, 2010, 25(4): 1937-4195.
[16] Ostrowski J, Wang J, Liu C. Transmission switching with connectivity-ensuring constraints[J]. IEEE Transactions on Power Systems, 2014, 29(6): 2621-2627.
[17] 张永康, 蔡泽祥, 李爱民, 等. 限制 500kV 电网短路电流的网架调整优化算法[J]. 电力系统自动化,2009, 33(22): 34-39.Zhang Yongkang, Cai Zexiang, Li Aimin, et al. An optimization algorithm for short-circuit current limitation of 500 kV power grid by adjusting power grid configuration[J]. Automation of Electric Power Systems, 2009, 33(22): 34-39.
[18] 黄根, 罗滇生, 李帅虎, 等. 基于综合灵敏度分析限流的最优断线措施[J]. 电网技术, 2016, 40(1):309-315.Huang Gen, Luo Diansheng, Li Shuaihu, et al. Optimal line-outage measure based on comprehensive sensitivity analysis to limit short-circuit current[J].Power System Technology, 2016, 40(1): 309-315.
[19] 应林志, 刘天琪, 王建全, 等. 基于改进蚁群优化限制短路电流的网架调整措施[J]. 电力系统自动化, 2018, 42(1): 144-150.Ying Linzhi, Liu Tianqi, Wang Jianquan, et al.Adjustment for power grid configuration to limit short-circuit current based on improved ant colony optimization[J]. Automation of Electric Power Systems, 2018, 42(1): 144-150.
[20] 田士君, 王秀丽, 齐世雄, 等. 计及短路电流限额的网架优化模型及启发式算法[J]. 西安交通大学学报, 2019, 53(9): 102-109.Tian Shijun, Wang Xiuli, Qi Shixiong, et al. Optimal transmission switching considering short circuit current limitation and heuristic algorithm[J]. Journal of Xi'an Jiaotong University, 2019, 53(9): 102-109.
[21] Yang Zhifang, Zhong Haiwang, Xia Qing, et al.Optimal transmission switching with short-circuit current limitation constraints[J]. IEEE Transactions on Power Systems, 2016, 31(2): 1278-1288.
[22] 覃岭, 林济铿, 戴赛, 等. 计及短路电流约束的机组组合问题[J]. 中国电机工程学报, 2016, 36(22):6049-6058.Qin Ling, Lin Jikeng, Dai Sai, et al. Short circuit constrained unit commitment[J]. Proceedings of the CSEE, 2016, 36(22): 6049-6058.
[23] 张伯明, 陈寿孙, 严正. 高等电力网络分析[M]. 北京: 清华大学出版社, 2007.
[24] 杨超, 梁海平, 顾雪平, 等. 多直流馈入异步受端电网恢复的分区方法[J]. 电力系统自动化, 2019,43(10): 162-175.Yang Chao, Liang Haiping, Gu Xueping, et al.Partition method for restoration of asynchronous receiving end power grid with multi-infeed HVDC[J].Automation of Electric Power Systems, 2019, 43(10):162-175.
[25] 顾雪平, 周光奇, 李少岩. 计及系统可观测性的网络化简与黑启动分区方案制定[J]. 电力系统自动化, 2019, 43(20): 114-128.Gu Xueping, Zhou Guangqi, Li Shaoyan. Network simplification and formation of black-start zone partitioning scheme considering system observability[J].Automation of Electric Power Systems, 2019, 43(20):114-128.
[26] 肖峻, 肖居承, 张黎元, 等. 配电网的严格与非严格安全边界[J]. 电工技术学报, 2019, 34(12): 2637-2648.Xiao Jun, Xiao Jucheng, Zhang Liyuan, et al. Strict and non-strict security boundary of distribution network[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2637-2648.
[27] 顾雪平, 刘雨濛, 王涛, 等. 基于结构平衡理论的电网自组织临界态辨识[J]. 电工技术学报, 2018,33(17): 4136-4145.Gu Xueping, Liu Yumeng, Wang Tao, et al. Self -organized critical state identification of power systems based on structural equilibrium theory[J].Transactions of China Electrotechnical Society, 2018,33(17): 4136-4145.
[28] Liu C, Wang J, Ostrowski J. Heuristic prescreening switchable branches in optimal transmission switching[J]. IEEE Transactions on Power Systems,2012, 27(4): 2289-2290.
[29] 谭玉东, 李欣然, 蔡晔, 等. 基于电气距离的复杂电网关键节点识别[J]. 中国电机工程学报, 2014,34(1): 146-152.Tan Yudong, Li Xinran, Cai Ye, et al. Critical node identification for complex power grid based on electrical distance[J]. Proceedings of the CSEE, 2014,34(1): 146-152.
[30] Blumsack S. Network topologies and transmission investment under electric-industry restructuring[D].Pittsburgh, PA, USA: Carnegie Mellon University,2006.