0 引言
随着新能源的大量并网运行、“西电东送”战略的实施以及大城市配电网的升级改造,传统交流输电技术已越来越不适应现代电力工业的发展。基于电压源型换流器(Voltage Sourced Converter, VSC)的多端柔性直流(Voltage Source Converter Multi-Terminal DC, VSC-MTDC)输电技术以其较高的灵活性、经济性和可靠性[1-4],在新电源并网运行、大容量远距离电能输送以及新增城市直流配电网等领域有着广泛的应用前景[5-7]。
相比于两端高压直流输电,VSC-MTDC系统控制策略更加复杂,控制方式也更灵活多变[8]。电压下垂控制的优势在于进行功率调节时不依赖于通信系统,可以确保每个具备功率调节能力的换流站都能参与不平衡功率的调节,提高系统的稳定性[9]。文献[9]提出了一种适用于功率共享的自适应下垂控制方法,针对换流站功率裕度的不同实现不平衡功率的灵活分配,但未考虑多个换流站间直流电压的误差会导致某一换流站直流电压达到允许的波动极限时其余换流站仍存在较大可用功率容量。文献[10]分析了直流电压偏差控制策略和直流电压斜率控制策略的优点和缺点,结合两种控制策略的优点,提出了一种新型的直流电压偏差斜率控制策略,实现了换流站直流功率的跟踪,具备较好的动态响应能力。文献[11]提出了一种包含功率共享的通用直流电压下垂控制策略,采用分层控制结构,结合三种控制模式,提高了电压下垂控制的功率共享能力,增强了系统的可操作性。文献[12]提出了一种基于功率共享指数的新型控制方法,可以实现功率的准确控制,当通信中存在一定的延迟时系统仍能保持稳定运行。文献[13]提出了一种改进直流电压下垂控制策略,同时引入一个公共直流参考电压参与下垂控制换流站的功率调整,但未考虑主站故障退出运行后直流电压波动超过最大限定值时的情况。文献[14]提出一种新型的直流电压斜率控制策略,采用包含处理层和执行层的分层控制方式来实现不平衡功率的最优分配,但需要依赖通信系统。以上文献在换流站间的功率协调方面都做出了很多突出贡献,但忽略了换流站间的直流电压误差对功率调节的影响。在功率的输送过程中会在输电线路上产生电压降落,导致换流站间存在一定的直流电压误差。在不应用通信系统的前提下,当以直流电压作为控制系统的全局信号时,换流站间的直流电压误差会降低不平衡功率分配的准确性,易导致部分换流站满载和直流电压越限等问题。在控制策略中应用通信可以实现很多功能,例如电力系统的全局优化使得经济成本最低、系统损耗最小等。但当通信中断时同样易导致部分换流站满载和直流电压越限等问题,而在柔性直流配电网中,因考虑投资成本等原因没有装设通信设备,因此,侧重于研究依据换流站的本地控制器来实现多个换流站之间的功率协调控制具有重要意义[15-19]。
针对 VSC-MTDC系统中无需通信或当通信中断的情况下多个换流站间功率协调控制的问题,提出了计及换流站间电压误差的自适应下垂控制策略。所提控制策略通过下垂系数的灵活调节,降低了换流站间电压误差对功率调节的影响,提高了按功率裕度分配不平衡功率的准确性,可以最大限度地利用换流站的有功功率容量,维持直流侧电压稳定。同时,该控制策略显著降低了直流电压波动,且在调节速度方面具备一定优势。
1 VSC-MTDC系统模型
四端柔性直流输电系统结构如图1所示。Gi(i=1,2, …, 4)为交流系统,Rs、Ls分别为交流侧的等效电阻和电感,Load为等效负荷,VSCi 为直流电网的换流站,Pi为换流站发出的有功功率,以注入直流电网为参考正方向。
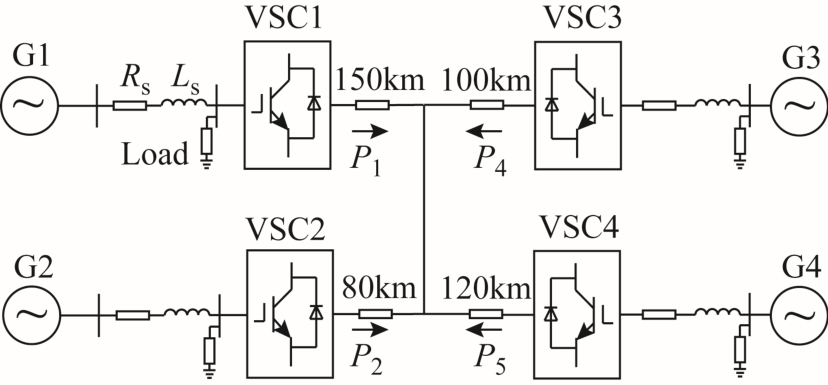
图1 四端柔性直流输电系统结构
Fig.1 Structure diagram of four-terminal VSC-MTDC transmission system
在 VSC-MTDC系统的整体协调控制中,选取一部分具备有功功率调节能力的换流站采用下垂控制,标记为 VSC1~VSCm,承担系统中的不平衡功率;其余换流站采用定有功功率控制,标记为VSC(m+1)~VSCn,主要用于新能源接入和向无源网络供电等。
模块化多电平变流器(Modular Multilevel Converter, MMC)拓扑结构如图2所示,Usj(j=a,b,c)为换流站所连交流系统的相电压,Uj为换流站三相输出点电压;Rarm、Larm分别为MMC桥臂电阻和电感。MMC三相中每一相都可分成上、下桥臂,每个桥臂由桥臂电阻、电感和 N个子模块(Sub-Module,SM)构成。每个子模块由两个带有反并联二极管的IGBT和一个并联电容Csm构成。
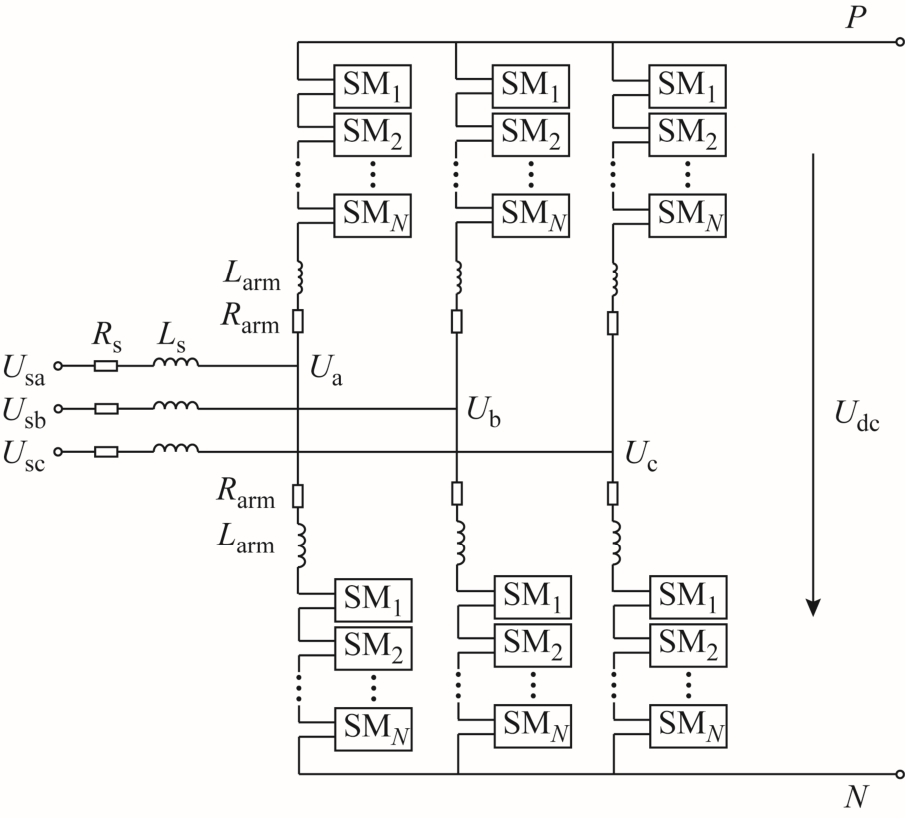
图2 MMC拓扑结构
Fig.2 MMC topological structure diagram
根据基尔霍夫电压定律得到换流站交流侧方程为
式中,Rm为MMC桥臂电阻和交流侧电阻串联后的等效电阻;Lm为MMC桥臂电感和交流侧电感串联后的等效电感;isj为交流系统输入到MMC换流站的电流。将式(1)从abc坐标系转换到dq旋转坐标系,变为
式中,id、iq分别为交流系统输入到MMC换流站电流矢量的d、q轴分量;Usd、Usq分别为交流系统相电压矢量的 d、q轴分量;Ud、Uq分别为换流站交流侧电压矢量的d、q轴分量;ω为电网电压矢量同步旋转角速度。
2 自适应下垂控制
在自适应下垂控制策略下,定义换流站可用功率变化量的绝对值|Pcan|为换流站的功率裕度。换流站可用功率变化量Pcan为
式中,Pdcmax为换流站的额定有功功率;P0为进行功率调节之前换流站的稳态有功功率;ΔUdc为换流站直流电压变化量,其表达式为
式中,Udc为换流站直流电压实时测量值;U0为进行功率调节之前的稳态直流电压。
设定采用自适应下垂控制换流站的下垂系数 K与换流站可用功率变化量Pcan成正比,目的是在直流电压变化量相同的情况下,可以使不平衡功率根据换流站的功率裕度进行合理分配;同时设定在直流电压达到允许的波动极限时所有采用自适应下垂控制的换流站同时达到满载状态,目的是最大限度地利用换流站的有功功率容量,将直流电压限制在允许范围内,则下垂系数K应满足
式中,H为符合设定的一个常数;Ucan为允许的直流电压变化量,其表达式为
式中,Udcmin和Udcmax分别为直流电压允许运行范围的下限、上限。
令下垂系数 K根据式(5)中的两个端点按Δ U dc的λ次非线性变化,则其表达式为
以 ΔUdc为自变量对式(7)积分可得换流站有功功率指令值变化量ΔP为
式中,C为积分常数。
ΔP应满足
结合式(7)~式(9)可得
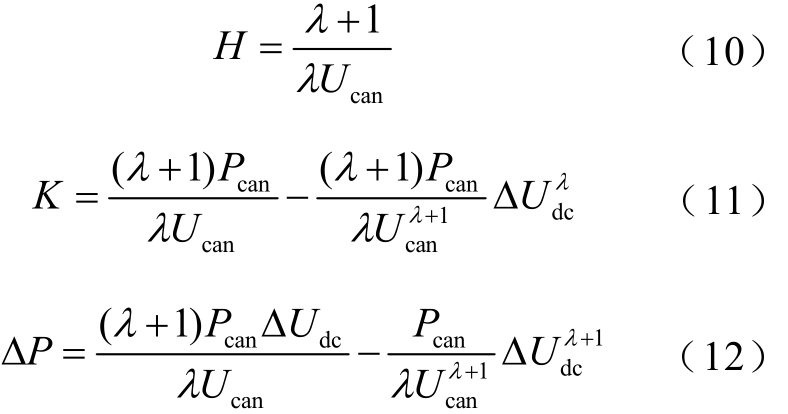
则换流站有功功率指令值Pref为
当λ=1时,即下垂系数K根据式(5)中的两个端点线性变化,将λ=1分别代入式(11)和式(12),可得
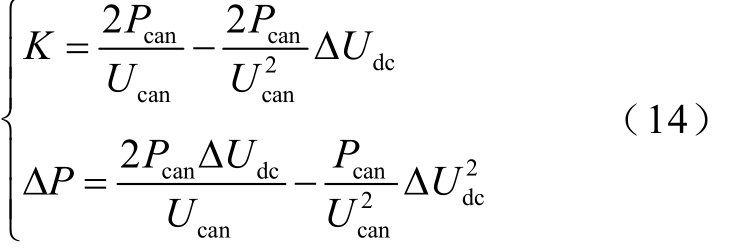
同理,作为对比,将 λ=0.5 代入式(11)和式(12),可得
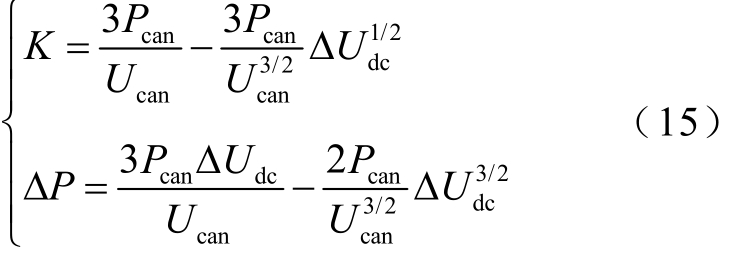
将λ= 2代入式(11)和式(12)得
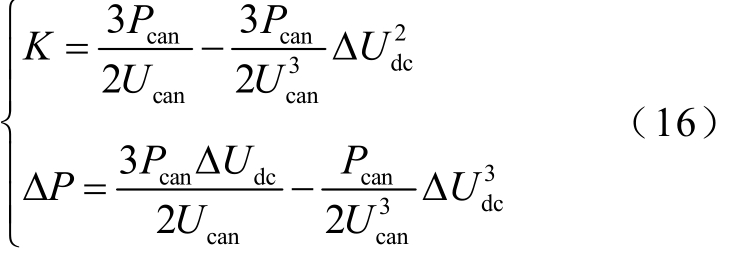
图 3为自适应下垂控制示意图。可以看出,λ的物理意义是以式(5)的两个端点作为边界条件,确定功率变化量 ΔP跟随电压变化量 ΔUdc的变化速率,即K值的变化。当换流站未满载时,自适应下垂控制较文献[9]方法在对应相同的ΔP时具备较小的ΔUdc,可以在功率调节过程中降低直流电压波动;且当ΔUdc接近Ucan时,采用自适应下垂控制的换流站更接近满载,降低了换流站间直流电压误差对功率调节的影响,更加充分地利用了换流站的有功功率容量。
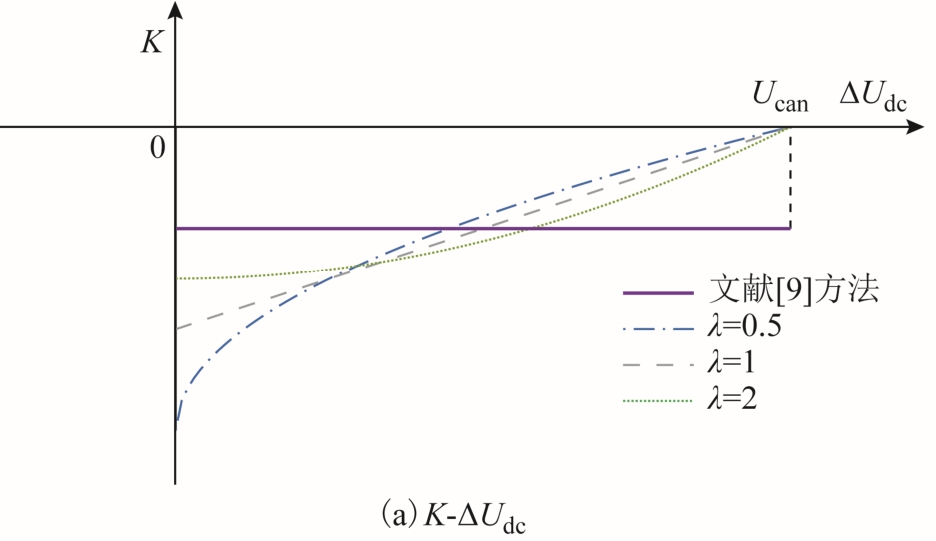
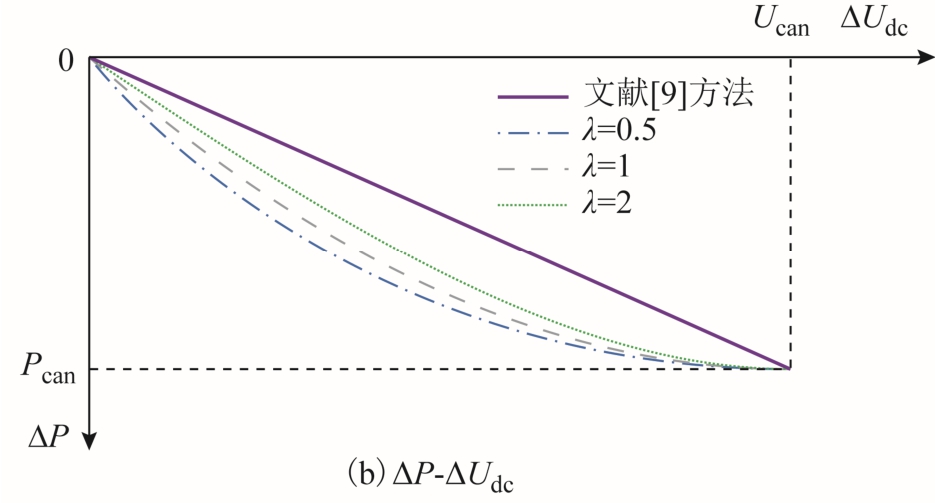
图3 自适应下垂控制示意图
Fig.3 Adaptive droop control schematic diagram
图 4为自适应下垂控制流程,Udm为调整有功功率指令值的电压阈值,目的是防止有功功率指令值的频繁调整。
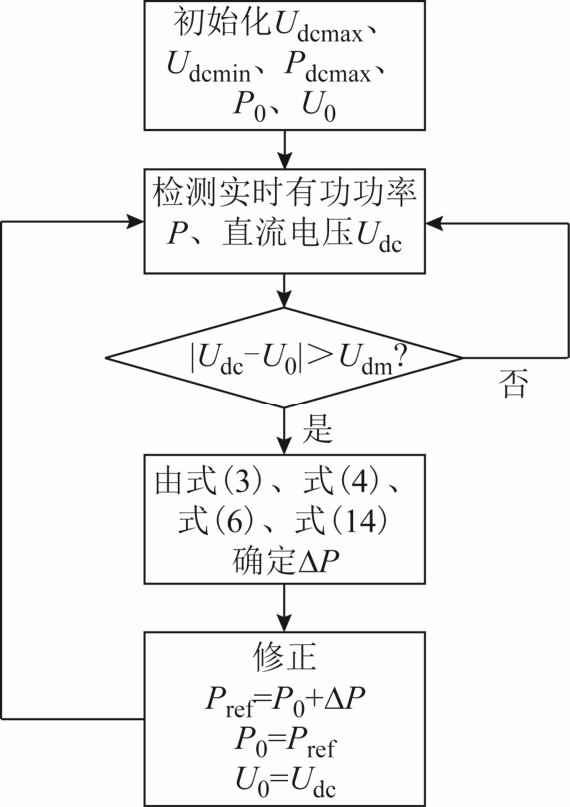
图4 自适应下垂控制流程
Fig.4 Flow chart of adaptive droop control
自适应下垂控制框图[20]如图5所示。定义KA=-K,系统换流站电流内环闭环传递函数为

图5 自适应下垂控制框图
Fig.5 Block diagram of adaptive droop control
式中,Kpi、Kii分别为电流内环PI控制器的比例系数和积分系数;KPMW为系统换流站放大特性比例增益,当开关频率足够高时,KPWM近似为1。设
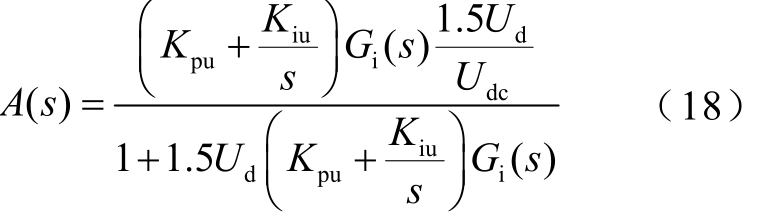
式中,Kpu、Kiu分别为电压外环PI控制器的比例系数和积分系数。换流站自适应下垂控制的闭环传递函数为
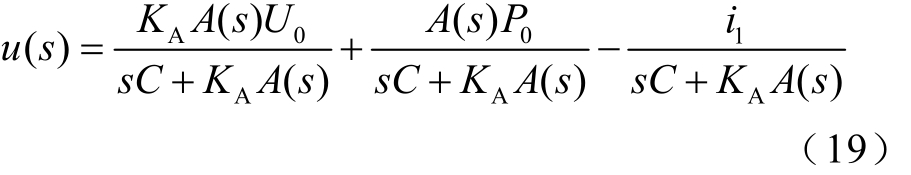
将 i1分量看作系统扰动量,则 udc-U0与 udc-P0的闭环传递函数分别为
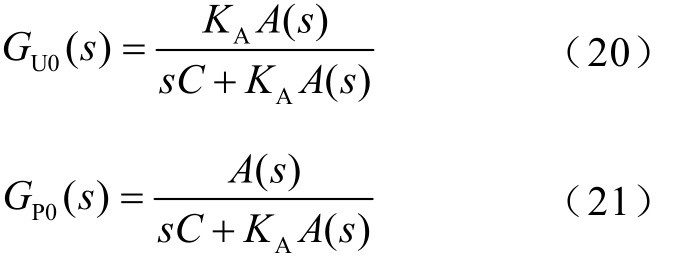
以KA为变量,通过对GU0(s)的推导计算,可得到KA由0变化到无穷时的根轨迹,如图6所示。当KA≠0时,系统的特征根实部均保持为负;当KA=0,即系统换流站达到满载时,系统的主导极点与原点重合,此时换流站由自适应下垂控制切换至定有功功率控制。由于主导极点与虚轴的距离变化较大,故换流站下垂系数的变化会影响系统的动态响应速度。
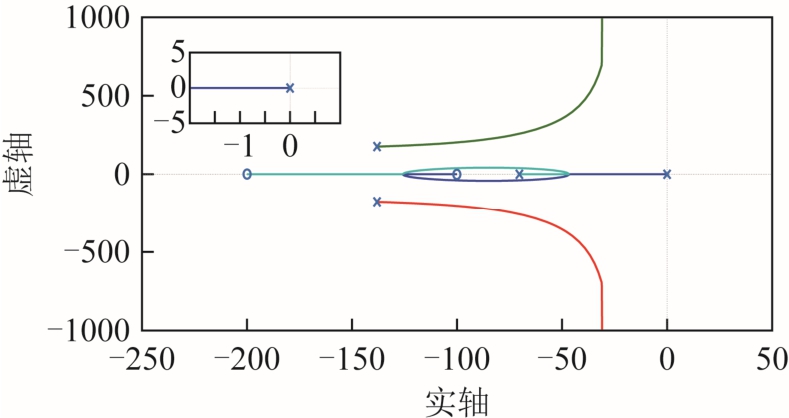
图6 udc-U0闭环传递函数的根轨迹
Fig.6 Root locus of udc-U0 closed-loop transfer function
以KA为变量,通过对GP0(s)的推导计算,可得到KA由0变化到无穷时的根轨迹,如图7所示。由于系统的特征根实部均保持为负,且主导极点与虚轴的距离有一定的变化范围,故当换流站的下垂系数变化时不会影响系统的稳定运行,但会在一定程度上影响系统的动态响应速度。
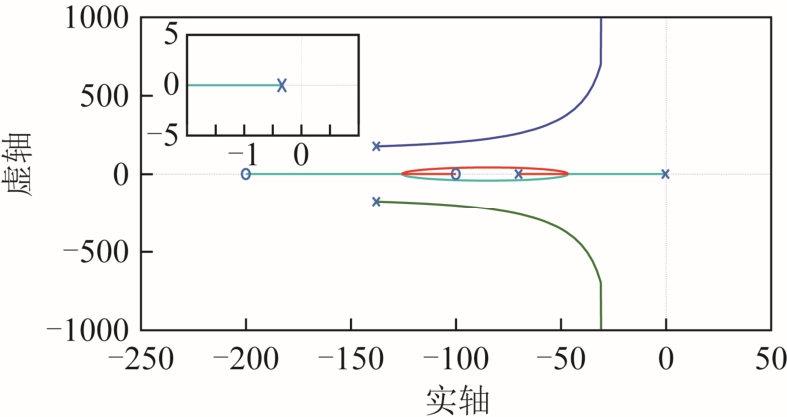
图7 udc-P0闭环传递函数的根轨迹
Fig.7 Root locus of udc-P0 closed-loop transfer function
自适应下垂控制(λ=1)关系曲线如图8所示,假设初始状态下换流站运行于A点,随着直流电压的变化,换流站的运行状态轨迹为A-B-C-D。由图8可以看出,当直流电压发生变化时,自适应下垂控制策略根据换流站的当前运行状态制定相应的关系曲线进行调节;当直流电压达到允许的波动极限时,换流站达到满载,平滑切换至定有功功率运行。
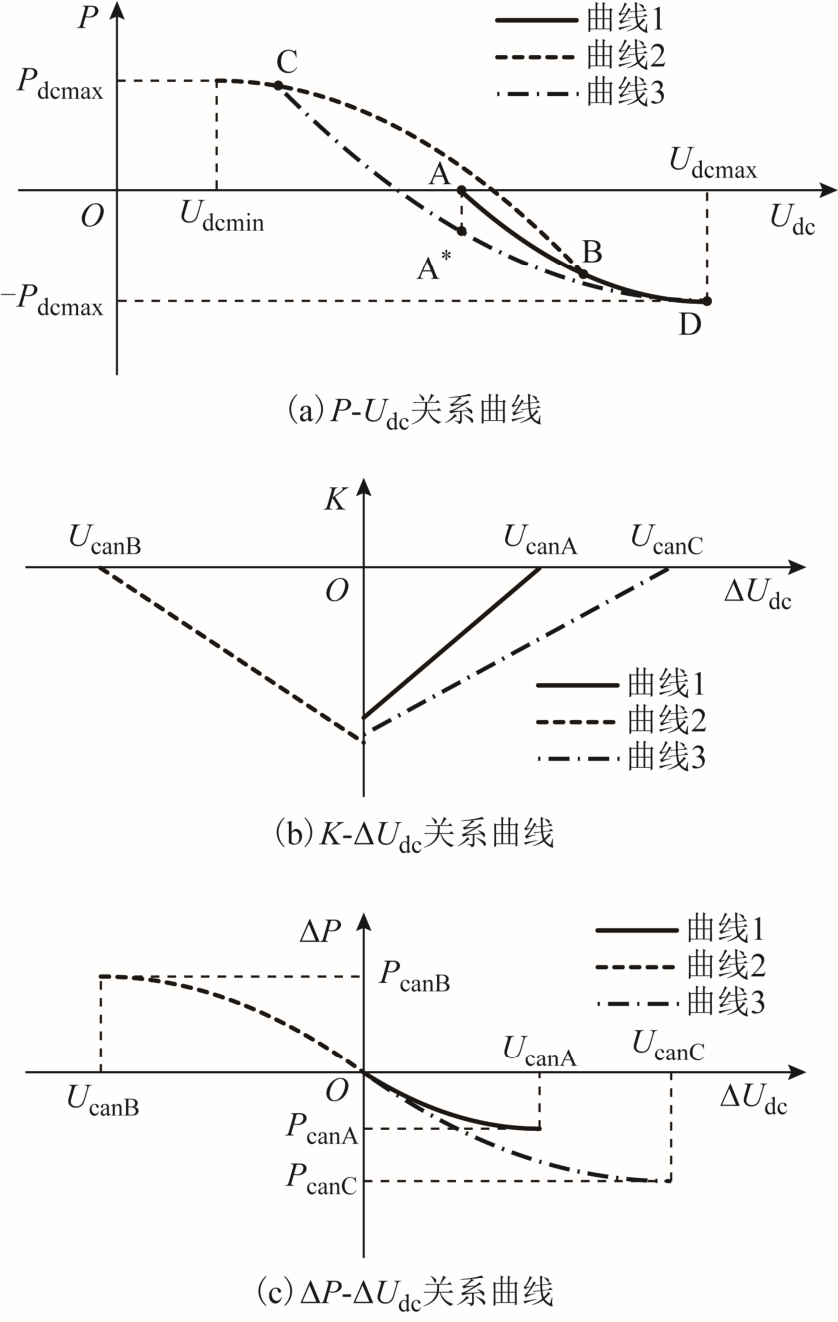
图8 自适应下垂控制关系曲线
Fig.8 Adaptive droop control relation curve
在图8a中,假设某一时刻换流站1的运行状态对应于A点,换流站2的运行状态对应于A*点。当直流电压升高时,换流站 1的P-Udc关系曲线对应曲线1的A-D段,换流站2的P-Udc关系曲线对应曲线 3的 A*-D段。由于自适应下垂控制策略可以将系统中的不平衡功率根据换流站的功率裕度进行合理分配,故直流电压的升高过程中换流站1和换流站 2的负载率逐渐接近,当直流电压达到Udcmax时,两个换流站同时满载,最大限度地利用了换流站的有功功率容量,同时将直流电压限制在允许范围内。
由图 8b、图8c可见,随着|ΔUdc|的增大,|K|逐渐减小,当|ΔUdc|变化较小时,|K|较大,|ΔUdc|单位变化时对应较大的调节功率,有利于减小直流侧电压波动;当|ΔUdc|逐渐接近至|Ucan|时,|K|逐渐减小至0,|ΔUdc|单位变化时对应较小的调节功率,ΔP变化趋缓,此时所有采用自适应下垂控制的换流站都接近满载,降低了换流站间直流电压的误差对于功率调节的影响。以图8a中A点为例进行说明:假设多个换流站间直流电压最大值与最小值之差为0.3%Udcref,Udcref为换流站的额定直流电压,直流电压允许波动范围为±3%Udcref,|Pcanmax|为当系统中任一换流站直流电压达到极限时,其余换流站的最大功率裕度。采用文献[9]方法时,可得
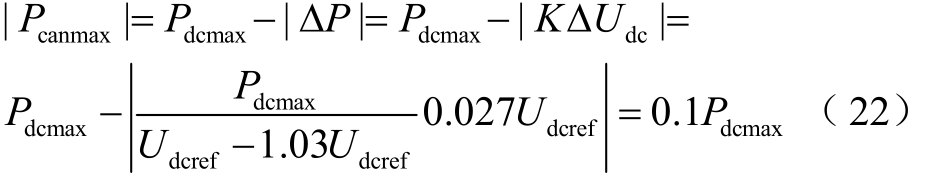
即当系统中任一换流站直流电压达到极限时,所有采用定斜率下垂控制的换流站功率裕度均处于[0,0.1Pdcmax]区间内,此时系统中仍存在较大可用功率容量。采用自适应下垂控制时,结合式(3)、式(4)、式(6)、式(14)可得
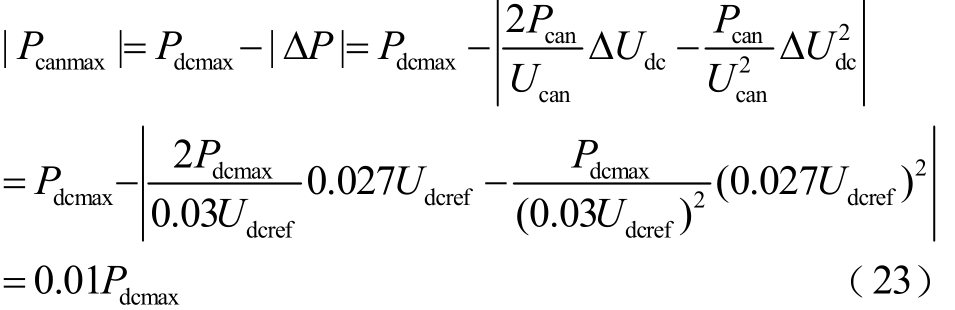
即当系统中任一换流站直流电压达到极限时,所有采用自适应下垂控制的换流站功率裕度均处于[0,0.01Pdcmax]区间内,充分利用了换流站的有功功率容量,降低了多个换流站间直流电压的误差对功率调节的影响。
由上述分析可知,自适应下垂控制策略将直流电压设定为系统的全局变量,根据换流站的功率裕度对系统中的不平衡功率进行合理分配;进行功率调节时以当前时刻换流站的运行状态为基准,制定调节关系曲线,根据换流站的可用功率变化量和允许电压变化量灵活调节下垂系数,显著减小了直流侧电压波动。当换流站接近满载时,下垂系数K逐渐趋近于 0,降低了多个换流站间直流电压误差对功率调节的影响,提高了不平衡功率分配的准确性;当任一换流站的直流电压达到允许的波动极限时,所有采用自适应下垂控制的换流站几乎同时达到或接近满载,充分利用了换流站的有功功率容量,维持直流电压稳定。
3 仿真结果分析
为验证本文所提控制策略的可行性和有效性,基于 PSCAD/EMTDC搭建了如图 1所示的四端柔性直流输电系统仿真模型。VSC1和 VSC2采用下垂控制,VSC3和VSC4采用定有功功率控制。通过算例1和算例2将文献[9]所提方法和本文所提方法进行了对比分析,算例3对不同的λ取值进行了对比分析,系统主要仿真参数见表1。
表1 系统主要仿真参数
Tab.1 Main simulation parameters of the system

参 数 数 值额定直流电压/ kV 320 VSC1~VSC4的额定功率/ MW 200, 300, 240, 260直流电压允许波动范围/ kV ±3%Udcref(310.4~329.6)交流系统电压/ kV 166 Rs/Ω 0.2 Ls/ mH 30输电线路分布电阻/(Ω/km) 0.011 4输电线路分布电感/(mH/km) 0.935 6输电线路分布电容/(μF/km) 0.012 3测量平滑时间常数/s 0.02子模块数量N 100 Rarm/Ω 0.2 Larm/ mH 60 Csm/μF 10 000 Udm/ kV 0.1 Kpu, Kiu 0.005, 1 Kpi, Kii 10, 1 000
3.1 算例1
初始条件下,VSC1和 VSC2的直流电压分别为 321.9kV和 320.4kV,两个换流站间电压误差约为0.47%Udcref,VSC1和 VSC2的有功功率分别为-48MW和-197MW,VSC3和VSC4的有功功率分别为100MW和150MW。2s时VSC3和VSC4的有功功率指令值分别变为 50MW 和 100MW;4s时VSC3和VSC4的有功功率指令值分别变为240MW和 260MW。换流站分别采用文献[9]所提方法和本文所提方法(λ=1)的仿真结果如图9所示。

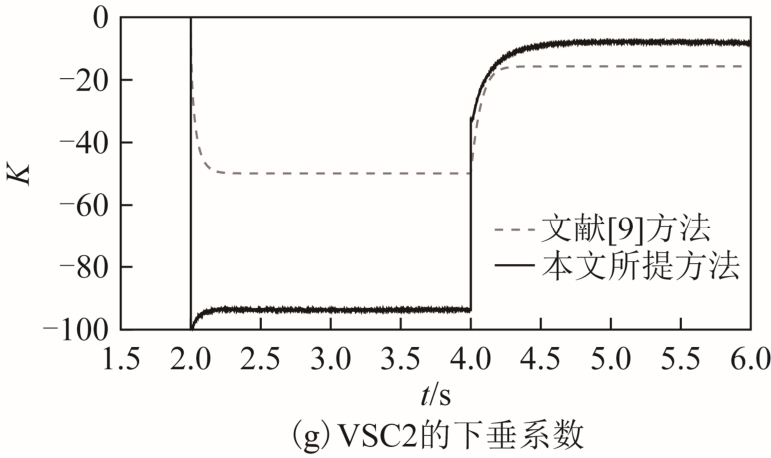
图9 功率变化的仿真结果
Fig.9 Simulation results of power change
由图 9可以看出,2s时 VSC3和 VSC4输出的有功功率减小后,系统中出现了-100MW 的不平衡功率,直流电压下降。此时VSC1和VSC2的功率裕度之比为 248MW:497MW,电压裕度之比为-11.5kV:10kV,当换流站采用文献[9]的方法时,可得VSC1对应的调节曲线为
VSC2对应的调节曲线为
当换流站采用本文所提方法时,VSC1对应的调节曲线为
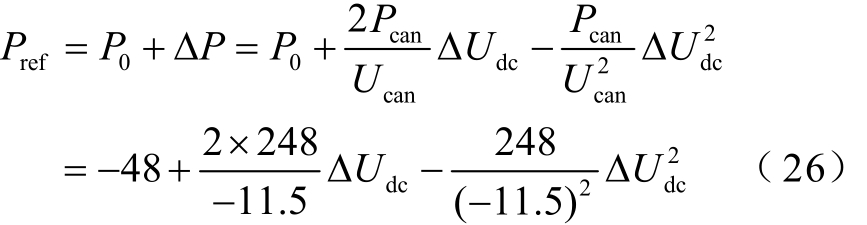
VSC2对应的调节曲线为
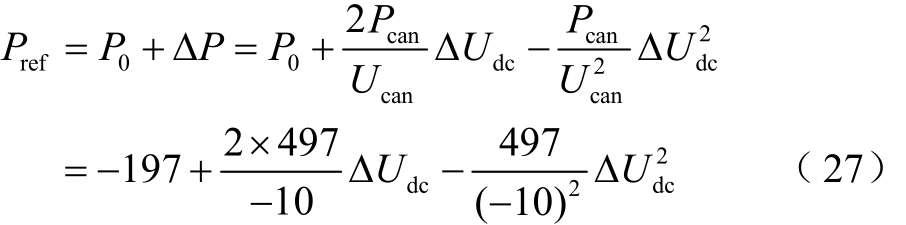
由于换流站间的电压误差和系统损耗随换流站的输出功率而变化,当换流站采用文献[9]的方法时,VSC1和VSC2的实际功率变化量约为36MW和62MW,实际直流电压变化量约为-1.35kV和-1.25kV;当换流站采用本文所提方法时,VSC1和VSC2的实际功率变化量约为41MW和57MW,实际直流电压变化量约为-0.60kV和-0.60kV。4s时VSC3和 VSC4输出的有功功率增大后,当换流站采用文献[9]的方法时,VSC1在调节过程未结束便达到满载,其余不平衡功率由VSC2独自承担。由于换流站间存在电压误差,当系统达到稳态时,VSC1直流电压已越限。当换流站采用本文所提方法时,VSC1和VSC2协调配合,当换流站接近满载时,下垂系数接近于 0,提高了按照换流站功率裕度分配不平衡功率的准确性,使两个换流站均未达到满载,降低了直流电压误差对功率调节的影响,且可以将直流电压限制在允许范围内。
由仿真结果对比可知,文献[9]所提方法和本文所提方法在功率调节过程中均可实现不平衡功率根据各换流站的功率裕度进行分配,不同之处在于本文所提方法考虑了换流站间直流电压误差对功率调节的影响,提高了不平衡功率按照换流站功率裕度分配的准确性,可以在一定程度上减少功率调节过程中某些换流站的直流电压越限现象,使下垂系数在功率调节过程中灵活变化来降低直流电压波动,且在调节速度方面具备一定优势。
3.2 算例2
初始条件下,VSC1的直流电压为322.35kV,VSC1和VSC2的有功功率分别为53MW和-100MW,VSC3和VSC4的有功功率分别为-50MW和100MW。2s时VSC2退出运行;4s时VSC3和VSC4的有功功率指令值分别变为-100MW和-50MW。换流站分别采用文献[9]所提方法和本文所提方法(λ=1)的仿真结果如图10所示。
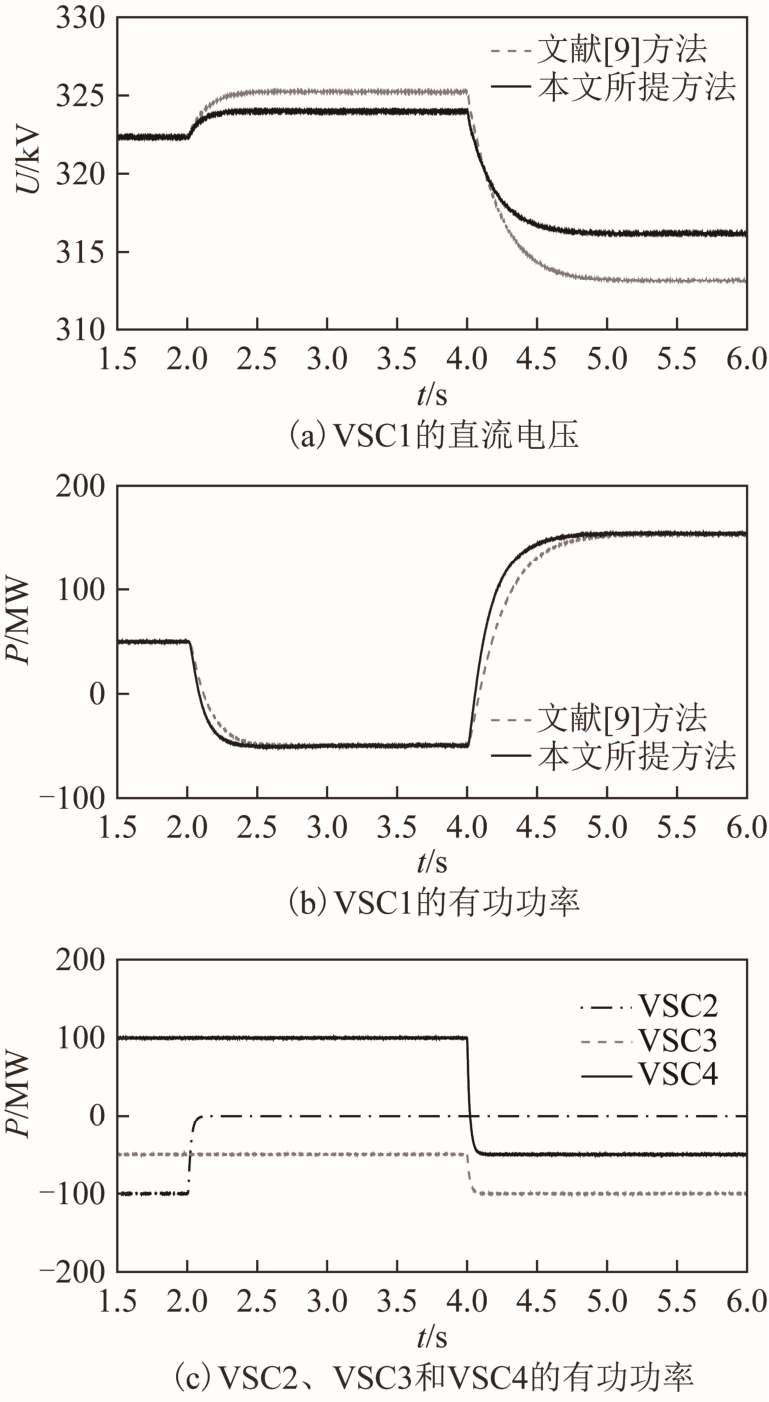
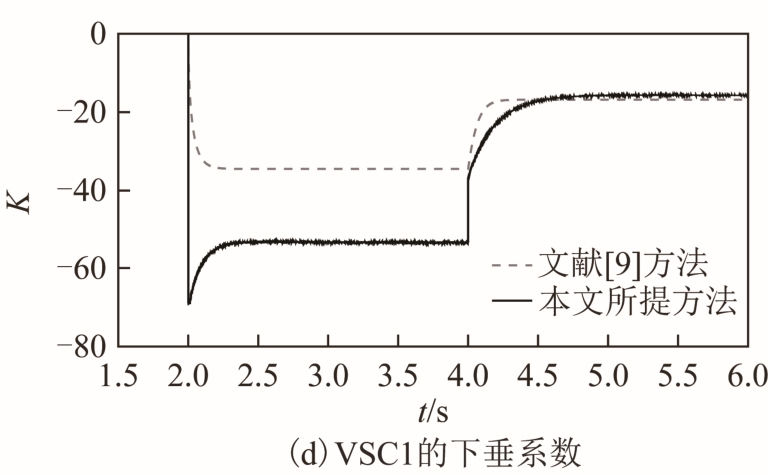
图10 VSC2退出运行的仿真结果
Fig.10 Simulation results of VSC2 exit operation
如图10所示,2s时VSC2退出运行后,系统中出现了100MW的不平衡功率,直流电压上升。VSC1检测到直流电压上升后,根据变化后的直流电压相应地调节输出的有功功率,此时VSC1的功率裕度为-253MW,VSC1的直流电压裕度为7.25kV。当换流站采用文献[9]所提方法时, VSC1对应的功率指令值的调节曲线为
当VSC1承担100MW的不平衡功率时,理论计算ΔUdc约为2.9kV,实际仿真结果约为2.8kV,仿真结果与理论计算结果一致。当换流站采用本文所提方法时,VSC1对应的功率指令值的调节曲线为
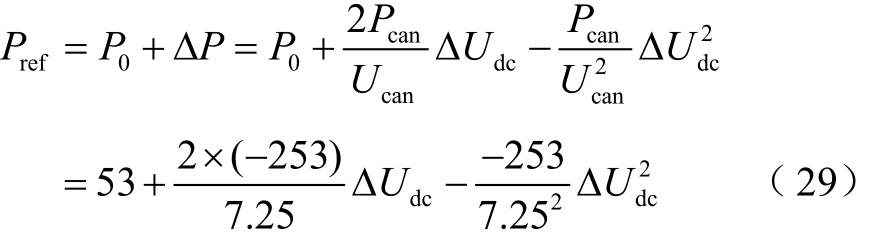
当 VSC1承担 100MW的不平衡功率时,理论计算 ΔUdc约为 1.6kV,实际仿真结果 ΔUdc约为1.6kV,仿真结果与理论计算结果一致。
4s时VSC3和VSC4输出的有功功率减小后,直流电压下降,VSC1承担200MW的不平衡功率。当换流站采用文献[9]所提方法时,实际仿真结果ΔUdc约为 12.1kV,当换流站采用本文所提方法时,实际仿真结果ΔUdc约为7.8kV。
由仿真结果对比可知,由于两次功率变化均由VSC1独自承担,故两种方法在 VSC1到达稳态后输出的有功功率相同。在两种控制方法下,某一换流站的退出不会影响到系统的稳定运行。与文献[9]的方法相比,本文所提方法可以显著降低直流电压波动,且在调节速度方面具备一定优势。
3.3 算例3
初始条件下,VSC1和VSC2的直流电压分别为321.9kV和320.4kV,两个换流站间电压误差约为0.47%Udcref;VSC1和VSC2的有功功率分别为-48MW和-197MW,VSC3和VSC4的有功功率分别为100MW和150MW。2s时VSC3和VSC4的有功功率指令值分别变为 50MW 和 100MW;4s时VSC3和VSC4的有功功率指令值分别变为240MW和260MW。λ分别为0.5、1、2的对比仿真结果如图11所示。

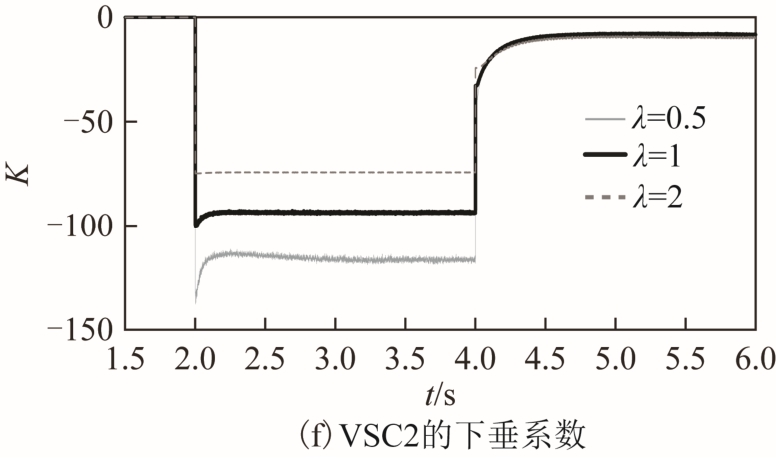
图11 不同λ值的对比仿真结果
Fig.11 Simulation results of comparison of different values of λ
由仿真结果可以看出,λ的取值不同,对不平衡功率的分配和直流电压的波动有一定的影响。λ的取值越小,计算得出的|K|越大,导致在功率调节过程中直流电压的波动越小,同时下垂系数K越容易受到直流电压稳态波动的影响。λ的取值较大时,虽然下垂系数 K不容易受到直流电压稳态波动的影响,但由于计算得出的|K|较小,导致在功率调节过程中直流电压的波动较大。故λ的取值虽不会对系统的稳定性造成影响,但由于稳态直流电压是在小范围内进行波动,λ的取值不宜过小;考虑到功率调节过程中的电压波动,λ的取值也不宜过大。
4 结论
针对 VSC-MTDC系统中无需通信,或当通信中断的情况下各换流站之间功率协调控制的问题,本文提出一种计及换流站间电压误差的 VSCMTDC系统自适应下垂控制策略。结果表明:
1)当换流站接近满载时,下垂系数K逐渐趋近于 0,降低了多个换流站间直流电压误差对功率调节的影响,提高了按换流站功率裕度分配不平衡功率的准确性。
2)换流站的下垂系数在功率调节过程中根据其功率裕度灵活变化,使换流站不易达到满载,且可以显著减小直流电压波动。
3)当任一换流站的直流电压达到允许的波动极限时,所有采用自适应下垂控制的换流站几乎同时达到或接近满载,充分利用了换流站的有功功率容量,维持了直流电压稳定。
[1] 吴杰, 王志新. 多端柔性直流输电系统的改进下垂控制策略[J]. 电工技术学报, 2017, 32(20): 242-248.Wu Jie, Wang Zhixin. Improved droop control strategy for multi-terminal voltage source converter-HVDC[J]. Transactions of China Electrotechnical Society, 2017, 32(20): 242-248.
[2] 陈鹏远, 黎灿兵, 周斌, 等. 异步互联电网 VSCHVDC紧急功率支援与动态区域控制偏差协调控制策略[J]. 电工技术学报, 2019, 34(14): 3025-3034.Chen Pengyuan, Li Canbing, Zhou Bin, et al.Coordination control strategy of emergency power support and dynamic regional control deviation for asynchronous interconnected power system VSCHVDC[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 3025-3034.
[3] 刘子文, 苗世洪, 范志华, 等. 基于自适应下垂特性的孤立直流微电网功率精确分配与电压无偏差控制策略[J]. 电工技术学报, 2019, 34(4): 795-806.Liu Ziwen, Miao Shihong, Fan Zhihua, et al. Accurate power allocation and voltage unbiased control strategy for isolated DC microgrid based on adaptive droop characteristics[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 795-806.
[4] 汤广福, 罗湘, 魏晓光, 等. 多端直流输电与直流电网技术[J], 中国电机工程学报, 2013, 33(10): 8-16.Tang Guangfu, Luo Xiang, Wei Xiaoguang, et al.Multi terminal DC transmission and DC grid technology[J]. Proceedings of the CSEE, 2013, 33(10):8-16.
[5] 周孝信, 鲁宗相, 刘应梅, 等. 中国未来电网的发展模式和关键技术[J]. 中国电机工程学报, 2014,34(29): 4999-5008.Zhou Xiaoxin, Lu Zongxiang, Liu Yingmei, et al.Development mode and key technologies of China's future power grid[J]. Proceedings of the CSEE, 2014,34(29): 4999-5008.
[6] 杨超, 梁海平, 顾雪平, 等. 基于电压源换流器HVDC联网的受端电网扩展黑启动方案[J]. 电工技术学报, 2017, 32(22): 207-215.Yang Chao, Liang Haiping, Gu Xueping, et al. The recovery strategy of the extended black-start for the receiving end system based on the voltage source converter-HVDC[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 207-215.
[7] 李梦柏, 谢竹君, 林卫星, 等. 一种适用于新能源并网的高增益单向直流变压器[J]. 电工技术学报,2018, 33(2): 301-309.Li Mengbo, Xie Zhujun, Lin Weixing, et al. Cascaded LC-AC transformer unidirectional DC-DC converter with high stepping ratio[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 301-309.
[8] 徐殿国, 刘瑜超, 武健. 多端直流输电系统控制研究综述[J]. 电工技术学报, 2015, 30(17): 1-12.Xu Dianguo, Liu Yuchao, Wu Jian. Review on control strategies of multi-terminal direct current transmission system[J]. Transactions of China Electrotechnical Society, 2015, 30(17): 1-12.
[9] 刘瑜超, 武健, 刘怀远, 等. 基于自适应下垂调节的 VSC-MTDC 功率协调控制[J]. 中国电机工程学报, 2016, 36(1): 40-48.Liu Yuchao, Wu Jian, Liu Huaiyuan, et al. Effective power sharing based on adaptive droop control method in VSC multi-terminal DC grids[J]. Proceedings of the CSEE, 2016, 36(1): 40-48.
[10] 唐庚, 徐政, 刘昇, 等. 适用于多端柔性直流输电系统的新型直流电压控制策略[J]. 电力系统自动化, 2013, 37(15): 125-132.Tang Geng, Xu Zheng, Liu Sheng, et al. A novel DC voltage control strategy for VSC-HVDC systems[J].Automation of Electric Power Systems, 2013, 37(15):125-132.
[11] Rouzbehi K, Miranian A, Candela J I, et al. A generalized voltage droop strategy for control of multiterminal DC grids[J]. IEEE Transactions on Industry Applications, 2015, 51(1): 607-618.
[12] Kirakosyan A, El-Saadany E F, El-Moursi M S, et al.Control approach for the multi-terminal HVDC system for the accurate power sharing[J]. IEEE Transactions on Power Systems, 2018, 33(4): 4323-4334.
[13] 阎发友, 汤广福, 贺之渊, 等. 基于 MMC 的多端柔性直流输电系统改进下垂控制策略[J]. 中国电机工程学报, 2014, 34(3): 397-404.Yan Fayou, Tang Guangfu, He Zhiyuan, et al.Improved droop control strategy for multi terminal HVDC system based on MMC[J]. Proceedings of the CSEE, 2014, 34(3): 397-404.
[14] 江斌开, 王志新, 邹建龙, 等. 计及不平衡功率最优分配的直流电压斜率控制策略研究[J]. 中国电机工程学报, 2017, 37(12): 3383-3390.Jiang Binkai, Wang Zhixin, Zou Jianlong, et al. Study of DC voltage slope control strategy considering optimal allocation of unbalanced power[J].Proceedings of the CSEE, 2017, 37(12): 3383-3390.
[15] Wang Weiyu, Li Yong, Cao Yijia, et al. Adaptive droop control of VSC-MTDC system for frequency support and power sharing[J]. IEEE Transactions on Power Systems, 2018, 33(2): 1264-1274.
[16] Li Xialin, Guo Li, Hong Chao, et al. Hierarchical control of multi-terminal DC grids for large-scale renewable energy integration[J]. IEEE Transactions on Sustainable Energy, 2018, 9(3): 1448-457.
[17] 朱瑞可, 王渝红, 李兴源, 等. VSC-MTDC系统直流电压自适应斜率控制策略[J]. 电力系统自动化,2015, 39(4): 63-67.Zhu Ruike, Wang Yuhong, Li Xingyuan, et al.Adaptive slope control strategy of DC voltage in VSCMTDC system[J]. Automation of Electric Power Systems, 2015, 39(4): 63-67.
[18] Kirakosyan A, El-Saadany E F, El-Moursi M S, et al.DC voltage regulation and frequency support in pilot voltage droop controlled multi terminal HVDC systems[J]. IEEE Transactions on Power Systems,2018, 33(3): 1153-1164.
[19] 孙黎霞, 陈宇, 宋洪刚, 等. 适用于 VSC-MTDC的改进直流电压下垂控制策略[J]. 电网技术, 2016,40(4): 1038-1039.Sun Lixia, Chen Yu, Song Honggang, et al. An improved DC voltage droop control strategy for VSCMTDC[J]. Power System Technology, 2016, 40(4):1038-1039.
[20] 刘盼盼, 荆龙, 吴学智, 等. 一种 MMC-MTDC 系统新型协调控制策略[J]. 电网技术, 2016, 40(1): 64-69.Liu Panpan, Jing Long, Wu Xuezhi, et al. A new coordinated control strategy for MMC-MTDC system and stability analysis[J]. Power System Technology,2016, 40(1): 64-69.