0 引言
风力发电是我国应用规模最大的新能源发电方式，目前我国风电总装机容量居于世界第一位[1]。随着新能源并网规模的日益扩大以及风火打捆输电方式的逐步实施，并网风电机组与同步发电机组之间的相互作用越来越明显，风电场对电力系统稳定性的影响也越来越显著。近年来，风电场并网引起的次同步振荡事故多发，严重影响了事故相关区域电网的安全稳定运行，引起了国内外电力系统稳定性研究领域的广泛关注[2-7]。含大规模风电电网的运行经验表明，风电的随机性、波动性及间歇性可能会引起电网各子系统间交换功率的快速变化，引入新的振荡模式，相应的机电耦合作用可能会进一步诱发同步机组轴系次同步扭振现象，因此探究风电场并网对同步机轴系稳定性的影响具有重要的现实意义和理论价值[8]。
风电场并网对同步机轴系次同步振荡稳定性的影响主要包括稳态潮流影响和动态交互作用影响两方面[9]。首先，对于稳态潮流影响，在研究中通常将风电场等效为恒功率源进行研究，通过不同渗透率下同步机出力变化及交流系统潮流变化来分析轴系次同步振荡稳定性变化。另外，对于风电机组与同步机组之间的动态交互作用影响，在研究中需充分考虑风电机的动态特性、换流器控制环节采取的控制方式及采用的控制参数对同步机轴系次同步振荡稳定性的影响。双馈风力发电机（Doubly-Fed Induction Generators, DFIG）是目前市场主流机型之一，该机型能够实现有功功率和无功功率的解耦控制，其转子回路通过变流器与外部电网相连，变流器中有许多复杂控制环节；定子回路则直接与外部电网相连，与外部电网有直接的耦合作用。因此，DFIG比直驱永磁同步机（Permanent Magnet Synchronous Generator, PMSG）等其他类型的风电机组更容易与同步机轴系之间产生动态交互作用，引发电力系统次同步振荡事故[10]。
目前，次同步振荡问题的研究方法主要包括频域分析法和模式分析法两大类[11-12]。复转矩系数法作为频域分析法的一种，不仅能够避免模式分析中常见的“维数灾”问题，而且能够给出任一待研究频段上系统的阻尼特性，具备明确的物理意义，尤其适合研究轴系扭振及新能源并网引发的次同步振荡，近年来在风电并网系统次同步振荡分析领域得到了广泛的应用[13-18]。文献[13]中基于复转矩系数法对并网风机轴系次同步振荡问题进行了研究，分析了系统参数变化对风机轴系电气阻尼的影响及相应抑制策略。文献[14-16]中采用复转矩系数法分析了并网风电机组变流器与线路串联补偿相互作用引发的电力系统次同步振荡，以系统机械阻尼与电气阻尼之和为负值作为风机引发系统次同步振荡的理论依据，在全频率段内研究了系统参数变化对稳定性的影响。文献[17]将风电场用恒功率源表示，研究了不同风电穿透率引起的潮流变化对系统阻尼的影响。文献[18]中应用复转矩系数法研究了影响并网DFIG感应发电机效应（Induction Generator Effect,IGE）的因素，指出串补度的增大、风速的减小及输电线路电阻的减小均可能增大系统的电气负阻尼，导致系统输出功率发散振荡。然而，传统的复转矩系数法只能用于分析系统的整体稳定性，无法研究并网风电机组和同步机组之间的动态交互作用，存在一定的应用局限性。同时，由于复转矩系数法最初提出时仅从物理意义出发，缺乏严格的数学证明，近年来有一些文献对其准确性进行了深入探究，表明该方法在某些特定场景下存在一定局限性[19-21]。
本文对复转矩系数法的稳定判据进行了改进和推广，将其扩展到含并网风电场的多输入多输出闭环互联模型的分析中，研究了 DFIG风电场接入对同步机轴系稳定性的影响，并从阻尼弱化的角度分析了风机并网引发的近似强模式耦合现象。本文所提出的分析方法与常用的模式分析法相比，不仅降低了计算量，并且分别考虑了风电场并网后系统潮流变化及动态交互作用对轴系稳定性的影响，能够从物理角度解释风机与同步机轴系之间的动态交互作用。
1 多输入多输出闭环互联系统模型
含有DFIG和n台同步发电机的多机电力系统结构如图1所示，各发电机的输出功率汇集到一起经交流线路输送到无穷大电网。将风机并网点机端电压幅值以及风机向电力系统注入的有功功率和无功功率的小信号增量作为风电场与多机电力系统之间的接口变量，分别记为wVΔ、wPΔ和wQΔ。
图1 含并网DFIG的多机电力系统结构
Fig.1 Diagram of multi-machine power system integrated with a grid-connected DFIG
对除 DFIG外的多机电力系统进行建模，该模块的输入量为wPΔ和wQΔ，输出量为wVΔ。根据自动控制原理[22]，该子系统的状态空间模型为
式中，gΔX为由除DFIG外，多机电力系统其余状态变量组成的列向量，包括同步机轴系状态变量、同步机电气状态变量以及表征输电网络动态的状态变量（输电线路电感的电流、节点对地电容的节点电压）；Ag为其对应的状态空间矩阵；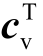
、bp、bq、dp、dq分别为相应的系数向量或系数。
并网DFIG的线性化状态空间模型为
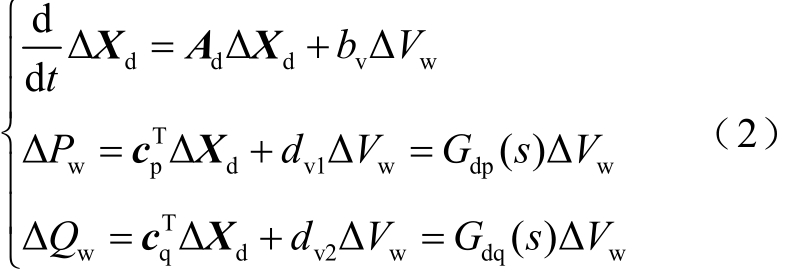
式中，ΔXd为由并网DFIG所有状态变量组成的列向量，包括异步发电机定转子绕组电流、轴系（双质量块）转速和角位移、转子侧换流器的内外环控制变量、DC环节的直流电容电压、网侧换流器的内外环控制变量、PLL环节的控制变量； A d为其对应的状态系数矩阵；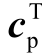
、
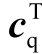、 bv、 d v 1、 d v 2分别为相应的系数向量或系数；Gdp(s)、Gdq(s)为相应的开环传递函数。
联立式（1）和式（2），可以得到图1所示含并网DFIG电力系统的线性化闭环互联模型为
式中，ΔXb为由系统全部状态变量组成的列向量。状态空间矩阵 A b 的表达式为
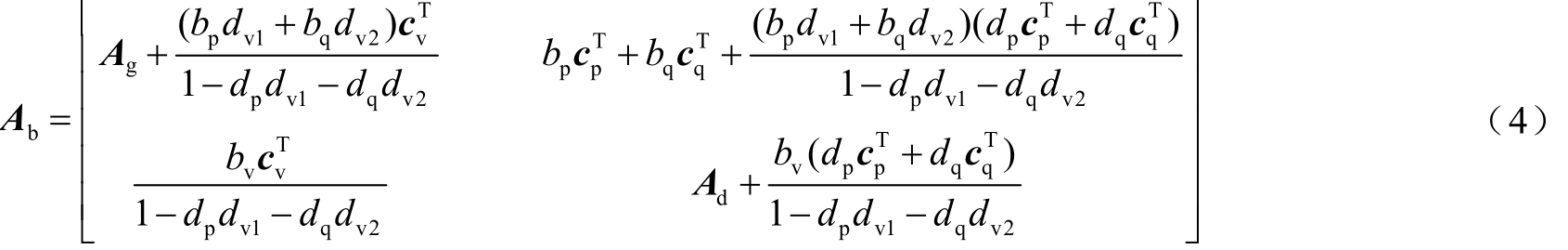
根据特征值灵敏度理论[23]，当闭环互联系统状态空间矩阵Ab的某一个特征值λa随着参数α的变化靠近Ab的另一个特征值λb时，特征值对参数的灵敏度∂λa/∂α和∂λb/∂α会单调增大，到两个特征值完全重合即 λ a =λb时，系统会发生强模式耦合现象，此时灵敏度趋于无穷大，两个特征值反向弹开，Δλa及 Δλb较大， λa或λb有可能成为不稳定的模式。在实际电力系统中，完全的强模式耦合不会发生，但可能会出现近似强模式耦合现象[24]，即闭环互联系统的两个特征值在参数α调整的过程中先不断靠近，在二者重合之前便会由于彼此之间的交互作用相互弹开。同步机轴系振荡模式和风机并网引入的振荡模式对应矩阵 A b中的两个特征根，当系统中参数调整不当时，这两个振荡模式之间可能发生强烈的动态交互作用，出现近似强模式耦合现象，进而导致多机电力系统轴系次同步失稳。
2 改进复转矩系数法
2.1 传统复转矩系数法原理及局限性
2.1.1 传统复转矩系数法原理
1982年，I. M. Canay博士首次提出了复转矩系数法，将闭环电力系统的电气和机械部分划分为独立子模块，用两个转矩系数 e()k s和 m()k s分别表示发电机组转子电气角位移受到小干扰δΔ后电气子系统和机械子系统感应出的等效电气转矩和等效机械转矩[25]。取jsω=，将转矩系数表示为复数的形式为
式中， eK、 eD分别为电气子系统的弹性系数和阻尼系数； mK、 mD分别为机械子系统的弹性系数和阻尼系数。复转矩系数法的数学模型如图2所示。
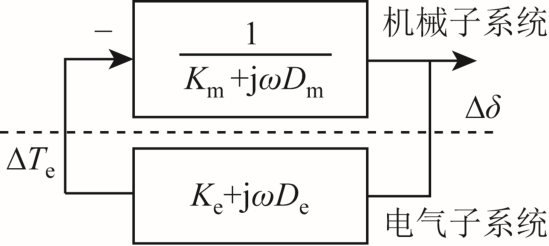
图2 复转矩系数法数学模型
Fig.2 Mathematical model of the complex torque coefficients method
在发电机轴系的自然扭振频率附近进行频率扫描，若在某角频率下满足总弹性系数为零这一条件，即
且同时满足系统总阻尼系数大于零的条件，即
则认为系统在该轴系振荡模式下是稳定的，反之系统存在发生次同步振荡的风险。
2.1.2 传统复转矩系数法的两点局限性
复转矩系数法物理意义明确，数学模型简单且易于实现，但存在一定的理论缺陷和应用局限。结合现有文献，复转矩系数法存在的问题主要包括以下两点[19-21]：
1）复转矩系数法根据弹性转矩系数之和为零识别系统轴系扭振频率，但由于默认jsω=，忽略了振荡模式实部及各模式间的耦合作用，可能检测不到某扭振模式或识别出错误的扭振频率。
2）复转矩系数法使用阻尼转矩系数之和的正负判断系统稳定性，但该判据在最初提出时进行了大量的化简，尤其当大规模电力电子设备集成到电力系统中时，可能无法获得正确的结论。
鉴于复转矩系数法的以上两点局限性，本文提出一种适用于分析含并网风电场的多机电力系统次同步振荡稳定性的改进复转矩系数法，基本思路如下：首先对待研究同步机轴系进行解耦建模，排除轴系各振荡模式间的相互耦合作用；之后对阻尼转矩稳定性判据进行修正，基于特征值灵敏度理论建立风电场并网对轴系振荡模式的动态作用与风电场注入多机系统的阻尼转矩之间的关系，更为准确地判断系统的稳定性及稳定裕度。
2.2 改进复转矩系数法
首先，建立适于改进复转矩系数法应用场景的闭环互联系统模型。设系统中共有n台同步发电机，其中第k台同步机有lk个轴系扭振模式，对同步机轴系部分进行解耦处理，过程如文献[26]所示，得到第k台同步机第i个轴系扭振模式kiλ对应的解耦方程为
式中，k=1,2,…,n；i=1,2,…,lk；上标(m)表示解耦模式量；
、
、
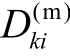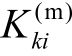分别为第k台同步机第i个轴系振荡模式对应的解耦惯性时间常数、解耦阻尼系数及解耦弹性系数；ΔTek为第k台同步机的电磁转 矩 增量； Δ δ k(im)为第k台同步机第i个模式的解耦等值转子角位移。第k台同步机各轴系振荡模式对应的解耦转子角位移小信号增量之和
等于实际转子角位移小信号增量Δδk[24]。当系统中发生第 i个扭振模式时，其他解耦模式等值质块的转子角位移约为0，此时
轴系解耦过程所进行的简化处理包括：
1）默认各轴系振荡模式之间无机械阻尼耦合。
2）在发生第 i个轴系扭振模式时忽略其余扭振模式对应的解耦角位移增量（小干扰条件下其值极小）。
以上简化处理对分析精度的影响极小。在轴系振荡模式kiλ下，根据轴系解耦方程式（8）和式（9），将式（1）分解表示为
式中，ωk为第k台同步机角速度；ΔXs为闭环互联系统除第 k台同步机轴系状态变量外的其余状态变量组成的列向量；状态变量[Δ δ Δω ΔX]T 之k k s前的矩阵为相应状态系数矩阵，与式（1）中的状态系数矩阵相比，考虑了轴系解耦后的具体表达形式；ΔPw和ΔQw之前的矩阵为相应输入矩阵，[cv 1 cv 2 C v 3]、 d p、 d q亦为相应的系数或系数矩阵。根据式（2）和式（10），得到经过同步机轴系解耦处理的含并网 DFIG风电场电力系统的闭环互联系统模型，如图 3所示。图 3中的电力系统闭环模型包含SG子系统及DFIG子系统，两个子系统的交互物理量为风电机组的端口电压ΔVw和输出功率ΔPw、ΔQw，其中SG系统输入为ΔPw和ΔQw，输出为ΔVw；DFIG子系统输入为ΔVw，输出为ΔPw和ΔQw。
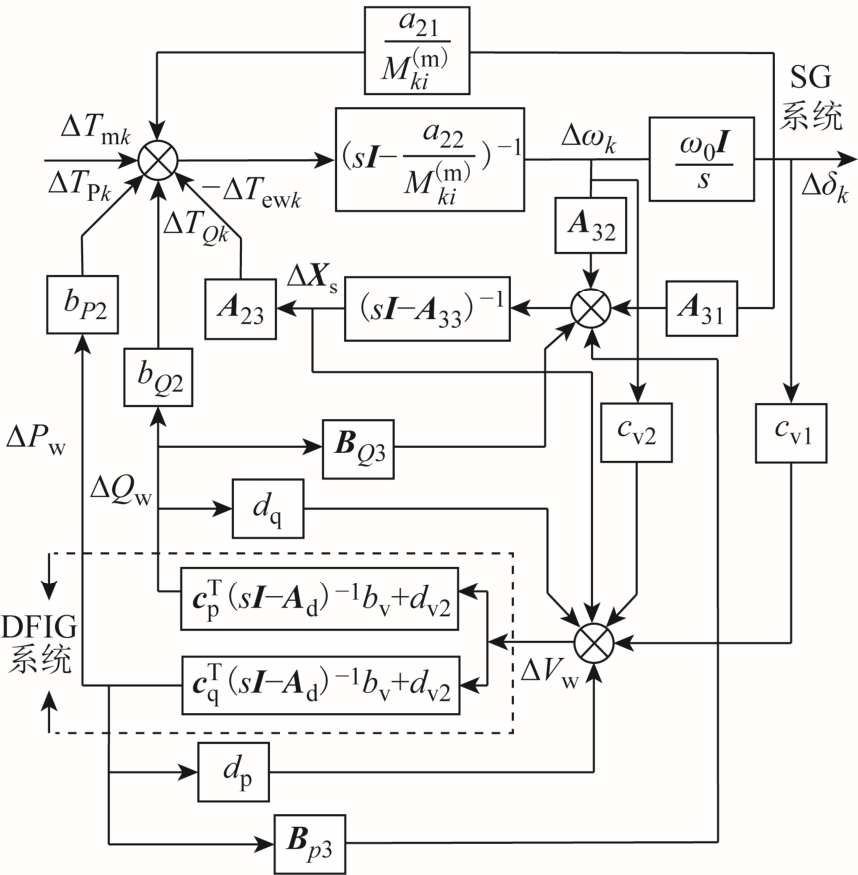
图3 适用于改进复转矩系数法的DFIG并网电力系统闭环互联模型
Fig.3 Closed-loop interconnected model of power system integrated with a grid-connected DFIG-based wind farm used for the improved complex torque coefficients method
下面将分别考虑风电场并网对同步机轴系次同步振荡模式的稳态潮流影响和动态交互作用影响。不失一般性，对于轴系振荡模式λki，记系统中未接入DFIG风电场时其值为λki0；在不考虑DFIG引入的次同步动态影响时，即DFIG作为恒功率源接入、ΔPw和ΔQw为零的情况下，记该振荡模式为λkif，其与λki0之间的差值代表系统稳态潮流变化对轴系振荡模式的影响。记 DFIG并网对该振荡模式的动态作用影响为Δλ ki，则 DFIG并网前后第k台同步机第 i个轴系振荡模式的总变化量为 λ kif - λ ki 0 +Δλ ki 。在计算λki0及λkif时，只需建立同步机部分的状态方程，计算较为便捷，因此研究的重点与难点集中在Δλ ki的计算上。为更准确地判断风机并网对轴系次同步振荡稳定性的影响，并且赋予近似强模式耦合现象更明确的物理意义，下面建立Δλki与风电场向同步机提供的阻尼转矩之间的关系。
首先计算由并网 DFIG风电场向多机电力系统注入的电气阻尼转矩。用ΔTPk及ΔTQk分别表示DFIG输出有功功率和无功功率在系统小干扰下对第k台同步机电磁转矩的动态作用分量，根据电磁转矩的相关定义[27]，对式（10）进行变换，将相应的传递函数分别表示为
将式（11）代入式（2），得到DFIG风电场的输入状态变量ΔVw与第k台同步机电磁转矩增量Δ T ewk之间的关系式为
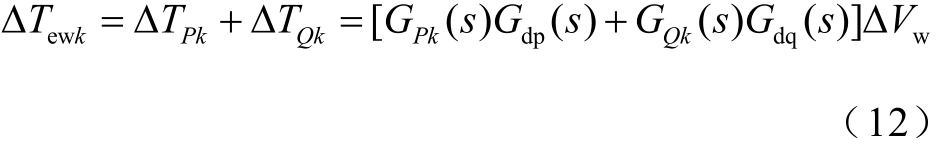
在轴系振荡模式kiλ下，从第k台同步机角速度增量kωΔ到DFIG机端电压wVΔ增量的传递函数可以表示为[28]
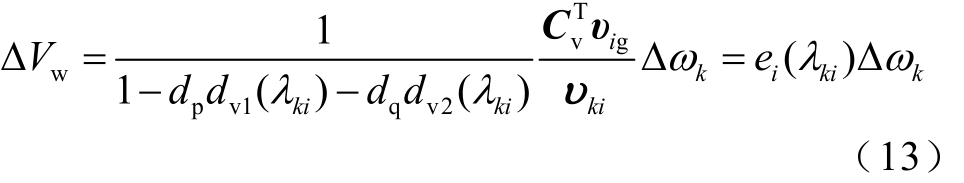
式中，giυ为由sΔX的全部特征向量构成的矩阵；kiυ为状态变量kωΔ对应的特征向量。联立式（12）和式（13），得到第k台同步机在振荡模式kiλ下电磁转矩增量与角速度变量的关系式为
相应地，由DFIG风电场向第k台同步机提供的电气阻尼转矩系数为
根据式（12）~式（15），由于在计算阻尼转矩系数Dw k时考虑了系统中其余同步发电机对所研究同步发电机电磁转矩的影响，因此所提方法适用于多机电力系统的分析。用该阻尼转矩系数 D w k表征第k台同步机轴系和风电场之间的动态交互，定义λki对Dwk的灵敏度为
式中，p和r为相应的左、右特征向量，且有pTr=1。由式（15）和式（16），有
式（17）即为所推导出的由阻尼转矩系数计算DFIG风电场对同步机轴系振荡模式动态作用的表达式。根据上述推导及控制系统状态空间模式分析理论[22]，考虑了DFIG并网潮流变化及动态交互作用的同步机轴系次同步振荡稳定性判据为
式中，λkif对应风电场并网引入的稳态潮流变化，Δλ ki对应并网风电场与同步机组轴系之间的动态交互作用。由此给出基于改进复转矩系数法的含并网风电场多机电力系统同步机轴系次同步振荡稳定性研究通用步骤如下：
1）建立如图3所示的多输入多输出系统模型。
2）计算风电场并网前同步机轴系振荡模式。对式（1）中不含风电场的多机电力系统状态系数矩阵 Ag进行模式分析，得到风电场并网前多机电力系统中待研究的第k台同步机第i个轴系解耦振荡模式0kiλ。
3）分析风电场并网对系统潮流的影响。将并网风电场看作恒功率源，对潮流重新分布后的系统状态系数矩阵Ag进行模式分析，计算此时第k台同步机第i个轴系振荡模式λkif。潮流变化引起的轴系振荡模式增量为 λ kif -λki0。
4）根据式（17）计算并网风电场对轴系振荡模式的动态作用，并根据式（18）判断轴系的次同步振荡稳定性。若λki满足式（18）的条件，说明风电场并网后该振荡模式仍处于复平面的左半平面，系统稳定；否则系统会发生轴系次同步振荡。
综上所述，所提出的改进复转矩系数法通过轴系解耦解决了传统方法可能出现的扭振频率检测问题；通过分别计及稳态潮流影响和动态交互作用影响，解决了传统方法在某些场景下可能存在的准确度不足的问题。
3 算例分析
3.1 算法验证
算例系统的结构如图1所示。表1、表2分别列出了含并网 DFIG风电场的 IEEE第一标准模型和IEEE第二标准模型的同步机轴系振荡模式的特征分析法计算值及改进复转矩系数法计算值，其中同步机和交流线路参数参考 IEEE标准测试系统[29-30]，DFIG模型和参数参考文献[31]，具体数值见附录。由于本文研究重点在于并网DFIG风电场与同步机轴系之间的交互作用，因此移除了模型中的串联补偿结构。表中0iλ表示风电场并网前同步机轴系振荡模式，λ if表示风机作为恒功率源接入系统时轴系振荡模式，λim表示由改进复转矩系数法计算出的考虑了风机与轴系之间动态交互作用的轴系振荡模式，λic表示采用特征值分析法计算出的风电场并网后轴系振荡模式。表1中模式1~5对应单同步机六质量块轴系的五个振荡模式，表2中模式6~8和模式9、10分别对应两台同步机的四质量块轴系和三质量块轴系的振荡模式。
表1 含并网DFIG的IEEE第一标准模型轴系振荡模式
Tab.1 Shaft torsional modes of IEEE first benchmark power system with grid-connected DFIG
模式0iλ f iλ miλ c iλ 1 -0.182 0+298.2i-0.181 9+298.2i -0.181 9+298.2i -0.181 9+298.2i 2 -0.641 1+203.1i-0.495 4+203.1i -0.515 6+203.1i -0.509 4+203.1i 3 -0.487 3+160.6i-0.418 0+160.7i -0.439 1+160.7i -0.444 1+160.7i 4 -0.727 7+127.0i-0.715 6+127.0i -0.737 6+127.0i -0.741 6+127.0i 5 -0.550 4+98.77i-0.623 9+99.16i 1.147 5+99.69i 1.157 9+99.67i
表2 含并网DFIG的IEEE第二标准模型轴系振荡模式
Tab.2 Shaft torsional modes of IEEE second benchmark power system with grid-connected DFIG
模式0iλ f iλ miλ c iλ 6 -0.153 7+356.6i-0.153 8+356.6i -0.153 9+356.6i -0.153 9+356.6i 7 -1.534 5+213.6i-1.542 5+213.6i -1.546 5+213.6i -1.547 8+213.6i 8 -0.496 6+117.9i-0.496 7+117.9i -0.642 6+117.9i -0.625 7+117.8i 9 -0.197 9+287.1i-0.194 0+287.1i -0.194 0+287.1i -0.194 0+287.1i 10 -0.678 4+123.6i-0.675 2+123.6i -0.686 1+123.6i -0.690 5+123.6i
由表1、表2的第3、4列可知，前文所提出的改进复转矩系数法与特征分析法之间的计算误差非常小（＜1%）。该误差随系统潮流、参数变化的具体情况见附录。因此可以认为，改进复转矩系数法能够在降低系统计算维数的情况下准确判断风电场并网后同步机轴系稳定性，且同时适用于单同步机系统及多同步机系统。为了更清晰地反映出风电场并网后系统潮流变化及动态交互作用分别对同步机轴系振荡模式的影响，图4给出了DFIG风电场并入IEEE第一标准模型前后同步机轴系振荡模式 2~5的矢量示意图，其中短虚线代表 DFIG风电场并网引入的潮流影响，线段起点为 DFIG风电场并网前同步机轴系振荡模式，终点为风电场作为恒功率源接入时的同步机轴系振荡模式；实线代表 DFIG风电场振荡模式与轴系振荡模式之间的动态交互作用影响，起点为风电场作为恒功率源接入时的同步机轴系振荡模式，终点为 DFIG风电场并网后由改进复转矩系数法计算出的轴系振荡模式；长虚线代表DFIG风电场并网对同步机轴系振荡模式的实际总影响，起点为 DFIG风电场并网前同步机轴系振荡模式，终点为风电场并网后的轴系振荡模式特征分析计算值。考虑到轴系振荡模式1在风电场并网前后数值变化非常小，难以直观地用图形表现出来，因此在图4中将其省略。
图4 DFIG并网前后IEEE第一标准模型轴系振荡模式
Fig.4 Diagram of the shaft torsional modes of IEEE first benchmark power system with and without DFIG
由图4和表1可知，风电场并网前后各轴系振荡模式的变化趋势不尽相同：轴系振荡模式1~4主要受到系统潮流变化的影响，且风机并网前后其变化量相对较小；而轴系振荡模式5受到的主要影响来自风电场与同步机之间的动态交互作用，并因此由稳定模式变为不稳定模式。为了找出可能与该轴系振荡模式发生近似强模式谐振的DFIG振荡模式，对式（2）中DFIG状态系数矩阵Ad进行模式分析，发现存在振荡模式-0.747 5+98.93i在数值上与风机并网前轴系振荡模式5十分接近。进一步计算DFIG各状态变量在此振荡模式中的参与因子，发现该振荡模式由转子侧换流器电流控制内环主导，因此将其定义为转子侧换流器电流控制内环振荡模式。下面针对这两个模式之间可能发生的近似强模式耦合现象，采用改进复转矩系数法分析不同因素带来的具体影响。
3.2 系统近似强模式谐振分析
3.2.1 DFIG换流器控制参数影响
将风电场并网后转子侧换流器电流控制内环振荡模式和同步机轴系次同步振荡模式5分别记作dλ和sλ，风电场并网前相应记作d0λ和s0λ。调节转子侧无功电流内环控制器的积分放大倍数Kqi，得到风机并网前后d0λ、dλ和sλ的变化轨迹，如图5所示。图中 Kqi变化区间为 5~30，取点间隔为 0.1；DFIG与同步机轴系之间发生最强烈动态交互作用时的Kqi约为 15.3。
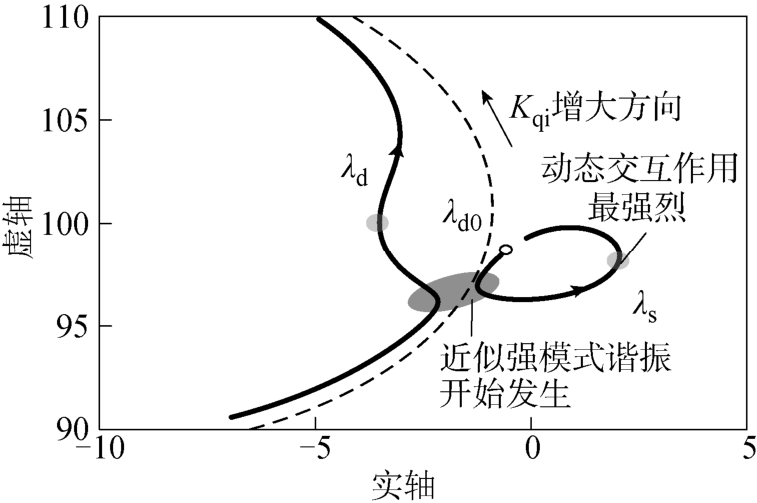
图5 dλ和sλ随qiK变化的根轨迹
Fig.5 Modal trajectories ofdλandsλwhenqiK was tuned
由图5可知，随着Kqi的增大，原本相距较远的两个振荡模式dλ和sλ逐渐靠近，当它们距离很小时（落入图5深灰色椭圆形区域），彼此开始产生交互作用。近似强模式谐振发生点对应着图5深灰色区域中两个特征值距离最近的点，但此时并非动态交互作用最强烈的位置，系统也并未失稳，说明近似强模式谐振理论只能作为一种失稳预判。随着参数Kqi的进一步增大，dλ和sλ沿着相反方向移动，在二者间距逐渐增大的同时，同步机轴系与 DFIG换流器控制环节之间的动态交互作用也不断增强，直至达到最强烈状态（落入图5浅灰色圆形区域）。在此过程中sλ到达不稳定区域，系统存在次同步振荡风险。当参数 Kqi继续增大，动态交互作用逐渐减弱，sλ再次回到稳定区域。
图6给出了Kqi分别取10、15、20时各状态变量在dλ及sλ中的参与因子，表征了Kqi调节过程中同步机轴系与 DFIG换流器控制环节之间的动态交互作用变化情况。Kqi的取值分别对应近似强模式谐振开始发生、动态交互作用最强烈、近似强模式谐振开始消除三种状态。由图6a和图6b可知，当Kqi取10时（对应于图5中的深灰色区域），dλ和sλ之间开始出现较弱的动态交互，DFIG状态变量在sλ中的参与度很小，轴系状态变量在dλ中的参与度也较小；随着Kqi增大到15（对应图5中的浅灰色区域），如图6c和图6d所示，dλ和sλ之间交互作用变强，DFIG状态变量与轴系状态变量在彼此振荡模式中的参与度均很高；随着 Kqi进一步增大到 20，dλ和sλ之间的动态相互作用再度减弱，它们各自的状态变量成为了自身主导因素，进一步验证了图 5的结论。
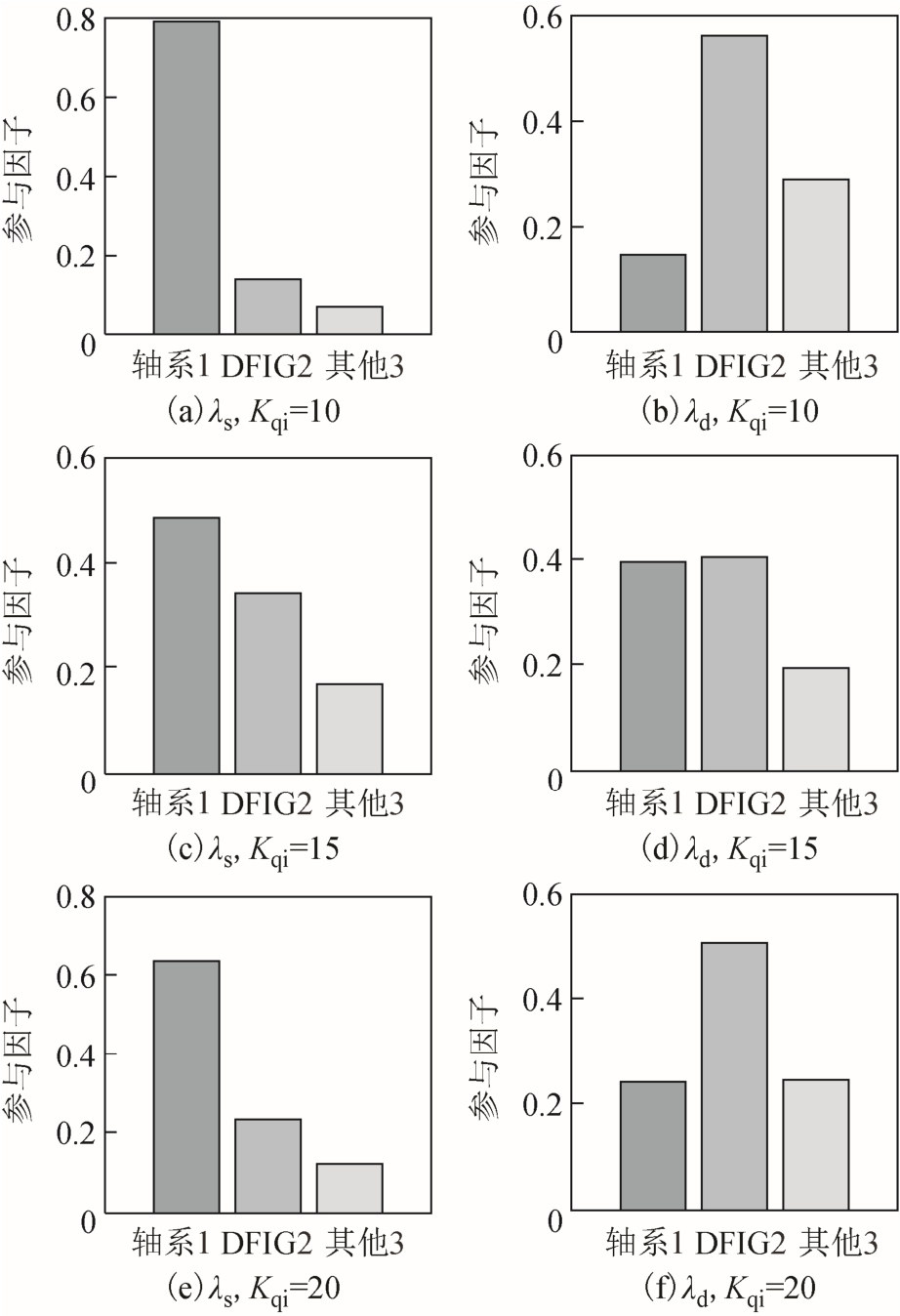
图6 不同qiK下dλ和sλ参与因子
Fig.6 Participation factor ofdλandsλwhenqiK was varied
图 7、图 8反映了同步机轴系振荡模式对参数Kqi的灵敏度 ∂λ s/∂Kqi以及DFIG风电场向轴系注入的阻尼转矩 D e w 随参数 Kqi变化的情况。由图 8可知，当系统中两个振荡模式发生动态交互后，振荡模式对所调参数的灵敏度将会迅速增大，并且在模式谐振最强烈的区域达到峰值（图中灰色区域，对应图5中圆形区域），此时DFIG换流器控制参数Kqi对轴系振荡模式稳定性的影响十分显著。同时，如图 7所示，DFIG注入同步机轴系的负阻尼转矩也达到了最大值，同步机轴系的次同步振荡稳定性最差。
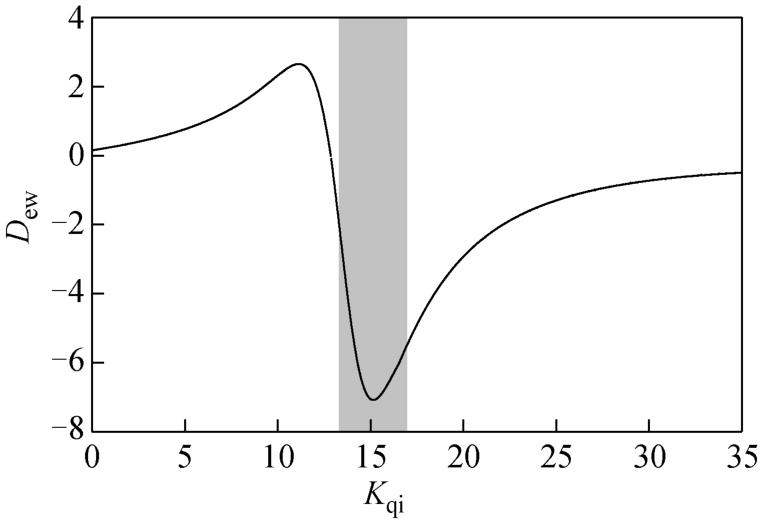
图7 qiK 变化过程中风机阻尼转矩 ewD
Fig.7 Change of damping torque ewD when qiK was tuned
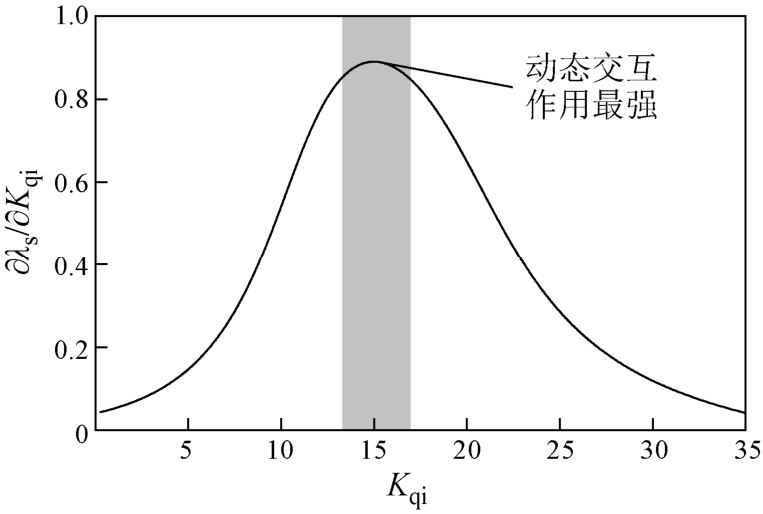
图8 K q i变化过程中灵敏度 ∂ λs/∂Kqi
Fig.8 Change of sensitivity ∂ λs/∂KqiwhenKqi was tuned
3.2.2 系统负荷大小对轴系稳定性的影响
在研究系统负荷对轴系稳定性的影响时，通过调整图 1所示电抗值 XL的大小等效调节发电机所供电负荷，其中XL包括传输线路本身电抗X1及等效负荷电抗X2。绘制 XL分别取 0.012(pu)、0.024(pu)、0.036(pu)时dλ和sλ的根轨迹，如图9所示，图中箭头方向代表Kqi增大方向。
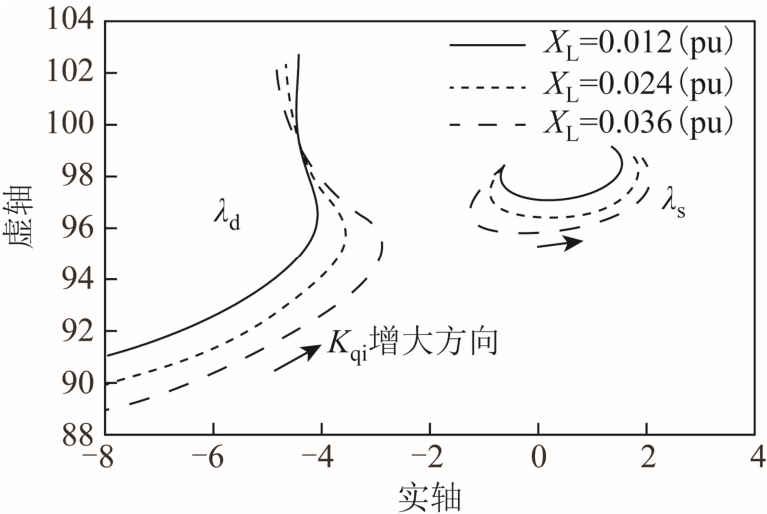
图9 不同负荷 LX 对应的根轨迹
Fig.9 Modal trajectories when LX was varied
对三种运行工况下dλ和sλ随Kqi变化的根轨迹进行对比分析。由图9可知，随着系统负荷 LX 的增大，同步机轴系不稳定区域逐渐扩大，DFIG换流器控制环节与同步机轴系之间的动态交互作用变强，dλ和sλ间的近似强模式谐振现象也变得更加明显。由此得出结论，同步机轴系发生次同步振荡的风险和系统所承担的负荷呈正相关的关系。
3.2.3 DFIG与同步机动态交互程度对近似强模式谐振现象的影响
为进一步分析 DFIG与同步机轴系之间动态交互作用对近似强模式耦合现象的影响，引入一个微小变量wε量化地反映二者间动态交互作用程度。将式（11）中从DFIG系统输出功率变量wPΔ、wQΔ到同步机转矩增量ΔTPk、ΔTQk的传递函数GP k (s)和GQ k(s)改写为 ε w G P 0(s)和 ε w G Q 0(s )。 G P 0(s)和 G Q 0(s)代表DFIG风电场并网后相应的传递函数。εw在0~1变化过程中λd和λs轨迹如图10所示。
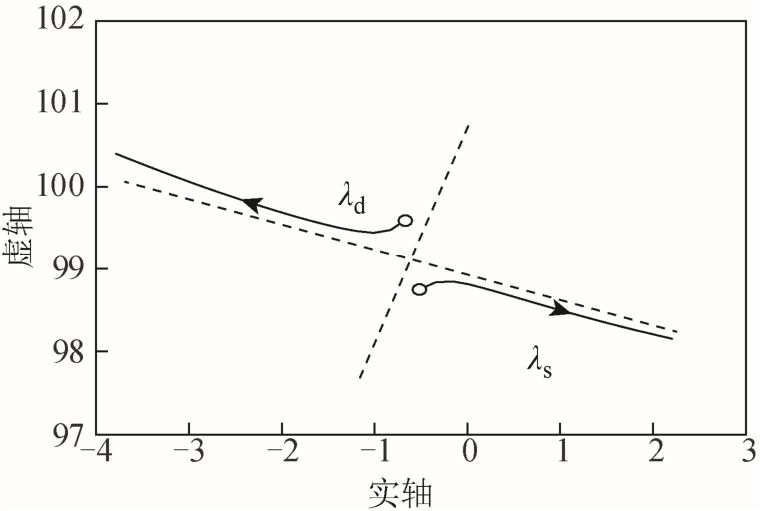
图10 wε变化下的根轨迹
Fig.10 Modal trajectories whenwεwas tuned
由图10可知，在DFIG换流器控制环节与同步机轴系之间的动态交互作用逐渐增强的过程中，dλ和sλ沿着相反的方向移动，运动轨迹符合近似强模式谐振理论。动态交互作用最终导致同步机轴系振荡模式sλ的实部由负变正，进入不稳定运行区域。
最后，为了验证本文线性化分析的正确性，图11给出了wε分别取0.1和0.8时系统非线性仿真图形。同步机在0.1s时发生20%的有功负荷扰动，持续 0.02s后恢复。分析同步机输出有功功率和无功功率的变化，发现当w0.1ε=时，随着扰动的消除，同步机输出功率很快趋于稳定，而当w0.8ε=时，同步机有功功率和无功功率在扰动消失后均发生振荡失稳，由此可知dλ和sλ之间的强交互作用引发了系统的次同步振荡。
图11 非线性仿真结果
Fig.11 Non-linear simulation results
4 结论
本文提出了一种改进复转矩系数法，通过建立含并网 DFIG电力系统的多输入、多输出闭环互联模型，研究了风电场并网引发的同步机组轴系次同步振荡，主要结论有：
基于特征值灵敏度理论，给出了并网风电场与同步机组轴系之间的动态交互作用计算指标，提出了一种用于分析并网风电场引发多机电力系统轴系次同步振荡的改进复转矩系数法。本文所提方法在计算量上较复转矩系数法略有增加，在计算精度上较复转矩系数法有显著的提升。该方法能够有效地判断风电场并网后同步机轴系振荡模式稳定性，且能分别反映稳态潮流变化和动态交互作用两方面的影响，解决了传统方法存在的局限性和准确性两方面问题。
从根轨迹、参与因子、参数灵敏度及阻尼转矩多个角度研究了 DFIG风电场振荡模式与同步机轴系振荡模式之间的近似强模式耦合现象，明确了其物理意义。
分析了风机换流器控制环节参数、输电系统负荷大小及风火发电机之间动态交互作用对同步机轴系与风机控制环节之间近似强模式耦合现象的影响，指出风机VSC参数的不合理、过大的线路负荷及动态交互作用均可能引发同步机轴系次同步振荡。
对 DFIG风电场并网引发单同步机系统和多同步机系统次同步振荡进行了算例研究，验证了所提出方法的正确性。
附 录
1. 仿真模型参数
附表1 第一标准模型同步发电机参数
App.Tab.1 Parameters of the synchronous generator
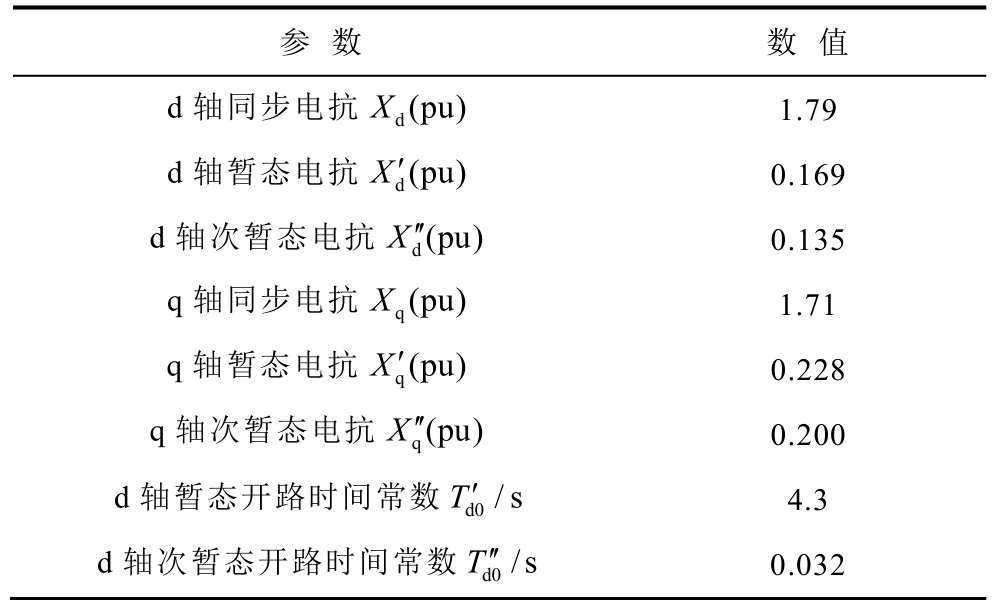
参 数 数 值d轴同步电抗 d(pu)X 1.79 d轴暂态电抗 d(pu)X′ 0.169 d轴次暂态电抗 d(pu)X′ 0.135 q轴同步电抗 q(pu)X 1.71 q轴暂态电抗 q(pu)X′ 0.228 q轴次暂态电抗 q(pu)X′ 0.200 d轴暂态开路时间常数 d0/sT′ 4.3 d轴次暂态开路时间常数 d0/sT′ 0.032
（续）
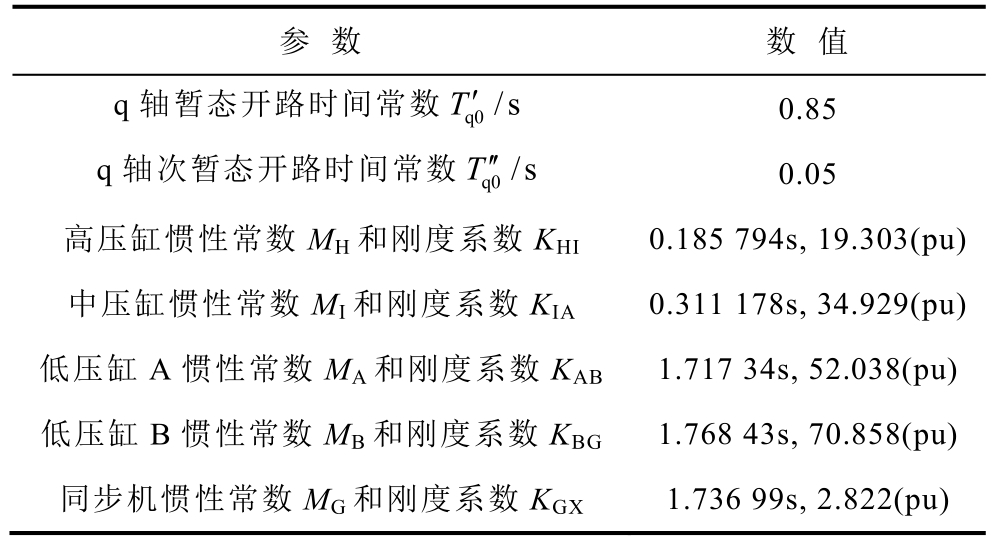
参 数 数 值q轴暂态开路时间常数 q0/sT′ 0.85 q轴次暂态开路时间常数 q0/sT′ 0.05高压缸惯性常数MH和刚度系数KHI 0.185 794s, 19.303(pu)中压缸惯性常数MI和刚度系数KIA 0.311 178s, 34.929(pu)低压缸A惯性常数MA和刚度系数KAB 1.717 34s, 52.038(pu)低压缸B惯性常数MB和刚度系数KBG 1.768 43s, 70.858(pu)同步机惯性常数MG和刚度系数KGX 1.736 99s, 2.822(pu)
附表2 DFIG参数
App.Tab.2 Parameters of DFIG
参 数 数 值定子绕组漏感Xls(pu) 0.092 31定转子绕组互感XM(pu) 3.952 79转子绕组漏感Xlr(pu) 0.099 55 GSC滤波电抗Xtg(pu) 0.1定子绕组电阻Rs(pu) 0.004 88转子绕组电阻Rr(pu) 0.005 49风机质量块惯性常数H2(pu) 4.29发电机质量块惯性常数H1(pu) 0.9风机、发电机质量块互阻尼D12(pu) 1.5轴系刚度系数K12(pu) 50 DC环节电容 C/μF 14 000 PLL环节PI控制参数 1, 10 RSC q轴（有功）外环控制PI参数 0.1, 5 RSC q轴电流内环控制PI参数 0.01, 20 RSC d轴（无功）外环控制PI参数 0.1, 10 RSC d轴电流内环控制PI参数 0.01, 20 GSC q轴直流电压外环控制PI参数 0.1, 5 GSC q轴电流内环控制PI参数 0.2, 10 GSC d轴电流内环控制PI参数 0.2, 10
附表3 输电线路及变压器参数
App.Tab.3 Parameters of transmission lines and transformers
参 数 数 值变压器 T1参数XT1(pu) 0.012变压器TD参数XTD(pu) 0.012变压器TN参数XTN(pu) 0.012输电线路RL(pu) 0.005输电线路XL(pu) 0.03
2. 改进复转矩系数法误差
对轴系振荡模式 5，随着 DFIG风电场出力变化及DFIG转子侧换流器有功电流内环控制参数 Kqi、转子侧换流器无功电流内环控制参数Kdi的变化，改进复转矩系数法与特征值分析法的计算误差见附表4。
附表4 改进复转矩系数法与特征值分析法误差
App.Tab.4 Error between the improved complex torque coefficients method and eigenvalue analysis method
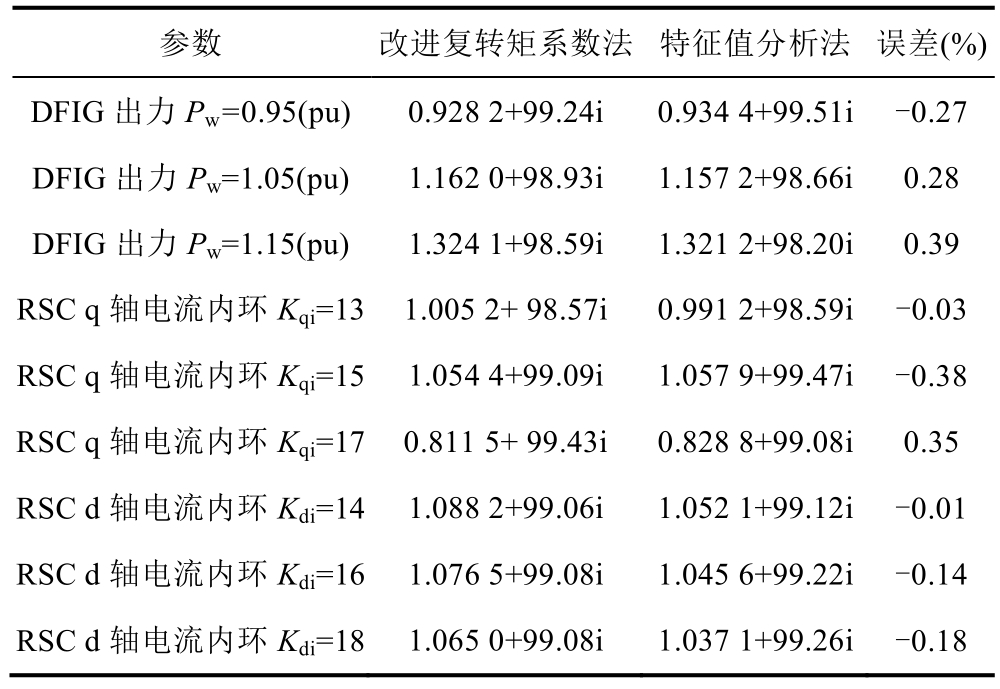
参数 改进复转矩系数法 特征值分析法 误差(%)DFIG出力Pw=0.95(pu) 0.928 2+99.24i 0.934 4+99.51i -0.27 DFIG出力Pw=1.05(pu) 1.162 0+98.93i 1.157 2+98.66i 0.28 DFIG出力Pw=1.15(pu) 1.324 1+98.59i 1.321 2+98.20i 0.39 RSC q轴电流内环Kqi=13 1.005 2+ 98.57i 0.991 2+98.59i -0.03 RSC q轴电流内环Kqi=15 1.054 4+99.09i 1.057 9+99.47i -0.38 RSC q轴电流内环Kqi=17 0.811 5+ 99.43i 0.828 8+99.08i 0.35 RSC d轴电流内环Kdi=14 1.088 2+99.06i 1.052 1+99.12i -0.01 RSC d轴电流内环Kdi=16 1.076 5+99.08i 1.045 6+99.22i -0.14 RSC d轴电流内环Kdi=18 1.065 0+99.08i 1.037 1+99.26i -0.18
[1] 张振宇, 王文倬, 王智伟, 等. 跨区直流外送模式对新能源消纳的影响分析及应用[J]. 电力系统自动化, 2019, 43(11): 174-181.Zhang Zhenyu, Wang Wenzhuo, Wang Zhiwei, et al.Impact analysis and application of cross-region HVDC delivery mode in renewable energy accommodation[J]. Automation of Electric Power Systems, 2019, 43(11): 174-181.
[2] 盛逸标, 林涛, 陈宝平, 等. 面向新能源外送系统次/超同步振荡的控制器参数协调优化[J]. 电工技术学报, 2019, 34(5): 983-993.Sheng Yibiao, Lin Tao, Chen Baoping, et al.Coordination and optimization of controller parameters for subsynchronous/super-synchronous oscillation in new energy delivery systems[J].Transactions of China Electrotechnical Society, 2019,34(5): 983-993.
[3] 张超, 王维庆, 王海云, 等. 风火打捆外送系统220kV电网次同步振荡监控策略研究[J]. 电力系统保护与控制, 2018, 46(11): 138-144.Zhang Chao, Wang Weiqing, Wang Haiyun, et al.Study on monitoring and control strategy of subsynchronous oscillation for 220kV power grid in wind-thermal-bundled transmission system[J]. Power System Protection and Control, 2018, 46(11): 138-144.
[4] 王玉芝, 王亮, 姜齐荣. 基于 STATCOM 的风电场SSCI附加阻尼抑制策略[J]. 电力系统自动化, 2019,43(15): 49-59.Wang Yuzhi, Wang Liang, Jiang Qirong. STATCOM based supplementary damping mitigation strategy for subsynchronous control interaction in wind farms[J].Automation of Electric Power Systems, 2019, 43(15):49-59.
[5] 苏田宇, 杜文娟, 王海风. 多直驱永磁同步发电机并联风电场次同步阻尼控制器降阶设计方法[J].电工技术学报, 2019, 34(1): 116-127.Su Tianyu, Du Wenjuan, Wang Haifeng. A reduced order design method for subsynchronous damping controller of multi-PMSGs parallel wind farm[J].Transactions of China Electrotechnical Society, 2019,34(1): 116-127.
[6] 陈宝平, 林涛, 陈汝斯, 等. 直驱风电场经 VSCHVDC并网系统的多频段振荡特性分析[J]. 电工技术学报, 2018, 33(增刊1): 176-184.Chen Baoping, Lin Tao, Chen Rusi, et al.Characteristics of multi-band oscillation for direct drive wind farm interfaced with VSC-HVDC system[J]. Transactions of China Electrotechnical Society, 2018, 33(S1): 176-184.
[7] Chowdhury M A, Shafiullah G M. SSR mitigation of series-compensated DFIG wind farms by a nonlinear damping controller using partial feedback linearization[J]. IEEE Transactions on Power Systems,2017, 33(3): 2528-2538.
[8] 肖湘宁, 罗超, 廖坤玉. 新能源电力系统次同步振荡问题研究综述[J]. 电工技术学报, 2017, 32(6): 85-97.Xiao Xiangning, Luo Chao, Liao Kunyu. Review of the research on subsynchronous oscillation issues in electric power system with renewable energy sources[J]. Transactions of China Electrotechnical Society, 2017, 32(6): 85-97.
[9] Du Wenjuan, Wang Yang, Wang Haifeng, et al.Concept of modal repulsion for examining the subsynchronous oscillations caused by wind farms in power systems[J]. IEEE Transactions on Power Systems, 2018, 34(1): 518-526.
[10] 张剑, 肖湘宁, 高本锋, 等. 双馈风力发电机的次同步控制相互作用机理与特性研究[J]. 电工技术学报, 2013, 28(12): 142-149.Zhang Jian, Xiao Xiangning, Gao Benfeng, et al.Mechanism and characteristic study on subsynchronous control interaction of a DFIG-based wind-power generator[J]. Transactions of China Electrotechnical Society, 2013, 28(12): 142-149.
[11] 陈晨, 杜文娟, 王海风. 风电场接入引发电力系统次同步振荡机理综述[J]. 南方电网技术, 2018,12(1): 84-93.Chen Chen, Du Wenjuan, Wang Haifeng. Review on mechanism of sub-synchronous oscillations caused by grid-connected wind farms in power systems[J].Southern Power System Technology, 2018, 12(1):84-93.
[12] 任必兴, 杜文娟, 王海风. UPFC与系统的强动态交互对机电振荡模式的影响[J]. 电工技术学报, 2018,33(11): 2520-2534.Ren Bixing, Du Wenjuan, Wang Haifeng. Impact of strong dynamic interaction between UPFC and system on electromechanical oscillation mode[J].Transactions of China Electrotechnical Society, 2018,33(11): 2520-2534.
[13] Badrzadeh B, Sahni M, Zhou Yi, et al. General methodology for analysis of sub-synchronous interaction in wind power plants[J]. IEEE Transactions on Power Systems, 2013, 28(2): 1858-1869.
[14] 高本锋, 李忍, 杨大业, 等. 双馈风电机组次同步振荡阻尼特性与抑制策略[J]. 电力自动化设备,2015, 35(12): 11-20.Gao Benfeng, Li Ren, Yang Daye, et al. Damping characteristics and countermeasure of DFIG subsynchronous oscillation[J]. Electric Power Automation Equipment, 2015, 35(12): 11-20.
[15] 刘晋. 双馈风电机组并网的次同步控制相互作用问题研究[D]. 北京: 华北电力大学, 2015.
[16] Hu Jiaobin, Wang Bo, Wang Weisheng, et al. Small signal dynamics of DFIG-based wind turbines during riding through symmetrical faults in weak AC grid[J].IEEE Transactions on Energy Conversion, 2017, 32(2):720-730.
[17] 杨琳. 新能源电力系统的次同步振荡与阻尼控制特性研究[D]. 北京: 华北电力大学, 2015.
[18] 吕勇, 雷涛, 黄国华, 等. 并网双馈风力机感应发电机效应研究[J]. 电力系统保护与控制, 2016,44(24): 154-158.Lü Yong, Lei Tao, Huang Guohua, et al. Induction generator effect analysis of doubly-fed wind generator connected to the power system[J]. Power System Protection and Control, 2016, 44(24): 154-158.
[19] Tabesh A, Iravani R. Frequency-response analysis of torsional dynamics[J]. IEEE Transactions on Power Systems, 2004, 19(3): 1430-1437.
[20] Tabesh A, Iravani R. On the application of the complex torque coefficients method to the analysis of torsional dynamics[J]. IEEE Transactions on Energy Conversion, 2005, 20(2): 268-275.
[21] 吕世荣, 刘晓鹏. 次同步谐振分析中复转矩系数与特征值之间的关系[J]. 电力系统自动化, 1999,23(3): 16-18.Lü Shirong, Liu Xiaopeng. Relationship between complex torque coefficients and eigenvalues in subsynchronous resonance analysis[J]. Automation of Electric Power Systems, 1999, 23(3): 16-18.
[22] 王积伟. 现代控制理论与工程[M]. 北京: 高等教育出版社, 2003.
[23] Seyranian A P. Sensitivity analysis of multiple eigenvalues[J]. Journal of Structural Mechanics, 1993,21(2): 261-284.
[24] Dobson I. Is strong modal resonance a precursor to power system oscillations?[J]. IEEE Transactions on Circuits and Systems, 2001, 48(3): 340-349.
[25] Canay I M. A novel approach to the torsional interaction and electrical damping of the synchronous machine part I: theory[J]. IEEE Transactions on Power Apparatus and Systems, 1982, 101(10): 3630-3638.
[26] 倪以信, 陈寿孙, 张宝霖. 动态电力系统的理论和分析[M]. 北京: 清华大学出版社, 2002.
[27] Demello F P. Concept of synchronous machine stability as affected by excitation control[J]. IEEE Transactions on Power Apparatus and Systems, 1969,88(4): 316-329.
[28] Du Wenjuan, Bi Jingtian, Cao Jun, et al. A method to examine the impact of grid connection of the DFIGs on power system electromechanical oscillation modes[J]. IEEE Transactions on Power Systems, 2016,31(5): 3775-3784.
[29] IEEE Subsynchronous Resonance Working Group.First benchmark model for computer simulation of subsynchronous resonance[J]. IEEE Transactions on Power Systems, 1977, 96(5): 1565-1572.
[30] IEEE Subsynchronous Resonance Working Group.Second benchmark model for computer simulation of subsynchronous resonance[J]. IEEE Transactions on Power Apparatus and Systems, 1985, 104(5): 1057-1066.
[31] Fan L, Kavasseri R, Miao Z L, et al. Modeling of DFIG-based wind farms for SSR analysis[J]. IEEE Transactions on Power Delivery, 2010, 25(4): 2073-2082.