0 引言
电网互联化和智能化的发展使得当今电网日趋复杂开放;在电网规模不断扩大的同时,不确定性风险因素也日益加剧[1-2]。这对电网的安全稳定分析提出了更高的要求。电力系统的暂态稳定评估即要求在发生一个较大扰动时,及时判断系统能否保持同步稳态。传统的以物理模型为依据的电力系统暂态稳定评估方法在面对复杂大电网时效率较低[3-4],难以满足实时在线的评估要求,且由于一些不得已的简化和假设可能会与实际情况造成偏差。目前,同步相量测量装置和广域测量系统[5]的发展使得实时采集海量的电力系统同步数据成为可能,这也为研究人员尝试从数据挖掘的角度解决该问题带来了新的思路。
基于数据挖掘的暂态稳定评估方法由于能够满足实时的在线评估要求以及具有较高的评估精度,近年来受到越来越多学者的关注。其将电力系统暂态稳定评估问题当作两分类的模式识别问题。通过建立一组与暂态稳定状态间强相关的暂态特征集合并采集大量的样本数据,利用分类模型对暂态特征集和暂态稳定状态间的非线性映射关系进行离线学习;进而利用训练完成的分类模型对新接收的电网采样数据进行在线评估,达到实时的暂态稳定评估要求。相较于传统的以物理模型驱动的暂态稳定评估方法,基于数据挖掘的暂态稳定评估方法由于以数据为驱动,其在满足评估快速性的基础上同时具有较高的评估精度。
目前针对基于数据挖掘的暂态稳定评估方法的研究主要包括特征选择和分类器的构造两方面。在特征选择的研究上,目前已有主成分分析[6-7]、文化算法[8]、支持向量机[9]等方法用于暂态特征提取,并取得了不错的效果。在分类器构造方面,目前的暂态稳定评估模型主要包括支持向量机[3,10-14]、决策树[15-17]和神经网络[6,18-19]等。其中文献[10]和文献[11]分别从模型参数和输入特征空间的角度提出基于集成多支持向量机的电网暂态稳定评估方法。文献[3]针对传统支持向量机进行改进,并提出一种正则化投影孪生支持向量机的暂态稳定评估方法。文献[15-16]则以决策树为基础设计预测模型。然而,以上所提方法皆为浅层模型,评估精度仍有待进一步提高。此外,浅层模型在处理大规模的电网数据时常常会存在泛化能力较差、训练效率低等问题[20]。相比之下,基于深度学习模型的暂态稳定评估方法则更具优势。一方面,通过多层串行的深度架构可以对特征进行抽象表征学习以加强特征量与标签属性间的非线性映射关系;另一方面,相较于浅层模型,深度学习方法的学习能力和泛化能力更强,评估精度更高。然而,深度学习模型通常需要建立在大量样本数据的基础上,在样本数量较少的情况下,由于对数据分布的拟合精度不足,评估精度通常较低。此外,为了对训练样本的分布进行无偏估计,现有的以深度置信网络为代表的深度学习方法[20-23]往往假设暂态稳定样本与暂态失稳样本间的分布均衡,且缺乏对暂态失稳样本的重视;在实际电网运行中,电网在绝大多数情况下都保持暂态稳定的状态,暂态失稳的情况十分少见,因此暂态稳定样本与暂态失稳样本在数据量上往往呈现明显不平衡关系。传统分类模型在学习训练时为了提高评估精度,往往会更加偏重样本数量占多数类的暂态稳定样本,从而造成对暂态失稳样本的分类精度较低。而在实际中,若将暂态失稳样本误判为暂态稳定样本,则会影响系统调度人员及时采取保护措施,对电网安全造成重大威胁。因此,在保证总的评估性能的基础上,应更注重对暂态失稳样本评估的准确率。
针对以上问题,本文提出一种融合邻域粗糙约简与深度森林的电力系统暂态稳定评估方法。将由决策树集成得到的森林进一步集成,并通过级联的方式达到对原始暂态特征的表征学习,以抽象地生成更利于分类学习的高维特征空间。利用邻域粗糙约简在不同粒度级别下寻找多组互具差异的最优特征子集以对原始特征空间进行再表征,来进一步强化深度森林的表征学习能力。通过引入加权投票机制,提高分类过程对暂态失稳样本的重视。实验结果表明,所提方法不仅能够提高评估精度,且可以有效降低对暂态失稳样本的误分率;相比传统的深度学习方法,所提方法在样本规模较小时也能取得较好的评估结果,且受无关特征以及样本集不平衡度的影响较小,具有一定的鲁棒性与适用性。
1 暂态特征集的构建
基于数据挖掘的暂态稳定评估方法核心在于设计分类模型对电网暂态特征量和暂态稳定状态间(类别)的复杂非线性映射关系进行学习拟合,因而,构建一组与电网暂态稳定状态高度相关的暂态特征集是此类方法的基础与关键。目前共有两种方式构建电网的初始暂态特征集合。第一种直接以故障发生前后系统的潮流量,如系统中各母线电压幅值、相位,有功、无功功率分布等构建初始暂态特征集合。该方法直接基于电网底层原始数据进行分类器学习,不依赖专家经验进行特征选取[18],但是所选暂态特征量的规模随着系统规模的变化有较大的浮动。在实际大系统中,过多的输入特征量不仅会造成严重的计算负担,降低分类学习算法的精度,同时容易出现“维数灾”现象[8]。第二种则是以故障前后系统参数的组合变量来构建初始特征集合。通过考虑在不同的时间和空间因素下选取一组系统的“组合特征量”,来对暂态稳定状态进行充分表征。该方法需要一定的专家经验知识,但优点在于所选特征集固定,不随系统对象的变化而变化,更具一般性。同时由于考虑到时空间上的完备性,其能够较好地反映出运行环境的改变对系统暂态稳定特性的冲击影响。本文选择第二种方法来构建初始暂态特征集。
利用“组合特征量”方法来构建初始暂态特征集时,通常要考虑系统性原则、主流性原则和实时性原则三个方面[8,19,24],即要求所选特征量要满足:①所选特征量的规模不随系统变化而改变,应为系统中各元件状态变量的组合指标;②所选特征量与暂态稳定状态之间存在较高的关联性;③所选特征量应在时间上具有完备性,要求能反映系统在故障发生前后的状态,以更充分地了解故障对系统造成的冲击影响。根据以上三个原则,在大量仿真实验的基础上,根据对现有文献的学习和总结[9-15,19-20,24-26],构建了表1所示的32维暂态特征量,表中t0、t1、t2分别表示故障发生前、故障发生时刻和故障清除时刻。
表1 暂态特征集
Tab.1 The transient feature set

特征 描述1 0t时刻机械功率平均值2 系统的平均功率调整3、4 1t时刻发电机所受有功冲击最大、最小值5 1t时刻发电机加速功率平均值6 1t时刻加速度最大的发电机的相对转子角度7 1t时刻相对转子角最大值8, 9 1t时刻转子加速度平均值、最大值10、11 1t时刻发电机转子加速度、加速功率的方差12 2t时刻发电机加速功率平均值13、14 2t时刻发电机转子动能最大值、平均值15 2t时刻转子加速度最大发电机的转子动能16 2t时刻对系统的冲击17 2t时刻转子动能最大的发电机的相对转子角度
(续)

特征 描述18 12,t t时刻相对转子角差值19 2t时刻相对转子角最大值20 12,t t时刻相对转子角速度差值21 2t时刻相对转子角速度最大值22 2t时刻发电机转子角速度极差值23 12,t t时刻相对转子加速度差值24 2t时刻相对转子加速度最大值25~27 2t时刻转子加速度、转子动能、动能变化率极差值28 2t时刻发电机有功功率总和29 2t时刻领前机与殿后机转子角差值30 2t时刻发电机加速功率方差31、32 2t时刻发电机转子角速度、机械功率平均值
从表1可以看出,本文所构建的暂态特征量不受系统规模的影响,皆为系统中各元件状态变量的组合指标。在时间上涵盖稳态时刻(特征 1和 2)、故障发生时刻(特征3~11)以及故障清除时刻(特征 12~32)三个不同阶段的系统状态量,能够充分反映故障给系统带来的冲击。在特征量上的选取以反映转子状态以及系统运行水平的系统物理量的组合指标为主。其中特征6、7、17~19、29与转子角有关,反映了发电机的同步运行状态;特征 5、8~15、20~27、30、31与转子速度和加速度有关,反映了扰动对转子运动产生的影响;特征 1~4、16、28、32与系统的运行水平有关,反映了故障对系统功率平衡的影响。因此所建立的暂态特征集能够很好地揭示故障冲击对系统稳定趋势带来的影响。
2 模型基本原理
从数据挖掘的观点来看,电力系统暂态稳定评估本质上为对相应数据集进行学习分类的过程。为了便于分析,本文将该分类任务描述成一个决策系统DS = U, C, D, f 的形式。式中, U = { x 1 , x 2 ,… ,xm}为数据集中所有样本 x i的集合, i = 1,2,…,m;C = { c 1 , c2 , … ,c 32}为样本的暂态特征集合,也称作条件属性。其中 ci对应表1中的第i条特征;D为样本的标签属性,也称作决策属性,代表样本的暂态稳定状态。若样本不稳定,则标签取为0,反之则取为1。f为一个信息函数,用来指定样本在相应特征属性下的取值,记样本 xi在特征c下的取值为 f ( xi, c)。
2.1 邻域粗糙约简
由于暂态特征的构建依赖于专家经验,在构建完初始暂态特征集后,通常可以对其做进一步的压缩或约简,以提取关键特征并减少特征集合的冗余性[9,12,26]。为此,本文引入邻域粗糙集[27]的方法来对初始暂态特征集做进一步的约简。
对于一个暂态稳定评估的分类任务DS=U, C, D, f,其中,C为条件属性(暂态特征)集合,B⊆C,∀xi∈U,定义xi在特征空间B中的邻域为
式中,δ为邻域阈值,为介于0和1之间的实数;![]() 为距离函数,表示样本 xi和样本 x j在特征空间 B下的相似度,ΔB ( x i , xj)越大,则表示在特征空间B下 xi和 x j的相似度越低。式(1)表示在特征集合B下,所有和样本 xi具有相似特征值的样本集合。δ则起到控制样本邻域粒度大小的作用,δ越小, xi的邻域样本与xi的相似度越高,邻域粒内的个体也越少。
为距离函数,表示样本 xi和样本 x j在特征空间 B下的相似度,ΔB ( x i , xj)越大,则表示在特征空间B下 xi和 x j的相似度越低。式(1)表示在特征集合B下,所有和样本 xi具有相似特征值的样本集合。δ则起到控制样本邻域粒度大小的作用,δ越小, xi的邻域样本与xi的相似度越高,邻域粒内的个体也越少。
进一步地,将整个样本集按照决策属性(标签属性)D划分为稳定样本集合 d1以及不稳定样本集合 d 0,则定义样本集关于特征集合B的正域为
其中
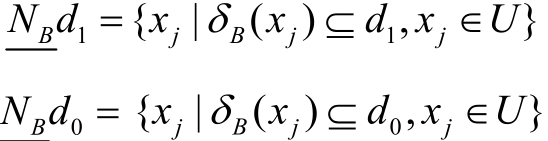
由式(2)可知,若某个样本在正域中,则所有与其有相似特征值的样本都拥有相同的标签类别。这说明在特征集合B下可以准确地对该样本进行分类。正域内的样本越多,则说明特征集合B的可分性越好,分类能力越强,越有利于分类算法的学习。类似地,称 B N B (D)= U - P OSB(D)为样本集关于特征集合B的边界域。边界域反映了样本集在特征集合B下相对标签属性的不一致程度。相比于正域内的样本,边界域的样本更容易被误分。正域的大小反映了不同特征集合的分类能力。为了对特征进行约简,只需寻找到一个特征子集,使其相对决策属性的正域大小与原特征集相同即可。为实现这一目标,可以使用基于filter算法的前向特征选择策略。将约简集合初始化为一个空集,每次添加使样本集相对当前约简集合的正域最大化的特征,不断重复上述过程直至满足停止条件。具体步骤如下:
1)对暂态稳定评估的分类任务DS = U, C, D, f,令约简集合RED=φ,给定邻域阈值δ。利用minmax标准化方法将数据归一化。
2)对每一个 C - R ED中的特征 a i,计算POSa i ∪RED (D), 找 出 满 足 POSal ∪RED (D)=maxi P OSai ∪RED (D)的特征 a l,并将其放入约简集合中,即RED = R ED ∪ a l。
3)若 P OS R ED (D ) ≠ P OSC (D),则继续转入步骤2)执行,否则输出约简特征集合RED。
通过设定不同的邻域阈值δ,可以控制样本的邻域粒大小,从而得到在不同粒度级别下的约简结果。
2.2 决策树森林
决策树是一种具有树形结构的分类模型,其从根节点出发,在每个子节点处进行特征选择以及样本划分以得到不同节点规则;每个子节点都对应一条特征,而每个节点规则代表在所选特征下对样本的一种划分方式。根据所得节点规则依次将不同样本分配到各个子节点中。递归以上过程,不断地对样本进行划分,直至到达叶节点。每个叶节点代表样本的一种类别标签。对于决策树而言,在各个节点处的特征选择以及样本划分方式至关重要。目前常用的用于决策树节点特征选择的度量方法通常包括信息增益比以及基尼指数两类。对于一个暂态稳定评估的分类任务DS = U, C, D, f,C为条件属性集合,c∈C;D为决策属性,其将样本集U划分为稳定样本集合 d1和不稳定样本集合 d 0。若根据特征c下的某一划分值将样本集 U划分为 U 1和 U 0两部分,则对于样本集U,信息熵定义为
特征c对数据集U的信息增益比定义为

对于样本集U,基尼指数定义为
特征c对数据集U的基尼指数定义为
通过对多棵决策树进行集成,可以进一步组成决策树森林。决策树森林属于集成学习模型,通过少数服从多数的方式进行投票并给出最终决策结果。由于其综合考虑了多个模型的预测结果,具有较高的评估精度以及较强的鲁棒性。根据子分类器的输入空间构成以及特征选择方式,决策树森林又可进一步分为随机森林[28]、完全随机树森林[29]与极端随机树等[30]。具体来说,对于含有n个输入特征的决策系统,随机森林通过随机选取 m ( m <n)个子特征作为每棵树的输入特征集,并在该随机子集内根据信息增益比或基尼指数寻找每个节点上的最佳特征及划分点。本文采用文献[28,31]推荐的经验值 作为子特征选择个数m的取值;完全随机树森林在每棵树的节点上随机从原始输入特征中选择一个特征并通过信息增益比或基尼指数来寻找最优划分点;而极端随机树在每棵树的节点上对特征以及划分点均做随机选择。
作为子特征选择个数m的取值;完全随机树森林在每棵树的节点上随机从原始输入特征中选择一个特征并通过信息增益比或基尼指数来寻找最优划分点;而极端随机树在每棵树的节点上对特征以及划分点均做随机选择。
3 融合邻域粗糙约简与深度森林的暂态稳定评估模型
深度森林[31]是一种深度架构下的基于决策树森林的集成模型,其通过将多个互异的决策树森林进一步集成来强化模型的多样化学习能力,通过逐级串联集成的森林以实现深度学习架构中的多层表征学习。深度森林主要包括级联结构及输入特征的加强再表征两部分。
3.1 级联森林结构与投票加权机制
深度森林是由多级学习层串行组成的,其中每一级的学习层都由数个决策树森林集成得到;每一层对样本标签的输出概率向量连同原始输入特征一起重新组成下一级学习层的输入特征,其级联结构如图1所示。

图1 深度森林的级联结构
Fig.1 The cascade structure of deep forest
决策树森林由若干决策树构成,每棵决策树均会输出相应的暂态稳定评估结果。对于学习层中的每一个决策树森林,通过计算森林中评估结果稳定的树和评估结果失稳的树的占比分布,来最终生成一个二维的类分布向量,表示样本位于不同暂态稳定状态下的概率。若每一级包含M个决策树森林,则每一层会输出M个关于类分布的2维概率向量,将其串联组成2×M维的增强特征。这2×M维增强特征将连同原始的32维输入特征一起连接起来,组成新的特征向量,作为下一级学习层的输入特征。通过对特征向量的逐级抽象强化,可以提取更有利于分类学习的高阶特征,达到深度学习框架中的多层表征学习效果。为了保证学习多样化,在每一级学习层中,本文选用基于信息增益比和基尼指数的随机森林(分别记为RFI和RFG),基于信息增益比和基尼指数的完全随机树森林(分别记为CRFI和CRFG)以及极端随机树(记为ERF)共五种不同类型的森林。
在电力系统暂态稳定评估问题中,暂态失稳样本往往较少,与暂态稳定样本在数量上呈现明显不平衡关系,因而分类器往往会倾向于有利于暂态稳定样本分类的方向学习。然而误判暂态失稳样本的代价更高,因此在实际中,要更加注重提高对暂态失稳样本的评估准确率。为此,在每一级生成类分布向量时,引入如图2所示的加权投票机制,来加强学习过程对暂态失稳样本的重视。对于一个暂态稳定评估的分类任务DS = U, C, D, f,U=U s ∪ U u, x∈U 。其中 U s和 U u分别为稳定样本与失稳样本。若决策树森林由Y棵决策树构成,其中评估结果为稳定的树共 Ys棵,评估结果为失稳的树共 Yu棵,则定义该森林关于类分布的概率为
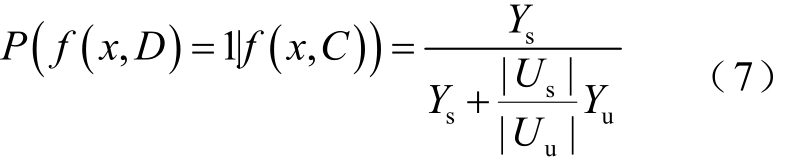

图2 加权投票机制
Fig.2 The weighted voting mechanism
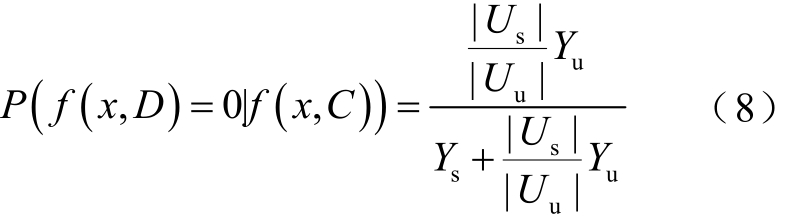
式(7)和式(8)分别表示在给定样本输入特征值时,评估结果为暂态稳定以及暂态失稳的条件概率。其根据两类样本间的不平衡程度,自适应地对类向量进行加权处理,给与暂态失稳样本更高的权值。样本的不平衡程度越严重,则对失稳样本赋予的权值越高。因而在学习过程中能够更好地加强对暂态失稳样本的重视,减少对暂态失稳样本的误判。
在深度森林的训练过程中,每增加一级都会在验证集上对准各级联森林进行验证评估;每输入一个预测样本,在每一级学习层对所有森林生成的概率向量取平均,概率输出最大的类别将作为样本的预测标签。若分类性能没有增长则停止训练。
3.2 输入特征加强再表征
相比浅层学习模型,深度学习方法的优势在于其强大的处理特征关系的能力。而通过将原始特征空间进行再表征,可以强化特征量与标签属性间的非线性映射关系,从而进一步加强深度森林的表征学习能力[31]。本文利用邻域粗糙约简在不同粒度级别下寻找多组互具差异的最优特征子集以对原始特征空间进行再表征,如图3所示。

图3 基于邻域粗糙集的多粒度约简与特征再表征
Fig.3 Multi-granulated reduction and feature rerepresentation based on neighborhood rough sets
在图3中,通过对邻域粗糙约简设置不同的邻域阈值,原始特征空间被约简为数个不同的特征子空间。分别在每个特征子空间下利用 RFI、RFG、CRFI、CRF、ERF五种森林对样本进行训练;每个森林将会生成一个关于类分布的2维概率向量,因此样本在每个特征子空间下共会生成10维的概率向量。将N个特征子空间下生成的概率向量串联起来,则原始的 32维初始特征向量将会被重新表征为10×N维的高阶特征。对输入特征的加强再表征提供了比原始特征空间更为充分的信息,且所选取的特征子空间差异越大,表征能力越强,学习效果也越好。
融合邻域粗糙约简与深度森林的整体评估模型如图4所示。利用邻域粗糙约简在不同粒度级别下寻找数个互具差异的特征子空间,在这些特征子空间下对原始特征向量进行再表征;深度森林的每一级学习层由五种不同类型的决策树森林构成,每一层都将输出10维的类向量,该类向量将会作为增强特征与再表征特征串联组成下一级学习层的输入特征。假设再表征特征维数为60,则每一级的输入都为70(=60+10)维的高阶抽象特征。最终模型将取最后一级五类森林生成的2维类向量的平均值,输出概率最大的标签作为模型预测结果。

图4 融合邻域粗糙约简与深度森林的评估模型结构
Fig.4 The structure of evaluation model integrating neighborhood reduction and deep forest
融合邻域粗糙约简与深度森林的暂态稳定评估流程所提暂态稳定评估模型框架如图 5所示。图 5中主要包括离线模型训练及在线暂态稳定评估两部分。在线下通过时域仿真采样特征数据,利用邻域粗糙约简确定特征子空间并对原始输入特征进行再表征,在此基础上进行深度森林模型训练。每当收到电网在线特征数据,在由线下邻域粗糙约简得到的特征子空间中将其进行再表征,随后送入训练完成的深度森林模型中进行同步评估,给出电网暂态稳定状态的预测结果,为电网调度人员做进一步决策提供支持。

图5 电力系统暂态稳定评估模型框架
Fig.5 The framework of power system transient stability assessment
4 实验分析
为验证本文所提评估模型的有效性,在IEEE 10机 39节点系统[32]上进行时域仿真,并根据表 1中的特征进行数据采集。在仿真中考虑标准系统拓扑以及N-1故障两种运行环境。在N-1故障环境下假设系统中任意一条传输线或变压器因故障而失效。以5%为步长,设置80%~125%共10个不同的负荷水平,同时发电机出力做出相应改变。在每种运行环境下随机选择20个故障位置,故障类型设置为三相短路,假设在0.1s发生故障,并分别在0.2s、0.25s、0.3s、0.35s时清除故障。故障清除后线路重合,系统拓扑结构不变。仿真时长设为5s。以仿真结束时系统中任意两台发电机的功角差是否超过180°来判断系统的暂态稳定状态,若超过180°则判定系统暂态失稳,相应的类别标签记为 0;否则判定系统稳定,类别标签记为1。以上仿真均在Matlab/Simulink中实现。仿真共生成8 000组样本数据,其中暂态稳定样本5 104组,暂态失稳样本2 896组。在完成样本采样后,采用Min-Max标准化方法对所有样本数据进行归一化,以消除属性量纲的差异对学习过程造成的影响。
4.1 模型评估指标
鉴于电力系统暂态稳定评估问题具有样本不平衡及错分代价不平衡的特点,为更加全面地描述模型性能,在实验中选择表2所示的分类准确率(AC)、安全度(SD)、G-means指标(GM)以及F-measures指标(FM)进行性能评估。表中 TS、FS、TU、FU分别表示正确分类的稳定样本数、错误分类的稳定样本数、正确分类的失稳样本数、错误分类的失稳样本数。其中,安全度反映模型对暂态失稳样本的分类准确率,安全度越大,则对暂态失稳样本的误分率越低,系统相对安全性越高;G-means指标综合考虑了对暂态稳定样本与暂态失稳样本的评估准确率,G-means值越大,模型对不同类别样本的学习越平衡,评估性能越好;F-measures指标则综合考虑了失稳样本评估准确率与召回率,F-measures值只有在对失稳样本分类准确率提高的同时保持对稳定样本分类水平低牺牲程度的情况下才会增大。为了避免实验结果的偶然性,本文在实验中均采用十折交叉验证的方式来计算以上各模型性能指标。
表2 模型度量指标
Tab.2 Model evaluation index

指标 表达式 性能度量AC +TSTU TSFSTU FU+ + + 模型对总样本的分类正确率SD TU TU FU+ 模型对失稳样本分类正确率GM TS TU TSFS TU FU+ +·模型对两类样本的综合分类评估性能FM TU TU TU FS TU FU+ +·模型对失稳样本在准确率与查全率上综合评估性能
4.2 模型参数影响
本文所提模型参数主要有两类,包括邻域粗糙约简阶段邻域阈值的设定以及模型中决策树森林包含的树的数量。在邻域粗糙约简阶段,首先按照文献[27]中推荐的邻域阈值范围[0.1,0.3],以 0.02为步长设定相应的邻域阈值进行约简运算,并挑选出其中差异性最大的若干组约简结果作为最终的特征子集。具体来说,所选的每对特征子集间应具有至少30%不同的特征以保证学习的多样性。此外,为保证再表征后的特征具有更好的分类性能,通常要将其映射到更高维的空间中进行高阶抽象,同时考虑到转换后数据的内存开销不宜过大,通常再表征的特征集规模可以取为原特征集的 2~4倍,相应的可以通过邻域粗糙约简方法取不同数量的特征子集。本文共选取6组特征子集,所得结果见表3。
表3 邻域粗糙约简结果
Tab.3 Results of neighborhood rough reduction

粒度级别 约简特征子集1 13,9,17,7,6,26,8,12,4,2,1,11,25,3,5,30 2 13,16,9,8,26,15,7,6,4,10,20,17,2,14,3,1,30,5,31,11,21 3 13,16,9,8,7,3,26,15,6,20,10,2,11,4,12,1,17,14,5,22,31,19,21 4 13,9,14,26,12,8,6,15,4,2,11,3,25,1,5,19,20,21,27,7,10,30,17 5 13,16,20,1,8,26,9,6,10,4,7,2,15,17,14,23,3,21,30,31,5,11,22,12,28 6 13,9,14,26,7,12,6,4,8,15,2,11,25,1,3,5,19,20,21,27,10,16,17,30,18,29
表3中特征的顺序按照在邻域粗糙约简算法中选择的顺序给出。最终选定的特征子集共有6组,通过在相应的特征子空间下对原始输入特征进行加强,可以得到60维的再表征特征,其将进一步与每一级学习层的10维类向量串联到一起组成70维的高阶抽象特征,作为下一级的输入特征参与学习。
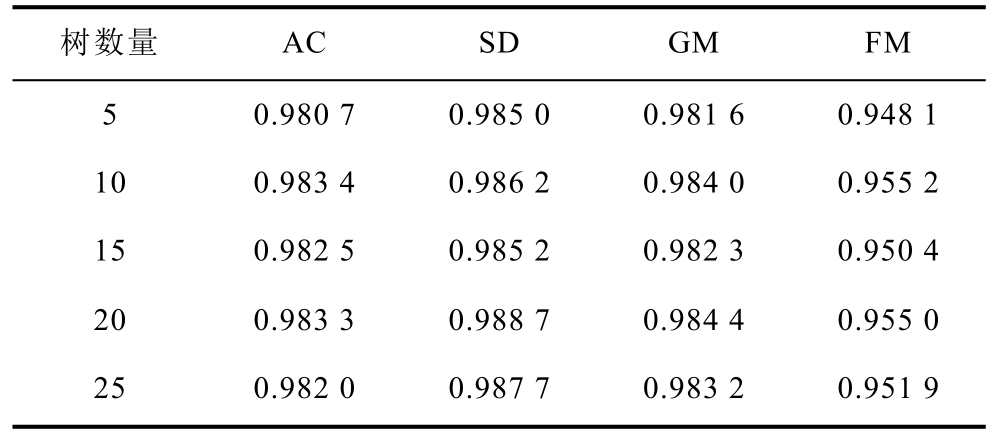
进一步研究决策树森林中所含树数量对模型性能的影响。以5为步长,设置决策树森林中的树数量从5变化到25。在不同参数下利用十折交叉验证对模型性能进行评估,结果见表4。
表4 不同数量树下的模型性能
Tab.4 Model performance with different number of trees
树数量 AC SD GM FM 5 0.980 7 0.985 0 0.981 6 0.948 1 10 0.983 4 0.986 2 0.984 0 0.955 2 15 0.982 5 0.985 2 0.982 3 0.950 4 20 0.983 3 0.988 7 0.984 4 0.955 0 25 0.982 0 0.987 7 0.983 2 0.951 9
从表4中可以看出,在每个决策树森林中包含超过10棵决策树时,模型性能不再有显著提高,并开始趋于稳定状态。为了减轻模型的计算负荷以及避免对存储空间的不必要浪费,在下文实验中,本文设定模型中每一个森林中包含10棵决策树。
4.3 不同模型性能对比
为验证模型性能,选取常用的电力系统暂态稳定评估分类器进行对比分析。选取的分类器模型包括 C4.5决策树、分类回归树(Classification and Regression Tree, CART)、朴素贝叶斯(Naïve Bayes,NB)、支持向量机(Support Vector Machine, SVM),以及人工神经网络(Artificial Neural Network, ANN)。其中,ANN采用三层隐层结构,训练算法采用动量梯度下降算法;SVM采用 Matlab工具箱的默认参数设置(线性核、序列最小最优化算法)。方便起见,本文算法在下文中简记为NRRDF。结果见表5。
表5 不同模型性能比较
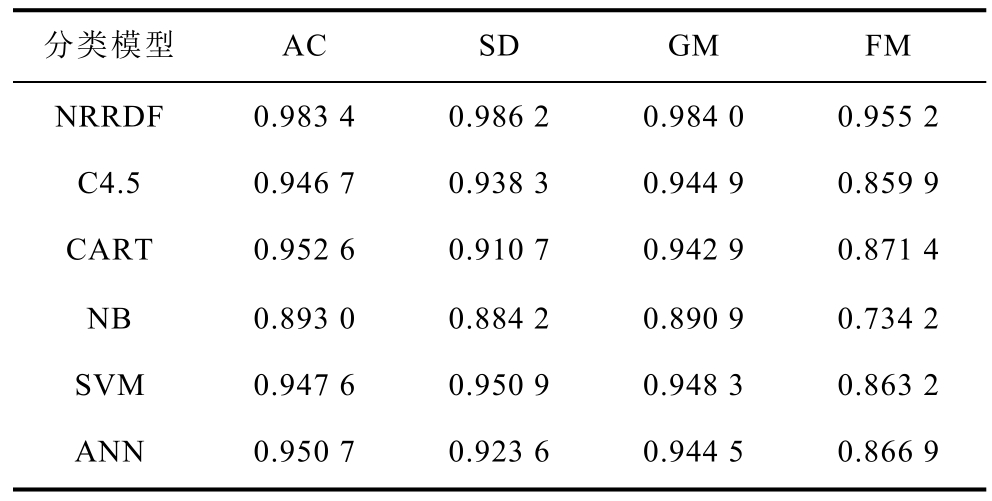
Tab.5 Performance comparison of different models
分类模型 AC SD GM FM NRRDF 0.983 4 0.986 2 0.984 0 0.955 2 C4.5 0.946 7 0.938 3 0.944 9 0.859 9 CART 0.952 6 0.910 7 0.942 9 0.871 4 NB 0.893 0 0.884 2 0.890 9 0.734 2 SVM 0.947 6 0.950 9 0.948 3 0.863 2 ANN 0.950 7 0.923 6 0.944 5 0.866 9
由表5可以看出,相比其他方法,本文所提方法在四个评估指标上均具有最佳的性能表现,其不仅具有较高的总体评估精度,同时能够提高对暂态失稳样本的重视,有效减少对暂态失稳样本的误判。以 ANN为例,本文所提模型在总的分类精度上提高了 3.27%,而对于暂态失稳样本的分类精度则提高了 6.26%。这是由浅层模型本身的学习局限性所造成的。一方面,浅层模型并不能对特征输入进行高效的表征学习,难以充分提取特征中的有用信息,因而对许多复杂非线性映射问题的泛化学习能力有限;另一方面,现有方法在学习过程中均假设不同类别的样本分布均匀,缺乏对样本不平衡性的重视。相比之下,本文所提模型在深度框架下通过对原始特征输入的加强再表征以及多级串行的特征学习结构,可以有效地对特征信息进行高阶抽象变换,挖掘更多隐含在数据中的丰富信息,提高模型的学习能力。此外,由于在学习过程中根据样本不平衡度自适应地对类向量进行加权处理,给予了暂态失稳样本更高的权值,因而模型能够有效提高对暂态失稳样本的重视,减少误判率。
为了进一步反映模型对未经训练的电网拓扑结构下特征数据的适应性,随机抽取某电网拓扑结构下采集的全部800组数据作为测试数据,剩余的在其他拓扑结构下采集的7 200组数据作为训练数据,对以上各模型性能进行测试,所得结果见表6。
表6 在未知电网拓扑结构下的模型性能比较
Tab.6 Peformance comparison of different models in unknown power network topology structure

分类模型 AC SD GM FM NRRDF 0.948 7 0.969 1 0.953 9 0.856 5 C4.5 0.910 0 0.849 4 0.893 1 0.738 6 CART 0.923 7 0.864 9 0.907 4 0.774 9 NB 0.667 5 0.942 1 0.710 6 0.464 4 SVM 0.890 0 0.764 5 0.852 2 0.672 7 ANN 0.908 7 0.866 9 0.929 3 0.778 8
从表6中可以看出,在未经训练的情况下,各个模型对于新的电网拓扑结构下特征数据的分类性能均有所下降。其中NB下降的最多,这是因为其是一种基于样本概率的算法,当对样本的概率分布学习不充分时会对性能产生较大影响。C4.5、CART、SVM、ANN等性能表现相对平稳,但是对于新拓扑结构下特征数据的安全度指标表现较差,这意味着其对新出现的暂态失稳样本的误分率较高。相比之下,NRRDF不仅表现相对平稳,且在四个指标上均具有最佳的性能表现,这说明其对于未经训练的电网拓扑结构下的特征数据也具有较好的适应性,在不同情况下的模型鲁棒性更强。
4.4 不同样本规模下的模型性能表现
进一步研究模型在不同样本规模下的性能表现。由于深度学习的特点之一是对大数据的高效学习能力,本节选择深度学习中最具代表性的深度置信网络(Deep Belief Network, DBN)进行性能比较。分别从原始的8 000组样本数据中以1 000为步长,随机抽取1 000~8 000组样本数据;在不同的样本规模下分别利用十折交叉验证来对所提模型以及 DBN的性能进行评估。DBN选定为{10-15-20}的 3层网络结构,该结构为根据经验法通过多次实验选取最优结果下的网络结构参数。实验结果如图6所示。


图6 模型性能随样本数量的变化(NRRDF vs. DBN)
Fig.6 Variation of model performance with number of samples (NRRDF vs. DBN)
从图6可以看出,在样本数量较少时,DBN的各项性能指标与NRRDF相比具有较大差距;随着样本数量的增加,DBN的各项性能指标逐渐提升,且样本数越少,通过增加样本带来的性能提升效果越明显;当样本数量达到4 000时,DBN的各项性能指标开始趋于饱和,呈缓慢增加的趋势。相比之下,本文所提模型受样本数量的影响较小,在不同样本规模下均具有较好的表现。在样本数量较少时,本文所提模型具有明显的优势。尽管随着样本数量增加,两者间的差距逐渐变小,但最终NRRDF在四个评估指标上均要优于 DBN。这是因为不同于DBN,NRRDF并不依赖大数据来对样本分布进行无偏估计。此外,DBN的模型深度通常为固定结构,而所提模型深度可以在学习过程中通过对训练过程的逐层评估自适应决定,因而在不同样本规模下,本文所提模型均具有良好的表现,具有较强的鲁棒性。
4.5 无关特征对模型性能的影响
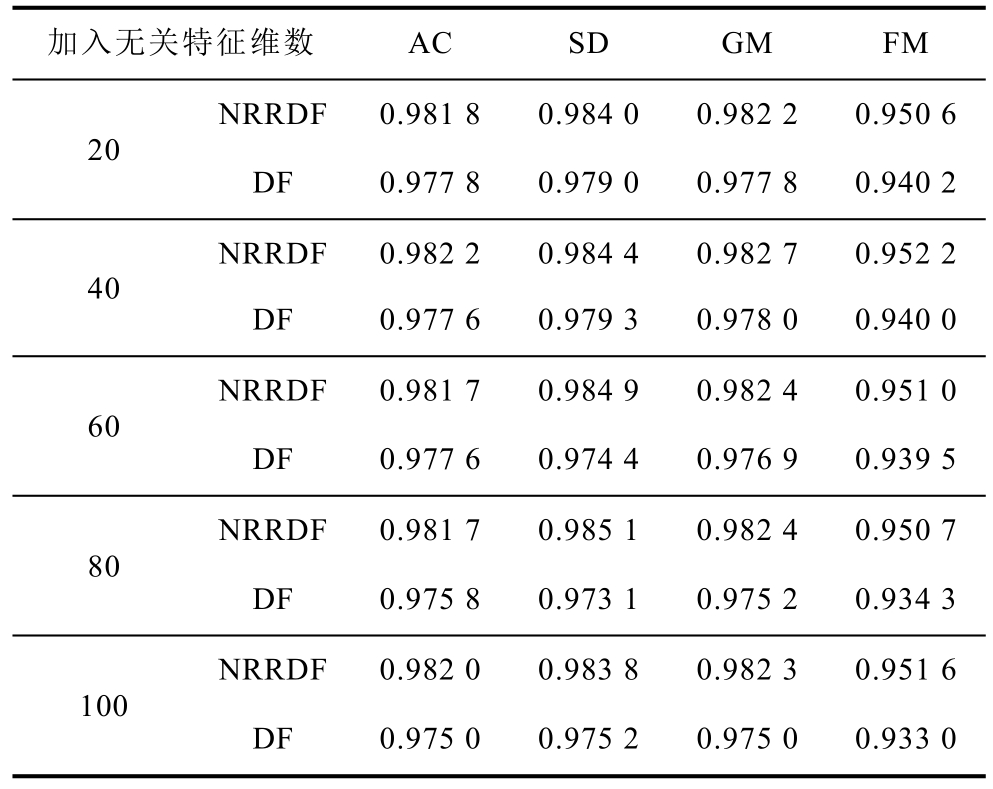
由于暂态特征集合的建立依赖专家经验,可能会受到一定的人为主观因素影响。本节研究无关特征对模型的影响。无关特征通过由服从标准正态分布的随机变量生成。分别向原始数据集中以20为步长,添加20~100维的无关特征,利用十折交叉验证计算模型在加入不同维度无关特征时的性能指标变化情况。为了更直观地展现所提模型性能,同时给出不采取邻域粗糙约简方法对输入特征进行加强再表征的原始深度森林模型(记为DF)的相应评估结果,结果见表7。从表7中可以看出,本文所提模型在加入不同数量的无关特征后的各项性能指标表现相对稳定,基本不受无关特征的影响。而DF的评估效果则随着无关特征数量的增加而逐渐降低。这是因为在所提模型中,原始输入特征经由邻域粗糙约简方法进行了加强再表征,而邻域粗糙约简可以有效地对关键特征集进行挖掘,其结果并不会受无关特征数量的影响。因而尽管增加了高维无关特征,再表征后的特征并不会受到影响。这说明本文所提方法具有较强的鲁棒性,在大量加入无关特征的情况下仍能保证较高的评估性能。
表7 模型性能随无关特征数量的变化
Tab.7 Variation of model performance with number of irrelevant features
加入无关特征维数 AC SD GM FM NRRDF 0.981 8 0.984 0 0.982 2 0.950 6 20 DF 0.977 8 0.979 0 0.977 8 0.940 2 NRRDF 0.982 2 0.984 4 0.982 7 0.952 2 40DF 0.977 6 0.979 3 0.978 0 0.940 0 NRRDF 0.981 7 0.984 9 0.982 4 0.951 0 60 DF 0.977 6 0.974 4 0.976 9 0.939 5 NRRDF 0.981 7 0.985 1 0.982 4 0.950 7 80 DF 0.975 8 0.973 1 0.975 2 0.934 3 NRRDF 0.982 0 0.983 8 0.982 3 0.951 6 100 DF 0.975 0 0.975 2 0.975 0 0.933 0
4.6 不同样本不平衡比下的模型性能比较
在实际电网运行过程中,由于电网暂态失稳的情况十分少见,因此实际电网数据中的暂态失稳样本往往占比较少。为了评估所提模型在不同的样本不平衡比下的性能表现,本文首先在总样本中随机抽取与暂态失稳样本等量的暂态稳定样本,使暂态失稳样本占比达到50%。随后在此基础上逐渐从暂态失稳样本中随机删除部分样本使暂态失稳样本占总样本的比例依次降到 40%、30%、20%和 10%。在不同的不平衡度下进行模型的性能评估,对各模型评估所得的G-means以及F-measures指标如图7所示。


图7 模型性能随暂态失稳样本占比的变化情况
Fig.7 Variation of model performance with ratio of unstable samples
从图7可以看出,在暂态稳定样本与暂态失稳样本数量平衡时,各模型的分类性能最佳。随着暂态失稳样本占比降低,两类样本间的不平衡度逐渐加剧,各模型的分类性能开始有所下降。从G-means指标来看,CART、C4.5及ANN受暂态失稳样本占比降低的影响较大,而NRRDF、SVM及NB的模型性能在不同的样本不平衡度下表现相对稳定,但是SVM、NB的评估性能较差。相比之下,所提模型在G-means指标下不仅性能最佳,且相对稳定。从F-measures指标来看,各类模型的性能总体上均随着暂态失稳样本占比的降低而降低。这是因为随着样本间的不平衡度逐渐加剧,各模型在学习过程中逐渐偏向数量更占优势的稳定样本,对于暂态失稳样本的误分率往往更高。而本文所提方法通过根据样本间的不平衡度自适应地调整暂态失稳样本的权重,可以在一定程度上加强对暂态失稳样本的重视,降低对失稳样本的误分,在各样本不平衡比下均具备较好的分类性能。
5 结论
针对当前电力系统暂态稳定评估方法存在浅层模型学习精度有限以及对暂态失稳样本重视不足的问题,提出一种融合邻域粗糙约简与深度森林的暂态稳定评估方法。在IEEE 10机39节点系统上对所提模型进行对比实验分析。实验结果表明:
1)相比目前常用的浅层学习模型,所提模型能够有效地提高分类性能。加权投票机制的引入在保证模型评估精度的基础上可以有效地提高模型在学习过程中对暂态失稳样本的重视,减少对暂态失稳样本的误判,并且在不同的样本不平衡度下均具有较好的表现。
2)相比以深度置信网络为代表的传统深度学习方法,所提方法具备较少的超参数。多级串行的结构不仅可以实现对输入特征的多层表征学习,且能够在学习过程中通过对训练过程的逐层评估自适应决定模型的深度,使得所提模型在不同规模数据下均具有良好的表现。
3)通过邻域粗糙约简方法对原始输入特征进行加强再表征不仅能够提供比原始特征空间更加充分的信息,同时使得模型在加入大量无关特征的情况下仍保持较高的分类性能,因此模型鲁棒性更强。
针对当前存在的一些问题,本文在深度学习架构下对电力系统暂态稳定评估问题进行研究。在实际中,由于测量装置损耗以及通信延迟等问题,可能会造成暂态特征数据的缺失。因而未来将完善所提模型在诸如数据缺失等情况下的可行性分析。
[1] 王毅, 张宁, 康重庆, 等. 电力用户行为模型: 基本概念与研究框架[J]. 电工技术学报, 2019, 34(10):2056-2068.Wang Yi, Zhang Ning, Kang Chongqing, et al.Electrical consumer behavior model: basic concept and research framework[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2056-2068.
[2] 陈国恩, 李伟, 张仲孝. 电网故障诊断方法及其系统架构的研究[J]. 电气技术, 2018, 19(1): 64-67.Chen Guoen, Li Wei, Zhang Zhongxiao. Research on power grid fault diagnosis method and its system architecture[J]. Electrical Engineering, 2018, 19(1):64-67.
[3] 姜涛, 王长江, 陈厚合, 等. 基于正则化投影孪生支持向量机的电力系统暂态稳定评估[J]. 电力系统自动化, 2019, 43(1): 141-148.Jiang Tao, Wang Changjiang, Chen Houhe, et al.Transient stability assessment of power system based on projection twin support vector machine with regularization[J]. Automation of Electric Power Systems, 2019, 43(1): 141-148.
[4] 谭本东, 杨军, 赖秋频. 基于改进 CGAN的电力系统暂态稳定评估样本增强方法[J]. 电力系统自动化, 2019, 43(1): 149-157.Tan Bendong, Yang Jun, Lai Qiupin. Data augment method for power system transient stability assessment based on improved conditional generative adversarial network[J]. Automation of Electric Power Systems, 2019, 43(1): 149-157.
[5] 罗深增, 李银红, 石东源. 广域测量系统可观性概率评估及其在 PMU优化配置中的应用[J]. 电工技术学报, 2018, 33(8): 1844-1853.Luo Shenzeng, Li Yinhong, Shi Dongyuan. Wide area monitoring system observability probabilistic evaluation and it’s application in optimal PMU placement[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1844-1853.
[6] Wahab N I A, Mohamed A, Hussain A. Fast transient stability assessment of large power system using probabilistic neural network with feature reduction techniques[J]. Expert Systems with Applications,2011, 38: 11112-11119.
[7] Wahab N I A, Mohamed A, Hussain A. Feature selection and extraction methods for power systems transient stability assessment employing computational intelligence techniques[J]. Neural Process Letter,2012, 35: 81-102.
[8] Gu Xueping, Li Yang, Jia Jinghua. Feature selection for transient stability assessment based on kernelized fuzzy rough sets and memetic algorithms[J].International Journal of Electrical Power & Energy Systems, 2015, 64: 664-670.
[9] 叶圣永, 王晓茹, 刘志刚, 等. 基于支持向量机的暂态稳定评估双阶段特征选择[J]. 中国电机工程学报, 2010, 30(31): 28-34.Ye Shengyong, Wang Xiaoru, Liu Zhigang, et al.Dual-stage feature selection for transient stability assessment based on support vector machine[J].Proceedings of the CSEE, 2010, 30(31): 28-34.
[10] 戴远航, 陈磊, 张玮灵, 等. 基于多支持向量机综合的电力系统暂态稳定评估[J]. 中国电机工程学报, 2016, 36(5): 1173-1180.Dai Yuanhang, Chen Lei, Zhang Weiling, et al. Power system transient stability assessment based on multisupport vector machines[J]. Proceedings of the CSEE,2016, 36(5): 1173-1180.
[11] 周艳真, 吴俊勇, 于之虹, 等. 用于电力系统暂态稳定预测的支持向量机组合分类器及其可信度评价[J]. 电网技术, 2017, 41(4): 1188-1196.Zhou Yanzhen, Wu Junyong, Yu Zhihong, et al.Support vector machine ensemble classifier and its confidence evaluation for transient stability prediction of power systems[J]. Power System Technology, 2017,41(4): 1188-1196.
[12] 王亚俊, 王波, 唐飞, 等. 基于响应轨迹和核心向量机的电力系统在线暂态稳定评估[J]. 中国电机工程学报, 2014, 34(19): 3178-3186.Wang Yajun, Wang Bo, Tang Fei, et al. Power system online transient stability assessement based on response trajectory and core vector machine[J].Proceedings of the CSEE, 2014, 34(19): 3178-3186.
[13] Wang Bo, Fang Biwu, Wang Yajun, et al. Power system transient stability assessment based on big data and the core vector machine[J]. IEEE Transactions on Smart Grid, 2016, 7(5): 2561-2570.
[14] 陈厚合, 王长江, 姜涛, 等. 基于投影能量函数和Pin-SVM的电力系统暂态稳定评估[J]. 电工技术学报, 2017, 32(11): 67-76.Chen Houhe, Wang Changjiang, Jiang Tao, et al.Transient stability assessment in bulk power grid using projection energy function and support vector machine with Pinball loss[J]. Transactions of China Electrotechnical Society, 2017, 32(11): 67-76.
[15] 张晨宇, 王慧芳, 叶晓君. 基于 XGBoost算法的电力系统暂态稳定评估[J]. 电力自动化设备, 2019,39(3): 77-89.Zhang Chenyu, Wang Huifang, Ye Xiaojun. Transient stability assessment of power system based on XGBoost algorithm[J]. Electric Power Automation Equipment, 2019, 39(3): 77-89.
[16] 石访, 张林林, 胡熊伟. 基于多属性决策树的电网暂态稳定规则提取方法[J]. 电工技术学报, 2018,33(23): 36-47.Shi Fang, Zhang Linlin, Hu Xiongwei. Power system transient stability rules extraction based on multiattribute decision tree[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 36-47.
[17] Rahmatian M, Chen Y C, Palizban A. Transient stability assessment via decision trees and multivariate adaptive regression splines[J]. Electric Power Systems Research, 2017, 142: 320-328.
[18] 朱乔木, 陈金富, 李弘毅. 基于堆叠自动编码器的电力系统暂态稳定评估[J]. 中国电机工程学报,2018, 38(10): 2937-2946.Zhu Qiaomu, Chen Jinfu, Li Hongyi. Transient stability assessment based on stacked autoencoder[J].Proceedings of the CSEE, 2018, 38(10): 2937-2946.
[19] 李扬, 李国庆, 顾雪平, 等. 基于集成 OS-ELM 的暂态稳定评估方法[J]. 电工技术学报, 2015, 30(14):412-418.Li Yang, Li Guoqing, Gu Xueping, et al. Transient stability assessment of power systems based on ensemble OS-ELM[J]. Transactions of China Electrotechnical Society, 2015, 30(14): 412-418.
[20] 朱乔木, 党杰, 陈金富. 基于深度置信网络的电力系统暂态稳定评估方法[J]. 中国电机工程学报,2018, 38(3): 735-743.Zhu Qiaomu, Dang Jie, Chen Jinfu. A method for power system transient stability assessment based on deep belief network[J]. Proceedings of the CSEE,2018, 38(3): 735-743.
[21] 胡伟, 郑乐, 闵勇. 基于深度学习的电力系统故障后暂态稳定评估研究[J]. 电网技术, 2017, 41(10):3140-3146.Hu Wei, Zheng Le, Min Yong. Research on power system transient stability assessment based on deep learning of big data technique[J]. Power System Technology, 2017, 41(10): 3140-3146.
[22] 尹雪燕, 闫炯程, 刘玉田. 基于深度学习的暂态稳定评估与严重度分级[J]. 电力自动化设备, 2018,38(5): 64-69.Yin Xueyan, Yan Jiongcheng, Liu Yutian. Deep learning based transient stability assessment and severity grading[J]. Electric Power Automation Equipment, 2018, 38(5): 64-69.
[23] 徐春华, 陈克绪, 马建, 等. 基于深度置信网络的电力负荷识别[J]. 电工技术学报, 2019, 34(19):4135-4142.Xu Chunhua, Chen Kexu, Ma Jian, et al. Recognition of power loads based on deep belief network[J].Transactions of China Electrotechnical Society, 2019,34(19): 4135-4142.
[24] 顾雪平, 李扬, 吴献吉. 基于局部学习机和细菌群体趋药性算法的电力系统暂态稳定评估[J]. 电工技术学报, 2013, 28(10): 271-279.Gu Xueping, Li Yang, Wu Xianji. Transient stability assessment of power systems based on local learning machine and bacterial colony chemotaxis algorithm[J].Transactions of China Electrotechnical Society, 2013,28(10): 271-279.
[25] Li Bingyang, Xiao Jianmei, Wang Xihuai. Feature reduction for power system transient stability assessment based on neighborhood rough set and discernibility matrix[J]. Energies, 2018, 11(1): 185.
[26] 唐飞, 王波, 查晓明, 等. 基于双阶段并行隐马尔科夫模型的电力系统暂态稳定评估[J]. 中国电机工程学报, 2013, 33(10): 90-97.Tang Fei, Wang Bo, Zha Xiaoming, et al. Power system transient stability assessment based on twostage parallel hidden Markov model[J]. Proceedings of the CSEE, 2013, 33(10): 90-97.
[27] Hu Qinghua, Yu Daren, Xie Zongxia. Neighborhood classifiers[J]. Expert Systems with Applications, 2008,34: 866-876.
[28] Breiman L. Random forests[J]. Machine Learning,2001, 45(1): 5-32.
[29] Liu F T, Ting Kaiming, Yang Yu. Spectrum of variable-random trees[J]. Journal of Artificial Intelligence Research, 2008, 32:355-384.
[30] Geurts P, Ernst D, Wehenkel L. Extremely randomized trees[J]. Machine Learning, 2006, 63: 3-42.
[31] Zhou Zhihua, Feng Ji. Deep forest: towards an alternative to deep neural networks[C]//Proceedings of the 26th International Joint Conference on Artificial Intelligence, Melbourne, Australia, 2017: 3553-3559.
[32] Pai A M. Energy function analysis for power system stability[M]. Bonston: Kluwer Academic Publishers,1989: 256.