0 引言
近年来随着可再生能源与主动式配电网的发展,对中、高压大功率电力电子变压器、储能变流器等新兴电力电子装备的研究逐渐兴起。为适配中高压交流电网的应用需求,采用级联H桥(Cascaded H Bridge, CHB)与高频DC-DC组成的前后多级变换结构成为此类电力电子变换装置研究的主流[1-5]。CHB结构作为变流器与交流电网连接的前级,降低了功率半导体开关的电压应力,实现了低耐压IGBT在中、高压变流场合的应用;与之相匹配的多电平调制技术,有效地提升了变流器的等效开关频率,降低了系统的损耗[6-8];同时,标准化的单元模块便于系统的设计与工业化生产[9]。
在CHB的控制上,要求各级联桥的直流侧电压相等,这是实现低耐压 IGBT在高电压环境下应用的基础。由于各级联桥单元的功率损耗、IGBT的触发延迟以及调制策略等因素会造成各级联桥直流侧电压的不均衡[10-11],尤其是当CHB作为整流级应用于多级结构时,后级不均衡的功率输出更会严重影响CHB中各级联桥的直流侧电压。如文献[12]在链式储能变流器的应用中,在对不同电池的SOC管理上,各级联桥会产生不均衡的直流侧功率输出。文献[13]采用两套 CHB与 n个隔离型中频 DC-DC,构建了一个对称结构的三相交流电网接口变流器。为保障有功功率传递时相间功率平衡,将整流级与逆变级的各级联桥进行了交叉互联,但当三相功率不平衡时,会导致相内各级联桥的功率不均衡,从而影响到级联桥的直流侧电压。
为避免这种多级结构下 CHB直流侧电压不平衡,国内外学者根据应用场合的要求,从电路拓扑、后级控制以及CHB级控制等几个方面开展了电压平衡控制的研究。文献[14]在CHB后级的每个DCDC变换单元中增加了一套不控的整流回路,实现了级联单元母线电压的自平衡。文献[15]为实现一个交-直-交的高、低压电网三端接口变流器,将CHB后级的 DC-DC变换单元的副边并联在了一起,通过调整 DC-DC级传递的功率,实现后级对CHB级直流侧电压的控制。文献[16-20]则是直接在CHB级施加控制,实现各级联桥的直流电压平衡。文献[16]采用了附加均压环的方法,将各桥均压环的输出作用到各级联桥交流侧的调制波上,改变各桥调制波的相位或幅值,从而影响各桥对电网有功能量的吸收,最终实现各桥直流电压平衡。但附加均压环的控制器设计会受到诸多因素的影响,如考虑某桥轻载时,设计的附加控制器饱和限与满载工作时直流电压快速平衡存在矛盾[17]。同时,附加的均压环会随着级联桥数量的增加而增多,这无疑会给控制系统的运算带来更大的压力。文献[18-19]利用多电平层叠载波调制时各桥损耗不同的原理,在每个开关周期中,根据各桥直流侧电压的高低,给各桥分配不同的调制波,从而改变各桥的有功功率吸收,实现直流电压平衡。这种平衡方法以下简称排序交换平衡法,其本质可看作是一种基于时间的滞环控制,相较于附加均压环控制法,其原理简单,调节速度也更快。文献[20]在排序交换平衡法的基础上,研究了两桥级联整流(Cascaded H Bridge Rectifier, CHBR)的直流电压快速平衡方法,通过在二维平面上规划调制轨迹,构建出两个新的调制波,使两桥级联桥在选择不同调制波时获得的有功能量差值更大,从而增强了两桥直流侧不平衡的带载能力,加快两桥的平衡速度。文献[17]将两桥级联的二维调制扩展成三桥级联的三维调制,原二维调制平面变成了三维调制空间,二维调制的调制轨迹线也相应地变成了调制轨迹面。根据多电平的阶梯分布对三维调制空间进行了分块,又根据调制平面内不同区域对各桥吸收有功能量的影响不同,对任意时刻的调制平面划分出了小扇区。为实现较好的平衡性能,选择了小扇区的边界进行调制。这种调制方法使得 CHB在每个开关周期内都可以选择最优的开关组合平衡直流侧电压,开关损耗对比移相载波PWM也颇具优势。但在更多桥级联时,该方法会变得相当复杂。文献[21]将n桥CHB的调制区间通过占空比形式统一到了二维平面上,采用了与文献[22]相同的调制轨迹平衡两桥CHB的直流侧电压,但并未就多桥CHB的扩展调制方法进行探讨。文献[23]总结了CHB多维调制的平衡原理,并对比分析了二维调制中,不同调制轨迹对系统等效开关频率与损耗的影响。并指出多桥级联会给调制波合成带来更多的自由度,从而可以根据优化的目标选择这些自由度,如对损耗、开关频率的优化等。随着级联桥数量的增长,调制空间由二维平面变成了多维空间,这种调制带来了自由度急剧增长,自由度的优化变得异常抽象和复杂。
为解决 CHBR多维调制多自由度的复杂优化问题。本文以 CHBR直流侧电压快速平衡为二维调制的自由度优化目标,选择了与文献[20]相同的二维调制轨迹。在此基础上,提出了一种n桥级联的多维扩展调制方法,并对此方法的调制逻辑进行了化简。之后,研究了多维扩展策略对二维调制自由度优化的继承性,从理论上对比分析了 CHBR单位功率因数运行时,多维扩展调制与二维调制的直流电压平衡性能,以及影响多维扩展调制平衡性能的主要因素。搭建了单相 CHBR实验平台,验证了所述方法和理论的有效性。最后,对比传统排序交换平衡法,验证了所提多维扩展调制电压平衡性能的优越性。
1 二维电压平衡调制
CHBR二维电压平衡调制的流程可分为:调制平面构建、调制轨迹规划以及排序交换平衡三个步骤。其中的步骤三与传统排序交换平衡法的原理相同,即在每个开关周期,按照级联桥直流电压高低,为各桥分配调制轨迹规划出的不同调制波,从而平衡CHBR的直流电压。下面将就调制平面构建与调制轨迹规划两个方面详细论述二维电压平衡调制的过程。
1.1 二维调制原理与调制平面构建
二维调制是针对如图1所示单相两桥级联的一种调制策略[22]。图中 us、is分别为电网电压与并网电流,uL为电感电压,iL1、iL2分别为 H1、H2的直流侧负载电流,udc1、udc2分别为H1、H2的直流侧输出电压,ucon为CHBR交流侧的合成电压。
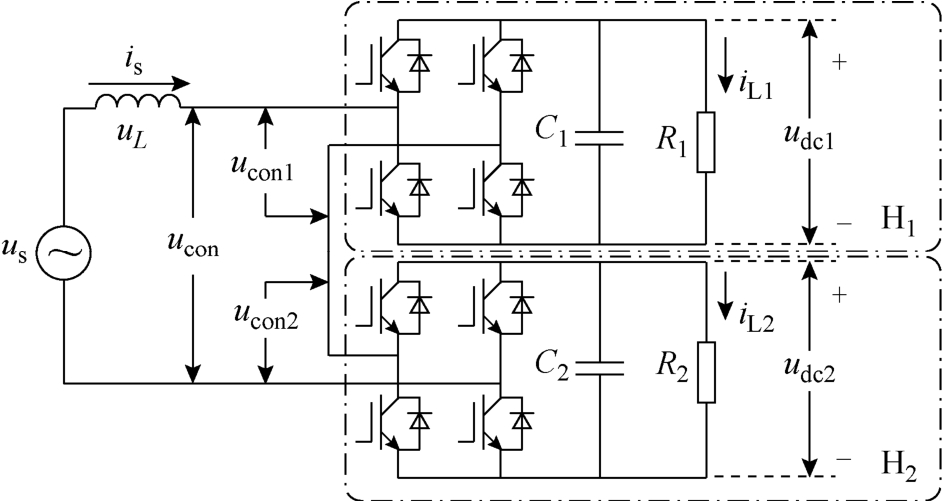
图1 两桥CHBR拓扑图
Fig.1 Topological diagram of two bridges CHBR
系统单位功率因数运行时,us、is分别为
式中,UsM、IsM分别为电网电压与并网电流的幅值。
ucon为
式中,UconM为ucon的幅值;θ为us与ucon基波电压的夹角。ucon1∈[-udc1,udc1]、ucon2∈[-udc2,udc2],ucon1、ucon2分别为H1、H2的交流侧电压,其与直流侧电压满足式(3)关系。
式中,d1、d2为两桥调制的占空比。由图1可知,ucon与 ucon1、ucon2满足
若 udc1=udc2=Udc,则 ucon1∈[-Udc,Udc],ucon2∈[-Udc,Udc],ucon∈[-2Udc,2Udc],其中 Udc是整流时 H桥直流侧电压的指令值。任意时刻合成的ucon可由ucon1和ucon2的无限种组合来实现。
1.2 电压平衡调制轨迹规划
二维调制平面以级联桥直流侧不平衡带载能力与直流电压平衡速度为优化目标,选择了与文献[20]相同的调制轨迹。
根据ucon与is的符号关系,在调制平面的边界规划了两条调制轨迹,尽可能地增大了两桥对有功能量吸收的偏差,从而增强了CHBR直流电压的平衡能力。若udc1<udc2,规划的调制轨迹如图2所示。
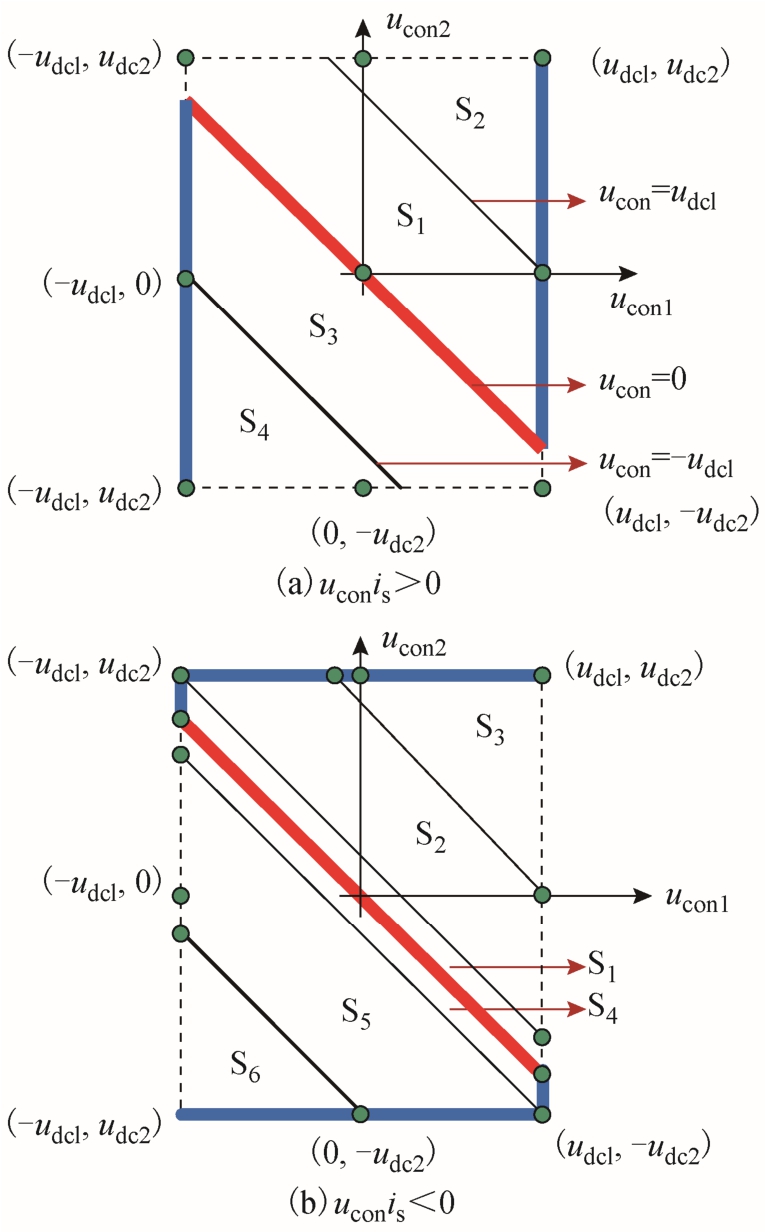
图2 二维平面内轨迹规划
Fig.2 Trajectory planning in a two-dimensional plane
调制扇区判断见表 1,两桥在各扇区内的占空比计算见表2。表中,|dx|=d1、|dy|=d2,dx与dy的符号表示ucon1与ucon2的电压方向。
表1 调制轨迹扇区判断
Tab.1 Judgment of modulated track sectors
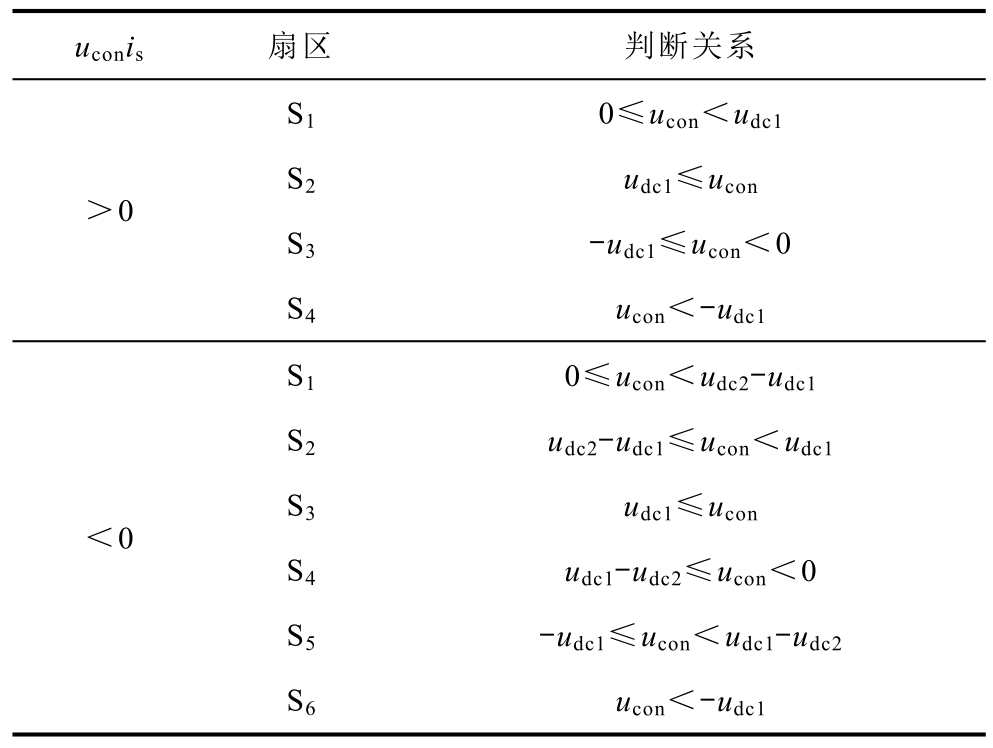
uconis 扇区 判断关系S1 0≤ucon<udc1>0 S2 udc1≤ucon S3 -udc1≤ucon<0 S4 ucon<-udc1 S1 0≤ucon<udc2-udc1<0 S2 udc2-udc1≤ucon<udc1 S3 udc1≤ucon S4 udc1-udc2≤ucon<0 S5 -udc1≤ucon<udc1-udc2 S6 ucon<-udc1
表2 CHBR占空比计算
Tab.2 CHBR duty cycle calculation

uconis 扇区 H1 H2 S1 dx=1 dy=(ucon-udc1)/udc2>0 S2 dx=1 dy=(ucon-udc1)/udc2 S3 dx=-1 dy=(ucon+udc1)/udc2 S4 dx=-1 dy=(ucon+udc1)/udc2 S1 dx=-1 dy=(ucon+udc1)/udc2<0 S2 dx=(ucon-udc2)/udc1 dy=1 S3 dx=(ucon-udc2)/udc1 dy=1 S4 dx=1 dy=(ucon-udc1)/udc2 S5 dx=(ucon+udc2)/udc1 dy=-1 S6 dx=(ucon+udc2)/udc1 dy=-1
1.3 规划轨迹的平衡性能分析
二维调制在控制CHBR直流电压时,两桥有功功率吸收的差值决定着平衡直流电压的性能,差值越大平衡能力越强,反之越弱。因此对电压平衡的性能分析,可从两桥对有功功率吸收的偏差入手,对1.2节调制轨迹的平衡性能进行研究。
系统单位功率因数运行时,ucon滞后 us的夹角为 θ;若仍假设 udc1<udc2,由表 1、表 2可得,在规划轨迹下,ucon1与ucon2的表达式分别为

式(5)、式(6)分别为 ucon1与 ucon2正半周期各个时刻的瞬时值,由于ucon1、ucon2正负半周奇对称,因此计算两桥吸收的有功功率仅需考虑正半周期即可。结合式(1),两桥吸收的有功功率可表示为

当两桥直流电压临界平衡时,平衡策略不会使各桥的调制波发生交换,udc1≈udc2≈Udc。将式(5)、式(6)代入式(7),化简后可得
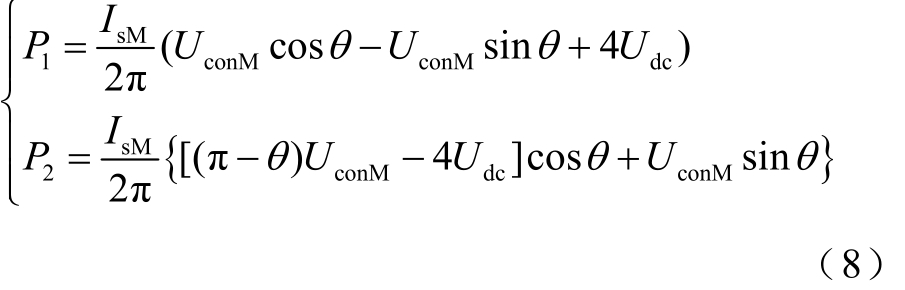
定义直流电压升压比m为
式中,n为级联桥的数量。将式(9)代入式(8),整理可得两桥对有功功率吸收的偏差ΔP2D为
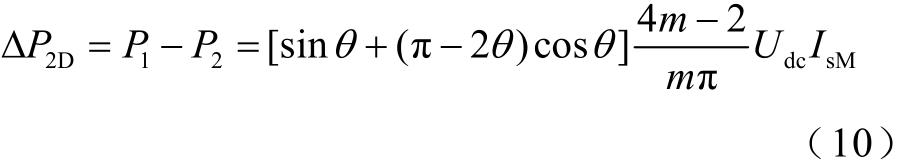
由于升压比 m≥1、夹角 θ<0.5π,因此ΔP2D>0,H1比H2可以获得更多的有功能量。随着直流电压或并网电流的增大,这种平衡策略会使两桥的不平衡带载能力进一步增强。
2 多桥级联扩展原理与调制逻辑化简
2.1 多桥级联扩展原理
在多桥 CHBR的电压平衡控制上,多电平层叠载波的调制波分配方案被广泛采用。从两桥CHBR的电压平衡性能上看,1.2节的调制方案比传统方案更具优势[20]。但在多桥应用时,若按二维调制的思路进行扩展,需首先构建多维空间,再规划调制轨迹,这使得调制自由度的优化变得异常抽象和复杂。
针对多桥CHBR的多维调制与调制轨迹规划问题,提出了如图3所示的多维扩展调制流程。采取先规划二维轨迹,优化调制的自由度,后扩展到多维的思路。将n维调制转换为n-1次二维调制,从而实现n维调制的降维。
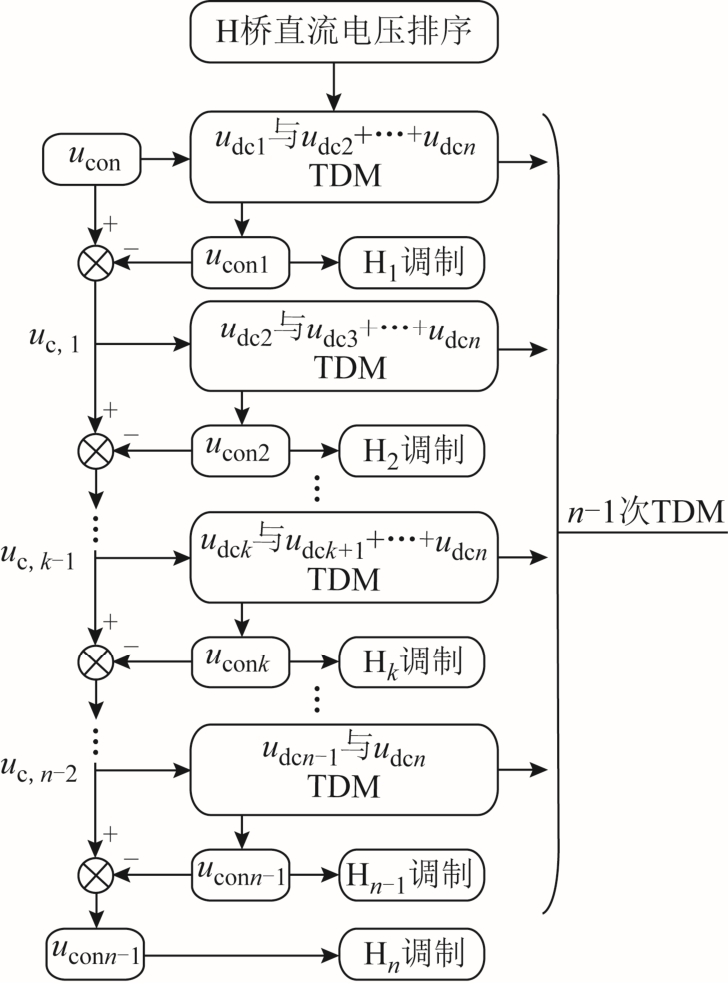
图3 n维调制降维流程
Fig.3 Dimension reduction flow chart of n-dimensional modulation
在合成ucon时,首先对n个H桥的直流电压进行排序,假设排序后udc1<udc2<…<udcn,将H1桥的直流电压udc1与其余n-1个H桥的直流电压之和按照1.2节规划的轨迹进行二维调制,得到H1的调制波ucon1,ucon-ucon1作为新的合成调制波uc,1,由其余H2~Hn合成,第1次二维调制结束;将H2桥的直流电压udc2与除H1和H2外的n-2个H桥的直流电压之和进行二维调制,得出 H2调制波 ucon2,uconucon1-ucon2作为新的合成调制波 uc,2,由其余 H3~Hn合成,第2次二维调制结束;依次类推,n-1次二维调制后,n个桥的调制波分配完毕。
2.2 多维扩展调制逻辑化简
下面将综合 1.2节的调制轨迹与 2.1节的调制扩展原理,对多维电压平衡调制的调制逻辑与占空比计算进行化简。
设参与第 k-1次二维调制的两直流电压分别为 udck、udckn,且 udck<udckn,其中 udck为第 k桥的直流电压;udckn为除第k桥与已完成调制波分配的桥之外,剩余H桥的直流电压之和,其满足式(11)关系。
定义表3的输入量A、B、C、D、E,其中uc,k-1为此次二维调制需合成的调制波。根据表2定义表4的输出量 Xi、Yi、Zi。
表3 输入变量
Tab.3 Input variable
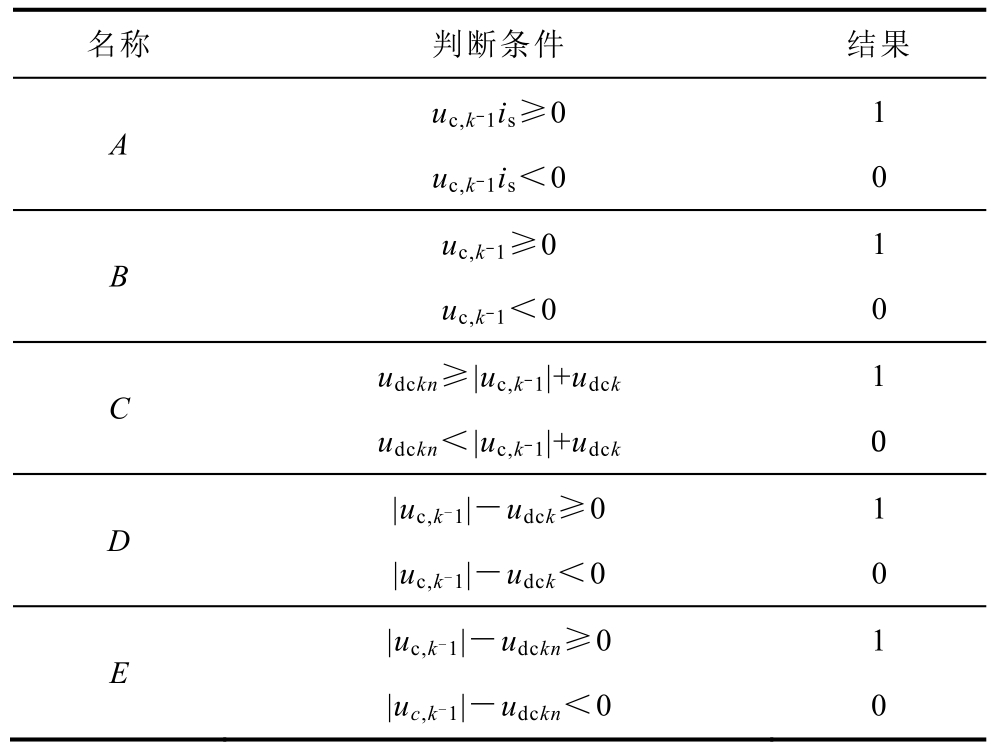
名称 判断条件 结果A uc,k-1is≥0 1 uc,k-1is<0 0 B uc,k-1≥0 1 uc,k-1<0 0 C udckn≥|uc,k-1|+udck 1 udckn<|uc,k-1|+udck 0|uc,k-1|-udck≥0 1 D|uc,k-1|-udck<0 0 E|uc,k-1|-udckn≥0|uc,k-1|-udckn<0 10
表4 输出变量
Tab.4 Output variable

名称 定义 结果d≥0 1 Xi d<0 0|d|=1 1 Yi |d|<1 0 Zi d=(uc,k-1-udcj)/udci 1 d=(uc,k-1+udcj)/udci 0
表中Xi判断调制波的正负;Yi判断占空比的绝对值是否为 1;当占空比绝对值小于 1时,Zi判断具体的计算公式。Xi、Yi、Zi三者共同确定某一时刻的占空比。表中,i=k或kn、j=k或kn,且i≠j。以i为例,当i=k时,d表示第k-1次二维调制时电压为udck的桥的占空比;i=kn时,d表示第k-1次二维调制时,电压为udckn的桥的占空比。
根据表4,设第k桥的输出为Xk、Yk、Zk,与k桥做二维调制的剩余桥输出量为 Xkn、Ykn、Zkn。结合图3,可构建输入量与输出量的真值表,见表5。根据真值表中输入、输出量间的关系,经过卡诺图化简,可得输入、输出量之间的逻辑关系式(12)。最后,通过如图4所示的多路选择器,即可得到多维扩展调制策略下,第k桥的调制占空比。
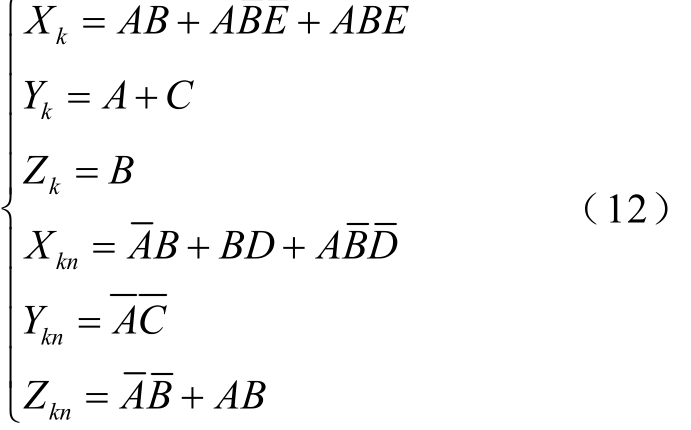
表5 真值表
Tab.5 Truth value table

A B C D E Xk Yk Zk Xkn Ykn Zkn 0 0 0 × 0 1 0 0 0 1 ×0 0 0 × 1 0 0 0 0 1 ×0 0 1 × 0 1 1 × 0 0 1 0 1 0 × 0 0 0 1 1 1 ×0 1 0 × 1 1 0 1 1 1 ×0 1 1 × 0 0 1 × 1 0 0 1 0 × 0 × 0 1 × 1 0 0 1 0 × 1 × 0 1 × 0 0 0 1 1 × 0 × 1 1 × 0 0 1 1 1 × 1 × 1 1 × 1 0 1
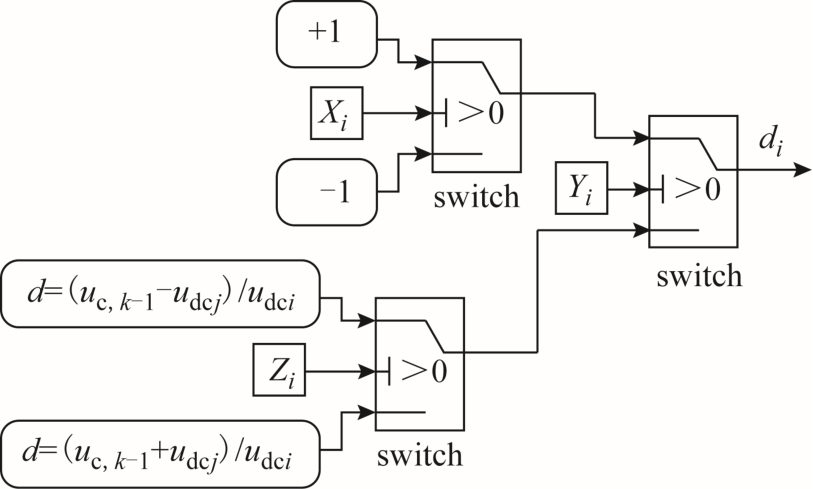
图4 输出占空比结果选择
Fig.4 Selection of output duty cycle results
3 二维调制多维扩展的性能分析
理想状态下,二维调制多维扩展后,直流电压偏差最大的两桥吸收的有功功率偏差最大,因而对多维扩展的性能分析仅考虑直流电压偏差最大的两桥。n桥级联时,假设直流侧电压满足:udc1<udc2<…<udcn,系统处于各直流侧电压临界平衡状态,即 udc1≈udc2≈…≈udcn≈Udc。
由扩展策略分析可得,直流电压最小的桥H1的ucon1在正半周期为Udc,在负半周期为-Udc;直流电压最大的桥 Hn的 uconn正、负半周奇对称,正半周期表达式为

其中
将式(9)代入式(14)化简可得
与 1.3节的计算方法相同,分段积分后,得到H1与 Hn从电网吸收的有功功率 P1、Pn,进而求得H1与 Hn对有功功率吸收的偏差 ΔPnD=P1-Pn。将ΔPnD与式(10)做差,考察多维扩展调制较二维调制对电压平衡性能的影响,得
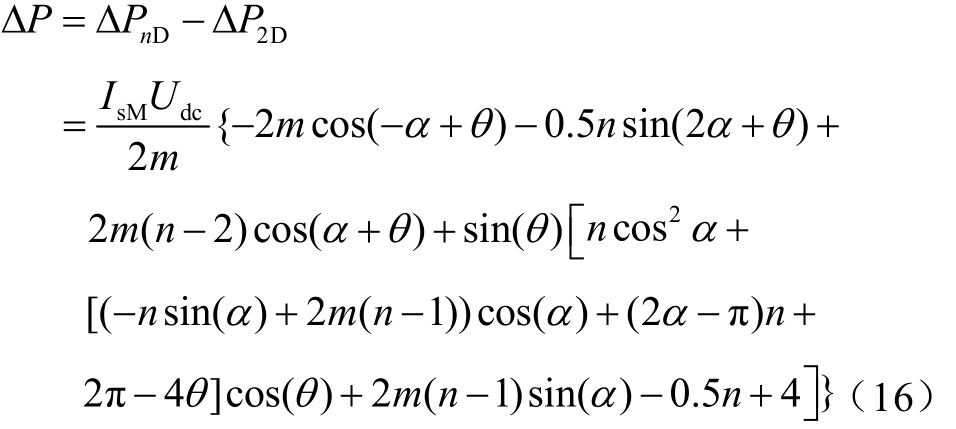
由式(16)分别绘制出升压比m、夹角θ、级联桥数量n与能量差ΔP的三维关系,如图5所示。图5a为夹角θ=π/12时,ΔP与m、n的三维关系;图5b为升压比m=1.1时,ΔP与θ、n的三维关系。图5中ΔP均大于0,且随着级联桥数量n的增加,ΔP随之增长,级联桥的直流侧带载能力会进一步提升,ΔP与IsMUdc成正比关系。

图5 ΔP与m、n、θ的三维关系
Fig.5 Three-dimensional relationship between ΔP and m, n, θ
根据文献[18-19]平衡调制策略,同理可得传统策略直流电压偏差最大的两桥,吸收的有功功率差为 ΔPTn,令 Δ P ′=ΔPnD-ΔPTn,可对比多桥级联时所提策略与传统策略电压平衡的性能,Δ P ′计算结果为
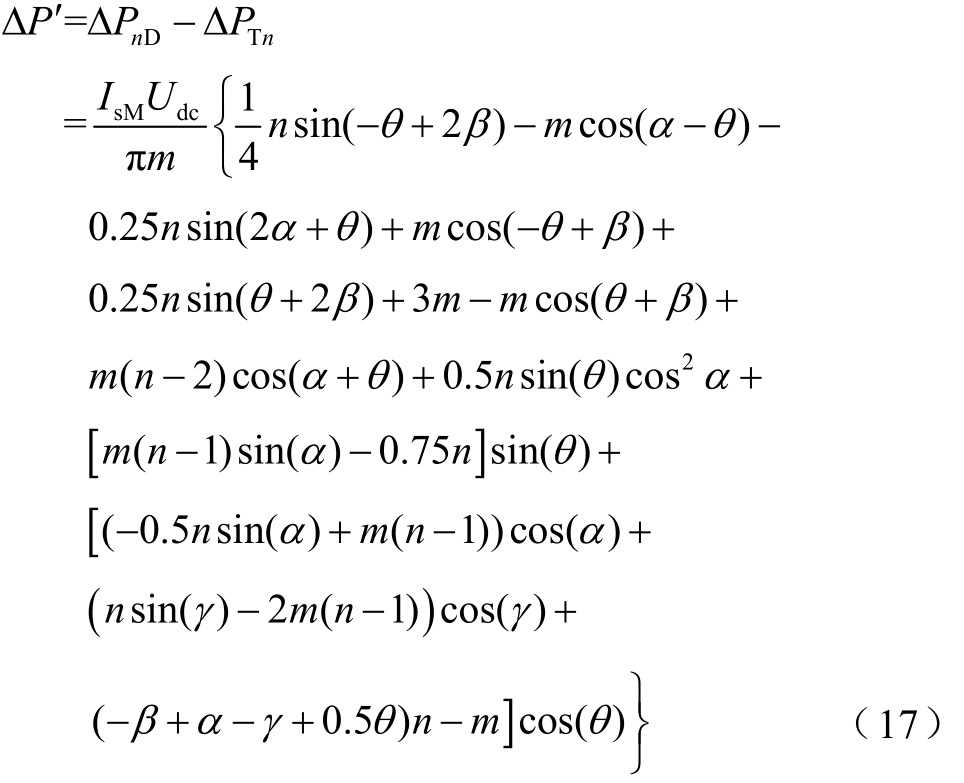
其中
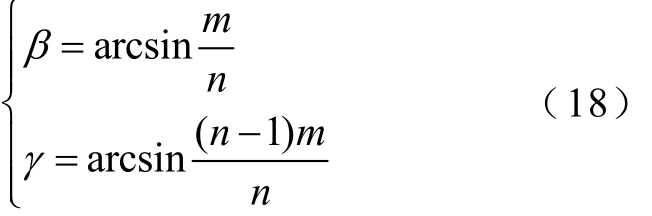
由式(17)可绘制 Δ P ′与m、n以及 Δ P ′与 θ、n的三维关系如图6所示。图6a为夹角θ=π/12时,Δ P ′与m、n的三维关系;图6b为升压比m=1.1时,ΔP ′与 θ、n的三维关系。

图6 传统策略与提出策略的性能对比
Fig.6 Performance comparison between traditional strategy nd popo
图中 Δ P ′≥0,说明与传统方法相比,提出的策略继承了二维调制规划轨迹的优势,具有更好的直流电压平衡性能;随着级联桥数量的增加,提出方法的性能优势会更加明显。
4 实验验证与结果分析
为了验证所提出的多维扩展策略的有效性,搭建了一套单相CHBR实验平台如图7所示。平台主控制器采用DSP TMS320F28335,利用硬件死区电路,将 DSP的 PWM 扩展为 16路互补带死区的PWM信号。CHBR交流网侧采用 L型滤波器,各级联H桥的直流电容相等,直流侧负载为纯阻性负载。实验平台的系统与控制参数见表6。

图7 单相CHBR实验平台
Fig.7 Single phase CHBR experimental platform
表6 单相四桥CHBR平台系统与控制参数
Tab.6 Single-phase four-bridge CHBR platform system and control parameters
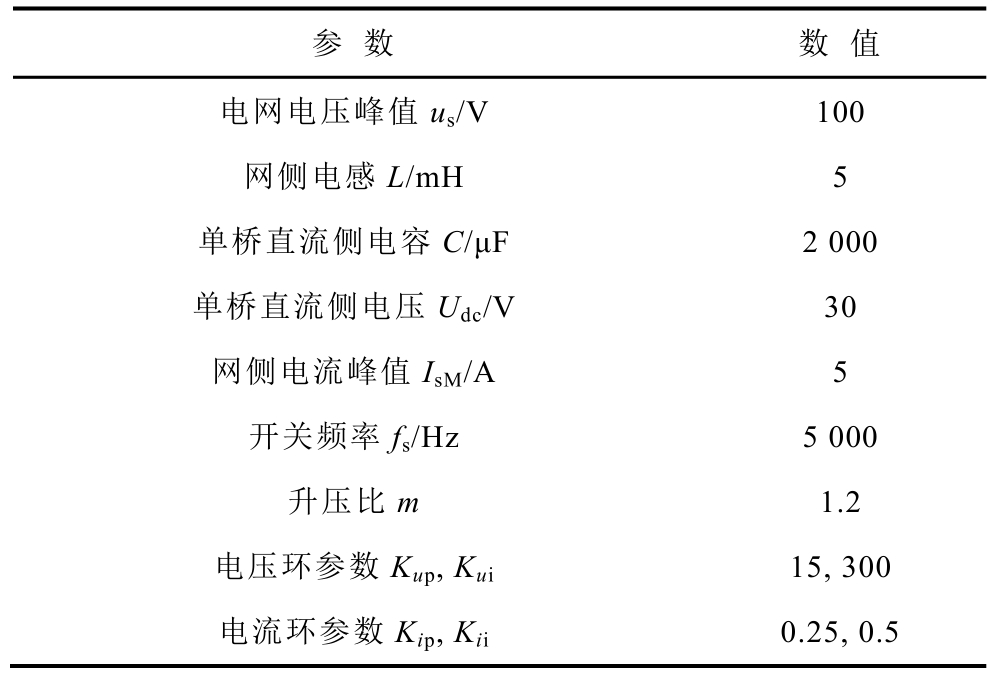
参 数 数 值电网电压峰值us/V 100网侧电感L/mH 5单桥直流侧电容C/μF 2 000单桥直流侧电压Udc/V 30网侧电流峰值IsM/A 5开关频率fs/Hz 5 000升压比m 1.2电压环参数Kup, Kui 15, 300电流环参数Kip, Kii 0.25, 0.5
系统采用与文献[24]相同的电压、电流双闭环控制。电流内环采用准PR控制器;将CHB直流侧总电压作为电压外环的控制对象,采用PI控制器;为验证所提出策略的性能,对比了传统排序平衡方法[18-19]的平衡效果。
图8为所提策略下单相4桥级联整流的稳态实验结果。四桥直流侧负荷分别为:R1=17Ω,R2=18Ω,R3=19Ω,R4=20Ω。图中可见:稳态时,所提调制扩展策略可以较好地配合电压电流的控制算法实现系统单位功率因数运行;传统方法与提出方法的并网电流THD分别为5.2%、4.8%,其谐波含量基本相同;调制算法使得 CHB的交流侧合成了 9电平阶梯波;4桥的直流侧电容电压平衡,由于各桥为单相结构,直流侧存在2次脉动,脉动值约为6%。

图8 4桥CHBR稳态实验波形
Fig.8 Steady-state experimental waveforms of 4-bridge CHBR
为验证所提调制扩展策略的平衡性能,与文献[18-19]的扩展方法进行了对比实验。实验结果如图9所示。

图9 4桥级联直流侧电压暂态波形
Fig.9 Four-bridge cascade DC-side voltage transient waveforms diagram
实验仍采用单相 4桥级联拓扑,过程分成四个阶段:第一阶段,R1=18Ω,R2=12Ω,R3=22Ω,R4=25Ω;第二阶段,减小 H4的直流输出功率,R4突变为40Ω,其余桥负载不变;第三阶段,增大H2直流输出功率,R2突变为6Ω,其余桥负载不变,进一步拉大各桥的不平衡功率;第四阶段,恢复第一阶段。通过对比不同阶段的波形,验证所提出策略的优越性。
图9a的0~3s为对比实验的第一阶段,此时各桥间带载功率偏差较小,两种调制策略均可实现各桥的直流侧电压平衡。第二阶段如图9a中3~4.5s所示,随着H4带载的减小,各桥的带载功率差被拉大,致使传统的平衡策略无法满足此时各桥的功率需求,各桥的直流侧电压不再平衡,CHB功率偏差最大的两桥直流电压偏差约为4V;对比之下,本文策略的各桥直流电压仍然保持平衡,如图9b所示。第三阶段如图9a中 4.5~6s所示,继续增大各桥直流的功率偏差,采用传统方法功率偏差最大的两桥直流电压偏差约为19V,与设定电压的最大偏差约为15V;而本文方法分别为13V和10V,分别减少了约32%与50%,如图9c所示。
为验证两种策略对不平衡电压的恢复速度影响情况,设置直流侧初始电阻为:R1=18Ω,R2=12Ω,R3=22Ω,R4=25Ω。首先,从不控整流进入平均功率调制,此时各桥的输出调制波相等,均为 ucon/4,此时的直流负载所需功率不同,因此直流侧电压无法平衡。在某一时刻分别施加传统调制方法和本文提出的调制方法,使其直流侧达到电压平衡,实验结果如图 10所示。在 0.2s时施加平衡调制策略,传统方法恢复电压平衡的时间约为 20ms,本文方法恢复时间约为 16ms,平衡速度提升约 20%。可见所提出的多维扩展策略继承了二维电压平衡调制的优化特性。
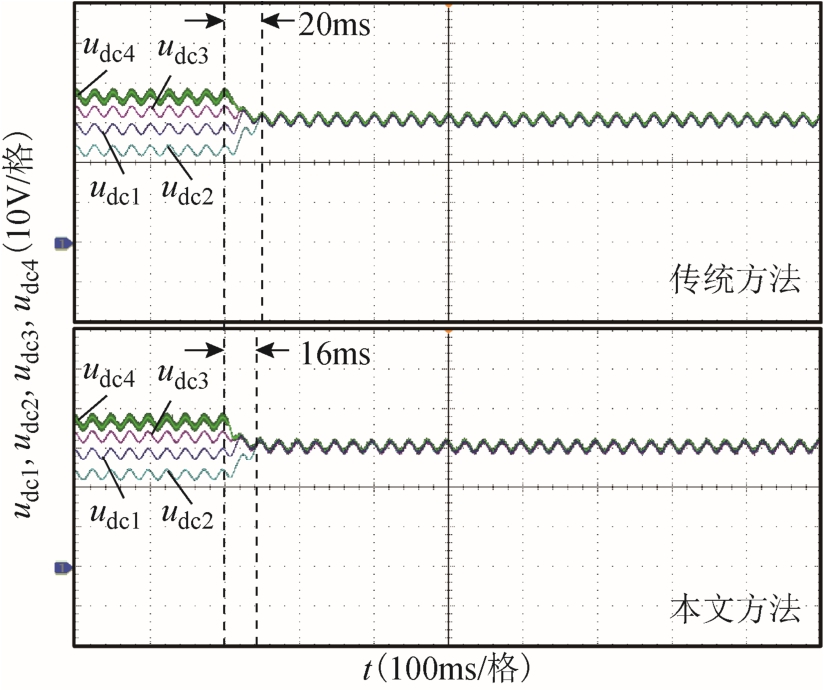
图10 电压平衡速度对比
Fig.10 Comparison of voltage balance velocity
为考察多维扩展调制逻辑化简效果,通过CCS(code composer studio)执行时钟对本文方法与传统方法执行时间进行分析,得到本文方法化简前后与传统方法执行时间的对比图,如图11所示。由于本文方法较传统方法的逻辑判断更为复杂,本文方法化简前的执行时间增幅明显,而化简后的执行时间与传统方法基本一致。
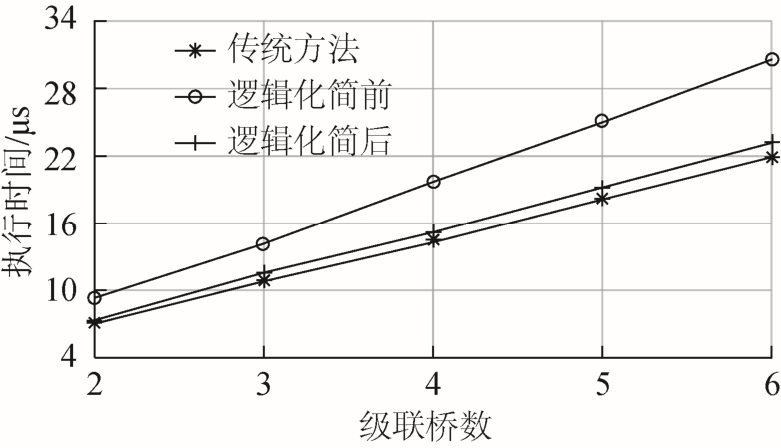
图11 逻辑化简效果对比
Fig.11 Comparison of logicalization effects
为进一步考察多维扩展策略的平衡性能,验证第3节的分析结论。分别就2~4桥CHBR进行了对比实验,实验波形如图12所示。为保障对比环境的一致性,对比实验忽略了升压比的变化,m取固定值1.2,各桥直流电压设定为Udc=30V,并网电流峰值IsM=5A。

图12 2~4桥CHB直流不平衡带载性能对比
Fig.12 Comparison of 2~4 bridge CHB DC unbalanced load performance
各级联桥直流电阻初始值均为 15Ω,4s时,2桥CHB直流电阻跳变为:R1=5Ω,R2=25Ω;3桥跳变为:R1=5Ω,R2=15Ω,R3=25Ω;4桥跳变为:R1=5Ω,R2=15Ω,R3=15Ω,R4=25Ω。6s时,各桥的直流电阻跳变回15Ω。在同样不平衡的带载下,4桥级联比2桥级联的电压偏差缩小了34%。这与第3节的理论分析一致,即直流侧电压的带载能力会随级联桥数量的增加而提升。
5 结论
为将两桥CHBR的二维调制优化策略扩展到多桥级联,降低多维调制优化的复杂度,提出了一种多维调制的降维策略,并对其调制逻辑进行了化简,从而为多维调制的自由度优化提供了一种较为简单的解决方案。通过对这种扩展策略性能的分析与实验得出如下结论:
1)稳态时,所提出的二维调制多维扩展策略与传统的调制方法均可实现n桥CHBR单位功率因数运行,在交流侧合成2n+1电平的阶梯波,实现各桥直流侧电压的平衡与可控。
2)多维扩展策略继承了二维调制自由度的优化特性,使得多维扩展策略的直流电压平衡能力较传统方法更好,且平衡性能会随着级联桥数量的增长而提高。
[1] Xu She, Huang A Q, Burgos R. Review of solid-state transformer technologies and their application in power distribution systems[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics,2013, 1(3): 186-198.
[2] 周柯, 葛钦, 葛平娟, 等. 不平衡负荷下输出并联型电力电子变压器的优化控制策略[J]. 电工技术学报, 2018, 33(1): 149-156.Zhou Ke, Ge Qin, Ge Pingjuan, et al. The research on the control strategy of PET under unbalanced load[J].Transactions of China Electrotechnical Society, 2018,33(1): 149-156.
[3] Xu She, Huang A Q, Ni Xijun. Current sensorless power balance strategy for DC/DC converters in a cascaded multilevel converter based solid state transformer[J].IEEE Transactions on Power Electronics, 2014, 29(1):17-22.
[4] Ferreira Costa L, De Carne G, Buticchi G. The smart transformer: a solid-state transformer tailored to provide ancillary services to the distribution grid[J]. IEEE Power Electronics Magazine, 2017, 4(2): 56-67.
[5] Chen Hao, Divan D. Design of a 10-kV·A softswitching solid-state transformer(S4T)[J]. IEEE Transactions on Power Electronics, 2018, 33(7): 5724-5738.
[6] 吴瑕杰, 熊成林, 冯晓云. 一种适用于单相级联 H桥型变换器的通用型多电平空间矢量PWM算法[J].电工技术学报, 2017, 32(14): 127-136.Wu Xiajie, Xiong Chenglin, Feng Xiaoyun. An universal multilevel space vector pulse-width modulation algorithm for single-phase cascaded H-bridge converter[J]. Transactions of China Electrotechnical Society, 2017, 32(14): 127-136.
[7] Kim S, Lee J, Lee K. A modified level-shifted PWM strategy for fault-tolerant cascaded multilevel inverters with improved power distribution[J]. IEEE Transactions on Industrial Electronics, 2016, 63(11):7264-7274.
[8] Moeini A, Zhao Hui, Wang Shuo. Improve control to output dynamic response and extend modulation index range with hybrid selective harmonic current mitigation-PWM and phase-shift PWM for fourquadrant cascaded H-bridge converters[J]. IEEE Transactions on Industrial Electronics, 2017, 64(9):6854-6863.
[9] 何英杰, 付亚斌, 段文岩. 一种星接 H 桥级联型SVG 直流侧电压均衡控制方法研究[J]. 电工技术学报, 2016, 31(11): 13-21.He Yingjie, Fu Yabin, Duan Wenyan. Research on DC voltage balancing control method of star connection cascaded H bridge static var generator[J].Transactions of China Electrotechnical Society, 2016,31(11): 13-21.
[10] 耿俊成, 刘文华, 袁志昌. 链式 STATCOM 电容电压不平衡现象研究(一)仿真和试验[J]. 电力系统自动化, 2003, 27(16): 53-57, 86.Geng Juncheng, Liu Wenhua, Yuan Zhichang.Research on voltage unbalance of chain statcom capacitor (I) simulation and test[J]. Automation of Electric Power Systems, 2003, 27(16): 53-57, 86.
[11] 耿俊成, 刘文华, 袁志昌. 链式 STATCOM 电容电压不平衡现象研究(二)数学模型[J]. 电力系统自动化, 2003, 27(17): 35-39.Geng Juncheng, Liu Wenhua, Yuan Zhichang.Research on voltage unbalance of chain STATCOM capacitor (Ⅱ) mathematical model[J]. Automation of Electric Power Systems, 2003, 27(17): 35-39.
[12] Ge Baoming, Liu Yushan, Abu-Rub H, et al. State-ofcharge balancing control for a battery energy stored quasi Z source cascaded multilevel inverter based photovoltaic power system[J]. IEEE Transactions on Industrial Electronics, 2018, 65(3): 2268-2279.
[13] Bifaretti S, Zanchetta P, Watson A, et al. Advanced power electronic conversion and control system for universal and flexible power management[J]. IEEE Transactions on Smart Grid, 2011, 2(2): 231-243.
[14] 葛俊杰, 赵争鸣. 级联型电压自平衡固态变压器[J].清华大学学报: 自然科学版, 2013, 53(4): 459-464.Ge Junjie, Zhao Zhengming. Cascaded voltage selfbalancing solid state teansformer[J]. Journal of Tsinghua University: Science&Technology, 2013,53(4): 459-464.
[15] Wang Liang, Zhang Donglai, Wang Yi, et al. Power and voltage balance control of a novel three-phase solid-state transformer using multilevel cascaded H-bridge inverters for microgrid applications[J]. IEEE Transactions on Power Electronics, 2016, 31(4): 3289-3301.
[16] Zhao Tiefu, Wang Gangyao, Bhattacharya S, et al.Voltage and power balance control for a cascaded H-bridge converter-based solid-state transformer[J].IEEE Transactions on Power Electronics, 2013, 28(4):1523-1532.
[17] She Xu, Huang A Q, Wang Gangyao. 3-D space modulation with voltage balancing capability for a cascaded seven-level converter in a solid-state transformer[J]. IEEE Transactions on Power Electronics, 2011, 26(12): 3778-3789.
[18] Lin B R, Lu H H. New multilevel rectifier based on series connection of H-bridge cell[J]. IEE Proceedings-Electric Power Applications, 2000,147(4): 304-312.
[19] Iman-Eini H, Schanen J, Farhangi S. A modular strategy for control and voltage balancing of cascaded H-bridge rectifiers[J]. IEEE Transactions on Power Electronics, 2008, 23(5): 2428-2442.
[20] 王聪, 张国澎, 王俊, 等. 一种适用于级联 H 桥整流直流侧电容电压快速平衡的新型调制方法[J].电工技术学报, 2013, 28(8): 120-127.Wang Cong, Zhang Guopeng, Wang Jun, et al. A novel modulation method for fast balancing DC-link capacitor voltages of cascaded H-bridge rectifier[J].Transactions of China Electrotechnical Society, 2013,28(8): 120-127.
[21] Liang Weihua, Liu Yushan, Ge Baoming, et al. DC-link voltage balance control strategy based on multidimensional modulation technique for quasi-Z-source cascaded multilevel inverter photovoltaic power system[J]. IEEE Transactions on Industrial Informatics, 2018, 14(11): 4905-4915.
[22] Leon J I, Vazquez S, Portillo R, et al. Twodimensional modulation technique for multilevel cascaded H-bridge converters[C]//IEEE International Conference on Industrial Technology, Gippsland, VIC,Australia, 2009: 1-6.
[23] Napoles J, Leon J I, Franquelo L G, et al.Multidimensional modulation technique for cascaded multilevel converters[J]. IEEE Transactions on Industrial Electronics, 2011, 58(2): 412-420.
[24] 高吉磊, 林飞, 郑琼林. 基于网压预测的单相PWM 整流器比例谐振控制[J]. 电工技术学报,2011, 26(5): 45-51.Gao Jilei, Lin Fei, Zheng Qionglin. Proportionalresonant control of single-phase PWM rectifiers based on grid voltage prediction[J]. Transactions of China Electrotechnical Society, 2011, 26(5): 45-51.