0 引言
断路器是配用电网络中的重要电气设备,主要提供电气回路的过载、短路等保护功能,其保护特性对于保障配用电网络安全具有重要作用。国家标准规定,断路器出厂之前需要对其保护特性进行校验,用于保证产品质量与可靠性。文献[1]针对小型断路器中保护特性中的反时限特性建立了基于双金属变形非线性的电-热结构模型,较准确地预测了反时限保护的变形和温度变化。采用电流变换器对断路器保护特性进行在线校验,是对断路器进行性能检测的重要方法[2-3]。早期的断路器保护特性测试装置,主要采用调压器和升流器的组合方式,通过手动、电机控制等方式改变调压器电压,以获得不同测试电流。如文献[4]设计的断路器保护特性实验装置,可进行断路器保护特性测试,但是受调压器的限制,体积较大,且断路器测试精度和效率均受限。随着电力电子技术的发展,基于电力电子变流技术和自动控制理论相结合的电流变换器逐渐成为断路器保护特性测试的新方向[5-8],但目前这些方案缺乏功率因数补偿,没有考虑整流过程中输入电流畸变所带来的谐波污染问题;同时,测试过程没有考虑负载变化对于电流精度的影响,测试准确性有待提高。
功率因数校正(Power Factor Correction, PFC)是减小谐波污染的重要手段,主要可分为有源式与无源式两种。相比于无源功率因数校正,有源功率因数校正在校正效果、体积等方面具有优势[9-12]。文献[9]搭建了基于电压外环、电流内环控制的PFC变换器模型,为解释变换器工作原理提供了依据。文献[10]结合DSP实现了双闭环 PFC变换器的设计,提升了变换器的数字化程度。文献[11]设计了一种用于断路器保护特性测试的交-交电流变换器,基于双闭环方案进行了功率因数补偿和电流控制,但是系统基于传统PI控制进行实现,在控制精度和动态特性上有待提高。文献[12]利用双前馈控制策略改善了电压外环输出侧的稳定性,但其实现过程较为复杂,硬件成本较高。
随着智能控制理论的发展,模糊控制的应用越来越广泛[13-15],由于不需要准确的数学模型,其设计过程简单,易于实现。模糊控制的关键在于模糊规则的确定,传统方法主要基于工程经验对模糊规则进行设计。文献[16]在模糊控制器中引入伸缩因子,与上次运算的论域相乘得到新的论域,消除了控制精度与模糊规则数量的矛盾,增加了系统稳态精度。文献[17-18]利用模糊控制与PID算法融合的方法,建立模糊PID复合系统,利用工程经验建立模糊矩阵表,实现PID输出参数的自适应调整,改善了系统的自适应能力。这些方案虽然提高了控制器的控制性能,但因其模糊控制规则主要基于工程经验,效率和控制精度有待进一步提升。
为了进行改善,一些学者采用人工智能算法对模糊规则进行设计和优化。文献[19]采用改进遗传算法对模糊控制规则进行了优化设计,利用免疫算法的个体记忆、抗体多样性等特点确保系统收敛于全局最优解,有利于改善模糊控制器的性能。文献[20]利用径向基函数对模糊规则进行设计,提高模糊控制的自适应能力。由于涉及复杂的智能算法,这一类方法浮点运算要求较高,得到的模糊规则面存在较明显的凹凸点,即存在一定的无效规则。
为解决上述问题,本文提出一种基于PI控制的Sugeno型模糊控制器模糊规则设计方法,通过PI控制生成模糊控制规则,减小模糊控制过程中存在的凹凸点。以该模糊控制为基础,在输入端,增加测试装置前级的有源功率因数校正(Active Power Factor Correction, APFC)的模糊控制单元,提高系统功率因数水平。在输出端,为减小负载回路阻抗对输出电流精度的影响,采用离散采样积分的方法对负载阻抗自适应在线识别,并进行前馈补偿,提高电流输出精度,整体上提升电流变换器的输入和输出性能。
1 系统结构
电流变换器采用AC-DC-AC结构,其结构如图1所示,可按图中点画线框分为前级、后级两个子系统。前级由交流电源、整流桥、高频滤波电容C1以及升压斩波直流变换器组成;后级由全桥逆变电路、滤波电路、升流器以及负载组成。对前级子系统而言,交流电经过整流桥变为正弦半波,控制电路提取正弦半波相位得到基准电流的相位,正弦半波经过 Boost电路,在负载处得到较为平稳的直流输出电压,控制电路提取输出侧的电压与基准参考值进行求差,经过模糊控制器输出电压平衡直流量,作为参考电流的幅值。参考电流与实际电流送入滞环比较器得到一系列既可稳定输出电压又可提高功率因数的脉冲波形。对于后级子系统,逆变电路采用有限双极性调制,其输出SPWM波形经过滤波恢复成 50Hz工频电流,经过升流器为负载提供测试基准电流。后级子系统将负载电流与基准电流一起送入电流误差放大器,其输出加上经负载阻抗识别的前馈控制信号一同送入比较器与驱动器,进而控制逆变器的高频臂(VT1、VT2)。逆变器的低频臂(VT3、VT4)只需固定输入半个周期的高低电平即可。
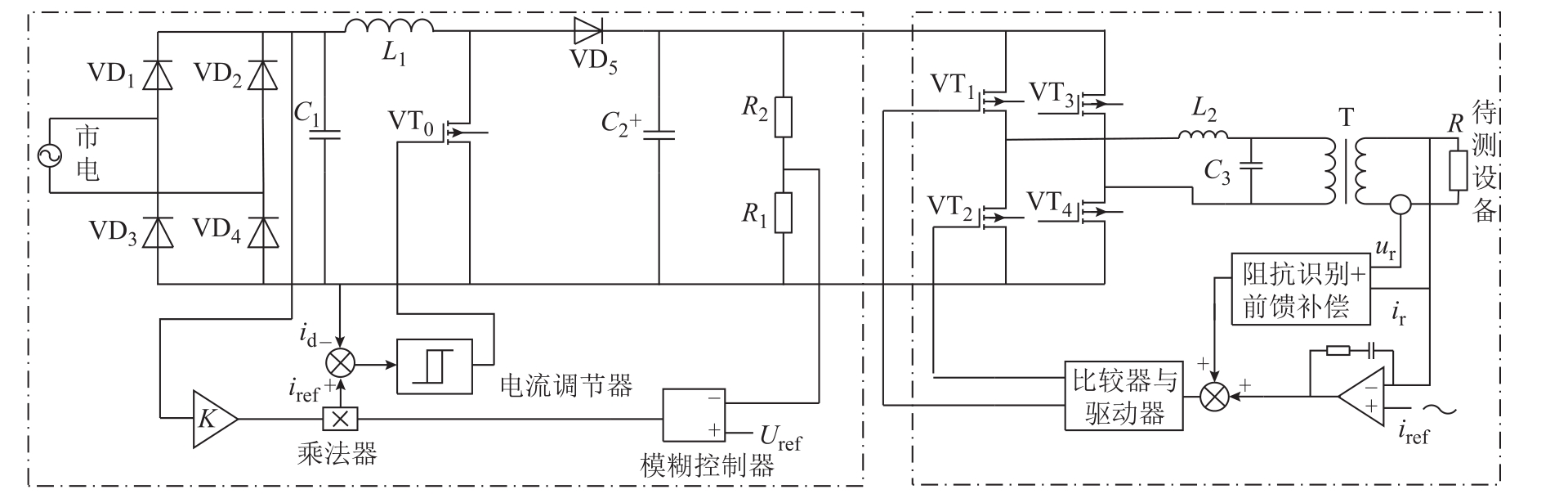
图1 基于电流自适应控制的断路器保护特性测试原理
Fig.1 Block diagram of circuit breaker protection characteristic test based on adaptive current control
2 系统控制算法与策略
2.1 PID控制
实现基于自适应电流控制的电流变换器系统,前级采用基于PID控制与模糊控制相结合的自适应控制方式,后级采用自适应前馈补偿与PID控制相组合的控制方法,系统前后级相结合实现对断路器保护特性测试电流大小以及频率的动态调节。PID技术根据实现方式分为数字PID和模拟PID,数字PID(位置式)的基本表达式为
基于式(1),增量式数字PID的表达式为
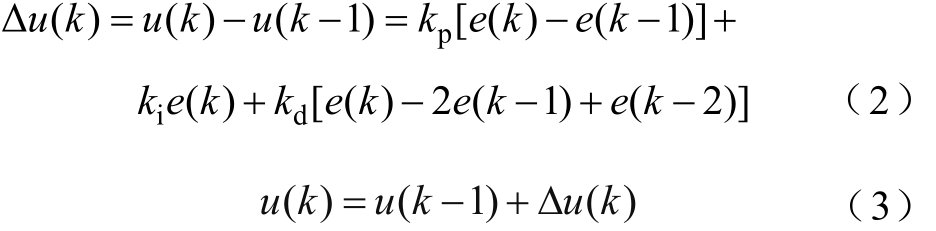
通过对比式(1)、式(3)不难发现,增量式PID控制算法不需要进行累加运算,计算误差影响较小,本系统的PID设计以增量式数字PID控制为基准。
2.2 PI型Sugeno模糊控制
为了提高电流变换器的功率因数水平,论文以Sugeno型模糊控制器为基础,在Sugeno模糊控制电压信号中引入跟踪误差信号进行补偿,提升前级电路对直流电压的跟踪能力,同时结合PI控制生成模糊控制规则,减小Sugeno模糊控制过程中存在的凹凸点,系统控制原理如图2所示,图中误差信号e(k)一方面进入模糊控制器得到控制电压Δu(t),另一方面经过PI控制输出uo(t),两者相加获得最终控制信号。其中,模糊控制器的重要参数m和n是关于kp、ki与Ts的函数,其大小取决于所设计的PI控制器参数。
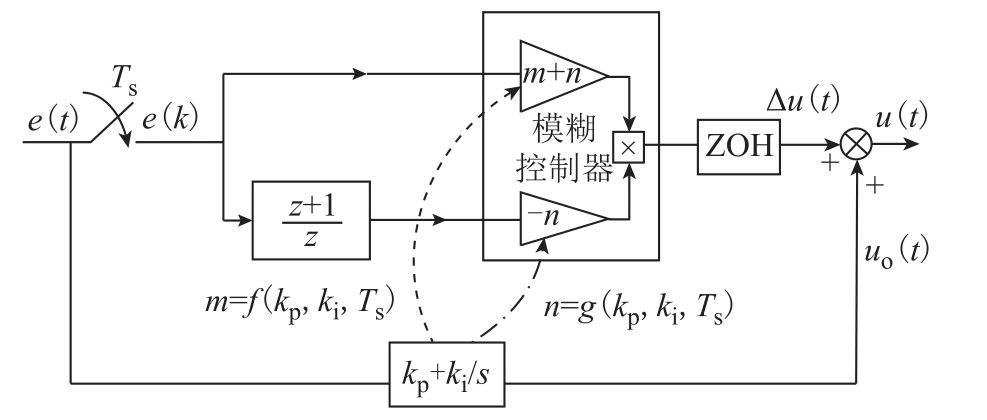
图2 PI型Sugeno模糊控制原理
Fig.2 Schematic diagram of PI-like Sugeno fuzzy control
文献[18]采用阶跃响应法对PI控制器的参数进行调节,所采用的PI控制传递函数G(s)为
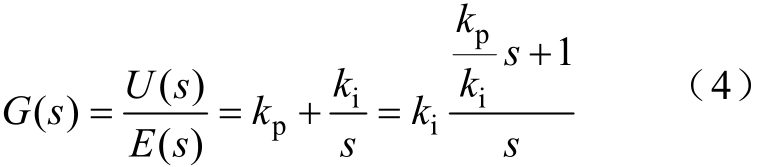
采用双极性变换法对式(4)进行离散后得到
由式(4)和式(5)可得
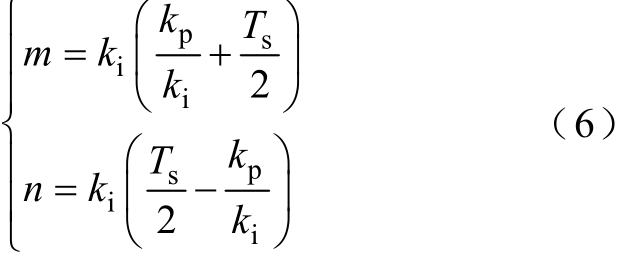
对式(5)进行分解后得到控制电压信号为
对式(7)再进行移项处理可以得到
式(8)即为基于Sugeno推理系统的模糊控制器设计原则。可以发现,控制器此刻的输出 u(k)等于上一个时刻的输出值 u(k-1)加上本时刻控制输出的变化值 Δu(k),理论上可以实现自适应控制的效果。然而式(8)中控制信号u(k)缺乏对当前跟踪误差信号 e(k)的设计,导致控制系统的抗干扰能力和参考输入跟踪能力存在不足。此外,式(8)中控制信号易受到采样时间Ts的影响,容易引起系统超调。针对该问题,论文提出在式(8)的基础上进一步引入跟踪误差信号作为参考,设计一种新的控制输出方式,即
其连续输出形式为
此方案一方面利用模糊控制产生系统控制变化量 Δ u ( t ),另一方面利用PI控制产生主控制信号,既结合了PI控制的特性增加系统稳态性能,又利用模糊控制提升了系统动态响应。
2.3 负载阻抗自适应补偿
对断路器进行保护特性测试时,不同断路器所引入的测试回路阻抗大小不同,对电流输出精度影响也不同。本文提出在电流变换器后级输出端采用离散采样积分的方法对负载阻抗自适应在线识别,并进行前馈补偿,提高测试电流精度,其控制原理如图3所示。
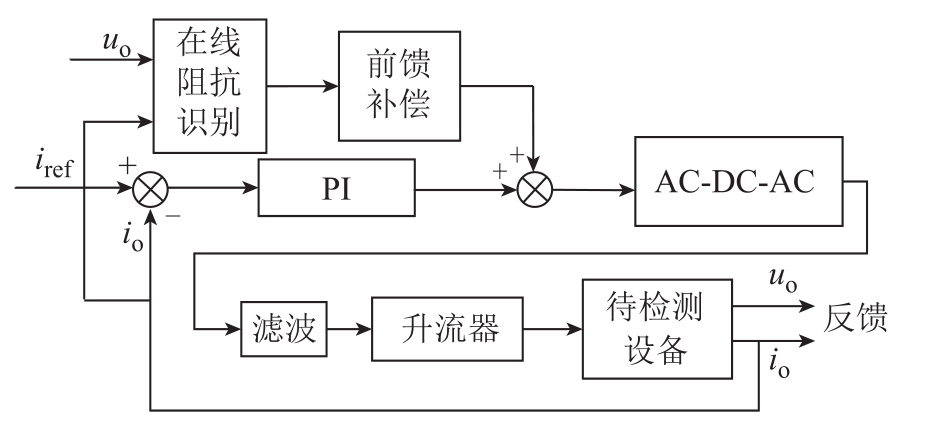
图3 基于阻抗识别的前馈补偿PI控制系统结构图
Fig.3 Diagram of PI feedforward compensation system based on impedance identification
断路器测试端口电压、电流信号作为自适应阻抗识别的输入,通过离散采样积分对阻抗自适应识别,同时结合 PI前馈控制对回路阻抗差异进行补偿。离散采样积分的基本原理如图4所示,断路器测试回路可以用RL串联模型表示,其微分方程描述为
式中,L为测试回路等效电感;R为等效电阻;uo、io分别为负载的端口电压与电流。对端口电压和电流进行离散采样,同时结合分段积分的方法对回路阻抗参数进行自适应在线识别。对式(11)两边同时进行积分运算,得到
式中,t0、t1分别为分段积分的起始和结束时间。分别选取不同分段积分时间,得到两组积分方程组,即
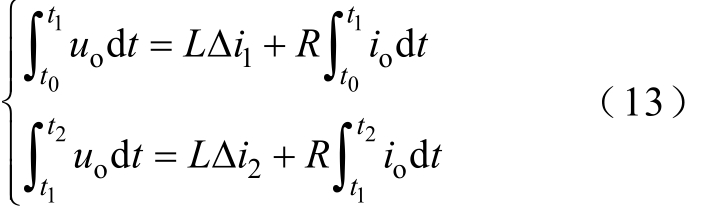
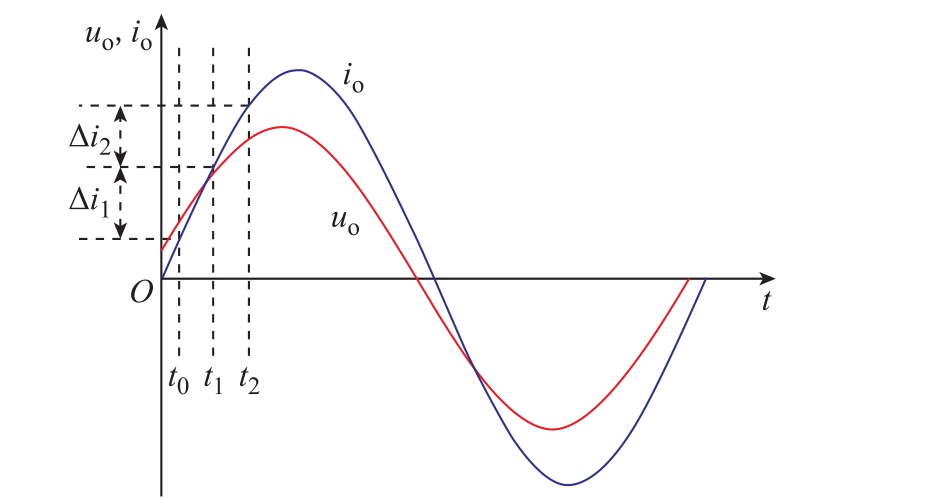
图4 断路器测试端口电压与电流
Fig.4 Voltage and current at the circuit breaker testing port
为了表述方便,分别定义数学符号为
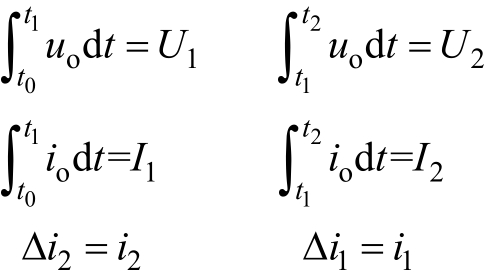
则式(13)可以简化为
联立求解式(14)可得
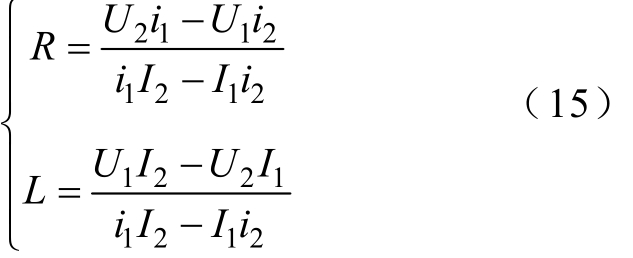
式(15)即为基于离散采样和分段积分的回路阻抗自适应识别模型,可通过断路器测试回路的端口电压、电流以及相应的积分运算,对不同大小的回路阻抗进行自适应在线识别。在此基础上,进一步结合前馈控制,可以减小回路阻抗大小对电流输出精度的影响。
采用状态空间平均法对断路器保护特性测试装置进行建模,设电流变换器前级直流电压幅值恒定,逆变器开关频率远大于输出基波频率,逆变桥可以等效为单相电压型PWM逆变器,如图5所示。
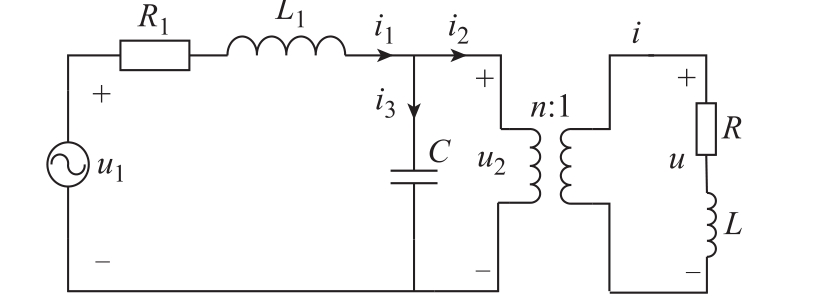
图5 单相电压型PWM逆变电路状态模型
Fig.5 State model of single-phase voltage type PWM inverter
图5 中测试系统的状态空间方程可描述为
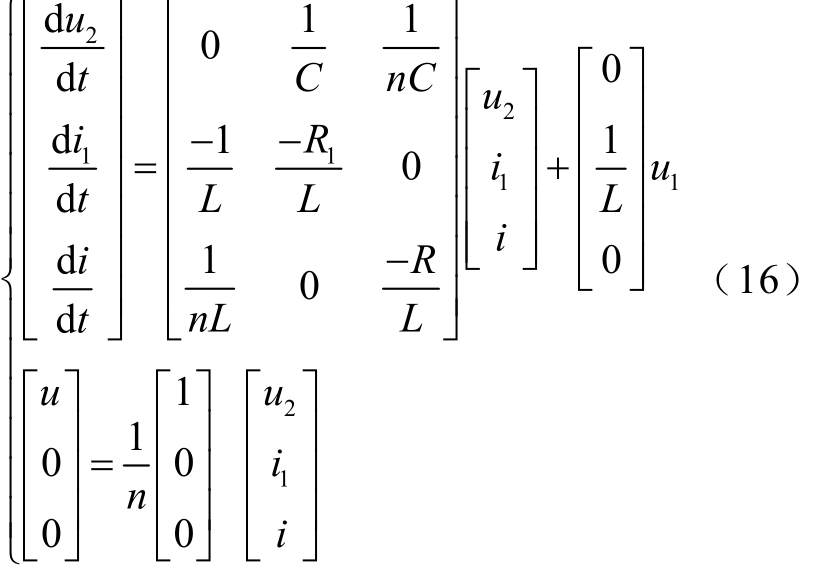
式中,u1为逆变桥的输出电压;u2为电容两端电压;L1和 C分别为滤波电感和电容;i为测试电流;n为升流器电流比;R1为滤波电感自阻。根据式(15)测试回路阻抗自适应识别的结果,可以通过式(16)反求逆变桥的输出控制电压 u1,从而对负载变化对测试电流精度的影响进行补偿,此时控制电压信号为
式中,![]() ;L和R分别为阻抗识别算法计算得到的负载特征值。由此,根据负载阻抗变化,并结合图 3所示的基于阻抗识别的前馈补偿 PI控制系统结构,可有效解决阻抗变化对于测试电流精度的影响,从而提高测试可靠性。
;L和R分别为阻抗识别算法计算得到的负载特征值。由此,根据负载阻抗变化,并结合图 3所示的基于阻抗识别的前馈补偿 PI控制系统结构,可有效解决阻抗变化对于测试电流精度的影响,从而提高测试可靠性。
3 系统仿真
3.1 PI型Sugeno模糊控制仿真
系统仿真结构如图6所示,Boost电路中电感、电容参数分别为0.5mH和0.6mF,滞环比较器上下幅度设置为±0.5,设直流电压跟踪误差为e,误差对时间的变化量为ec,该对组合作为模糊控制器的输入。设两个模糊子集个数均为 9,e的模糊子集为{A1, A2, A3, A4, A5, A6, A7, A8, A9},ec的模糊子集为{B1, B2, B3, B4, B5, B6, B7, B8, B9}。输入变量确定之后,需要确定隶属函数。三角函数曲线体现变量在模糊子集间分布平均,系统输出对参数比较敏感,故选择三角形函数曲线作为e和ec的隶属度函数,其分布如图7所示,其中Tu代表隶属函数,每个三角形表示一个三角函数,横坐标x表示输入模糊子集的取值。
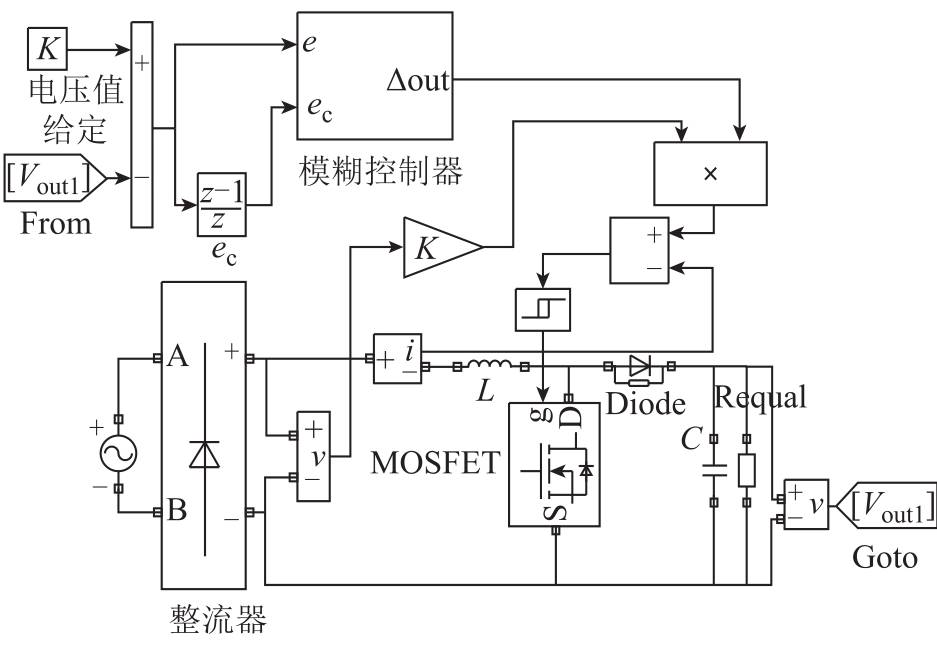
图6 基于PI型Sugeno模糊控制仿真原理图
Fig.6 Simulation diagram of PI-like Sugeno fuzzy control
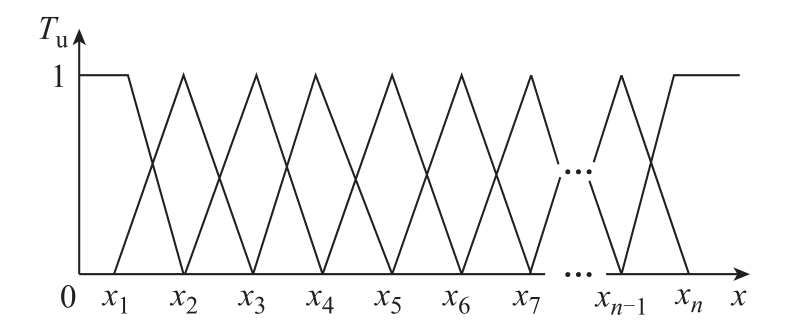
图7 输入模糊子集隶属函数分布图
Fig.7 The distribution map of membership function
模糊控制器的关键在于模糊规则的建立,采用Sugeno推理系统的模糊控制与 Mamdani推理系统的最大的区别在于它的输出是一个函数或者是常数,不需要指定输出模糊子集的隶属度函数。模糊规则库的变现形式为IF e is A1 AND ec is B1 THEN out is U11,…,IF e is A9 AND ec is B9 THEN out is U99。采用阶跃响应法对图 2中的 PI控制器参数进行调节,得到kp=0.02,ki=1 000,Ts取0.005s,将上述kp、ki参数代入式(6)和式(7)进一步求得m=2.52和n=2.48,在确定误差量化值的基础上(见表1),进而得到如表2所示的整体模糊规则,用于仿真和实验结果验证。
为了进行验证,将经典PI、文献[18]中的模糊控制(式(8))和本文提出的方法进行仿真对比(按顺序分别编号为第一、二、三组)。首先对比了系统上电初始时刻前级电路的电压稳定性,设直流电压参考输入为310V,电网电压为220V,电压输出结果如图8所示。可以发现,第一组对应的经典PI控制下电压输出波形在上电时刻产生较大超调,并且存在一定稳态误差。第二、三组在性能上均有改善。进一步比较二、三两组可以发现,本文提出的控制方案在电压波形的动态响应方面更快,并且波形在稳定性方面得到进一步提升。
表1 输入误差/误差变化量模糊化值
Tab.1 Fuzzy values of input error / error changes

A1/B1 A2/B2 A3/B3 A4/B4 A5/B5 A6/B6 A7/B7 A8/B8 A9/B9-3 -1 -0.1 -0.015 0 0.015 0.1 1 3
表2 Δu(k)输出变化模糊规则表
Tab.2 Fuzzy rules of Δu(k)

e ec B1 B2 B3 B4 B5 B6 B7 B8 B9 A1 -3.810 0 -6.270 0 -7.377 0 -7.481 6 -7.500 0 -7.518 5 -7.623 0 -8.730 0 -11.190 0 A2 1.190 0 -1.270 0 -2.377 0 -2.481 6 -2.500 0 -2.518 5 -2.623 0 -3.730 0 -6.190 0 A3 3.440 0 0.980 0 -0.127 0 -0.231 6 -0.250 0 -0.268 5 -0.373 0 -1.480 0 -3.940 0 A4 3.652 5 1.192 5 0.085 5 -0.019 1 -0.037 5 -0.056 0 -0.160 5 -1.267 5 -3.727 5 A5 3.690 0 1.230 0 0.123 0 0.018 5 0.000 0 -0.018 5 -0.123 0 -1.230 0 -3.690 0 A6 3.727 5 1.267 5 0.160 5 0.056 0 0.037 5 0.019 1 -0.085 5 -1.192 5 -3.652 5 A7 3.940 0 1.480 0 0.373 0 0.268 5 0.250 0 0.231 6 0.127 0 -0.980 0 -3.440 0 A8 6.190 0 3.730 0 2.623 0 2.518 5 2.500 0 2.481 6 2.377 0 1.270 0 -1.190 0 A9 11.190 0 8.730 0 7.623 0 7.518 5 7.500 0 7.481 6 7.377 0 6.270 0 3.810 0
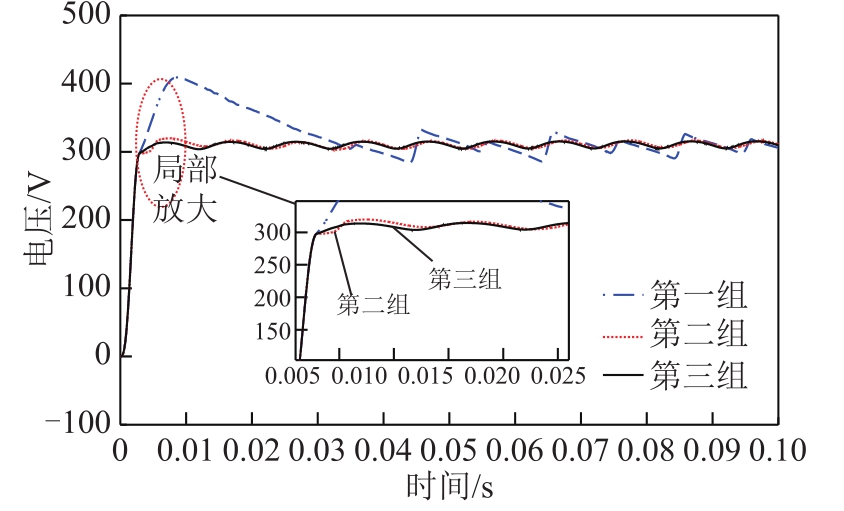
图8 上电时刻电流变换器前级电压输出波形对比
Fig.8 Voltage comparisons at the power-on stage
设电网电压波动,由220V变为180V,直流输出结果如图9所示,可以看到,第一组对应的经典PI控制无法稳态输出直流电压。基于式(8)的模糊控制方案可以较好改善PI控制的效果,但是由于式(8)中没有考虑系统跟踪误差信号e(t),在稳态误差方面有待改善。本文提出的模糊控制方案,其输出稳定在 310V附近,动态响应和稳态输出特性相比前两组结果较优。
此外,对比研究了三组控制方案在设定参考电压发生突变时的响应性能,设系统在 0.05s处参考输入由310V跳变为400V,观察直流电压输出波形,对比结果如图10所示。从图10中可以看到,经典PI控制下的输出电压偏离设定值,系统不稳定;基于式(8)的控制方案可以改善PI控制效果,但在参考输入波动出现时,该方法在电压跟踪的响应速度和稳定方面存在限制,到 0.09s时才趋于稳定。本文提出的控制方法动态响应时间约为 0.1s,在0.06s处达到稳定输出,且稳态误差较小,提高了电流变换器前级直流电压的控制精度。
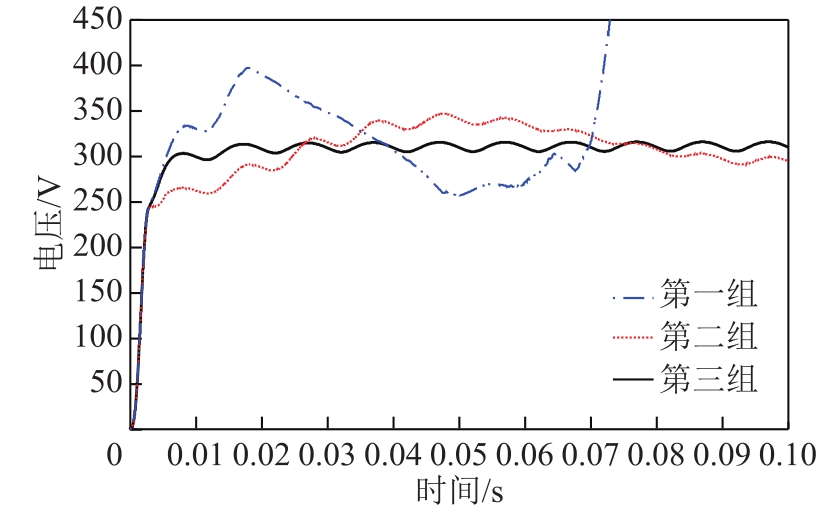
图9 180V电网电压时的电压输出波形对比
Fig.9 Voltage comparisons when the grid voltage is 180V
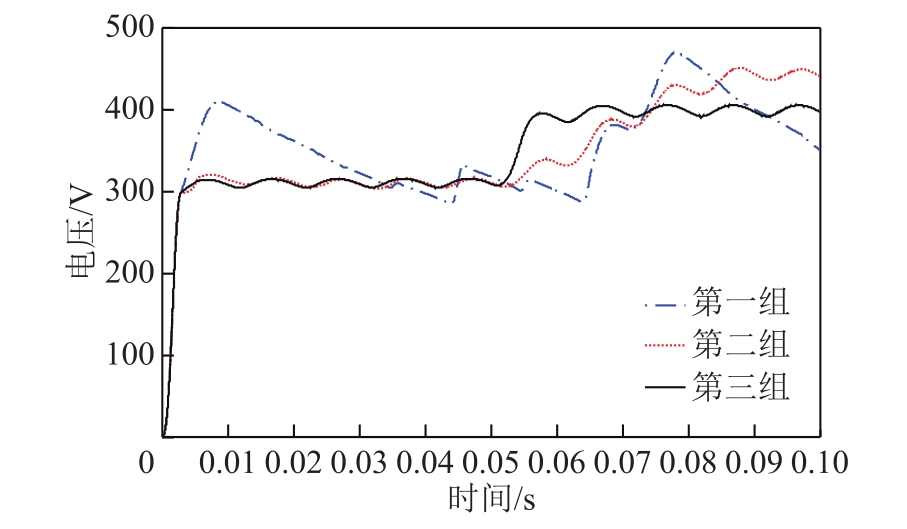
图10 直流参考输入由310V突变至400V时的电压输出波形对比
Fig.10 Voltage comparisons when reference is changed from 310V to 400V
为了对模糊规则的有效性进行对比,本文将所提出的PI型Sugeno模糊控制规则与遗传算法设计的规则进行对比,遗传算法实例以文献[12]中的方法为参考,对比结果分别如图11和图12所示。从图中可以看出,本文提出的方案中模糊规则平面较光滑,无凹凸点,设计的规则作用效果明显。相比于遗传算法产生的模糊控制规则,本文提出的模糊规则设计方法更能减少无效规则的产生,提高控制效率。
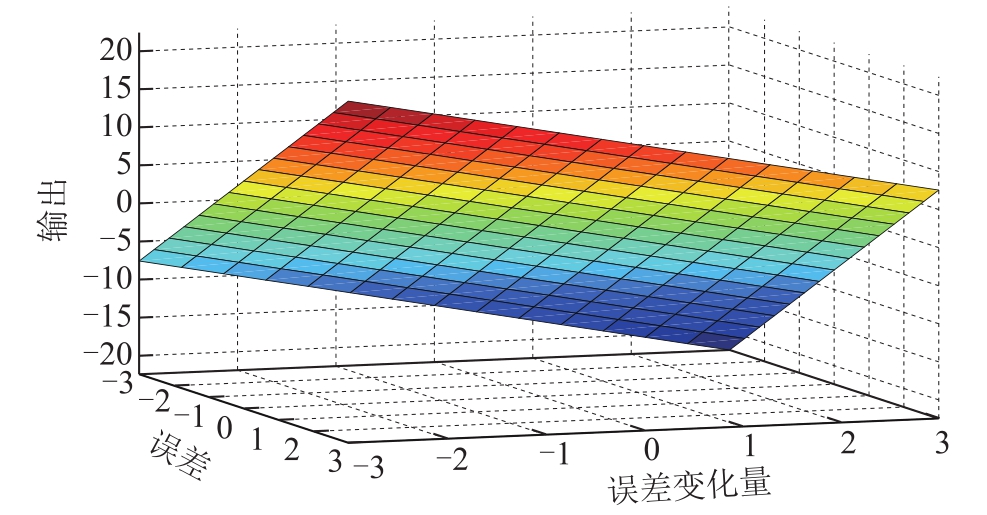
图11 所提出的PI型Sugeno模糊控制规则表面视图
Fig.11 Surface of the proposed PI-like Sugeno fuzzy rules
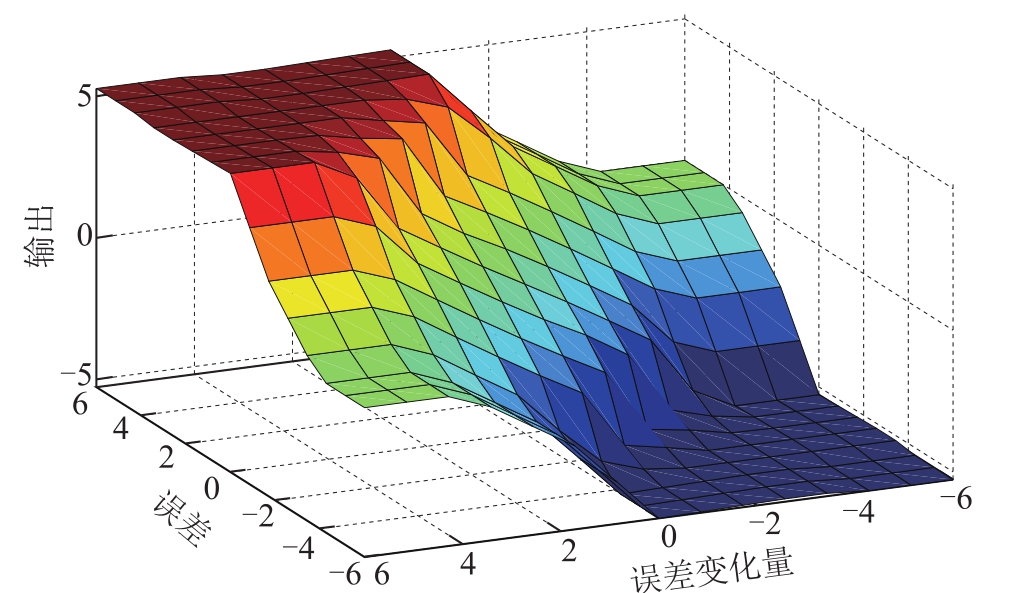
图12 基于遗传算法生成的模糊规则表面视图
Fig.12 Fuzzy rules based on genetic algorithm
3.2 后级电流自适应补偿控制策略仿真
在对电流变换器前级电压进行模糊控制的基础上,在后级电流输出回路中进行阻抗自适应识别并进行前馈补偿,系统仿真框图如图 13所示。图中功率因数校正单元即为前级电压跟踪单元,电流输出回路中,系统滤波电感L1取7.84mH,等效电阻 R1取 0.066Ω,滤波电容 C取 4.7μF,升流器电流比设置为 220/7,等效负载 RL串联模型参数为0.023 5Ω,1.575×10-5H,仿真结果如图14~图16所示。
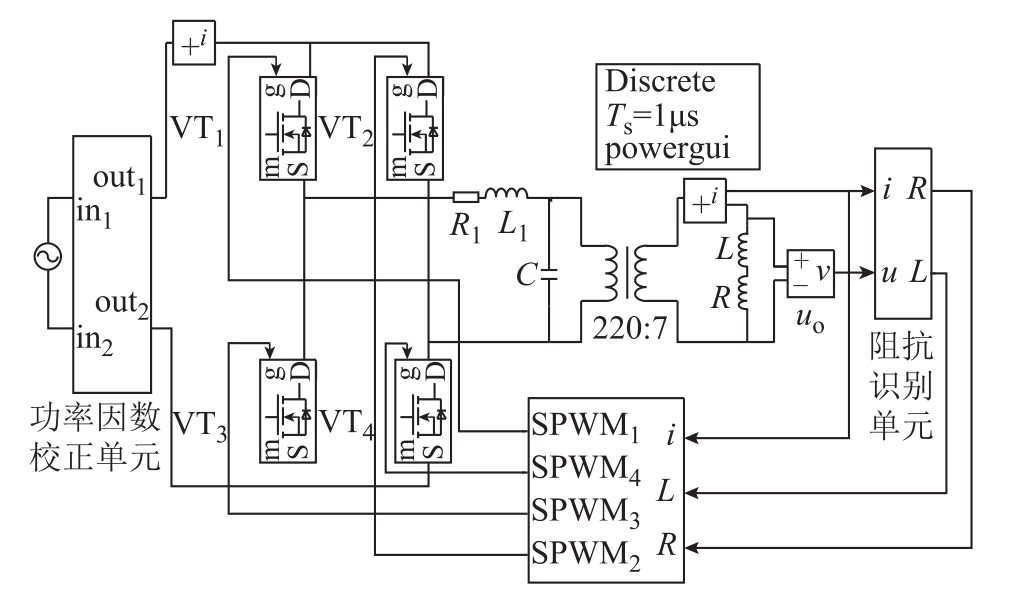
图13 电流变换器仿真原理
Fig.13 Simulation schematic diagram of the current converter
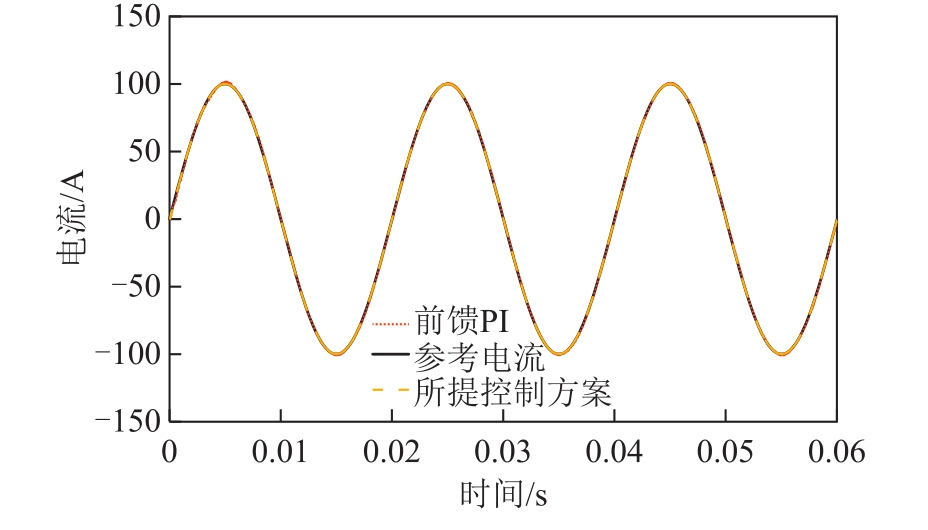
图14 电流变换器输出波形
Fig.14 Current comparisons of different control strategies
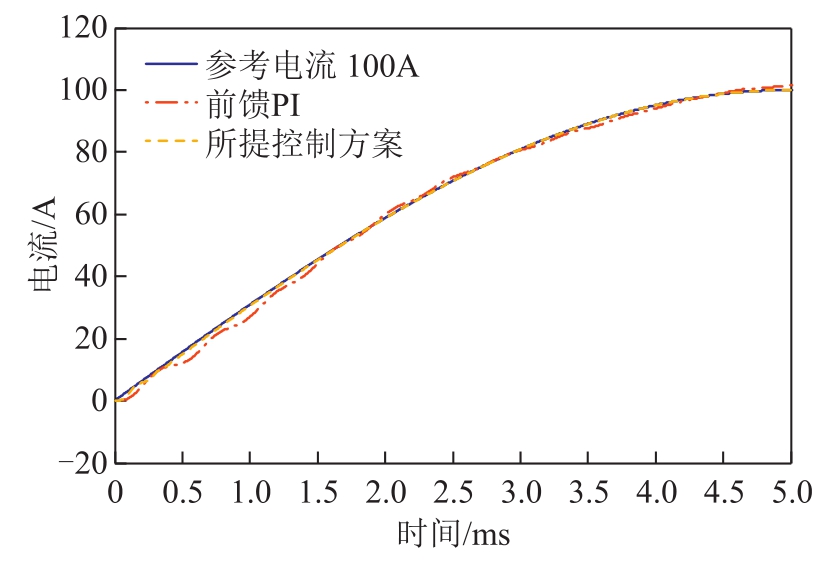
图15 电流变换器输出波形(局部放大)
Fig.15 Enlarged current waveform comparisons
图14 中测试电流参考值为100A,对应的三组曲线分别为参考输入、基于初始化负载参数的 PI前馈控制(前馈PI,负载RL模型初始化参数为0.02Ω,1.0×10-5H)和基于阻抗识别的前馈补偿控制下的电流输出波形。从图中可以看到,前馈PI控制和所提控制方案均可对电流波形进行控制,但是电流输出精度上有较大差异。将电流波形进行局部放大,对比结果如图15所示,可以发现,前馈PI控制相比所提出的控制方案,其响应速度较慢,并且误差较明显,将两组误差曲线直接进行对比,其结果如图16中的“第一组”所示,可以看到,所提出的控制方案在电流瞬态和稳态精度上均有提升。
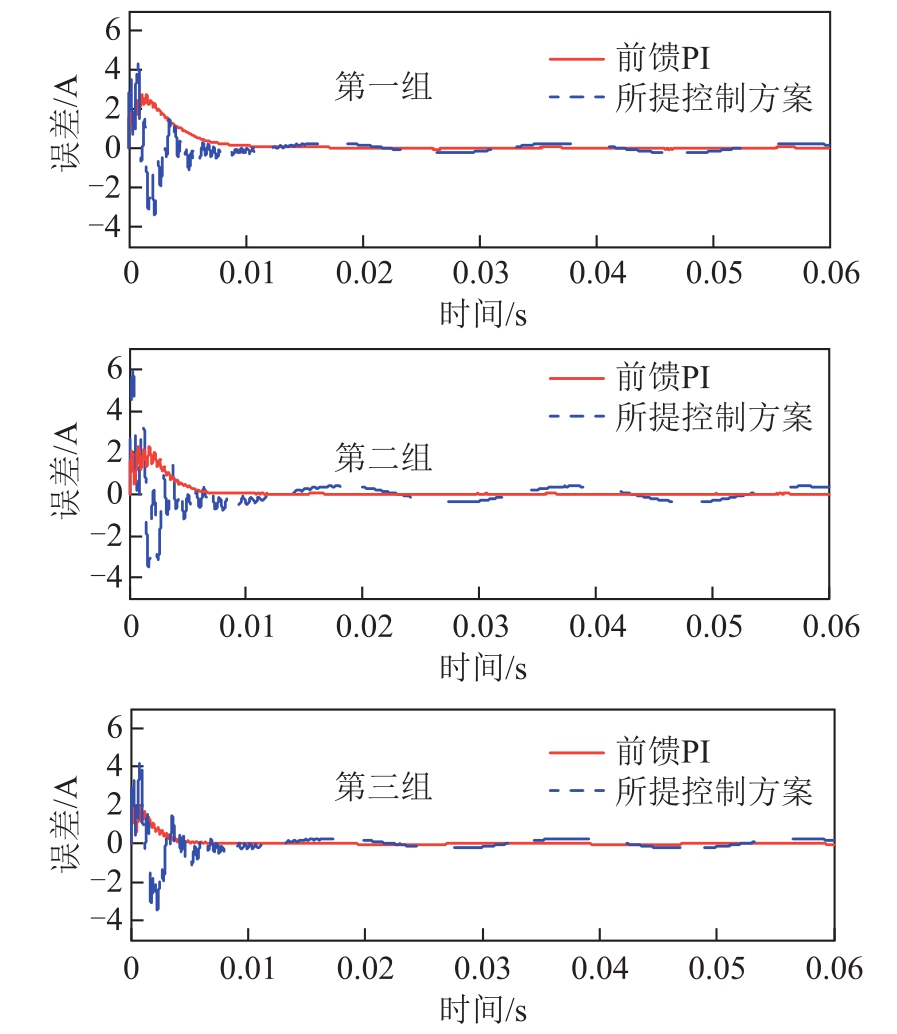
图16 电流变换器电流误差输出波形
Fig.16 Comparisons of current errors
此外,还对比了负载发生变化时不同控制方案的效果,其结果如图16中的“第二组”和“第三组”曲线所示,其中,第二组负载 RL串联模型参数为0.0141Ω和 0.945×10-5H,第三组 RL串联模型参数为0.007Ω和0.473×10-5H,前馈补偿和所提出控制方案中的参数不进行变化。对比误差曲线可以发现,当负载发生变化时,所提出的控制方案仍然可以保证较高的瞬态和稳态电流控制精度,对比稳态误差曲线,可以将前馈 PI控制中的电流精度±0.1A缩小至±0.02A,电流稳态时间缩短50%。说明基于阻抗识别的前馈补偿PI控制的电流误差输出更小,电流输出稳定,对于负载阻抗变化的适应性较强,从而能有效提高断路器保护特性的测试精度与稳定性。
4 样机研制及实验验证
选用STM32F103RBT6作为主控芯片,基于所提出的PI型Sugeno模糊控制和基于阻抗在线识别的前馈PI控制算法,研制了用于断路器保护特性测试的原型装置,其实物如图17所示。主要包括用于输出电流检测的电流互感器(300A/5A)、实现电流变换的升流变压器(220/7)、用于信号捕捉与显示的示波器、执行不同等级电流通路切换的交流接触器(吸持功率 25V·A)以及用于测试的小型断路器等。

图17 样机实物及测试装置
Fig.17 Converter prototype and experimental setup
为了对电流变换器前级电路特性进行对比,得到无功率因数校正和本文校正方案时输入电流波形对比如图18所示。由图18可知,未进行功率因数校正时,整个交流源系统的输入电流表现为一个周期内的正负尖脉冲波形,对图18中无校正波形进行傅里叶分析,如图19所示。由图19发现其包含大量的谐波成分,对电网产生较大谐波污染。采用所提出的控制方案进行功率因数校正后,输入电流中谐波含量明显降低,降低了谐波污染。
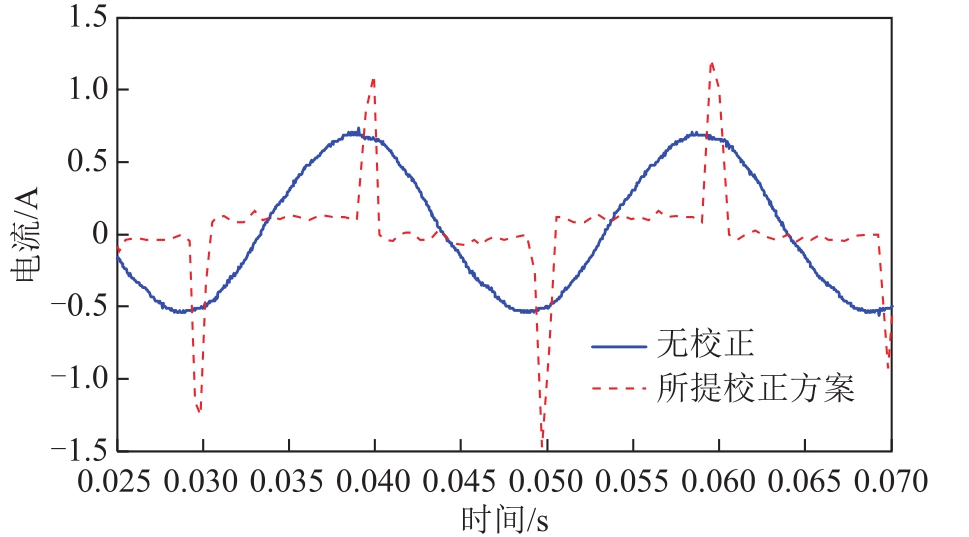
图18 输入电流波形对比
Fig.18 Comparison diagram of input current waveforms
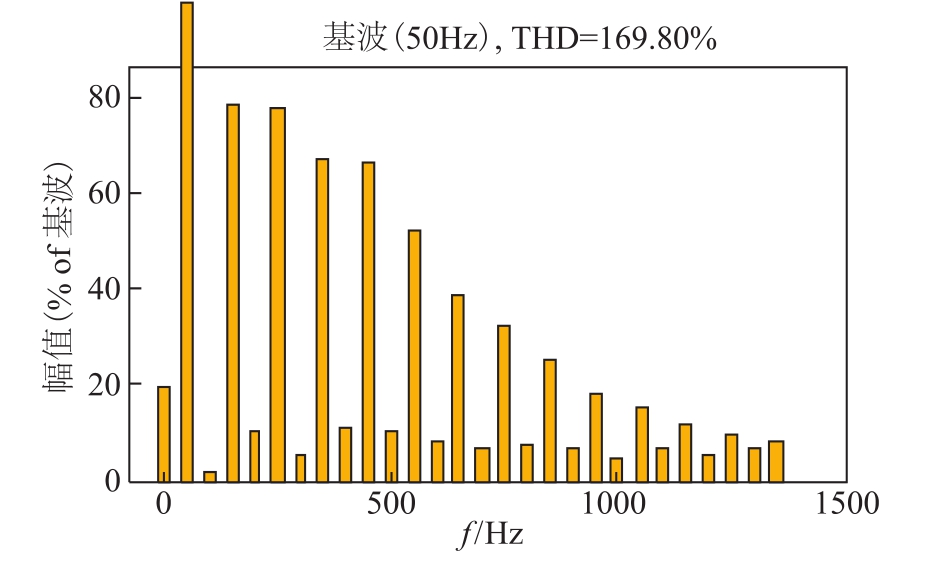
图19 无校正电流傅里叶分析
Fig.19 Fourier analysis of uncorrected current waveform
在对前级电路进行功率因数补偿的基础上,对后级控制策略下的电流输出波形进行了实验对比,分别研究了基于给定负载初始化参数的前馈 PI控制(图20中第一组)和所提出的阻抗在线识别自适应前馈补偿控制(图20中第二组)两种方案,电流输出结果如图20所示。对比可以发现,相比现有的前馈PI控制策略,所提出的控制方法可有效降低测试电流误差,误差小于1.2%,从而有效提高断路器保护特性测试的精度及可靠性。
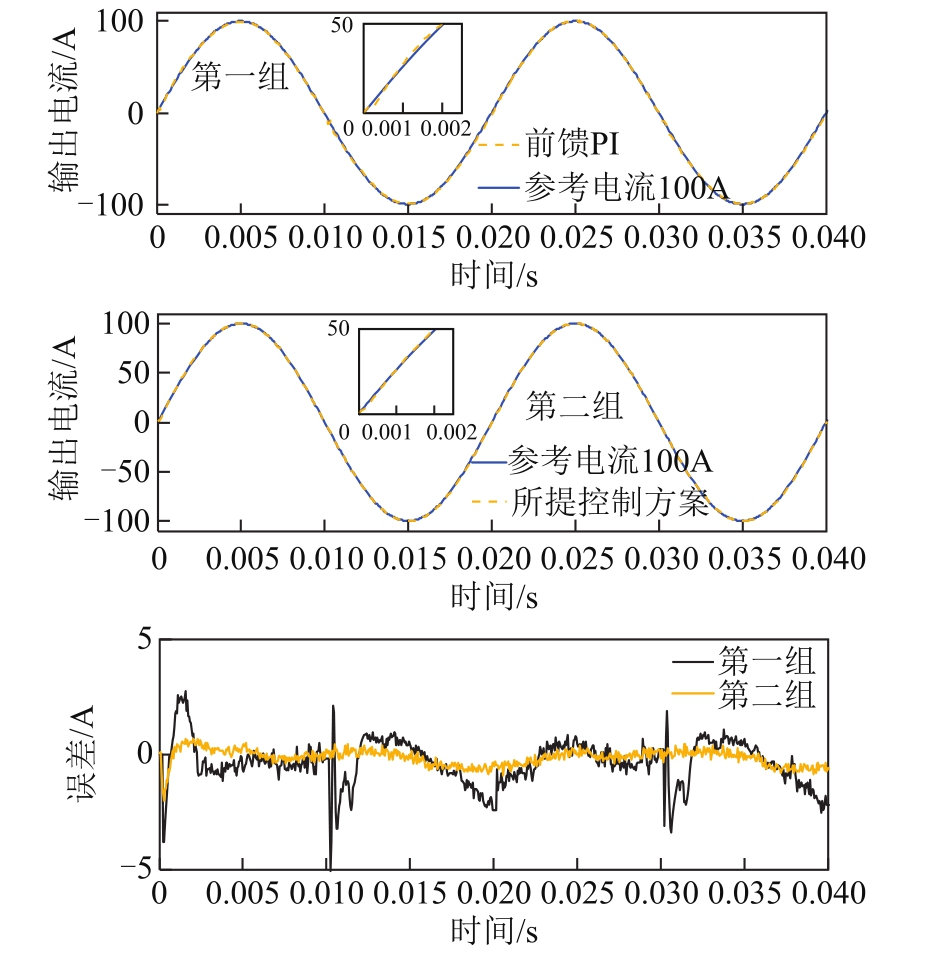
图20 输出电流对比曲线
Fig.20 Output current comparisons
为了验证模糊控制设计的合理性以及该控制效果对后级电路的影响。在保证系统后级进行在线阻抗识别前馈补偿的基础上,分别对比研究了电流变换器在不同输入电压下的综合性能,其结果见表3。
表3 电流变换器综合性能对比
Tab.3 Performance comparisons of the current converter
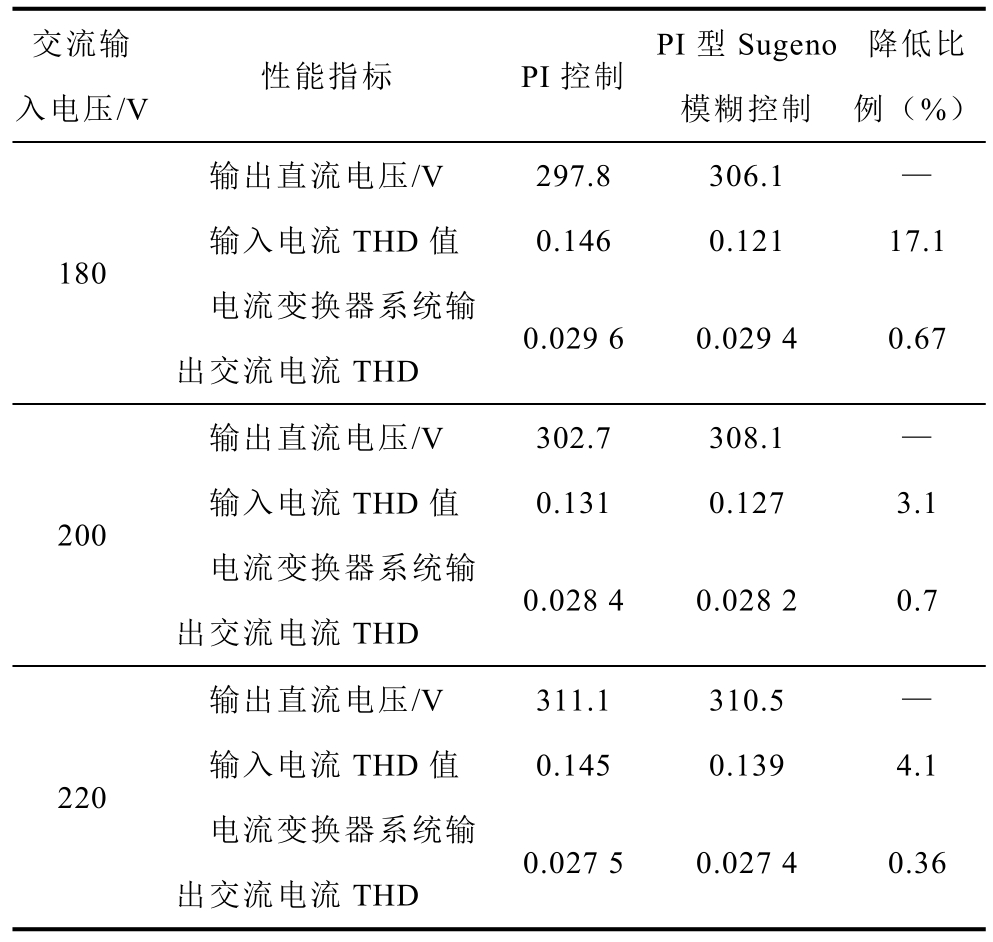
交流输入电压/V性能指标 PI控制PI型Sugeno模糊控制降低比例(%)输出直流电压/V 297.8 306.1 —180输入电流THD值 0.146 0.121 17.1电流变换器系统输出交流电流THD 0.029 6 0.029 4 0.67输出直流电压/V 302.7 308.1 —200输入电流THD值 0.131 0.127 3.1电流变换器系统输出交流电流THD 0.028 4 0.028 2 0.7输出直流电压/V 311.1 310.5 —220输入电流THD值 0.145 0.139 4.1电流变换器系统输出交流电流THD 0.027 5 0.027 4 0.36
根据表3的实验结果可知,对于不同的系统输入电压,相比于现有PI控制,本文提出的自适应模糊控制可以获得更稳定的直流电压(直流电压设定值为 310V),同时降低了输入、输出电流畸变。输入电流THD的降低比例分别为17.1%、3.1%和4.1%。所提出的前级功率因数补偿控制策略,对于减小后级输出电流的波形畸变也有一定效果,但是影响效果不明显,降低比例分别为0.67%、0.7%和0.36%。
5 结论
本文研究了断路器保护特性测试中的自适应电流控制策略,提出通过PI型Sugeno模糊控制对测试装置的前级电路进行功率因数补偿,所提出的模糊控制方案中模糊规则平面较光滑,无凹凸点,相比现有遗传算法的模糊控制生成规则,可有效减少无效规则的产生,提高控制效率。在后级电流输出端,提出通过离散采样积分的方法对负载阻抗自适应在线识别,结合前馈PI控制,将测试电流误差从3%降至1.2%,提高了测试电流精度。此外,研究了PI型Sugeno模糊控制策略对于输入、输出电流THD的影响,相比现有 PI控制方案,THD最大降低比例达到 17.1%,可有效减小波形失真,同时减少电网谐波污染。
[1] Shu Liang, Guo Liang, Wu Guichu, et al. Research of thermal protection characteristics for circuit breakers considering nonlinear electro-thermal-structural[J].Applied Thermal Engineering, 2019, 156: 85-94.
[2] 舒亮, 刘源, 崔永昊, 等. 断路器测试中电流和功率因数补偿的组合控制策略研究[J]. 电器与能效管理技术, 2019(10): 57-63.Shu Liang, Liu Yuan, Cui Yonghao, et al. Research on combined control strategy of current and power factor compensation in circuit breaker testing[J]. Electrical and Energy Management Technology, 2019(10): 57-63.
[3] Saugata S Biswas, Anurag K Srivastava, Dave Whitehead. A real-time data-driven algorithm for health diagnosis and prognosis of a circuit breaker trip assembly[J]. IEEE Transactions on Industrial Electronics, 2015, 62(6): 3822-3831.
[4] 凌荣耀, 潘益斌, 黄书杭, 等. 断路器保护特性实验装置的设计及实现[J]. 中国电力教育, 2012,226(3): 117-118.Ling Rongyao, Pan Yibin, Huang Shuhang, et al.Design and implementation of experimental device for protection characteristics of circuit breakers[J]. China Electric Power Education, 2012, 226(3): 117-118.
[5] 杨松, 李艳芳, 徐欣歌, 等. 基于H桥及SPWM调制的大功率交流恒流源[J]. 机电技术, 2011, 3: 80-85.Yang Song, Li Yangfnag, Xu Xinge, et al. High power AC constant current source based on H-bridge and SPWM modulation[J]. Journal of Electromechanical Technology, 2011, 3: 80-85.
[6] 赵升, 陈冲, 苏秀萍, 等. 大功率交流恒流源自适应 PWM 策略研究及其应用[J]. 电力电子技术,2014, 48(7): 66-70.Zhao Sheng, Chen Chong, Su Xiuping, et al. Selfadaption control strategy of pulse width modulation in high power AC source[J]. Power Electronics, 2014,48(7): 66-70.
[7] 赵琛, 刘维亭, 魏海峰. 低压电器检测用交流恒流源系统设计[J]. 电子设计工程, 2017, 25(13): 151-155.Zhao Chen, Liu Weiting, Wei Haifeng. Research on AC constant current source system for low voltage electrical apparatus testing[J]. Electronic Design Engineering, 2017, 25 (13): 151-155.
[8] Jitendra Solanki, Norbert Frohleke, Joachim Bocker,et al. High-current variable-voltage rectifiers: state of the art topologies[J]. ET Power Electronics, 2015, 8(6):1068-1080.
[9] 任海鹏, 刘丁. 基于Matlab的PFC BOOST变换器仿真研究与实验验证[J]. 电工技术学报, 2006,21(5): 29-35.Ren Haipeng, Liu Ding. Simulation on power factor correction BOOST converter based on Matlab and itis experimental verification[J]. Transactions of China Electrotechnical Society, 2006, 21(5): 29-35.
[10] 马皓, 郎芸萍. 一种关于单相 Boost功率因数校正器数字控制的改进算法[J]. 电工技术学报, 2006,21(2): 83-87.Ma Hao, Lang Yunping. An improved algorthm DSP implementation of Boost PRC converter[J].Transactions of China Electrotechnical Society, 2006,21(2): 83-87.
[11] Kitcharoenwat S, Konghirun M, Sangswang A. A novel single-phase AC-AC converter for circuit breaker testing application[J]. IEEE Transactions on Industrial Applications, 2014, 50(6): 3867-3875.
[12] 任小永, 白雷, 惠琦, 等. 一种快速动态响应低电压纹波功率因数校正变换器的控制策略[J]. 电工技术学报, 2019, 34(14): 2937-2945.Ren Xiaoong, Bai Lei, Hui Qi, et al. Control strategy of power factor correction converter for fast dynamic response and low output voltage ripple[J]. Transactions of China Electrotechnical Society, 2019, 34(14):2937-2945.
[13] 朱熀秋, 杜伟. 基于模糊神经网络逆系统的无轴承永磁同步电机解耦控制[J]. 中国电机工程学报,2019, 39(4): 1190-1198.Zhu Huangqiu, Du Wei, Decoupling control of bearingless permanent magnet synchronous motor based on inverse system using the adaptive neuralfuzzy inference system[J]. Proceeding of the CSEE,2019, 39(4): 1190-1198.
[14] 卢浩, 王群京, 陈权, 等. 三相光伏逆变器软起动改进模糊控制研究[J]. 电力电子技术, 2015, 49(6):74-77.Lu Hao, Wang Jingqun, Chen Quan, et al. Soft start of three-phase photovoltaic inverter based on modified segmentation fuzyzy control[J]. Power Electronics,2015, 49(6): 74-77.
[15] Sun Xiaodong, Long Chen, Yang Zebin. Overview of bearingless permanent magnet synchronous motors[J].IEEE Transactions on Industrial Electronics, 2013,60(12): 5528-5538.
[16] 刘和祥, 胡敏强, 余海涛, 等. 基于磁悬浮小车系统的自适应模糊滑模-PID混合控制方案[J]. 电工技术学报, 2013, 28(6): 93-100.Liu Hexiang, Hu Minqiang, Yu Haitao, et al. Scheme of variable universe fuzzy sliding mode adaptive and PID hybrid controller for magley vehicle[J].Transactions of China Electrotechnical Society, 2013,28(6): 93-100.
[17] 张博彦, 齐铂金, 周阳, 等. 基于模糊 PID 算法的半桥DC/DC控制器的优化设计[J]. 电力电子技术,2018, 52 (9): 74-77.Zhang Boyan, Qi Bojin, Zhou Yang, et al. Optimal design of half-bridge DC/DC controller based on fuzzy PID algorithm[J]. Power Electronics, 2018, 52(9): 74-77.
[18] Alexander G Perry, Feng Guang, Liu Yanfei, et al. A design method for PI-like fuzzy logic controllers for DC-DC converter[J]. IEEE Transactions on Industrial Electronics, 2007, 54(5): 2688-2696.
[19] 郭亦文, 李军, 耿林霄, 等. 基于遗传算法获取模糊规则[J]. 计算机应用, 2014, 34(10): 2899-2903.Guo Yiwen, Li Jun, Geng Linxiao, et al. Fuzzy rule extraction based on genetic algorithm[J]. Journal of Computer Applications, 2014, 34(10): 2899-2903.
[20] 张景元. 基于神经网络的自适应模糊控制系统[J].计算机工程与设计, 2014, 34(10): 3613-3684.Zhang Jingyuan. Self-adaptive fuzzy control systems based on neural networks[J]. Computer Engineering and Design, 2014, 34(10): 3613-3684.