0 引言
随着新能源发电、储能应用、柔性直流输电等技术的发展，现代电力系统正逐渐演变为以电力电子设备高渗透率为特征的电力电子化电力系统[1-2]。基于虚拟同步发电机（Virtual Synchronous Generator,VSG）技术的逆变器控制策略能够全面地模拟同步发电机的运行特性，在实现一次调频和一次调压功能的同时能够在动态过程中为系统提供惯性、阻尼支撑[3-5]。该技术的发展为分布式电源的友好消纳提供了良好途径，具有广阔的应用前景。
虚拟同步机技术方案包括静止同步机（Static Synchronous Generator, SG）方案、虚拟同步机（VISMA）方案、虚拟同步发电机方案、“Synchronverter”方案和发电机模拟控制方案等[6]。文献[7]通过时域仿真对几种不同结构的VSG控制算法进行了综合比较。随着虚拟同步控制技术研究的深入，文献[8]进一步以Phillips-Heffron模型为基础对典型电压源型并网变换器（Voltage Source Converters, VSCs）控制策略的等效惯量阻尼参数进行了归纳总结。
目前，单台VSG接入的研究已经比较广泛，而多台VSG接入的研究还不够深入。针对多类型VSG的研究主要集中于以下两个方面：一方面是VSG接入交流系统后，自身控制策略的优化及其控制参数的选择。在多机并列运行情况下，稳态时并列机组通常按调差系数进行功率分配。在动态过程中，当参数配置合理时，多机系统能够实现频率和电压的稳定控制；当参数配置不合理时，多机并联运行易出现低频振荡现象[9-11]。同类型虚拟同步机通过参数匹配实现扰动功率的一致响应[12-16]，不同类型的虚拟同步机通过协调控制实现多机系统整体动态响应的优化[10,17]。另一方面是VSG接入后对交流系统稳定性的影响。文献[1]通过频率响应传递函数的范数对多 VSG接入的电力系统频率响应特性进行了定量分析。基于含多个VSG的交流系统线性化互联模型，文献[11]采用阻尼转矩法分析了VSG接入对系统机电振荡模式的影响机理并进行了论证，给出了参数设定的建议。文献[18]定义了微电网中多VSG相对于惯性中心的相位差，用于多 VSG微电网的暂态稳定性评估，并采用自适应惯量的方法提高大扰动后微电网的暂态稳定性。
上述研究所采用的小信号分析方法可分为频域分析法和时域分析法[19]。时域分析法需要建立系统的状态空间小信号模型，该方法可以详尽地描述系统中的每一个状态变量，可完整地获取系统的动态性能。但状态空间矩阵规模会随着控制策略和微电网网络结构的复杂程度增加而急剧增加，致使模型更为复杂[20-21]。文献[22-23]建立了微电网中逆变器并联系统完整的状态空间小信号模型。文献[24-26]建立了包含不同类型微源的微电网完整小信号模型。频域分析法需要依靠系统的传递函数。该类方法应用于VSG时，根据变流器的电压电流闭环控制带宽远高于功率环控制带宽，对内、外环分别进行分析[27]。其中，内环采用阻抗分析法[28-29]，通过二端口网络模型能够方便地扩展到多机并联系统中[2]；外环将并网逆变器等效为一个理想受控电压源与一个恒定的输出阻抗串联的形式。在此基础上，一些学者提出了用于分析VSG功率环（低频域）特性的简化模型，包括Phillips-Heffron模型[8,30-31]和忽略有功与无功控制环耦合影响的简化小信号模型[9-10]（功率耦合可通过虚拟阻抗等方法降低[32]）。详细的小信号模型由于模型阶数很高，通常用于分析单机或双机并联系统的稳定性；简化的小信号模型可灵活地选择时域类分析法或频率类分析法用于单机或双机并联系统的理论研究，但扩展到三机及以上系统时同样面临模型复杂的问题。
针对上述问题，文献[33]以有功和无功功率环解耦为基础，建立了下垂控制逆变器的P/ω和Q/U“导纳”模型，应用该模型分析了逆变器并联系统的稳定性。文献[34]运用P/ω“导纳”模型分析了并联VSG的功频调节特性。P/ω“导纳”模型将VSG描述为二端口网络，能够方便地扩展到两台及以上的多机并联系统中，但现有并联VSG系统的P/ω“导纳”模型仅考虑了角频率参考值输入和负载扰动情况下各台 VSG输出功率的响应，未考虑各台 VSG输出角频率的响应。然而，实际中更加关注的是有功指令值输入和负载扰动情况下各台 VSG输出功率和角频率的响应。因此，本文建立了拓展的 P/ω“导纳”模型来全面而精确地描述多VSG并联系统的功频响应特性，并进一步推导了多机系统参数匹配时各台VSG的功频最优响应形式。
1 P/ω“导纳”基础模型
1.1 单机模型
VSG主电路拓扑和控制结构如图 1所示[4-5]。逆变器通过LC滤波器及连接线路接到公共母线上。控制部分主要包括有功和频率控制环、无功和电压控制环、电磁方程、电流控制环和 SVPWM 调制。
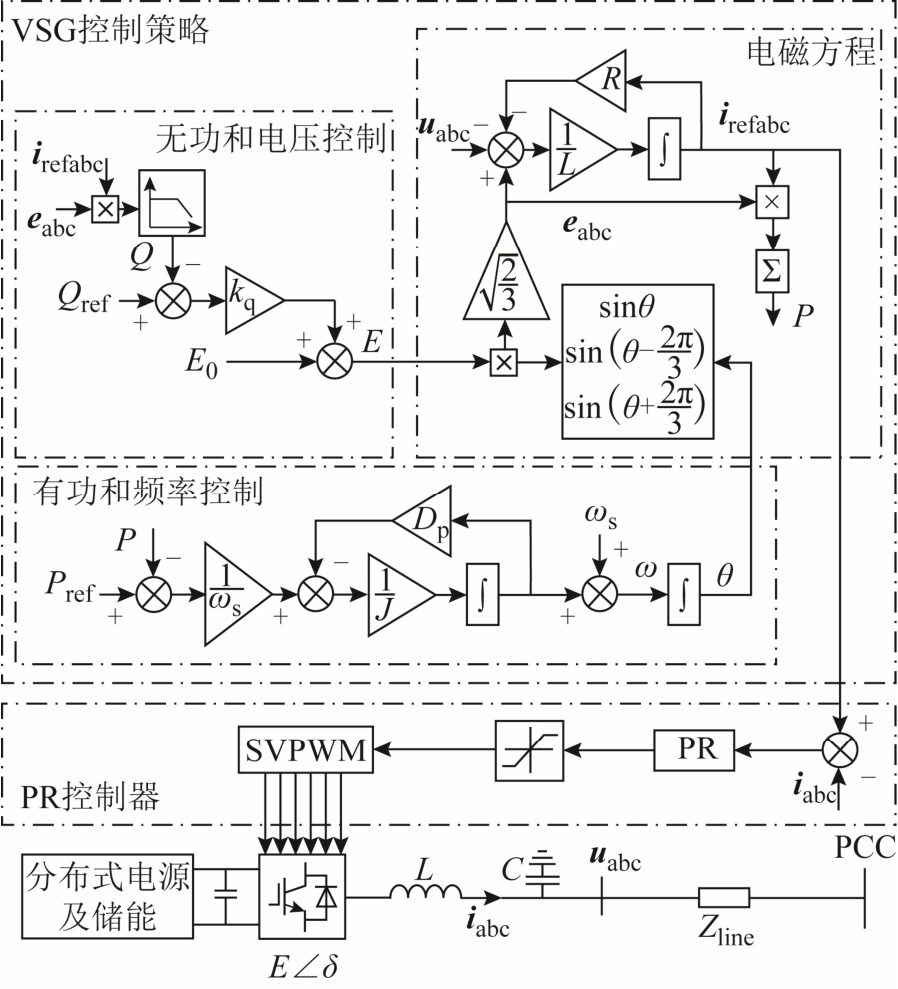
图1 VSG的控制策略
Fig.1 Control scheme of VSG
由图1中的有功和频率控制环路可得频率和有功功率关系为
式中，Pref为功率参考值；ωs为系统参考角频率；ω为内禀角频率；P为VSG输出的电磁功率；J为VSG转动惯量； PD为阻尼/下垂系数；kq为无功下垂系数。
文献[35]研究了单台VSG的功频调节特性。单机离网模式下，由于输出相位和功率的调节是解耦的，功频响应的传递函数即为式（1）。单机并网模式下，当VSG参数设置合理时，可忽略有功和无功控制耦合的影响，此时功频调节特性分析模型如图2所示。图中，cˆω为公共交流母线频率的小扰动量，KP=EUPCCcosδ/Z，Z为 VSG传输阻抗（输出阻抗与线路阻抗Zline之和），E为VSG内电势幅值，UPCC为交流母线电压幅值，δ为相位差。
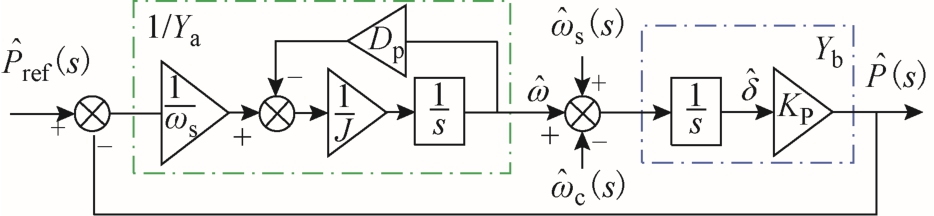
图2 并网模式下VSG功频小信号模型
Fig.2 Power/frequency small-signal model of VSG under grid-connected mode
基于图 2可得式（2）~式（5），式中 ΦI（s）、ΦΠ(s)和 Yp(s)为传递函数。
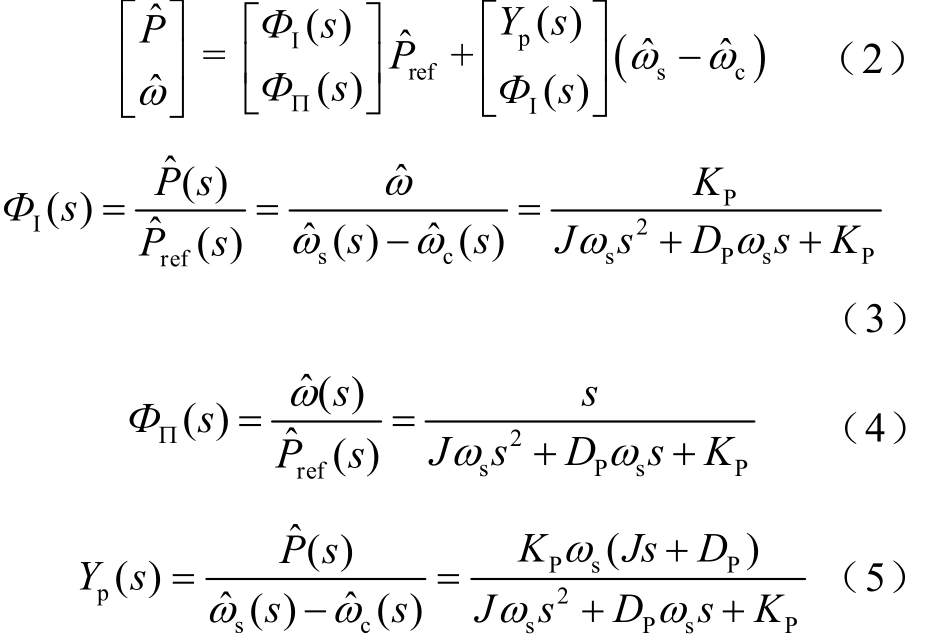
1.2 VSG并联系统的P/ω“导纳”基础模型
将式（5）改写成
式（6）形式上与电路理论中描述一个开路电压ωˆs(s)、输出导纳为Yp(s)、输出电流为Pˆ( s)、输出电压为ωˆc(s)的二端网络的方程一致，进而多VSG并联系统的频率（有功）模型可以用多个二端网络并联组成，如图3所示[33]。其中，电流源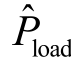
(s)为公共有功负载扰动，Yp,i(s)为第 i台 VSG的 P/ω“导纳”。
图3 VSG并联系统频率等效模型
Fig.3 Equivalent frequency model for multi-parallel VSGs
根据叠加定理可求得各逆变器输出的功率，写成矩阵形式为
展开为
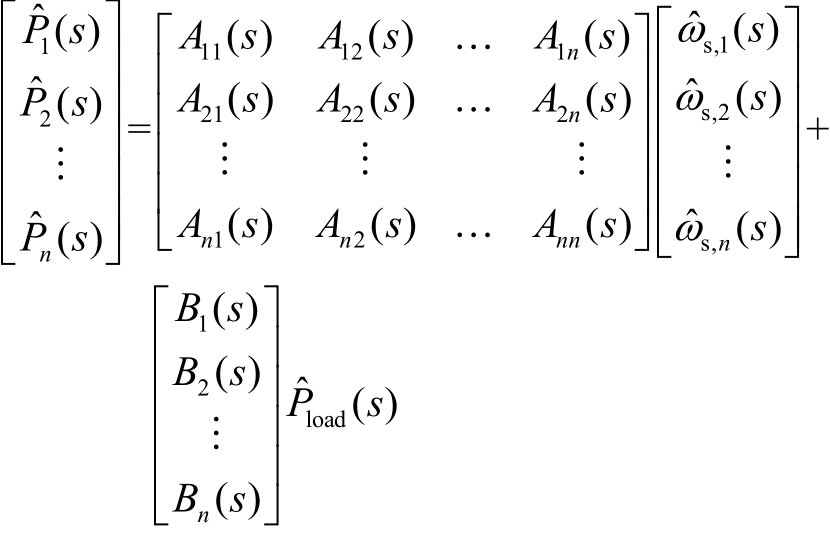
其中
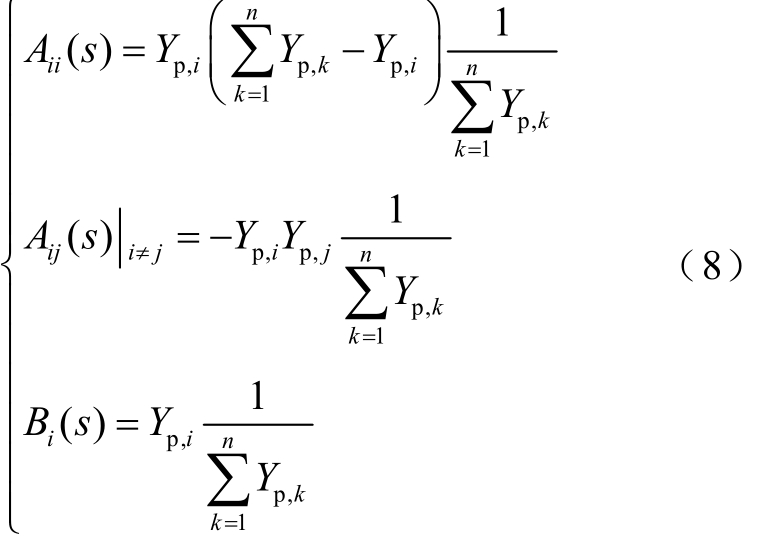
式中，Aij(s)为VSGj角频率参考值输入情况下VSGi输出功率的传递函数；Bi(s)为负载扰动下第i台VSG输出功率的传递函数。
2 拓展P/ω“导纳”模型
文献[33]应用上述构建的 P/ω“导纳”基础模型对多VSG并联系统的稳定性进行了分析，但该模型仅考虑了角频率参考值输入和负载扰动情况下各台VSG输出功率的响应，未考虑各台VSG输出角频率的响应。而实际中更加关注的是有功指令值输入和负载扰动情况下各台 VSG输出功率和角频率的响应。
为了全面反映有功指令值输入和负载扰动情况下VSG输出功率和角频率的响应，提出将图2的功频小信号模型集成为1/Ya(s)=GPω(s)和Yb(s) =KP/s两部分。不考虑扰动源sˆω的影响，集成之后的小信号模型满足关系式（9）。
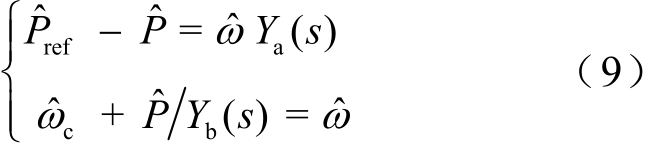
式（9）可以描述为图4a所示功率环路等效的二端网络。其中，Ya(s)称为VSG的第一P/ω“导纳”，Yb(s)称为VSG的第二P/ω“导纳”。图4a的二端网络能够全面反映 VSG在输入和扰动作用下的输出功率和角频率的响应，传递函数计算公式为
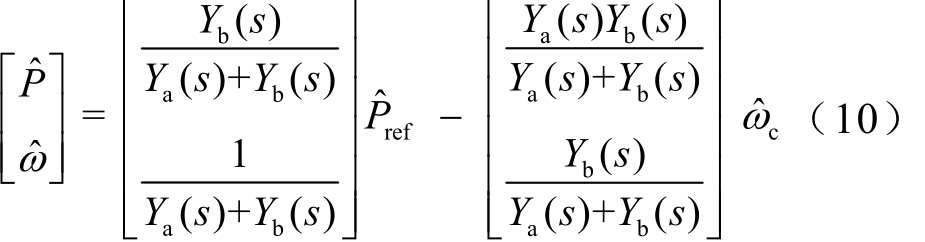
进一步，构建多VSG并联系统的拓展P/ω“导纳”模型，如图 4b所示。由图4b，根据叠加定理可求得各台VSG输出功率和角频率的响应，写成矩阵形式为
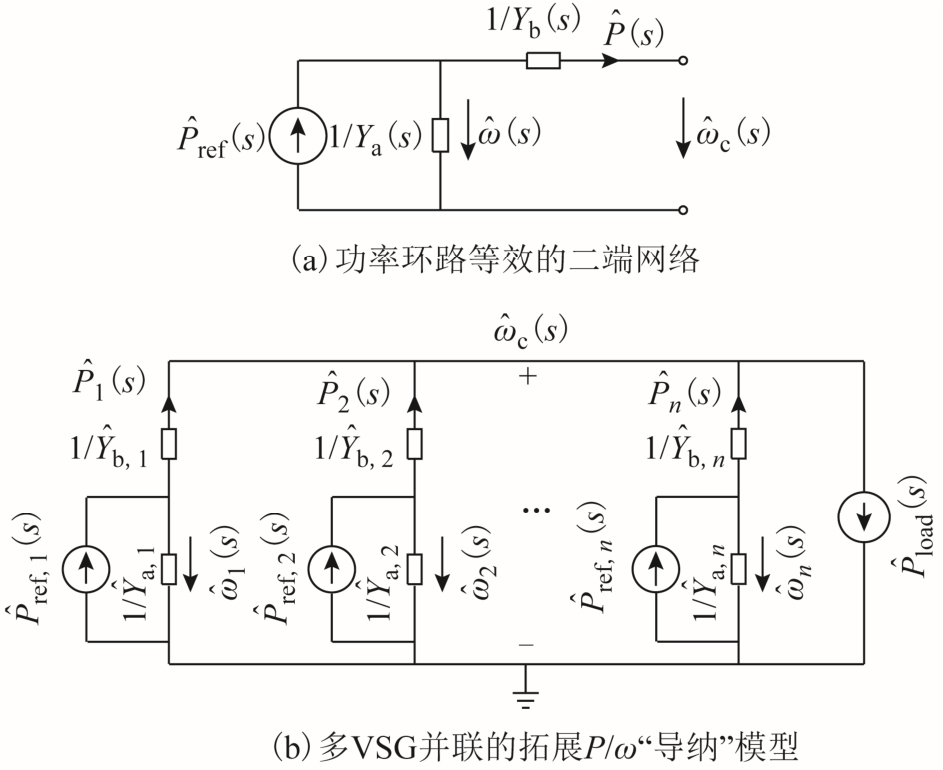
图4 拓展P/ω“导纳”模型
Fig.4 The extended P/ω “admittance” model
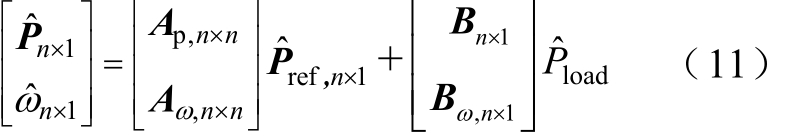
其中
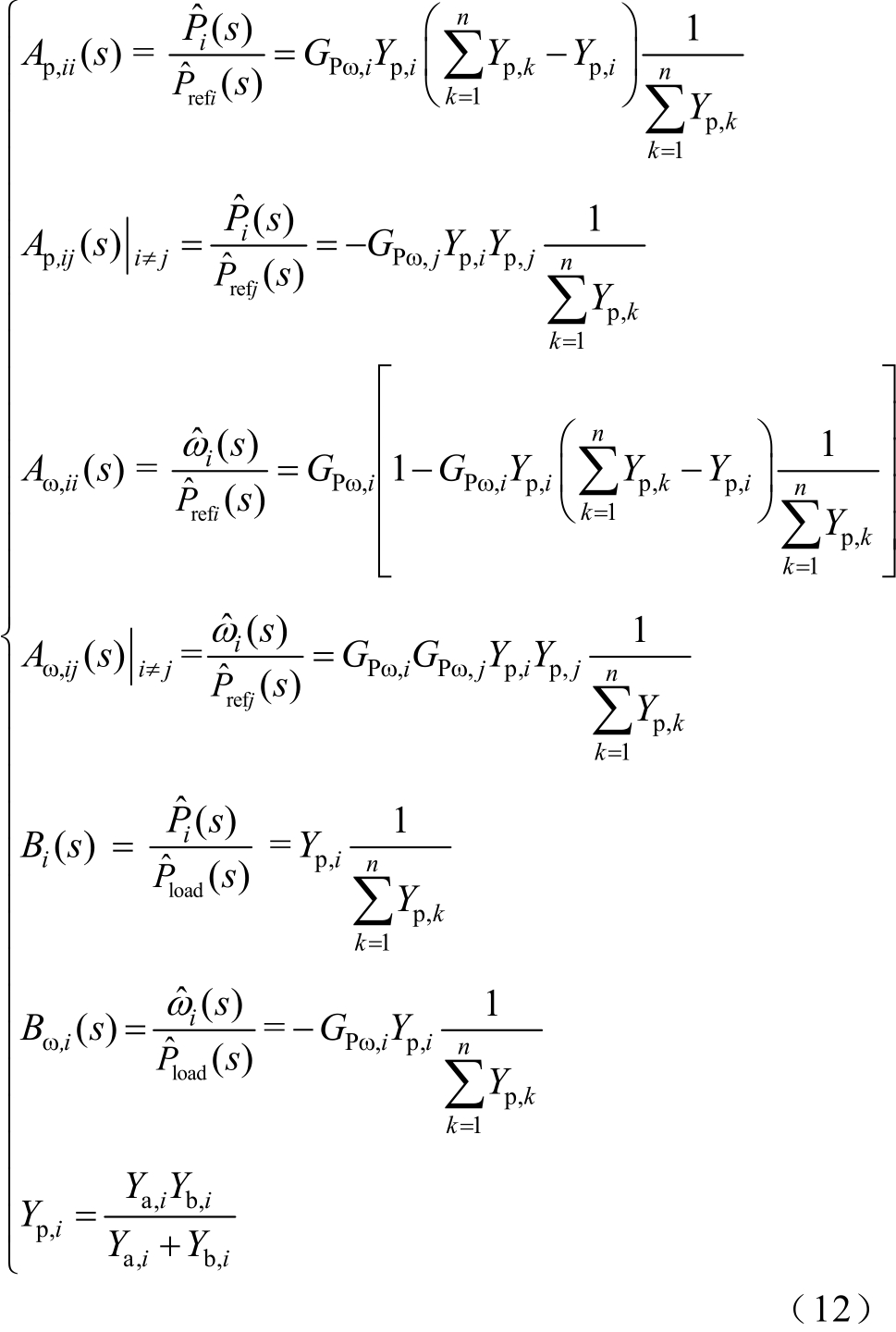
式中，Ap,ij(s)为 VSGj有功指令值输入情况下 VSGi输出功率的传递函数；Aω,ij(s)为VSGj有功指令值输入情况下VSGi输出角频率的传递函数；Bω,i(s)为负载扰动下第i台VSG输出角频率的传递函数。
相比于式（7）的P/ω“导纳”基础模型，式（11）构建的拓展 P/ω“导纳”模型能够全面地描述多机系统的功频调节特性。
3 关键性结论
为按照容量比例分配功率，多机系统中各VSG应采用与容量成正比关系的下垂系数、虚拟惯量，以及与容量成反比关系的传输阻抗[16]。当多机系统的参数匹配时，各VSG的P/ω“导纳”成比例关系，此时，并联系统的有功功率和角频率具有最优的响应形式。
设n台VSG的P/ω“导纳”具有式（13）的比例关系。
式中，αi为比例系数，i=1,2…,n，并且α1=1。
式（13）代入式（12）可得
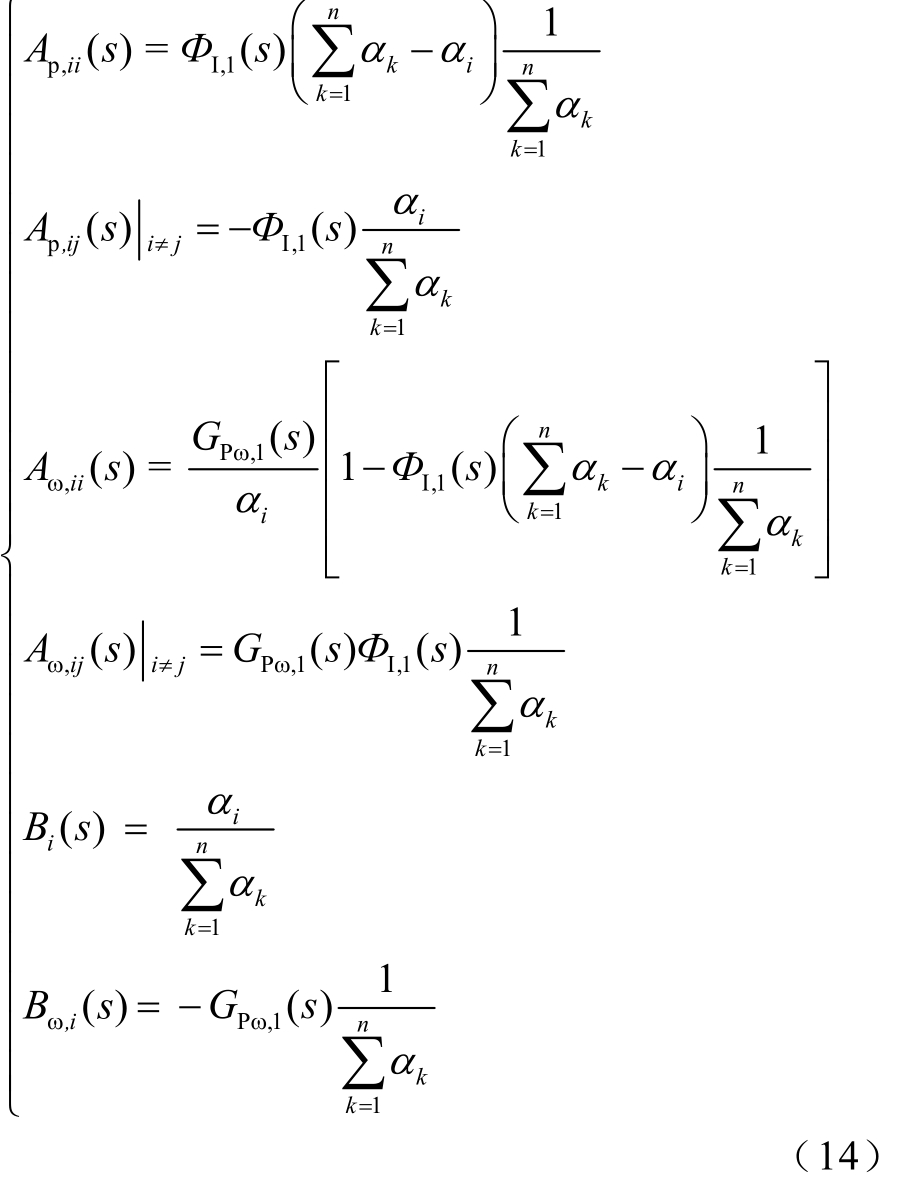
由式（14）可得：
1）负载扰动情况下，各台VSG的有功功率响应与扰动功率只呈现比例关系而不包含任何s项，因此直接进入按比例系数进行功率分配的稳态过程；各台VSG角频率的响应具有一致性，动态响应特性由GPω,1(s)决定，与单机离网模式相同，稳态响应幅值与比例系数α2、α3及阻尼系数D有关。
2）有功指令值输入情况下，各台VSG有功功率的动态响应具有一致性，均由 ΦI,1(s)决定，与单机并网模式相同，稳态响应幅值与比例系数α2、α3有关；各台 VSG角频率的动态响应由 ΦI,1(s)和GPω,1(s)共同决定，稳态响应幅值与比例系数α2、α3和阻尼系数D有关。
当多VSG并联系统的参数匹配时，各台VSG有功功率和角频率的响应特性最优，且最优响应特性与单机并/离网模式下的响应具有对应关系，具体见表1和表2。此外，易验证，多台VSG稳态响应幅值的分析与通过稳态下垂方程组求解的结果一致。
表1 有功功率动态响应特性
Tab.1 Dynamic response characteristics of active power
扰动类型 单机离网模式 单机并网模式 多机并联模式负载功率扰动 迅速响应 — 迅速响应有功指令值输入 无响应 ΦI,1(s) ΦI,1(s)电网频率扰动 — Yp,1(s) —
表2 角频率动态响应特性
Tab.2 Dynamic response characteristics of frequency
扰动类型 单机离网模式 单机并网模式 多机并联模式负载功率扰动 GPω,1(s) — GPω,1(s)有功指令值输入 GPω,1(s) — ΦI,1(s)和 GPω,1(s)
4 仿真和实验验证
4.1 仿真分析
为验证 P/ω“导纳”拓展模型的准确性，搭建了由三台VSG和两组负载构成的仿真系统，具有三种运行模式，仿真系统示意图如图5所示。三台VSG的容量比为1:1:2，主要仿真参数见表3，其余参数见文献[36]。
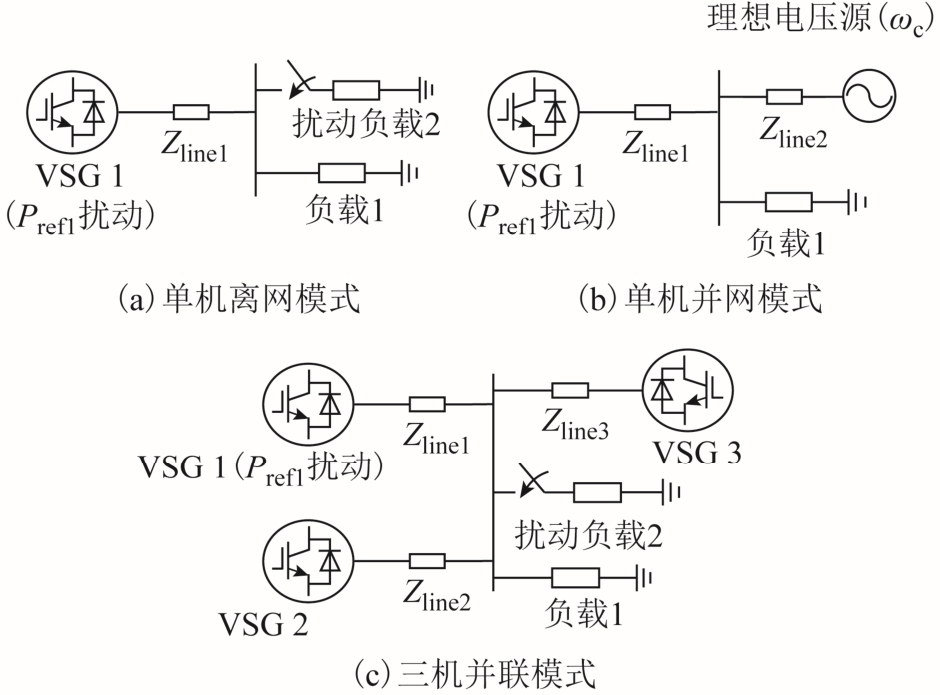
图5 仿真系统示意图
Fig.5 The structure diagram of simulation platform
表3 仿真参数
Tab.3 Simulation parameters
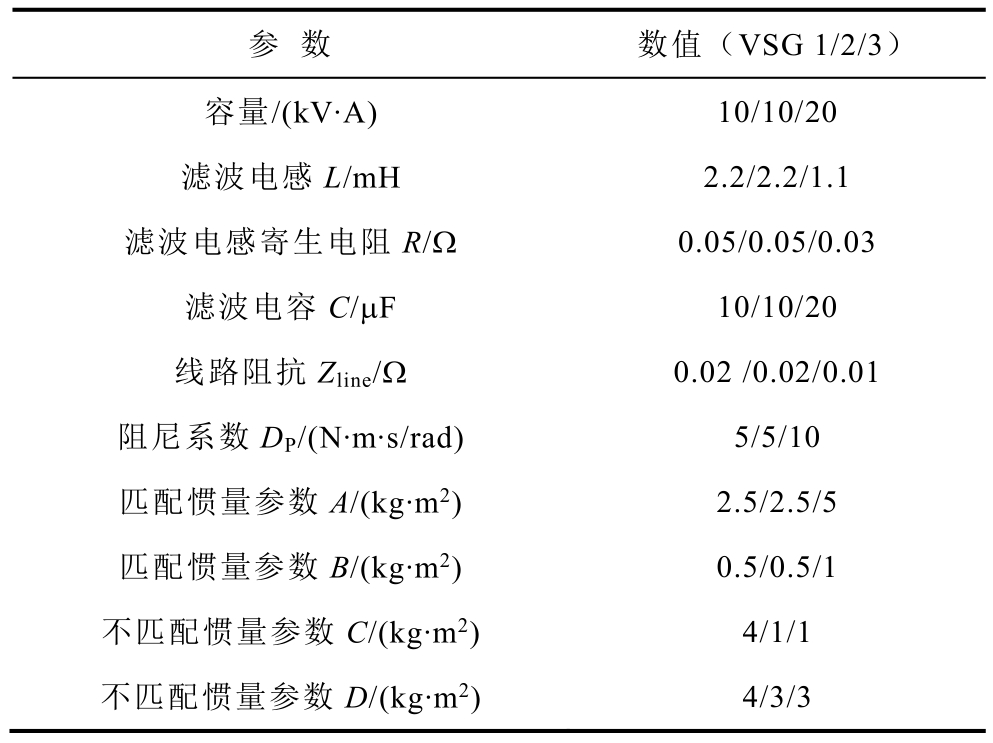
参 数 数值（VSG 1/2/3）容量/(kV·A) 10/10/20滤波电感L/mH 2.2/2.2/1.1滤波电感寄生电阻R/Ω 0.05/0.05/0.03滤波电容 C/μF 10/10/20线路阻抗 Zline/Ω 0.02 /0.02/0.01阻尼系数 DP/(N·m·s/rad) 5/5/10匹配惯量参数A/(kg·m2)匹配惯量参数B/(kg·m2)不匹配惯量参数C/(kg·m2)不匹配惯量参数D/(kg·m2)2.5/2.5/5 0.5/0.5/1 4/1/1 4/3/3
为验证表1及表2的结论，设置匹配惯量参数B，图6给出了三种运行模式下输入响应（左）和扰动响应（右）的仿真结果。作为对比，图7给出了不匹配惯量参数 C在三机并联模式下的输入响应（左）和扰动响应（右）的仿真结果。其中，左图为在 0.3s对 VSG1施加 ΔPref1=2.5kW 的有功指令后的响应，右图为在0.3s施加ΔPload=4kW的扰动负载 2或电网频率阶跃-0.2Hz后的响应。初始参考功率为Pref1=Pref2= 0.5Pref3=5kW，单机模式下负载 1的初始功率为 4kW，三机模式下负载 1的初始功率为13kW。
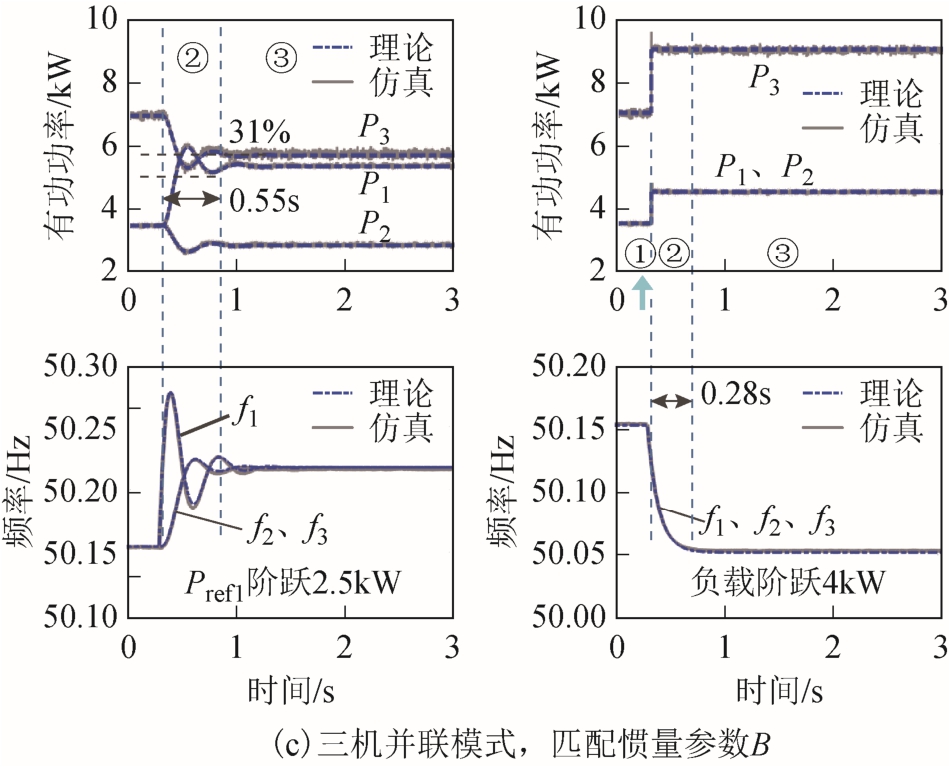
图6 不同工况和扰动下VSG的仿真结果
Fig.6 Simulation results of VSG under different operating conditions and disturbances
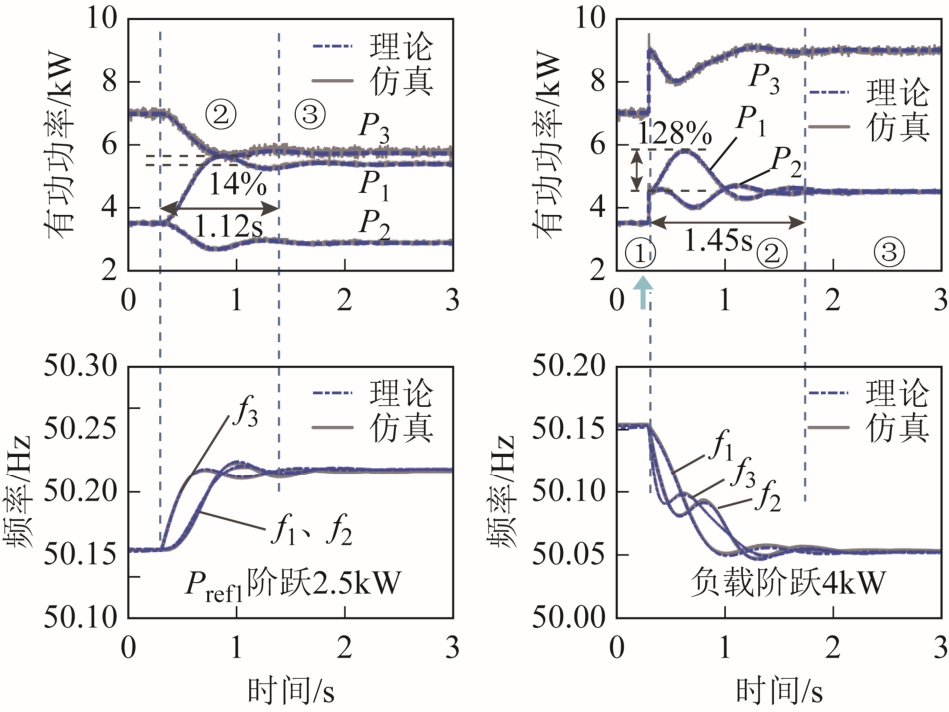
图7 三机并联模式下不匹配惯量参数C的仿真结果
Fig.7 Simulation results with mismatched inertia parameters C in three paralleled VSGs mode
4.1.1 关键结论验证
不同工况和扰动下 VSG的仿真结果如图 6所示，三机并联模式下不匹配惯量参数C的仿真结果如图7所示。由图6和图7可知，在输入和扰动工况下，仿真结果与理论值均能够较好地吻合，表明P/ω“导纳”拓展模型具有准确度高且适用于分析两机以上系统的特点。
VSG输入和扰动响应过程具有差异：有功指令输入下，各台VSG输出功率的分配包括由惯量参数决定的动态过程②和阻尼/下垂系数决定的稳态过程③；而负载扰动下输出功率的分配除包含过程②、③之外，还包含过程②之前的扰动瞬间自然功率分配[37]阶段①。
与关键结论一致，三种运行模式下的功频响应具有对应关系。当惯量参数匹配时，有功指令值输入下三台VSG输出功率响应具有一致的波动过程。负载扰动下输出功率响应则直接进入稳态过程而没有发生波动，这是由于关键参数匹配[16]时阶段①、②、③的有功功率分配目标值相同，均与容量成正比关系分配；因此，在阶段①有功功率分配过程已完结，仅有频率在阶段②体现出惯量响应特性。
与惯量匹配相比，当惯量参数不匹配时，有功指令值输入响应的调节时间变长，超调量减小，负载扰动响应过程中出现了显著的有功功率超调量。
4.1.2 过程②有功功率动态环流分析
在三机并联模式下，以 VSG1作为参考，通过式（15）求取ΔAp,1_2(s)和ΔAp,1_3(s)可以反映有功指令输入情况下三台 VSG的有功功率环流特性，如图8a、图 8b所示；通过式（16）求取ΔB1_2(s)和ΔB1_3(s)可以反映负载扰动过程中三台 VSG的有功功率环流特性，如图8c、图8d所示。图中，A、B、C、D分别表示不同的惯量参数值，见表 3，三机系统总惯量满足关系式（17）。图8c和图8d未展示惯量参数A、B的曲线，是由于参数A、B的惯量匹配，对应的ΔB1_2=ΔB1_3=0(pu)=-∞ dB。
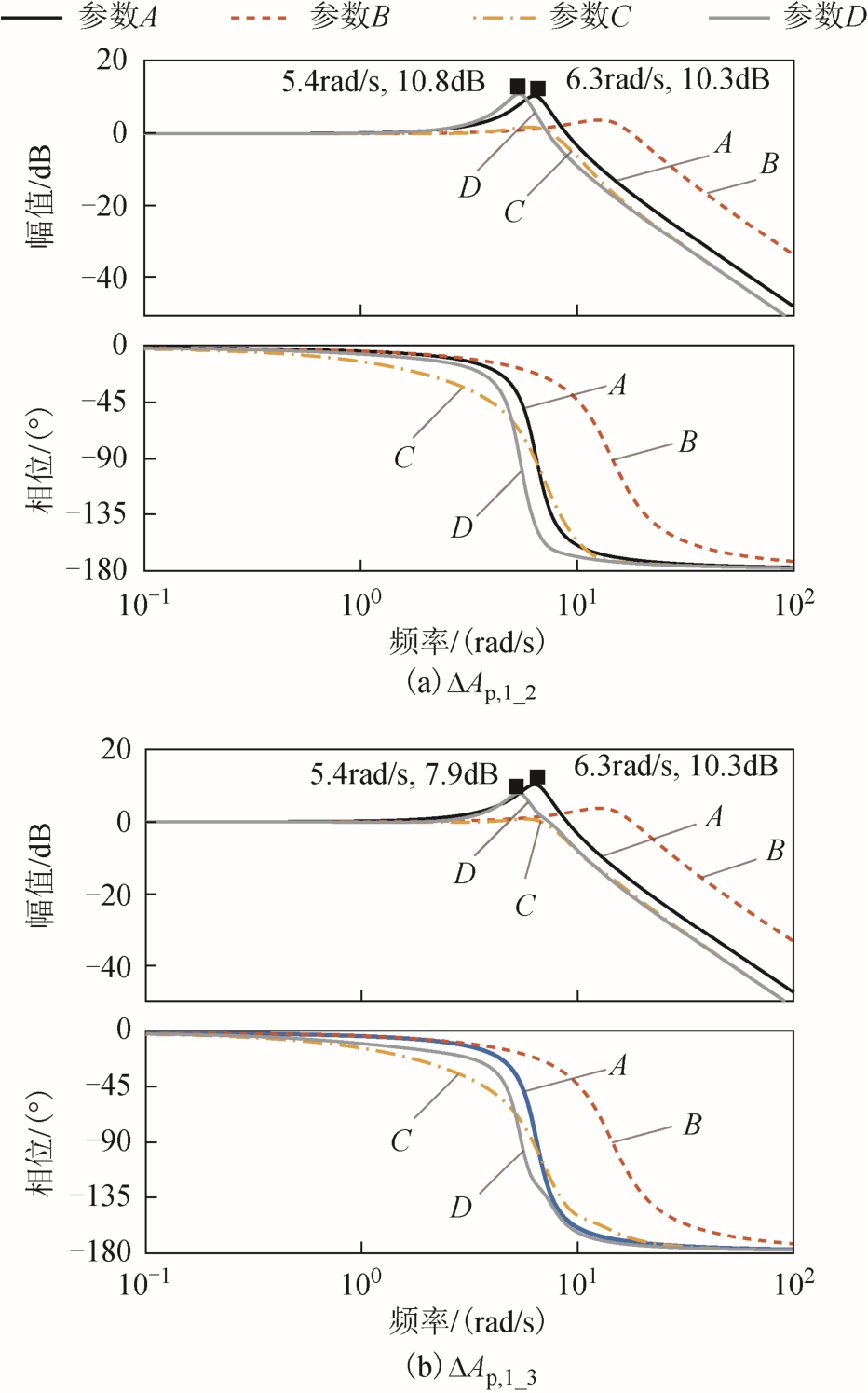
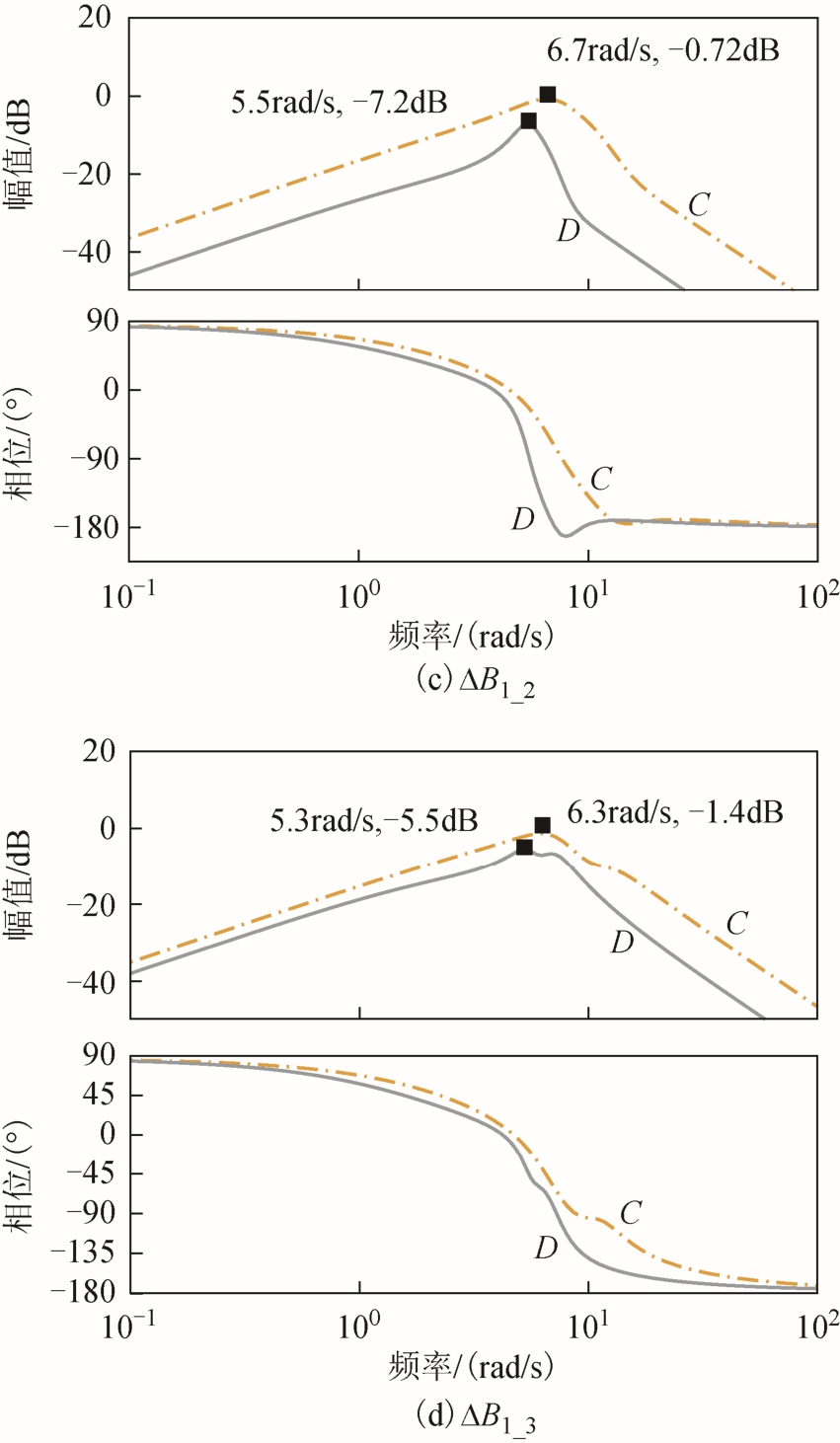
图8 三机系统不同惯量参数时有功功率环流的伯德图
Fig.8 Bode diagrams of active power difference with different Ji in three paralleled VSGs mode
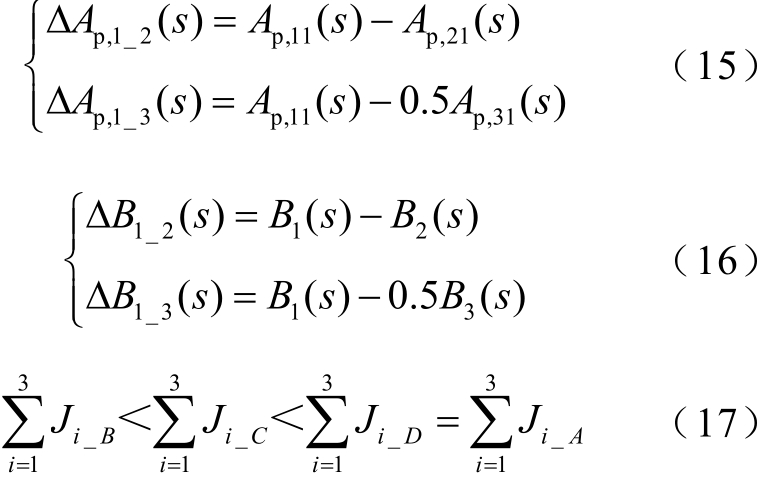
由图8可知，相比于参数A，相同惯量水平的参数 D在输入指令下（图 8a、图 8b）带宽略有减小，而峰值增益的影响相反——ΔAp,1_2(s)的增益增加ΔAp,1_3(s)的增益减小。相比于参数 B，参数 C在输入指令下带宽和峰值增益均大幅减小，参数D在输入指令下带宽大幅减小但出现了谐振尖峰。不匹配惯量参数C、D在扰动作用下（图8c、图8d）呈现出带通特性，并且参数C的通带宽度和通带中心处的增益均大于参数D。
图9的仿真结果与频域特性的对比一致，表明惯量参数对输入响应和扰动响应的影响是不同的。惯量匹配控制无法抑制输入指令下的有功动态环流。惯量参数C能够减小输入指令下的动态环流但会显著增大扰动作用下的动态环流；而与惯量参数A相比，D会减小输入指令下的动态环流但却引发了扰动作用下的动态环流及振荡。
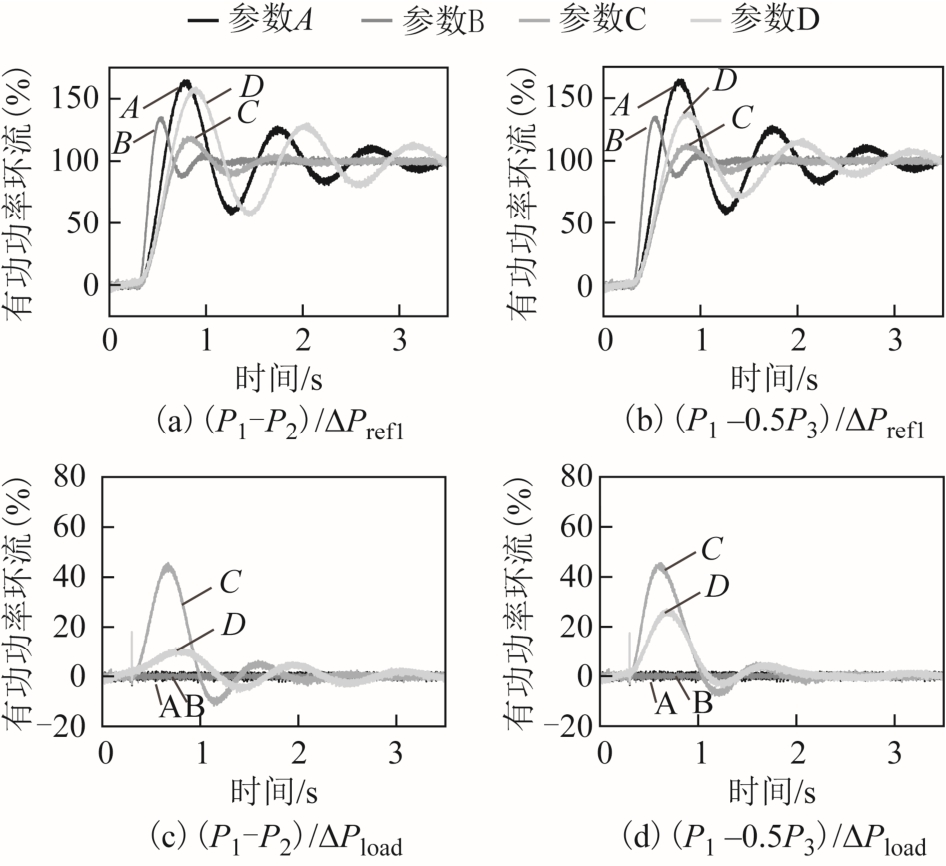
图9 不同虚拟惯量参数时有功功率环流的仿真结果
Fig.9 Simulation results of active power difference with different Ji
4.2 实验验证
搭建了两台VSG半实物仿真实验平台，包括硬件设计和和软件设计。硬件的主电路部分为直流电源（艾诺AN510）、电网模拟器（艾诺FP030A）、全桥逆变电路、LC 滤波器、阻性负载；硬件的控制部分包括信号采样电路、调理电路、IGBT驱动电路和基于SpaceR的快速原型控制器。软件部分包括VSG的核心算法以及保护回路。整体实验平台结构如图10所示，两台VSG的具体实验参数见表4。
图10 VSG实验平台
Fig.10 The experiment platform of VSG
4.2.1 关键结论验证
为验证表1及表2的结论，设置惯量参数A，即 J1=2kg·m2，J2=4kg·m2，图 11 给出了在三种运行模式下有功指令输入响应和扰动响应的实验结果。图中，左图为有功指令输入响应，右图为扰动响应。三种模式下的动态响应指标见表5~表7。
表4 实验参数
Tab.4 Experimental parameters
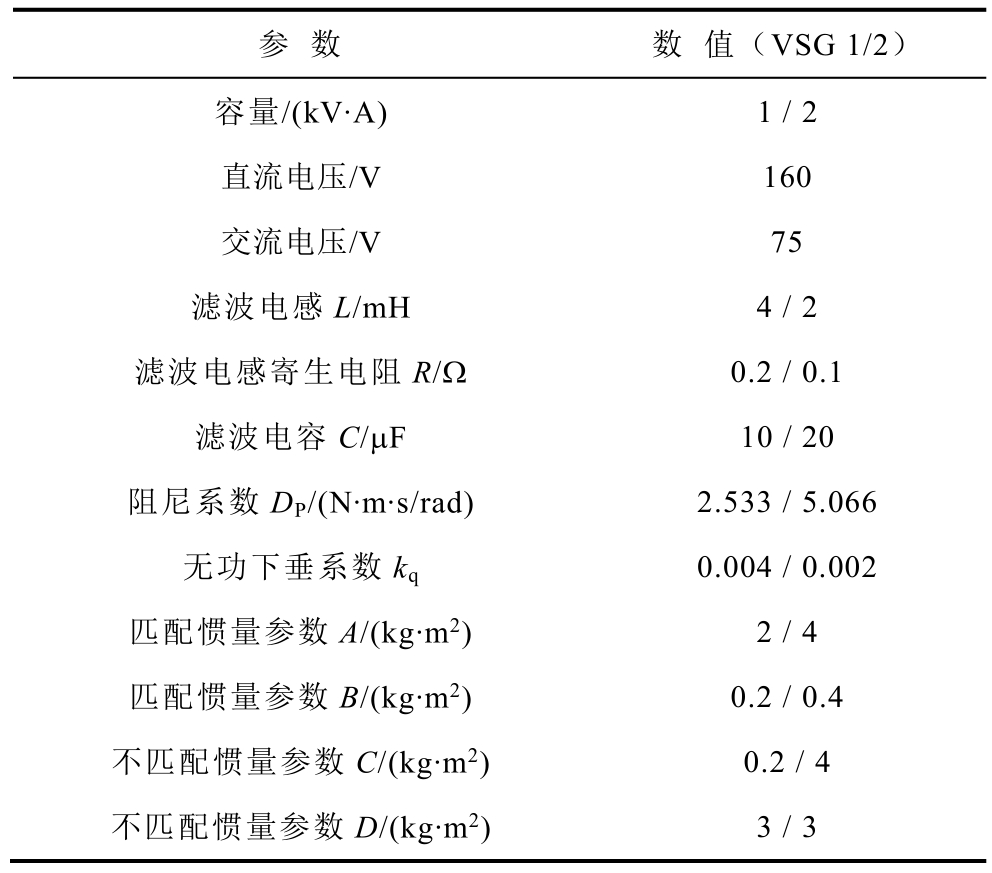
参 数 数 值（VSG 1/2）容量/(kV·A) 1 / 2 160 75滤波电感L/mH 4 / 2滤波电感寄生电阻R/Ω 0.2 / 0.1滤波电容 C/μF 10 / 20阻尼系数 DP/(N·m·s/rad) 2.533 / 5.066无功下垂系数kq 0.004 / 0.002匹配惯量参数A/(kg·m2)匹配惯量参数B/(kg·m2)不匹配惯量参数C/(kg·m2)不匹配惯量参数D/(kg·m2)直流电压/V交流电压/V 2 / 4 0.2 / 0.4 0.2 / 4 3 / 3
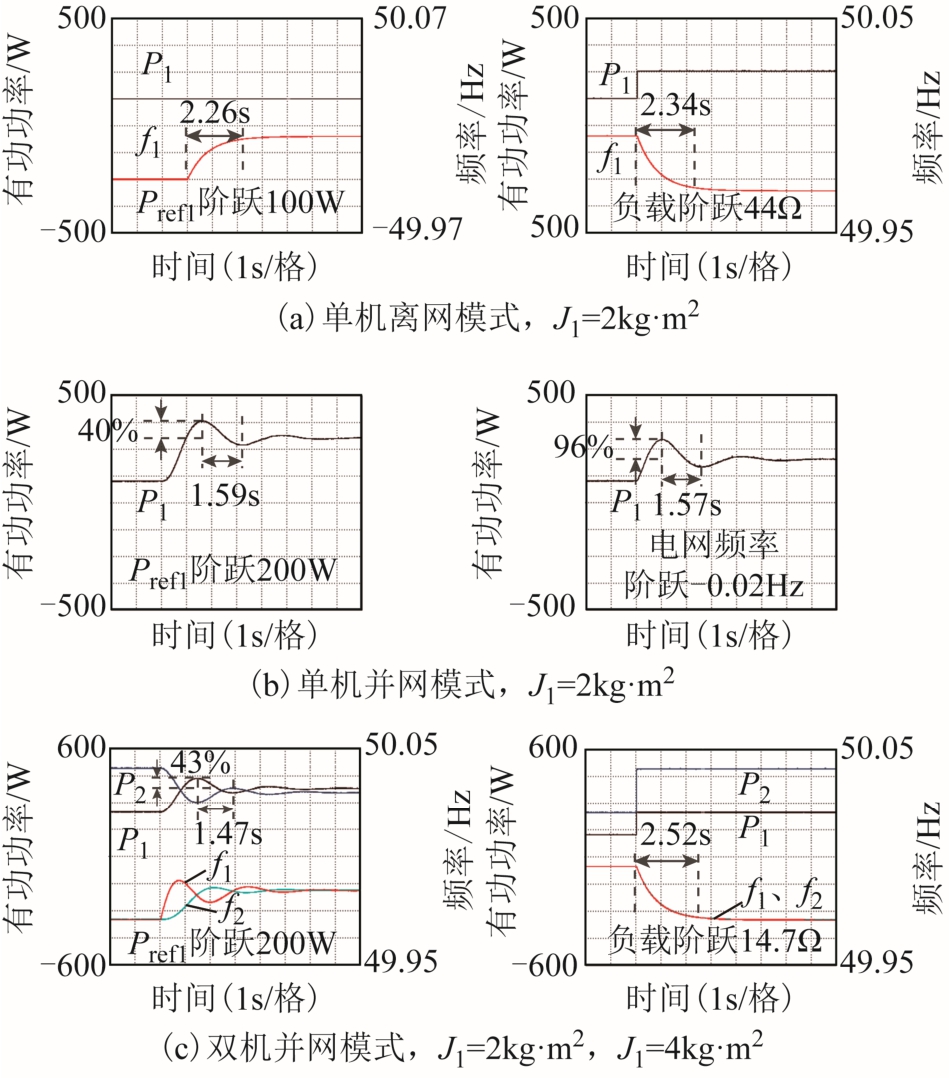
图11 不同工况和扰动下VSG的实验结果
Fig.11 Experimental results of VSG under different operating conditions and disturbances
表5 有功功率超调量对比
Tab.5 Dynamic response characteristics of active power
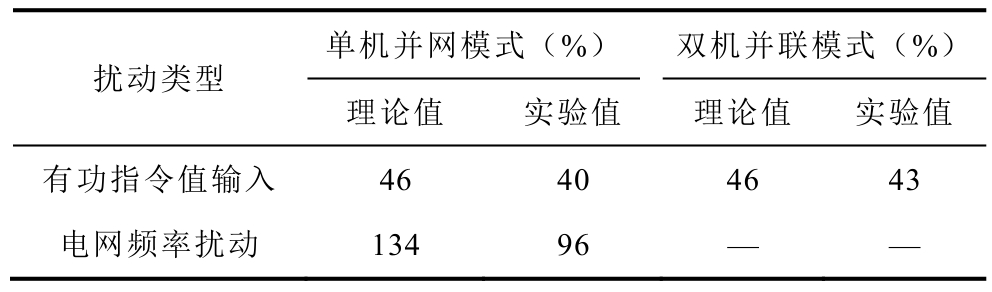
单机并网模式（%） 双机并联模式（%）扰动类型理论值 实验值 理论值 实验值有功指令值输入 46 40 46 43电网频率扰动 134 96 — —
表6 有功功率响应时间对比
Tab.6 Dynamic response characteristics of active power
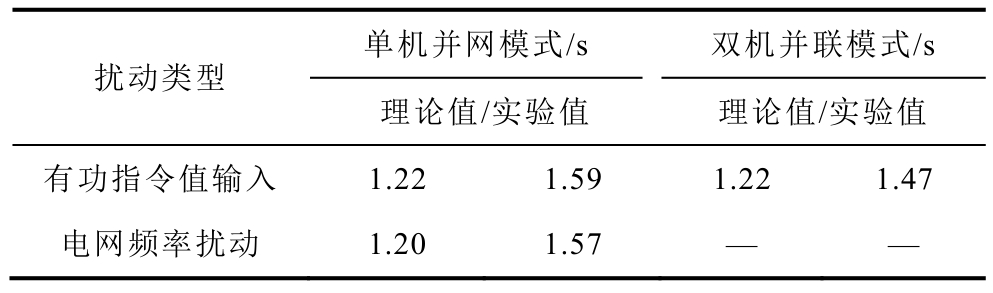
单机并网模式/s 双机并联模式/s扰动类型理论值/实验值 理论值/实验值有功指令值输入 1.22 1.59 1.22 1.47电网频率扰动 1.20 1.57 — —
表7 角频率响应时间对比
Tab.7 Dynamic response characteristics of frequency
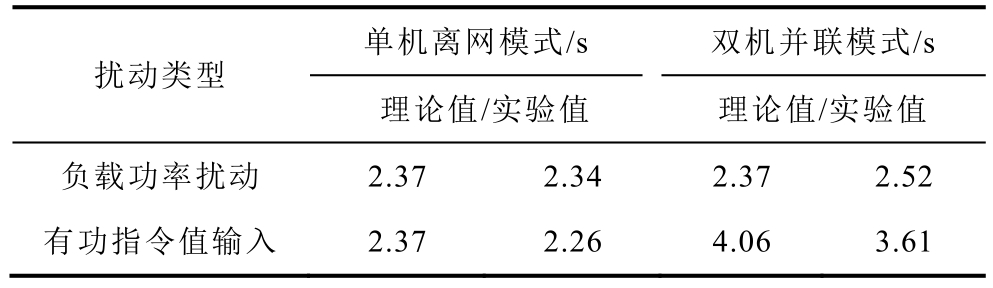
单机离网模式/s 双机并联模式/s扰动类型理论值/实验值 理论值/实验值负载功率扰动 2.37 2.34 2.37 2.52有功指令值输入 2.37 2.26 4.06 3.61
由表5及图11可知，Pref1扰动下有功功率响应的超调量实验值与理论值偏差较小，而电网频率扰动下有功功率超调量偏差较大，达到 38%。由表 6及图 10可知两种扰动下有功功率响应时间的实验值（峰谷值时间）均大于理论值，单机并网模式下两种扰动的偏差均为0.37s，双机并联模式下有功指令输入响应的偏差为0.25s。由表7及图10可知，除双机并联模式在有功指令输入下的响应外，频率响应时间（特指 f1响应到达 5%误差范围所需的时间）具有一致性。综上所述，不同模式下的实验结果与理论分析均具有较好的一致性，表明关键结论的正确性。
4.2.2 有功功率动态环流分析
双机并联模式下，设置两台VSG的初始参考功率为Pref1=0.5Pref2=100W，初始负载1为25Ω，分别对 VSG1施加 ΔPref1=200W 的功率指令及向系统中投入 14.7Ω(ΔPload=380W)的扰动负载，分析不同虚拟惯量参数时的有功功率动态环流，如图12所示。其中，左图为不同惯量参数时的有功指令输入响应，右图为不同虚拟惯量参数时的负载扰动响应。
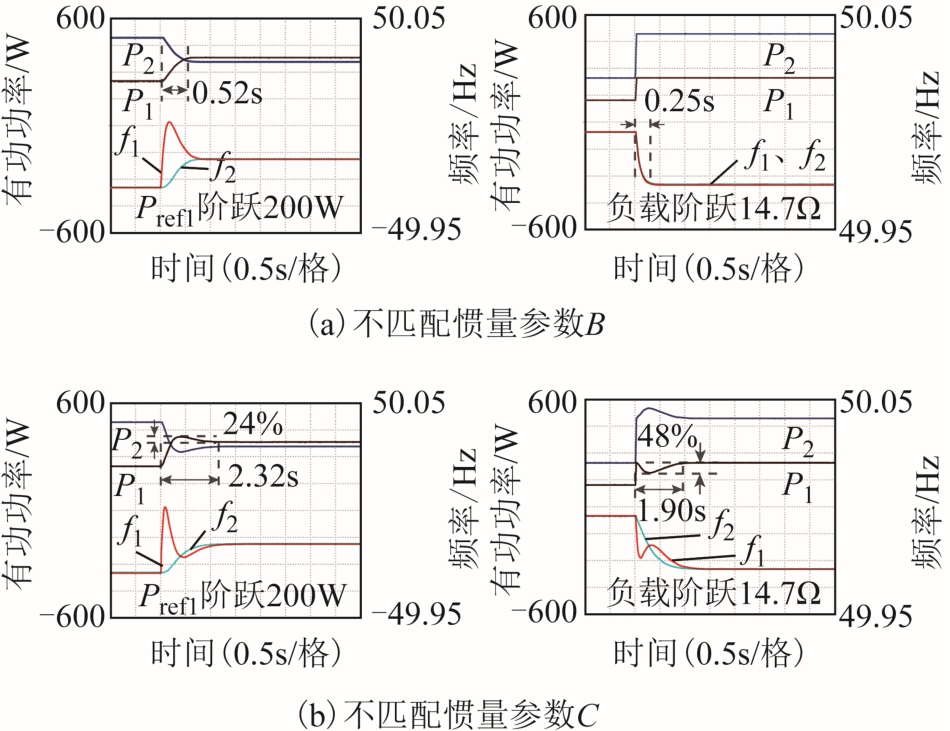
图12 双机并联模式下不同虚拟惯量参数时的实验结果
Fig.12 Experimental results with different Ji in two paralleled VSGs mode
四组惯量参数下，双机系统总惯量（ J ∑ =J1 + J2)满足关系 J ∑ _ B ＜ J ∑ _ C ＜ J ∑ _ D = J ∑_A 。双机并联模式下由于P1+P2=Pload，扰动发生后P1、P2具有互补的动态过程，故通过超调量指标来反映有功动态环流。四组惯量参数的有功功率超调量实验结果如下：输入响应分别为43%、0、24%和30%；扰动响应分别为0%、0、48%和35%。
与4.1.2节的有功功率环流分析一致，图12表明惯量参数对输入响应和扰动响应的影响是不同的。匹配惯量控制无法抑制输入指令下的有功动态环流，见图11c。减小惯量参数后，图12a中输入响应和扰动响应过程中均无有功动态环流，但减小惯量意味着频率响应变快和频率稳定度降低。不匹配参数C能够减小输入指令下的动态环流但会显著增大扰动作用下的动态环流；而不匹配参数D在输入和扰动响应过程中均存在环流，且有功功率调节时间均是最长。
5 结论
本文针对现有P/ω“导纳”模型未考虑各台VSG有功指令输入和角频率输出的情况，构建了多VSG并联系统的拓展 P/ω“导纳”模型，主要得出以下结论：
1）该模型能够全面而准确地描述有功指令输入和负载扰动情况下各台 VSG输出功率和角频率的响应特性。当各台VSG参数匹配时，其P/ω“导纳”成比例关系。
2）匹配惯量在负载扰动情况下，各台VSG的有功功率响应直接进入稳态过程；各台VSG的角频率响应具有一致性，其动态响应特性与任一VSG在单机离网模式下的响应特性相同。
3）匹配惯量在有功指令值输入情况下，各台VSG的有功功率动态响应具有一致性，与任一VSG在单机并网模式下的响应特性相同；角频率的动态响应由任一 VSG在单机离网和并网模式下的响应特性共同决定。
4）应用拓展P/ω“导纳”模型对多机并列运行的参数配置和暂态有功环流问题进行了理论分析。下一步将应用该模型对不同类型 VSG的协调控制和不同VSG技术方案的比较进行研究。
[1] 黄林彬, 辛焕海, 黄伟, 等. 含虚拟惯量的电力系统频率响应特性定量分析方法[J]. 电力系统自动化, 2018, 42(8): 31-38.Huang Linbin, Xin Huanhai, Huang Wei, et al.Quantified analysis method of frequency response characteristics for power systems with virtual inertia[J]. Automation of Electric Power Systems,2018, 42(8): 31-38.
[2] 曾正, 赵荣祥, 吕志鹏, 等. 光伏并网逆变器的阻抗重塑与谐波谐振抑制[J]. 中国电机工程学报,2014, 34(27): 4547-4558.Zeng Zheng, Zhao Rongxiang, Lü Zhipeng, et al.Impedance reshaping of grid-tied inverters to damp the series and parallel harmonic resonances of photovoltaic systems[J]. Proceedings of the CSEE,2014, 34(27): 4547-4558.
[3] 石荣亮, 张兴, 徐海珍, 等. 光储柴独立微电网中的虚拟同步发电机控制策略[J]. 电工技术学报,2017, 32(23): 127-139.Shi Rongliang, Zhang Xing, Xu Haizhen, et al. A control strategy for islanded photovoltaic-batterydiesel microgrid based on virtual synchronous generator[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 127-139.
[4] 吕志鹏, 盛万兴, 钟庆昌, 等. 虚拟同步发电机及其在微电网中的应用[J]. 中国电机工程学报, 2014,34(16): 2591-2603.Lü Zhipeng, Sheng Wanxing, Zhong Qingchang, et al.Virtual synchronous generator and its applications in mcrogrid[J]. Proceedings of the CSEE, 2014, 34(16):2591-2603.
[5] 曾正, 邵伟华, 冉立, 等. 虚拟同步发电机的模型及储能单元优化配置[J]. 电力系统自动化, 2015,39(13): 22-31.Zeng Zheng, Shao Weihua, Ran Li, et al.Mathematical model and strategic energy storage selection of virtual synchronous generators[J].Automation of Electric Power Systems, 2015, 39(13):22-31.
[6] Bevrani H, Ise T, Miura Y. Virtual synchronous generators: a survey and new perspectives[J].International Journal of Electrical Power & Energy Systems, 2014, 54: 244-254.
[7] Alsiraji H A, El-Shatshat R. Comprehensive assessment of virtual synchronous machine based voltage source converter controllers[J]. IET Generation, Transmission & Distribution, 2017, 11(7):1762-1769.
[8] Tan Shulong, Geng Hua, Yang Geng. Modeling framework of voltage-source converters based on equivalence with synchronous generator[J]. Journal of Modern Power Systems and Clean Energy, 2018,6(6):1291-1305.
[9] Liu Jia, Miura Y, Ise T. Comparison of dynamic characteristics between virtual synchronous generator and droop control in inverter-based distributed generators[J]. IEEE Transactions on Power Electronics, 2016, 31(5): 3600-3611.
[10] Hirase Y, Sugimoto K, Sakimoto K, et al. Analysis of resonance in microgrids and effects of system frequency stabilization using a virtual synchronous generator[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2016, 4(4): 1287-1298.
[11] 付强, 杜文娟, 王海风. 多虚拟同步发电机接入对电力系统机电振荡模式的影响[J]. 中国电机工程学报, 2018, 38(19): 5615-5624.Fu Qiang, Du Wenjuan, Wang Haifeng. Influence of multi virtual synchronous generators on power system electromechanical oscillation mode[J]. Proceedings of the CSEE, 2018, 38(19): 5615-5624.
[12] 张波, 颜湘武, 黄毅斌, 等. 虚拟同步机多机并联稳定控制及其惯量匹配方法[J]. 电工技术学报,2017, 32(10): 42-52.Zhang Bo, Yan Xiangwu, Huang Yibin, et al. Stability control and inertia matching method of multi-parallel virtual synchronous generators[J]. Transactions of China Electrotechnical Society, 2017, 32(10): 42-52.
[13] 涂春鸣, 杨义, 兰征, 等. 含多虚拟同步发电机的微电网二次调频策略[J]. 电工技术学报, 2018, 33(10):2186-2195.Tu Chunming, Yang Yi, Lan Zheng, et al. Secondary frequency regulation strategy in microgrid based on VSG[J]. Transactions of China Electrotechnical Society, 2018, 33(10): 2186-2195.
[14] 任碧莹, 邱姣姣, 刘欢, 等. 基于虚拟同步发电机双机并联系统的参数自调节优化控制策略[J]. 电工技术学报, 2019, 34(1): 128-138.Ren Biying, Qiu Jiaojiao, Liu Huan, et al.Optimization control strategy of self-adjusting parameter based on dual-parallel virtual synchronous generators[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 128-138.
[15] 张辉, 王帆, 李晓强, 等. 虚拟同步发电机并联运行的阻抗匹配策略[J]. 电力系统自动化, 2018,42(9): 69-74.Zhang Hui, Wang Fan, Li Xiaoqiang, et al. Impedance matching strategy for parallel virtual synchronous generators[J]. Automation of Electric Power Systems,2018, 42(9): 69-74.
[16] Mao Meiqin, Qian Cheng, Ding Yong. Decentralized coordination power control for islanding microgrid based on PV/BES-VSG[J]. CPSS Transactions on Power Electronics and Applications, 2018, 3(1): 14-24.
[17] Aderibole A, Zeineldin H H, El-Moursi M S, et al.Domain of stability characterization for hybrid microgrids considering different power sharing conditions[J]. IEEE Transactions on Energy Conversion, 2018, 33(1): 312-323.
[18] Alipoor J, Miura Y, Ise T. Stability assessment and optimization methods for microgrid with multiple vsg units[J]. IEEE Transactions on Smart Grid, 2018,9(2): 1462-1471.
[19] 王东东. 同步电机及虚拟同步电机的等效 Lorenz模型及稳定性分析[D]. 广州: 华南理工大学, 2017.
[20] Sun Jian. Small-signal methods for AC distributed power systems: a review[J]. IEEE Transactions on Power Electronics, 2009, 24(11): 2545-2554.
[21] 刘倪, 张昌华, 段雪, 等. 并网逆变器小信号建模方法对比及其适用性分析[J]. 电力系统自动化,2018, 42(23): 134-141.Liu Ni, Zhang Changhua, Duan Xue, et al.Comparison and applicability analysis of small- signal modeling methods for grid-connected inverter [J].Automation of Electric Power Systems, 2018, 42(23):134-141.
[22] Leitner S, Yazdanian M, Mehrizi-Sani A, et al. Smallsignal stability analysis of an inverter- based microgrid with internal model-based controllers [J].IEEE Transactions on Smart Grid, 2018, 9(5): 5393-5402.
[23] 颜湘武, 刘正男, 张波, 等. 具有同步发电机特性的并联逆变器小信号稳定性分析[J]. 电网技术,2016, 40(3): 1-11.Yan Xiangwu, Liu Zhengnan, Zhang Bo, et al. Smallsignal stability analysis of parallel inverters with synchronous generator characteristics[J]. Power System Technology, 2016, 40(3): 1-11.
[24] 杜威, 姜齐荣, 洪芦诚, 等. 光伏微电网孤岛运行时多种振荡模式的小信号建模分析[J]. 电力系统自动化, 2014, 38(10): 17-23.Du Wei, Jiang Qirong, Hong Lucheng, et al. Small signal analysis of multiple oscillation modes in a photovoltaic microgrid[J]. Automation of Electric Power Systems, 2014, 38(10): 17-23.
[25] Katiraei F, Iravani M R, Lehn P W. Small-signal dynamic model of a micro-grid including conventional and electronically interfaced distributed resources[J].IET Generation, Transmission & Distribution, 2007,1(3): 369-378.
[26] Tang Xisheng, Deng Wei, Qi Zhiping. Investigation of the dynamic stability of microgrid[J]. IEEE Transactions on Power Systems, 2014, 29(2): 698-706.
[27] 孟潇潇, 周念成, 王强钢. 逆变型分布式电源模型的多时间尺度降阶分析及稳定一致性证明[J]. 中国电机工程学报, 2018, 38(13): 3813-3825.Meng Xiaoxiao, Zhou Niancheng, Wang Qianggang.Multi-time scale model order reduction and stability consistency of IIDG system[J]. Proceedings of the CSEE, 2018, 38(13): 3813-3825.
[28] Tao Yong, Liu Quanwei, Deng Yan, et al. Analysis and mitigation of inverter output impedance impacts for distributed energy resource interface[J]. IEEE Transactions on Power Electronics, 2015, 30(7): 3563-3576.
[29] Yao Wei, Chen Min, Matas J, et al. Design and analysis of the droop control method for parallel inverters considering the impact of the complex impedance on the power sharing[J]. IEEE Transactions on Industrial Electronics, 2011, 58(2):576-588.
[30] 陈昕. 基于小信号模型的虚拟同步发电机稳定性分析与设计研究[D]. 成都: 电子科技大学, 2017.
[31] 李伟龙, 安军, 周毅博. 基于两机扩展 Heffron-Phillips模型的励磁系统调差系数对系统阻尼特性的影响[J]. 电网技术, 2017, 41(1): 222-229.Li Weilong, An Jun, Zhou Yibo, et al. Research on impact of excitation system adjustment coefficient on system damping characteristics based on extended two-machine Heffron-Phillips model[J]. Power System Technology, 2017, 41(1): 222-229.
[32] 袁敞, 丛诗学, 徐衍会. 应用于微电网的并网逆变器虚拟阻抗控制技术综述[J]. 电力系统保护与控制, 2017, 45(9): 144-154.Yuan Chang, Cong Shixue, Xu Yanhui. Overview on grid-connected inverter virtual impedance technology for microgrid[J]. Power System Protection and Control, 2017, 45(9): 144-154.
[33] 张平, 蔡环宇, 石健将, 等. 应用 P/w(Q/E)“导纳”的逆变器并联系统稳定性分析方法[J]. 中国电机工程学报, 2016, 36(9): 2486-2493.Zhang Ping, Cai Huanyu, Shi Jianjiang, et al. Stability analysis of parallel inverter systems using a P/w(Q/E)“admittance”[J]. Proceedings of the CSEE, 2016,36(9): 2486-2493.
[34] 颜湘武, 贾焦心. VSG一次调频和转速振荡阻尼的解耦控制方案[J]. 电网技术, 2019, 43(5): 1566-1575.Yan Xiangwu, Jia Jiaoxin. Decoupling control of primary frequency regulation and rotational speed damping of VSG[J]. Power System Technology, 2019,43(5): 1566-1575.
[35] 颜湘武, 王俣珂, 贾焦心, 等. 基于非线性最小二乘曲线拟合的虚拟同步发电机惯量与阻尼系数测量方法[J]. 电工技术学报, 2019, 34(7):168-178.Yan Xiangwu, Wang Yuke, Jia Jiaoxin, et al. A VSG inertia and damping measurement method based on nonlinear least-squares curve fitting[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 168-178.
[36] 颜湘武, 贾焦心, 王德胜, 等. 虚拟同步发电机的并网功率控制及模式平滑切换[J]. 电力系统自动化, 2018, 42(9): 91-99.Yan Xiangwu, Jia Jiaoxin, Wang Desheng, et al.Power control and smooth mode switchover for gridconnected virtual synchronous generators[J].Automation of Electric Power Systems, 2018, 42(9):91-99.
[37] 张也. 微网逆变电源的功率分配控制和同步运行特性研究[D]. 北京: 华北电力大学, 2016.