0 引言
目前电流差动保护仍然是变压器主保护,需要面临空载合闸时励磁涌流防误动问题。近年来,国内外学者提出了众多新型励磁涌流识别方法[1-5]。现场一般采用二次谐波制动和波形特征制动的方式识别励磁涌流。Y-d接线变压器因其改善波形的优势广泛应用于各电压等级电网中,其差动保护需要转角接线。目前差动保护的转角方式主要有两种:一种是基于相间差动方式的转角方式;另一种是基于相电流减零序电流的差动保护方式。
文献[6]指出两种转角方式在应用中都存在问题。因转角后的谐波特征会减弱,国内一些厂家将Y侧CT也按Y联结接入保护装置,当差流二次谐波未能制动时,进一步用一次电流中的二次谐波进行制动。GE公司提出利用一次电流中二次谐波幅值与相位特征的自适应二次谐波制动方案,其原理基于典型励磁涌流二次谐波与基波的相位差为 90°。但一次侧三相涌流的波形并非总是与典型单相励磁涌流一致,一次侧某相电流可能会出现对称性涌流或波形畸变,这与二次侧环流的助增作用密切相关,因此上述方法的可靠性会受到影响。当二次侧是星形联结时,一次电流就是典型的励磁涌流(非连续的截断正弦波形态)。而当二次侧是三角形联结时,三角绕组中有电流流过。此时励磁涌流应为一次电流与二次侧三角绕组环流之和。文献[6-7]采用助增作用解释了上述非典型涌流现象,并提出了基于“绕组电流”的方法,即利用环流对一次电流进行补偿,得到具有典型特征的真实励磁涌流。
目前广泛应用的新型高阻抗变压器结构发生了变化,多次发生了零序过电流保护误动问题。基于一次侧零模电流和环流的线性关系,需要研究变压器结构改变后二次侧高漏感特性对环流的影响以及该环流对一次电流的影响[8]。然而,目前环流的产生机理及助增作用尚存在机理解释不清晰、因果关系混乱的问题,且模糊处理了变压器接地与不接地两种情况,忽视了二次侧漏感的影响等,导致无法分析环流的影响因素。为了研究新型变压器结构及阻抗特性对环流的影响,以及完善利用环流补偿一次电流的方法,改善差动保护动作性能,解决基于典型励磁涌流特征的涌流制动判据应用时可靠性不高的问题,需要进一步完善环流理论,从物理意义上厘清环流的产生机理、助增作用以及影响因素。
利用环流补偿一次电流可以改善差动保护的灵敏度。500kV及以上电压等级变压器的环流可测,但220kV及以下电压等级变压器的三角绕组内部环流无法直接测量。许多学者提出了环流的求取方法。文献[9-11]假设系统三相电压平衡,根据变压器回路微分方程计算环流,得出了环流和Y侧零模电流的比例关系,分别通过各自的方法求得比例系数,进而根据零模电流求取环流。但这些方法仅适用于变压器中性点接地的情况,当中性点不接地时无效。此外,系统三相电压平衡的假设忽略了系统运行时电压扰动造成的不平衡[12-15],这些方法可能在外部扰动时失效。文献[16-17]所提方法适用于中性点不接地的情况,但该方法需要获取变压器中性点电压,现场不易获得此电压,该方法的基本原理和实现方案均需进一步完善。因此,目前尚缺乏一种适用性强、可靠实用的环流求取方法。
针对目前变压器三角环流在产生机理、助增作用、求解方法等方面研究不足的问题,本文通过变压器回路微分方程和相量分析,厘清和完善了环流的产生机理、助增作用及影响因素。基于环流的产生机理以及环流与不饱和相一次电流的关系,提出利用一次电流分段代替的工程用环流求取方法,用于补偿一次电流以改善差动保护动作性能。该方法与接地方式无关,且不要求系统电压平衡对称,适用性强,可靠性高。该方法的应用有利于差流的准确计算,有助于改善差动保护动作性能。数字仿真和现场录波验证了该方法的有效性。
1 二次电流的去磁作用
变压器空投时二次侧三角形绕组漏感为感性负载,二次绕组电流滞后于电压,二次电流形成的磁场与一次电流形成的磁场相反,二次电流起到去磁作用[18]。双绕组单相变压器原理如图1所示,取三相电路中的A相做具体分析。一、二次电流iA、ia的正方向如箭头所示,图中的电量已归算到高压侧。对于一次侧,系统电压uA是电源,系统电感Ls、一次侧漏感Lσ、励磁电感Lm是负荷。对于二次侧,感应电动势ea是电源,二次侧漏感LσD是负荷。
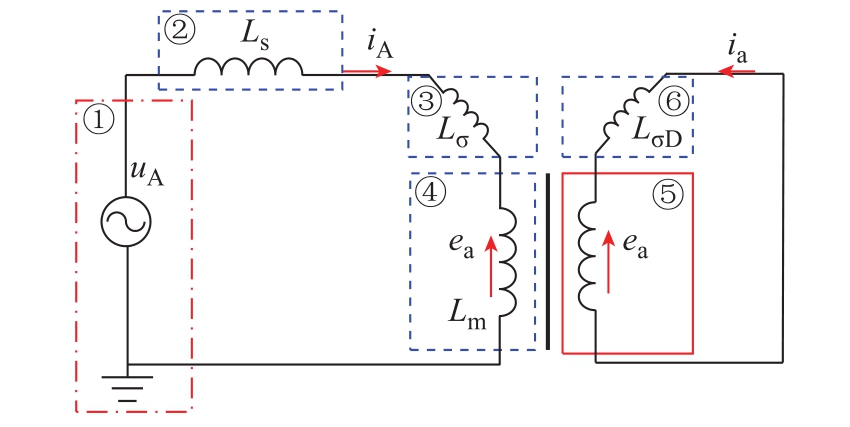
图1 双绕组单相变压器原理图
Fig.1 Two-winding single-phase transformer
忽略电阻的影响,根据图1列出变压器磁链电压微分方程为
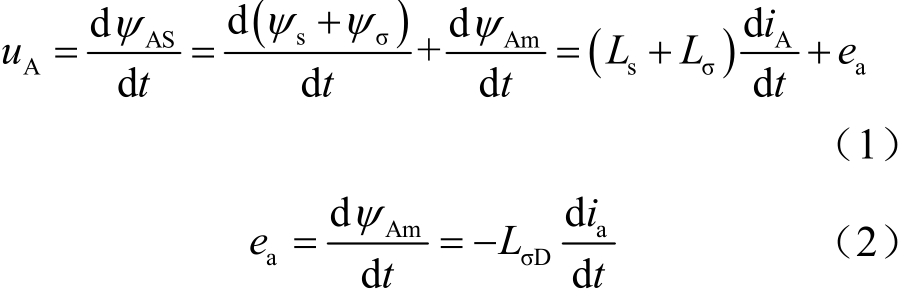
式中,ψAS为使微分方程左右平衡所需的总磁链。ψA S包括系统磁链ψ(s对应线性电感Ls)、一次侧漏磁链ψσ(对应线性电感Lσ)和互感磁链ψAm(对应非线性电感 Lm,励磁特性曲线如图 2所示)三部分。图2中,Lm为线圈的励磁电感,Lμ0为饱和后的励磁电感,im为励磁电流,ψ为通过线圈的磁链,ψS at为饱和磁链。由式(1)可知电压是激励,电流是响应。电流流过各电感产生与激励“相抵”的电动势以维持等式平衡。去磁作用相量图如图3所示。图3中,ψA、ψa为一、二次电流产生的互感磁链,ψa的方向与ψA相反(相角差180°),起去磁作用,两者合成后为互感磁链ψAm,再加上一次侧线性磁链ψA(lψAl=ψs+ψσ),得到总磁链ψAS。当铁心不饱和时,励磁电流很小,iA几乎为0,线性磁链ψA1忽略不计,可以认为 ψ AS =ψAm,即总磁链全部由互感磁链提供。
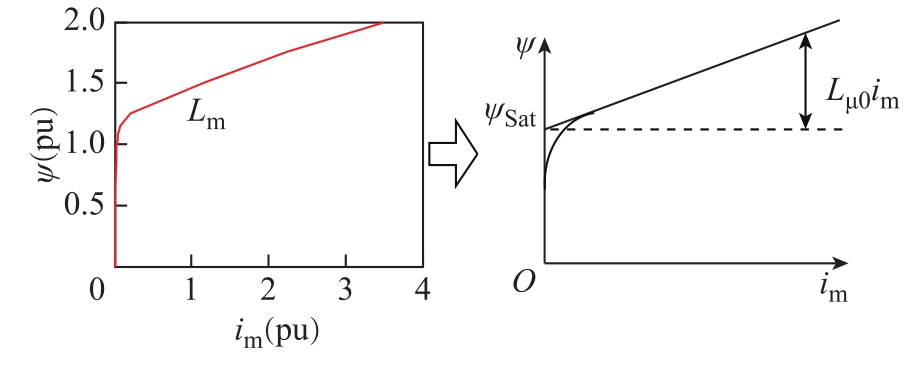
图2 铁心励磁特性曲线
Fig.2 Core magnetizing characteristic curve
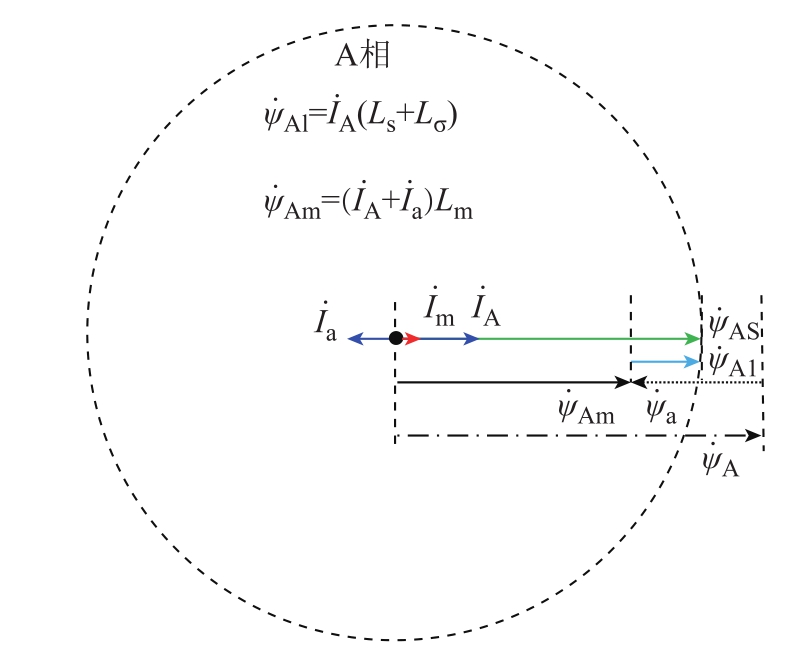
图3 去磁作用相量图
Fig.3 Phasor diagram of demagnetization
2 三角绕组环流的产生机理和助增作用
2.1 环流的产生机理
目前,国内外文献关于环流产生机理的解释普遍为[6,19-20]:当仅 A相铁心饱和具备产生涌流条件时,A相涌流iA必分两路经BC相绕组返回,这时B相和C相就有涌流了(即iB=iC=-0.5iA),再根据变压器一、二次侧的磁动势平衡条件,B相和C相二次侧就必须有方向与一次电流相反的涌流(即iD=0.5iA),且二次侧为三角形封闭回路,所以A相二次电流也为 iD。A相励磁涌流 iAm=iA+iD=1.5iA,BC相铁心没有产生涌流条件,iBm=iCm≈0,一、二次电流相抵消。上述解释中有两点说法尚待商榷:其一,在中性点接地时,A相产生的涌流不必分两路经 BC相绕组返回,而是流入了大地,有必要按接地与否分别说明;其二,认为环流是二次侧抵消不饱和相一次电流而产生的,这样将会忽略二次电感对环流的影响,使因果关系错误。
总之,上述环流产生的机理的解释说服力不强,因果关系模糊。为了准确揭示环流产生机理,采用图4所示Y-d联结变压器说明。图4中,uA、uB、uC为系统电压;ua、ub、uc为变压器二次电压;uN为Y形侧中性点电压,若中性点接地则uN=0;Ls、Ls0分别为系统正序和零序电感;Lσ为变压器一次侧漏感;LσD为二次侧漏感;ea、eb、ec为变压器三相励磁支路感应电动势;iD为三角绕组环流。图中忽略了电阻,且电量已归算到高压侧。
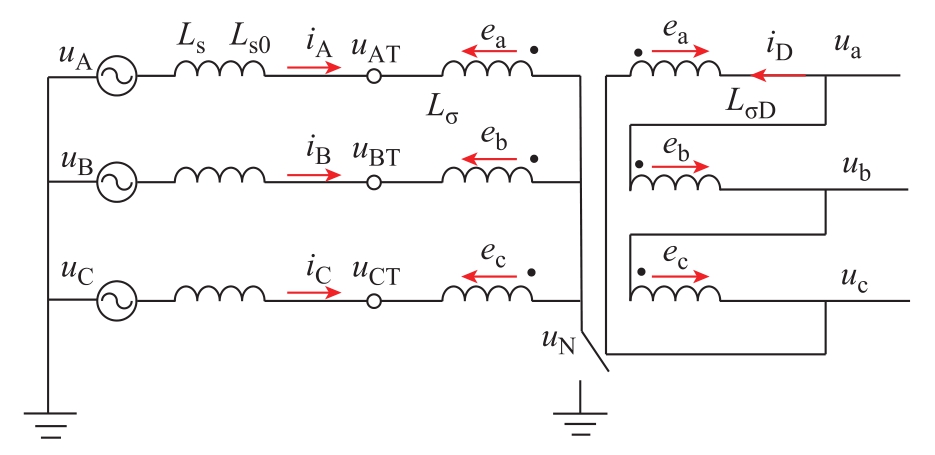
图4 Y-d联结变压器接线图
Fig.4 Wiring diagram of Y-d-connected transformer
根据自互感理论列写三相电压回路方程,文献[19]虽然采用了文献[20]相量方程的方法,但认为其在理论上不严格或不成立。本文采用严格成立的微分方程进行分析,列出A相系统电压至变压器中性点的回路方程为
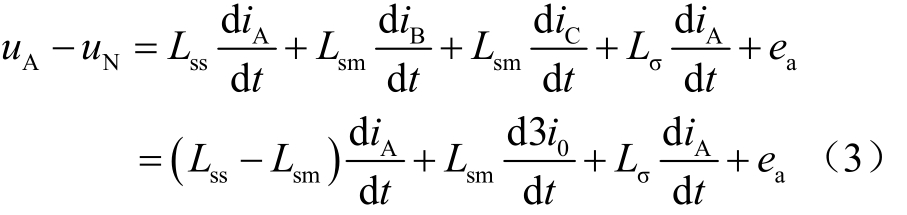
因为 Ls=Lss-Lsm,Ls0=Lss+2Lsm,iA+iB+iC=3i0,进一步得到
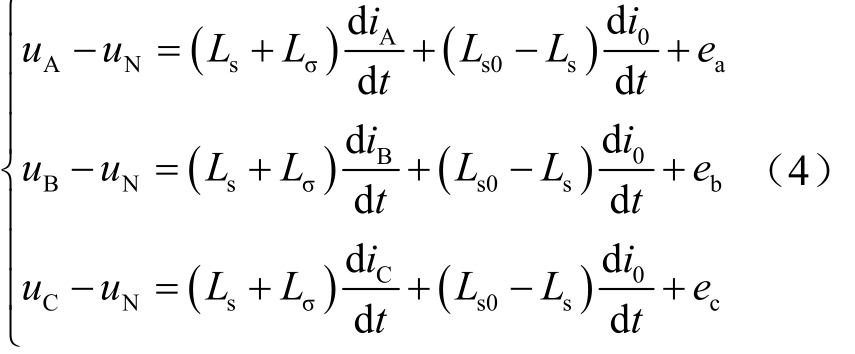
二次侧满足方程
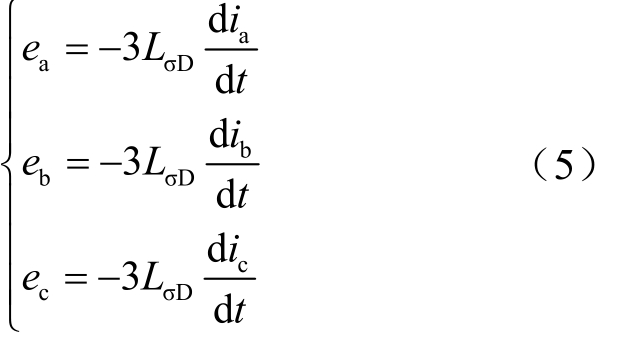
参考式(2),ia、ib、ic为三相对应的去磁电流,根据叠加定理,得到环流表达式为
无论是否接地,当Y-d三相变压器三相铁心均不饱和时,三相二次侧均会产生各自的去磁电流,且三相对称,三者和为零,即环流为零。当发生变压器空投等铁心饱和的暂态过程时,二次侧会产生环流,下面按接地与否分别说明。
接地时,三相绕组与大地进行电荷交换,一次侧三相电流相互独立,无耦合关系。当铁心不饱和时,iA几乎为 0,系统电动势全由变压器互感电动势(互感磁链变化率)提供平衡。当某相铁心饱和时,采用图 5所示的仅有一相饱和的情况来说明。由图5可知饱和后曲线微分电感值很小,互感电动势变小,将不足以与系统电动势平衡(如图 5c所示),系统电动势和互感电动势之间的电动势差落在了线性电感上(如图5b所示),因此一次侧产生了涌流(如图5d所示)。此时互感磁链和线性磁链的关系如图 5a所示。因为互感电动势减小,结合式(5)可知,该饱和相二次侧去磁电流削弱(如图5d所示),原有的二次侧三相去磁电流对称关系被打破,电流和不再为零,产生了环流(如图 5e所示)。注意,上述过程虽无时间上的前后关系,但有明确的因果关系。
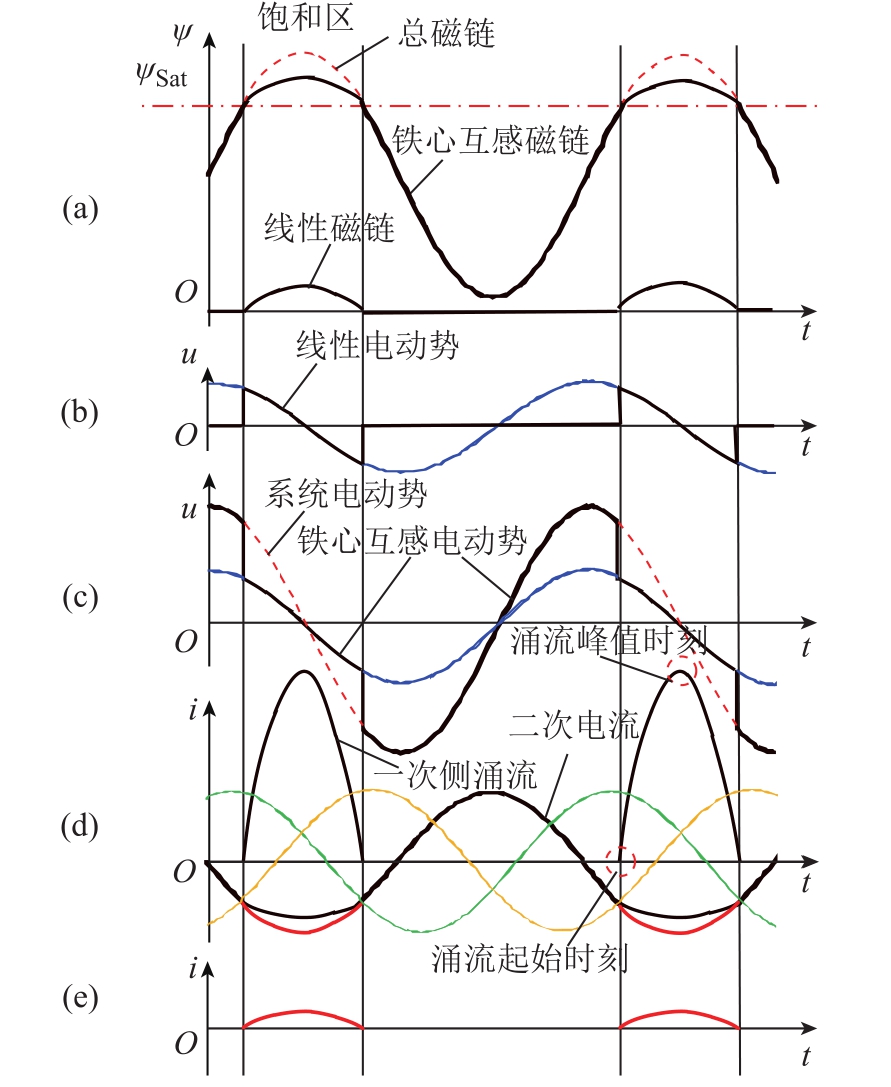
图5 环流产生机理的示意图
Fig.5 The generating mechanism of circulating current
环流流过不饱和相二次侧时,该不饱和相的互感电动势将发生改变,因而该互感电动势与对应相系统电动势产生了电动势差,落在线性电感上,因此不饱和相一次侧产生了电流,并与环流“相抵”。图6a为接地时环流产生的因果关系示意图,饱和相互感电动势的削弱使二次侧产生了不平衡的环流,环流进而影响了不饱和相的互感电动势,使一次侧不饱和相产生了与环流“相抵”的电流。

图6 环流产生机理的因果关系
Fig.6 Causal relationship for the generating mechanism of circulating current
以上描述了变压器接地时饱和相涌流、环流、不饱和相电流产生的因果逻辑关系。对于变压器中性点不接地时,环流的产生机理基本相同。仅有的区别是除了一、二次侧之间的互感电动势耦合以及二次侧环流对一次电流的反馈影响外,还有一次侧三相电流瞬时值之和为零的约束。为了满足上述所有约束,中性点电压不再为零,根据式(3)的回路方程,所需的总磁链将同时受系统电动势和中性点电压的影响。因而,励磁电流出现的时间和大小将不会与接地时一样。励磁电流是由“分配”在励磁互感上的电动势(磁链变化率)决定的。接地时,该电动势就是端口电压。不接地时,需要端口电压减去中性点电压。因此,不接地时,中性点电压总是“抑强扶弱”,起维持平衡的作用,自动调节使两侧满足约束条件。
2.2 环流的助增作用
文献[20]最早介绍了助增作用(Helping Effect),国内外对助增作用的解释均为[6, 20]:因饱和相的一次电流流过非饱和相,非饱和相的二次侧感应出来“抵消”该电流的反向环流正好与饱和相一次电流同向,起到了“帮助作用”。显然,根据上文的环流机理分析,该说法忽略了接地情况且因果关系倒置。根据图5及机理说明,饱和相的二次侧去磁电流减小,而“和电流”为原该相去磁电流的反方向,也就是和一次电流同方向(相位差为0°),此为“助增作用”。上文中为了便于阐释物理机理,提到的去磁都是反方向(相位差为180°)的去磁,助磁都是同方向(相位差为0°)的助磁。文献[6]提到环流对非饱和相是去磁,对饱和相是助磁。事实上,“去磁”和“助磁”的内涵更为丰富。
无论是“去磁”还是“助磁”都是针对相量来说的,对于瞬时值没有意义。根据图2的模型,可以认为饱和与不饱和存在较明显的界限。观察图5,虽然进出饱和区时电动势和电流都发生了变化,但前后波形仍然可视为正弦的一部分,因此可以进行相量分析。下面通过相量分别介绍接地时两种饱和情形下的去磁作用和“助增作用”。当变压器中性点不接地时,相量图中中性点不再为圆心处,而是根据平衡条件动态变化。
图7为一相饱和与两相饱和时的相量示意图。当只有一相饱和时,对于饱和的A相,环流与一次电流同向(相位差0°),虽然是助磁,但其互感电动势是三相中最小的;对于不饱和的B相和C相,环流的去磁作用与第1节介绍的不同,去磁电流不是反向(相位差180°),而是比180°小的钝角。
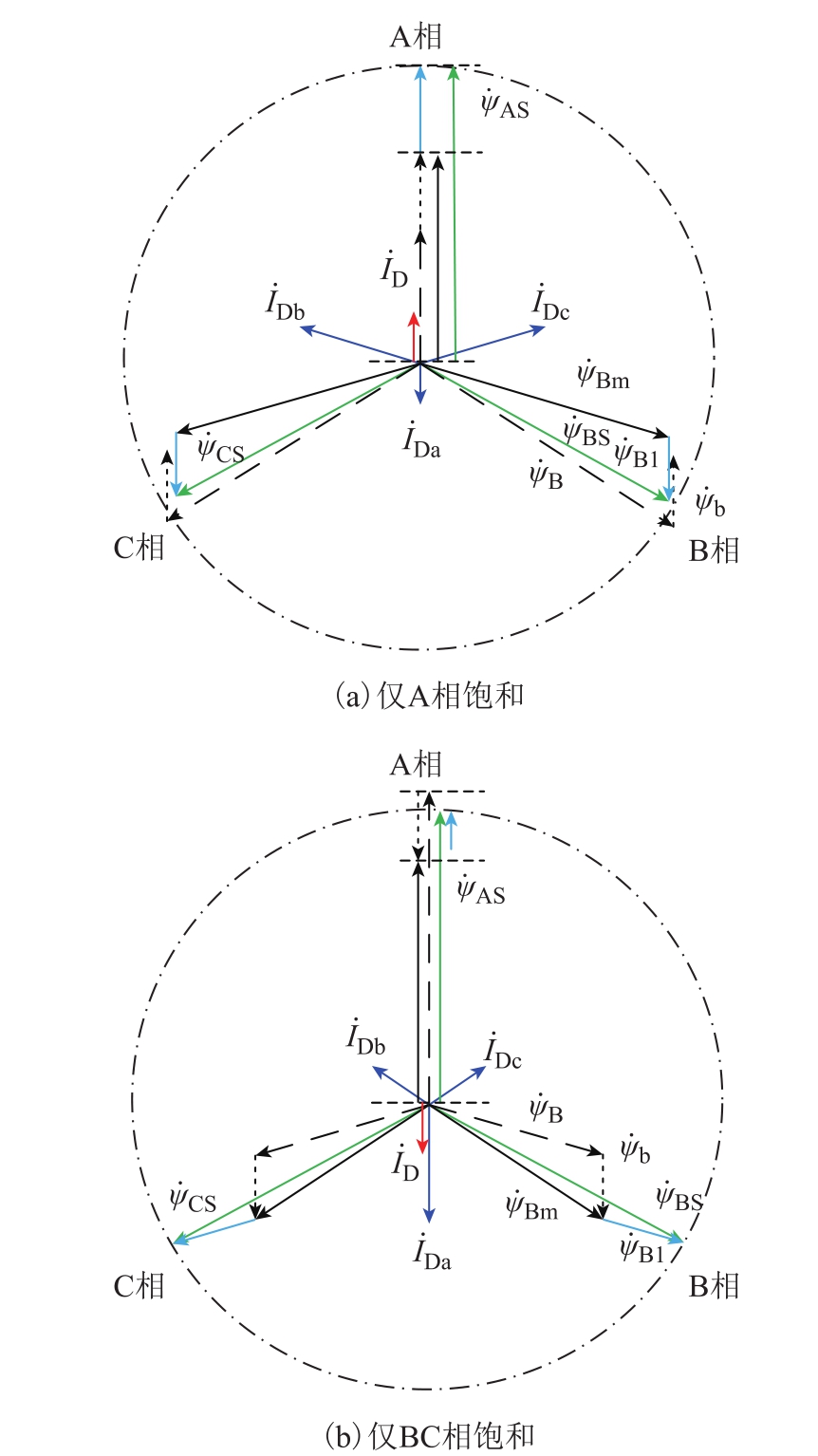
图7 助增作用相量图
Fig.7 Phasor diagram of helping effect
当两相饱和时,对于不饱和的A相,环流与一次电流反向(相位差180°),是典型的去磁作用,但其互感电动势是三相中最大的;对于饱和的B相和C相,环流的助磁作用与第1节介绍的不同,助增电流不是同向(相位差 0°),而是比 0°大的锐角。这里通过相量图更清晰地认识了助增作用的内涵。
2.3 环流的影响因素
文献[6,19-20]认为环流是因二次侧抵消不饱和相一次电流而产生的,因果关系错误且忽略了二次电感对环流的作用,难以分析环流的影响因素。根据上述分析,从最根本的物理意义上认识了环流的产生机理及其助增作用,有利于分析环流的影响因素。
除了剩磁、合闸角等环境因素外[21],环流还受多方面及变压器自身因素的影响。是否接地是影响环流的首要因素,从前文的中性点分析来看,当不接地时,为了满足平衡条件,中性点电压总是起“抑强扶弱”的作用:能在接地时产生最大涌流的相的涌流会被削弱,而较小涌流甚至无涌流的相的涌流会增强,而二次侧较小的涌流与环流“相抵”。因此,当只有“是否接地”这一个变量时,不接地变压器三角形绕组环流将大于接地变压器三角形绕组环流。根据前文机理的分析可知,环流是在“不平衡互感电动势”下产生的,那么相同电动势下二次侧漏感越小,环流越大。互感电动势又与空心电感(励磁特性曲线饱和的后微分电感)正相关。因此,二次侧漏感和空心电感越大,环流越小,即环流随着 LσD、Mair增大而减小。
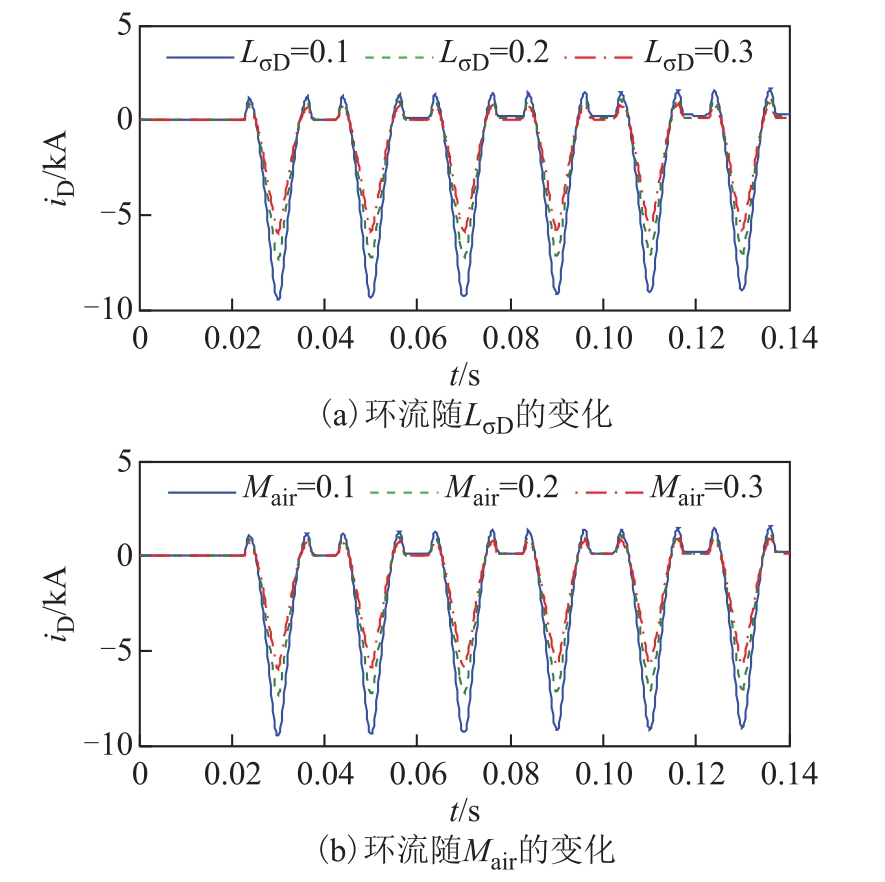
图8 接地时环流的影响因素
Fig.8 Factors affecting circulating currents when neutral grounding
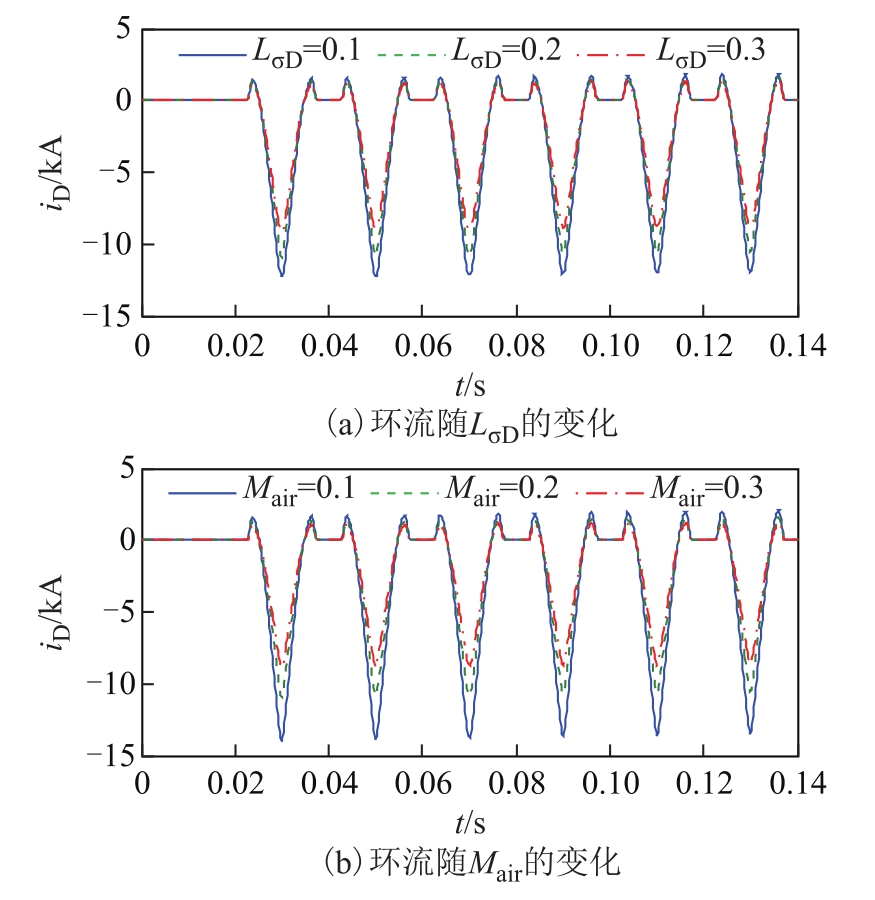
图9 不接地时环流的影响因素
Fig.9 Factors affecting circulating currents with isolated neutral
图8 和图9分别为同一个剩磁、合闸角下变压器接地和不接地时,环流随 LσD、Mair的变化情况的仿真结果。对比图8和图9中接地和不接地的环流,发现不接地时,环流更大。从图中可以看出,环流随着LσD、Mair增大而减小,仿真结果证明了理论的正确性。
3 三角形绕组环流的工程求取方法
环流的助增作用会使二次电流产生畸变,影响基于典型励磁涌流特征的差动保护涌流制动判据的可靠性,需要对二次电流进行补偿。目前的环流求取方法会受到接地方式、系统电压平衡等因素的限制,尚缺乏一种适用性强、简单可靠的环流计算方法。本节基于环流的产生机理以及环流与一次侧不饱和相电流的关系,提出一种工程中实用的环流求取方法。
3.1 原理介绍及方法实现
根据上述理论,一次侧不饱和相电流的产生是在环流影响下的一次侧“抵消”电流,因此可用不饱和相的一次电流来代替环流,但不饱和相并非总是不饱和,一个周期内饱和与不饱和交替出现。文献[9]证明了总存在一相电流饱和区间大于 1/3,但未论证三相电流饱和时间区间对一个周期时间的覆盖程度。若能在证明三相电流的不饱和区间能尽可能地覆盖整个周期,那么环流iD或许可以用一次侧三相电流来分段代替。此分段电流的集合定义为“准环流iDk”。下面说明三相电流不饱和的时间区间对一个时间周期的覆盖程度。
设 A相电源电压为 umsin(ωt+α),α为合闸角,不考虑电阻的影响,磁通可表示为
式中,mψ为额定磁通幅值;rAψ为剩磁通。式(7)除以mψ,标幺化后得到A相、B相、C相的饱和程度系数TA、TB和TC分别为
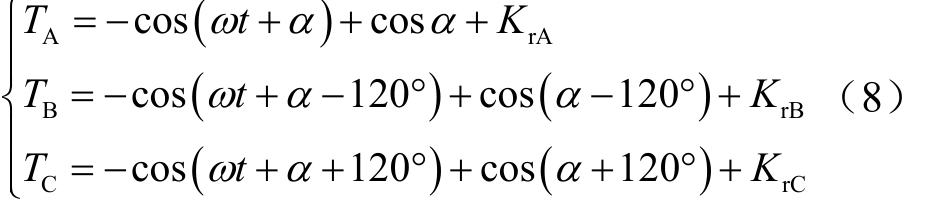
式中,KrA、KrB、KrC为各相剩磁占比。显然,当|T|≤1时,该相铁心不饱和;当|T|>1时,该相铁心饱和。
若不考虑剩磁(Kr=0),图10为式(8)代表的相量图。以A相为例,深色相量代表cosα,浅(红)色相量代表-cos(ωt+α)。两条竖线中间的区域代表只要某相末端端点落在该区域,则该相不饱和,该区域称为“不饱和区”。图10为三相相量末端端点尽可能都避免落入“不饱和区”的边界情况。可以发现,无论何时,总存在一相相量末端端点落在“不饱和区”,满足-1≤T≤1的关系,即任意时刻总有一相不饱和。因此,不考虑剩磁时,在整个连续周期内都可以由准环流代替环流。
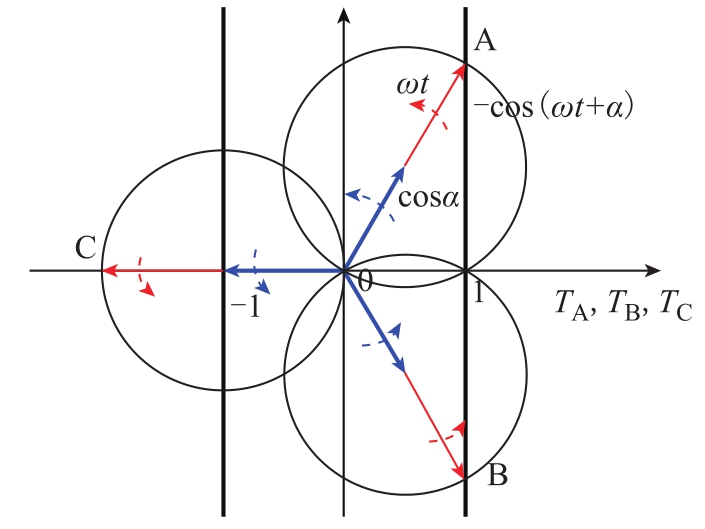
图10 无剩磁时饱和状态判断相量图
Fig.10 Phasor diagram for saturated state judgment without remanence
一般而言,不饱和电流为三相电流中绝对值最小的,因此求取环流算法为每个时刻均取三相电流中绝对值最小的那相,即准环流为三相电流中绝对值较小段的集合。对于每个时刻的值,考虑到涌流受电流互感器误差的影响以及其他扰动造成的直流偏移[22],准环流为三相一次电流的中间值,即被另两相“夹在中间”。对于每个时刻的值,由式(9)决定。
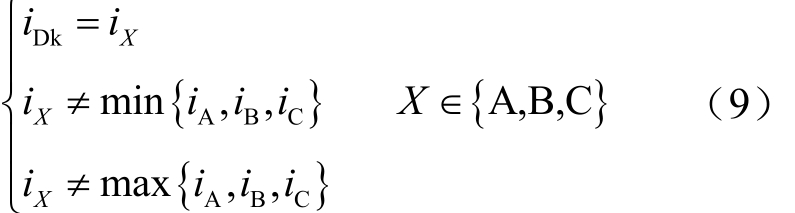
3.2 剩磁影响的分析
当考虑剩磁时,电力系统实际运行中,变压器铁心剩磁主要考虑两类[23]:一类为断路器开断电路所产生的剩磁,由于电力系统三相电压的对称性,这种情况下,铁心的三相剩磁之和为零,称之为“三相平衡性剩磁”。由经典铁磁学磁畴理论以及实验测试可知,当断路器突然断开,变压器三相铁心剩磁并不会维持在断开前时刻的值,而是会瞬间减弱并缓慢衰减至新的稳态。此类剩磁稳态值最大能达到饱和剩磁的70%[24-25],由式(10)决定[26-27]。另一类为由于直流电阻测试或直流偏磁等原因造成的铁心剩磁,此类剩磁具有三相方向相同的特征,称之为“三相非平衡性剩磁”,此类剩磁一般很小。
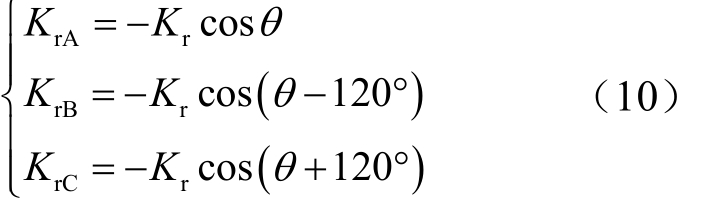
式中,θ为分闸角;Kr为剩磁系数,对于平衡性剩磁,若断开后铁心剩磁不衰减,即 Kr=1,图 11所示为剩磁系数为1时饱和状态判断相量图。图11中虚线相量代表剩磁通。此时最极端的理想情况下单个周期中存在 60°的时间段三相均饱和,且该时间段发生在一相刚进入饱和另一相即将退出饱和时,三相相量端点都在“非饱和区”之外。因此该时间段内三相均不同程度饱和。一个周期内能用一次侧不饱和电流代替环流的时间“有效占比”为83%。因为现实中不存在剩磁系数为 1,该论证只是求取一个达不到的极限边界值。
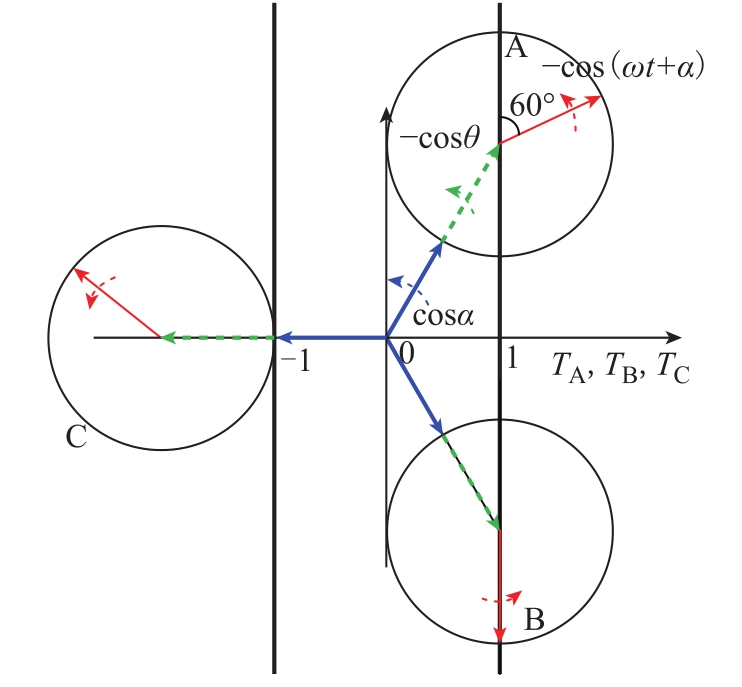
图11 剩磁系数为1时饱和状态判断相量图
Fig.11 Phasor diagram for saturation judgment when Kr=1
若考虑实际衰减,剩磁系数最大时Kr=0.7,如图12所示,虚线相量代表的剩磁长度减小,经过计算,此时一个周期中仍存在42.7°的时间段三相都饱和,准环流理论有效占比为88%。显然,当剩磁系数更小时,三相均饱和的时间区间会进一步减小,有效占比越来越接近100%。但只要考虑剩磁,一个周期内必定会存在三相都饱和的时间区间。总之,严格地说,在某些情况下 iDk≠iD,准环流不能严格完美地代替环流。
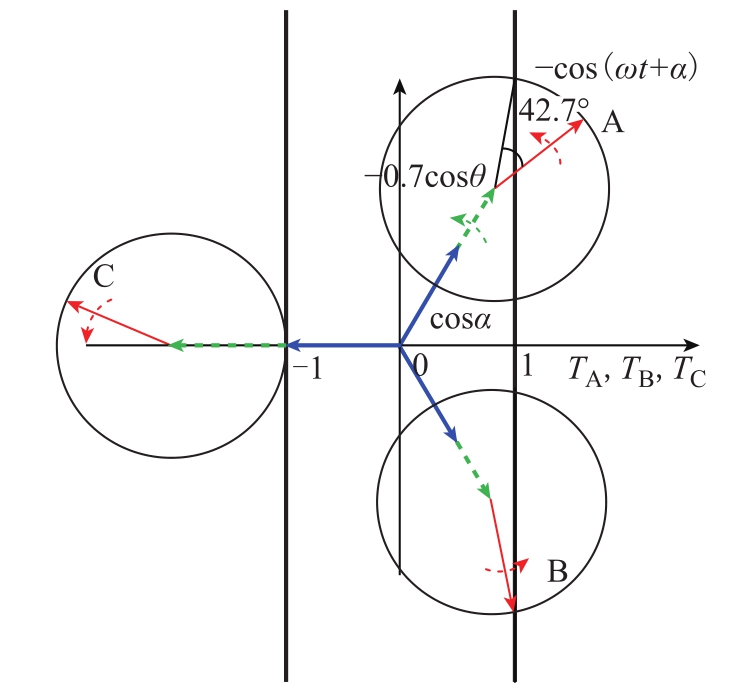
图12 剩磁系数为0.7时饱和状态判断相量图
Fig.12 Phasor diagram for saturation judgment when Kr=0.7
图13为剩磁系数为0.7时,根据式(8)计算得到的各种分合闸组合准环流代替环流的有效占比大小分布。从图中可以得到最小的有效占比为88%,与前文相量分析结论相符。从整个面积分布来看,即使在最大剩磁系数 0.7时,绝大部分分合闸角度组合下有效占比为 100%(图中深(红)色部分),准环流能够完全地代替环流。现实中,剩磁系数一般比0.7小,而且恰好为最严重分合闸角度的概率也很低,所以这里的论证是求取一个小概率能达到的边界值。下面分析三相饱和时,准环流代替环流的误差是否影响补偿一次电流。
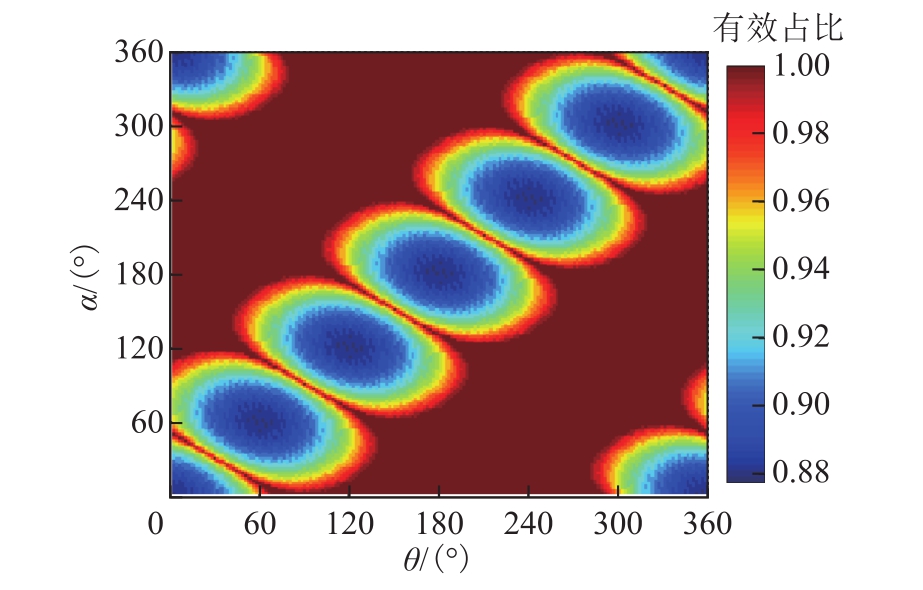
图13 剩磁系数为0.7时有效占比分布
Fig.13 Effective proportion distribution when Kr=0.7
上文提到,三相均不饱和总是发生在一相刚进入饱和另一相即将退出饱和的过渡区。此时这两相(如图11中A、B相)饱和程度都比较浅,补偿后的励磁涌流应该在起始时刻附近(如图5d所示),第三相(如图11中C相)饱和程度较深,补偿后的励磁涌流应该在峰值时刻附近(如图5d所示)。而越接近饱和边缘时,准环流和环流数值相差并不大,理论上可以近似代替,下面通过仿真说明。
3.3 仿真实验分析
“有效占比”是一种理论的数学计算。尽管83%现实中达不到,88%也只是小概率才能达到,但也要评估这些情况下,准环流代替实际环流的效果。这里采用仿真分析准环流和环流的误差情况。利用PSCAD V4.6软件建立变压器仿真系统模拟实际情况。以容量为 240MV·A/240MV·A/80MV·A,额定电压比为220kV /110kV /10.5kV的高阻抗变压器为原型进行仿真。
图14a为Kr=1时一次电流ip、环流和准环流以及励磁涌流im。图14b为Kr=0.7时二次电流、三角形环流及励磁涌流。可以发现,即使是现实中无法达到的极端情况 Kr=1,环流和准环流贴合度也很高,偏差时间角度的仿真值小于其理论值60°,仅在较小区域内存在较小误差。而当 Kr=0.7时,误差更是微乎其微,偏差时间角度的仿真值几乎为 0°,远小于其理论值42.7°。因此,即便是现实中小概率达到的边界情况,准环流的替代效果也很好。本文的环流求解计算的目的在于采用环流补偿二次电流,使之最大程度上还原典型的励磁涌流特征。因此从工程实用角度可以用准环流代替环流进行计算。
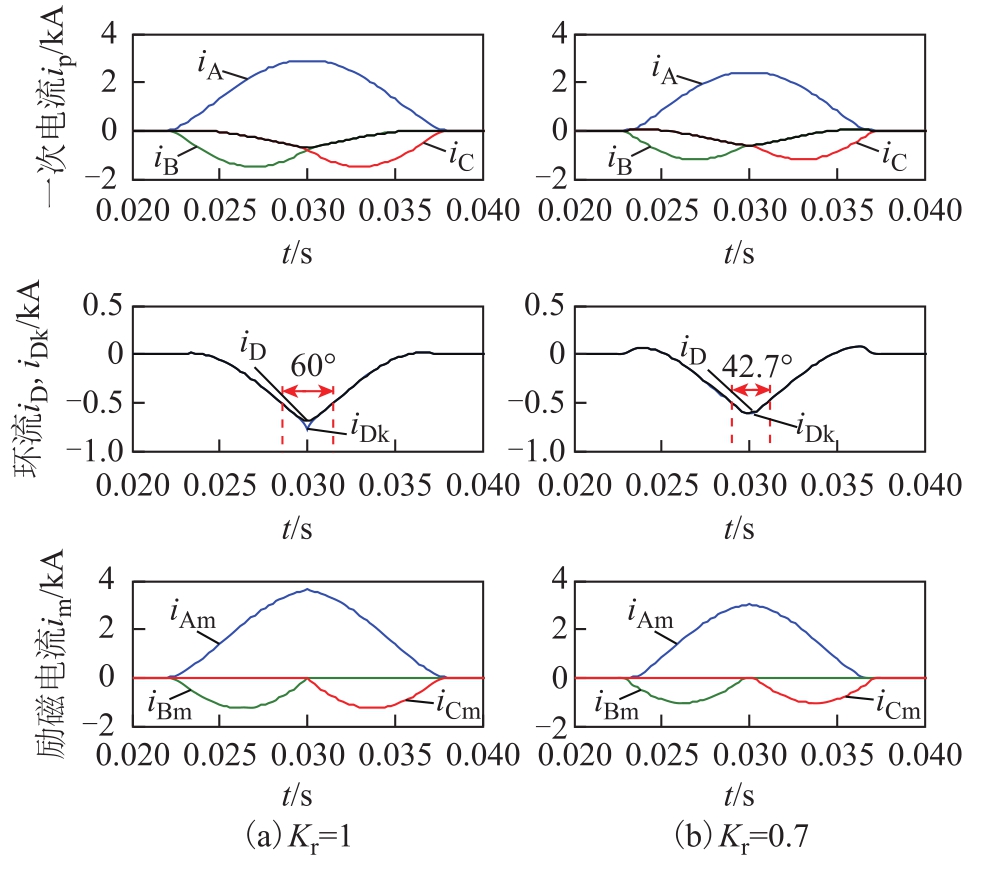
图14 剩磁系数对环流还原程度的影响
Fig.14 Effect of remanence coefficient on degree of circulating reduction
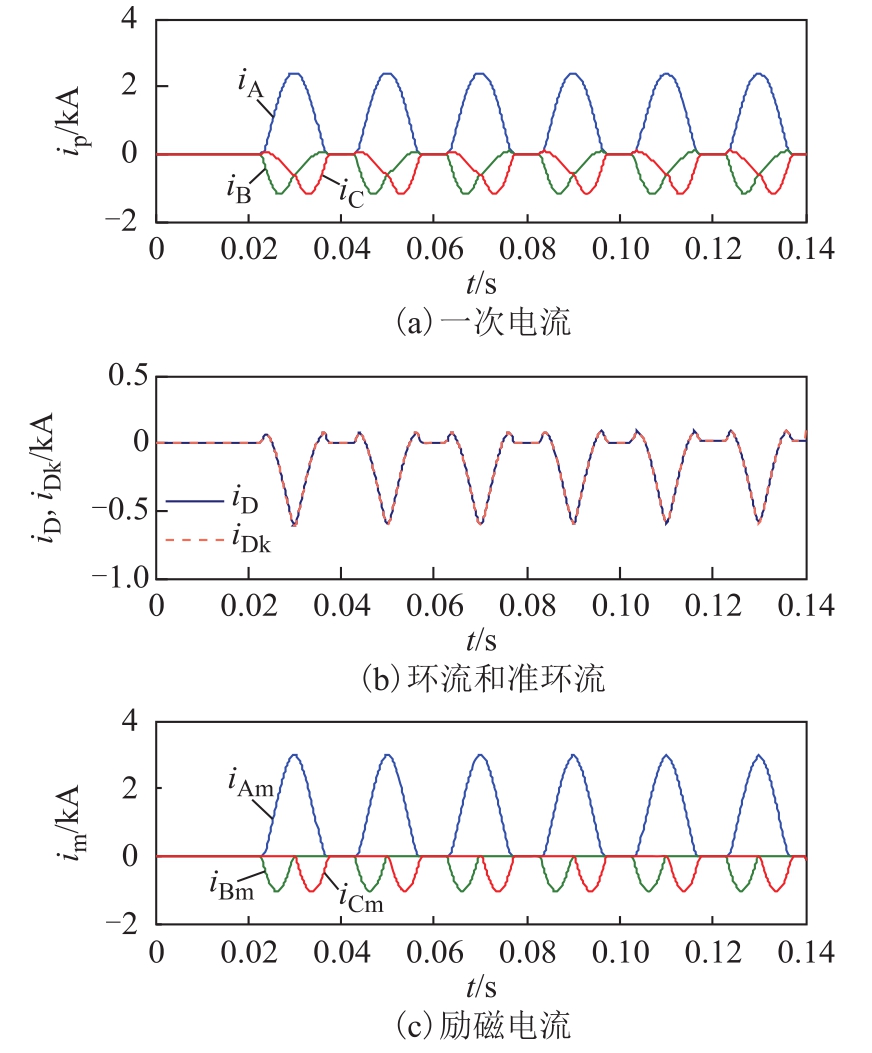
图15 中性点接地时补偿效果
Fig.15 Compensation effect when neutral point is grounded
考虑产生最严重涌流的条件,设置变压器仿真模型的三相剩磁为分闸角θ=180°,剩磁系数Kr=0.7时的大小(0.70, -0.35, -0.35);A相合闸角α=0°。图 15、图 16分别为接地和不接地时,系统电压平衡情况下空投变压器产生的三相二次电流、环流和准环流、补偿后的励磁涌流。可以发现,环流和准环流拟合度非常好。二次电流受环流影响,产生了畸变,而经过准环流的补偿后,得到了具有典型励磁涌流特征的电流,将有利于提高差动保护动作性能。

图16 中性点不接地时补偿效果
Fig.16 Compensation effect when neutral point is not grounded
接地和不接地时环流的拟合效果均较良好,说明本文方法通用性强。另外从图中得到,在相同条件下,接地时的一次电流大于不接地时的一次侧对应相电流,而环流相反,接地时的环流小于不接地时的环流,验证了前述理论的正确性。

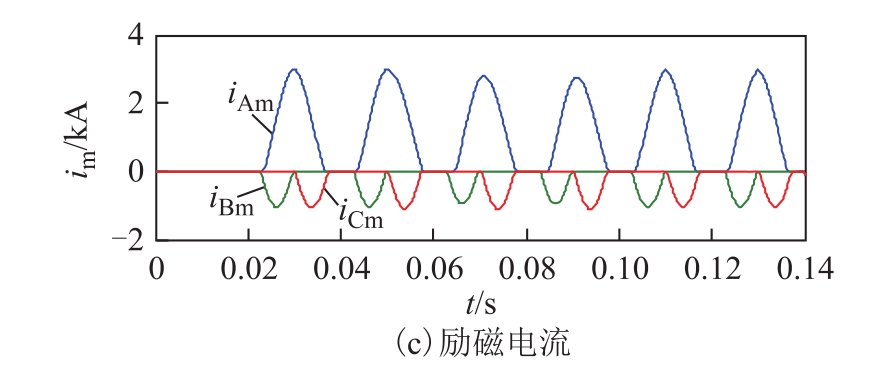
图17 电压扰动且中性点接地时补偿效果
Fig.17 Compensation effect when neutral point is grounded and the voltage is disturbed
图 17、图 18为系统电压发生扰动时,接地和不接地情况下本文方法的使用效果。发现准环流和环流依旧贴合度很高,补偿后的一次电流具有典型的励磁涌流特征,仅仅是整体波形大小发生了变化,说明本文方法抗干扰性强。

图18 电压扰动且中性点不接地时补偿效果
Fig.18 Compensation effect when neutral point is not grounded and the voltage is disturbed
3.4 录波结果
某变压器(SSZ11-240 MVA/220 kV)进行高压侧空载合闸充电,三相电流录波数据如图19a所示;通过本文提出的方法得到的准环流如图19b所示;一次电流经过补偿后得到了具有典型励磁涌流特征的波形,如图19c所示。经过准环流补偿后的涌流比一次侧原始涌流的特征更加明显,显示出典型的非连续截断正弦波形态,这将有利于提高差动保护的灵敏性。
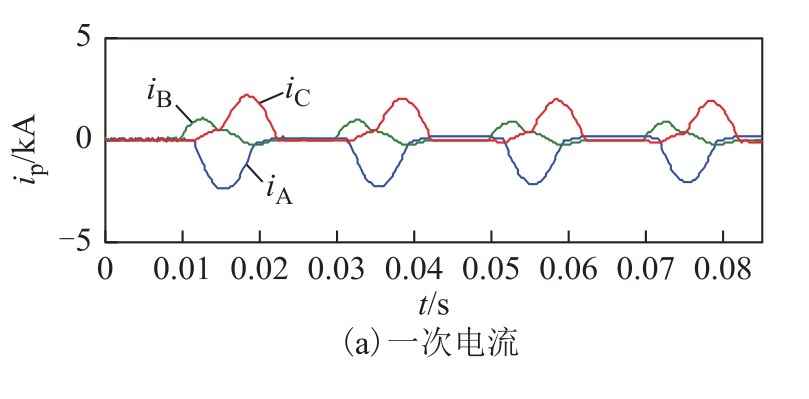
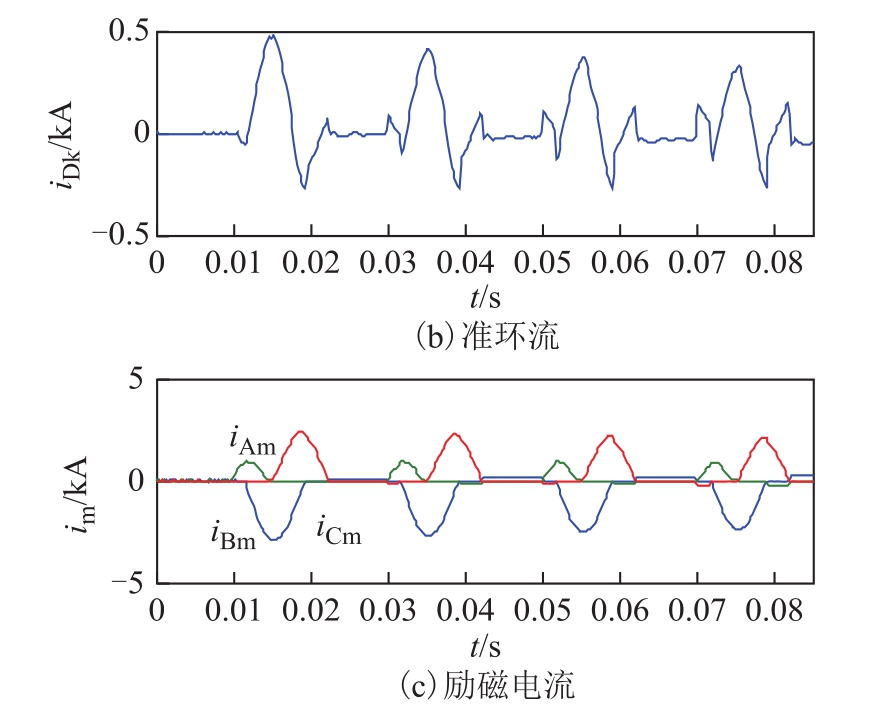
图19 实际录波的补偿效果
Fig.19 Compensation effect of recorded waveform
4 结论
Y-d联结变压器中差动保护的转角方式会减弱谐波特征,国内外研究人员提出了直接利用涌流谐波和相位特征的涌流制动判据,但三角形绕组环流可能会使一次侧某相电流出现对称性涌流或波形畸变,可靠性受到影响。针对目前关于变压器三角环流在产生机理、助增作用、求解方法等方面研究不足的问题,本文通过变压器回路微分方程和相量分析,厘清和完善了环流的产生机理、助增作用及影响因素,指出环流是因为饱和相二次侧去磁电流变小,打破三相不饱和时三相二次侧去磁电流对称关系而产生的不平衡电流。其他条件一致,不接地时环流大于接地时环流,且环流随空心电感和二次侧漏感增大而减小。基于环流的产生机理以及环流和一次侧不饱和电流的关系,提出一次电流分段代替的工程实用环流求取方法,用于补偿一次电流以改善差动保护动作性能。该方法与接地方式无关,且不要求系统电压平衡对称,工程实用性强,可靠性高。该方法的应用有利于差流的准确计算,有助于改善差动保护动作性能。数字仿真和现场录波验证了该方法的有效性。
[1] 郑涛, 陆格野, 赵彦杰, 等. 基于虚拟等效电感的特高压调压变压器励磁涌流判别算法[J]. 电工技术学报, 2016, 31(7): 118-125.Zheng Tao, Lu Geye, Zhao Yanjie, et al. A discriminating algorithm for identifying inrush of UHV voltage-regulating transformer based on virtual equivalent inductance[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 118-125.
[2] 潘超, 金明权, 蔡国伟, 等. 基于变压器励磁电流辨识的直流失稳与抑制策略[J]. 电工技术学报,2018, 33(18): 4267-4276.Pan Chao, Jin Mingquan, Cai Guowei, et al. DC instability and suppression strategy of transformer based on exciting-current identification[J]. Transactions of China Electrotechnical Society, 2018, 33(18):4267-4276.
[3] 王业, 袁宇波, 高磊, 等. 基于 FSAD 及非周期分量的励磁涌流鉴别算法[J]. 电工技术学报, 2015,30(21): 127-135.Wang Ye, Yuan Yubo, Gao Lei, et al. A algorithm to identify magnetizing inrush current based on FSAD and aperiodic components[J]. Transactions of China Electrotechnical Society, 2015, 30(21): 127-135.
[4] Wu Wencong, Ji Tianyao, Li Mengshi, et al. Using mathematical morphology to discriminate between internal fault and inrush current of transformers[J].IET Generation, Transmission & Distribution, 2016,10(1): 73-80.
[5] 周念成, 李春艳, 王强钢. 基于多变量多尺度熵的变压器励磁涌流识别方法[J]. 电工技术学报, 2018,33(15): 3426-3436.Zhou Niancheng, Li Chunyan, Wang Qianggang. An algorithm to identify transformer inrush currents based on multivariate multiscale sample entropy[J].Transactions of China Electrotechnical Society, 2018,33(15): 3426-3436.
[6] 袁宇波, 陆于平, 李澄, 等. 三相涌流波形特征分析及差动保护中采用二次谐波相位制动的原理[J].中国电机工程学报, 2006, 26(19): 23-28.Yuan Yubo, Lu Yuping, Li Cheng, et al. The characteristic analysis of three phase transformer inrush and the discussion of second harmonic restrained method using phase angle and amplitude[J].Proceedings of the CSEE, 2006, 26(19): 23-28.
[7] 袁宇波, 陆于平, 陈久林, 等. 变压器三角形侧零序环流助增对差动保护的影响[J]. 电力系统自动化, 2006, 30(3): 44-50.Yuan Yubo, Lu Yuping, Chen Jiulin, et al. Influence of add-assist circulation current at delta side on Y/delta transformer different protection[J]. Automation of Electric Power Systems, 2006, 30(3): 44-50.
[8] 尹项根, 曹文斌, 潘远林, 等. 高阻抗电力变压器涌流特性及其对保护影响的研究[J]. 电力系统保护与控制, 2018, 46(20): 1-11.Yin Xianggen, Cao Wenbin, Pan Yuanlin, et al. Inrush current characteristic of high-impedance transformers and its impact on protective relays[J]. Power System Protection and Control, 2018, 46(20): 1-11.
[9] 凌光, 姚文熙. Y/Δ接线变压器三角形侧环流计算新方法[J]. 电力自动化设备, 2015, 35(10): 157-162.Ling Guang, Yao Wenxi. Circulating current calculation for delta windings of transformer with Y/Δ connection[J]. Electric Power Automation Equipment,2015, 35(10): 157-162.
[10] 王雪, 王增平. 新型变压器三角形侧绕组环流计算方法[J]. 电力系统自动化, 2011, 35(24): 59-62.Wang Xue, Wang Zengping. A new method of calculating current in delta windings of transformers[J]. Automation of Electric Power Systems, 2011, 35(24): 59-62.
[11] 夏石伟, 郑涛. Y,d接线变压器三角形侧绕组中环流求取方法[J]. 电力系统自动化, 2008, 32(24): 60-64.Xia Shiwei, Zheng Tao. Calculation of circulating current in delta winding of transformers with Y,d connection[J]. Automation of Electric Power Systems,2008, 32(24): 60-64.
[12] 潘超, 衣双园, 蔡国伟, 等. 交直流混杂模式下变压器励磁-振动特性研究[J]. 电工技术学报, 2019,34(18): 3788-3796.Pan Chao, Yi Shuangyuan, Cai Guowei, et al.Excitation-vibration characteristics of transformer in AC-DC hybrid operation[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3788-3796.
[13] 潘超, 王格万, 蔡国伟, 等. 交直流混杂模式下变压器励磁电流谐波与箱体损耗映射研究[J]. 电工技术学报,2019, 34(13): 2830-2838.Pan Chao, Wang Gewan, Cai Guowei, et al. Research on maping from excitation current harmonic to tank loss for AC-DC hybrid operation of transformer[J].Transactions of China Electrotechnical Society, 2019,34(13): 2830-2838.
[14] 张学广, 张雅阁, 方冉, 等. 弱电网下双馈风电机组电网电压扰动补偿控制策略[J]. 电力系统自动化, 2020, 44(6): 146-159.Zhang Xueguang, Zhang Yage, Fang Ran, et al.Control strategy of disturbance compensation for grid voltage of DFIG based wind turbine in weak grid[J].Automation of Electric Power Systems, 2020, 44(6):146-159.
[15] 徐少博, 陈嘉敏, 徐永海, 等. 级联型电力电子变压器三相电压暂降隔离能力分析[J]. 电力系统自动化, 2020, 44(4): 168-183.Xu Shaobo, Chen Jiamin, Xu Yonghai, et al. Analysis of three-phase voltage sag isolation capability of cascaded power electronic transformer[J]. Automation of Electric Power Systems, 2020, 44(4): 168-183.
[16] 郑涛, 刘强, 夏石伟. 基于变压器回路方程的三角形侧绕组中环流求取新方法[J]. 电力系统自动化,2009, 33(15): 43-46, 111.Zheng Tao, Liu Qiang, Xia Shiwei. New calculation method of the circulating current in delta side based on voltage loop equation of transformer[J].Automation of Electric Power Systems, 2009, 33(15):43-46, 111.
[17] 毕大强, 梁武星, 柴建云, 等. 变压器三角形绕组中环流的构造方法[J]. 电力系统自动化, 2008,32(1): 39-43.Bi Daqiang, Liang Wuxing, Cai Jianyun, et al.Research on constructing algorithm of circulating current in delta winding of transformers[J].Automation of Electric Power Systems, 2008, 32(1):39-43.
[18] 李发海, 朱东起. 电机学[M]. 北京:科学出版社,2013.
[19] 王维俭.发电机变压器继电保护应用[M].北京:中国电力出版社,1998.
[20] Sonnemann W K, Wagner C L, Rockefeller G D.Magnetizing inrush phenomena in transformer banks[J]. Transactions of the American Institute of Electrical Engineers. Part III: Power Apparatus and Systems, 1958, 77(3): 884-892.
[21] Hamilton R. Analysis of transformer inrush current and comparison of harmonic restraint methods in transformer protection[J]. IEEE Transactions on Industry Applications, 2013, 49(4): 1890-1899.
[22] 王瑞田, 肖飞, 范学鑫, 等. 三电平移相全桥直流变换器的变压器直流偏置分析与抑制[J]. 电工技术学报, 2019, 34(16): 3345-3354.Wang Ruitian, Xiao Fei, Fan Xuexin, et al. Analysis and suppression of transformer DC-bias for DC-DC converter with three-level phase-shift full-bridge topology[J]. Transactions of China Electrotechnical Society, 2019, 34(16): 3345-3354.
[23] 焦在滨, 行武, 王钊, 等. 变压器励磁涌流负序二次谐波特征及机理[J]. 电力系统自动化, 2015,39(11): 146-151.Jiao Zaibin, Xing Wu, Wang Zhao, et al. Features and mechanism of negative-sequence second harmonics of magnetizing inrush current in transformers[J].Automation of Electric Power Systems, 2015, 39(11):146-151.
[24] Santagostino E C A G. Results of the inquiries on actual network conditions when switching magnetizing and small inductive and on transformer and shunt reactor saturation characteristics[J]. Electra, 1984(94):35-53.
[25] Brunke J H, Frohlich K J. Elimination of transformer inrush currents by controlled switching-part i:theoretical considerations[J]. IEEE Transactions on Power Delivery, 2001, 16(2): 276.
[26] 王育学, 曹文斌, 黄明辉, 等. 变压器零模涌流解析分析及其等值电路[J]. 电网技术, 2018, 42(12):3960-3968.Wang Yuxue, Cao Wenbin, Huang Minghui, et al.Mathematical analysis for zero-mode inrush current of transformer and its equivalent circuit[J]. Power System Technology, 2018, 42(12): 3960-3968.
[27] 尹项根, 曹文斌, 潘远林, 等. 高阻抗变压器零模涌流特性与动模试验研究[J]. 电力系统保护与控制, 2020, 48(5): 1-9.Yin Xianggen, Cao Wenbin, Pan Yuanlin, et al. Study on zero-mode inrush current characteristics and dynamic physical simulation tests of high-impedance transformer[J]. Power System Protection and Control,2020, 48(5): 1-9.