0 引言
一般金属构件的寿命周期可以分为早期的性能退化、损伤的起始与积累、断裂失效三个阶段[1]。由于拉伸、交变等载荷以及环境因素的作用,铝合金板材在其服役期间会出现诸如塑性变形和微裂纹等早期损伤[2-4]。由于塑性损伤(位错、滑移等)造成的缺陷在材料内部分布不均匀,使得声阻抗难以反映其变化。材料早期塑性损伤不会在信号传播过程中引起明显的反射和散射,同时对声速、衰减等线性特征参量的影响也不显著,常规的超声检测方法对于材料由塑性变形引起的早期力学性能退化检测困难。而非线性超声检测是利用微小缺陷对材料非线性的影响,其检测的特征参数不受限于缺陷的几何尺寸,被广泛应用于早期塑性损伤的检测[5-8]。
通过对材料力学的研究发现,材料的宏观力学性能与微观组织结构之间存在一定的内在联系。文献[9]提出了利用位错、滑移造成的累积塑性表征金属损伤程度的方法,该方法指出位错、滑移在晶界处的堆积使得位错附近产生局部非线性应力应变,进而导致在材料中传播的超声波产生高次谐波。文献[10]通过建立位错单极模型研究了位错密度、位错弦长度、应力大小和二次谐波幅值之间的关系。模型可以较好地表征由于单个位错引发二次谐波的原理,并且在位错密度小、位错弦长的单晶体材料中得到了很好的验证。文献[11]在位错单极模型的基础上建立了位错偶模型,通过进一步研究发现,在较大位错密度情况下,不但位错长度、应力大小会对二次谐波幅值产生明显影响,而且与位错在结构中的排列密切相关。位错单极模型、位错偶模型在某一程度上反映出超声非线性与材料的微观组织之间的关系,但是不能够完整地阐述二者之间的关系。基于以上两种模型,文献[12]从金属材料的塑性变形是位错动力学的结果出发,提出了一种预测非线性声学系数的方法,建立了弹塑性变形声学非线性系数的量化模型。该模型没有直接将声学非线性系数与位错结构联系起来,而是考虑位错的连续化,即塑性应变。采用塑性应变这一宏观力学参数表征位错信息,使位错演化与声学非线性之间建立间接联系,并利用晶体塑性理论对晶体金属累积塑性应变的演化进行了广泛研究。本文在弹塑性模型基础上进一步研究应力应变、塑性损伤、超声非线性系数三者之间的关系,利用声学非线性系数与塑性应变之间的关系模型,以期完整地表征材料力学全周期寿命。
在塑性损伤实验检测方面,文献[13-14]利用非线性Lamb波评价6061-T6和1100-H14铝合金薄板的塑性损伤情况,实验结果表明通过累积的二次谐波可以对材料结构损伤进行评价;文献[15]利用非线性纵波对 AZ31镁铝合金在拉伸载荷下的塑性变形进行了实验研究,验证了声学非线性参数(Acoustic Nonlinear Parameter, ANP)随塑性损伤单调增加;文献[16]针对 SS41钢的性能退化,利用非线性超声的方法进行检测,实验结果表明纵波非线性系数与产生塑性变形的加载应力呈等比关系;文献[17]利用激光表面波实现了对变形 2024-T4铝合金非线性系数的测量;文献[18]利用非线性电磁超声对铝合金拉伸变形进行评价,论证了电磁超声纵波基于非线性理论对塑性拉伸载荷变形评估的可行性。综上所述,基于二次谐波幅值的声学非线性系数能够作为表征铝合金塑性变形的特征参量。
电磁超声检测技术具有无需耦合剂、对材料表面要求较低和可重复性好等特点,在金属材料的非线性超声检测领域具有一定优势[19-22]。本文基于表面波波动方程以及非线性理论,建立电磁超声非线性弹塑性有限元时域仿真模型,并同时考虑表面波对塑性变形铝合金的非线性响应特性,建立应力应变-塑性损伤-超声非线性系数之间的关系,以期达到评估材料力学寿命的目的。
1 非线性电磁超声表面波检测的基本原理
当电磁超声换能器(Electromagnetic Acoustic Transducer, EMAT)激发的超声波通过应变大小不同的塑性区时,材料内部结构的非线性应力应变关系使得超声波发生非线性畸变,产生以二次谐波为主的高次谐波。
塑性变形属于材料硬化阶段的不可逆变形,位错结构自身周围的应力应变关系与周围区域紧密连接,因此表现为局部区域的非线性应力应变,使得传播至该局部区域的超声应力波产生非线性扰动,进而产生高次谐波。
固体介质的非线性应力应变关系可以表示为
式中,σ为应力;ε为应变;E为弹性模量;β和γ分别为二阶、三阶非线性弹性常数。
表面波是由非均匀纵波与横波叠加而成,位移分量可以分解成纵向分量和剪切分量。由于三阶弹性常数的对称性,各向同性材料中剪切波声学非线性消失,因此纵波分量是表面波中声学非线性的主要原因。
在一维、非线性介质应变较小情况下,应变与位移的关系可以表示为
式中,u(x,t)为x方向上的位移分量。
忽略散射和衰减的影响,波动方程可以表示为
式中,ρ为介质密度;(,)x tσ为x方向上的正应力。将式(1)、式(2)代入式(3),忽略二阶以上的高阶项,可得
根据微扰动解法,设
式中, 1(,)u x t为线性位移分量; 2(,)u x t为非线性位移分量。则波动方程的解近似为
式中, A1为基波幅值;ω为角频率;k为波数。令二次谐波幅值 A 2=β k2 A12 x/8,则非线性系数可表示为
当频率和传播距离一定时,可以简化相对非线性系数为
2 电磁超声非线性弹塑性建模与分析
2.1 弹塑性仿真模型的建立
本文采用COMSOL Multiphysics有限元仿真软件,根据弹塑性材料本构方程,建立电磁超声表面波时域仿真模型,如图1所示。仿真模型在多物理场耦合方面涉及电磁场、声场和力场三个物理场,其中,电磁场选择AC/DC模块的磁场,力场和声场选择固体力学模块;电磁场计算范围涵盖所有区域,而固体力学场仅计算铝板区域;将铝板下端面与两侧面设置为低反射边界,减少检测点波形信号中来自该边界的反射波的混合,从而降低模型的计算量,提高计算速度。在铝材的材料属性中选择塑性属性,与常规采用拟合函数作为材料硬化函数不同,本文通过导入实际应力应变曲线作为材料硬化函数,以拉伸距离为辅助扫描参数,改变材料内部塑性应变大小,模拟不同程度的塑性损伤。铝板的具体材料参数见表1。铝板和EMAT线圈之间的提离距离为0.2mm,铝板为100mm×10mm。永磁体剩余磁通密度为 1.2T,磁场方向竖直向下;空气域为18mm×8mm,相对磁导率为1,电导率为0。激发线圈频率为1.6MHz,表面波长λ=1.82mm,相邻曲折线圈间距d=λ/2。激发线圈具体参数见表2,激励电信号的激励电流幅值为30A。仿真模型不再设置接流信号采用汉宁窗函数调制的5个周期的tone-burst收端 EMAT,选择表面波的传播路径上的点(10,-0.1)作为观察点,研究该点的质点位移的时域信号波形,并通过傅里叶变换对其进行频谱分析。

图1 仿真模型示意图
Fig.1 Simulation model diagram
表1 铝板参数
Tab.1 Parameters of aluminum plate

参 数 数 值密度/(kg/m3) 2 700泊松比 0.33电导率/(S/m) 3.5×10-7弹性模量/Pa 7×1010相对磁导率 1
表2 EMAT线圈参数
Tab.2 Parameters of EMAT coil

参 数 数 值导线截面宽/mm 0.05导线截面长/mm 0.2线间距/mm 0.91磁导率/(H/m) 4π×10-7电导率/(S/m) 2.67×10-7
2.2 弹塑性模型仿真结果
曲折线圈在铝板内部产生的涡流分布如图2所示,可以看出两相导线下方感生的涡流方向相反,而且涡流主要集中分布在试件近表面,随试件深度的增加而迅速减小。
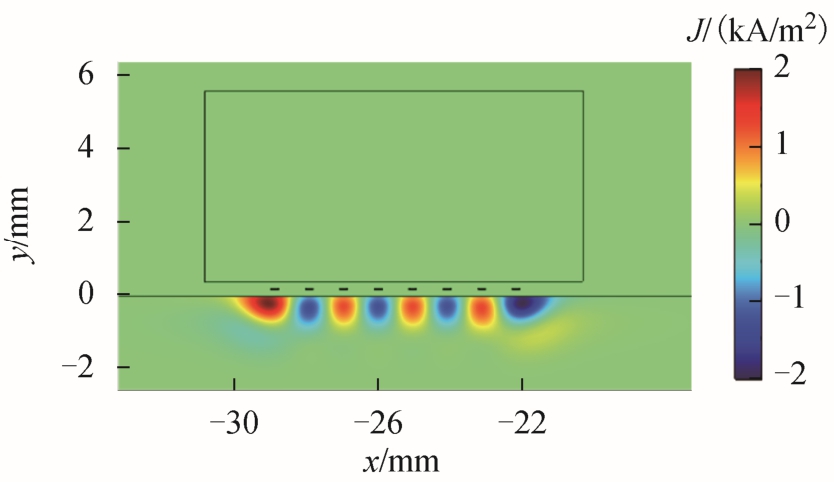
图2 t =65μs时刻涡流分布
Fig.2 Eddy current distribution at time t=65μs
图3 为铝板内质点的表面波面内位移分布图,可以看出曲折线圈EMAT可以在铝板中激发出表面波,其能量主要集中在距离试件约2mm(一个表面波长)深度范围内,同时也激发出在铝板内部传播的体波,但是其能量相较于表面波极其微弱。随着传播时间的增加,体波位移相较于表面波衰减很快。
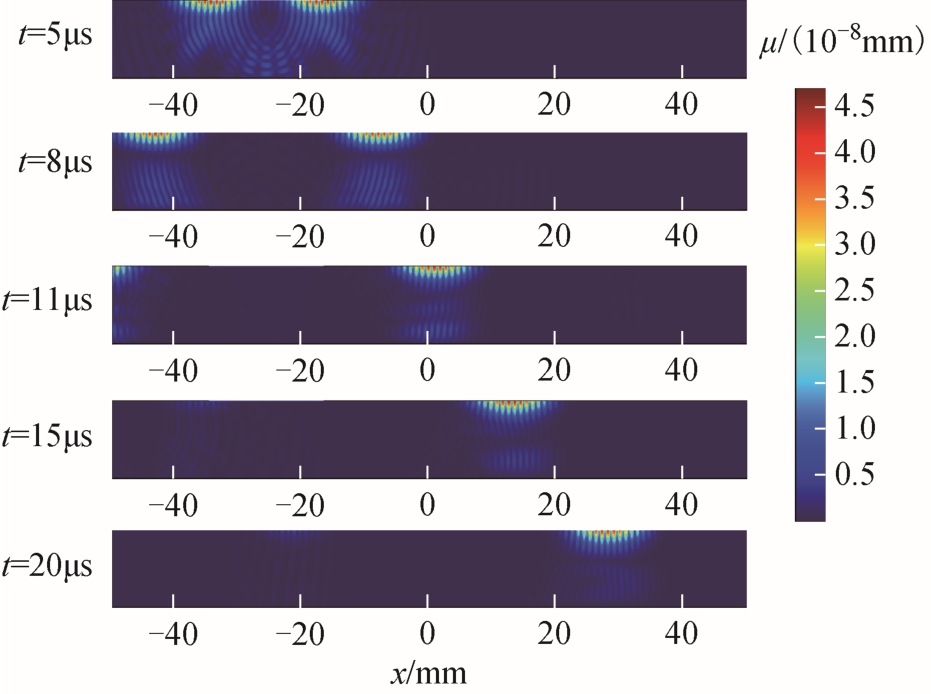
图3 不同时刻应力波在铝板中的传播情况
Fig.3 Propagation of stress wave in aluminum plates at different time
图 4为不同应变下铝板的内部应力变化。由图可知,随着应变量的增加,铝板内部应力不断增加,并在铝板中部出现颈缩现象,且应力在颈缩处集中。
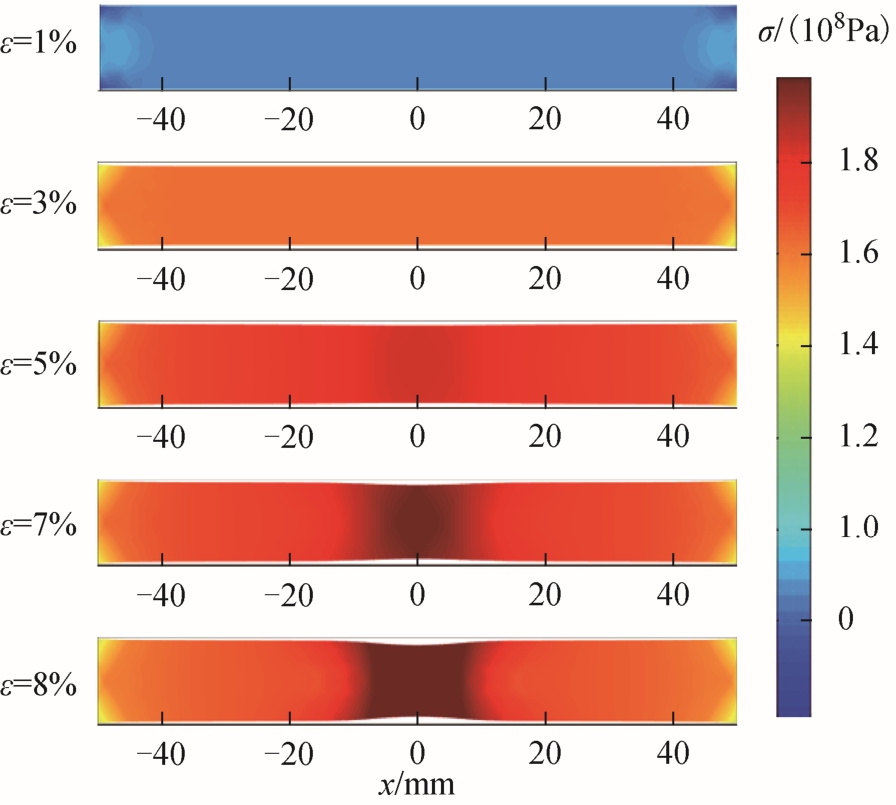
图4 不同应变下材料的内部应力变化
Fig.4 Internal stress changes of materials under different strains
图5 为不同拉伸位移参数下得到的应力应变曲线。由图5可知,在材料的弹性阶段和屈服硬化阶段,应力随应变分别呈近似线性增加(斜率不同);当材料内部应力达到屈服点应力时,塑性变形开始发生;当材料内部应力达到饱和流动应力后,材料中部出现颈缩现象,材料内部应力到达最大值并短暂保持不变。
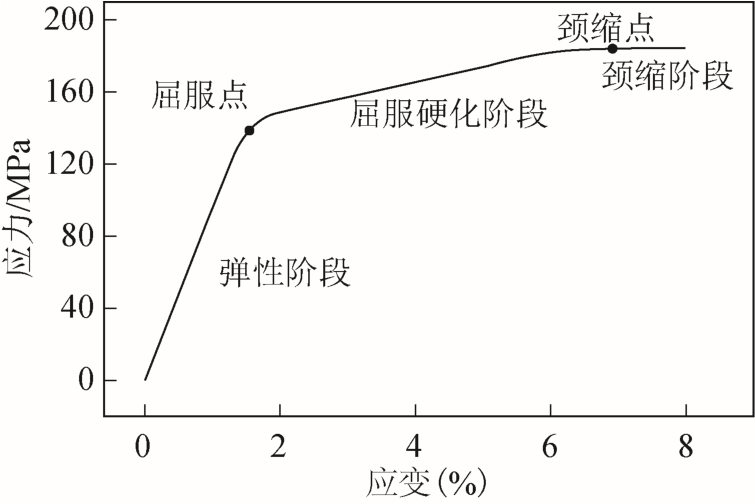
图5 应力应变曲线
Fig.5 Stress-strain curve
依据图5所示曲线,在0~8%应变范围内选取9个不同应变量,对拉伸到不同程度塑性应变的板材进行电磁超声检测,进而得到9组不同的时域波形,其中,图6为=6%ε时所采集到的时域波形。

图6 采集信号的时域波形(ε=6%)
Fig.6 Time domain waveform of acquisition signal(ε=6%)
对9组时域信号波形进行频域变换并提取基波和二次谐波幅值,分别绘制试件不同塑性损伤程度与表面波二次谐波幅值和相对非线性系数的关系曲线,具体结果如图7和图8所示。
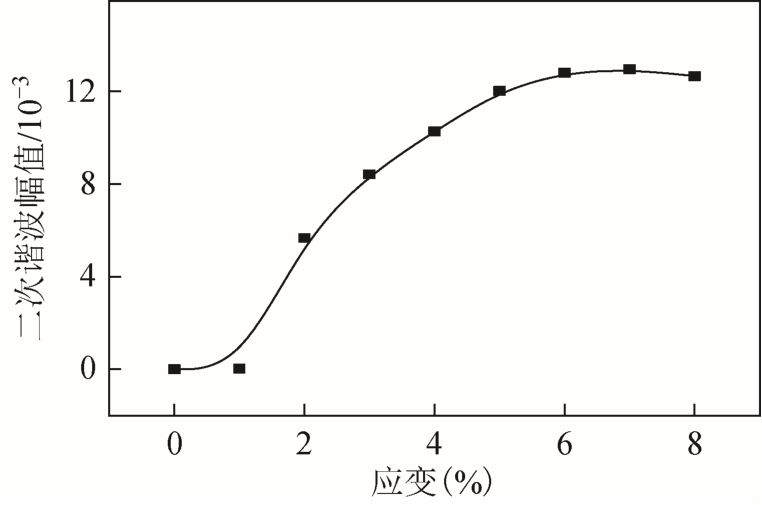
图7 不同应变程度下的二次谐波幅值
Fig.7 Second harmonic amplitude under different strain degree
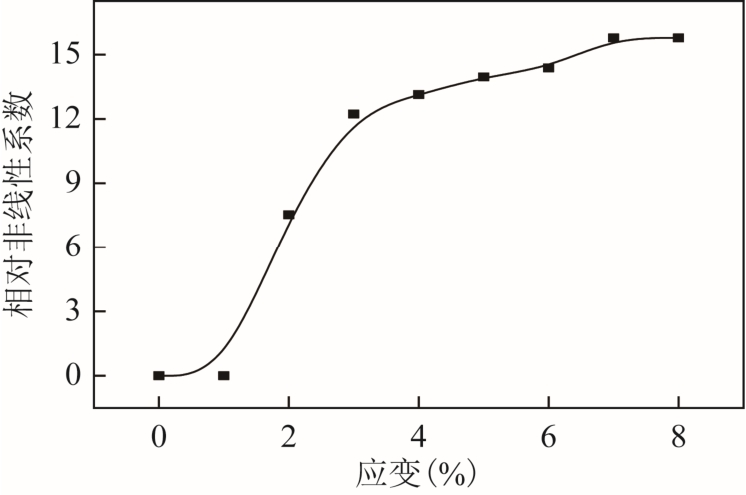
图8 不同应变程度下的相对非线性系数
Fig.8 Relative nonlinear parameter under different strain degree
由图7可知,在材料变形的弹性阶段,应变的增加并不会引起二次谐波幅值的明显变化;随着变形的加剧,材料内部应力迅速增长,超过材料本身屈服应力时塑性变形发生,二次谐波幅值随塑性应变不断增加,增长较为明显;在材料的屈服硬化阶段的后期,当材料表面出现颈缩时,应力增长放缓,二次谐波增幅也逐渐趋于平缓。
由图8不同应变程度下的相对非线性系数曲线可知,在材料变形的弹性阶段,相对非线性系数未出现明显上升,其值保持在较低水平;在材料的屈服硬化阶段,相对非线性系数随材料内部应力的增加增长迅速,虽然出现轻微波动,整体上仍呈增长趋势且增幅趋于平缓;当塑性应变的材料应力达到饱和流动应力时,结合图5可知铝板中部出现颈缩现象,应力在颈缩处集中但不再增加,相对非线性系数也保持相对平稳。
3 塑性损伤检测实验结果及分析
3.1 非线性电磁超声检测系统
在室温条件下,对厚度为 10mm的 6061铝合金材料按照GB/T 228.1—2010《金属材料拉伸试验第1部分:室温试验方法》制备拉伸试件[23]。制备试件的具体尺寸参数如图9所示。
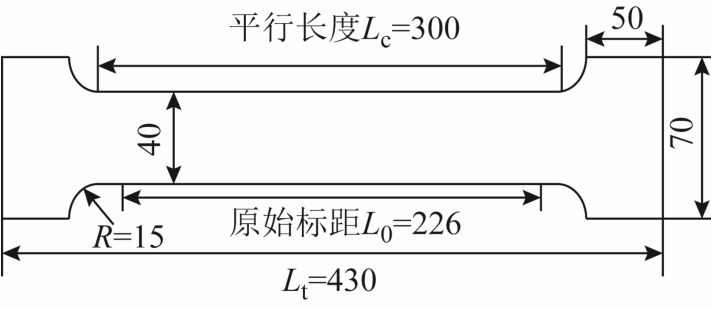
图9 标准试件尺寸示意图
Fig.9 Schematic diagram of standard specimen size
应用CMT-5205微机控制电子万能试验机对试件进行准静态拉伸,为保证加载处于准静态加载范畴,选用2.0mm/min的加载速率。为了使试件中间部分应力集中产生塑性变形,在试件中部预制一对长3mm、宽0.2mm的开口。本实验采用离线测量的方式,对加载至不同应变的标准试件卸载后进行非线性电磁超声检测。
非线性电磁超声检测系统包括激发端 EMAT、接收端PZT、Ritec-SNAP-5000、阻抗匹配电路、放大器、滤波器、示波器和被测试件,如图10所示。磁铁剩余磁通密度1.2T,激发线圈频率1.6MHz。
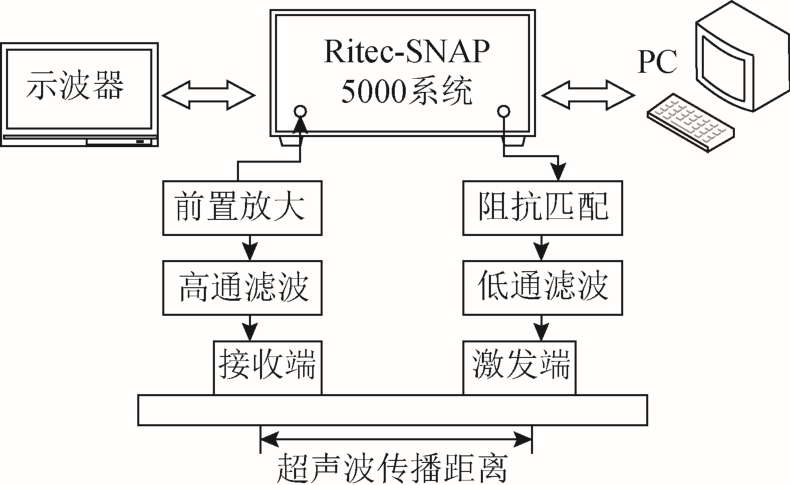
图10 非线性超声检测系统
Fig.10 Nonlinear acoustic detection system
实验设置七个试件,A0试件为完好试件,作为参考;A6试件为拉断试件,得到材料应力应变曲线如图11所示;A1~A5试件分别导入不同程度的拉伸变形,试件制作的具体参数见表3。
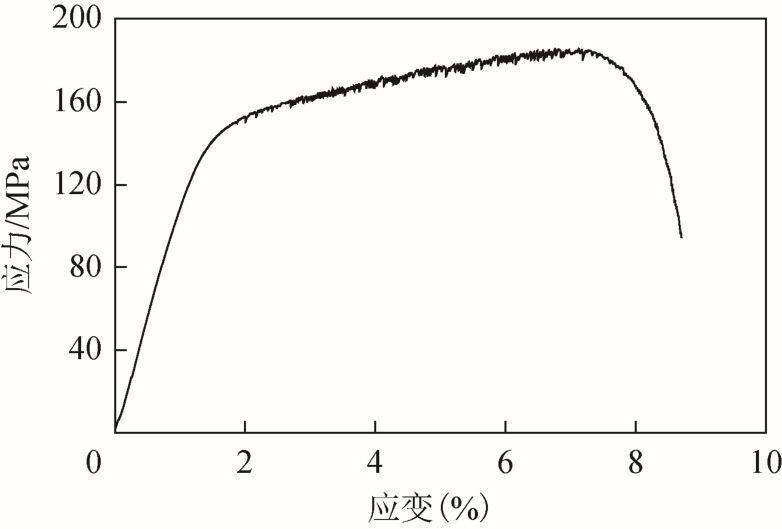
图11 拉伸断裂实测的应力应变曲线
Fig.11 Stress strain curve measured by tensile fracture
表3 不同应变试件制备参数
Tab.3 Preparation parameters of different strain specimens

试件编号拉伸载荷Fmax/kN 应力/MPa 应变(%) 加载速率/(mm/min)A0 0 0 0 0 A1 43.475 108.69 1 2 A2 64.531 161.33 3 2 A3 70.733 176.83 5 2 A4 73.297 183.24 7 2 A5 66.984 167.46 8 2 A6 37.768 94.42 8.7 2
为了消除波的重叠效应,同时考虑仿真与实验的良好对照,实验中激发信号为中心频率1.6MHz、5个周期的汉宁窗函数调制的tone-burst信号,激励电流信号波形如图12所示。

图12 激励电流信号波形
Fig.12 Waveform of excitation current signal
由于拉伸载荷的作用在材料中引入了非线性应力应变,当电磁超声换能器在试件趋肤层激发出的超声表面波进入被测铝板时,超声波将与材料非线性应力应变相互作用产生畸变,利用接收端表面波PZT探头采集畸变的超声波并对该信号波形进行结果分析。
3.2 检测结果分析
以不同塑性损伤的试件为样本,保持每个试件的检测位置完全一致,对试件进行三次实验,记录二次谐波幅值大小,实验结果取平均值。对接收端采集到的信号进行处理,采集除主冲击波外的第一个波形信号做频谱分析,提取信号频谱中的基波幅值与二次谐波幅值作为基本参量对相对非线性系数进行计算。
对采集到的时域波包数据进行频域变换。为了使得到的频域波形更加容易观测,分别对二次谐波部分进行了放大(如图13所示)和对Y轴取对数处理(如图14所示)。
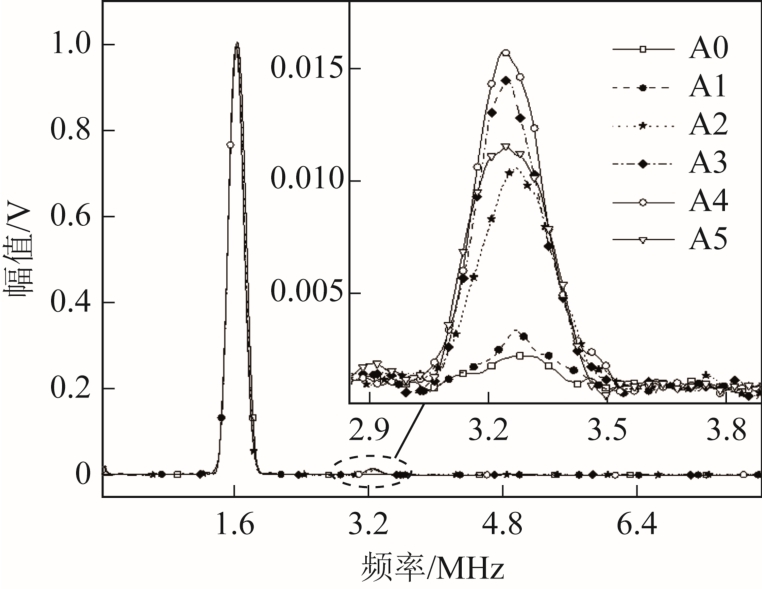
图13 归一化频谱幅值(局部放大)
Fig.13 Normalized spectral amplitude (local amplification)
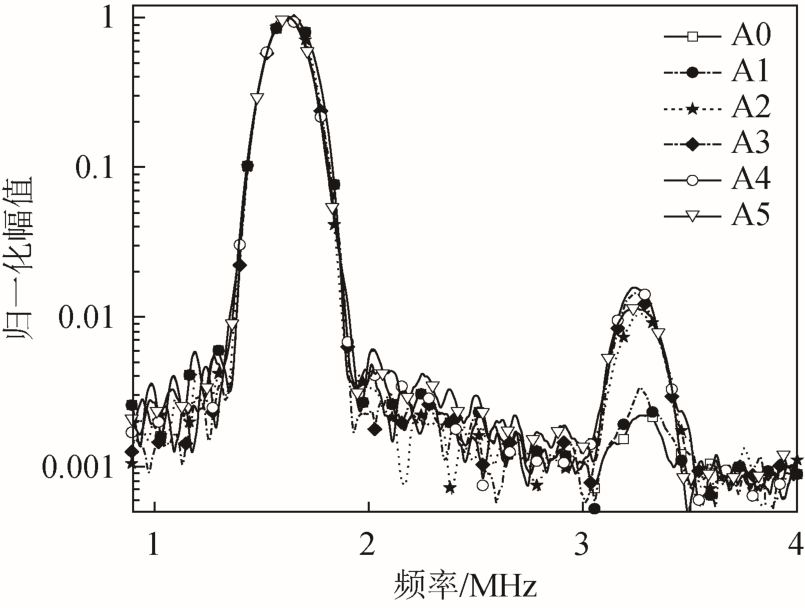
图14 归一化频谱幅值(Y轴取对数)
Fig.14 Normalized spectrum amplitude (logarithm of Y-axis)
图13 中,通过二次谐波放大图可以看出,在A0~A4试件中,随着塑性损伤程度的增加,二次谐波幅值逐渐增大;A5试件的二次谐波幅值较A3、A4试件明显减小。
图14中,为保持激励水平一致,对基波幅值进行了归一化处理。通过双Y轴取对数,使二次谐波幅值与基波幅值在同窗下可见。可以明显看出在A0~A4试件中二次谐波幅值随塑性损伤程度的增加而增加,在A5试件中二次谐波幅值明显降低。
对实验结果进一步分析,研究二次谐波幅值变化规律以及相对非线性系数与塑性损伤程度之间的关系,具体实验结果如图15和图16所示。

图15 不同塑性应变程度下的谐波幅值
Fig.15 Harmonic amplitude under different plastic strain degrees
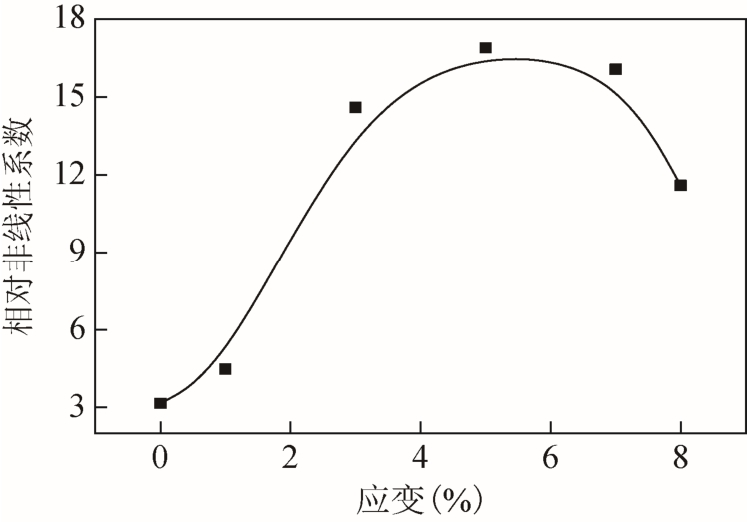
图16 不同塑性应变程度下相对非线性系数
Fig.16 Relative nonlinear coefficients under different plastic strain degrees
由图15可知,引入不同应变的塑性损伤试件的二次谐波幅值均高于完好试件,这是由于试件中的塑性损伤区域使得超声波在传播过程中产生了以二次谐波为主的高次谐波;在A1~A4试件中,随着塑性损伤程度的增加,超声波与材料中的非线性应力应变作用更加显著,使超声波产生的畸变也更加明显;A5试件由于拉伸中部出现较为明显颈缩,颈缩切面的空隙形成不连续微裂纹区域从而造成二次谐波幅值突然下降。
从图 16中不同塑性应变程度下的归一化相对非线性系数可以看出,在应变为0时(完好试件),相对非线性系数在较低水平并不为零,考虑到材料的制备、加工成型过程中可能存在夹杂、气泡等微小缺陷,因此会存在一定的固有非线性。在材料屈服硬化阶段早期(A1~A3试件),随着被测试件中导入塑性应变量的增大,相对非线性系数增长迅速;在材料屈服硬化阶段后期(A4试件),相对非线性系数不断趋于平缓,检测结果和仿真结果基本一致;在材料塑性应变程度超过7%时(A5试件),非线性系数突然减小。结合仿真(图5)与实测的应力应变图(图11)可以看出,当应变超过7%时,材料均出现颈缩现象,且实际铝合金试件中的应力也出现了突然下降,这是由于颈缩面内部微裂纹形成的不连续区域造成超声波能量损失,二次谐波幅值下降,进而导致了非线性系数的明显下降。
4 结论
1)根据弹塑性材料本构方程,建立了电磁超声非线性有限元仿真模型,与常规采用拟合函数作为材料硬化函数有所不同,本文通过导入实际应力-应变曲线作为材料硬化函数,通过改变材料内部塑性应变大小,模拟不同程度的塑性损伤。仿真分析结果表明:在材料的屈服硬化阶段,随着塑性损伤程度的增加,材料内部应力不断增加,超声二次谐波幅值增大,相对非线性系数增大。
2)搭建了非线性电磁超声表面波检测系统,对导入不同塑性变形的试件进行非线性检测。在材料屈服的硬化阶段早期(5%ε≤),随着被测试件中导入塑性应变量的增加,相对非线性系数增加迅速;在材料屈服硬化阶段后期(5%7%ε<≤),随塑性损伤程度的增加,相对非线性系数变化逐渐趋于平缓;在材料出现颈缩后(7%ε>),材料内部应力的降低导致相对非线性系数出现明显下降。据此,研究应力应变-塑性损伤-超声非线性系数之间的关系,可以对塑性损伤的变化情况进行有效监测,并进一步评估材料的力学寿命。
[1] 税国双, 汪越胜, 曲建民. 材料力学性能退化的超声无损检测与评价[J]. 力学进展, 2005, 35(1): 52-68.Shui Guoshuang, Wang Yusheng, Qu Jianmin.Advances in nondestructive test and evaluation of material degradation using nonlinear ultrasound [J].Progress in mechanics, 2005, 35(1): 52-68.
[2] Kim G, In C W, Kim J Y, et al. Air-coupled detection of nonlinear Rayleigh surface waves in concreteapplication to microcracking detection [J]. NDT & E International, 2014, 67(4): 64-70.
[3] 张剑锋, 轩福贞, 项延训. 材料损伤的非线性超声评价研究进展[J]. 科学通报, 2016, 61(14): 1536-1550.Zhang Jianfeng, Xuan Fuzhen, Xiang Yanxun.Evaluation of material damage using nonlinear ultrasonic wave[J]. Chinese Science Bulletin, 2016,61(14): 1536-1550.
[4] Matlack K H, Kim J Y, Jacobs L J, et al. Review of second harmonic generation measurement techniques for material state determination in metals [J]. Journal of Nondestructive Evaluation, 2015, 34(1): 273-296.
[5] 刘素贞, 庄东超, 商士博, 等. 高频涡流加载下闭合裂纹的动态响应特性[J]. 电工技术学报, 2015,30(18): 246-253.Liu Suzhen, Zhuang Dongchao, Shang Shibo, et al.Dynamic response characteristics of closed cracks under high frequency eddy current loading[J].Transactions of China Electrotechnical Society, 2015,30(18): 246-253.
[6] Jhang K Y. Nonlinear ultrasonic techniques for nondestructive assessment of micro damage in material: a review[J]. International Journal of Precision Engineering and Manufacturing, 2009, 10(1): 123-135.
[7] 张闯, 曹晓琳, 刘素贞, 等. 基于累积效应的铝材塑性损伤电磁超声非线性检测[J]. 电工技术学报,2019, 34(19): 3961-3967.Zhang Chuang, Cao Xiaolin, Liu Suzhen, et al.Electromagnetic ultrasonic nonlinear detection of aluminum with plastic damage based on cumulative effect[J]. Transaction of China Electrotechnical Society, 2019, 34(19): 3961-3967.
[8] 金亮, 寇晓斐, 郭富坤, 等. 基于电磁超声换能器的铁磁材料电磁声发射检测方法[J]. 电工技术学报, 2017, 32(18): 98-105.Jin Liang, Kou Xiaofei, Guo Fukun, et al.Electromagnetic acoustic emission detection method for ferromagnetic materials based on electromagnetic ultrasonic transducer[J]. Transactions of China Electrotechnical Society, 2017, 32(18): 98-105.
[9] Cantrell J H. Substructural organization, dislocation plasticity and harmonic generation in cyclically stressed wavy slip metals[J]. Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences, 2004, 460(2043): 757-780.
[10] Hikata A, Sewell F A, Elbaum C. Generation of ultrasonic second and third harmonics due to dislocations II[J]. Physical Review, 1966, 151(2): 442-449.
[11] Cantrell J H. Nonlinear dislocation dynamics at ultrasonic frequencies[J]. Journal of Applied Physics,2009, 105(4): 043520.
[12] Kim J Y, Qu Jianmin, Jacobs L J, et al. Acoustic nonlinearity parameter due to microplasticity[J]. Journal of Nondestructive Evaluation, 2006, 25(1): 28-36.
[13] Bermes C, Kim J Y, Qu Jianmin, et al. Nonlinear Lamb waves for the detection of material nonlinearity[J]. Mechanical Systems and Signal Processing, 2008, 22(3): 638-646.
[14] Pruell C, Kim J Y, Qu Jianmin, et al. A nonlinearguided wave technique for evaluating plasticitydriven material damage in a metal plate[J]. NDT&E International, 2009, 42(3): 199-203.
[15] Shui G, Wang Y S, Gong F. Evaluation of plastic damage for metallic materials under tensile load using nonlinear longitudinal waves[J]. NDT & E International,2013, 55: 1-8.
[16] Jhang K Y, Kim K C. Evaluation of material degradation using nonlinear acoustic effect[J].Ultrasonics, 1999, 37(1): 39-44.
[17] Choi S, Seo H, Jhang K Y. Noncontact evaluation of acoustic nonlinearity of a laser-generated surface wave in a plastically deformed aluminum alloy[J]. Research in Nondestructive Evaluation, 2015, 26(1): 13-22.
[18] 刘素贞, 李礼, 蔡智超, 等. 非线性电磁超声对铝合金拉伸变形评价研究[J]. 声学学报, 2017(1): 60-66.Liu Suzhen, Li li, Cai Zhichao, et al. Evaluation of tensile deformation of aluminum alloy by nonlinear electromagnetic ultrasound[J]. Acta Acustica, 2017(1):60-66.
[19] 吕敬祥, 刘国强. 磁声电无损检测及改进的EMD消噪方法[J]. 电工技术学报, 2018, 33(17): 3935-3942.Lü Jingxiang, Liu Guoqiang. Magnetoacousto electrical NDT and improved EMD de-noising algorithm[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 3935-3942.
[20] Xie Yuedong, Yin Liyuan, Liu Zenghua, et al. A novel variable-length meander-line-coil EMAT for side lobe suppression[J]. IEEE Sensors Journal, 2016, 16(16):6279-6287.
[21] 孙文秀, 刘国强, 夏慧, 等. 非铁磁材料的电磁超声接收过程数值模拟及实验研究[J]. 电工技术学报, 2018, 33(19): 4443-4449.Sun Wenxiu, Liu Guoqiang, Xia hui, et al. Numerical simulation and experimental study on electromagnetic ultrasonic receiving process of non-ferromagnetic materials[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4443-4449.
[22] Rueter D, Morgenstern T. Ultrasound generation with high power and coil only EMAT concepts[J].Ultrasonics, 2014, 54(8): 2141-2150.
[23] GBT 228.1—2010 金属材料 拉伸试验 第 1部分:室温试验方法[S]. 北京: 中国标准出版社, 2010.