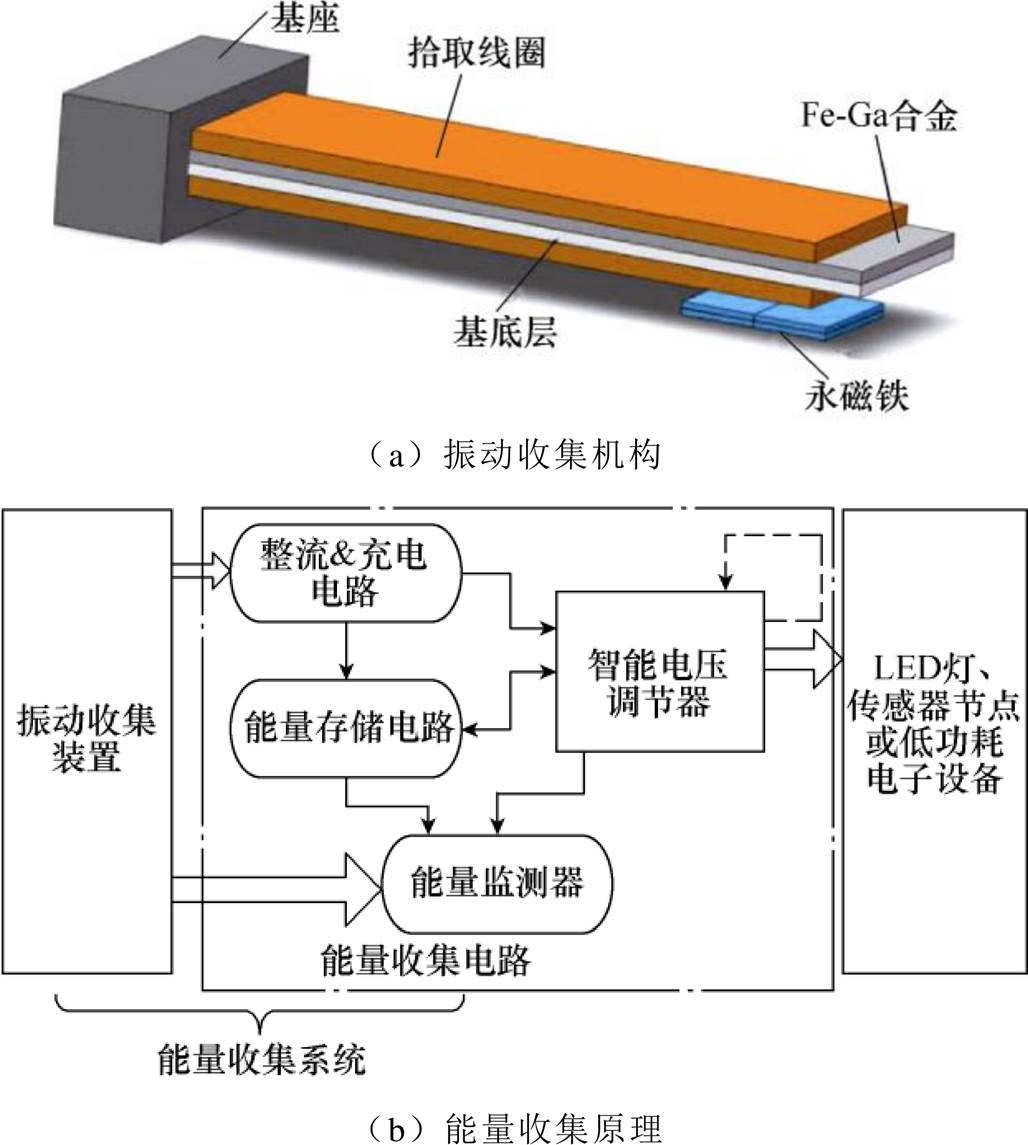
图1 悬臂式铁镓合金振动收集装置原理结构
Fig.1 Schematic diagram of cantilever gallium-iron alloy vibration collecting device
摘要 基于悬臂式铁镓合金的动力学模型、等效电路模型和伏安特性建立悬臂式铁镓合金振动能量收集装置的输出电压和输出功率模型，设计能量存储电路，搭建了铁镓合金振动能量收集装置实验平台。实验结果表明，在67Hz固有频率、外接17W 负载时，样机的最大输出功率为116mW，对应的功率密度约为271mW/cm3；电压智能调解电路的最大输出电压可保持在5.1V，且可为锂电池提供4.18V的充电电压，实验验证了振动收集装置的输出电压经过所设计的能量存储电路可有效地为超级电容器和锂电池充电，实现对能量的存储；样机可持续点亮LED灯和数码管，进一步证明了文中涉及的振动收集装置及存储电路的有效性，并为其在无线传感器节点供电中的实际应用提供了基础。
关键词：悬臂式 铁镓合金 振动能量收集 能量存储
振动能量收集技术属于利用环境废弃振动能量产生电能的研究领域，该研究可以应用于许多无需人工干涉即可长期运行的实际问题中，如无线传感器网络[1-2]、健康监测[3]、心脏起搏器[4]、自供电传感器[5]等。传统上，电池是此类设备的主要电源。然而，每年对数十亿个废弃电池的处置会引发严重的环境问题，并且有限的使用寿命对设备的长期、自主运行亦构成了挑战。因此，收集环境中的振动能源是实现便携式和无线电子设备可持续绿色供电的有效途径，该技术引起了学术界的广泛关注。压电及磁致伸缩等智能材料已经被证明能够依靠材料固有的特性实现对轮胎[6-8]、风[9]、人体运动[10]等形式的环境振动能量进行收集。压电材料振动能量收集是一种直接简单、较为流行的方法，其是通过正向压电效应将材料的应变能转化为电能[11]，由于无笨重的附件以及易于与微机电系统（Microelectro- mechanical System, MEMS）沉积融合的优势，目前对它的研究较为广泛。例如，Zhou Maoying等研究了一种基于压电复合材料的悬臂管流致振动的能量收集系统[12]。M. Febbo等提出了一种安装到轮毂上的压电片旋转能量回收系统，旨在为低频环境下的无线自主监测系统提供能量[13]。S. Orrego等提出了一种倒置压电旗子的风能收集系统，室外实验表明，所收集的环境风能能够为温度传感器进行有效的供电，该研究可能是能量收集装置首次在实际环境条件下使用。压电振动收集方法具有电容特性，可以产生较高输出电压和较低电流。另外，压电材料中也存在去极化、电荷泄漏、最佳输出功率需要很高匹配负载阻抗等缺点[14]。
为了克服这些局限性，近几年尝试基于磁致伸缩材料（Magnetostrictive Materials, MsM）的Villari效应[15]实现收集振动能量。基于MsM的能量收集方法是利用了其结构振荡所引起的磁场变化，进而在拾取线圈中产生电动势。近些年出现的磁致伸缩球墨铸铁合金（称为Galfenol）[16]和玻璃纤维金属化合物（例如Metglas）[17]等MsM具有高强度、优异的延展性、良好的鲁棒性、较高的饱和磁致伸缩系数和机电耦合系数，尤其是优异的可加工性。这为需要通过与弯曲结构灵活配合来完成振动能量收集提供了一种更合适的核心元件材料。并且，这些材料没有去极化问题，可显著提高系统运行的可靠性。然而，在低振动激励下时，磁致伸缩装置表现出几百毫伏的低电压和几十微瓦的低功率。因此，有必要设计一种高效的能量采集系统，以实现最大功率的跟踪与能量存储，以满足负载端的要求。课题组利用铁镓合金研制了一种悬臂式振动能量收集系统，可实现源于基极振动及瞬态自由振动的收集。本文针对此装置的特点，通过数学建模及实验的方式分析了系统的输出功率特性，在Multisim软件中设计并仿真了两种信号处理与能量收集电路，实验证明了该方法对电压整流及为超级电容和锂电池充电的有效性，并且通过利用样机持续点亮多个LED灯和数码管，验证振动收集装置的可持续发电能力及能量存储方法的有效性。
悬臂式铁镓合金振动收集装置原理结构如图1所示。基于悬臂式铁镓合金的振动能量收集装置有两个单元：一个是振动收集机构，包括铁镓MsM层，铁镓层粘合在基底上并由拾取线圈缠绕包裹，如图1a所示，该装置总体上是一个复合悬臂梁结构，铁镓层与基底以及拾取线圈层由3MDP100双组分环氧胶粘剂固化；另一个是能量收集和存储电路。铁镓合金的易磁化轴沿纵向，在压缩应力下对该材料进行应力退火，以提供内置的单轴各向异 性[18]，从而在压缩和拉伸应力下磁通量均能产生变化。当振动通过基座激励或自由激励作用在梁上时，该结构会像悬臂一样弯曲，即梁内产生弯曲应变和应力。弯曲引起的振动应变将通过Villari效应改变铁镓层的磁通量，由周期性弯曲变形引起的变化磁通量会通过法拉第电磁感应在拾取线圈上产生感应电压。最后，能量采集与存储电路将感应电压作为电能进行采集和存储，并根据电子元件的电压与功率要求向其供电，如图1b所示。
图1 悬臂式铁镓合金振动收集装置原理结构
Fig.1 Schematic diagram of cantilever gallium-iron alloy vibration collecting device
铁镓合金复合悬臂梁的机械结构与动力学结构简图如图2所示，悬臂梁长和宽分别为l和b，在基座施加的位移激励y(t)作用下，悬臂梁自由端所产生的位移为z(t)。基于平均应变，推导出等效系统单自由度质量-弹簧-阻尼近似模型（见图2b），该模型仅在基本固有频率范围内有效，当工作在更高频率时，需要研究更加严谨的模型。
图2 铁镓合金复合悬臂梁的机械与动力学结构简图
Fig.2 Mechanical and dynamic schematic diagram of gallium-iron alloy composite cantilever beam
根据建立的动力学模型，可得到悬臂梁自由的运动方程[19]为
（1）式中，M、c、K分别为等效质量、机械阻尼系数、弹簧刚度。
考虑磁场的作用。铁镓材料的应变、应力、磁场、磁感应强度间的关系用本构方程[21]表示为
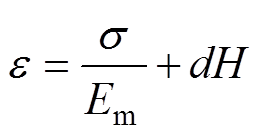（2）
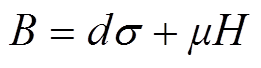（3）
式中，B为磁感应强度；H为磁场强度；m 为磁导率；d为磁致伸缩系数；Em为铁镓合金的杨氏模量；s 和e 分别为弯曲应力和应变。
悬臂梁的应力与应变关系由胡克定律表示为
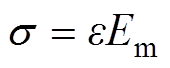（4）假设拾取线圈为理想的线圈，磁场强度与电流的关系可以由安培环路定律表示为
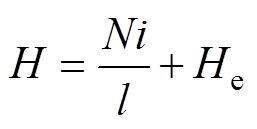（5）
式中，i为电流；N为线圈总匝数；He为直流偏置磁场。
当悬臂梁受外部激励作用产生弯曲形变时，铁镓合金中的磁感应强度将因磁畴偏转而发生变化，致使在其周围的拾取线圈中产生感应电压。
根据法拉第定律，拾取线圈无穷小部分（Dl）的电压[20]表示为
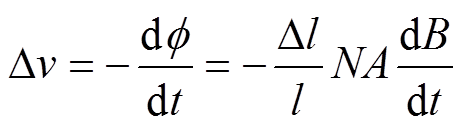（6）式中，A为线圈截面积；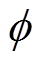
为穿过线圈的磁通；
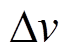为线圈无穷小部分的感应电压。
将式（2）、式（3）、式（5）代入式（6），并对式（6）在l范围内进行积分，得到拾取线圈的总输出电压为
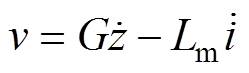（7）式中，G为悬臂梁的机电耦合系数；Lm为与铁镓合金层及线圈相关的等效电感，有
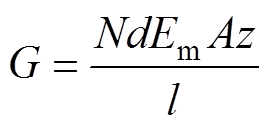（8）
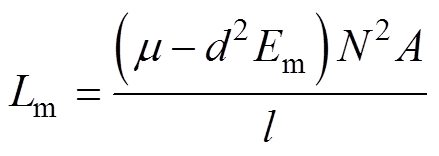（9）线圈中的电流为
（10）
式中，C为等效电容。
根据式（1）～式（7），在激励F作用下结构的运动方程写为
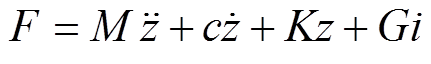（11）如果悬臂梁受到的基座振动激励是按简谐规律变化，则有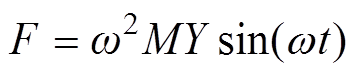
，其中，w 为悬臂梁的振动频率，Y为基座的位移。
将式（7）、式（10）和式（11）联立起来求解，得到输出电压的微分方程模型为
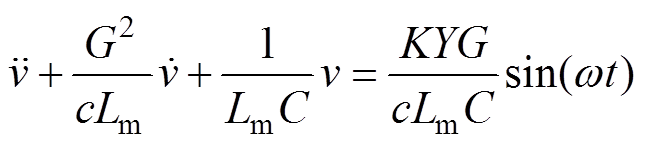（12）式（12）的初始条件为
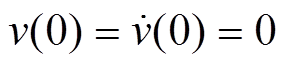
为了分析振动能量收集系统的输出功率特性，将式（1）与式（7）结合，建立能量收集系统的等效电路模型，如图3所示。左侧为机械部分，对应的机械阻抗为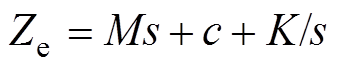
，
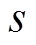为拉普拉斯变量；
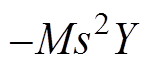为作用在基座上的力，即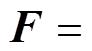
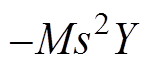。右侧为电学部分，
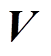和
分别为系统输出电压和电流。
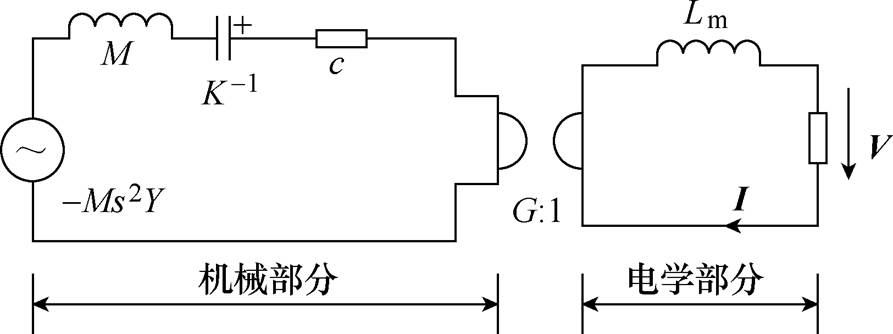
图3 能量收集装置的等效电路模型
Fig.3 Equivalent circuit model of energy collecting device
对上述等效电路模型中的输出力和电压分别建立微分方程，得到系统稳态方程的拉普拉斯表示形式[20]为
（13）式中，U为相对速度。
式（13）中有3个未知参数：、和
，为消除速度，给出了如图4所示的能量收集装置伏安特性。
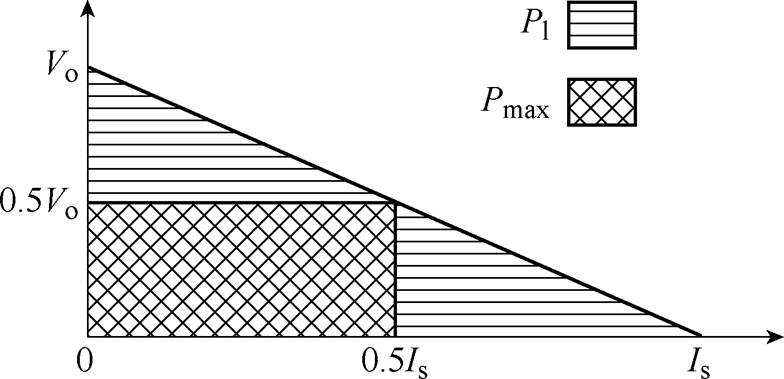
图4 能量收集装置的伏安特性
Fig.4 Volt-ampere characteristics of an energy collector
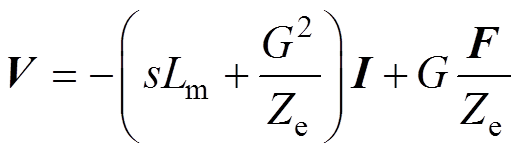（14）分别通过设置式（14）中的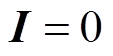
和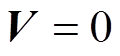
，得到系统输出的开路电压
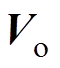和短路电流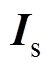
分别为
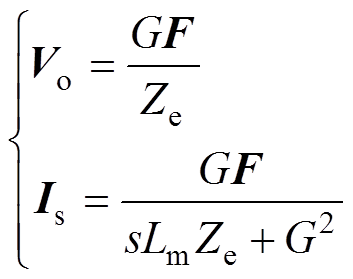（15）
机械输入功率Pe为
（16）当电流为零时，机械输入功率为
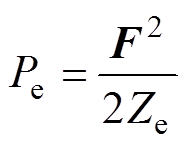（17）
在图4中，伏安特性线下的横线区域与电功率有关，由此得到输出电功率为
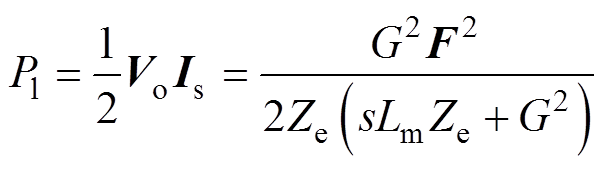（18）根据文献[21]，可知振动收集装置的机电耦合系数kg为
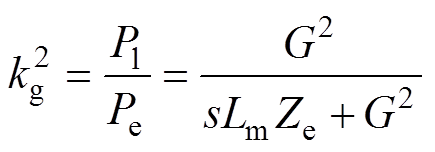（19）
通过改变图4伏安特性曲线中的斜线的斜率使下方矩形达到最大，得到收集装置的最大输出功率为
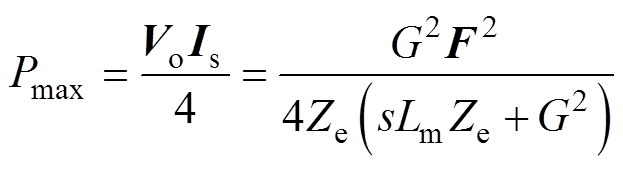（20）相应地，最优负载电阻为
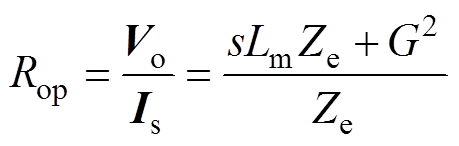（21）
铁镓合金能量收集装置所输出的电压通常不稳定且较低，因此需要对其进行整流滤波并将电能存储在储能元件中，进而根据电子元件要求向其供电。目前，主要利用超级电容器和锂电池两种方法存储电能。超级电容器的最大优势在于能够在很小体积情况下达到法拉级的电容量，但自放电特性较明显，且放电过程难于实现精准控制；而锂电池作为新型储能电池，其能量密度高、容量大，并且能够反复充放电。本文提出将上述两种储能方法结合，选用超级电容作为暂时存储元件，锂电池作为最终存储元件。本文所设计的铁镓合金能量存储电路原理如图5所示，其主要由四部分组成：倍压整流电路、超级电容、电压调节电路和储能管理电路。
振动能量收集装置中拾取线圈输出的交流电压通常很小，不足以为储能元件充电；并且，由于整流电路中的二极管自身存在正向电压降，导致全波或半波整流后的直流电压会更低。针对此问题，本文设计了一个四倍压整流电路，如图5中的第一个点画线框所示。当电压处于负半周时，二极管VD1和VD3工作，而VD2和VD4断开，此时电容C1和C3两端的电压等于电源电压Vm；当处于正半周时，C1和C3不能通过VD1和VD3进行放电，VD2导通，C1上的电压加到电源电压上，将C2充电到2Vm；同样地，C4亦被充电到2Vm；此时，C2和C4两端电压为4Vm，实现了四倍压整流过程。由此可见，文中设计的四倍压整流电路可实现整流、滤波，同时还具有放大提高输出直流电压的作用。
图5 信号处理与能量存储电路原理
Fig.5 Schematic diagram of signal processing and energy storage circuit
采用NI Multisim13.0仿真软件，对设计的四倍压整流电路进行仿真分析，仿真结果如图6所示。当收集装置产生0.5V交流电压时，经过整流后的直流电压理想输出应为2.0V（0.5V´4=2.0V），但事实上，稳态直流电压的仿真结果约为1.7V，这是由于二极管存在的正向电压降致使在整流过程中存在能量损耗所致。
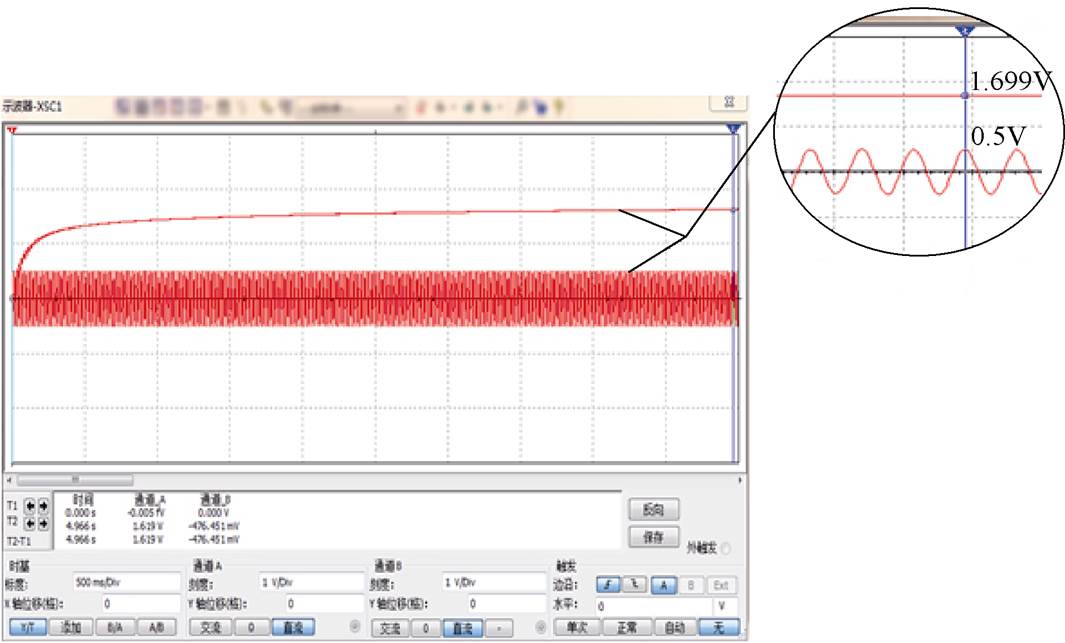
图6 能量收集装置输出电压的整流仿真结果
Fig.6 Rectifier simulation results of output voltage of energy collection device
为了进一步提升上述整流输出的稳定性及输出电压值，本文又利用美信公司生产的MAX1795芯片设计了二次升压稳压的智能电压调解电路，如图5中的第二个点画线框所示。它仅消耗25mA的静态电流和2mA的关断电流，其内部具有的同步整流器与MOSFET功率开关电阻可最低限度地降低能量损耗，转换效率高达95%。输出电压范围为+2.0～+5.5V，可利用电阻分压原理对输出电压值调节。输出电压与分压电阻R2和R3之间的关系为
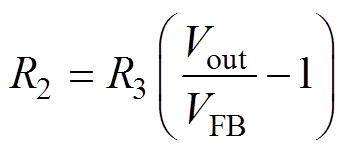（22）式中，Vout为输出电压值，参考电压值VFB=+1.245V，R3阻值应小于250kW，本文在实验过程中选取R3= 220kW；设定输出电压目标值Vout=5.1V（输入为510mV），由式（22）计算确定R2=680kW。
由于MAX1795的工作阈值为+0.85V，而能量装置输出的电压值取决于环境振动的实际情况，可能时大时小。因此，本文提出在智能电压调节电路的前端并联一个超级电容器C5，将一次整流后的电能暂存在C5中，当电压达到启动电压时，MAX1795即可正常工作进行二次升压稳压。另外，本文利用MAX1811芯片设计了锂电池储能管理电路，如图5中的第三个点画线框所示，用于为电能的最终存储提供恒压恒流。
图5中所设计的信号处理与能量存储电路经过印制电路板（Printed Circuit Board, PCB）设计与加工后，最终制作出的电路实物如图7所示，其尺寸为58mm×45mm。
图7 信号处理与能量存储电路实物（与一元硬币比较）
Fig.7 Physical diagram of signal processing and energy storage circuit (compared with one-dollar coin)
振动收集装置的结构参数是影响其能量收集性能的重要因素，包括核心材料铁镓合金梁的尺寸、基底弹性层与铁镓梁的布置形式、梁的尺寸、预磁化磁场的布置位置及方式等[22]，这些参数对系统工作性能的影响及系统性能优化设计将在另一篇文章里给予专门阐述。本文采用课题组已经设计的悬臂式铁镓振动能量收集装置进行实验，该装置的核心材料为薄片状铁镓合金，其尺寸为40mm´15mm´ 0.5mm；基底弹性层材料为铍铜，其尺寸为55mm´ 15mm´0.3mm；二者构成一个复合梁。拾取线圈缠绕在复合梁的外侧，匝数1 000匝，其绕线为0.15mm直径的铜漆包线，电阻为17W。预磁化磁场由方形钕铁硼提供，作用在铁镓合金周围的预磁化场强度约为48.73kA/m。
为验证对振动能量收集过程的模型预测、测试信号处理与能量存储电路对输出电压信号的整流性能及充放电过程，搭建了如图8所示的实验装置平台。关键的实验设备是一台JZK-20型电磁激振器，用于提供一个频率和激励幅值可控的机械能量源。振动收集装置样机通过基座与激振器的输出端连接。YE1311型函数信号发生器可产生任意频率的小幅值正弦信号，其输出信号经过YE5837A型功率放大器放大后，用于驱动激振器。激振器通过样机的基座向其施加振动激励，激励形式为加速度。CA-YD- 130型加速度传感器（频响范围2～5 000Hz，灵敏度为3pC/g）用于测量悬臂的加速度，悬臂梁自由端的位移通过非接触式激光位移传感器测得。示波器用来记录样机的加速度、输出电压以及电路板的输出电压信号。
图8 实验装置平台
Fig.8 Experimental device platform
在频率为80Hz的正弦振动激励下，测量了有无预磁化场时的振动收集装置输出电压，结果如图9所示。可以看出，随着振动加速度的增加，无论有、无预磁化场，输出电压都逐渐增大，并且其变化趋势亦相似。当振动幅度相同时，具有预磁化场的收集装置所产生的电压比无预磁化场的大很多，预磁化场对提高其振动收集能力具有很大的作用。以下实验均在带有该预磁化磁场的条件下进行。
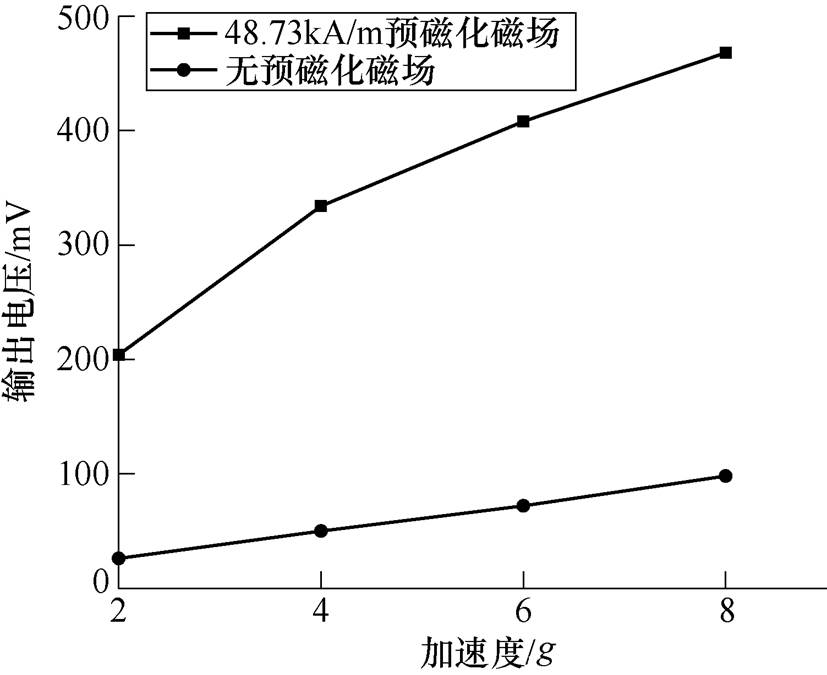
图9 有无预磁化场时的输出电压-振动加速度
Fig.9 Output voltage-vibration accelerationwith or without premagnetized field
在不同振动幅度条件下测量了40～110Hz范围内的输出电压值，实验结果如图10所示。输出电压值在大约67Hz的振动激励下达到了极大值，如图中虚线所示，该频率为系统的一阶谐振频率[22]，在谐振状态下其产生的电压最大，具有最佳的振动收集能力，能够将8g（g=9.8m/s2）的振动转换为约468mV的电压输出。另外，当振动幅度从2g增大到4g时，谐振处的最大电压由204mV增加到334mV，增幅达到63.73%；而当加速度从4g增加到6g，从6g增大到8g时，电压增幅分别约为22.16%和4.71%。可以看出，随着加速度的增大，输出电压的增加幅度相比于开始阶段下降很多，产生这种现象的原因可能是：加速度的增加导致了器件自身的结构阻尼和空气阻尼也在增大，减弱了器件的振动特性及铁镓合金梁内部的应变及应力，进而导致收集装置所产生的电压降低。由此得出如下结论，应使振动收集装置的谐振频率与环境振源的频率相一致，在未来，应进一步开展振动收集装置谐振频率的调整（调谐）方法。本文在后续的实验中，都是在一阶谐振频率下工作。
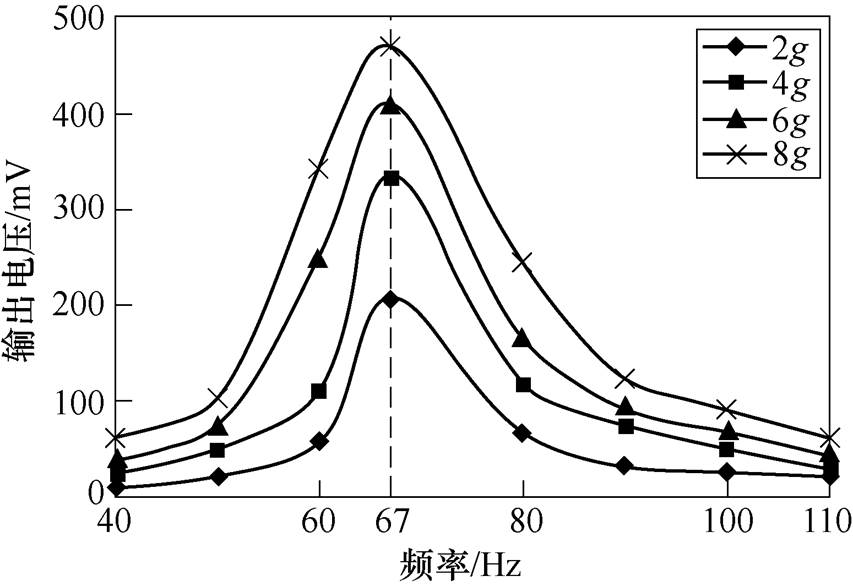
图10 输出电压峰-峰值的频率响应曲线
Fig.10 Frequency response curves of output voltage peak-peak
为了明确悬臂式铁镓合金振动能量收集装置为负载供电的特性，通过在拾取线圈两端连接1～100W 的纯电阻负载，测量分析了负载两端的工作电压及功率与外接负载之间的关系，如图11～图14所示。其中，由虚线所表示的理论值是通过上述模型预测得到的。从图11和图12看出，通过实验测得的电压值与模型预测得到的理论值之间存在着一定的误差，但误差较小，产生这种现象的原因可能是由实际测得的等效阻尼系数引起的。分析图13可知，负载两端电压随其阻值的增大而逐渐增大，最后趋于饱和稳定，负载电压的饱和值接近100mV。分析图14可知，作用在负载上的功率随着负载电阻的增加先逐渐增大，在17W 时的输出功率达到最大，再随着负载电阻的增大，功率逐渐降低。最大功率约为116mW，对应的功率密度约为271mW/cm3，与其匹配的最佳外接电阻值与拾取线圈的阻抗值基本相等（文中样机拾取线圈的电阻和电感分别为17W 和6.7mH）。由此可见，负载电阻对产生的功率有很大的影响，可以通过对负载电阻进行微调以提高输出功率。与压电式振动收集装置（＞1MW）相比，文中设计的铁镓振动收集装置的最佳电阻负载是一个非常小的值（小于100W）。因此，所设计的振动收集装置不适合于驱动高电阻负载，这与压电式收集装置恰好相反。
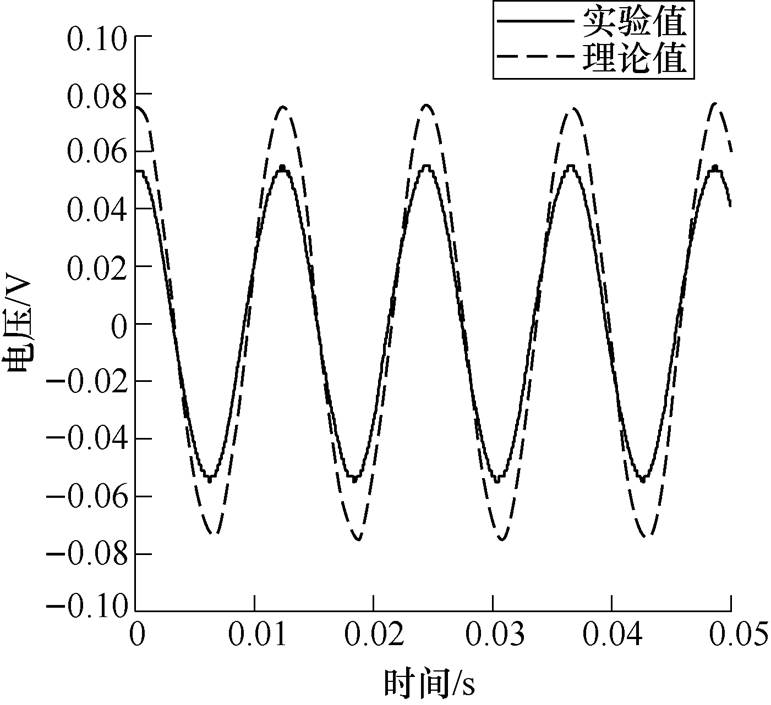
图11 外接33W 负载时输出电压的理论值与实验值对比
Fig.11 33Wexternal load when the output voltage of the theoretical value and experimental value contrast figure
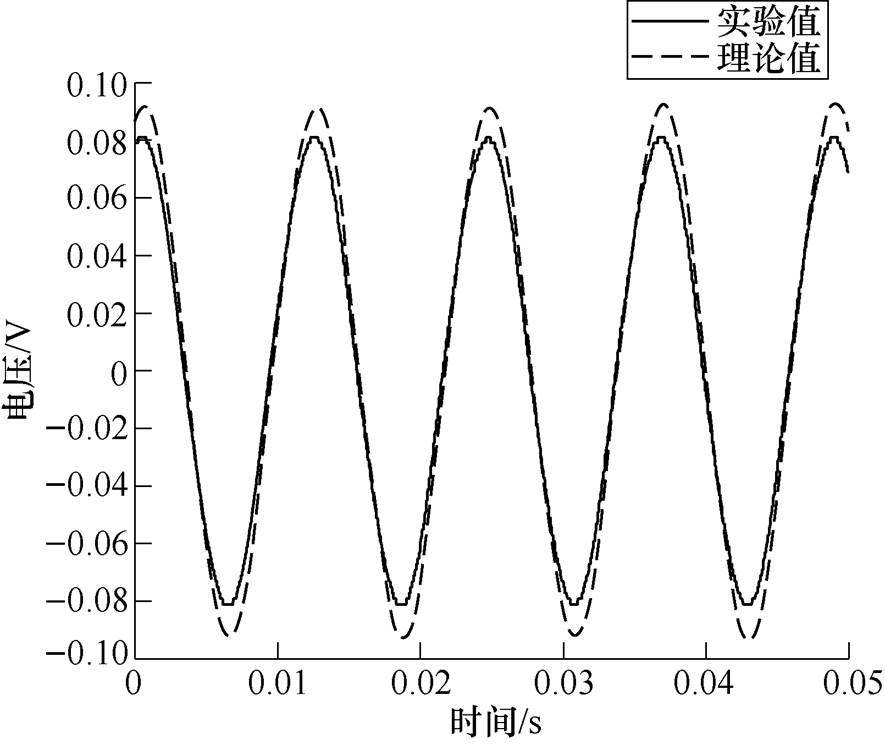
图12 外接75W 输出电压的理论值与实验值对比
Fig.12 75W external load when the output voltage of the theoretical value and experimental value contrast figure
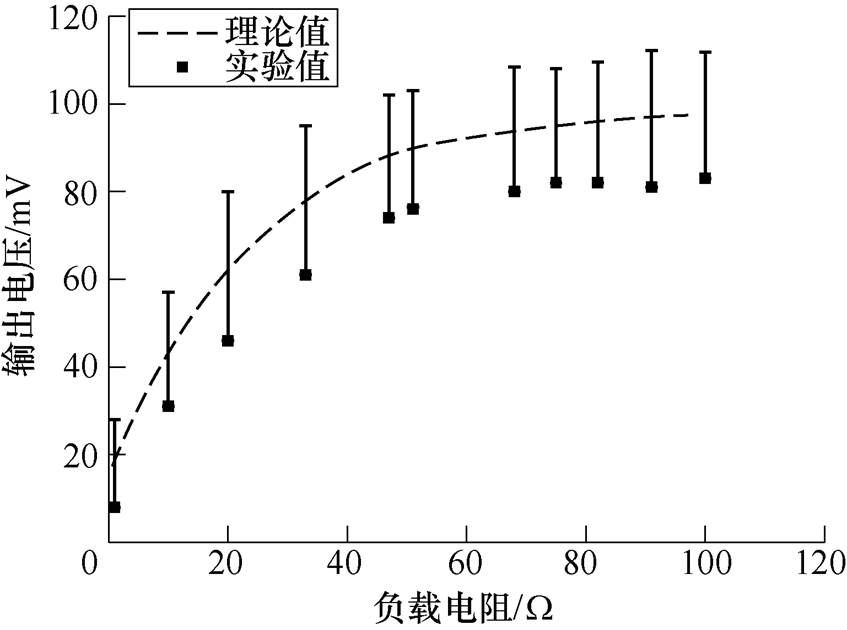
图13 输出电压与负载电阻的关系曲线（振动幅度为2g）
Fig.13 Relation curve between output voltage and load resistance (vibration amplitude is 2g)
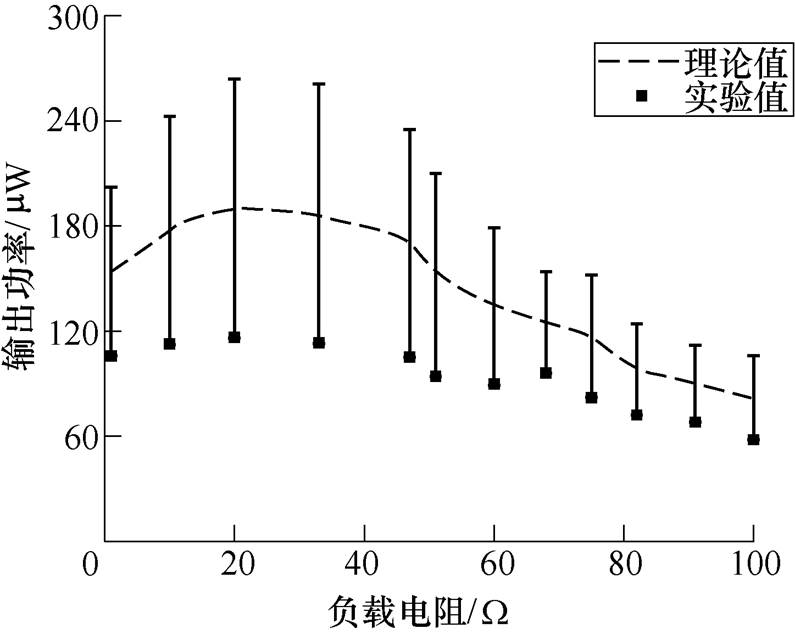
图14 输出功率与负载电阻的关系曲线
Fig.14 Relation curve between output power and load resistance
然而，该装置产生的电压低于二极管的正向电压降，直接将其应用于实际是不现实的，需要通过电压倍增器进行升压处理。
向样机施加幅度为9.4g的振动，对样机输出的电压利用倍压整流电路进行处理。图15显示了作用于收集装置上振动的加速度、拾取线圈的交流电压和四倍整流电路的直流输出的实测波形。从图中可以看出，振动收集装置输出的交流电压峰值为510mV，经过四倍压整流电路处理后，所输出的直流电压理论值应该为2.04V（用虚线表示），但是由于肖特基二极管1N5711存在着正向电压降，实际测得的直流电压电平约为1.6V（用点画线表示）。
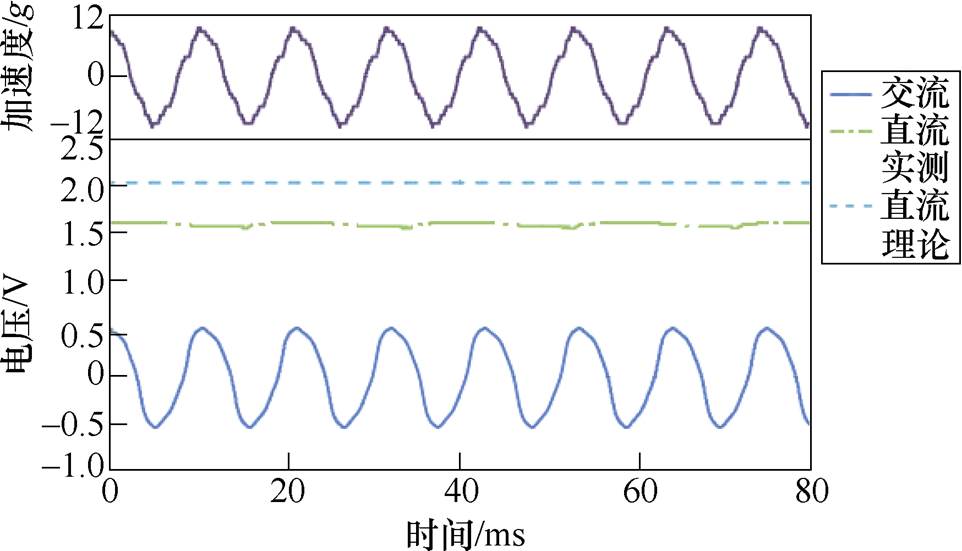
图15 收集装置的交流输出以及整流后的直流输出
Fig.15 AC output of collecting device and DC output after rectification
接下来针对振动收集装置对超级电容器的充电性能进行评估，并对智能电压调解电路的性能进行测试。在超级电容器C5上的电压达到1.6V后，通过在其后端接1kW 的负载电阻测量超级电容器的放电过程，得到的实验结果如图16所示。图16a显示了超级电容器的充/放电，图16b为对应智能电压调节器的直流电压输出。超级电容器电压在充电周期和放电周期内分别呈现指数增加和线性衰减的规律。当其两端电压高于0.9V时，电压智能调解芯片MAX1795开始自启动，输出电压保持在设定的目标值5.1V。当超级电容器的电压低于0.9V时，则电压智能调解芯片自动关断，避免了减小能量耗散。从两组曲线中可以看出，尽管超级电容器在充/放电过程中，其两端电压会出现波动变化，但只要电压高于0.9V（见图16a中实线），电压智能调解芯片的输出电压就会保持在某个恒定值（本文为5.1V）（见图16b中实线），直到超级电容器的电压小于0.9V。由于悬臂式铁镓振动能量收集装置从环境振动中收集所产生的电能量较小，因此使3F的超级电容器充满电大约需要3h。
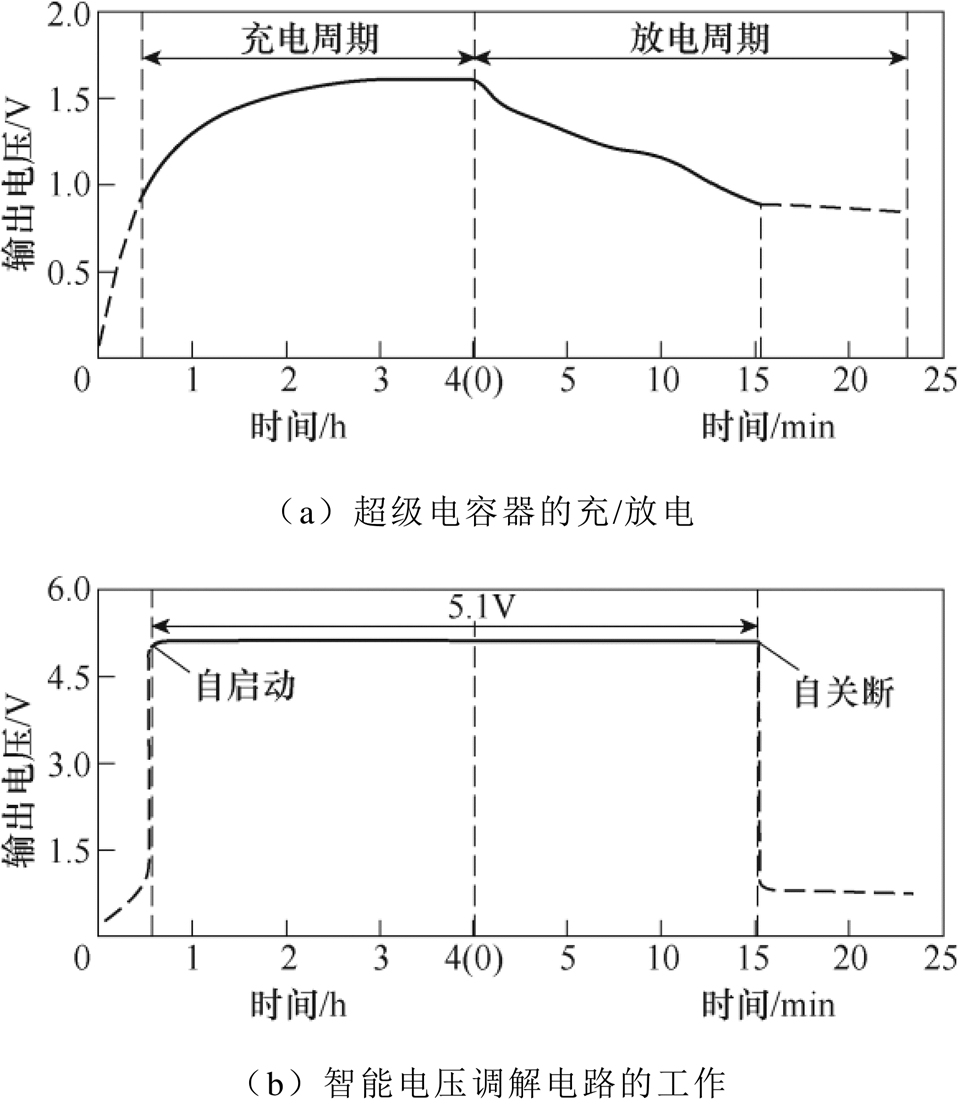
图16 超级电容器及智能电压调解电路的工作过程实验结果
Fig.16 Experimental results of working process of supercapacitor and intelligent voltage regulating circuit
将PCB电路连接在振动能量收集样机的两端，综合测试整个系统的输出电压特性，结果如图17所示。分析图17可知，振动能量收集样机收集振动后产生了0.51V的交流电，经四倍压整流电路整流成直流电后开始给超级电容器充电，大约需要3h充满至1.6V。当超级电容器电压高于0.9V时，电压智能调解芯片MAX1795和储能管理芯片MAX1811开始工作，测得能量存储电路所输出的电压为4.18V。此时，在能量存储电路后端连接一锂电池，即可为锂电池提供4.18V的充电电压，设定充电电流为100mA，使250mA·h 502030型号的锂电池完成充电大约需要4h。
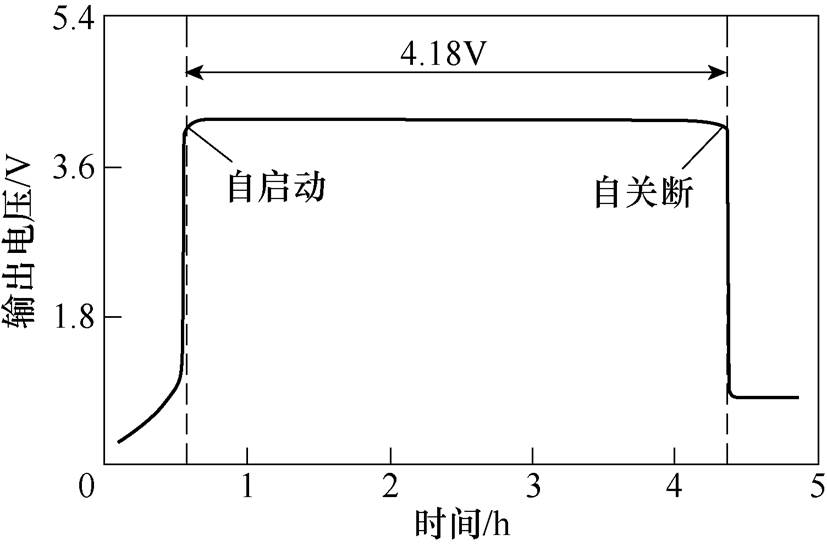
图17 能量存储电路的输出电压监测结果
Fig.17 Output voltage monitoring results of energy storage circuit
使用连接有PCB电路的振动能量收集样机系统所输出的直流电压为并联的低功耗LED灯和数码管供电，其实验结果如图18和图19所示。从图中可以看出，只要振动能量收集样机通过收集振动而产生的交流电压经过整流后达到0.9V以上，PCB电路即可正常工作，其输出的直流电成功地持续点亮了10个并联的红色LED灯或3个数码管。本实验验证了样机的发电能力及信号处理与能量存储电路的工作性能，并对悬臂式铁镓合金振动能量收集装置在LED指示装置、智能手机、智能手环、LED随身灯、无线传感器网络节点等方面的应用提出了思路。今后，课题组将进一步针对提高收集振动能力的性能优化、系统调谐等内容展开研究。
图18 样机为多个并联的LED灯供电
Fig.18 Prototype power supply for multiple parallel LED lights
图19 样机为多个数码管供电
Fig.19 Prototype power supply for multiple nixie tubes
1）将铁镓合金复合悬臂梁结构近似简化为单自由度质量-弹簧-阻尼系统，建立了悬臂式铁镓合金振动能量收集装置的输出电压模型，并依据其等效电路模型和伏安特性，对能量收集装置在外接负载电阻时的输出功率进行理论分析。
2）由于悬臂式铁镓合金振动能量收集装置产生的电压是交流电，并且电压较小，不能直接用于为电子元器件供电。针对此问题，设计了四倍压整流电路，用于对收集装置输出的交流电进行升压与整流；采用MAX1795和MAX1811芯片设计了电压调节电路和储能管理电路，进一步提高了直流输出电压，最大值可达到5.1V，同时可为超级电容器和锂电池充电，实现对能量的存储。
3）开发了悬臂式铁镓合金振动能量收集样机，并搭建了实验平台。综合测试了样机的发电能力与能量存储电路的性能，结果表明，样机系统输出的直流电能够持续点亮了多个并联LED灯或数码管，进一步验证了样机的发电能力及信号处理与能量存储电路的工作性能。
参考文献
[1] Deepak S, Amritesh O, Amol P B. Heterogeneity consideration in wireless sensor networks routing algorithms: a review[J]. The Journal of Supercom- puting, 2019, 75(5): 2341-2394.
[2] 赵军, 李乃梁, 王磊, 等. 电动汽车无线充电系统对人体及体内植入器件电磁安全研究[J]. 电工技术学报, 2018, 33(1): 27-33.
Zhao Jun, Li Nailiang, Wang Lei, et al. Research on electromagnetic safety of wirelesscharging system of electric vehicle to human body andimplanted device[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 27-33.
[3] Shi Shuxin, Yue Qiuqin, Zhang Zuwei. A self- powered engine health monitoring system based on L-shaped wideband piezoelectric energy harvester[J]. Micromachines, 2018, 9(12): 1-12.
[4] Alrashdan M H S, Hamzah A A, Majlis B. Design and optimization of cantilever based piezoelectric micro power generator for car diacpacemaker[J]. Microsystem Technologies-Micro-and Nanosystems-Information Storage and Processing Systems, 2015, 21(8): 1607- 1617.
[5] 李志. 基于自供电的无线传感器网络MAC层协议研究[D]. 南京: 南京航空航天大学, 2014.
[6] Liu Huifang, Wang Shijie, Zhang Yu. Study on the giant magnetostrictive vibration-power generation method for battery-less tire pressure monitoring system[J]. Proceedings of the Institution of Mechancial Engineers Part C-Journal of Mechancial Engineering Science, 2015, 229(9): 1639-1651.
[7] 菅新乐. 基于压电陶瓷的汽车轮胎压力监测系统无源化研究[D]. 吉林: 吉林大学, 2007.
[8] 罗洪波. 压电发电在汽车轮胎报警器上的应用基础研究[D]. 吉林: 吉林大学, 2008.
[9] 乔印虎. 压电板壳风力机叶片设计与振动控制研究[D]. 合肥: 合肥工业大学, 2014.
[10] Khan M B, Kim D H, Han J H, Performance improvement of flexible piezoelectric energy harvester for irregular human motion with energy extraction enhancement circuit[J]. Nano Energy, 2019, 58: 211-219.
[11] 王光庆, 徐文潭, 杨斌强. T型直线超声波电动机的运行机理及其特性分析[J]. 电工技术学报, 2017, 32(15): 111-119.
Wang Guangqing, Xu Wentan, Yang Binqiang. The operation mechanism and characteristic analysis of T-line ultrasonic motor[J]. Transactions of China Electrotechnical Society, 2017, 32(15): 111-119.
[12] Zhou Maoying, Al-Furjan M S H, Wang Ban. Modeling and efficiency analysis of a piezoelectric energy harvester based on the flow induced vibration of a piezoelectric composite pipe[J]. Sensors, 2018, 18(12): 1-15.
[13] Febbo M, Machado S P, Gatti C D, et al. An out- of-plane rotational energy harvesting system forlow frequency environments[J]. Energy Conversionand Management, 2017, 152(12): 166-175.
[14] Orrego S, Shoele K, Ruas A, et al. Harvesting ambient wind energy with an inverted piezoele- ctricflag[J]. Applied Energy, 2017, 194: 212-222.
[15] 赵争鸣, 王旭东. 电磁能量收集技术现状及发展趋势[J]. 电工技术学报, 2015, 30(13): 1-11.
Zhao Zhengming, Wang Xudong. Current situation and development trend of electromagneti energy collection technology[J]. Transactions of China Electrotechnical Society, 2015, 30(13): 1-11.
[16] 杨庆新, 阎荣格, 陈海燕. 新型高性能电工材料应用特性建模技术研究[J]. 电工技术学报, 2006, 21(1): 2-6.
Yang Qingxin, Yan Rongge, Chen Haiyan. Research on applied characteristic modeling technology of new high performance electrical materials[J]. Transa- ctions of China Electrotechnical Society, 2006, 21(1): 2-6.
[17] Vivek S, Geetha P, Saravanan V, et al. Magneto- electric coupling in strained strontium titanate and Metglas based magnetoelectric trilayer[J]. Journal of Alloys and Compounds, 2018, 789: 1056-1061.
[18] 贲彤, 陈龙, 阎荣格. 考虑磁化及磁致伸缩特性各向异性的感应电机铁心电磁应力分析[J]. 电工技术学报, 2019, 34(1): 67-74.
Ben Tong, Chen Long, Yan Rongge. Electromagnetic stress analysis of the core of an induction motor considering the anisotropy of magnetization and magnetostriction characteristics[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 67-74.
[19] Wang Lei, Yuan F G. Energy harvesting by magneto- strictive material (MsM) for powering wireless sensors in SHM[C]//International Symposium on: Smart Structures & Materials & Nondestructive Evaluation & Health Monitoring. International Society for Optics and Photonics, Carolina, USA, 2007: 1-12.
[20] 赵冉, 卢全国, 刘柳. 磁致伸缩悬臂梁振动能量采集器建模与仿真[J]. 南昌工程学院学报, 2016, 35(4): 10-12.
Zhao Ran, Lu Quanguo, Liu Liu. Modeling and simulation of vibration energy collector for magneto- strictive cantilever beam[J]. Journal of Nanchang Institute of Engineering, 2016, 35(4): 10-12.
[21] Wang Qingming, Du Xiaohong, Xu Baomin. Elec- tromechanical coupling and output efficiency of piezoelectric bending actuators[J]. IEEE Transa- ctionson Ultrasonics Ferroelectrics and Frequency Control, 1999, 46(3): 638-646.
[22] Liu Huifang, Chen Cong, Qiang Zhao. Comprehen- sive analysis of the energy harvesting performance of a Fe-Ga based cantilever harvester in free excitation and base excitation mode[J]. Sensors, 2019, 19(15): 1-25.
The Method of Vibration Energy Collection and Storage of Cantilever Gallium-Iron Alloy
Abstract Based on the dynamic model, equivalent circuit model and volt-ampere characteristics of the cantilever Gallium-iron alloy, the output voltage and output power models of the cantilever Gallium-iron alloy vibration energy collecting device were established, the energy storage circuit was designed, and the experimental platform of the Gallium-iron alloy vibration energy collecting device was built. The experimental results show that at the natural frequency of 67Hz and the external load of 17W, the maximum output power of the prototype is 116mW, and the corresponding power density is about 271mW/cm3. The maximum output voltage of the intelligent voltage mediation circuit can be maintained at 5.1V, and the charging voltage of 4.18V can be provided for the lithium battery. The experiment verifies that the output voltage of the vibration collection device can effectively charge the supercapacitor and lithium battery through the energy storage circuit designed in this paper, realizing the storage of energy. The prototype can continuously light up the LED lamp and digital tube, which further proves the effectiveness of the vibration collection device and storage circuit mentioned in this paper, and can provides the a basis for its practical application in the power supply of wireless sensor nodes.
keywords：Cantilever, gallium-iron alloy, vibration energy harvesting, energy storage
DOI: 10.19595/j.cnki.1000-6753.tces.190794
中图分类号：TM9
刘慧芳 女，1983年生，博士，副教授，博士生导师，主要研究方向为功能材料精密驱动与控制技术。E-mail: hfliu@sut.edu.cn
曹崇东 男，1995年生，硕士研究生，主要研究方向为功能材料精密驱动与控制技术。E-mail: caochongdong@126.com（通信作者）
收稿日期2019-06-28
改稿日期 2019-12-30
国家自然科学基金项目（51775354）、沈阳市高层次创新人才项目（RC180061）和辽宁省创新人才计划项目资助。
（编辑 崔文静）