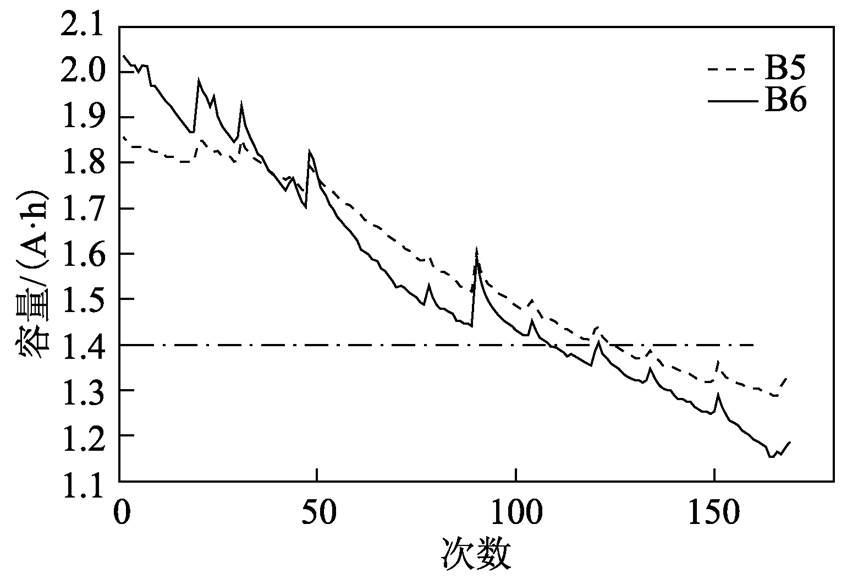
图1 B5和B6电池容量衰减曲线
Fig.1 The capacity decay curves of B5 and B6 batteries
摘要 随着电池使用次数的增加,电池会出现老化问题。通过对电池的剩余容量进行预测,可以为设备系统中电池管理系统提供可靠的数据支撑。该文采用支持向量机(SVM)对锂离子电池剩余容量进行预测,并采用改进鸡群算法(ICSO)对SVM参数进行优化,从而建立了ICSO-SVM预测模型。为验证预测模型的可行性,首先,采用db5小波对B5和B6电池容量衰减数据进行多尺度分解,进而重构去噪后的信号;其次,对鸡群优化算法(CSO)进行了改进,提出了ICSO优化算法,经测试ICSO算法的收敛精度明显高于粒子群优化算法(PSO)和传统CSO算法;最后,采用两组实验对CSO-SVM模型和ICSO-SVM模型进行验证。通过分析发现,ICSO-SVM模型的平均偏差(AAD)值在1.5%以下,RMSE值在2%以下,R2均值为0.972 6。
关键词:锂离子电池 支持向量机 优化算法 小波去噪 容量预测
锂离子电池由于其能量密度大、使用寿命长和绿色环保等优点被广泛应用于手机、计算机、电动汽车、航天等领域[1-3]。随着锂离子电池使用次数的增加,电池会出现老化问题,失效的电池将会影响设备的正常运行[4]。因此,锂离子电池的安全性和可靠性成为国内外学者研究的热点。通过对锂离子电池容量进行预测,及时发现失效的电池,可以有效降低由于电池失效带来的危害。
电池管理系统包括电压与电流测量、温度检测、荷电状态估计(State of Charge, SOC)和健康状态管理(State of Health, SOH)等功能[5-7]。常见的锂离子电池剩余容量预测方法有两种:一种是基于数据驱动的方法;另一种是基于模型的方法。由于锂电池具有复杂的电化学动态特性,基于模型的方法实现起来相对困难。基于数据驱动的预测方法不需要考虑锂电池复杂的电化学特性,通过直接测取的数据(电流、电压、内阻等参数)来反映锂电池的健康状态信息,从而实现锂电池的容量预测。且基于数据驱动的方法可以克服基于模型方法普适性差的缺点。
文献[8]提取了恒压充电曲线的几何特征,将其作为锂离子电池在不完全放电情况下的一种新的老化特征,并提出了一种基于量子粒子群优化支持向量机的锂电池容量估计框架,将提取的特征作为模型的输入。该方法可以不依赖完整的放电过程。文献[9]研究了磷酸铁锂电池的低温性能,并采用反向传播(Back Propagation, BP)神经网络模型对低温环境下的放电容量进行了预测。BP模型具有较强的非线性映射能力,但是BP模型存在局部最小化和收敛速度慢的缺点。文献[10]提出了一种新的基于数据驱动的锂离子电池剩余寿命预测方法,该方法将自动编码器与深度神经网络(Deep Neural Networks, DNN)相结合,采用自编码模型的多维特征提取方法用于模拟电池健康退化,采用DNN对锂离子电池剩余寿命进行预测。与支持向量机(Support Vector Machine, SVM)相比,DNN需要更
多的训练样本。文献[11]提出了一种基于高斯过程混合(Gaussian Processes Mixture, GPM)的新型锂离子电池容量预测方法。该方法采用不同的高斯过程回归(Gaussian Process Regression, GPR)模型拟合不同的轨迹段,从而可以揭示这些段之间的微小差异。相比SVM,GPM模型的建模过程更加复杂。文献[12]分析了放电时间、截止电流、开路电压与动力电池容量损耗之间的关系,并建立了电池容量损耗非线性模型对电池的容量进行预测。文献[13]采用极限学习机(Extreme Learning Machine, ELM)对锂离子电池寿命进行预测,并采用遗传蚂蚁算法对ELM的参数进行寻优。测试结果表明,相比BP方法,该方法预测更准确。与SVM相比,ELM的鲁棒性和预测稳定性较差。文献[14]采用改进鸟群优化算法(Improved Bird Swarm Algorithm, IBSA)对最小二乘支持向量机(Least Square Support Vector Machine, LSSVM)参数进行寻优,建立了IBSA- LSSVM预测模型对锂离子电池容量进行预测。但该方法没有对原始数据进行预处理,原始信号中的噪声信号会对预测效果产生一定影响。文献[15]提出锂电池健康状态离线预测方法,该方法不再依赖电池的历史充放电数据,构建了三种健康因子,分别为均值内阻、最小内阻和内阻-SOC 曲线,同时建立了三种健康寿命模型,实现了对不同锂电池健康状态的预测。
通过分析上述文献中提出的预测方法发现,有的预测模型对样本数的依赖性较强,有的预测模型在预测前并没有对数据进行预处理,还有的预测模型本身鲁棒性和预测稳定性较差。针对以上方法的不足,本文建立了改进鸡群优化(Improve Chicken Swarm Optimization, ICSO)-SVM预测模型对电池的剩余寿命进行预测。SVM本身具有较强的非线性映射能力、良好的“鲁棒性”和适用于小样本的优点。通过ICSO算法对SVM的超参数进行寻优得到ICSO-SVM模型。相比其他传统预测模型,ICSO- SVM模型具有预测可靠性高且需要训练样本少的优点。首先,对鸡群优化算法(Chicken Swarm Optimization, CSO)进行了改进,引入了ICSO优化算法。其次,采用db5小波对B5和B6电池容量衰减数据进行去噪,通过对原始数据中的噪声信号进行抑制,从而减少噪声信号对预测精度的影响。最后,采用两组实验对CSO-SVM模型和ICSO-SVM模型进行测试,验证两个模型的可行性。
本文采用NASA PCoE研究中心提供的锂离子电池数据。选取的电池型号分别为B5和B6。B5和B6两个型号电池的额定容量为2A·h。实验测试在25℃恒温下进行,具体的实验步骤如下:
(1)首先对B5和B6电池进行恒流恒压充电。电池的充电电流为1.5A,充电电压为4.2V。
(2)然后对B5和B6电池进行恒流放电。B5和B6电池的放电电流为2A,B5、B6电池的放电截止电压分别为2.7V、2.5V。B5和B6电池的容量衰减曲线如图1所示。

图1 B5和B6电池容量衰减曲线
Fig.1 The capacity decay curves of B5 and B6 batteries
如图1所示,B5和B6电池的容量衰减轨迹并不是平滑的曲线,衰减曲线上存在尖点。其中点画线表示B5和B6电池的失效阈值。
通过实验获取锂离子电池容量衰减数据是寿命预测的第一步,同时也是最关键的一步。由于在实验过程中受室内温度变化、放电倍率、充电电压等因素的影响,锂离子电池容量衰减数据中夹杂着一些噪声信号。如果不对原始数据进行预处理,直接用原始数据进行训练和预测,则会影响模型的预测精度。因此,在进行寿命预测之前,要对数据进行预处理,去除电池容量衰减数据中的噪声信号。
传统的滤波方法主要有线性滤波方法和非线性滤波方法,如中值滤波、Wiener滤波等。传统的滤波方法只能将信号全部变换到时域或全部变换到频域,无法描述信号的非平稳特性,且无法得到信号的相关性。小波变换具有良好时域特性和频域特性,并且具有低熵性、多分辨率、小波基选择多样性和去相关性等优点。因此,小波变换被广泛应用在降噪领域[16-19]。
小波降噪流程如下:
(1)利用小波基函数将含噪信号进行分解,分解为高频信号和低频信号。一般情况下低频信号为真实信号,高频信号为噪声信号。
(2)对高频信号进行阈值处理。
(3)小波重构并输出降噪后的信号。
本文选用db5小波作为小波基函数。db5小波是一种常用的小波变换,具有计算简单的优点。采用db5将原始信号分解成三层,并且采用启发式阈值和软阈值函数。
采用db5小波对B5和B6电池数据进行去噪,去噪后的容量衰减曲线如图2所示。小波去噪并没有破坏数据的原始特征,去噪后的数据保留了原始数据的尖峰点。相比于原始数据,去噪后的容量衰减数据更加平滑。小波去噪在最大程度保留原始数据真实性的同时去除了原始数据中的噪声信号。
SVM是基于统计学习理论,对结构风险最小化的近似实现[20-23]。
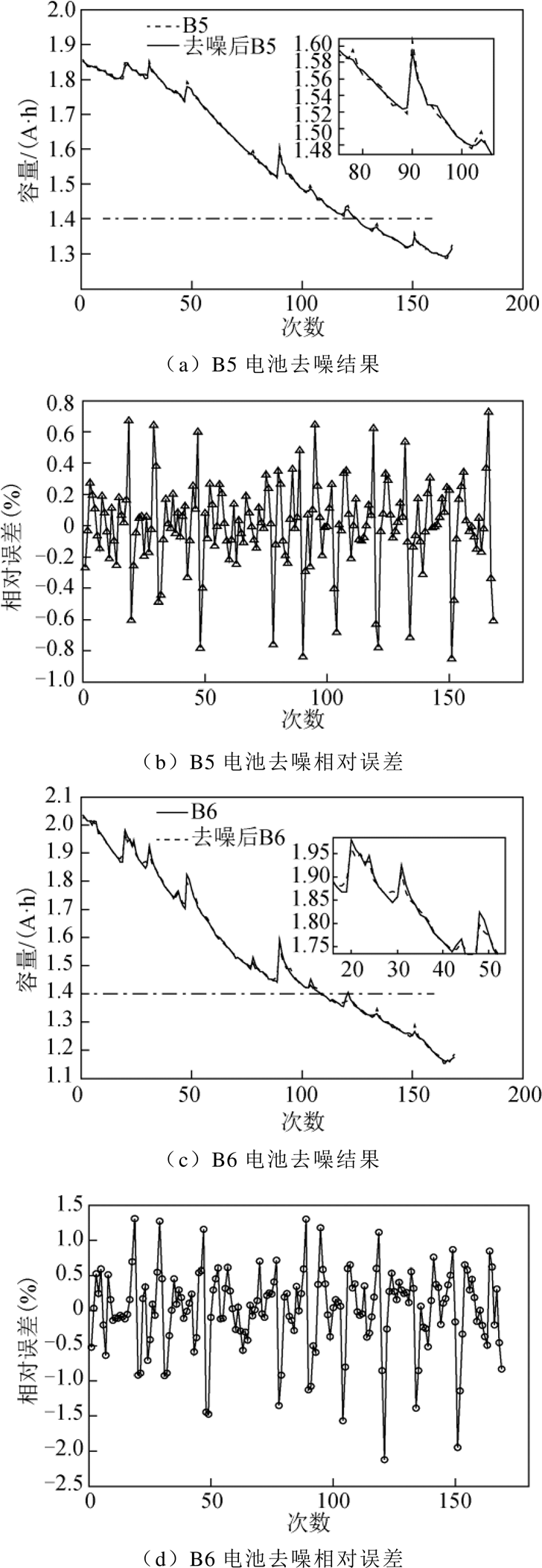
图2 db5小波去噪结果
Fig.2 db5 wavelet denoising
设样本集为
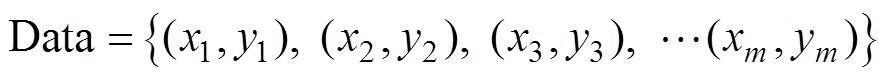
式中,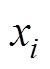 为第
为第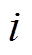 个样本输入值,
个样本输入值,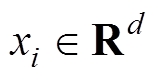 ;
;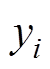 为第
为第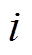 个样本输出值,
个样本输出值,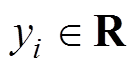 。SVM的回归函数为
。SVM的回归函数为
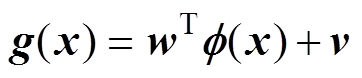 (1)
(1)
式中,w为权值;f(×)为映射函数,将输入映射到高维空间;v为偏移量。
建立拉格朗日函数[24-25]为
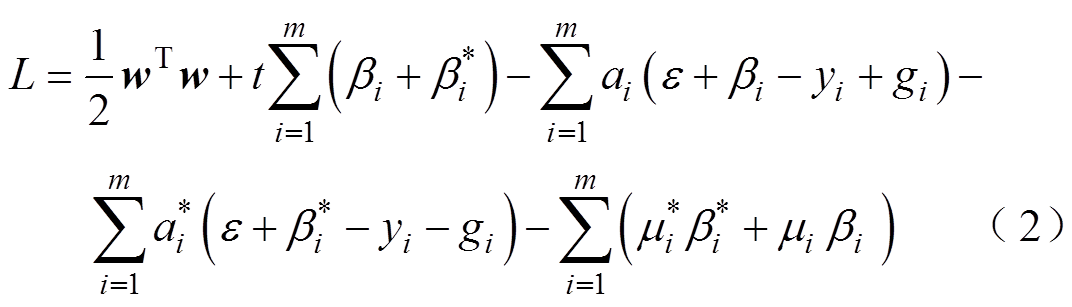
式中,ai和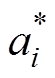 为拉格朗日乘子;t为惩罚参数;
为拉格朗日乘子;t为惩罚参数;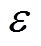 为不敏感损失函数;b 为松弛变量。
为不敏感损失函数;b 为松弛变量。
最终得到回归函数[26]为
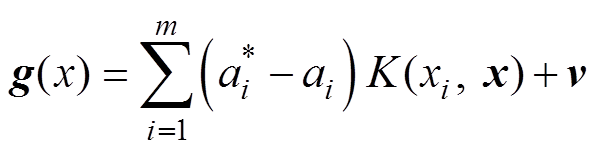 (3)
(3)式中,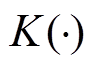 为核函数。本文采用径向基核函数,其计算式为
为核函数。本文采用径向基核函数,其计算式为
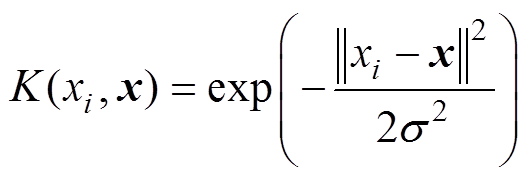 (4)
(4)
式中,s 为核宽度。
在SVM中,核宽度s 和惩罚系数t对回归效果有较大的影响。SVM中的惩罚参数t主要用来对支持向量的复杂度与误差率进行平衡。当t较大时,支持向量增加,导致模型变复杂;当t较小时,支持向量减少,模型变简单。核宽度s 主要反映了单个样本对超平面的影响。当s 较小时,单个样本对超平面的影响较小;当s 较大时,单个样本对超平面的影响增大。
如果核宽度s 和惩罚系数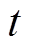 选取不合适会使回归效果变差。因此,为找到合适的核宽度s 和惩罚系数
选取不合适会使回归效果变差。因此,为找到合适的核宽度s 和惩罚系数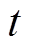 ,采用优化算法对核宽度s 和惩罚系数
,采用优化算法对核宽度s 和惩罚系数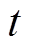 进行寻优。
进行寻优。
文献[27]于2014年提出了鸡群优化算法(CSO)。CSO算法模拟了鸡群的等级制度及觅食行为。
第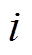 只公鸡在第
只公鸡在第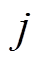 维空间的觅食位置为[28-30]
维空间的觅食位置为[28-30]
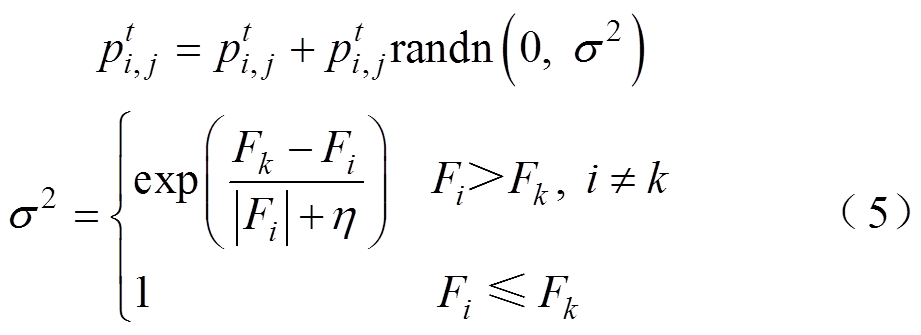
式中,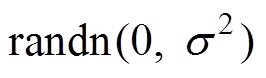 为高斯分布,其均值为0,标准差为
为高斯分布,其均值为0,标准差为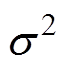 ;
;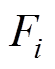 为第
为第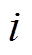 只公鸡的适应度值;
只公鸡的适应度值;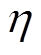 为无穷小数;t为当前迭代次数。
为无穷小数;t为当前迭代次数。
第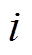 只母鸡在第j维空间的觅食位置为[31-32]
只母鸡在第j维空间的觅食位置为[31-32]
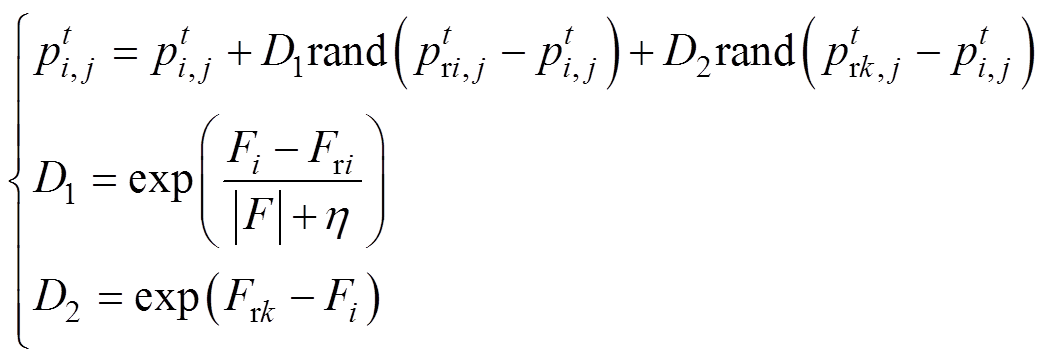 (6)
(6)式中,rand为[0,1]区间的随机数;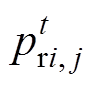 为母鸡所在群组中的公鸡位置;
为母鸡所在群组中的公鸡位置;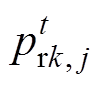 为其他群组中公鸡位置,且
为其他群组中公鸡位置,且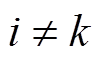 。
。
第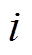 只小鸡在第
只小鸡在第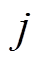 维空间的觅食位置为
维空间的觅食位置为
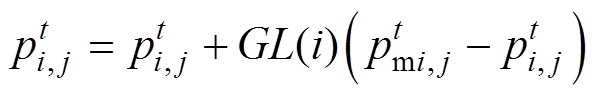 (7)
(7)式中,GL(i)为跟随系数,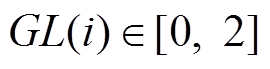 ;
;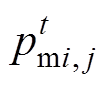 为第
为第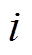 只小鸡跟随的母鸡的位置。
只小鸡跟随的母鸡的位置。
由于CSO算法本身存在局限性,在处理较复杂问题时CSO算法容易陷入局部最优。公鸡粒子在鸡群中占主导地位,且觅食能力最强,搜寻范围最广。当公鸡粒子陷入局部最优时会导致整个算法陷入局部最优。本文对公鸡粒子的位置更新公式进行了改进,在位置更新公式中引入了非线性惯性权重。通过非线性惯性权重来提高公鸡粒子的全局搜索能力和局部搜索能力。在鸡群中,小鸡粒子的觅食能力最差,搜索范围最小。而且鸡群中的小鸡粒子只能在母鸡身边觅食,从而导致小鸡粒子很容易陷入局部最优值。通过在小鸡粒子位置更新公式中引入向公鸡粒子学习部分,来提高小鸡粒子的搜索能力。
改进后的公鸡粒子位置更新公式为
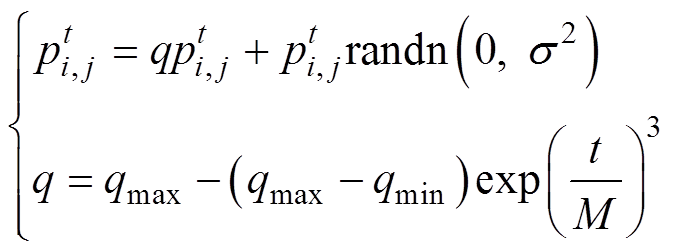 (8)
(8)式中,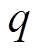 为非线性惯性权重;M为最大迭代次数;经试验测试当qmax=0.9,qmin=0.6时,测试效果最佳。
为非线性惯性权重;M为最大迭代次数;经试验测试当qmax=0.9,qmin=0.6时,测试效果最佳。
从式(8)中可以看出随着迭代次数的增加,权值逐渐减小。在迭代初期,惯性权重加强了公鸡粒子的全局搜索能力;在迭代后期,惯性权重加强了公鸡粒子的局部搜索能力。
改进后的小鸡粒子位置更新公式为
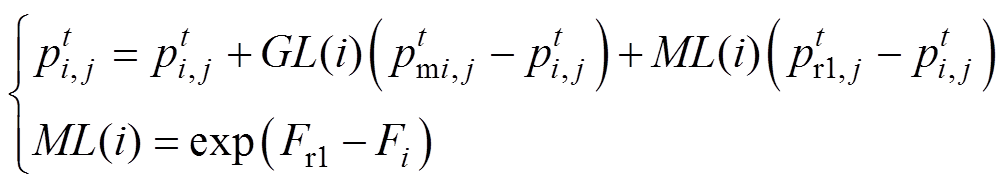 (9)
(9)式中,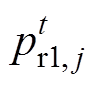 为鸡群中公鸡粒子位置;
为鸡群中公鸡粒子位置;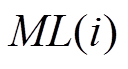 为小鸡粒子的学习系数。
为小鸡粒子的学习系数。
为了测试ICSO算法的收敛性能,采用四个标准测试函数分别对粒子群优化算法(Particle Swarm Optimization, PSO)、CSO和ICSO进行测试。四个测试函数分别对三种优化算法重复测试10次,测试维数为40维。为了使测试数据更具有说服力,采用统一的测试平台。
四个标准测试函数见表1,三种优化算法的参数设置见表2。
如表2所示,三种优化算法种群规模N为50个,最大迭代次数M为300。PSO算法的学习系数c1=c2=1.494,权值w为0.729。CSO和ICSO算法种群状态更新时刻G为7。鸡群中共有10只公鸡,30只母鸡和10只小鸡。测试结果见表3。
如表3所示,PSO算法的运行时间是最短的,但是收敛精度较差。对于标准测试函数g1、g3和g4,PSO算法的收敛精度都是最差的,说明PSO算法容易陷入局部最优值。CSO算法和ICSO算法的收敛时间相近,说明改进后的ICSO算法并没有明显增加运行成本。相比于PSO算法和CSO算法,ICSO算法的收敛精度最高。对于标准测试函数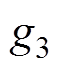 ,ICSO算法收敛到了全局最优值0。通过分析以上数据发现,对CSO算法进行改进之后,ICSO算法的收敛效果明显优于CSO算法,且ICSO算法的运行成本没有明显增加。
,ICSO算法收敛到了全局最优值0。通过分析以上数据发现,对CSO算法进行改进之后,ICSO算法的收敛效果明显优于CSO算法,且ICSO算法的运行成本没有明显增加。
表1 标准测试函数
Tab.1 Standard test function

函数式最优值取值范围 0[-100, 100] 0[-100, 100] 0[-600, 600] 0[-10, 10]
表2 算法参数
Tab.2 Parameter setting

算法参 数 PSON=50 M=300 c1=c2=1.494 w=0.729 CSON=50 M=300 G=7 Nr=10 Nh=30 Nc=10 ICSON=50 M=300 G=7 Nr=10 Nh=30 Nc=10
表3 测试结果
Tab.3 Test results
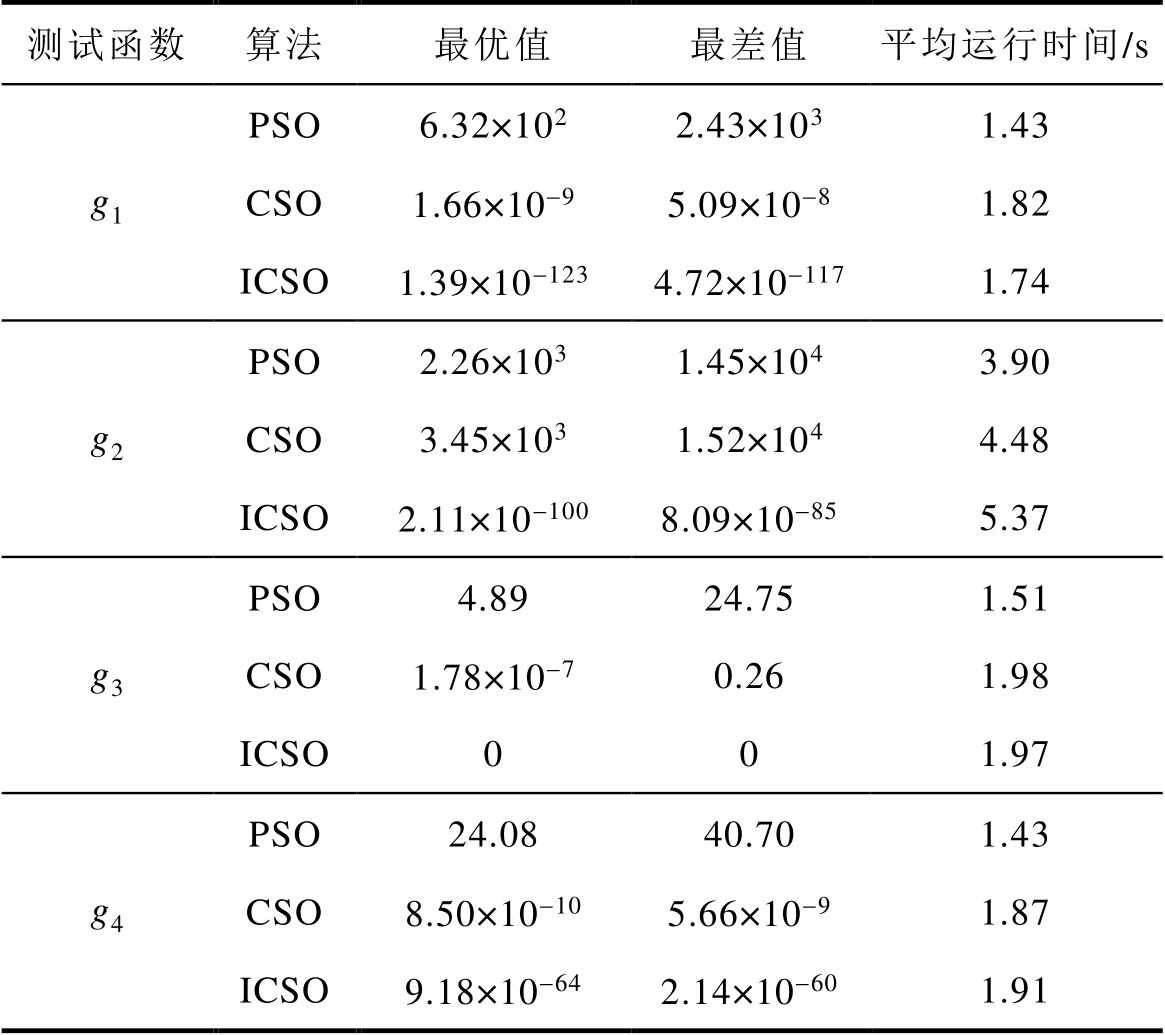
测试函数算法最优值最差值平均运行时间/s g1PSO6.32×1022.43×1031.43 CSO1.66×10-95.09×10-81.82 ICSO1.39×10-1234.72×10-1171.74 g2PSO2.26×1031.45×1043.90 CSO3.45×1031.52×1044.48 ICSO2.11×10-1008.09×10-855.37 g3PSO4.8924.751.51 CSO1.78×10-70.261.98 ICSO001.97 g4PSO24.0840.701.43 CSO8.50×10-105.66×10-91.87 ICSO9.18×10-642.14×10-601.91
为更加直观地比较三种优化算法的收敛情况,对算法的适应度值取对数。三种优化算法的收敛曲线如图3所示。
由图3可以更加直观地看到对于四个标准测试函数,ICSO算法的收敛曲线均明显低于CSO算法和PSO算法的收敛曲线,说明ICSO算法的收敛精度最高。

图3 收敛曲线
Fig.3 The convergence curves
本节的实验数据采用的是去噪之后的B5和B6电池数据。采用ICSO-SVM模型对B5和B6电池剩余容量预测分为两步。首先,将B5和B6电池数据分为测试样本和训练样本,采用训练样本对预测模型进行训练。然后,利用训练好的模型对测试样本进行预测,并对模型预测效果进行评估。
采用平均偏差(Average Absolute Deviation, AAD)、方均根误差(Root Mean Square Error, RMSE)和决定系数(R2)作为预测效果评定指标。其中R2越接近1,说明模型的拟合程度越高。
平均偏差(AAD)、方均根误差(RMSE)和决定系数(R2)的计算公式为
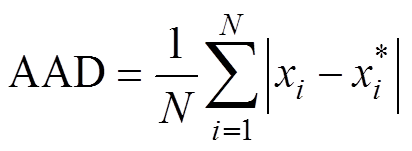 (10)
(10)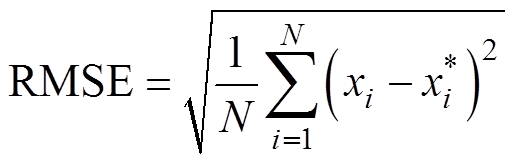 (11)
(11)
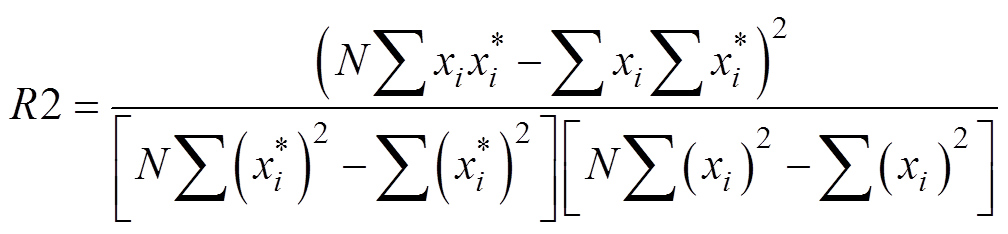 (12)
(12)
式中,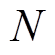 为测试样本个数;
为测试样本个数;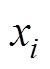 为测试样本真实值;
为测试样本真实值;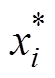 为测试样本预测值。
为测试样本预测值。
采用ICSO-SVM模型对锂电池剩余容量进行预测的流程如图4所示。
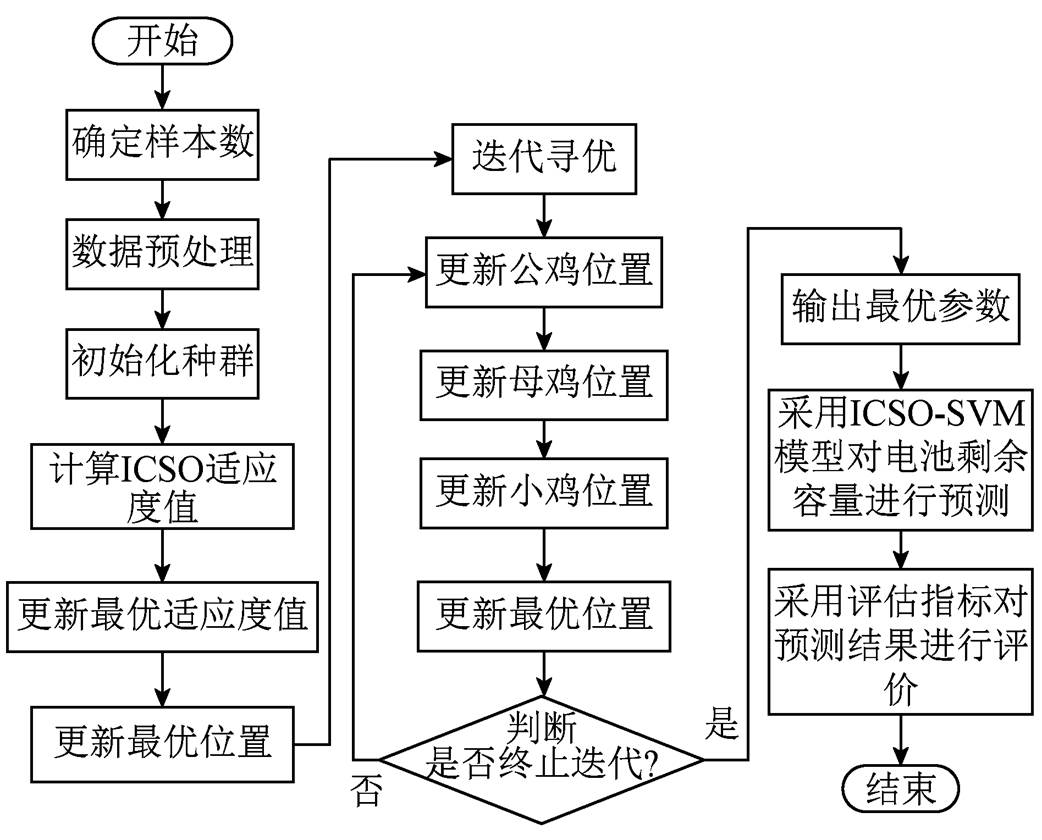
图4 锂离子电池剩余容量预测流程
Fig.4 The flow chart of lithium-ion battery remaining capacity prediction
首先,选定B5和B6电池的训练样本和测试样本,见表4。由表4可知,仿真分两组进行。B5电池的训练样本个数分别为110个和100个,测试样本分别50个和60个。B6电池的训练样本个数分别为110个和100个,测试样本为50个和60个。
表4 训练样本和测试样本个数
Tab.4 The number of training samples and test samples
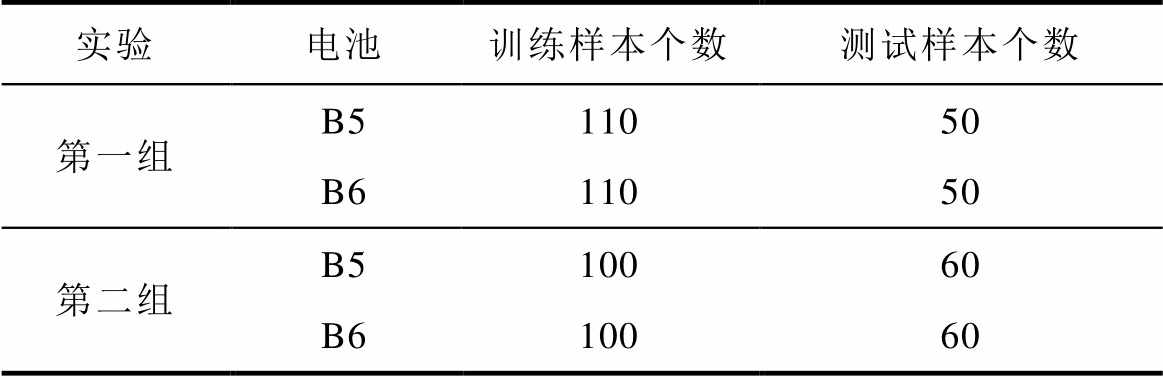
实验电池训练样本个数测试样本个数 第一组B511050 B611050 第二组B510060 B610060
首先,进行第一组实验。当B5电池的训练样本为110个、测试样本50个时,CSO-SVM和ICSO- SVM模型的预测结果如图5所示。
图5a所示为两个模型的预测值。从图5a中可以发现,两个模型的预测效果比较接近,且两个模型的拟合程度较高。
图5b为两个模型预测的相对误差。从图5b中可以发现,CSO-SVM模型的预测误差波动区间为[-1.41%, 0.75%];ICSO-SVM模型的预测误差波动区间为[-1.08%, 0.51%]。
图5c所示两个模型预测误差直方图。从图中可以看出CSO-SVM模型的预测误差主要分布在[-0.5%, 0.5%]区间内,ICSO-SVM模型的预测误差主要分布在[-0.2%, 0.4%]区间内。
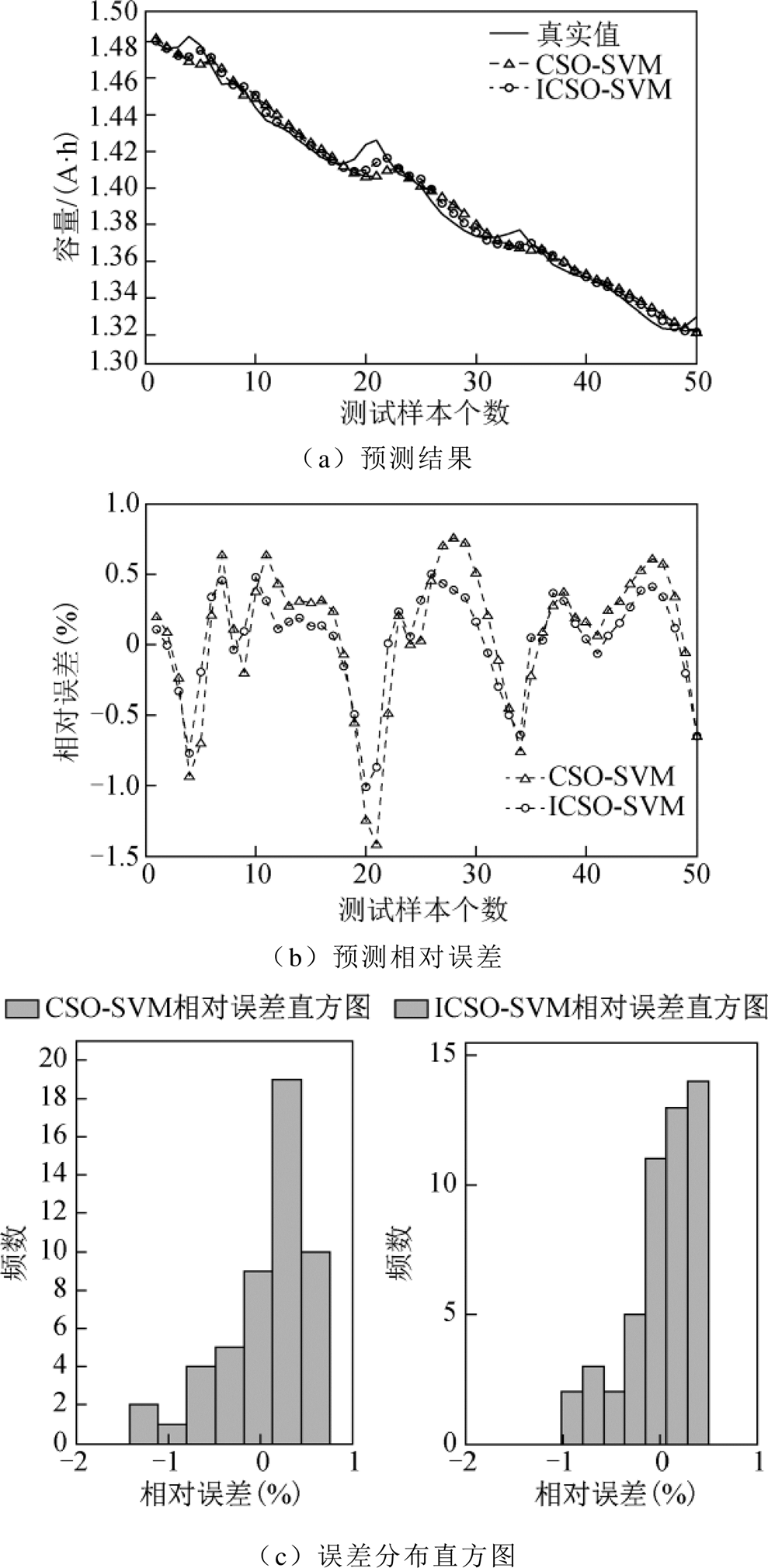
图5 110个训练样本时B5电池预测结果
Fig.5 The prediction results of B5 batteries for 110 training samples
当B6电池的训练样本为110个,测试样本为50个时,CSO-SVM和ICSO-SVM模型的预测结果如图6所示。
图6a所示为两个模型对B6电池剩余容量的预测值。其中黑色曲线表示真实值曲线。从图6a中可以发现,两个模型展现了较强的预测稳定性。
图6b展示的是两个模型的预测相对误差。从图6b中可以发现,CSO-SVM模型的预测误差波动区间为[-0.67%, 1.01%];ICSO-SVM模型的预测误差波动区间为[-0.65%, 1.06%]。
图6c展示的是两个模型预测误差直方图,通过直方图可以得到模型预测误差的分布区间。两个模型的预测误差分布差别较小,都分布在[-0.5%, 1%]区间内。

图6 110个训练样本时B6电池预测结果
Fig.6 The prediction results of B6 batteries for 110 training samples
其次,进行第二组实验。设定B5电池的训练样本为100个,测试样本为60个;B6电池的训练样本为100个,测试样本为60个。当B5电池的训练样本为100个,测试样本为60个时,CSO-SVM和ICSO-SVM模型的预测结果如图7所示。
图7a所示为两个模型对B5电池剩余容量的预测值。相比图5a的拟合程度,图7a中的三角曲线和圆形曲线与黑色曲线的拟合程度明显降低。在预测后期ICSO-SVM模型的预测误差小于CSO-SVM模型的预测误差。

图7 100个训练样本时B5电池预测结果
Fig.7 The prediction results of B5 batteries for 100 training samples
从图7b中可以发现,CSO-SVM模型的预测误差波动区间为[-1.01%, 2.31%];ICSO-SVM模型的预测误差波动区间为[-0.95%, 2.01%]。ICSO-SVM模型的预测误差波动小于CSO-SVM模型。相比图5b中的相对误差曲线,图7b中的相对误差曲线波动幅度明显增大。
当B6电池的训练样本为100个,测试样本为60个时,CSO-SVM和ICSO-SVM的预测结果如图8所示。
100个训练样本时,两个模型对B6电池剩余容量的预测结果如图8a所示。从图8a中可以发现,在预测后期CSO-SVM模型的预测稳定性较差。随着测试样本数的增加,预测误差也逐渐增大。
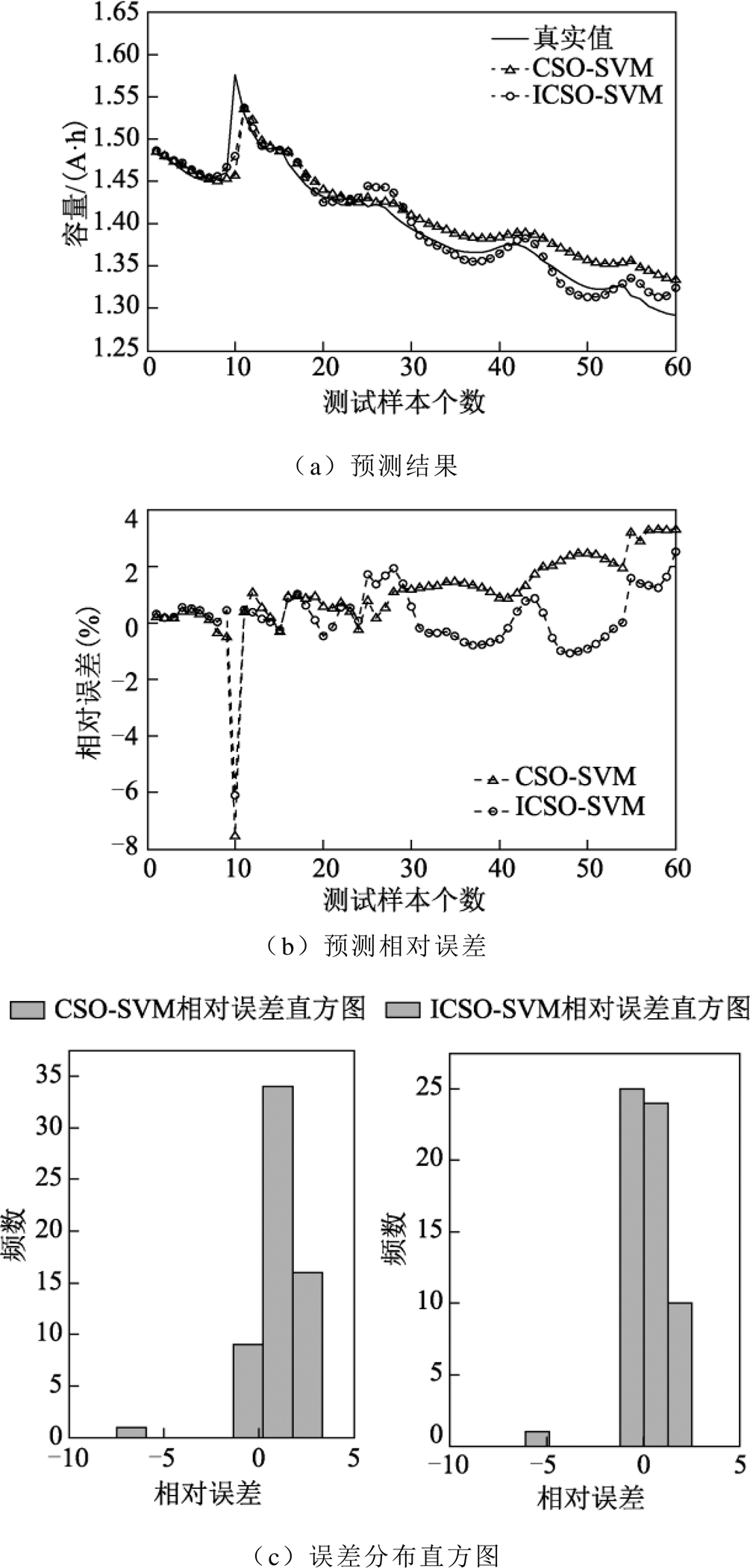
图8 100个训练样本时B6电池预测结果
Fig.8 The prediction results of B6 batteries for 100 training samples
从图8b中可以发现CSO-SVM模型的预测误差波动区间为[-7.51%, 3.32%]; ICSO-SVM模型的预测误差波动区间为[-6.09%, 2.51%]。ICSO-SVM模型的误差幅值小于CSO-SVM模型的误差幅值。
通过以上两组仿真实验,可以得到两个模型的测试结果见表5。
表5 测试结果分析
Tab.5 Analysis of test results
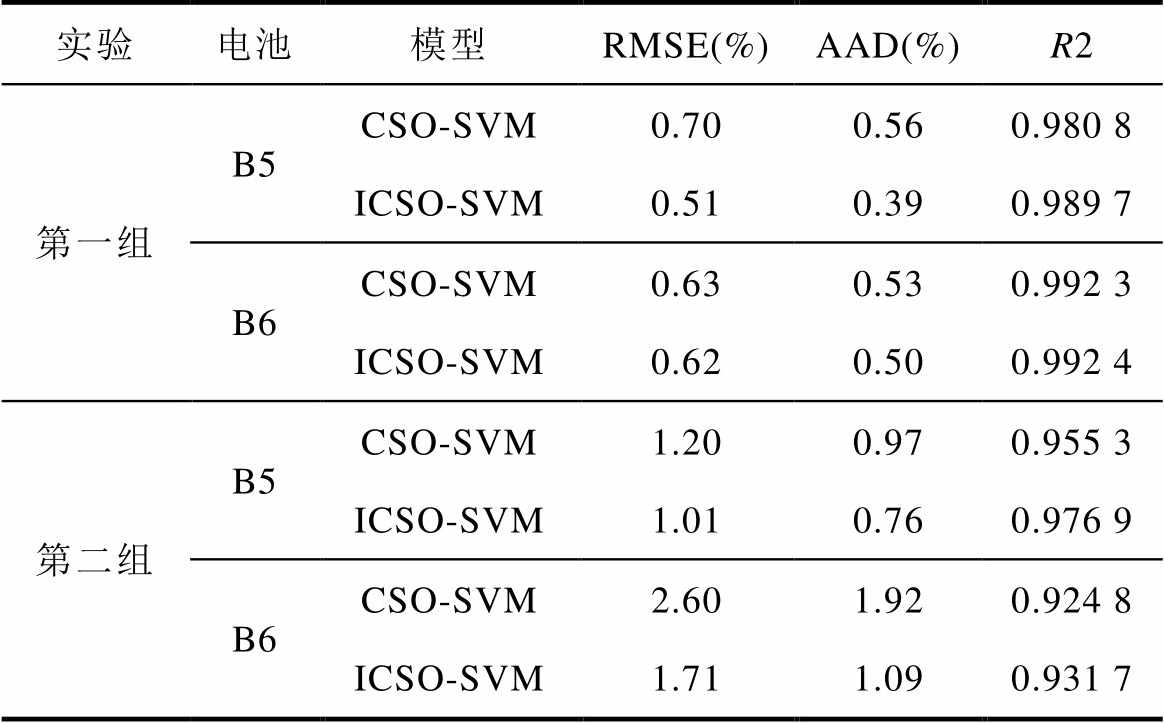
实验电池模型RMSE(%)AAD(%)R2 第一组B5CSO-SVM0.700.560.980 8 ICSO-SVM0.510.390.989 7 B6CSO-SVM0.630.530.992 3 ICSO-SVM0.620.500.992 4 第二组B5CSO-SVM1.200.970.955 3 ICSO-SVM1.010.760.976 9 B6CSO-SVM2.601.920.924 8 ICSO-SVM1.711.090.931 7
如表5所示,第一组实验中两个预测模型的RMSE值和AAD值均低于第二组实验中两个预测模型的RMSE值和AAD值。对于B5电池,第二组实验中两个预测模型的RMSE平均值是第一组实验中两个预测模型的RMSE平均值的2.5倍;第二组实验中的AAD平均值是第一组实验中AAD平均值的2.3倍多。对于两组仿真实验,ICSO-SVM模型的AAD均值为0.68,RMSE均值为0.96,R2均值为0.972 6;CSO-SVM模型的AAD均值为0.99,RMSE均值为1.28,R2均值为0.963 3。通过分析发现,相比CSO- SVM模型,ICSO-SVM模型剩余容量预测更加精确,且ICSO-SVM模型的R2均值高于CSO-SVM模型,说明其拟合效果更好。
本文采用NASA电池数据作为实验数据,并采用SVM作为基本预测模型。为提高SVM的预测能力,采用ICSO算法优化SVM的超参数,建立了ICSO-SVM预测模型对电池寿命进行预测,并得出以下结论:
1)采用db5小波对B5和B6电池数据的噪声信号进行抑制,从而降低了噪声信号对预测精度的影响。
2)传统的CSO算法容易陷入局部最优,本文对CSO算法进行了改进,并采用标准测试函数对改进效果进行验证。对于标准测试函数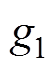 、
、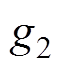 、
、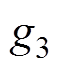 和
和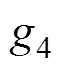 ,ICSO算法的最优值分别收敛到了1.39×10-123、2.11×10-100、0和9.18×10-64。测试结果表明:相比CSO算法,ICSO算法的收敛精度有了明显提高。
,ICSO算法的最优值分别收敛到了1.39×10-123、2.11×10-100、0和9.18×10-64。测试结果表明:相比CSO算法,ICSO算法的收敛精度有了明显提高。
3)ICSO-SVM模型的RMSE值和AAD值均低于CSO-SVM模型。ICSO-SVM模型的AAD值控制在1.5%以下,RMSE值控制在2%以下。ICSO-SVM模型的R2均值为0.963 3,保持了较好的拟合效果。仿真结果表明ICSO-SVM预测模型可以满足实际 需求。
本文建立的锂离子电池剩余容量预测模型是对单个电池的剩余容量进行预测,并不是对整个电池组的剩余容量进行评估。后续的工作主要对整个电池组的剩余容量进行评估。
参考文献
[1] 葛少云, 朱林伟, 刘洪, 等. 基于动态交通仿真的高速公路电动汽车充电站规划[J]. 电工技术学报, 2018, 33(13): 2991-3001.
Ge Shaoyun, Zhu Linwei, Liu Hong, et al. Optimal deployment of electric vehicle charging stations on the highway based on dynamic traffic simulation[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 2991-3001.
[2] 刘飘, 林培霞, 罗致远, 等. 基于闲置手机锂电池的多功能移动电源[J]. 电源技术, 2017, 41(4): 558-561.
Liu Piao, Lin Peixia, Luo Zhiyuan, et al. Multi- functional movable power based on idle cellular Li-ion battery[J]. Chinese Journal of Power Sources, 2017, 41(4): 558-561.
[3] 任仁良, 袁鹏. 航空锂电池故障检测与诊断[J]. 电源技术, 2018, 42(12): 1837-1840.
Ren Renliang, Yuan Peng. Fault detection and diagnosis of lithium battery used in aviation[J]. Chinese Journal of Power Sources, 2018, 42(12): 1837-1840.
[4] 李晓宇, 徐佳宁, 胡泽徽, 等. 磷酸铁锂电池梯次利用健康特征参数提取方法[J]. 电工技术学报, 2018, 33(1): 9-16.
Li Xiaoyu, Xu Jianing, Hu Zewei, et al. The health parameter estimation method for LiFePO4 battery echelon use[J]. Transactions of China Electro- technical Society, 2018, 33(1): 9-16.
[5] 陈英杰, 杨耕, 祖海鹏, 等. 基于恒流实验的锂离子电池开路电压与内阻估计方法[J]. 电工技术学报, 2018, 33(1): 9-16.
Chen Yingjie, Yang Geng, Zu Haipeng, et al. An open circuit voltage and internal resistance estimation method of lithium-ion batteries with constant current tests[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 9-16.
[6] 谢长君, 费亚龙, 曾春年, 等. 基于无迹粒子滤波的车载锂离子电池状态估计[J]. 电工技术学报, 2018, 33(17): 3958-3964.
Xie Changjun, Fei Yalong, Zeng Chunnian, et al. State-of-charge estimation of lithium-ion battery using unscented particle filter in vehicle[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(17): 3958-3964.
[7] 程泽, 孙幸勉, 程思璐. 一种锂离子电池荷电状态估计与功率预测方法[J]. 电工技术学报, 2017, 32(15): 180-189.
Cheng Ze, Sun Xingmian, Cheng Silu. Method for estimation of state of charge and power prediction of lithium-ion battery[J]. Transactions of China Elec- trotechnical Society, 2017, 32(15): 180-189.
[8] Wang Zengkai, Zeng Shengkui, Guo Jianbin, et al. Remaining capacity estimation of lithium-ion batteries based on the constant voltage charging profile[J]. Plos One, 2018, 13(7): 22.
[9] 张伟, 卿鑫慧, 王一军, 等. 磷酸铁锂电池低温性能及放电容量预测研究[J]. 电源技术, 2019, 43(3): 430-433.
Zhang Wei, Qing Xinhui, Wang Yijun, et al. Study on discharge performance and discharge capacity prediction of lithium iron phosphate battery at low- temperature[J]. Chinese Journal of Power Sources, 2019, 43(3): 430-433.
[10] Ren Lei, Zhao Li, Hong Sheng, et al. Remaining useful life prediction for lithium-ion battery: a deep learning approach[J]. IEEE Access, 2018, 6: 50587- 50598.
[11] Li Lingling, Wang Pengchong, Chao Kuei-Hsiang, et al. Remaining useful life prediction for lithium-ion batteries based on gaussian processes mixture[J]. Plos One, 2016, 11(9): e0163004.
[12] 赵美红, 刘佳庚. 基于非线性模型的动力电池容量损耗的预测[J]. 可再生能源, 2016, 34(7): 1067- 1071.
Zhao Meihong, Liu Jiageng. The prediction of capacity loss of power battery based on nonlinear model[J]. Renewable Energy Resources, 2016, 34(7): 1067-1071.
[13] 刘柱, 姜媛媛, 罗慧, 等. 基于最优权阈值ELM算法的锂离子电池RUL预[J]. 电源学报, 2018, 16(4): 168-173.
Liu Zhu, Jiang Yuanyuan, Luo Hui, et al. Prediction of lithium-ion battery RUL based on optimalweight and threshold using ELM algorithm[J]. Chinese Journal of Power Sources, 2018, 16(4): 168-173.
[14] Li Lingling, Liu Zhifeng, Tseng Minglang. Enhancing the lithium-ion battery life predictability using a hybridmethod[J]. Applied Soft Computing Journal, 2019, 74: 110-121.
[15] 孙冬, 许爽. 梯次利用锂电池健康状态预测[J]. 电工技术学报, 2018, 33(9): 2121-2129.
Sun Dong, Xu Shuang. State of health prediction of second-use lithium-ion battery[J]. Transactions of China Electrotechnical Society, 2018, 33(9): 2121- 2129.
[16] Bi Fengrong, Ma Teng, Wang Xu. Development of a novel knock characteristic detection method for gasoline engines based on wavelet-denoising and EMD decomposition[J]. Mechanical Systems and Signal Processing, 2019, 117: 517-536.
[17] Rajaee T, Jafari H. Utilization of WGEP and WDT models by wavelet denoising to predict water quality parameters in rivers[J]. Journal of Hydrologic Engineering, 2018, 23(12): 17.
[18] Ding Y, Selesnick I W. Artifact-free wavelet denoising: non-convex sparse regularization, convex optimi- zation[J]. IEEE Signal Processing Letters, 2015, 22(9): 1364-1368.
[19] 李化, 杨新春, 李剑, 等. 基于小波分解尺度系数能量最大原则的GIS局部放电超高频信号自适应小波去噪[J]. 电工技术学报, 2012, 27(5): 84-91.
Li Hua, Yang Xinchun, Li Jian, et al. The maximum energy of wavelet decomposition approximation- related adaptive wavelet de-nosing for partial dis- charge UHF pulse in GIS[J]. Transactions of China Electrotechnical Society, 2012, 27(5): 84-91.
[20] 彭道刚, 陈跃伟, 钱玉良, 等. 基于粒子群优化-支持向量回归的变压器绕组温度软测量模型[J]. 电工技术学报, 2018, 33(8): 1742-1749, 1761.
Peng Daogang, Chen Yuewei, Qian Liangyu, et al. Transformer winding temperature soft measurement model based on particle swarm optimization-support vector regression[J]. Transactions of China Electro- technical Society, 2018, 33(8): 1742-1749, 1761.
[21] 邱思语, 杨洪耕. 改进的加权支持向量机回归的谐波发射水平估计方法[J]. 电工技术学报, 2016, 31(5): 85-90.
Qiu Siyu, Yang Honggeng. Assessment method of harmonic emission level based on the improved weighted support vector machine regression[J]. Transactions of China Electrotechnical Society, 2016, 31(5): 85-90.
[22] Ertekin S, Bottou L, Giles C L. Nonconvex online support vector machines[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2011, 33(2): 368-381.
[23] Han B, Davis L S. Density-based multifeature background subtraction with support vector machine[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2012, 34(5): 1017-1023.
[24] Hussain S F. A novel robust kernel for classifying high-dimensional data using support vector machines[J]. Expert Systems with Applications, 2019, 131: 116- 131.
[25] Parhizkar E, Saeedzadeh H, Alunadi F, et al. Partial least squares-least squares-support vector machine modeling of ATR-IR as a spectrophotometric method for detection and determination of iron in pharma- ceutical formulations[J]. Iranian Journal of Pharma- ceutical Research, 2019, 18(1): 72-79.
[26] Feng Tianpei, SunYuedong, Wang Yansong, et al. Sound feature space effects on the performance of annoyance evaluation model based on support vector machine[J]. Applied Acoustics, 2019, 154: 99-113.
[27] Meng Xianbing, Liu Yu, Gao Xiaozhi, et al. A new bio-inspired algorithm: chicken swarm optimi- zation[J]. Advances in Swarm Intelligence, 2014, 5: 86-94.
[28] Liang Jianhui, Wang Lifang, Ma Miao, et al. A fast SAR image segmentation method based on improved chicken swarm optimization algorithm[J]. Multimedia Tools and Applications, 2018, 77(24): 31787-31805.
[29] Wu Zhongqiang, Yu Danqi, Kang Xiaohua. Appli- cation of improved chicken swarm optimization for MPPT in photovoltaic system[J]. Optimal Control Applications & Methods, 2018, 39(2): 1029-1042.
[30] Liu Dong, Liu Chunlei, Fu Qiang, et al. Projection pursuit evaluation model of regional surface water environment based on improved chicken swarm optimization algorithm[J]. Water Resources Manage- ment, 2018, 32(4): 1325-1342.
[31] Wang Zhifang, Wang Shuatao, Kong Deming, et al. Methane detection based on improved chicken algorithm optimization support vector machine[J]. Applied Sciences-Basel, 2019, 9(9): 15.
[32] Yu Xiwu, Zhou Lixing, Li Xiangyang. A novel hybrid localization scheme for deep mine based on wheel graph and chicken swarm optimization[J]. Computer Networks, 2019, 154: 73-78.
Capacity Prediction of Lithium-Ion Batteries Based on Wavelet Noise Reduction and Support Vector Machine
Abstract As battery usage increases, the battery will age. By predicting the remaining capacity of the battery, reliable data support can be improved for the battery management system in the equipment system. In this study, support vector machine (SVM) is used to predict the remaining capacity of lithium-ion batteries. The improved chicken swarm algorithm (ICSO) is used to optimize the parameters of SVM. The ICSO-SVM model is established. In order to verify the feasibility of the prediction model, the following work has been done. Firstly, the capacity degradation data of B5 and B6 batteries were decomposed by db5 wavelet. And then the denoised signal was reconstructed. Secondly, the chicken swarm optimization algorithm (CSO) was improved and ICSO optimization algorithm was proposed. The convergence accuracy of ICSO is higher than that of PSO and CSO algorithms. Finally, two groups of experiments were used to verify the validity of the CSO-SVM model and the ICSO-SVM model. It is found that the average absolute deviation (AAD) value of ICSO-SVM model is less than 1.5%, RMSE value is less than 2% and average of R2 value is 0.972 6.
keywords:Lithium-ion battery, support vector machine, optimization algorithm, wavelet denoising, capacity prediction
DOI: 10.19595/j.cnki.1000-6753.tces.190620
中图分类号:TM572.2
张婷婷 女,1984年生,硕士,讲师,研究方向为数字信号处理,数字图像处理和计算机视觉。E-mail: zhangtingting@hebut.edu.cn
于 明 男,1964年生,教授,博士生导师,研究方向为数字信号处理,图像视频理解,智能视频处理和模式识别。E-mail: yuming@hebut.edu.cn(通信作者)
收稿日期 2019-05-22
改稿日期 2019-06-12
中国科学院自动化研究所模式识别国家重点实验室开放课题(201900043)、河北省教育厅青年基金(QN2019207)、天津科技发展战略研究计划(18ZLZXZF00660)和河北省自然科学基金面上项目(F2019202381, F2019202464)资助项目。
(编辑 郭丽军)