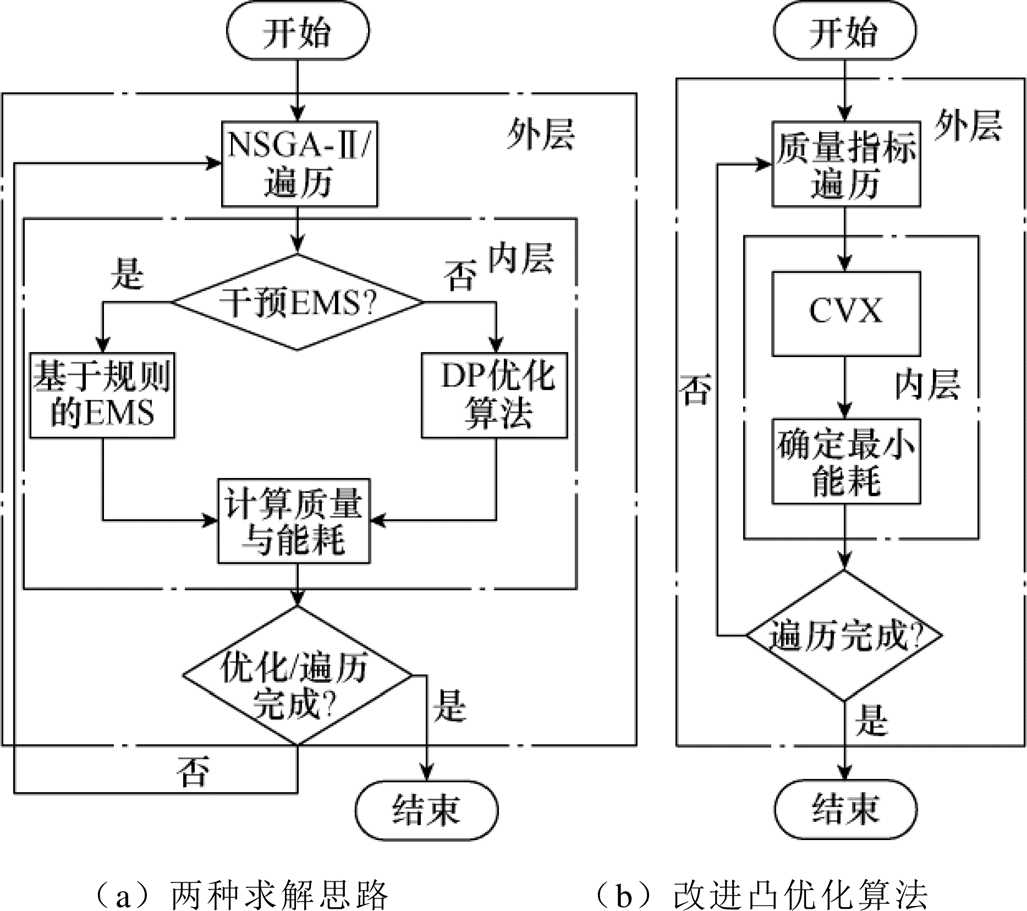
图1 两种求解思路与改进凸优化算法
Fig.1 Two solutions and improved convex optimization algorithm
摘要 容量配置影响混合储能有轨电车的运行可行性与经济效益,是设计混合储能系统的基础环节。能量管理策略(EMS)与容量配置互相耦合,互为影响,基于这一特点,该文提出一种协同优化容量配置与能量管理策略的改进型凸优化(CVX)算法,求解容量配置的可行域,在可行域内构建一族等质量线,在每一条等质量线下寻找能耗最小的容量配置与EMS的最优组合解,获得混合储能系统质量与能耗的双目标帕累托前沿。与单储能系统相比较,混合储能系统质量轻、体积小,适合在对质量、体积要求严苛的情况下使用,在严苛的质量限制下,混合储能系统仍然是一种不可替代的解决方案。仿真结果对比表明,协同优化的EMS效率高,功率分配合理。
关键词:有轨电车 混合储能系统 容量配置 凸优化 帕累托解集
有轨电车环保节能、运量适中,适合在中等城市推广使用[1]。目前实际运行的有轨电车的动力来源多是牵引网,一方面,牵引网的架设影响城市的美观;另一方面,牵引网在雨雪天气有不安全隐患,且运行期间会对电网造成一定的冲击。近年来,随着清洁能源政策的推行,储能式有轨电车[2-4]开始出现并被广泛地研究,逐渐替代了牵引网式的有轨电车。
常应用于储能式有轨电车中的储能元件主要有锂电池与超级电容。二者之间特性互补,近年来,将二者结合起来的混合储能系统应用得越来越广泛。但是,双源系统的引入增加了容量配置与功率分配的复杂度[5-7]。如何合理地配置电池、超级电容的数量,使有轨电车储能系统的配置既能满足运行需求,又不至于出现配置冗余的情况,成为一个热点问题。
容量配置的求解有两个难点:如何解决能量管理策略(Energy Management Strategy, EMS)与容量配置的耦合关系及如何处理容量配置多目标优化问题。
(1)容量配置和EMS相互关联,彼此耦合。不同的学者采用不同的方法来处理两者之间的耦合关系。一种方法是基于确定的EMS优化容量配置[8-15],该方法所得到的容量配置与人为事先确定好的EMS有关,不具备一般性;另一种方法是同时优化EMS和容量配置,该方法的准确分析需要极其复杂的计算和极大的计算成本,为了减少计算时间和复杂度,有学者提出将原问题近似为凸优化(Convex, CVX)问题,以提高计算速度[16-20]。
(2)容量配置的求解是一个多目标的优化问题。处理多目标优化问题,文献[8-15]的解决思路是将多目标加权求和得到一个综合指标,将多目标优化问题转化为单目标优化问题,进行求解。为了避免人为设立权重的不合理性,文献[21-24]基于多目标优化非支配解的概念,获得了优化问题的帕累托(Pareto)前沿,该帕累托前沿可以使决策者更好地了解优化问题的结果,做出更为合理的决策。文献[22]基于大量的仿真数据构建了容量配置的帕累托前沿,以验证DIRECT算法的合理性。文献[23-24]基于非支配排序遗传算法-II(Non-dominated Sorting Genetic Algorithm-II, NSGA-II)求解了容量配置的Pareto解集。
求解帕累托前沿,有两种思路,两种求解思路与改进凸优化算法如图1所示。文献[8, 13, 15]的思路是将问题转化为一个外层优化的双层嵌套问题,进行迭代优化,先确定一种基于规则的能量管理策略作为内层的子程序,再利用NSGA-II等优化算法对外层的储能系统(Energy Storage System, ESS)配置进行寻优,但是这种求解方法无法得到全局最优结果,所得到的容量配置受事先人为确定的EMS的影响,不具有一般性。另一种思路是将问题转化为双层优化的嵌套问题,外层ESS配置的寻优通过进化算法来实现,内层嵌入动态规划算法(Dynamic Programming, DP)来优化在该容量配置下的最优功率分配方式,再将得到的能耗与质量指标传给主程序,经过进化算法的非支配排序、交叉与变异得到下一代种群,这一思路虽然避免了人为干预EMS的缺点,但是计算量大,极大地浪费了人力、物力,只是一种理想的处理方式,对容量配置的求解不具有实际的指导意义。

图1 两种求解思路与改进凸优化算法
Fig.1 Two solutions and improved convex optimization algorithm
本文为了解决这两个难点,提出了改进型凸优化算法,基于国内某有轨电车的实际运行功率数据,得到了混合储能系统容量配置的帕累托前沿。并将其优化结果与单储能系统进行比较,仿真结果表明,混合储能系统质量轻、体积小,适合在对质量、体积要求严苛的情况下使用。
本文的有轨电车模型是基于国内某实际线路的现运营车辆来搭建的,该有轨电车的储能系统由钛酸锂电池与超级电容两部分组成,采用电池半主动的拓扑结构,即电池通过DC-DC变换器并联接入直流母线,超级电容直接接入直流母线,混合储能系统拓扑结构如图2所示。有轨电车全线无牵引网,运行途中仅由混合储能系统供电,停站时,其受电弓抬升,连接充电桩补充能量。
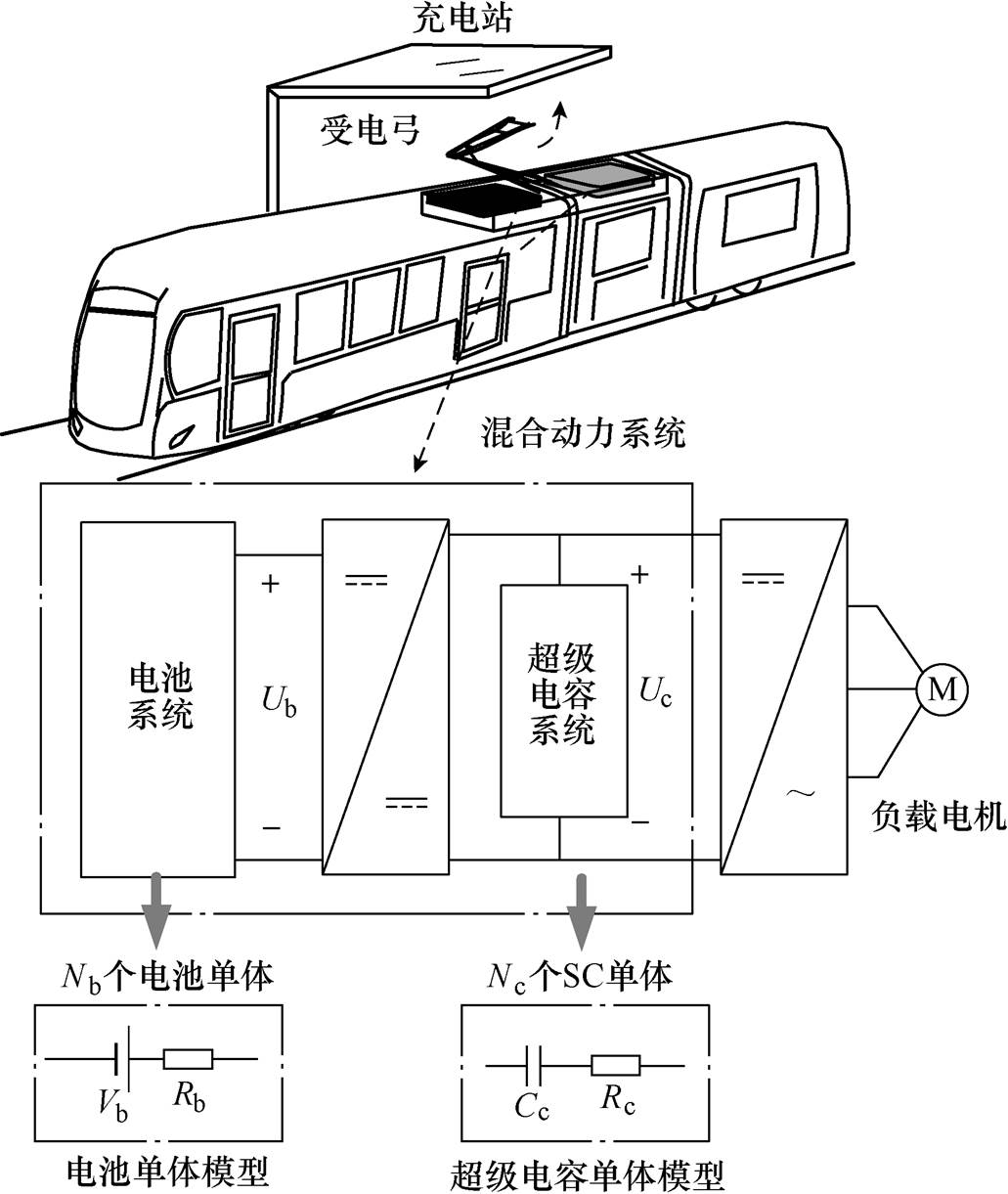
图2 混合储能系统拓扑结构
Fig.2 Hybrid energy storage system topology
超级电容的功率密度大,因此在设计混合储能系统时,超级电容承担大功率的输出与吸收。相比双DC-DC的拓扑结构,采用电池半主动方式,可以降低变换器的功率等级,减小整个储能系统的体积与质量,减少在DC-DC变换器上的能量损耗。
锂电池模型如图2所示。Vb是电池单体开路电压,Rb是电池单体欧姆内阻。电池的开路电压会随着荷电状态(State of Charge, SOC)的变化而变化,为了尽量延长电池寿命,避免电池过充与过放,其SOC的使用区间应该在[0.4, 0.8]。图3所示为基于混合功率脉冲(Hybrid Pulse Power Characteristic, HPPC)实验得到的电池单体开路电压与SOC之间的关系,SOC在[0.4, 0.8]区间,电池的Vb与SOC之间呈线性关系,对二者的关系进行近似处理,有
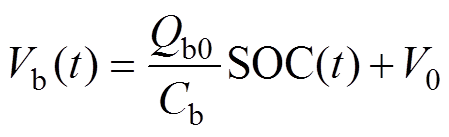 (1)
(1)式中,V0为拟合曲线在电池SOC=0时的电压;Qb0为电池的额定容量;Cb为电池的等效电容。
为了构建锂电池[25]的凸模型,需要分析其功率流动的数学表达式,以放电为例,锂电池单体的功率流动模型如图4所示,Vb两端的功率为Pb/Nb,Rb上消耗的功率为Pbloss/Nb,电池两端所释放的功率为Pbt/Nb,电池所储存的能量为Eb/Nb。
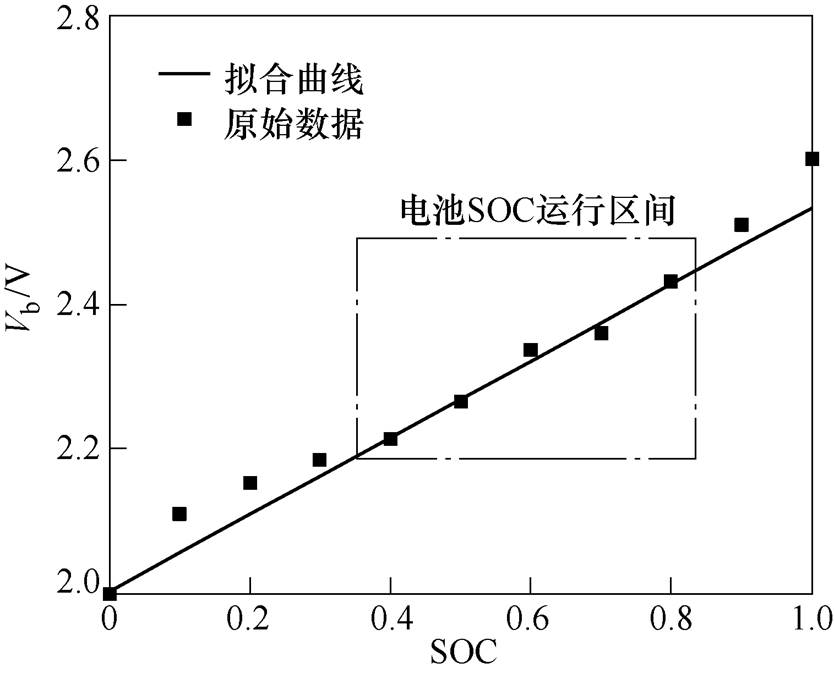
图3 基于HPPC实验所得电池电压曲线
Fig.3 Battery voltage curve based on HPPC experiments
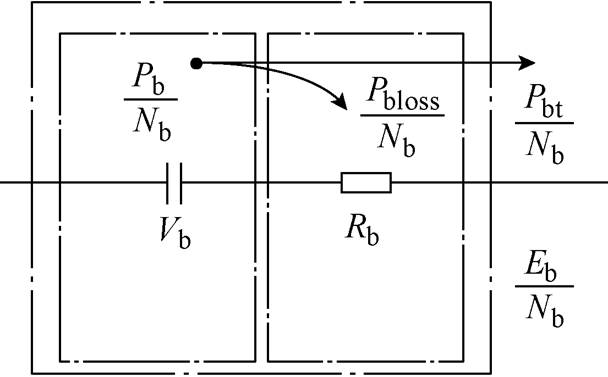
图4 锂电池单体的功率流动模型
Fig.4 Power flow model of lithium battery
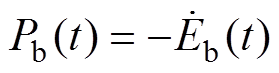 (2)
(2)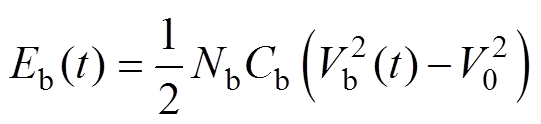 (3)
(3)
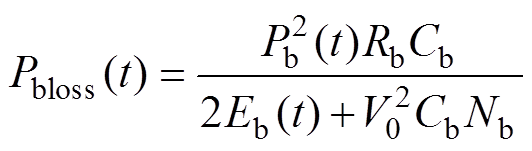 (4)
(4)
为了保持问题的凸性,将式(1)代入式(3),并将式(3)的简化结果代入式(4),使得Pbloss成为Pb与Eb的函数。充电或制动工况下的公式与放电工况下的公式完全相同,推导过程类似,此处不再赘述。
超级电容单体的功率流动模型如图5所示。超级电容容值为Cc,其两端的功率为Pc/Nc,Rc上消耗的功率为Pcloss/Nc,超级电容两端所释放的功率为Pct/Nc。超级电容所储存的能量为Ec/Nc。
超级电容的开路电压Vc与其所带电荷量Qc的关系为
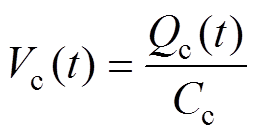 (5)
(5) 超级电容功率流动模型中变量的数学表达式为
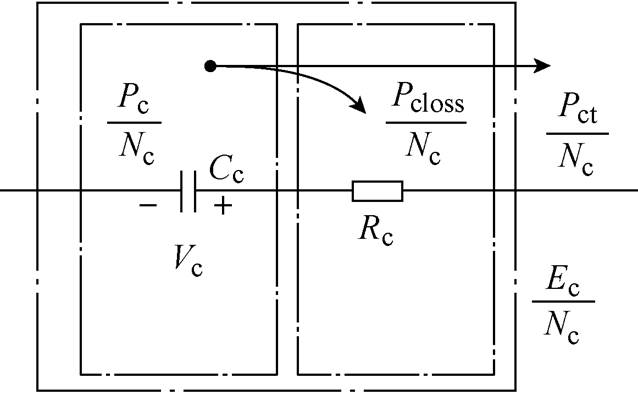
图5 超级电容单体的功率流动模型
Fig.5 Power flow model of supercapacity
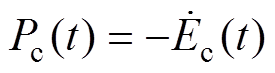 (6)
(6)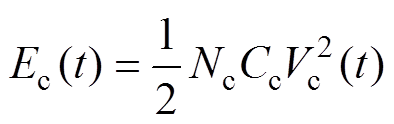 (7)
(7)
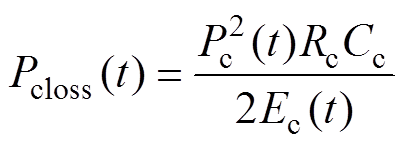 (8)
(8)
基于该有轨电车混合储能系统的凸模型,通过改进型凸优化算法,可以获得EMS与ESS协同优化的帕累托解集,有效地减少计算复杂度与计算时间。
凸优化问题的优化模型为
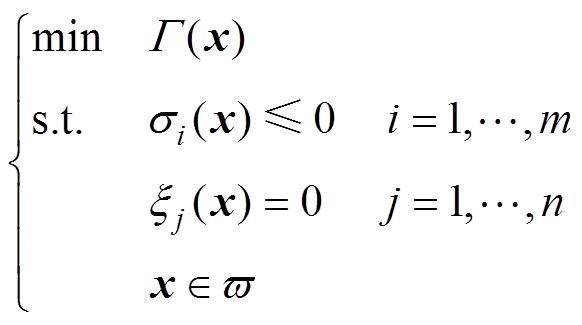 (9)
(9)式中,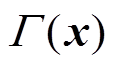 为目标函数。在混合储能型有轨电车系统中,系统效率是影响有轨电车运行经济性的主要因素,有
为目标函数。在混合储能型有轨电车系统中,系统效率是影响有轨电车运行经济性的主要因素,有
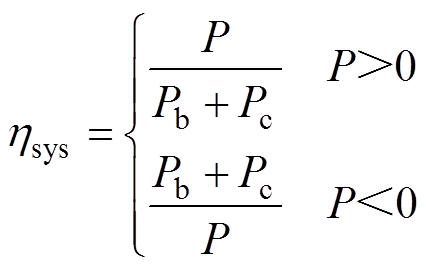 (10)
(10)
式中,Pb为Nb个电池单体释放或吸收的总功率;Pc为Nc个超级电容单体释放或吸收的总功率;P为直流母线侧需要的功率。
牵引时,系统效率是指母线侧功率与混合储能系统总功率的比值;制动时,系统效率是指混合储能系统总功率与母线侧功率的比值。可以看出,在牵引阶段,混合储能系统释放的功率越小,效率越高;在制动阶段,混合储能系统吸收的功率越大,效率越高。表明效率越高,总耗能越小,因此,设电池与超级电容的总耗能为目标函数[16-17, 26],有
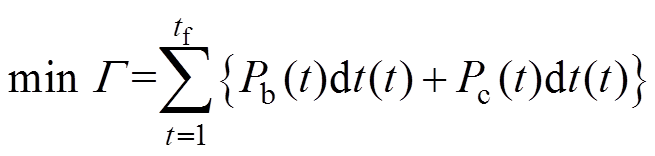 (11)
(11)限制条件的第一项中,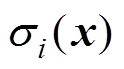 是凸函数。在这个优化问题中,需要满足两个等式条件:功率守恒与质量匹配,有
是凸函数。在这个优化问题中,需要满足两个等式条件:功率守恒与质量匹配,有
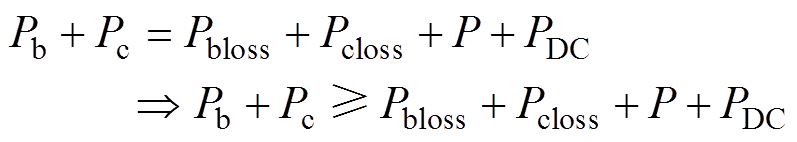 (12)
(12)
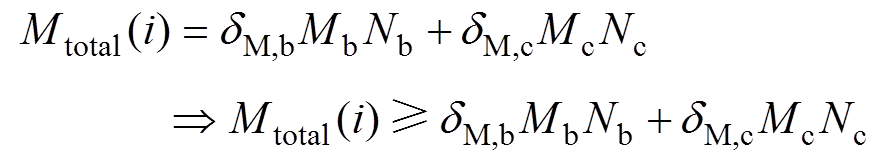 (13)
(13)式中,Pbloss为Nb个电池单体内阻消耗的功率;Pcloss为Nc个超级电容单体内阻消耗的功率;PDC为在DC-DC变换器消耗的功率;Mtotal(i)为指混合储能系统的总质量限制;i为索引值,该值的引入可以在不同的质量指标下寻得对应的最优结果;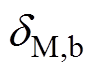 、
、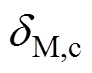 分别为电池、超级电容的封装系数[24];Mb、Mc分别为电池与超级电容的单体质量;Nb、Nc分别为电池与超级电容的数量。
分别为电池、超级电容的封装系数[24];Mb、Mc分别为电池与超级电容的单体质量;Nb、Nc分别为电池与超级电容的数量。
为了保持问题的凸性,需要将这式(12)和式(13)松弛为不等式,显然,通过该变换,优化问题的结果是不变的。
由于能量流动在DC-DC变换器上产生的损耗为PDC,其表达式为
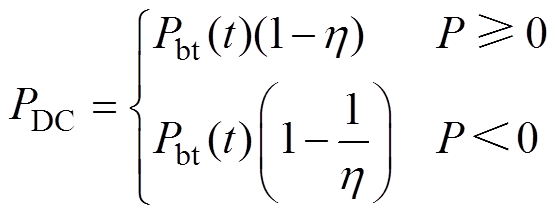 (14)
(14)PDC在充电与放电情况下的计算公式由于能量流动方向不同而不同,在此,为了构建模型的方便、提升计算速度,基于文献[6, 15],考虑有轨电车的功率等级,将DC-DC变换器的效率h 视为定值95%。
式(9)第二项限制条件中,xj(x)是仿射函数,该限制条件由超级电容凸模型与电池凸模型的公式构成,即式(1)~式(8)。
式(9)中,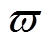 表示凸集,
表示凸集,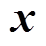 需要满足凸集的特性。在本文的混合储能系统实例中,优化变量
需要满足凸集的特性。在本文的混合储能系统实例中,优化变量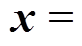
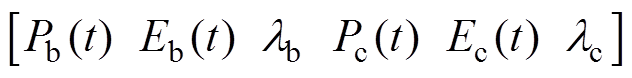 ,lb、lc作为配置系数引入到该凸优化问题中,Nb0、Nc0分别表示电池与超级电容的基数,与配置系数相乘得到电池与超级电容的实际数量,有
,lb、lc作为配置系数引入到该凸优化问题中,Nb0、Nc0分别表示电池与超级电容的基数,与配置系数相乘得到电池与超级电容的实际数量,有
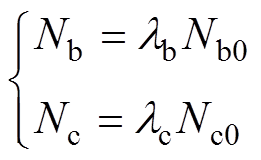 (15)
(15)
在这个优化问题中,Ec、Eb、Pc、Pb、lb、lc这些优化变量需要进行限制,有
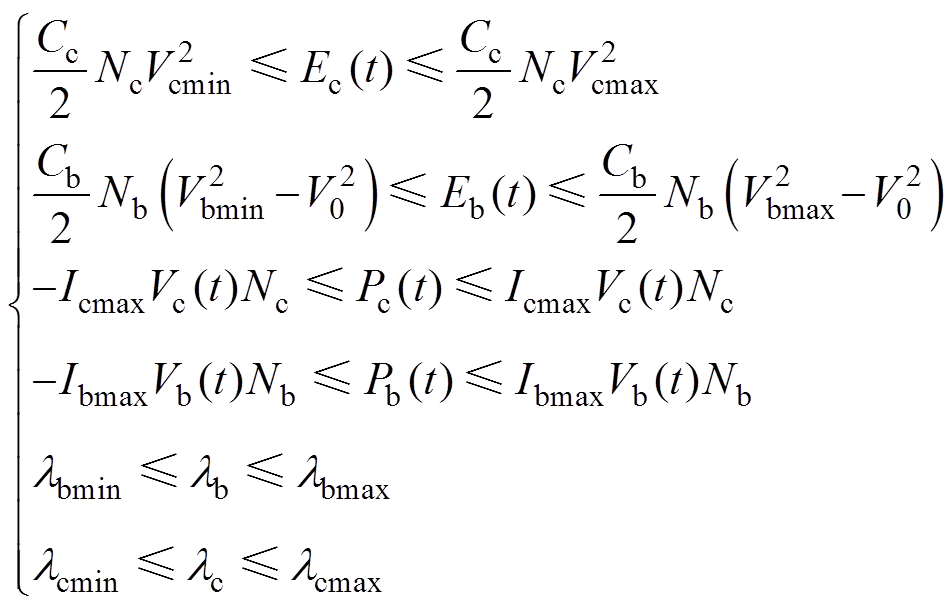 (16)
(16)式中,Vcmin、Vcmax和Vbmin、Vbmax分别为超级电容与锂电池适宜工作区间的下限电压、上限电压;Icmax、Ibmax分别为超级电容与锂电池的最大电流;lbmin、lbmax、lcmin、lcmax分别为储能元件配置系数的最小值与最大值。这些限制使得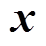 满足了凸集的特性。
满足了凸集的特性。
据式(9)~式(16)得到的凸优化问题,可以通过Matlab的凸优化工具包进行求解,可以求得在给定的质量Mtotal(i)下最优的ESS配置与功率分配序列,即得到一组最优解,有
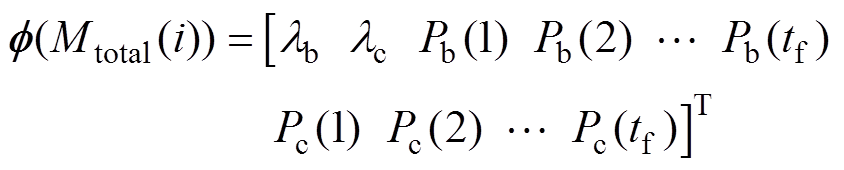 (17)
(17)传统的凸优化算法是单目标优化方法,本文所研究的混合储能系统在优化系统效率的基础上,还应考虑该车辆实际的储能系统质量限制,需要引入质量指标,构建能耗-质量帕累托前沿(E-M前沿)。
为了更好地理解本节内容,首先对帕累托非支配解与帕累托前沿进行介绍。
帕累托非支配解:一个可行域内的解,如果在改善任意一个目标函数的同时,必然会使得至少一个目标函数变差,那么这个解即为非支配解。
帕累托前沿:由非支配解构成的解集即为帕累托前沿。
为了求得E-M前沿,将该优化问题转为双层嵌套的优化问题,内层嵌入凸优化算法,外层遍历质量指标,在某一质量下,求得的最小能耗所对应的ESS配置即为帕累托非支配解,这是因为如果要降低能耗,必然要增加质量,即无法找到该解的支配解了。为了寻找帕累托前沿,需要在不同的质量目标下,利用CVX,寻找能耗最小的ESS配置。经过多次运行凸优化程序,可以得到n组最优解,有
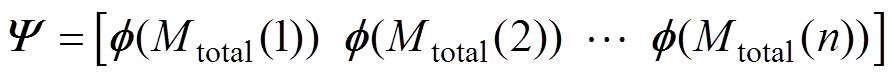 (18)
(18)这n组最优解,对应着n个点(Nb0lb(1), Nc0lc(1)), (Nb0lb(2), Nc0lc(2)),…,(Nb0lb(n), Nc0lc(n)),由这n个点组成的解集即为帕累托前沿的子集。通过数值计算无法获得完整的帕累托前沿,工程分析中也没有必要穷尽所有可能,结合实际情况,选定合适的质量步长,来获得较为平滑的解集即可。
基于改进型凸优化算法求解EMS与ESS协同优化的帕累托解集,需要以一定的步长遍历质量指标来求得帕累托非支配解,为了减少质量遍历的范围,需要先求解混合储能系统的可行域,在可行域的范围内遍历质量指标,可以增加运算的效率。
本文以国内某有轨电车线为研究对象,通过对7天内从首班车7:30到末班车20:00连续采集的母线电压、电流与车辆速度数据进行分析,将能耗最大的区间作为本文的仿真对象。
为了使得配置的ESS可以承受最严苛的情况,在该区间上,对比多天不同时段的功率曲线,选取某工作日早高峰的实际功率曲线与速度曲线来做容量配置优化。其实际功率与速度如图6所示。该区间的最大能耗为14.65kW·h,峰值功率为903.336kW。该有轨电车的车体允许装设2.5t、2m3的储能系统。
本文的仿真所采用的储能元件单体是钛酸锂电池与超级电容,其参数见表1。
ESS的设计需考虑功率、能量、质量与体积限制,这些要素决定了ESS配置的可行范围。电池与超级电容最大功率的和应大于该有轨电车在指定线路上运行时的最大功率,电池与超级电容所携带的能量应大于该有轨电车的最大能耗,而储能系统的质量与体积也应受到实际情况的限制,将这些限制条件联立不等式组求解可行域,有
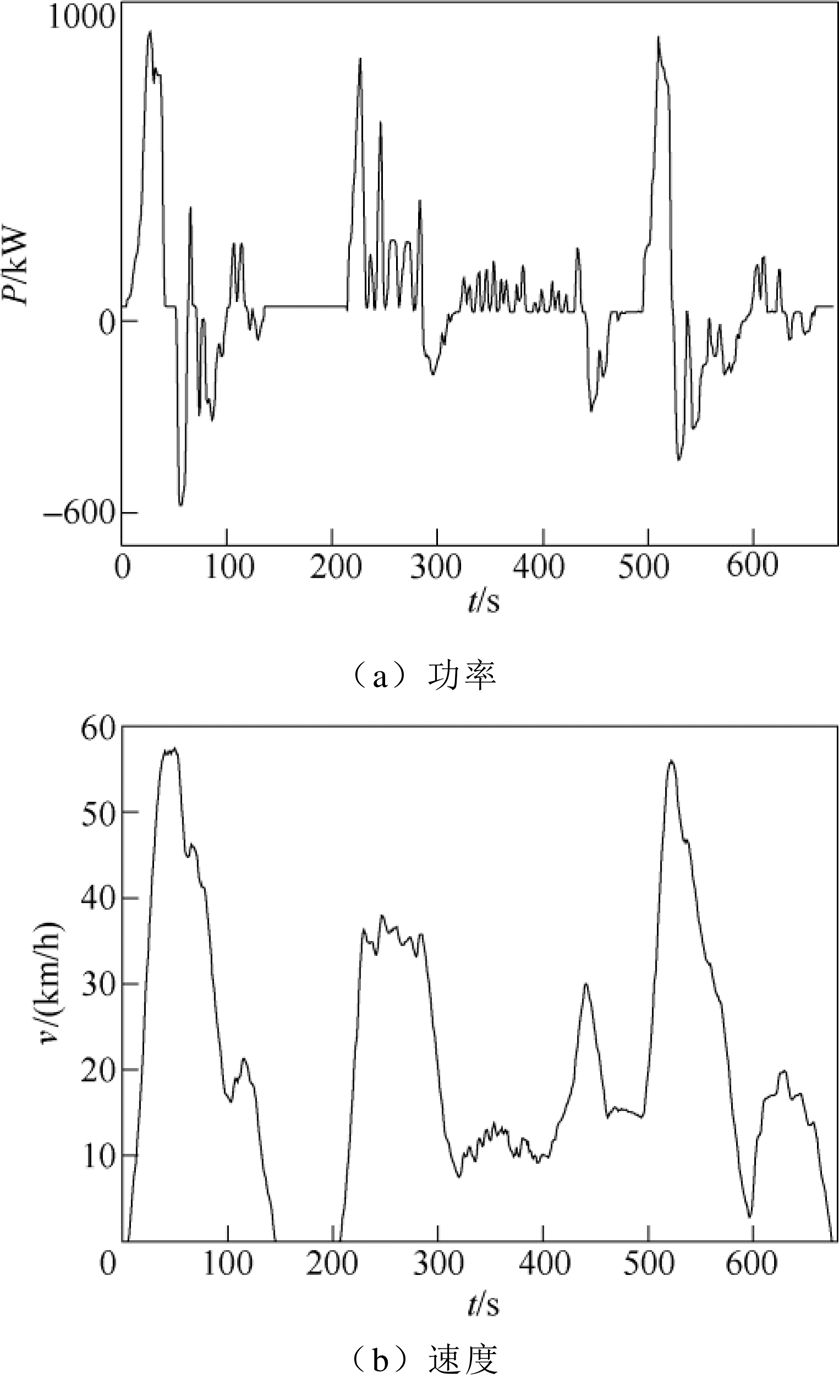
图6 有轨电车实际功率与速度
Fig.6 The actual power and speed curves of tramcar
表1 储能元件参数
Tab.1 Energy storage element parameters
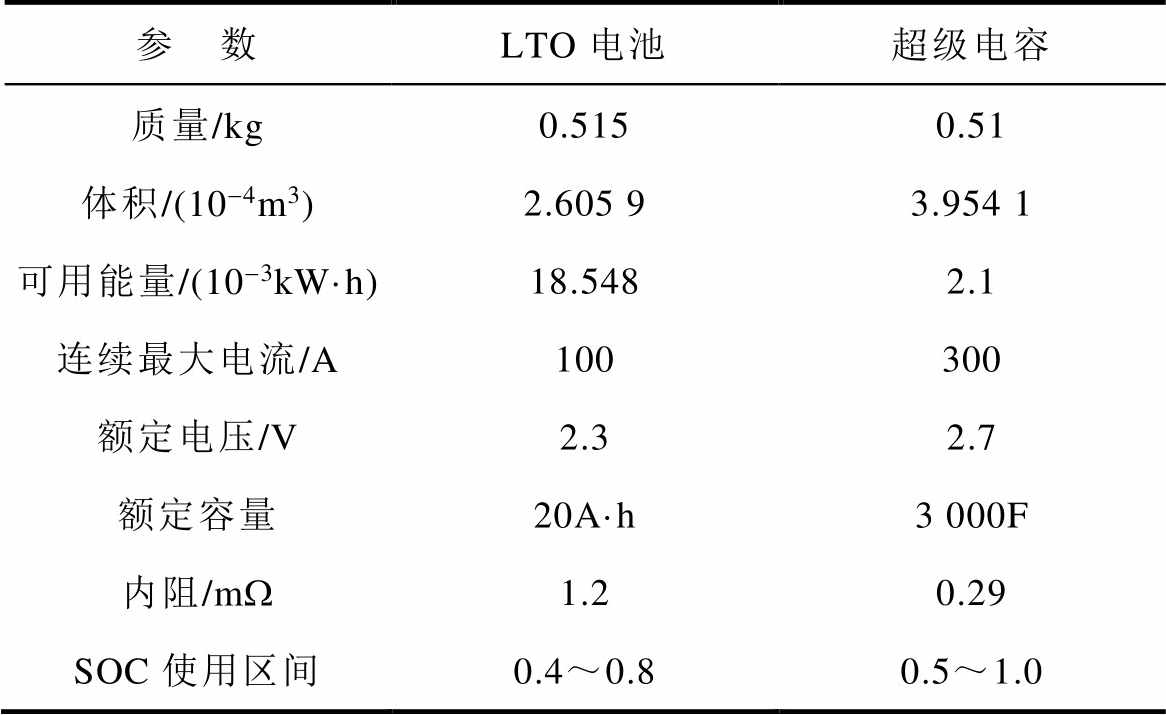
参 数LTO电池超级电容 质量/kg0.5150.51 体积/(10-4m3)2.605 93.954 1 可用能量/(10-3kW·h)18.5482.1 连续最大电流/A100300 额定电压/V2.32.7 额定容量20A·h3 000F 内阻/mW1.20.29 SOC使用区间0.4~0.80.5~1.0
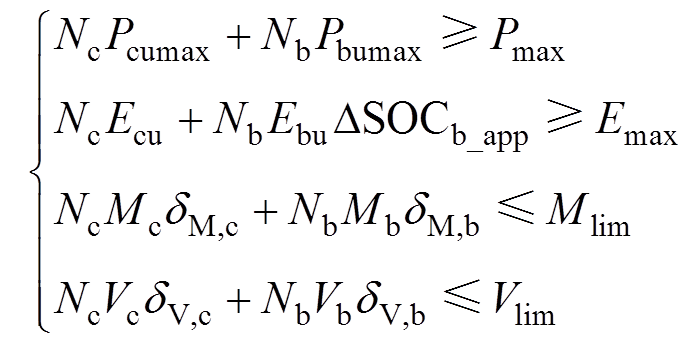 (19)
(19)式中,Pcumax、Pbumax分别为超级电容单体、电池单体的最大功率;Ecu、Ebu分别为超级电容单体、电池单体的最大储能量;dM,c、dV,c,dM,b、dV,b分别为超级电容、电池的质量、体积封装系数,显然,电池与电容的最大功率在其最大电流处取得。由以上4个限制不等式可以在Nb、Nc的坐标系中得到该ESS配置的可行域,如图7所示。
其中,电池单体与超级电容单体的最大功率在最大电流处取得,有
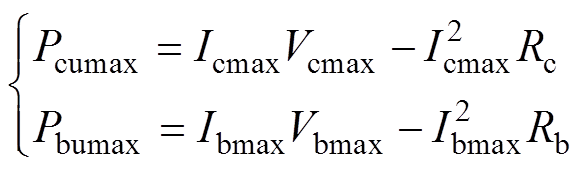 (20)
(20)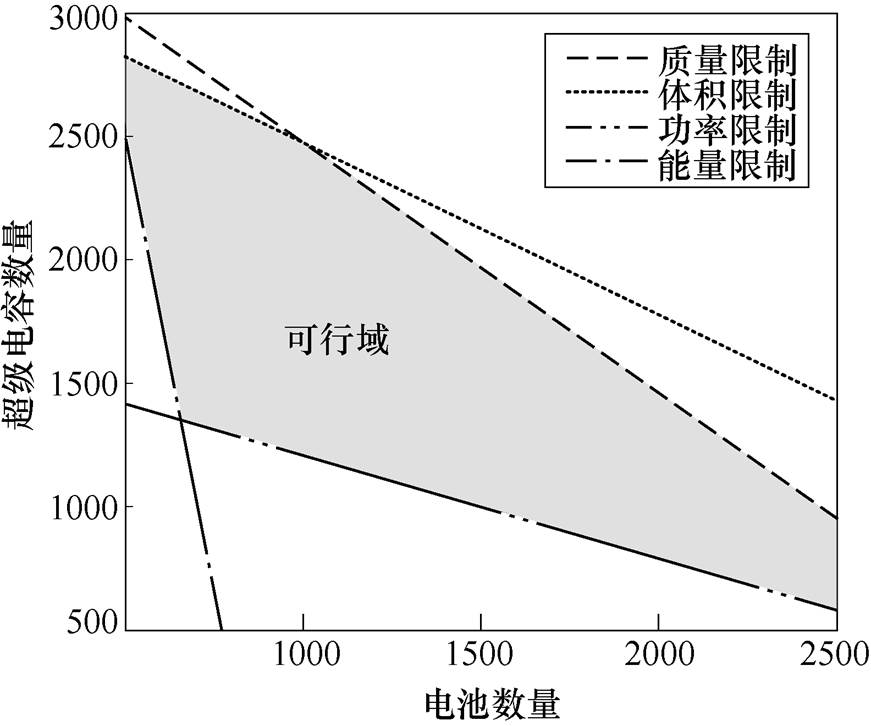
图7 ESS配置的可行域
Fig.7 Feasible domain of ESS configuration
在该可行域内,基于改进型凸优化算法求取帕累托解集的步骤如下:
(1)外层遍历质量指标。基于工程经验,选定合适的质量指标步长,通过向下平移质量限制曲线来改变质量这一目标。
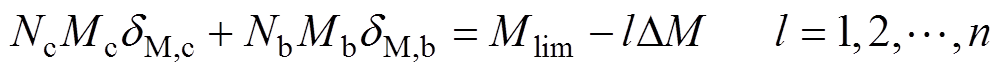 (21)
(21)式中,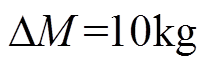 ,依照该步长,可得到一族间隔为10kg的等质量线。
,依照该步长,可得到一族间隔为10kg的等质量线。
(2)内层优化。在质量指标确定的情况下,通过凸优化,确定能耗最小的EMS与ESS,得到帕累托非支配解。
(3)重复步骤(1)和步骤(2),直至凸优化算法在某一质量指标下无法得到可行解,退出循环。
ESS的帕累托前沿如图8所示,这些解组成的解集是帕累托前沿的较为光滑的子集[23],可用来分析工程问题。
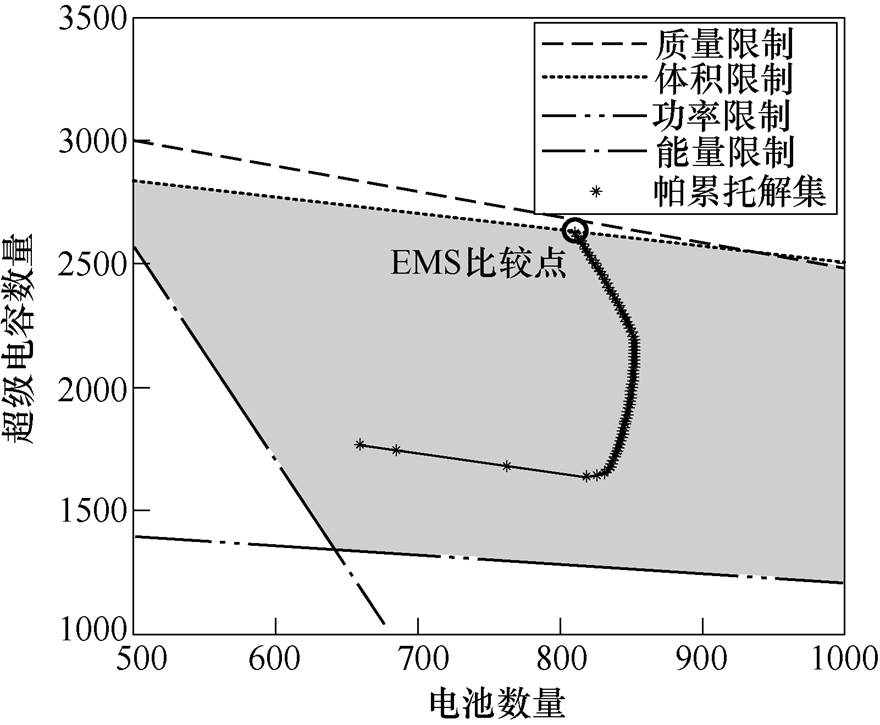
图8 ESS的帕累托前沿
Fig.8 Pareto frontier of ESS
基于改进型的凸优化算法,对EMS与ESS进行了协同优化,本节分别对EMS与ESS的优化结果进行分析。
3.3.1 EMS优化结果分析与比较
以图8的EMS比较点为例,对三种能量管理策略比例法、阈值法[13]与凸优化所得到的功率分配方法进行分析比较。
最优比例法(Optimal Proportion, OP)、最优阈值法(Optimal Threshold, OT)中参数的选取原则是能够使有轨电车完整运行并且耗能最小。优化所得参数比例值为0.51,阈值为140kW。其功率曲线如图9所示。
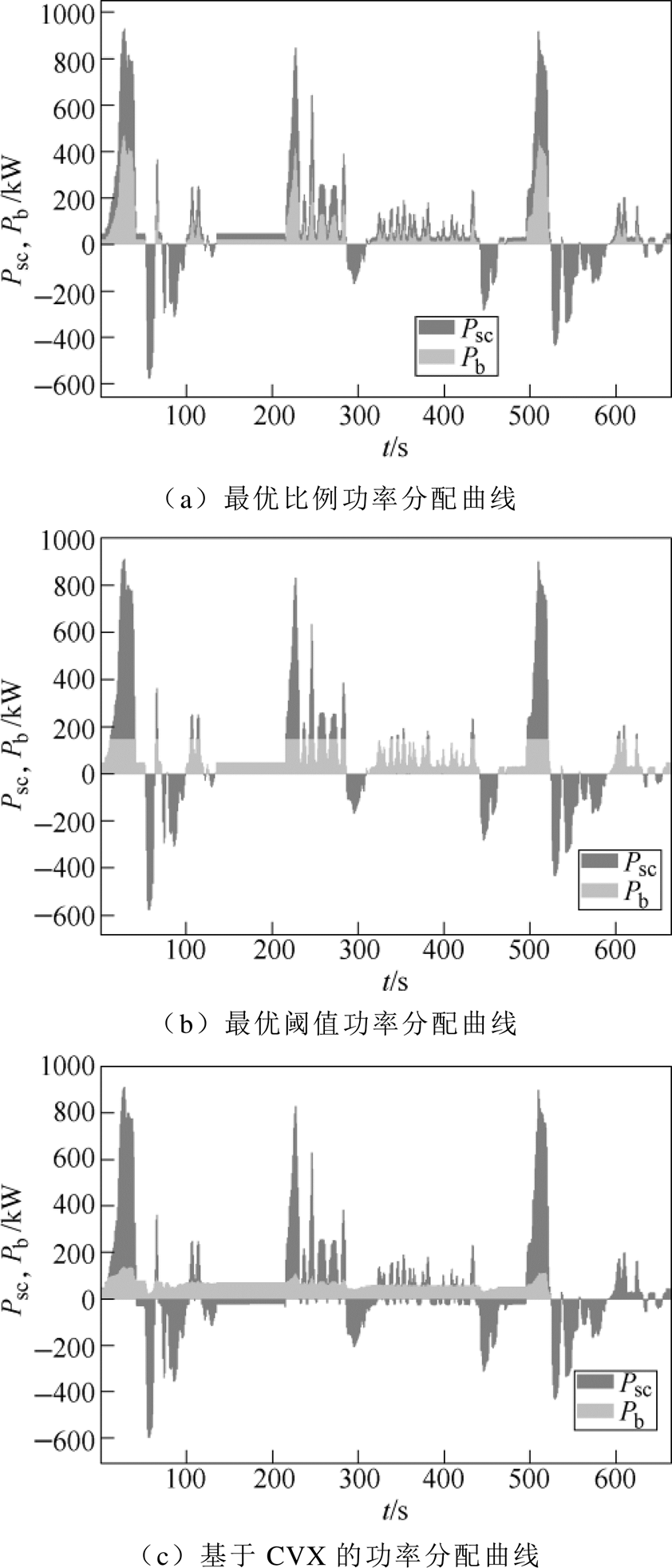
图9 三种EMS的功率分配曲线
Fig.9 Power distribution curves of three EMS
为了对三种EMS下的电池与超级电容的工作情况进行深入分析,对其效率点的分布作了仿真,并将其画在等效率曲线图上,如图10所示。图中,三种EMS的超级电容的工作点基本都分布在效率大于98%的区域,从三者的超级电容工作点的分布来看,其所导致三种EMS之间的能耗差很小,而电池的工作点差异则比较明显。CVX的电池工作点基本上都处于效率97%区域以内,主要集中在98%附近;比例法的电池工作点则有一部分超出了电池的功率限制[20],对电池寿命极为不利;阈值法的工作点基本上都处于效率图95.5%区域以内。
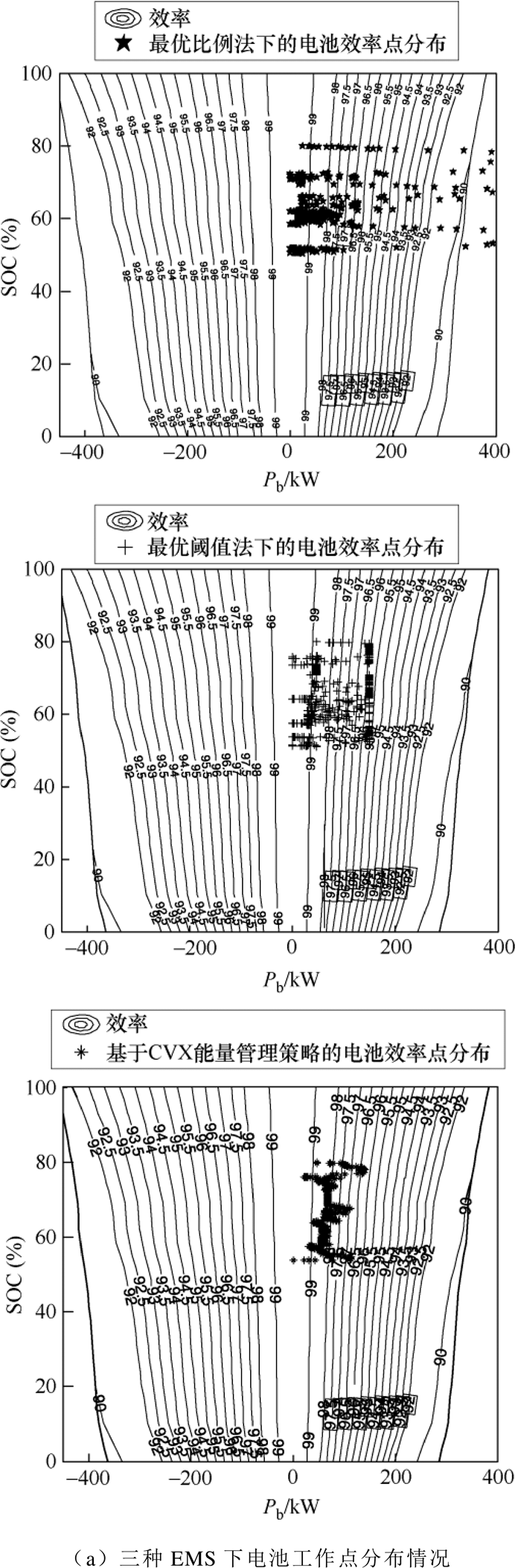
图10 三种EMS下电池与超级电容的工作点分布
Fig.10 Distribution of operating points of batteries and supercapacitors under three EMS
CVX得到的能量管理策略存在电池与超级电容能量交互的时段,能量交互能够使得电池的功率波动减小,电池工作在效率更高的工作状态,而且也可以在需求功率比较小的时候给超级电容充电,使超级电容尽可能地工作在高电压状态,即高效率状态。
对三种EMS的能量损耗[16-17, 26]进行计算,不同EMS能耗比较见表2,可以看到,CVX所得的EMS效率是最高的,其能量损耗相比于OP、OT,分别减少了39.58%、14.75%。
表2 不同EMS能耗比较
Tab.2 Comparison of different EMS energy consumption
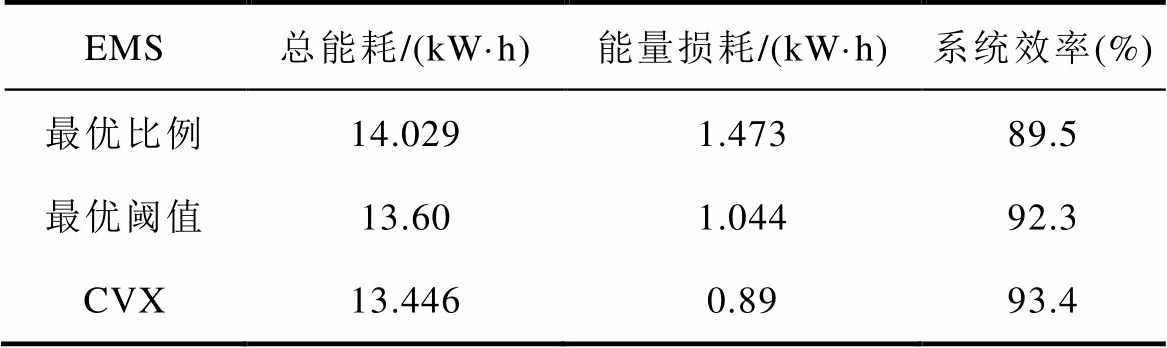
EMS总能耗/(kW·h)能量损耗/(kW·h)系统效率(%) 最优比例14.0291.47389.5 最优阈值13.601.04492.3 CVX13.4460.8993.4
3.3.2 ESS优化结果分析与比较
目前应用于有轨电车的储能系统主要分为单储能和混合储能系统[1-4],单储能系统主要指的是电池(Battery, BAT)单储能系统与超级电容(Super Capacitor, SC)单储能系统。为了对三种储能系统的性能优劣作对比,分别对三种储能系统的耗能指标与质量指标做了比较。
图11是基于实际功率曲线仿真得到的三种ESS的能耗-质量(E-M)帕累托前沿,可以看出,三种混合储能系统分别适于在不同的质量范围内使用。
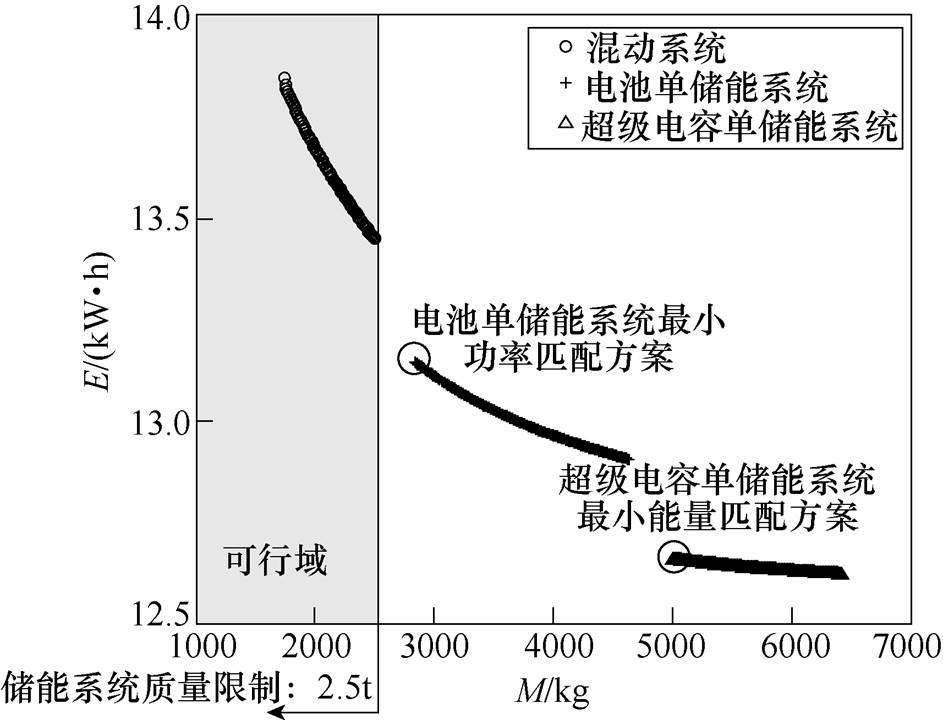
图11 三种ESS的E-M双指标帕累托前沿
Fig.11 E-M double index Pareto frontier of three ESS
对BAT系统来说,功率限制是其制约因素,对SC系统来说,能量限制是其制约因素,这些限制都导致了单储能系统的质量过大,当然,在车体的质量限制宽松的情况下,安装SC系统是最合算的。SC系统的耗能是最小的,其次是BAT系统,对混合储能系统来说,因为增加了DC-DC变换器,导致其能耗增加。但是该有轨电车储能系统的质量限制是2.5t,由图11可得,只有混合储能系统可以满足要求。
本文为了解决混合储能系统EMS与ESS协同优化的问题,在凸优化算法的基础上,提出了一种改进型的凸优化算法。在质量一定的条件下,寻找能耗最小的非支配解,通过质量指标的遍历,得到混合储能系统的能耗-质量双目标帕累托前沿。
相比于最优比例法、最优阈值法,改进型凸优化算法得到的EMS的电能损耗分别降低了39.58%、14.75%,改进型凸优化算法所得到的功率分配方式能够有效地提升系统效率,降低系统损耗。
相比于单储能系统,混合储能系统质量轻,体积小,但是耗能比较大。在质量限制宽松时,优先选用SC与BAT单储能系统。但是储能系统过重会给有轨电车带来过大的负担,挤占有轨电车的运营空间。混合储能系统与单储能系统的选取需要结合实际情况具体分析。在严苛的质量限制下,混合储能系统仍然是一种不可替代的解决方案。
参考文献
[1] Ratniyomchai T, Tricoli P, Hillmansen S. Recent developments and applications of energy storage devices in electrified railways[J]. IET Electrical Systems in Transportation, 2014, 4(1): 9-20.
[2] Mir L, Etxeberria-Otadui I, Arenaza I P D, et al. A supercapacitor based light rail vehicle: system design and operations modes[C]//IEEE Energy Conversion Congress and Exposition, San Jose, CA, 2009: 1632- 1639.
[3] Lhomme W, Delarue P, Barrade P, et al. Design and control of a supercapacitor storage system for traction applications[C]//IEEE Industry Applications Conference, Fourtieth IAS Annual Meeting, Kowloon, HongKong, China, 2005, DOI: 10.1109/IAS.2005. 1518724.
[4] Fernandez L M, Garcia P, Carlos Andrés Garcia, et al. Hybrid electric system based on fuel cell and battery and integrating a single DC/DC converter for a tramway[J]. Energy Conversion and Management, 2011, 52(5): 2183-2192.
[5] 张纯江, 董杰, 刘君, 等. 蓄电池与超级电容混合储能系统的控制策略[J]. 电工技术学报, 2014, 29(4): 335-340.
Zhang Chunjiang, Dong Jie, Liu Jun, et al. A control strategy for battery-ultracapacitor hybrid energy storage system[J]. Transactions of China Electro- technical Society, 2014, 29(4): 334-340.
[6] 程龙. 新能源城轨车辆车载储能系统的关键技术研究[D]. 北京: 北京交通大学, 2018.
[7] 诸斐琴, 杨中平, 林飞, 等. 基于加速时间预测的现代有轨电车储能系统能量管理与容量配置优化研究[J]. 电工技术学报, 2017, 32(23): 158-166.
Zhu Feiqin, Yang Zhongping, Lin Fei, et al. Research on acceleration-time-prediction-based energy manage- ment and optimal sizing of onboard energy manage- ment system for modern trams[J]. Transactions of China Electrotechnical Society, 2017, 32(23): 158- 166.
[8] Mesbahi T, Khenfri F, Rizoug N, et al. Combined optimal sizing and control of Li-ion battery/ supercapacitor embedded power supply using hybrid particle swarm-nelder-mead algorithm[J]. IEEE Transactions on Sustainable Energy, 2017, 8(1): 59-73.
[9] Shen Junyi, Dusmez S, Khaligh A. Optimization of sizing and battery cycle life in battery/ultracapacitor hybrid energy storage systems for electric vehicle applications[J]. IEEE Transactions on Industrial Informatics, 2014, 10(4): 2112-2121.
[10] Herrera V I, Gaztanaga H, Milo A, et al. Optimal energy management of a battery-supercapacitor based light rail vehicle using genetic algorithms[C]//IEEE Energy Conversion Congress and Exposition, Montreal, QC, 2015: 1359-1366.
[11] García Pablo, Fernández Luis M, Torreglosa J P, et al. Operation mode control of a hybrid power system based on fuel cell/battery/ultracapacitor for an electric tramway[J]. Computers & Electrical Engineering, 2013, 39(7): 1993-2004.
[12] 王玙, 杨中平, 林飞, 等. 有轨电车车载混合储能系统动态比例分配策略[J]. 电工技术学报, 2019, 34(增刊1): 405-413.
Wang Yu, Yang Zhongping, Lin Fei, et al. Dynamic proportion allocation strategy of hybrid energy storage system on tram [J]. Transactions of China Electrotechnical Society, 2019, 34(S1): 405-413.
[13] 王玙, 杨中平, 李峰, 等. 有轨电车混合动力系统能量交互型管理策略与容量配置协同优化研究[J]. 电工技术学报, 2019, 34(8): 1780-1788.
Wang Yu, Yang Zhongping, Li Feng, et al. Research on collaborative optimization of energy interaction management strategy and capacity configuration for tram hybrid system[J]. Transactions of China Elec- trotechnical Society, 2019, 34(8): 1780-1788.
[14] Herrera V, Milo A, Gazta Aga H, et al. Adaptive energy management strategy and optimal sizing applied on a battery-supercapacitor based tramway[J]. Applied Energy, 2016, 169(1): 831-845.
[15] Wang Yu, Yang Zhongping, Fei Lei. Optimization of energy management strategy and sizing in hybrid storage system for tram[J]. Energies, 2018, 11(4): 752-769.
[16] Hu Xiaosong, Murgovski N, Johannesson L M, et al. Optimal dimensioning and power management of a fuel cell/battery hybrid bus via convex program- ming[J]. IEEE/ASME Transactions on Mechatronics, 2015, 20(1): 457-468.
[17] Murgovski N, Johannesson L, Hu Xiaosong, et al. Convex relaxations in the optimal control of elec- trified vehicles[C]//IEEE American Control Con- ference, Chicago, IL, 2015: 2292-2298.
[18] Zhang Shuo, Xiong Rui, Cao Jiayi. Battery dura- bility and longevity based power management for plug-in hybrid electric vehicle with hybrid energy storage system[J]. Applied Energy, 2016, 179(1): 316-328.
[19] Hu Xiaosong, Murgovski N, Johannesson L M, et al. Comparison of three electrochemical energy buffers applied to a hybrid bus power train with simultaneous optimal sizing and energy management[J]. IEEE Transactions on Intelligent Transportation Systems, 2014, 15(3): 1193-1205.
[20] 李秀磊, 耿光飞, 季玉琦, 等. 考虑实际运行的配电网电池储能系统的优化配置研究[J]. 电力系统保护与控制, 2017, 45(9): 88-94.
Li Xiulei, Geng Guangfei, Ji Yuqi, et al. Research on optimal configuration of battery energy storage system in distribution network considering actual operation[J]. Power System Protection and Control, 2017, 45(9): 88-94.
[21] Knoke T, Romaus C, Bocker J, et al. Energy management for an onboard storage system based on multi-objective optimization[C]//IECON 2006-32nd Annual Conference on IEEE Industrial Electronics, Paris, 2006: 4677-4682.
[22] Shen Junyi, Dusmez S, Khaligh A. Optimization of sizing and battery cycle life in battery/ultracapacitor hybrid energy storage systems for electric vehicle applications[J]. IEEE Transactions on Industrial Informatics, 2014, 10(4): 2112-2121.
[23] 张弛. 现代有轨电车车载混合储能系统能量管理优化研究[D]. 北京: 北京交通大学, 2018.
[24] 诸斐琴, 杨中平, 林飞, 等. 城轨交通牵引供电系统参数与储能系统容量配置综合优化[J]. 电工技术学报, 2019, 34(3): 135-144.
Zhu Feiqin, Yang Zhongping, Lin Fei, et al. Comprehensive optimization of urban rail transit traction power supply system parameters and energy storage system capacity allocation[J]. Transactions of China Electrotechnical Society 2019, 34(3): 135-144.
[25] 吴寿松. 蓄电池技术发展综述[J]. 电气技术, 2005, 6(4): 7-10.
Wu Shousong. Summary of battery technology deve- lopment[J]. Electrical Engineering, 2005, 6(4): 7-10.
[26] 丁若星, 董戈, 吴和平, 等. 混合储能系统功率分配效果的表征参数研究[J]. 电工技术学报, 2016, 31(增刊1): 184-189.
Ding Ruoxing, Dong Ge, Wu Heping, et al. Research on power sharing results parameterization of hybrid energy storage system[J]. Transactions of China Electrotechnical Society 2016, 31(S1): 184-189.
Pareto Solution Set of Tram Hybrid Energy Storage System Capacity Allocation Based on Improved Convex Optimization
Abstract Capacity allocation affects the operational feasibility and economic benefits of hybrid electric tram, which is the basic link in the design of hybrid electric system. Energy management strategy (EMS) and capacity allocation are coupled and influenced each other. Based on this characteristic, an improved convex (CVX) optimization algorithm for collaborative optimization of capacity allocation and energy management strategy is proposed. Firstly, the feasible region of capacity allocation is solved, and a family of equal weight lines is constructed in the feasible region. Under each equal weight line, the optimal group point of capacity allocation and EMS with minimum energy consumption is found. The dual-objective Pareto frontier of hybrid power system weight and energy consumption is obtained. Compared with the single energy storage system, the hybrid energy storage system is light in weight and small in volume. It is suitable for the situations with strict requirements on weight and volume. The simulation comparison shows that the EMS of collaborative optimization is efficient and the power distribution is reasonable.
keywords:Tramcar, hybrid energy storage system, capacity configuration, convex optimization, Pareto solution set
DOI: 10.19595/j.cnki.1000-6753.tces.190712
中图分类号:TM921
安星锟 男,1994年生,硕士研究生,研究方向为城市轨道交通车载混合储能技术。E-mail: 17121411@bjtu.edu.cn
杨中平 男,1970年生,教授,博士生导师,研究方向为轨道交通电力牵引传动和节能技术。E-mail: zhpyang@bjtu.edu.cn(通信作者)
收稿日期 2019-06-12
改稿日期 2019-11-22
中央高校基本科研业务费专项资金(2018YJS153)和国家重点研发计划项目(“十三五”计划)(2017YFB1201105)资助。
(编辑 崔文静)