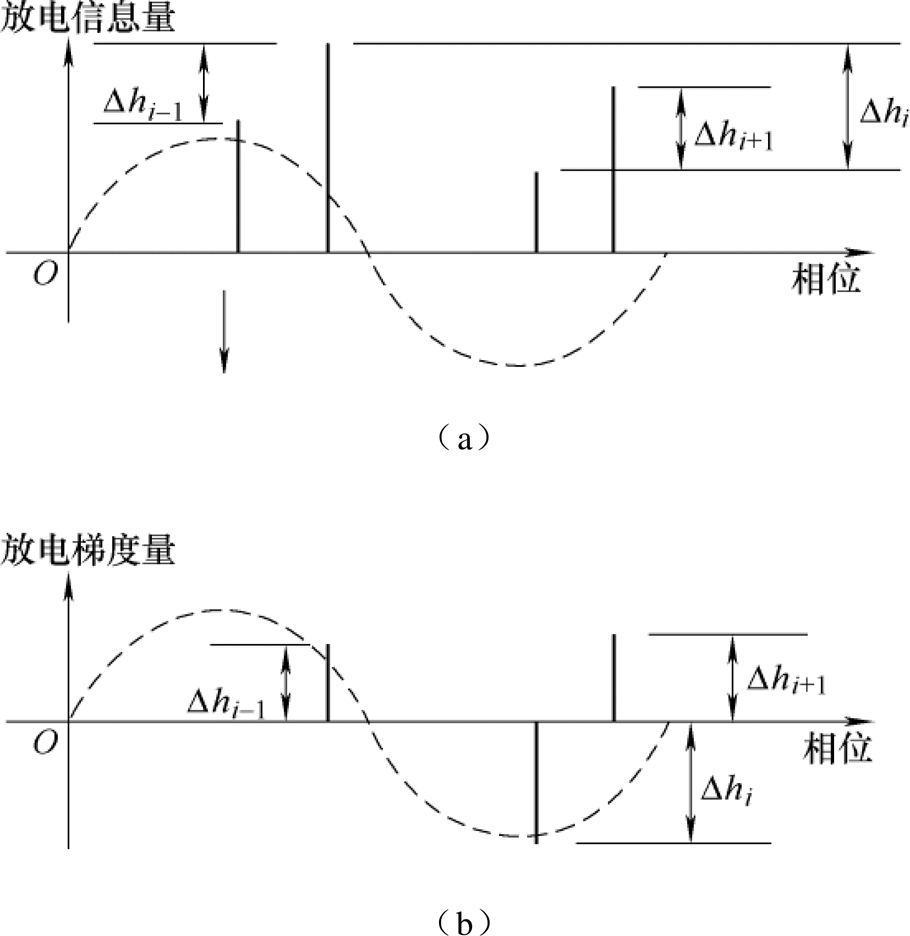
图1 构造“相位-梯度”谱图
Fig.1 Constructing "phase-gradient" spectra
摘要 针对局部放电中可能出现新的不属于已知放电类型的未知样本，提出一种基于变量预测-谷本相似度（VPM-Tanimoto similarity）的未知类型信号识别方法。构建梯度谱图实现未知信号的表达，并使用两个指标来对样本分区域过滤以分离出未知类。首先，构建j-Dj、j-Du、j-Dqmax、j-Dn梯度模式和j-n谱图模式并提取特征。其次，对各已知类放电建立相应的VPM模型组并预测样本的特征向量。再次，计算样本和各已知类放电的Tanimoto相似度，获得与样本最匹配的已知类别。然后，计算识别结果的可靠率（IDAR）并划分可靠率空间，不同的区域有不同的判定方法。最后，利用Tanimoto相似度和各区域的IDAR对所有信号进行双重过滤以判定并分离出未知样本。实验结果表明，该方法取得了一定的识别效果。
关键词：局部放电 未知类型 谱图 谷本相似度 可靠率
电力变压器的绝缘状态会直接影响电网的安全稳定运行，局部放电（Partial Discharge, PD）是变压器内部绝缘劣化的重要先兆[1]。不同的放电类型一般有不同的发展趋势和不同的发生位置[2]，及时识别放电类型有助于进一步实施检修工作。
在PD信号的特征提取领域，通常先构造具有一般性的图谱模式，再提取统计参数指纹特征，以形成特征指纹库。常见的谱图模式有局部放电脉冲序列分布模式（Phase Resolved Pulse Sequence, PRPS）和局部放电相位模式（Phase Resolved Partial Discharge, PRPD）[3]。PRPS模式包含CIGRE提出的标准局部放电形式的全部放电信息[4-5]，可以直观地体现放电量与放电相位、放电时间的关系。PRPD模式是统计PRPS序列在多个周期内的放电指标，形成简洁的j-n、j-qsum、j-qave、j-qmax谱图[6]。
在PD信号的分类领域，众多学者使用机器学习算法识别放电类型，主要有支持向量机[7]（Support Vector Machine, SVM）、聚类[8-9]、概率神经网络[10]和卷积神经网络[11]等。
上述方法能满足常规的放电信号分类问题，但随着电力设备制造工艺、材料方面的改进，可能会有新放电类型或者别的非放电信号出现。这些信号不属于放电库中的常规已知放电类，它们可能取决于放电材料、放电强度、电磁干扰等，本文将此称为“未知类”。监督学习分类方法只能识别已知的常规类型，若有不属于已知类的新信号出现，则会被误判为某种已知类别。放电信号的识别中应包含一个对未知类的识别分支。
有关未知类信号判定和分离方面的研究非常少。文献[12-13]通过智能算法得到训练集和待识别样本集的某一指标，并在该指标上选取一个合适的阈值隔开样本里的已知、未知类。文献[14]将所有已知类样本用一个图形围合，以隔开未知类。上述文献默认了测试集中含有未知样本并对未知放电类型进行了有效分离，然而测试集中是否含有未知类型正是需要判定的。此外，未知类型也可能并不是放电信号。实际上，由于未知类型的种类复杂度高，很难找到一个合适的指标、一个合适的阈值能够满足所有未知类的分离要求。
针对现有未知类信号识别研究的不足，本文从特征提取和分类算法两方面展开研究：特征提取方面，考虑到未知类型可能为非放电信号，常用的放电谱图可能不满足所有未知信号的特征表达，本文初步分析PRPS序列的各放电参数，构造了j-Dj、j-Du、j-Dqmax和j-Dn梯度模式并结合j-n谱图形成了5个模式组，试图实现未知信号的清晰表达；分类算法方面，由于未知信号种类繁多，难以统一衡量，故考虑从多个角度分析已知类样本特点，用多个指标对样本过滤，只要有一个指标不满足已知类要求，就判为未知类型。本文从Tanimoto相似度和可靠率（Integrator Discriminant Analysis Rule, IDAR）两方面挖掘已知类信号特点，并对IDAR分区域讨论。提出了基于变量预测-谷本相似度（Variable Predictive Model and Tanimoto similarity, VPM-Tanimoto）的方法识别未知类信号。VPM能有效地提取各类放电特征间的关系并生成符合某一类型特点的新向量。Tanimoto相似度可从模值和角度两方面体现向量差异，还未用于放电信号的匹配。可靠率IDAR反应了相似度的可信程度，可作为相似度指标的补充。利用Tanimoto相似度和IDAR对所有放电信号进行双重过滤来识别各已知、未知类局部放电。针对现有研究中未知类定义的单一性，本文增加了未知类样本复杂度，使用实验室模型生成的板对板放电、不同电压不同材料的悬浮颗粒放电、电晕、多尖对板放电、染噪样本和白噪声进行识别效果测试。
学者Patch和Hoof指出局部放电的再次发生很大程度上取决于电压梯度而非电压值本身[5]。文献[15]基于PRPS模式构造了j-Dj 图谱，使用相位梯度信息避免了测量环境的影响。梯度相当于对信号求导，在一定程度上更能反映信号的本质规律，有助于已知、未知类信号更好的表达。基于此点，本文构造梯度谱图。传统的PRPD二维图谱统计了某相位处的放电量q、放电次数n。故与局部放电信号有关的量共有8个：时间t、相位j、电压u；放电发生时对应的时刻值t0、相位j0、电压值u0；某一相位处的放电量q和放电次数n。局部放电是一个复杂的过程，难以直接描述，可以选取与局部放电有关的量作为局部放电的结果，这些与局部放电有关的量就可认为是因变量。上述8个量中，前3个为自变量；中间3个是产生局部放电的原因，可以理解为只有t、j、u达到了某一限值才能发生放电，属于因变量；最后2个是对局部放电的统计结果，也属于因变量。“自变量-因变量”的构造能够体现放电过程。
时间和相位信息存在冗余，本文以相位j 作为自变量，对j0、u0、q和n构造“相位-因变量梯度”图谱。此外放电产物q和n是重要的放电信息，但q值极易受干扰，故只取j-n谱图。
PRPD谱图为统计谱图，比较稳定，本文在PRPD谱图的基础上求梯度谱图，这里取j-qmax图谱。该谱图中的每一个非零值的横坐标代表在此相位处会发生放电，即可以监测一个周期内放电发生时的相位，这样便可得到j-j 谱图。由放电发生时的相位可求得此刻的外施电压，得到j-u谱图。
“相位-梯度”谱图的构造过程如图1所示。图1a的横坐标为相位j，纵坐标表示与放电相关的信息量，包括j、u、qmax和n，即可用图1a表示j-j、j-u、j-qmax和j-n谱图。图1a中某一相位处的放电信息与相邻的前一个放电信息之差即为图1b中该相位处的放电梯度Dhi，据此处理得到j-Dj、j-Du、j-Dqmax和j-Dn谱图。j-j 谱图的值递增，由图1b可知j-Dj 谱图的值为正；j-Du、j-Dqmax和j-Dn这3个谱图的值有正有负。需将这3个谱图整体向纵坐标正方向平移，直至恰好没有负值。这样可得到j-Dj、j-Du、j-Dqmax、j-Dn和j-n共5个谱图。
图1 构造“相位-梯度”谱图
Fig.1 Constructing "phase-gradient" spectra
本文先判断待识别样本所属的具体已知类型，再使用相似度和可靠率衡量这些样本是否真的是已知类。过滤掉的样本可认为是未知类。
2.1.1 VPMCD基本原理
基于变量预测模型的模式识别（Variable Predictive Model based on Class Discriminate, VPMCD）是由Rahuraj等提出的一种模式识别方法[12]。不同类样本特征间的相互关系不同。VPM可通过式（1）实现特征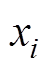
的表征。式（1）包含了线性模型（L）、线性交互模型（LI）、二次交互模型（QI）和二次模型（Q）[16]。
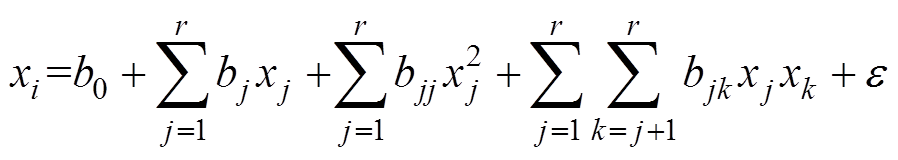（1）式中，b0、bj、bjk、bjj为模型参数；r为模型阶数；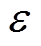
为预测误差；VPM可自动对式（1）进行参数寻优。
假设表征样本需要p维特征，第k类样本经训练可得到该类的p个变量预测模型VPM，记作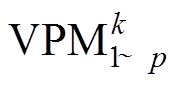
。VPMCD通常以特征预测误差二次方和最小为依据对模型寻优并将样本分类，即
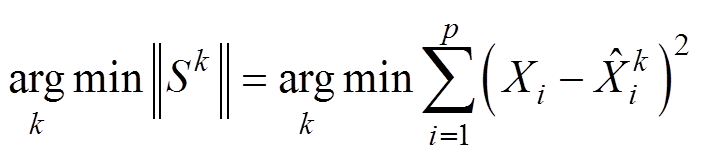（2）2.1.2 Tanimoto相似度
常用的相似性度量有余弦相似度（cosine similarity）、修正余弦相似度（adjusted cosine similarity）和皮尔逊相似度（pearson correlation similarity）。余弦相似度仅反映向量间的角度差异，后两者对其稍有改进。谷本相似度（Tanimoto similarity）主要用在匹配用户爱好、文档相似性等互联网领域，未曾用于局部放电。本文的相似度计算方法[17-18]为
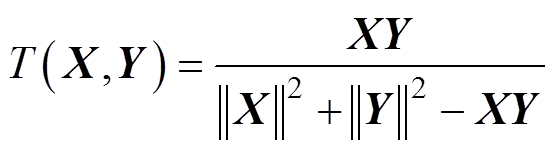（3）式中，X、Y为特征向量。
Tanimoto相似度考虑了向量的夹角和数值差异，值域为-1～1。值越大，向量越相似；值越小，越不相似。
2.1.3 VPM-Tanimoto识别已知放电类型
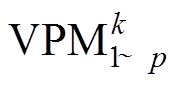可有效提取放电特征间的函数关系。若模型和输入向量的类别对应，则新向量和原向量相似；反之，不相似。这为匹配相似度创造了有利条件，而Tanimoto相似度可全面衡量向量差异，二者相辅相成。设训练样本共g类，每个样本的特征向量可表示为X=[x1 x2 … xp]。待识别样本的特征向量为F=[f1 f2 …fp]。识别已知类型的步骤如下：
（1）用训练集训练好每类放电的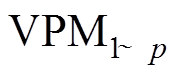
，可得到VPMg×p=
。
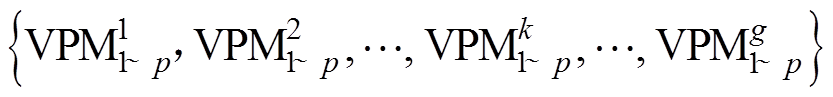（2）将某一Fk样本分别输入g类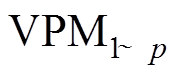中，得到各类模型对该样本的特征预测矩阵F=[F1F2…Fk …Fg]。
（3）分别计算各个Fk与原始向量Fk的Tamimoto相似度，可得T=[T1 T2 …Tk …Tg]。
（4）在矩阵T中找到最大相似度并记录其下标，若Tk为Tmax，则k为样本类别。
2.1.4 相似度识别分析
为了验证VPM-Tanimoto方法识别已知放电类型的效果，以VPM-Pearson和VPMCD分类方法作为对比，识别板对板、电晕、悬浮和多尖对板放电。结果见附表1。两种相似度方法都优于VPMCD，表明相似度更能细腻地刻画向量差距。
对样本相似度分析，发现若样本属于某一类别，则与该类别的相似度必然明显高于其他类别；若样本不属于任一类别，则会缩小相似值间的差异度。所以最大相似度和次大相似度的相对距离可反映识别结果的可靠率。基于此点，参照文献[19]中定义的相对识别因子，定义IDAR为
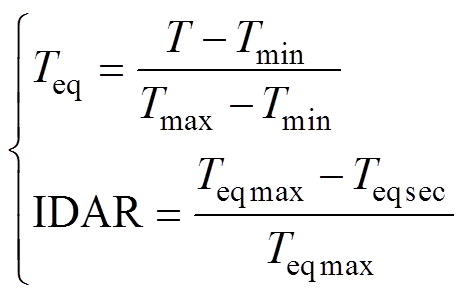（4）式中，Teq是将相似度从-1～1归一化到0～1区间后的值；Teqmax、Teqsec分别是归一化后的最大、次大相似度。下文中出现的相似度都是指归一化后的值。IDAR的取值范围在0～1间。
Teqmax和Teqsec的值相近时，IDAR接近于0；当二者差距较大时，IDAR的值接近于1。一般地，IDAR可将可靠率空间划分为三个区域：当IDAR＞50%时，区分明显、识别可靠；当IDAR＜25%时，识别不可靠；当25%＜IDAR＜50%时，识别较可靠[20]。
本文以已知类型为目标，以最大相似度和可靠率为条件对所有样本进行筛选，只要有一个指标不满足已知类要求，就判为未知类型。IDAR是由相似度计算得来，它所受的影响条件更复杂，可作为相似度指标的补充，在最大相似度达到一定值时对样本进行二次过滤。
当Tmax＜50%时，相似度还不到一半，认为是未知类型；当Tmax＞50%时，需结合IDAR判断样本是否为已知类。IDAR＞50%，可靠率高，是已知类；IDAR＜25%，可靠率不满足要求，认为是未知类；若IDAR在25%～50%之间，则样本属于模糊样本，不易直接判断是否为已知类型，需结合Tmax指标进一步设置判断规则，以防止样本的“误报”“漏报”。由于Tmax、IDAR的值域都为0～1，可将两个指标结合构造数学模型[21]为
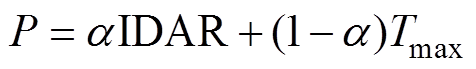（5）式中，a 为松弛因子；P值分布在0～1区间。调节a 得到一个合适的阈值以判断模糊区间的样本类型。
模糊样本的Tmax、IDAR分别在50%～100%、25%～50%区间。区间的端点值50%、100%、25%和50%是经验值。使用这些经验值定义模糊区间的识别阈值P，以提高模型的泛化能力。当Tmax、IDAR各取50%时，最大相似度明显高于次大相似度，即样本明显接近于某一类型，但Tmax的值刚达到要求，可认为刚达到识别概率门槛；当Tmax、IDAR各取100%，25%时，样本完全相似，但IDAR刚跨出不可靠边界，也可认为刚达到识别概率门槛。联立两个概率门槛如式（6）所示，可解得a =2/3，概率门槛P1，P2为50%。即P≥50%为已知类，否则为未知类。
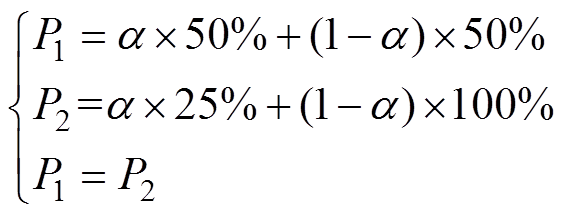（6）（1）构建j-n谱图和4个“相位-梯度”谱图，提取统计参数特征。
（2）训练好各已知类别放电的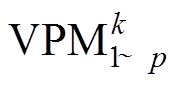模型。
（3）由2.1.3节识别步骤确定各待识别样本所属的具体已知类别。
（4）由最大相似度和次大相似度计算待识别样本的可靠率IDAR。
（5）由图2所示流程对样本进行筛选，确定未知类，图2中“已知类”为Tmax所在类别。
实验室分别构造板对板、电晕、悬浮和多尖对板放电模型，如附图1所示。其中悬浮放电包括悬浮小颗粒、36.5kV和29kV的悬浮大颗粒放电。试验标准为IEC 60270-2000，试验方法是采用并联测试电路并用脉冲电流法标定放电量，采用TWPD-2F局部放电综合分析仪[13]，采样频率为20～80MHz，带宽为40～300kHz。每个工频周期记录一个放电 数据。
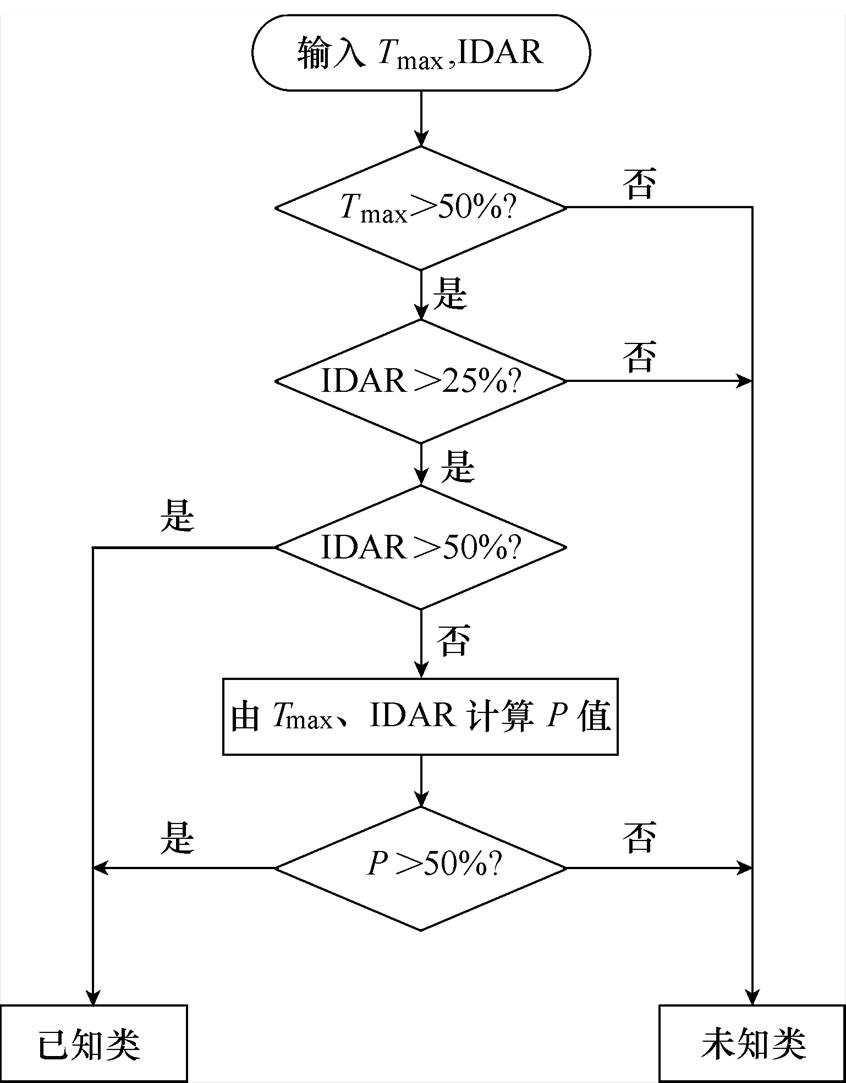
图2 流程
Fig.2 Flow chart
根据第1节方法可做出放电信号的梯度谱图，这里给出“板对板”放电的5个谱图如附图2所示。将板对板、电晕、36.5kV的悬浮大颗粒和多尖对板放电各取一例染噪，信噪比为0.2dB；另生成5例均值为0，方差为0.01的噪声样本。对“相位-梯度”及j-n谱图并提取统计特征。其主要有反应图谱形状差异的正、负半周偏斜度Sk、陡峭度Ku、局部峰值点数Pe和相位中值Mv以及反映轮廓差异的互相关系数CC、放电量因数QF和修正互相关系数Mcc共11个原始特征[22]。此外对传统的j-n、j-qsum、j-qave和j-qmax这4个谱图也提取前述特征作为对比。采用主成分分析降维（Principal Component Analysis, PCA）将所有特征降到两维，二维特征对比如图3所示。另给出板对板、电晕、36.5kV的悬浮大颗粒和多尖对板放电三维特征对比如附图3所示。
由图3可知，本文所提模式谱图能将噪声和板对板放电区分开，使36.5kV的悬浮大颗粒和多尖对板放电的差异更明显，各放电类型整体区分度比PRPD图谱高。附图3展示了不同类放电的三维特征差异，可见梯度谱图特征更简明集中，分散性小，类间差异更明显，有利于样本的进一步分类。
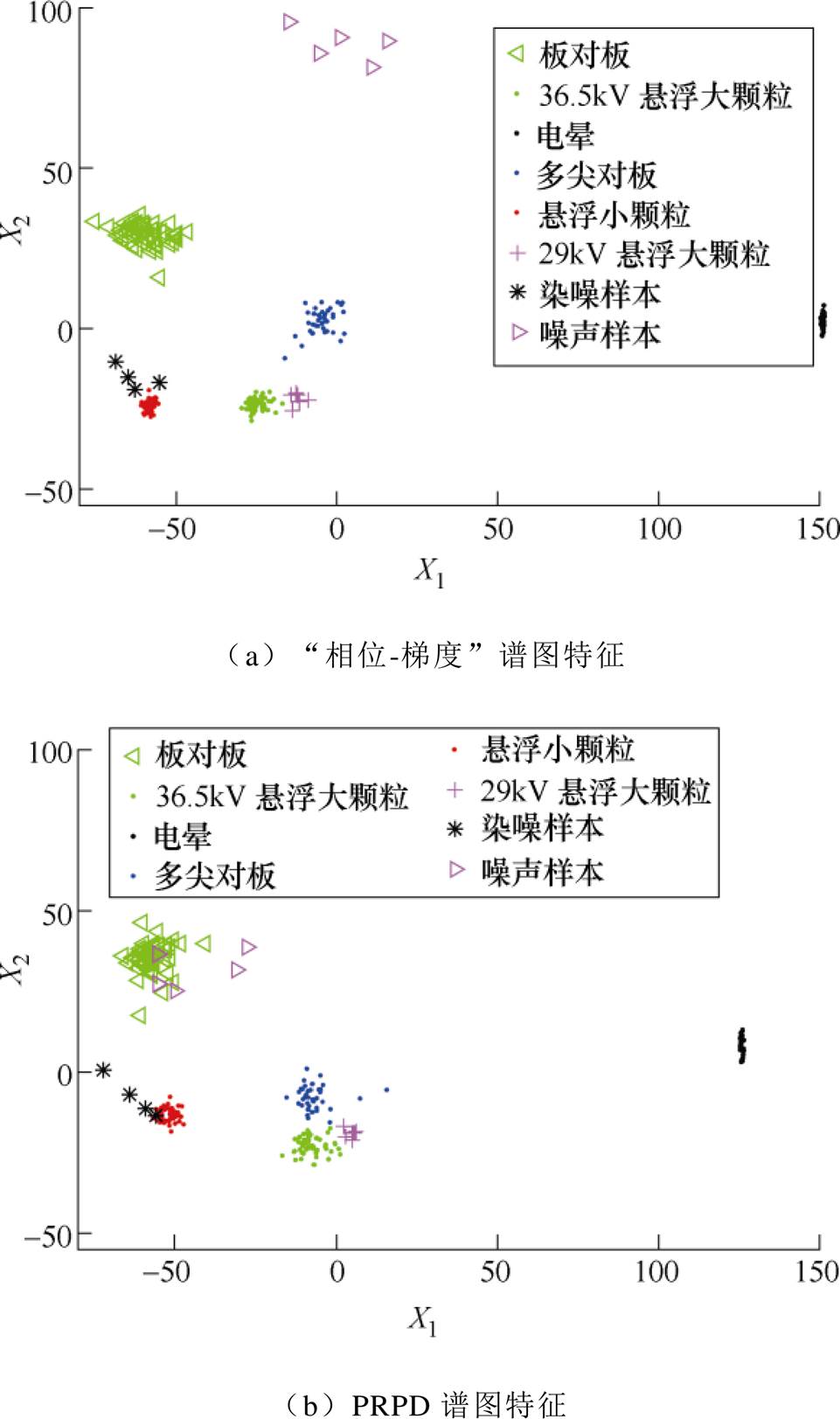
图3 二维特征对比
Fig.3 Two-dimensional feature contrast
VPM模型的特征参数一般取5个[23]，采用PCA算法将梯度谱图特征降到五维。在板对板、36.5kV的悬浮大颗粒中各抽取40组放电数据作为训练集。取上述两种放电各10组，另分别针对放电类型、材料、电场强度、样本污染等因素再取10组电晕和10组多尖对板、10组悬浮小颗粒、6组29kV悬浮大颗粒、4组染噪样本和5组噪声样本作为测试集。
由训练集可分别得到两种已知类型放电的VPM模型组，分别用两种VPM组生成特征向量，计算相似度，取最大相似度的VPM组的类别作为样本的已知类别，再由Tmax和IDAR筛选出未知类信号。另使用PRPD图谱作为对比，对测试集的识别结果见表1。
表1 测试集识别结果
Tab.1 Test set identification results
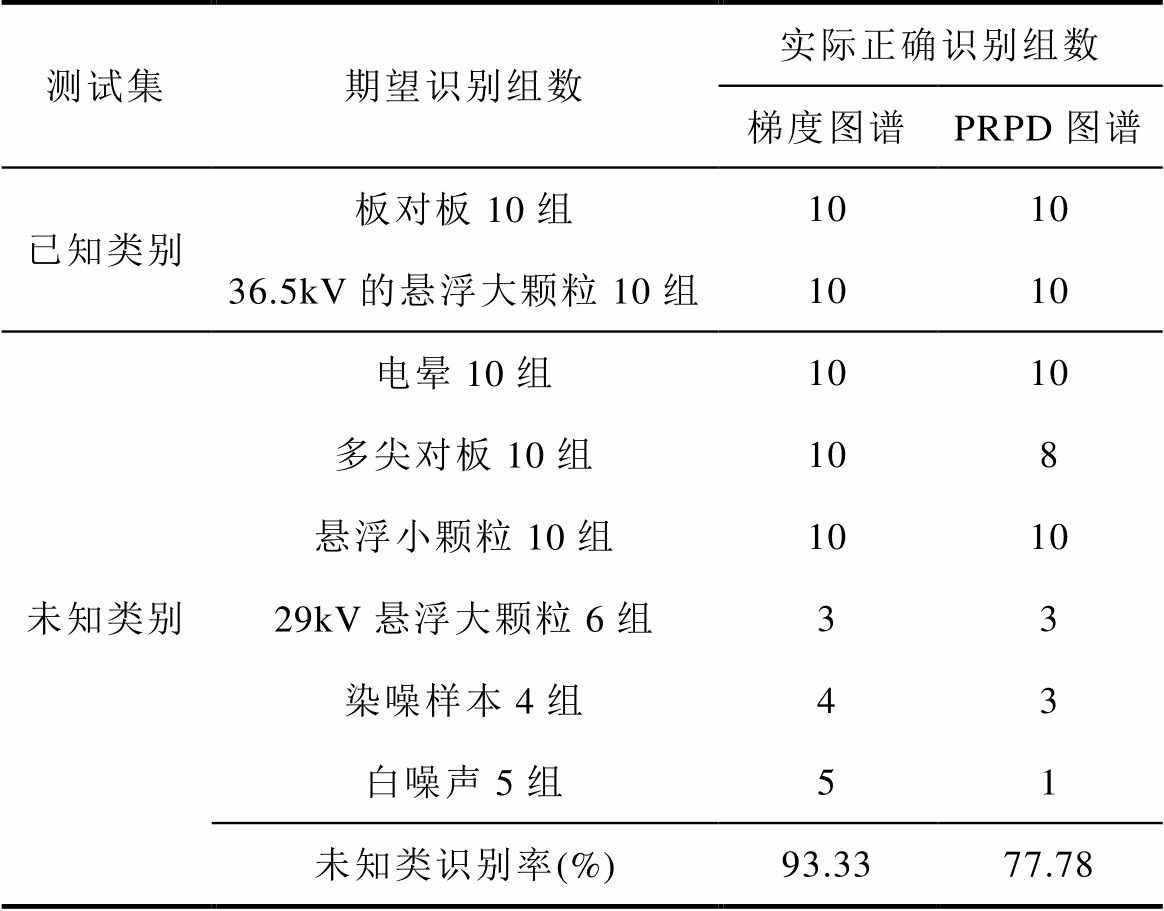
测试集期望识别组数实际正确识别组数 梯度图谱PRPD图谱 已知类别板对板10组1010 36.5kV的悬浮大颗粒10组1010 未知类别电晕10组1010 多尖对板10组108 悬浮小颗粒10组1010 29kV悬浮大颗粒6组33 染噪样本4组43 白噪声5组51 未知类识别率(%)93.3377.78
由表1可知本文方法对已知、未知类放电信号都有不错的识别效果。而PRPD图谱对复杂度高的未知类型信号特别是噪声样本的表征能力较差，如图3b所示，识别效果不如梯度谱图。
为了分析Tanimoto相似度和IDAR的作用，列出的本文方法测试集的Tmax和IDAR见表2。1～10组为板对板，11～20组为36.5kV的悬浮大颗粒，它们是已知类；21～30组为电晕，31～40组为多尖对板，41～50组为悬浮小颗粒，51～56组为29kV悬浮大颗粒，57～60组为染噪样本，61～65组为白噪声，它们为未知类。
由表2可知：
（1）由Tanimoto相似度计算得来的IDAR值较为稳定，说明这里的IDAR具有一定的参考价值。
（2）1～20组已知类测试样本的Tmax都高，接近于1。1～10组和15～20组测试样本（已知类）Tmax＞50%，IDAR在25%～50%区间。它们是通过进一步计算P值而将样本正确分类的。
（3）未知类样本的Tmax整体差距较大。大部分未知样本都可以通过Tmax＜50%过滤出来。第36组未知类样本的Tmax＞50%，它们是由于IDAR＜25%而被正确分类的。第39、40、51、52和56组未知样本Tmax＞50%，通过计算P值而被正确分类。即Tanimoto相似度和IDAR可有效监督放电信号。
将本文方法中的Tanimoto相似度换为Pearson相似度，对测试集的识别结果见表3。测试集的最大皮尔逊相似度和可靠率的值见附表2。
由表3可知，Pearson相似度对已知类样本的测试准确率没有影响，而未知类的准确率下降了很多。这是因为已知类测试样本和各已知类训练集的特征关系一致，那么由VPM预测的特征向量便接近于样本真实特征向量。两个本就相似的向量对相似度的计算方法要求低，故用Pearson相似度计算出的相似度依然很高，具体可见附表2的1～20组中Pmax差异。而未知类放电和已知类放电训练集存在部分不同之处，必须选择较好的相似度计算方法才能体现这种差异。故附表2中未知类相似度有的在0附近，有的接近于1，极不稳定。此外未知类IDAR的值也不稳定，这也是受Pearson相似度的影响，用其识别未知类不太可靠，逊于VPM-Tanimoto方法。
表2 测试集的Tmax和IDAR
Tab.2 Tmax and IDAR of test samples
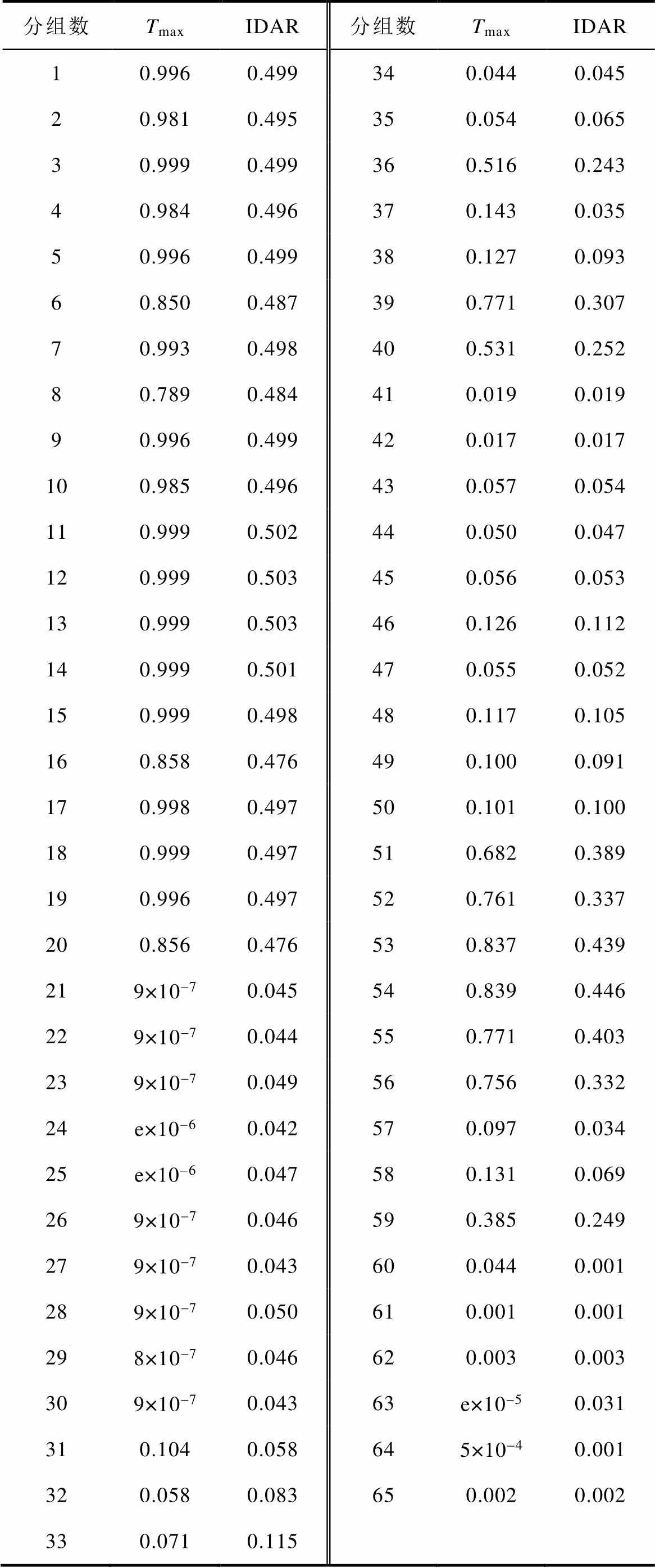
分组数TmaxIDAR分组数TmaxIDAR 10.9960.499340.0440.045 20.9810.495350.0540.065 30.9990.499360.5160.243 40.9840.496370.1430.035 50.9960.499380.1270.093 60.8500.487390.7710.307 70.9930.498400.5310.252 80.7890.484410.0190.019 90.9960.499420.0170.017 100.9850.496430.0570.054 110.9990.502440.0500.047 120.9990.503450.0560.053 130.9990.503460.1260.112 140.9990.501470.0550.052 150.9990.498480.1170.105 160.8580.476490.1000.091 170.9980.497500.1010.100 180.9990.497510.6820.389 190.9960.497520.7610.337 200.8560.476530.8370.439 219×10-70.045540.8390.446 229×10-70.044550.7710.403 239×10-70.049560.7560.332 24e×10-60.042570.0970.034 25e×10-60.047580.1310.069 269×10-70.046590.3850.249 279×10-70.043600.0440.001 289×10-70.050610.0010.001 298×10-70.046620.0030.003 309×10-70.04363e×10-50.031 310.1040.058645×10-40.001 320.0580.083650.0020.002 330.0710.115
表3 VPM-Pearson识别结果
Tab.3 VPM-Pearson recognition results
测试集Pearson识别率(%) 已知类20组100 未知类45组73.33
将本文方法与传统不含未知类分支的SVM方法、文献[13]的FCM加权聚类未知信号识别方法对比。分别对不含未知类的测试集、含有未知类的测试集进行识别，结果见表4、表5。SVM选用高斯核，调节高斯核参数。当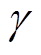
=0.18，C =3时，识别效果最好。
表4 不含未知类的测试集识别结果
Tab.4 Test set identification results without unknown types
测试集期望识别组数实际正确识别组数 SVMFCM本文方法 已知类别板对板10组101010 36.5kV的悬浮大颗粒10组10010
表5 含未知类的测试集识别结果
Tab.5 Test set identification results with unknown types
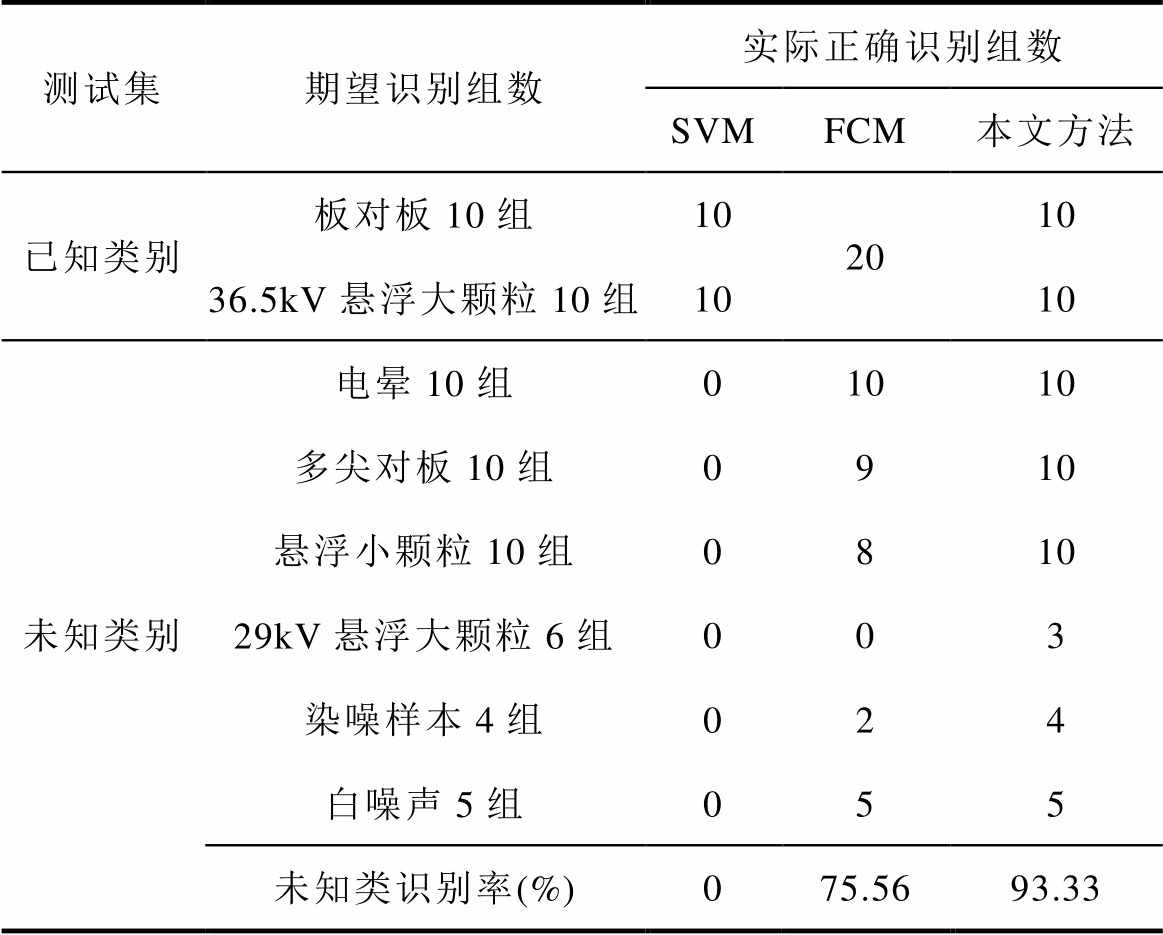
测试集期望识别组数实际正确识别组数 SVMFCM本文方法 已知类别板对板10组102010 36.5kV悬浮大颗粒10组1010 未知类别电晕10组01010 多尖对板10组0910 悬浮小颗粒10组0810 29kV悬浮大颗粒6组003 染噪样本4组024 白噪声5组055 未知类识别率(%)075.5693.33
由表4可知，测试集不含未知类时，SVM和本文方法都能识别各已知类型。FCM识别方法默认样本集含有未知类型，其将36.5kV悬浮大颗粒放电误判为了未知类。
由表5可知，测试集含有未知类时，由于SVM方法没有对未知类的识别分支，故对未知类没有识别能力，将未知类误判为了已知类型。FCM方法能识别未知类，但不能判定已知类样本的具体类型，此外FCM方法使用一个指标对未知类的识别效果逊于本文方法。本文将Tmax和IDAR两个指标结合来筛选出已知类样本，使未知类的识别更可靠，但对29kV的悬浮大颗粒识别效果不好，这可能是因为29kV和36.5kV的悬浮大颗粒属于同一类型不同电压的信号，其位置较近，如图3a所示，识别效果不够理想。
本文构造了“相位-梯度”模式谱图组，并提出了基于VPM-Tanimoto的未知类型信号识别方法。基于实验室的放电数据得到如下结论：
1）“相位-梯度”模式谱图能反映信号的特质，提取的特征比传统二维PRPD谱图分布集中。
2）本文扩展了未知类型样本的复杂度，由Tanimoto相似度和IDAR两个指标筛选放电信号，取得了一定的识别效果。
3）将VPM和Tanimoto相似度的优点结合，使得已知、未知类间的Tmax差异、IDAR差异更明显。
4）能够对待识别样本集中是否含有未知类进行判定，并能判断已知类样本的具体类别。
附 录
附表1 各方法对已知类放电识别结果
App.Tab.1 The identification results of known discharge types by each method （单位: %）
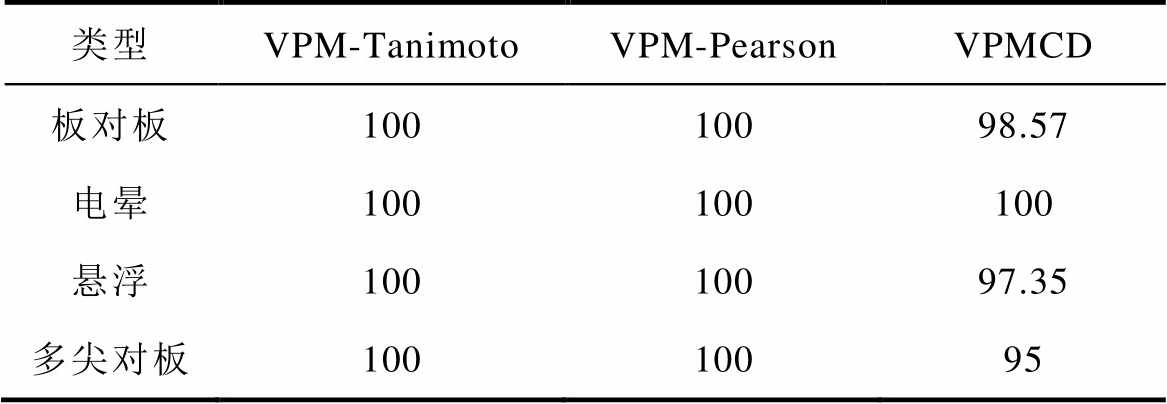
类型VPM-TanimotoVPM-PearsonVPMCD 板对板10010098.57 电晕100100100 悬浮10010097.35 多尖对板10010095
附表2 测试集的Pmax和IDAR
App.Tab.2 Pmax and IDAR of test samples
分组数PmaxIDAR分组数PmaxIDAR 10.9980.56070.9980.538 20.9960.55580.8850.517 30.9990.55690.9980.591 40.9960.555100.9980.559 50.9970.554110.9990.339 60.8860.528120.9990.353
（续）
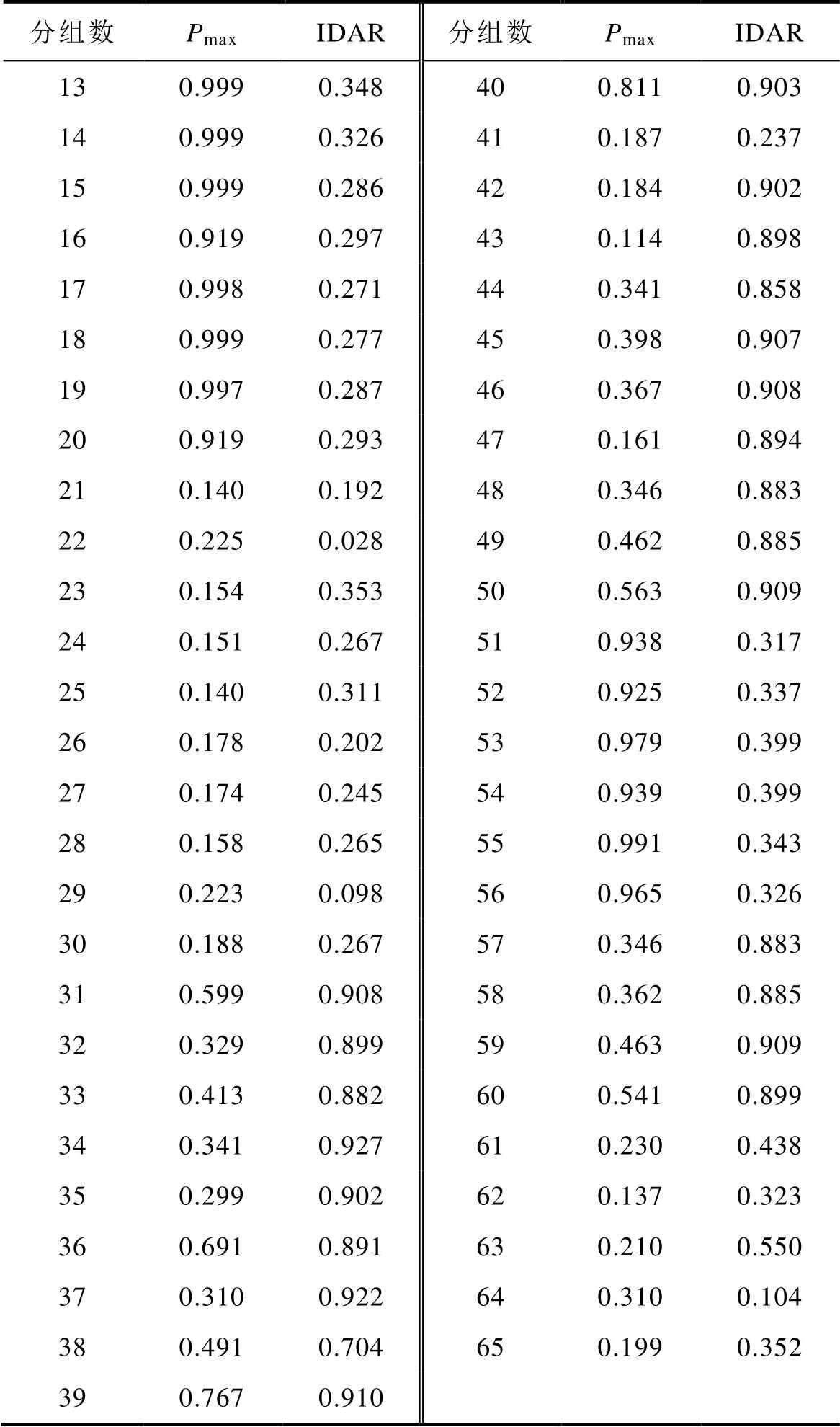
分组数PmaxIDAR分组数PmaxIDAR 130.9990.348400.8110.903 140.9990.326410.1870.237 150.9990.286420.1840.902 160.9190.297430.1140.898 170.9980.271440.3410.858 180.9990.277450.3980.907 190.9970.287460.3670.908 200.9190.293470.1610.894 210.1400.192480.3460.883 220.2250.028490.4620.885 230.1540.353500.5630.909 240.1510.267510.9380.317 250.1400.311520.9250.337 260.1780.202530.9790.399 270.1740.245540.9390.399 280.1580.265550.9910.343 290.2230.098560.9650.326 300.1880.267570.3460.883 310.5990.908580.3620.885 320.3290.899590.4630.909 330.4130.882600.5410.899 340.3410.927610.2300.438 350.2990.902620.1370.323 360.6910.891630.2100.550 370.3100.922640.3100.104 380.4910.704650.1990.352 390.7670.910
附图1 放电模型
App.Fig.1 Discharge models
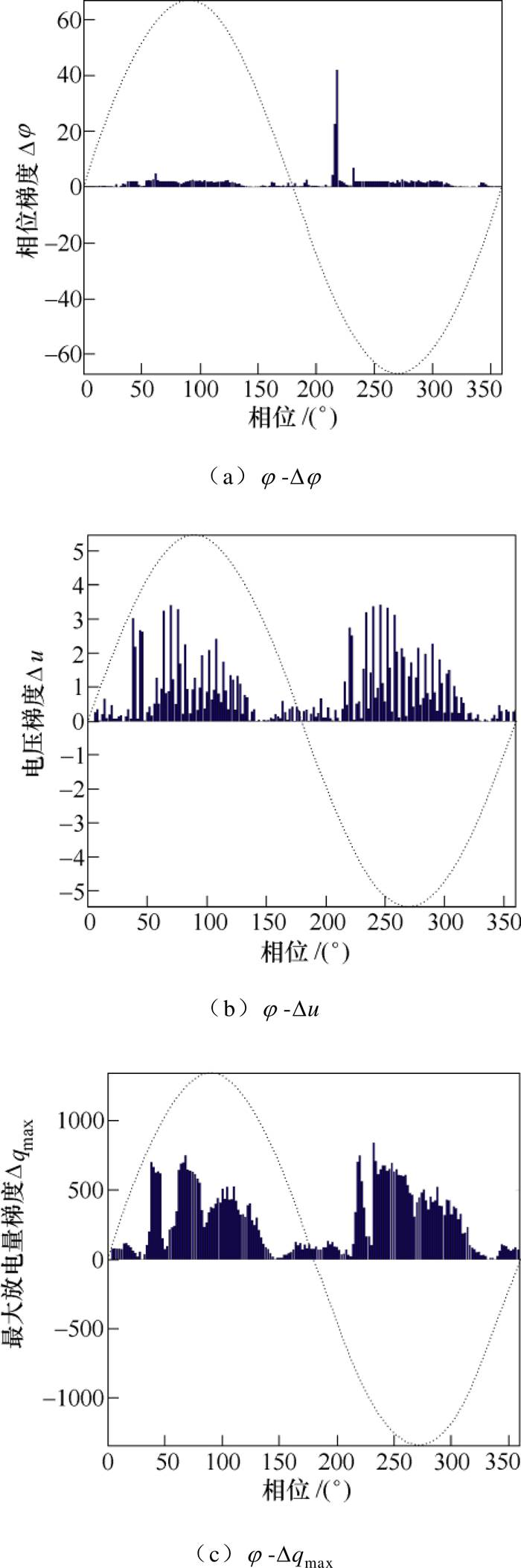
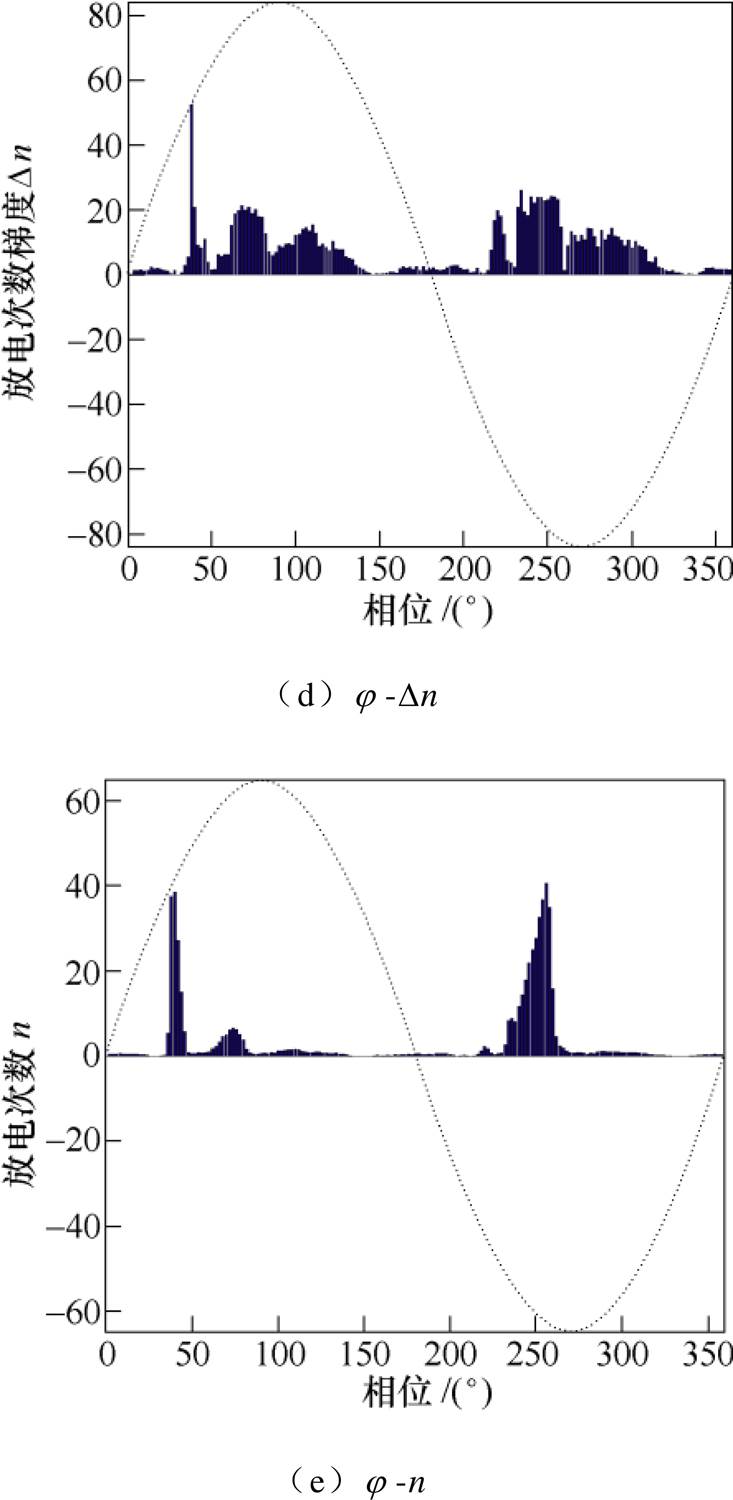
附图2 “板对板放电”的5种谱图
App.Fig.2 Five spectra of “board-to-board discharge”
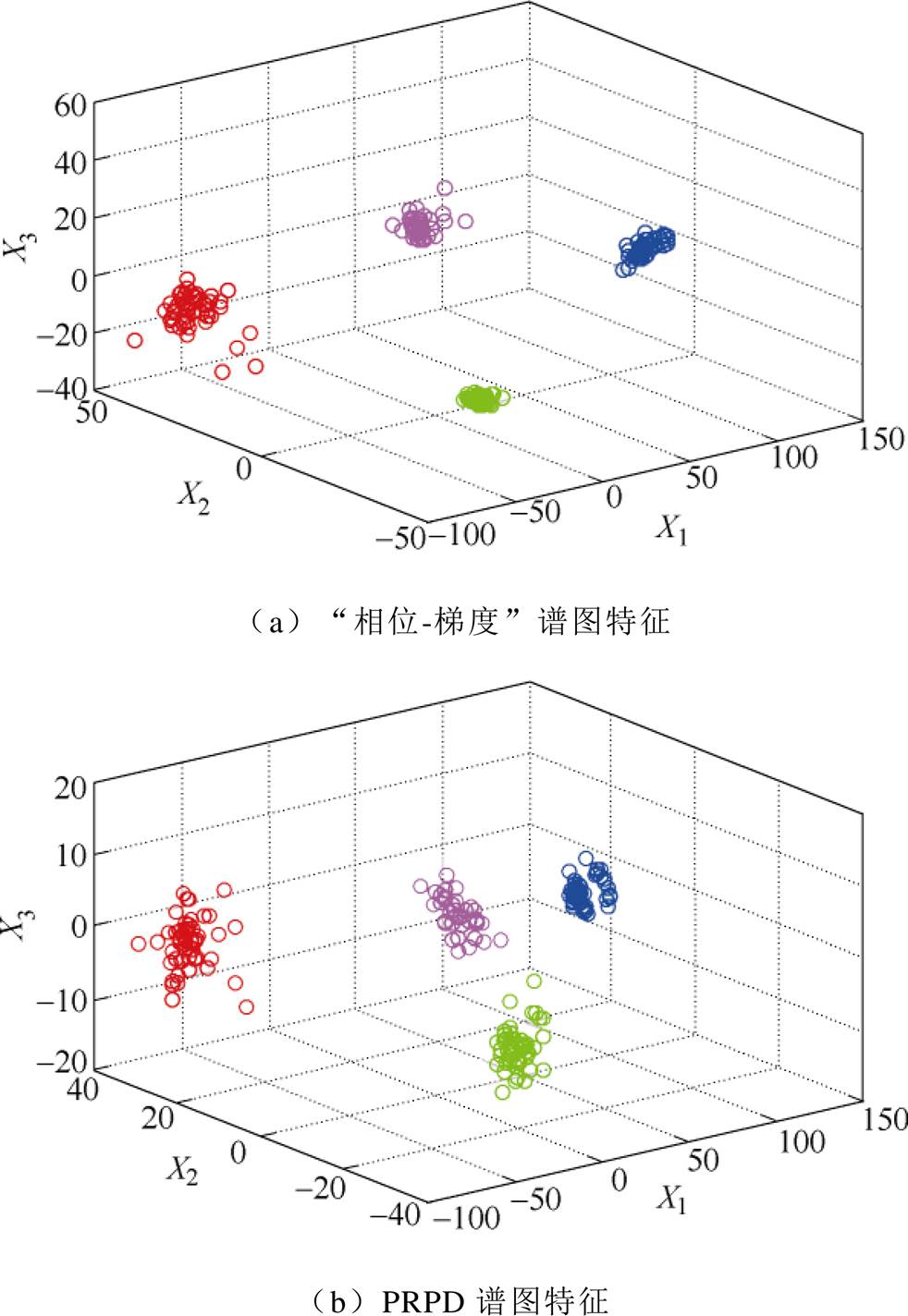
附图3 三维特征对比
App.Fig.3 Three-dimensional feature contrast
参考文献
[1] 杜伯学, 朱闻博, 李进, 等. 换流变压器阀侧套管油纸绝缘研究现状[J]. 电工技术学报, 2019, 34(6): 1300-1309.
Du Boxue, Zhu Wenbo, Li Jin, et al. Research status of oil-paper insulation of valve side bushing of converter transformer[J]. Transactions of China Elec- trotechnical Society, 2019, 34(6): 1300-1309.
[2] 张伟超, 董青青, 赵洪, 等. 液-固复合介质对光纤法-珀局部放电超声响应强度影响分析[J]. 电工技术学报, 2019, 34(10): 2230-2238.
Zhang Weichao, Dong Qingqing, Zhao Hong, et al. Analysis of the influence of liquid-solid composite media on the ultrasonic response strength of optical fiber-perot partial discharge[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2230- 2238.
[3] 王彩雄. 基于特高频法的GIS局部放电故障诊断研究[D]. 北京: 华北电力大学, 2013.
[4] Lapp A, Kranz H G. The use of the CIGRE data format for PD diagnosis applications[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2000, 7(1): 102-112.
[5] 唐志国, 唐铭泽, 李金忠, 等. 电气设备局部放电模式识别研究综述[J]. 高电压技术, 2017, 43(7): 2263-2277.
Tang Zhiguo, Tang Mingze, Li Jinzhong, et al. Summary of research on partial discharge pattern recognition of electrical equipment[J]. High Voltage Engineering, 2017, 43(7): 2263-2277.
[6] 王国强. 油纸绝缘局部放电的特征提取与模式识别[D]. 保定: 华北电力大学, 2014.
[7] 龙嘉川, 王先培, 代荡荡, 等. 基于改进S变换的超高频局部放电信号特征提取及分类[J]. 高电压技术, 2018, 44(11): 3649-3656.
Long Jiachuan, Wang Xianpei, Dai Dangdang, et al. Feature extraction and classification of uhf partial discharge signals based on improved S transform[J]. High Voltage Technology, 2018, 44(11): 3649- 3656.
[8] 李恩文, 王力农, 宋斌, 等. 基于混沌序列的DGA数据并行聚类分析[J]. 电工技术学报, 2019, DOI: 10.19595/j.cnki.1000-6753.tces.181894.
Li Enwen, Wang Linong, Song Bin, et al. Parallel clustering analysis of DGA data based on chaotic sequence[J]. Transactions of China Electrotechnical Society, 2019, DOI: 10.19595/j.cnki.1000-6753.tces. 181894.
[9] 李恩文, 王力农, 宋斌, 等. 基于改进模糊聚类算法的变压器油色谱分析[J]. 电工技术学报, 2018, 33(19): 4594-4602.
Li Enwen, Wang Linong, Song Bin, et al. Analysis of transformer oil chromatography based on improved fuzzy clustering algorithm[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 4594-4602.
[10] 李正明, 钱露先, 李加彬. 基于统计特征与概率神经网络的变压器局部放电类型识别[J]. 电力系统保护与控制, 2018, 46(13): 55-60.
Li Zhengming, Qian Luxian, Li Jiabin. Partial discharge type identification of transformer based on statistical features and probabilistic neural net- works[J]. Power System Protection and Control, 2018, 46(13): 55-60.
[11] 王菲菲, 阮爱民, 魏刚, 等. 基于卷积神经网络的开关柜局部放电故障识别[J]. 电气技术, 2019, 20(4): 76-81.
Wang Feifei, Ruan Aimin, Wei Gang, et al. Discognition of partial discharge faults of switchgear based on convolutional neural network[J]. Electrical Engineering, 2019, 20(4): 76-81.
[12] 高佳程, 曹雁庆, 朱永利, 等. 基于KELM-VPMCD方法的未知局部放电类型的模式识别[J]. 电力自动化设备, 2018, 38(5): 141-147.
Gao Jiacheng, Cao Yanqing, Zhu Yongli, et al. Pattern recognition of unknown partial discharge type based on KELM-VPMCD method[J]. Electric Power Automation Equipment, 2018, 38(5): 141-147.
[13] 贾亚飞, 朱永利, 高佳程, 等. 基于样本加权FCM聚类的未知类别局部放电信号识别[J]. 电力自动化设备, 2018, 38(12): 107-112.
Jia Yafei, Zhu Yongli, Gao Jiacheng, et al. Identi- fication of partial discharge signals in unknown category based on sample weighted FCM clustering[J]. Electric Power Automation Equipment, 2018, 38(12): 107-112.
[14] 高佳程, 朱永利, 贾亚飞, 等. 基于改进SVDD算法与马氏距离的未知局部放电类型的识别[J]. 电工技术学报, 2018, 33(15): 3510-3517.
Gao Jiacheng, Zhu Yongli, Jia Yafei, et al. Identi- fication of unknown partial discharge types based on improved SVDD algorithm and Mahalanobis distance[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3510-3517.
[15] Chan J C, Hui Ma, Saha T K. Automatic blind equalization and thresholding for partial discharge measurement in power transformer[J]. IEEE Transa- ctions on Power Delivery, 2014, 29(4): 1927-1938.
[16] 马利洁, 朱永利, 郑艳艳. 基于并行变量预测模型的变压器故障诊断及优化研究[J]. 电力系统保护与控制, 2019, 47(6): 82-89.
Ma Lijie, Zhu Yongli, Zheng Yanyan. Research on transformer fault diagnosis and optimization based on parallel variable prediction model[J]. Power System Protection and Control, 2019, 47(6): 82-89.
[17] 曾佳, 樊红, 徐强. 互联网大众点评与商圈空间分布的餐饮商家协同推荐研究[J]. 测绘地理信息, 2018, 43(4): 92-94.
Zeng Jia, Fan Hong, Xu Qiang. Research on the collaborative recommendation of catering business based on Internet public comment and business space distribution[J]. Surveying and Mapping Geographic Information, 2018, 43(4): 92-94.
[18] 汤燕彬, 许榕生. 基于Tanimoto系数的JPEG碎片数据识别方法[J]. 计算机应用与软件, 2011, 28(9): 80-81, 92.
Tang Yanbin, Xu Rongsheng. A JPEG fragment data recognition method based on tanimoto coefficient[J]. Computer Applications and Software, 2011, 28(9): 80-81, 92.
[19] Kranz H G, Krump R. Partial discharge diagnosis using statistical optimization on a PC-based system[J]. IEEE Transactions on Electrical Insulation, 1992, 27(1): 93-98.
[20] 朱德恒, 严璋, 谈克雄, 等. 电气设备状态监测与故障诊断技术[M]. 北京: 中国电力出版社, 2009.
[21] 文俊浩, 舒珊. 一种改进相似性度量的协同过滤推荐算法[J]. 计算机科学, 2014, 41(5): 68-71.
Wen Junhao, Shu Shan. A collaborative filtering recommendation algorithm for improving similarity measures[J]. Computer Science, 2014, 41(5): 68-71.
[22] 王刘旺, 朱永利, 李莉, 等. 基于特征子集的变压器局部放电小样本类型识别[J]. 电测与仪表, 2015, 52(24): 40-45.
Wang Liuwang, Zhu Yongli, Li Li, et al. Identi- fication of small sample types of partial discharge of transformer based on feature subset[J]. Journal of Electric Measurement & Instrumentation, 2015, 52(24): 40-45.
[23] 罗颂荣, 程军圣, 杨宇. 基于本征时间尺度分解和变量预测模型模式识别的机械故障诊断[J]. 振动与冲击, 2013, 32(13): 43-48.
Luo Songrong, Cheng Junsheng, Yang Yu. Mechanical fault diagnosis based on pattern recognition of intrinsic time scale decomposition and variable prediction model[J]. Journal of Vibration and Shock, 2013, 32(13): 43-48.
Pattern Recognition of Unknown Types in Partial Discharge Signals Based on Variable Predictive Model and Tanimoto
Abstract For new samples that may not belong to the known discharge types in the partial discharge, a method based on variable predictive model and Tanimoto (VPM-Tanimoto) similarity is proposed to recognize the unknown types. The expression of unknown signals is achieved by constructing gradient pattern spectra, and two indicators are used to separate the unknown signals by filtering all signals in different areas. Firstly, j-Dj、j-Du、j-Dqmax、j-Dn and j-n spectral patterns were built to extract features. Secondly, the corresponding VPM model group was established for each known type of discharge to predict the features for samples. Subsequently, the Tanimoto similarities between the samples and each known type of discharge were calculated to obtain the best match known category for each sample. Then, the reliability integrator discriminant analysis rule (IDAR) of the recognition results was calculated and the reliability space was divided. Different regions had different determination methods. Finally, the Tanimoto similarity and the IDAR of each region were used to double filter all discharge signals to determine and separate unknown samples. Experimental results show that the method has certain recognition effects.
keywords：Partial discharge, unknown types, spectrum, Tanimoto similarity, integrator discriminant analysis rule
DOI: 10.19595/j.cnki.1000-6753.tces.190777
中图分类号：TM85
邓 冉 女，1995年生，硕士研究生，研究方向为高压设备局部放电信号分析与故障诊断。E-mail: liferan@foxmail.com
朱永利 男，1963年生，教授，博士生导师，研究方向为输变电设备网络化监测与信息分析处理。E-mail: yonglipw@163.com（通信作者）
收稿日期 2019-06-27
改稿日期 2019-08-20
国家自然科学基金项目（51677072），中央高校基本科研业务费专项资金项目（2017XS118）资助。
（编辑 陈 诚）