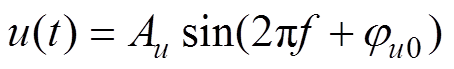（1）
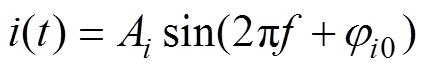（2）
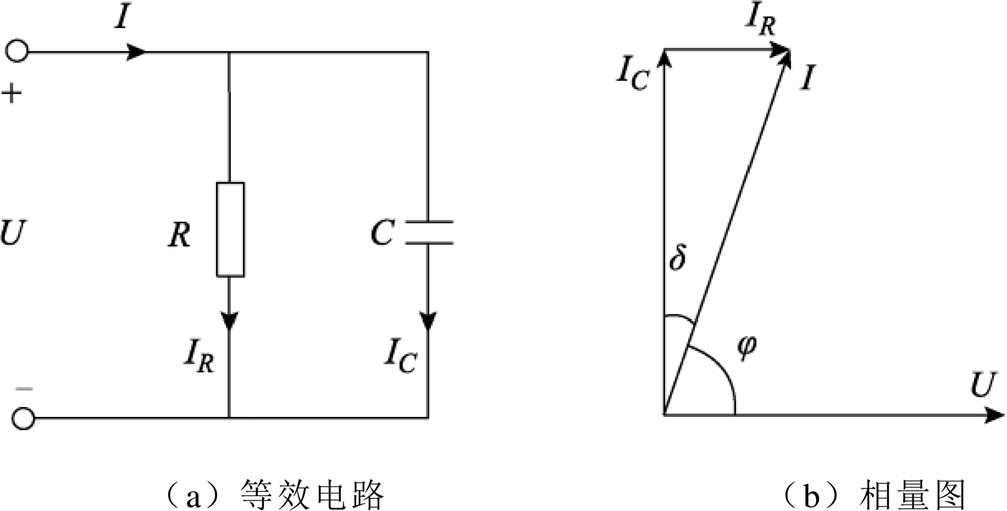
图1 电介质等效电路
Fig.1 Dielectric equivalent circuit
摘要 由于快速傅里叶算法在实际应用中存在栅栏效应和频谱泄漏的问题，且用于测量介质损耗角的精度不高，该文提出一种基于混合卷积窗和改进全相位的高精度介质损耗角测量方法。用主、旁瓣性能更好的混合卷积窗对信号截断以减小频谱泄露，用全相位傅里叶变换具有的“相位不变性”以消除栅栏效应，并针对全相位傅里叶提出差分式相位校正方法。分别在基波频率变动、信噪比变化、谐波含量变化及采样点数的影响下对比验证，结果表明所提方法的检测精度高于加窗插值的傅里叶变换算法，尤其在非同步采样时，其优势更加显著。
关键词：全相位 傅里叶变换 混合卷积窗 介损角
高压电容器广泛用于补偿电力系统感性无功的设备，介质损耗角（简称介损角）是反映高压电容型设备绝缘性能的重要指标[1-3]。电介质在电压作用下的能量损耗简称为介质损耗，通过检测介损角可以反映绝缘材料的损耗程度，反映绝缘介质老化、受潮和绝缘中气体放电等绝缘缺陷。快速准确地监测介损角对电力系统稳定运行具有重要意义[4-5]。
在介损角检测中，目前有硬件和软件两种测量方法。硬件方法实现简单，但易受外界干扰，测量误差较大[6]。软件法具有更低的成本，对信号的处理也更加快速和准确，其中谐波检测方法由于其易实现且抗干扰能力强应用最为广泛[7-8]。谐波检测法中最常用的方法为快速傅里叶变换法（Fast Fourier Transform, FFT），但FFT存在栅栏效应和频谱泄漏问题，造成测量精度不高[9-11]。介损角通常在0.001～0.02rad范围，很容易被误差所覆盖[12]，因此一些学者提出加窗处理和插值校正提高FFT算法的精度[13-14]，该方法虽被证明有较明显减小频谱泄漏和栅栏效应的效果，但鉴于介损角的特殊性，仍然有待精度更高的算法。文献[15]提出了全相位快速傅里叶变换（all-phase Fast Fourier Transform, apFFT）分析算法，apFFT由于具有“相位不变性”，不存在栅栏效应，无需再做插值校正，并且从理论和仿真验证了apFFT还能够有效地抑制频谱泄漏问题。
本文基于文献[15]中Hanning窗预处理的apFFT算法，提出用主瓣较窄的Hanning窗和旁瓣衰减较快的Nuttall窗做卷积运算构造一种混合卷积窗来做信号截断。apFFT本身不存在栅栏效应并且具有一定的抑制频谱泄漏能力，用性能更好的混合窗函数来做信号预处理再次减小了频谱泄漏，测量精度显著增加。apFFT只能得到数据中心样点x(0)处的相位，而实际中有时还需要其他时刻的相位值，本文又提出了apFFT的差分式校正算法，经校正后能获得采样数据中任意一点对应时刻的相位。最后分别在频率变动、白噪声、含有谐波和不同采样点数的情况下检验所提算法的性能。结果表明，提出的方法在以上条件下所测介损角误差均最低，且能很好地抑制这些变化带来的影响，明显地提高了介损角的测量精度。
在正弦交流电压下，高压电容型设备的介质等效为电阻R和电容C的并联形式，介质两端的电压U和流过的电流I的相位差为j。图1所示是高压电容型设备的等效电路和电压电流的相量图，图中d即为该介质的损耗角。
设电介质两端电压和流过的电流分别为
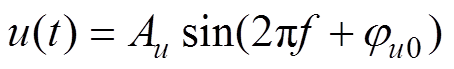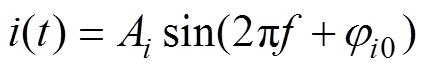（1） （2）
图1 电介质等效电路
Fig.1 Dielectric equivalent circuit
式中，f为基波频率；Au和Ai分别为电压、电流的幅值；ju0和ji0分别为电压、电流的初相位。
由图1b电压和电流的相量图可见，经过电介质的电流与所加电压间的相位是j，显然介质损耗角d 为电压电流的相位差j 的余角，即介损角d 为
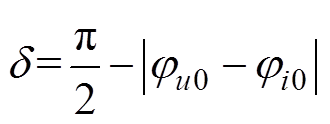（3） 式（3）所示，测量介损角问题转换为测量电介质的电压和电流相位的问题。用apFFT算法求介损角的流程如图2所示。
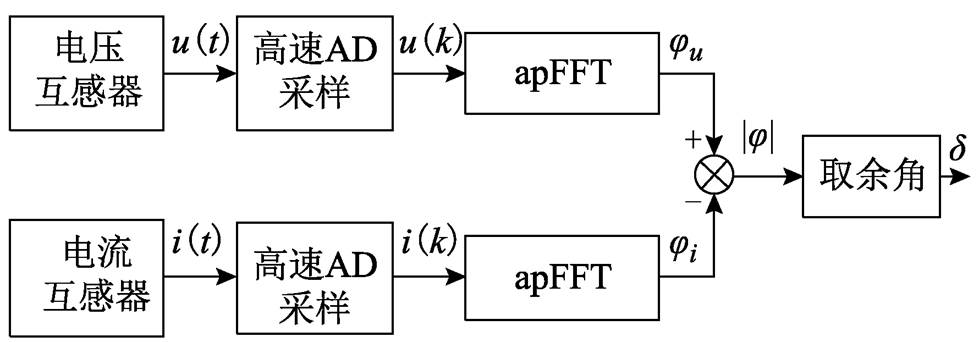
图2 apFFT算法测量介损角
Fig.2 apFFT algorithm for measuring dielectric loss angle
长度都为N的窗函数w1(n)和w2(n)构成的一阶混合卷积窗(1-HCW)的定义为
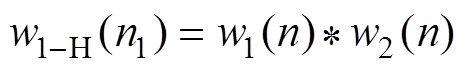（4）其频域表达式为
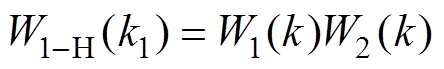（5）
由L个一阶混合卷积做自卷积构成的L阶混合卷积窗(L-HCW)的定义为
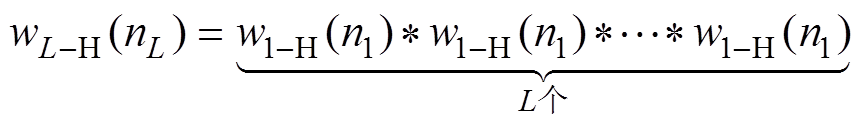（6）其频域表达式为
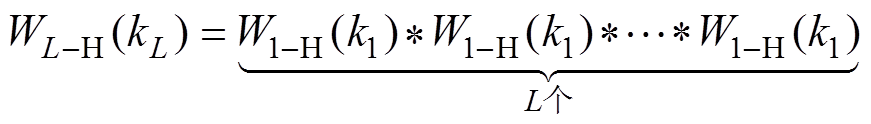（7）
本文选用主瓣较窄的Hanning窗和旁瓣衰减较快的四项三阶Nuttall窗做卷积，Hanning窗和四项三阶Nuttall窗的时域表达分别为
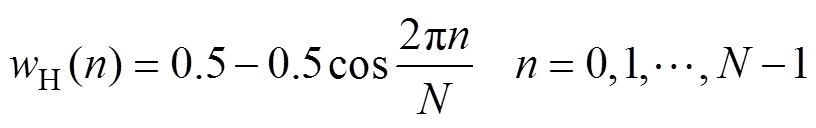（8）
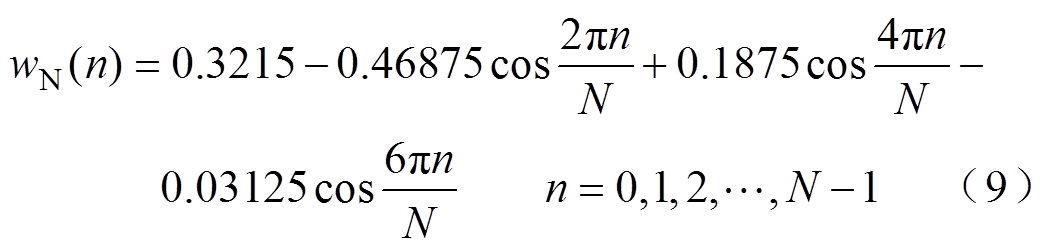
分别对其做离散傅里叶变换所得频域表达式分别为
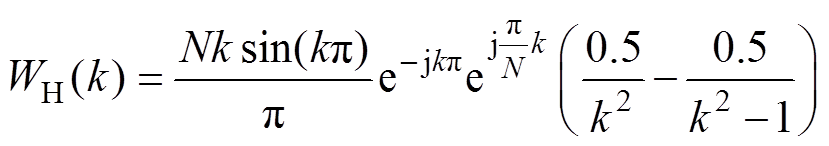（10）
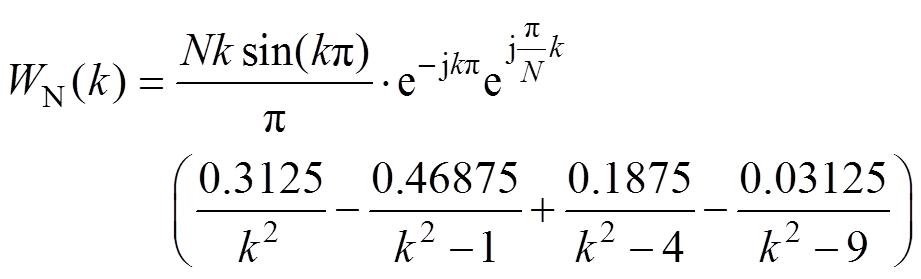（11）
根据上述给出的混合卷积窗的定义，则由Hanning窗与Nuttall窗构成的一阶混合卷积频域表达式为
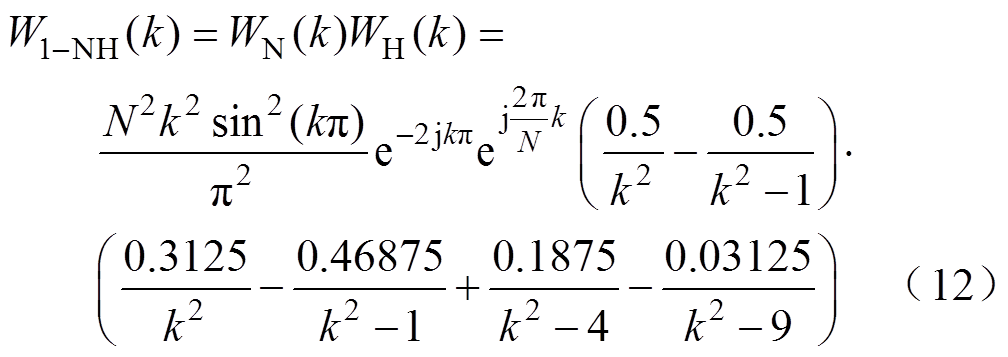
根据式（7）得二阶混合卷积频域表达式为
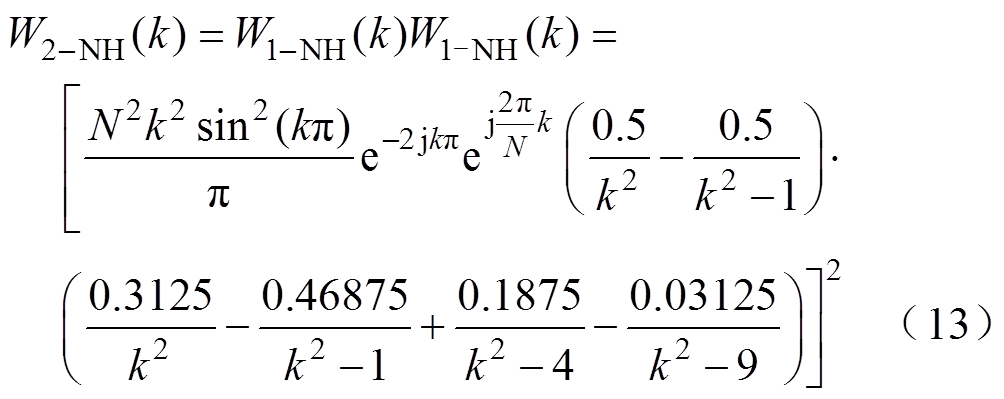
根据式（10）、式（11）和式（12）窗函数的表达式可分析其幅频响应，Hanning窗、四项三阶Nuttall窗及其构成的一阶混合卷积窗的归一化频谱图如图3所示。
由图3和文献[16]对混合卷积窗的分析可知，混合卷积窗主瓣宽度与母窗中较窄窗函数宽度相同，旁瓣衰减速率是两个窗函数旁瓣衰减速率相加，旁瓣峰值在Hanning窗旁瓣峰值处时，其值等于两母窗在此处的旁瓣幅值之和。
根据式（13）所示二阶混合窗频域表达式，对二阶混合卷积窗做频谱分析，结果如图4所示。
由图4可知，二阶混合窗与一阶混合窗相比，二阶混合窗的旁瓣峰值更低，衰减速度也更快。二阶混合卷积窗性能明显比一阶混合卷积窗性能好，用其对信号截断时，具有更小的频谱泄漏。
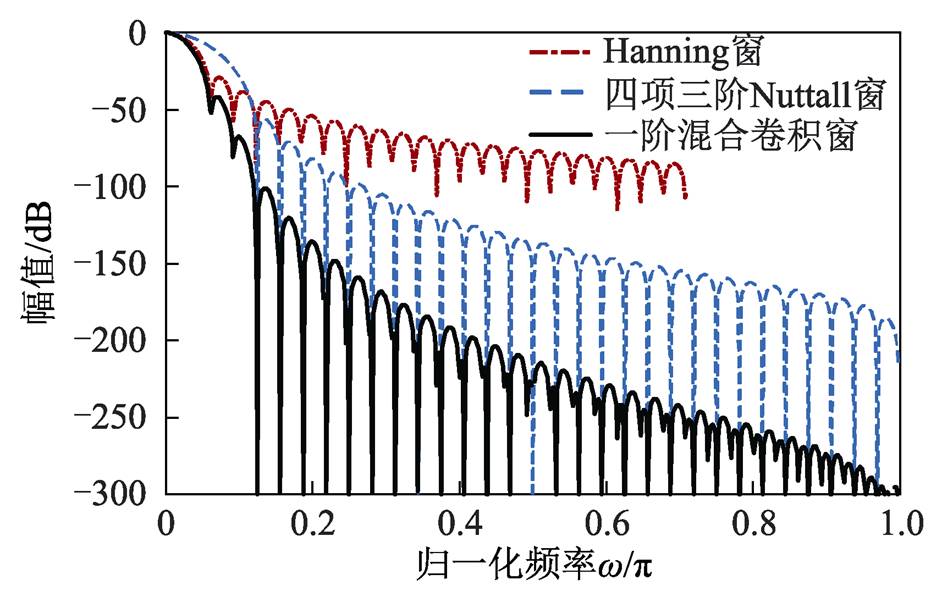
图3 一阶混合卷积窗的归一化频谱图
Fig.3 Normalized spectrogram of first-order mixed convolution window
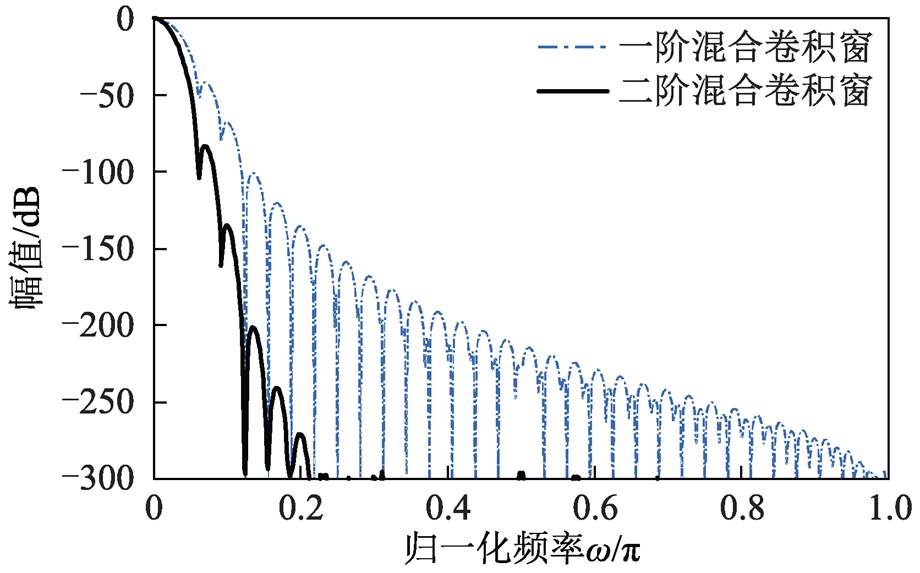
图4 一、二阶混合窗频谱对比
Fig.4 First- and second-order mixed window spectrum comparison
由于实际电网电压存在波动，很难做到同步采样，必然导致传统FFT算法存在栅栏效应，王兆华教授提出在做FFT之前先对信号做全相位处理，处理后的信号不仅具有更小的频谱泄漏，还具有“相位不变性”。
全相位FFT的处理过程为：首先将长度为2N-1的信号用长度为2N-1的窗函数wc加权截断；然后把间隔为N的数据点两两相加，得到长度为N的数据，该过程称为全相位处理；最后再把点数为N的处理后的信号做FFT分析。以上过程即为apFFT分析，如图5所示。
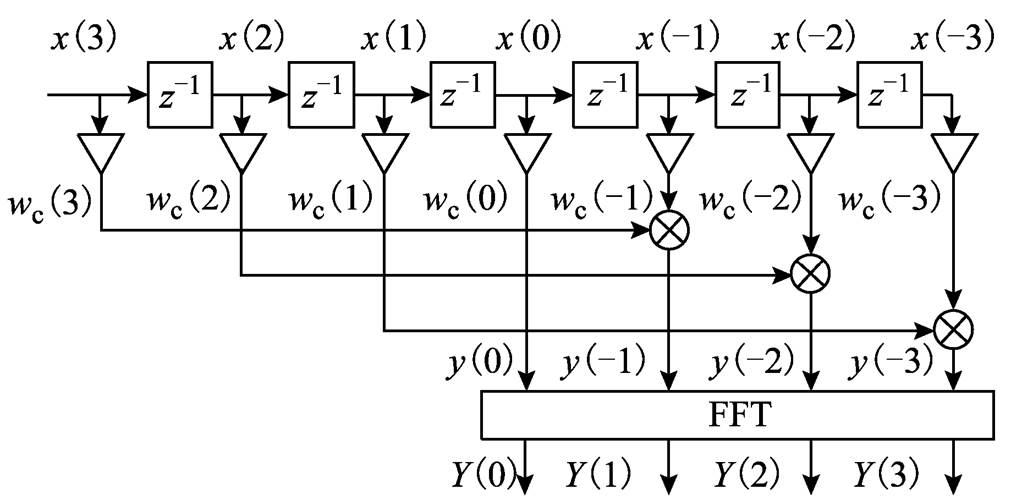
图5 全相位频谱理论分析图
Fig.5 All-phase spectrum theory analysis
图5中长度为2N-1的窗函数wc由长度均为N的前窗f和翻转的后窗b线性卷积产生[17]，即
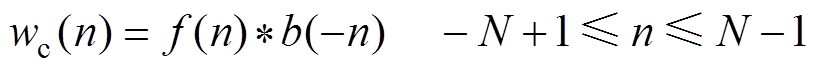（14）根据前窗和后窗的情况分为无窗全相位、单窗全相位和双窗全相位。
为展示apFFT的优越性，选择如式（15）所示输入信号，对其分别做传统FFT和apFFT分析。
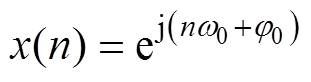（15）式中，w0为序列的数字角频率；j0为序列的初相位。
采用传统FFT的输出结果为
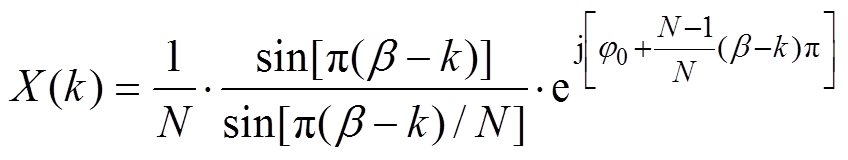（16）而采用apFFT计算输出结果为
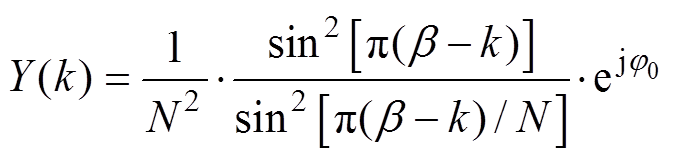（17）
对比式（16）、式（17）可见，在幅值上，经过全相位处理的信号傅里叶变换的幅值谱是直接做傅里叶变换幅值谱的二次方[18]。这意味着apFFT的主瓣更为突出，旁瓣的衰减也更快，频谱泄漏也就更小。在相位上，传统FFT的相位与频率偏差有关，而apFFT谱的相位始终等于中心样点x(0)的相位值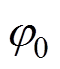
，即apFFT的相位具有“相位不变性”[19]。
对式（15）的输入信号，取频率为30Hz，初相位为60°，分别做FFT和apFFT分析，相频谱如图6所示。
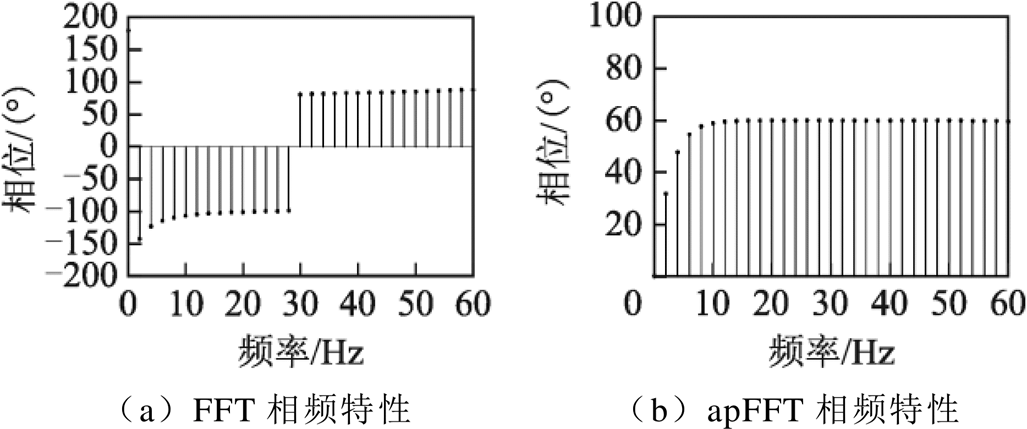
图6 apFFT和FFT相频特性
Fig.6 Phase frequency characteristics of apFFT and FFT
由图6可知，apFFT在同一频率时，其相位始终等于中心样点x(0)的相位，频域离散就不会有栅栏效应，直接在相位谱上的该频率附近选择一根谱线，即为该频率分量的初始相位[20]。此外，相比FFT算法，apFFT无需再做插值校正，得出更加精确相位的同时又减小了运算量。
经以上分析，apFFT只能获得中心样点x(0)处的相位，而实际往往需要的相位值可能是采样序列中任意一点的相位值，若想获得其他序列点的相位，本文提出apFFT算法的差分式相位校正方法。
首先，从寄存器取第1～2N-1段序列，对其做apFFT分析，求得该段数据的中心样点x(0)处的相位j0；然后再取第L～2N-1+L段序列，做apFFT分析得到该段数据的中心样点x(L)处的相位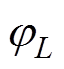
；则相位的差分量Dj 为
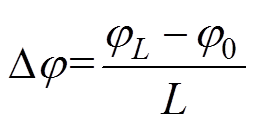（18）由于相位的取值在[-p, p]，故L的取值不宜过大，应使其满足
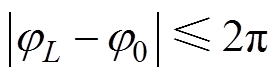（19）
则距中心样点k个距离的序列点的相位jk的修正公式为
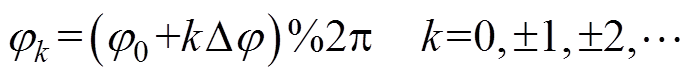（20）式中，运算符“%”表示取余运算。
由式（20）得到k时刻的真实相位。差分式相位校正流程如图7所示。
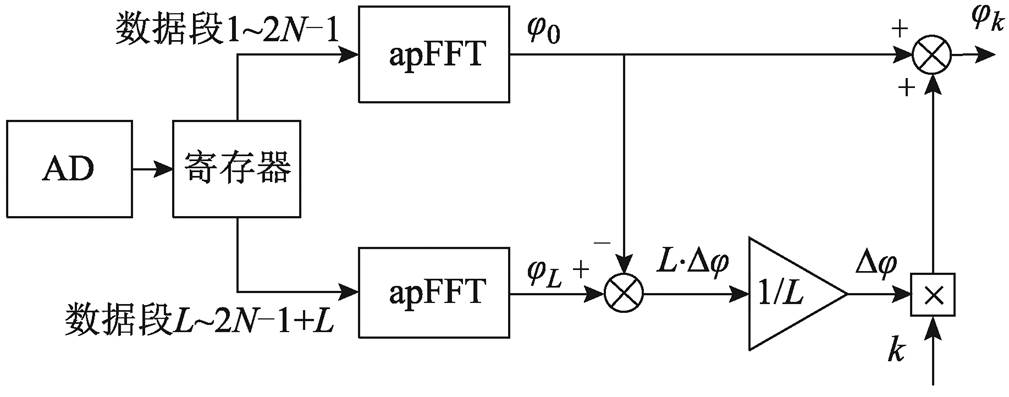
图7 差分式相位校正流程
Fig.7 Differential phase correction flow chart
利用上述方法，分别求得电压和电流同一时刻的相位值，代入式（3），即可求出介损角d。
基于混合窗的改进apFFT介损角测量流程如图8所示。
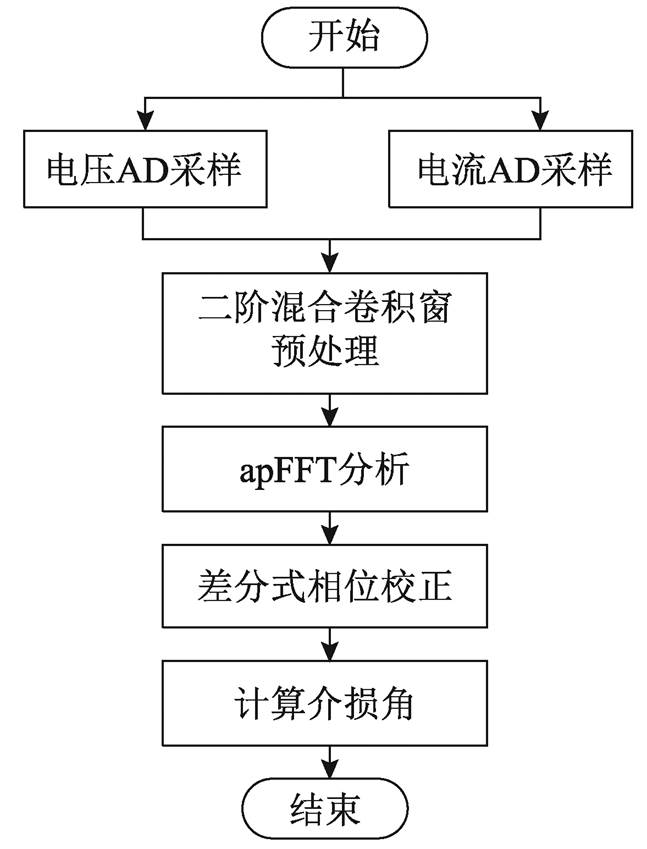
图8 改进apFFT介损角测量流程
Fig.8 Flow chart of algorithm measurement in this paper
测量电路如图9所示，绝缘介质采用电容和电阻的并联形式等效，仿真电路中，用三个电压源分别表示基波、3次谐波和5次谐波模型。
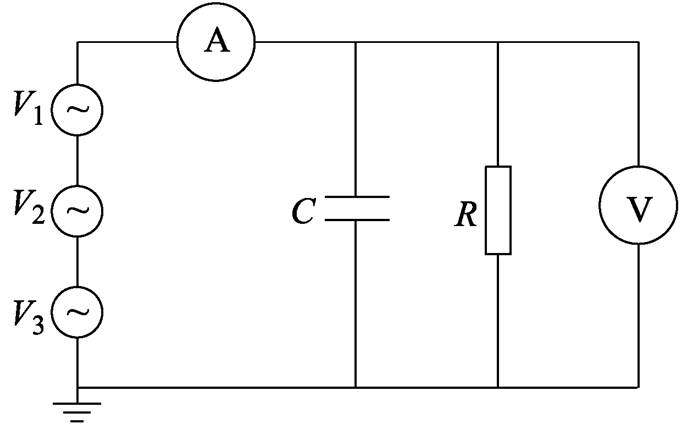
图9 介损角测量电路
Fig.9 Dielectric loss angle measurement circuit
图9中C=519.02pF，R=22.67kΩ。采用并联等效电路，三个电压源信号分别设置为基波、3次谐波、5次谐波电压。电压源信号为
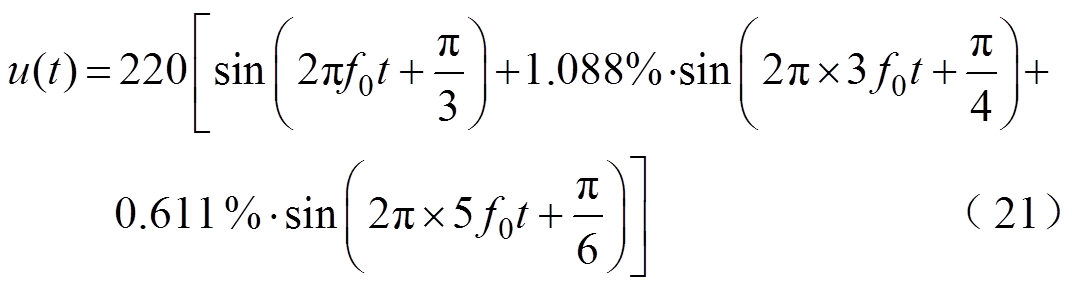
式中，基波频率f0=50Hz。
用上述仿真参数分别在频率波动、含不同比例的白噪声、含有谐波和不同采样点数的情况下，分析所提算法的性能。
考虑实际电网允许频率在(50±0.2)Hz范围波动，设置仿真信号基波频率范围为49.8～50.2Hz，对本文算法与Hanning窗的双谱线插值算法和Nuttall窗的三谱线插值算法分别测量介损角。设采样频率为2 500Hz，采样点数为512。三种算法测量的相对误差如图10所示。
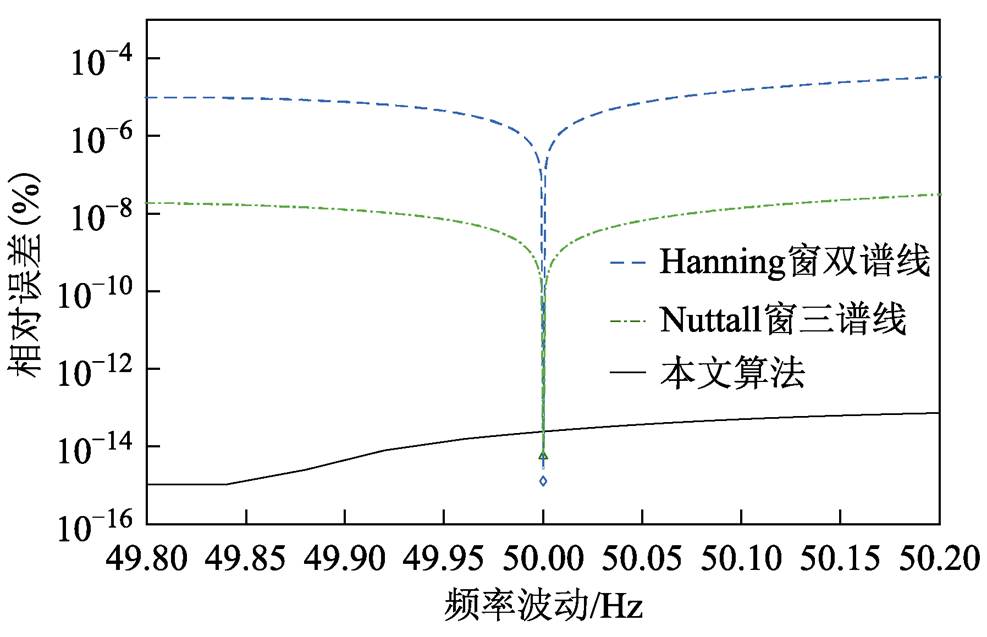
图10 频率波动的影响对比图
Fig.10 Contrast chart of frequency fluctuation
由图10可见，本文算法精确度比传统加窗插值FFT算法精度提高了7～10个数量级，本文算法的相对误差可达10-15数量级。由于采样频率设置为2 500Hz，基波频率为50Hz时相当于同步采样，不存在栅栏效应，加窗插值FFT算法的误差很小，即便如此，本文算法也和加窗插值FFT算法的精度相差不大。在实际电网中，由于负荷消耗的有功功率实时变动，电网的频率难免变动，同步采样要求采样频率能够追踪系统频率变化，所以很难做到同步采样。当频率偏离50Hz时，传统加窗插值FFT算法的误差迅速增大，而本文混合窗改进的apFFT算法对频率波动、精度变化很小，对频率变动的敏感度极低，更适合实际应用。
在实际情况中，不可避免会有噪声干扰，噪声对相位检测会有一定的影响，从而影响介损角的测量精度。对此，添加不同信噪比的白噪声进行仿真分析。选用Hanning窗双谱线插值算法、Nuttall窗三谱线插值算法和本文算法对介损角进行测量，对比分析。设采样频率为2 500Hz，采样点数为512。仿真结果如图11所示。
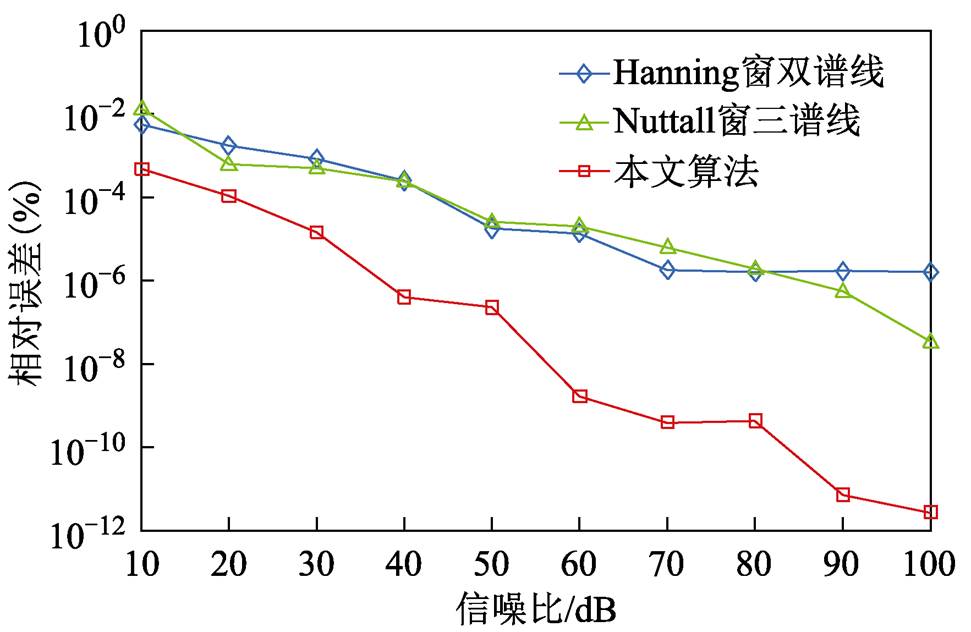
图11 白噪声的影响对比图
Fig.11 Contrast chart of the effect of white noise
由图11可知，随着信号的信噪比的增加，三种算法的测量精度都在增大，但是本文算法无论信噪比取值多大相对误差都最小，在信噪比为100dB时，相对误差达到10-12数量级。本文算法与传统FFT算法，测量精度均受噪声的影响，但在各信噪比的噪声下，本文算法的测量精度始终较传统FFT更高。
当有谐波分量存在时，谐波分量产生频谱泄漏会给基波带来误差，尤其是离基波频率最近的3次和5次谐波的频谱泄漏的影响最大。设置仿真信号的基波频率为50.12Hz，加入3次谐波分量并设置谐波含量在0～8%变化，设采样频率为2 500Hz，采样点数为512。分析三种算法在谐波分量变化时对介损角的测量误差情况的对比图如图12a所示，本文算法在谐波分量变化时的误差详细情况如图12b所示。
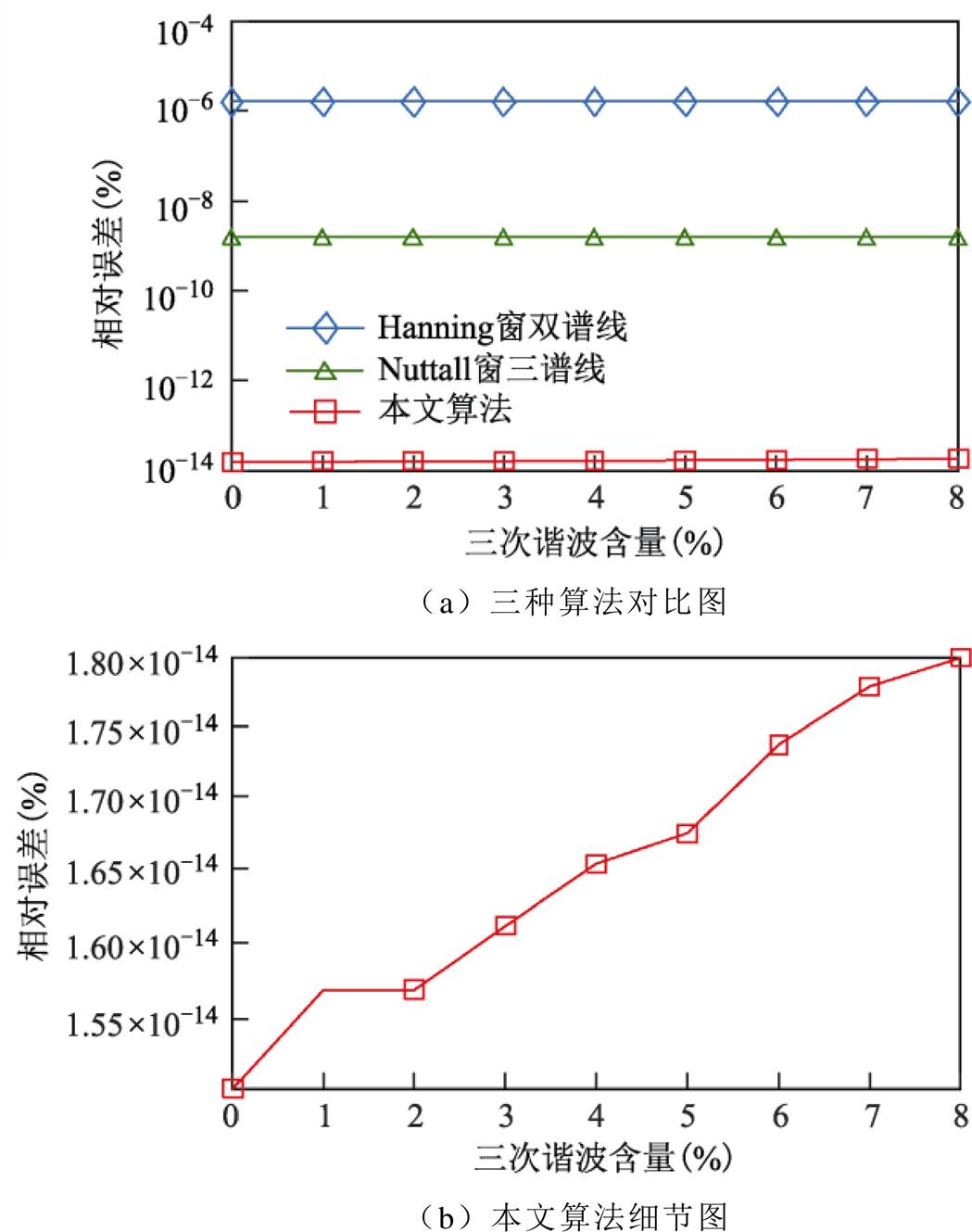
图12 3次谐波含量的影响对比图
Fig.12 Contrast chart of third harmonic content
由图12a可知，三次谐波含量变化时，三种算法的测量精度都几乎没有波动，这可以说明三种算法几乎不受谐波含量变化的影响。本文算法采用的是Hanning窗与Nuttall窗构成的二阶混合窗，该窗的主瓣更为突出，旁瓣小且衰减快，故频谱泄漏很少，由图12b也可看出，随着谐波含量增加，本文算法相对误差有略微增加，但都在同一数量级10-14上变化，测量精度几乎不受谐波含量的影响。
固定频率为4 200Hz，采样点数分别取为256、512、1 024、2 048、4 096。再选用Hanning窗双谱线插值算法、Nuttall窗三谱线插值算法和本文算法对介损角进行测量对比，三种算法误差对比如图13所示。
由图13可知，随着采样点数增加，三种算法检测的相对误差都呈下降趋势，但是本文算法检测误差最低，在采样点数为4 028时，相对误差达到10-15数量级，已具有很高的精确度。
针对算法的计算复杂度问题，对算法做了耗时测试。计算机的CPU主频3.10GHz，操作系统为Win7旗舰版64位，运行环境为Matlab2016a。测试中Nuttall窗三谱线插值算法耗时0.003 726s，本文算法耗时0.002 271s。本文算法无需做插值校正，耗时约为Nuttall窗三谱线插值算法的60%。
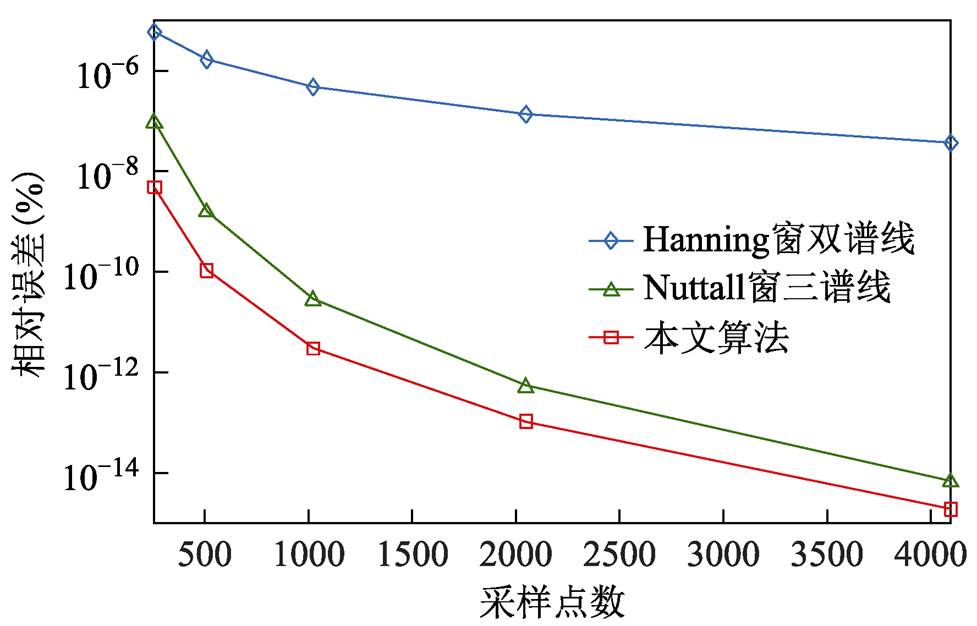
图13 采样点数的影响对比图
Fig.13 Contrast chart of the impact of sampling points
在实际应用中，测量精度还受AD采样精度、电磁干扰和温度漂移等影响，测量精度不及理想仿真情况。为验证本文算法应用的可行性，搭建如图13所示的实际电路采样、计算机分析构成的试验系统。
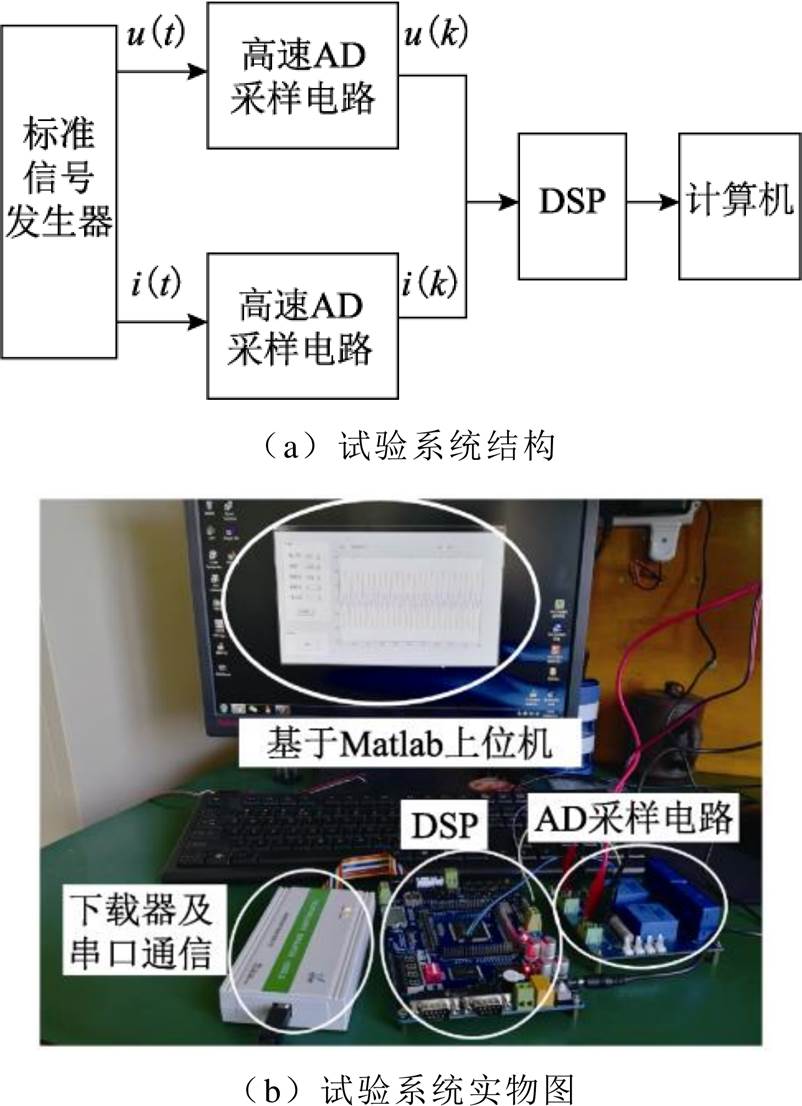
图14 算法试验系统
Fig.14 Algorithmic test system
由标准功率发生器产生相位相差(p/2-0.006)rad的两个标准正弦信号，其中相位超前的信号模拟流过介质的电流，滞后的信号模拟介质两端的电压，等效介损角的真值为0.006rad；经两路AD采样电路将数据传至DSP处理器，DSP访问AD的频率为4 000Hz，DSP每记录0.5s的数据用串口上传至计算机，其中AD采样芯片选择的是ADI公司的AD9645模数转换芯片，采样精度为14位；DSP采用ADI公司的ADSP-BF56数字信号处理芯片，主频为600MHz；信号发生器选用Fluke 6 100A功率电能质量标准源，其相位调节的分辨率为10×10-6rad。在计算机中将数据导入Matlab中分别用传统加窗插值FFT和本文算法计算介损角，测量结果见表1。
表1 介损角测量结果
Tab.1 Measurement results of dielectric loss angle d
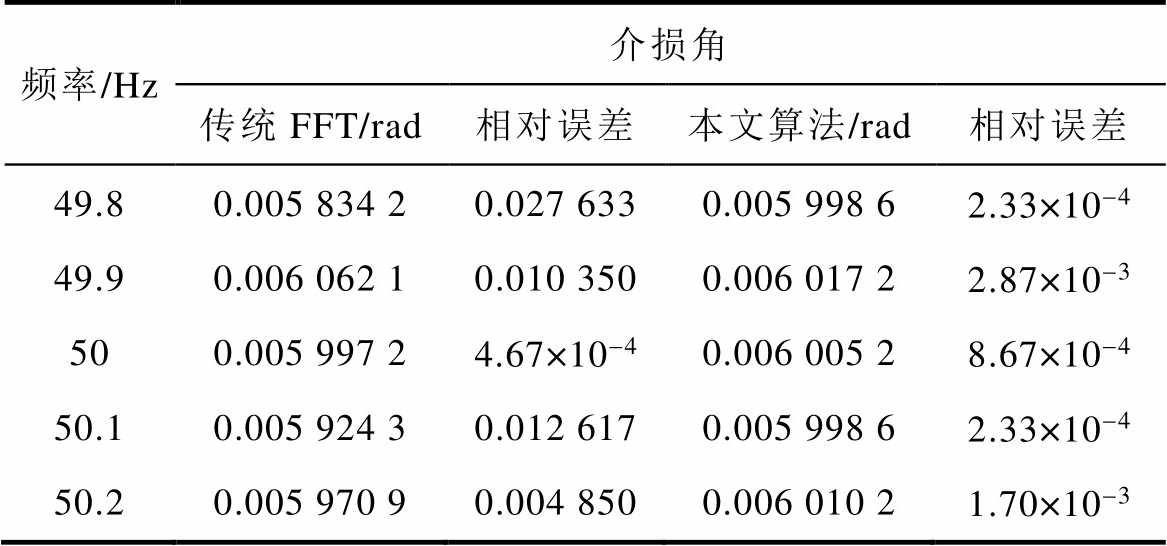
频率/Hz介损角 传统FFT/rad相对误差本文算法/rad相对误差 49.80.005 834 20.027 6330.005 998 62.33×10-4 49.90.006 062 10.010 3500.006 017 22.87×10-3 500.005 997 24.67×10-40.006 005 28.67×10-4 50.10.005 924 30.012 6170.005 998 62.33×10-4 50.20.005 970 90.004 8500.006 010 21.70×10-3
文中主要贡献及结论如下：
1）给出了Nuttall窗和Hanning窗构成的二阶混合窗的频域表达式，根据表达式分析了窗函数具有很好的主瓣和旁瓣特性，并将其应用在apFFT的全相位处理。
2）用全相位预处理，不仅具有抑制信号截断引起的频谱泄漏能力，还具有“相位不变性”，不存在栅栏效应，因此能够进行高精度相位检测，非常适合应用在高精度介损角的测量。
3）相比传统FFT，apFFT只是在全相位处理时多做了N次加法运算，但由于不存在栅栏效应，得到相位谱后无需再做插值校正，故从算法的复杂度上讲，apFFT也具有更小计算量。
4）在频率变动、白噪声、谐波含量变化及采样点数的影响下，验证了本文算法较传统傅里叶加窗插值算法精度提高了多个数量级，且此算法相对传统加窗插值FFT，省去了插值的过程，算法复杂度更低，更适合用于绝缘介质介损角的在线检测。
参考文献
[1] 王晓辉, 朱永利, 王艳, 等. 基于深度学习的电容器介损角在线辨识[J]. 电工技术学报, 2017, 32(15): 145-152.
Wang Xiaohui, Zhu Yongli, Wang Yan, et al. On-line identification of capacitor dielectric loss angle based on deep learning[J]. Transactions of Electrical Engin- eering, 2017, 32(15): 145-152.
[2] Yu Xinliang, Yi Bing, Liu Fang, et al. Prediction of the dielectric dissipationtan factor tand of polymers with an ANN model based on the DFT calculation[J]. Reactive and Functional Polymers, 2008, 68(11): 1557-1562.
[3] 张俊敏, 刘开培, 汪立, 等. 基于主瓣宽度多谱线插值的高精度快速谐波分析算法[J]. 电工技术学报, 2018, 33(增刊1): 121-128.
Zhang Junmin, Liu Kaipei, Wang Li, et al. High- precision fast harmonic analysis algorithm based on multi-line interpolation of main lobe width[J]. Transa- ctions of Electrical Engineering, 2018, 33(S1): 121-128.
[4] 徐志钮. 噪声对介质损耗角正切计算结果的影响[J]. 电力自动化设备, 2013, 33(11): 69-74.
Xu Zhiniu. Influence of noise on accuracy of dielectric loss factor calculation[J]. Electric Power Automation Equipment, 2013, 33(11): 69-74.
[5] 赵文清, 严海, 王晓辉. BP神经网络和支持向量机相结合的电容器介损角辨识[J]. 智能系统学报, 2019, 14(1): 134-140.
Zhao Wenqing, Yan Hai, Wang Xiaohui. Identi- fication of dielectric loss angle of capacitors based on BP neural network and support vector machine[J]. Journal of Intelligent Systems, 2019, 14(1): 134-140.
[6] 董爽, 李天云, 王永, 等. 在线检测介质损耗角的矩阵束方法[J]. 电工技术学报, 2015, 30(18): 229-236.
Dong Shuang, Li Tianyun, Wang Yong, et al. Matrix beam method for detecting dielectric loss angle on-line[J]. Transactions of China Electrotechnical Society, 2015, 30(18): 229-236.
[7] 高云鹏, 李峰, 陈婧, 等. 改进能量算子Nuttall窗频谱校正的闪变测量方法[J]. 仪器仪表学报, 2014, 35(4): 745-753.
Gao Yunpeng, Li Feng, Chen Jing, et al. Flicker measurement method for improved energy operator Nuttall window spectrum correction[J]. Chinese Journal of Scientific Instrument, 2014, 35(4): 745-753.
[8] 王永, 滕召胜, 李建闽, 等. 基于采样序列重构的高精度介质损耗角测量方法[J]. 电工技术学报, 2018, 33(23): 5607-5615.
Wang Yong, Teng Zhaosheng, Li Jianbiao, et al. High-precision dielectric loss angle measurement method based on sample sequence reconstruction[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5607-5615.
[9] 华敏, 陈剑云. 一种高精度六谱线插值FFT谐波与间谐波分析方法[J]. 电力系统保护与控制, 2019, 47(11): 9-15.
Hua Min, Chen Jianyun. A high accuracy six-line interpolation FFT method for harmonic and inter- harmonic analysis[J]. Power System Protection and Control, 2019, 47(11): 9-15.
[10] 杨名, 陈红卫. 一种基于小波包和apFFT的间谐波检测方法[J]. 电力系统保护与控制, 2017, 45(15): 112-117.
Yang Ming, Chen Hongwei. An interharmonics detection method based on wavelet packet and apFFT[J]. Power System Protection and Control, 2017, 45(15): 112-117.
[11] 范晋龙, 黄晓峰, 王建辉, 等. 绝缘材料的介质损耗角在线检测方法研究[J]. 计算机测量与控制, 2019, 27(1): 17-21.
Fan Jinlong, Huang Xiaofeng, Wang Jianhui, et al. On-line detection method of dielectric loss angle of insulating materials[J]. Computer Measurement & Control, 2019, 27(1): 17-21.
[12] 朱国威, 王先培, 龙嘉川, 等. 基于Kalman基频跟踪的介损角测量算法[J]. 高电压技术, 2016, 42(4): 1282-1289.
Zhu Guowei, Wang Xianpei, Long Jiachuan, et al. Dielectric loss angle measurement algorithm based on Kalman fundamental frequency tracking[J]. High Voltage Engineering, 2016, 42(4): 1282-1289.
[13] 张超, 王维庆, 邱衍江, 等. 大规模风电并网地区次同步谐波检测方法[J]. 高电压技术, 2019, 45(7): 2194-2202.
Zhang Chao, Wang Weiqing, Qiu Yanjiang, et al. Subsynchronous harmonic detection method for large-scale wind power grid-connected area[J]. High Voltage Technology, 2019, 45(7): 2194-2202.
[14] 王保帅, 肖霞. 一种用于谐波分析的高精度多谱线插值算法[J]. 电工技术学报, 2018, 33(3): 553-562.
Wang Baoshuai, Xiao Xia. A high precision multi- line interpolation algorithm for harmonic analysis[J]. Transactions of China Electrotechnical Society, 2018, 33(3): 553-562.
[15] 王兆华, 黄翔东, 杨尉. 全相位FFT相位测量法[J]. 世界科技研究与发展, 2007, 29(4): 28-32.
Wang Zhaohua, Huang Xiangdong, Yang Wei. All phase FFT phase measurement method[J]. World Sci- Tech Research and Development, 2007, 29(4): 28-32.
[16] 孙仲民, 何正友, 臧天磊. 一种混合卷积窗及其在谐波分析中的应用[J]. 电工技术学报, 2016, 31(16): 207-214.
Sun Zhongmin, He Zhengyou, Zang Tianlei. A hybrid convolution window and its application in harmonic analysis[J]. Transactions of China Electrotechnical Society, 2016, 31(16): 207-214.
[17] 黄翔东, 王兆华, 罗蓬, 等. 全相位FFT密集谱识别与校正[J]. 电子学报, 2011, 39(1): 172-177.
Huang Xiangdong, Wang Zhaohua, Luo Peng, et al. Discrimination and correction for dense all-phase FFT spectrums[J]. Acta Electronica Sinica, 2011, 39(1): 172-177.
[18] 黄翔东, 王兆华. 全相位时移相位差频谱校正法[J]. 天津大学学报, 2008, 41(7): 815-820.
Huang Xiangdong, Wang Zhaohua. All-phase time- shift phase difference correcting spectrum method[J]. Journal of Tianjing University, 2008, 41(7): 815-820.
[19] 黄翔东, 王兆华. 基于全相位频谱分析的相位差频谱校正法[J]. 电子与信息学报, 2008, 30(2): 293-297.
Huang Xiangdong, Wang Zhaohua. Phase difference spectrum correction method based on all phase spectrum analysis[J]. Journal of Electronics & Infor- mation Technology, 2008, 30(2): 293-297.
[20] 张鸿博, 蔡晓峰, 鲁改凤. 基于全相位FFT改进相位差法的自动准同期并列参数测量[J]. 电力系统保护与控制, 2016, 44(4): 76-83.
Zhang Hongbo, Cai Xiaofeng, Lu Gaifeng. Auto- mated synchronous parallel parameter measurement based on improved phase difference method of all phase FFT[J]. Power System Protection and Control, 2016, 44(4): 76-83.
High Precision Dielectric Loss Angle Measurement Based on Improved All-Phase Algorithm
Abstract The fast Fourier algorithm has the problems of fence effect and spectrum leakage in practical application. The accuracy of dielectric loss angle measurement by fast Fourier algorithm is not high. A high precision dielectric loss angle measurement method based on hybrid convolution window and improved all-phase was proposed. The mixed convolution window with better main and side lobes was used to truncate the signal to reduce the spectrum leakage. The "phase invariance" of all-phase Fourier transform was used to eliminate the fence effect. A differential phase correction method was proposed for all-phase Fourier transform. It is compared under the influence of fundamental frequency variation, signal-to-noise ratio change, harmonic content change and sampling points and the results show that the detection accuracy of the proposed method is higher than that of the windowed interpolation Fourier transform algorithm, especially in asynchronous sampling.
keywords：All-phase, Fourier transform, mixed convolution window, dielectric loss angle
DOI: 10.19595/j.cnki.1000-6753.tces.190673
中图分类号：TM835
张家军 男，1993年生，硕士研究生，研究方向为电力谐波分析。E-mail: 1624236670@qq.com
张新燕 女，1964年生，教授，博士生导师，研究方向为新能源发电控制与并网技术。E-mail: xjcxzxy@126.com（通信作者）
国家自然科学基金资助项目（51667018）。
收稿日期 2019-06-03
改稿日期 2019-07-08
（编辑 郭丽军）