图1 DAB变换器拓扑
Fig.1 The topology of DAB converter
摘要 为提升能量路由器中双有源桥(DAB)变换器的传输效率,同时改善系统的动态特性,该文提出一种基于扩展移相的输出电压模型预测控制与梯度下降算法实现回流功率优化的混合控制策略。首先,建立DAB变换器在单移相和扩展移相控制下的传输功率数学模型,分析回流功率产生机理,并推导扩展移相控制下的输出电压状态空间平均化方程;其次,在DAB变换器输出电压模型预测控制基础上提出基于梯度下降算法的回流功率优化策略。搭建小功率实验样机,并与传统单移相控制进行对比,实验结果证明了该文所提控制策略的有效性及正确性。
关键词:双有源桥变换器 扩展移相控制 回流功率优化 动态响应 梯度下降算法
近年来,随着环境污染的日益严峻及可再生能源的快速发展,现有电网难以满足未来发展的需要。以高速发展的互联网技术、先进的电力电子装备及分布式控制为基础的能源互联网(Energy Internet, EI)得到了学者的广泛关注[1-3]。其中,电力电子能量路由器(Electric Energy Router, EER)作为能源互联网的核心设备,具有可实现高低压侧电气隔离、多电压等级接口、便于可再生能源及储能设备接入的多种优点[4-6]。此外,双有源桥(Dual-Active- Bridge, DAB)直流变换器因具有电气隔离、结构对称、功率双向传输及易于模块化扩展等优势,被广泛地应用于光伏、电动汽车、储能及直流配电网等场合,并逐渐成为EER的核心设备之一[7-9]。
在DAB变换器控制方法中,移相控制为最常用的控制方式之一[10],但其采用单移相(Single- Phase-Shift, SPS)控制时,通常存在较大回流功率和电流应力,不利于提升变换器效率[11-12]。文献[13]提出了一种扩展移相(Extended-Phase-Shift, EPS)控制方法,在一次侧H桥中加入内移相比D1,增加了控制自由度,并在一定程度上降低了变换器的回流功率。文献[14-15]则基于双重移相控制展开研究,在外移相比的基础上,同时在两侧H桥中引入了相同的内移相比,根据对DAB变换器的软开关特性、回流功率等影响因素的分析,采用分段线性的控制方法来改善回流功率。文献[16]提出了一种三重移相控制策略,但在该控制下DAB变换器工作模态较多,回流功率数学模型过于复杂,因此在实际工程应用中难以推广。
此外在实际应用中,DAB变换器动态特性尤为重要。文献[17]为改善负载阶跃时的动态特性,提出了一种基于DAB变换器谐波模型的前馈补偿控制策略,但其谐波数学模型的求解较为复杂,不利于该算法的推广应用。为此文献[18]建立了基于二阶广义状态空间平均法的三相DAB模型,在此基础上提出了一种优化限幅的闭环控制方法,能够改善系统的动态响应。文献[19]提出了一种基于SPS的直接功率优化控制方案,但其在负载突变的工况下并不能很好地改善系统的动态性能。文献[20]提出了一种基于双重移相的模型预测控制策略,在输入电压及负载突变的工况下改善了动态特性。类似地,Y. Jeung等在文献[21]中提出了一种双线性积分滑模控制策略,但是其推导过程过于复杂并且优化程度有限。
为综合改善DAB回流功率及动态性能,本文基于EPS提出了一种输出电压模型预测控制和梯度下降算法(Model Predictive Control and Gradient Descent algorithm, MPC-GD)优化回流功率的混合控制策略。首先推导了传输功率及回流功率数学模型,并与传统SPS控制进行对比。在此基础上,建立DAB输出电压状态空间平均化模型,提出了一种输出电压模型预测控制,同时采用梯度下降算法实现回流功率的优化。最终将梯度下降算法与模型预测控制相结合形成混合控制策略,并与传统SPS控制进行对比实验验证。
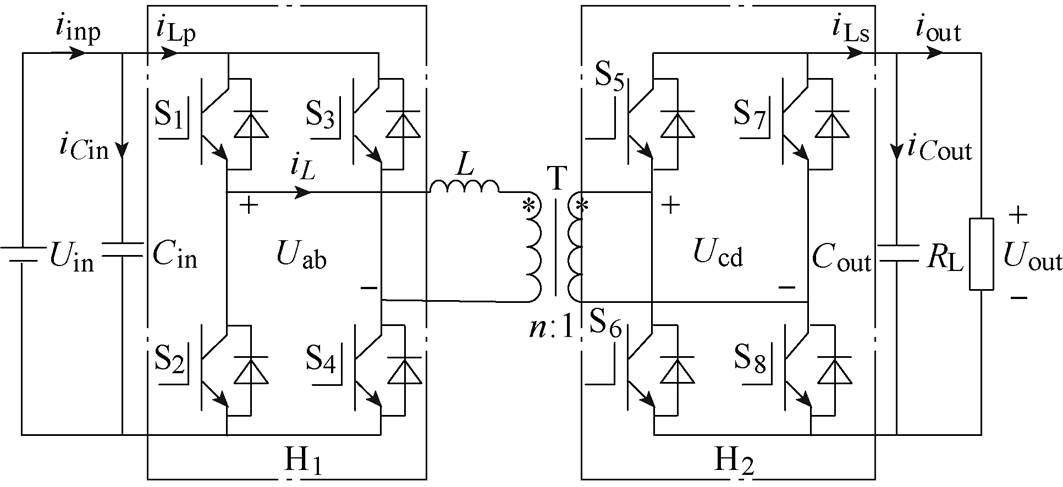
图1为典型DAB变换器主电路拓扑,主要由两个H桥(H1和H2)和隔离变压器T组成。图中,Cin、Cout分别为输入和输出电容,Uin、Uout分别为输入和输出电压。iinp和iCin分别为一次侧电源电流和直流母线电容电流,iL为电感电流,iLp和iLs分别为一次侧输入电流和二次侧输出电流。iCout和iout分别为输出侧母线电容电流和负载电流,Uab和Ucd分别为H1输出电压和H2输入电压。规定图1中箭头方向为电流正方向,L为变压器漏感和辅助电感之和,RL为负载等效电阻,变压器电压比为n。

图1 DAB变换器拓扑
Fig.1 The topology of DAB converter
由图1可知,DAB变换器电路微分方程可分别表示为
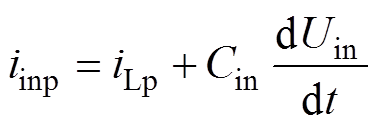 (1)
(1)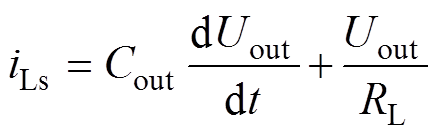 (2)
(2)
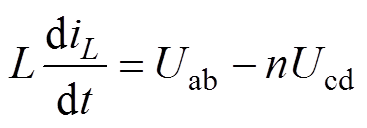 (3)
(3)
DAB变换器在EPS控制下的工作波形如图2所示,其中,Ths为半个开关周期,UL为电感电压, Pt(EPS)为传输功率。D1为S1(S2)和S4(S3)之间的内移相比,0≤D1≤1;D2为H1和H2之间的外移相比,0≤D2≤1且0≤D1+D2≤1。与传统SPS控制相比,增加了控制系统的灵活性与自由度。
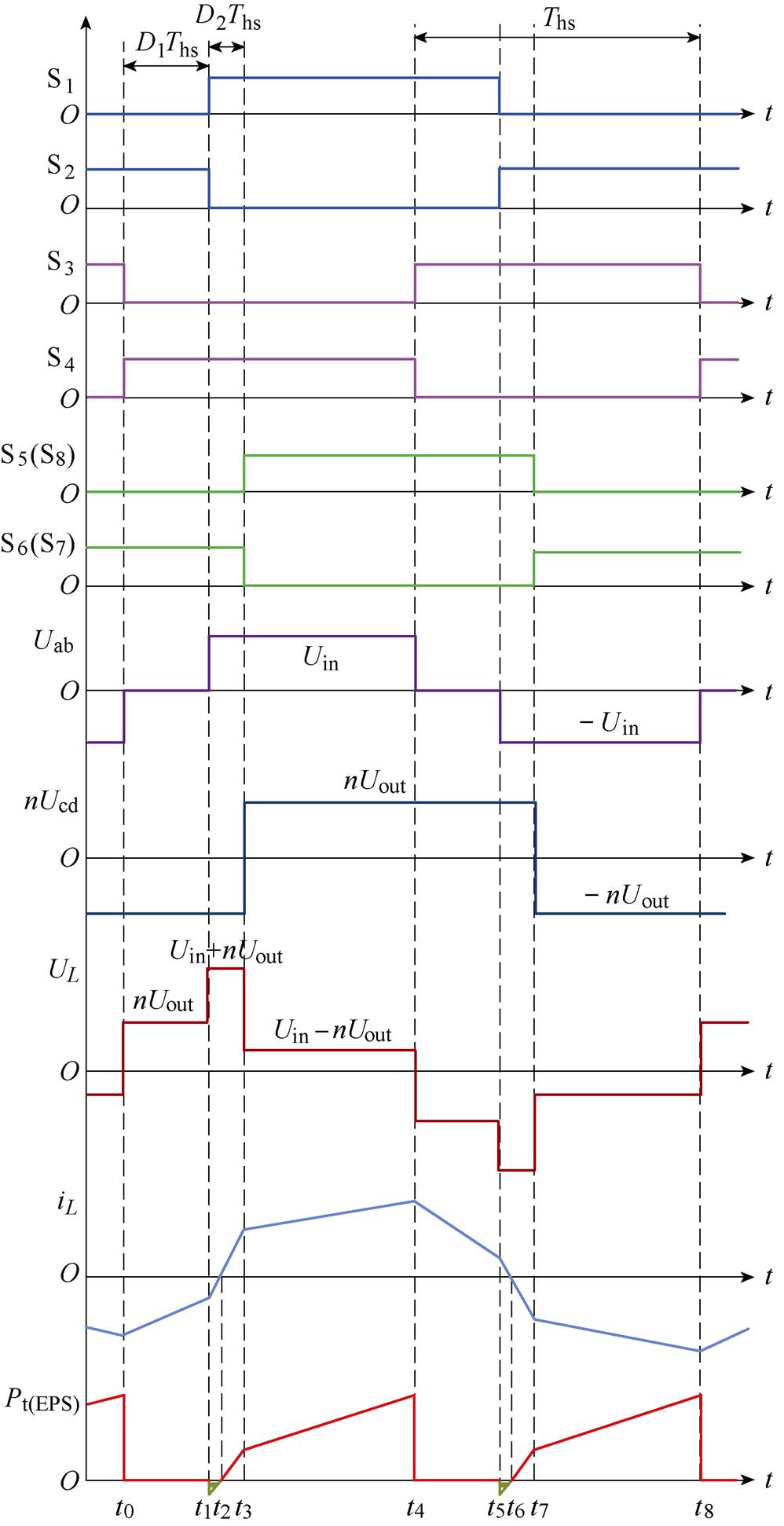
图2 EPS控制下DAB变换器工作波形
Fig.2 Working waveforms of DAB converter under EPS control
由图2可知,在一个开关周期内,同时考虑电感电流的对称性,在各个时刻的电感电流为
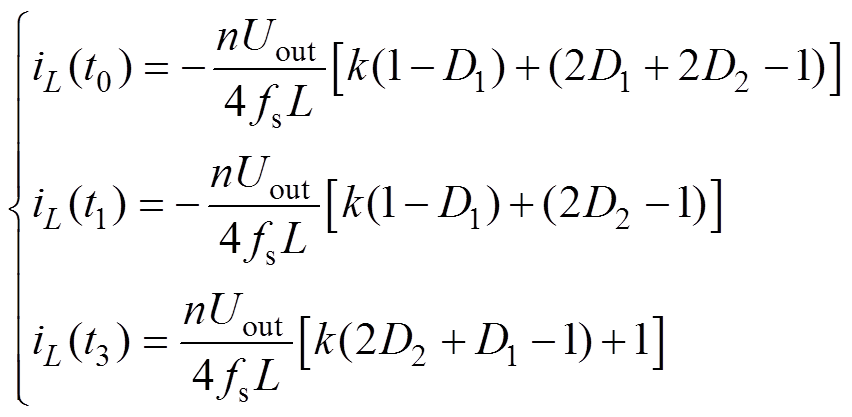 (4)
(4)式中,fs为开关频率;k为设DAB变换器的电压转换比,为简化分析,k=Uin/(nUout)。
根据式(1)~式(4)并结合图2中电感电流在一个开关周期内的工作模态及对称性可求得,DAB变换器在EPS控制下的输出电压状态空间平均化方程为
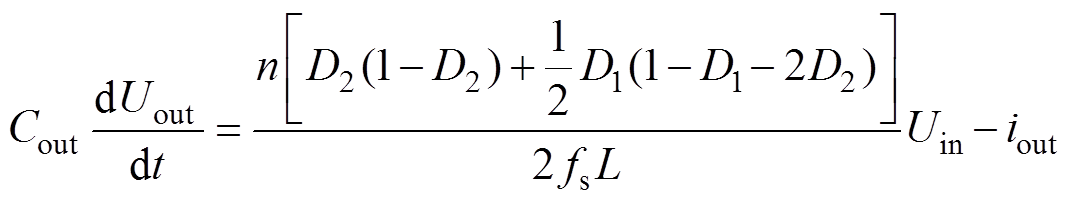 (5)
(5)由前述EPS工作模态分析可知,当变换器的传输功率从一次侧传递至二次侧时,在EPS控制下DAB的传输功率Pt(EPS)和回流功率Pbf(EPS)表达式分别为
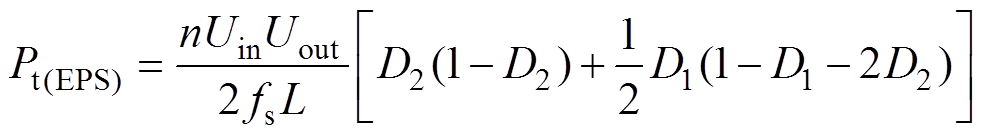 (6)
(6)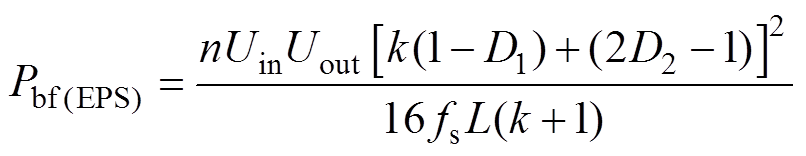 (7)
(7)
类似地,由式(4)可知,EPS控制下DAB变换器的电流应力可表示为
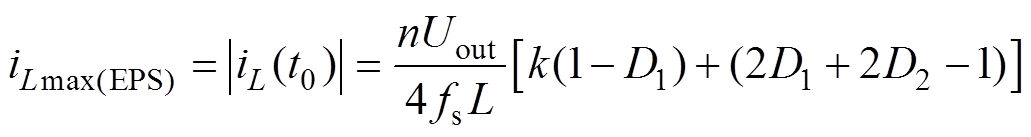 (8)
(8)同理可得,在SPS控制下传输功率Pt(SPS)、回流功率Pbf(SPS)和电流应力iLmax(SPS)的表达式分别为
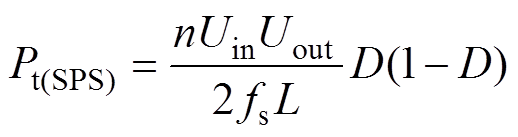 (9)
(9)
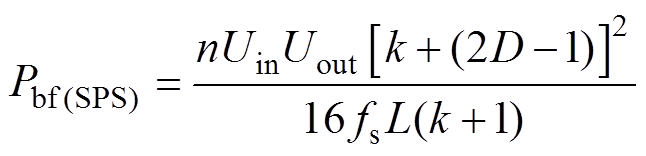 (10)
(10)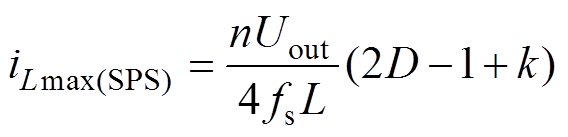 (11)
(11)
式中,D为SPS控制移相比。
选取DAB变换器在EPS控制下的最大传输功率为PN,电流应力额定值为iN,则可分别表示为
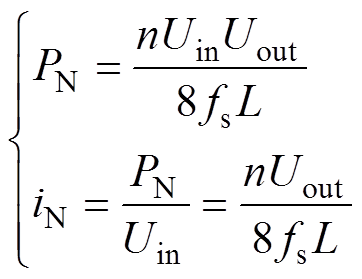 (12)
(12)为便于对比分析,将SPS与EPS控制下的传输功率、回流功率和电流应力分别进行标幺化可得
 (13)
(13)
式中,p(SPS)和p(EPS)分别为SPS与EPS控制下的传输功率标幺值;Mbf(SPS)和Mbf(EPS)分别为SPS与EPS控制下的回流功率标幺值;A(SPS)和A(EPS)分别为SPS与EPS控制下的电流应力标幺值。
在SPS和EPS控制下,当DAB变换器的传输功率相同时,可得
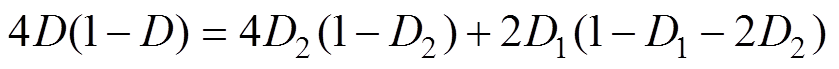 (14)
(14)对式(14)进行求解可得
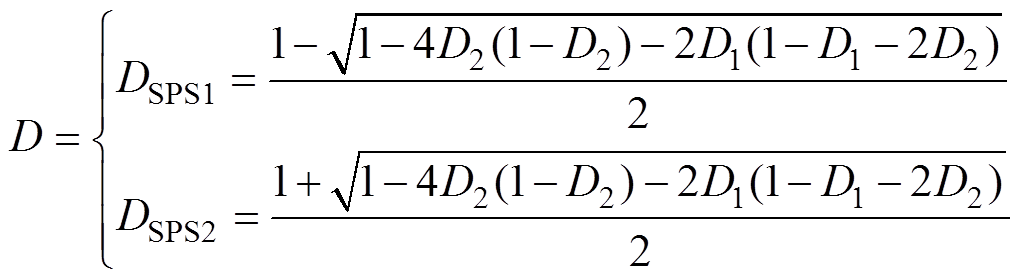 (15)
(15)
根据式(13)和式(15)可得,当SPS和EPS控制在传输功率相同的情况下,电压转换比k=3时,回流功率和电流应力在SPS与EPS控制下的三维曲线如图3所示。
采用SPS控制时,移相比DSPS1所对应的回流功率和电流应力明显小于DSPS2所对应的回流功率及
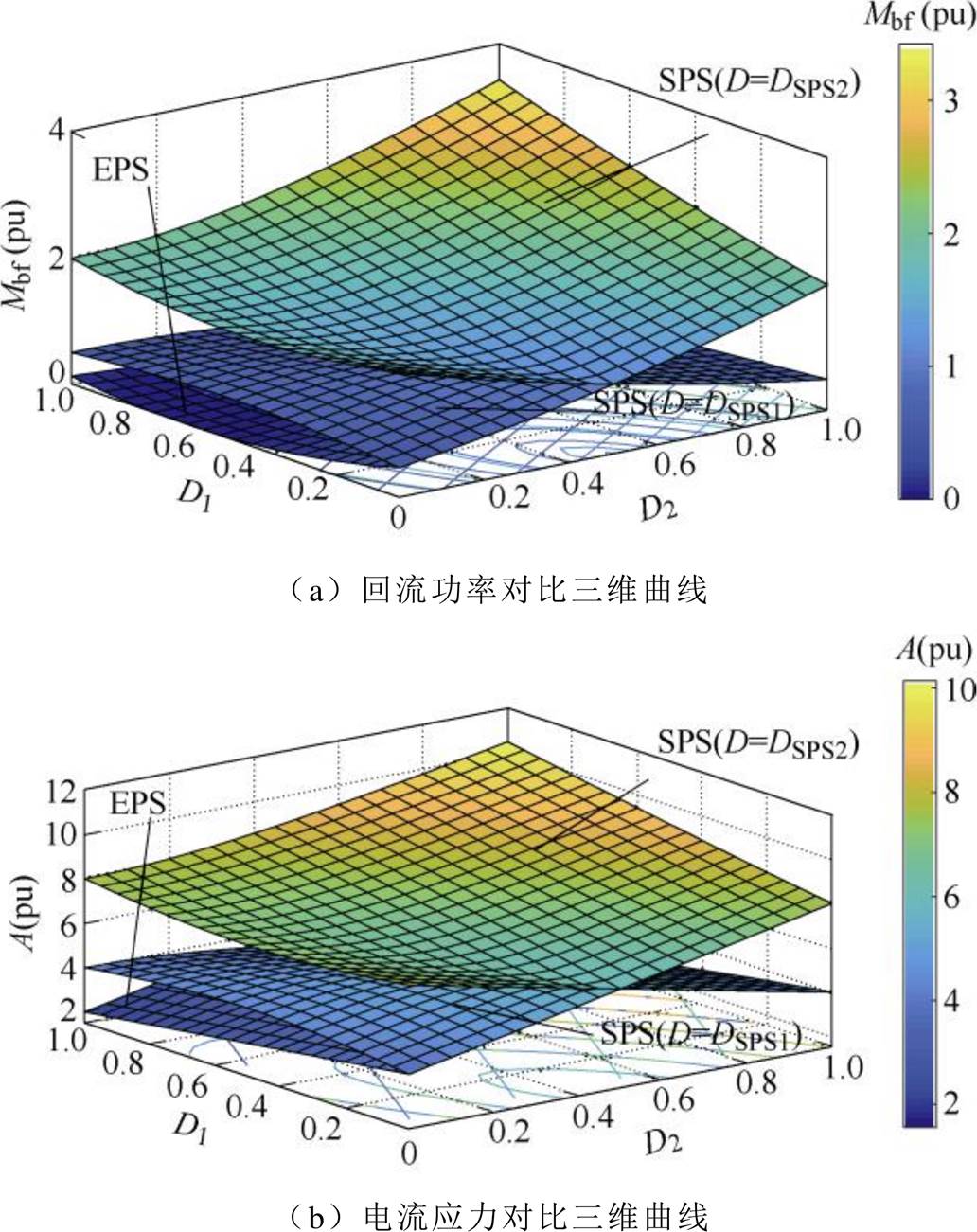
图3 回流功率与电流应力三维曲线
Fig.3 Three-dimensional curves of backflow power and current stress
电流应力。同时可知,相同传输功率下采用EPS控制时,电流应力及回流功率较SPS控制均明显降低,由此可知,EPS相对SPS控制对回流功率有较好的抑制效果。
由式(5)输出电容电压微分方程可预测输出电压的变化趋势,由此采用前向欧拉法对式(5)进行离散化处理,可得
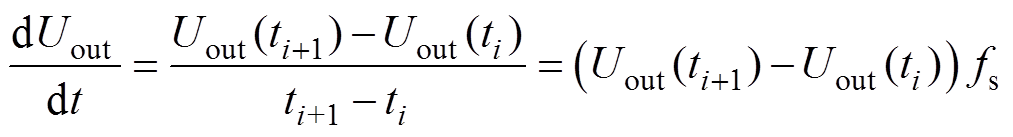 (16)
(16)联立式(5)和式(16)可得输出电压预测控制方程可表示为
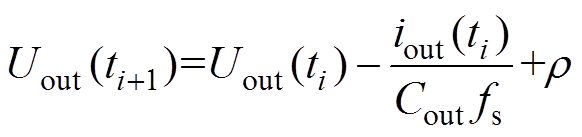 (17)
(17)
其中
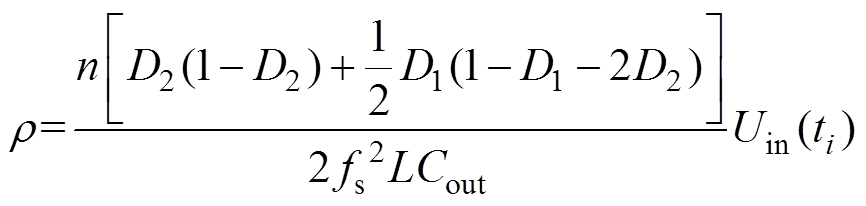 (18)
(18)式中,r 为等效输入电压分量;Uout(ti)和Uin(ti)分别为ti(i=1,2,…)时刻输出电压和输入电压采样值;iout(ti)为ti时刻输出电流采样值;Uout(ti+1)为ti+1时刻输出电压预测值。
根据式(17)和式(18),选取输出电压价值函数J(i)为
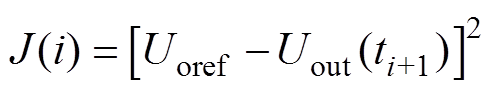 (19)
(19)式中,Uoref为输出电压给定值。
将式(17)代入式(19),并且为使得控制器输入与输出相匹配,同时增强控制系统的抗干扰能力,对输出电压进行标幺化处理,由此可得到预测控制优化外移相比D2可表示为
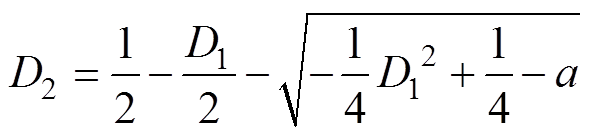 (20)
(20)其中
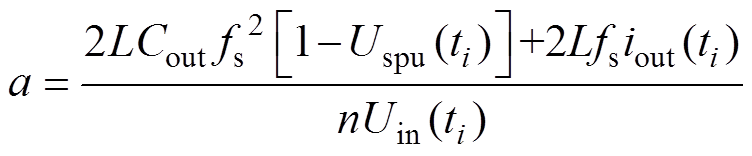 (21)
(21)
式中,Uspu(ti)为变换器输出电压标幺值,Uspu(ti)= Uout(ti)/Uoref。
根据式(20)可得标幺化输出电压Uspu(ti)与预测优化外移相比D2之间的关系曲线如图4所示。其中,电路参数为:输入电压Uin=80V,输出电压Uout= 200V,输出电容Cout=2 000mF,变压器电压比n=1/4,负载电阻为100W,给定内移相比D1=0.1。当输出电压与给定电压偏差较大时,系统将以最大优化能力提高(D2=0.5)或降低(D2=0)输出电压,从而使得输出电压快速恢复至给定值。当DAB输出电压在给定值附近时,能够平滑地调节输出电压,快速准确地跟踪输出电压给定值。
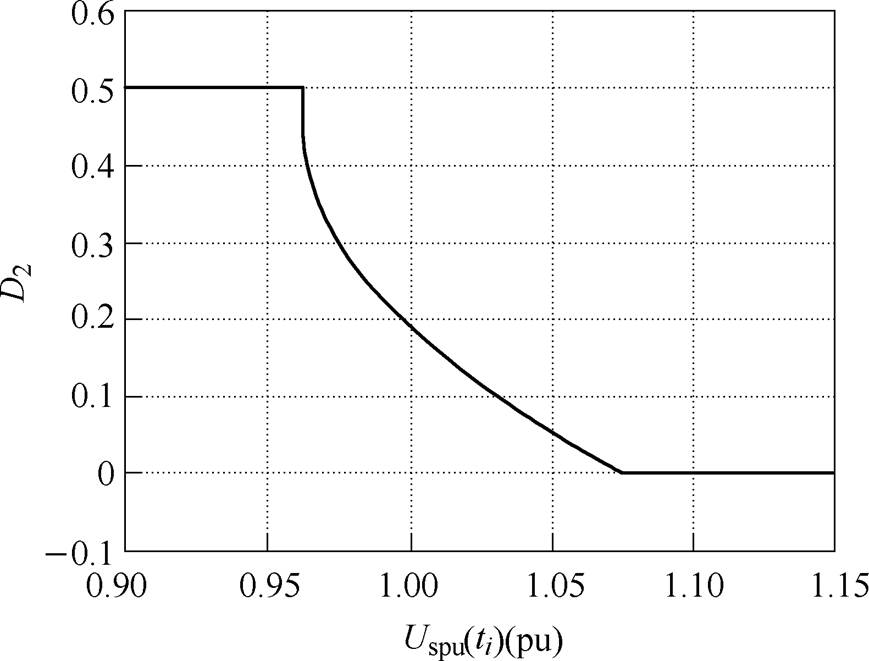
图4 预测外移相比D2与输出电压标幺值曲线
Fig.4 The curve between predictive outer phase-shift ratio D2 and the normalized output voltage
在实际电路中,由于开关管的压降及开通关断延迟、电感电容参数测量误差、变换器死区时间以及控制系统的采样传输延迟等因素的影响,使得式(20)中的预测优化外移相比与实际真实值之间存在偏差,从而导致控制系统的不精确。为消除上述控制偏差,引入误差校正因子b 对偏差进行补偿。b 可由输出电压误差通过PI控制器后,与校正因子基准值相叠加,最后经过校正因子限幅所获得。误差校正因子b的控制框图如图5所示。
将b 与式(20)中的预测外移相比D2相乘,可得到加入校正因子b 后的预测优化外移相比D2final的表达式为
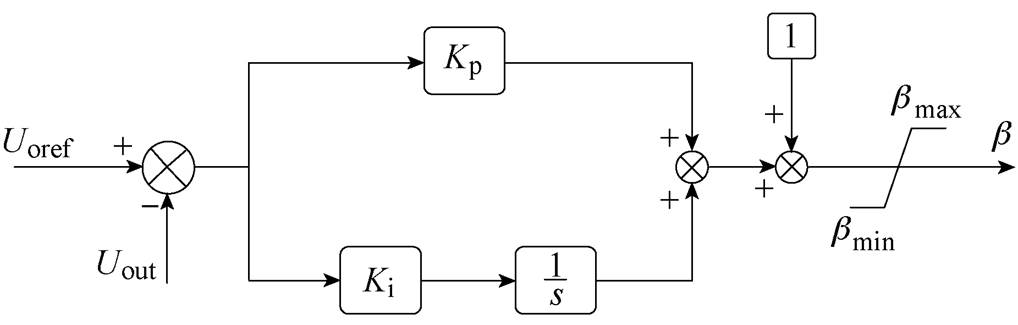
图5 误差校正因子控制框图
Fig.5 Control block diagram of error correction factor
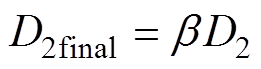 (22)
(22)由此可得到,EPS控制下DAB变换器的回流功率Mbfn(EPS)最终可表示为
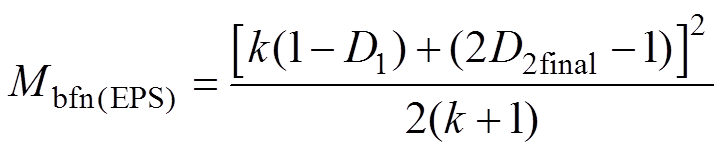 (23)
(23)
梯度下降算法是用于求解强化学习优化问题常用的方法,用于逼近所建立控制对象数学模型的极值,求得最优解[22]。本文基于梯度下降算法对EPS控制下DAB变换器回流功率进行优化,减小回流功率,进而提高系统传输效率。
定义EPS控制下回流功率的梯度表达式为
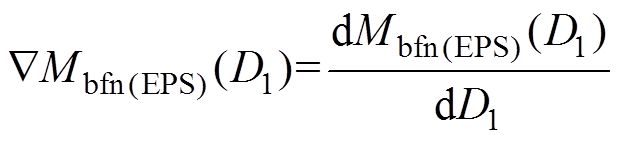 (24)
(24)对于EPS控制下DAB变换器回流功率优化问题,可得到回流功率基本优化迭代方程为
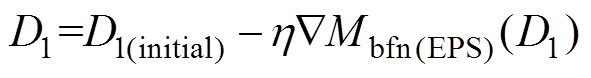 (25)
(25)
式中,h 为学习率;D1(initial)为内移相比初始值;D1为根据式(25)迭代更新之后的内移相比。
选取合适的学习率h 尤为重要,当h 过小时,会导致系统的迭代次数增加,收敛速度变慢;当h过大时,虽然系统的迭代次数有所减少,但可能会导致系统的振荡甚至不稳定。合适的学习率可以使得回流功率精确快速地到达最小值,从而提升控制系统的准确性和良好的动态特性。
为了减小求解系统回流功率优化时陷入局部最优的风险,在原有迭代方程的基础上加入冲量,形成冲量梯度下降回流功率优化算法。则原有的梯度下降方程式(24)可更新为
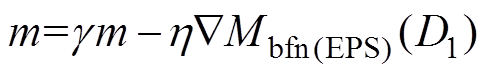 (26)
(26)式中,m为加入冲量优化之后的等效梯度步进数值;g 为冲量比例系数。由此可得到,加入冲量之后的内移相比D1的迭代公式为
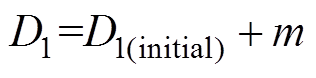 (27)
(27)
由式(26)和式(27)可知,当D1更新时不仅考虑了当前梯度值,而且加入了冲量g m。相比原有梯度下降算法,当梯度与冲量方向一致时,冲量增加,加速了系统的求解;反之,冲量减小,降低系统的超调与振荡。
由以上推导分析可得到回流功率梯度下降算法的具体实现流程如图6所示。
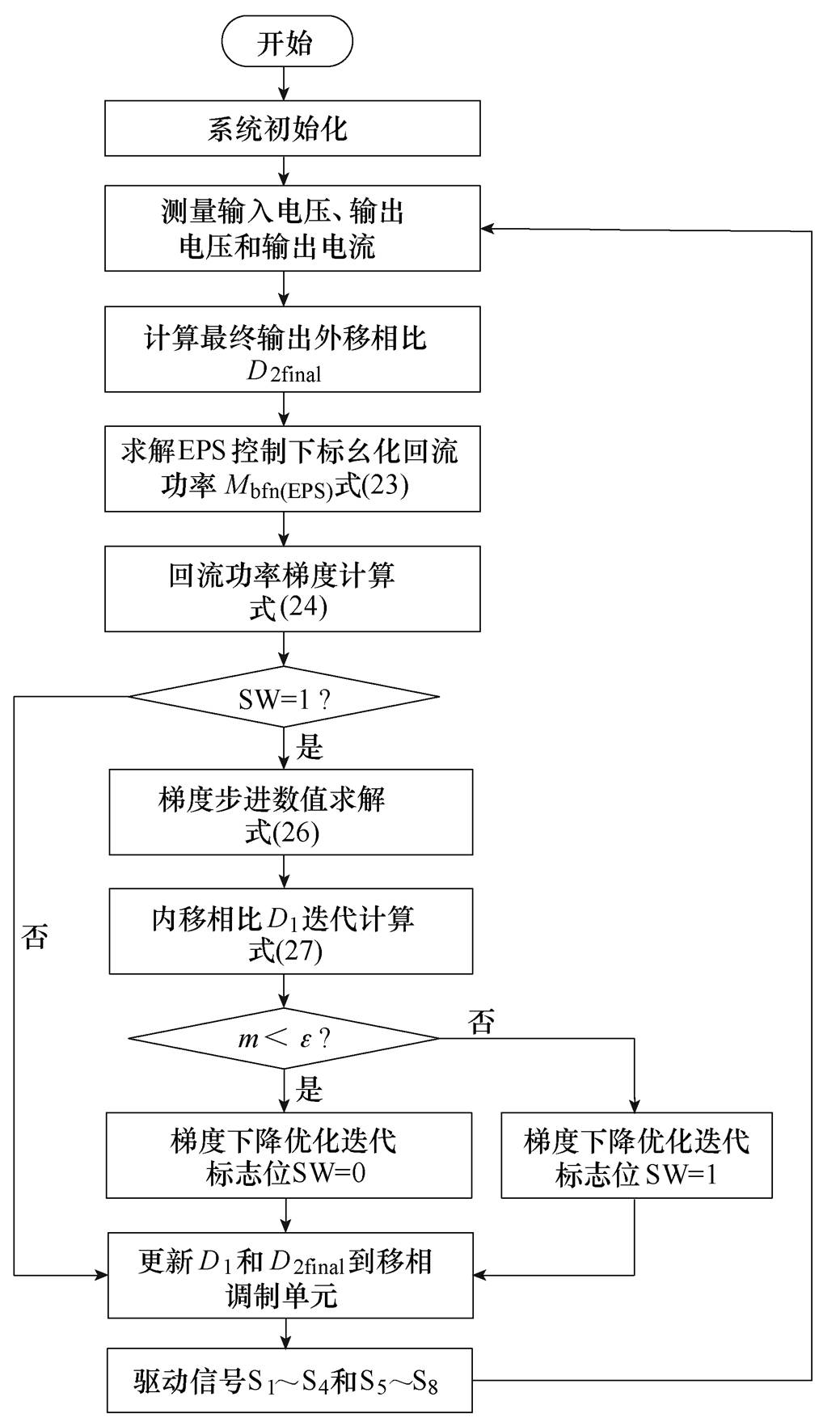
图6 梯度下降算法流程
Fig.6 Flow chart for the gradient descent algorithm
首先启动系统进行初始化设置,分别测量输入和输出电压及输出电流,根据测量值求解EPS控制下的标幺化回流功率Mbfn(EPS)。然后,判断梯度下降优化迭代标志位SW是否为1:若为1,则进行回流功率梯度下降迭代计算如式(26)和式(27)所示,判断梯度步进数值m是否小于给定阀值e,若满足,则将SW置0;否则,SW仍为1;若SW不为1,则将梯度下降优化算法旁路,不再进入运算。最后,均输出更新之后的D1和D2final到移相调制单元,进而生成相对应的门极驱动信号实现EPS优化控制。
将梯度下降回流功率优化算法与加入误差校正因子b 的输出电压模型预测控制相结合,可得基于EPS的输出电压模型预测控制与梯度下降算法回流功率混合优化整体控制框图,如图7所示。
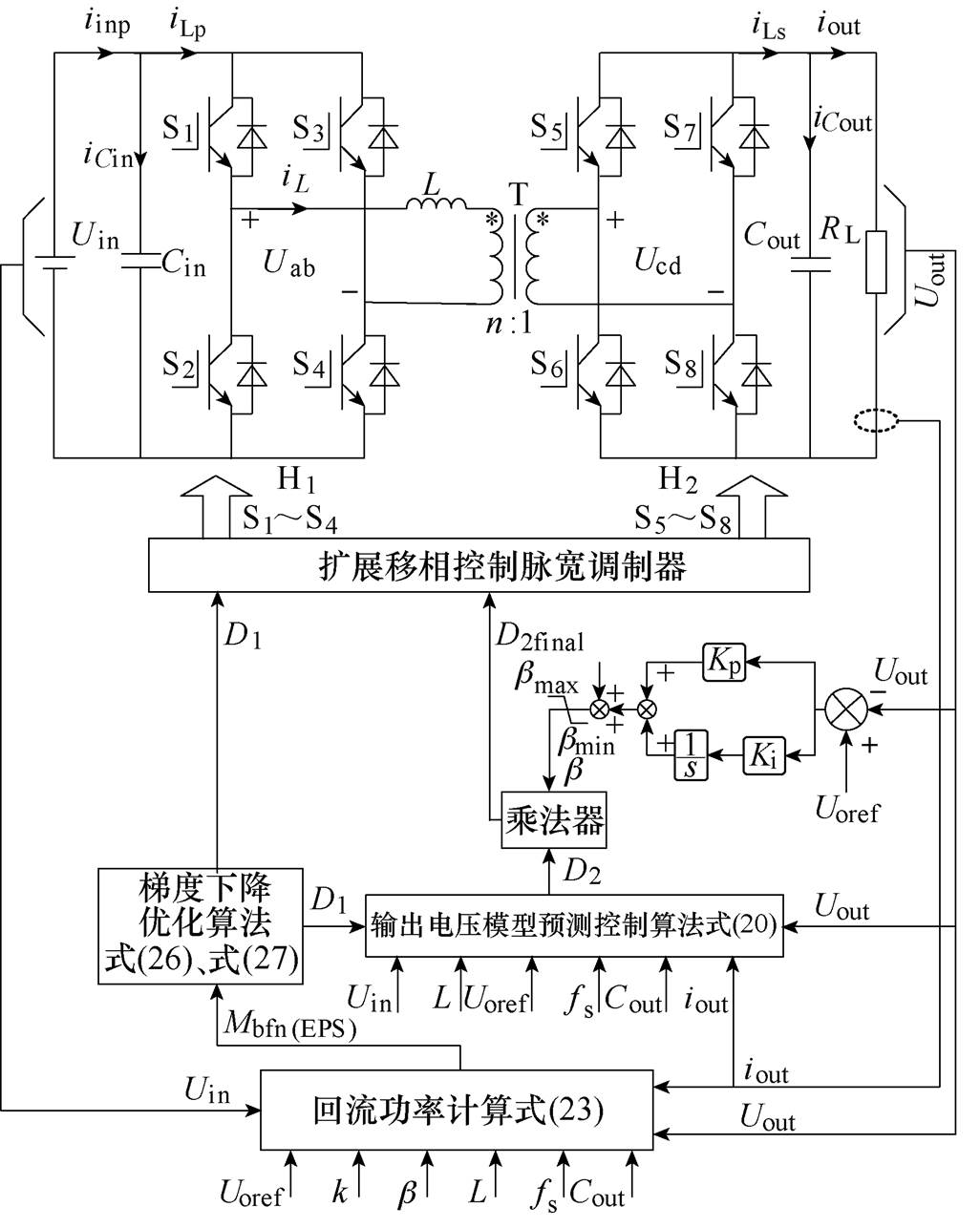
图7 基于MPC-GD-EPS的DAB变换器控制框图
Fig.7 Control block diagram of DAB converter based on MPC-GD-EPS
为验证本文所提控制策略的有效性,搭建了DAB变换器小功率实验样机。其主要实验电路参数见表1,并将MPC-GD-EPS控制策略与传统SPS控制进行对比。
表1 DAB变换器样机实验电路参数
Tab.1 The experimental circuit parameters of DAB converter prototype
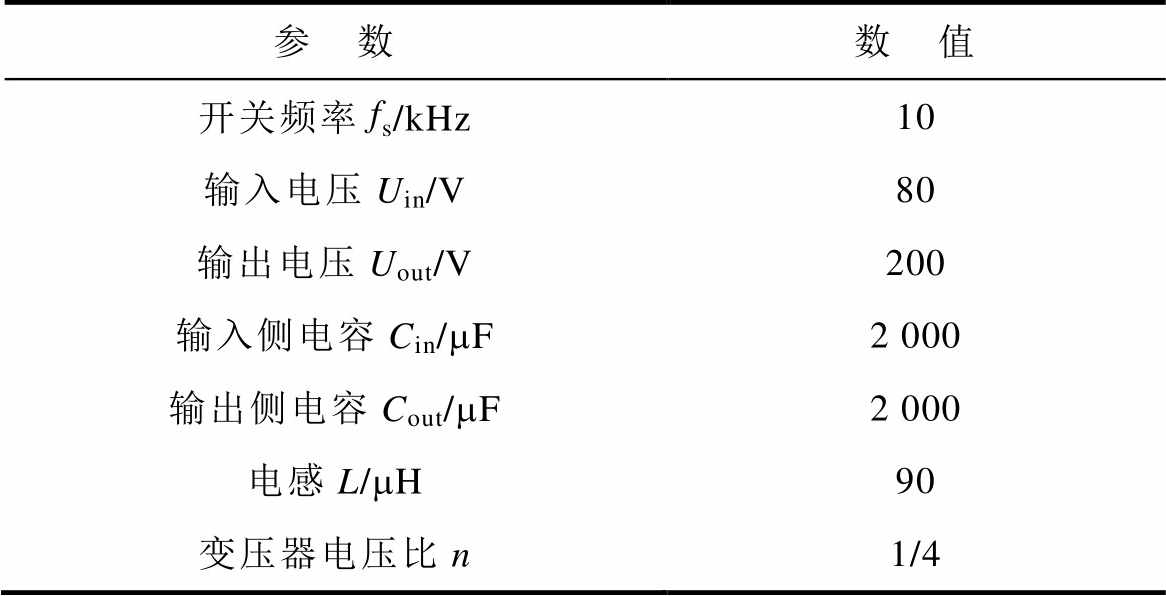
参 数数 值 开关频率fs/kHz10 输入电压Uin/V80 输出电压Uout/V200 输入侧电容Cin/mF2 000 输出侧电容Cout/mF2 000 电感L/mH90 变压器电压比n1/4
当系统输出电压Uout=200V,负载电阻为200W,输入电压由80V突降至60V时,SPS与MPC-GD- EPS控制下的电压、电流实验波形如图8所示。
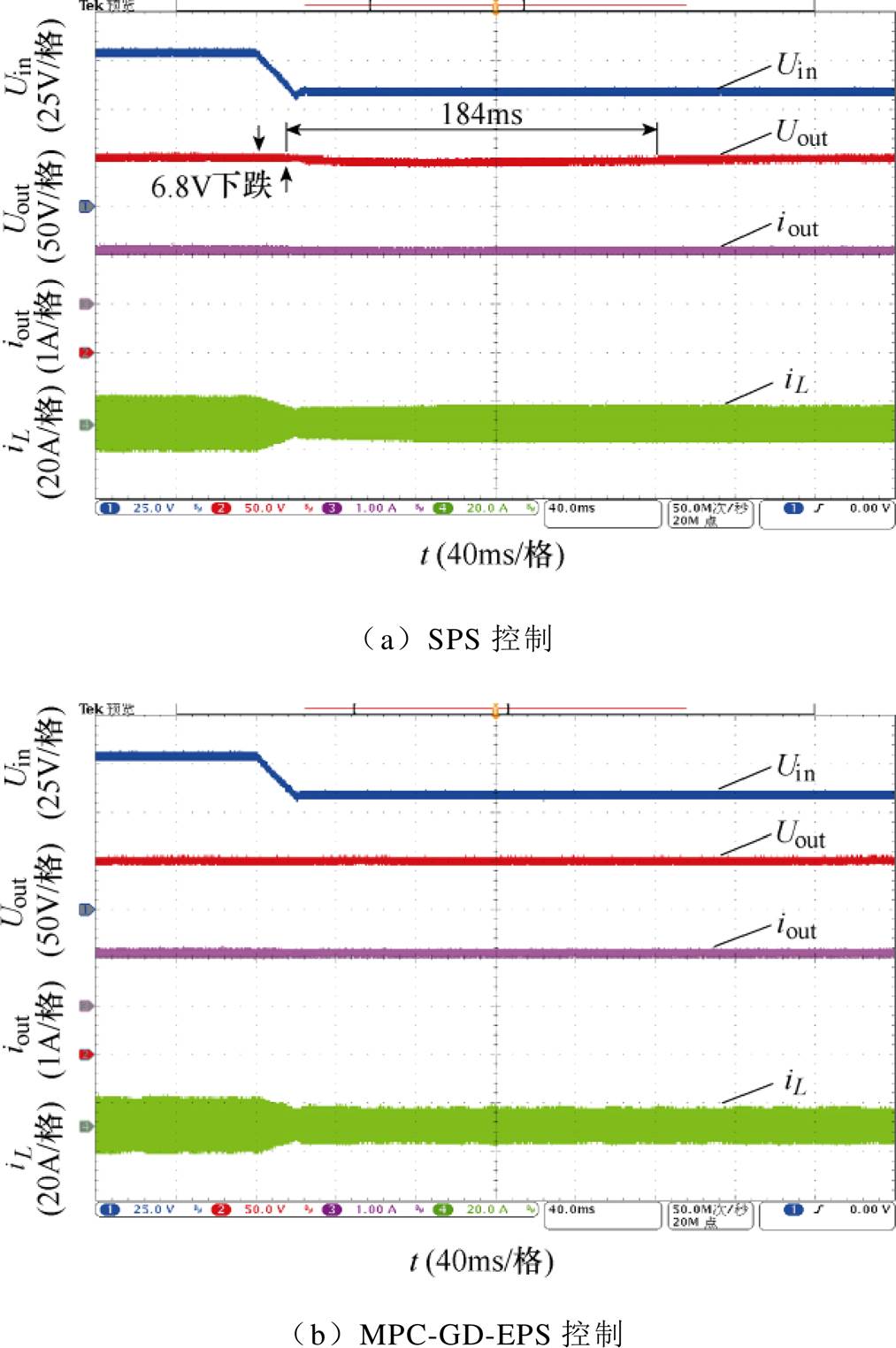
图8 输入电压突降时SPS与MPC-GD-EPS控制下的电压、电流实验波形
Fig.8 Voltage and current experimental waveforms under SPS and MPC-GD-EPS control when the input voltage steps down
由图8可知,DAB变换器采用传统SPS输出电压闭环控制时,输出电压动态调节时间较长,约为184ms,同时输出电压存在跌落,约为6.8V。而当采用本文所提出的MPC-GD-EPS控制策略时,可知系统输出电压几乎不存在波动,其动态响应时间为零。
当系统输出电压Uout=200V,负载电阻为200W,输入电压由60V突增至80V时,SPS与MPC-GD- EPS控制下的电压、电流实验波形如图9所示。
由图9可知,DAB变换器在采用SPS控制时,输出电压动态调节时间较长,约为189ms,同时存在电压超调,约为10V。而在MPC-GD-EPS控制下系统输出电压调节时间约为34ms,较SPS控制减小了155ms,并且输出电压超调约为2.1V,相比SPS控制降低了7.9V。
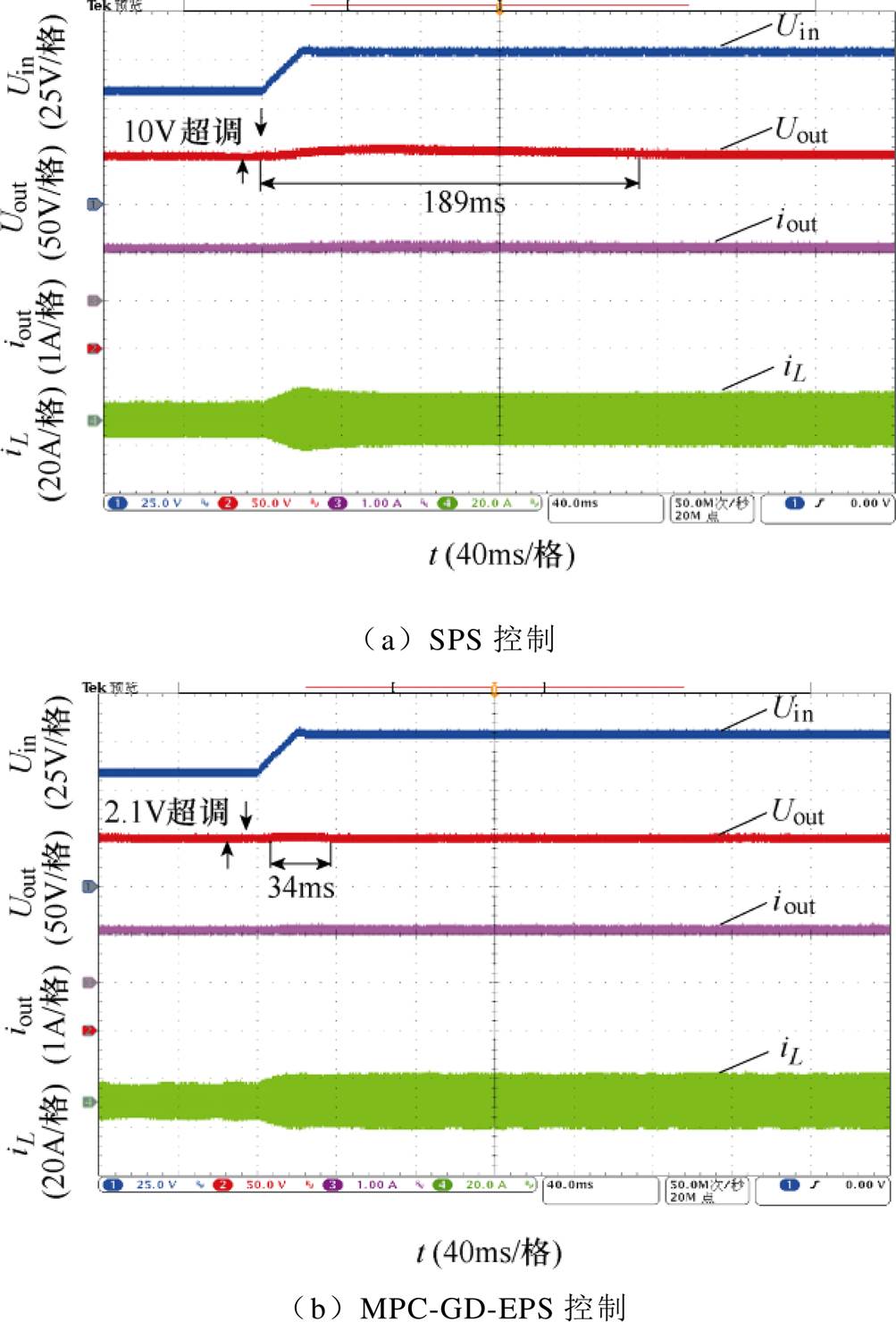
图9 输入电压突增时SPS与MPC-GD-EPS控制下的电压、电流实验波形
Fig.9 Voltage and current experimental waveforms under SPS and MPC-GD-EPS control when the input voltage steps up
当输入电压为Uin=80V,输出电压Uout=200V,负载电阻由200W 切换至120W 时,SPS与MPC-GD- EPS控制下的电压、电流实验波形如图10所示。
由图10可知,采用SPS控制时,输出电压动态调节时间约为192ms,同时存在约9.6V的电压跌落。而在MPC-GD-EPS控制下可以很好地提升DAB变换器动态响应,输出电压一直稳定在200V且无波动,动态响应时间为零。
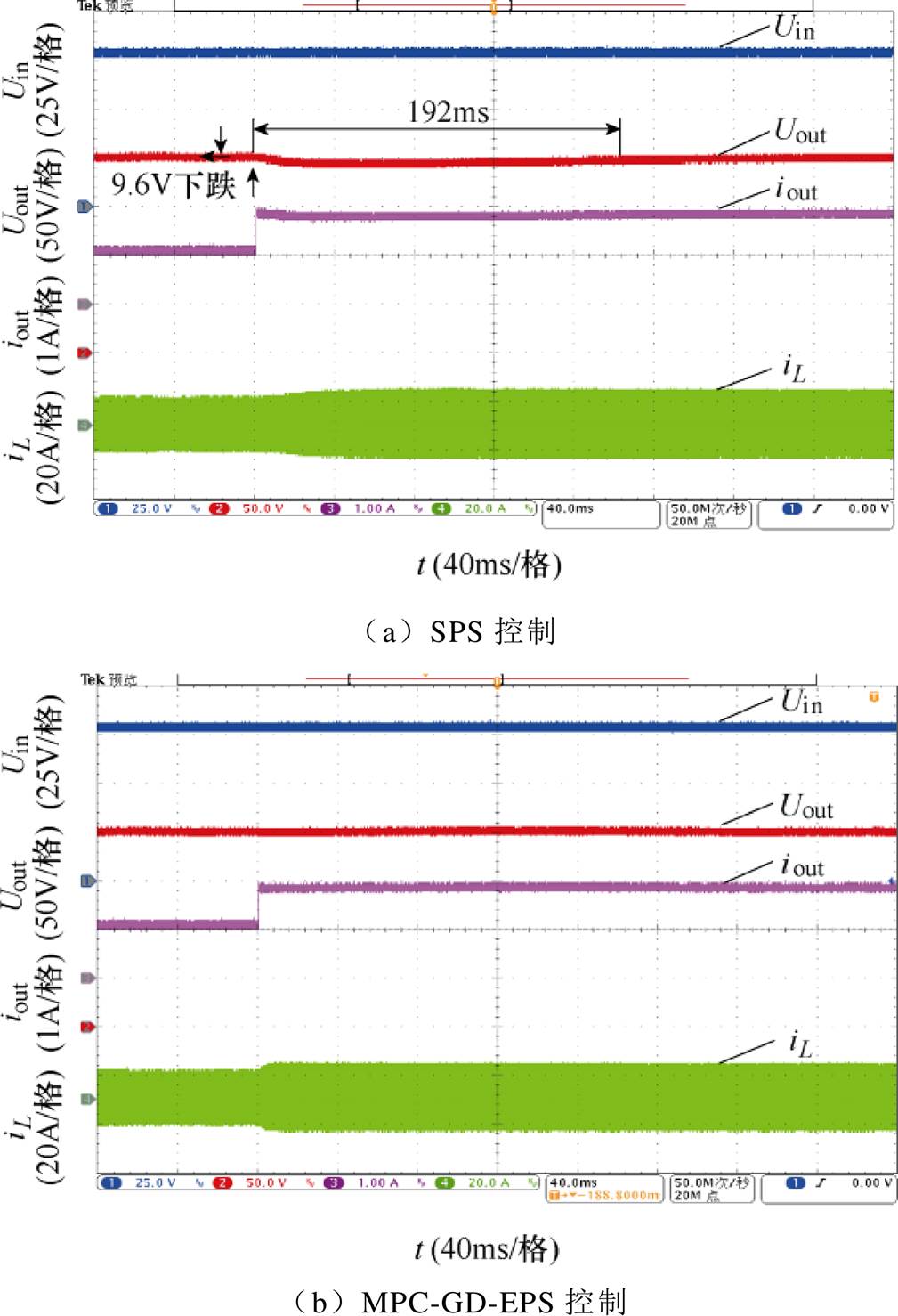
图10 负载突增时SPS与MPC-GD-EPS控制下的电压、电流实验波形
Fig.10 Voltage and current experimental waveforms under SPS and MPC-GD-EPS control when load steps up
当输入电压Uin=80V,输出电压Uout=200V,负载电阻由120W 切换至200W 时,SPS与MPC-GD- EPS控制下的电压、电流实验波形如图11所示。
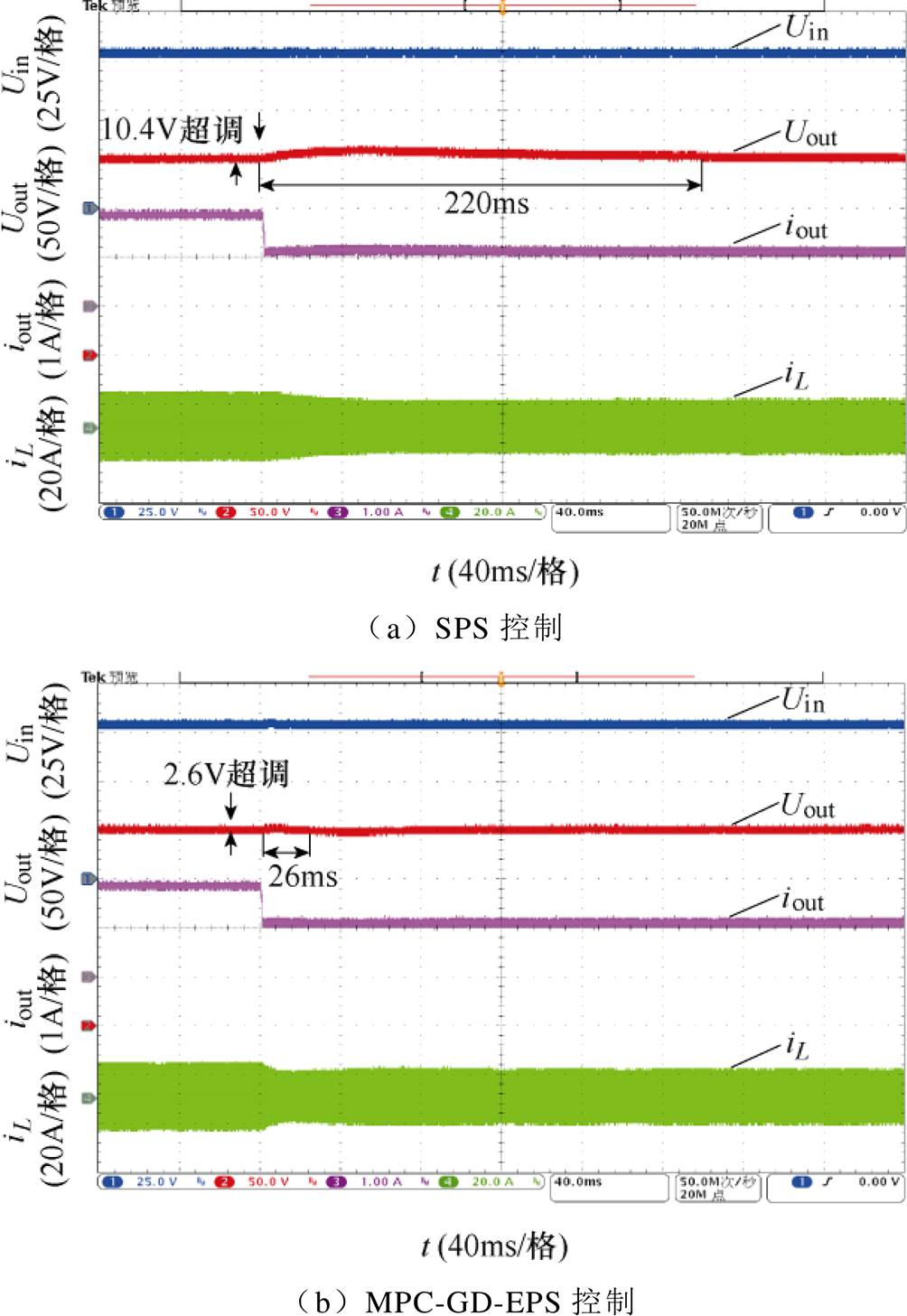
图11 负载突降时SPS与MPC-GD-EPS控制下的电压、电流实验波形
Fig.11 Voltage and current experimental waveforms under SPS and MPC-GD-EPS control when load steps down
由图11可知,采用SPS控制时,输出电压动态调节时间较长,约为220ms,电压超调,约为10.4V。而在MPC-GD-EPS控制策略下,可知系统输出电压的调节时间和超调分别为26ms和2.6V,较SPS控制分别减小了194ms和7.8V,动态特性优异。
图12为当输入电压为Uin=80V,输出电压Uout= 200V,负载电阻为RL=120W 时,SPS与MPC-GD- EPS控制下一次侧H桥交流输出电压Uab、二次侧H桥交流输入电压Ucd、电感电流iL及计算得出的DAB变换器传输功率Pt的实验波形。
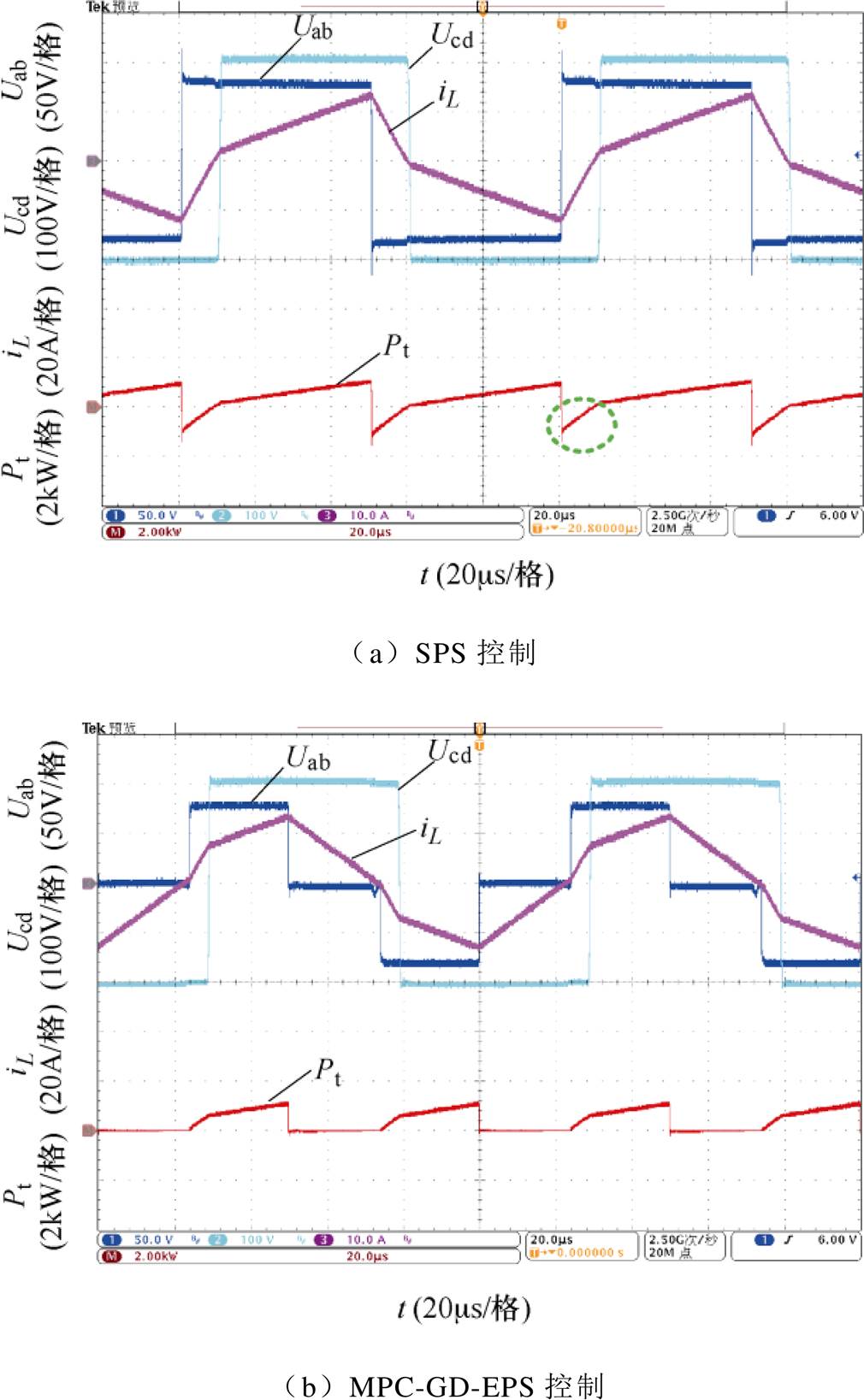
图12 SPS与MPC-GD-EPS控制下的电压、电流及传输功率实验波形
Fig.12 Experimental waveforms of voltage, current and transmission power under SPS and MPC-GD-EPS control
采用SPS控制时,如图12a所示。传输功率在每个开关周期内均包含负值,存在较大的回流功率。而采用MPC-GD-EPS控制,从图12b中可知,系统的回流功率基本被优化至零,验证了本文所提控制策略的正确性和有效性。
图13为DAB变换器在SPS与MPC-GD-EPS控制下的效率曲线。其运行工况为输入电压Uin= 80V,输出电压Uout=200V,DAB变换器传输功率从50W逐渐增加至250W,可知,MPC-GD-EPS控制下的传输效率整体高于SPS控制。当传输功率为250W时,SPS控制下的传输效率为87.48%;而在MPC-GD-EPS控制下变换器效率为90.50%。因此本文所提出的MPC-GD-EPS控制能够有效地提升了DAB变换器的效率并降低功率传输损耗。
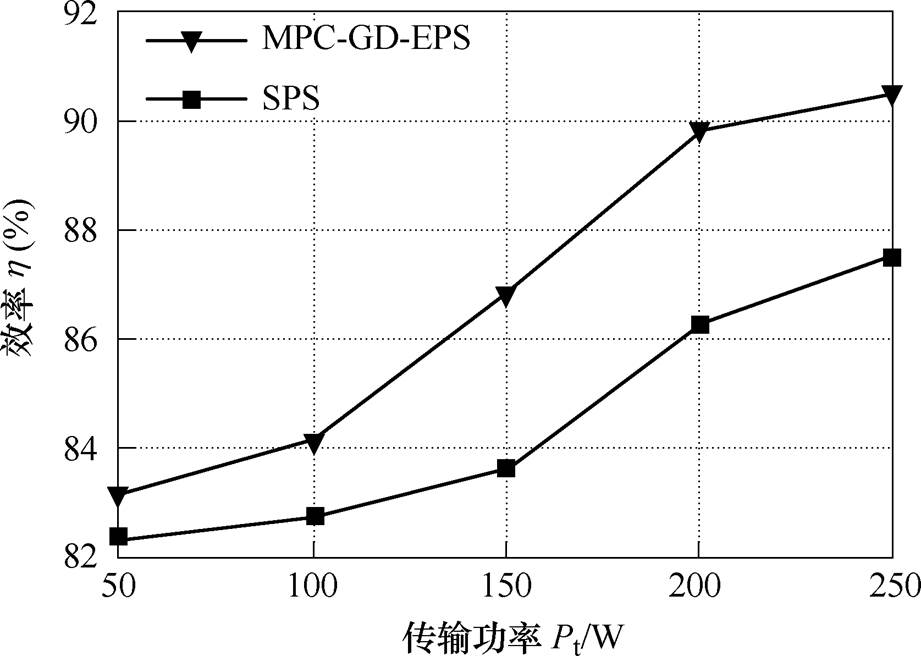
图13 SPS与MPC-GD-EPS控制下随着传输功率变化的DAB变换器效率曲线
Fig.13 Efficiency curves of DAB with transmission power variation under SPS and MPC-GD-EPS control
本文通过对EPS控制下DAB变换器传输功率和回流功率模型的推导,并考虑变换器动态性能的优化,提出了一种基于EPS的输出电压模型预测控制与梯度下降回流功率优化算法的混合控制策略,与SPS输出电压闭环控制对比,理论分析和实验结果表明:
1)EPS控制相比SPS控制,增加了DAB变换器控制自由度,增强了控制灵活性。
2)本文所提控制策略在输入电压及负载功率突变时,DAB变换器输出电压基本保持稳定,显著地提高了系统的动态响应速度。
3)所提控制策略能够很好地优化变换器的回流功率,有效地提升系统的传输效率。
参考文献
[1] 我国能源互联网关键装备获新突破—交直流混合10kV/1MW电能路由器研制成功[J]. 电气技术, 2019, 20(6): 7.
China's energy internet key equipment has achieved new breakthroughs-AC/DC hybrid 10kV/1MW power router developed successfully[J]. Electrical Engin- eering, 2019, 20(6): 7.
[2] 兰征, 涂春鸣, 肖凡, 等. 电力电子变压器对交直流混合微网功率控制的研究[J]. 电工技术学报, 2015, 30(23): 50-57.
Lan Zheng, Tu Chunming, Xiao Fan, et al. The power control of power electronic transformer in hybrid AC-DC microgrid[J]. Transactions of China Electro- technical Society, 2015, 30(23): 50-57.
[3] 刘海军, 李刚, 王志凯, 等. 面向中高压智能配电网的电力电子变压器建模方法与控制策略研究[J]. 电力系统保护与控制, 2017, 45(2): 85-93.
Liu Haijun, Li Gang, Wang Zhikai, et al. Research on medium and high-voltage smart distribution gird oriented power electronic transformer modeling and control strategies[J]. Power System Protection and Control, 2017, 45(2): 85-93.
[4] 冯高辉, 赵争鸣, 袁立强. 基于能量平衡的电能路由器综合控制技术[J]. 电工技术学报, 2017, 32(14): 34-44.
Feng Gaohui, Zhao Zhengming, Yuan Liqiang. Synthetical control technology of electric energy router based on energy balance relationship[J]. Transactions of China Electrotechnical Society, 2017, 32(14): 34-44.
[5] 辛德锋, 安昱, 郜亚秋, 等. 适用ISOS拓扑的高压DC/DC变换器研究[J]. 电力系统保护与控制, 2017, 45(13): 64-70.
Xin Defeng, An Yu, Gao Yaqiu, et al. Study on high voltage DC/DC converter based on ISOS topology[J]. Power System Protection and Control, 2017, 45(13): 64-70.
[6] Ge Junjie, Zhao Zhengming, Yuan Liqiang, et al. Energy feed-forward and direct feed-forward control for solid-state transformer[J]. IEEE Transactions on Power Electronics, 2015, 30(8): 4040-4047.
[7] 安峰, 杨柯欣, 王嵩, 等. 基于模型前馈的双有源全桥DC-DC变换器电流应力优化方法[J]. 电工技术学报, 2019, 34(14): 2946-2956.
An Feng, Yang Kexin, Wang Song, et al. Current stress optimized scheme with model-based feedfor- ward for dual-active-bridge DC-DC converters[J]. Transactions of China Electrotechnical Society, 2019, 34(14): 2946-2956.
[8] 涂春鸣, 孟阳, 肖凡, 等. 一种交直流混合微网能量路由器及其运行模态分析[J]. 电工技术学报, 2017, 32(22): 176-188.
Tu Chunming, Meng Yang, Xiao Fan, et al. An AC- DC hybrid microgrid energy router and operational modal analysis[J]. Transactions of China Electro- technical Society, 2017, 32(22): 176-188.
[9] 金莉, 刘邦银, 段善旭. 三电平双有源全桥DC-DC变换器回流功率最小的移相控制[J]. 电工技术学报, 2018, 33(24): 5864-5873.
Jin Li, Liu Bangyin, Duan Shanxu. Minimum reflux power strategy of three-level dual active bridge DC-DC converter with phase shift control[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(24): 5864-5873.
[10] Mi Chunting, Bai Hua, Wang Chongwu, et al. Oper- ation, design and control of dual H-bridge-based isolated bidirectional DC-DC converter[J]. IET Power Electronics, 2008, 1(4): 507-517.
[11] 卢林煜, 王鲁杨, 柏扬, 等. 面向能源互联网的固态变压器中双有源桥直流变换器研究[J]. 电力系统保护与控制, 2019, 47(6): 141-150.
Lu Linyu, Wang Luyang, Bai Yang, et al. Research on dual-active-bridge DC-DC converter in solid state transformer for energy internet[J]. Power System Protection and Control, 2019, 47(6): 141-150.
[12] 李婧, 袁立强, 谷庆, 等. 一种基于损耗模型的双有源桥DC-DC变换器效率优化方法[J]. 电工技术学报, 2017, 32(14): 66-76.
Li Jing, Yuan Liqiang, Gu Qing, et al. An efficiency optimization method in dual active bridge DC-DC converter based on loss model[J]. Transactions of China Electrotechnical Society, 2017, 32(14): 66- 76.
[13] Zhao Biao, Yu Qingguang, Sun Weixin. Extended- phase-shift control of isolated bidirectional DC-DC converter for power distribution in microgrid[J]. IEEE Transactions on Power Electronics, 2012, 27(11): 4667-4680.
[14] 张勋, 王广柱, 商秀娟, 等. 双向全桥DC-DC变换器回流功率优化的双重移相控制[J]. 中国电机工程学报, 2016, 36(4): 1090-1097.
Zhang Xun, Wang Guangzhu, Shang Xiujuan, et al. An optimized strategy based on backflow power of bi-directional dual-active-bridge DC-DC converters with dual-phase-shifting control[J]. Proceedings of the CSEE, 2016, 36(4): 1090-1097.
[15] 吴俊娟, 孟德越, 申彦峰, 等. 双重移相控制与传统移相控制相结合的双有源桥式DC-DC变换器优化控制策略[J]. 电工技术学报, 2016, 31(19): 97- 105.
Wu Junjuan, Meng Deyue, Shen Yanfeng, et al. Optimal control strategy of dual active bridge DC-DC converter with combined dual-phase-shift and traditional- phase-shift controls[J]. Transactions of China Elec- trotechnical Society, 2016, 31(19): 97-105.
[16] Huang Jun, Wang Yue, Li Zhuoqiang, et al. Unified triple-phase-shift control to minimize current stress and achieve full soft-switching of isolated bidirectional DC-DC converter[J]. IEEE Transactions on Industrial Electronics, 2016, 63(7): 4169-4179.
[17] Segaran D, Holmes D G, McGrath B P. Enhanced load step response for a bidirectional DC-DC con- verter[J]. IEEE Transactions on Power Electronics, 2013, 28(1): 371-379.
[18] 宋胜利, 李卓强, 姚志, 等. 三相双有源桥式直流变换器建模与控制方法[J]. 电工技术学报, 2019, 34(增刊2): 573-585.
Song Shengli, Li Zhuoqiang, Yao Zhi, et al. Modeling and closed loop control of three phase double active bridge DC transformer[J]. Transactions of China Electrotechnical Society, 2019, 34(S2): 573-585.
[19] 侯聂, 宋文胜, 武明义. 全桥隔离DC/DC变换器的直接功率控制方法[J]. 电力系统自动化, 2016, 40(17): 204-209.
Hou Nie, Song Wensheng, Wu Mingyi. Direct power control scheme of full-bridge isolated DC/DC converters[J]. Automation of Electric Power Systems, 2016, 40(17): 204-209.
[20] An Feng, Song Wensheng, Yu Bin, et al. Model predictive control with power self-balancing of the output parallel DAB DC-DC converters in power electronic traction transformer[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(4): 1806-1818.
[21] Jeung Y, Lee D. Voltage and current regulations of bidirectional isolated dual-active-bridge DC-DC converters based on a double-integral sliding mode control[J]. IEEE Transactions on Power Electronics, 2019, 34(7): 6937-6946.
[22] Hanna A I, Mandic D P. A fully adaptive normalized nonlinear gradient descent algorithm for complex- valued nonlinear adaptive filters[J]. IEEE Transa- ctions on Signal Processing, 2003, 51(10): 2540- 2549.
Multi-Objective Optimization Control Strategy of Dual-Active-Bridge DC-DC Converter in Electric Energy Router Application
Abstract For improving the transmission efficiency and dynamic characteristics of dual- active-bridge (DAB) converter, a hybrid control strategy for backflow power optimization is proposed based on extended-phase-shift output voltage model predictive control and gradient descent algorithm. Firstly, the transmission power mathematical models of DAB converter under single-phase-shift and extended-phase-shift control are established. The mechanism of backflow power is analyzed, and the output voltage state space averaging equation under extended-phase-shift control is also derived. Secondly, based on the output voltage model predictive control of DAB converter, a backflow power optimization strategy based on gradient descent algorithm is proposed. A scale-down experimental prototype of DAB converter was built and compared with the traditional single-phase-shift control. The experimental results have verified the effectiveness and correctness of the proposed control strategy.
keywords:Dual-active-bridge converter, extended-phase-shift control, backflow power optimi- zation, dynamic response, gradient descent algorithm
DOI: 10.19595/j.cnki.1000-6753.tces.191278
中图分类号:TM464
周兵凯 男,1995年生,硕士研究生,研究方向为双有源桥DC-DC变换器控制技术与应用。E-mail: 18121554@bjtu.edu.cn
杨晓峰 男,1980年生,副教授,博士生导师,研究方向为多电平变换器技术、柔性直流输电技术、电力电子技术在轨道交通中的应用。E-mail: xfyang@bjtu.edu.cn (通信作者)
收稿日期 2019-09-30
改稿日期 2020-01-10
国家重点研发计划(2016YFE0131700)和捷克共和国青年和体育英才计划(LTACH-17001)资助项目。
(编辑 陈 诚)