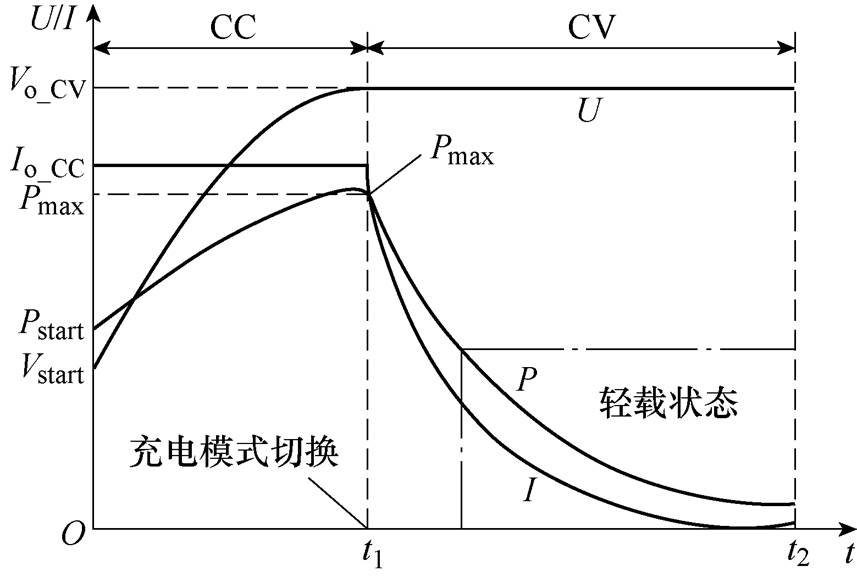
图1 阶段式充电曲线
Fig.1 Staged charging curves
摘要 提出一种基于并联变压器切换控制的LLC（ST-LLC）多谐振腔软开关直流变换器。基于变电感比值k的设计思想，采用多变压器间接并联方法以及切换控制策略构建新的变拓扑结构LLC，在保持软开关特性的同时，实现对变换器效率的有效提升以及对变压器热点的分散设计。对拓扑电压增益特性以及主要工作模态进行详细分析，为变换器工作模式设置提供了理论依据。给出变压器切换控制逻辑，并在此基础上，提出一种最优负荷分区控制策略，拓宽了LLC变换器的高效工作范围。此外，详细推导变压器切换控制点最大功率解析式，给出电路主要元件参数设计流程，并设计制作了一台约1kW的电源样机，通过仿真和实验共同验证了所提方案的可行性，样机实现了在82%的负载范围内保持90%以上的工作效率。
关键词：LLC变换器 并联变压器切换 效率优化 最优负荷分区控制
高效率与高功率密度是开关电源变换器一直以来追求的目标与发展方向。各类软开关电源拓扑的提出与改进，极大地提升了电源变换器的工作效 率[1-5]，其中，LLC谐振变换器因其优异的软开关特性被广泛应用于电动汽车充电电源和数据中心电源系统等各类DC-DC变换场合[6-8]。
在LLC谐振变换拓扑的基础上，相关学者进一步对其变换效率的提高进行了大量研究。文献[9]基于四变压器输入串联、输出并联LLC拓扑结构，对变换器主要元件进行损耗分析，并借助电磁仿真软件对平面变压器进行优化设计，提高了变换效率。文献[10]在对LLC工作模态和谐振电流分析的基础上，提出了峰值增益配置的优化设计方法，在所需增益范围内将导通损耗最小化，样机最大效率超过98%。文献[11]通过推导LLC拓扑损耗与死区时间的定量关系，提出一种基于死区时间和励磁电感最优解的LLC谐振参数设计方法，通过优选死区时间和励磁电感提高整机效率。然而，以上文献仅考虑对整机最大效率进行优化提升，忽略了变换器在不同负载范围内的效率趋势。
对于动力电池充电电源等典型的变功率输出变换器，其负载情况随充电过程的进行而明显改变。图1为典型的阶段式充电曲线，在整个充电过程中，最大功率点Pmax只出现在恒压（Constant Current, CC）与恒流（Constant Voltage, CV）模式切换时刻，其他阶段皆处于非满载工作状态，并且在恒压充电后期，将保持长时间的轻载运行。然而，LLC谐振变换器往往以额定功率点为设计需求进行谐振参数设计，虽然确保了全负载范围内的电压增益能够满足需求，但同时也忽略了轻载状态下变换器效率偏低的问题。由此可见，高轻载效率水平LLC谐振变换器具有极高的研究价值与应用前景。
图1 阶段式充电曲线
Fig.1 Staged charging curves
目前，提高LLC谐振变换器轻载效率的研究方向主要集中于对变换器控制策略以及拓扑结构的改进。在控制策略上，现阶段多采用引入Burst控制模式提高LLC轻载效率。文献[12-15]采用在轻载状态下引入Burst工作模式的优化方法，对变换器轻载效率具有明显的提升效果，但Burst控制模式可能导致电流噪声，同时该模式往往在极轻负载阶段以及空载阶段投入使用，因此效率提升范围相对较小。文献[16]在Burst控制模式的基础上提出一种分段控制方法，将LLC的Burst控制模式分为三个过程，并仔细分析每个过程的损耗分布，找到降低功率损耗的规则，确保在不同负载点达到最高效率，该方法使变换器在0～15%负载范围内的效率明显提高，但其作用范围仍然较小。在改进拓扑结构上，文献[17]提出一种变电感比值k的设计思想，采用可变励磁电感变压器，一定程度上提高了变换器效率，但变压器设计困难，且需要添加直流偏置电源控制电路，实现难度相对较大。文献[18]同样基于变电感比值k的设计思想，利用并联变压器的方式改变变压器励磁电感，但其参数设计流程中并未直接给出谐振电感以及谐振电容的计算公式，而是采用反复迭代的方法确定谐振参数，因而设计过程较为繁琐。同时，文中并未对变压器切换点的选择进行分析讨论，无法确保效率优化区域尽量达到最大。文献[19]引入模块集成变换器（Module Integrated Converter, MIC），提出一种并联直流MIC的双谐振模式变换拓扑，该拓扑结构可以根据工作条件自适应调节谐振模式，在较大范围内实现了变换器效率的提高，但增益调节范围稍显不足。
本文采用基于变压器并联的变拓扑结构式LLC谐振变换器，在传统LLC谐振变换器的基础上，采用两台高频变压器间接并联形成可控变压器组。在脉冲频率调制（Pulse Frequency Modulation, PFM）的基础上，提出变压器切换控制策略和最优负荷分区控制方法，根据负载情况的不同灵活投切变压器，从而可以对不同的负荷区域分配相应的变电感比值k，以达到拓宽高效率范围的目的。
基波分析法（First Harmonic Approximation, FHA）是将非线性LLC谐振拓扑转换为线性等效电路进行简化分析的有效手段，对图2所示的半桥LLC谐振变换器（Half-Bridge LLC, HB-LLC）进行FHA等效，得到其交流等效电路如图3所示。图中，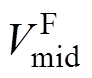
为谐振腔输入方波电压基波分量，
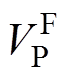为归算到变压器一次侧的输出电压基波分量，Rac为归算到一次侧的交流等效负载电阻。变频控制LLC谐振腔阻抗随工作频率变化而改变，调节开关管驱动信号频率即能改变谐振腔与输出阻抗的分压比，进而实现控制输出的作用。
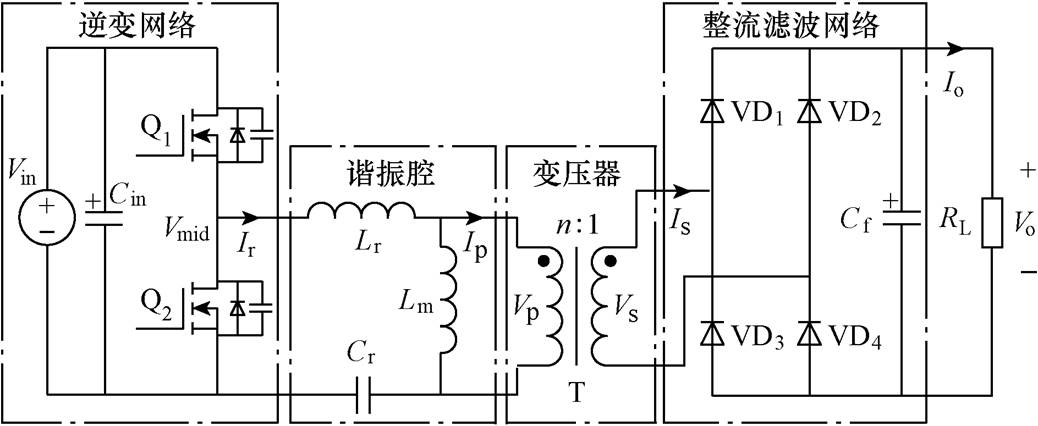
图2 半桥LLC谐振变换拓扑
Fig.2 Topology of HB-LLC resonant converter
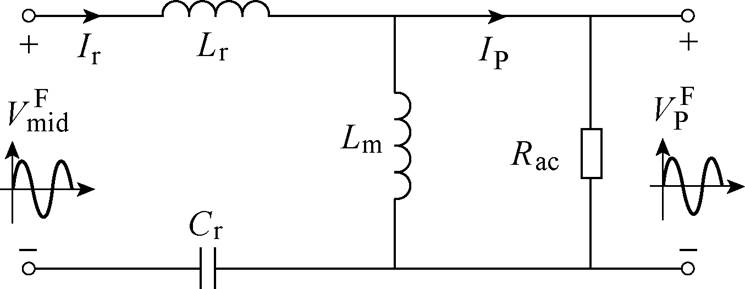
图3 LLC交流等效电路
Fig.3 AC equivalent circuit of LLC
由图3所示交流等效电路，可推导出半桥LLC谐振腔直流电压增益表达式为
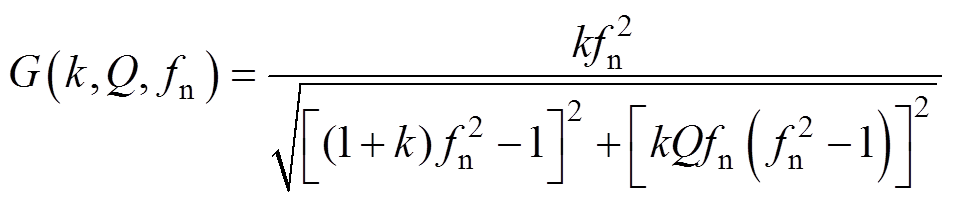（1）式中，变电感比值k=Lm/Lr；Q为品质因数；fn为归一化频率。进一步可得其与输出电压的关系表达式为
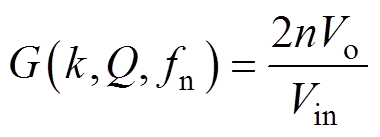（2）
从上述直流电压增益表达式可以看出，变电感比值k与品质因数Q是影响LLC谐振变换器增益特性的关键参数。绘制LLC增益特性与两者之间的关系曲线，分别如图4a和图4b所示。从图中可以看出，变换器可达最大直流电压增益与变电感比值k以及品质因数Q均近似成反比关系。
由品质因数基本公式推导出其与输出功率Po和输出电压Vo之间的关系为
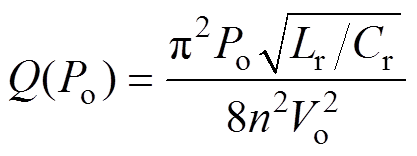（3） 随着负载加重，Q值增大，LLC可达峰值电压增益不断降低，其在重载情况下对电压增益要求更为苛刻，因此，通常以满负载情况作为LLC谐振变换器的设计参考。
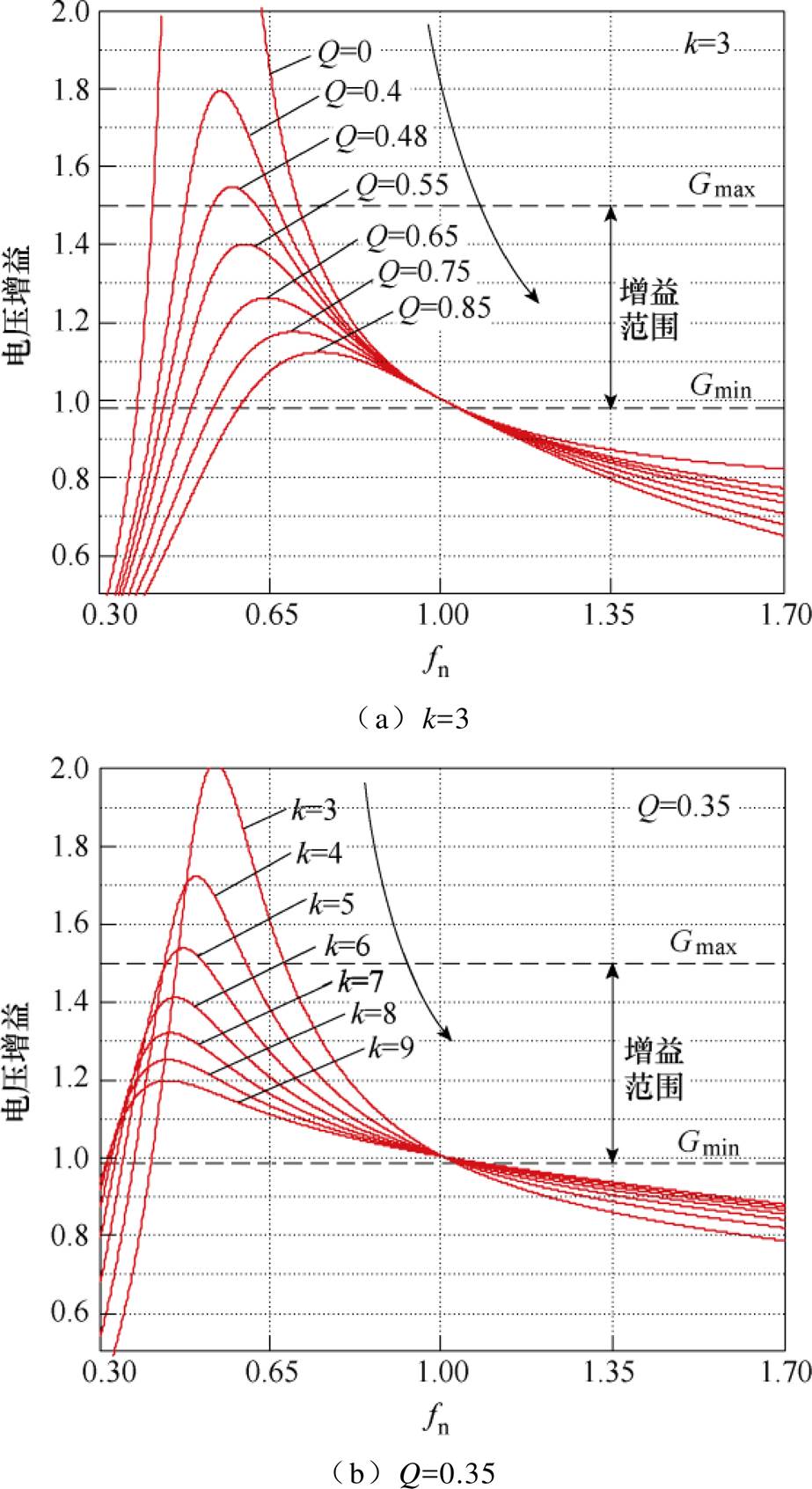
图4 电压增益与k和Q关系曲线
Fig.4 The relation curves of voltage gain with k & Q
品质因数Q随负载而变化，然而传统LLC谐振变换器k值固定。文献[20]经过详细分析得出了变电感比值k与LLC损耗之间的关系曲线，提高k值可明显降低变换器损耗，但一味地增大k值又无法满足增益需求。因此，k值的选取需要综合考虑增益需求与变换器效率。
对于恒压输出LLC谐振变换器，假设输入电压不变，则由式（2）可知其所需电压增益为固定值（Gneed）。而随着负载功率降低，Q值减小，电压增益曲线不断抬高，这相当于造成了增益浪费，如图5所示。由以上分析可知，造成该增益浪费的原因正是运行过程中Q值随负载变动而k值无法改变，固定的k值难以同时满足全负载范围内变换器对高增益与高效率的要求。因此，本文采用变电感比值k的设计思想，从改进拓扑结构的角度引入多变压器并联切换机制，使变换器在运行过程中可随负载情况改变变压器组的等效励磁电感，进而改变谐振腔变电感比值k。
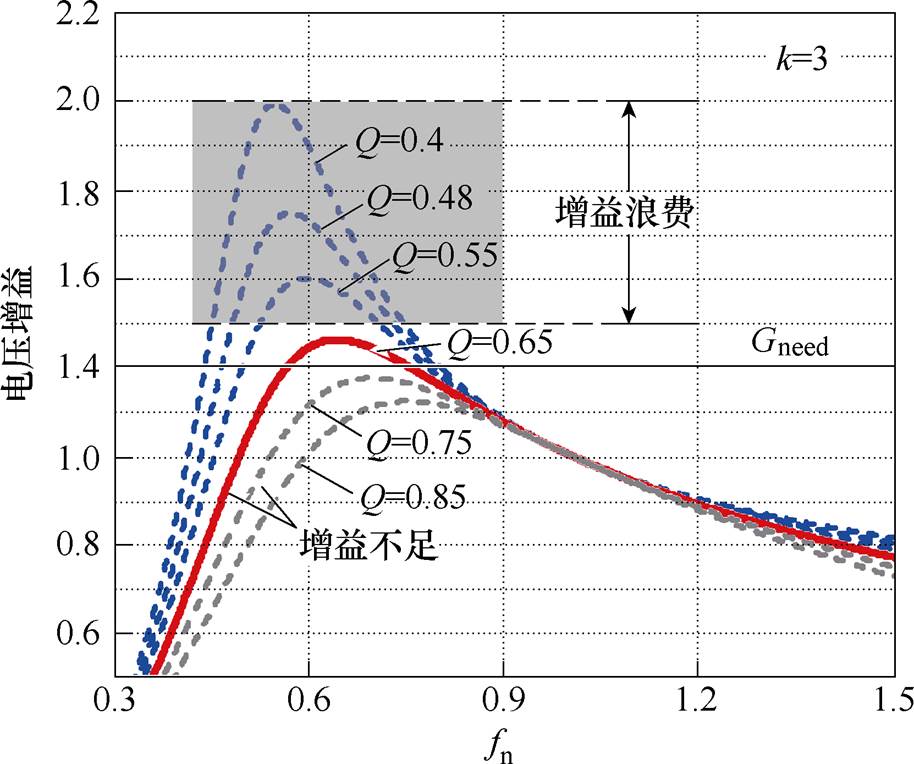
图5 电压增益浪费示意图
Fig.5 Schematic diagram of voltage gain waste
以半桥拓扑为例，图6给出了所述变压器切换控制的半桥LLC（Switching Transformer-Based Half Bridge, STHB-LLC）谐振变换器拓扑。其同样由逆变网络、谐振网络、变压器网络以及整流滤波网络构成。相对于传统的半桥LLC谐振变换器，所提拓扑结构采用两台高频变压器并联形成变压器组，通过切换开关Q3控制变压器的投入或者切除。
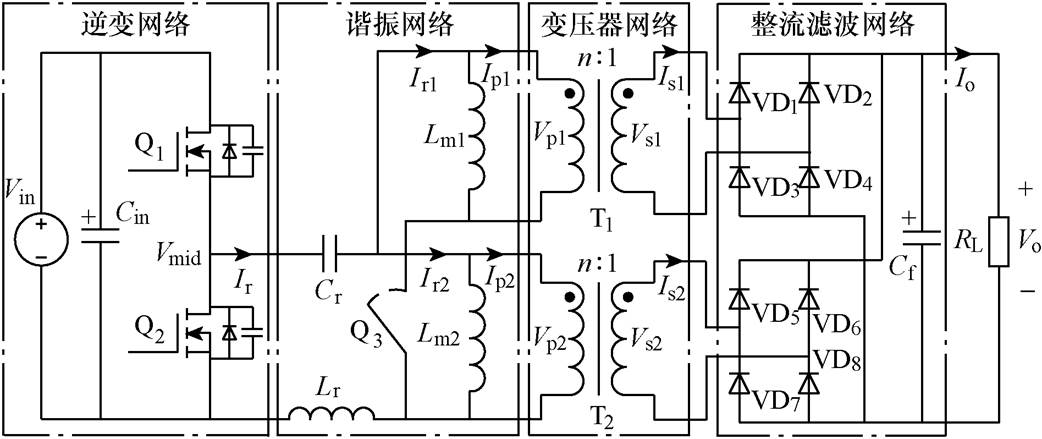
图6 STHB-LLC谐振变换拓扑
Fig.6 Topology of STHB-LLC resonant converter
为限制因两台变压器参数差异形成的环流，两台变压器采用间接并联方式，即一次绕组直接并联，二次绕组经整流环节后再做并联（Primary Parallel & Secondary Indirect Parallel, PPSIP）。间接并联方式利用二极管的单相导电性阻断二次侧环流回路，一次绕组并联节点处的电压受输入侧电源电压钳位，因而所提拓扑结构可以有效避免环流的影响。同时，重载情况下流过变压器组的电流由两台变压器均分，在不计环流影响的条件下可有效降低变压器发热程度，延长磁心寿命。
图7为STHB-LLC谐振变换器对应交流等效电路，由图可知，两变压器励磁电感呈可控并联状态，控制开关Q3的导通与关断决定变压器组的等效励磁电感。为方便叙述，忽略变压器切换过程，将变压器切换前后的等效励磁电感统一称为复合励磁电感Lm。
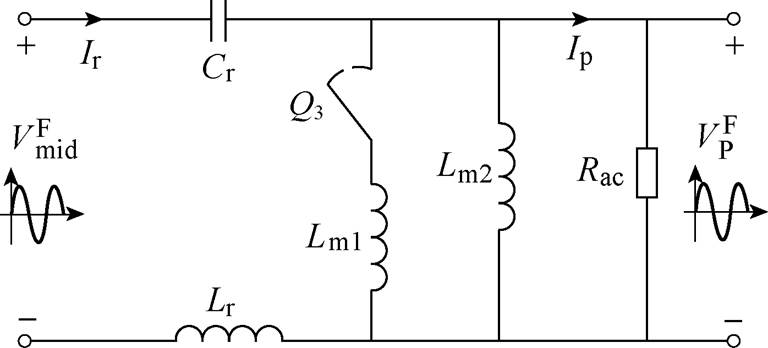
图7 STHB-LLC交流等效电路
Fig.7 AC equivalent circuit of STHB-LLC
为尽量减小高频变压器制作工艺中形成的参数差异，所提方案中使两台变压器参数保持一致，不妨令Lm1=Lm2=LT，假设实际投入运行的变压器数量为N，则复合励磁电感表达式为
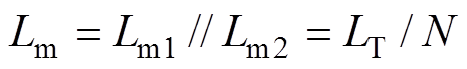（4）式中，LT为变压器励磁电感。
进一步可得复合励磁电感Lm与谐振变电感比值k的表达式为
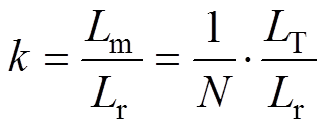（5）复合励磁电感的改变将直接影响变电感比值k的大小，最终在满足各分段区域内电压增益的基础上对LLC谐振变换器的工作效率进行优化提升。
独特的三元件（Lr，Lm，Cr）串并联结构使LLC谐振变换器具有两个谐振频率。谐振电感Lr和谐振电容Cr发生谐振时，复合励磁电感Lm两端电压被输出侧钳位而不参与谐振，变压器向二次侧传递能量，称此时的谐振频率为第一谐振频率（额定谐振频率）fr，有
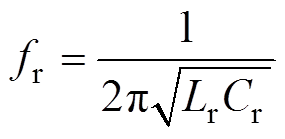（6）当谐振电感Lr、复合励磁电感Lm与谐振电容Cr共同谐振时，变压器一次侧励磁电感不再受输出侧电压钳位，变压器不会向二次侧传递能量，称此时的谐振频率为第二谐振频率fm。与传统LLC谐振变换器不同，所述STHB-LLC谐振变换拓扑在小k值工作模式下，两变压器励磁电感均可参与谐振，因此，其具有两个第二谐振频率，有
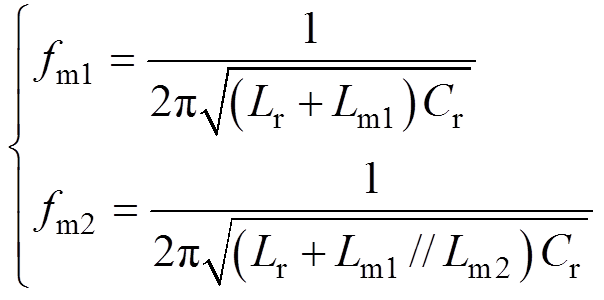（7）
变频控制LLC谐振变换器通过改变变换器工作频率fs稳定输出，fr与fm将整个LLC工作区间划分为三部分：①容性区域fs＜fm；②弱感性区域fm＜fs＜fr；③强感性区域fs＞fr。容性区域内，谐振腔电压与电流相位关系不符合MOS管的零电压开通（Zero Voltage Switching, ZVS）条件，应当避免；强感性区域内，整流二极管工作于电流连续模式（Continue Conduction Mode, CCM）而无法实现零电流关断（Zero Current Switching, ZCS）；弱感性区域内，谐振腔电流滞后电压，且整流二极管工作于电流断续模式（Discontinuous Conduction Mode, DCM），因此可同时实现一次侧MOS管的ZVS与二次侧整流二极管的ZCS，称之为理想工作区。
额定谐振频率fr是强感性区与弱感性区的分界频率，因此其对LLC工作频率范围的设置至关重要。由式（6）可知，相对于改变谐振电感Lr的大小来改变变电感比值k的方式，所述STHB-LLC谐振变换拓扑在变压器切换过程中并不会改变额定谐振频率fr，因此，极大地降低了工作区间的设置难度。虽然变压器切换前后变换器频率区域划分宽度有所不同，但各区域内工作模态及主要工作波形仍然相同，故而仍可对各区域模态进行统一分析。单变压器运行模式下，所述STHB-LLC谐振变换器工作模态与传统HB-LLC一致，因此不做讨论，下面重点对理想工作区域内双变压器运行状态下的工作模态进行详细分析。
图8为STHB-LLC弱感性区域内变换器主要工作波形，此时，整流管工作于DCM，复合励磁电感电流Im等于两变压器励磁电感电流之和。从图中可以看出，一个工作周期内，DCM可分为12个工作阶段，由于正负半周的工作模态完全对称，这里仅对半个周期的6个阶段进行分析，各阶段分别对应图9所示电路等效模型，具体过程如下。
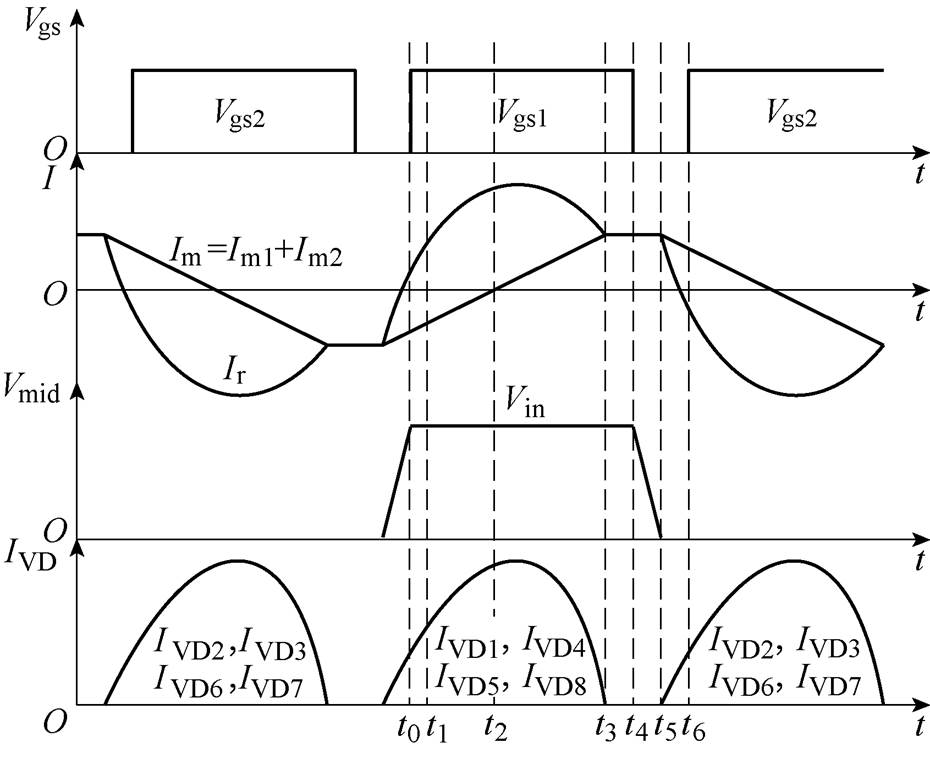
图8 STHB-LLC弱感性区工作波形
Fig.8 Working waveform of STHB-LLC in weakly inductive area
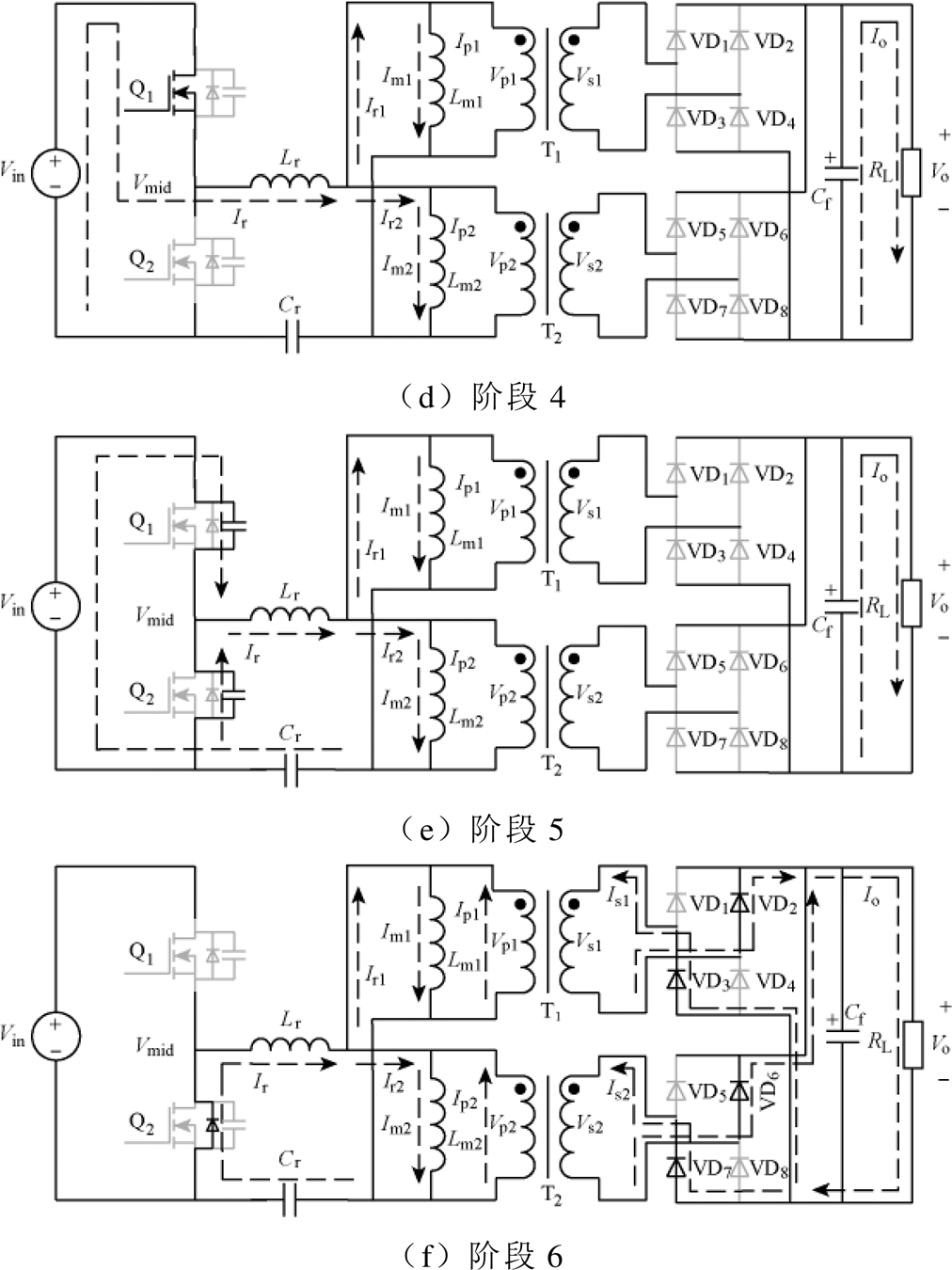
图9 STHB-LLC弱感性区等效模型
Fig.9 The equivalent mode in weakly inductive area
阶段1[t0, t1]：在t0时刻前电路进入死区阶段，反向的谐振电流Ir经过MOS管Q1体内寄生二极管进行续流，将Q1端电压钳位在零。t0时刻，Q1管开始导通，反向谐振电流Ir转移至Q1进行续流，由此实现Q1管的ZVS。由工作波形可知，该阶段内谐振电流ir在数值上小于复合励磁电流Im，则此时正向电流Ip流入变压器一次侧，向二次侧传输能量，二极管VD1、VD4、VD5、VD8导通，两变压器励磁电感被输出电压钳位在nVo。
阶段2[t1, t2]：t1时刻，谐振电流Ir减小至零，之后逐渐正向增大，流过MOS管Q1，该阶段内整流二极管VD1、VD4、VD5、VD8保持导通，变压器励磁电感两端电压继续被输出侧钳位，一次侧电源不断向二次侧传输能量。
阶段3[t2, t3]：t2时刻，复合励磁电流Im减小至零并开始正向增大，谐振电流Ir持续正向流通，变压器励磁电感与二次侧电路继续维持上一阶段的工作状态。
阶段4[t3, t4]：t3时刻，复合励磁电感电流Im与谐振电流Ir大小相等，两变压器励磁电感摆脱输出侧钳位并参与谐振，因此变压器不向二次侧传输能量，流过二次侧整流二极管的电流也逐渐减小至零，实现了二极管的ZCS。该阶段内，输入侧与输出侧断开，所有整流管都处于关断状态，负载能量全部由输出侧滤波电容提供。
阶段5[t4, t5]：t4时刻，MOS管Q1关断，重新进入死区状态，该阶段内仍然没有能量传输至二次侧，复合励磁电流Im对Q1管寄生电容进行充电，对Q2管寄生电容进行放电。
阶段6[t5, t6]：t5时刻，寄生电容充放电过程结束，复合励磁电感电流Im与谐振电流Ir出现数值差且两电流逐渐减小，Ir流经Q2内部的体二极管进行续流。该阶段内，整流二极管VD2、VD3、VD6、VD7开始导通，两变压器向二次侧传输能量，励磁电感再次被输出侧电压重新钳位而退出谐振。
对于所述STHB-LLC谐振变换器，通过比较实测输出功率Po与变压器切换点设定功率Pswitch的大小即可判断当前所属负荷区间，其逻辑关系如图10所示。恒压模式下，若位于重载区域则保持两台变压器并联运行，即变压器切换控制信号为0；若位于轻载区域则保持单台变压器运行，即变压器切换控制信号为1，由此产生的驱动信号经驱动电路后控制变压器切换开关做出相应动作。
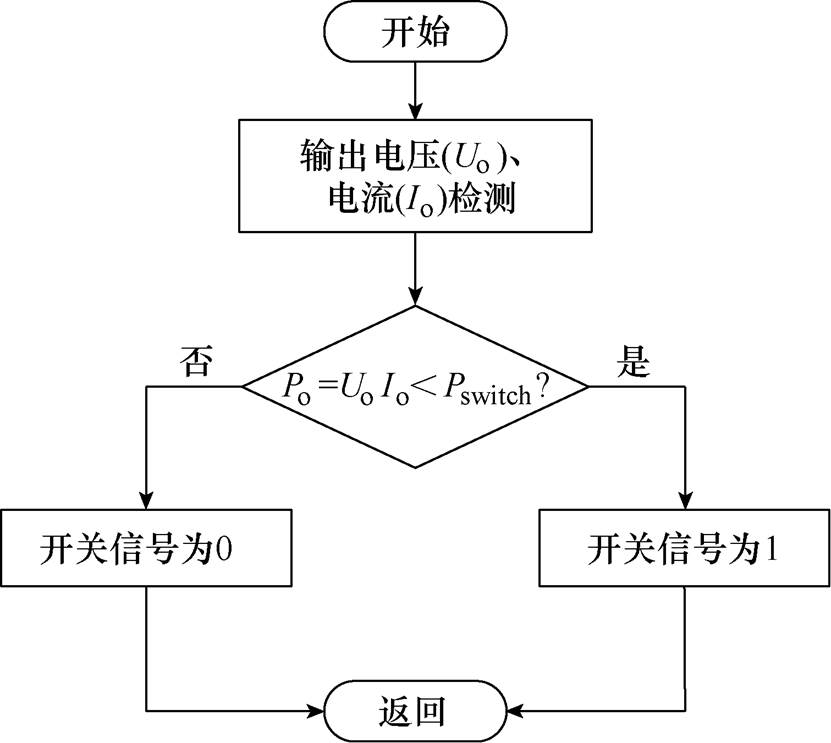
图10 变压器切换控制逻辑
Fig.10 Logic of transformer switching control
为了实现上述控制效果，需要采用负荷分区控制策略与之匹配，其核心控制思想为：
（1）重载区域内，两台高频变压器并联工作，即保持较小的k值运行以满足重载区域内变换器对电压增益的严格要求。
（2）轻载区域内，单台变压器运行，在满足电压增益需求的同时保持较大k值运行以提高轻载阶段效率。
对于轻载和重载的概念，传统定义方式往往根据变换器额定功率的大小直接取某一百分值，这样的分区方式不够明确且无法使效率优化范围尽可能扩大。问题的关键在于负荷分区点功率Pswitch的确定，若Pswitch选择过大，则可能导致变换器无法满足重载区域对增益的严格要求；反之，若Pswitch选择过小，则会导致效率优化范围降低。为此，本文提出一种最优负荷分区控制策略，通过解析法给出了变压器可切换点最大功率Pswitch_max的求解过程，在理论上使STHB-LLC谐振变换器的效率优化范围达到最大。下面对所提STHB-LLC最优负荷分区控制策略进行详细分析。
假设轻载区域内分配的变电感比值为kmax，重载区域内分配的变电感比值为kmin，由于涉及功率计算，因此从品质因数Q入手，采用逆推的方式求解变压器切换点最大功率Pswitch_max，具体计算步骤如下：
（1）根据设计需求合理选定重负荷区变电感比值kmin，并以最恶劣工况点（额定工作点）确定变换器相关参数：变压器电压比n、所需最大电压增益Gmax、谐振电感Lr以及谐振电容Cr。
（2）将轻负荷区域变电感比值kmax代入最大品质因数与k值关系表达式（8），得出其对应的最大品质因数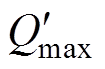
为
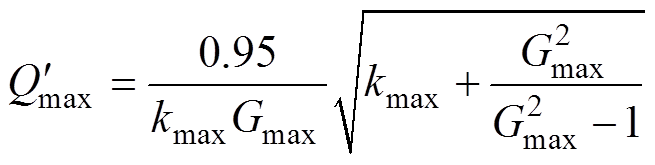（8）（3）将上述计算所得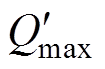代入品质因数与输出功率关系表达式（3），此时所求得的功率即为变压器切换点最大功率Pswitch_max为
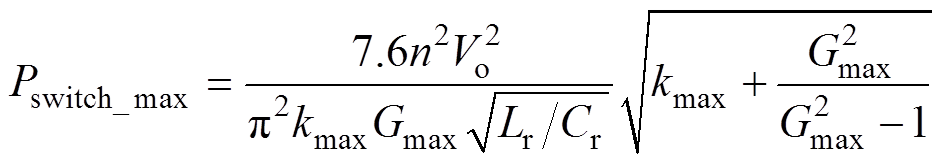（9）
考虑基波分析法自身误差，取适当的下降裕度确定变压器切换点功率Pswitch，以确保重载情况能够获得足够的电压增益。
（4）绘制Q3切除前后变换器增益曲线，观察是否满足电压增益需求且未造成太大的增益浪费，如不满足，则返回步骤（3）重新选择变压器切换点功率Pswitch。
根据以上最优负荷分区控制策略，即可确定所述STHB-LLC谐振变换器的变压器切换点功率，该分区方法给出了负荷分区点最大功率解析值的求解过程，使效率提升区域最大化，从而可使高效率范围显著拓宽。
谐振电感Lr、谐振电容Cr和变压器励磁电感Lm是LLC谐振变换器的灵魂元件，三谐振元件参数大小直接决定变换器性能。由第1节分析可知，所述STHB-LLC谐振变换器等效拓扑与传统LLC类型一致，因此，仍可基于FHA分析方法进行参数计算。根据设计需求，在选择额定谐振频率fr1和小变电感比值kmin之后，需要首先确定变压器比率n。从式（2）可以看出，当输入电压固定时，额定谐振频率（G=1）下LLC输出电压直接由变压器匝比n确定。因此，n的计算公式对于设定工作区域至关重要。图11给出了主要参数计算流程，具体计算步骤如下：
（1）明确设计需求。确定电源相关参数设计指标，选择额定谐振频率fr以及变电感比值kmin、kmax，见表1。
（2）变压器匝比n。变压器匝比对LLC谐振变换器工作区域的设置至关重要，为确保变换器在整个工作过程中均位于理想工作区域内，应将最小输出电压对应的工作频率设置于额定谐振频率处，则
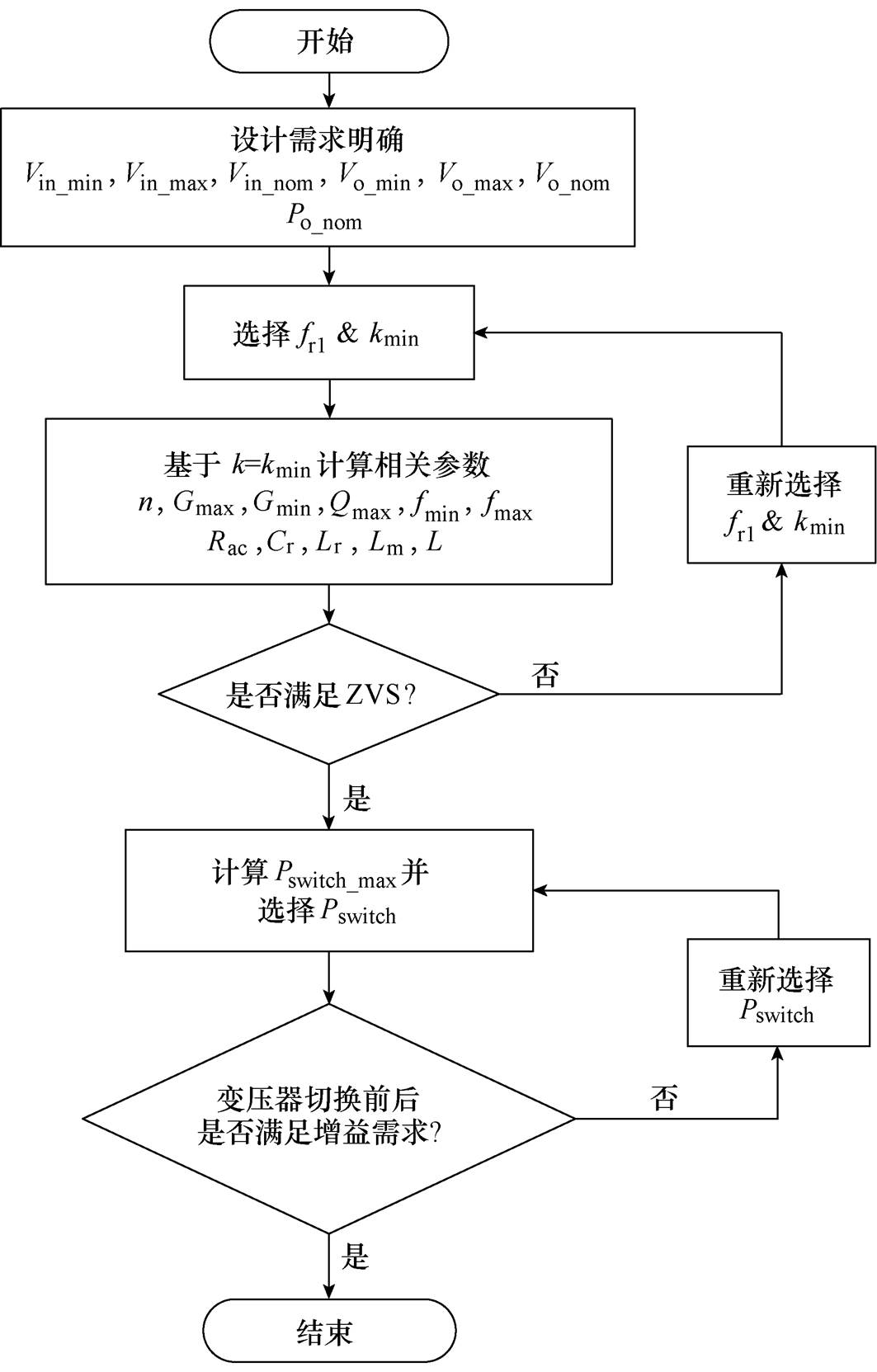
图11 STHB-LLC参数设计流程
Fig.11 Parameters design procedure of STHB-LLC
表1 电源参数设计指标
Tab.1 Main design index of the power supply
参 数符号及单位 输入电压范围Vin_min～Vin_max/V 额定输入电压Vin_nom/V 输出电压范围Vo_min～Vo_max/V 额定输出电压Vo_nom/V 额定输出电流Io_nom/A 额定输出功率Po_nom/W 额定谐振频率fr/kHz 变电感比值kmin/kmax
变压器电压比计算公式为
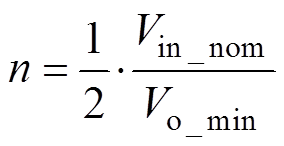（10）（3）最大与最小电压增益。最大与最小电压增益分别对应两种极限工作状态，最大电压增益Gmax对应输入电压最小且输出电压最大，最小电压增益Gmin对应输入电压最大而输出电压最小。同时，对于所需最大电压增益还要考虑一定的裕度，以确保具有一定的过载能力，则Gmax与Gmin的计算公式分别为
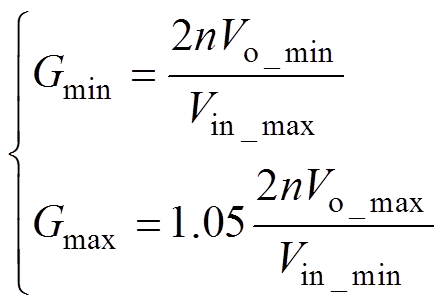（11）
（4）交流等效负载Rac为
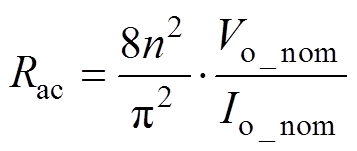（12）（5）满载、小k值对应最大品质因数Qmax为
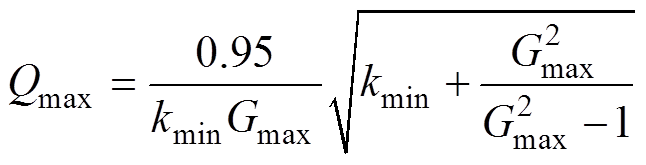（13）
（6）最大与最小工作频率分别为
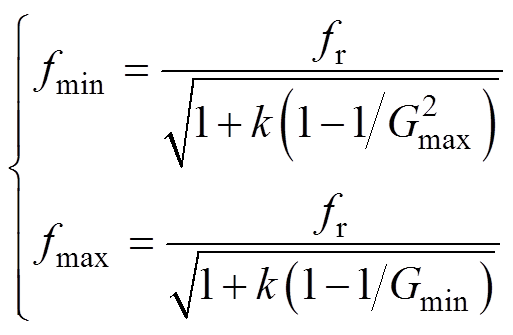（14）fmin与fmax是电源控制器中频率限幅器设置的重要参考依据，无论是在软件仿真还是在实验验证时，频率限幅器上下限的设定值都将影响验证结果。若限幅器设定值不够合理，严重时将会导致变换器无法按照要求稳定输出。由于所设计的STHB-LLC谐振变换器在变压器切换前后具有两种变电感比值k，因此，要分别计算两种k值情况下所对应的最大、最小工作频率，在频率限幅器参数设定时，需综合考虑两种k值情况下的频率范围。
（7）计算谐振元件参数Lr、Cr、Lm及变压器励磁电感LT。
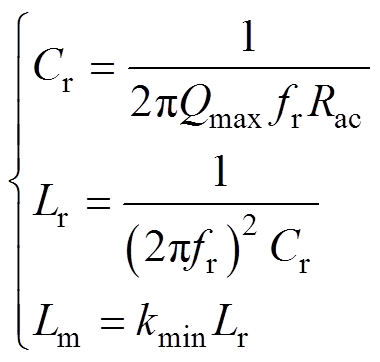（15）此时所得励磁电感Lm是以小k值进行计算，即为两台变压器并联励磁电感，因此单台变压器励磁电感值为
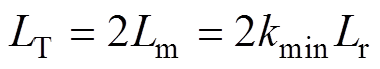（16）
（8）ZVS条件验证。通过步骤（2）中变压器电压比的计算已能将整个工作区域限制在理想工作区内，而步骤（5）中也已经对品质因数上限进行的限制，因此只要确保死区时间内谐振腔电流能够完成对总寄生电容的充放电即可实现MOS管的ZVS。分别计算死区时间Td内谐振腔电感电流最小峰值Imp_min和寄生电容所需充放电电流IZVS，有
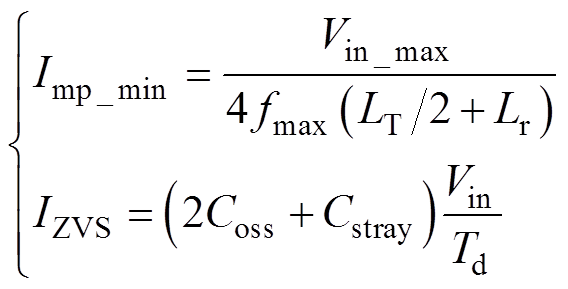（17）式中，Coss为开关管两端寄生电容；Cstray为桥臂中点对地电容。若Imp_min＜IZVS，则不满足软开关条件，需返回步骤（1）重新选择额定谐振频率fr以及变电感比值k。
（9）计算变压器可切换最大功率点Pswitch_max并选择切换点功率Pswitch。
根据前述STHB-LLC最优负荷分区控制策略，计算变压器可切换最大功率点Pswitch_max，同时，为了确保变压器切换前后均能满足电压增益的需求，对所求Pswitch_max取一定的下降裕度后选定切换点功率Pswitch。
为了验证所提拓扑结构性能与最优负荷分区控制策略的正确性，搭建了一台额定功率约1kW且具有恒压与恒流两种输出模式的电源样机。按图11所示参数设计流程计算得到样机主要参数指标见 表2，图12为电源样机实物。
表2 样机主要参数指标
Tab.2 Main parameters of the prototype
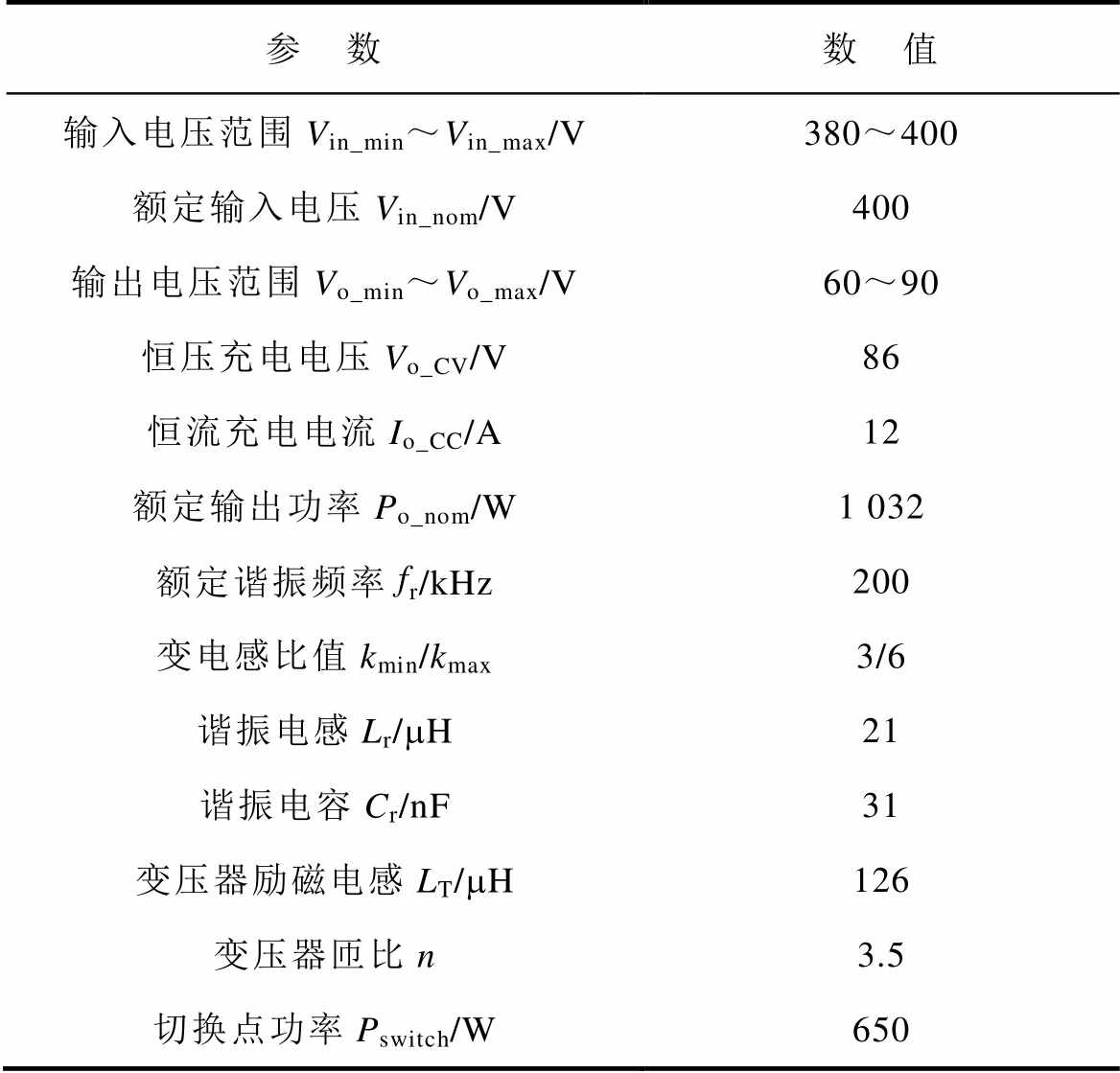
参 数数 值 输入电压范围Vin_min～Vin_max/V380～400 额定输入电压Vin_nom/V400 输出电压范围Vo_min～Vo_max/V60～90 恒压充电电压Vo_CV/V86 恒流充电电流Io_CC/A12 额定输出功率Po_nom/W1 032 额定谐振频率fr/kHz200 变电感比值kmin/kmax3/6 谐振电感Lr/mH21 谐振电容Cr/nF31 变压器励磁电感LT/mH126 变压器匝比n3.5 切换点功率Pswitch/W650
图12 充电电源实验样机
Fig.12 Prototype of the charging power supply
根据负荷分区最大功率点计算方法得出变压器可切换点最大功率Pswitch_max=727W，绘制变压器切换前后直流电压增益曲线如图13所示。图13表明，切换前后直流电压增益均能满足变换器增益需求，且未造成太大的增益浪费。实验过程中取5%～10%的下降裕度，设置变压器切换点功率为Pswitch=650W。
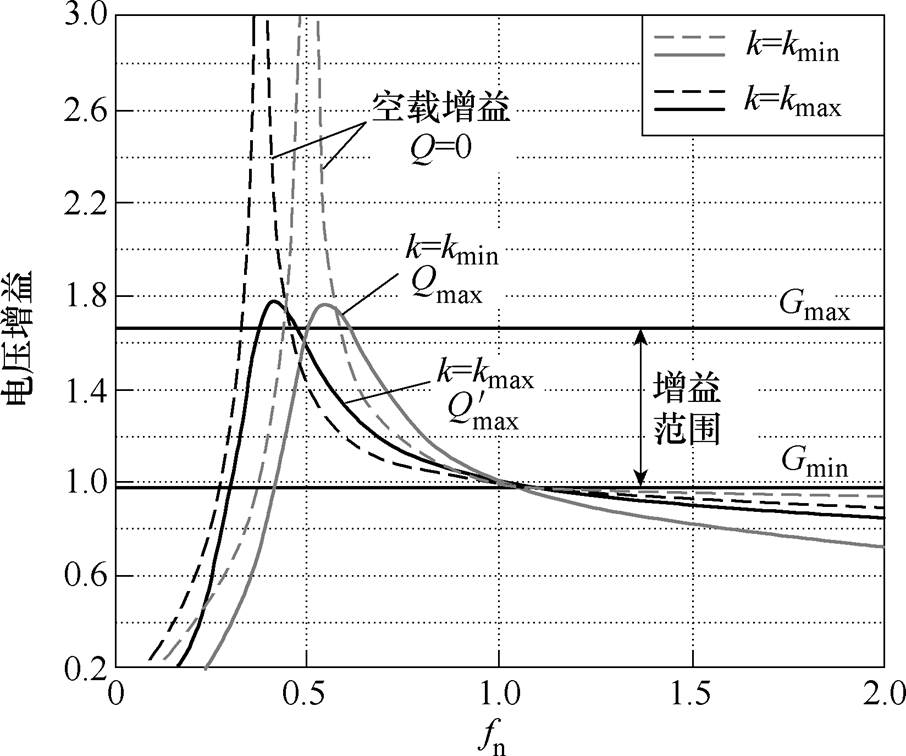
图13 变压器切换前后电压增益曲线对比
Fig.13 Comparison of voltage gain curves before and after transformer switching
图14为86V恒压模式下，变换器从空载到满载范围内主要负荷等级下的ZVS波形以及谐振电流Ir波形。其中，图14a～图14c为输出功率小于变压器切换功率Pswitch时的工作波形，即变换器工作于大k值模式；图14d～图14f为输出功率大于Pswitch时的工作波形，因此为小k值工作模式。
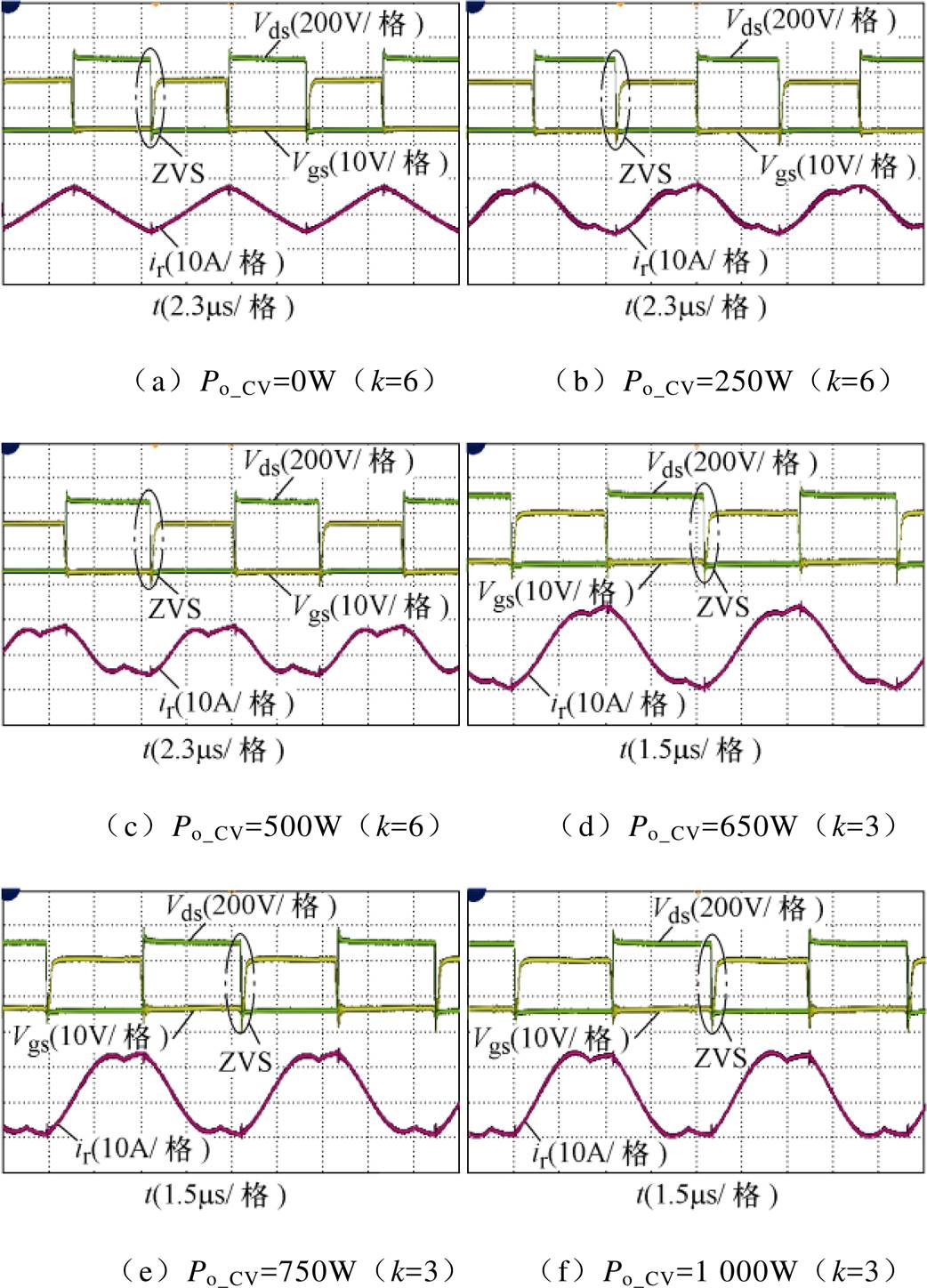
图14 恒压模式ZVS和Ir波形
Fig.14 Waveforms of ZVS and Ir in CV mode
图15为12A恒流模式下，主要输出电压等级对应的ZVS与谐振电流Ir波形，由于其为恒流阶段工作波形，因此属于小k值工作模式。
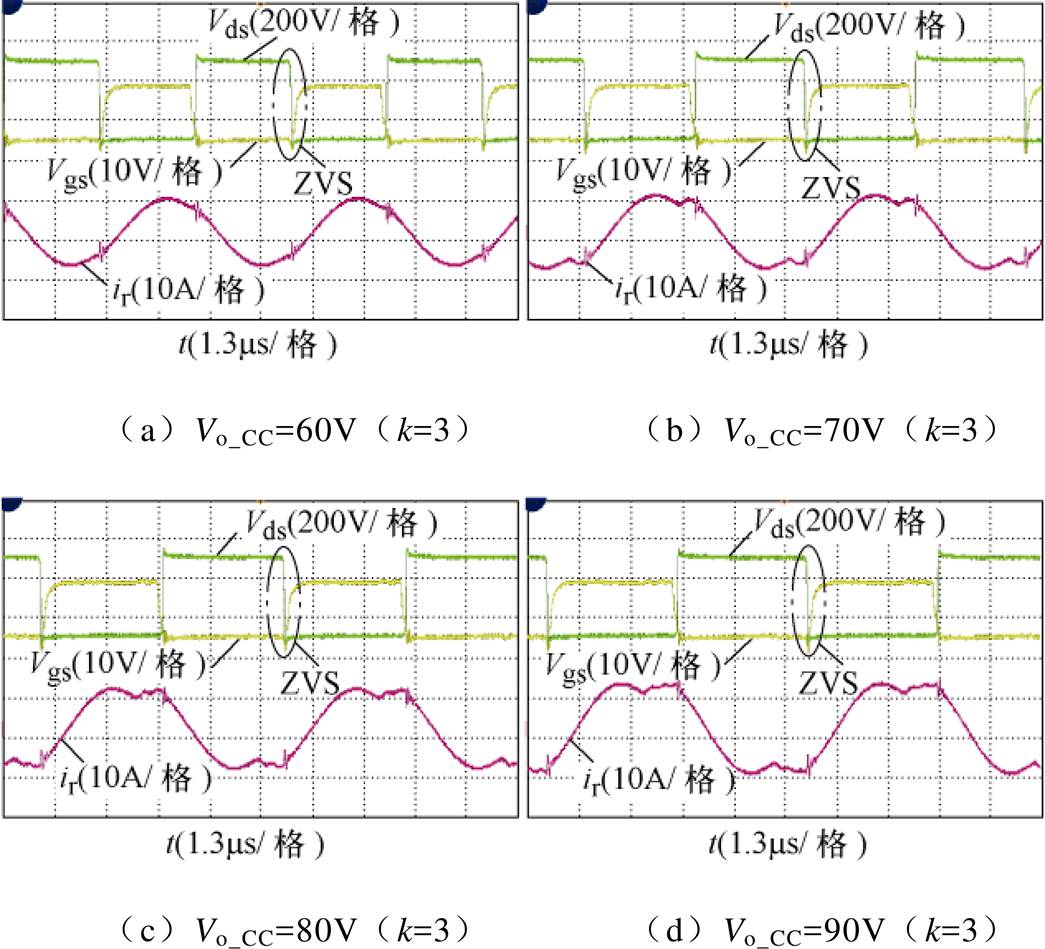
图15 恒流模式ZVS和Ir波形
Fig.15 Waveforms of ZVS and Ir in CC mode
进一步，对所设计电源样机整流二极管的ZCS实现情况进行实验测试。由于LLC谐振变换器整流管的ZCS波形主要受输出电压影响较大，因此，图16给出了样机工作于恒流状态时各主要电压等级对应的整流二极管ZCS波形。
从图14和图15中可以看出，在MOS管开通阶段，当漏源两端电压Vds降至零电平时驱动电压Vgs才开始建立；从图16可以看出，电源样机无论工作于何种工作模式，都能够实现MOS管的ZVS 以及整流管的ZCS，并且从谐振电流波形可以看出，变换器一直工作于理想工作区。此外，从图15a和图16a中可以看出，当变换器以60V电压输出时，谐振电流Ir接近于完美正弦波，且整流二极管端电压波形的上升沿与下降沿平台最小。这说明输出电压为60V时，变换器工作频率fs接近额定谐振频率fr，而在其他电压等级下，工作频率fs小于额定谐振频率fr，这也说明了变换器在整个负载范围内均位于理想工作区域内。
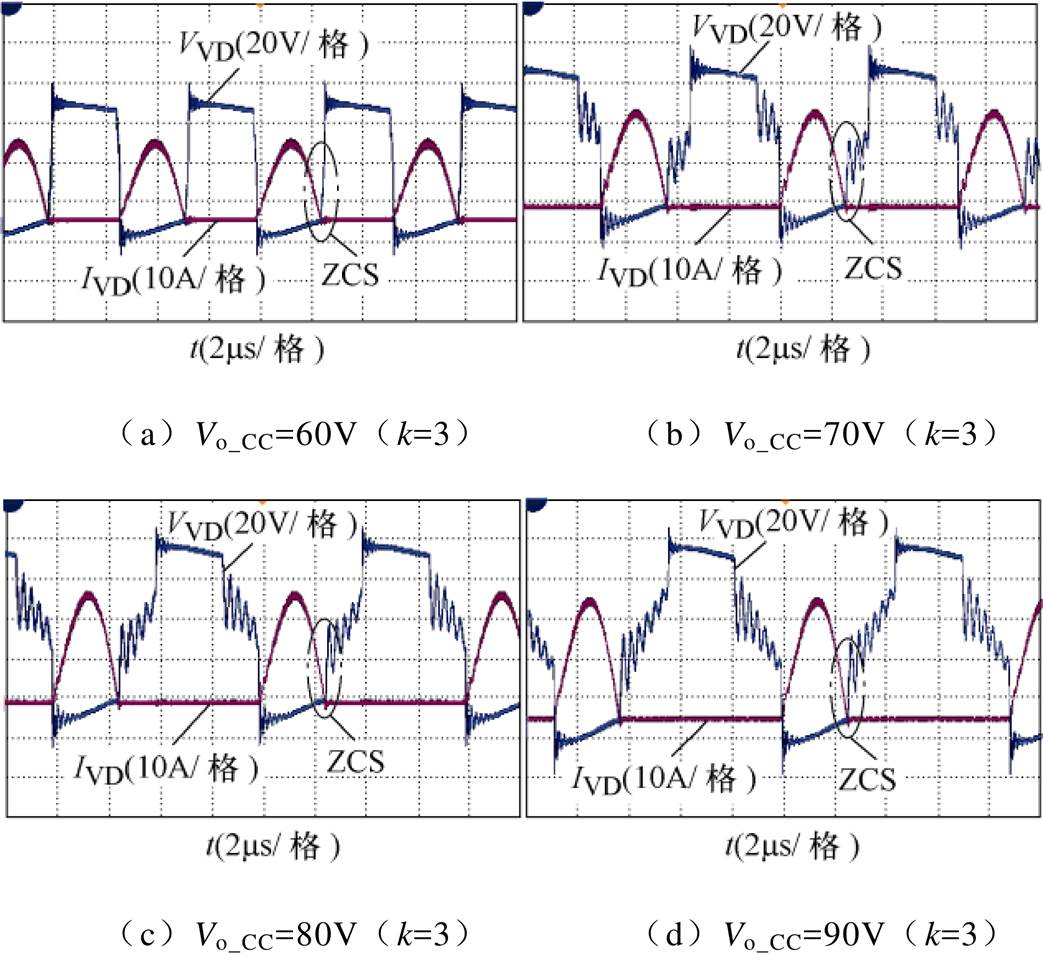
图16 不同电压等级下的ZCS波形
Fig.16 ZCS waveforms at the main voltage level
由于Q3切除时会断开该条支路上的励磁电流，因此会产生一定的电压尖峰。图17为变压器控制开关Q3连续开断时触头两端的电压波形，从图中可以看出，该电压尖峰相对较小，且能够快速恢复稳定。
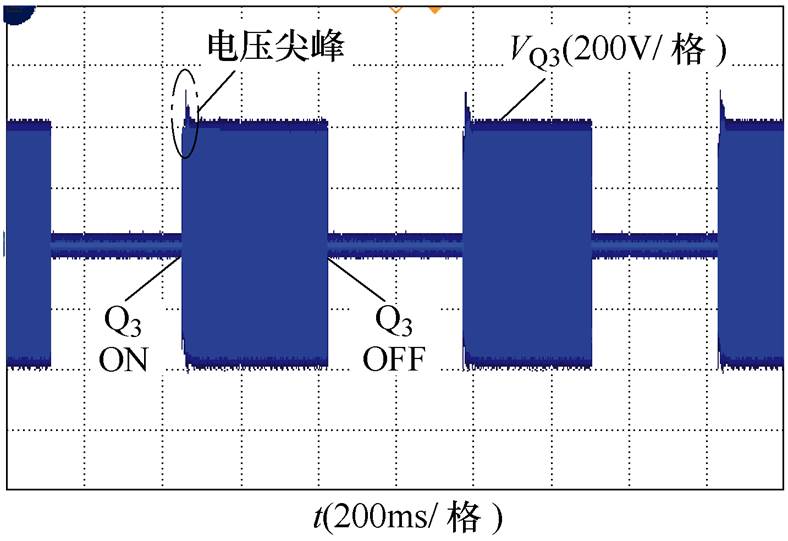
图17 Q3端电压波形
Fig.17 Voltage waveform of Q3
图18a和图18b分别为变压器连续投切时的输出电压波形以及负载连续切换时的输出电压、电流波形。可以看出，实验样机在各种切换情况下均能快速恢复稳定，说明了所提STHB-LLC谐振变换拓扑的可行性。
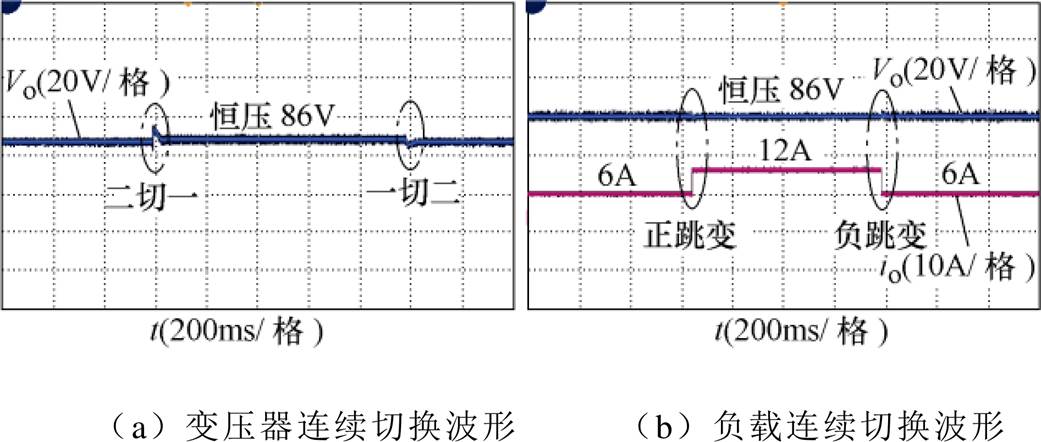
图18 切换实验波形
Fig.18 Switching test waveforms
图19为变压器一切二暂态过程中谐振电流以及ZVS波形，其中，图19a和图19b分别为变压器投入及局部放大波形。从图中可看出，存在ZVS部分丢失现象，但由于时间较短，从实验结果上来看并不会引起开关管温度的明显升高以及产生振荡现象。
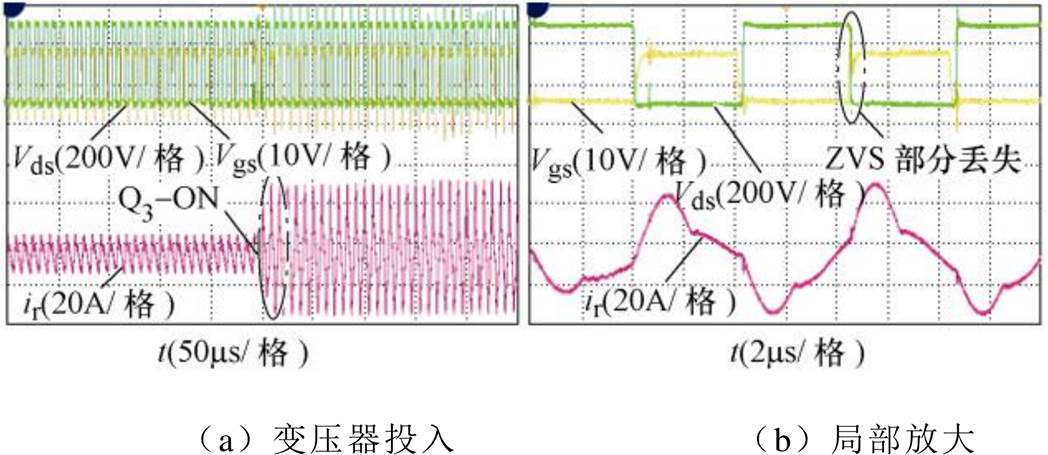
图19 变压器一切二的暂态响应
Fig.19 Transient response to switch-on two transformers
图20为传统HB-LLC与所述STHB-LLC实验样机满载情况下的变压器热成像对比，从图中可明显看出，所提STHB-LLC拓扑可以有效降低功率变压器的工作温度，延长磁心寿命。同时，分散热点的工作特性也能降低变换器对整体散热要求，对于所设计电源样机，在全负载范围内仅需自然冷却即可，无需添加散热风扇。
图20 变压器热成像对比
Fig.20 Transformer thermal imaging comparison
图21为所设计STHB-LLC电源样机与传统HB- LLC实验样机在恒压模式下的实测效率曲线对比。图中虚线为传统HB-LLC实验样机在全负载范围内的效率曲线，而实线为所述STHB-LLC谐振变换器效率曲线。可以看出，所提方案最大效率可达95%，且在180W处效率就超过了90%，而传统方案在500W处效率才能达到89.91%。因此，采用所提方案实现了在较宽负载范围内对LLC谐振变换器的效率提升。
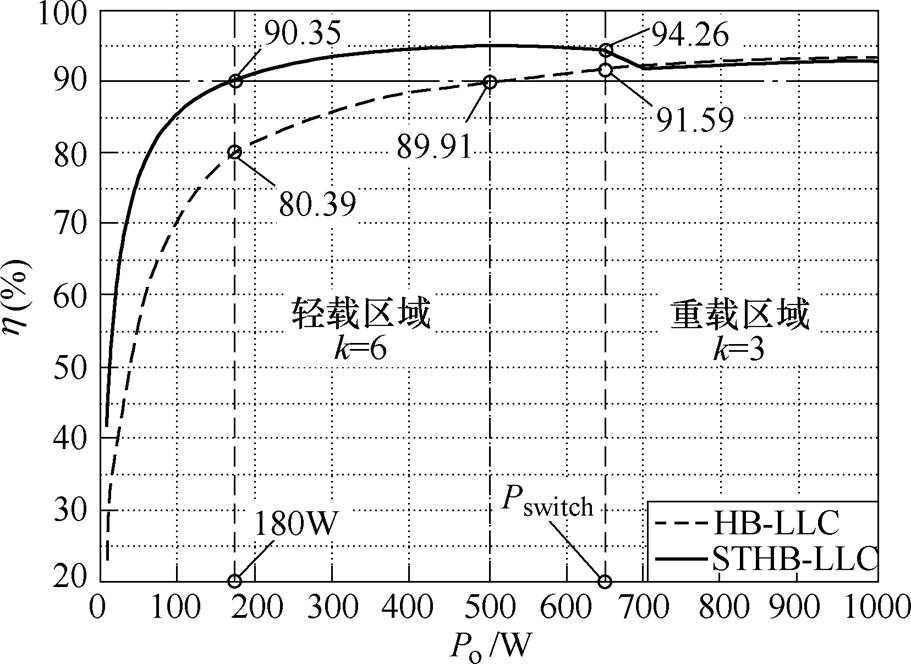
图21 样机效率曲线对比
Fig.21 Prototype efficiency curves comparison
本文针对LLC谐振变换器轻载效率提升问题，基于变电感比值k的设计思想，对LLC谐振变换拓扑进行优化改进，结合变压器切换控制策略，对负荷区域进行分区控制。主要内容与贡献如下：
1）提出变压器切换控制LLC（ST-LLC）谐振变换拓扑，对负载区间进行分区控制，重点提高了变换器轻载效率。
2）根据所述拓扑提出最优负荷分区控制策略，详细分析了负荷分区最大功率点Pswitch_max的计算方法，有效拓宽了效率优化范围。
3）给出了所述STHB-LLC谐振变换器核心参数的详细设计流程，并以一台约1kW的电源实验样机验证了所提拓扑结构、相关控制方法以及参数设计流程的正确性。实验样机最高效率达到了95%，可在82%的负载范围内保持90%以上的工作效率。
参考文献
[1] Lo Y K, Lin C Y, Hsieh M T, et al. Phase-shifted full-bridge series-resonant DC-DC converters for wide load variations[J]. IEEE Transactions on Industrial Electronics, 2010, 58(6): 2572-2575.
[2] Lo Y K, Pai K J. Feedback design of a piezoelectric transformer-based half-bridge resonant CCFL inver- ter[C]//IEEE 2007 International Aegean Conference on Electrical Machines and Power Electronics, Bodrum, Turkey, 2007: 162-167.
[3] 胡杨良, 王议锋, 陈博, 等. 一种双CLT谐振软开关直流变换器设计与实现[J]. 电工技术学报, 2018, 33(7): 1461-1471.
Hu Yangliang, Wang Yifeng, Chen Bo, et al. The design and implementation of a dual-CLT resonant soft-switching DC-DC converter[J]. Transactions of China Electrotechnical Society, 2018, 33(7): 1461- 1471.
[4] 林雪凤, 许建平, 周翔. 谐振软开关耦合电感高增益DC-DC变换器[J]. 电工技术学报, 2019, 34(4): 747-755.
Lin Xuefeng, Xu Jianping, Zhou Xiang. Soft- switched high step-up DC-DC converter with coupled inductor of resonance[J]. Transactions of China Electrotechnical Society, 2019, 34(4): 747-755.
[5] 钱城晖, 钱挺. 辅助半桥调节的定频LLC谐振功率变换器[J]. 电工技术学报, 2019, 34(7): 1459-1467.
Qian Chenghui, Qian Ting. A fixed-frequency LLC resonant converter adjusted by auxiliary half- bridge[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1459-1467.
[6] Wang Haoyu, Dusmez S, Khaligh A. Design and analysis of a full-bridge LLC-based PEV charger optimized for wide battery voltage range[J]. IEEE Transactions on Vehicular technology, 2013, 63(4): 1603-1613.
[7] Huang Daocheng, Kong Pengju, Lee F C, et al. A novel integrated multi-elements resonant converter[C]// IEEE Energy Conversion Congress and Exposition, Phoenix, AZ, USA, 2011: 3808-3815.
[8] 徐恒山, 尹忠东, 黄永章. 考虑最大输出电压和效率的LLC谐振变流器的设计方法[J]. 电工技术学报, 2018, 33(2): 331-341.
Xu Hengshan, Yin Zhongdong, Huang Yongzhang. Design method of LLC resonant converter considering maximum output voltage and efficiency[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(2): 331-341.
[9] 冯雪. LLC谐振变换器损耗分析与效率优化[D]. 北京: 北京交通大学, 2017.
[10] 胡海兵, 王万宝, 孙文进, 等. LLC谐振变换器效率优化设计[J]. 中国电机工程学报, 2013, 33(18): 48-56, 16.
Hu Haibing, Wang Wanbao, Sun Wenjin, et al. Optimal efficiency design of LLC resonant con- verters[J]. Proceedings of the CSEE, 2013, 33(18): 48-56, 16.
[11] 任仁, 张方华, 刘硕. 基于LLC直流变压器(LLC- DCT)效率优化的死区时间与励磁电感设计[J]. 电工技术学报, 2014, 29(10): 141-146.
Ren Ren, Zhang Fanghua, Liu Shuo. Optimal design for efficiency based on the dead time and magnetizing inductance of LLC DC transformer[J]. Transactions of China Electrotechnical Society, 2014, 29(10): 141- 146.
[12] Feng Weiyi, Lee F C, Mattavelli P. Optimal trajectory control of Burst mode for LLC resonant converter[J]. IEEE Transactions on Power Electro- nics, 2013, 28(1): 457-466.
[13] Yang C H, Liang T J, Chen K H, et al. LLC resonant converter controller with novel light load control[C]// International Power Electronics and Application Conference and Exposition, Shanghai, China, 2014: 131-135.
[14] Chen Jian, Sato T, Yano K, et al. An average input current sensing method of LLC resonant converters for automatic burst mode control[J]. IEEE Transa- ctions on Power Electronics, 2016, 32(4): 3263-3272.
[15] Fei Chao, Li Qiang, Lee F C. Digital implementation of light-load efficiency improvement for high- frequency LLC converters with simplified optimal trajectory control[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2018, 6(4): 1850-1859.
[16] Wang Bin, Xin Xiaoni, Wu S, et al. Analysis and implementation of LLC burst mode for light load efficiency improvement[C]//Twenty-Fourth Annual IEEE Applied Power Electronics Conference and Exposition, Washington DC, USA, 2009: 58-64.
[17] Jeong Y, Moon G W, Kim J K. Analysis on half- bridge LLC resonant converter by using variable inductance for high efficiency and power density server power supply[C]//IEEE Applied Power Elec- tronics Conference and Exposition (APEC), Tampa, FL, 2017: 170-177.
[18] Hua C C, Fang Y H, Chen Weilin. LLC resonant converter for electric vehicle battery chargers[J]. IET Power Electronics, 2016, 9(12): 2369-2376.
[19] Liang Zhigang, Guo Rong, Li Jun, et al. A high- efficiency PV module-integrated DC/DC converter for PV energy harvest in FREEDM systems[J]. IEEE Transactions on Power Electronics, 2011, 26(3): 897- 909.
[20] Yang Bo, Lee F C, Zhang A J, et al. LLC resonant converter for front end DC/DC conversion[C]// Seventeenth Annual IEEE Applied Power Electronics Conference and Exposition, Dallas, TX, USA, 2002: 1108-1112.
Wide Range Efficiency Optimization Control Strategy for LLC Resonant Converter Based on Parallel Transformer Switching
Abstract A parallel switching transformer-based LLC (ST-LLC) multi-resonant converter was proposed in this paper. The transformer indirect parallel method and switching control strategy were used to construct a novel variable topology LLC based on the idea of variable inductance ratio k. The efficiency of the converter was effectively improved and the decentralized design of the transformer hot-spot was achieved, while maintaining soft switching characteristics. Detailed analysis for characteristics of voltage gain and the main operating modes was given. Besides, an optimal load partition control strategy was proposed based on the logic of transformer switching control, and wide range of high efficiency was achieved. Furthermore, the analytical formula of the maximum power of the transformer switching point was derived, and the design process of the main component parameters of the circuit was also given. A 1kW prototype was designed and manufactured, and the feasibility of the proposed scheme was verified by simulation and experiment. The working efficiency of the prototype could maintain more than 90% in the 82% load range.
keywords：LLC converter, parallel transformer switching, efficiency optimization, optimal load partition control
DOI: 10.19595/j.cnki.1000-6753.tces.190778
中图分类号：TM46
刘晓东 男，1971年生，博士，教授，研究方向为电力电子功率变换技术以及非线性控制。E-mail: lxdong168@sina.com
刘宿城 男，1981年生，博士，副教授，研究方向为电力电子系统建模与控制、直流微电网。E-mail: liusucheng@gmail.com（通信作者）
收稿日期 2019-06-26
改稿日期 2019-09-01
国家自然科学基金（51407003）、安徽省自然科学基金（1708085ME106）和安徽高校自然科学研究重点（KJ2017A067）资助项目。
（编辑 崔文静）