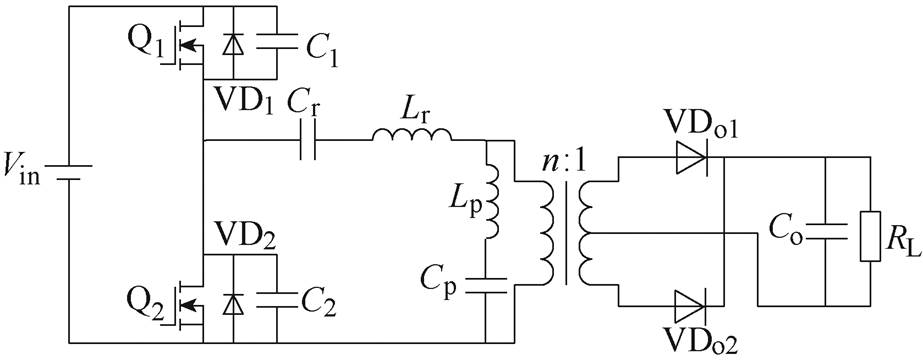
图1 单向半桥LCLC谐振变换器
Fig.1 Half bridge unidirectional LCLC resonant converter
摘要 为了解决双向DC-DC变换器输入、输出电压范围过窄的问题,该文提出一种高增益对称双向LCLC谐振变换器。提出的谐振变换器不是利用变压器的励磁电感参与谐振,而是在变压器的一次侧并联一个LC支路代替变压器励磁电感的作用,使得变换器在电感比较大的情况下仍有较高的增益,兼顾了LLC型谐振变换器在谐振点的高效率和宽的增益范围,且能保证一次侧和二次侧的软开关特性,实现谐振变换器的对称双向运行。该文基于基波分析法建立基波等效模型,推导出变换器的增益公式,分析谐振参数对直流增益特性的影响。最后搭建一台100~200V/24~48V、500W的实验样机,实验结果验证了理论分析的正确性和所提出拓扑结构的可行性及有效性,样机的最大效率达到96.3%。
关键词:双向LCLC谐振变换器 并联LC支路 高增益 软开关
目前双向DC-DC变换器已经广泛应用于电动汽车、微电网、能量存储系统等多种场合[1-4]。很多双向DC-DC变换器都要求有一个比较宽的输入输出电压范围[5],因此研究高增益、高效率的双向DC-DC变换器很有必要。
LLC谐振变换器可以在全负载范围内实现一次侧开关管的零电压开通(Zero Voltage Switching, ZVS)和二次侧整流二极管的零电流关断(Zero Current Switching, ZCS),减小开关损耗的同时实现高效率,因此成为近些年研究的热点[6-13]。双向LLC谐振变换器继承了单向LLC谐振变换器软开关优点[13],损耗小、效率高,已经成为双向DC-DC功率变换应用的最优选择之一。
传统的LLC谐振变换器工作在变频控制下,为了获得比较高的增益,不得不扩大工作频率范围或减小电感比[14-15],前者对磁性元件的优化和设计是一个挑战,这会增加磁性元件的体积;后者使得LLC谐振变换器不得不设计较小的励磁电感。然而,小的励磁电感需要较大的气隙,容易造成变压器发热,损耗增加;另外,小的励磁电感会引起循环电流的增加,导致较大的开关管导通损耗和关断损耗。因此大部分LLC谐振变换器的设计是在增益满足要求的基础上尽可能去取最大的励磁电感。所以传统的LLC谐振变换器不能满足高增益宽范围的要求[15-16],目前大多数LLC谐振变换器的归一化增益在1.5以内,达到2的很少。
为了获得较高的增益,近些年来国内外学者提出了一系列LLC谐振变换器的新型拓扑结构和控制方法[17-21]。文献[17]提出了一种混合桥双模式LLC谐振变换器的控制策略,通过控制滞后或超前桥臂开关管下管的常开与上管的常闭,变换器可以实现半桥LLC与全桥LLC 之间的切换,这样就可以扩大变换器的增益范围,但增益只是减小一半,不能应用在对称双向高增益结构中。文献[18]提出了一种变频-移相的混合控制策略,变频工作模式和普通LLC的工作过程一样,移相工作使得归一化增益低于1甚至为0,但当移相等效占空比较小时不能实现ZVS。文献[19]提出了一种倍压整流方案,可以使得变换器的增益是传统LLC谐振变换器的2倍,但它用到了大于串联谐振频率点的一段增益曲线,这部分工作范围不能实现ZCS。文献[20]提出了一种非对称的双向LLC谐振变换器,正反向输入电压范围都比较宽,但是其励磁电感与谐振电感的比值比较小,只有3,而且变换器也有一部分工作在大于串联谐振频率点,不能实现ZCS,此外工作频率调节范围过宽,且其实际最大增益并未达到2。
文献[21]提出了单向半桥LCLC谐振变换器如图1所示,用来增加电源断电时的持续时间,但并没有分析各谐振元件对增益的影响和其高增益特性。对称型双向LLC谐振变换器[13]如图2所示,因其可以双向运行,且结构对称,正反向运行的增益特性相同,设计简单,近些年来受到了广泛关注。但是大部分学者让其工作在增益为1附近,其电感比取值较大,这大大限制了它的应用范围。本文结合文献[13, 21]提出了如图3所示的一种高增益双向LCLC谐振变换器。本文提出对称双向LCLC谐振变换器,是在传统的对称双向LLC谐振器的基础上,在变压器一次侧并联一个电感电容支路代替变压器励磁电感的作用,没有利用变压器励磁电感参与谐振,变压器不需要开气隙,在大的电感比情况下,仍可以实现较大的增益。

图1 单向半桥LCLC谐振变换器
Fig.1 Half bridge unidirectional LCLC resonant converter
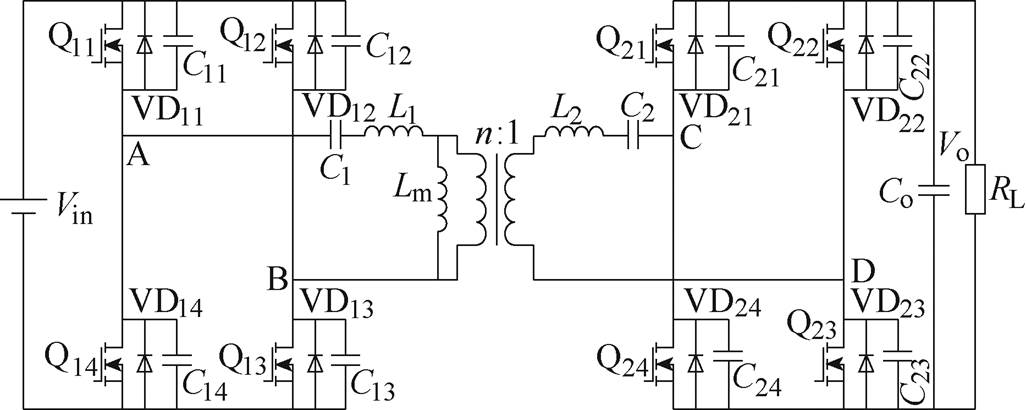
图2 对称双向LLC谐振变换器
Fig.2 Traditional symmetric bidirectional LLC resonant converter
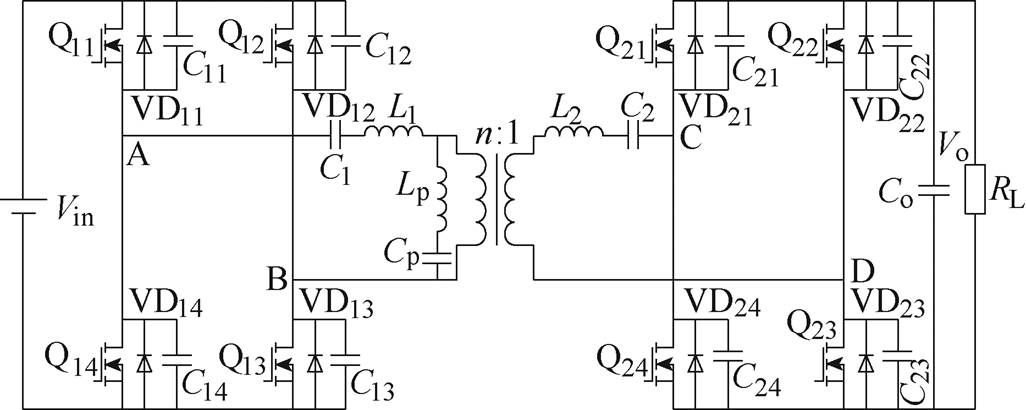
图3 提出的对称双向LCLC谐振变换器
Fig.3 Proposed symmetric bidirectional LCLCresonant converter
如图3所示,开关管Q11、Q12、Q13和Q14构成一次侧的H桥,Q21、Q22、Q23和Q24构成二次侧的H桥。图中与开关管并联的二极管和电容是相应开关管的寄生二极管和寄生电容。正向工作时,一次侧同一桥臂的开关管Q11和Q14、Q12和Q13以50%的占空比互补导通,不同桥臂对角的开关管Q11和Q13、Q12和Q14以50%的占空比同时导通;二次侧的开关管不导通,相应的反并联二极管构成整流桥,进行全桥整流。反向工作时与此类似。图中L1 和L2,C1和C2分别为一次侧和二次侧的谐振电感和谐振电容,Cp和Lp为并联支路的电容和电感。
提出的变换器采用传统LLC变换器变频控制的方法,其工作方式分为工作频率小于等于串联谐振频率和大于串联谐振频率。当工作在大于串联谐振频率时,变换器工作在归一化增益小于1的状态,此时不能实现二次侧ZCS,损耗增加,应尽可能避免工作在这个状态;当工作在小于等于串联谐振频率时,变换器工作在归一化增益大于等于1的状态,可以实现一次侧的ZVS和二次侧的ZCS,此时工作的主要波形如图4所示,提出的对称双向LCLC谐振变换器各阶段工作的电路如图5所示。接下来将对这一情况下的工作过程分阶段进行详细分析。图4中,Vgs为开关管驱动脉冲,iLp为流过电感Lp的电流,VC1为电容C1两端的电压,iVD21、iVD22、iVD23和iVD24分别为流过VD21、VD22、VD23和VD24的电流。
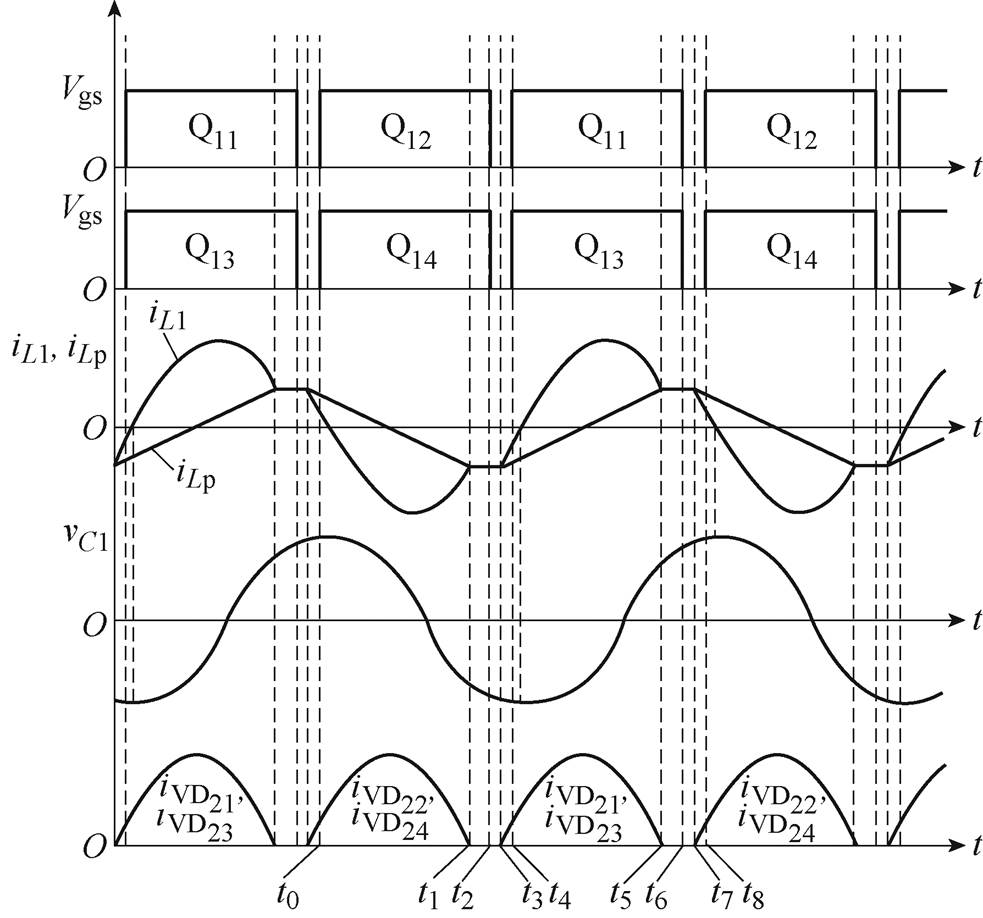
图4 提出的变换器主要工作波形
Fig.4 Key operating waveforms of the proposed converter
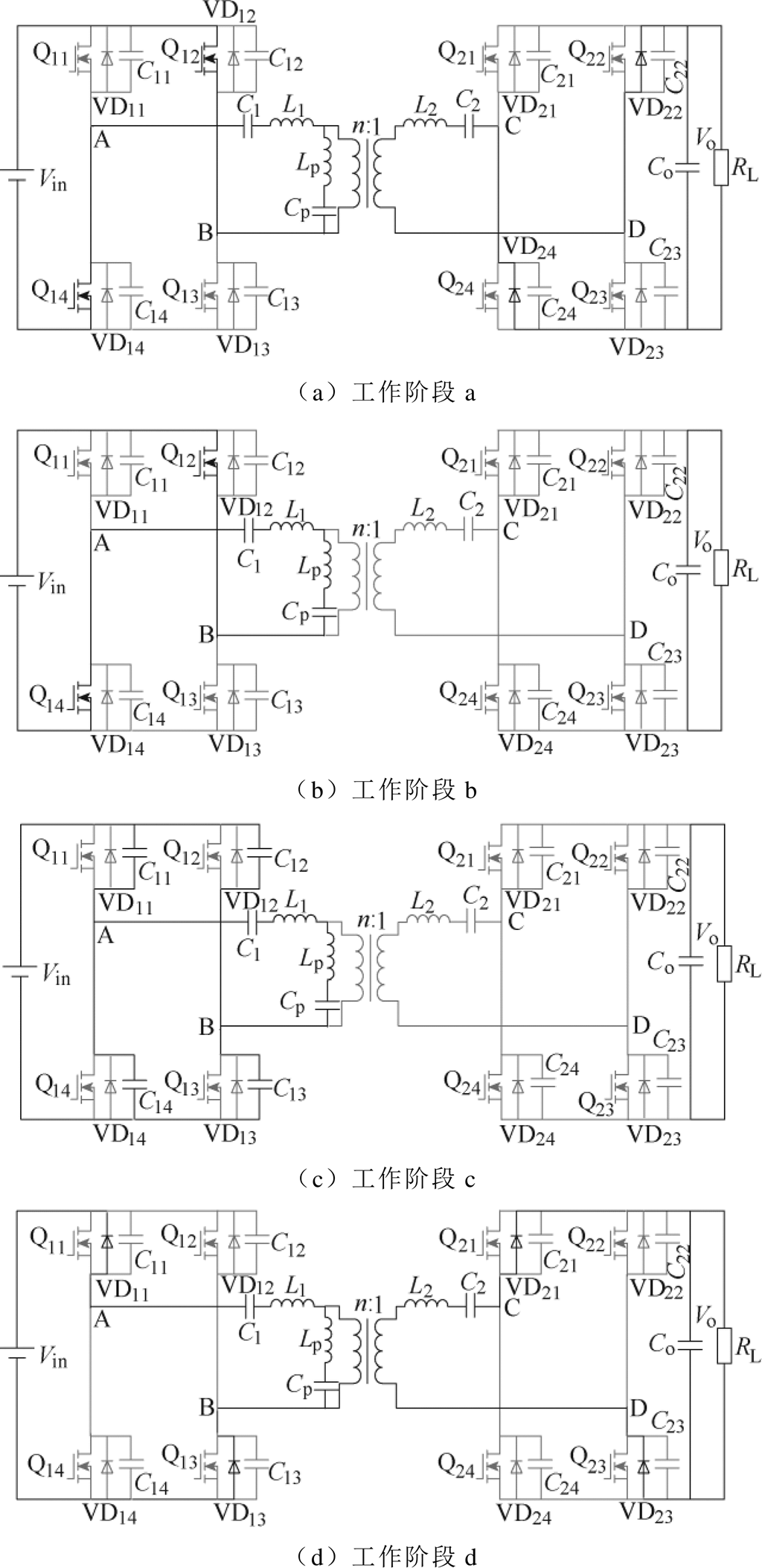
图5 提出的对称双向LCLC谐振变换器各阶段工作的电路
Fig.5 Operational stages of the proposed symmetric bidirectional LCLC resonant converter
工作阶段a[t0, t1]:t0时刻Q12和Q14实现ZVS并向二次侧传递能量,输入电压Vin加在AB两端,C1和L1发生谐振,谐振电流iL1呈正弦下降,由于二次电压的钳位作用,电流ip呈线性下降,且iL1电流下降速度要快于ip,二次侧二极管VD22和VD24导通,进行整流,直到电流iL1=ip,C1和L1退出谐振,此阶段结束。
工作阶段b[t1, t2]:t1时刻iL1=ip,二次侧停止传递能量,二次电流iL2=0,二次侧二极管VD22和VD24零电流关断,实现了ZCS。此时没有二次电压的钳位作用,C1、L1、Cp和Lp一起发生谐振,由于此时的谐振周期很大,谐振电流缓慢上升,近似看作线性上升,直到Q12和Q14关断,此阶段结束。
工作阶段c[t2, t3]:t2时刻Q12和Q14关断,Q11和Q13还没有导通,此时死区的第一阶段开始,谐振电流iL1向Q12和Q14的寄生电容C12和C14充电,Q11和Q13的寄生电容C11和C13放电,直到充放电完成,当C11和C13两端的电压降为零时,死区的第一个阶段结束。
工作阶段d[t3, t4]:t3时刻C11和C13两端的电压为零,为Q11和Q13的零电压导通准备条件。此时Q11和Q13体二极管VD11和VD13开始反向导通,而Q11和Q13仍然没有导通,iL1和ip开始增加,且iL1增加较快,两电流不相等,开始向二次侧传递能量,二次侧二极管VD21和VD23导通。
由图4工作波形可知,变换器的前半周期工作过程与后半周期工作过程相似,是对称运行的,所以这里详细分析了半个周期的工作过程。由于本文提出的变换器是对称运行的,反向工作过程与正向工作过程一样,因此这里不再赘述。
本文提出的高增益对称双向LLC谐振变换器采用变频控制的方式,以下采用基波等效分析法(First Harmonic Approximation, FHA)对变换器的增益特性进行分析。提出的双向LCLC谐振变换器基波等效模型如图6所示。为了方便分析,这里做出以下假设:①开关管、电感、电容都为理想元器件;②负载是纯阻性;③变压器为理想变压器;④输出电容足够大,输出电压为恒值。为了简化分析,这里取变压器的匝比为1 1,所提出的谐振变换器是对称双向运行的,所以有
1,所提出的谐振变换器是对称双向运行的,所以有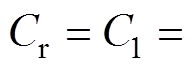
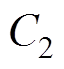 ,
,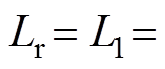
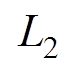 ,当匝比为n
,当匝比为n 1时,有
1时,有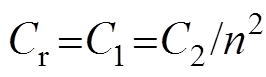 ,
,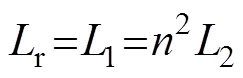 。
。
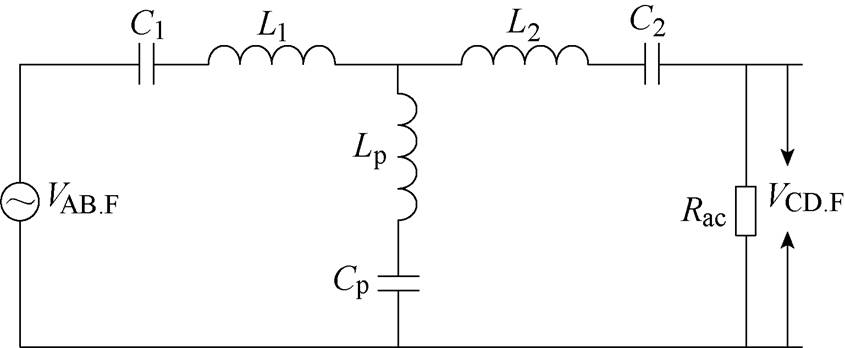
图6 提出的双向LCLC谐振变换器基波等效模型
Fig.6 FHA model of the proposed symmetric bidirectional LLC resonant converter
输入电压经过一次侧H桥的逆变作用,将直流电压Vin变成为从-Vin到+Vin的纯方波,将其进行傅里叶展开可得
 (1)
(1)式中,fs为开关频率,在应用基波分析法时,将方波等效成基波忽略高次谐波,此时vAB的基波表达式为
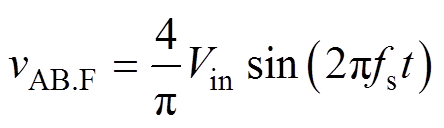 (2)
(2)
有效值VAB.F为
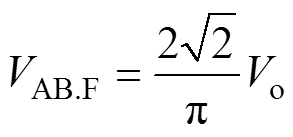 (3)
(3)同理,谐振腔输出电压的傅里叶展开为
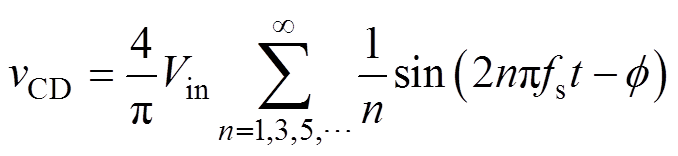 (4)
(4)
式中,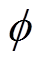 为输入电压与输出电压之间的相位差;uCD.F基波表达式为
为输入电压与输出电压之间的相位差;uCD.F基波表达式为
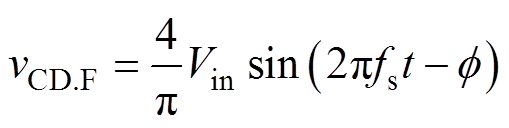 (5)
(5)其有效值为
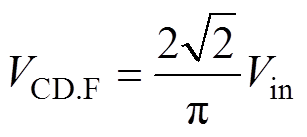 (6)
(6)
等效负载上的电流可以用求式(2)的方法得到其基波表达式为
 (7)
(7)等效负载上的电流iac的平均值等于输出电流Io。由此得输出电流为
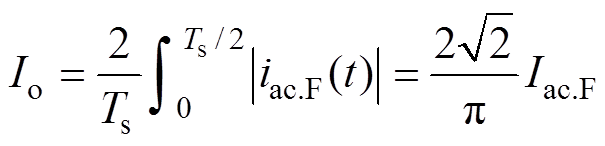 (8)
(8)
由式(6)式和(8)可得等效交流电阻为
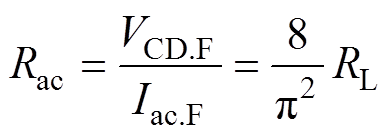 (9)
(9)当变压器的电压比为n 1时,得
1时,得
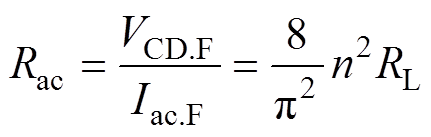 (10)
(10)
本文将通过基波等效模型来推导变换器的增益公式,为增益特性分析做铺垫。等效模型中谐振腔内所有的电容值、电感值分别用C和X表示,对应的电容值和电感值可以分别表示为
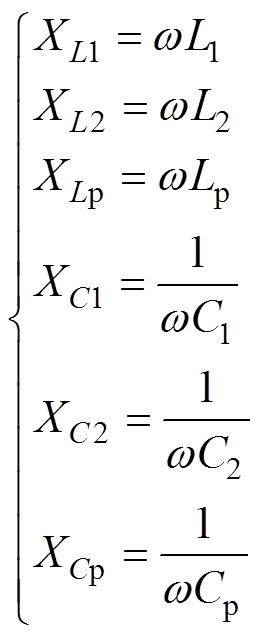 (11)
(11)每条支路的电抗可以表示为
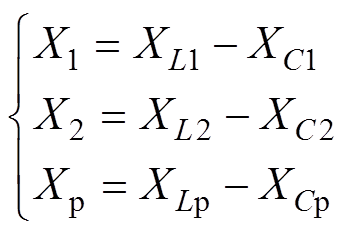 (12)
(12)
式中,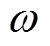 为开关管的开关角频率,
为开关管的开关角频率,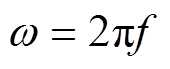 ,f为开关管的开关频率。
,f为开关管的开关频率。
归一化频率定义为
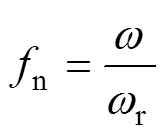 (13)
(13)式中,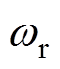 为串联谐振角频率,表示为
为串联谐振角频率,表示为
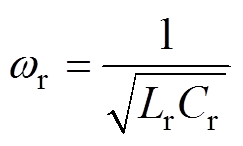 (14)
(14)
为了方便增益公式推导,取下列参数作为基准,进行归一化推导: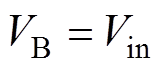 ,
,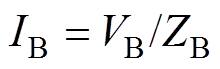 ,
,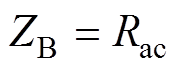 ,
,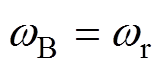 。
。
由图5所示变换器的基波等效电路,可得电压增益为
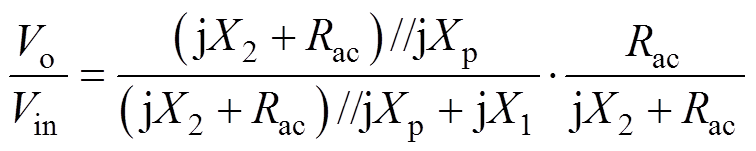
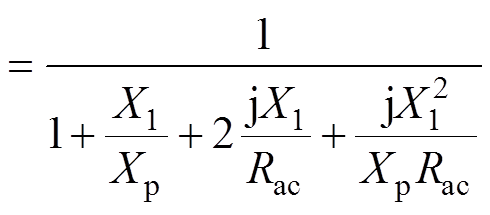
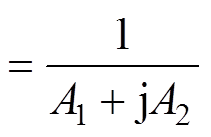 (15)
(15)
其中
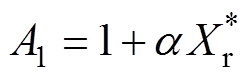 (16)
(16)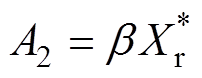 (17)
(17)
式中,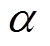 、
、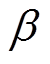 分别表示为
分别表示为
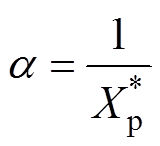 (18)
(18)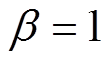 (19)
(19)
式中,右上角带*的分别是对应参数的标幺值,如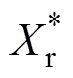 、
、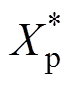 分别为Xr、Xp的标幺值,
分别为Xr、Xp的标幺值,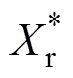 、
、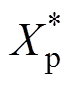 可以分别表示为
可以分别表示为
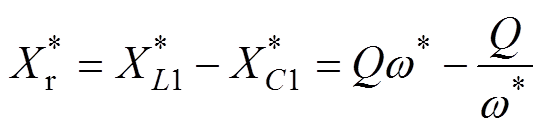 (20)
(20)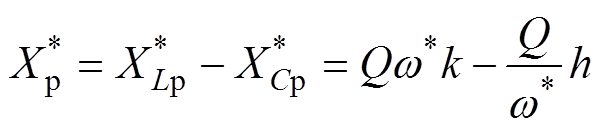 (21)
(21)
式中,Q为品质因数;k为并联电感与谐振电感的比值;h为谐振电容与并联电容的比值,其表达式分别为
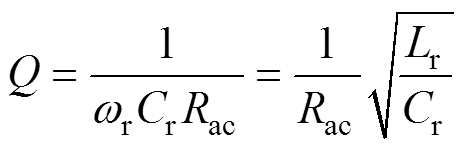 (22)
(22)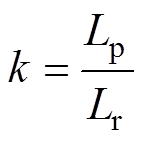 (23)
(23)
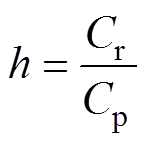 (24)
(24)
归一化增益G可以表示为
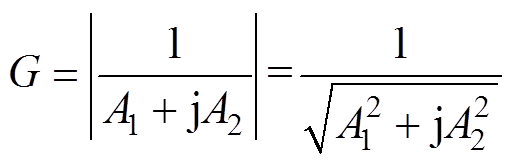 (25)
(25)2.2节通过建立基波等效模型,推导出归一化直流增益公式(25),本节将对基波等效模型进行增益特性的分析,分析谐振腔各个元件参数变化对增益的影响,这也是设计提出的谐振变换器的主要依据。根据式(15)~式(25),用数学软件可以画出如图7所示的归一化增益G与品质因数Q和归一化频率fn三维关系曲线。
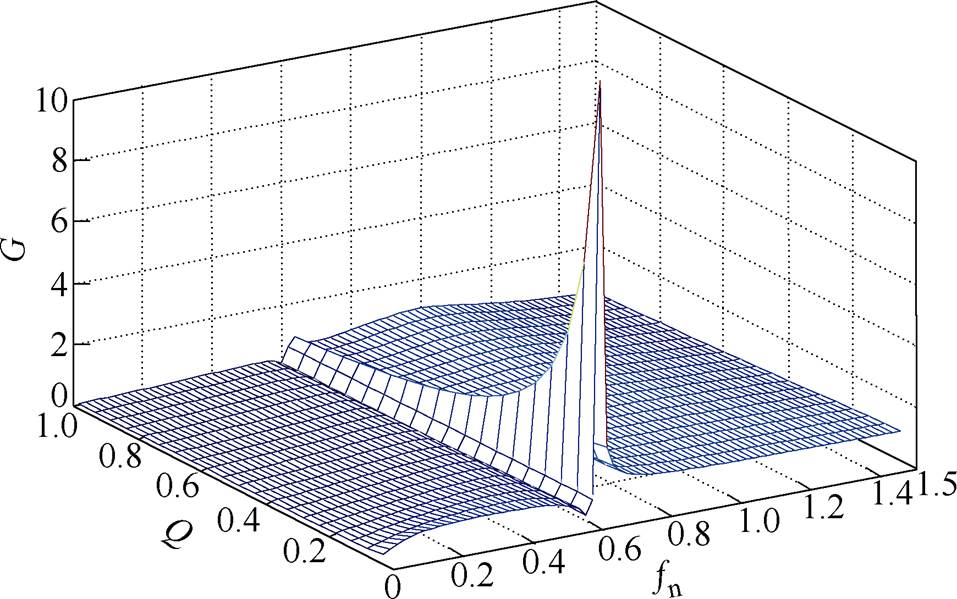
图7 归一化增益G与Q和fn的三维曲线
Fig.7 Three-dimensional gain G curvesversus Q andfn
为了更加直观地分析品质因数Q对归一化增益的影响,画出如图8所示的在不同的品质因数Q下,归一化增益G与归一化频率fn的曲线。由Q的表达式(22)可以看出,在谐振参数确定的情况下,品质因数Q和负载电阻呈反比,所以可以用Q来反映负载大小的情况。从图7可以看出,Q越大,峰值增益越小,且Q的大小对从峰值增益到增益为1的频率变化范围影响不明显,这和传统LLC增益特性相似。
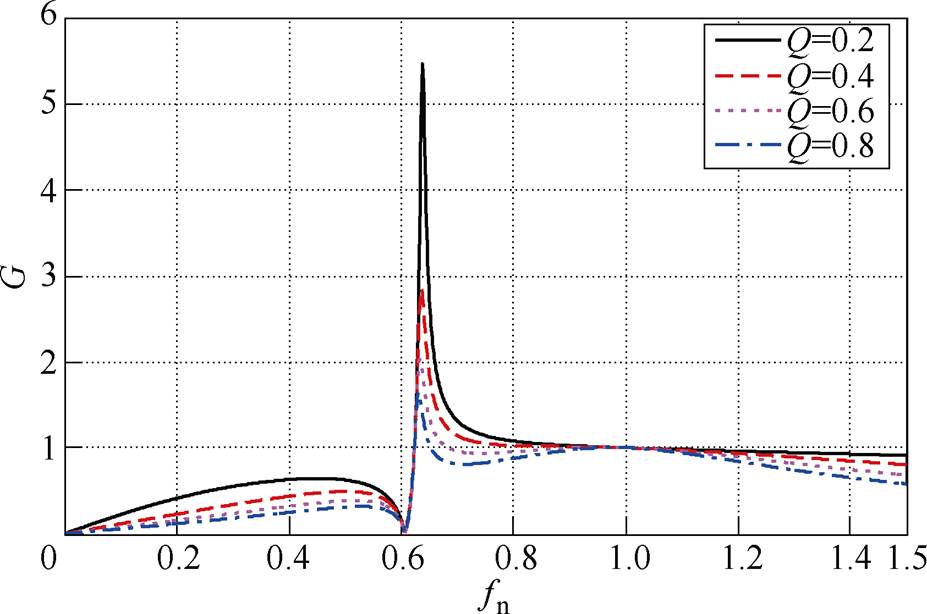
图8 不同Q值下归一化增益G与fn的关系曲线
Fig8 The normalized gain G versusfnunder different Q
图9所示为提出对称双向LCLC谐振变换器在不同的并联电感和谐振电感比k下,归一化增益G与归一化频率fn的关系曲线。从图9中可以看出,k越小,峰值增益越大,且峰值增益点的频率越大,调频范围越小,增益曲线变得越陡峭。所以k的取值既要满足增益要求,又不能太陡,调频范围不能太宽,需要综合考量。
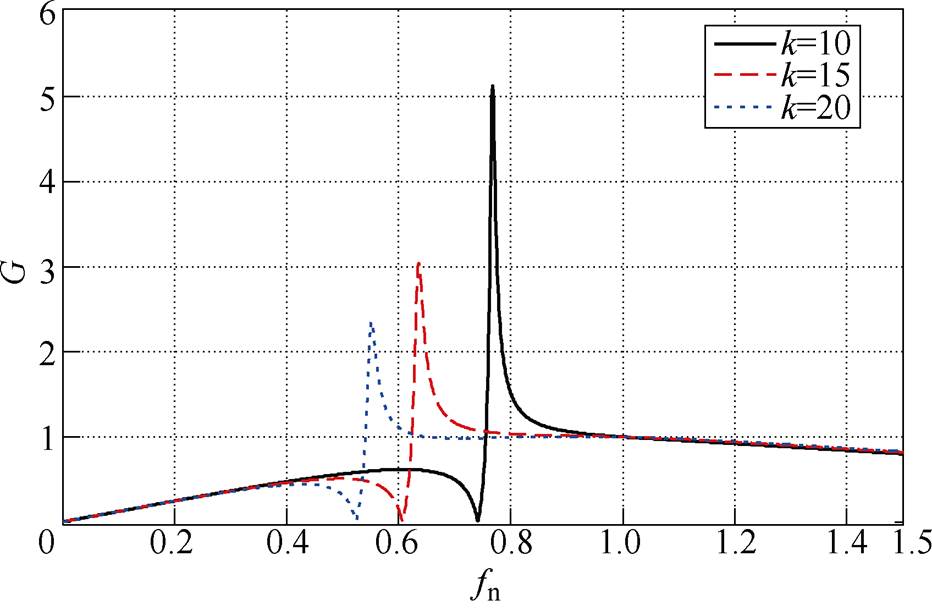
图9 不同k值下归一化增益G与fn的关系曲线
Fig.9 The normalized gain G versus fn under different k
图10所示为在不同谐振电容和并联电容比h下,归一化增益G与归一化频率fn的关系曲线。从图10中可以看出,电容比h越大,峰值增益越大,而且峰值增益点的频率越大,则调频范围变得更窄,但是增益曲线越陡,因此电容比h的选取需要综合以上三个因素进行折中考虑。
在谐振电感Lr、谐振电容Cr、品质因数Q(也即负载)相同时,利用基波等效法求出传统对称双向LLC谐振变换器增益公式(26),具体推导过程参见文献[16],画出其归一化增益曲线,比较如图2

图10 不同h值下归一化增益G与fn的关系曲线
Fig.10 The normalized gain G versus fn under different h
所示的传统对称双向LLC谐振变换器和如图3所示的提出的对称双向LCLC谐振变换器的增益范围和调频范围,进行变换器的特性对比分析如图11所示。
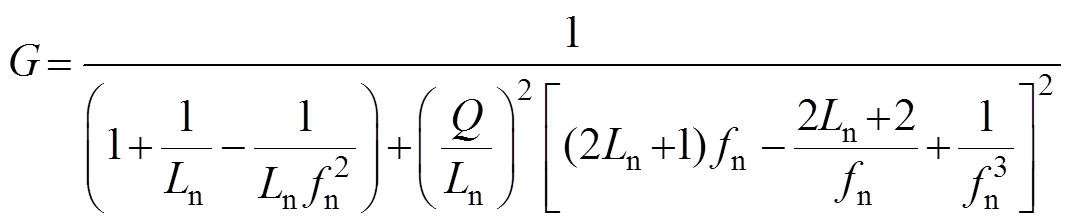 (26)
(26)式中,Ln为励磁电感与谐振电感之比。
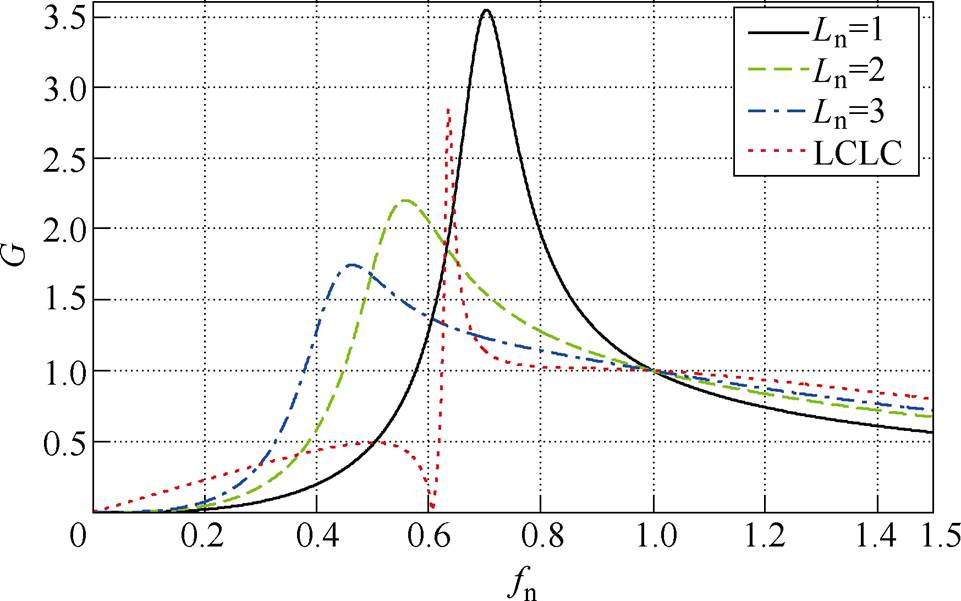
图11 提出变换器和传统对称双向LLC谐振变换器增益特性比较
Fig.11 Gain characteristic comparison of the proposed converter and traditional symmetric bidirectional LLC resonant converter
1)增益特性比较
图11所示的点线为提出拓扑的归一化增益曲线,实线、虚线和点画线分别为传统对称双向LLC谐振变换器在励磁电感与谐振电感比Ln=1、2、3时的归一化增益曲线。从图中可以看到,提出的变换器可以达到高增益(G=2);传统的拓扑达到相同的增益,电感比必须取得较小,Ln=2,事实上,电感比越小,励磁电流越大,损耗也会越大,所以一般在实际应用设计中传统的LLC电感比尽可能取得大,很少会低于3,因此传统的LLC不适用于高增益场合。
2)频率范围比较
通过对比图11可以看出,在G=2时,提出的拓扑的峰值增益点频率较高,工作频率范围相对较窄,虽然实线也能达到G=2时,频率范围较小,但是此时Ln=1,非常小的电感比会导致损耗增大,实际应用中绝对不会取这么小,因此提出的拓扑工作频率范围更窄,更有利于磁件的设计。所以选择合适的并联电感Lp,并联电容Cp可使提出的变换器比传统对称双向LLC谐振变换器的增益更大且频率变化范围小。
3)并联支路的本质
电感电容并联支路其本质是一个随频率增加而增大的可变电感,电路工作在增益较小(1附近)时,工作频率较高,可变电感的值较大,相当于传统LLC的电感比Ln很大,损耗降低、效率增加。而当电路需要工作在高增益时,降低开关频率,可变电感值变小,电感比变小,以此来提高增益。而传统的LLC谐振变换器要达到高增益,必须有很小的电感比,这样无论工作在较低增益还是较高增益,电感比都很小,效率比较低。
以上的增益特性分析都是基于没有考虑变压器励磁电感的影响,但实际上变压器的励磁电感却是真实存在,且无法避免的。考虑励磁电感的基波等效模型如图12所示。考虑励磁电感的直流增益计算方法仍可以用基波等效法,与上述方法类似,但会更复杂,这里不再进行具体的推导。同样应用Matlab画出励磁电感对增益影响的对比曲线如图13所示。
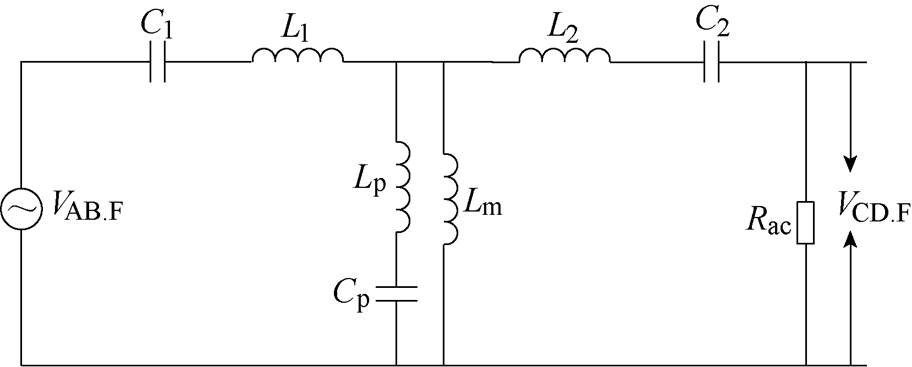
图12 考虑Lm的对称双向LCLC谐振变换器的基波等效模型
Fig.12 FHA model of the symmetric bidirectional LCLC resonant converter with Lm
图13是考虑变压器励磁电感大小和不考虑变压器励磁电感参与谐振情况下的直流增益对比曲线。从图中可以看出,A点以左增益曲线差别比较大,考虑励磁电感的增益曲线会多出一个拐点,这是因为多了一个电感,电路高了一阶,相应地多出一个谐振点,但是变换器不工作在这一部分曲线范围,所以对变换器的实际工作没有影响,可以不用考虑;B点以右,即变换器工作的增益曲线范围,励磁电感Lm对增益变化有影响,从图13可以看出,励磁电感Lm越小影响越大,当Lm=1mH时,增益相差不超过0.1,在可接受范围内。实际上由于变压器不开气隙,励磁电感会很大,很容易达到1mH以上,所以励磁电感对增益特性影响有限。因此设计谐振参数时可以忽略励磁电感对变换器增益变化的影响。
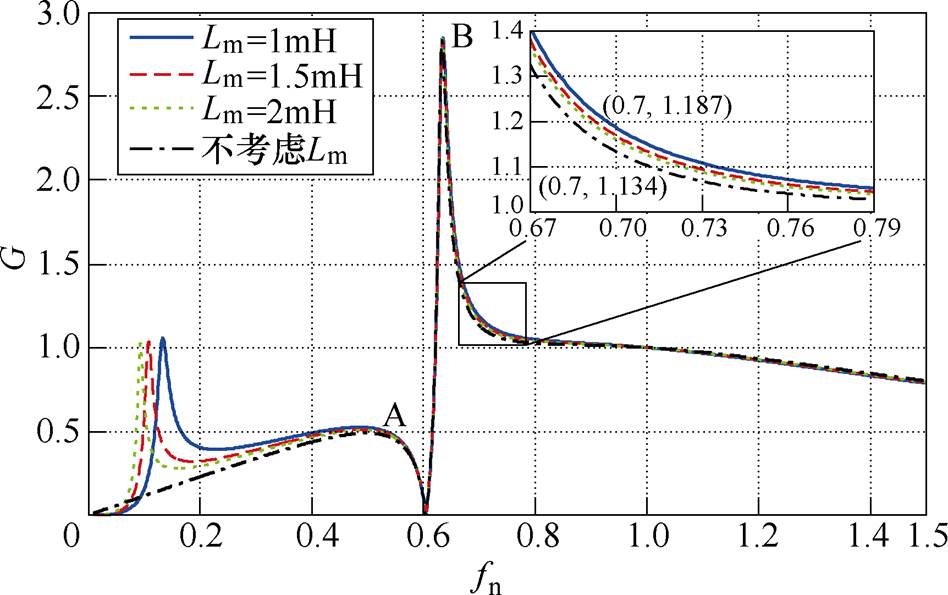
图13 考虑不同的Lm和不考虑Lm的对称双向LCLC谐振变换器的归一化增益比较
Fig.13 The normalized gain comparison of the symmetric bidirectional LCLC resonant converter with different Lm and without Lm
本文提出的高增益对称双向LCLC是以LLC谐振变换器为基础的,其参数设计过程与LLC谐振变换器的参数设计有相似之处,但是由于多了一个LC并联支路,所以参数设计过程较为复杂。
变压器的匝比可以用输入、输出额定电压之比求出。谐振参数设计过程的重点是求取合适的Q、k和h。第2节已经分析了Q、k、h对变换器的特性影响,根据仿真得出的增益特性曲线,选择合适的Q、k、h,通过式(27)求出谐振电容Cr,根据所要求的谐振频率fr通过式(14)得出Lr,通过k、h由式(23)、式(24)可求Lr、Cr,最后通过匝比将一次侧参数折算到二次侧。参数求解过程中可以根据实际情况对Q、k、h进行适当的调整。最后式(28)验证是否满足ZVS条件。
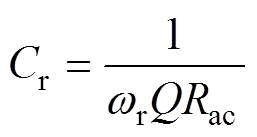 (27)
(27)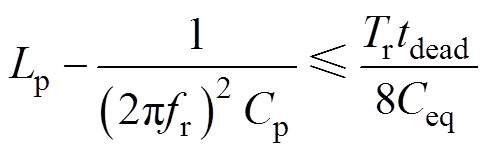 (28)
(28)
式中,Tr为串联谐振周期;tdead为死区时间;Ceq为开关管寄生等效电容。
为了验证提出的高增益对称双向LCLC谐振变换器的特性,按如图3所示的电路拓扑,制作了一台双向运行的500W实验样机。样机同一桥臂的两个MOS管的死区设为150ns,对称双向LCLC谐振变换器具体的工作模式:①正向运行模式:输入电压范围为100~200V,其中额定输入电压200V,输出电压48V,满载为500W;②反向运行模式:输入电压范围为24~48V,其中额定输入电压48V,输出电压200V,满载为500W。具体实验样机的参数见表1。
表1 样机参数
Tab.1 The parameters of prototype
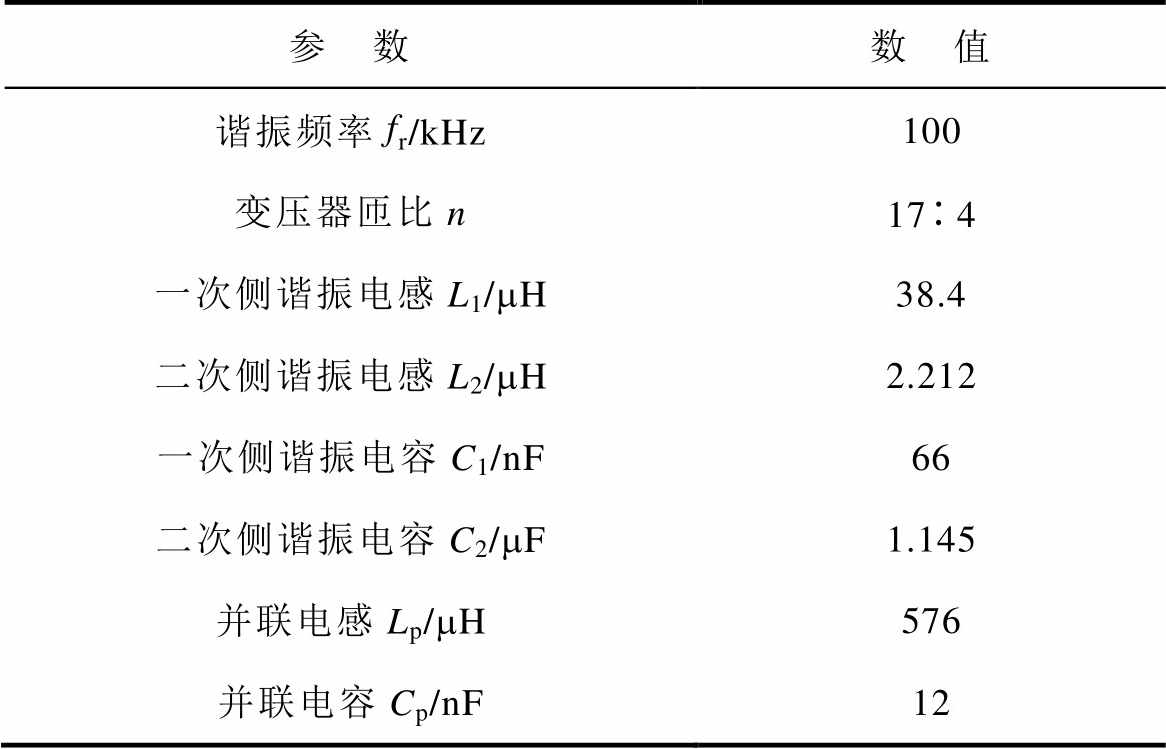
参 数数 值 谐振频率fr/kHz100 变压器匝比n174 一次侧谐振电感L1/mH38.4 二次侧谐振电感L2/mH2.212 一次侧谐振电容C1/nF66 二次侧谐振电容C2/mF1.145 并联电感Lp/mH576 并联电容Cp/nF12
图14和图15分别是实验在满载情况下各元器件正向及反向的运行实验波形。图14中的波形分别为输入200V、150V、100V,输出48V时,满载500W情况下输出电压、一次侧的谐振电流、MOS管Q14的栅源驱动电压和漏源电压的实验波形。类似地,图15中的波形分别为输入48V、36V、24V,输出200V时,满载500W情况下输出电压、二次侧的谐振电流、MOS管Q24的栅源驱动电压和漏源电压的实验波形。
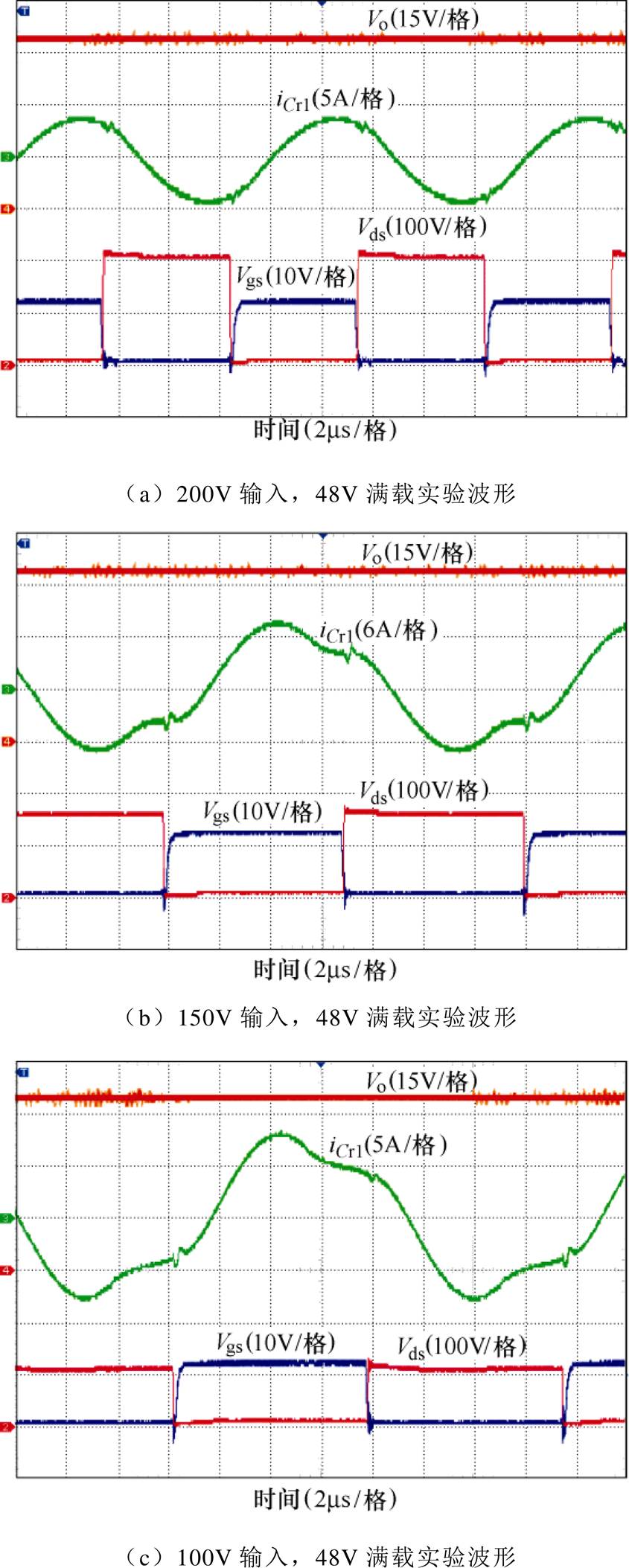
图14 正向运行实验波形
Fig.14 Experimental waveforms of forward operation
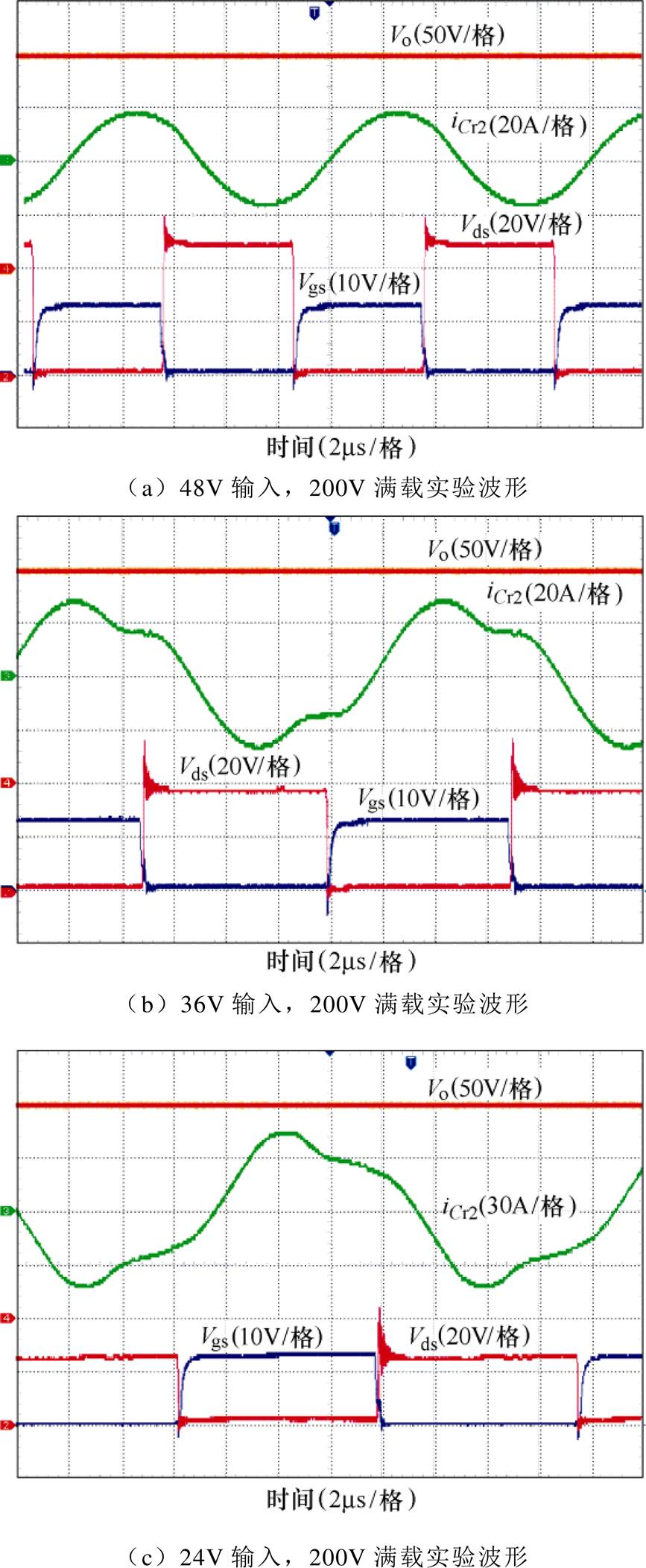
图15 反向运行实验波形
Fig.15 Experimental waveforms of backward operation
从实验的波形上可以明显看出,无论正向运行还是反向运行,在栅源驱动电压到来之前,漏极源极之间的电压已经降为0,即在全负载范围内实现了零电压开通,所以本文所提出的高增益拓扑具有传统LLC的特性,而且能够实现高增益。从谐振电流波形上可以看出,提出的高增益拓扑在额定输入情况下电流值较小,说明循环电流小,因此通过减小导通损耗和MOS管的关断损耗,提高变换器的效率。
图16和图17分别为提出的对称双向LCLC变换器和传统的对称双向LLC变换器(见图11中的Ln=2)额定输入、输出时正反向工作在不同负载下所测量的效率曲线对比。提出的变换器正向运行时,在80%的满载下,效率最大达到95.7%,满载效率能达到96%;反向运行时,在70%的满载下,效率最大达到96.3%,满载时效率为96.1%。从图中可以看出,无论正反向,本文提出的拓扑均比传统的高2%~3%,这验证了2.4节中与传统LLC变换器的对比分析结果。
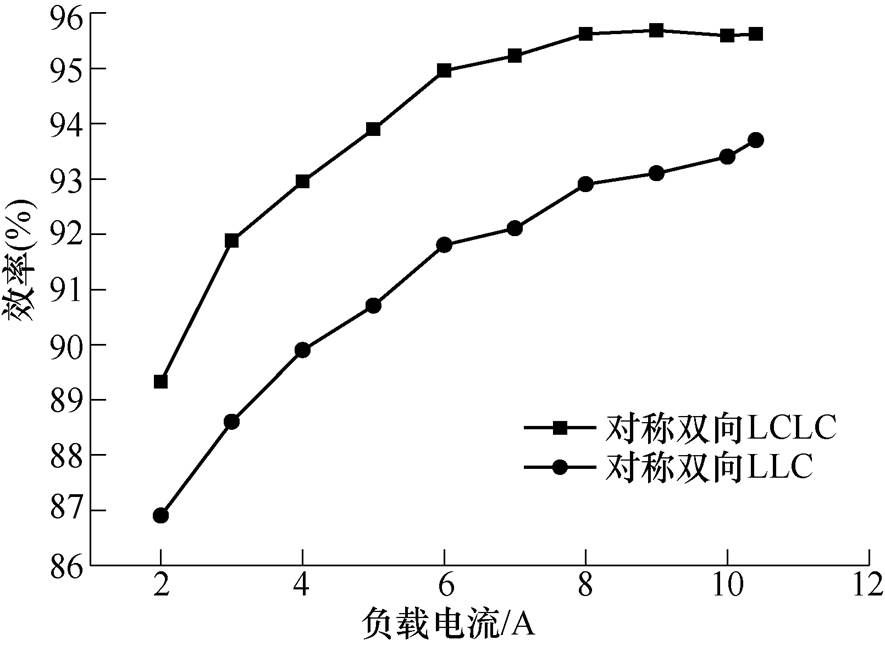
图16 不同负载下正向效率曲线
Fig.16 Efficiency curves in forward operation at different load
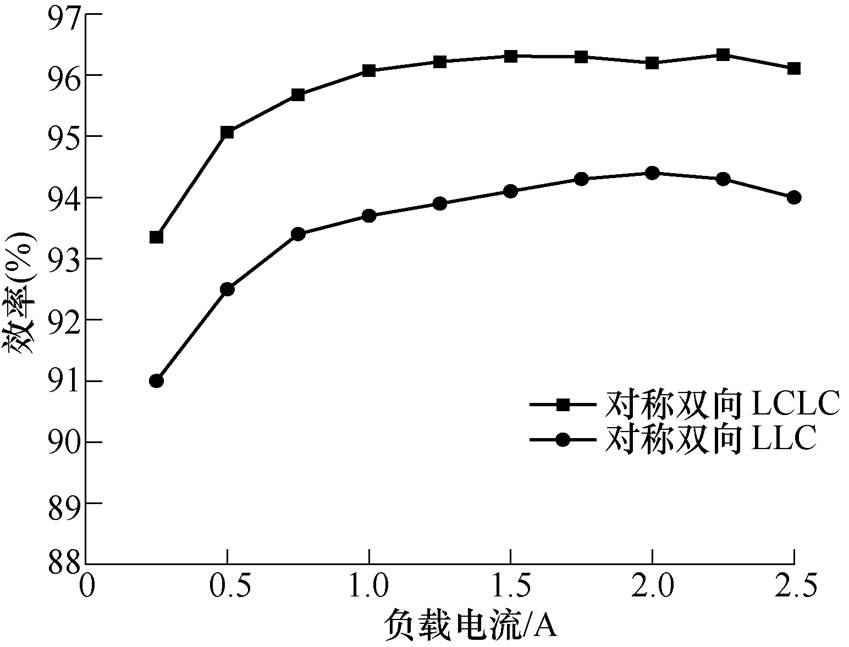
图17 不同负载下反向效率曲线
Fig.17 Efficiency curves in backward operation at different load
图18和图19分别为提出的变换器在不同的负载、不同的输入电压下正向和反向工作时的频率负载曲线。其中正向运行时的频率变化范围为65.5~111.2kHz,反向运行时的频率变化范围为65~137.6kHz,实际与理论总存在误差,所以正反向的频率变化范围不完全相同。
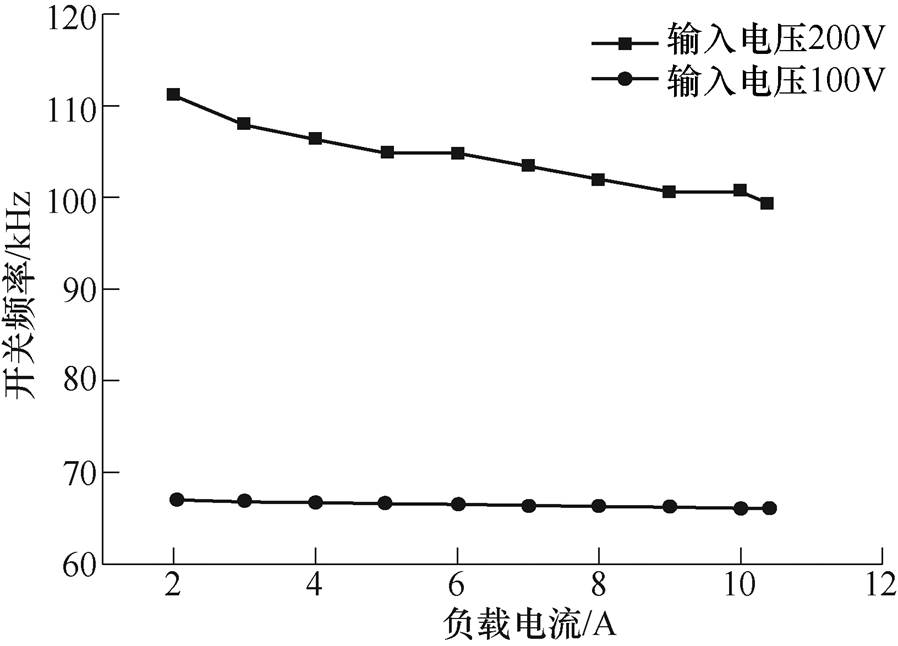
图18 不同负载下正向频率曲线
Fig.18 Frequency curves in forward operation at different load
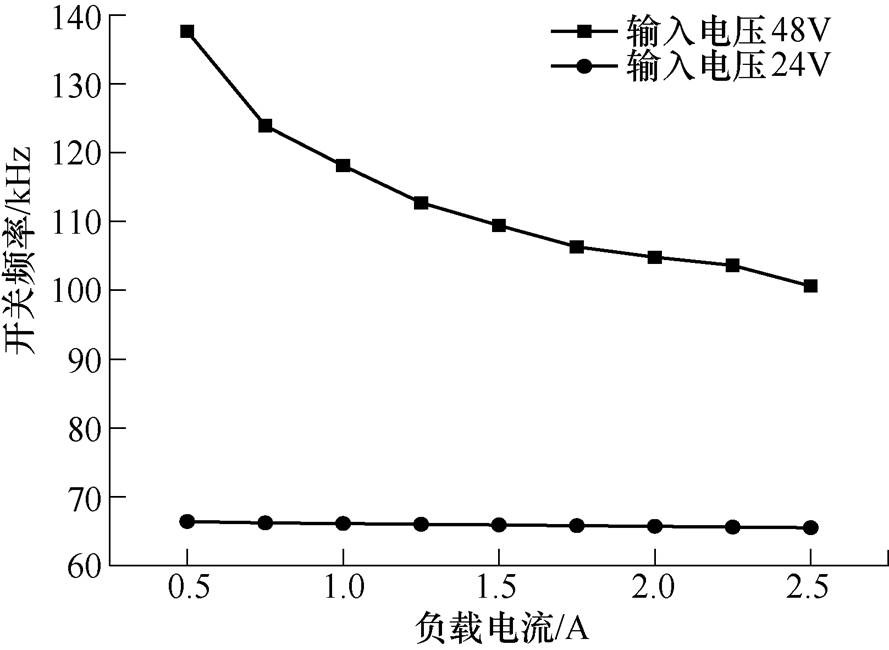
图19 不同负载下反向频率曲线
Fig.19 Frequency curves in backward operation at different load
图20为在满载情况下,FHA等效模型下的理论增益与实际正反向实验电压增益曲线对比。从图20中明显看出,提出的变换器的实际增益比理论增益高,这是因为FHA等效模型只是一种近似的分析方法,只考虑了基波的作用,忽略了其他高次谐波的作用。由于变压器实际电压比和理论电压比有差别,实际元器件数值和设计值也存在差异,所以正反向实际增益会存在误差,但已经较好地符合理论分析。
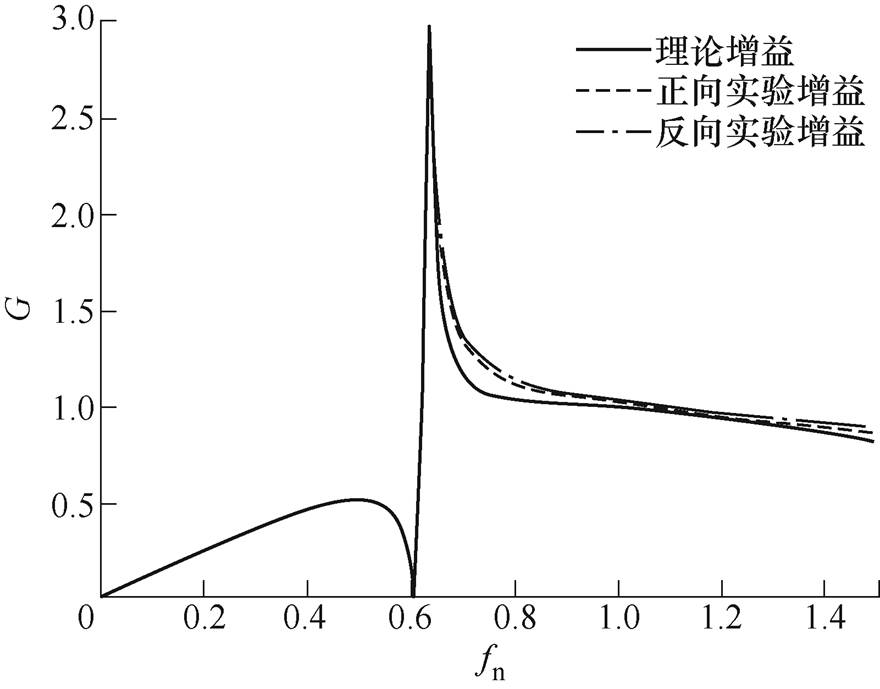
图20 理论增益与实际增益比较
Fig.20 The normalized gain comparison of the FHA method and the measured results
本文提出了一种高增益对称双向LCLC谐振变换器,无论正反向均有传统LLC谐振变换器的特性。本文通过建立基波等效模型,推出增益公式,分析提出的变换器的电压增益特性,阐明了各个参数对增益变化的影响,并研究了励磁电感对增益的影响,给出参数设计过程。最后制作了一台500W的实验样机来验证理论分析和所提拓扑的优越性。实验证明,在宽电压输入和全载情况下,所有的一次侧MOS管都能实现ZVS,所有的二次侧整流二极管可以实现ZCS,而且可以提高额定输入输出时的效率。从实验结果可以看出,所提出的拓扑可以作为高增益高效率的双向DC-DC变换器应用的最优选择之一。
参考文献
[1] Deng Junjun, Mi C C, Ma Ruiqing, et al. Design of LLC resonant converters based on operation-mode analysis for level two PHEV battery chargers[J]. IEEE/ASME Transactions on Mechatronics, 2014, 20(4): 1-12.
[2] Moon D, Park J, Choi S. New interleaved current-fed resonant converter with significantly reduced high current side output filter for EV and HEV appli- cations[C]//2014 International Power Electronics Conference (IPEC-Hiroshima 2014 ECCE-ASIA), Hiroshim, Japan, 2014: 1394-1399.
[3] 江添洋, 张军明, 汪槱生. 同步控制双向LLC谐振变换器[J]. 电工技术学报, 2015, 30(12): 87-96.
Jiang Tianyang, Zhang Junming, Wang Yousheng. Synchronous control bidirectional LLC resonant converter[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 87-96.
[4] Tsang C W, Foster M P, Stone D A, et al. Analysis and design of LLC resonant converters with capacitor-diode clamp current limiting[J]. IEEE Transactions on Power Electronics, 2015, 30(3): 1345-1355.
[5] 王暄, 王广柱, 孙晓伟, 等. 具有宽范围输出电压的三电平半桥LLC谐振变换器控制策略[J]. 电工技术学报, 2017, 32(21): 24-33.
Wang Xuan, Wang Guangzhu, Sun Xiaowei, et al. Research on control strategy of three-level half-bridge LLC resonant converter with wide output voltage range[J]. Transactions of China Electrotechnical Society, 2017, 32(21): 24-33.
[6] 杨玉岗, 吴晗, 关婷婷. 交错并联LLC谐振变换器的磁集成均流特性[J]. 电工技术学报, 2019, 34(12): 2529-2538.
Yang Yugang, Wu Han, Guan Tingting. Magnetic integrated current sharing characteristics of inter- leaved LLC resonant converter[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2529- 2538.
[7] Yang Bo, Lee F C, Zhang A J, et al. LLC resonant converter for front end DC/DC converter[C]//IEEE Applied Power Electronics Conference & Exposition, Dallas, TX, USA, 2002: 1108-1112.
[8] Lu Bing, Liu Wendou, Liang Yan, et al. Optimal design methodology for LLC resonant converter[C]// Twenty-First Annual Applied Power Electronics Conference and Exposition, Dallas, TX, USA, 2006: 533-538.
[9] Hu Zhiyuan, Qiu Yajie, Liu Yanfei, et al. A control strategy and design method for interleaved LLC converters operating at variable switching frequ- ency[J]. IEEE Transactions on Power Electronics, 2014, 29(8): 4426-4437.
[10] Feng Weiyi, Lee F C, Mattavelli P. Optimal trajectory control of burst mode for LLC resonant converter[J]. IEEE Transactions on Power Electro- nics, 2013, 28(1): 457-466.
[11] Yang Gang, Dubus P, Sadarnac D. Double-phase high-efficiency, wide load range high-voltage/low- voltage LLC DC/DC converter for electric/hybrid vehicles[J]. IEEE Transactions on Power Electronics, 2015, 30(4): 1876-1886.
[12] Guo Zhiqiang, Sha Deshang, Liao Xiaozhong. Hybrid phase-shift-controlled three-level and LLC DC-DC converter with active connection at the secondary side[J]. IEEE Transactions on Power Electronics, 2015, 30(6): 2985-2996.
[13] Jung J, Kim H, Ryu M, et al. Design methodology of bidirectional CLLC resonant converter for high- frequency isolation of DC distribution systems[J]. IEEE Transactions on Power Electronics, 2013, 28(4): 1741-1755.
[14] Beiranv R, Zolghadri M R, ZolghadriM R, et al. Using LLC resonant converter for designing wide- range voltage source[J]. IEEE Transactions on Industrial Electronics, 2011, 58(4): 1746-1756.
[15] Sun Xiaofeng, Li Xiaohua, Shen Yanfeng, et al. A dual-bridge LLC resonant converter with fixed- frequency PWM control for wide input appli- cations[J]. IEEE Transactions on Power Electronics, 2016, 32(1): 1-1.
[16] 陈启超, 纪延超, 王建赜. 双向CLLLC谐振型直流变压器的分析与设计[J]. 中国电机工程学报, 2014, 34(18): 2898-2905.
Chen Qichao, Ji Yanchao, Wang Jianze. Analysis and design of bidirectional CLLLC resonant DC-DC transformer[J]. Proceedings of the CSEE, 2014, 34(18): 2898-2905.
[17] Liang Zhigang, Guo Rong, Wang Gangyao, et al. A new wide input range high efficiency photovoltaic inverter[C]//IEEE Energy Conversion Congress and Exposition, Atlanta, GA, USA, 2010: 2937-2943.
[18] 李菊, 阮新波. 全桥LLC谐振变换器的混合式控制策略[J]. 电工技术学报, 2013, 28(4): 72-79.
Li Ju, Ruan Xinbo. Hybrid control strategy of full bridge LLC converter[J]. Transactions of China Electrotechnical Society, 2013, 28(4): 72-79.
[19] Zong Sheng, Fan Guoxing, Yang Xiaobo. Double voltage rectification modulation for bidirectional DC/DC resonant converters for wide voltage range operation[J]. IEEE Transactions on Power Electro- nics, 2018, 34(7): 6510-6521.
[20] Chen Wei, Rong Ping, Lu Zhengyu. Snubberless bidirectional DC-DC converter with new CLLC resonant tank featuring minimized switching loss[J]. IEEE Transactions on Industrial Electronics, 2010, 57(9): 3075-3086.
[21] Chen Yang, Wang Hongliang, Hu Zhiyuan, et al. LCLC resonant converter for hold up mode oper- ation[C]//Energy Conversion Congress & Exposition, Montreal, QC, Canada, 2015: 556-562.
Research on High-Gain Symmetric Bidirectional LCLC Resonant Converter
Abstract The input and output voltage ranges of the bidirectional DC-DC converter are too small. Therefore, a high gain symmetric bidirectional LCLC resonant converter is proposed. The proposed resonant converter does not use the magnetizing inductor of transformer to participate in resonance, but connects a parallel LC branch on the primary side of the transformer. Thus, the converter still has a large gain with a large inductor ratio, which takes into account the efficiency and a wide gain range at the resonance point. The proposed resonant converter can also ensure the soft switching both on the primary and secondary sides, and realize the symmetric bidirectional operation. This paper establishes the fundamental wave equivalent model by the first harmonic approximation method, obtains the gain formula, and analyzes the effect of resonant parameters on DC gain characteristics. Finally, a bidirectional experimental prototype of 100-200V/24-48V 500W was built, and the experimental results verified the theoretical analysis and the proposed topology. The maximum efficiency of the prototype could reach 96.3%.
keywords:Bidirectional LCLC resonant converter, parallel LC branch, high gain, soft switching
DOI: 10.19595/j.cnki.1000-6753.tces.190701
中图分类号:TM46
杨玉岗 男,1967年生,博士,教授,博士生导师,研究方向为电力电子技术及磁集成技术。E-mail: 447987957@qq.com
赵金升 男,1993年生,硕士研究生,研究方向为电力电子技术及磁集成技术。E-mail: 1262517923@qq.com(通信作者)
收稿日期 2019-06-12
改稿日期 2019-10-17
国家自然科学基金项目(U1510128),辽宁省特聘教授项目(55770007008)和辽宁省教育厅重点实验室基础研究项目(LZ2015045)资助。
(编辑 陈 诚)