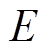）。当d轴绕组中流过电流id时，因ed=0，其对电磁转矩无贡献；id产生的磁动势对转子永磁体磁场的影响即d轴电枢反应有助磁或去磁效果。其中，id＜0时为去磁，反之为助磁。当q轴绕组中流过电流iq时，将会产生电磁转矩，对转子永磁体磁场的影响很小。其中，iq＞0时q轴绕组产生顺时针方向电磁转矩，推动转子逆时针旋转，反之顺时针旋转。其电磁转矩表达式为摘要 无刷直流电机由于非正弦的主磁场分布和反电动势波形，在方波电流驱动下产生较大转矩脉动。为此提出一种基于转子永磁体磁场定向的转矩脉动抑制方法。首先，通过分析无刷直流电机转子永磁体磁场定向dq同步旋转坐标系下的等效模型，得出该坐标系下d轴电枢反应和电磁转矩各自取决于dq轴电流的结果；其次，给出了以变换前后绕组产生的d轴电枢反应和电磁转矩不变为原则的三相电流和dq轴电流之间变换方法；最后，利用该变换方法，得到所需dq轴电流对应的三相电流，并对该电流进行闭环控制，进而实现无助磁和去磁的瞬时恒定转矩控制。所提方法通过Matlab仿真和DSP实验验证了其可行性和有效性。
关键词：无刷直流电机 转子永磁体磁场定向 转矩脉动抑制 d轴电枢反应
无刷直流电机（Brushless Direct Current Motor, BLDCM）以其高功率密度、大输出转矩及简单的内部结构等特点在数控机床、电动汽车以及航空航天等领域得到广泛的应用[1-3]；但是由于非正弦的主磁场分布和反电动势波形，在传统的方波电流驱动下将产生较大的转矩脉动。转矩脉动使得电机在其运行过程中容易产生电机噪声、扭转振动等诸多问题[4]，影响其在高精度、高稳定性场合上的应用[5-6]。
为解决上述问题，国内外学者通过采用新型拓扑结构调节直流母线电压[7-9]，采用不同调制方式[10-13]或采用直接转矩控制[14-18]等多种控制方法来有效抑制无刷直流电机的转矩脉动。文献[7]通过使用准Z源网络与开关选择电路为逆变器直流侧提供电压，以便通过调整母线电压保证非换相相电流维持不变来抑制换相转矩脉动。文献[8]采用Cuk电路与开关选择电路提供直流侧母线电压并采用中点钳位（Neutral Point Clamped, NPC）电路作为主电路来减少电流谐波从而抑制转矩脉动。文献[9]采用三电平逆变器作为主电路来减小电流谐波，并对单端初级电感变换器（Single Ended Primary Inductor Converter, SEPIC）电路进行改进后与开关选择电路结合来提供直流电压抑制转矩脉动。文献[10]引入了合成电流变量并得到其与非换相相电流的关系，根据合成电流变量正比于电机瞬时转矩的特点，通过对非换相相电流进行控制进而控制瞬时转矩，并改变调制方式重新分配占空比来达到抑制转矩脉动的目的。文献[11]通过相电流整形避免因反电动势（Electro- motive Force, EMF）非理想造成的转矩脉动并推导换相期间占空比关系，采用双闭环调速方法抑制转矩脉动。文献[12]考虑电流滞后对转矩脉动的影响并提出超前换相控制策略，推导出提前换相时间的表达式。文献[13]提出反电动势空间矢量定向方法，通过控制与瞬时转矩成正比的q轴电流来抑制转矩脉动。文献[14]根据霍尔信号划分扇区并给出最优导通相电压矢量选择表，也提出了转矩观测的方法，实现了无刷直流电机的直接转矩控制。文献[15]给出了不同扇区零电压矢量的定义方式并依此改进了电压矢量查询表，提出一种基于零电压矢量的适用于两相导通的直接转矩控制策略。文献[16]提出滞环结合脉冲宽度调制（Pulse Width Modulation, PWM）方式下的直接转矩控制技术，解决了因采用一个周期一个电压矢量和低电感引起的较大转矩脉动问题，同时通过在换相和非换相期间设置不同占空比来抑制换相转矩脉动。文献[17]在换相期间将两相和三相导通方式结合起来达到换相转矩脉动抑制的目的，并给出了与之相对应的开关管状态查询表。文献[18]提出无磁链环的直接转矩控制方案，其瞬时转矩实际值通过查询离线获得的线反电动势常数数据库后经计算得到。另外，相关文献提出适用于回馈制动与发电状态的转矩脉动控制策略，文献[19]针对回馈制动过程提出，在120°开关管导通期间前30°PWM、中间60°关断、后30°PWM的方式，在实现高效回馈制动的同时可以做到抑制非导通相续流从而达到抑制转矩脉动的效果。文献[20]考虑了无刷直流电机的发电状态，提出了一种运用于电动状态与发电状态的电流滞环控制策略，在其换相期间将非换相的相电流控制在一定阈值范围来抑制转矩脉动。
本文提出一种转子永磁体磁场定向的无刷直流电机转矩脉动抑制方法，该方法以转子永磁体磁场定向dq同步旋转坐标系下的无刷直流电机等效模型为基础，利用其dq轴电枢电流各自决定d轴电枢反应和电磁转矩的特点，实现无刷直流电机无助磁去磁的瞬时恒定转矩控制。为此，以变换前后绕组产生的d轴电枢反应和电磁转矩不变为原则，把所需dq轴电枢电流变换到三相静止绕组电流，并对该电流进行闭环控制。所提方法通过相应Matlab数值仿真和DSP驱动实验，验证了其可行性和有效性。
所提出的转矩脉动抑制方法以无刷直流电机的dq同步旋转坐标系下等效模型为前提。图1给出了其dq同步旋转坐标系下等效模型示意图。图中，定子侧的dq轴绕组在空间上正交，且以同步转速w 即转子永磁体磁场旋转速度逆时针旋转。其中，d轴绕组始终位于转子永磁体磁场正方向位置，q轴绕组位于相对d轴绕组空间上超前90°电角度的位置。该模型与正弦波永磁同步电机的区别在于，转子永磁铁产生的磁场在沿定子内表面的分布为非正弦波。由图1可知，随着转子旋转，转子永磁体磁场与d轴绕组交链的主磁链yd始终维持最大值（记为ymax），且转子永磁体磁场在d轴绕组产生的感应电动势ed始终为0。同理，转子永磁体磁场与q轴绕组交链的主磁链yq始终为0，转子永磁体磁场在q轴绕组产生的感应电动势eq始终维持最大值（记为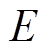）。当d轴绕组中流过电流id时，因ed=0，其对电磁转矩无贡献；id产生的磁动势对转子永磁体磁场的影响即d轴电枢反应有助磁或去磁效果。其中，id＜0时为去磁，反之为助磁。当q轴绕组中流过电流iq时，将会产生电磁转矩，对转子永磁体磁场的影响很小。其中，iq＞0时q轴绕组产生顺时针方向电磁转矩，推动转子逆时针旋转，反之顺时针旋转。其电磁转矩表达式为
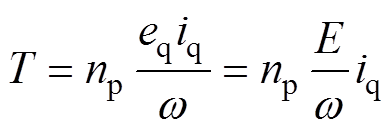（1）式中，np为无刷直流电机的极对数；w 为转子电角速度（rad/s）。
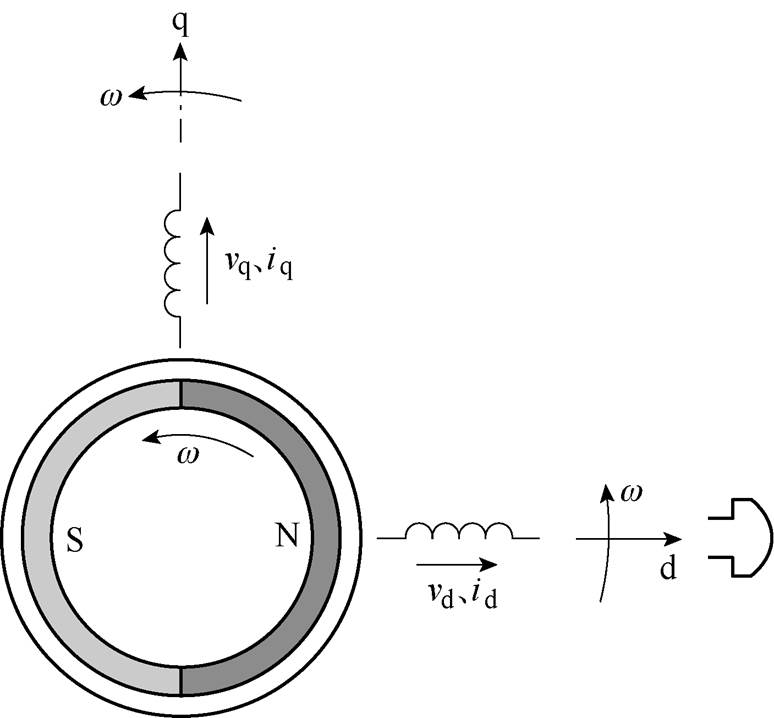
图1 dq同步旋转坐标系下的等效模型示意图
Fig.1 Schematic diagram of equivalent model in d, q synchronous rotation coordinate system
由以上分析可知，id和iq各自作用于转子永磁体磁场和电磁转矩，可实现无刷直流电机的磁链与转矩的解耦控制。具体为，若能够做到iq始终保持恒值，则可以实现平滑的瞬时恒定转矩控制；若能够做到id=0，则可实现无去磁和助磁控制；甚至通过id＜0，可实现弱磁升速。
正弦波永磁同步电机中，对称三相绕组到dq轴绕组的变换以变换前后的多相绕组产生的合成磁势不变为原则。基于此原则，能够做到变换前后功率和转矩不变，且绕组变换所需变换矩阵为正交矩阵。对于无刷直流电机，因转子永磁体磁场在空间上的非正弦分布，致各相绕组磁链与电动势为非正弦波，经过三相空间矢量合成得到的合成磁链与合成电动势矢量轨迹并非圆形，其空间矢量的旋转速度也与转子转速不同步且非恒值，得不到图1所示等效模型。
为此，本文提出以变换前后绕组产生的d轴电枢反应和电磁转矩不变为原则，把每相绕组的电流变换到dq轴绕组。以A相绕组为例，如图2所示，基于d轴电枢反应不变原则，变换前后的d轴电枢反应为
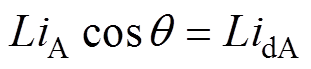（2） 式中，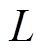
为一相绕组的等效电感；
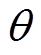为当前时刻转子永磁体磁场的位置；iA、idA分别为A相电流和其变换到d轴后的电流。
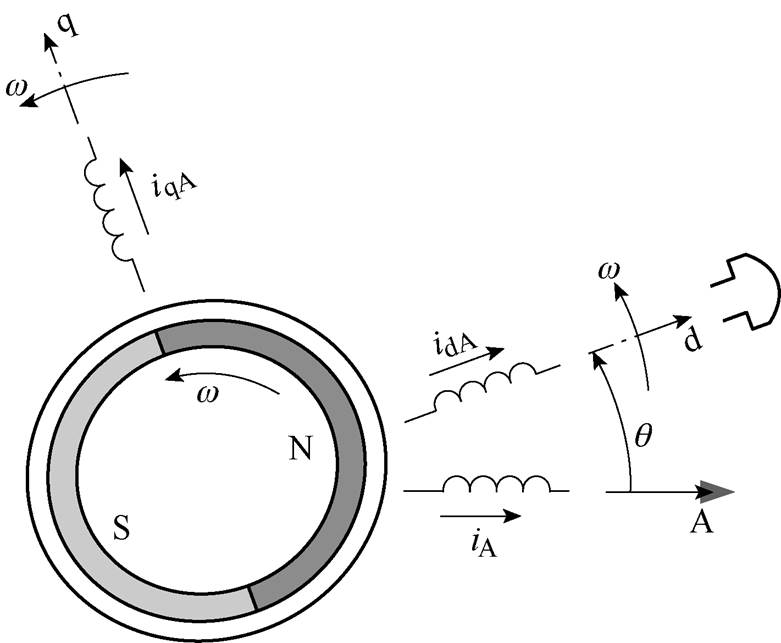
图2 A相绕组与dq轴绕组之间关系示意图
Fig.2 Diagram of relationship between phase A winding and axis d and q winding
基于电磁转矩不变原则，变换前后的电磁转矩为
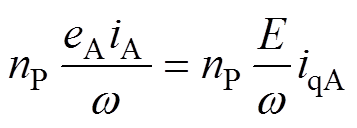（3）式中，eA为当前时刻A相绕组的反电动势；iqA为A相电流变换到q轴后的电流。
由式（2）和式（3），可得A相绕组电流和其变换到dq轴的电流之间关系，有
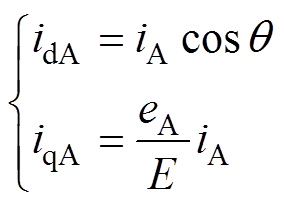（4）同理，可得到B、C两相绕组电流变换到dq轴后的电流。
在理想方波驱动下，无刷直流电机的理想反电动势和方波电流波形如图3所示。根据方波驱动方式的特点，可将转子位置分成6个扇区，其标号分别记为Ⅰ～Ⅵ。在该理想梯形反电动势和方波电流驱动下，无刷直流电机能够产生无转矩脉动的恒定电磁转矩，在此着重分析此时的d轴电枢反应。
图4给出了三相绕组通入如图3所示的理想方波电流时的转子永磁体磁通与气隙合成磁通关系。图中，主磁通曲线的每个点到圆心之间的距离代表对应转子位置下转子永磁铁产生的每极磁通量；气隙合成磁通曲线的每个点到圆心之间距离代表对应转子位置下定子三相电流产生的d轴电枢反应磁通与主磁通之和。
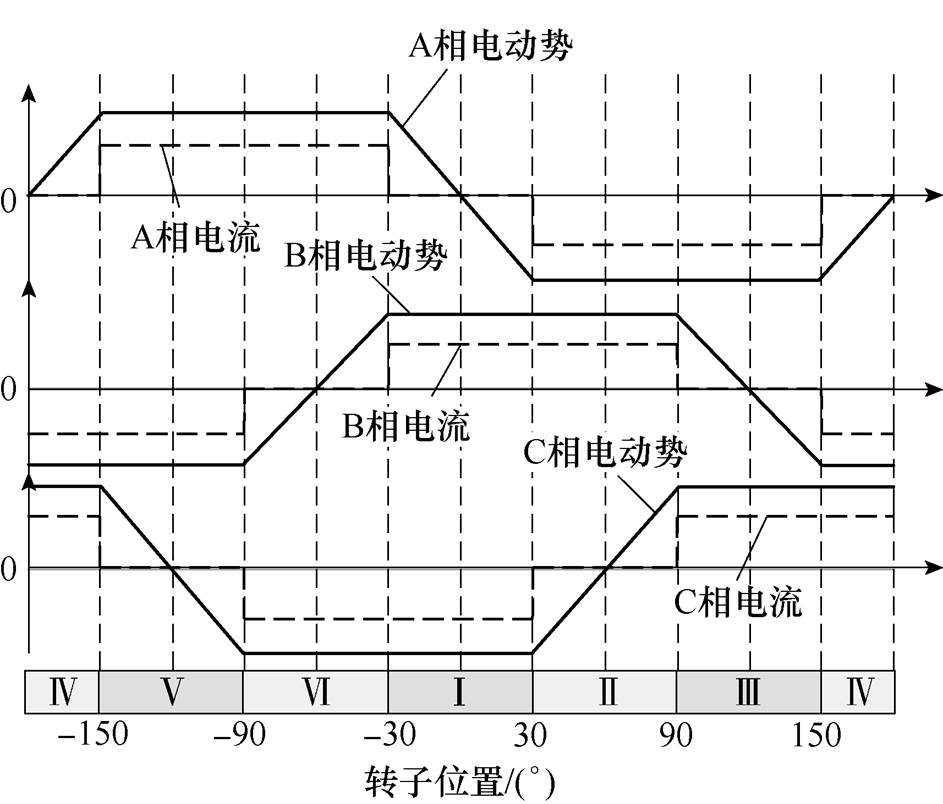
图3 理想反电动势与方波电流波形
Fig.3 Ideal back EMF and square current waveforms
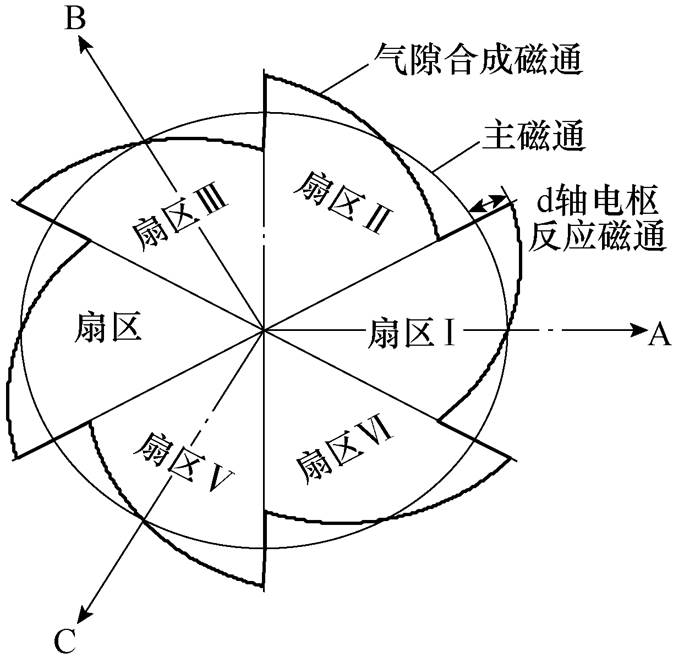
图4 理想方波驱动下，转子永磁体磁通与气隙合成磁通的关系
Fig.4 The relationship between the rotor permanent magnet flux and the air gap composite flux driven under the ideal square waveform
产生d轴电枢反应磁通的id为
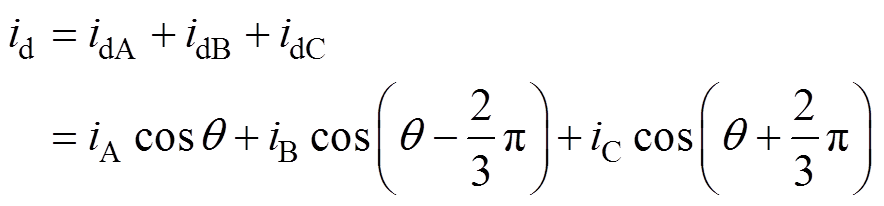（5）由图4可看出，随着无刷直流电机的正向旋转，每个扇区都会经历由去磁到助磁的单调变化过程。如转子转到30°即刚进入第Ⅱ扇区时，因B相绕组轴线与转子永磁体磁场恰好正交，B相电流不会产生d轴方向磁场，使得A、B相电流产生的d轴电枢反应磁场仅由A相电流产生。此时，因A相电流为负，且转子位置角为30°，故电枢反应磁场的d轴分量与转子永磁体磁场方向相反，为去磁。随着转子位置角增加，A相电流产生的d轴电枢反应（去磁）逐渐减小，而B相电流产生的d轴电枢反应（助磁）逐渐增加，使得在60°转子位置时，A、B相电流产生的d轴电枢反应既不助磁又不去磁，而在90°转子位置时助磁效果最强。
在已知dq轴电流的前提下，根据1.2节提供的绕组变换方法，易计算得到对应的三相电流。根据式（4）和式（5），可列出三相电流的联立方程为
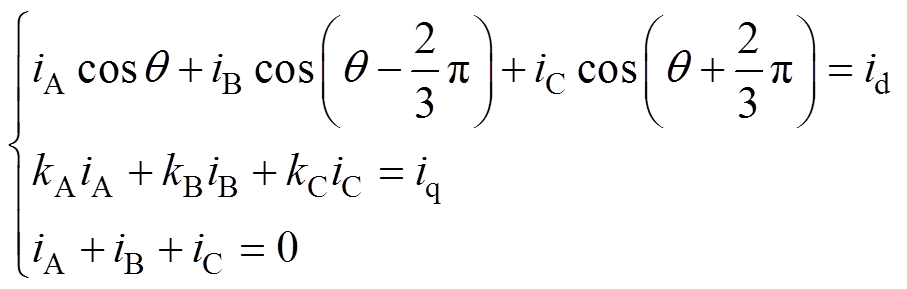（6）式中，kA、kB和kC分别为各自绕组的反电动势eA、eB、eC与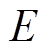的比值，是随转子位置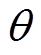变化的物理量，且满足
。
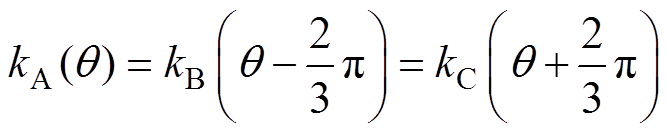由式（6），可得三相电流与dq轴电流之间的表达式为
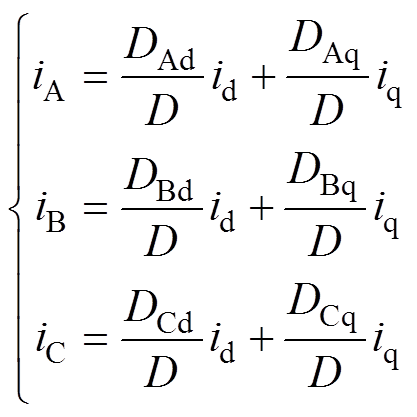（7）其中
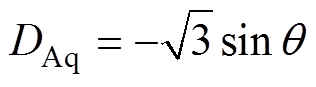
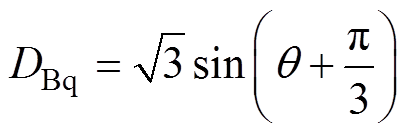
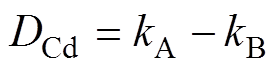
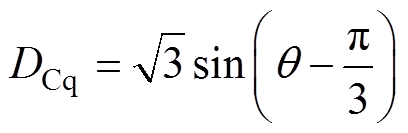
图5给出了理想梯形反电动势下，d轴电流等于0即无助磁和去磁时的三相电流波形。为便于比较，同时给出了理想方波电流波形。理想方波电流最大值为1/2的q轴电流。由图5可知，为了在任意转子位置处都实现无助磁和去磁，无刷直流电机需要运行于三相导通方式。以第Ⅱ扇区为例，当刚进入该扇区即转子转到30°时，B相绕组与转子永磁体磁场正交，B相电流不产生d轴电枢反应，而A相电流为负，产生去磁效果的d轴电枢反应，为抵消该电枢反应，须给C相通入负向电流；随着转子旋转，B相电流产生助磁效果的d轴电枢反应，且逐渐增强，致使C相产生助磁所需电流逐渐减小；当转子转到60°即C相绕组处于d轴位置时，C相电流为0；转子继续旋转即转子位置超过60°时，A相电流产生的去磁效果逐渐减弱，C相需通入产生去磁效果的正向电流。
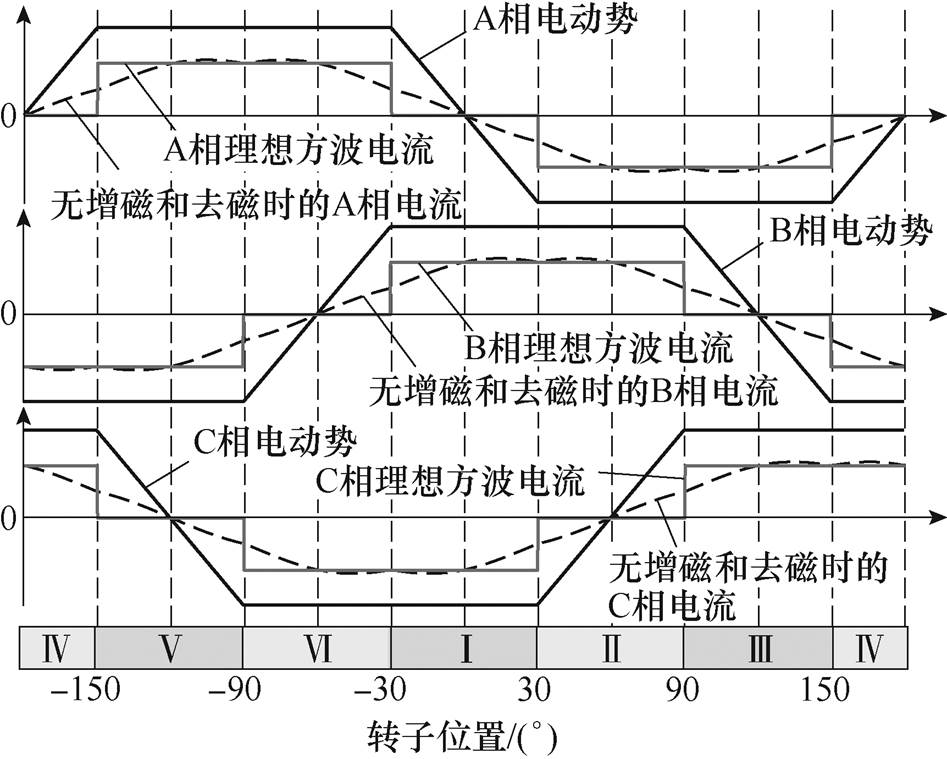
图5 理想梯形反电动势下，无助磁和去磁所需三相电流波形
Fig.5 Required three-phase current waveforms for no magnetization and demagnetization under ideal trapezoid back EMF
基于上述理论，构建如图6所示的基于转子永磁体磁场定向的无刷直流电机控制系统。系统中，q轴参考电流由速度控制器直接给出；三相参考电流由式（7）计算得到。根据图5给出的三相电流波形的特点，重新划分6个扇区，如图7所示。每个扇区内的三相电流中，其中一相总是电流近似不变，而其余两相总是电流快速上升和下降。此时对电流上升或下降对应的相电流与剩余一相电流进行相减得到新的两相电流，分别记为上升相和下降相，并对该两相进行电流闭环控制。如在第Ⅱ扇区，A、B相电流相减构成上升相，A、C相电流相减构成下降相。为减少开关损耗，令每个扇区仅有两个开关管进行PWM，各个扇区对应开关管状态见表1。表中，开关管状态中的每个位分别为A、B、C相上下桥臂开关管的状态；0和1分别表示截止和导通，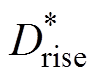
和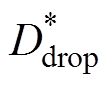
分别表示该开关管进行占空比为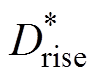和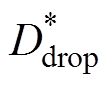的PWM。此外，图6中的占空比补偿单元用于获得电流闭环控制中反电动势相关的占空比，由转子位置q 查询反电动势常数后，再乘以转速得到。
图6 整体系统框图
Fig.6 The block diagram of the control system
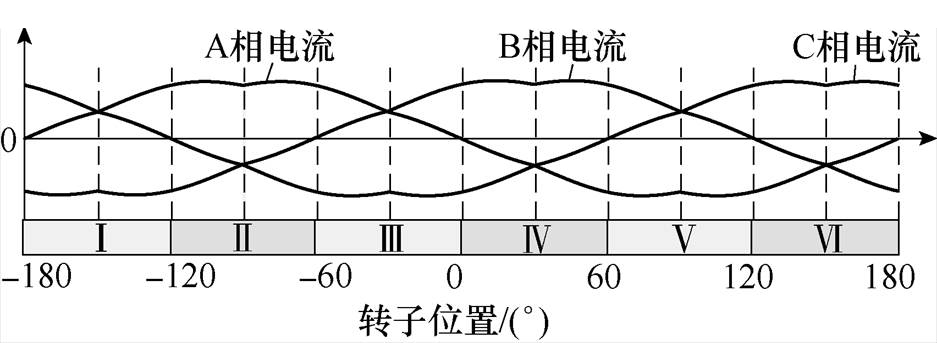
图7 新的扇区划分
Fig.7 New sector division
以第Ⅲ扇区为例，上升相电流与下降相电流分别为B、A两相电流与C相电流之差，进行PWM的两个开关管分别为B、A两相的上桥臂开关管，且C相下桥臂开关管恒通。此时，无刷直流电机的三相电压方程为
表1 各扇区的开关状态查询
Tab.1 Switching table for each sector
扇区S开关管状态 Ⅰ Ⅱ Ⅲ Ⅳ Ⅴ Ⅵ
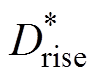（8）式中，和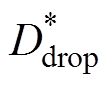分别为B、A相上桥臂开关管的占空比；Udc为功率变换电路的直流母线电压；Un为无刷直流电机中性点对直流母线负极的电压；R和L分别为每相绕组的电阻和等效电感。
由式（8）可得，上升、下降相电流的微分方程为
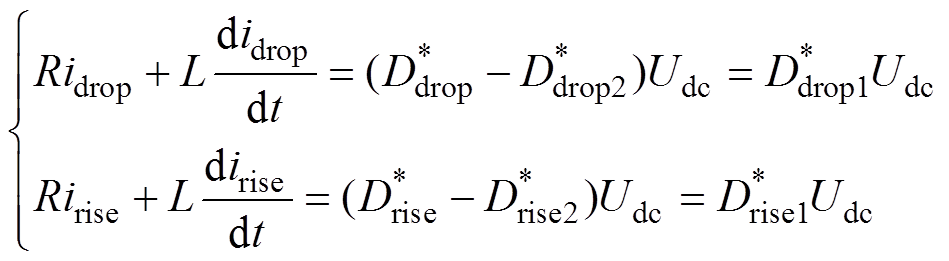（9）式中，
、
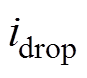分别为上升、下降相电流；
、
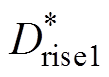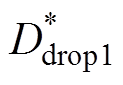分别为上升、下降相阻感压降对应占空比；
、
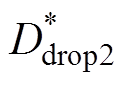分别为上升、下降相反电动势对应占空比，即
、
。
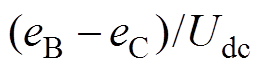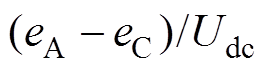由式（9）可知，若分别对上升、下降两相电流进行PI控制得到
、
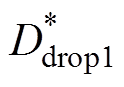，再分别与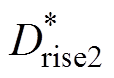
、
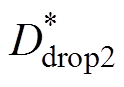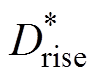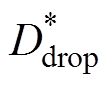相加可获得所需上升、下降相电流对应的和。其中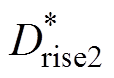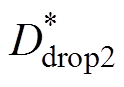，、由图6中的占空比补偿单元获得。因无刷直流电机的三相电流之和始终为零，使得所需三相电流和上升、下降相电流之间存在一一对应关系，故由上升、下降相电流取代三相电流进行闭环控制，可有效减小进行PWM的开关管数量。
实验系统中的电机为5对极三相无刷直流电机。具体电机参数为：额定电压、额定转速和额定功率分别为300V、3 000r/min和400W；定子侧相电阻和等效电感分别为3.05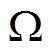
和17mH。仿真及实验中的电流采样和控制周期皆为50ms，速度控制周期为500ms，其控制实验系统如图8所示。功率变换电路中的直流母线电压为300V，转子位置信息由分辨率为2048PPR/r的增量式光电编码器获取，数字信号处理（Digital Signal Processor, DSP）芯片为TMS320F28335-150，负载采用Magtrol公司的磁滞测功机（HD-705-8NA-0100型），由同一家公司的DSP6001型控制器提供独立于转速的负载转矩。
图8 无刷直流电机控制实验系统
Fig.8 Control experiment system of BLDCM
实验用无刷直流电机的实际反电动势波形不会是理想梯形波，故通过离线实验检测得到了如图9所示的三相反电动势波形，给出了d轴电流为0即无助磁和去磁时的三相电流波形。由图9可看出，其与理想梯形反电动势下的三相电流波形（见图5、图7）差异较大。下面以差异明显的-120°和-90°两处位置为例，理论分析下反电动势波形不一致引起的三相电流波形的区别。
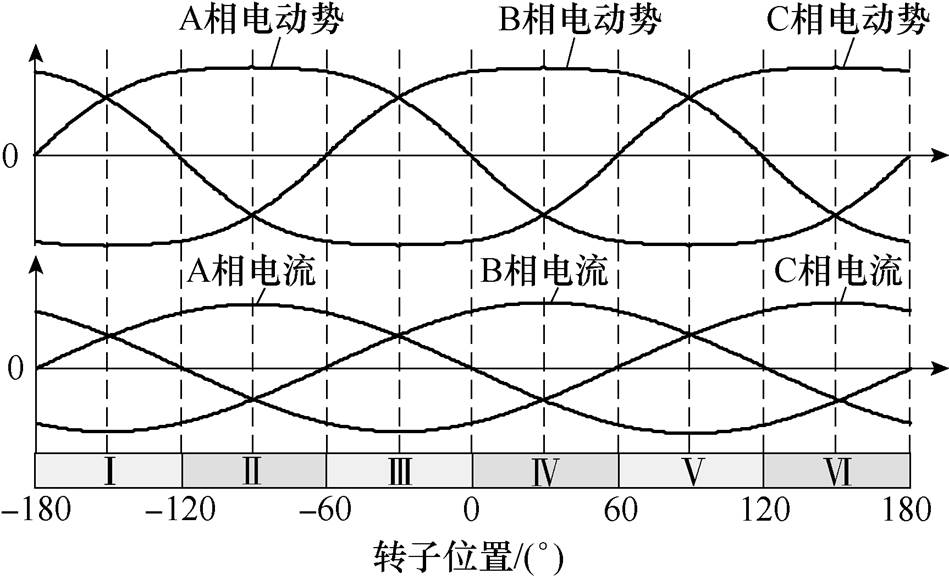
图9 实际反电动势下，无助磁和去磁所需三相电流波形
Fig.9 Required three-phase current waveform for no magnetization and demagnetization under real back EMF
在-120°转子位置处，把q=-120°代入式（7）可得三相电流分别为
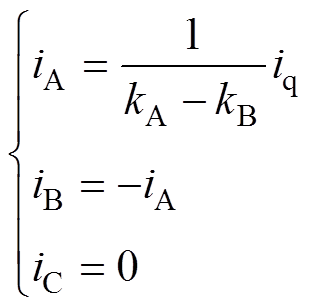（10）在理想梯形反电动势下，kA=1、kB=-1，代入式（10）可得iA=-iB=0.5iq；而在实际反电动势下，kA和kB的绝对值小于等于1且接近1，代入式（10）可得，iA和iB的绝对值大于等于0.5iq且接近0.5iq。
在-90°转子位置处，把q =-90°代入式（7）可得三相电流分别为
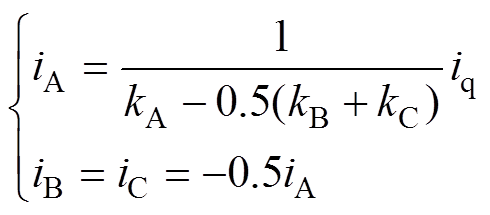（11）在理想梯形反电动势下，kA=1、kB=kC=-1，代入式（11）可得，iA=0.5iq，与-120°位置处的iA相等；而在实际反电动势下，kA=1、kB和kC的绝对值明显小于1，使得-90°位置处的iA要明显大于-120°位置处。
图10、图11给出了转速分别为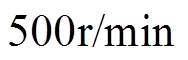
和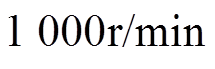
时，参考转矩由轻载阶跃增加到额定转矩（1.27N·m）再阶跃减小到轻载时的转子永磁体磁场定向电流闭环控制系统的仿真和实验结果。该仿真和实验的系统框图为图6中除速度环以外的电流内环控制系统。其中，d轴参考电流设定为0，q轴参考电流把参考转矩代入电磁转矩式（1）计算得到；三相参考电流根据式（7），离线获得DAq/D、DBq/D、DCq/D与转子位置q 之间的数值关系并制作数据库后代入q轴参考电流计算得到；电流闭环用的上升和下降相电流的计算与调制方法已在1.5节中阐述。作为仿真结果，分别给出了实际转矩、三相参考电流和实际电流及电压波形；而作为实验结果，分别给出了实际转矩、A相参考电流和实际电流及电压波形。仿真和实验结果中的电压为功率变换电路三相引出线与直流母线负极之间的电压。
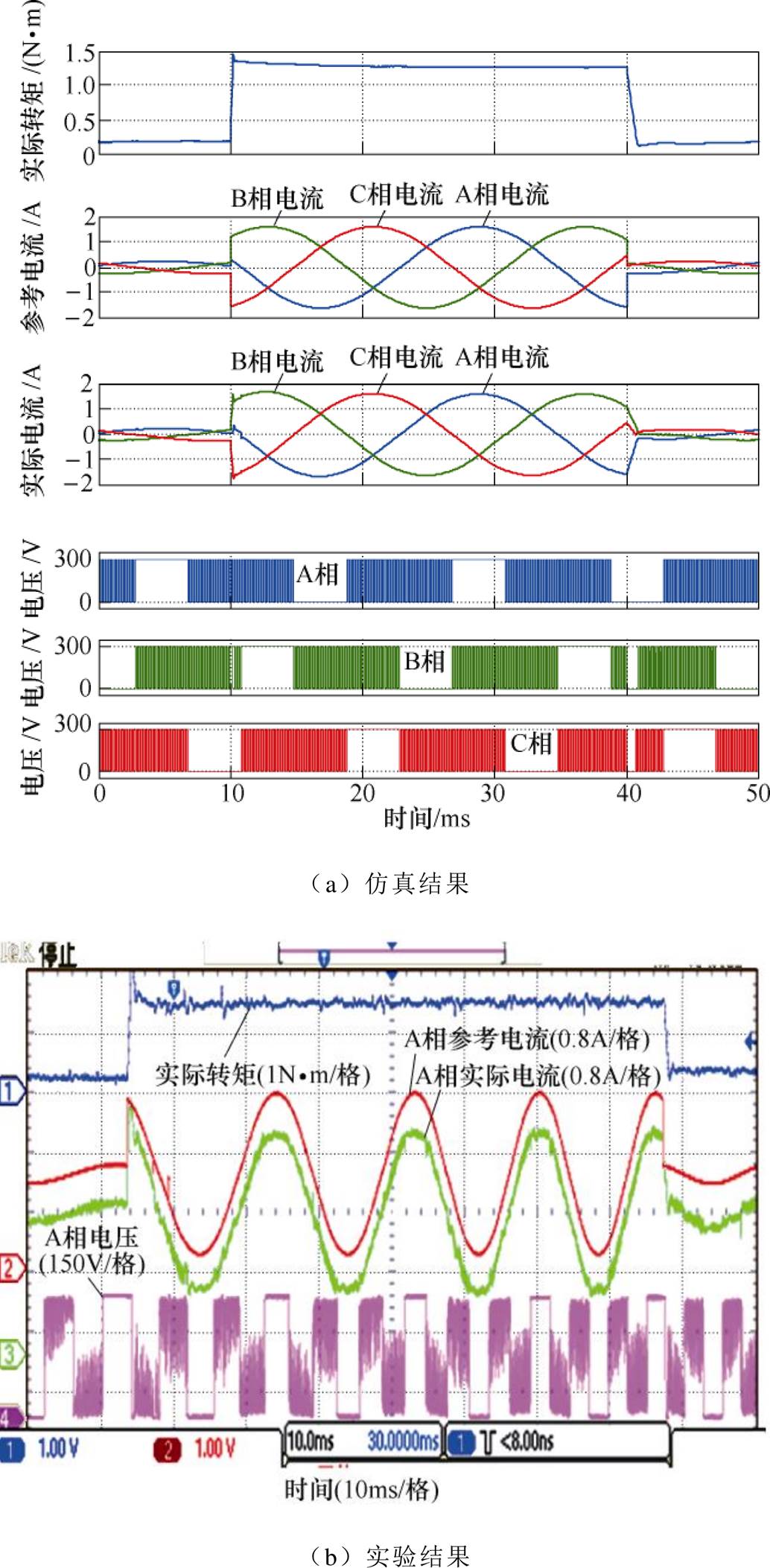
图10 阶跃参考转矩下的仿真及实验结果（500r/min）
Fig.10 The simulation and experiment results under the step reference torque (500r/min)
由图10、图11中的实际转矩波形可知，虽然参考转矩阶跃下降时因调制策略原因，实际转矩稍微滞后参考转矩，但是整体跟踪效果良好，且转矩较为平稳，转矩脉动小于10%，也不存在换相转矩脉动。由实际转矩波形还可看出，每次参考转矩阶跃变化时，都有一定超调，这是因为电流PI闭环控制本身存在超调的缘故。由图10、图11中的电流和电压波形可看出，功率变换电路中开关管的通断符合表1给出的调制方式。如图10a中的参考转矩阶跃增加时刻，该转子位置处于第Ⅲ扇区，B、C 相电流相减构成上升相，A、C相相减构成下降相，根据表1可知，A、B相上桥臂开关管进行PWM，因在该时刻B、C相参考电流分别阶跃增加和减小，使上升相参考电流阶跃增加很多，故B相上桥臂开关管出现如同B相电压所示的短暂全通。
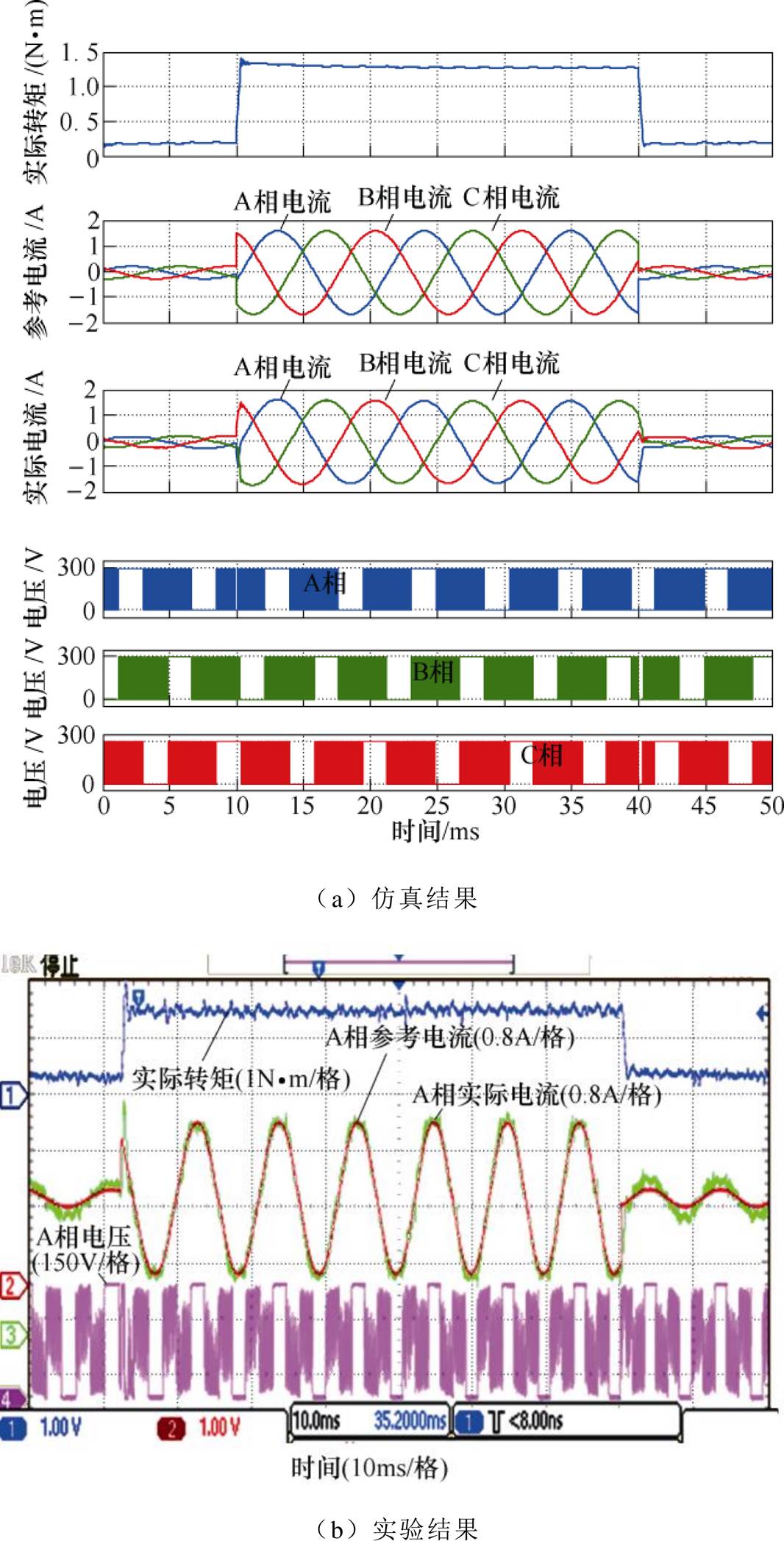
图11 阶跃参考转矩下的仿真及实验结果（1 000r/min）
Fig.11 The simulation and experiment results under the step reference torque (1 000r/min)
图12给出了一半额定负载和额定负载下，无刷直流电机由500r/min阶跃增加至1 000r/min，再阶跃减小至500r/min的双闭环速度控制系统实验结果。作为实验结果，分别给出了实际转速和转矩、A相实际电流及电压波形。由该实验结果可看出，速度PI控制有一定超调，速度控制整体效果良好。
本文利用转子永磁体磁场定向同步旋转坐标系下的dq轴电枢电流各自决定d轴电枢反应和电磁转矩的特点，提出一种能够实现无助磁和去磁的无刷直流电机转矩脉动抑制方法，并得出以下结论：
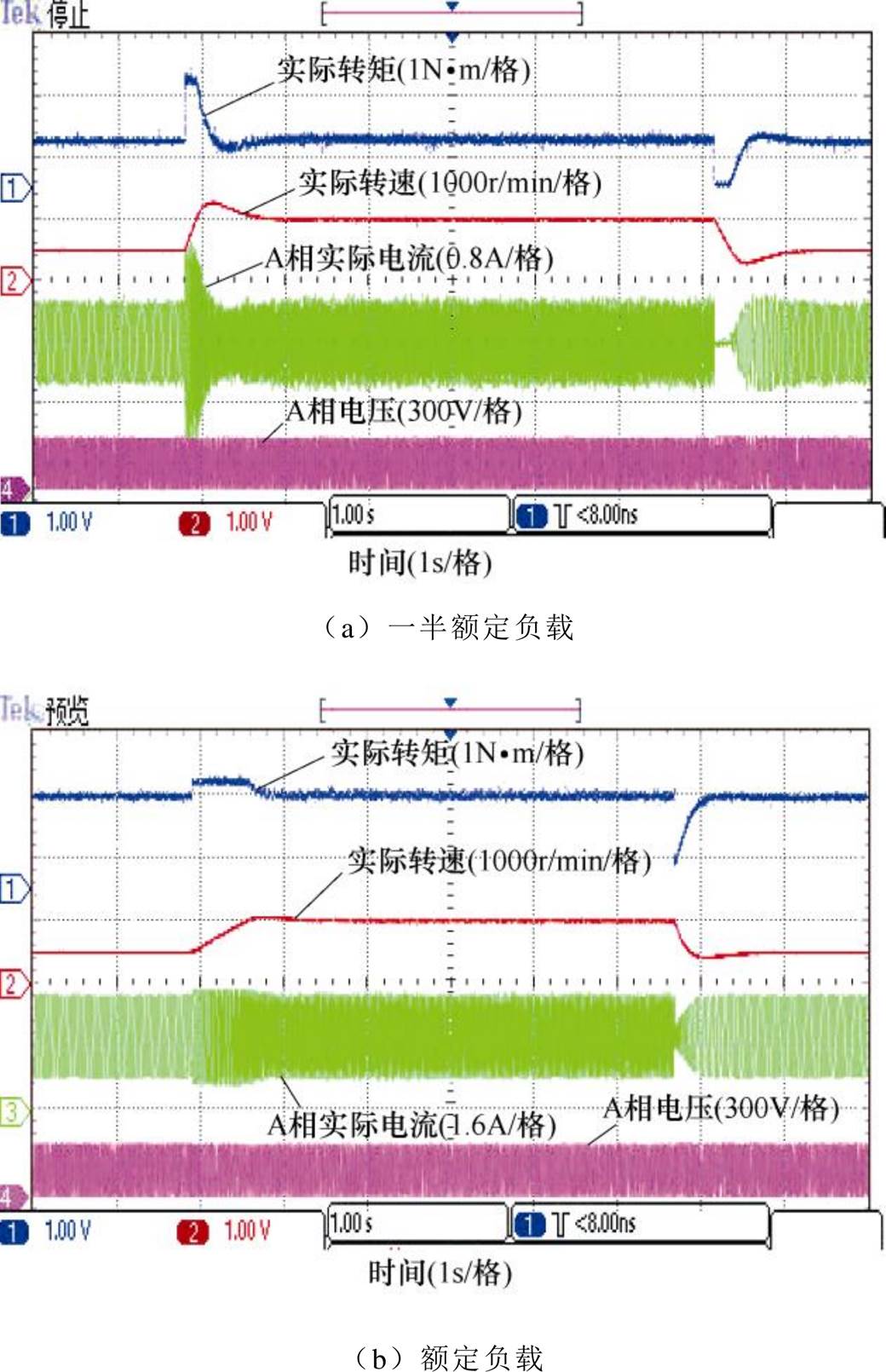
图12 阶跃参考转速下的实验结果（500→1 000→500r/min）
Fig.12 Experimental result under the step reference speed (500→1 000→500r/min)
1）转子永磁体磁场定向dq同步旋转坐标系中，d轴电流决定d轴电枢反应效果，对电磁转矩无贡献；q轴电流决定电磁转矩大小。
2）传统的坐标变换不能用于三相静止坐标系和转子永磁体磁场定向dq同步坐标系之间的变换。为此，本文以变换前后绕组产生的d轴电枢反应和电磁转矩不变为原则，进行了三相电流和dq轴电流之间的变换。
3）方波电流驱动下，不仅因非理想梯形反电动势和相电流非理想换相等因素引起较大转矩脉动，而且在电机旋转过程中，每个扇区都会重复由去磁到助磁的单调变化过程。
4）所提转子永磁体磁场定向转矩脉动抑制方法，无需外接额外硬件，仅需事先知道反电动势波形数据，具有结构简单、容易实现的特点。
参考文献
[1] Liu Yue, Hu Jianhui, Dong Shili. A torque ripple reduction method of small inductance brushless DC motor based on three-level DC converter[C]//2019 14th IEEE Conference on Industrial Electronics and Applications, Xi’an, China, 2019: 1669-1674.
[2] Sun Lihui, Yu Jun. Design of vector control system for brushless DC motor based on hall sensor[C]//2018 International Symposium on Communication Engin- eering & Computer Science, Hohhot, China, 2018: 416-422.
[3] 施晓青, 王晓琳, 徐同兴, 等. 高速无刷直流电机自寻优换相校正策略[J]. 电工技术学报, 2019, 34(19): 3997-4005.
Shi Xiaoqing, Wang Xiaolin, Xu Tongxing, et al. Self-optimization commutation correction strategy for high-speed brushless DC motor[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 3997-4005.
[4] Zhu Chong, Zeng Zhiyong, Zhao Rongxiang. Com- prehensive analysis and reduction of torque ripples in three-phase four-switch inverter-fed PMSM drives using space vector pulse-width modulation[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5411-5424.
[5] 姚绪梁, 鲁光旭, 王景芳, 等. 基于最优电流矢量的无刷直流电机换相转矩脉动抑制方法[J]. 中国电机工程学报, 2019, 39(14): 4272-4280, 4301.
Yao Xuliang, Lu Guangxu, Wang Jingfang, et al. Commutation torque ripple suppression method of brushless DC motor based on optimal current vector[J]. Proceedings of the CSEE, 2019, 39(14): 4272-4280, 4301.
[6] 朱熀秋, 郝正杰, 潘伟, 等. 无轴承无刷直流电机的研究、应用及发展趋势[J]. 电工技术学报, 2019, 34(21): 4428-4440.
Zhu Huangqiu, Hao Zhengjie, Pan Wei, et al. Research, application and development trends of bearingless brushless DC motor[J]. Transactions of China Elec- trotechnical Society, 2019, 34(21): 4428-4440.
[7] 夏鲲, 朱琳玲, 曾彦能, 等. 基于准Z源网络的永磁无刷直流电机换相转矩脉动抑制方法[J]. 中国电机工程学报, 2015, 35(4): 971-978.
Xia Kun, Zhu Linling, Zeng Yanneng, et al. Researches on the method of suppressing com- mutation torque ripple for brushless DC motors based on a quasi-Z-source net[J]. Proceedings of the CSEE, 2015, 35(4): 971-978.
[8] 朱俊杰, 刘浩然, 蒋峰, 等. 无刷直流电机转矩脉动抑制系统的新型拓扑研究[J]. 电工技术学报, 2018, 33(17): 4060-4068.
Zhu Junjie, Liu Haoran, Jiang Feng, et al. A new topology research on torque ripple suppression system of brushless motor[J]. Transactions of China Electrotechnical Society, 2018, 33(17): 4060-4068.
[9] Viswanathan V, Seenithangom J. Commutation torque ripple reduction in the BLDC motor using modified SEPIC and three-level NPC inverter[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(1): 535-546.
[10] 李珍国, 王江浩, 高雪飞, 等. 一种合成电流控制的无刷直流电机转矩脉动抑制系统[J]. 中国电机工程学报, 2015, 35(21): 5592-5599.
Li Zhenguo, Wang Jianghao, Gao Xuefei, et al. Torque ripple reduction systems for brushless DC motors with resultant current control[J]. Proceedings of the CSEE, 2015, 35(21): 5592-5599.
[11] 李珍国, 周生海, 王江浩, 等. 无刷直流电动机双闭环调速系统的转矩脉动抑制研究[J]. 电工技术学报, 2015, 30(15): 156-163.
Li Zhenguo, Zhou Shenghai, Wang Jianghao, et al. The research on the brushless DC motor double-loop speed control system for torque ripple reduction[J]. Transactions of China Electrotechnical Society, 2015, 30(15): 156-163.
[12] 王大方, 朱洪彪, 金毅, 等. 抑制BLDCM换相转矩脉动的超前换相控制策略[J]. 电机与控制学报, 2018, 22(10): 77-86.
Wang Dafang, Zhu Hongbiao, Jin Yi, et al. Advance commutation control method to suppress com- mutation torque ripple of brushless DC motors[J]. Electric Machines and Control, 2018, 22(10): 77-86.
[13] Li Zhenguo, Gao Xuefei, Wang Jianghao, et al. Phase back EMF space vector oriented control of brushless DC motor for torque ripple minimization[C]//2016 IEEE 8th International Power Electronics and Motion Control Conference, Hefei, China, 2016: 2564-2570.
[14] 张兰红, 唐慧雨, 何坚强. 基于霍尔位置信号的无刷直流电机直接转矩控制[J]. 电机与控制学报, 2018, 22(9): 56-63.
Zhang Lanhong, Tang Huiyu, He Jianqiang. Direct torque control of brushless DC motor based on hall position signals[J]. Electric Machines and Control, 2018, 22(9): 56-63.
[15] 杨建飞, 曹伟, 李德才, 等. 两相导通无刷直流电机直接转矩控制零电压矢量特性分析[J]. 电工技术学报, 2019, 34(23): 4948-4956.
Yang Jianfei, Cao Wei, Li Decai, et al. Analysis on zero voltage vector in two-phase conduction direct torque control of brushless DC motor[J]. Transa- ctions of China Electrotechnical Society, 2019, 34(23): 4948-4956.
[16] 李珍国, 章松发, 周生海, 等. 考虑转矩脉动最小化的无刷直流电机直接转矩控制系统[J]. 电工技术学报, 2014, 29(1): 139-146.
Li Zhenguo, Zhang Songfa, Zhou Shenghai, et al. Direct torque control of brushless DC motor conside- ring torque ripple minimization[J]. Transactions of China Electrotechnical Society, 2014, 29(1): 139-146.
[17] Liu Yong, Zhu Ziqiang, Howe D. Commutation- torque-ripple minimization in direct-torque-controlled PM brushless DC drives[J]. IEEE Transactions on Industry Applications, 2007, 43(4): 1012-1021.
[18] Li Zhenguo, Wang Lu, Zhang Songfa, et al. Torque ripple reduction in direct torque controlled brushless DC motor[C]//2011 International Conference on Electrical Machines and Systems, Beijing, China, 2011: 1749-1752.
[19] 边春元, 段鹏飞, 肖鸿权, 等. 一种用于无刷直流电机回馈制动的PWM调制方式[J]. 中国电机工程学报, 2019, 39(17): 5247-5256, 5305.
Bian Chunyuan, Duan Pengfei, Xiao Hongquan, et al. A PWM scheme for regenerative braking of brushless DC motor[J]. Proceedings of the CSEE, 2019, 39(17): 5247-5256, 5305.
[20] 王培侠, 姜卫东, 王金平, 等. 基于电流滞环控制的无刷直流电机多状态换相转矩脉动抑制方法[J]. 电工技术学报, 2018, 33(22): 5261-5272.
Wang Peixia, Jiang Weidong, Wang Jinping, et al. A current hysteresis control method for brushless DC motor in multi-state with commutation torque ripple reduction[J]. Transactions of China Electrotechnical Society, 2018, 33(22): 5261-5272.
Torque Ripple Reduction of Brushless DC Motor Based on Rotor Permanent Magnet Field Orientation
Abstract Due to the non-sinusoidal waveforms of main magnetic field distribution and back-EMF, there are large torque ripples in brushless DC motor under the driving with square wave current. Therefore, a torque control strategy to reduce torque ripple based on the rotor permanent magnet field orientation is proposed in this paper. Firstly, by analyzing the equivalent model for BLDCM rotor permanent magnet field orientation under d-q synchronous rotating coordinate system, it is shown that the armature reaction of d-axis and electromagnetic torque are determined by the current of d-axis and q-axis, respectively. Secondly, based on the principle that the d-axis armature reaction and the electromagnetic torque are unchanged after conversion, the transformation method between the three-phase current and the d- and q-axis currents is presented. Finally, the three-phase currents from the required d-axis and q-axis currents are obtained. These currents are regulated in closed loop form to realize the instantaneous constant torque control without magnetization and demagnetization. The test results obtained from Matlab simulation and DSP experiment show the feasibility and effectiveness of the proposed method.
keywords：Brushless DC motor (BLDCM), rotor permanent magnet field orientation, torque ripple reduction, d-axis armature reaction
DOI: 10.19595/j.cnki.1000-6753.tces.200061
中图分类号：TM351
李珍国 男，1973年生，博士，副教授，研究方向为电力电子与电力传动。E-mail: lzg@ysu.edu.cn（通信作者）
孙启航 女，1997年生，硕士研究生，研究方向为电力电子与电力传动。E-mail: 1018525294@qq.com
收稿日期 2020-01-14
改稿日期 2020-04-12
国家自然科学基金（61873226）和河北省自然科学基金（E2017203320）资助项目。
（编辑 崔文静）