 效应或分散层效应[9,11-12]。Frumkin修正是考虑双电层结构的一种更准确的处理方法,并假设电子转移过程发生在Helmholtz平面上,它给出了两方面的修正[9,13-15]:
效应或分散层效应[9,11-12]。Frumkin修正是考虑双电层结构的一种更准确的处理方法,并假设电子转移过程发生在Helmholtz平面上,它给出了两方面的修正[9,13-15]:摘要 为了研究不同质量分数氯化钠溶液中腐蚀电场的Frumkin修正效果,采用电化学阻抗谱测试得到921A钢电极在腐蚀电位下的双电层电容,并由此计算分散层电位的实验值,根据双电层的Stern模型,推导分散层电位与双电层电位、支持电解质质量分数的理论关系,并得到分散层电位的理论值。根据Frumkin修正理论,对阴极和阳极的电极过程动力学分别进行修正,得到与分散层电位相关的修正后的Tafel方程式。分别以修正前后的Tafel方程式作为921A钢板腐蚀电场边界元模型的边界条件,得到修正前后的腐蚀电场分布,并与实测腐蚀电场进行对比。结果表明,修正后的电场模量幅值与实验结果更为接近,说明在仿真过程中对Tafel边界条件进行修正是有必要的,当氯化钠溶液质量分数分别为1.5%、2.5%和3.5%时,修正效果分别为12.2%、10.8%和9.4%。
关键词:腐蚀电场 Frumkin修正 双电层 分散层电位 921A钢 边界元法
舰船腐蚀及防腐电流在其附近产生的电流场称为舰船腐蚀相关电场[1],相关研究表明[2-3],舰船腐蚀相关电场是一种新型的水下信号源。舰船腐蚀电场的实船测量不仅成本高、周期长,且难以测得舰船周围全空间的电场分布情况,而边界元法是一种非常适合求解开域问题的高精度数值计算方法[4],已被广泛应用于石油钻井平台、舰船等海洋结构件的腐蚀防护问题的仿真[5-6],近年来,已有学者开始将其应用于舰船腐蚀电场的仿真研究[7-8]。腐蚀电场边界元模型的边界条件为描述电极过程动力学的Butler-Volmer方程,在Butler-Volmer方程的推导过程中,均假设双电层电位完全分布于紧密层中,即分散层电位为零,而更接近真实情况的Stern双电层结构模型表明[9-10],双电层电位包括紧密层电位和分散层电位两部分,因此,Butler-Volmer方程忽略了双电层结构变化对电化学反应速度的影响。
电极过程动力学理论中,考虑分散层电位对电荷传递速度的影响被称为Frumkin修正,又叫 效应或分散层效应[9,11-12]。Frumkin修正是考虑双电层结构的一种更准确的处理方法,并假设电子转移过程发生在Helmholtz平面上,它给出了两方面的修正[9,13-15]:
效应或分散层效应[9,11-12]。Frumkin修正是考虑双电层结构的一种更准确的处理方法,并假设电子转移过程发生在Helmholtz平面上,它给出了两方面的修正[9,13-15]:
(1)驱动电子转移的有效电位不是金属相和溶液相之间的电位差,而是电极表面电位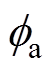 和Helmholtz平面电位
和Helmholtz平面电位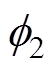 之间的电位差
之间的电位差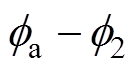 。
。
(2)Helmholtz平面上的反应粒子质量分数不是溶液体质量分数,而是由Boltzmann分布给出的,有
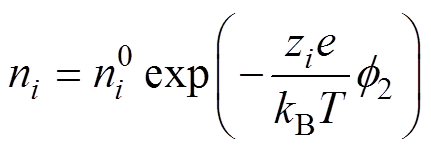 (1)
(1)式中,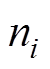 为粒子
为粒子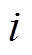 在Helmholtz平面的质量分数;
在Helmholtz平面的质量分数;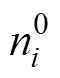 为溶液中
为溶液中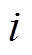 粒子的体质量分数;
粒子的体质量分数;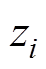 为粒子
为粒子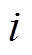 所带电荷数;
所带电荷数;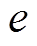 为元电荷电量;
为元电荷电量;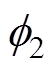 为Helmholtz平面电位;
为Helmholtz平面电位;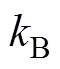 为Boltzmann常数;
为Boltzmann常数;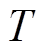 为热力学温度。Frunkin修正理论从1933年提出至今,已被应用于腐蚀[16-17]、纳米电极[18-19]和化学电池[15, 20]等多个领域,Z. Nagy等指出,当电解质质量分数低于0.1M(1M=1mol/L)或者电极电位接近零电荷电位时,若不考虑双电层结构的影响,由实测极化曲线定义的腐蚀速度与实际值之间的误差达到10%以上[17]。
为热力学温度。Frunkin修正理论从1933年提出至今,已被应用于腐蚀[16-17]、纳米电极[18-19]和化学电池[15, 20]等多个领域,Z. Nagy等指出,当电解质质量分数低于0.1M(1M=1mol/L)或者电极电位接近零电荷电位时,若不考虑双电层结构的影响,由实测极化曲线定义的腐蚀速度与实际值之间的误差达到10%以上[17]。
综上所述,应用Butler-Volmer方程作为舰船腐蚀电场边界元模型的边界条件可能会使仿真得到的电场与实测结果之间存在较大的误差,因此,本文依据电化学相关理论并采用电化学测试技术主要研究两个问题:①探索对Butler-Volmer边界条件进行Frumkin修正的必要性;②考虑到不同海域和江河入海口的海水具有不同的电导率,研究了模拟海水的氯化钠溶液质量分数分别为1.5%、2.5%和3.5%时的Frumkin修正效果。为了将研究问题简化,本文研究对象为船体常用材料的921A钢板自腐蚀产生的电场,为后续舰船腐蚀电场边界元模型的建立奠定基础。
电极/溶液界面双电层结构主要有Helmholtz模型、Gouy-Chapman模型和Stern模型三种[21],其中,Stern模型综合考虑了溶液中带电粒子的静电作用和热运动,认为离子双电层是由静电作用引起的紧密层和由热运动引起的分散层构成,相应地,双电层电位包括紧密层电位和分散层电位两部分。Stern模型中分散层电位分布满足Poisson-Boltzmann方程,对于NaCl溶液(1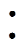 1型电解质),求解Poisson- Boltzmann方程得到分散层中的电位分布[13],有
1型电解质),求解Poisson- Boltzmann方程得到分散层中的电位分布[13],有
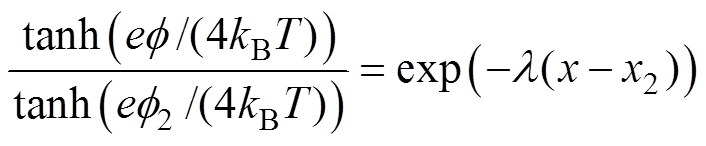 (2)
(2)式中,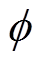 为距离电极表面
为距离电极表面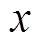 处的电位;
处的电位;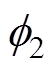 为分散层电位;
为分散层电位;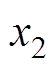 为紧密层厚度;
为紧密层厚度;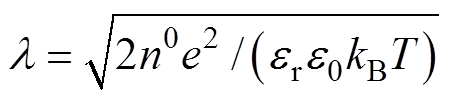 ,
,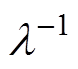 为Debye长度,即分散层的有效厚度,
为Debye长度,即分散层的有效厚度,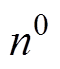 为NaCl溶液的数量质量分数,
为NaCl溶液的数量质量分数,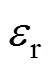 和
和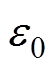 分别为水溶液的相对介电常数和真空介电常数。由于整个紧密层区域内不存在剩余电荷,
分别为水溶液的相对介电常数和真空介电常数。由于整个紧密层区域内不存在剩余电荷,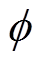 与
与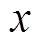 的关系是线性的,且紧密层电位曲线斜率[9, 13]为
的关系是线性的,且紧密层电位曲线斜率[9, 13]为
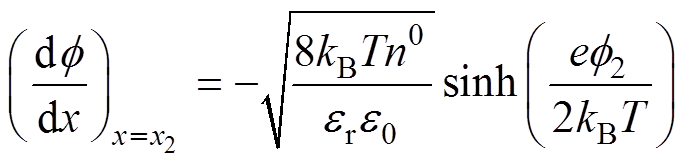 (3)
(3)
电极表面电荷密度[13]为
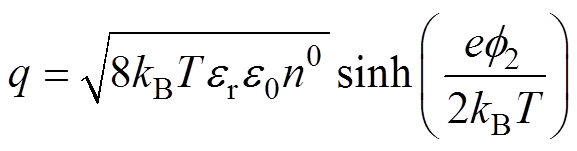 (4)
(4)将紧密层作为平行板电容器处理,假设水分子直径和水合阳离子的半径不随双电层电位变化,其微分电容为恒定值,即 ,由
,由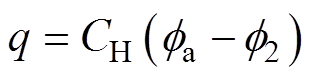 [9]得到
[9]得到
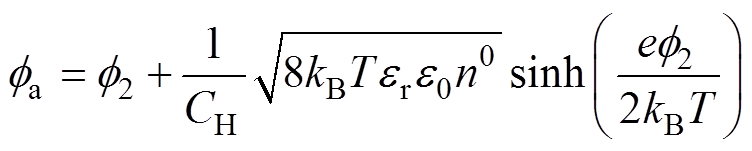 (5)
(5)式中,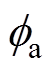 为双电层电位,式(5)为分散层电位与双电层电位、支持电解质质量分数的理论关系。
为双电层电位,式(5)为分散层电位与双电层电位、支持电解质质量分数的理论关系。
采用三电极体系在CS310电化学工作站上测试921A钢的动电位极化曲线和阻抗谱,实验介质为氯化钠溶液,质量分数分别为1.5%、2.5%和3.5%。工作电极为采用环氧树脂封装的921A低合金钢,试样尺寸为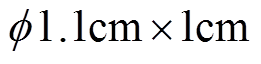 ,金属暴露面积为1cm2,用SiC湿砂纸逐级打磨至1 000目,丙酮脱脂,并依次用乙醇和蒸馏水冲洗,然后置于干燥箱中烘干;参比电极为Ag/AgCl电极;辅助电极为面积
,金属暴露面积为1cm2,用SiC湿砂纸逐级打磨至1 000目,丙酮脱脂,并依次用乙醇和蒸馏水冲洗,然后置于干燥箱中烘干;参比电极为Ag/AgCl电极;辅助电极为面积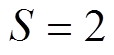 cm2的铂片电极。工作电极先在溶液中浸泡一段时间,等到开路电位基本稳定后开始测试,极化曲线的电位扫描范围为-1.1~-0.1V(相对参比电极),扫描速率为1.0mV/s;阻抗谱的直流电位设定为921A钢在相应质量分数氯化钠溶液中的腐蚀电位,交流幅值为10mV,频率扫描范围为105~10-2Hz。
cm2的铂片电极。工作电极先在溶液中浸泡一段时间,等到开路电位基本稳定后开始测试,极化曲线的电位扫描范围为-1.1~-0.1V(相对参比电极),扫描速率为1.0mV/s;阻抗谱的直流电位设定为921A钢在相应质量分数氯化钠溶液中的腐蚀电位,交流幅值为10mV,频率扫描范围为105~10-2Hz。
金属平板腐蚀电场测量的实验布置如图1a所示,实验水池为塑料水箱,将尺寸为14cm×10cm× 0.2cm的921A钢板水平置于水域,并以水域中心为坐标原点。电场传感器固定在非金属结构架上,如图1b所示,1~6分别为1号~6号传感器,1号和2号传感器组成测量电场X分量的电极对,3号和4号传感器组成测量电场Y分量的电极对,5号和6号传感器组成测量电场Z分量的电极对,电极对的两个传感器之间的距离均为10cm,分别连接在多通道水下电场采集系统的3个通道上。每个通道记录相应分量的电位差,用U1~U3分别表示3个通道上记录的电位差,根据电场强度计算公式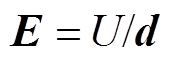 ,其中,d为电极对的两个传感器之间的距离,则电场的计算公式为
,其中,d为电极对的两个传感器之间的距离,则电场的计算公式为
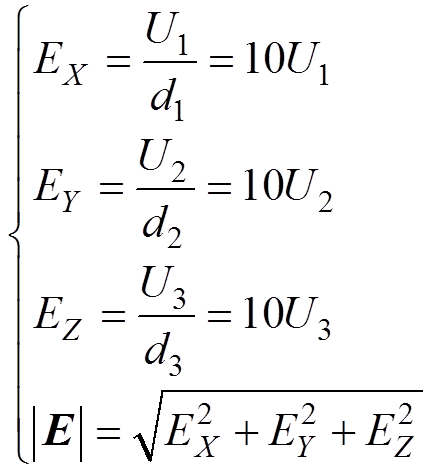 (6)
(6)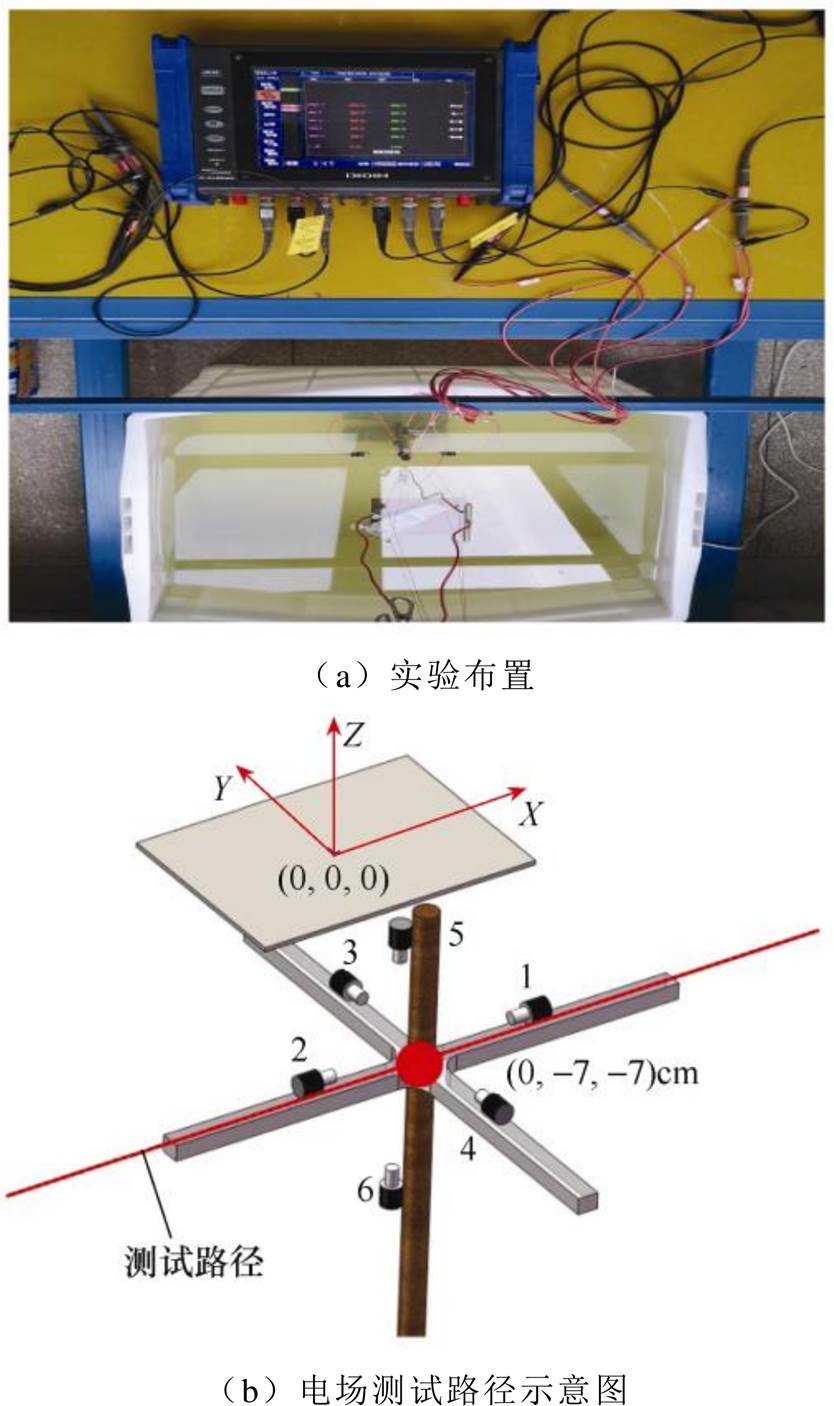
图1 腐蚀电场测量实验布置和测试路径
Fig.1 Experimental setup for corrosion electric field measurement and schematic diagram of the observation path
调整氯化钠溶液的质量分数模拟不同电导率的海水,将实验钢板置于水池中浸泡两天,待腐蚀电场稳定之后再进行实验。传感器架中心置于(0, -7, -7)cm处,通过行车带动钢板前进,以测试钢板通过电场传感器时的电场曲线,用通过性曲线等效钢板附近的腐蚀电场分布。
采用COMSOL Multiphysics仿真软件中电流分布(边界元)接口建立钢板腐蚀电场边界元模型,海水域和钢板的尺寸、坐标系统及其原点的选择均与实验保持一致,钢板6个面均直接与氯化钠溶液接触。整个模型的求解域及边界条件设定如下:①无限空区域为氯化钠溶液,电导率分别为2.18S/m、3.60S/m和4.80S/m(与1.5%、2.5%和3.5%氯化钠溶液质量分数对应);②钢板6个电极表面均同时发生铁的氧化与氧的还原两个共轭反应,铁氧化和氧还原的动力学过程分别由阳极Tafel方程和阴极Tafel方程描述,将修正前后的Tafel方程分别作为边界条件仿真得到Frumkin修正前后的腐蚀电场。为了与实验测试路径保持一致,在钢板附近选取以点(-75, -7, -7)cm和点(75, -7, -7)cm为端点的路径作为观测对象。
921A钢在1.5%、2.5%和3.5%三个质量分数氯化钠溶液中的极化曲线如图2所示,相关的电化学参数见表1,其中,电极反应的平衡电位由Nernst方程得到,拟合极化曲线的Tafel区得到钢的腐蚀电位、腐蚀电流和电极反应的Tafel斜率,由以上参数结合Tafel方程式可计算得到电极反应的交换电流密度,传递系数由Tafel斜率计算得到。腐蚀电流密度随着氯化钠溶液质量分数的增加而增大,这是因为氯离子对钢表面的腐蚀氧化膜具有破坏作用,氯离子质量分数越大,对保护性氧化膜的破坏越明显,钢的腐蚀速度也越大。
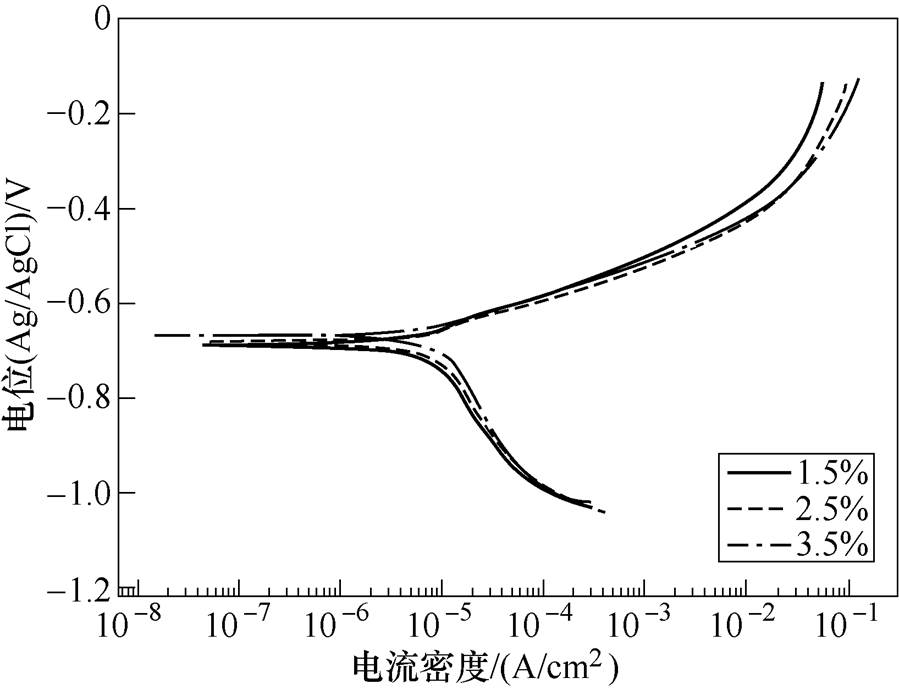
图2 921A在1.5%、2.5%和3.5%氯化钠溶液中的极化曲线
Fig.2 Polarization curves of 921A in 1.5%, 2.5% and 3.5% sodium chloride solution
表1 钢腐蚀过程中的电化学参数
Tab.1 Electrochemical parameters of steel corrosion
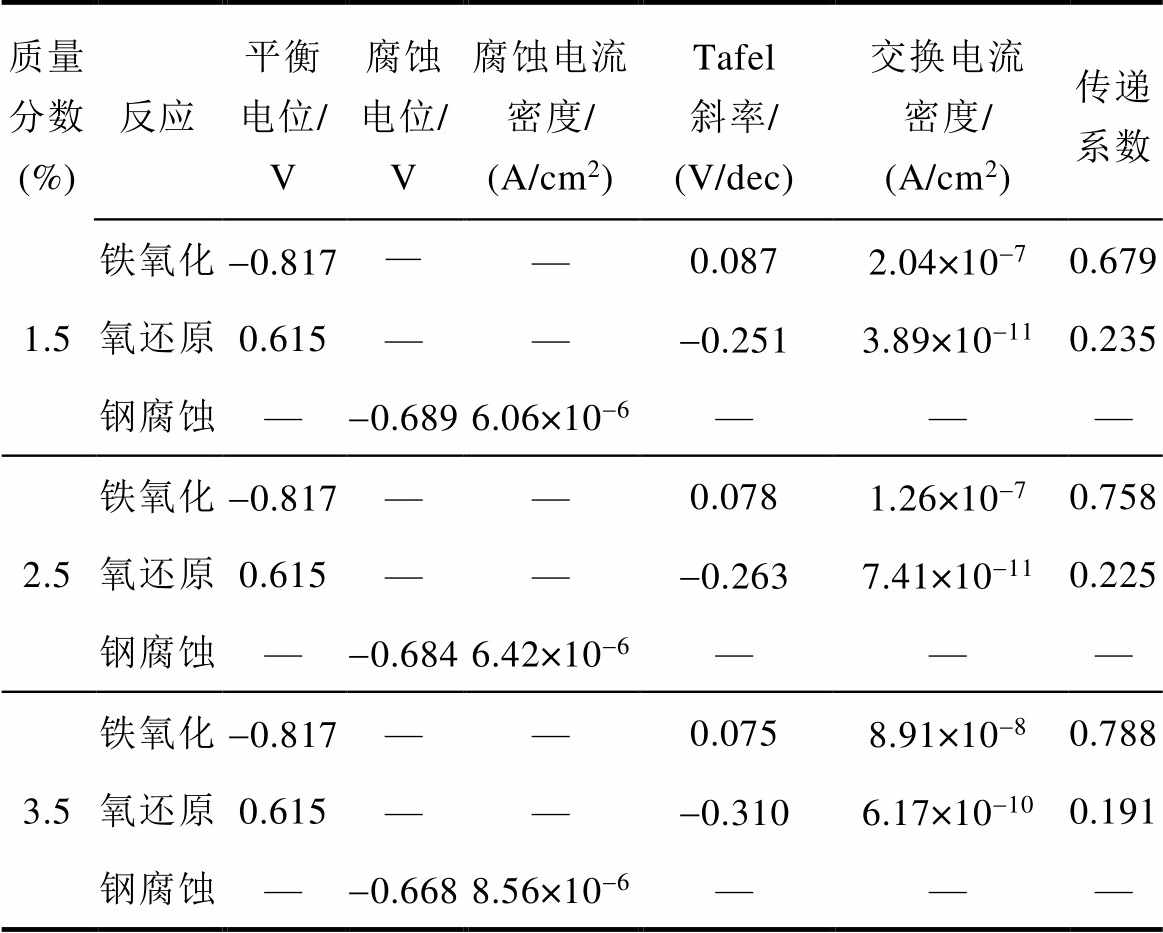
质量分数 (%)反应平衡电位/ V腐蚀电位/ V腐蚀电流密度/ (A/cm2)Tafel斜率/ (V/dec)交换电流密度/ (A/cm2)传递系数 1.5铁氧化-0.817——0.0872.04×10-70.679 氧还原0.615——-0.2513.89×10-110.235 钢腐蚀—-0.6896.06×10-6——— 2.5铁氧化-0.817——0.0781.26×10-70.758 氧还原0.615——-0.2637.41×10-110.225 钢腐蚀—-0.6846.42×10-6——— 3.5铁氧化-0.817——0.0758.91×10-80.788 氧还原0.615——-0.3106.17×10-100.191 钢腐蚀—-0.6688.56×10-6———
921A钢在1.5%、2.5%和3.5%氯化钠溶液中的阻抗谱和Bode图如图3所示。考虑到阻抗谱的“弥散效应”,用常相位角元件代替纯电容对阻抗谱进行拟合,常相位角元件(Constant Phase Element, CPE)的阻抗定义为
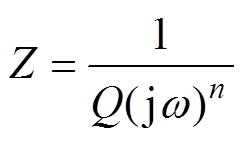 (7)
(7)式中,Z和Q分别为CPE的阻抗和导纳;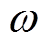 为扰动信号的角频率;
为扰动信号的角频率;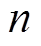 为弥散指数,
为弥散指数,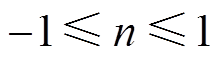 。双电层电容与常相位角元件参数之间的关系[22]为
。双电层电容与常相位角元件参数之间的关系[22]为
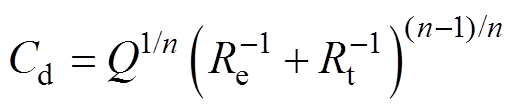 (8)
(8)
式中,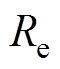 为Luggin毛细管与工作电极表面的溶液电阻,其值随着氯化钠质量分数的增大而减小;Rt为电极反应的电荷传递电阻。
为Luggin毛细管与工作电极表面的溶液电阻,其值随着氯化钠质量分数的增大而减小;Rt为电极反应的电荷传递电阻。
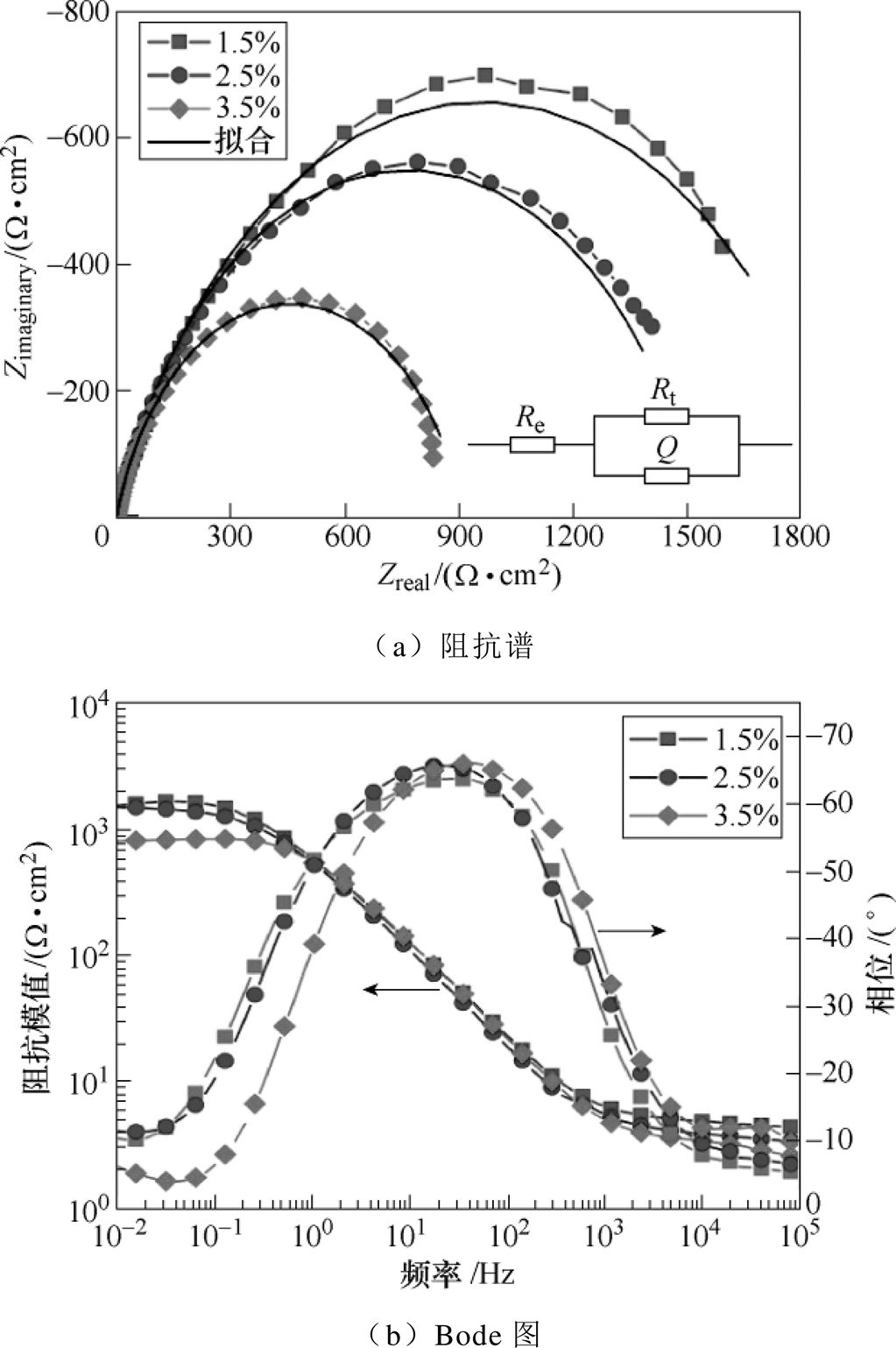
图3 921A在1.5%、2.5%和3.5%氯化钠溶液中的阻抗谱和Bode图
Fig.3 EIS and Bode plot of 921A in 1.5%, 2.5% and 3.5% sodium chloride solution
当溶液电阻远小于电荷传递电阻时,式(8)简化为
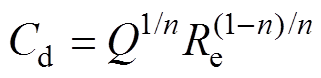 (9)
(9)对电化学阻抗谱(Electrochemical Impedance Spectroscopy, EIS)进行拟合得到等效电路中各元件的参数见表2,再根据式(9)计算钢/溶液界面的双电层(Electric Double Layer, EDL)电容。由第3.1节分析可知,氯化钠溶液质量分数越大,钢的腐蚀速度越大,即电极反应速度越大,因此,电荷传递电阻越小;Cd为钢/溶液界面的双电层电容,其值随着氯化钠质量分数的增大而增大,这是因为氯化钠溶液质量分数增大,分散层的有效厚度(Debye长度)减小,从而分散层电容增大,而紧密层电容不随质量分数变化而改变,因此,双电层的总电容增大。
表2 阻抗谱拟合参数及双电层电容
Tab.2 Fitting parameters by EIS and capacitance of EDL

质量分数 (%)n 1.50.7923.384.491.9161.5 2.50.8043.433.861.5368.2 3.50.8113.583.140.91373.6
电极电位包括剩余电荷引起的离子双电层电位、带电粒子特性吸附双电层电位、极性分子的偶极子层电位和金属表面因短程作用力形成的金属表面电位[23],只有第一种情况形成双电层电位,而后三种情况形成金属的零电荷电位。根据式(5)可得分散层电位与双电层电位、支持电解质质量分数的理论关系,如图4所示,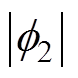 随着
随着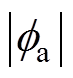 的增大而增大,但是前者增大的速度要小于后者,即随着
的增大而增大,但是前者增大的速度要小于后者,即随着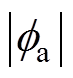 的增大,
的增大,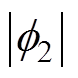 在整个双电层电位中所占的比例越来越小,当
在整个双电层电位中所占的比例越来越小,当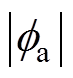 增大到一定程度时,可忽略
增大到一定程度时,可忽略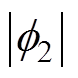 的影响,其次,在同一双电层电位下,溶液质量分数的增大会使
的影响,其次,在同一双电层电位下,溶液质量分数的增大会使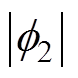 减小,说明双电层结构的分散性随溶液质量分数的增大而减小。取紧密层厚度为0.5nm[13],根据式(2)和式(3)可得钢电极表面电位随距离的变化曲线,如图5所示,氯化钠溶液质量分数越大,电位的绝对值随电极距离的增大而减小得越快,这同样说明了双电层结构的分散性随电解质质量分数的增大而减小。
减小,说明双电层结构的分散性随溶液质量分数的增大而减小。取紧密层厚度为0.5nm[13],根据式(2)和式(3)可得钢电极表面电位随距离的变化曲线,如图5所示,氯化钠溶液质量分数越大,电位的绝对值随电极距离的增大而减小得越快,这同样说明了双电层结构的分散性随电解质质量分数的增大而减小。
对于整个双电层结构来说,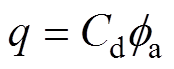 ,结合式(4)可得
,结合式(4)可得
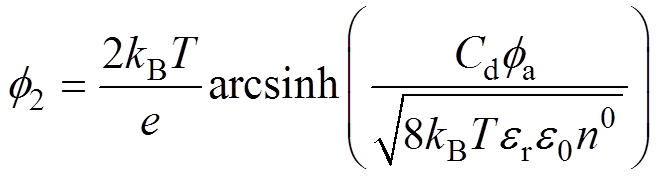 (10)
(10)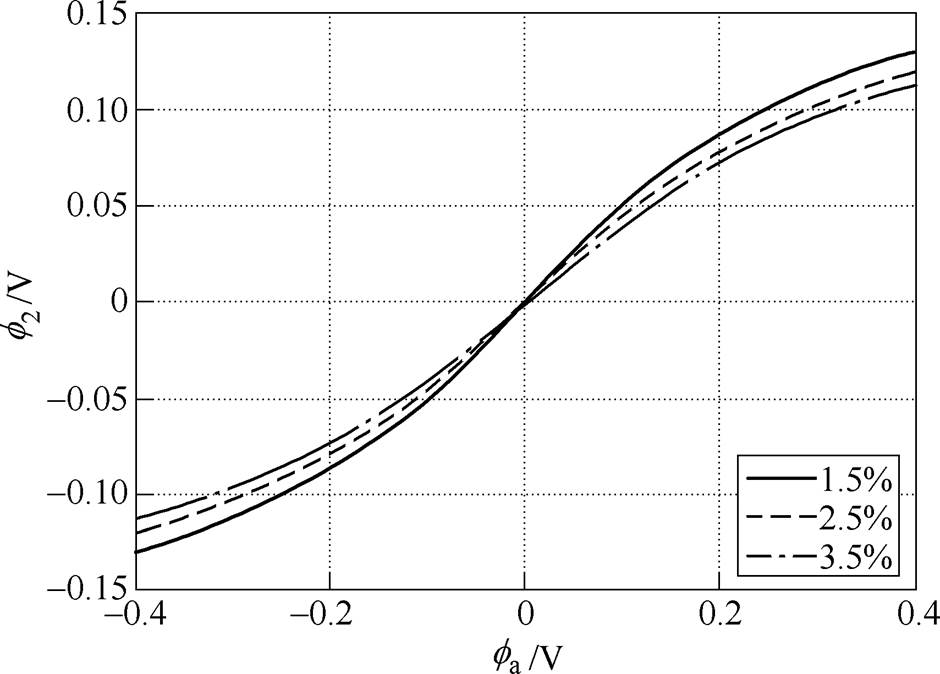
图4 分散层电位与双电层电位、电解质质量分数的理论关系
Fig.4 The theoretical relationship between diffuse layer potential and potential of EDL and concentration of electrolyte
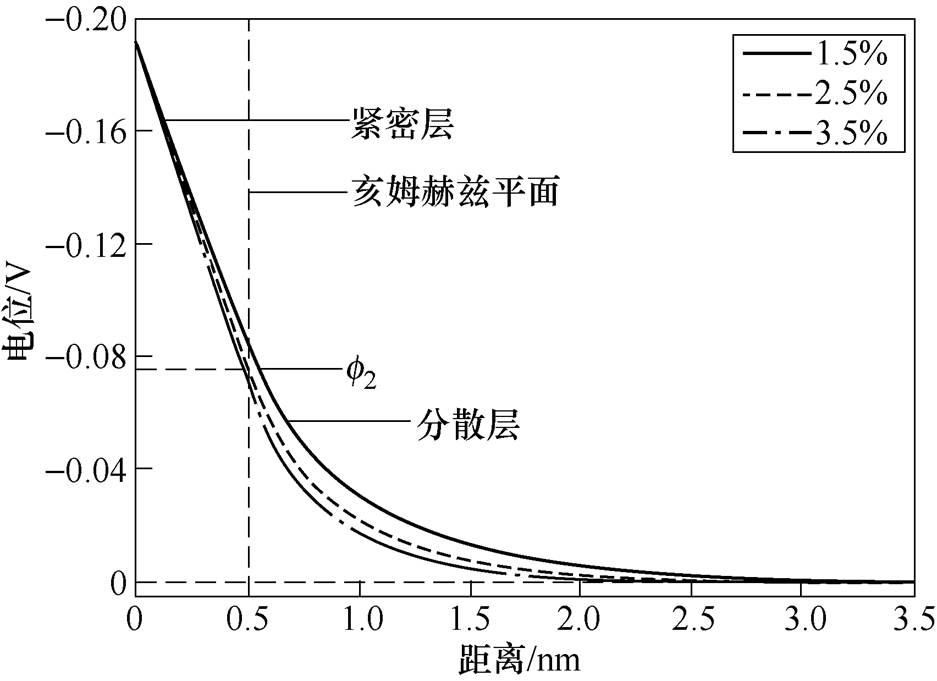
图5 921A电极表面电位随距离的变化
Fig.5 Surface potential of 921A electrode changes with distance
式中,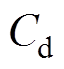 为3.2节实验所测双电层电容。将实验所测的双电层电容和腐蚀电位代入式(10)可得分散层电位的实验值。由图4得到的分散层电位理论值和实验所得的实验值见表3,分散层电位理论值和实验值的绝对值均随着氯化钠溶液质量分数的增大而减小,理论值和实验值的误差在10%左右。实验值和理论值之间的误差可能是由以下两方面原因引起的:一方面,电化学阻抗谱的测试时间较短,电极表面没有足够的时间形成稳定的分散层,导致分散层电位的绝对值比理论值小;另一方面,在计算分散层电位的理论值时,假设紧密层厚度为0.5nm且保持不变,而实际的紧密层厚度并不等于0.5nm,从而引起理论值与实验值存在一定的误差。
为3.2节实验所测双电层电容。将实验所测的双电层电容和腐蚀电位代入式(10)可得分散层电位的实验值。由图4得到的分散层电位理论值和实验所得的实验值见表3,分散层电位理论值和实验值的绝对值均随着氯化钠溶液质量分数的增大而减小,理论值和实验值的误差在10%左右。实验值和理论值之间的误差可能是由以下两方面原因引起的:一方面,电化学阻抗谱的测试时间较短,电极表面没有足够的时间形成稳定的分散层,导致分散层电位的绝对值比理论值小;另一方面,在计算分散层电位的理论值时,假设紧密层厚度为0.5nm且保持不变,而实际的紧密层厚度并不等于0.5nm,从而引起理论值与实验值存在一定的误差。
以阴极还原反应为例推导Frumkin修正后的Tafel方程式,对于多电子电极反应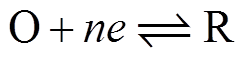 ,还原反应的绝对速度[9]为
,还原反应的绝对速度[9]为
表3 分散层电位理论值与实验值
Tab.3 Theoretical and experimental value of diffuse layer potential
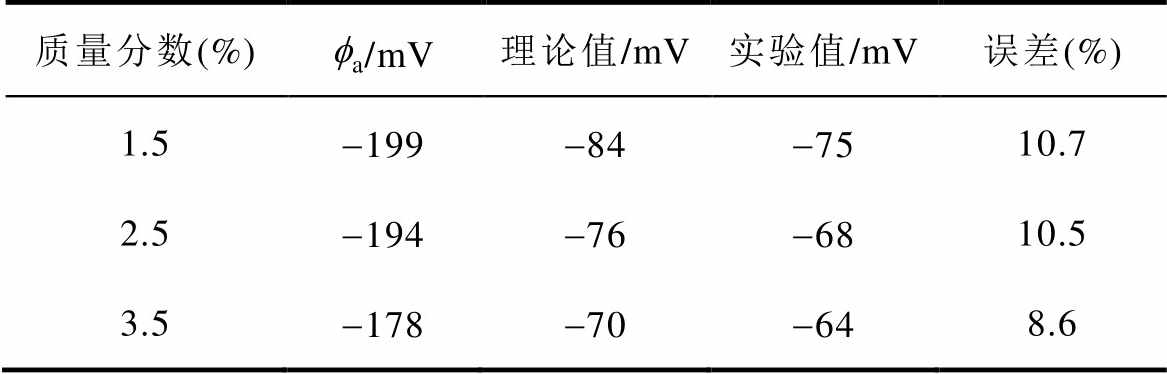
质量分数(%)fa/mV理论值/mV实验值/mV误差(%) 1.5-199-84-7510.7 2.5-194-76-6810.5 3.5-178-70-648.6
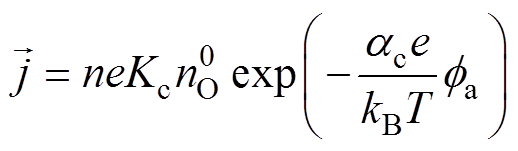 (11)
(11)式中,n为电极反应转移的电子数;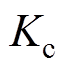 为还原反应总速度常数;
为还原反应总速度常数;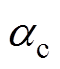 为还原反应总传递系数。考虑Frumkin修正,分别将紧密层电位和Helmholtz平面的反应物质量分数代替式(11)中的双电层电位和溶液体质量分数,则电极过程动力学公式(11)修正为
为还原反应总传递系数。考虑Frumkin修正,分别将紧密层电位和Helmholtz平面的反应物质量分数代替式(11)中的双电层电位和溶液体质量分数,则电极过程动力学公式(11)修正为
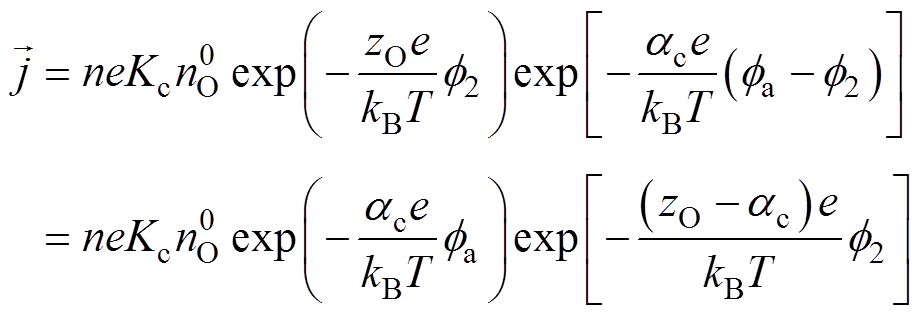 (12)
(12)
吸氧腐蚀过程中,阴极反应的反应物为电中性,氧化剂的电化学反应数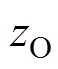 =0,因此,高过电位下阴极动力学方程(阴极Tafel方程)修正为
=0,因此,高过电位下阴极动力学方程(阴极Tafel方程)修正为
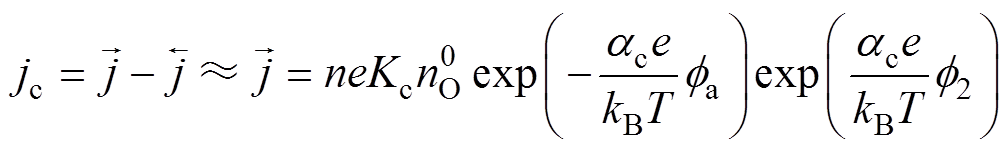 (13)
(13)同理,阳极Tafel方程修正为
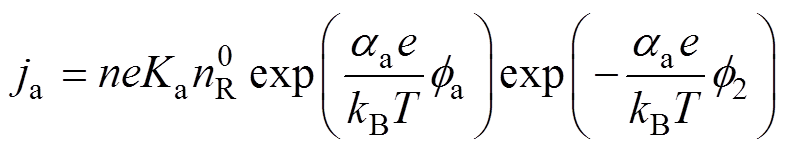 (14)
(14)
式中,Ka为氧化反应总速度常数;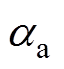 为氧化反应总传递系数。
为氧化反应总传递系数。
将修正前后的Tafel方程分别作为边界条件仿真得到Frumkin修正前后的腐蚀电场,将修正前后的电场模量在指定路径上的分布与实验结果进行对比,如图6所示,其中,图6a~图6c分别为氯化钠溶液质量分数为1.5%、2.5%和3.5%时的电场模量分布。由图6可知,修正前后的电场模量分布形状保持不变,但修正后的幅值较修正前有所增大,电场模量分布的仿真结果与实验结果吻合度很高,且修正后的电场模量幅值与实验结果更为接近,当氯化钠质量分数为3.5%时,修正前的电场模量幅值与实验结果的误差为12.6%,而修正后这一误差降到了4.3%,这说明了本文所建立的腐蚀电场边界元模型的有效性,而且,在仿真过程中对Tafel边界条件进行修正是有必要的。表4给出了指定路径上电场模量幅值和电流密度幅值随氯化钠溶液质量分数的变化,修正效果定义为

图6 Frumkin修正前后的电场模量与实验结果对比
Fig.6 Comparison of electric field modulus before and after Frumkin correction and experimental results
表4 Frumkin修正前后的电场模量和电流密度模量幅值随氯化钠溶液质量分数的变化
Tab.4 The amplitude of electric field modulus and current density modulus before and after Frumkin correction changes with sodium chloride solution concentration
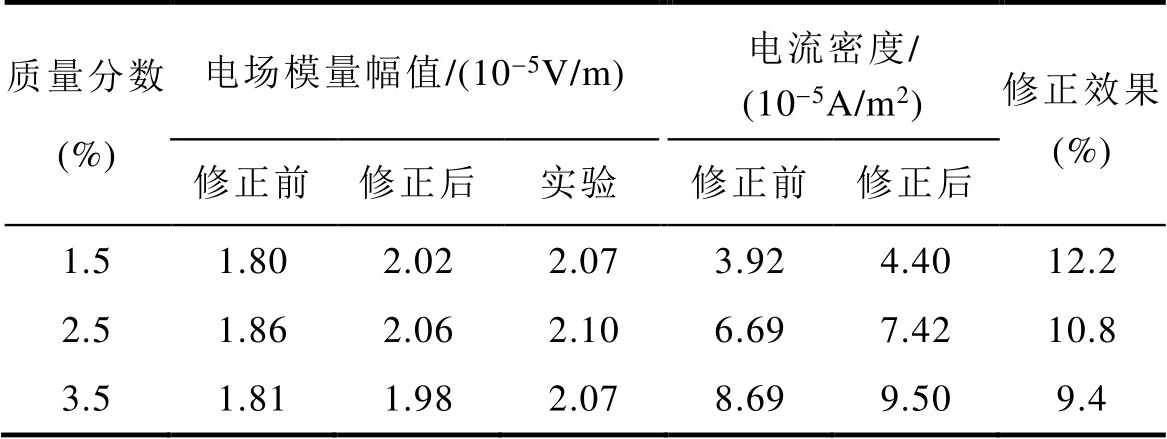
质量分数(%)电场模量幅值/(10-5V/m)电流密度/ (10-5A/m2)修正效果 (%) 修正前修正后实验修正前修正后 1.51.802.022.073.924.4012.2 2.51.862.062.106.697.4210.8 3.51.811.982.078.699.509.4
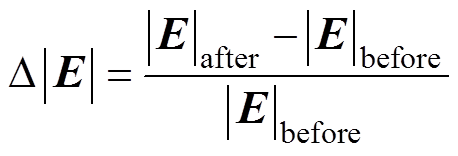 (15)
(15)式中,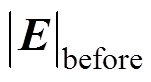 和
和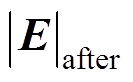 分别为修正前、后的电场模量幅值,当氯化钠溶液质量分数分别为1.5%、2.5%和3.5%时,修正效果分别为12.2%、10.8%和9.4%,说明电解质溶液质量分数越小,修正效果越明显,这是因为溶液质量分数越小,分散层电位在整个双电层电位所占的比例大,越有修正的必要。另外,腐蚀电流密度j随着氯化钠溶液质量分数的增大而增大,而腐蚀电场几乎不随溶液质量分数变化,这是因为溶液质量分数增大的同时电导率s 也同样增大,由
分别为修正前、后的电场模量幅值,当氯化钠溶液质量分数分别为1.5%、2.5%和3.5%时,修正效果分别为12.2%、10.8%和9.4%,说明电解质溶液质量分数越小,修正效果越明显,这是因为溶液质量分数越小,分散层电位在整个双电层电位所占的比例大,越有修正的必要。另外,腐蚀电流密度j随着氯化钠溶液质量分数的增大而增大,而腐蚀电场几乎不随溶液质量分数变化,这是因为溶液质量分数增大的同时电导率s 也同样增大,由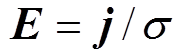 可知,氯化钠溶液质量分数增大时,腐蚀电流密度和电导率同比增大,使得电场强度值几乎保持不变。
可知,氯化钠溶液质量分数增大时,腐蚀电流密度和电导率同比增大,使得电场强度值几乎保持不变。
基于Frumkin修正理论,对921A钢板腐蚀电场边界元模型的Tafel边界进行了修正,并研究了氯化钠溶液质量分数对腐蚀电场Frumkin修正效果的影响,得到以下结论:
1)当氯化钠溶液质量分数增大时,分散层的有效厚度(Debye长度)减小,从而分散层电容增大,而紧密层电容不随质量分数变化而改变,因此,双电层的总电容增大。
2)电解质溶液质量分数越小,双电层的分散性越大,因此,分散层电位理论值和实验值的绝对值均随着氯化钠溶液质量分数的减小而增大,理论值和实验值的误差在10%左右。
3)修正后的电场强度模量幅值与实验结果更为接近,说明有必要在仿真过程中对Tafel边界条件进行修正,电解质溶液质量分数越小,双电层结构的分散性越大,修正效果越明显。
4)仿真得到的电场模量分布与实验结果具有很高的吻合度,验证了本文所建立的腐蚀电场边界元模型的有效性,为舰船腐蚀电场的仿真研究提供了建模依据。
参考文献
[1] 王向军, 嵇斗. 舰船电场防护原理[M]. 武汉: 海军工程大学出版社, 2016.
[2] Kim Y S, Lee S K, Chung H J, et al. Influence of a simulated deep sea condition on the cathodic protection and electric field of an underwater vehicle[J]. Ocean Engineering, 2018, 148: 223-233.
[3] Wang Jinhong, Li Bin, Chen Lianping, et al. A novel detection method for underwater moving targets by measuring their ELF emissions with inductive sensors[J]. Sensors, 2017, 17(8): 56-67.
[4] 王泽忠, 石雨鑫. 三维电场多极子曲面边界元方法研究[J]. 电工技术学报, 2018, 33(24): 5797-5804.
Wang Zezhong, Shi Yuxin. Fast multipole curved boundary element method for 3D electrostatic field[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5797-5804.
[5] Kim Y S, Kim J, Choi D, et al. Optimizing the sacrificial anode cathodic protection of the rail canal structure in seawater using the boundary element method[J]. Engineering Analysis with Boundary Elements, 2017, 77: 36-48.
[6] Xing S H, Li Yan, Song H Q, et al. Optimization the quantity, locations and output currents of anodes to improve cathodic protection effect of semi- submersible crane vessel[J]. Ocean Engineering, 2016, 113: 144-150.
[7] Kim Y S, Seok S, Lee J S, et al. Optimizing anode location in impressed current cathodic protection system to minimize underwater electric field using multiple linear regression analysis and artificial neural network methods[J]. Engineering Analysis with Boundary Elements, 2018, 96: 84-93.
[8] Wang Xiangjun, Xu Qinglin, Zhang Jianchun, et al. Simulating underwater electric field signal of ship using the boundary element method[J]. Progress in Electromagnetics Research M, 2018, 76: 43-54.
[9] 李荻. 电化学原理[M]. 2版. 北京: 北京航空航天大学出版社, 2007.
[10] Biesheuvel P M, Van S M, Bazant M Z. Imposed currents in galvanic cells[J]. Electrochimica Acta, 2009, 54(21): 4857-4871.
[11] Aoki K J, Chen Jingyuan, Zeng Xiangdong, et al. Decrease in the double layer capacitance by faradaic current[J]. RSC Advances, 2017, 7(36): 22501-22509.
[12] Lin Chuhong, Laborda E, Batchelor M C, et al. Electrical double layer effects on ion transfer reactions[J]. Physical Chemistry Chemical Physics, 2016, 18(14): 9829-9837.
[13] Bard A J, Faulkner L R. Electrochemical methods: fundamentals and applications[M]. 2nd ed. New York: John Wiley & Sons, 2001.
[14] Liu Yuwen, Zhang Qianfan, Chen Shengli. The voltammetric responses of nanometer-sized elec- trodes in weakly supported electrolyte: a theoretical study[J]. Electrochimica Acta, 2010, 55(27): 8280- 8286.
[15] Van S M. Frumkin-butler-volmer theory and mass transfer in electrochemical cells[J]. Russian Journal of Electrochemistry, 2012, 48(6): 570-579.
[16] Van S M, Mavinkurve A, Rongen R T H, et al. Theory of aluminum metallization corrosion in microelectronics[J]. Electrochimica Acta, 2010, 55(19): 5459-5469.
[17] Nagy Z, Schultz P F. Effect of double layer structure on the determination of corrosion rates from polari- zation measurements[J]. Electrochemical Science and Technology, 1988, 135(11): 2700-2706.
[18] Van Soestbergen M. Ionic currents exceeding the diffusion limitation in planar nano-cavities[J]. Elec- trochemistry Communications, 2012, 20: 105-108.
[19] Figueiredo M C, Hiltrop D, Sundararaman R, et al. Absence of diffuse double layer effect on the vibrational properties and oxidation of chemisorbed carbon monoxide on a Pt(111) electrode[J]. Elec- trochimica Acta, 2018, 281: 127-132.
[20] Dickinson E J F, Compton R G. Influence of the diffuse double layer on steady-state voltammetry[J]. Journal of Electroanalytical Chemistry, 2011, 661(1): 198-212.
[21] 赵洋, 梁海泉, 张逸成. 电化学超级电容器建模研究现状与展望[J]. 电工技术学报, 2012, 27(3): 188- 195.
Zhao Yang, Liang Haiquan, Zhang Yicheng. Review and expectation of modeling research on electro- chemical supercapacitor[J]. Transactions of China Electrotechnical Society, 2012, 27(3): 188-195.
[22] Hirschorn B, Orazem M E, Tribollet B, et al. Determination of effective capacitance and film thickness from constant-phase-element parameter[J]. Electrochimica Acta, 2010, 55(21): 6218-6227.
[23] 胡敏, 何湘宁. 脉冲电源印染污水处理的双电层电容效应分析[J]. 电工技术学报, 2007, 22(11): 130- 134.
Hu Min, He Xiangning. Analysis on electric double layer of dye wastewater purified by electro- coagulation with pulsed power supply[J]. Transa- ctions of China Electrotechnical Society, 2007, 22(11): 130-134.
Frumkin Correction of Corrosion Electric Field Generated by 921A Steel
Abstract In order to study the Frumkin correction effect of corrosion electric field in different concentrations of sodium chloride solution, the electric double layer (EDL) capacitance of 921A steel electrode at the corrosion potential was acquired by electrochemical impedance spectroscopy (EIS) Accordingly the experimental value of diffuse layer potential was calculated. The theoretical relationship between diffuse layer potential and potential of EDL and concentration of supporting electrolyte was derivedaccording to the Stern model of EDL. Therefore, the theoretical value of diffuse layer potential was obtained. According to the Frumkin correction theory, the electrode kinetics of cathode and anode were corrected respectively, and the modified Tafel equation related to diffuse layer potential was acquired. The uncorrected and corrected Tafel equation was used as the boundary condition of the boundary element model (BEM) of corrosion electric fieldfor 921A steel plate, so the corrosion electric field distributions before and after Frumkin correction were obtained and compared with the experimental results. The results show that the corrected amplitude of electric field modulus is closer to experimental values, indicating that it is necessary to correct the Tafel boundary condition during simulation process. Moreover, when the concentration of sodium chloride solution is 1.5%, 2.5% and 3.5%, the correction effectis 12.2%, 10.8%, and 9.4%, respectively.
keywords:Corrosion electric field, Frumkin correction, electric double layer, diffuse layer potential, 921A steel, boundary element model
DOI: 10.19595/j.cnki.1000-6753.tces.190741
中图分类号:TM15
徐庆林 男,1991年生,博士研究生,研究方向为电磁环境与防护技术。E-mail: csuxql@163.com
王向军 男,1973年生,教授,博士生导师,研究方向为电磁环境与防护技术。E-mail: wxjnue@hotmail.com(通信作者)
收稿日期 2019-06-18
改稿日期2019-12-05
国家自然科学基金面上项目(41476153)、武汉科技大学城市学院科学基金项目(2018CYZDKY002)资助。
(编辑 崔文静)