0 引言
双馈风力发电机（Doubly-Fed Induction Generator,DFIG）因损耗小、效率高、成本低，成为目前风力发电的主流机型[1-4]。其并网运行时，转子侧通过背靠背式变流器与电网相连，针对发电机轴系动能特点是否因此隔离，大量学者做了广泛研究[5-8]。与同步发电机相比，电力电子设备使双馈风机系统更具灵活性，也因此在频率响应、阻尼特性等方面表现出与传统电力系统的不同，随着风机并网比例的增加，这一差异将不容忽略[9-12]。对此，国内外学者类比同步发电机的机电特性，提出了虚拟同步机（Virtual Synchronous Generator，VSG）的概念[13-18]。DFIG系统中常见的VSG控制策略有基于同步机动能方程的虚拟惯量控制[19-21]、预留容量的改进最大功率跟踪（Maximum Power Point Tracking，MPPT）曲线控制[22-25]、基于直流电压的惯性支撑控制[26-27]等。可见，为系统提供与同步机相似的频率响应特性，是大多数VSG控制策略的目标。
不同VSG控制策略的控制效果、频率支撑特性多基于稳定性判断及时域仿真分析。稳定性判断时广泛采用模态分析法，根据控制参数变化观察特征根轨迹，进行定性分析[28-29]。但高阶系统特征根因控制参数随动的轨迹趋势并非完全一致，需要锁定主导特征根才可判断系统稳定走向。时域仿真分析时，通过观察负荷变化[20,27]、风速变化[19]和装机容量增大时[21]系统的动态响应曲线，对不同 VSG控制提供的惯性进行定性描述。总的来说，所采用的大多数方式是定性分析，缺乏定量的描述指标对控制效果进行判别。文献[30]基于变流器提出了关于系统频率响应的定量描述方法，开辟了系统频率稳定分析的新角度。
本文围绕系统传递函数矩阵范数与系统频率抑制能力之间的联系，从物理层面讨论了H 2/ H∞范数与双馈风机系统频率振荡抑制能力的量化关系。利用H 2
H∞范数，对三种 VSG控制提供的惯性进行量化分析，重点对比了三种VSG控制策略下的系统频率响应特性。最后，通过仿真分析证明了此方法的有效性。
1 系统频率响应的范数描述
对于任何一个矩阵G，可以通过范数将该矩阵与一个实数联系起来，这个实数能提供矩阵大小的度量，如
分别表示矩阵G的列模、谱模和行模。同样对于任何一个系统，其传递函数矩阵的范数可以作为度量该系统输入输出增益的指标[31]。假设某系统状态空间模型为
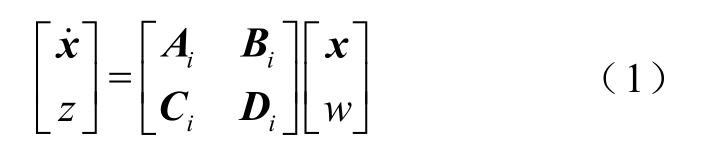
式中，x为系统的状态变量；w为系统外部扰动输入；z为系统的输出； A i、Bi、Ci、Di为系数矩阵。则系统传递函数矩阵为[32]
式中，I为单位矩阵；s为拉普拉斯算子。
在度量系统输入输出增益的指标中，H2、H∞范数通常作为衡量系统对输入抑制能力的定量指标。由系统伯德图可知[31]，H2范数对应伯德图幅值特性曲线下方的面积，故与系统超调量相关；而H∞范数对应幅值曲线峰值，与系统阻尼相关。对于一个系统，其传递函数矩阵T(s)的H2和H∞范数的计算公式分别为[31,33]
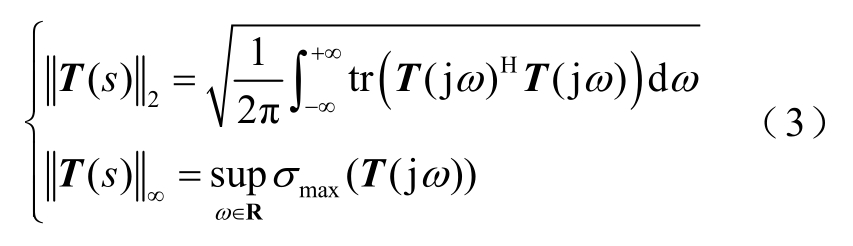
式中，tr表示矩阵的迹；上标 H表示共轭转置；
表示最大奇异值的峰值。
根据Parseval定理可知[31]，传递函数矩阵T(s)的H2范数的二次方
等于外部扰动w为脉冲输入时系统输出信号的总输出能量。而
的计算公式为系统传递函数矩阵的最大奇异值的峰值，恰好等于系统输出信号能量与扰动输入信号能量比的峰值[33]，即
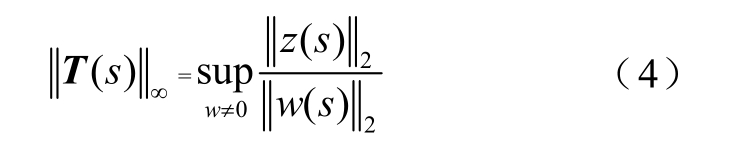
由式（4）可得，对于单输入单输出系统
数值上等于其在能量有界的扰动输入w的激励下，输出信号z与w能量之比的峰值。当w为能量有界的干扰时，为了减小其响应z，应尽量减小
的值。因此可以看出，H2、H∞范数与传统的系统抑制能力分析手段相比，具有显著的优势。可以从能量的角度定量描述系统抑制外部扰动的能力，并且其数值越小，系统抗扰动能力越强。
当传递函数矩阵以系统频率为输出，与频率有关的扰动量为输入时，传递函数矩阵的H2、H∞范数成为度量系统对频率扰动抑制能力的指标。此时，T ( s)的H2范数代表系统对于全频段输入扰动的抑制能力，用来评价输出信号z的总能量；T(s)的H∞范数为系统频率响应的最大奇异值的峰值，其物理意义为闭环系统对谐振频率扰动的抑制能力。可以理解为，H2范数反映的是系统关于扰动输入的平均情况，H∞范数为最严重的扰动输入下系统的响应情况。
对于整个系统来说，H2范数和H∞范数越小，系统的频率扰动抑制能力也就越强。从物理意义上看，H2范数和H∞范数都反映系统抑制干扰的能力，且与系统振荡能量有关，但两者存在细微差别：H2范数反映全部频段输入的平均抑制能力；H∞范数表示系统对全频段中最严重输入的抑制能力。由以上分析可得，H 2/H∞范数组合指标的互补性强，考虑系统整体情况的同时，又兼顾了极限情况。因此，可用于分析评估系统的频率响应能力。
2 虚拟同步机控制系统频率响应模型
本文主要研究DFIG在不同VSG控制策略下系统的频率扰动抑制能力，因此选择锁相环（Phase Locked Loop, PLL）模型中的旋转角速度 ω s_ PL L变量作为输出信号（详见附录中锁相环模型），所采用的系统如图1所示。
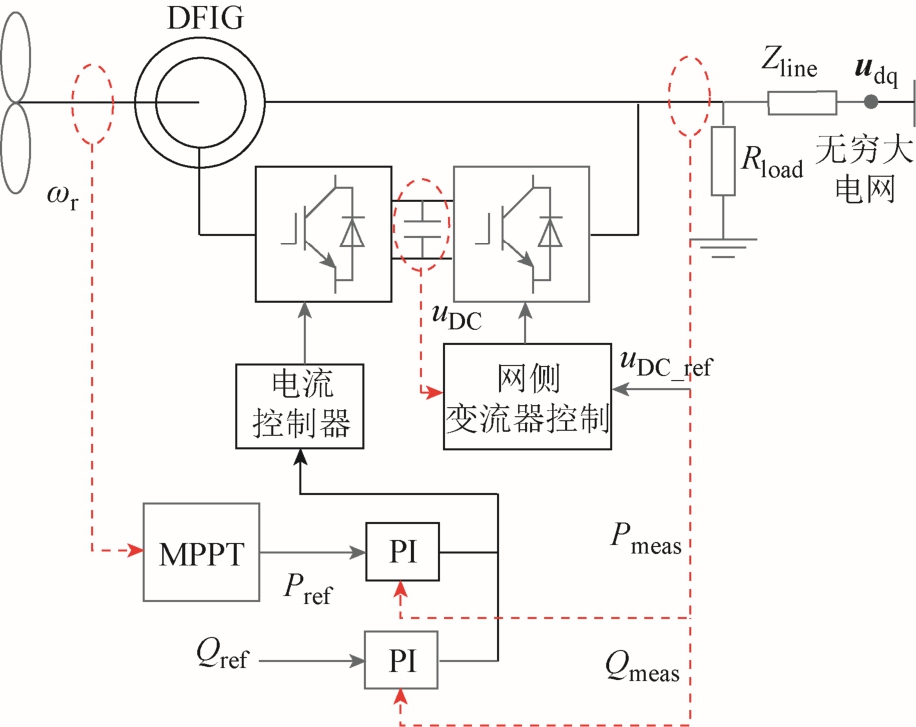
图1 双馈风机单机无穷大系统
Fig.1 Single machine infinite system of DFIG
图1中，ωr为风机转速，Pref为MPPT控制模块输出的有功参考值，Qref为无功参考值，uDC、 uDC_ref分别为直流端电压采集值与参考值，ud、uq分别为远端电网电压的d、q轴分量，Pmeas、Qmeas分别为有功、无功测量值。双馈风力发电机、线路阻抗、有功负荷的主要参数见表1。
表1 双馈风机系统主要参数
Tab.1 The main parameters of DFIG system
参 数 数 值定子电阻Rs(pu)定子电感Ls (pu)0.007 6 0.171 0.005 0.156定转子漏感Lm(pu) 3.5坐标系旋转角速度ωs(pu) 1.0风机转子角速度ωr(pu) 1.2时间常数Hr/s 0.5直流端电容C/F 0.06直流端电压初值uDC0/V 1 200额定容量S/MW 1.5负荷/MW 0.5线路参数 line 1 j1转子电阻Rr(pu)转子电感Lr(pu)Z =R+X(pu) 0.015+j0.4负载Rload(pu) 1.0转速基准值ωb/(rad/s) 314
2.1 虚拟惯量VSG控制
传统控制模式下，双馈风机运行在最大风能追踪状态，转子转速不会因电网频率变化而变化。为了使双馈风机具备同步发电机的惯量特性，在虚拟同步机控制中，常将虚拟惯量控制环节引入 DFIG的最大功率追踪模块[20]，如图2所示。
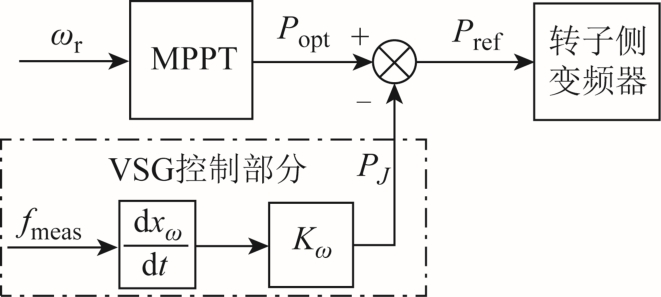
图2 虚拟惯量控制框图
Fig.2 Block diagram of virtual inertia control
控制策略可描述为
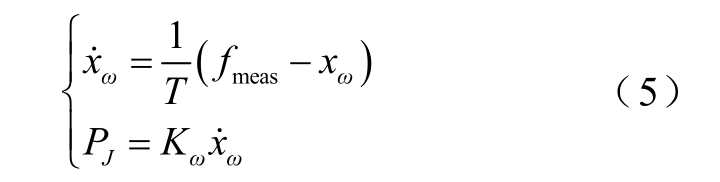
式中，xω为引入的中间变量，与系统频率相关；T为微分环节时间常数； fm eas =ωs_ PL L/(2π)，由锁相环测量得到；PJ为虚拟惯量控制的功率输出信号；Kω为虚拟惯量控制环节的比例系数。
因此，转子侧变流器控制部分的有功功率参考值Pref变为
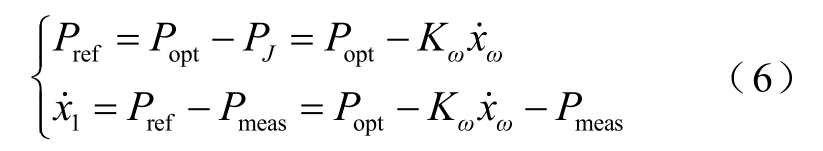
式中，Popt为 MPPT控制输出功率；x1为转子侧变流器控制部分模型搭建引入的中间变量。
选取输出信号为
式中，Δωs_PLL为ωs_PLL的扰动变化量。
由于相位的变化等效于有功功率的变化，而有功功率扰动和频率扰动是相关的[34]。所以这里将输入扰动Δω加在锁相环模型中的相位上，即
DFIG机电部分和控制部分的状态方程见附录，将系统模型进行线性化处理[35]，并消掉中间变量即可得系统的状态空间模型。其中，状态变量
为控制部分引入的中间变量，
。
此时，系统状态空间模型的系数矩阵A1、B1、C1D1分别如下所示，其中下角标0为各变量初始值。
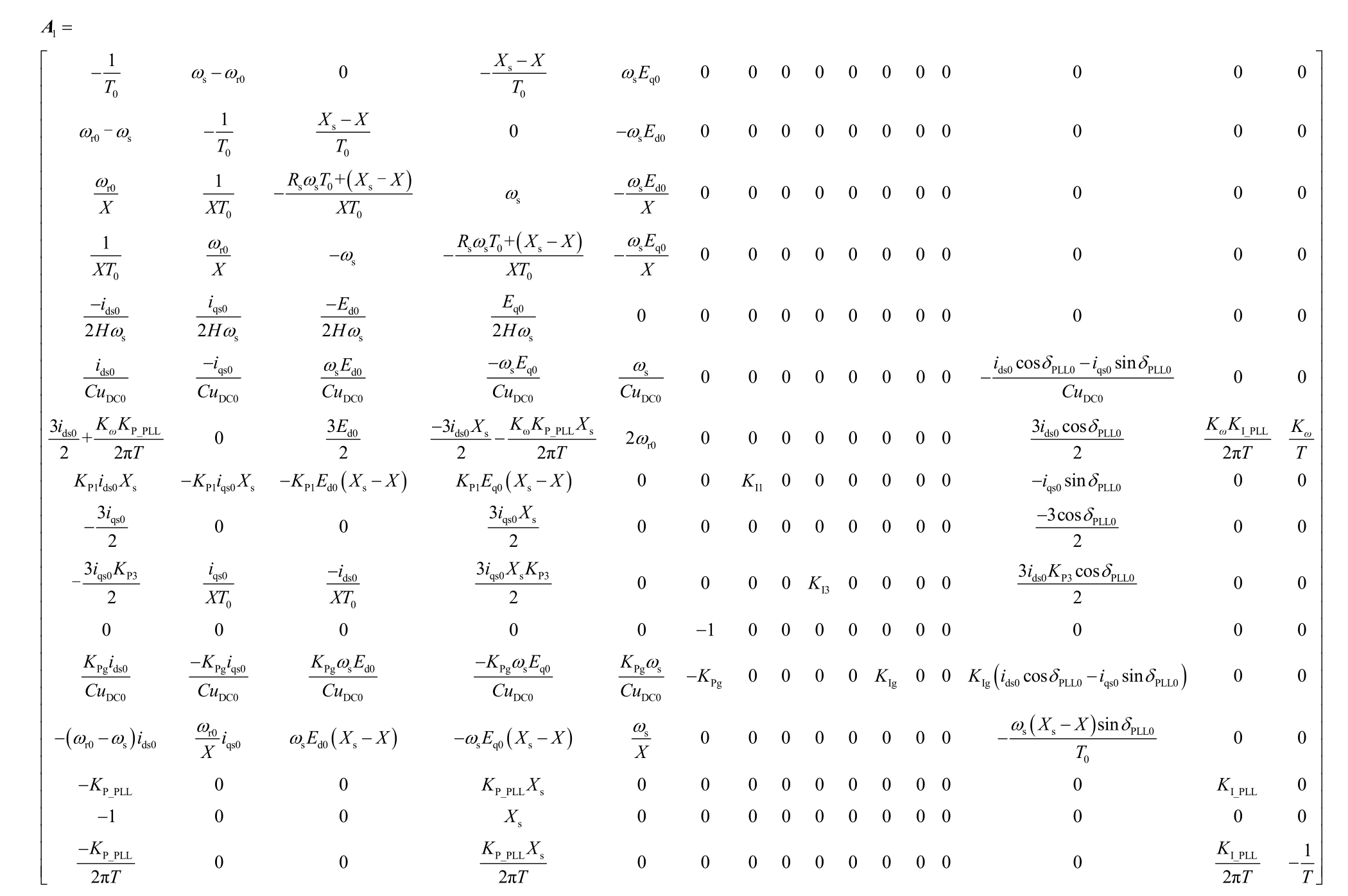
由式（2）可得该系统的闭环传递函数T1(s)。
2.2 直流电容VSG控制
双馈风机系统中，可以将转子侧变流器输入功率与网侧变流器输出功率之差视为直流侧电容元件吸收或释放的功率[26]。为实现虚拟同步机控制，可将直流电容的功率变化趋势与同步机动能方程进行等效，将同步机的惯性常数引入直流电压参考值[27]，即
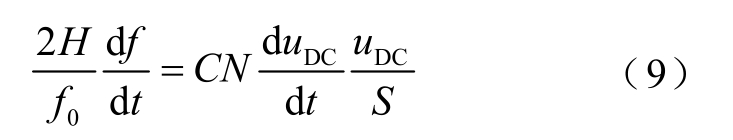
式中，H为同步机惯性时间常数；f为系统频率；C为直流侧电容值；N为电容个数，在双馈风力发电机并网系统中，该电容个数一般取 1；S为变流器的容量； f0为额定频率，取工频50Hz则有
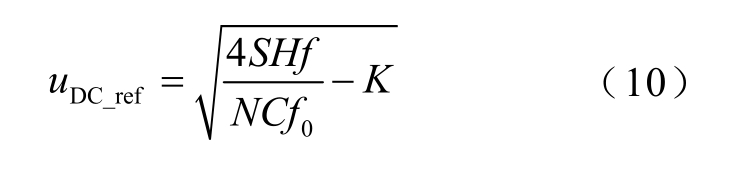
式中，K为一个与惯性常数和直流电压初值uDC0相关的常数。
附加惯性控制过程如图3所示，实时测量系统频率的变化，根据上述公式计算得到电压的参考值与直流侧电容电压的实测值，在网侧变流器控制中进行PI控制。
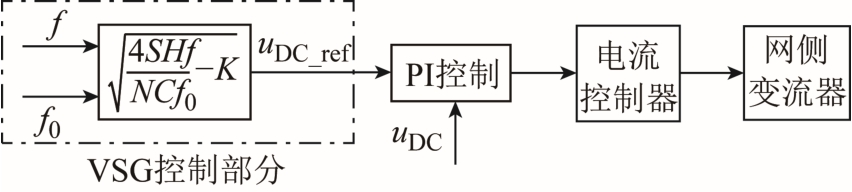
图3 附加惯性控制框图
Fig.3 Block diagram of additional inertia control
将电容电压参考值计算公式引入网侧变流器控制部分的状态方程中，即
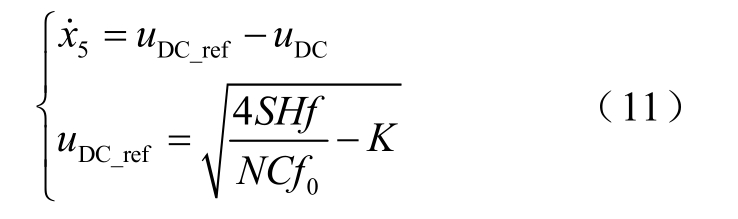
式中，x5为网侧变流器控制部分模型搭建而引入的中间变量。
效仿2.1节，可得系统的闭环传递函数T2(s)。其中，状态变量
分别为系统状态空间模型的系数矩阵（详见附录）。
2.3 MPPT曲线优化VSG控制
双馈风力发电机一般采取MPPT控制风机的功率输出，将功率与风机转速的关系进一步拟合为二次曲线，即
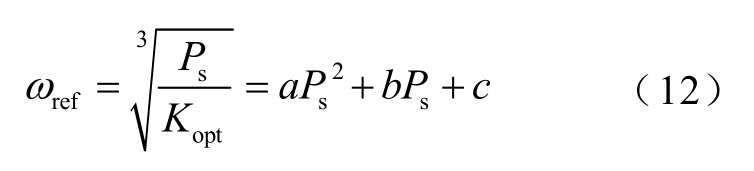
式中，ωref为转速参考值； Ps为定子的电磁功率；K o pt为功率计算系数；a、b、c分别为拟合系数。
第三种VSG控制方法就是在式（12）中引入比例系数Kv[22]，对 MPPT曲线进行优化，从而实现转子动能随频率波动而释放，控制框图如图4所示。
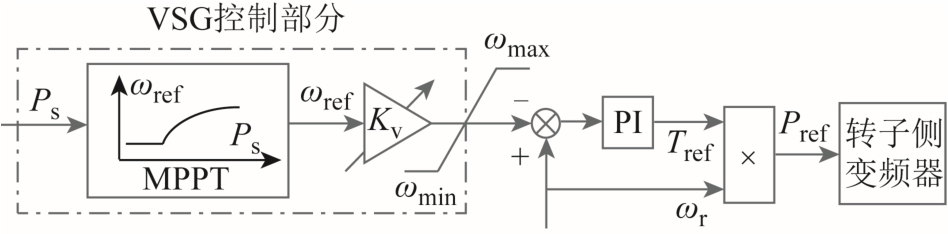
图4 曲线优化控制框图
Fig.4 Block diagram of curve optimization control
加入比例系数Kv后，转速由ω0经过Δωr变化到ω1，有
式中，
为曲线变化后功率计算系数；ω0和ω1分别为转速改变前后的转子转速稳态值；ωe为电力系统同步角速度；Δωe为电力系统的同步角速度变化量；γ 为转速调节系数，
由式（13）可得
将功率参考值计算公式引入到转子侧变流器控制部分的状态方程中，即
效仿2.1节得到该系统的闭环传递函数T3(s)。其中，状态变量
分别为系统状态空间模型的系数矩阵（详见附录）。
3 DFIG不同控制策略下的频率特性
利用H2、H∞范数，对上述三种VSG控制策略下的 DFIG系统进行频率响应特性研究。由式（3）分别计算传递函数T1(s)、T2(s)和T3(s)的H2、H∞范数，并采用模态分析法，计算三种VSG控制下系统的特征值和参与因子，分析各控制参数Kω、K和Kp从1到10变化时，对系统特征值的影响程度，得到其主导特征值的分布轨迹。范数与控制参数间的变化规律以及主导特征值的分布轨迹如图5所示，图中箭头为特征值移动方向。
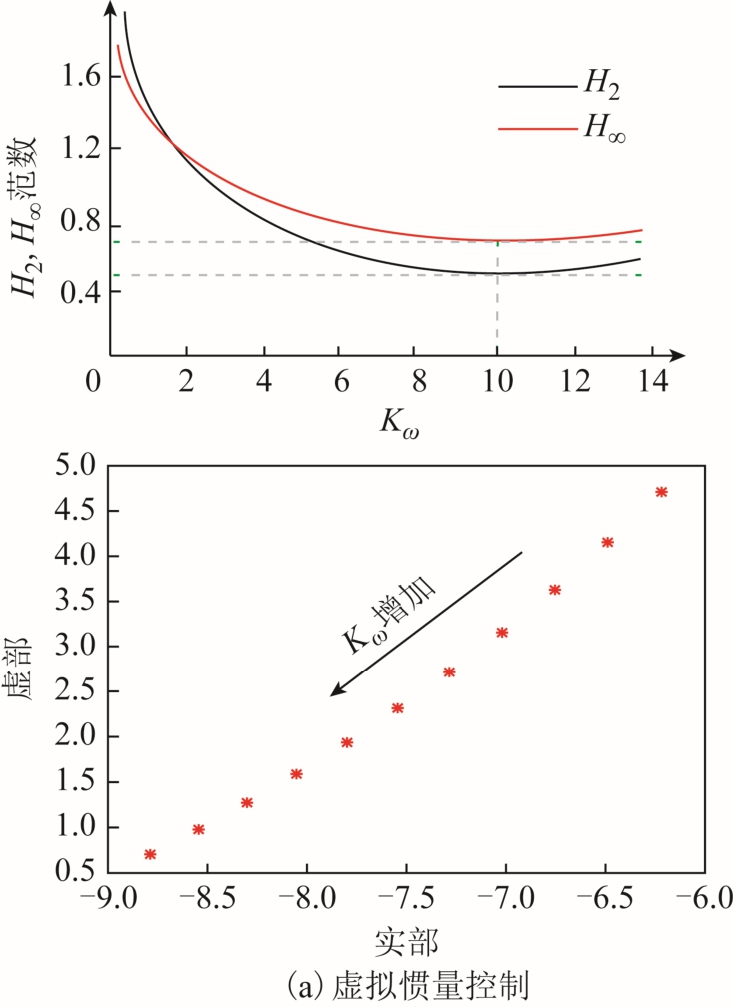
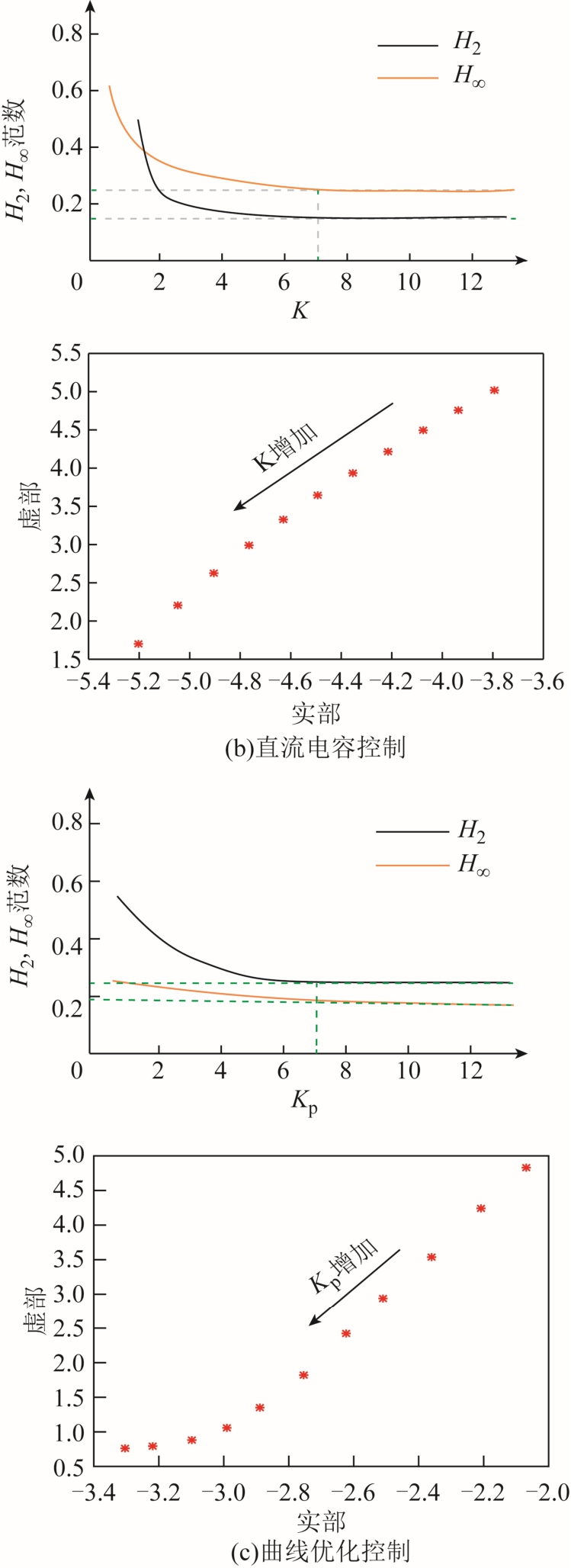
图5 三种VSG控制下系统H2、 H ∞范数
Fig.5 H2、 H ∞norm of system under three VSG controls
由图5可知，当Kω＜5、K＜2和Kp＜4时，H2、H∞范数值较大，此时主导特征值靠近右半平面，且其阻尼小。随着控制参数的增大，三种控制方式的H2和H∞范数都呈下降趋势，三个主导特征值也逐渐向左半平面移动，阻尼逐渐变大。由此可以看出，H2和H∞范数能够说明系统的频率稳定特性，并且其值越小，系统关于频率扰动的抑制能力就越强。
由于三种 VSG控制策略均基于系统惯性补偿的控制思想，曲线变化规律说明惯性对于风机系统频率扰动抑制的正面影响。对比三种控制策略下的范数结果，虚拟惯量控制方式的平均抑制能力及谐振抑制能力都要弱于其他两种控制策略；第二种 VSG控制方式下的全部频段输入的平均抑制能力更强；第三种VSG控制方式下的对最坏输入的抑制能力更强。
4 仿真验证
采用Matlab/Simulink建立系统仿真模型，对比研究三种VSG控制下的系统响应，如图6所示。图中，双馈风机为 1.5MW，有功负荷为 0.5MW。在t=10s时切除负荷，观察系统响应。
图6 系统仿真模型
Fig.6 Simulation model of system
根据前述分析，H2范数和H∞范数在反映系统频率响应时侧重角度不同，前者体现系统频率振荡的平均抑制能力，后者代表频率振荡的极限情况，因此H2范数更具一般性，故以其为衡量标准，取H2范数为相同值时，对比观察三种控制手段的频率响应波形。由图5可知，当Kω、K和Kp分别取 9、1.5和1时，系统H2范数均为0.5。此时，三种VSG控制手段下的系统频率响应如图7所示。
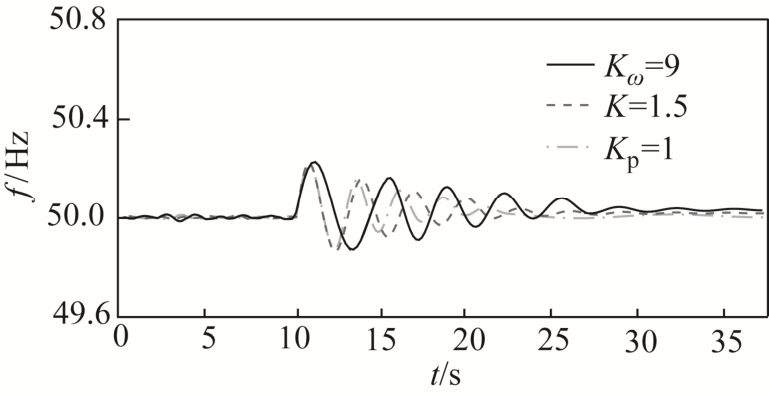
图7 系统频率响应
Fig.7 Frequency response of system
由图7可知，当H2范数相同时，不同VSG控制下的频率响应趋势基本一致，响应曲线的整体波动范围均介于 49.83～50.23Hz之间，差异率约为0.1%，说明H2范数具有评价系统响应超调量指标的能力。但因三种控制策略在H2范数相同时H∞范数并不一致，导致频率响应曲线在响应时间上存在微小差异，以±0.1Hz为频率稳定误差[36]，列出控制策略下响应时间分别为 15s、10s、8s。由此可见，范数可以作为定量指标，横向比较不同控制策略对系统频率响应的影响。
图8为一台 200MW同步发电机取不同惯性时间常数H时，系统的频率响应。在t = 10s时，切掉50MW的有功负荷，系统由于功率不平衡而产生频率波动。当惯性时间常数H取0.2s时，系统频率波动明显，并且持续时间长。随着惯性时间常数H的增大，系统频率波动幅值降低，持续时间减小。可见，惯性时间常数H的增大，使系统抑制频率振荡的效果更加显著。
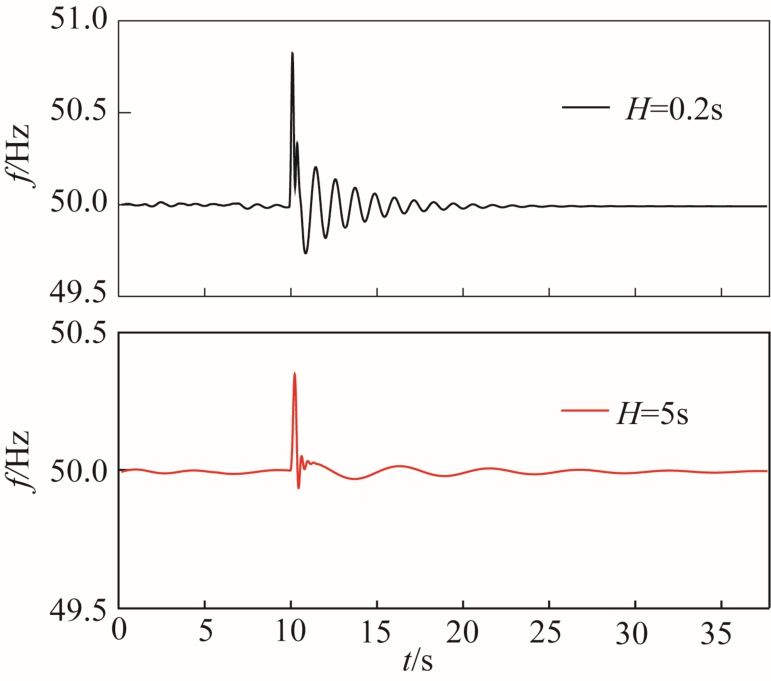
图8 同步机并网系统频率响应
Fig.8 Frequency response of synchronous machine grid-connected system
图9为双馈风机在不同VSG控制下，主导控制参数变化时系统频率的响应曲线。可以看出，控制参数的增大使系统的频率扰动抑制能力更加显著，这与图8的同步机频率响应分析结果相类似。由图5可以看出，三种VSG策略的控制参数大小与H2、H∞范数大小变化趋势相反。也就是说，当选择H2、H∞范数较大时的控制参数时，系统频率响应波动明显；当选择H2、H∞范数变小时的控制参数时，系统频率波动状态明显减小。可见H2和H∞范数越小，表征系统的频率扰动抑制能力就越强。
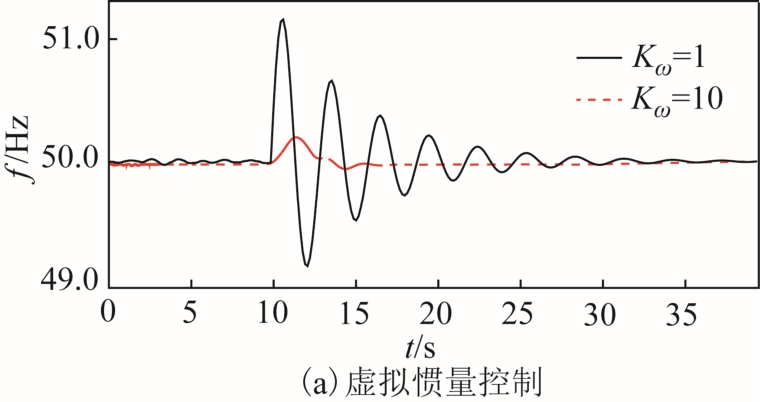
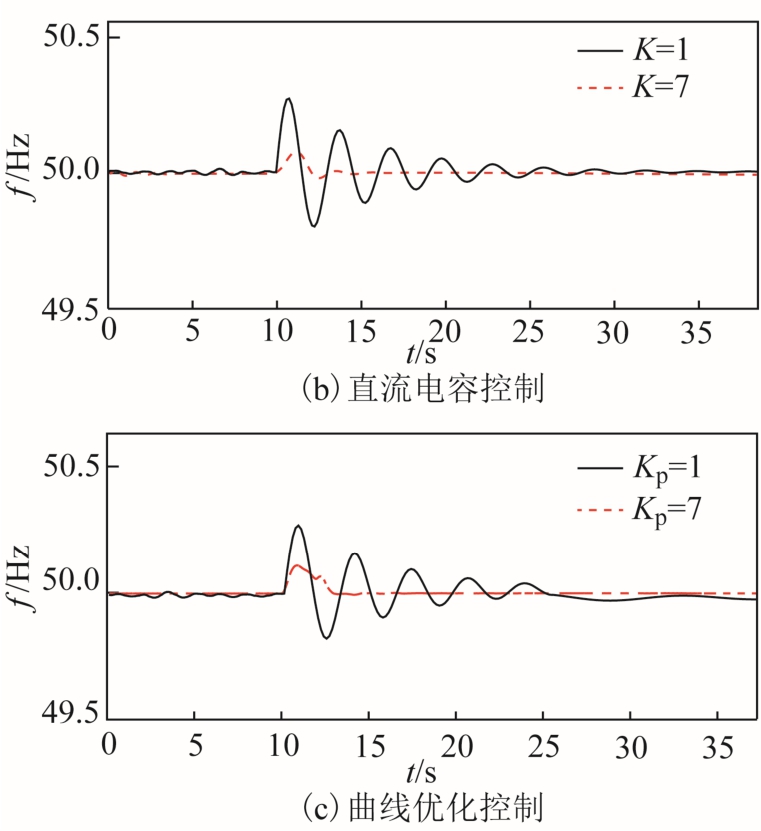
图9 三种VSG控制的频率响应
Fig.9 Frequency response of three VSG controls
综合上述分析，取三种VSG控制下的系统H2范数最小值情况做进一步对比分析。根据图5的虚线标记可知，此时各控制参数取值为Kω=10，K=7，Kp=7。对比不同控制策略下投切负荷时双馈风机系统频率及转子转速的时域响应波形，如图10和图11所示。
表2为投切负荷时，三种VSG控制下系统的响应参数。其中切除负荷时，虚拟惯量控制下的转子转速上升幅度最小，约为 0.04(pu)；系统频率振荡峰值最大，约为50.2Hz；响应恢复时间最长，约为7s。而直流电容控制、曲线优化控制对频率波动的抑制能力较强，曲线振荡幅度较小，恢复到稳定状态的时间较短。并且，第二种控制下的转子转速上升幅度最大，由 0.04(pu)提高至0.08(pu)。同时，此控制下系统的频率峰值最小，由50.2Hz改善为50.11Hz。第三种控制下的系统频率恢复时间最短，由 7s缩短为 2s。同理，当投入负荷时可得类似结果。由此可知，虽然三种VSG控制方式令双馈风机系统具备与同步机一样的调速能力，实现了惯性补偿，但是其控制效果的侧重点存在差异。这与前面范数分析结果相一致。
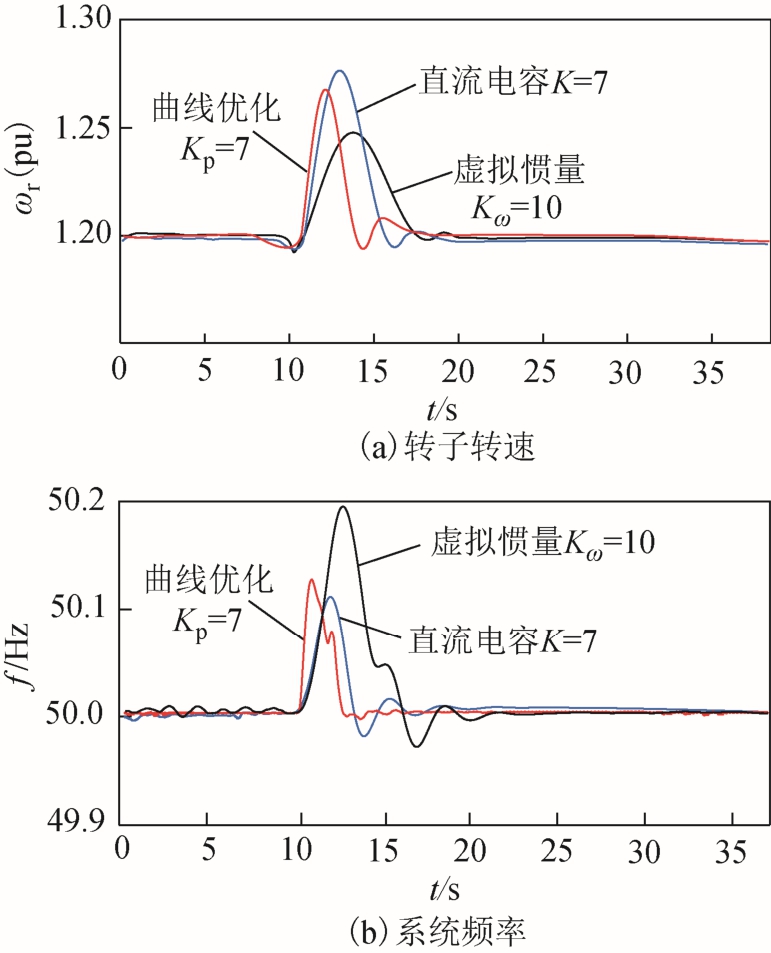
图10 切除负荷系统的响应
Fig.10 System response to remove load
图11 投入负荷系统的响应
Fig.11 System response in loading
表2 系统响应参数
Tab.2 The parameters of system response
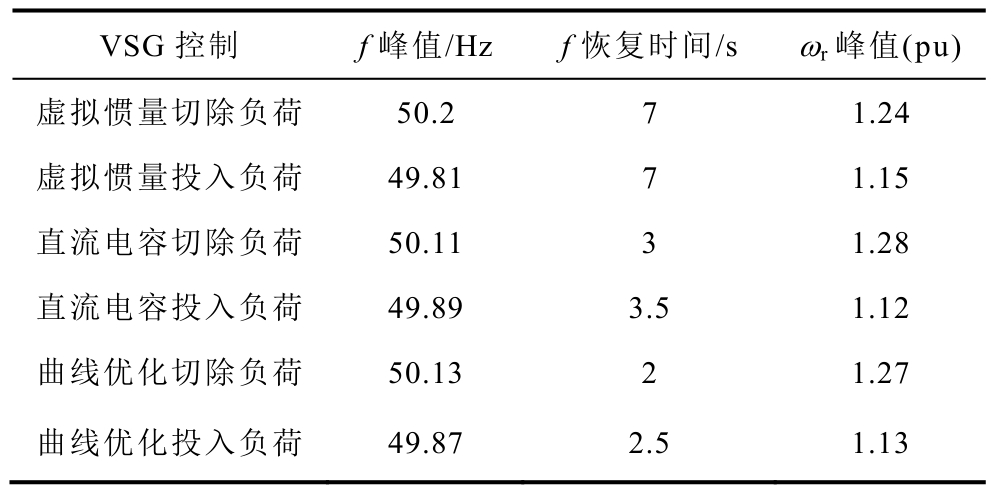
VSG控制 f峰值/Hz f恢复时间/s ωr峰值(pu)虚拟惯量切除负荷 50.2 7 1.24虚拟惯量投入负荷 49.81 7 1.15直流电容切除负荷 50.11 3 1.28直流电容投入负荷 49.89 3.5 1.12曲线优化切除负荷 50.13 2 1.27曲线优化投入负荷 49.87 2.5 1.13
过上述仿真，验证了H2、H∞范数从能量角度定量刻画系统频率扰动抑制能力的有效性，且其数值越小，系统频率扰动的抑制能力就越强。同时，由第3节分析得到，第二种VSG控制方式对应的H2范数较小，其关于全频段输入的平均抑制能力更强；第三种VSG控制方式对应的H∞范数较小，其关于最坏输入的抑制能力更强。将此分析结果与系统频率的仿真结果联系，可得：系统传递函数的H2范数和系统频率的超调量有很大的相关性，而系统传递函数的H∞范数和系统频率恢复时间快慢有很大的相关性。因此，当系统对超调量或响应时间存在具体控制要求时，可通过系统传递函数矩阵H2范数和H∞范数的计算，对其所对应的变量进行针对性的分析和讨论。
5 结论
VSG技术为双馈风机提供了惯性支撑，使之在并网时具备类似于同步机的频率响应特性，进而友好地接入电网。本文基于系统传递函数矩阵的H2和H∞范数，对三种附加VSG控制的DFIG系统进行了定量描述，分析了传递函数矩阵范数与系统频率扰动抑制能力之间的联系。以系统传递函数矩阵的H2和H∞范数为指标，对三种 VSG技术在惯性支撑上的贡献进行分析。搭建系统状态空间模型，横向比较了三种主流VSG的频率响应差异。通过对比特征根稳定分析方法，论证了H2、H∞范数对DFIG系统频率抑制能力描述的可行性，并选择不同的控制参数进行仿真分析。最后得出，系统传递函数矩阵的H 2/H∞范数与双馈风机系统频率振荡抑制能力之间存在量化关系，可以从惯性补偿的角度为控制策略提供参数选择。同时，也为评价不同形式的VSG控制提供了一种行之有效的方法依据。
后续研究工作中，可根据H 2/H∞范数对控制方式进行指导优化，并进一步通过半实物仿真校验其控制效果。
附 录
1.双馈风机系统状态方程
选定dq旋转坐标系下，定转子电压与磁链方程[37]为
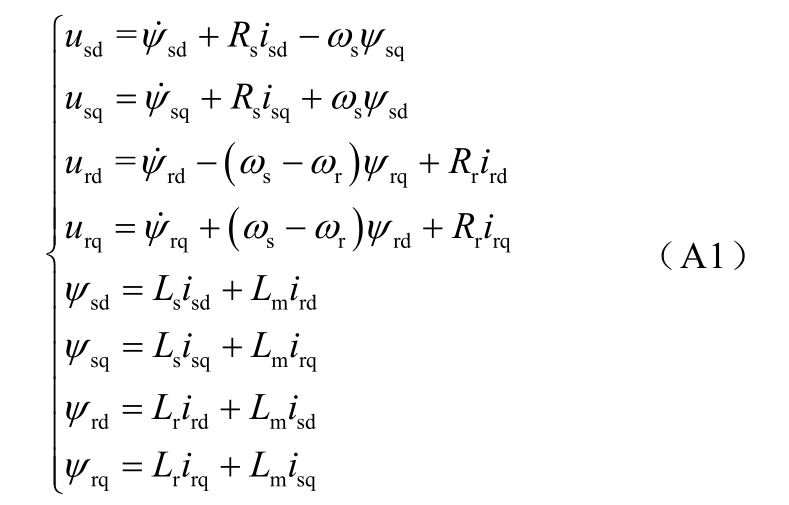
式中，u为电压；i为电流；ψ为磁链；下标s表示定子，r表示转子；ωs为坐标系的旋转角速度；ωr为风机转子角速度；Rs为定子电阻；Rr为转子电阻；Ls为定子自感；Lr为转子自感；Lm为定子与转子互感。
消掉定子磁链和转子电流，得
转子侧变流器控制系统模型为
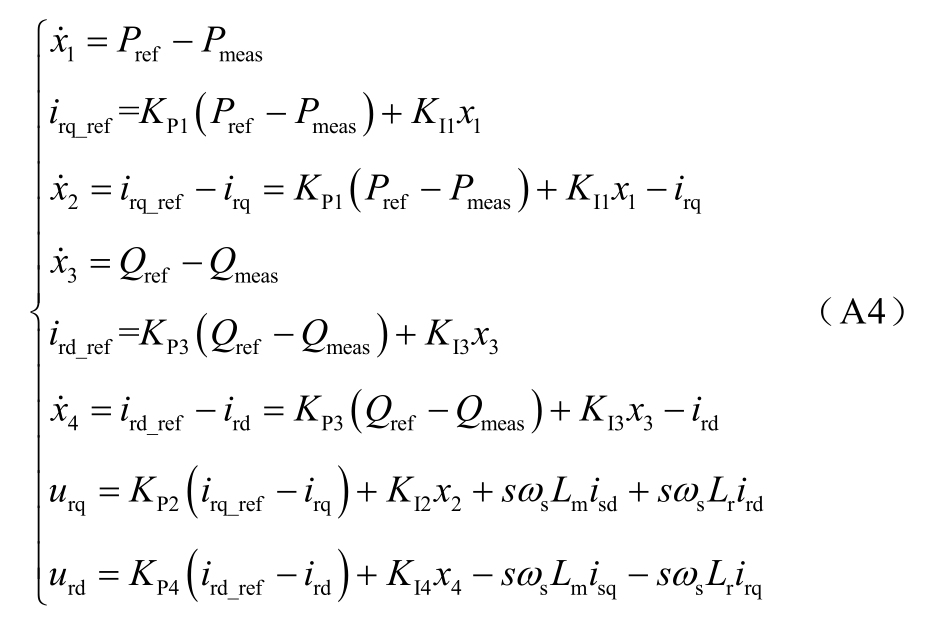
式中，x1、x2、x3、x4为转子侧控制环节引入的中间变量；KP1、KI1、KP3、KI3分别为功率外环的两个 PI控制器的 PI控制参数；KP2、KI2、KP4、KI4分别为电流内环的两个 PI控制器的 PI控制参数；ird_ref、irq_ref为转子电流参考值；s为转差率。
网侧变流器控制系统模型为
式中，x5、x6、x7为网侧控制环节引入的中间变量；udg、u q g为网端电压；idg、iqg为网端电流；KPg、KIg分别为网侧变流器系统电流内环的PI控制参数。
驱动链模型为
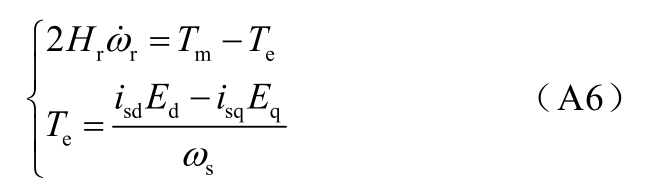
式中，Hr为发电机的惯性时间常数；Tm为风力机的机械转矩；Te为发电机的电磁转矩。
变流器和直流电容模型为
锁相环模型为
式中，xPLL为跟踪定子d轴电压的误差积累；δPLL为锁相环相位；ωs_ PL L 为锁相环测得的旋转角速度；K P _PLL 、KI_PLL分别为锁相环的PI控制参数。
远端母线电压表示为
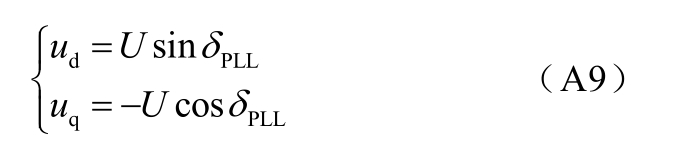
式中，U为电压幅值，取1.0 (pu)。
2.系数矩阵
[1]贺益康, 胡家兵, 徐烈.并网双馈异步风力发电机运行控制[M].北京: 中国电力出版社, 2012.
[2]康祎龙, 郑婷婷, 苗世洪, 等.不平衡电网电压下双馈感应发电机系统串联和并联网侧变换器协调控制策略[J].电工技术学报, 2018, 33(增刊 1):193-204.Kang Yilong, Zheng Tingting, Miao Shihong, et al.Coordinated control strategy of series and parallel grid side converters for DFIG system under unbalanced grid voltage[J].Transactions of China Electrotechnical Society, 2018, 33(S1): 193-204.
[3]马少康, 耿华, 马进, 等.双馈型风电场详细模型建模方法[J].电工技术学报, 2017, 32(增刊1): 1-10.Ma Shaokang, Geng Hua, Ma Jin, et al.An approach to establish detailed model of DFIG based wind farm[J].Transactions of China Electrotechnical Society, 2017, 32(S1): 1-10.
[4]刘瑞芳, 任雪娇, 陈嘉垚.双馈异步风力发电机的轴电流分析[J].电工技术学报, 2018, 33(19):4517-4525.Liu Ruifang, Ren Xuejiao, Chen Jiayao.Analysis of bearing currents in doubly-fed induction wind turbines[J].Transactions of China Electrotechnical Society, 2018, 33(19): 4517-4525.
[5]张海燕, 王杰.不平衡电网电压下双馈风力发电机高阶滑模控制方法[J].电机与控制学报, 2019,23(4): 37-48.Zhang Haiyan, Wang Jie.High-order sliding mode control method for doubly-fed wind power generator under unbalanced grid voltage[J].Electric Machines and Control, 2019, 23(4): 37-48.
[6]Chen Lei, Min Yong, Chen Yiping, et al.Evaluation of generator damping using oscillation energy dissipation and the connection with modal analysis[J].IEEE Transactions on Power Systems, 2014, 29(3):1393-1402.
[7]Hu Jiabing, Sun Li, Yuan Xiaoming, et al.Modeling of type 3 wind turbine with df/dt inertia control for system frequency response study[J].IEEE Transactions on Power Systems, 2017, 32(4): 2799-2809.
[8]王磊, 张琛, 李征, 等.双馈风电机组的虚拟同步控制及弱网运行特性分析[J].电力系统保护与控制, 2017, 45(13): 85-90.Wang Lei, Zhang Chen, Li Zheng, et al.Virtual synchronous generator control for DFIG wind turbines and its operation characteristics in weak grid[J].Power System Protection and Control, 2017,45(13): 85-90.
[9]刘斯伟, 李庚银, 周明.双馈风电机组对接入区域系统暂态功角稳定性的影响分析[J].电力系统保护与控制, 2016, 44(6): 56-61.Liu Siwei, Li Gengyin, Zhou Ming.Impact analysis of doubly-fed induction generator on the transientangle stability of the region with wind power integrated[J].Power System Protection and Control,2016, 44(6): 56-61.
[10]Ma Jing, Qiu Yang, Li Yinan, et al.Research on the impact of DFIG virtual inertia control on power system small-signal stability considering the phase-locked loop[J].IEEE Transactions on Power Systems, 2017, 32(3): 2094-2105.
[11]孙丽玲, 王艳娟, 许伯强.DFIG高电压穿越暂态特性分析及控制策略改进[J].电机与控制学报, 2019,23(2): 27-34.Sun Liling, Wang Yanjuan, Xu Boqiang.Transient analysis and control strategy improvement of high voltage ride through of DFIG[J].Electric Machines and Control, 2019, 23(2): 27-34.
[12]Geng Hua, Xi Xinze, Yang Geng.Small-signal stability of power system integrated with ancillary controlled large-scale DFIG based wind farm[J].IET Renewable Power Generation, 2016, 11(8): 1191-1198.
[13]Beck H P, Hesse R.Virtual synchronous machine[C]// Proceedings of 2007 9th International Conference on Electrical Power Quality and Utilisation, Barcelona, 2007: 1-6.
[14]Zhong Qingchang.Virtual synchronous machines: a unified interface for grid integration[J].IEEE Power Electronics Magazine, 2016, 3(4): 18-27.
[15]葛俊, 刘辉, 江浩, 等.虚拟同步发电机并网运行适应性分析及探讨[J].电力系统自动化, 2018,42(9): 26-35.Ge Jun, Liu Hui, Jiang Hao, et al.Analysis and investigation on grid-connected operation adaptability of virtual synchronous generators[J].Automation of Electric Power Systems, 2018, 42(9): 26-35.
[16]杨明, 高龙将, 王海星, 等.电网不平衡下虚拟同步发电机功率-电流协调控制策略[J].电力系统保护与控制, 2019, 47(6): 17-23.Yang Ming, Gao Longjiang, Wang Haixing, et al.Coordinate control of power and current for virtual synchronous generator under unbalanced grid voltage[J].Power System Protection and Control,2019, 47(6): 17-23.
[17]陈文倩, 辛小南, 程志平.基于虚拟同步发电机的光储并网发电控制技术[J].电工技术学报, 2018,33(增刊 2): 538-545.Chen Wenqian, Xin Xiaonan, Cheng Zhiping.Control of grid-connected of photovoltaic system with storage based on virtual synchronous generator [J].Transactions of China Electrotechnical Society, 2018,33(S2): 538-545.
[18]缪惠宇, 梅飞, 张宸宇, 等.基于虚拟阻抗的虚拟同步整流器三相不平衡控制策略[J].电工技术学报, 2019, 34(17): 3622-3630.Miao Huiyu, Mei Fei, Zhang Chenyu, et al.Three phase unbalanced control strategy for virtual synchronous rectifier based on virtual impedance [J].Transactions of China Electrotechnical Society, 2019,34(17): 3622-3630.
[19]赵晶晶, 吕雪, 符杨, 等.基于可变系数的双馈风机虚拟惯量与超速控制协调的风光柴微电网频率调节技术[J].电工技术学报, 2015, 30(5): 59-68.Zhao Jingjing, Lü Xue, Fu Yang, et al.Frequency regulation of the wind/photovoltaic/diesel microgrid based on DFIG cooperative strategy with variable coefficients between virtual inertia and over-speed control[J].Transactions of China Electrotechnical Society, 2015, 30(5): 59-68.
[20]马静, 李益楠, 邱扬, 等.双馈风电机组虚拟惯量控制对系统小干扰稳定性的影响[J].电力系统自动化, 2016, 40(16): 1-7.Ma Jing, Li Yinan, Qiu Yang, et al.Impact of virtual inertia control of DFIG wind turbines on system small-signal stability[J].Automation of Electric Power Systems, 2016, 40(16): 1-7.
[21]赵晶晶, 吕雪, 符杨, 等.基于双馈感应风力发电机虚拟惯量和桨距角联合控制的风光柴微电网动态频率控制[J].中国电机工程学报, 2015, 35(15):3815-3822.Zhao Jingjing, Lü Xue, Fu Yang, et al.Dynamic frequency control strategy of wind/photovoltaic/diesel microgrid based on DFIG virtual inertia control and pitch angle control[J].Proceedings of the CSEE,2015,35 (15): 3815-3822.
[22]彭晓涛, 贾继超, 周际城, 等.优化风电惯性响应的变比例系数调速策略[J].中国电机工程学报,2018, 38(19): 5625-5635.Peng Xiaotao, Jia Jichao, Zhou Jicheng, et al.Speed regulation strategy based on variable proportion coefficient for optimizing inertial response of windgenerator[J].Proceedings of the CSEE, 2018, 38(19):5625-5635.
[23]周天沛, 孙伟.高渗透率下变速风力机组虚拟惯性控制的研究[J].中国电机工程学报, 2017, 37(2):486-495.Zhou Tianpei, Sun Wei.Study on virtual inertia control for DFIG-based wind farms with high penetration[J].Proceedings of the CSEE, 2017, 37(2):486-495.
[24]李和明, 张祥宇, 王毅, 等.基于功率跟踪优化的双馈风力发电机组虚拟惯性控制技术[J].中国电机工程学报, 2012, 32(7): 32-39.Li Heming, Zhang Xiangyu, Wang Yi, et al.Virtual inertia control of DFIG-based wind turbines based on the optimal power tracking[J].Proceedings of the CSEE, 2012, 32(7): 32-39.
[25]周凌辉, 谷志华, 彭晓涛.一种构造双馈风机虚拟惯性的自适应风功率跟踪策略[J].船电技术, 2017,37(3): 51-57.Zhou Linghui, Gu Zhihua, Peng Xiaotao.An adaptive wind power tracking strategy for constructing virtual inertia of doubly-fed induction generator-based wind turbine[J].Marine Electric & Electronic Technology,2017, 37(3): 51-57.
[26]Zhu J, Booth C D, Adam G P, et al.Inertia emulation control strategy for VSC-HVDC transmission systems[J].IEEE Transactions on Power Systems,2013, 28(2): 1277-1287.
[27]Zhang H, Zhu J, Guerrero J M, et al.A generic inertia emulation controller for multi-terminal VSC-HVDC systems[C]// 2nd IET Renewable Power Generation Conference, Beijing, 2014: 109-114.
[28]陈润泽, 吴文传, 孙宏斌, 等.双馈风电机组惯量控制对系统小干扰稳定的影响[J].电力系统自动化, 2014, 38(23): 6-12.Hen Runze, Wu Wenchuan, Sun Hongbin, et al.Impact of inertia control of DFIG wind turbines on system small-signal stability[J].Automation of Electric Power Systems, 2014, 38(23): 6-12.
[29]王清, 毕天姝, 薛安成.基于相似性的双馈风机小干扰稳定性分析及锁相环的影响[J].电力系统自动化, 2016, 40(6): 30-34, 84.Wang Qing, Bi Tianshu, Xue Ancheng.Similarity-based small-signal stability analysis of DFIG-based wind turbines and influence of phase-locked loop[J].Automation of Electric Power Systems, 2016, 40(6): 30-34, 84.
[30]黄林彬, 辛焕海, 黄伟, 等.含虚拟惯量的电力系统频率响应特性定量分析方法[J].电力系统自动化, 2018, 42(8): 31-38.Huang Linbin, Xin Huanhai, Huang Wei, et al.Quantified analysis method of frequency response characteristics for power systems with virtual inertia[J].Automation of Electric Power Systems,2018, 42(8): 31-38.
[31]俞立.鲁棒控制:线性矩阵不等式处理方法[M].北京: 清华大学出版社, 2002.
[32]Gopal M.Modern control system theory[M].England:Wiley, 1993.
[33]梅生伟, 申铁龙, 刘康志.现代鲁棒控制理论与应用[M].北京: 清华大学出版社, 2008.
[34]Simpson-Porco J W, Bullo F.Synchronization and power sharing for droop-controlled inverters in islanded microgrids[J].Automatica, 2013, 49(9):2603-2611.
[35]王锡凡.现代电力系统分析[M].北京: 科学出版社, 2003.
[36]Ackermann T.Wind power in power systems[M].2nd ed.London: Wiley, 2014.
[37]周双喜.风力发电与电力系统[M].北京: 中国电力出版社, 2011.