0 引言
电磁超声技术因具有非接触、灵敏度高、无需耦合剂等优势被广泛应用于无损检测领域,但接收到的信号存在信噪比低、特征信号难以辨别的问题,导致电磁超声技术的发展受到了一定的限制。为满足无损检测设备智能化的需要,基于计算机语言的数学算法被应用到接收信号处理之中,也推动着电磁超声乃至其他无损检测技术在信号处理方面得到发展[1-3]。
针对接收信号微弱、噪声严重等问题,常规电磁超声信号处理方法主要采用低噪前置放大器等高抗干扰电路[4]、计算机算法降噪[5]等方法,但这些方法无法高效、精确地提取特征信号。随着计算机算法的不断发展,利用高效的算法并嵌入到带有片上系统(System of Chip,SOC)的硬件设备中来取代硬件功能电路[6],基于各种数学算法的数据处理方法成为目前发展快速、应用广泛、功能强大的信号处理手段之一。
采集到的超声信号常存在信噪比低的特点,为有效地辨别超声信号时域信息,文献[7]采集多组缺陷回波信号样本,采用小波包降噪和小波包变换提取时频信息,以实现对实验样本缺陷的有效识别。文献[8]采用四倍平均算法改善接收波的信噪比,实现对 P60钢轨人工缺陷的定位。文献[9]提出一种基于解析小波阈值的去噪方法,用于降低磁声电无损检测中的噪声。对于小波降噪方法,由于小波基需根据不同信号进行选择,且上述文献采用的平均算法均对输入信号存在一定限制,使其适用范围受限,通用性差。而对于信号特征提取,文献[10]采用微分算法对超声信号进行特征提取,实现管道壁厚的不均匀性检测,但并未提取频域特征。文献[11]采用小波包分析和快速傅里叶变换(Fast Fourier Transformation, FFT)分析确定接收信号在各频段的能量分布,实现对铁磁性材料的损伤评定,但是也受困于小波基选择的局限性。而传统信号提取方法多采用自相关算法,对于多频率信号特征提取相对较弱。
非线性超声技术对材料应力疲劳损伤、微裂纹检测更为敏感,但非线性超声信号相对于线性超声信号幅值较低,因而从噪声信号中提取到幅值较高的非线性信号至关重要[12-14]。针对非平稳、非线性信号的特征提取,N.E.Huang提出了经验模态分解(Empirical Mode Decomposition, EMD)方法,该方法被应用于超声检测及无损评估中并取得了显著成果。文献[15]提出EMD方法与短时傅里叶变换相结合的超声导波信号处理方法,用于层状复合材料的无损评估。文献[16]在对薄层金属材料厚度检测过程中,采用 EMD对非平稳信号进行降噪处理,实现对峰值信号到达时刻的准确获取。文献[17]采用EMD方法将兰姆波分解为一组固有模态函数,用于区分不同目标的重叠散射信号,以用于板结构的无损检测。文献[18]采用集合EMD算法与信号最小化算法对奥氏体不锈钢样品进行缺陷信号重构,实现50mm厚的粗晶奥氏体不锈钢内缺陷检测。文献[19]基于 EMD方法提取复合材料结构损伤程度状态特征,并根据距离和形状相似性定义材料损伤指数。采用由数据驱动的 EMD方法进行特征提取具有明显优势,且通用性较好[20]。
针对电磁超声信号的非平稳、非线性特性,以及信噪比低、特征信号难以辨别等问题,本文提出将 EMD方法与自适应滤波算法相融合,并经现场可编辑门阵列(Field-Programmable Gate Array,FPGA)硬件逻辑实现该方法。本方法为基于线性方均误差准则和经验模态分解相融合的数字信号处理方法,主要适用于具有非线性、非平稳特性的电磁超声信号,且对信噪比低、特征难以提取的微弱信号均有积极作用,方法的通用性较高,能最大程度地保留原始信号的非线性,对噪声抑制表现优秀,时频提取高效。本方法采用FPGA实现,对带有微裂纹、塑性损伤的薄铝板进行实验,验证该方法的有效性,为实现信号的识别、定位和非线性分析奠定基础。
1 电磁超声信号平稳性评估
在信号缺陷检测过程中,缺陷信息往往由特征信号的幅值、频率或相位表征,但由于被测试件本身和传输环境复杂性,导致电磁超声信号在激发、传输和接收过程中引入噪声,造成超声信号混杂,需确定超声信号非线性和非平稳特性。
1.1 电磁超声信号平稳性检验
将采集到的电磁超声信号长度设为 n,将其分为k段,每段有m=n/k个数据,则k个子序列中任一子序列与原始数据的关系可以表征为
式中, i = 1 , 2, … ,k ;j = 1 , 2, … , m。
并构建统计量z
式中,R为轮次数;μR为独立随机序列轮次数的期望;σR为独立随机序列轮次数的方差。
假设数据具备平稳性,则在给定显著性水平 a的条件下(选取产生错误结论的最大概率为0.1,即a= 0.1;对于大样本数据,式(2)中数据则可以利用正态分布来近似),记作平稳性检测参数Za。根据式(2),若统计量 z ≤Za ,则数据具备平稳性;反之,则数据不具备平稳性。
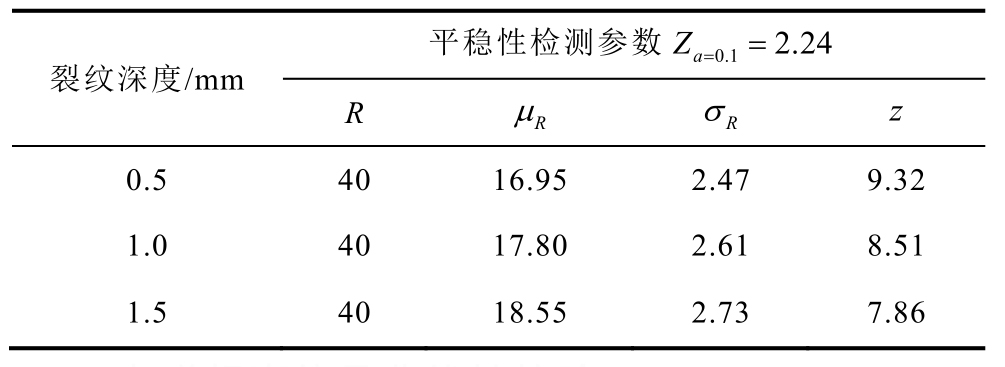
本文对标准裂纹试块H—80上宽度为0.1mm的三种深度的裂纹进行电磁超声检测,激励信号选用1MHz的超声信号,对每个裂纹深度连续采样,得到相对应的平稳性检验结果,见表1。
由表1计算得到的统计结果可知,三种裂纹深度下,通过超声实验采样得到的统计量均大于给定显著性水平a的平稳性检测参数,故接收到的电磁超声信号为非平稳性信号。
表1 电磁超声信号的平稳性检验
Tab.1 Stationarity test of electromagnetic ultrasonic signals
平稳性检测参数 0.1 2.24 Z= =a裂纹深度/mm R μR σR z 0.5 40 16.95 2.47 9.32 1.0 40 17.80 2.61 8.51 1.5 40 18.55 2.73 7.86
1.2 电磁超声信号非线性检验
在非线性检验方法中,由于重复幅度匹配傅里叶变换(Iterated Amplitude Adjusted Fourier Transform,IAAFT)算法能够提供很好地匹配原始数据的傅里叶频谱和概率密度分布,因此在数据非线性检验中得到广泛应用。
采用IAAFT算法生成替换数据,直到替换数据与原始数据有相似的功率谱密度,进而选择具有时间不对称的三阶统计量偏斜度和检验非线性成分的三阶统计量自相关,作为电磁超声观测数据的特征值,其数学表达式如下。
偏斜度
三阶自相关
式中,τ 为时间延迟量;xn为时间序列第n个值;N为时间序列的长度。
为验证电磁超声信号的非线性特性,对 1.1节中的实验数据进行非线性参数计算,得到相对应的非线性检验结果见表2。
表2 电磁超声信号的非线性检验结果
Tab.2 Nonlinear test of electromagnetic ultrasonic signals

裂纹深度/mm偏斜度 三阶自相关实验数据 替代数据 实验数据 替代数据0.5 -12.316 -4.501 -949.267 -245.420 1.0 -0.076 0.002 108.992 193.113 1.5 -0.046 0.003 31.872 77.650
由表2可看出,电磁超声实验数据和替代数据在偏斜度和三阶自相关存在明显差异,表明电磁超声信号存在非线性,即在超声检测中的应力波存在非线性,该非线性不是由于测量函数引起的,而是所测试件本身缺陷与超声波相交互作用所引起的非线性。
2 电磁超声自适应算法建模及FPGA实现
针对电磁超声信号的非平稳、非线性特性及信噪比低、特征信号难以辨别等问题,本文提出一种电磁超声信号自适应滤波和 EMD分解相融合的数据处理算法,其模型如图1所示。
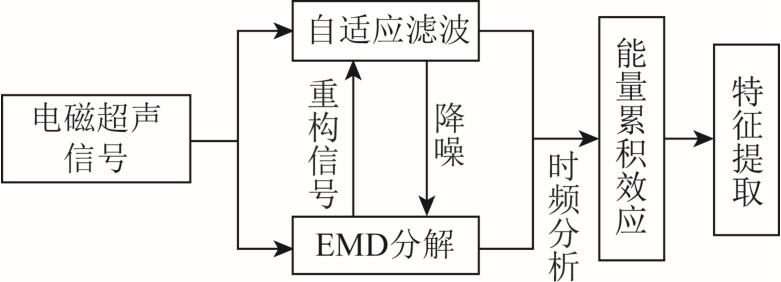
图1 自适应处理算法模型
Fig.1 Adaptive processing algorithm model schematic
如图1所示,自适应滤波器采用最小方差(Least Mean Square, LMS)准则计算自适应滤波器的系数,EMD分解则根据LMS算法估计权值,使得重构信号逼近原始信号。一旦有电磁超声信号输入本算法时,自适应滤波与EMD分解在LMS算法下相互作用,EMD分解得到的本征模函数重构效果可最优采用LMS算法估计权值,而LMS算法也在进行自适应滤波处理,保证在重构信号时噪声影响系数较小,EMD分解得到的本征模函数可信度更高。EMD分解得到的噪声频率传递给自适应滤波器,经LMS算法进行消除。该融合方法并不会使得系统自适应赘余,反而得到效果更佳的时频信息。本自适应处理算法原理如图2所示。

图2 自适应处理算法原理图
Fig.2 Adaptive processing algorithm schematic
输入信号的时序序列为X[n],LMS算法的权值迭代更新方式:利用一种寻找式实时逼近的替代方法,摒弃了相关函数的严格度量,利用下一个权值等于当前权值加上正比于梯度的一个改变量,得到
式中,μ为控制算法稳定性和算法收敛速度的步长,FPGA数据处理选择二进制代码,一般选取 μ为 2的整数次幂分之一。
经过自适应算法处理后的时域信号为 Y[n],EMD分解得到噪声频率并传递给自适应滤波器进行噪声滤除,得到信噪比较高的时域信号Z[n],H[n]为重构信号,则得到
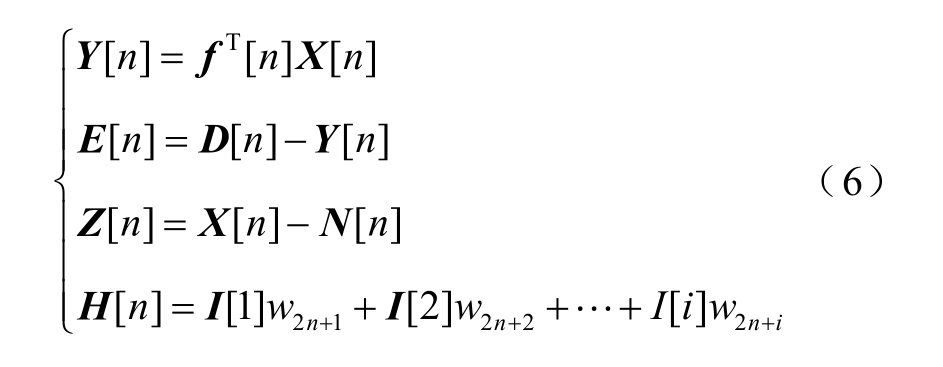
式中,E[n]为误差函数;D[n]为期望响应;f为LMS权值;N[n]为EMD分解后噪声函数;I[i]为本征模函数。
数字 LMS算法中的权值均可对电磁超声输入信号进行调整,而期望信号D[n]可在系统中经式(6)计算后确定一些参数,EMD提取到的主成分频率和干扰噪声频率等信息不受权值调整。期望信号若选择噪声信号,则该系统相当于干扰抵消系统,同样可以得到较好的滤波效果,LMS算法的误差信号E[n]即为本系统自适应滤波器的输出结果。
经过自适应处理算法后得到的时频信息成分存在数量较大,则定义单位频率内的能量密度函数为G(ω),超声信号的频谱函数为F(jω),由帕塞瓦尔定理可得超声信号能量为

式中,由能量密度函数表示各阶 IMF的频谱函数,即G(ω) = [F(jω) ]2 。
为选取超声信号的主要成分在整个时域内的主成分,即选取能反映特征信号信息的本征模函数,通常取能量比率累积(Energy Ratio Accumalation,ERA)≥95%时的IMF阶数作为最大阶数[21],记为k,则前k阶IMF能量比率系数(Energy Proportion Coefficient, EPC)为
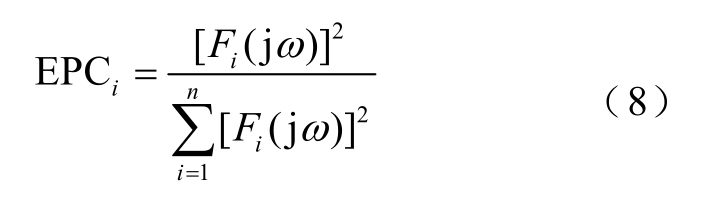
式中,i为IMF阶数次序,i≤k。
由式(8)可计算出前 i阶 IMF所占的能量比率,进一步反映电磁超声信号本身能量分布,对确定特征信号信息意义重大。
本文自适应滤波和 EMD分解相融合的数据处理算法基于FPGA实现,利用硬件描述语言Verilog编写,将该算法综合成可用于FPGA的功能模块,利用片上硬件逻辑资源实现算法功能,采用 QuartusII编写顶层程序,对于算法模块进行端口声明并进行模块与数据端口连接操作,最终将程序编译、布局布线、配置到FPGA中,图3所示为FPGA程序编译后的RTL级功能电路图。
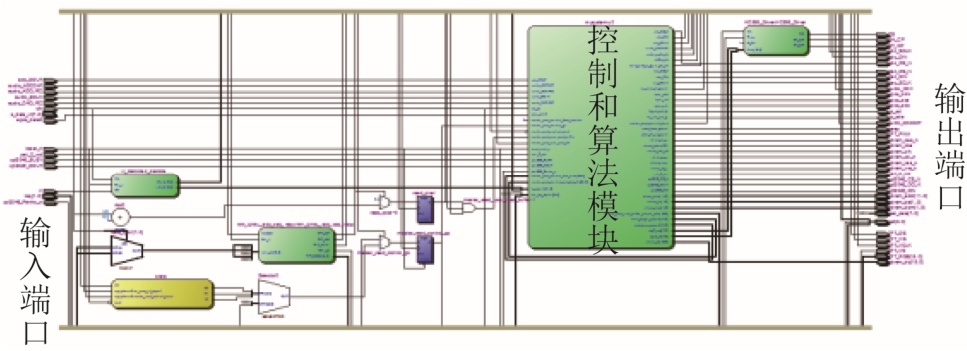
图3 RTL级功能电路
Fig.3 RTL level function circuit diagram
3 实验研究与结果分析
3.1 电磁超声对裂纹缺陷检测
为了验证本算法的性能,对带有裂纹的薄铝板进行缺陷检测,实验铝板尺寸为600mm×60mm× 1mm,裂纹在铝板正中位置,裂纹尺寸为 30mm×0.5mm×1mm。基于 FPGA兰姆波的无损检测系统如图4所示,采用一发一收电磁超声换能器(Electromagnetic Acoustic Transducer, EMAT)在铝板中激发和接收兰姆波。激发探头距离左端面边界50mm,接收探头距离左端面边界150mm,裂纹距离左端面边界300mm,激发探头和接收探头采用双层三分裂五匝线圈结构与方形磁铁结构相结合,均为1MHz的宽带频率探头。通过低噪放大电路和10MHz的模数转换电路采集原始数据,输送给带有SOC的硬件设备进行数据处理,运行本文所提出的自适应算法,进行自适应降噪、时频特征提取、波包到达时刻提取等。
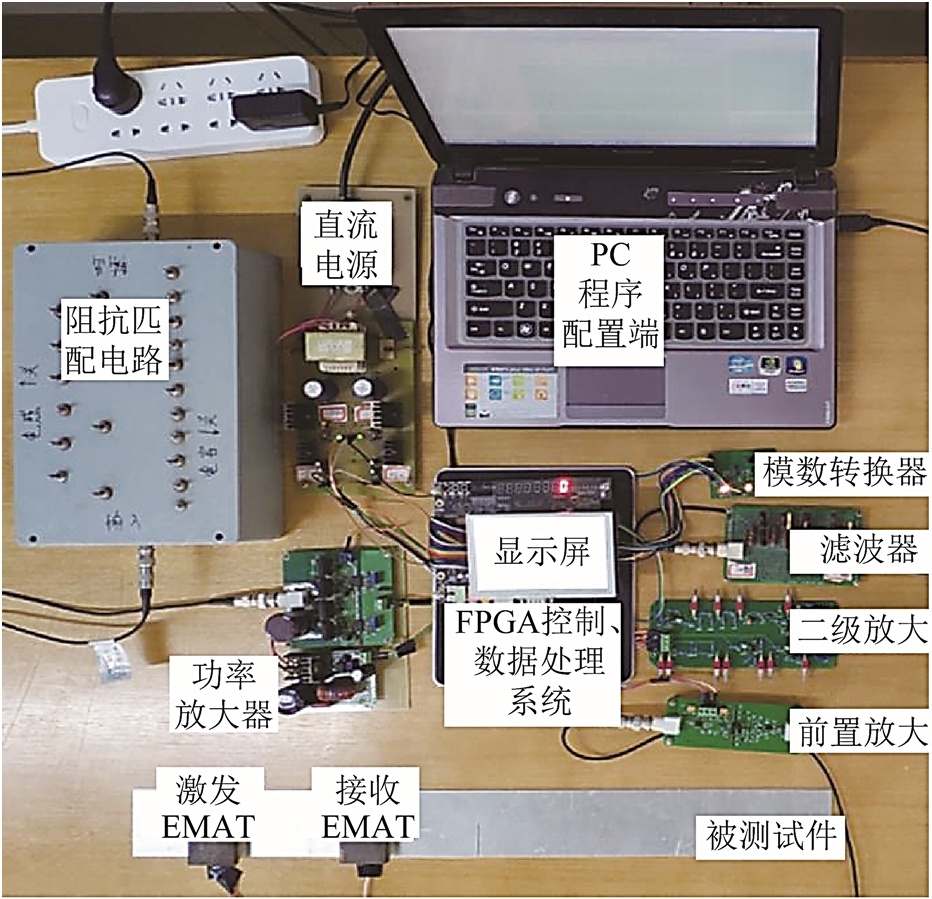
图4 基于FPGA的兰姆波检测系统实物图
Fig.4 Physical map of Lamb wave detection system based on FPGA
为验证自适应算法的降噪效果,采集处理后数据和传入数据处理模块前的信号进行对比,如图5所示。图5a为输入超声信号,只是把接收换能器采集到的初始信号经过前置放大器后将微弱信号放大,特征信号波包被噪声湮没,难以辨别;图5b为自适应算法状态 1采集到的实验波形,μ相对较大,估计误差为0.05;图5c为滤除杂波后获得的信号,且估计误差为 0.025时采集到的波形,降噪后的特征信号明显,信噪比较高。随着自适应反馈调节滤波器的系数、滤波器自相关性逐渐增强,所实现的降噪效果也会越来越明显。
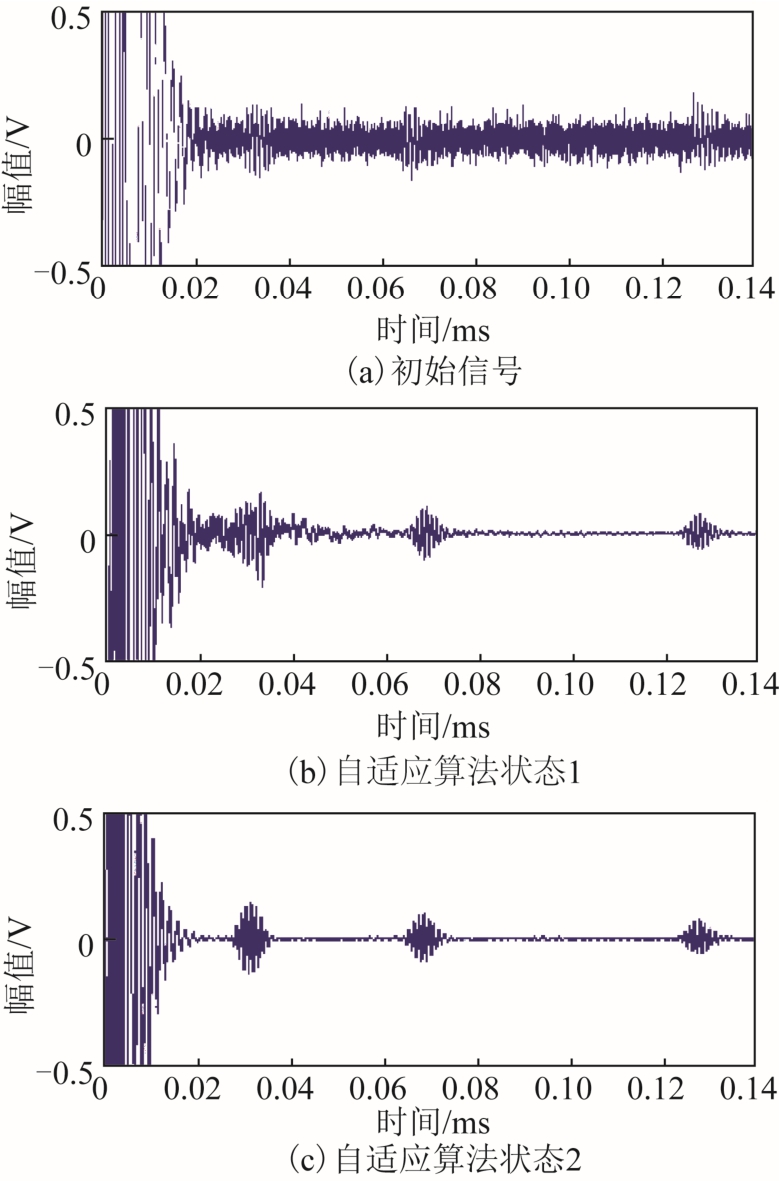
图5 自适应算法的实验效果
Fig.5 Experimental effect of adaptive method
图6为经过EMD分解后的前8阶IMF。由图6可知,EMD方法可将电磁超声信号分解为在同一时间刻度上的不同表征,主要特征集中在前三阶IMF,从中可提取到波包到达时刻,并且可根据不同缺陷信号本身尺度特征进行信号识别。
根据图6分解得到的电磁超声IMF成分,分别选取不同阶数IMF重构还原超声信号,如图7所示。由图7可知,信号主要成分集中在前几阶IMF中,且包含噪声成分极少,还原超声信号较好,表明超声原始信号能量主要分布于前几阶IMF。

图6 EMD分解的各阶IMF
Fig.6 Experimental effect of adaptive method
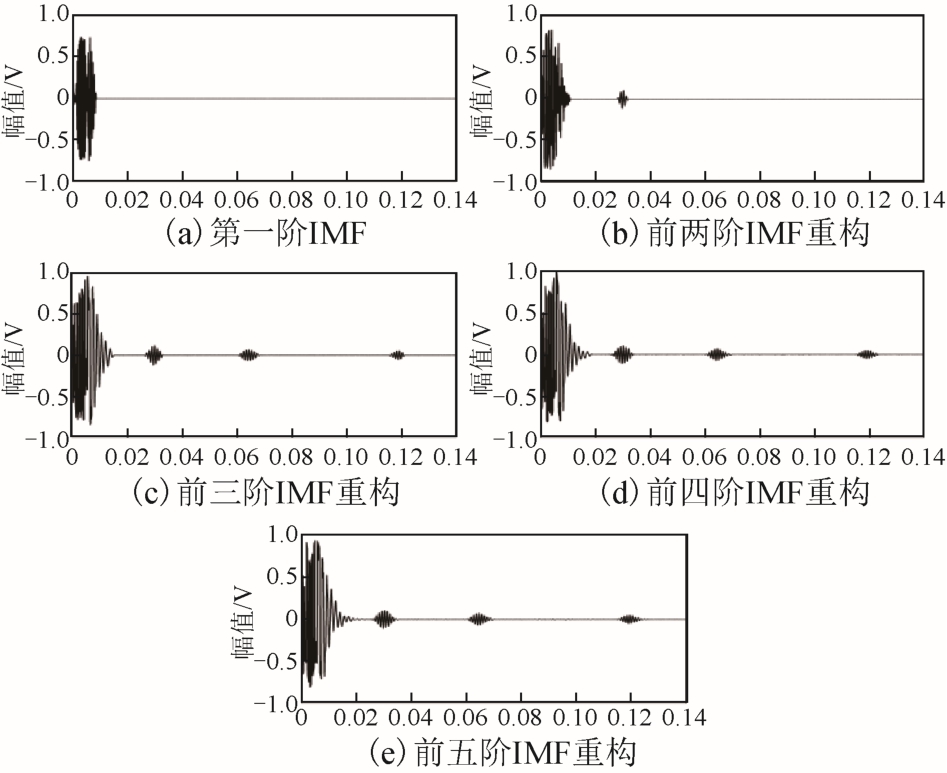
图7 EMD分解重构图
Fig.7 EMD reconstruction diagram
各阶IMF能量占比见表3。由表3可知,能量主要集中在前五阶 IMF,经计算 ERA=99.67%,所以选取前五阶IMF足以能够表征电磁超声特征信号的信息,且有一小部分低频噪声信号,在能量占比中可忽略不计。
表3 各阶IMF能量占比
Tab.3 IMF EPC of each order

IMF分量 能量J 能量占比(%)IMF1 2 158 55.87 IMF2 1 039 26.90 IMF3 494 12.79 IMF4 94 2.43 IMF5 65 1.68 IMF6 12 0.31 IMF7 0.5 0.01 IMF8 0.03 0
图8为前8阶本征模函数所对应的频域图。由图8可知,特征信号频段均在1MHz,表明在信号的传播过程中,并未产生新频率的信号,可反映出实验铝板内部结构并未发生影响频率变化的改变。另外,EMD分解在高信噪比的条件下,能清晰地表征特征信号能量分布,在时频分析方面具有实用价值。

图8 各阶IMF频域图
Fig.8 Each order IMF frequency domain diagram
图9为经过自适应算法得到的带裂纹铝板的接收信号时域图,图中显示的波包依次为在铝板中传递过程中采集到的直达波、左端面回波、裂纹回波。

图9 带有裂纹铝板的接收信号时域图
Fig.9 Time domain diagram of received signal with microcracked aluminum plate
根据采集到的时频信息,对铝板中裂纹可实现定位。激发和接收线圈位置由线圈中间位置确定,各个波包起振时刻作为波包到达时刻,波速根据兰姆波在铝板中的频散曲线获取,则裂纹距左端面位置可计算为
式中,Vg为兰姆波在铝板中传播的A0模态群速度,Vg=3.15m/ms;t1为左端面到达接收探头时刻,t1=63μs;t2为直达波到达裂纹后的返回波时刻,t2=127μs。
由式(9)计算结果可得到,检测到的裂纹位置与实际裂纹位置(裂纹距离左端面300mm)误差较小,能够较准确地定位裂纹。
3.2 电磁超声对塑性损伤检测
基于本文设计的兰姆波无损检测系统,对通过拉伸实验得到带有塑性损伤的铝板进行检测。激发探头和接收探头放置在裂纹两侧,激发信号频率为1MHz。经过快速傅里叶变换(Fast Fourier Transform, FFT)得到纵坐标以分贝方均根的频域图,如图10所示。由EMD分解得到的前4阶IMF频域图,如图11所示。
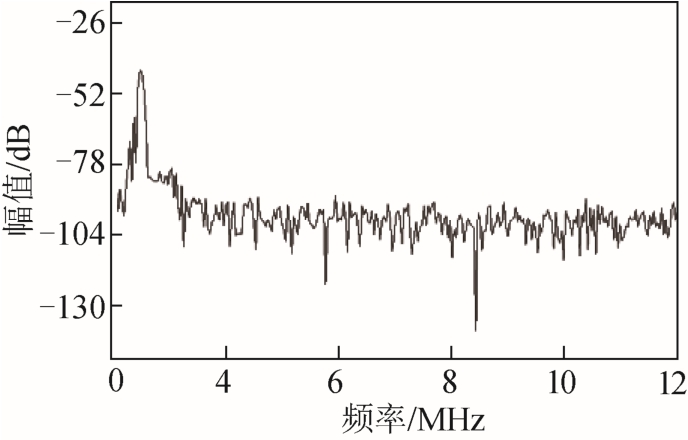
图10 FFT方法下塑性损伤铝板特征频谱图
Fig.10 Spectral spectrum of plastic damage aluminum plate based on FFT method

图11 EMD方法下塑性损伤铝板特征频谱图
Fig.11 Spectral spectrum of plastic damage aluminum plate based on EMD method
由图10和图11得到的塑性损伤铝板特征频谱图可知,图10中的 2次谐波相对于主频率能量较小,较难分辨出2次谐波及高次谐波,图10为透射波包得到的频率图,受到指定波包的限制,容易出现波包能量的泄露或掺杂进其他波包能量,能量占比存在误差较大,从而导致出现波包频率截断效应;图11则是由数据本身得到的频谱图,不存在波包的选择,且混入噪声能量较小,相对幅值较高。
材料存在塑性损伤时,电磁超声波在传播过程中受到材料非线性应力应变作用会产生以2次谐波为主的高次谐波。图11中,接收信号中出现了2MHz的谐波信息,谐波频率为激发信号频率的2倍,表明被拉伸的铝板产生了塑性损伤,因此本文提出的算法适用于铝材塑性损伤的检测。
4 结论
电磁超声无损检测容易受到外界干扰影响,造成接收端信号信噪比低,甚至影响后续信号的特征提取和识别精度。考虑自适应滤波器与经验模态分解特性,本文将自适应滤波算法与 EMD分解相融合,该融合方法噪声滤除效果明显、时频信息提取高效、软硬件结合友好。
本方法不仅能够对非线性、非稳态信号进行数据处理,并能滤除特定频率噪声,大大提高系统的信噪比,还能够针对电磁超声信号进行特征提取,且提取效果显著,选取的IMF能够很好地表征特征信号的信息,可靠性较高、自适应能力强。在实际缺陷检测中,能够准确定位裂纹位置,对塑性损伤进行谐波分析。本方法具有较好的通用性,适用范围广泛,为微裂纹、塑性的损伤检测奠定了基础,且本方法基于FPGA实现,对于检测设备便携化提供了可行性方案。
[1]王淑娟, 康磊, 李智超, 等.电磁超声换能器三维有限元分析及优化设计[J].中国电机工程学报,2009, 29(30): 123-128.Wang Shujuan, Kang Lei, Li Zhichao, et al.3-D finite element analysis and optimum design of electromagnetic acoustic transducers[J].Proceedings of the CSEE, 2009, 29(30): 123-128.
[2]Ashigwuike E C, Ushie O J, Mackay R, et al.A study of the transduction mechanisms of electromagnetic acoustic transducers (EMATs) on pipe steelmaterials[J].Sensors and Actuators A: Physical, 2015,229: 154-165.
[3]孙文秀, 刘国强, 夏慧, 等.非铁磁材料的电磁超声接收过程数值模拟及实验研究[J].电工技术学报,2018, 33(19): 4443-4449.Sun Wenxiu, Liu Guoqiang, Xia Hui, et al.Numerical simulation and experimental study of electromagnetic acoustic transducer receiving process in nonferromagnetic material[J].Transactions of China Electrotechnical Society, 2018, 33(19): 4443-4449.
[4]刘素贞, 李丽滨, 蔡智超, 等.电磁超声检测系统中消除电磁干扰电路的设计[J].电工技术学报,2016, 31(1): 80-84.Liu Suzhen, Li Libin, Cai Zhichao, et al.The Design for electromagnetic interference eliminating circuits in electromagnetic ultrasonic testing systems[J].Transactions of China Electrotechnical Society, 2016,31(1): 80-84.
[5]Talebhaghighi Z, Bazzazi F, Sadr A.Design and simulation of ultrasonic denoising algorithm using wavelet transform and ICA[C]//The 2nd International Conference on Computer & Automation Engineering,Singapore, 2010, 1: 739-743.
[6]梁子千, 玄文博, 王婷, 等.基于二维阻抗特征的管道环焊缝缺陷涡流检测[J].仪器仪表学报, 2017,38(9): 54-61.Liang Ziqian, Xuan Wenbo, Wang Ting, et al.Eddy current NDT for the cracks of girth welds of pipes based on 2D impedance characteristics[J].Chinese Journal of Scientific Instrument, 2017, 38(9): 54-61.
[7]汪开灿, 许霁, 翟国富.基于电磁超声的铝板缺陷识别方法[J].浙江大学学报(工学版), 2014, 48(11):2031-2038.Wang Kaican, Xu Ji, Zhai Guofu.Defect identification method for aluminum plate based on electromagnetic acoustic technique[J].Journal of Zhejiang University:Engineering Science, 2014, 48(11): 2031-2038.
[8]南钢洋, 王启武, 张振振, 等.基于激光超声方法的钢轨缺陷检测(英文)[J].红外与激光工程, 2017,6(1): 132-137.Nan Gangyang, Wang Qiwu, Zhang Zhenzhen, et al.Rail steel flaw inspection based on laser ultrasonic method [J].Infrared and Laser Engineering, 2017,6(1): 132-137.
[9]Lü Jingxiang, Liu Guoqiang.Noise reduction in magneto-acousto-electrical NDT using analytic wavelet thresholding [C]// 2017 IEEE 3rd Information Technology and Mechatronics Engineering Conference(ITOEC), 2017: 585-588.
[10]曹建树, 罗振兴, 姬保平.应用微分算法处理特种管道测厚激光超声信号[J].光学精密工程, 2017,25(5): 1197-1205.Cao Jianshu, Luo Zhenxing, Ji Baoping.Laser ultrasonic signal processing by differential aloorithm in special pipeline thickness measurement [J].Optics and Precision Engineering, 2017, 25(5): 1197-1205.
[11]金亮, 寇晓斐, 郭富坤, 等.基于电磁超声换能器的铁磁材料电磁声发射检测方法[J].电工技术学报, 2017, 32(18): 98-105.Jin Liang, Kou Xiaofei, Guo Fukun, et al.Electromagnetic acoustic emission detection method of ferromagnetic materials based on the EMAT[J].Transactions of China Electrotechnical Society, 2017,32(18): 98-105.
[12]张剑锋, 轩福贞, 项延训.材料损伤的非线性超声评价研究进展[J].科学通报, 2016, 61(34): 1536-1550.Zhang Jianfeng, Xuan Fuzhen, Xiang Yanxun.Evaluation of material damage using nonlinear ultrasonic wave[J].Chinese Science Bulletin, 2016,61(34): 1536-1550.
[13]刘素贞, 李礼, 蔡智超, 等.非线性电磁超声对铝合金拉伸变形评价研究[J].声学学报, 2017, 42(1):60-66.Liu Suzhen, Li Li, Cai Zhichao, et al.Evaluation of the tensile deformation of aluminum alloy using EMAT for nonlinear ultrasonic detection[J].Acta Acustica, 2017, 42(1): 60-66.
[14]王大为, 王召巴.一种强噪声背景下微弱超声信号提取方法研究[J].物理学报, 2018, 67(21): 65-77.Wang Dawei, Wang Zhaoba.Weak ultrasonic signal detection in strong noise[J].Acta Physica Sinica, 2018,67(21): 65-77.
[15]Xu Hanhui, Xu Chunguang, Zhou Shiyuan.A new ultrasonic guided wave signal processing method for UNDE of laminated composite material[C]//1st International Conference on Mechanic Automation &Control Engineering, Wuhan, China, 2010: 2542-2545.
[16]刘永强, 杨世锡, 甘春标.一种基于激光超声的薄层金属材料厚度检测方法研究[J].振动与冲击,2018, 37(12): 147-152.Liu Yongqiang, Yang Shixi, Gan Chunbiao.Thickness measurement for thin metal material with the use of laser generated ultrasound[J].Journal of Vibration and Shock, 2018, 37(12): 147-152.
[17]Ma Ding, Shi Lihua, Cao Hongfu.Combination of wavelet transform with EMD to distinguish overlapped Lamb wave packets[C]//11th IEEE International Conference on Electronic Measurement& Instruments, Harbin, China, 2013, 1: 159-165.
[18]Zhang Guangming, Harvey David M.Contemporary ultrasonic signal processing approaches for nondestructive evaluation of multilayered structures[J].Nondestructive Testing & Evaluation, 2012, 27(1):1-27.
[19]Cui Jianguo, Wang Qingtian, Hua Jiaojiao, et al.Structure damage prediction of the composite material based on EMD[C]//Proceedings of the 33rd Control Conference, IEEE, Nanjing, China, 2014: 7784-7788.
[20]乐静, 郭俊杰, 朱虹.基于 EMD和 Snakes模型信息融合的表面缺陷检测方法[J].仪器仪表学报,2006, 27(12): 1664-1669.Le Jing, Guo Junjie, Zhu Hong.Surface defect defection method based on information fusion of EMD and Snakes model[J].Chinese Journal of Scientific Instrument, 2006, 27(12): 1664-1669.
[21]吕敬祥, 刘国强.磁声电无损检测及改进的 EMD消噪方法[J].电工技术学报, 2018, 33(17): 3935-3942.Lü Jingxiang, Liu Guoqiang.Magneto-acoustoelectrical NDT and improved EMD de-noising algorithm[J].Transactions of China Electrotechnical Society, 2018, 33(17): 3935-3942.