0 引言
为应对日益严峻的能源和环境问题,大力发展多种能源互联互济的综合能源系统(Integrated Energy System, IES)[1]逐渐成为国内外能源领域的共识。近年来,随着燃气机组[2]装机比例的增加、电驱动压缩机的广泛使用[3]和电转气技术[4]的发展,电力和天然气系统的耦合越加紧密,电力-天然气联合系统(以下简称“电-气联合系统”)已成为综合能源系统的一种典型形式。
与常规电力系统/天然气系统一样,电-气联合系统中也存在电/气负荷变化、电/气源出力波动等大量不确定因素。但不同的是,这些不确定因素的影响可能通过耦合环节在电、气子系统之间传递而加剧不确定因素影响的复杂性。因此,定量评估不确定因素的影响是电-气联合系统规划与运行的一项重要任务。
目前,已有大量文献研究如何定量评估不确定因素对电-气联合系统的影响,包括概率能流[5-7]、区间能流[8]、概率-模糊能流[9]、概率最优能流[10]以及可靠性评估[11-13]等。事实上,除能流分析和可靠性评估,灵敏度分析也是一种定量评估不确定因素影响的有效工具。灵敏度分析通过量化输出与输入之间的关系来评估不确定因素的影响程度,帮助运行人员识别影响系统运行的关键因素或者薄弱环节。然而,目前仅有少量关于电-气联合系统灵敏度分析的研究,其中,文献[14]基于电-气联合系统的灵敏度矩阵定量评估电网节点注入功率对天然气节点压力的影响,而文献[15]基于电压-电负荷、压力-气负荷以及热电分配系数-热电联产机组热/电出力的灵敏度关系分别评估电负荷对电压、气负荷对压力,以及电/热出力对分配系数的影响程度。
文献[14-15]中灵敏度分析的基本思路是根据输出变量(如节点电压或压力)相对于输入变量(如节点负荷)的一阶偏微分关系来评估输入对输出的影响程度,其实质是局部灵敏度分析方法。从原理上讲,局部灵敏度分析是一种基于输入变量局部线性化的确定性分析方法,仅能量化输入变量在线性化点附近对输出变量的影响程度,难以计及输入变量概率特性及输入变量间的相关性对灵敏度分析结果的影响。与之相对,全局灵敏度[16]分析则能有效地考虑输入变量的概率特性及变量之间的相关性,从而可以有效地弥补局部灵敏度分析的不足。近年来,国内外学者开始应用全局灵敏度方法评估不确定因素对电力系统的影响,特别是基于方差分析的全局灵敏度方法已在配电网潮流[17]、微电网潮流[18]、电压稳定[19]、小干扰稳定[20]、可用传输容量分析[21]以及阻塞管理[22]等研究中得到广泛应用。然而,目前尚未见全局灵敏度在电-气联合系统中的研究报道。
为此,本文提出一种区域电-气联合系统的全局灵敏度分析方法,并研究该方法在配电网、配气网耦合形成的区域电-气联合系统[23]中的应用。以基于Sobol′方法[16,18]和稀疏多项式混沌展开(sparse Polynomial Chaos Expansion, sPCE)[24]的全局灵敏度理论为基础,定量评估电/气负荷、光伏出力、天然气管道参数等多种不确定性及其相关性对区域电-气联合系统运行状态的影响。算例仿真结果证明所提方法的有效性,以及对具有三相不对称特性的区域电-气联合系统的适应性。
1 区域电-气联合系统的稳态能流模型
1.1 配电网的三相潮流模型
考虑到配电网(特别是35kV及以下的中、低压配电网)具有显著不对称特性,采用三相潮流模型[25]

式中,![]() 分别为节点i的φ相注入有功功率和无功功率;
分别为节点i的φ相注入有功功率和无功功率;![]() 分别为节点i的φ相电压模值和相角;
分别为节点i的φ相电压模值和相角;![]() 分别为三相配电网节点导纳矩阵对应节点 i、k及 φ、ψ相的电导和电纳;φ,ψ∈{a,b,c};Ne为配电网节点总数。
分别为三相配电网节点导纳矩阵对应节点 i、k及 φ、ψ相的电导和电纳;φ,ψ∈{a,b,c};Ne为配电网节点总数。
1.2 配气网的能流模型
考虑压力等级小于 75mbar(1bar=105Pa)的低压配气网,管道i-j的流量方程[6]为
式中,下标p表示管道;i、j为管道首末两端节点号;Fp,ij为流经管道i-j的流量;pi和pj分别为节点i、j的压力;Kij为管道i-j的综合参数,其大小与管道物理特性(如直径、长度、摩擦系数等)、天然气气体成分及周围环境(如温度、土壤湿度)等诸多因素有关;sp,ij为方向变量,若pi>pj,则sp,ij=1,否则sp,ij= -1。
由式(2)可知,沿气流方向有压力损失,通常要配置压缩机来补偿压力损失、满足用户的压力需求。压缩机可由燃气或电机驱动,燃气驱动压缩机模型为[10]

式中,下标 c表示压缩机;i、j分别为压缩机入、出口对应的节点号;Hc,ij为压缩机用于升压消耗的功率,单位为马力(1马力=735.499W);τc,ij为Hc,ij对应耗气量;Fc,ij为流入压缩机的气流量;Bc,ij和Zc,ij为与压缩机温度、效率及压缩因子有关的常数;αc、βc、γc为燃气机组的燃料比率常数。
天然气网络中的节点满足
式中,Fi为节点 i的注入流量;j∈i表示与 i直接相连的节点集合;sc,ij为压缩机方向变量,若i为压缩机入口节点,则 sc,ij=1,若为出口节点,则sc,ij=-1。
1.3 耦合元件模型
考虑燃气机组和电驱动压缩机两类耦合元件。燃气机组以天然气为燃料向电力网络供电,其消耗的天然气流量Fg与输出电功率Pg满足[26]

式中,下标g表示燃气机组;αg、βg、γg为燃气机组的燃料比率常数,单位分别为 MJ/h、MJ/(kW·h)、MJ/[(kW)2·h];CLHV为天然气低热值,取CLHV=39.12MJ/ m3。
电驱动压缩机的模型[6]为

式中,下标k为电力网络的节点编号;Pc,k为压缩机消耗的等效电功率,MW。
1.4 区域电-气联合系统的稳态能流方程
结合上述配电网三相潮流方程、配气网能流方程以及耦合元件的稳态模型,以配电网节点电压模值、相角和配气网节点压力为状态变量,则区域电-气联合系统的稳态能流方程可以表示为
式中,Vφ、δφ分别为配电网所有待求节点电压模值和相角;p为配气网所有待求节点压力。上述稳态能流模型的求解存在统一求解和交替求解两种思路,本文采用配电网、配气网交替迭代的求解方法。
需要指出,区域电-气联合系统的稳态能流方程与其电压和气压等级有关。对于中压气网,需要采用中压管道方程;而对于高压配电网,则可以采用更为简化的对称潮流模型。采用不同的能流方程并不会对本文所提全局灵敏度分析方法及其应用带来实质影响。
2 区域电-气联合系统的不确定能流模型
2.1 不确定因素及其模型
区域电-气联合系统中的源、荷具有明显的随机性,也是现有研究广泛考虑的不确定因素。本文用正态分布描述电、气负荷的随机变化,用Beta分布描述光伏出力的随机变化,并假设配电网中所有光伏单相接入。受天气、用户用能习惯等因素的影响,电、气负荷以及光伏出力之间往往具有一定的相关性。本文采用秩相关系数描述这些不确定因素之间的相关性,并基于高斯Copula函数进行处理,具体步骤参见文献[27]。
与源、荷不同,仅有少量研究(如文献[6])考虑天然气管道参数的不确定性。事实上,如式(2)所示,管道参数与管道物理特性、天然气成分以及周围环境等诸多因素有关,难以准确计算或测量,一般仅能给出经验值或典型取值范围。因此,本文将管道参数同样视为不确定因素,并根据管道参数的典型取值区间,分别用均匀分布和正态分布描述其不确定性。
2.2 计及不确定因素的概率能流模型
当考虑区域电-气联合系统中负荷、光伏出力以及管道参数的不确定性时,运行人员所关心的任一输出变量y(如配电网中的节点电压、支路潮流或者配气网中的节点压力、管道流量等),均可以表示为式(8)所示的概率能流问题。
式中,X为表示源、荷不确定性的n维变量,X=[X1 X2 … Xn]T;Z为表示管道参数不确定性的m维变量,Z=[Z1 Z2 … Zm]T。
3 基于Sobol′法的全局灵敏度分析
Sobol′法[16]是数学家 I.M.Sobol′提出的一种全局灵敏度分析方法。该方法基于方差分析量化系统各输入变量及其相互作用对系统输出变量的影响,基本原理如下。
设有一个平方可积函数 y=f(ξ),ξ=[ξ1 ξ2 … ξN]T为N维独立随机变量,0≤ξi≤1, i=1, …, N。基于函数的高维模型表达理论,f(ξ)可分解为 2N个子函数之和[16]。

式中,f0为 0 阶常数项,也是 f(ξ)的期望;fi(ξi)为 ξi的 1 阶子函数;fij(ξi, ξj)为与 ξi和 ξj有关的 2 阶子函数;f1,2,···,N(ξ1,··,ξN)为与所有输入变量有关的 N 阶子函数。
当任一子函数满足式(10)条件时,式(9)分解唯一。

式(10)表征了任一非0阶子函数的期望始终为0。结合式(9)和式(10)可知,各个子函数之间具有正交性。

结合随机变量方差的定义,将式(9)等式两边平方并积分,可以得到f(ξ)的方差 D[f(ξ)]为

由于各非 0阶子函数的期望为 0,D[f(ξ)]可以进一步用子函数的方差表示为

式中,Di=D[f(ξi)],表示 1 阶子函数 f(ξi)的方差;Dij为 2 阶子函数 f(ξi, ξj)的方差;D1,2,…,N为N阶子函数 f1,2,…,N(ξ1,··,ξN)的方差。
Sobol′定义输入变量的全局灵敏度指标为

将式(13)两边除以D[f(ξ)],可得各输入变量全局灵敏度指标满足

由上述推导可知,任何输入变量的全局灵敏度指标本质上是该变量对输出变量方差的贡献程度。Si是1阶灵敏度指标,表征输入变量ξi的不确定性对于输出变量的影响;Sij为2阶灵敏度指标,表征输入变量ξi和ξj之间的交互作用对于输出变量的影响,以此类推直至 S 1,2,…, N 。
一般可采用蒙特卡罗模拟(Monte Carlo Simulation, MCS)计算全局灵敏度指标[18]。通过抽取两组独立输入随机变量样本,可以估算输出变量及各子函数的方差。假设每组样本数为NMCS,为估计区域电-气联合系统中某输入变量对指定输出变量的全局灵敏度指标,需要进行2NMCS次确定性能流计算。基于MCS的全局灵敏度计算过程简单,但为达到一定的计算精度需要大量样本,限制了MCS方法对大规模系统的适应性。因此,本文将基于sPCE建立区域电-气联合系统中输出变量的逼近模型,从而实现全局灵敏度的快速计算。
4 基于sPCE的全局灵敏度计算
4.1 稀疏多项式混沌展开理论
4.1.1 正交多项式混沌展开
对于含 N个独立随机变量的函数 y=f(ξ),根据多项式混沌展开理论[24],f(ξ)可以用以下各输入变量对应的正交多项式混沌展开形式逼近。
式中,i=[i1 i2··iN]表示多阶下标,满足|i|=i1+ i2+··+iN;Φi(ξ)为多变量多项式基函数; ai为Φi(ξ)对应的待求展开系数。
多变量多项式基函数 Фi(ξ)可以分解为各单变量基函数的张量积。
式中,φ i1(ξj)为变量 ξj的第 ij阶正交多项式。一般来说,各个输入变量对应的正交多项式取决于该输入变量的分布类型,例如,当输入变量为标准正态分布变量,则 Hermite正交多项式为最优基函数,而对于[-1,1]的均匀分布变量,其最优基函数为Legendre正交多项式。其他典型变量类型对应的基函数详见文献[24]。
实际上,计算如式(16)的逼近模型时,一般会限定最高展开阶数r,以实现逼近模型的有限项截断。
也可将式(18)采用向量形式表示为
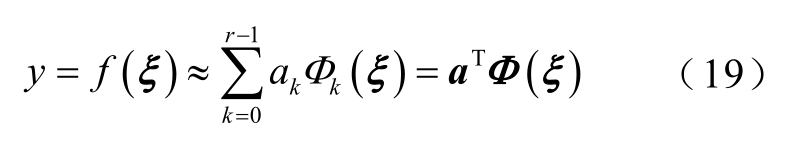
式中,a为展开系数向量,a=[a0 a1 … ar-1]T,ak(k=0,1,··, r-1)表示第 k阶多项式对应的展开系数;Ф(ξ)为基函数向量,Ф(ξ)=[1 Ф1(ξ) … Фr-1(ξ)]T。
截断后逼近模型的展开项数R为

一般来说,最高展开阶数r越大,多项式展开式越精确,但展开项数也会相应增多。对于一般的工程问题,r取 2~3即能保证较高计算精度。本文取r=2,则输出变量y的逼近模型为

式中,Ф1(ξi)为与变量 ξi对应的 1阶正交多项式;Ф2(ξi, ξj)为变量 ξi和 ξj对应的 2 阶正交多项式。
根据最小二乘原理,可通过以下最小化残差问题来计算式(21)中各项展开系数[17]为

式中,NED为样本数量;ξ(i)为输入变量第i组样本;y(ξ(i))为由原始模型 y=f(ξ)计算得到输出变量的第 i个样本。
为保证最小二乘的求解精度,一般要求样本数NED为展开项数R的2~3倍。由式(20)可知,R取决于输入变量数量N和最大展开阶数r。对于本文所研究的区域电-气联合系统,即使取r=2,由于不确定因素众多,R可能很大,直接求解式(22)需要大量计算。为提高计算效率,本文基于稀疏多项式的思想,并采用压缩感知技术中的正交匹配追踪(Orthogonal Matching Pursuit, OMP)[24]算法实现展开系数的快速计算。
4.1.2 稀疏展开系数求解
如前所述,在构造多项式混沌展开模型过程中,展开项数会随着输入变量个数和最大展开阶数的增加而大幅增加。然而,大部分高阶展开项的数值往往很小,甚至接近于0,基本上可以忽略这些项;另外,即使是低阶项,不同输入变量对同一输出变量的影响也有所区别,对于影响较小的展开项,也可以近似认为其展开系数为 0。因此,多项式混沌展开具有显著稀疏性[24],可以仅求取对输出变量影响较大的项而降低计算量。根据这一思想,问题(22)转换为最小化展开系数向量a中非零元素最少的优化问题。
式中,||·||0表示0范数,||a||0可表示a中非零元素数量;![]() 为输出变量样本向量;
为输出变量样本向量;![]() 为输入变量样本对应的正交多项式矩阵;ε为最大允许误差。
为输入变量样本对应的正交多项式矩阵;ε为最大允许误差。
利用OMP求解问题式(23)的基本思想是不断选取H矩阵中与残差向量最相关的列,再利用最小二乘求取与这些列对应的展开系数。基本步骤如下:
(1)输入参数。包括输出变量向量yED、正交多项式矩阵H、最大允许误差ε。
(2)变量初始化。设置迭代次数k=0,展开系数a(k)=0,残差r(k)=yED-Ha(k),项数索引集Λ(k)=φ。
(3)确定正交多项式矩阵 H中与残差 r(k)最相关的列,即计算C(k)=r(k)TH,选取行向量C(k)中数值最大的项并记录对应的列数j(k)。
(4)令 k=k+1,将 j(k)添加至 Λ(k),Λ(k)=Λ(k-1)∪j(k)。
(5)基于最小二乘法,求解展开系数a,即求解a(k)=arg mina||yED-H(k)a||2,H(k)为 H 中索引集 Λ(k)对应列数的向量构成的矩阵。
(6)更新残差 r(k)=yED-Ha(k),判断是否满足||r(k)||2>ε,若满足则返回步骤(3),否则计算结束,输出a(k)为优化结果。
4.2 基于sPCE计算全局灵敏度指标
基于 4.1节内容可建立输出变量关于输入变量的 sPCE模型,并基于该模型直接得到输出变量的期望 E[f(ξ)]和方差 D[f(ξ)]。
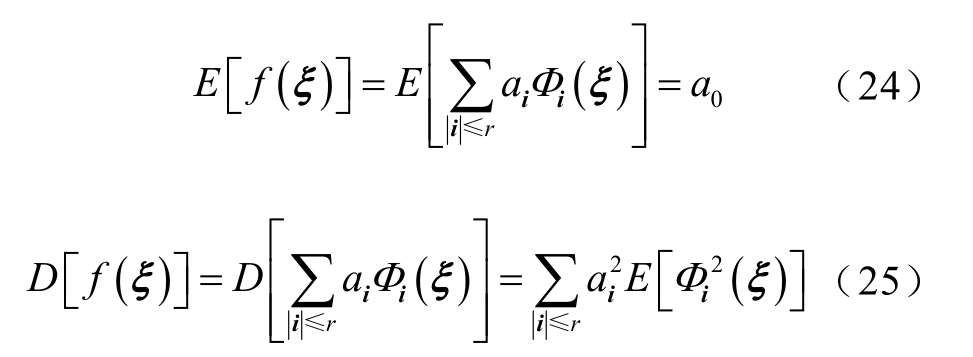
定义下标集合α为
则包含下标 α 的多项式 Фα(ξ1,··, ξs)为
因任意变量 ξi的 0阶正交多项式 φ0(ξi)恒为1[24]。为便于表示,定义集合 Ωi1,··,is包含 α 中所有非0元素。
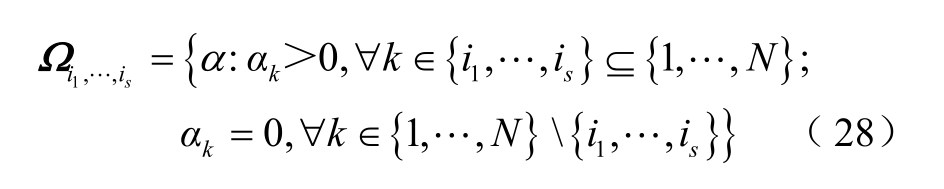
借助上述定义,可以将变量(ξ1,··, ξs)的各阶正交多项式统一表示,则式(18)可以改写为

根据 Sobol′分解唯一性,对比式(29)与式(9),有
可见,Sobol′分解式中变量(ξ1,··, ξs)的 s 阶子函数就是 sPCE模型中含相同变量的 s阶正交多项式之和。
在此基础上结合式(14)、式(24)和式(25),可根据 sPCE 直接求得输入变量(ξ1,··, ξs)的全局灵敏度指标。

由此可知,基于 sPCE计算全局灵敏度指标方法仅需要 NED次确定性能流计算,与 MCS方法相比,可以大幅度提高计算效率。
5 区域电-气联合系统全局灵敏度计算
基于Sobol′分解和sPCE逼近模型,本文所提区域电-气联合系统全局灵敏度指标的计算流程如下:
(1)输入区域电-气联合系统的基本参数,包括配电网、配气网、耦合元件的参数,电、气负荷及光伏出力向量X=[X1 X2··XN]T的分布类型和秩相关系数,管道参数Z=[Z1 Z2··ZM]T的分布类型及参数。
(2)采用拉丁超立方抽样技术生成对应X的N维独立标准正态随机向量 ξ=[ξ1 ξ2··ξN]T 的样本,并根据 Z的分布生成对应的 M维独立标准正态随机向量或在[-1,1]均匀分布的独立变量 λ=[λ1 λ2··λM]T的样本,样本数均为NED。利用高斯Copula函数建立X与ξ的转换关系,并得到X的样本值;根据等概率变换原则,由λ计算得到Z的样本值。
(3)根据X和Z的每组样本,对区域电-气联合系统进行确定性能流计算,得到目标输出变量样本 yED。
(4)根据ξ和λ构造相应的正交多项式矩阵H。对于ξ中各变量,选择Hermite正交多项式;对于λ,选取 Legendre正交多项式(对应均匀分布的管道参数)或 Hermite正交多项式(对应正态分布的管道参数)。
(5)基于yED和H,采用OMP计算稀疏展开系数a。
(6)根据所得sPCE模型,基于式(31)求解目标输出变量对各输入不确定变量的全局灵敏度指标。
6 算例分析
6.1 算例数据
用图1所示的区域电-气联合系统进行算例仿真,该系统由IEEE 13配电网[28]和11节点配气网[6]耦合形成。燃气轮机NGU输出功率为0.1MW,取αg=γg=0,βg=7MJ/(kW·h);配气网节点 9~11 接有特殊用户,其压力需求均为38mbar,在各节点出口处配置电力驱动压缩机,并由配电网节点4、11和12供电,压缩机参数中与压缩机温度、效率及压缩因子有关的常数统一取为Bc=226.02,Zc=0.233 35;配电网节点 13和节点 8的 a相分别接入容量为0.15MW的单相光伏电源PV1和PV2。考虑系统中所有的电/气负荷以及光伏出力的随机性,假定所有电/气负荷服从以基态负荷为均值、标准差为均值5%的正态分布,光伏出力均服从形状参数为0.95和0.8的 Beta分布。各变量之间的秩相关系数为![]() 下标E、G、P分别表示电/气负荷及光伏。本文所提方法基于Matlab R2014a平台实现,经 COM 接口驱动OpenDSS[29]实现配电网的三相交流潮流计算。
下标E、G、P分别表示电/气负荷及光伏。本文所提方法基于Matlab R2014a平台实现,经 COM 接口驱动OpenDSS[29]实现配电网的三相交流潮流计算。

图1 区域电-气联合系统算例
Fig.1 Regional electricity and gas integrated system sample
6.2 本文方法与MCS方法的比较
为验证所提全局灵敏度计算方法的正确性和高效性,本节将对比分析本文方法与 MCS方法所得的全局灵敏度指标。本节仅考虑区域电-气联合系统中电、气负荷及光伏出力的随机性。取 sPCE的最大展开阶数为2,样本数NED为1 000;以配电网有功损耗的方差系数作为 MCS方法的收敛判据[30],仿真发现样本数为20 000时的方差系数小于0.3%,因此以20 000次MCS方法的结果作为本文方法的验证标准。
以图1中配电网节点13的a相电压( )作为输出变量,图2、图3分别为
)作为输出变量,图2、图3分别为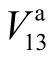 对配电网与配气网中各输入变量的全局灵敏度指标。图2中
对配电网与配气网中各输入变量的全局灵敏度指标。图2中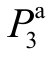 表示配电网3节点a相负荷的有功功率、PPV1表示光伏PV1的出力,图3中 F2表示配气网节点 2的气负荷,余类推。为减小计算结果的分散性,图中全局灵敏度指标均为 10次计算结果的平均值。由图2、图3可见,两种方法所得全局灵敏度指标基本一致,验证了本文方法的正确性。
表示配电网3节点a相负荷的有功功率、PPV1表示光伏PV1的出力,图3中 F2表示配气网节点 2的气负荷,余类推。为减小计算结果的分散性,图中全局灵敏度指标均为 10次计算结果的平均值。由图2、图3可见,两种方法所得全局灵敏度指标基本一致,验证了本文方法的正确性。
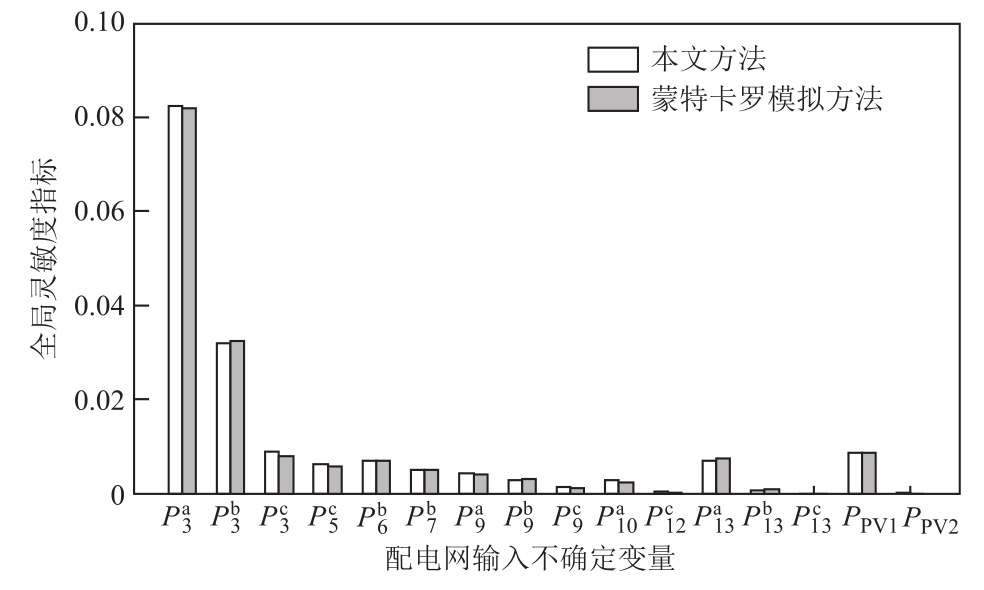
图2 配电网中各输入不确定变量的全局灵敏度指标
Fig.2 Global sensitivity indexes for all input uncertain variables in the power distribution network
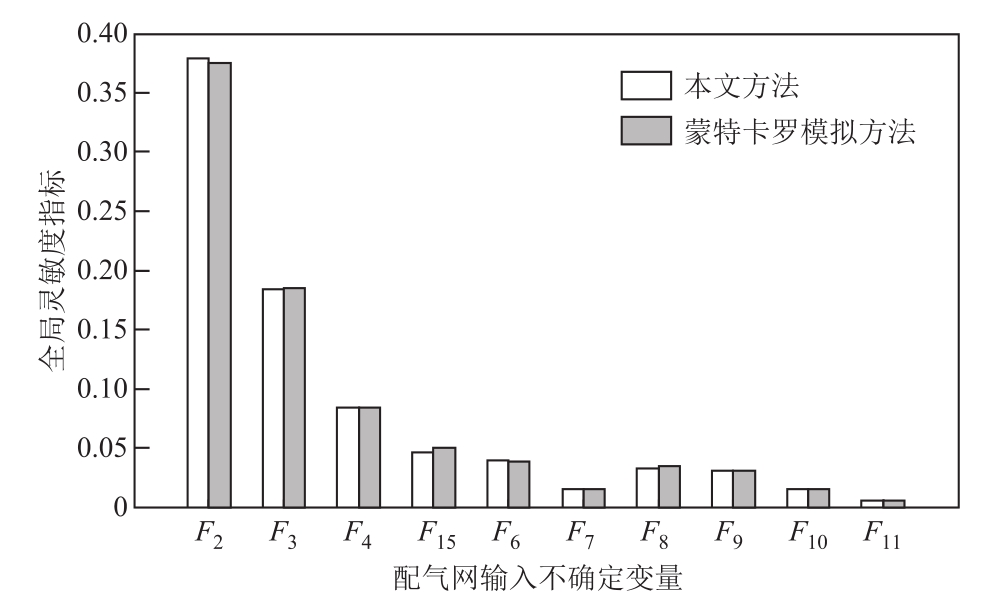
图3 配气网各输入不确定变量的全局灵敏度指标
Fig.3 Global sensitivity indexes for all input uncertain variables in the gas distribution network
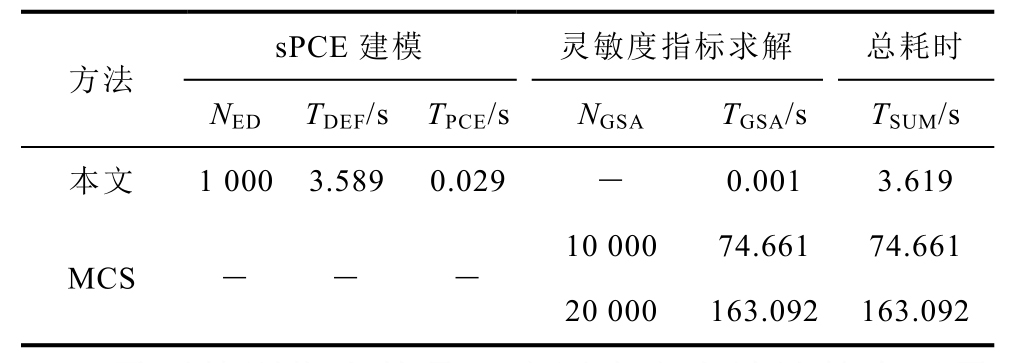
表1对比了本文方法与 MCS方法(样本数分别为10 000和20 000)的计算时间,其中本文方法的总耗时 TSUM由确定性能流计算时间 TDEF、sPCE模型求解时间 TPCE以及全局灵敏度指标计算时间TGSA三部分构成。TDEF包含输入变量相关性的处理、样本生成、NED次确定性能流计算的时间,TPCE则包含正交多项式的计算和展开系数求解的时间。由表1可见,本文方法所需时间远小于MCS方法,而MCS方法的时间基本与样本数成比例。不难推算,本文方法用时与500次MCS相当,而计算结果则与20 000次MCS基本一致。此外,本文方法的大部分时间用于确定性能流计算,sPCE模型一旦形成,便可快速得到全局灵敏度指标。
表1 两种方法的计算时间
Tab.1 Computational time of the two methods
sPCE建模 灵敏度指标求解 总耗时方法NED TDEF/s TPCE/s NGSA TGSA/s TSUM/s本文 1 000 3.589 0.029 - 0.001 3.619 MCS - - -10 000 74.661 74.661 20 000 163.092 163.092
需要特别指出的是,应用本文方法计算全局灵敏度指标时,可以直接根据 sPCE模型一次性得到所有输入变量的全局灵敏度指标,而 MCS方法每次仅能计算某一个输入变量的全局灵敏度指标。可以预见,随着所研究系统不确定输入变量的增加,本文方法在计算效率上的优势将更为明显。
6.3 源荷不确定性及相关性的影响
如前所述,全局灵敏度分析可以量化系统中所有不确定变量对输出变量的影响程度,从而为识别影响系统运行状态的关键因素提供参考。本节分别以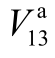 和支路3-12的a相有功功率
和支路3-12的a相有功功率 为输出变量,基于全局灵敏度指标,分析负荷及光伏出力的不确定性及相关性对区域电-气联合系统的影响。
为输出变量,基于全局灵敏度指标,分析负荷及光伏出力的不确定性及相关性对区域电-气联合系统的影响。
在“不考虑相关性”和“考虑相关性”两种情况下,应用本文方法所得 对配电网、配气网中不确定变量的全局灵敏度指标分别如图4、图5所示。其中,“考虑相关性”时按6.1节设置各变量的相关系数。
对配电网、配气网中不确定变量的全局灵敏度指标分别如图4、图5所示。其中,“考虑相关性”时按6.1节设置各变量的相关系数。
由图4可见,是否考虑输入变量之间的相关性,对全局灵敏度指标的计算结果有显著影响。具体而言,不考虑相关性时,对 影响最大的变量(本文称之为“最重要变量”)是
影响最大的变量(本文称之为“最重要变量”)是 和 PPV1,而其余变量的影响较小。这是因为此时所考虑的输出变量
和 PPV1,而其余变量的影响较小。这是因为此时所考虑的输出变量 是节点13的a相电压,
是节点13的a相电压, 和PPV1分别为同一节点(13节点)、同一相别(a相)的负荷和光伏电源。当考虑相关性后,
和PPV1分别为同一节点(13节点)、同一相别(a相)的负荷和光伏电源。当考虑相关性后, 和PPV1虽然对
和PPV1虽然对 仍有较大影响,但“最重要变量”变为
仍有较大影响,但“最重要变量”变为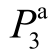 、
、 和
和 ,这是因为3节点与13节点的电气距离较近,而与电气距离更近的节点 12比较,节点3的负荷(
,这是因为3节点与13节点的电气距离较近,而与电气距离更近的节点 12比较,节点3的负荷(  、
、 和
和 )均显著大于节点12的负荷(
)均显著大于节点12的负荷( )。可见,全局灵敏度指标与电气距离、相别、负荷水平以及变量之间的相关性等多个因素有关,并无简单的规律可循,是区域电-气联合系统中各输入变量及其相关性综合作用的结果。
)。可见,全局灵敏度指标与电气距离、相别、负荷水平以及变量之间的相关性等多个因素有关,并无简单的规律可循,是区域电-气联合系统中各输入变量及其相关性综合作用的结果。
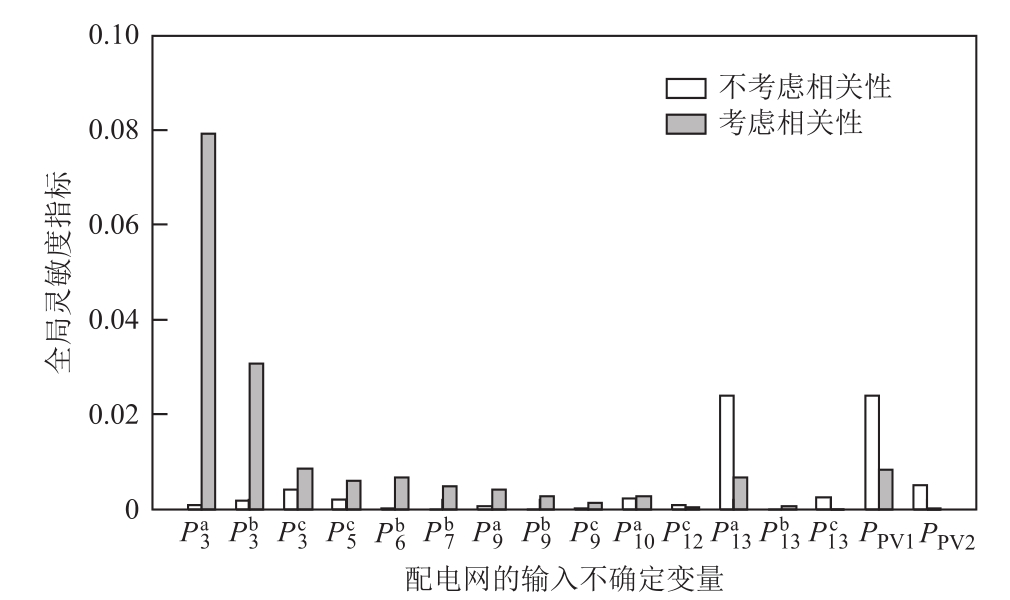
图4 考虑/不考虑变量相关性时 关于配电网各输入不确定变量的全局灵敏度指标
关于配电网各输入不确定变量的全局灵敏度指标
Fig.4 Global sensitivity indexes of 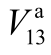 for input uncertain variables in the power distribution network with/without considering the correlation of variables
for input uncertain variables in the power distribution network with/without considering the correlation of variables

图5 考虑/不考虑变量相关性时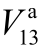 关于配气网各输入不确定变量的全局灵敏度指标
关于配气网各输入不确定变量的全局灵敏度指标
Fig.5 Global sensitivity indexes of  for input uncertain variables in the gas distribution network with/without considering the correlation of variables
for input uncertain variables in the gas distribution network with/without considering the correlation of variables
与图4类似,图5同样表明输入变量的相关性对全局灵敏度指标有显著影响。不考虑相关性时,对 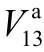 而言“最重要变量”是 F9和 F8;而考虑相关性后,“最重要变量”是F2和F3。然而,无论是配气网节点 2、3还是节点 8、9,都不是与配电网节点 13电气距离最近的节点或者耦合最为紧密的节点,表明电-气系统之间的灵敏度关系并不简单取决于电气距离或者耦合程度,同样是电-气联合系统中各种因素综合作用的结果。
而言“最重要变量”是 F9和 F8;而考虑相关性后,“最重要变量”是F2和F3。然而,无论是配气网节点 2、3还是节点 8、9,都不是与配电网节点 13电气距离最近的节点或者耦合最为紧密的节点,表明电-气系统之间的灵敏度关系并不简单取决于电气距离或者耦合程度,同样是电-气联合系统中各种因素综合作用的结果。
为进一步验证图4、图5的分析结果,在计及输入相关性情况下,不考虑对 影响较小变量(例如
影响较小变量(例如 和PPV2)的不确定性,应用本文方法计算
和PPV2)的不确定性,应用本文方法计算 对其余不确定变量的全局灵敏度指标如图6和图7所示。从理论上讲,不计影响较小变量(本文称之为“非重要变量”),对全局灵敏度指标的影响应该很小。由图6、图7不难发现,对于“考虑
对其余不确定变量的全局灵敏度指标如图6和图7所示。从理论上讲,不计影响较小变量(本文称之为“非重要变量”),对全局灵敏度指标的影响应该很小。由图6、图7不难发现,对于“考虑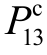 和PPV2的不确定性”和“不计
和PPV2的不确定性”和“不计 和PPV2的不确定性”两种情况,全局灵敏度指标的差异很小,与理论分析一致,从而证明了本文所提全局灵敏度计算方法的正确性。此外,由图6、图7可知,当电-气联合系统所涉及的不确定变量数量较多时,也可以借助全局灵敏度指标识别出影响很小、可以忽略的“非重要”变量,从而降低问题规模,简化联合系统的分析。
和PPV2的不确定性”两种情况,全局灵敏度指标的差异很小,与理论分析一致,从而证明了本文所提全局灵敏度计算方法的正确性。此外,由图6、图7可知,当电-气联合系统所涉及的不确定变量数量较多时,也可以借助全局灵敏度指标识别出影响很小、可以忽略的“非重要”变量,从而降低问题规模,简化联合系统的分析。

图6 考虑/不考虑 和PPV2不确定性时
和PPV2不确定性时 关于配电网各输入不确定变量的全局灵敏度指标
关于配电网各输入不确定变量的全局灵敏度指标
Fig.6 Global sensitivity indexes of  for input uncertain variables in the power distribution network with/without considering the uncertainties of
for input uncertain variables in the power distribution network with/without considering the uncertainties of  and PPV2
and PPV2

图7 考虑/不考虑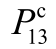 和PPV2不确定性时
和PPV2不确定性时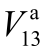 关于配气网各输入不确定变量的全局灵敏度指标
关于配气网各输入不确定变量的全局灵敏度指标
Fig.7 Global sensitivity indexes of  for input uncertain variables in the gas distribution network with/without considering the uncertainties of
for input uncertain variables in the gas distribution network with/without considering the uncertainties of  and PPV2
and PPV2
除节点电压幅值外,支路功率同样是描述配电网运行状态的重要参数,也会受到输入变量相关性的影响。为此,进一步以 为输出变量,应用本文方法计算
为输出变量,应用本文方法计算 对各不确定变量的全局灵敏度指标,如图8、图9所示。
对各不确定变量的全局灵敏度指标,如图8、图9所示。
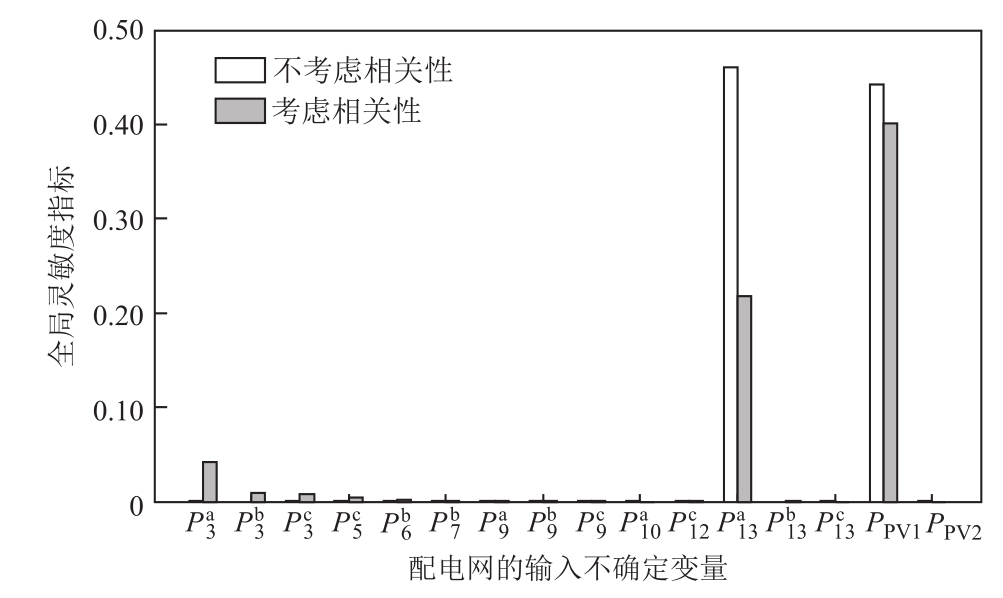
图8 考虑/不考虑变量相关性时 关于配电网各输入不确定变量的全局灵敏度指标
关于配电网各输入不确定变量的全局灵敏度指标
Fig.8 Global sensitivity indexes of  for all input uncertain variables in the power distribution network with/without considering the correlation of variables
for all input uncertain variables in the power distribution network with/without considering the correlation of variables

图9 考虑/不考虑变量相关性时  关于配气网各输入不确定变量的全局灵敏度指标
关于配气网各输入不确定变量的全局灵敏度指标
Fig.9 Global sensitivity indexes of  for all input uncertain variables in the gas distribution network with/without considering the correlation of variables
for all input uncertain variables in the gas distribution network with/without considering the correlation of variables
由图8可见,当不考虑相关性时, 是影响
是影响 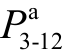 的“最重要变量”、PPV1其次,配电网中其余随机变量的影响基本可以忽略;考虑相关性后,PPV1变为“最重要变量”、
的“最重要变量”、PPV1其次,配电网中其余随机变量的影响基本可以忽略;考虑相关性后,PPV1变为“最重要变量”、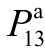 其次,同时该支路首节点的a相注入功率(
其次,同时该支路首节点的a相注入功率( 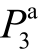 )也表现出一定影响。图9显示不考虑相关性时,配气网中影响
)也表现出一定影响。图9显示不考虑相关性时,配气网中影响 的“最重要变量”是F9和F8,但灵敏度指标均小于0.02;而考虑相关性后,“最重要变量”变为F2和F3,且灵敏度指标出现显著升高(分别超过 0.14和 0.06),变化趋势与图5基本一致。图8、图9再次表明全局灵敏度分析中考虑变量相关性的必要性。
的“最重要变量”是F9和F8,但灵敏度指标均小于0.02;而考虑相关性后,“最重要变量”变为F2和F3,且灵敏度指标出现显著升高(分别超过 0.14和 0.06),变化趋势与图5基本一致。图8、图9再次表明全局灵敏度分析中考虑变量相关性的必要性。
6.4 管道参数不确定性的影响
在考虑源、荷不确定性基础上,本节设计以下五种场景,以量化分析管道参数不确定性的影响。
场景 1:仅考虑电、气负荷及光伏出力的不确定性及相关性。
场景2:在场景 1基础上,考虑所有管道参数的不确定性,取经验公式计算结果[31]为基准值(设为K),假设所有管道参数在[0.95K, 1.05K]均匀分布。
场景3:在场景 2基础上,增大管道参数分布区间,即假设所有管道参数在[0.9K, 1.1K]均匀分布。
场景4:在场景 1基础上,假设所有管道参数服从均值μK=K的正态分布,并根据文献[6]所述3σ原则,按[μK-3σK, μK+3σK]对应[0.95K, 1.05K]确定正态分布的标准差,即取σK=0.05K/3。
场景5:类似场景4,假设所有管道参数服从均值μK=K的正态分布,但按场景2中均匀分布的方差设置各正态分布变量的方差。
根据上述设置,五种场景的特点见表2。
表2 五种场景的特点
Tab.2 Main features of the five scenarios

场景 1 2 3 4 5管道参数确定 √均匀分布 √ √正态分布 √ √方差 较小 最大 最小 较小(同2)
分别以配电网 和配气网管道4-7流量(F4-7)为输出变量,应用本文方法计算上述五种场景下各输入变量的全局灵敏度指标,并从大到小进行排序。为直观显示指标的相对大小,用图10、图11所示的圆形比例面积图分别表示对
和配气网管道4-7流量(F4-7)为输出变量,应用本文方法计算上述五种场景下各输入变量的全局灵敏度指标,并从大到小进行排序。为直观显示指标的相对大小,用图10、图11所示的圆形比例面积图分别表示对 和F4-7影响最大的输入变量及其灵敏度指标,图中圆形面积与灵敏度指标成正比;K2-3表示配气网中管道2-3的参数,余类推;场景1取排名前十的变量,场景2、3取排名前十四的输入变量。
和F4-7影响最大的输入变量及其灵敏度指标,图中圆形面积与灵敏度指标成正比;K2-3表示配气网中管道2-3的参数,余类推;场景1取排名前十的变量,场景2、3取排名前十四的输入变量。

图10 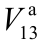 对各输入不确定变量全局灵敏度指标的示意图
对各输入不确定变量全局灵敏度指标的示意图
Fig.10 Schematic diagram of global sensitivity indexes of to input uncertain variables
to input uncertain variables

图11 F4-7对各输入不确定变量全局灵敏度指标的示意图
Fig.11 Schematic diagram of global sensitivity indexes of F4-7 to input uncertain variables
由图10可见,管道参数的不确定性对 灵敏度指标有显著影响。当不考虑管道参数的不确定性时(场景1),对
灵敏度指标有显著影响。当不考虑管道参数的不确定性时(场景1),对 影响最大的前十个变量,按重要度排序,依次为 F2>F3>F4>
影响最大的前十个变量,按重要度排序,依次为 F2>F3>F4> >F5>F6>F8>
>F5>F6>F8> >F9>F7;考虑管道参数的不确定性后(场景2~5),尽管上述变量的相对排序未发生明显变化,但在场景2、3中,K2-3和K7-9成为影响
>F9>F7;考虑管道参数的不确定性后(场景2~5),尽管上述变量的相对排序未发生明显变化,但在场景2、3中,K2-3和K7-9成为影响 的“重要变量”,其影响程度超过F6;特别是当管道参数变化范围较大(场景3)时,K2-3、K7-9对
的“重要变量”,其影响程度超过F6;特别是当管道参数变化范围较大(场景3)时,K2-3、K7-9对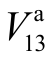 的影响程度与排名第二的变量(F3)相当;相对于均匀分布(场景2、3),正态分布管道参数(场景4、5)对
的影响程度与排名第二的变量(F3)相当;相对于均匀分布(场景2、3),正态分布管道参数(场景4、5)对 灵敏度指标影响较小。此外,场景2和3表明,均匀分布管道参数的方差对
灵敏度指标影响较小。此外,场景2和3表明,均匀分布管道参数的方差对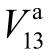 灵敏度指标有显著影响,而对比场景4和5可知正态分布管道参数的方差影响较小。进一步对比场景2和5可知,尽管两种场景下管道参数的方差相同,但场景 2中 K2-3、K7-9和K1-2的重要程度显著高于场景5,表明管道参数的分布类型对灵敏度指标有明显影响。
灵敏度指标有显著影响,而对比场景4和5可知正态分布管道参数的方差影响较小。进一步对比场景2和5可知,尽管两种场景下管道参数的方差相同,但场景 2中 K2-3、K7-9和K1-2的重要程度显著高于场景5,表明管道参数的分布类型对灵敏度指标有明显影响。
由图11同样可见,管道参数的不确定性对配气网变量F4-7的全局灵敏度指标有显著影响,且该影响大于对配电网 的影响。例如,在场景1下,对F4-7影响最大的变量是F3和F4,而在场景2、3下,K2-4和K2-3取代F3和F4,成为对F4-7影响最大的变量;同时,对于管道参数变化范围较大的场景 3,K4-7也成为仅次于K2-4和K2-3的“重要变量”。与图10类似,相对均匀分布(场景2、3)而言,正态分布管道参数(场景4、5)对F4-7灵敏度指标的影响同样较小,但其程度超过对
的影响。例如,在场景1下,对F4-7影响最大的变量是F3和F4,而在场景2、3下,K2-4和K2-3取代F3和F4,成为对F4-7影响最大的变量;同时,对于管道参数变化范围较大的场景 3,K4-7也成为仅次于K2-4和K2-3的“重要变量”。与图10类似,相对均匀分布(场景2、3)而言,正态分布管道参数(场景4、5)对F4-7灵敏度指标的影响同样较小,但其程度超过对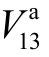 的影响。具体来说,场景 4、5下,各管道参数对
的影响。具体来说,场景 4、5下,各管道参数对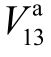 的影响程度均在第9位之后,而管道参数 K2-4对 F4-7的影响在场景 4下排位第7,在场景5则进一步上升到第4位。
的影响程度均在第9位之后,而管道参数 K2-4对 F4-7的影响在场景 4下排位第7,在场景5则进一步上升到第4位。
此外,与图10的结论类似,由图11中场景2和3可知,均匀分布管道参数的方差对F4-7的灵敏度指标有显著影响,而对比场景4和5可知正态分布管道参数的方差则影响较小。进一步对比图11中场景2和5可知,尽管两种场景下管道参数的方差相同,但场景2中K2-4和K2-3的重要程度显著高于场景 5,同样表明管道参数的分布类型对 F4-7灵敏度指标有明显影响。
以上结果表明管道参数的不确定性对全局灵敏度指标有显著影响,是区域电-气联合系统全局灵敏度分析中不可忽略的不确定因素。
此外,对比图10、图11中相同场景的计算结果发现,对 而言“最重要变量”是配气网中的F2而非配电网的变量,而对 F4-7而言,K2-4的重要程度超过管道 4-7本身的参数 K4-7,再次表明某个输入变量对应的全局灵敏度指标不仅取决于该输入变量与输出变量之间的耦合关系或密切程度,而是系统中各个输入变量及其相互作用的综合结果。
而言“最重要变量”是配气网中的F2而非配电网的变量,而对 F4-7而言,K2-4的重要程度超过管道 4-7本身的参数 K4-7,再次表明某个输入变量对应的全局灵敏度指标不仅取决于该输入变量与输出变量之间的耦合关系或密切程度,而是系统中各个输入变量及其相互作用的综合结果。
7 结论
本文考虑电/气负荷、光伏出力和天然气管道参数的不确定性,提出一种基于 Sobol′方法和 sPCE的区域电-气联合系统的全局灵敏度分析方法。算例分析表明本文方法能够定量评估各种不确定因素及其相关性对区域电-气联合系统的影响。主要结论如下:
1)与基于MCS的全局灵敏度方法相比,本文方法在保证正确性的同时显著提高了计算效率。
2)在区域电-气联合系统全局灵敏度分析中需要考虑不确定变量之间的相关性,忽略相关性将严重影响全局灵敏度指标及不确定变量的“重要性排序”。
3)天然气管道参数的不确定性同样对全局灵敏度指标及“重要性排序”有显著影响,是区域电-气联合系统全局灵敏度分析中不可忽略的不确定因素。
4)全局灵敏度指标是联合系统中多种不确定因素相互作用、相互影响的综合结果,有助于揭示电-气联合系统运行状态与各种不确定因素之间的复杂关系,从而有效辨识影响联合系统运行的关键因素。
本文以区域电-气联合系统为研究对象,但本文所提全局灵敏度分析方法容易推广应用于跨区域电-气联合系统或者其他形式的综合能源系统。
[1]余晓丹, 徐宪东, 陈硕翼, 等.综合能源系统与能源互联网简述[J].电工技术学报, 2016, 31(1): 1-13.Yu Xiaodan, Xu Xiandong, Chen Shuoyi, et al.A briefreview to integrated energy system and energy internet[J].Transactions of China Electrotechnical Society, 2016, 31(1): 1-13.
[2]罗毅, 邵周策, 张磊, 等.考虑风电不确定性和气网运行约束的鲁棒经济调度和备用配置[J].电工技术学报, 2018, 33(11): 2456-2467.Luo Yi, Shao Zhouce, Zhang Lei, et al.Robust economic dispatch and reserve configuration considering wind uncertainty and gas network constraints[J].Transactions of China Electrotechnical Society, 2018, 33(11): 2456-2467.
[3]赵霞, 杨仑, 瞿小斌, 等.电-气综合能源系统能流计算的改进方法[J].电工技术学报, 2018, 33(3): 467-477.Zhao Xia, Yang Lun, Qu Xiaobin, et al.An improved energy flow calculation method for integrated electricity and natural gas system[J].Transactions of China Electrotechnical Society, 2018, 33(3): 467-477.
[4]韩佶, 苗世洪, 李超, 等.计及相关性的电-气-热综合能源系统概率最优能量流[J].电工技术学报,2019, 34(5): 1055-1067.Han Ji, Miao Shihong, Li Chao, et al.Probabilistic optimal energy flow of electricity-gas-heat integrated energy system considering correlation[J].Transactions of China Electrotechnical Society, 2019,34(5): 1055-1067.
[5]陈胜, 卫志农, 孙国强, 等.电-气混联综合能源系统概率能量流分析[J].中国电机工程学报, 2015,35(24): 6331-6340.Chen Sheng, Wei Zhinong, Sun Guoqiang, et al.Probabilistic energy flow analysis in integrated electricity and natural-gas energy systems[J].Proceedings of the CSEE, 2015, 35(24): 6331-6340.
[6]Yang Lun, Zhao Xia, Hu Xiaoyun, et al.Probabilistic power and gas flow analysis for electricity-gas coupled networks considering uncertainties in pipeline parameters[C]//2017 IEEE Conference on Energy Internet and Energy System Integration (EI2),Beijing, 2017: 1-6.
[7]Hu Yuan, Lian Haoran, Bie Zhaohong, et al.Unified probabilistic gas and power flow[J].Journal of Modern Power Systems and Clean Energy, 2017, 5(3):400-411.
[8]Qiao Zheng, Huang Shangyuan, Li Rui, et al.An interval gas flow analysis in natural gas and electricity coupled networks considering the uncertainty of wind power[J].Applied Energy, 2017, 201: 343-353.
[9]赵霞, 胡潇云, 杨仑, 等.考虑参数不确定性的区域电-气联合系统的概率-模糊能流评估[J].电力自动化设备, 2019, 39(2): 135-142.Zhao Xia, Hu Xiaoyun, Yang Lun, et al.Probabilisticpossibilistic energy flow evaluation of regional electricity-gas system considering parameter uncertainties[J].Eletric Power Automation Equipment,2019, 39(2): 135-142.
[10]孙国强, 陈霜, 卫志农, 等.计及相关性的电—气互联系统概率最优潮流[J].电力系统自动化, 2015,39(21): 11-17.Sun Guoqiang, Chen Shuang, Wei Zhinong, et al.Probabilistic optimal power flow of combined natural gas and electric system considering correlation[J].Automation of Electric Power Systems, 2015, 39(21):11-17.
[11]Chaudry M, Wu J, Jenkins N.A sequential Monte Carlo model of the combined GB gas and electricity network[J].Energy Policy, 2013, 62: 473-483.
[12]余娟, 马梦楠, 郭林, 等.含电转气的电-气互联系统可靠性评估[J].中国电机工程学报, 2018,38(3): 708-715.Yu Juan, Ma Mengnan, Guo Lin, et al.Reliability evaluation of integrated electrical and natural-gas system with power-to-gas[J].Proceedings of the CSEE, 2018, 38(3): 708-715.
[13]Chen Juanwei, Yu Tao, Xu Yue, et al.Fast analytical method for reliability evaluation of electricity-gas integrated energy system considering dispatch strategies[J].Applied Energy, 2019, 242: 260-272.
[14]骆柏锋, 穆云飞, 赵波, 等.基于统一潮流模型的电-气耦合综合能源系统静态灵敏度分析[J].电力系统自动化, 2018, 42(13): 29-35.Luo Bofeng, Mu Yunfei, Zhao Bo, et al.State sensitivity analysis of integrated electricity and gas system based on unified power flow model[J].Automation of Electric Power Systems, 2018, 42(13):29-35.
[15]秦佳倩, 马瑞.电-气耦合系统概率Pareto最大负荷裕度及灵敏度分析[J].电网技术, 2019, 43(1): 58-65.Qin Jiaqian, Ma Rui.Probability Pareto maximum load margin and sensitivity analysis for electricity-gascoupling system[J].Power System Technology, 2019,43(1): 58-65.
[16]Sobol' I M.Global sensitivity indices for nonlinear mathematical models and their Monte Carlo estimates[J].Mathematics and Computers in Simulation, 2001, 55: 271-280.
[17]Ni F, Nijhuis M, Nguyen P H, et al.Variance-based global sensitivity analysis for power systems[J].IEEE Transactions on Power Systems, 2018, 33(2): 1670-1682.
[18]何琨, 严正, 徐潇源, 等.基于 Sobol'法的孤岛微电网潮流全局灵敏度分析[J].电力系统自动化,2018, 42(14): 99-106.He Kun, Yan Zheng, Xu Xiaoyun, et al.Sobol' method based global sensitivity analysis of power flow in inlanded microgrid[J].Automation of Electric Power Systems, 2018, 42(14): 99-106.
[19]Xu Xiaoyuan, Yan Zheng, Shahidehpour M, et al.Power system voltage stability evaluation considering renewable energy with correlated variabilities[J].IEEE Transactions on Power Systems, 2018, 33(3):3236-3245.
[20]Hasan, Nazmul K, Preece R.Influence of stochastic dependence on small-disturbance stability and ranking uncertainties[J].IEEE Transactions on Power Systems,2017, 33(3): 3227-3235.
[21]孙鑫, 王博, 陈金富, 等.基于稀疏多项式混沌展开的可用输电能力不确定性量化分析[J].中国电机工程学报, 2019, 39(10): 1-10.Sun Xin, Wang Bo, Chen Jinfu, et al.Sparse polynomial chaos expansion based uncertainty quantification for available transfer capability[J].Proceedings of the CSEE, 2019, 39(10): 1-10.
[22]宋梦, 于继来, 李碧君, 等.HDMR在电网潮流概率评估与调控中的应用[J].电网技术, 2014, 38(6):1585-1592.Song Meng, Yu Jilai, Li Bijun, et al.Application of high dimensional model representation in probability assessment and regulation of power flow[J].Power System Technology, 2014, 38(6): 1585-1592.
[23]王伟亮, 王丹, 贾宏杰, 等.考虑天然气网络状态的电力-天然气区域综合能源系统稳态分析[J].中国电机工程学报, 2017, 37(5): 1293-1305.Wang Weiliang, Wang Dan, Jia Hongjie, et al.Steady state analysis of electricity-gas regional integrated energy system with consideration of NGS network status[J].Proceedings of the CSEE, 37(5): 1293-1305.
[24]Sun Xin, Tu Qingrui, Chen Jinfu.Probabilistic load flow calculation based on sparse polynomial chaos expansion[J].IET Generation, Transmission &Distribution, 2018, 11(12): 2735-2744.
[25]Hansen C W, Debs A S.Power-system state estimation using three-phase models[J].IEEE Transactions on Power System, 1995, 10(2): 818-824.
[26]Zeng Qing, Fang Jiakun, Li Jinghua, et al.Steady-state analysis of the integrated natural gas and electric power system with bi-directional energy conversion[J].Applied Energy, 2016, 184: 1483-1492.
[27]Peng Sui, Tang Junjie, Li Wenyuan.Probabilistic power flow for AC/VSC-MTDC hybrid grids considering rank correlation among diverse uncertainty sources[J].IEEE Transactions on Power Systems, 2016, 32(5): 4035-4044.
[28]IEEE PES AMPS DSAS.Test feeder working group[EB/OL].http://sites.ieee.org/pes-testfeeders/resources/.
[29]Electric power research institute.Simulation tool -OpenDSS[EB/OL].http://smartgrid.epri.com/Simulati onTool.aspx
[30]任洲洋.光伏时空概率模型及其在电力系统概率分析中的应用[D].重庆: 重庆大学, 2014.
[31]Abeysekera M, Wu J, Jenkins N, et al.Steady state analysis of gas networks with distributed injection of alternative gas[J].Applied Energy, 2016, 164: 991-1002.