0 引言
一直以来,发、输、配、售电垂直化管理的传统运行模式作为我国电力系统运行的支柱,维持着居民日常生活中的电力运营。然而,随着我国经济规模扩大带来的用电需求剧增,传统的电力市场运行模式出现越来越多的问题[1]。其中,电力价格的僵化以及缺乏竞争机制是造成这种现象的重要原因,而在市场环境下进行电力改革则是对其进行有效处理的关键措施[2-3]。
同时,随着新能源发电技术的快速发展[4-5],为了将新能源电力引入现阶段的电力市场并提升新能源发电的经济性,由新能源发电技术有机结合而成的混合能源系统被视为实现该目标的重要手段。此外,在一些可再生能源资源(太阳能、风能、水力资源)丰富但当地配电设施并不完善的偏远地区,建立混合能源系统并网是对当地用电需求进行补充的有效方法[6]。考虑混合能源系统在项目周期的经济效益,合理有效的容量配置是混合能源系统在电力市场中具备竞争力的关键。
已有大量的研究针对混合能源系统的运行以及容量配置等问题进行探讨。针对几千kW规模的孤立微电网,文献[7]构建风光蓄混合能源系统满足当地电力需求,并在技术经济评价等方面对混合能源系统进行优化。同样针对容量较小的微电网系统,文献[8]提出一种建立在碳排放计算模型下的风光储多能源互补微电网以及并网日前调度的优化方法。文献[9]基于双层决策模型,兼顾系统稳定性和经济性,研究风光储联合发电系统中储能容量优化配置问题,通过不同季节下储能容量之间的比较验证方法的有效性。文献[10]在风光储三个主体之外,还考虑利用燃气轮机等多种形式能源进行综合供能,且以综合供能系统年均成本最小为目标,提出风光燃储系统的优化配置方法。文献[11-12]则提出在考虑需求侧响应下的光储微电网联合配置优化方法。综上所述,目前针对混合能源系统的研究主要集中在风光储系统的运行及容量配置等问题上,考虑到我国西部省份丰富的水力资源[13]以及水光互补特性[14],将水电站这一成熟的可再生能源发电技术整合进混合能源系统中无疑将为混合能源系统在我国发展带来重大飞跃。本研究依托于国家重点研发计划在四川小金县示范区的水光储系统,探讨存在外部大电网供电基础下并网的水光储系统规划。
涉及混合能源系统具体的容量配置方案设计,由于需要考虑投资成本、系统稳定性、环境保护等诸多因素,故而通常采用多目标算法求解。文献[15]关注考虑电动汽车的风水火联合系统的规划运行,文中采用发电成本及排放因子两个目标进行运行优化。文献[16]则提出一个多目标的长期优化模型,该模型关注电力输出过程的平稳性和系统的年发电量。
此外,采用双层规划模型求解混合能源系统优化问题也得到广泛认可,文献[17]基于上、下层目标函数为满足置信水平的年利润最大和考虑主动管理的分布式风光有功削减最小的双层规划模型,对主动配电网中的分布式风光最优潮流优化配置进行研究。考虑风力发电的不确定性,文献[18]建立以系统投资成本最小为目标函数的上层模型和关注系统运行可行性的下层模型组成的双层规划模型,目的在于提高综合电力和天然气系统可再生能源渗透率。在文献[19]的岛屿能源系统中,为了使太阳能集成到当地制冷供热和电力部门,采用双层规划模型研究最优容量配置以优化海水淡化需求和能源系统的结合,结果表明,容量配置结果取决于其经济和环境目标。文献[20]中,以最小化系统投资成本和运营成本为目标的双层规划模型被应用在天然气与电力一体化系统容量研究上,并且分别采用二进制粒子群优化算法和内点法求解其上、下层函数。类似地,多目标粒子群算法也被用于求解为优化混合电力系统组件容量配置而构建的双层规划模型中[21]。相较于上述文献中的双层规划模型,本文采用完全不同的上、下层求解算法。上层混合能源系统规划问题具有强非线性特性,启发式算法是解决此种问题的较好选择,因此,本文采用线性递减惯性权重粒子群(Linearly Decreasing Inertia Weight, LDIW)算法对其求解,并对比其他算法证明其优越性;而下层运行问题则运用序列二次规划(Sequential Quadratic Programming, SQP)算法求解。
通过以上文献回顾,很少有容量配置相关的文献计及实际中存在的投资成本规模效应,即生产规模增大带来的边际成本递减,而对系统容量配置结果产生偏差。为了更精确地估计现实中的系统建造成本以及填补目前以小水电站为主体的混合能源系统研究空白,本文建立在我国西南地区较有特色的,以光伏电站、小水电站和抽水蓄能电站为主体的混合能源系统,并提出在上、下层各具目标函数的双层规划模型基础上,探索混合能源系统投资成本与售电收益间的关系,最终得到整个项目周期内最大经济效益的系统容量优化配置。最后,算例仿真结果表明文中模型容量配置优化方案可显著提高混合能源系统的经济性。
1 光伏/小水电/抽水蓄能电站系统模型
1.1 光伏电站模型
由于太阳能分布广泛、永不枯竭的特点,光伏发电技术已成为新能源发电的重要方式。光伏发电技术的发电原理是光伏电池在太阳光的照射下,经由电池板的光生伏特效应将太阳能转换为电能[22]。
光伏电池面板的发电主要受到太阳光强度、温度、电池板倾角等因素的影响。因此,可构建出小时级别的光伏功率波动特性模型[22],即
式中,PPV1为光伏电池额定功率;ηinv为逆变器效率;ηloss为光伏电池损耗效率;ηref为光伏电池模块在参考温度下的效率;kT为光伏电池板的功率温度系数;T0为运行光伏组件的温度;Tref为光伏组件的参考温度;Gα为光伏待建地区地表太阳辐射强度的小时均值。式中多数参数都可从光伏电池板制造商提供的数据手册中找到。
考虑到光伏电站出力在极大程度上受当地天气和时空特性影响,为保证数据精确性,本文采取收集整年的光伏电池板温度以及当地太阳辐射强度数据的方法,针对每日24个时段,全年共计8 760个时段进行计算,从而准确地模拟光伏电站出力特性。
1.2 小水电站模型
小水电站因其较小的建造规模和发电过程的灵活性,被视为填补地区供电缺口的有效措施。小水电站的发电原理是利用上游库容聚集附近的天然水源来冲击水轮发电机,从而将水流的势能转换为可用的电能[23-24]。
制约发电规模的主要是天然水源的流量和上下游的高度差(即水头),小水电站的实际输出功率PHS可以表示为
式中,η为水电站的能量转换效率,一般用水轮机效率 η1与发电机效率 η2的乘积表示;H0为小水电站的净水头;E的取值是由该水电站的规模以及设备的先进程度共同确定,小水电站的 E值通常在6.5~7.5。
考虑到现实情况下的小水电站运行方式,在本研究中采用的小水电站将具有维持某一水位的可控性,即小水电站的实际发电功率可调节,以维持发电上网后电网、负荷的稳定。
1.3 抽水蓄能电站模型
鉴于新能源发电技术具有间歇性、不确定性等特点,目前技术成熟、成本较低的抽水蓄能电站被选择为混合能源系统的储能方式。
抽水蓄能电站使用可逆式水泵水轮机,因而可在电网电力负荷需求较低时,吸收电网过剩电能用于抽水并储存在上游水库中,而在电网负荷高峰期将电能释放出来,满足电力需求[25]。抽水蓄能电站在这个过程中不仅可以保证电能质量,而且可实现机组发电的平稳过渡,便于电力系统的控制和调节。
抽水蓄能电站的模型主要由可逆式水泵水轮机装机容量Ppump_power和上游水库库容Vpump_cap构成,抽水蓄能电站的模型和出力约束将在2.2节中展示。
1.4 混合能源系统的运行方式
针对上述光伏/小水电/抽水蓄能电站组成的混合能源系统模型,基于电力市场现实电价的前提,结合系统三个主体特点,考虑现实情况提出三者互补且共同优化以获得最大的售电利益的混合能源系统运行方式:
1)若当前的电网售电电价处于一天内电价的较高区间,光伏电站与小水电站会选择将自身所发的电力直接上网售卖,抽水蓄能电站也将在满足相应约束的条件下尽量释放自身储水量发电以获得最大的经济效益。
2)若当前的电网售电电价处于一天内电价的较低区间,光伏电站会将自身所发的电力输送至抽水蓄能电站储存起来,不能储存的部分才直接上网售卖。小水电站则会将天然流量储存在自身上游库容中,不能储存的部分才选择输送至抽水蓄能电站储存或直接发电上网售卖,抽水蓄能电站不仅储存系统内生产的电力,还可以从电网中购入电力并抽水储存,以待电价高峰期售出获利。
因此,可以看出在混合能源系统中,各个主体的容量配置与各自的运行方式之间存在博弈关系。对三个电站主体进行容量配置时,其投资成本与运行收益有着直接的矛盾,如何平衡这两者之间的关系从而获得混合能源系统建造周期内的最大经济效益则是本文主要研究的问题。
2 基于电力市场的混合能源系统双层规划模型
不同于常规的单目标或者多目标优化问题,双层规划模型是一类具有主从递阶关系结构的模型[3,17-21,26]。它一般的数学模型表达式为
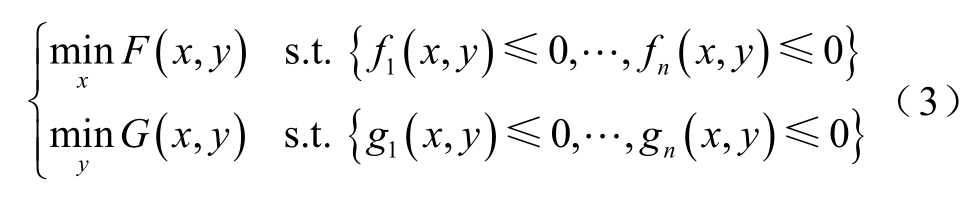
式中,x和 y分别为上层、下层决策变量;F(x,y)和G(x,y)分别为上层、下层目标函数; fn (x ,y)和g n (x ,y)分别为上层、下层的约束限制条件。
双层规划模型主要由两个各具目标函数和各自约束条件的主体构成,并且两个主体之间有着非协作方式的互相作用关系。上层目标函数在自身约束条件下将配置方案传递给下层,下层目标函数在具体配置方案的基础上对每个方案进行优化运行模拟,并将所得的优化结果传递给上层,再对上层的决策产生指导作用。
2.1 上层优化模型
2.1.1 目标函数
上层优化属于系统投资决策问题,优化目标是系统中三个主体的总投入成本与年运行收益之比,即投入成本回收年限最小。总成本包含每个主体的投资成本以及整个周期中的替换成本、运维成本。
具体的数学表达式为
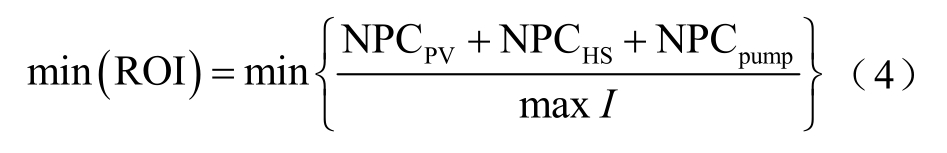
式中,ROI为在一定的容量配置下混合能源系统在最大化经济效益时的投入成本回收年限;NPCPV为光伏电站的总成本;NPCHS为小水电站的总成本;NPCpump为抽水蓄能电站的总成本;I为一年内混合能源系统通过优化运行所获得的售电收益。
1)光伏电站总成本
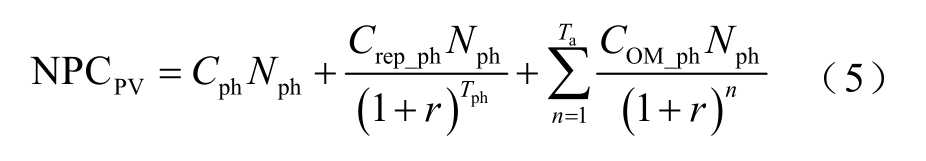
式中,Nph为光伏电站中光伏电池的数量;Cph为光伏电池的单价;Crep_ph为单位光伏电池的替换成本;Tph为光伏电池的寿命周期;COM_ph为单位光伏电池的运行维护成本;r为折现率;Ta为本项目的周期。
2)小水电站总成本
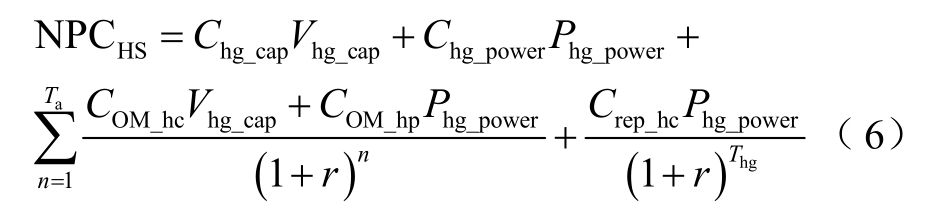
式中,Vhg_cap为小水电站中的上游库容的体积;Phg_power为小水电站水轮机的装机容量;Chg_cap为小水电站上游库容每立方米的单价;Chg_power为小水电站水轮机装机容量每千瓦的单价;Crep_hc为小水电站水轮机的替换成本;Thg为小水电站水轮机的寿命周期;COM_hc为小水电站上游库容每立方米的运行维护成本;COM_hp为小水电站每千瓦的运维成本。
3)抽水蓄能电站总成本

式中,Vpump_cap为抽水蓄能电站上游库容的体积;Ppump_power为抽水蓄能电站可逆式水泵水轮机的装机容量;Cpump_cap为抽水蓄能电站上游库容每立方米的单价;Cpump_power为抽水蓄能电站水轮机装机容量每千瓦的单价;Crep_pp为抽水蓄能电站水轮机的替换成本;Tpump为抽水蓄能电站水轮机的寿命周期;COM_pc为抽水蓄能电站上游库容每立方米的运行维护成本;COM_pp为抽水蓄能电站每千瓦的运维成本。
2.1.2 约束条件
1)光伏电池数量约束
式中,Nph为光伏电站中光伏电池的数量,Nphmax为光伏电站中光伏电池数量的上限。
2)小水电站上游库容容量约束
式中,Vhg_cap为小水电站中的上游库容的体积;Vhg_capmin为小水电站上游库容体积的下限;Vhg_capmax为小水电站上游库容体积的上限。
3)小水电站装机容量约束
式中,Phg_power为小水电站水轮机的总装机容量;Phg_powermax为小水电站水轮机装机容量的上限。
4)抽水蓄能电站上游库容容量约束
式中,Vpump_cap为抽水蓄能电站上游库容的体积;Vpump_capmax为抽水蓄能电站上游库容体积的上限。
5)抽水蓄能电站装机容量约束
式中,Ppump_power为抽水蓄能电站水轮机的总装机容量;Ppump_powermax为抽水蓄能电站水轮机装机容量的上限。考虑到现实情况,在简化模型的前提下,将小水电站以及抽水蓄能电站的下游水库视为库容无限的海平面。
2.2 下层优化模型
2.2.1 目标函数
下层优化属于系统运行优化问题,优化目标是系统的三个主体在设计的运行方式下获得的年售电收益最大。具体的数学表达式为
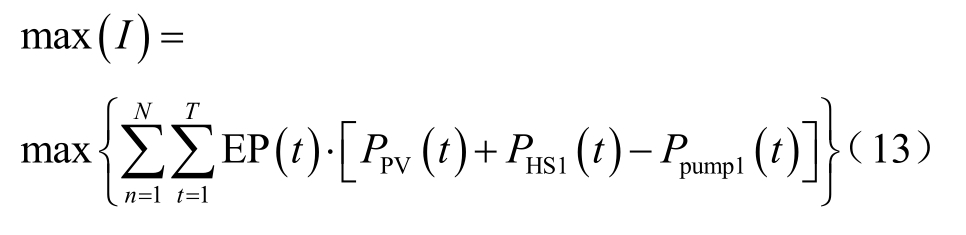
式中,EP(t)为t时刻的电价;PPV(t)为t时刻光伏电站上网售卖的输出电量;PHS1(t)为 t时刻小水电站上网售卖的输出电量;Ppump1(t)为t时刻抽水蓄能电站的输入电量;I为一年中通过优化运行所获得的售电收益;N为一年中的天数,365d;T为一天中的小时数,24h。
抽水蓄能电站输入电量为
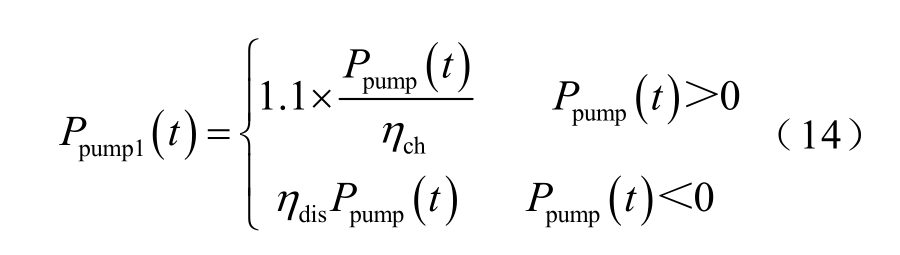
式中,Ppump1(t)为抽水蓄能电站的输入电量;Ppump(t)为抽水蓄能电站上游库容中水量的可发电量,正值代表抽水蓄能电站正处于抽水状态,负值代表抽水蓄能电站正处于放水状态;ηch和ηdis分别为抽水蓄能电站抽水、放水的效率;1.1是购电增益,表示抽水蓄能电站向电网购电电价为当前向电网售电电价的1.1倍。
2.2.2 约束条件
1)小水电站运行过程约束限制
(1)运行功率约束
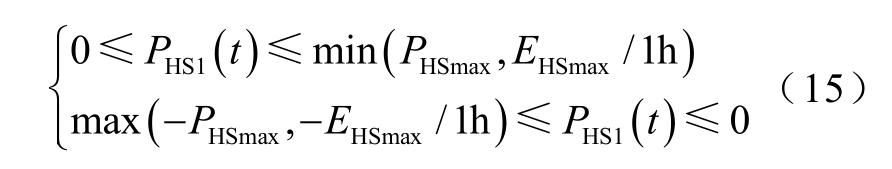
式中,PHSmax为小水电站水轮机的最大装机容量;EHSmax为小水电站上游库容最大体积所对应的发电量。限制小水电站任意时刻的发电功率不得超过水轮机最大装机容量和上游库容最大可发电量中的较小值。
(2)上游库容容量约束
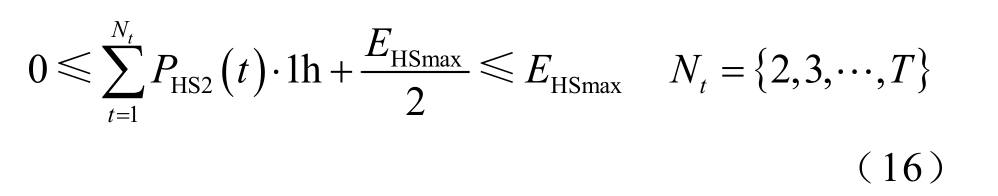
式中,PHS2(t)为t时刻小水电站储存在自身上游库容中的电量。限制在任意时刻小水电站上游库容所蓄水量不得超过设定的上游库容体积,且在初始时刻,小水电站上游库容的水量设置为库容体积的一半。
(3)进、出水量约束

式中,PHS(t)为t时刻小水电站进水的可发电量。限制一天中小水电站的进水量和出水量相同。
2)抽水蓄能电站运行过程约束限制
(1)运行功率约束
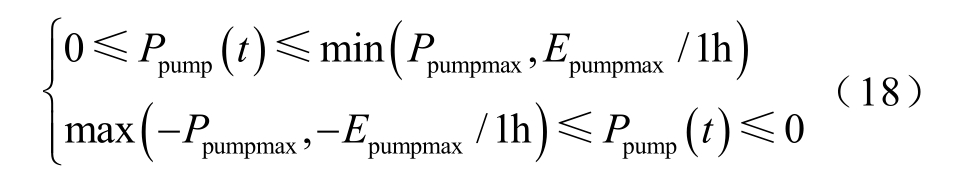
式中,Ppumpmax为抽水蓄能电站可逆式水泵水轮机的最大装机容量;Epumpmax为抽水蓄能电站上游库容最大体积所对应的发电量。限制抽水蓄能电站任意时刻的抽水、放水功率不得超过可逆式水泵水轮机最大装机容量和上游库容最大可发电量中的较小值。
(2)上游库容容量约束

限制在任意时刻,抽水蓄能电站上游库容所蓄水量不得超过设定的上游库容体积,且在初始时刻,抽水蓄能电站上游库容的水量设置为库容体积的一半。
(3)进、出水量约束

限制一天中抽水蓄能电站的进水量和出水量相同。
2.3 双层规划模型上、下层之间的动态联系
上层规划模型以三个主体的容量配置为决策变量,以系统中三个主体的总投入成本与年运行收益之比最小为优化目标,先将容量配置方案传递给下层。下层的优化目标是系统的三个主体在上层给定的容量配置下,以 1.4节中的运行方式售电获得总收益最大。在下层规划模型运行过程中,将根据全年电价信息通过算法优化每一小时中三个主体的运行行为获得最大的售电收益,并将该收益结果返回给上层。此时上层规划模型根据容量配置更新各主体容量配置投入成本,再结合下层传递的收益结果求解得出投入成本回收年限。
上层规划模型针对上层目标函数结果进行对比优化,探索出新的容量配置方案,周而复始地进行上述步骤,在满足上、下层约束条件的前提下,得到混合能源系统的最优容量配置方案。本文提出的双层规划模型结构如图1所示。

图1 双层规划模型结构
Fig.1 Bi-level programming model architecture
3 基于LDIW以及SQP算法的模型求解
由于涉及多目标的双层规划模型是复杂的非线性问题,本文将采用基于LDIW算法和SQP算法对该模型的上、下层分别进行求解。其中,利用LDIW算法来处理上层规划模型中的系统成本决策问题,对下层规划模型的系统运行优化问题,则运用SQP算法求解。
3.1 LDIW算法求解上层规划模型
相比于其他进化算法,粒子群(Particle Swarm Optimization, PSO)算法不仅保留基于群体的整体优化搜索方式,其独特的记忆模型还能够动态顺延现阶段的搜寻状况,调整自身的搜寻战略,因而能够在较少迭代次数内搜寻最优结果,最终达到计算速度快的目的[3,20-21]。
对混合能源系统容量配置方案中具体参数,即光伏电站的光伏电池数、小水电站和抽水蓄能电站的上游库容体积和装机容量,基于实际情况确定各电站容量的上、下限,并随机生成满足容量约束的粒子群。再根据容量约束定义粒子飞行的初速度,使其可在解的空间充分迭代搜索,并实时调整自身位置搜寻最优解。在每一次迭代过程中,粒子将依据两个“极端值”不断变换自身的位置:一个是单粒子通过比较每次迭代过程的位置得出的个体最优解pi,j;另一个是粒子群在比较每次迭代结果后现阶段的群体最优解pg,j。当两个“极端值”确定后,每个粒子将依据式(21)和式(22)来调整自身的速度以及位置。
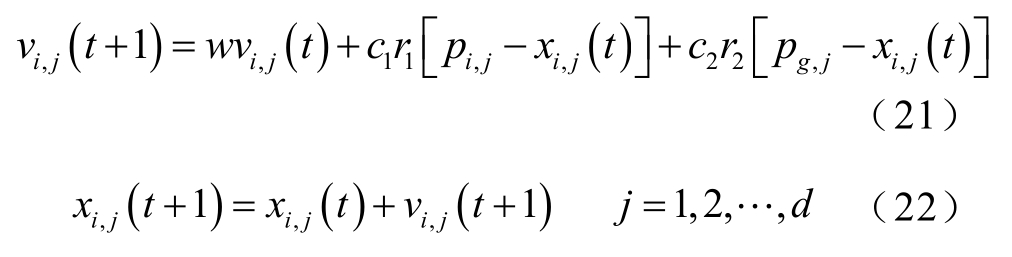
式中,i为粒子的个数;j为需解决问题的维数;vi,j(t)为第i个粒子在第t次迭代中第j维的速度;w为惯性权重;c1和c2为学习因子,分别称为认知学习因子和社会学习因子;r1和 r2为 0~1之间的随机数。粒子不断根据当前最优解来调节自身的位置,向全局最优解前进。
惯性权重是PSO可调整参数中最重要参数,较大的惯性权重有利于粒子逃出局部最优解,提升整体搜寻能力,而较小的惯性权重则便于算法收敛,提升PSO的局部搜寻能力。因此,在迭代过程采用以线性规律变动的惯性权重是解决PSO算法末期易在全局最优解的值附近发生振荡问题的有效措施。
3.2 SQP算法求解下层规划模型
下层规划模型在给定容量配置下,需要解决在满足小水电站和抽水蓄能电站的运行功率约束、上游库容容量约束以及进出水量约束条件下的优化运行问题。基于全年的电价来规划每个时刻下各个主体的运行行为达到获取最大售电收益的目的。SQP等经典分区分块算法是对约束优化等问题进行求解的有效优化算法之一[27]。
SQP算法的主要思想是在求解约束优化问题时,在一系列的初始迭代点构造一群 QP子问题,其目标函数是亟待求解的优化问题在一定条件下的近似,约束条件则是亟待求解的优化问题在线性情况下的靠近,将 QP子问题的解作为迭代搜索的方向,确定迭代搜索的步长,通过不断求解上述QP子问题修正其解,直到最终的结果逼近原非线性规划问题的解为止。
3.3 混合能源系统双层规划模型求解流程
采用 LDIW 与 SQP算法求解本文中搭建的双层规划模型的具体流程如图2所示。
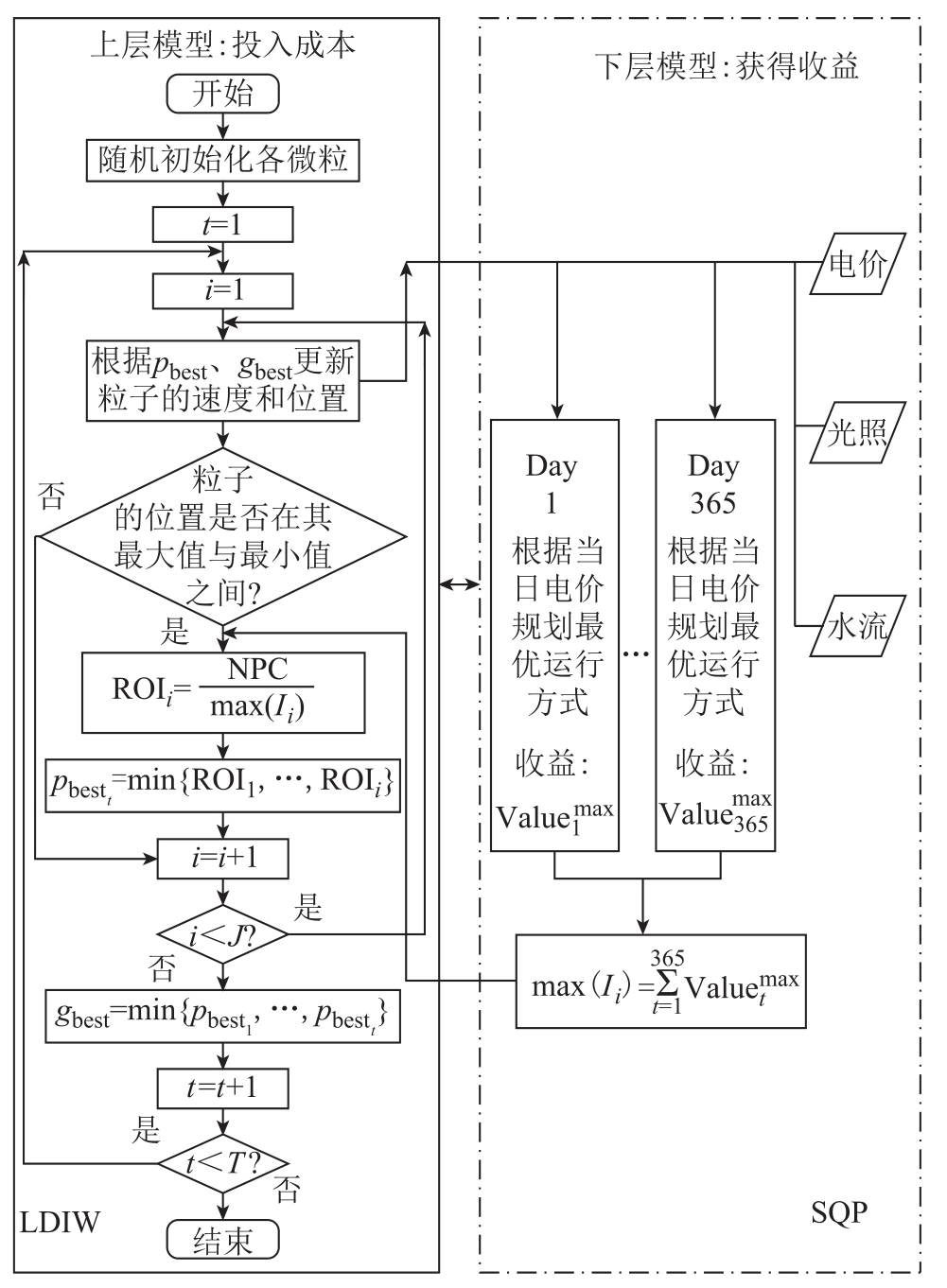
图2 混合能源系统容量优化配置求解流程
Fig.2 Flow chart for capacity optimization allocation of hybrid energy system
4 算例仿真及其结果分析
4.1 算例系统参数
参考电价:由于本文研究考虑市场机制下混合能源系统的最优容量配置方案,现实电力市场电价的获取对于优化容量配置至关重要。
本研究采用丹麦全年的市场电价进行下层规划模型中的系统运行优化,数据来自于文献[6,28]。全年电价波动趋势如图3a所示,电价平均值为0.52元/(kW·h),图3b以全年前5天为例展示详细电价。

图3 全年电价数据
Fig.3 Annual electricity price data
光伏电站参数:光伏电池的出力预计依赖当地光照情况,因此在预测其出力时采用历史全年光照数据。参考温度设置为25℃,每片光伏电池的功率设置为0.1kW,光伏电池的使用周期为10年,即10年后须更换。考虑项目实际情况,光伏电池数目上限为10万片,且规划过程中数目应为整数。全年的光伏电站出力情况如图4a所示,图4b选取全年前5天展示其小时级别出力。结合国内实际情况,设光伏电站的投资成本、运行维护成本和替换成本见表1。此外,本文光伏电池的投资成本预测遵循规模效应,即当企业生产光伏电池规模达到一定水平后,由于生产要素有机结合,光伏电池的单位成本将下降,其下降的趋势如图5所示。
表1 光伏电站建造成本
Tab.1 Construction cost of photovoltaic power station

images/BZ_94_1285_2921_1964_2986.pngimages/BZ_94_1964_2921_2254_2986.pngimages/BZ_94_1285_2988_1964_3053.pngimages/BZ_94_1964_2988_2254_3053.pngimages/BZ_94_1285_3053_1964_3118.pngimages/BZ_94_1964_3053_2254_3118.pngimages/BZ_94_1285_3118_1964_3183.pngimages/BZ_94_1964_3118_2254_3183.png
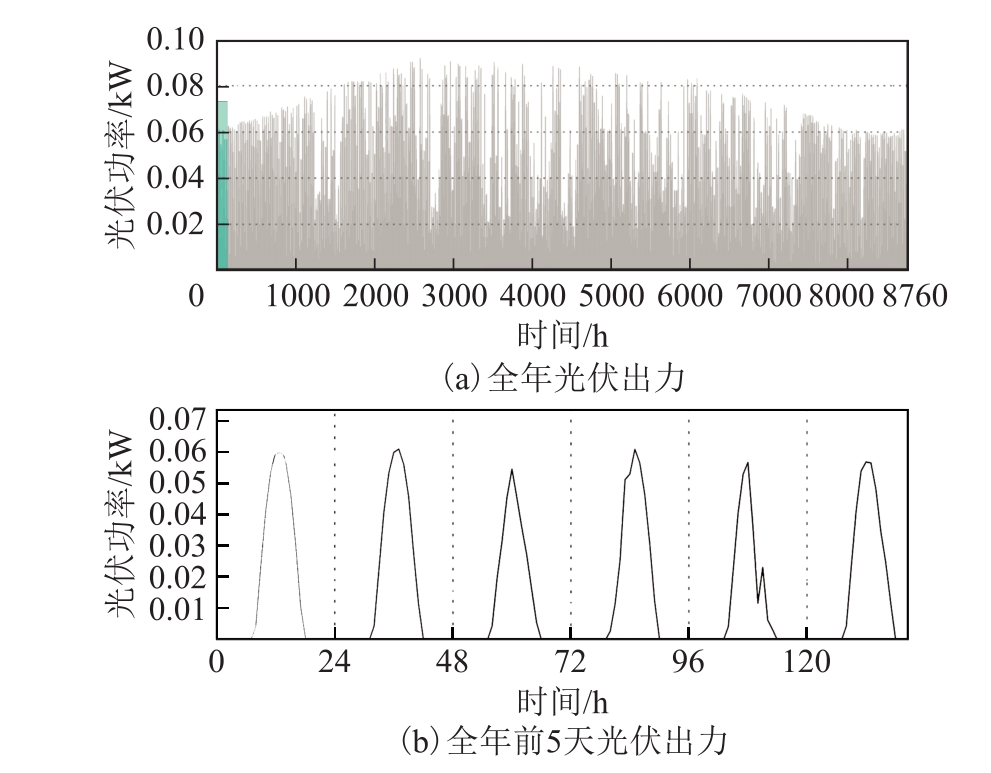
图4 全年光伏功率数据
Fig.4 Annual photovoltaic power data

图5 投资成本规模效应
Fig.5 Scale effect of investment cost
小水电站参数:与光伏发电出力类似,小水电站的出力预测主要取决于小水电站建造地区的天然水流流量情况。不同区域的水流流量存在季节性差异,一般分为枯水季和丰水季,我国大多数河流的流量特点是夏秋多,冬季少甚至断流。在本文中,采用历史全年天然水流流量数据用以预测小水电站出力。本研究中设计建造的小水电站水头设置为60m,小水电站的水轮机效率设置为 85%,发电机效率设置为85%,水轮机的使用周期设置为15年。由于小水电站上游库容寿命通常较长,上游库容的使用周期设定为全项目周期。考虑到当地实际地理因素,小水电站上游库容最大体积对应的可发电量被设置为50 000kW·h,而水轮机装机容量的上限被设置为10 000kW。全年的小水电站流量趋势如图6a所示,图6b选取全年中 5天为例详细展示当地小时级别的天然水流流量趋势。结合国内实际情况,设小水电站上游库容的建造成本、运行维护成本以及水轮机的投资成本、运行维护成本和替换成本见表2。小水电站的上游库容建造成本以及水轮机的投资成本在本文中同样遵循规模效应,如图5所示。
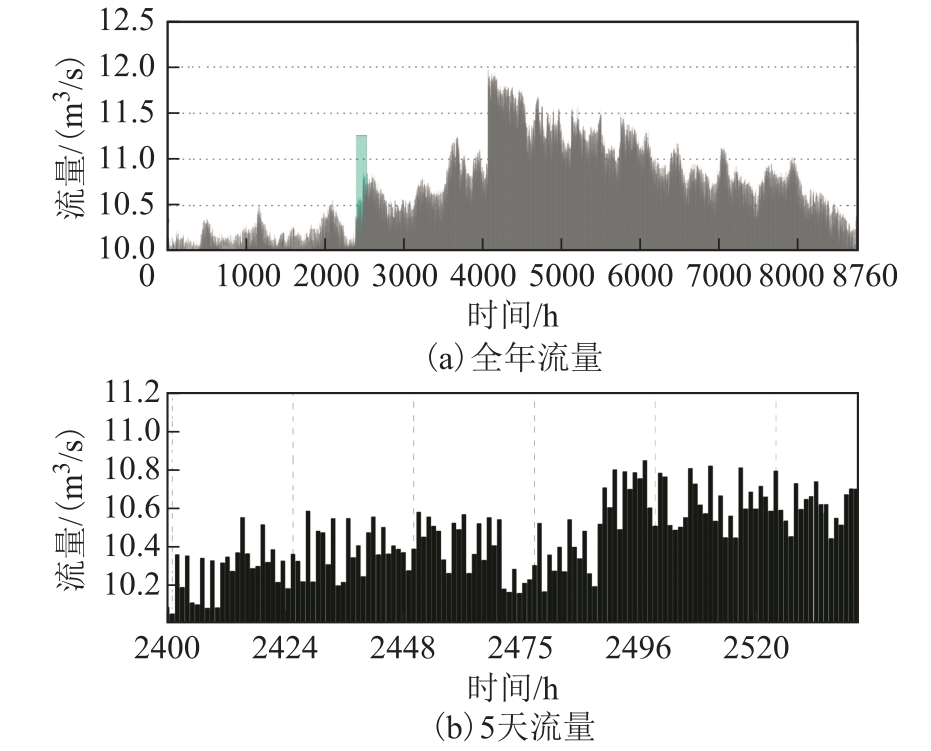
图6 全年流量数据
Fig.6 Annual flow data
表2 小水电站建造成本
Tab.2 Construction cost of small hydropower station

images/BZ_95_1285_1614_1964_1679.pngimages/BZ_95_1964_1614_2254_1679.pngimages/BZ_95_1285_1681_1964_1746.pngimages/BZ_95_1964_1681_2254_1746.pngimages/BZ_95_1285_1746_1964_1811.pngimages/BZ_95_1964_1746_2254_1811.pngimages/BZ_95_1285_1811_1964_1876.pngimages/BZ_95_1964_1811_2254_1876.pngimages/BZ_95_1285_1876_1964_1941.pngimages/BZ_95_1964_1876_2254_1941.pngimages/BZ_95_1285_1941_1964_2006.pngimages/BZ_95_1964_1941_2254_2006.png
抽水蓄能电站参数:本研究中的抽水蓄能电站水头设置为100m,可逆式水泵水轮机的抽水效率为80%,发电效率为90%,使用周期为15年。与小水电站的上游库容相同,抽水蓄能电站的上游库容的使用周期被视为全项目周期。其上游库容最大体积对应可发电量被设置为50 000kW·h,可逆式水泵水轮机装机容量的上限被设置为10 000kW。结合国内实际情况,设抽水蓄能电站上游库容的建造成本、运行维护成本以及可逆式水泵水轮机的投资成本、运行维护成本和替换成本见表3。抽水电站的上游库容建造成本以及水轮机的投资成本在本文中同样遵循规模效应,如图5所示。
表3 抽水蓄能电站建造成本
Tab.3 Construction cost of pumped storage power station

images/BZ_95_1283_2859_2050_2924.pngimages/BZ_95_2073_2859_2234_2924.pngimages/BZ_95_1283_2926_2050_2991.pngimages/BZ_95_2073_2926_2234_2991.pngimages/BZ_95_1283_2991_2050_3056.pngimages/BZ_95_2073_2991_2234_3056.pngimages/BZ_95_1283_3056_2050_3121.pngimages/BZ_95_2073_3056_2234_3121.pngimages/BZ_95_1283_3121_2050_3186.pngimages/BZ_95_2073_3121_2234_3186.pngimages/BZ_95_1283_3186_2050_3251.pngimages/BZ_95_2073_3186_2234_3251.png
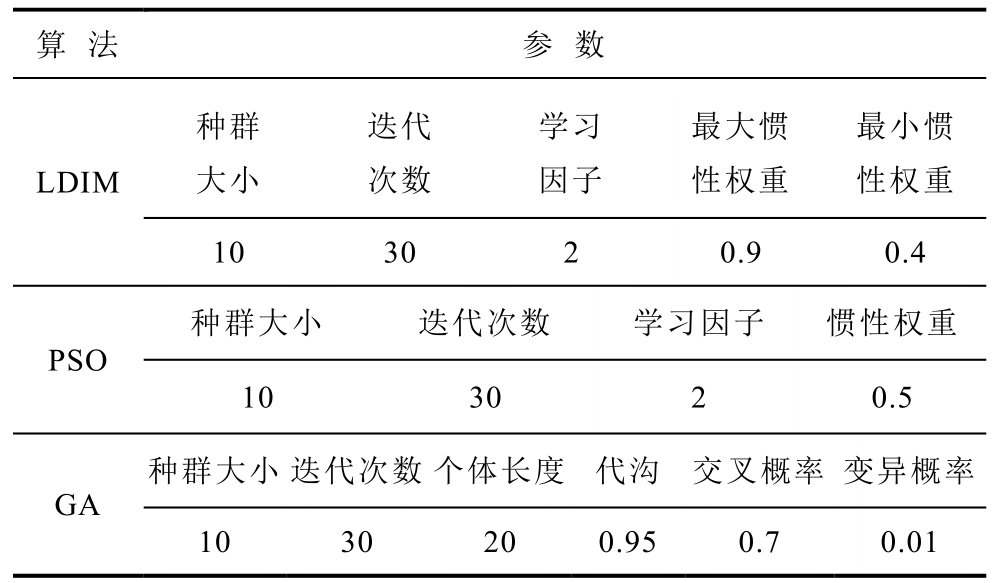
双层规划模型参数:上层规划模型采用的 LDIW算法中,粒子的种群规模设为10个,按需解决问题个数将每个粒子维数设为5维,算法迭代次数为30次,学习因子的数值均设为 2。惯性权重基于线性规律变换,将从最大值按线性规律减小到最小值,在本研究中,将惯性权重的最大值设置为0.9,最小值设置为0.4。
下层规划模型运用的SQP算法中,以一天为单位优化一天中的混合能源系统各个主体24h的运行行为,为获取年售电效益下层模型将优化运行365次。
本文计算系统配置:Inter Xeon W-2123 3.6GHz CPU和64GB内存。本文的混合能源系统模型和所提算法均采用 Matlab R2018a平台进行搭建和编程求解。在工作站运行软件求解容量配置结果的时间约为 30h。由于本研究针对现实混合能源系统,求解的是考虑同时优化系统中三个电站主体运行的规划问题,而此类项目的建设周期一般为数年。因此,在项目开始建设之前就可以根据现实数据进行容量优化配置,程序求解时间对于规划问题是可接受的。
4.2 结果分析
为分析混合能源系统中储能方式对系统各个电站主体的运行方式和项目周期内经济效益等方面的作用从而验证利用文中提出的双层规划模型进行混合能源系统容量配置优化的可行性,本文将从有储能方式(考虑抽水蓄能电站)与无储能方式(不考虑抽水蓄能电站)两个方面进行对比。
基于 4.1节中设置的混合能源系统模型参数和成本参数,利用文中提出的双层规划模型,采用LDIW-SQP算法对模型进行求解,计算得到混合能源系统在有储能方式与无储能方式下的容量优化配置方案,其结果见表4。由表4可以看出,在混合能源系统中是否考虑抽水蓄能电站作为储能方式将显著改变系统中另外两个电站主体的容量配置,进而影响容量配置方案在整个周期范围内的经济性。
表4 两种方式下的系统最优容量配置
Tab.4 Optimal capacity allocation of system in two modes

images/BZ_96_225_2746_820_2811.pngimages/BZ_96_819_2746_1009_2811.pngimages/BZ_96_1032_2746_1175_2811.pngimages/BZ_96_225_2813_820_2878.pngimages/BZ_96_819_2813_1009_2878.pngimages/BZ_96_1032_2813_1175_2878.pngimages/BZ_96_225_2878_820_2943.png images/BZ_96_819_2878_1009_2943.pngimages/BZ_96_1032_2878_1175_2943.pngimages/BZ_96_225_2943_820_3008.pngimages/BZ_96_819_2943_1009_3008.pngimages/BZ_96_1032_2943_1175_3008.pngimages/BZ_96_225_3008_820_3073.png images/BZ_96_819_3008_1009_3073.pngimages/BZ_96_1032_3008_1175_3073.pngimages/BZ_96_225_3073_820_3138.pngimages/BZ_96_819_3073_1009_3138.pngimages/BZ_96_1032_3073_1175_3138.pngimages/BZ_96_225_3140_820_3205.pngimages/BZ_96_819_3140_1009_3205.pngimages/BZ_96_1032_3140_1175_3205.pngimages/BZ_96_225_3205_820_3270.pngimages/BZ_96_819_3205_1009_3270.pngimages/BZ_96_1032_3205_1175_3270.png
在有储能方式的情况下,双层规划模型得到的混合能源系统容量配置方案对小水电站以及光伏电站电池数量给出的容量规划更高。在更大的容量配置前提下,小水电站的弃水情况相对于无储能方式下的混合能源系统可得到很大程度上的缓解。
以下将从混合能源系统运行方式和系统经济效益两个方面,对采用双层规划模型得到的系统最优容量配置进行分析,用以验证双层规划模型在解决混合能源系统容量优化配置问题的有效性。
4.2.1 系统运行方式
为探讨混合能源系统中有、无储能方式对系统运行方式的影响,选取同一天分别在有储能方式下和无储能方式下的小水电站按照运用 SQP算法的下层规划模型得出的运行方式,并进行对比,结果如图7所示。

图7 两种模式下小水电站优化运行结果
Fig.7 Optimal operation results of small hydropower station in two modes
从图7中可以看出,在当日电力市场电价下,小水电站在系统中存在抽水蓄能电站时,针对当日上网电价除初始时刻外的低谷期,即 2:00~5:00时,会做出将天然流量储存至其上游水库的决策。若上游库容储水达到上限时,则将多余的电量输送至抽水蓄能电站储存起来。在当日上网电价的高峰期,即 8:00~20:00时,小水电站将上游水库中储存的水量在满足水轮机约束的情况下不断放水发电,从而直接获利。
同样关注系统经济性,小水电站在系统无抽水蓄能电站时的运行方式是将天然流量利用水轮机不断放水发电并上网售卖,此时只有超出水轮机规划装机容量的很小一部分才可被储存起来在电价高峰期售出,这是因为双层规划模型规划的水轮机装机容量不大,最终获得的年售电收益相对较低,这一点在表4中同样得到体现。
具备储能方式的混合能源系统中,给出抽水蓄能电站在同一天经过优化的最佳运行方式,抽水蓄能电站的上游库容储水量变化和可逆式水泵水轮机每小时的抽放水量如图8所示。

图8 有储能系统中抽水蓄能电站优化运行结果
Fig.8 Optimal operation results of pumped storage power station in system with electricity storage
在下层规划模型优化的运行方式中,抽水蓄能电站在电价低谷期(2:00~5:00时)不仅接收光伏电站及小水电站生产的电力,而且可以从电网中购入电力,并且在电价高峰阶段(15:00~17:00时)放水发电,满足系统售电获利。通过添加抽水蓄能电站,混合能源系统更加丰富了系统的供电方式,对年售电收益的提高产生极大影响。
4.2.2 系统经济效益
基于混合能源系统电站成本数据,将系统在有储能方式及无储能方式下的投入成本回收年限进行对比,结果见表4。
具备抽水蓄能电站作为储能方式的混合能源系统经由 LDIW 算法收敛到最优值,其最优的成本回收年限为9.92年,而无储能方式下混合能源系统的最优成本回收年限为11.38年。这表明满足混合能源系统优化运行方式的前提下,相对于无储能方式的系统,有储能方式的系统具有更快的成本回收速度,原因是抽水蓄能电站的建造使小水电站的弃水量减小并将弃水量有效利用进行发电,从而可获得较高的售电收益,用以抵消添加储能方式带来的成本提升。
除混合能源系统的成本回收年限之外,混合能源系统在全项目周期获得的总收益也是衡量系统经济性的重要指标。基于系统在项目周期内的年售电收益与初期投入成本,可计算系统在有储能方式与无储能方式情况下分别获得的总收益,结果如图9所示。由图9可见,在无储能方式下混合能源系统的成本回收年限不仅高于有储能方式,而且具备抽水蓄能电站的系统每年获得的售电收益为310.84万元,达到无储能方式下的年售电收益的2.41倍。

图9 两种模式下系统在项目周期内所获总收益
Fig.9 The economic benefits of the system in the project cycle under two modes
在整个项目周期内,有储能方式的混合能源系统的收益为6 242万元,较之无储能方式的系统获得的收益 2 397万元提高了 2.6倍。这表明具备抽水蓄能电站的混合能源系统在整个项目周期能够带来经济效益上的巨大提升,对新能源发电企业的发展以及投资具有关键作用。
4.3 算法性能对比
为衡量本文中提出的双层规划模型中利用LDIW 算法求解上层问题的优越性及效率,在相同种群规模下,采用 PSO算法、遗传算法(Genetic Algorithm, GA)对双层规划模型进行多次求解,从中选取其最优解。其中各算法的详细参数设置见表5。
表5 各算法参数设置
Tab.5 Parameter configuration of various algorithms
images/BZ_97_1283_2170_1414_2235.pngimages/BZ_97_1436_2170_2234_2235.pngimages/BZ_97_1283_2237_1414_2443.pngimages/BZ_97_1436_2252_1562_2306.pngimages/BZ_97_1607_2252_1734_2306.pngimages/BZ_97_1413_2237_1585_2375.pngimages/BZ_97_1585_2237_1756_2375.pngimages/BZ_97_1779_2252_1905_2306.pngimages/BZ_97_1756_2237_1928_2375.pngimages/BZ_97_1928_2237_2096_2375.pngimages/BZ_97_2118_2252_2234_2306.png images/BZ_97_2118_2306_2234_2360.pngimages/BZ_97_1413_2377_1585_2443.pngimages/BZ_97_1585_2377_1756_2443.pngimages/BZ_97_1756_2377_1928_2443.pngimages/BZ_97_1928_2377_2096_2443.pngimages/BZ_97_2118_2378_2234_2443.pngimages/BZ_97_1283_2445_1414_2591.png images/BZ_97_1413_2445_1642_2517.pngimages/BZ_97_1642_2445_1870_2517.pngimages/BZ_97_1870_2445_2070_2517.pngimages/BZ_97_2092_2448_2234_2513.pngimages/BZ_97_1413_2519_1642_2591.pngimages/BZ_97_1642_2519_1870_2591.pngimages/BZ_97_1870_2519_2070_2591.pngimages/BZ_97_2092_2522_2234_2587.pngimages/BZ_97_1283_2593_1414_2732.png images/BZ_97_1413_2593_1556_2665.pngimages/BZ_97_1556_2593_1699_2665.pngimages/BZ_97_1699_2593_1842_2665.pngimages/BZ_97_1842_2593_1956_2665.pngimages/BZ_97_1956_2593_2104_2665.pngimages/BZ_97_2127_2596_2234_2661.pngimages/BZ_97_1413_2667_1556_2732.pngimages/BZ_97_1556_2667_1699_2732.pngimages/BZ_97_1699_2667_1842_2732.pngimages/BZ_97_1842_2667_1956_2732.pngimages/BZ_97_1956_2667_2104_2732.pngimages/BZ_97_2127_2667_2234_2732.png
各算法求解双层规划模型所得最优解中投入成本回收年限ROI、计算时间t见表6。
表6 各算法结果对比
Tab.6 Comparison of various algorithms
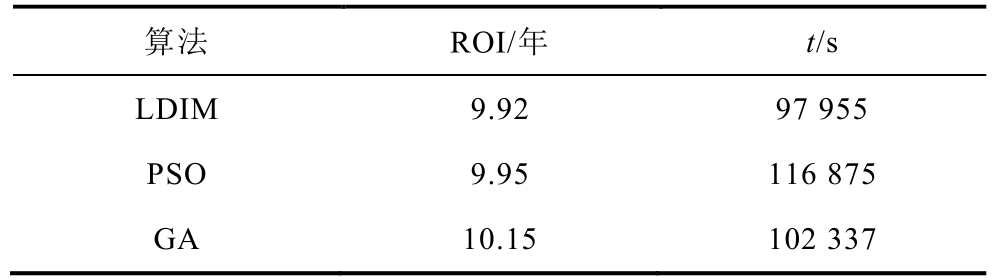
images/BZ_97_1283_3000_1612_3065.pngimages/BZ_97_1612_3000_1929_3065.pngimages/BZ_97_1951_3000_2234_3065.png images/BZ_97_1283_3067_1612_3132.png images/BZ_97_1612_3067_1929_3132.pngimages/BZ_97_1951_3067_2234_3132.pngimages/BZ_97_1283_3132_1612_3197.png images/BZ_97_1612_3132_1929_3197.pngimages/BZ_97_1951_3132_2234_3197.pngimages/BZ_97_1283_3197_1612_3262.png images/BZ_97_1612_3197_1929_3262.pngimages/BZ_97_1951_3197_2234_3262.png
由表6可以看出,GA算法的结果远大于其他两种算法,即其寻优效果较差。PSO算法的计算结果与LDIW接近,但计算时间最长。LDIW算法的寻优结果明显优于其他两种算法,计算时间也最低,这表明了本文采取LDIW算法求解双层规划上层模型的有效性及优越性。
5 结论
本文以面向电力市场的新能源发电技术为背景,建立由光伏电站、小水电站以及抽水蓄能电站组成的混合能源系统模型,并基于该模型提出了一种混合能源系统的容量配置优化方案,最后基于现实数据在Matlab平台进行仿真验证,得到以下结论:
1)以投入成本和获得收益作为上、下层目标函数,并采用LDIW以及SQP算法对上、下层进行求解的双层规划模型,将容量配置与运行方式相结合,同时考虑各个主体投资成本的规模效应,为提高新能源发电技术的经济性提供行之有效的方法。
2)相较于无储能方式的系统,具备抽水蓄能电站的混合能源系统不仅可以在很大程度上缓解小水电站的弃水情况以实现更好的社会效益,而且在系统项目周期内也体现出更加优良的经济性,这令混合能源系统的发展更具前景。
由于本文仅采用电力市场中的现实电价对混合能源系统的容量配置进行优化,缺乏更加深入的市场机制研究,在未来的工作里可进一步结合电力市场机制分析混合能源系统容量优化配置。此外,未来还将进一步讨论添加其他储能方式的可能,充分地探索混合能源系统发展的多样性。
[1]肖云鹏, 王锡凡, 王秀丽, 等.面向高比例可再生能源的电力市场研究综述[J].中国电机工程学报,2018, 38(3): 663-674.Xiao Yunpeng, Wang Xifan, Wang Xiuli, et al.Review on electricity market towards high proportion of renewable energy[J].Proceedings of the CSEE,2018, 38(3): 663-674.
[2]陈亦杰, 刘故帅, 张忠会.考虑电动汽车群和新增实体的电力市场多方交易策略研究[J].电力系统保护与控制, 2018, 46(13): 33-40.Chen Yijie, Liu Gushuai, Zhang Zhonghui.A study on multi-party trading strategy of electricity market considering electric vehicle group and new entity[J].Power System Protection and Control, 2018, 46(13):33-40.
[3]姜欣, 郑雪媛, 胡国宝, 等.市场机制下面向电网的储能系统优化配置[J].电工技术学报, 2019,34(21): 4601-4610.Jiang Xin, Zheng Xueyuan, Hu Guobao, et al.Optimization of battery energy storage system locating and sizing for the gird under the market mechanism[J].Transactions of China Electrotechnical Society, 2019, 34(21): 4601-4610.
[4]赖昌伟, 黎静华, 陈博, 等.光伏发电出力预测技术研究综述[J].电工技术学报, 2019, 34(6): 1201-1217.Lai Changwei, Li Jinghua, Chen Bo, et al.Review of photovoltaic power output prediction technology[J].Transactions of China Electrotechnical Society, 2019,34(6): 1201-1217.
[5]申建建, 张秀飞, 曹瑞, 等.水电富集电网大规模水电站群短期实用化调度方法[J].中国电机工程学报, 2019, 39(10): 2816-2828.Shen Jianjian, Zhang Xiufei, CaoRui, et al.Practical method for short-term operations of large-scale hydropower plants in power grids with rich hydropower[J].Proceedings of the CSEE, 2019,39(10): 2816-2828.
[6]Xu Xiao, Hu Weihao, Cao Di, et al.Optimized sizing of a standalone PV-wind-hydropower station with pumped-storage installation hybrid energy system[J].Renewable Energy, 2020, 147: 1418-1431.
[7]Ma Tao, Yang Hongxing, Lu Lin, et al.Optimal design of an autonomous solar-wind-pumped storage power supply system[J].Applied Energy, 2015, 160: 728-736.
[8]朱晔, 兰贞波, 隗震, 等.考虑碳排放成本的风光储多能互补系统优化运行研究[J].电力系统保护与控制, 2019, 47(10): 127-133.Zhu Ye, Lan Zhenbo, Wei Zhen, et al.Research on optimal operation of wind-PV-ES complementary system considering carbon emission cost[J].Power System Protection and Control, 2019, 47(10): 127-133.
[9]李建林, 郭斌琪, 牛萌, 等.风光储系统储能容量优化配置策略[J].电工技术学报, 2018, 33(6): 1189-1196.Li Jianlin, Guo Binqi, Niu Meng, et al.Optimal configuration strategy of energy storage capacity inwind/PV/storage hybrid system[J].Transactions of China Electrotechnical Society, 2018, 33(6): 1189-1196.
[10]朱青, 曾利华, 寇凤海, 等.考虑储能并网运营模式的工业园区风光燃储优化配置方法研究[J].电力系统保护与控制, 2019, 47(17): 23-31.Zhu Qing, Zeng Lihua, Kou Fenghai, et al.Research on optimal allocation method of wind, photovoltaic,gas turbine and energy storage in industrial parks considering energy storage’s grid-connected operation modes[J].Power System Protection and Control, 2019,47(17): 23-31.
[11]赵波, 包侃侃, 徐志成, 等.考虑需求侧响应的光储并网型微电网优化配置[J].中国电机工程学报,2015, 35(21): 5465-5474.Zhao Bo, Bao Kankan, Xu Zhicheng, et al.Optimal sizing for grid-connected PV-and-storage microgrid considering demand response[J].Proceedings of the CSEE, 2015, 35(21): 5465-5474.
[12]王树东, 杜巍, 林莉, 等.基于合作博弈的需求侧响应下光储微电网优化配置[J].电力系统保护与控制, 2018, 46(1): 129-137.Wang Shudong, Du Wei, Lin Li, et al.Optimal allocation of photovoltaic energy storage microgrid under the demand side response based on cooperative game[J].Power System Protection and Control, 2018,46(1): 129-137.
[13]Zhang Dahai, Wang Jiaqi, Lin Yonggan, et al.Present situation and future prospect of renewable energy in China[J].Renewable and Sustainable Energy Reviews,2017, 76: 865-871.
[14]Notton G, Mistrushi D, Stoyanov L, et al.Operation of a photovoltaic-wind plant with a hydro pumpingstorage for electricity peak-shaving in an island context[J].Solar Energy, 2017, 157: 20-34.
[15]Zhang Yachao, Le Jian, Liao Xiaobing, et al.Multiobjective hydro-thermal-wind coordination scheduling integrated with large-scale electric vehicles using IMOPSO[J].Renewable Energy, 2018, 128: 91-107.
[16]Li Fangfang, Qiu Jun.Multi-objective optimization for integrated hydro-photovoltaic power system[J].Applied Energy, 2016, 167: 377-384.
[17]刘佳, 徐谦, 程浩忠, 等.计及主动配电网转供能力的可再生电源双层优化规划[J].电工技术学报,2017, 32(9): 179-188.Liu Jia, Xu Qian, Cheng Haozhong, et al.Bi-level optimal renewable energy sources planning considering active distribution network power transfer capability[J].Transactions of China Electrotechnical Society, 2017, 32(9): 179-188.
[18]Wang Xu, Bie Zhaohong, Liu Fan, et al.Bi-level planning for integrated electricity and natural gas systems with wind power and natural gas storage[J].International Journal of Electrical Power and Energy Systems, 2020, 118: 105738.
[19]Luo Xi,Zhu Ying,Liu Jiaping, et al.Design and analysis of a combined desalination and standalone CCHP (combined cooling heating and power) system integrating solar energy based on a bi-level optimization model[J].Sustainable Cities and Society,2018, 43: 166-175.
[20]Zeng Qing,Zhang Baohua,Fang Jiakun, et al.A bilevel programming for multistage co-expansion planning of the integrated gas and electricity system[J].Applied Energy, 2017, 200: 192-203.
[21]Zhu Jianyun, Chen Li, Wang Xuefeng, et al.Bi-level optimal sizing and energy management of hybrid electric propulsion systems[J].Applied Energy, 2020,260: 114134.
[22]张迪, 苗世洪, 赵健, 等.分布式发电市场化环境下扶贫光伏布点定容双层优化模型研究[J].电工技术学报, 2019, 34(10): 1999-2010.Zhang Di, Miao Shihong, Zhao Jian, et al.A bi-level locating and sizing optimal model for poverty alleviation PVs considering the marketization environment of distributed generation[J].Transactions of China Electrotechnical Society, 2019,34(10): 1999-2010.
[23]侯贸军, 罗春辉, 隗霖捷, 等.基于微分进化算法的水火电短期优化调度的研究[J].电力系统保护与控制, 2015, 43(9): 54-61.Hou Maojun, Luo Chunhui, Wei Linjie, et al.Study on short-term hydrothermal scheduling based on defferential evolution[J].Power System Protection and Control, 2015, 43(9): 54-61.
[24]葛晓琳, 钟俊玲, 符杨.考虑来水多区间不确定集的跨年梯级水电鲁棒优化调度[J].中国电机工程学报, 2018, 38(17): 5097-5106, 5306.Ge Xiaolin, Zhong Junling, Fu Yang.Robust biennial scheduling of cascade hydropower system considering with the multi-band uncertainty set of the inflow[J].Proceedings of the CSEE, 2018, 38(17): 5097-5106,5306.
[25]吕翔, 刘国静, 周莹.含抽水蓄能的风水火联合机组组合研究[J].电力系统保护与控制, 2017, 45(12):35-43.Lü Xia, Liu Guojing, Zhou Ying.Research on combined unit commitment of wind power-hydro power-thermal power for the power system with pumped hydro storage[J].Power System Protection and Control, 2017, 45(12): 35-43.
[26]林晓明, 张勇军, 陈伯达, 等.计及多评价指标的园区能源互联网双层优化配置[J].电力系统自动化, 2019, 43(20): 8-15.Lin Xiaoming, Zhang Yongjun, Chen Boda, et al.Bilevel optimal configuration of park energy internet considering multiple evaluation indicators[J].Automation of Electric Power Systems, 2019, 43(20):8-15.
[27]徐雨田, 廖清芬, 刘涤尘, 等.市场环境下考虑主动管理措施的双层综合能源规划方法[J].电力系统自动化, 2018, 42(18): 114-126.Xu Yutian, Liao Qingfen, Liu Dichen, et al.Bi-level integrated energy planning method considering active management measures in electricity market environment[J].Automation of Electric Power Systems, 2018, 42(18): 114-126.
[28]Hou P, Enevoldsen P, Eichman J, et al.Optimizing investments in coupled offshore wind-electrolytic hydrogen storage systems in Denmark[J].Journal of Power Sources, 2017, 359: 186-197.