0 引言
在化石能源紧张、环境污染、气候变化等问题的涌现下,依赖于传统能源的生产和消费方式已经难以为继[1-2],发展以水、风、光为代表的清洁可再生能源发电已成为中国乃至世界上大多数国家的战略选择。然而,受限于自然资源的随机性与间接性,可再生能源发电特性曲线往往与负荷用电特性曲线相距甚远,导致了一系列问题的产生,诸如可再生能源的消纳问题、含可再生能源的电网运行调度问题、可再生能源的合理规划设计问题等。这其中,合理选取可再生能源规划方案具有重要意义,其规划合理与否,将影响系统今后运行的可靠性、经济性、电能质量、网络结构及其未来的发展[3]。
随着电网所含元素的不断增多,电源规划的建模、求解难度大幅增加[4-6]。而指标体系评估决策,又称多准则决策(Multi Criteria Decision Making,MCDM)[7]则为解决这类包含复杂因素的电源规划决策问题提供了有效的思路,并得到了广泛的应用。相较于经典的建模优化,采用 MCDM 方法的合理性和意义在于:①决策者可将多种甚至是相互冲突的指标纳入目标中,而不似建模优化可能付出巨大的代价;②不仅可以找到最优方案,还能输出次优、第三优等候选方案,更符合工程实际需求(规划设计者的方案往往不等同于实际建设方案,如考虑现场施工等因素该方案被否决,则次优方案的备用便极为重要);③由于设计方案由多维度指标共同确定,决策者在某些情况下可能会在不否决该方案的前提下,对该方案的某些技术或经济参数进行折中调整,此时,MCDM可提供各指标的相对重要程度等信息,帮助决策者做出最优调整[7]。
在含可再生能源的评估决策方面,文献[8-9]分别从多时间尺度及需求侧资源出发,构建了衡量可再生能源消纳程度的综合评价体系。文献[10-11]构建了高比例可再生能源接入下的系统灵活性的度量指标,前者构建了灵活性供给、需求、裕量指标计算模型,后者提出了上调、下调的灵活性不足期望、概率指标。这些安全性、灵活性评估指标中不乏需要经过运行模拟计算得到的指标,但就笔者所知,尚未有文献实现将稳态与暂态安全稳定指标相结合的综合评估体系的构建。阻碍这项研究的难点之一在于其需要通过软件仿真的途径实现,而这往往意味着“非自动化”,难以适应可再生能源的“多变”特性。正如文献[12]所指出的,高比例可再生能源接入下的规划方案评估决策难点在于生产模拟运行结果与潮流自动生成技术的结合,传统人工调整潮流方式难以适应海量数据分析要求,其核心在于将生产模拟运行结果数据转换为满足特定仿真计算软件(如BPA)所需方式的数据。
针对上述不足,本文构建了包含稳暂态指标的适用于评估区域多可再生能源系统的多准则决策指标体系,提出了基于PSD-BPA软件的稳、暂态联合仿真模拟方法,并对TOPSIS决策方法做出了一定改进。
1 区域多可再生能源系统评价体系
1.1 区域多可再生能源系统评价体系的构建
本文从系统安全性、稳定性、经济性以及区域电网同主网间交互性四个方面构建了区域多可再生能源系统评估指标体系,用以全面、综合地评估规划方案的合理性、优劣性并进行优选,如图1所示。稳态仿真指标即需要经过稳态潮流仿真计算才可得到的指标,暂态仿真指标即需要经过暂态仿真模拟才可得到的指标,其他指标则指的是无需经过仿真模拟便可得到的指标。

图1 区域多可再生能源规划方案评估指标体系
Fig.1 Evaluation index system of regional multirenewable energy planning schemes
由图1可知,区域多可再生能源系统评估指标体系是综合而全面的。一方面,该评估指标体系综合考虑了系统的安全性、稳定性、交互性、经济性,涵盖了系统规划、运行的关键要素;另一方面,该评估体系结合了投资决策指标与生产模拟指标,而生产模拟指标中,不仅包含稳态潮流运行方面的指标,还纳入了暂态仿真模拟方面的指标。
1.2 评价指标的确定
1.2.1 安全性指标
安全性指标包含线路载流比μ与节点电压偏差ν两个底层指标,分别表征线路传输与节点电压方面的安全性。线路载流比与节点电压偏差随着节点/线路位置以及观测时间的不同而各异,此处取加权平均值计算安全性指标值。采用加权平均值计算指标大小的相对合理性在于:①相较于中位数、众数等统计学中的统计量,平均数更受极端值影响,而这是作为安全性指标所需要的;②依据系统中众多线路、节点的重要性程度进行加权赋值,能有效地避免重点线路/节点与不重要的线路/节点指标值上下偏差很大时,平均值仍处于正常量的情况的发生。线路载流比与节点电压偏差指标的计算式为

式中,μ、ν分别为线路载流比指标与节点电压偏差指标;m、n分别为线路总数与节点总数;T0为仿真模拟起始时间;T为采样周期,一般取典型日的24h;Ij,t为t时刻j线路的载流量;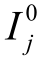 为j线路的额定载流量;ΔUi,t为t时刻i节点的电压偏移量;
为j线路的额定载流量;ΔUi,t为t时刻i节点的电压偏移量;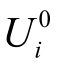 为节点电压的额定值;κj、χi分别为各线路、节点的重要性赋权值。
为节点电压的额定值;κj、χi分别为各线路、节点的重要性赋权值。
1.2.2 稳定性指标
稳定性指标由静态电压稳定和暂态电压稳定两个方面刻画。其中静态电压稳定由节点静态电压稳定裕度指标描述,而暂态电压稳定由节点暂态电压曲线的超调量与恢复时间来描述。
1)静态电压稳定
采用文献[13]中的基于戴维南等效和支路传输功率极限的电压稳定评估方法对静态电压稳定进行计算评估。主要步骤与计算式如下:
(1)对于一个N节点系统,选取第k个负荷节点为评估对象,其负荷功率为 S k = P k , 0 + j Q k,0,其节点电压相量为 。
。
(2)保持系统其余参数不变,单独增大该负荷节点的功率至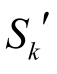 ′= λ (P k , 0 + j Q k,0),重新计算系统潮流,得到节点电压相量
′= λ (P k , 0 + j Q k,0),重新计算系统潮流,得到节点电压相量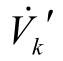 ′。
′。
(3)根据式(3)、式(4)计算两节点戴维南等效系统的等值参数。

式中, 与Zth分别为戴维南等值电压、阻抗参数;
与Zth分别为戴维南等值电压、阻抗参数;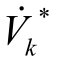 为相量
为相量 的共轭相量。
的共轭相量。
(4)根据式(5)~式(7)计算负荷节点k的静态电压稳定裕度ηk,ηk在0~1之间,且ηk的值越小,代表该节点电压稳定性越薄弱。

式中, Y k t ∠ θ kt 为节点 k与节点 t之间互阻抗的极坐标形式; Y kk ∠ θkk 为节点 k的自阻抗的极坐标形式;Pk , max为负荷节点k的有功功率极限。
(5)对系统中所有负荷节点重复以上步骤。根据式(8)计算系统的静态电压稳定性指标ηsys。ηsys既反映当前状态距离电压崩溃临界点的距离,又指出了全系统电压最薄弱的节点。
2)暂态电压稳定
暂态电压稳定包含两个底层指标,超调量Vmd与恢复时间trec。其中超调量又称最大偏差,指的是节点电压在振荡过程中距离稳定点的最大偏差值;恢复时间指节点电压振幅衰减至可接受范围内时所经历的振荡时间。图2直观描述了超调量指标与恢复时间指标。

图2 暂态电压稳定指标
Fig.2 Transient voltage stability indicators
1.2.3 交互性指标
考虑主网作为坚强后备的区域不易产生严重可靠性问题,因此选取交互性指标作为衡量区域多可再生能源方案优劣的评判依据之一。选取区域电网与主网间交互功率的峰谷差指标Kvp及波动性指标K v ol作为衡量含多可再生能源的区域电网与外部主网交互性优劣的判据,其计算式分别为

式中,Pjh,t为区域电网与主网在t时刻的交互功率,Pjh,t > 0 表示该区域发电量有余向外送电, P jh,t<0表示该区域发电量不足从主网吸收电能;PG,t为t时刻区域电源总出力。可见,波动性的定义即为周期 T内前后相邻时刻交互功率的最大差值与周期T内区域电源总出力平均值的比值。
1.2.4 经济性指标
经济性指标包含投资成本Cinv、售电利润Cpro和网损费用Closs三个底层指标,均折算至当年。考虑到可再生能源的发电边际成本近乎为 0,且维修费用一般为常数,因此忽略运维成本。经济性指标的计算式为[14]

式中,k为可再生能源的种类,即风、光、水等;K为区域包含的可再生能源种类总数;r为贴现率;yk为可再生能源k的寿命; Wk为可再生能源k的装机容量;λinv,k为可再生能源k的单位容量投资成本;τk为可再生能源k的年等效利用小时数;ρt为t时段的购售电价;ρs为上网电价;ρb为购电电价;Plo s s,t为t时刻的网络损耗功率。
2 基于稳暂态联合仿真模拟的指标计算方法
区域多可再生能源系统评估体系中的某些指标需要通过对目标系统进行模拟运行得出,且既包含稳态层面又涉及暂态层面。因此,立足于可再生能源出力生产运行模拟结果,本文基于PSD-BPA潮流及暂态稳定仿真平台,设计了潮流自动生成程序与暂态稳定自动仿真程序,以实现海量生产模拟数据下的稳暂态自动化联合仿真。
之所以要将稳态、暂态仿真进行联合运行,一方面是因为经过商业软件(PSD-BPA)计算得到的潮流、仿真数据具有普信度与说服力;另一方面是因为 PSD-ST暂态稳定仿真程序是与 PSD-PF潮流程序结合起来运行的,二者不可分割。
2.1 适应BPA仿真环境的稳态运行指标计算方法
可再生能源发电出力具有时序性、随机性等特性。时序性指电源出力随时间呈现周期性、规律性的变化,常以日/月/年为循环单位;随机性指因风、光等自然因素的预测误差而导致的电源出力与预想值出现偏差的现象。因此,对于含可再生能源的规划、运行问题,常采用的方法是Monte Carlo模拟等时序仿真方法,即在每个步长下采样获得源荷出力数据,从而计算系统潮流分布与电压电流等运行数据。但该方法的弊端在于计算时间长、占用内存大,尤其是若想通过 PSD-PF潮流仿真的途径实现时序仿真,以一年研究周期为例,需要准备8 760h的潮流数据输入文件(.dat),进行上万次计算,工作量巨大。
本文基于python语言,设计了潮流自动生成程序与稳态指标计算程序。潮流自动生成程序利用BPA文件的数据卡规范,编制潮流输入文件(.dat)中指定卡的识别、读取、替换程序模块,以实现潮流文件的自动更新及运行。而稳态指标计算程序通过编制 BPA潮流输出文件(.pfo)的读取程序模块,实现电压、电流等物理量的读取,再通过不同的指标计算程序模块,实现稳态仿真指标——线路载流比、节点电压偏差、静态电压稳定、交互功率峰谷差及波动性、网损指标的计算。潮流自动生成程序使得PSD-PF潮流仿真能在不更换潮流输入文件(.dat)的前提下,仅通过更改潮流输入文件(.dat)中的部分数据,实现多时刻(如8 760h)的滚动潮流仿真与所需指标值的计算。这使得所需文件由8 760个甚至更多的潮流输入文件(.dat),缩减至一个基态潮流文件即可,大大降低了占用内存。而自动化计算替代仿真所依赖的手动输入,则大大降低了计算时间。
2.2 基于BPA暂态仿真的暂态恢复能力计算方法
暂态仿真的第一步是搭建多可再生能源动态仿真模型。对于水电,通过水轮机模型(发电机模型MF卡+次暂态参数模型M卡)+励磁模型(直流励磁旋转系统EA卡)+调速器和原动机模型(GH卡)来描述。对于光伏,通过光伏发电模型(PV卡)+并网换流器模型(BC、BC+卡)来描述。对于抽水蓄能(简称抽蓄),当其处于发电状态时,与水电动态模型类似,但调速器和原动机模型部分改为电子调节器模型(GM、GM+卡)+导叶执行机构模型(GA、GA+卡)+原动机模型(TW卡)[15];当其处于抽水状态时,采用马达模型(ML卡)来描述。
本文考察区域电网在故障下的暂态电压恢复能力。考虑到暂态仿真程序本身耗时便较长,因此,暂态稳定自动仿真程序选取典型故障的种类、位置、发生时刻,对故障下的观测节点电压进行仿真记录,从而计算出暂态仿真指标——超调量与恢复时间。
与稳态潮流仿真类似,基于python语言,设计了暂态仿真自动生成程序与暂态指标计算程序,实现暂态稳定计算基态输入文件(.swi)中特定卡的识别、读取、替换,并从暂态稳定计算输出文件(.out与.swx)中读取所需信息,对暂态仿真指标进行计算。
3 多准则决策方法与模型
在构建好区域多可再生能源系统评估指标体系,并通过稳暂态联合仿真模拟方法进行计算得到待选方案的各指标值后,便需要通过一定指标评价方法,实现区域多可再生能源系统的多准则决策,即依据一定方法原则,对待选方案进行评分、排序和优选。
MCDM以决策矩阵为输入,以各方案的评分为输出。决策矩阵为

式中,行数m代表方案数量;列数n代表指标数量;元素X(i,j)代表方案 i的第 j个指标值,1≤i≤m,1≤j≤n。
3.1 指标分类与无量纲化
首先将各底层指标分为正指标、负指标两类,见表1。其中正指标代表该指标值越大,整体评分越高,即“越大越好”;负指标代表该指标值越大,整体评分越低,即“越小越好”。
对于不同类型的指标,无量纲化(或称标准化)的计算方法不同,正指标、负指标的无量纲化处理分别为
表1 区域多可再生能源规划评估体系指标分类
Tab.1 Index classification of regional multi-renewable energy planning evaluation system

指标名称 指标类型线路载流比 负指标节点电压偏差 负指标静态电压稳定性 正指标超调量 负指标恢复时间 负指标交互功率峰谷差 负指标交互功率波动性 负指标投资成本 负指标售电利润 正指标网损费用 负指标

式中,xij为方案i在指标 j下的原始数值;![]() 为方案 i在指标 j下的无量纲化值;
为方案 i在指标 j下的无量纲化值;![]()
![]() 。
。
3.2 基于主客观权重的指标权重计算方法
指标赋权是MDCM的前提条件。主观赋权法操作容易,对原始数据依赖性低,但主观随意性大;客观赋权法能够较好地反映指标之间的内在联系,但对原始数据依赖性高且计算复杂[16]。因此,本文采用 G1-熵权法的主客观结合方法对指标权重进行计算。
G1法[17]是一种由层级分析法衍生而出的主观权重计算方法。首先对n个评价指标进行由大到小的重要性排序,排序后将这些指标用 α 1,α2,…,αn − 1 ,αn( α1+ α 2 + … + α n=1)指代,其重要程度依次降低;随后依据一定原则(见表2),确定排序后相邻指标αk-1与αk的相对重要程度rk(1≤ rk <2 );根据式(17)、式(18),即可计算 α i(i = 1,… ,n )的值;而区域多可再生能源系统评价指标的主观权重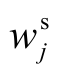 与 α i一一对应,仅是顺序不同,采用相同计算方法。
与 α i一一对应,仅是顺序不同,采用相同计算方法。
表2 相对重要程度赋值
Tab.2 Assignment of relative importance

rk 说明1.0 指标αk-1与指标αk有相同的重要性1.2 指标 αk-1比 αk稍微重要1.4 指标 αk-1比 αk明显重要1.6 指标 αk-1比 αk强烈重要1.8 指标 αk-1比 αk极其重要

熵权法是一种根据各指标容纳信息量的多少来确定指标权重的客观权重计算方法。对于某指标而言,其熵越小,代表该指标值的变异程度越大,提供的信息量越多,在评价中起的作用越大,则该指标对应权重也应当越大[18]。对于决策矩阵Xm×n,首先计算第j项指标下第i个评价对象的特征比重pij,然后计算第j项指标的熵值ej与熵权βj,分别为
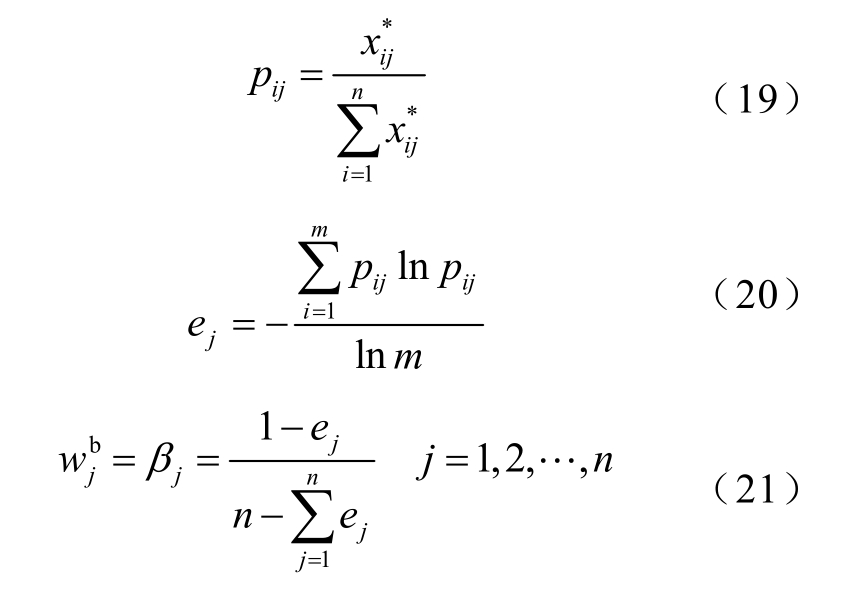
得到指标j的主观权重 与客观权重
与客观权重 后,采用乘法综合集成权重计算方法(Multiplication Synthesis Combination Weighting Method, MSCWM)[19]对主客观结合的综合权重进行计算,即
后,采用乘法综合集成权重计算方法(Multiplication Synthesis Combination Weighting Method, MSCWM)[19]对主客观结合的综合权重进行计算,即

3.3 基于改进TOPSIS的评估决策方法
TOPSIS(technique for order preference by similarity to ideal solution)法通过衡量每个方案到正理想点 与负理想点
与负理想点 的距离
的距离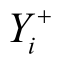 与
与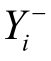 确定最佳方案[20],即
确定最佳方案[20],即
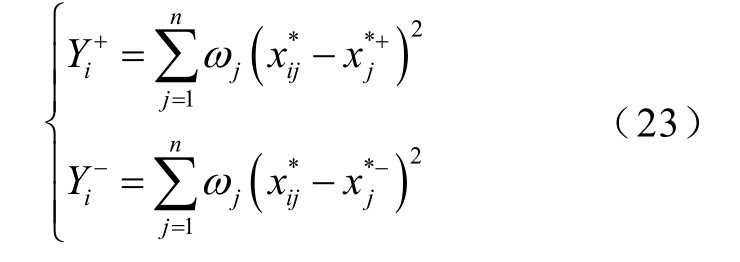
最佳备选方案应距离正理想点最近,距离负理想点最远。对于正、负指标j而言,正理想点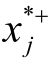 分别为不同方案下该指标值的最大、最小值,负理想点
分别为不同方案下该指标值的最大、最小值,负理想点 分别为不同方案下该指标值的最小、最大值。对于方案 i,用距离正理想点的贴近度 D i来评判方案优劣,见式(24)。Di越大,该方案越优。
分别为不同方案下该指标值的最小、最大值。对于方案 i,用距离正理想点的贴近度 D i来评判方案优劣,见式(24)。Di越大,该方案越优。

考虑到百分制评分更便于决策者进行方案对比评估,对TOPSIS法做如下改进:
用SCOREi替代Di作为候选方案的评分,能够使方案评分值基本落在 60~100的区间内,有利于决策者根据评分数值做出直观决策。
4 算例分析
4.1 算例说明
本文选取四川省某示范区为研究对象,其电网结构如图3所示。该区域向主电网输送清洁电能,其电源结构包含水电、待建抽蓄及待建分布式光伏,源荷容量及位置见表3,其中节点 3为待建抽蓄位置,节点4、5、9水电站为蓄水式水电站,其余水电为径流式水电站。

图3 示范区电网结构示意图
Fig.3 Network diagram of demonstration area
表3 示范区源荷容易及位置分布
Tab.3 Generation and load distribution

源荷类型 容量(负荷峰值)/位置水电60/4, 45/5, 36/9, 20/11, 24/12, 20/13, 4/15, 7.5/20,20/25, 10/29, 6.9/32, 4.8/40, 6.4/46, 4/47负荷19.8/14, 19.8/16, 2.8/18, 18.3/21, 5.7/23, 2.8/28,3.6/33, 1.8/34, 3.6/37, 1.4/39, 0.9/45, 2.9/42, 1.4/44
针对可再生能源出力的时序性与不确定性,基于场景分析的思路,以小时为时间尺度,选取典型日内场景开展研究。根据区域水光荷历史数据,运用 FCM聚类技术[21]得到如图4所示的典型日内组合场景,其中水电的三种场景分别为枯水期、平水期、丰水期,且在三种水电场景下,分别包含光伏的阴、晴、雨三类场景(分别对应场景1~3)。
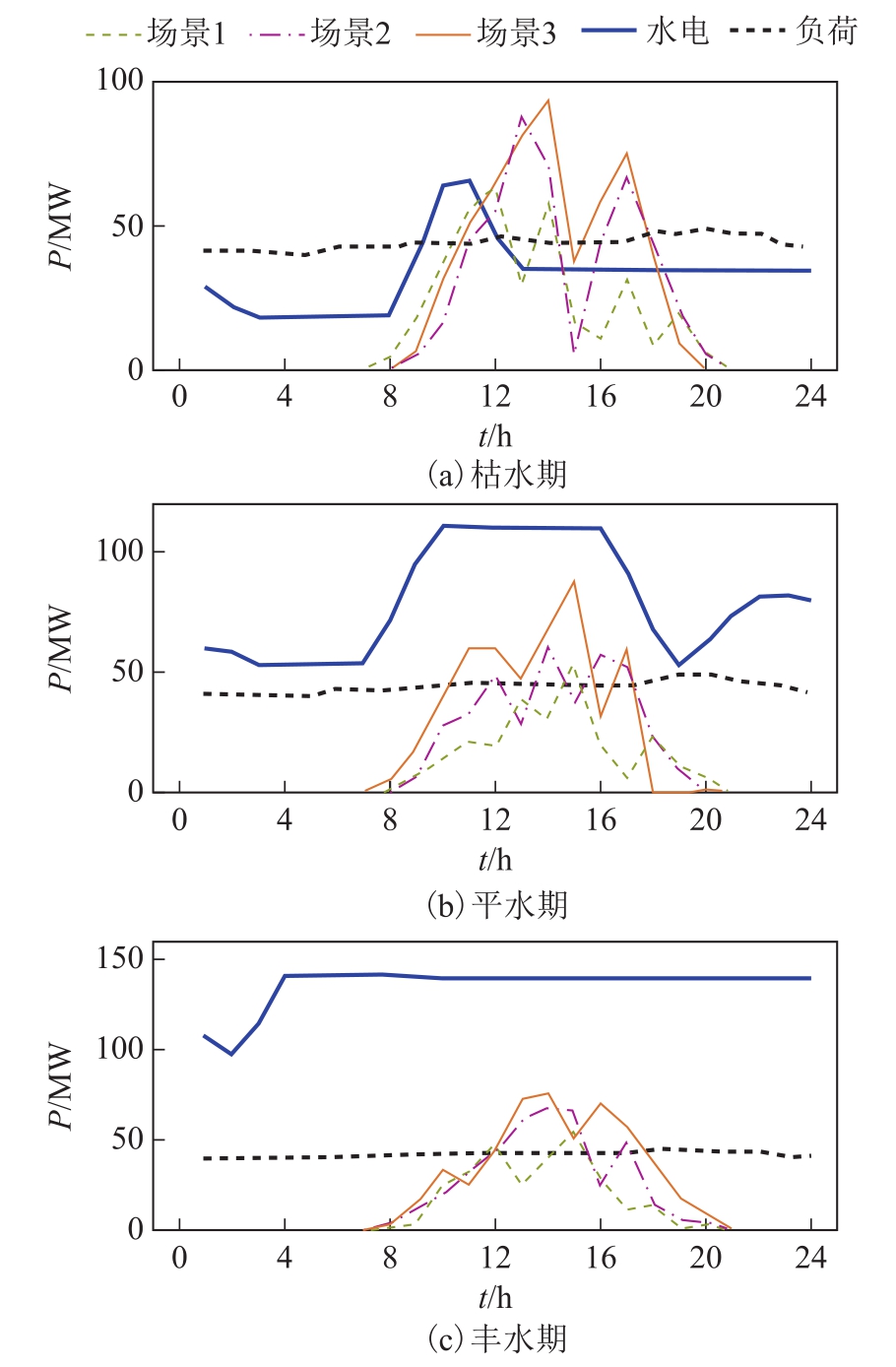
图4 小时级水光荷典型场景
Fig.4 Hourly scenes of hydro, photovoltaic and load
对 10年后的小金县电源进行扩展规划,年负荷增长率取 5%。经过调研与初步容量配置,得到水电、抽蓄、光伏的新增总容量分别为 47MW、22.2MW、210MW,具体待选方案见表4。蓄水式水电站及抽蓄具有出力可调节的特性,出力不仅取决于来水情况还服从电网调度,其运行特性如图5所示。设上网电价为0.4元/(kW·h),购电电价为0.6元/(kW·h),单位容量水电、抽蓄、光伏建设成本分别为1.4万元/kW、0.6万元/kW、0.8万元/kW,水电、抽蓄、光伏寿命分别为50年、35年、25年[22],贴现率为5%。

图5 可调节水电及抽蓄运行特性
Fig.5 Operation characteristics of adjustable hydropower and pumped storage
4.2 仿真模拟与指标计算
分别在平水期、枯水期、丰水期下,考虑雨、阴、晴天,在九类场景下,基于典型日小时级源荷数据,利用潮流自动生成程序,展开稳态潮流仿真,计算包含线路载流比、节点电压偏差、静态电压稳定性、主网交互峰谷差与波动性、网损在内的稳态仿真指标值。在稳态仿真的基础上,基于暂态稳定自动仿真程序,选择典型故障位置(节点8-24支路)、故障时刻(负荷峰值时刻)、故障类型(单相接地故障),进行暂态恢复能力仿真,得到观测节点的电压恢复曲线,从而计算超调量与恢复时间两个暂态仿真指标。将方案4的评价指标的仿真模拟数据部分图形化展示如图6所示,指标计算结果见表5。
表4 水光蓄扩展规划待选方案Tab.4 Alternatives of hydro, photovoltaic and pumped storage

方案水电容量/MW/位置抽蓄容量/MW/位置光伏容量/MW/位置1 20/4, 15/5, 12/9 22.2/3 80/6, 80/7, 30/10, 30/24 2 20/4, 15/5, 12/9 22.2/3 3 20/4, 15/5, 12/9 22.2/3 4 20/4, 15/5, 12/9 22.2/3 6/31,7/37,9/7,11/38,3/22,12/34,6/42,3/10,13/17,14/28,14/14,5/6,8/16,3/41,5/43,6/2,10/24,8/19,6/26,4/45,15/23,3/30,15/33,5/8,11/18,8/39 6/36,7/34,9/22,11/14,3/10,12/43,6/45,3/27,13/41,14/33,14/23,5/19,8/26,3/31,5/21,6/42,10/39,8/37,6/24,4/8,15/7,3/44,15/35,5/18,11/30,8/6 6/16,7/44,9/19,11/28,3/35,12/42,6/27,3/22,13/21,14/18,14/30,5/26,8/17,3/41,5/23,6/45,10/10,8/33,6/34,4/36,15/2,3/43,15/31,5/14,11/38,8/39

图6 方案4评价指标仿真模拟展示
Fig.6 Display of evaluation index simulation of scheme four
表5 待选方案指标计算值
Tab.5 Indicator calculated values of alternatives

指标名称 μ ν ηsys Vmd trec/s Kvp/MW Kvol Cinv/万元 Cpro/万元 Closs/万元方案1 0.296 2 0.034 1 0.841 1 0.134 9 1.361 7 118.78 0.151 2 1633 8 185 25 2 570.8方案2 0.256 9 0.020 3 0.945 5 0.026 1 0.792 0 106.47 0.132 0 1633 8 189 71 1 335.3方案3 0.253 3 0.020 3 0.945 0 0.021 2 0.738 3 105.47 0.132 0 1633 8 188 60 1 221.2方案4 0.243 7 0.020 1 0.940 1 0.023 1 0.860 6 111.88 0.141 6 1633 8 192 75 849.8
4.3 待选方案多准则决策
待选方案底层指标计算值即为决策矩阵,下一步即为多准则决策。将决策矩阵标准化,即

考虑到待选方案的各类可再生能源建设总容量相同,投资成本指标值相同,该指标的权重为0,在决策中属于无效指标,因此将投资成本指标去除。随后,客观权重即可通过式(26)计算得出,主观权重经过对各指标进行重要性排序、评级后可计算得出,指标权重赋值见表6。最后进行方案评分排序,可知方案 4为最优方案,待选方案的 TOPSIS指标评估值及评分展示见表7。
将待选方案的安全性、静态电压稳定性、暂态电压稳定性、与主网交互性以及经济性评分做直观对比,如图7所示。方案1与方案2、3、4进行对比,说明分布式光伏对区域电网安全性、稳定性、交互性、经济性上的支撑均要优于集中接入方式。方案2、3、4进行对比,可见方案2、3较为相似,其在交互性、静态电压稳定性与暂态电压恢复能力方面表现突出,而方案4除去交互性,其余指标均表现优异,鉴于交互性指标的权重相对较小,因此综合而言,方案4的整体评分最高,为最佳方案。

图7 待选方案对比
Fig.7 Comparison of alternatives
表6 指标权重赋值
Tab.6 Index weight assignment

指标名称 μ ν ηsys Vmd trec Kvp Kvol Cpro Closs主观权重 0.156 5 0.156 5 0.130 4 0.108 7 0.108 7 0.053 9 0.064 7 0.090 6 0.090 6客观权重 0.107 4 0.104 7 0.104 8 0.104 7 0.106 1 0.117 9 0.120 6 0.125 4 0.108 4综合权重 0.159 9 0.155 8 0.130 0 0.108 3 0.109 7 0.060 4 0.074 2 0.108 2 0.093 4
表7 待选方案TOPSIS评估值
Tab.7 TOPSIS evaluation value

方案 μ ν ηsys Vmd trec Kvp Kvol Cpro Closs 方案评分1 89.483 9 89.483 9 89.483 9 89.483 9 89.483 9 89.483 9 89.483 9 89.483 9 89.483 9 89.483 9 2 97.245 0 99.841 4 100.0 99.522 3 99.047 5 99.168 7 100.0 95.596 2 96.914 1 98.618 4 3 97.988 8 99.841 4 99.946 8 100.0 100.0 100.0 100.0 94.037 0 97.630 7 99.002 0 4 100.0 100.0 99.426 9 99.814 5 97.843 8 94.789 6 94.595 9 100.0 100.0 99.295 7
4.4 灵敏度分析
指标权重的选取对方案优选决策结果至关重要,因此,对指标权重的赋值展开灵敏度分析。首先,基于表6,分别将仅采用主观权重赋值、客观权重赋值与上文中的综合权重赋值方法三种赋权方法进行对比,观察方案的排序情况,如图8所示。然后,只采用主观权重赋值法,改变主观权重赋值中的指标重要性排序,设置六种场景,场景1~6分别代表所有指标均等重要、安全性重要程度最高、静态电压稳定重要程度最高、暂态电压恢复重要程度最高、交互性重要程度最高、经济性重要程度最高(重要性程度最高的指标合占0.4权重,剩余0.6权重其余指标平均分配),观察方案排序情况如图9所示。

图8 赋权方法对比
Fig.8 Comparison of weighting methods
由图8可以看出,改变赋权方法并不会影响方案的排序。而由图9可以看出,在均等重要程度、安全性重要程度最高、静态电压稳定性重要程度最高、经济性重要程度最高四种场景下,方案排序相同,方案4为最优方案;而在暂态电压恢复重要程度最高和交互性重要程度最高两种场景下,方案 3超越方案4成为最佳方案。因此,对于决策者而言,在重视安全性/静态电压稳定性/经济性或是无特殊重视指标的情况下,方案4为推荐建设的最佳规划方案;而在重视暂态电压恢复能力/交互性的场景下,方案3为推荐建设的最佳规划方案。
5 结论
本文的主要创新点与贡献在于:

图9 主观权重排序对比
Fig.9 Comparison of subjective weight ranking
1)从安全性、静态电压稳定性、暂态电压恢复能力、经济性以及与主网交互性多个维度出发,构建了适用于区域多可再生能源系统评价的多准则决策指标模型体系。
2)提出了基于PSD-BPA仿真平台的稳暂态联合仿真模拟方法,实现了指标的自动化仿真与计算。
3)对TOPSIS决策方法做出了一定改进,实现了多准则决策模型的输出评分的直观化。
通过算例分析得到以下结论:
1)本文提出的稳暂态联合仿真模拟方法能够完备地实现区域电网的生产模拟与指标计算。
2)本文提出的区域多可再生能源系统评估体系能够客观、合理地实现待选规划方案的评估、优选、决策。
3)可通过灵敏度分析快速寻找最优方案以外的可替代技术方案,各指标重要性程度不同会产生不同的结果。
4)本文所提评估决策方法可以为面向含多可再生能源的区域电网提供诸如建设集中式还是分布式光伏的参考意见。
[1]白建华, 辛颂旭, 刘俊, 等.中国实现高比例可再生能源发展路径研究[J].中国电机工程学报, 2015,35(14): 3699-3705.Bai Jianhua, Xin Songxu, Liu Jun, et al.Roadmap of realizing the high penetration renewable energy in China[J].Proceedings of the CSEE, 2015, 35(14):3699-3705.
[2]李建林, 马会萌, 惠东.储能技术融合分布式可再生能源的现状及发展趋势[J].电工技术学报, 2016,31(14): 1-10.Li Jianlin, Ma Huimeng, Hui Dong.Present development condition and trends of energy storage technology in the integration of distributed renewable energy[J].Transactions of China Electrotechnical Society, 2016, 31(14): 1-10.
[3]程浩忠.电力系统规划[M].北京: 中国电力工业出版社, 2008.
[4]易文飞, 张艺伟, 曾博, 等.多形态激励型需求侧响应协同平衡可再生能源波动的鲁棒优化配置[J].电工技术学报, 2018, 33(23): 5541-5554.Yi Wenfei, Zhang Yiwei, Zeng Bo, et al.Robust optimization allocation for multi-type incentive-based demand response collaboration to balance renewable energy fluctuations[J].Transactions of China Electrotechnical Society, 2018, 33(23): 5541-5554.
[5]张迪, 苗世洪, 赵健, 等.分布式发电市场化环境下扶贫光伏布点定容双层优化模型研究[J].电工技术学报, 2019, 34(10): 1999-2010.Zhang Di, Miao Shihong, Zhao Jian, et al.Bi-level locating and sizing optimal model for poverty alleviation PVs considering the marketization environment of distributed generation[J].Transactions of China Electrotechnical Society, 2019, 34(10): 1999-2010.
[6]唐程辉, 张凡, 张宁, 等.基于风电场总功率条件分布的电力系统经济调度二次规划方法[J].电工技术学报, 2019, 34(10): 2069-2078.Tang Chenghui, Zhang Fan, Zhang Ning, et al.Quadratic programming for power system economic dispatch based on the conditional probability distribution of wind farms sum power[J].Transactions of China Electrotechnical Society, 2019, 34(10):2069-2078.
[7]Kumar A, Sah B, Singh A R, et al.A review of multi criteria decision making (MCDM) towards sustainable renewable energy development[J].Renewable and Sustainable Energy Reviews, 2017, 69: 596-609.
[8]刘敦楠, 李奇, 秦丽娟, 等.电网多时间尺度接纳可再生能源能力评估指标体系[J].电力建设, 2017,38(7): 44-50.Liu Dunnan, Li Qi, Qin Lijuan, et al.Evaluation of grid accepting renewable energy in multi-time scale[J].Electric Power Construction, 2017, 38(7): 44-50.
[9]孙盛鹏, 刘凤良, 薛松.需求侧资源促进可再生能源消纳贡献度综合评价体系[J].电力自动化设备,2015, 35(4): 77-83.Sun Shengpeng, Liu Fengliang, Xue Song.Comprehensive evaluation system for contribution degree of demand-side resources to renewable energy source integration[J].Electric Power Automation Equipment, 2015, 35(4): 77-83.
[10]鲁宗相, 李海波, 乔颖.高比例可再生能源并网的电力系统灵活性评价与平衡机理[J].中国电机工程学报, 2017, 37(1): 9-20.Lu Zongxiang, Li Haibo, Qiao Ying.Flexibility evaluation and supply/demand balance principle of power system with high-penetration renewable electricity[J].Proceedings of the CSEE, 2017, 37(1):9-20.
[11]李海波, 鲁宗相, 乔颖, 等.大规模风电并网的电力系统运行灵活性评估[J].电网技术, 2015, 39(6):1672-1678.Li Haibo, Lu Zongxiang, Qiao Ying, et al.Assessment on operational flexibility of power grid with gridconnected large-scale wind farms[J].Power System Technology, 2015, 39(6): 1672-1678.
[12]程浩忠, 李隽, 吴耀武, 等.考虑高比例可再生能源的交直流输电网规划挑战与展望[J].电力系统自动化, 2017, 41(9): 19-27.Cheng Haozhong, Li Jun, Wu Yaowu, et al.Challenges and prospects for AC/DC transmission expansion planning considering high proportion of renewable energy[J].Automation of Electric Power Systems, 2017, 41(9): 19-27.
[13]李禹鹏, 冯煜尧, 冯楠, 等.基于戴维南等值和支路传输功率极限的电压稳定评估方法[J].智慧电力, 2019, 47(1): 13-18.Li Yupeng, Feng Yuyao, Feng Nan, et al.Evaluation method for voltage stability based on Thevenin equivalent and transfer power limit of branches[J].Smart Power, 2019, 47(1): 13-18.
[14]林君豪, 张焰, 陈思, 等.考虑可控负荷影响的主动配电系统分布式电源优化配置[J].电力自动化设备, 2016, 36(9): 46-53.Lin Junhao, Zhang Yan, Chen Si, et al.Optimal DG allocation considering effect of controllable load for active distribution system[J].Electric Power Automation Equipment, 2016, 36(9): 46-53.
[15]韩文杰.抽水蓄能机组调速系统实测建模与仿真研究[J].水电站机电技术, 2018, 41(4): 1-5.Han Wenjie.Modelling and simulation of pumped storage unit regulating system[J].Mechanical &Electrical Technique of Hydropower Station, 2018,41(4): 1-5.
[16]张世翔, 吕帅康.面向园区微电网的综合能源系统评价方法[J].电网技术, 2018, 42(8): 2431-2439.Zhang Shixiang, Lü Shuaikang.Evaluation method of park-level integrated energy system for microgrid[J].Power System Technology, 2018, 42(8): 2431-2439.
[17]郭亚军.综合评价理论、方法及应用[M].北京: 科学出版社, 2007.
[18]罗毅, 李昱龙.基于熵权法和灰色关联分析法的输电网规划方案综合决策[J].电网技术, 2013, 37(1): 77-81.Luo Yi, Li Yulong.Comprehensive decision-making of transmission network planning based on entropy weight and grey relational analysis[J].Power System Technology, 2013, 37(1): 77-81.
[19]Alsayed M, Cacciato M, Scarcella G, et al.Multicriteria optimal sizing of photovoltaic-wind turbine grid connected systems[J].IEEE Transactions on Energy Conversion, 2013, 28(2): 370-379.
[20]李彦斌, 于心怡, 王致杰.采用灰色关联度与TOPSIS法的光伏发电项目风险评价研究[J].电网技术, 2013, 37(6): 1514-1519.Li Yanbin, Yu Xinyi, Wang Zhijie.Comprehensive decision-making of transmission network planning based on entropy weight and grey relational analysis[J].Power System Technology, 2013, 37(6):1514-1519.
[21]李恩文, 王力农, 宋斌, 等.基于改进模糊聚类算法的变压器油色谱分析[J].电工技术学报, 2018,33(19): 4594-4602.Li Enwen, Wang Linong, Song Bin, et al.Analysis of transformer oil chromatography based on improved fuzzy clustering algorithm[J].Transactions of China Electrotechnical Society, 2018, 33(19): 4594-4602.
[22]Ma Tao, Yang Hongxing, Lu Lin, et al.Optimal design of an autonomous solar-wind-pumped storage power supply system[J].Applied Energy, 2015, 160: 728-736.