0 引言
光伏太阳能、风能的开发利用是全球能源结构调整与转型的重大措施。近年来，在国家政府的扶持下，光伏发电已经进入规模化、产业化的发展阶段[1]。截至2018年底，国家能源局发布了我国2018年全年太阳能光伏发电新增装机容量44 260MW，仅次于2017年新增装机，为历史第二高，其中，集中式和分布式光伏电站分别新增 23 300MW 和 20 960MW[2]。但由于光伏发电受气象因素影响，具有较强的间歇性和随机性，这些特性使得高渗透率并网光伏给电力系统的稳定性与经济性带来了巨大的挑战[3]，并且严重制约了光伏的100%消纳。
采用新能源互补发电技术是全额消纳新能源的有效途径[4]，即在最大功率跟踪模式下，利用储能设备及时有效地提供功率支撑来抑制并网点功率波动。同时，储能设备的接入提高了并网新能源系统的等效惯量水平、阻尼系数和同步能力[5-8]，实现了互补系统与大电网之间的平滑对接。通过调节新能源互补发电系统的等效参数来缓解风速、光照等因素的间歇性变化引起的区域间功率振荡，可以使新能源发电系统主动参与大电网响应。但在实际应用时由于全网各个储能设备之间的相互影响，使得控制器参数优化整定异常困难，且难以实时更新以响应新能源系统的变化。
根据上级调度系统的功率调度指令向电网平稳输送功率的直接功率控制能有效地避免集群控制参数的设计与整定带来的困难。文献[9]提出了一种基于指数平滑的功率爬坡控制策略。文献[10]提出了一种分布式模型预测控制方法有效地求解了高渗透率新能源参与的经济调度问题。文献[11]为解决新能源的间歇性出力带来传统发电机组爬坡/卸荷频繁的问题，提出了一种限制爬坡约束的经济调度鲁棒优化模型。文献[12]提出了一种分布式屋顶光伏与储能互补的智能实时能量调度系统，实现了互补系统响应大电网的实时电价以获取最大利益。文献[13]基于虚拟电厂提出了储能系统在市场参与模式下支持大规模、高渗透率的新能源备用辅助服务的最优潮流模型。文献[14]分析了在分时电价模式下，储能参与分布式光伏配网电压调节综合运行控制策略。文献[15]提出了一种集中式风-光互补的随机优化经济调度策略，并分析了不同置信区间下的机会约束模型对整个互补系统的经济效益与备用服务能力的影响。
然而，基于直接功率控制的日前或随机优化调度策略性能与源/荷预测的精度强相关[16-17]，在保证系统能量动态平衡的准则下，若预测精度偏低则系统实际出力会偏离最优策略，此时系统经济性难以保证。随机优化以一定的置信区间考虑了预测误差问题，最优解带有一定的风险水平，但难以适应实际工程应用。
因此，迫切需要找到一种能够适应新能源发电特点的实时智能调度方法。强化学习（Reinforcement Learning, RL）受到行为主义心理学的启发，关注智能体在与动态随机环境的交互过程中的累积回报奖励[18]。在电力系统中，该奖励则可表现为系统的运行指标，如运行利润最大、稳定裕度最高。智能体与环境的交互过程如图1所示，智能体向环境施加动作，环境则向智能体反馈该动作的奖励值以及动作对环境改变后的状态信息。
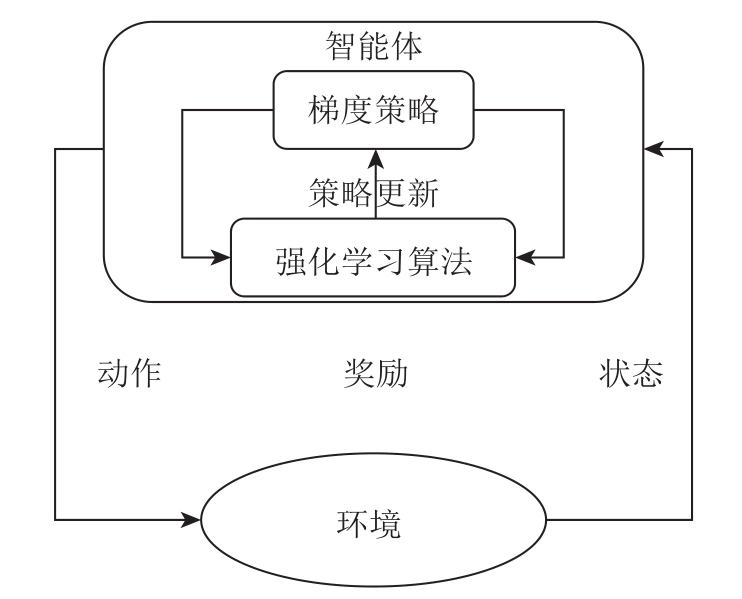
图1 智能体与环境的交互过程
Fig.1 Interaction process of reinforcement learning
人工智能在电力系统及综合能源系统中的应用面临着诸多机遇与挑战[19-20]。最早的强化学习算法如Q学习针对由离散的状态与动作构成的问题，通过查表的方式获得状态的奖励[21]。然而，复杂环境往往是由高维状态组成，此时传统的 RL算法将会面临“维数灾”，且在将连续的动作离散化的过程中会造成信息的丢失，难以找到最优解。深度强化学习（Deep Reinforcement Learning, DRL）则是结合了深度神经网络的非线性感知能力和强化学习的动态决策能力[22]，利用深度神经网络实现对动作值函数的逼近。如文献[23-24]采用深度Q学习研究了油电混动公交与能源互联系统的能量管理策略。文献[25]采用深度Q学习建立了含有大规模光伏与电动汽车的在线调度策略。深度Q学习算法通过神经网络有效地实现了状态空间的连续化，但所能应对的动作空间仍是离散的。
鲜有文献采用先进的连续型深度强化学习算法分析电力系统的智能经济调度问题，特别是对含有大规模储能和新能源的互补发电系统的智能随机经济调度问题。对此，本文以光伏-抽蓄（Photovoltaic-Pump Hydro Storage, PV-PHS）互补发电系统为研究对象，考虑光伏发电的不确定性，以100%消纳光伏为前提，构建并网点功率波动约束和抽水蓄能经济效益模型。针对抽水蓄能出力连续可调的特点，将智能调度问题转换为马尔可夫决策过程，详细描述了多约束优化问题向无约束强化学习任务转换的过程；并针对固定学习率的深度确定性策略梯度（Deep Deterministic Policy Gradient, DDPG）算法存在训练效率低、容易陷入局部最优的缺陷，提出基于周期衰减学习率（Cycling Decay Learning Rate, CDLR）的改进型深度确定性策略梯度算法，优化抽蓄的实时运行策略。最后以四川省小金县某光伏电站的实际出力数据为例，验证了本文构建模型和采用方法的可行性和通用性。
1 光-蓄互补系统描述
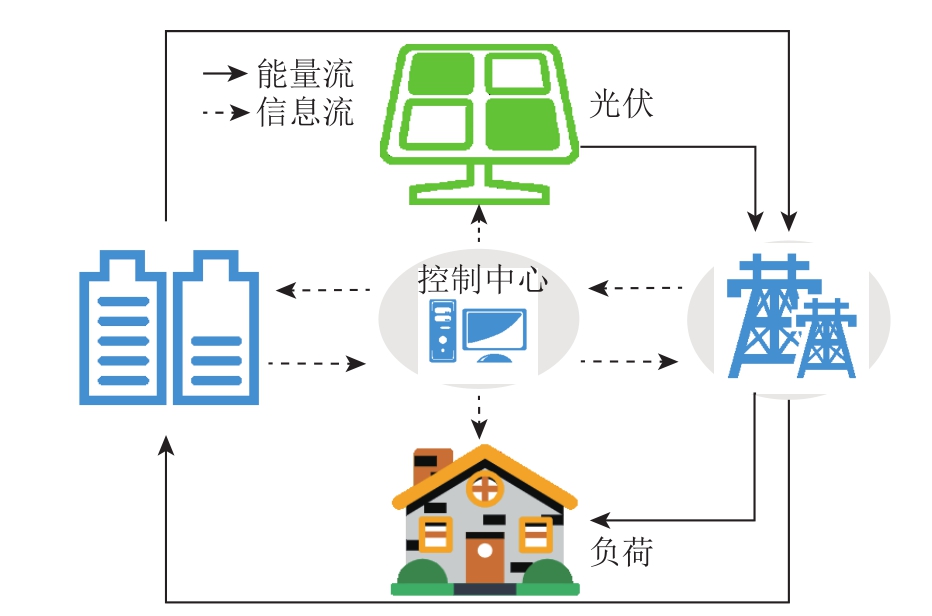
图2 光-蓄互补模型
Fig.2 Integrated energy system with PV and pump hydro storage
本文以光伏发电与抽水蓄能所构成的互补系统为研究对象，其示意图如图2所示，其中能量流表示系统能量流向，信息流表示系统内部信息传递以及与上级电网之间的通信，即光伏电站根据实际发出功率全额送入电网，抽水蓄能通过控制中心传递的光伏电站当前发电情况来提供功率支撑。
1.1 抽水蓄能的数学模型
本文研究的光-蓄互补发电系统要求全额消纳光伏，即认为光伏为不可控电源，因此不讨论光伏的发电模型。同时，本地负荷以恒功率模型表示。抽水蓄能可在不同时段承担着电源/负荷双重角色[26]。
抽水蓄能工作在发电模式下的数学模型为
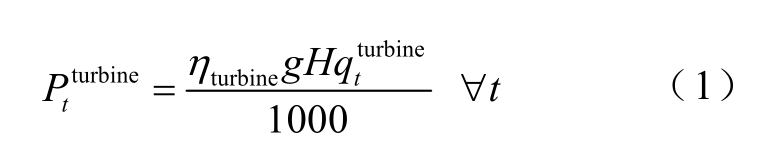
式中，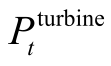
为抽水蓄能在t时刻的发电量，MW；ηtu rb ine为发电效率；g为重力加速度；H为水头高度，m； 
为t时刻的发电水流量，m3/s。
抽水蓄能工作在抽水模式下的数学模型为
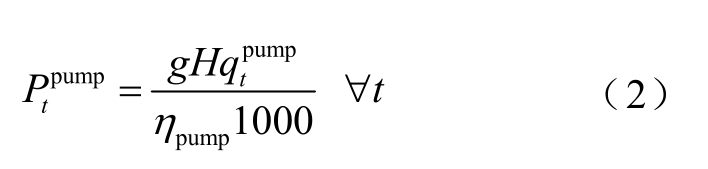
式中，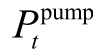
为抽水蓄能在t时刻的用电量，MW；ηp um p 为水泵效率；
为t时刻的抽水水流量，m3/s。
上游水库水量的变化可由式（3）计算。
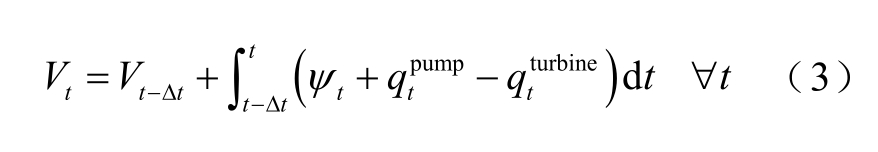
式中，Vt为t时刻的剩余水量，m3；Δt为优化时间间隔，h；tψ为t时刻其他支流的流入水流量，m3/s。
上游水库的剩余水量可以类比蓄电池的荷电状态（State of Charge, SOC），数学定义为
式中，SOCt为t时刻的剩余可用水量百分比；Vur为上游水库最大容量，m3。
1.2 优化模型
本文考虑全额消纳光伏时，抽水蓄能作为功率支撑设备来缓解并网点功率波动。在实时电价模式下，最大化抽水蓄能的经济收益，同时将功率波动转换为经济惩罚，构成优化目标为
式中，ERt为t时刻的收益，$；T为运行周期；λt为t时刻的电价，$/(MW·h)；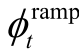
为功率波动的经济惩罚，$，其定义为
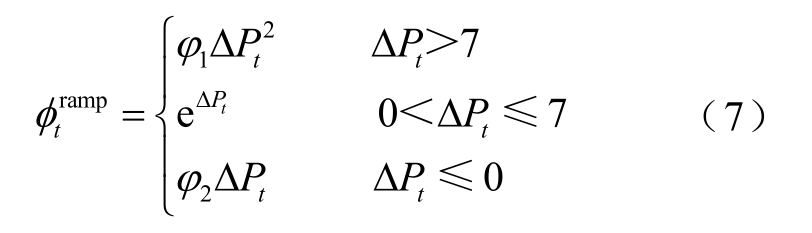
式中，φ1、φ2为波动罚金系数，单位分别为$/MW2和$/MW；ΔPt为Δt时间内的功率波动量，MW，Δt =1h定义为
式中，
分别为抽蓄参与调节前后t时刻并网点传递的功率，MW，定义为
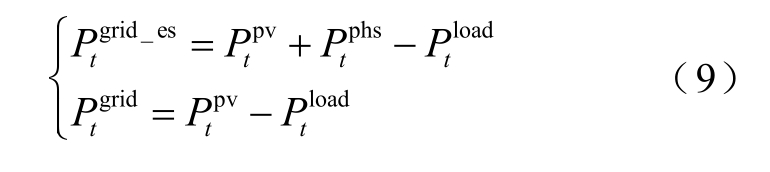
式中，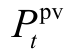
为t时刻光伏的实发功率，MW；
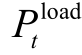为t时刻的负荷功率，MW；
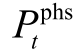为t时刻抽水蓄能的发出或吸收功率，MW。定义
1.3 约束条件
忽略系统内部网损，互补系统需要满足以下约束条件：
1）功率平衡约束，如式（9）。
2）抽水蓄能最大用/发电功率约束。
3）上游水库水量约束。
1.4 优化变量
定义优化变量x为抽水蓄能在t时刻的用/发电功率。
2 深度强化学习建模
马尔可夫过程（Markov Process, MP）表示系统在下一个时刻的状态只与当前时刻的状态相关[27]。由于本文所研究的智能调度问题是在一个含有随机性光伏出力的环境中做出的最优决策，因此，可以将该问题建模成一种离散的、有限步骤的马尔可夫决策过程（Markov Decision Process, MDP）[28]。
2.1 智能调度问题向强化学习任务的转换
对于一个强化学习问题必须具备智能体与环境两个条件，其学习过程表现为：根据智能体策略和环境信息，智能体采取相应的动作使得累积奖励最大。深度强化学习最初应用于游戏领域，并取得了非凡的成就[29]；但电力系统模型不同于游戏环境，因此，如何将电力系统问题转换为适应强化学习任务是其成功应用于电力系统的关键。
本文所研究的光-蓄互补系统可作为动态随机环境，抽水蓄能的发/用电功率作为智能体的动作at，即
光-蓄互补系统中，对于任意时刻t，光伏的实际发电量、负荷、电价、并网点功率差、抽蓄的工况和上游水库剩余水量作为状态，状态st定义为
在at作用下环境反馈的奖励值可由优化目标ERt体现（见式（5）），即
由于智能体在学习过程中的目标是最大化奖励，但是最优策略*π必须满足互补模型中的约束条件，因此，需将约束条件合理地转换为奖励函数的一部分。互补模型中，能量平衡约束由式（9）自动满足，抽水蓄能的最大用/发电功率约束体现在对动作值的限幅，因此，只需转换上游水库水量约束（SOC），本文以惩罚函数的形式表示为
式中，3φ、4φ为惩罚系数，$/MW，通常取值较大且与模型相关。
从状态st开始的一次探索过程所对应的累积奖励Rt为
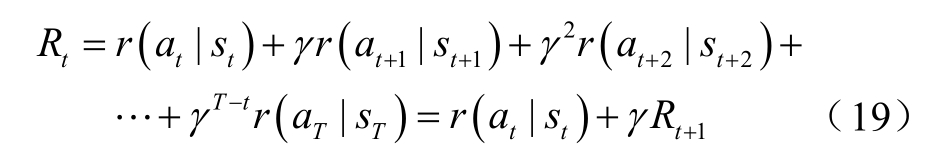
式中， γ 为奖励折扣系数， γ ∈ [ 0,1]。
对于策略π，从状态st开始并执行动作at的一次探索过程所期望的累积回报可由动作价值函数Qπ (s ,a )来描述。
综上所述，互补模型的智能调度问题可以转换为
2.2 CDLR-DDPG算法与网络结构
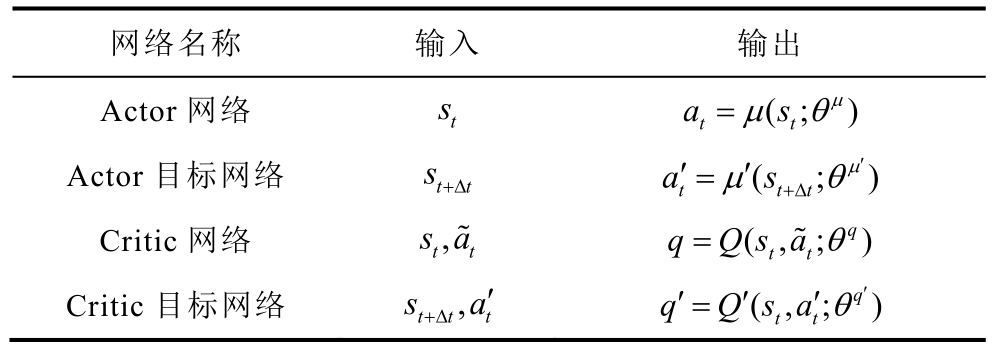
DDPG算法基于Actor-Critic架构结合了DQN的思想和DPG算法，并在连续控制问题中取得了很好的效果。本文采用DDPG算法来训练一个能够实时为光-蓄互补系统做出最优决策的智能体。在DDPG算法中，智能体通过与环境之间的交互所获得的累积奖励见式（21），并最大化累积奖励以获得最优策略π*。DDPG算法的Actor-Critic架构分别由四个全连接层神经网络实现，见表1。表中， θ μ为Actor网络参数；θq为Critic网络参数。Critic网络中
表示随机噪声。
表1 DDPG算法网络结构
Tab.1 The network structure of DDPG
网络名称 输入 输出Actor网络 st (; )a s μ μ θ t t=Actor目标网络 st+Δt ( ; )a s μ t ′ ′=μ θ′t+ Δt= ~Critic目标网络 ,Critic网络 s,a~ (,;q)t t q Qsaθ t t s a t t t+Δ ′ (, ;q)q Qsaθ′′′′=t t
训练时，Actor网络参数的优化通过梯度下降策略，即
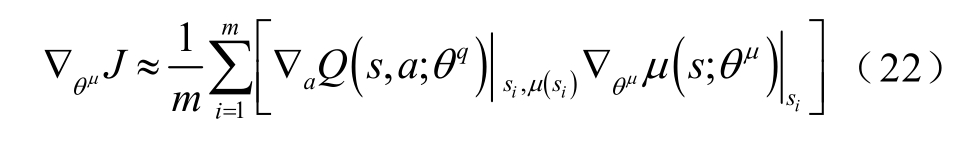
而Critic网络的更新则是通过最小化损失函数，即
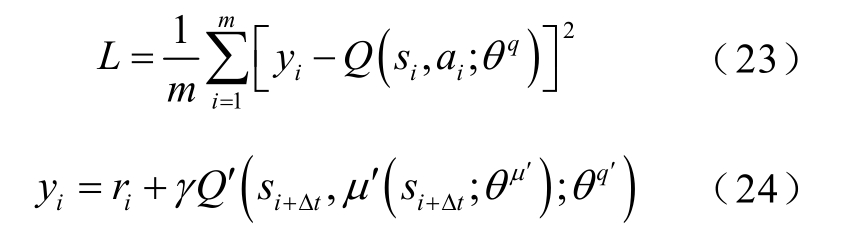
实现Actor、Critic网络参数更新后，与之对应的两个目标网络参数的更新则通过软更新（Soft Update）方式，即
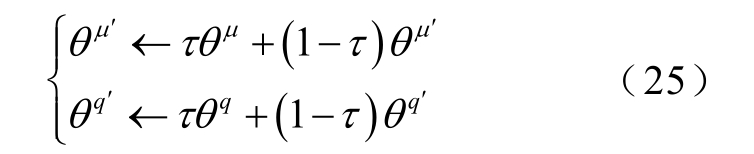
式中，θ μ′为Actor目标网络参数；θq′为Critic目标网络参数；τ为软更新系数（0＜τ≪1）。
为了增强DDPG算法的稳定性，引入了经验回放机制并将整个训练过程分为探索、学习和收敛三个阶段：①探索阶段，将从环境中观察的信息和反馈奖励值所构成的元组 ei={st, at, rt, st+1}放入大小为D的经验记忆库d中，d={e1, e2, …, eM}，当经验记忆库被存满时，新的元组将替换原有的旧元组，并进入学习阶段；②学习阶段，将经验记忆库中均匀采样的一小批元组信息用于更新Actor、Critic网络的参数；③收敛阶段，智能体学到了一条应对随机环境的策略，并保持累积奖励处于平稳状态。
由于元组信息中的状态与奖励均来自互补系统中实时输入信息与优化目标，因此，整个智能调度优化模型由互补模型和DDPG算法构成。互补优化模型结构如图3所示。
图3 互补优化模型结构
Fig.3 Framework of the PV-PHS system with DDPG-based reinforcement learning
原始DDPG算法在连续控制领域有着较大的优势，但是固定学习率的DDPG算法存在着训练效率低，容易陷入局部最优等缺陷。由于网络权值θ的更新速度受到学习率η的影响，如式（26）所示，在常规训练中通常选取较小的学习率来保证算法收敛性，但此时损失函数的梯度下降速度慢，收敛时间效率低且容易陷入局部最优。
为提升算法性能，本文提出采用周期衰减学习率的改进型深度确定性策略梯度算法，即在训练过程中将总回合数N划分为n个周期，并在一个周期内使学习率按照式（27）衰减规律进行更新。
式中，α为学习率；ε为衰减因子，εi表示ε的i次幂； i = 0,… ,n −1。第j个回合的学习率ηj为
式中，mod(⋅)定义为取余算子。
采用CDLR-DDPG算法流程见表2。
表2 CDLR-DDPG算法流程
Tab.2 Flow of the PV-PHS system with CDLR-DDPG algorithm
随机初始化Actor、Critic网络参数 μ θ′←θ ；初始化经验记忆库D；For j=1, N do:复位整个环境，并返回一个初试状态s1；通过式（28）更新学习率η；For t=1, T do:由当前策略π和噪声Nt，产生一个动作at；执行at并返回 tr和新状态st+1；存储{st, at, rt, st+1}到记忆库d；从d中均匀采样m个{st, at, rt, st+1}；通过式（22）和式（26）更新Actor网络参数；通过式（23）和式（26）更新Critic网络参数；通过式（25）更新Actor、Critic目标网络；End for End for θ；初始化Actor、Critic目标网络参数 μ μ θ、 q θ′←θ 、 q q
3 算例分析
本文利用Python3.7和 TensorFlow架构来实现改进型CDLR-DDPG算法对光-蓄互补发电系统智能调度问题的求解，并采用序列二次规划（Sequential Quadratic Programming, SQP）算法和拉丁超立方抽样场景分析法（Scenario Analysis, SA）与之进行对比分析。仿真模型如图2所示，互补模型主要参数见表3。
为进一步阐述本文所提互补模型与优化方法，以四川省小金县某实际光伏电站的出力数据做算例分析,其求解流程如图4所示，具体实施步骤如下：
（1）初始化互补模型的参数，CDLR-DDPG算法超参数以及神经网络的权重与偏置。
（2）随机读入训练集中某一天的光伏、电价、负荷数据。
表3 互补模型主要参数
Tab.3 The parameters of hybrid model
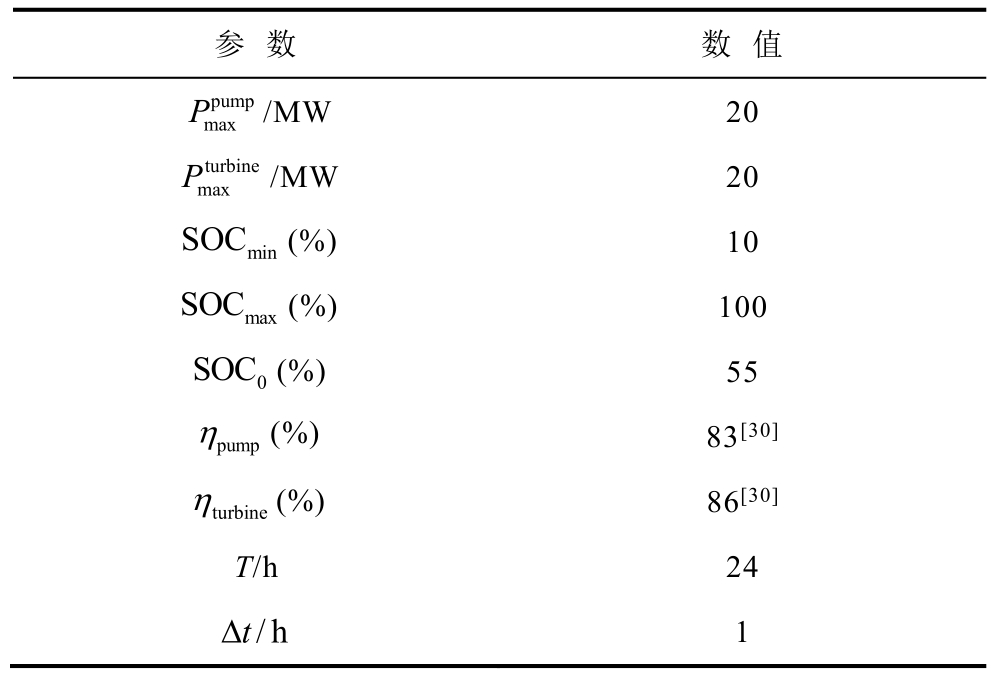
参 数 数 值P /MW 20 pump max P /MW 20 tur mxbine a SOC (%) 10 min SOC (%) 100 max SOC(%) 55 0 η (%) 83[30]pump η (%) 86[30]T/h 24 t/h turbine Δ 1
图4 光伏-抽蓄实施流程
Fig.4 The flowchart of PV-PHS hybrid energy system
（3）复位强化学习环境，更新学习率，并返回初始状态s1。
（4）根据当前策略和随机噪声输出的动作和读入的已知数据，由式（21）计算当前时刻的即时奖励。
（5）向经验记忆库中存入当前时刻的状态、动作及即时奖励和下一个时刻的状态，且记忆库容量计数器加1。
（6）判断经验记忆库是否存满，若存满，则选择m个{st, at, rt, st+1}并根据式（22）、式（23）和式（25）更新神经网络参数，然后更新状态和累积奖励；否则只更新状态和累积奖励。
（7）更新时刻，并判断当前训练是否结束，若结束，则输出当前回合的累积奖励，然后重复步骤（2）～步骤（7）；否则，重复步骤（4）～步骤（7）。
3.1 CDLR-DDPG算法训练
深度强化学习算法主要依赖于深度神经网络。因此，神经网络层数和每层神经元的个数也直接决定了算法的性能。本算例中将CDLR-DDPG算法的四个神经网络设置为相同结构，即神经网络有三个隐藏层，分别含256、256、128个神经元，CDLRDDPG的超参数见表4。
表4 CDLR-DDPG算法的超参数
Tab.4 The hyperparameters of CDLR-DDPG
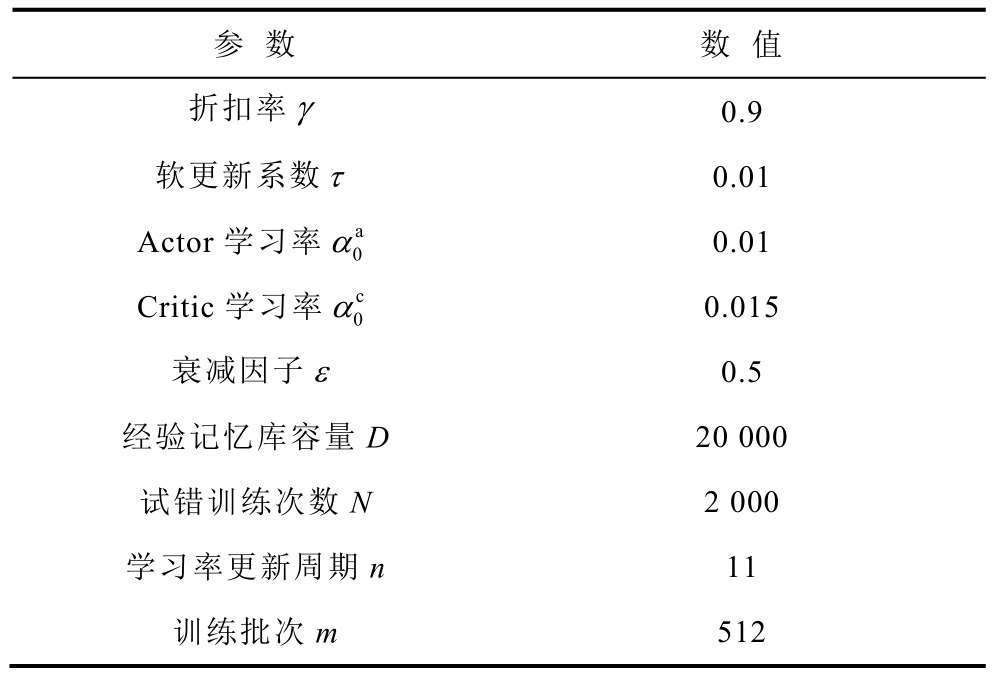
参 数 数 值折扣率γ 0.9软更新系数τ 0.01 Actor学习率 a0α 0.01 Critic学习率 c0α 0.015衰减因子ε 0.5经验记忆库容量D 20 000试错训练次数N 2 000学习率更新周期n 11训练批次m 512
本算例选取了一年小时级数据中的358天作为神经网络的训练样本，连续7天作为测试数据。根据表2所示的算法流程对智能体进行训练；为保证训练效果，本算例对智能体进行2 000次试错训练。每一次训练的 24个时刻点所对应的累积奖励变化趋势如图5所示。结果表明：①第1～839次训练为探索阶段；第840～1 500次训练为学习阶段，此阶段根据式（22）、式（23）和式（25）对神经网络参数进行修正与更新，以应对光伏与负荷的随机变化并使得累积奖励增大；②第1 500次之后，智能体学会了如何应对随机环境并保持累积奖励；③改进前后训练结果的差异主要表现在学习和收敛阶段。由于固定学习率取值为一个周期衰减学习率的平均值，因此，其对应的学习速度略快于周期衰减学习率；但是固定学习率缺乏探索速度的多样性，提早陷入且难以跳出局部最优。采用周期衰减学习率在训练过程中使得网络参数的更新速度呈周期性变化，探索速度丰富多样，易于跳出局部最优。
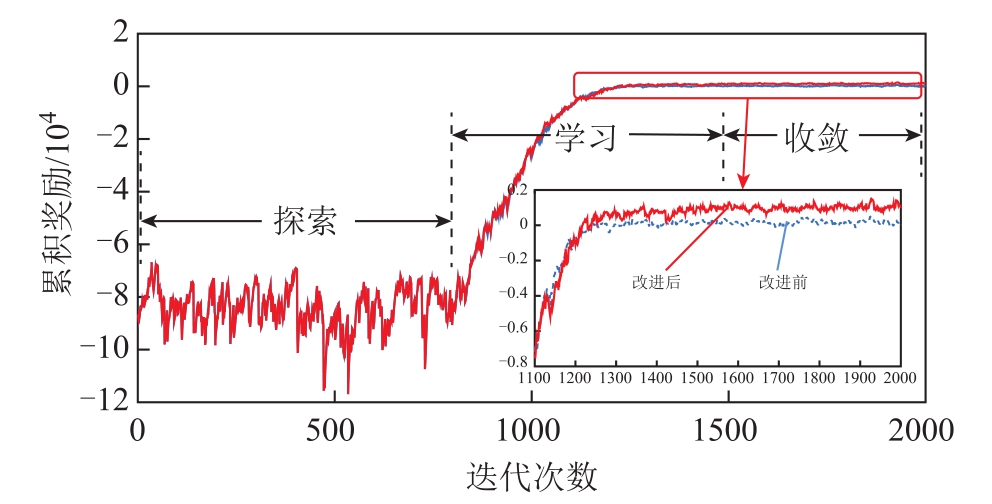
图5 改进前后累积奖励变化趋势
Fig.5 Cumulative reward change with episode during the training process after improvement
3.2 CDLR-DDPG算法性能测试
智能体在由互补模型构成的环境中被训练2 000次之后，便可以根据实时状态（光伏、负荷和电价）来决定抽水蓄能的出力。
为验证智能体在随机环境中持续运行的能力，本算例对智能体进行了连续7天的性能测试。优化前、后并网点功率波动情况对比如图6所示。图6表明：在抽水蓄能的作用下，并网点功率波动情况得到了改善，智能体能够根据光伏与负荷的当前和上一时刻的发/用电情况来决定抽水蓄能的出力，以达到缓解功率波动的目的。
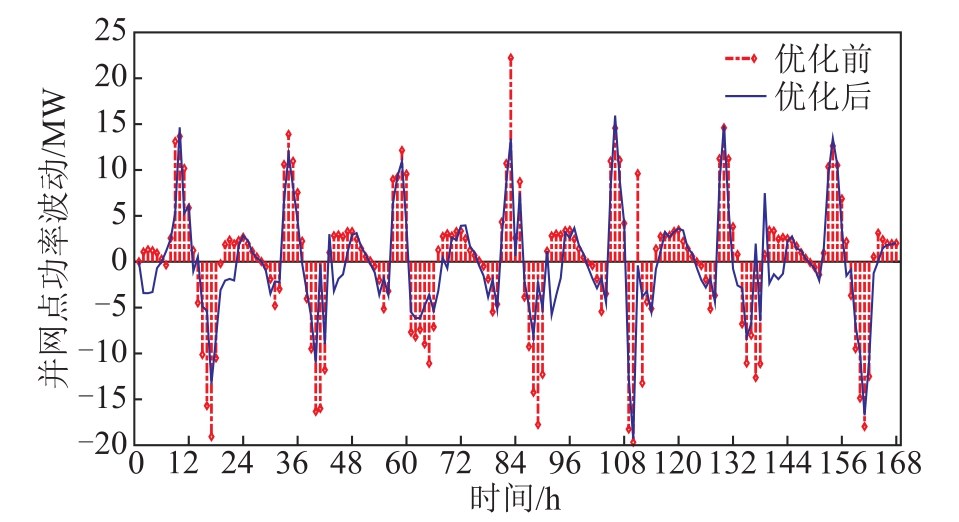
图6 优化前后并网点功率波动情况对比
Fig.6 Comparative analysis of power fluctuation on point of common coupling after PHS participating
智能体对抽水蓄能运行工况的选择来自于两个信息：①抽蓄参与调节之前的功率波动；②当前节点电价。综合考虑上述两个信息后，抽蓄的运行情况如图7所示。图中∆P表示抽蓄参与调节之前的功率波动；Pphs表示抽蓄的运行情况，式（10）、式（11）定义了Pphs大于零表示放水发电，反之表示用电抽水；Eprice表示实时电价。
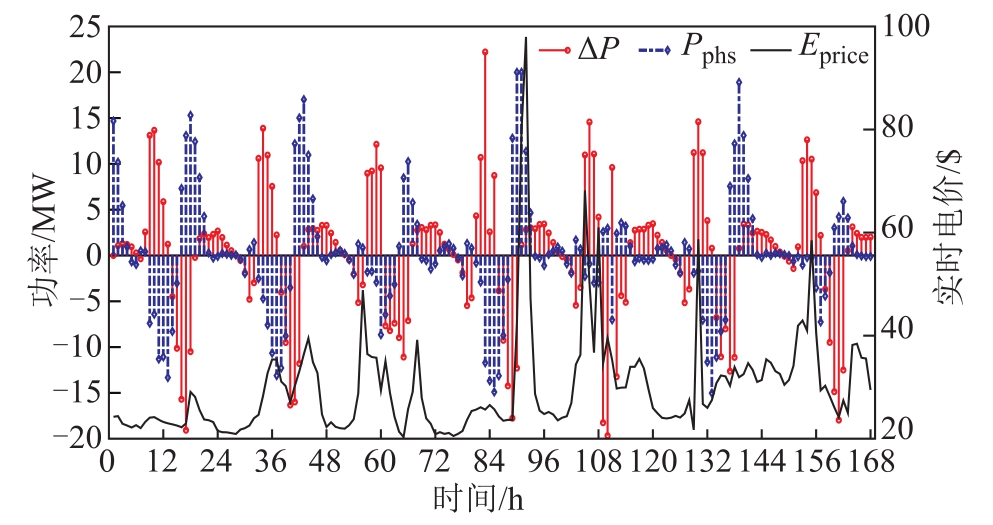
图7 兼顾功率波动与节点电价的抽蓄运行工况
Fig.7 The operation of PHS takes into account the power fluctuation and price
图7表明：根据电价的变化趋势，智能体能够很好地决定抽水蓄能的用/发电情况，即电价偏高时，抽蓄进入发电工况，反之则进入用电抽水工况，但在第36h、84h、130h和161h附近存在违反这一规律的情况。由式（8）可知，∆P的绝对值越大（越偏离横轴）表明功率波动越严重。由于在这些时段并网点的功率波动幅度较大，因此，为了减小∆P的幅值，智能体必须控制抽蓄向∆P的反方向运行；即出现了高电价抽水、低电价发电的反电价变化趋势运行的情况。
智能体控制抽蓄的运行与 SOC的变化情况如图8所示。
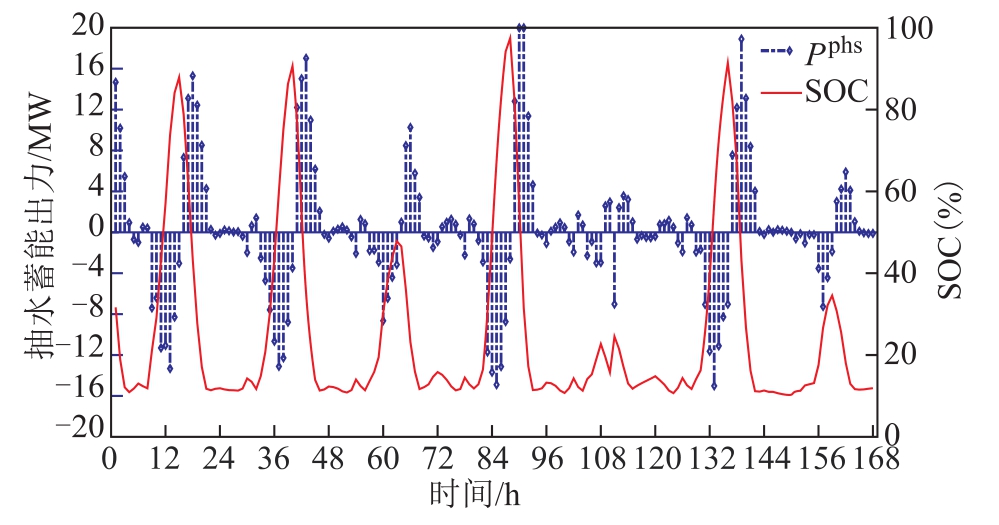
图8 抽蓄的运行与上游水库水量变化情况
Fig.8 Relationship of the operation of PHS and SOC variation
图8表明：
（1）智能体能够控制抽蓄在SOC约束范围内运行，表明该智能控制策略能使抽蓄在满足安全约束的前提下应对随机环境并寻求利益最大化。
（2）抽蓄在夜间几乎处于待机模式，既不参与发电也不参与抽水，原因是：①连续测试过程中智能体获得累积奖励的持续时间为24h，即每天的累积奖励是独立的，但是每天的 SOC1是以前一天的SOC24为基础的。因此在凌晨时段即便电价较低抽蓄参与抽水也会造成累积奖励减小，又由于SOC已经靠近约束下限，故也不可能发电。②夜间光伏出力为0，并网点功率波动主要是由负荷引起，而大电网可以平抑负荷的小范围波动，不需抽蓄参与调节。
上述分析表明：本文研究的光-蓄互补发电系统稳定运行时，智能体能够在随机环境中准确地控制抽蓄，既能缓解并网功率波动，同时也能保证其收益最大。此外，抽蓄在凌晨几乎处于待机模式且SOC较低，该状态有利于抽蓄应对电网功率突变，从而增强电力系统安全稳定能力。
3.3 CDLR-DDPG算法与SQP算法和SA算法的对比分析
为分析 CDLR-DDPG实现光-蓄互补智能调度的性能，本文采用序列二次规划（SQP）法和基于拉丁超立方的场景分析法（SA）与之对比。由于算例中将 CDLR-DDPG法进行了连续一周的实时测试，而 SQP法进行求解调度问题时，需要对未来源/荷数据进行预测，故本文将 CDLR-DDPG法测试过程中的实时数据（光伏、负荷与电价）作为光伏的准确预测值，并通过Matlab/Yalmip实现SQP法和SA法[31]。
图9～图11表示光伏预测精度为100%的对比结果。图9给出了CDLR-DDPG与SQP下的并网点功率波动情况，图10为两种算法下抽蓄跟随实时电价的运行工况，图11为两种算法所对应的SOC变化情况。结果表明：①CDLR-DDPG能在有效地缓解功率波动的同时保证抽蓄的收益。②采用 SQP时，抽蓄能得到全局最优的控制策略从而保证互补系统的经济性和稳定性。但是，获得该全局最优策略的前提是无预测误差存在。③CDLR-DDPG算法在做决策时智能体只需感知到当前和过去的环境状态，不需要参考未来环境中的状态，即智能体只能根据过去的表现来决策当前。④SQP法控制抽蓄时所对应的SOC变化幅度较大，即抽蓄在发电与抽水两种模式之间循环；而CDLR-DDPG则主要控制抽蓄在大功率波动条件下参与调节，抽蓄表现出发电、抽水和待机模式。
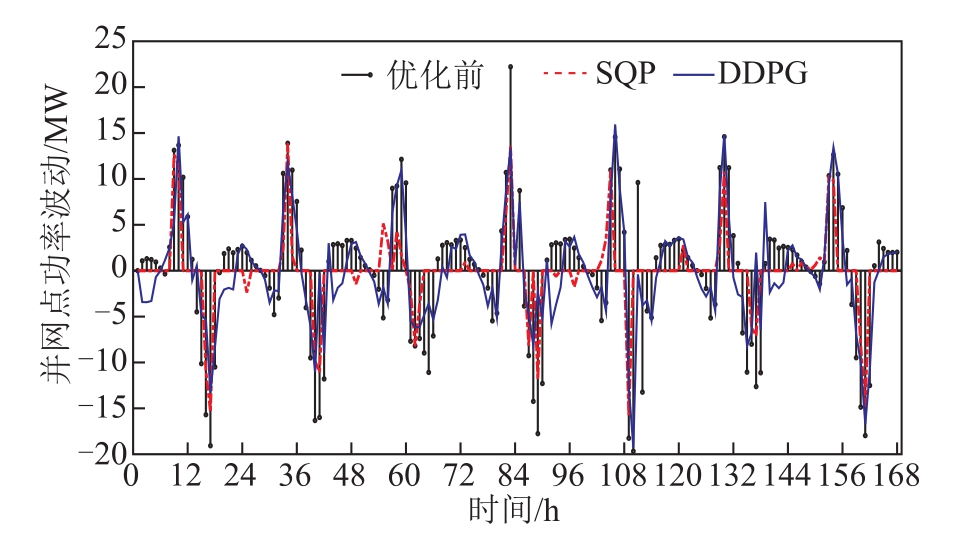
图9 SQP和CDLR-DDPG算法缓解并网点功率波动的对比分析
Fig.9 Comparative analysis of power fluctuation on PCC between SQP and CDLR-DDPG algorithm
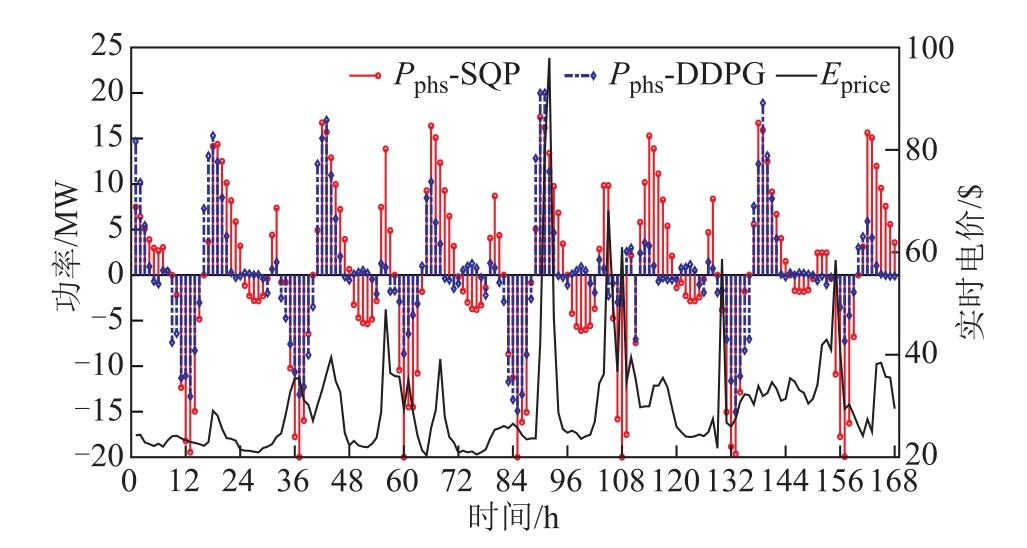
图10 SQP和CDLR-DDPG算法下抽蓄跟随电价的运行情况
Fig.10 The operation of PHS with SQP and CDLR-DDPG algorithm considering the price
图11 SQP和CDLR-DDPG算法下上游水库水量变化
Fig.11 Relationship of the operation of PHS and SOC variation under different optimization algorithm
由于当前预测技术的限制[32]，其精度不能达到100%，对此，本文考虑了光伏在不同预测精度下改进前后的CDLR-DDPG算法与SQP算法以及SA算法的对比计算结果见表5。其中，波动率定义为运行周期内并网点功率波动量的总和与并网点功率绝对值总和之比，收益增长率定义为抽蓄的收益与光-蓄的总收益之比。由表5可知：当无抽蓄参与调节时，并网点功率波动率为45.67%；由CDLR-DDPG算法实现抽蓄的经济调度时其波动率与收益增长率分别提升了12.70%和4.95%；同时改进后的CDLRDDPG算法相对于原始的DDPG算法，波动率下降了1.05%，经济效益提高了0.08%；基于SA法时，其波动率降低了 15.55%同时抽蓄的经济收益增长了4.98%；当利用SQP法求解时，预测精度为100%所对应的波动率降低了31.84%，同时抽蓄的收益增长了 5.48%，为全局最优值；若正常预测精度为90%[33]时，只能抑制 10.2%的并网功率波动率、提升 4.33%的抽蓄经济收益。同时，当极端天气下的预测精度不大于85%[34]时，互补系统的稳定性与经济效益均较差。因此，当预测误差大于15%时，采用 SQP法求解的效果不如 CDLR-DDPG法的实时决策性能。CDLR-DDPG法针对当前与历史信息的决策过程免去了对源/荷的预测，能够适应随机动态环境，而SQP法在随机环境中优化调度的效果会受到预测精度的影响。若同时考虑光伏、负荷和电价的预测误差以及预测成本，则CDLR-DDPG算法更适合在随机环境中做出决策。
表5 不同预测精度下波动率与收益的对比结果
Tab.5 Comparative analysis of the power flucuation and revenue under different forecast accuracy
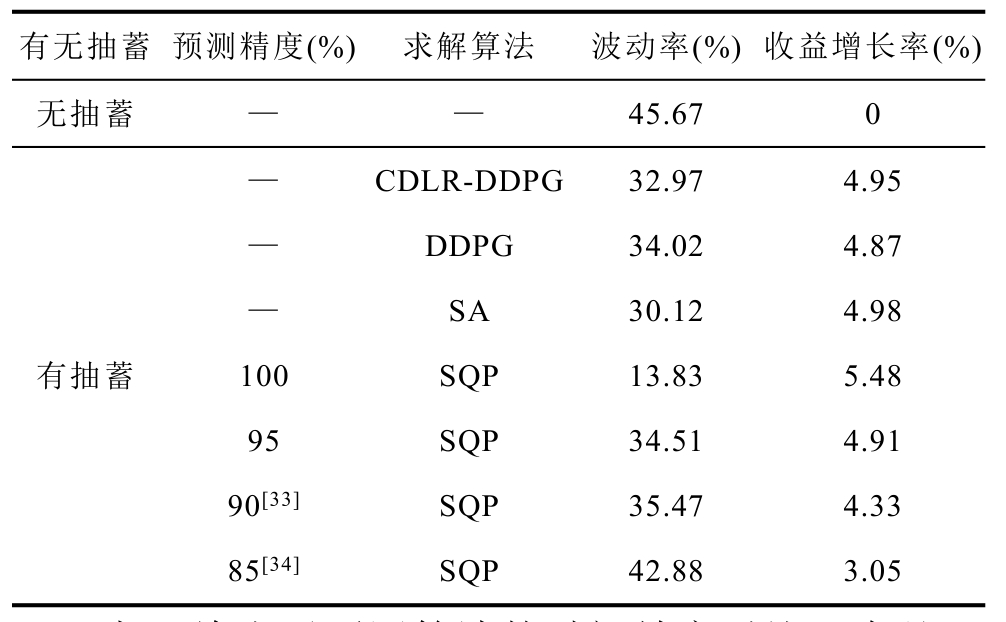
有无抽蓄 预测精度(%) 求解算法 波动率(%) 收益增长率(%)无抽蓄 — — 45.67 0— CDLR-DDPG 32.97 4.95有抽蓄— DDPG 34.02 4.87— SA 30.12 4.98 100 SQP 13.83 5.48 95 SQP 34.51 4.91 90[33] SQP 35.47 4.33 85[34] SQP 42.88 3.05
表6给出了不同算法的时间效率对比，在处理器为Inter(R) Core(TM) i9-9820X CPU @ 3.30GHz的硬件平台上，由python3.7实现本文所采用的CDLRDDPG算法求解所建立的经济调度模型总共耗时237.282s，其中包含测试 168个时刻点所消耗的0.043 8s；由 Matlab实现 SQP算法来求解时耗时2.683s；基于抽样的场景分析法耗时 1 324.85s。可见 CDLR-DDPG算法在实现光伏-抽蓄互补系统的在线经济调度时，模型离线训练相对耗时；若在线实时应用已经训练好的模型，则可根据当前的光伏出力和实时电价瞬间给出在满足并网功率波动约束的条件下抽蓄的工况；SQP法直接求解耗时为CDLR-DDPG算法的 61.25倍；从抑制波动性和提升经济性的角度来评估时，SA法略优于 CDLRDDPG法，但是在同一硬件平台上采用 SA求解所消耗的时间是训练 CDLR-DDPG法的 5.58倍。因此，对于这种强随机性互补系统的经济调度，基于抽样的SA法的计算成本即时间效益远低于数据驱动型的CDLR-DDPG算法。
表6 算法时间效益对比
Tab.6 Comparative analysis of the different algorithm efficient
求解算法 训练时间/s 测试时间/s CDLR-DDPG 237.282 0.043 8 SQP — 2.683 SA — 1 324.854
4 结论
本文针对光伏-抽蓄互补发电系统，从并网点功率波动和抽水蓄能的经济收益等角度出发，采用改进的DDPG算法（CDLR-DDPG），研究了全额消纳光伏时抽水蓄能的实时经济调度问题；并通过不同算法对比了 CDLR-DDPG算法在应对光-蓄随机环境而实时做出决策的有效性。结果表明：
1）CDLR-DDPG算法在控制抽水蓄能，缓解功率波动和跟随电价方面，能够取得较佳的效果，使得并网点功率波动降低了12.70%的同时增加4.95%的互补系统收益。此外，改进后的CDLR-DDPG算法相对于原始的DDPG算法，并网功率波动率降低了1.05%，抽蓄的经济效益提高了0.08%。
2）与 SQP相比，CDLR-DDPG算法更能够合理地控制抽水蓄能在凌晨时段处于待机状态，避免了抽蓄设备进行频繁的低效能工况切换，有利于延长抽蓄的寿命。
3）当光伏的预测误差大于10%时，使用CDLRDDPG算法实现光-蓄互补系统的调度策略，无论是在抑制并网波动率还是提升抽蓄的经济收益方面均具有绝对优势。
4）CDLR-DDPG算法在线应用的时间效益远大于SQP法和SA法实现调度的时间效益，进而降低了计算成本。本文所研究的光-蓄互补发电系统的智能调度策略为电力系统经济调度提供了一种新思路，有助于多能耦合智能调度的分析与设计。
[1]太阳能发展“十三五”规划[EB/OL].国家能源局,2016-12-08.http://zfxxgk.nea.gov.cn/auto87/201612/t20161216_2358.htm.
[2]2018年光伏发电统计信息[EB/OL].国家能源局，2019-03-19.http://www.nea.gov.cn/2019-03/19/c_137907428.htm.
[3]孙玉树, 张国伟, 唐西胜, 等.风电功率波动平抑下的MPC双储能控制策略研究[J].电工技术学报,2019, 34(3): 571-578.Sun Yushu, Zhang Guowei, Tang Xisheng, et al.Research on MPC and dual energy storage control strategies with wind power fluctuation mitigation[J].Transactions of China Electrotechnical Society, 2019,34(3): 571-578.
[4]李建林, 牛萌, 周喜超, 等.能源互联网中微能源系统储能容量规划及投资效益分析[J].电工技术学报, 2020, 35(4): 874-884.Li Jianlin, Niu Meng, Zhou Xichao, et al.Energy storage capacity planning and investment benefit analysis of micro-energy system in energy interconnection[J].Transactions of China Electrotechnical Society, 2020, 35(4): 874-884.
[5]Shah R, Mithulananthan N, Lee K Y.Large-scale PV plant with a robust controller considering power oscillation damping[J].IEEE Transactions on Energy Conversion, 2013, 28(1): 106-116.
[6]Miao Zhixin, Fan Lingling, Osborn D, et al.Control of DFIG-based wind generation to improve interarea oscillation damping[J].IEEE Transactions on Energy Conversion, 2009, 24(2): 415-422.
[7]Zhu Yongli, Liu Chengxi, Sun Kai, et al.Optimization of battery energy storage to improve power system oscillation damping[J].IEEE Transactions on Sustainable Energy, 2019, 10(3): 1015-1024.
[8]熊连松, 修连成, 王慧敏, 等.储能系统抑制电网功率振荡的机理研究[J].电工技术学报, 2019,34(20): 4373-4380.Xiong Liansong, Xiu Liancheng, Wang Huimin, et al.Mechanism of energy storage system to suppress grid power oscillations[J].Transactions of China Electrotechnical Society, 2019, 34(20): 4373-4380.
[9]Sukumar S, Mokhlis H, Mekhilef S, et al.Ramp-rate control approach based on dynamic smoothing parameter to mitigate solar PV output fluctuations[J].International Journal of Electrical Power & Energy Systems, 2018, 96: 296-305.
[10]Velasquez A, Barreiro-Gomez J, Quijano N, et al.Distributed model predictive control for economic dispatch of power systems with high penetration of renewable energy resources[J].International Journal of Electrical Power & Energy Systems, 2019, 113:607-617.
[11]Moarefdoost M, Lamadrid J, Zuluaga L.A robust model for the ramp-constrained economic dispatch problem with uncertain renewable energy[J].Energy Economics, 2016, 56: 310-325.
[12]Nge C, Ranaweera I, Midtgard O, et al.A real-time energy management system for smart grid integrated photovoltaic generation with battery storage[J].Renewable Energy, 2019, 130: 774-785.
[13]Banshwar A, Sharma N, Sood Y, et al.Market-based participation of energy storage scheme to support renewable energy sources for the procurement of energy and spinning reserve[J].Renewable Energy,2019, 135: 326-344.
[14]李佳琪, 陈健, 张文, 等.高渗透率光伏配电网中电池储能系统综合运行控制策略[J].电工技术学报, 2019, 34(2): 437-446.Li Jiaqi, Chen Jian, Zhang Wen, et al.Integrated control strategy for battery energy storage systems in distribution networks with high photovoltaic penetration[J].Transactions of China Electrotechnical Society, 2019, 34(2): 437-446.
[15]Zhao Shuqiang, Fang Yuchen, Wei Ziyu.Stochastic optimal dispatch of integrating concentrating solar power plants with wind farms[J].International Journal of Electrical Power & Energy Systems, 2019, 109:575-583.
[16]Yin Yue, Liu Tianqi, He Chuan.Day-ahead stochastic coordinated scheduling for thermal-hydro-windphotovoltaic systems[J].Energy, 2019, 187: 115944.
[17]Hang S, Jiakun F, Xiaomeng A, et al.Stochastic optimization of economic dispatch for microgrid based on approximate dynamic programming[J].IEEE Transactions on Smart Grid, 2019, 10(3): 2440-52.
[18]Sutton R S, Barto A G.Reinforcement learning: an introduction[M].Cambridge: The MIT Press, 1998.
[19]杨挺, 赵黎媛, 王成山.人工智能在电力系统及综合能源系统中的应用综述[J].电力系统自动化,2019, 43(1): 2-14.Yang Ting, Zhao Liyuan, Wang Chengshan.Review on application of artificial intelligence in power system and integrated energy system[J].Automation of Electric Power Systems, 2019, 43(1): 2-14.
[20]安灵旭, 唐其筠, 李中成, 等.人工智能在配电网运维中的应用研究[J].电气技术, 2019, 20(10): 103-106.An Lingxu, Tang Qijun, Li Zhongcheng, et al.Research on the application of artificial intelligence in operation maintenance of distribution system[J].Electrical Engineering, 2019, 20(10): 103-106.
[21]Wei Qinglai, Liu Derong, Shi Guang, A novel dual iterative Q-learning method for optimal battery management in smart residential environments[J].IEEE Transactions on Industrial Electronics, 2015 62(4): 2509-2518.
[22]Qiao Junfei, Wang Gongming, Li Wenjing, et al.An adaptive deep Q-learning strategy for handwritten digit recognition[J].Neural Networks, 2018, 107: 61-71.
[23]Wu Jingda, He Hongwen, Peng Jiankun, et al.Continuous reinforcement learning of energy management with deep Q network for a power split hybrid electric bus[J].Applied Energy, 2018, 222:799-811.
[24]Hua Haochen, Qin Yuchao, Hao Chuantong, et al.Optimal energy management strategies for energy Internet via deep reinforcement learning approach[J].Applied Energy, 2019, 239: 598-609.
[25]Mocanu E, Mocanu D C, Nguyen P H, et al.On-line building energy optimization using deep reinforcement learning[J].IEEE Transactions on Smart Grid, 2019, 10(4): 3698-3708.
[26]Ardizzon G, Cavazzini G, Pavesi G.A new generation of small hydro and pumped-hydro power plants:advances and future challenges[J].Renewable and Sustainable Energy Reviews, 2014, 31: 746-761.
[27]Jordan M I, Mitchell T M.Machine learning: trends,perspectives, and prospects[J].Science, 2015, 349:255-260.
[28]Olivier S, Olivier B.Markov decision process in artificial intelligence[M].Piscataway: John Wiley &Sons, Inc, 2013.
[29]最终决战！OpenAI将挑战Dota2最强战队TI8冠军OG[OL].新浪体育, 2019-03-27, http://sports.sina.com.cn/go/2019-03-27/doc-ihtxyzsm0868576.shtml.
[30]Aneke M, Wang Meihong.Energy storage technologies and real-life applications - a state of the art review[J].Applied Energy, 2016, 179: 350-377.
[31]Yalmip R20190425 < https://yalmip.github.io/ >[Z].
[32]赖昌伟, 黎静华, 陈博, 等.光伏发电出力预测技术研究综述[J].电工技术学报, 2019, 34(6): 1201-1217.Lai Changwei, Li Jinghua, Chen Bo, et al.Review of photovoltaic power output prediction technology[J].Transactions of China Electrotechnical Society, 2019,34(6): 1201-1217.
[33]Das U K, Tey K S, Mehdi S, et al.Forecasting of photovoltaic power generation and model optimization: a review[J].Renewable and Sustainable Energy Reviews, 2018, 81: 912-928.
[34]Rana M, Koprinska I, Agelidis V G.Forecasting solar power generated by grid connected PV systems using ensembles of neural networks[C]//2015 International Joint Conference on Neural Networks (IJCNN),Killarney, 2015: 1-8.