0 引言
随着经济的发展,人类社会对电力的需求越来越大。鉴于化石能源的不可再生性和其造成的环境压力,新能源发电技术越来越受到世界各国的重视。风力发电是新能源发电中重要的一部分,在 2018年,全球风电装机容量规模达到597GW,中国的风电装机容量规模占据全球第一,超过200GW[1]。随着风电渗透率的不断增加,由于风速的随机性和不确定性,风电功率的波动会对电网的安全性造成影响[2-3]。风电功率主要由风速决定[4-5],准确的风速预测可用于指导设计高效的风电控制策略,进而减小对电网不利影响[6]。但由于一个风电场中的风机广泛分布在不同的地理位置上,每个风机的风速都不相同[7]。若能精细化地预测风电场中每台风机的本地风速,则可为风电场控制提供更为充分的信息,进而提升风电场控制的灵活性和最优性[8]。
近年来,国内外学者已经对风速预测做了大量的研究,并且也取得了很多成果。文献[9-10]利用历史数据的潜在规律,实现单一风机风速的预测,文献[11-15]利用小波变换等机器学习方法将一个风电场中的所有风机作为一个整体进行风速预测,但这些研究均是对单个风机或者将整个风电场的风机当为整体进行预测。相较于欧美地区,我国季风区在冬季风、夏季风时期的风速有较高的空间相关性[16],故在进行风速预测时,此自然条件应予以充分利用,即应考虑风速和风向的空间相关性。文献[17-18]利用风速的时间相关性进行多风机风速等预测,但是其均没有考虑不同位置下风速和风向的空间相关性。文献[19-21]虽然考虑了风场内多风机风速间的空间相关性,但是没有考虑各风速序列内部的时间相关性。文献[22]使用环境和地理参数(如湿度、温度、大气压力等)预测多风机风速,虽然考虑了风速的时空相关性,但是计算代价大,参数依赖性强。文献[23]利用卷积神经网络(Convolutional Neural Network, CNN)和长短期记忆网络(Long Short-Term Memory, LSTM)进行多风机风速预测,但神经网络输入仅为风机风速,输入特征较为单一,且计算代价较大。
一个风电场往往会有多台风机,相应地其数据量也较大,所以需要有高效的处理工具来挖掘其内含的特征信息。深度学习是在海量数据中寻找复杂规律的有效工具,随着特征数据的增大,其表征数据特征的能力会不断提升。因此,风电场内多风机风速预测问题非常适合使用深度学习来解决。准确的风速预测模型需要尽可能地获取到有效信息,所以多风机风速预测需要同时考虑风速及风向的时间相关性和空间相关性。现有基于时空相关性的多风机预测模型的输入特征仅有风速,但多风机之间的时空相关性依赖实时风向,且随风向实时变化。因此,一个有效的空间时域预测模型应同时将多风机的风速和风向作为输入特征。在时间相关性方面,考虑风向之后,特征维数增大,不仅模型计算代价大,而且捕捉不同时刻间风电场整体风速和风向分布动态特性的难度变大,所以需要更加有效,且能减小计算代价的时间域建模方法。
鉴于此,本文提出了一种基于深度学习的风电场多风机风速集成预测模型。该模型同时学习多风机间风速和风向的时空相关性。风速和经三角函数处理的风向构成三维输入矩阵,此特征输入矩阵与彩色图像RGB三维通道的结构类似。而CNN非常适合处理具有类似彩色图像结构的数据,CNN每一个卷积层中具有多个卷积核,可以逐层学习到数据在多个方面的特征,所以在空间相关性方面使用CNN进行空间特征提取。将经过CNN处理后、蕴含空间信息的数据再进行时间特征提取。在时间相关性方面,由于简单循环单元(Simple Recurrent Unit, SRU)不仅具有并行处理能力,能极大地减小计算代价,而且可以有效地缓解梯度消失问题,解决长期依赖问题[24-25],因此可使用 SRU进行时间特征提取。
1 风电场多风机风速预测问题描述
本文所采用的时空集成预测模型是基于风电场中每台风机的历史风速数据和历史风向数据,采用CNN和 SRU集成预测模型,提取到上述风机特征数据之间内在的时空相关性,进而得到风电场中每台风机精细化风速预测结果。
进行风电场中每台风机精细化风速预测需要详细的风机数据,此风机数据必须真实地反映风电场中多个风机的时空相关性。本文所采用的数据来源于美国国家可再生能源实验室(National Renewable Energy Laboratory, NREL)提供的风能综合国家数据集(Wind Integration National Dataset, WIND),WIND是迄今为止公开可用的最大最完整的风能数据集,通过其网站可以十分容易地获取所需风能数据。WIND现已公开提供2007年~2012年美国本土超过 12.6万个陆基和海基处的风向、风速、温度、表面空气压力和空气密度等数据,其数据每5min采集一次,即时间分辨率为5min。本文仿真案例选择2012年数据,地点位于怀俄明州的梅迪辛博和埃尔克芒廷之间的144台风机测量点。其中,最大风速为27.353m/s,最小风速为0.061m/s,144台风机测量点以12×12的矩阵形状排列,各风机测量点轮毂高度一致,均为100m,每两个相邻的风机测量点间距2km,如图1所示。此研究对象可视作拥有多台位于不同地理位置风机风电场的一般案例。

图1 WIND中美国怀俄明州12×12风机矩阵
Fig.1 The wind turbine array of 12×12 in Wyoming of WIND, USA
2 多风机风速序列间空间相关性和风向序列间空间相关性建模
在集成预测模型中,CNN负责多风机风速序列间空间相关性和风向序列间空间相关性的建模。CNN是深度学习领域中重要的一种学习模型,于1998年被Y.LeCun等提出[26],它非常适合处理图像类结构的数据。在很多领域,CNN都得到了广泛的应用,如图像识别、语言识别和气候预测等。与常见的神经网络相比,CNN最主要的特征在于卷积层[26],即卷积操作。CNN一般由输入层(INPUT)、卷积层(CONV)、池化层(POOL)和全连接层(FC)构成。
2.1 卷积神经网络设计基本思想
在 CNN中,输入层的数据一般先由卷积层进行特征提取,为保持卷积之后的特征图尺寸不变,卷积核尺寸不应为偶数,并且卷积过程中需进行零填充操作。由于卷积层中有多个卷积核,卷积层输出往往具有较大的参数量,而池化层可以减小数据和参数的数量,所以卷积层后一般会加上池化层。为了提取最显著的特征,避免平均池化造成的模糊化效果,选用最大池化。由于在线性模型中加入非线性激活函数可以实现去线性化,故卷积层中每个神经元的输出通过一个修正线性单元(Rectified Linear Uint, ReLU)激活函数进行处理。使用多个较小尺寸的卷积核代替较大尺寸的卷积核,不仅可以减小参数,减轻过拟合,而且还增加了多层的非线性扩展能力。在卷积神经网络的底层构建全连接层,对所得到的高维特征进行综合处理,做出最后的决策输出。在卷积层中,其学习复杂结构的能力应该被保证。为了定量衡量卷积层的学习能力,定义卷积层学习能力C为

为了保证卷积层学习复杂结构的能力,每个卷积层的C值都应该大于某一最小值,一般可设1/6为此下界[27]。此外,当最深层网络神经元的感受野大于输入图像的尺寸时,单个神经元已经可以学习到整幅图像的特征,故不应再继续加深网络层数,以免产生过拟合现象,即最深层网络神经元的感受野必须略大于输入图像的尺寸。如果其感受野比输入图像尺寸小,那么此神经网络丧失了学习高级特征的能力。相反,若最深层网络神经元的感受野比输入图像尺寸大得多,不仅过深的卷积网络对整体网络性能没有帮助,而且增加了过拟合的风险,可能会对最终结果造成不好影响[27]。
2.2 卷积神经网络具体设计
综合考虑硬件平台和上述设计思想,本文构建如图2所示的CNN模型,其输入层为三维数据,每一维是 12×12矩阵,CNN结构中具有 2个卷积层,2个池化层和2个全连接层,卷积中最后的一个全连接层也被视为回归层。

图2 卷积神经网络结构
Fig.2 The CNN structure
卷积层中卷积核输入通道数应与输入卷积层数据的维度一致,故两个卷积层的卷积核输入通道数分别为 3和 6。令卷积核尺寸为 5×5,C2和 C1卷积层中卷积核输出通道数分别为16和6。采用自顶向下的方法来计算每层网络层的感受野[28],当卷积核尺寸为 5,第二层卷积层 C2的感受野尺寸为 6,故其学习能力C=5/6大于其下限值1/6,满足设计要求,采用自顶向下的计算方式得到第二个池化层P2的感受野为 14,略大于输入图像尺寸 12,满足设计要求,故在第二个池化层P2后,不应再新增卷积层。因池化层中的滑动步长大于3时提纯操作过于剧烈,故一般设步长为2。
2.3 卷积神经网络
2.3.1 卷积层
卷积层是 CNN中的基本操作,视作是加权求和的过程。通过卷积运算,原始数据的局部低维特征被映射到高维特征。对于输入到卷积层的每个局部区域,卷积计算是这个局部窗口内的所有元素和卷积核的内积,这个内积为下一层的对应元素。通过遍历上一层的所有局部进行卷积,即可得到通过卷积层运算的下一层。其卷积计算公式为
式中,i为局部区域内的元素;k为卷积核;g为卷积计算后的元素。
图3给出一个二维卷积的例子,当局部区域 时,滑动步长为1,卷积后的内积输出g=0。
时,滑动步长为1,卷积后的内积输出g=0。
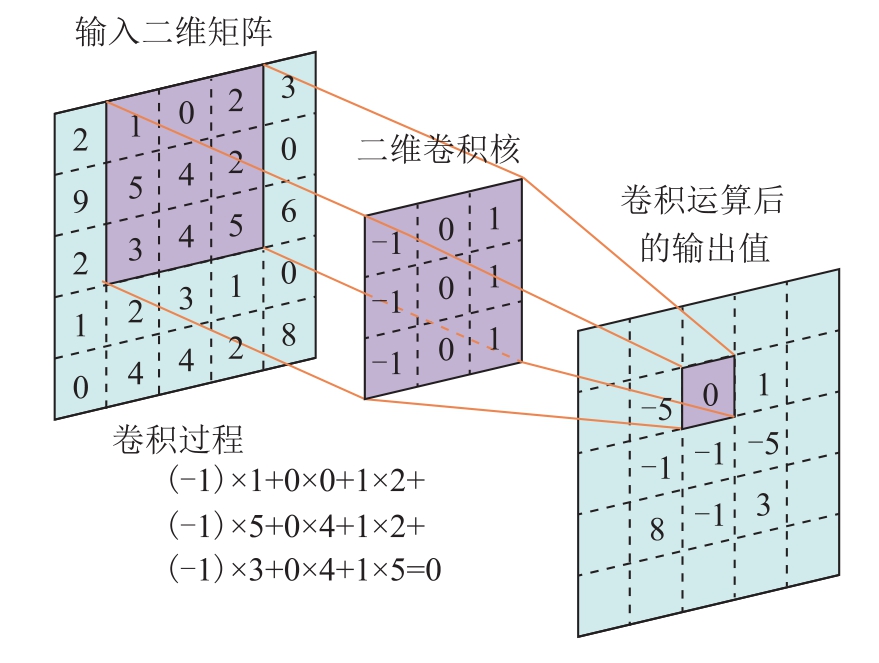
图3 二维卷积示例
Fig.3 The example of two-dimensional convolution
风速和三角函数化的风向构成三维矩阵输入,需要对其进行三维卷积操作。三维卷积与二维卷积类似,三维卷积的每一个维度都进行二维卷积,最后将每个维度上面的卷积结果叠加即是三维卷积的结果,故三维卷积的最终结果也是一个 1×1的数,如图4所示。

图4 三维卷积示例
Fig.4 The example of three-dimensional convolution
2.3.2 池化层
经过卷积层提取特征之后,一般会进行池化操作。由于一幅图像的相邻局部区域往往具有相同的特征,所以CNN对其进行池化操作,以达到防止过拟合的作用,并且经过池化操作后的数据对应原始输入数据的感受野也不断增大,可以提取到更高维的特征,这种操作也可以认为是一种下采样操作。池化操作最常见的是最大池化(Max Pooling),其次是平均池化(Average Pooling)。图5给出了最大值池化操作示例,池化窗口2×2,步长2。
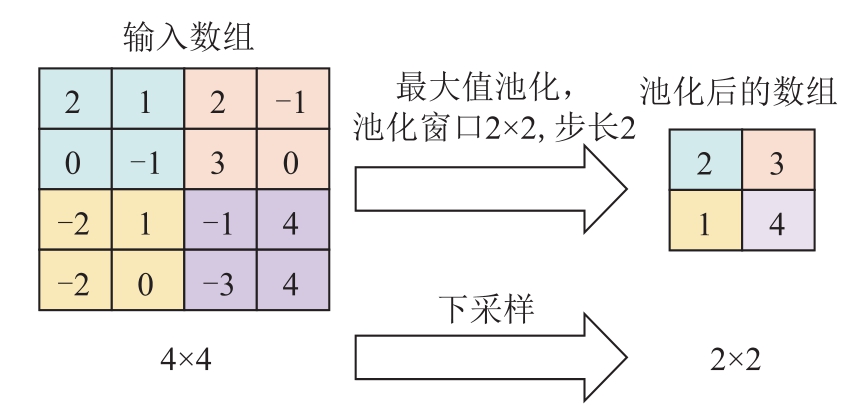
图5 最大值池化操作示例
Fig.5 The example of max pooling
3 多风机风速序列内时间相关性和风向序列内时间相关性的建模
循环神经网络(Recurrent Neural Network, RNN)是一种专门用来处理具有时序特征数据的深度神经网络,于1980年被J.J.Hopfield等提出。RNN广泛应用在自然语言处理、计算机视觉、地球科学和计算生物学等领域[29]。RNN根据“未来的状态与过去和现在的状态相关”提出,因此RNN非常适合分析时间序列数据,并且它可以将任意长度的序列作为输入预测未来的输出。
3.1 简单循环单元
深度学习研究的进展常常涉及更大更深的深层神经网络,虽然 RNN被设计为利用具有时序特征的历史数据做出当前时刻的决策输出,但 RNN对最近输入的历史数据非常敏感,而更早之前的历史数据会随着时间的推移,其辅助作用越来越弱,这种问题被称为长期依赖问题。LSTM 和门控循环单元(Gated Recurrent Unit, GRU)的提出解决了长期依赖问题。
但LSTM和GRU的“细胞”之间的计算具有前后的依赖性,所以它们只能串行计算,计算代价大。SRU是RNN的一种变体形式,它于2017年被Tao Lei等提出[25],SRU通过将每一时间步的主要计算部分优化为不依赖之前时间步的计算,从而可以实现并行化计算,进而减小计算成本。因此SRU不仅有利用长时间信息的优势,解决有着复杂时间相关性的长期依赖问题,而且可以大幅减小计算成本。SRU的结构如图6所示,SRU的计算公式为
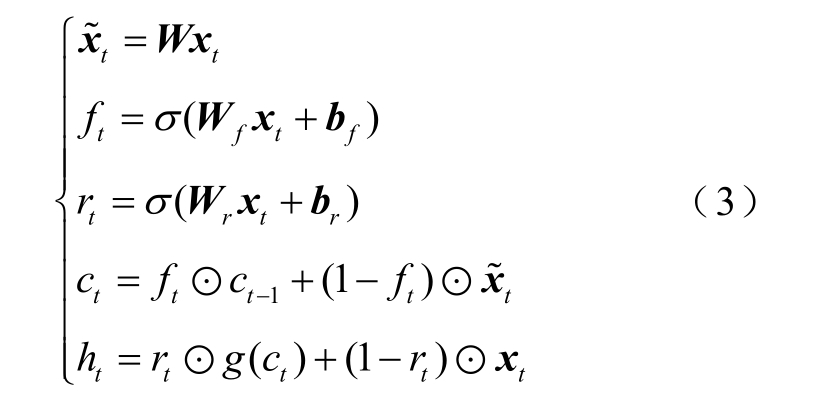
式中,W、Wf和 Wr分别为对应输入的权重矩阵;bf和 br为偏置向量;xt为在 t时刻的输入向量;ht为t时刻的输出;σ为激活函数sigmoid函数;ct-1为在t-1时刻的SRU的单元状态;⊙表示Hadamard运算。值得说明的是,ct-1虽然表示t-1时刻的单元状态,但是包含了从t-k到t-1时刻的输入序列对t时刻预测输出的影响,故ct−1记录了过去的输入状态对t时刻输出的影响。
由式(3)可知:ht计算不依赖于ht-1。故SRU可以实现并行计算,大幅减小计算成本。而 LSTM和GRU的ht均依赖于ht-1,破坏了独立性和并行性,故与LSTM和GRU相比,SRU能减小计算代价。

图6 SRU结构框图
Fig.6 SRU structure block diagram
3.2 基于SRU的时间相关性学习模型
本文所提的集成预测模型使用 SRU进行空间时域建模,其中采用的是单层网络结构的SRU,如图7所示。该时域预测模型使用 t-k至 t时刻的历史数据给出未来时刻的预测数据。值得说明的是:由于SRU的输出是一维向量形式,在计算损失函数的时候,需要将 144个风机组所构成的风速预测12×12矩阵映射为1×144向量,进而计算损失函数。
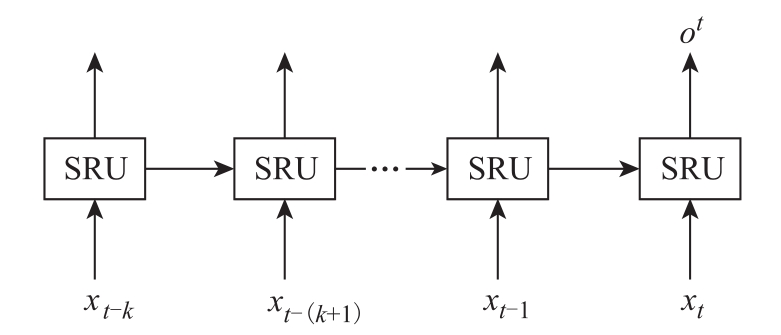
图7 单层SRU连接
Fig.7 The connection of single layer SRU
4 空间相关性和时间相关性的深度集成预测模型
4.1 数据处理
风机风向数据的范围在0°~360°之间,但是位于最大值附近(例如 359°)和最小值附近(例如 1°)的风向数据,对于风机扇叶来说相差并不大,若不进行任何处理直接将此风向数据输入到集成预测模型中,因实际风向的物理角度相差并不大,但是输入的风向数据却相差较大,故向集成预测模型输入相差较大的风向数据并不是合理有效的信息,会导致预测误差较大,因此需要对风向数据进行预先处理。本仿真案例中采用三角函数化处理,即 sin风向和 cos风向[30]。在每一个采样时刻k,用12×12×3的三维矩阵 I k将此时刻风电场中的12×12个风机的风速,cos风向和sin风向构成的三维信息存储起来,Ik具体结构如图8所示,此三维输入矩阵可视为类似于彩色图像的三维RGB结构。
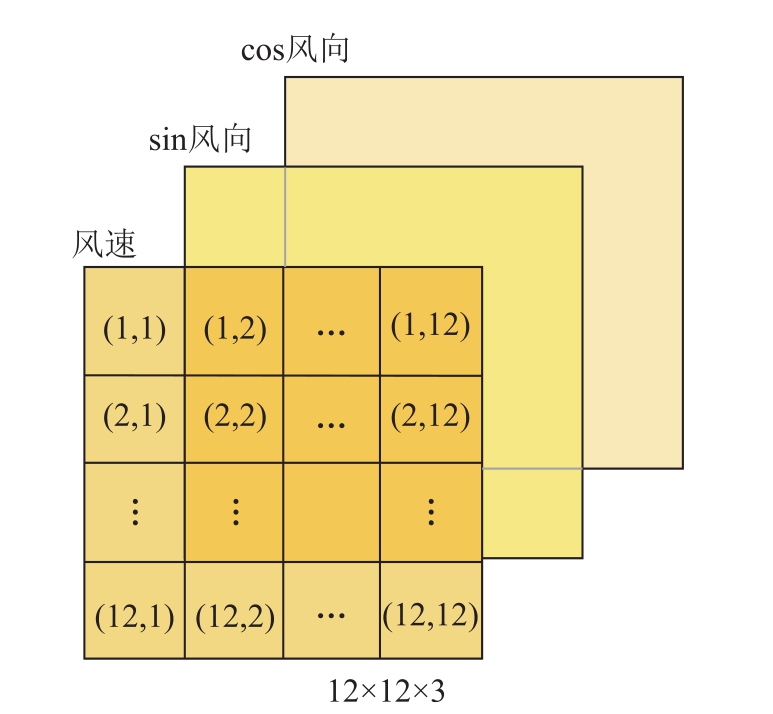
图8 三维矩阵特征
Fig.8 Three-dimensional matrix feature
4.2 时空集成预测
本文采用的方法通过考虑风电场中 144台风机阵列风速和风向的时空相关性来实现时空联合预测。首先使用CNN提取要预测时刻前20个时刻的三维矩阵的各自空间特征,再将CNN提取到的空间特征依次输入到20个SRU中提取时序特征,由最后一个 SRU的输出作为最终的多风机风速预测。时空集成预测模型的整体结构如图9所示,预测值为
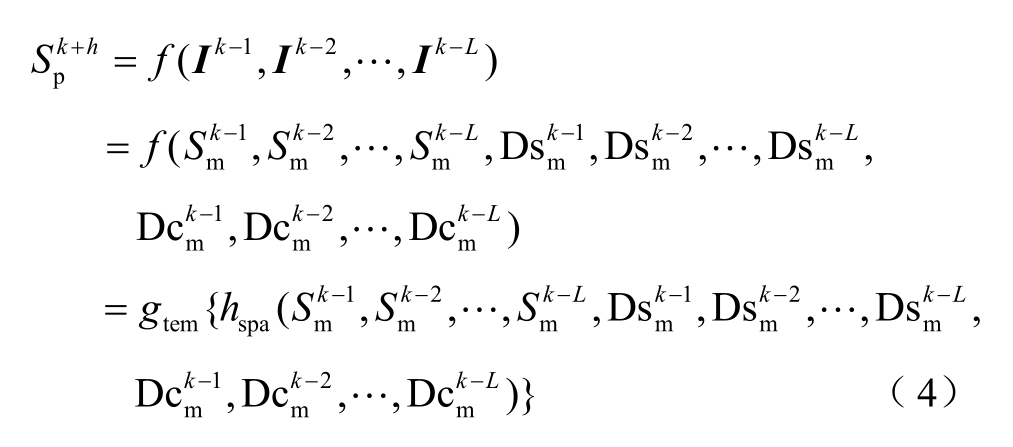
式中, 为在k+h在时刻的预测风速值,即h为预测时域; I k为 k时刻下由风速和三角函数化风向构成的三维矩阵;
为在k+h在时刻的预测风速值,即h为预测时域; I k为 k时刻下由风速和三角函数化风向构成的三维矩阵;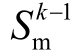 为在k-1时刻风速的测量值;
为在k-1时刻风速的测量值;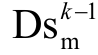 为 k-1时刻的 sin风向测量值;
为 k-1时刻的 sin风向测量值; 为k-1时刻的 cos风向测量值;gtem和hspa分别为以12×12排列风机的风速和风向内在的时间相关性和空间相关性。
为k-1时刻的 cos风向测量值;gtem和hspa分别为以12×12排列风机的风速和风向内在的时间相关性和空间相关性。

图9 集成预测模型结构
Fig.9 Integrated forecast model structure
对于确定的预测时域 h=h1和输入历史序列长度 L=L1,本案例采用滚动预测的方法进行多步预测,即迭代式。具体而言,在任意时刻k,都基于历史序列长度L1的风机特征数据![]() 预测出未来h1时刻的风速
预测出未来h1时刻的风速![]() ,当在下一个时刻k+1时,根据历史序列长度 L1的风机特征数据
,当在下一个时刻k+1时,根据历史序列长度 L1的风机特征数据![]() )预测出未来h1时刻的风速
)预测出未来h1时刻的风速![]() 。如此循环迭代下去,即为迭代预测过程。
。如此循环迭代下去,即为迭代预测过程。
5 仿真算例
5.1 仿真设置
本次仿真基于Tensorflow框架的python语言实现,利用统一计算设备架构(Compute Unified Device Architecture,CUDA)加速,仿真硬件平台设置:CPU为Intel Core i5-7400 3.40GHz,内存RAM为16GB,GPU为Nvidia GeFore GTX 1060 3G。
在本次仿真案例中使用风速和风向作为特征,设置预测时域h为 1。又本案例中风电场风机特征数据每隔5min更新一次,故当预测时域h为1时,即预测当前时刻后未来5min的多风机风速。
相较于仅给出风电场单一整体的风速预测结果,进行风电场每台风机精细化风速预测需要更加综合的评价指标,以衡量风电场中所有风机的整体预测效果。本案例采用方均根误差(Root Mean Square Error, RMSE)和平均误差(Mean Error, ME)作为仿真的综合评估损失函数。RMSEk和MEk用于衡量在k时刻风电场中每台风机精细化风速预测的综合误差大小,分别为
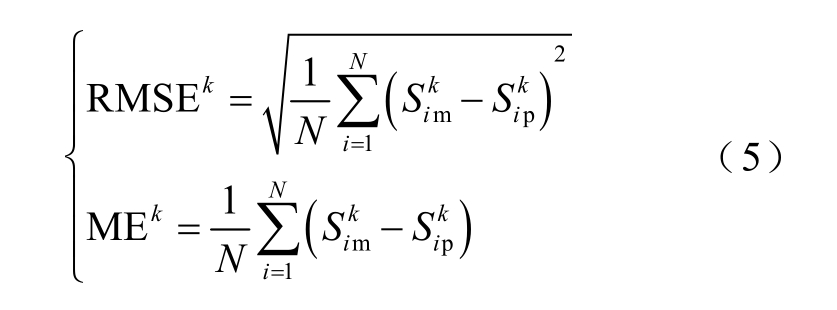
式中,RMSEk为k时刻风电场每台风机精细化风速预测的方均根误差;MEk为k时刻风电场每台风机精细化风速预测的平均误差;N为预测的总风机数量,在本次仿真N=144,即认为此风电场中共有144台风机;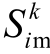 为在k时刻风电场中第i台风机风速的测量值;
为在k时刻风电场中第i台风机风速的测量值; 为在k时刻风电场中第i台风机风速的预测值。
为在k时刻风电场中第i台风机风速的预测值。
由于采用迭代预测,若风电场中每台风机总计滚动迭代预测M步,则在整个 M步迭代预测中,风电场中每台风机精细化风速预测的综合评价指标RMSE和ME分别为
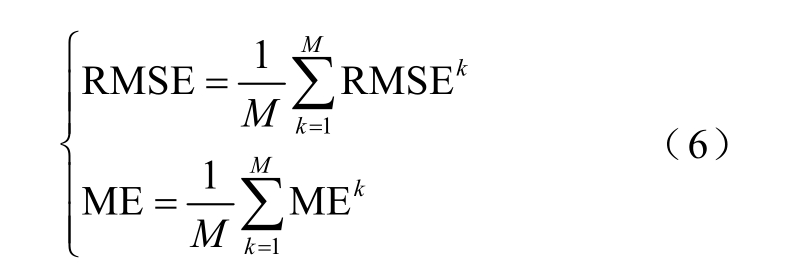
由式(6)可知,综合评价指标RMSE和ME使用总计M步迭代预测中每一步中的RMSEk和MEk进行计算,因此,RMSEk和MEk表示迭代预测过程中,在k时刻,此步的精细化风速预测的误差。RMSE和ME表示在整个迭代预测过程中的综合误差评价指标。
本次仿真首先将数据划分为训练集、验证集和测试集。训练集用来训练深度神经网络的各种参数,验证集用来验证模型是否建立合适,而测试集用来进行实际的预测。使用所获得的数据前50 000条作为仿真数据,在时间尺度上对应1~6月的风机数据,取其中0~40 000条数据作为训练集,40 000~45 000条数据作为验证集,45 000~50 000条数据作为测试集。由于深度神经网络模型中的参数采用随机梯度下降法进行训练,所以一般会将同样的一批数据多次输入该模型中,这样能保证模型中的权重值和偏置值训练得更加充分,将这样的一次训练过程叫作Epoch。在本次仿真中,设置Epoch=100,且为了实时了解训练的效果,在训练的过程中,每训练 200次进行一次验证集的测试。
对于输入集成预测模型的历史特征序列长度 L的选定来说,需要综合考虑网络参数的训练时间成本和先验知识的完备程度。若L太大,网络训练的时间成本及复杂程度会上升,网络参数优化不佳,且过于复杂的模型训练可能会影响参数的最终优化效果,进而影响预测的准确性;若L太小,则先验知识不完备,历史特征序列蕴含的预测知识欠缺,从而限制了预测精度。因此,需要折中考虑L的选定。文献[14,22]中分别选定历史特征序列长度L为12和32,随后采用人工试探的方法。参考上述选定经验,设置L在12~32之间,在采用上述仿真条件下只改变L参数计算得到风速预测误差RMSE,由所计算的若干仿真结果点,得到RMSE=f(L)在L⊂ ( 12,32)定义域内的散点图如图10所示。由图10可知,随着L的逐渐增大,历史特征序列长度不断增加,其蕴含的预测先验知识逐渐完善,所以RMSE逐渐降低。当L增加到某一临界点后,随着L的继续增加,历史特征序列长度过于冗长,网络参数没有得到合适的训练,影响了预测效果,又或是在此仿真设置中,数据训练迭代次数Epoch过小,过长的历史特征序列没有得到充分利用,反而导致网络参数没有得到最优或次优解,故RMSE又较缓慢增加。

图10 历史输入序列长度L与方均根误差RMSE关系(预测时域h=1,Epoch=100)
Fig.10 The graph of historical input sequence length L and RMSE(forecast horizon h=1, Epoch=100)
故在本仿真案例所用条件下,综合考虑选定经验和人工试探结果,最终选定输入集成预测模型的历史序列长度L=20,即使用前20个时刻的风速和风向特征来预测下一预测时域的风速。
5.2 仿真结果
给出 144个风机阵列在某一个时刻的预测结果,同时给出多个不同编号风机在多个时刻的迭代预测结果,如图11~图16所示。在图11中,将某一时刻144台风机的风速预测误差RMSE中最小值-1.098m/s置为青色(RGB分别为0, 255, 255),最大值1.057m/s置为品红色(RGB分别为 255, 0, 255),预测误差RMSE中间值采用线性插值方法得到相应RGB,最后得到对应的颜色。本次仿真算例中,测试集中风电场精细化风速预测综合误差评价指标 RMSE=0.661m/s,集成预测模型神经网络参数训练耗时为1 987.3s。
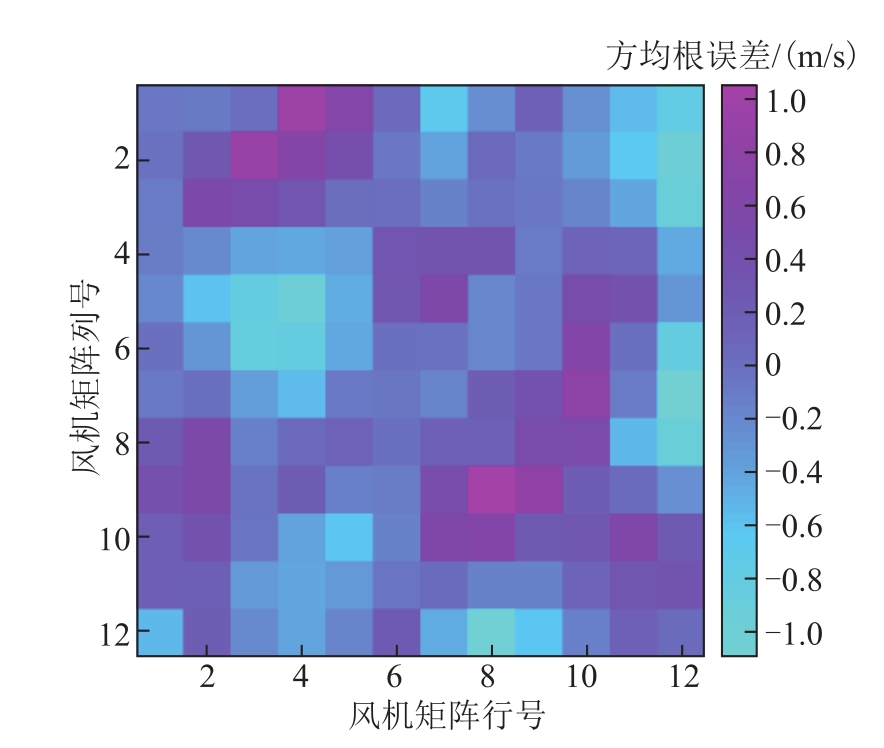
图11 144台风机在某一时刻的预测输出误差热力图(预测时域h=1,即预测未来5min的多风机风速)
Fig.11 Loss thermodynamic graph of the forecasted output of 144 wind turbines at a certain time (forecast horizon h = 1, that is to forecast the wind speed of multiple wind turbines in the next 5 minutes)
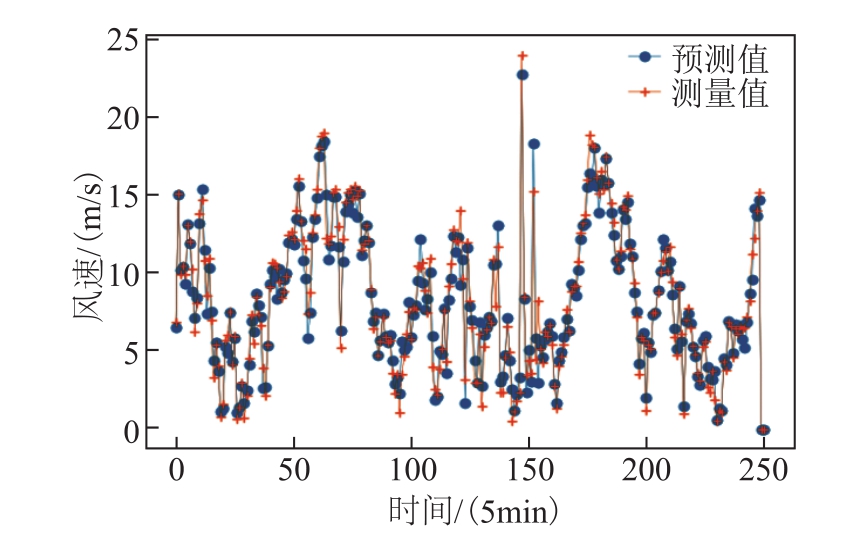
图12 编号1风机的风速预测结果(预测时域h=1,即预测未来5min的多风机风速)
Fig.12 Forecasted output of site ID 1 wind turbine(forecast horizon h = 1, that is to forecast the wind speed of multiple wind turbines in the next 5 minutes)
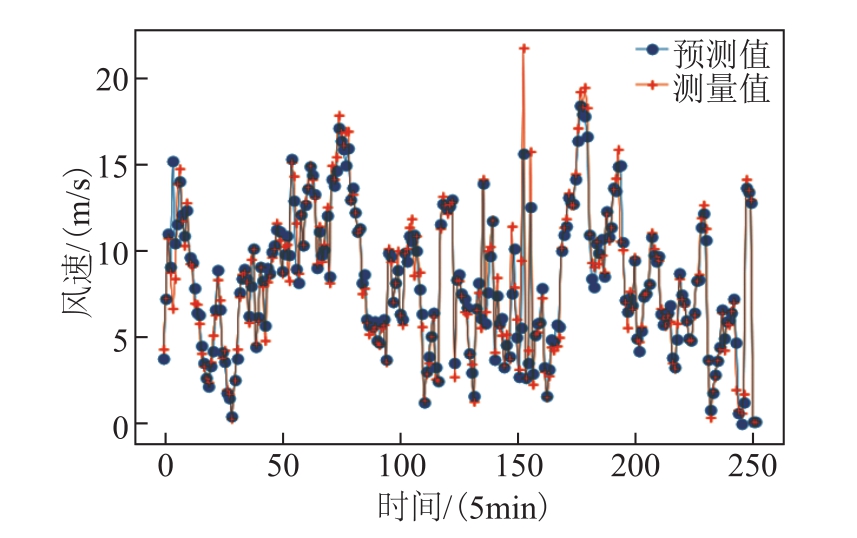
图13 编号20风机的风速预测结果(预测时域h=1,即预测未来5min的多风机风速)
Fig.13 Forecasted output of site ID 20 wind turbine(forecast horizon h = 1, that is to forecast the wind speed of multiple wind turbines in the next 5 minutes)
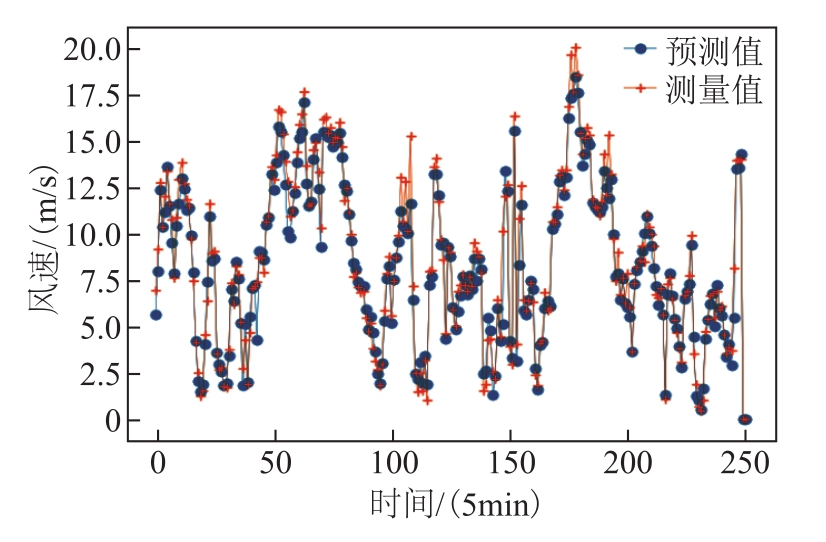
图14 编号40风机的风速预测结果(预测时域h=1,即预测未来5min的多风机风速)
Fig.14 Forecasted output of site ID 40 wind turbine(forecast horizon h = 1, that is to forecast the wind speed of multiple wind turbines in the next 5 minutes)
针对工程中风速预测中常见的多步时域预测问题,本文也给出了多个预测时域的预测结果,预测时域h分别为1、2、5和10,即预测当前时刻后未来 5min、10min、25min和 50min的多风机风速。集成预测模型参数训练耗时和风电场中每台风机精
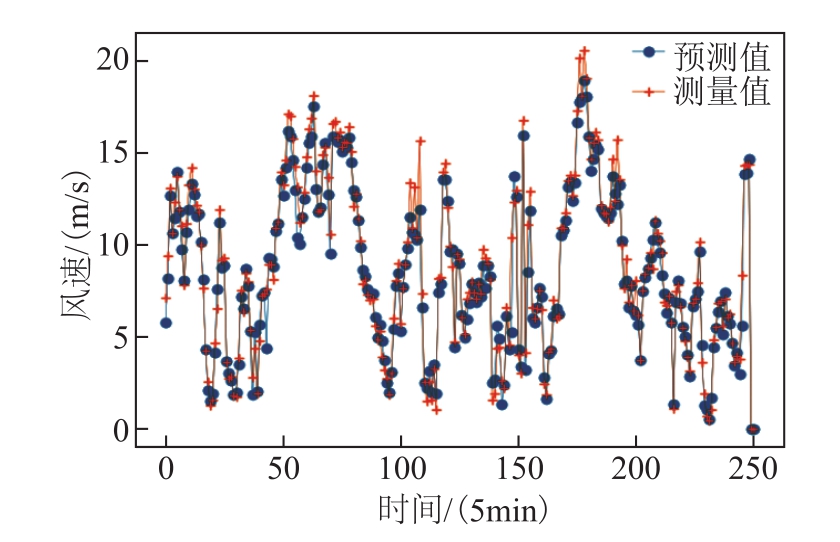
图15 编号60风机的风速预测结果(预测时域h=1,即预测未来5min的多风机风速)
Fig.15 Forecasted output of site ID 60 wind turbine(forecast horizon h = 1, that is to forecast the wind speed of multiple wind turbines in the next 5 minutes)
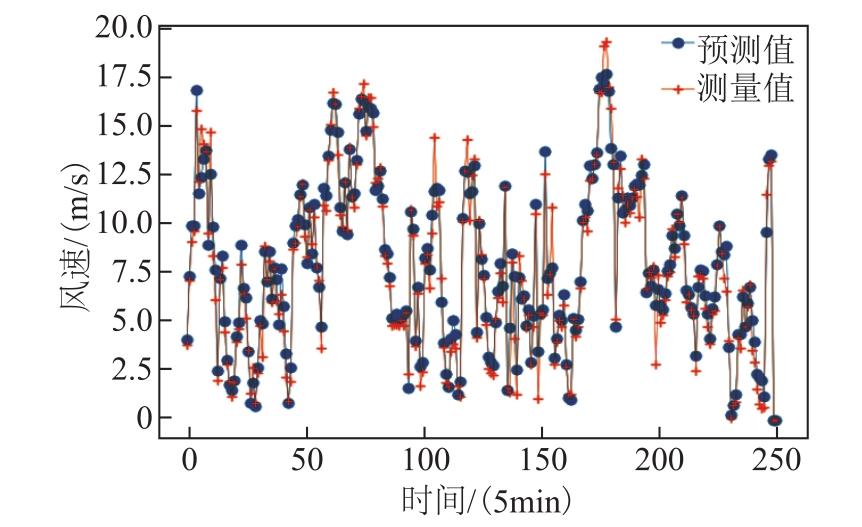
图16 编号80风机的风速预测结果(预测时域h=1,即预测未来5min的多风机风速)
Fig.16 Forecasted output of site ID 80 wind turbine(forecast horizon h = 1, that is to forecast the wind speed of multiple wind turbines in the next 5 minutes)细化风速预测误差的仿真结果见表1。
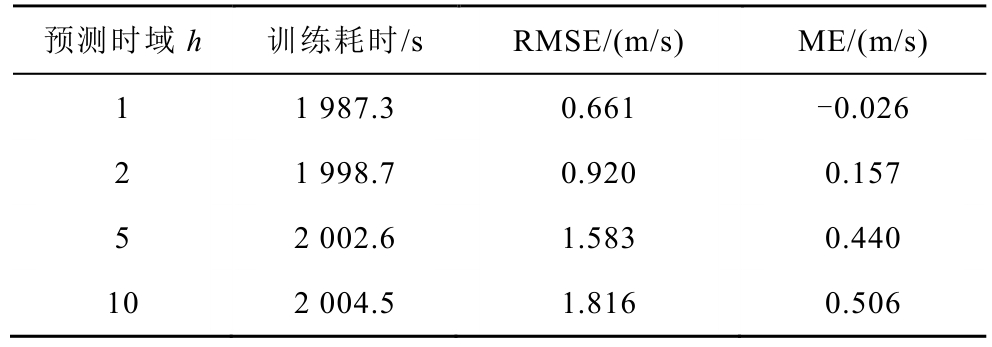
表1 预测性能与预测时域关系
Tab.1 Relationship between forecast performance and forecast horizon
images/BZ_26_1283_2357_1503_2422.png images/BZ_26_1503_2357_1728_2422.png images/BZ_26_1728_2357_2011_2422.pngimages/BZ_26_2033_2357_2234_2422.pngimages/BZ_26_1283_2424_1503_2489.pngimages/BZ_26_1503_2424_1728_2489.pngimages/BZ_26_1728_2424_2011_2489.pngimages/BZ_26_2033_2424_2234_2489.pngimages/BZ_26_1283_2489_1503_2554.pngimages/BZ_26_1503_2489_1728_2554.pngimages/BZ_26_1728_2489_2011_2554.pngimages/BZ_26_2033_2489_2234_2554.pngimages/BZ_26_1283_2554_1503_2619.pngimages/BZ_26_1503_2554_1728_2619.pngimages/BZ_26_1728_2554_2011_2619.pngimages/BZ_26_2033_2554_2234_2619.pngimages/BZ_26_1283_2619_1503_2684.pngimages/BZ_26_1503_2619_1728_2684.pngimages/BZ_26_1728_2619_2011_2684.pngimages/BZ_26_2033_2619_2234_2684.png
由表1可以看出,随着预测时域的增加,RMSE逐渐增大,预测效果逐渐变差。预测时域增加的同时,输入到CNN和SRU集成预测模型的特征将越来越偏离预测时刻的特征,所以取得的预测效果也相对比较差。但在预测时域h<10的情况下对风电场中所有风机进行精细化本地风速预测仍能取得相对比较好的预测效果。若在工程中需要取预测时域h>10时,即预测50min后的风速,可以考虑增大Epoch来提高预测的准确率。
5.3 对比分析
表2给出使用CNN和SRU集成预测模型,但使用不同的数据特征在多个预测时域的仿真结果。
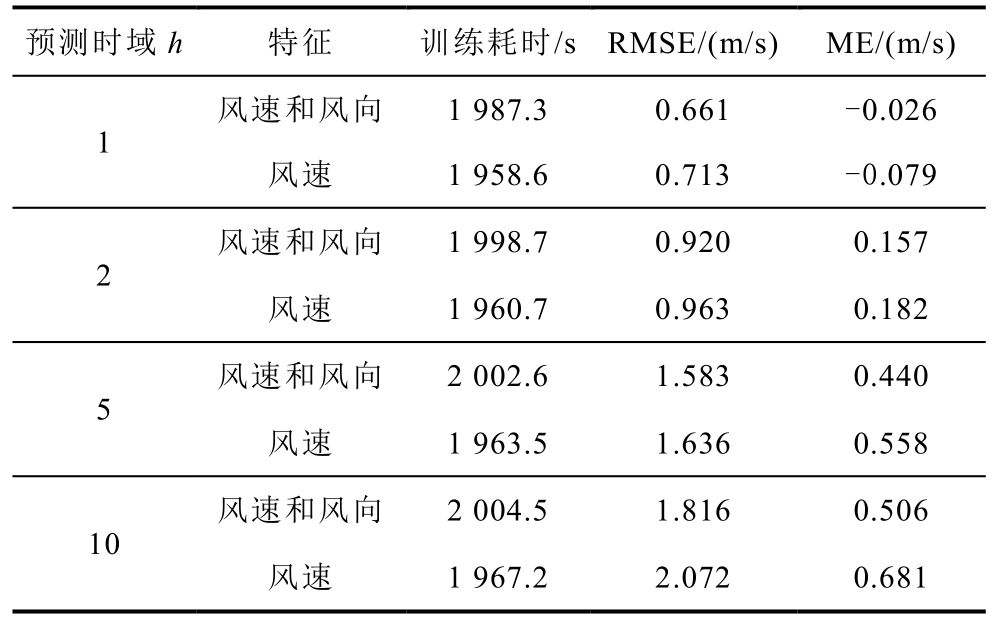
表2 风向特征对预测性能的提升表
Tab.2 Improvement table of wind direction characteristic for forecast performance
images/BZ_27_225_809_408_874.png images/BZ_27_408_809_618_874.pngimages/BZ_27_618_809_802_874.png images/BZ_27_802_809_1009_874.pngME/(m/s)images/BZ_27_225_876_408_1006.png-0.026images/BZ_27_408_876_618_941.pngimages/BZ_27_618_876_802_941.pngimages/BZ_27_802_876_1009_941.pngimages/BZ_27_408_941_618_1006.pngimages/BZ_27_618_941_802_1006.pngimages/BZ_27_802_941_1009_1006.png-0.079images/BZ_27_225_1008_408_1140.png0.157images/BZ_27_408_1008_618_1073.pngimages/BZ_27_618_1008_802_1073.pngimages/BZ_27_802_1008_1009_1073.pngimages/BZ_27_408_1075_618_1140.pngimages/BZ_27_618_1075_802_1140.pngimages/BZ_27_802_1075_1009_1140.png0.182images/BZ_27_225_1142_408_1274.png0.440images/BZ_27_408_1142_618_1207.pngimages/BZ_27_618_1142_802_1207.pngimages/BZ_27_802_1142_1009_1207.pngimages/BZ_27_408_1209_618_1274.pngimages/BZ_27_618_1209_802_1274.pngimages/BZ_27_802_1209_1009_1274.png0.558images/BZ_27_225_1276_408_1408.png0.506images/BZ_27_408_1276_618_1341.pngimages/BZ_27_618_1276_802_1341.pngimages/BZ_27_802_1276_1009_1341.pngimages/BZ_27_408_1343_618_1408.pngimages/BZ_27_618_1343_802_1408.pngimages/BZ_27_802_1343_1009_1408.png0.681
由表2可知,较仅使用风速作为特征,使用风速和风向作为特征来预测风速可取得更好的预测效果。因为在一个风电场中,众多风机分布在不同的地理位置下,不仅风速具有时空相关性,风向也同样具有时空相关性,而且多风机风速序列的空间相关性主要受风向影响。通过同时考虑风速和风向的时空相关性,可以获得更加丰富和有效的信息,更有利于进行风速预测。
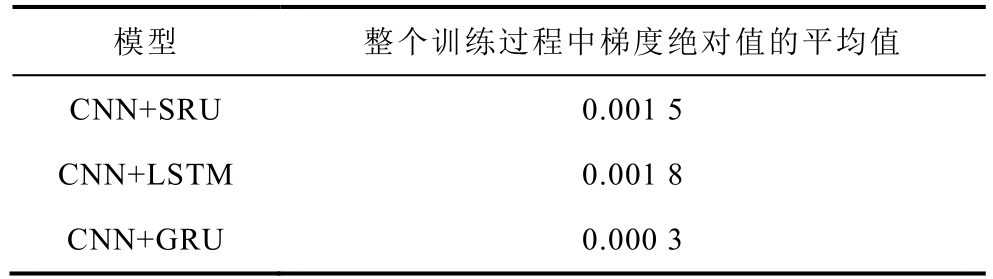
为了说明本文所提方法的优越性,给出了多个不同预测方法的对比仿真。由之前仿真的对比分析可知,使用风速和风向作为特征取得的预测效果更佳,所以在下文的对比分析中,均采用风速和风向为特征。对比的预测方法包括:CNN和SRU集成预测模型、CNN和LSTM集成预测模型、CNN和GRU集成预测模型、CNN及简单人工神经网络(Artificial Neural Network, ANN)。在预测时域为1时,图17~图21分别给出不同预测模型的训练误差、网络中某一参数及其梯度随训练次数的变化。表3给出了不同预测模型在训练过程中网络某一参数梯度绝对值的平均值。由图中可知,在训练过程中,较其他两种集成预测模型,CNN和SRU集成预测模型的RMSE下降最快。LSTM和GRU分别在训练的前期和后期存在一定的梯度消失问题,但SRU整个训练过程中一直存在较大的梯度。故在神经网络参数迭代过程中,SRU可以有效地缓解梯度消失问题,其参数收敛得更快,预测效果更好。为了说明在不同预测时域的预测结果,给出了h=1、h=2、h=5、h=10的预测时域,相关仿真数据见表4。
表3 不同预测模型梯度绝对值的平均值
Tab.3 Average value of the absolute gradient in different forecast models
images/BZ_27_225_2996_492_3061.pngimages/BZ_27_515_2996_1175_3061.pngimages/BZ_27_225_3063_492_3128.png images/BZ_27_515_3063_1175_3128.pngimages/BZ_27_225_3128_492_3193.png images/BZ_27_515_3128_1175_3193.pngimages/BZ_27_225_3193_492_3258.png images/BZ_27_515_3193_1175_3258.png
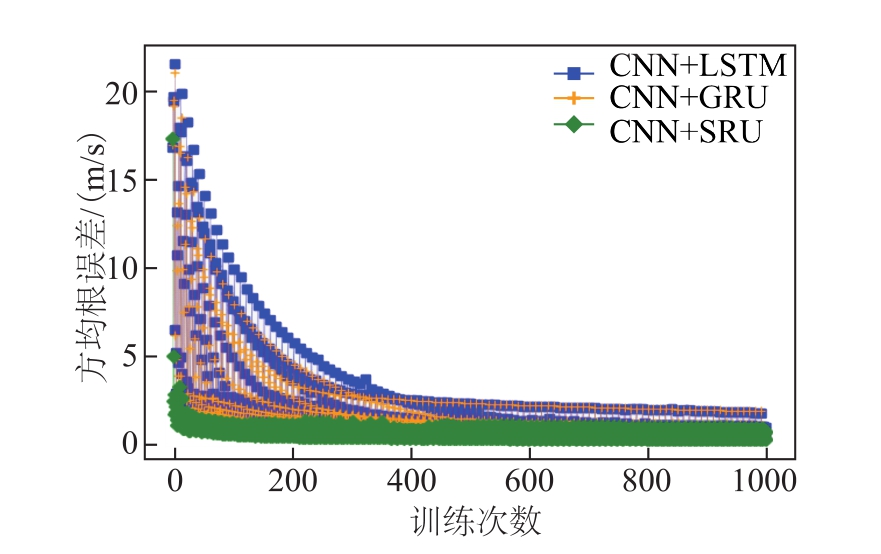
图17 预测误差随训练次数变化对比
Fig.17 Comparison graph of forecasted loss with the training times
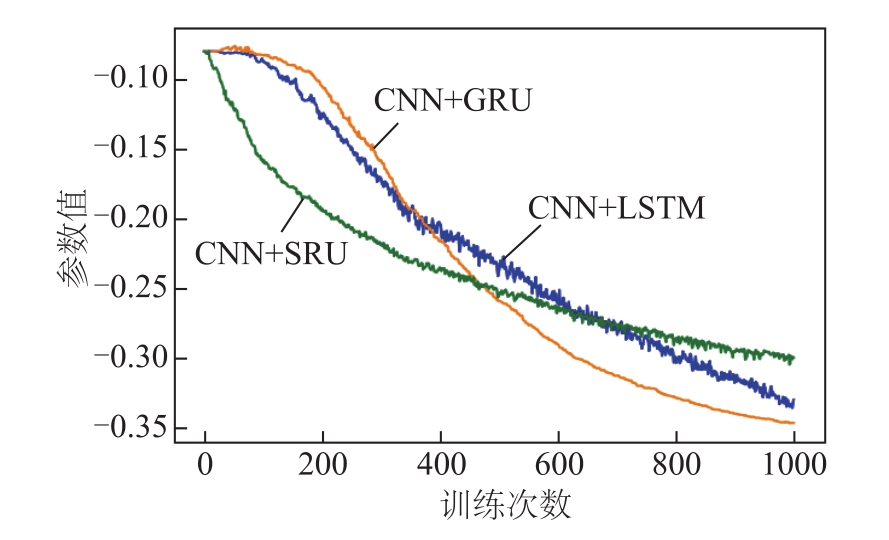
图18 网络中某一参数随训练次数变化对比
Fig.18 Comparison graph of a parameter in the network varies with the training times

图19 CNN和SRU集成预测模型中梯度变化
Fig.19 Gradient variation graph in the integrated forecast model of CNN and SRU

图20 CNN和LSTM集成预测模型中梯度变化
Fig.20 Gradient variation graph in the integrated forecast model of CNN and LSTM

图21 CNN和GRU集成预测模型中梯度变化
Fig.21 Gradient variation graph in the integrated forecast model of CNN and GRU
表4 不同预测模型仿真结果对比表
Tab.4 Comparison table of simulation results of different forecast models

images/BZ_28_227_1829_407_1896.png images/BZ_28_407_1829_629_1896.pngimages/BZ_28_629_1829_819_1896.png images/BZ_28_819_1829_1035_1896.png)images/BZ_28_1057_1829_1173_1895.pngimages/BZ_28_227_1898_407_2238.pngimages/BZ_28_407_1898_629_1968.png images/BZ_28_629_1898_819_1968.pngimages/BZ_28_841_1900_1012_1965.pngimages/BZ_28_1057_1900_1173_1965.pngimages/BZ_28_407_1967_629_2035.png images/BZ_28_629_1967_819_2035.pngimages/BZ_28_819_1967_1035_2035.pngimages/BZ_28_1057_1969_1173_2034.pngimages/BZ_28_407_2035_629_2103.png images/BZ_28_629_2035_819_2103.pngimages/BZ_28_819_2035_1035_2103.pngimages/BZ_28_1057_2036_1173_2102.pngimages/BZ_28_407_2103_629_2171.png images/BZ_28_629_2103_819_2171.pngimages/BZ_28_819_2103_1035_2171.pngimages/BZ_28_1057_2104_1173_2169.pngimages/BZ_28_407_2171_629_2238.png images/BZ_28_629_2171_819_2238.pngimages/BZ_28_819_2171_1035_2238.pngimages/BZ_28_1057_2172_1173_2237.pngimages/BZ_28_227_2241_407_2581.pngimages/BZ_28_407_2241_629_2311.png images/BZ_28_629_2241_819_2311.pngimages/BZ_28_819_2241_1035_2311.pngimages/BZ_28_1057_2243_1173_2308.pngimages/BZ_28_407_2311_629_2378.png images/BZ_28_629_2311_819_2378.pngimages/BZ_28_819_2311_1035_2378.pngimages/BZ_28_1057_2312_1173_2377.pngimages/BZ_28_407_2378_629_2446.png images/BZ_28_629_2378_819_2446.pngimages/BZ_28_819_2378_1035_2446.pngimages/BZ_28_1057_2380_1173_2445.pngimages/BZ_28_407_2446_629_2514.png images/BZ_28_629_2446_819_2514.pngimages/BZ_28_819_2446_1035_2514.pngimages/BZ_28_1057_2447_1173_2512.pngimages/BZ_28_407_2514_629_2581.png images/BZ_28_629_2514_819_2581.pngimages/BZ_28_819_2514_1035_2581.pngimages/BZ_28_1057_2515_1173_2580.pngimages/BZ_28_227_2583_407_2924.pngimages/BZ_28_407_2583_629_2653.png images/BZ_28_629_2583_819_2653.pngimages/BZ_28_819_2583_1035_2653.pngimages/BZ_28_1057_2586_1173_2651.pngimages/BZ_28_407_2653_629_2721.png images/BZ_28_629_2653_819_2721.pngimages/BZ_28_819_2653_1035_2721.pngimages/BZ_28_1057_2655_1173_2720.pngimages/BZ_28_407_2721_629_2789.png images/BZ_28_629_2721_819_2789.pngimages/BZ_28_819_2721_1035_2789.pngimages/BZ_28_1057_2723_1173_2788.pngimages/BZ_28_407_2789_629_2857.png images/BZ_28_629_2789_819_2857.pngimages/BZ_28_819_2789_1035_2857.pngimages/BZ_28_1057_2790_1173_2855.pngimages/BZ_28_407_2857_629_2924.png images/BZ_28_629_2857_819_2924.pngimages/BZ_28_819_2857_1035_2924.pngimages/BZ_28_1057_2858_1173_2923.pngimages/BZ_28_227_2926_407_3267.pngimages/BZ_28_407_2926_629_2996.png images/BZ_28_629_2926_819_2996.pngimages/BZ_28_819_2926_1035_2996.pngimages/BZ_28_1057_2929_1173_2994.pngimages/BZ_28_407_2996_629_3064.png images/BZ_28_629_2996_819_3064.pngimages/BZ_28_819_2996_1035_3064.pngimages/BZ_28_1057_2998_1173_3063.pngimages/BZ_28_407_3064_629_3132.png images/BZ_28_629_3064_819_3132.pngimages/BZ_28_819_3064_1035_3132.pngimages/BZ_28_1057_3065_1173_3130.pngimages/BZ_28_407_3132_629_3199.png images/BZ_28_629_3132_819_3199.pngimages/BZ_28_819_3132_1035_3199.pngimages/BZ_28_1057_3133_1173_3198.pngimages/BZ_28_407_3199_629_3267.png images/BZ_28_629_3199_819_3267.pngimages/BZ_28_819_3199_1035_3267.pngimages/BZ_28_1057_3201_1173_3266.png
由表4可以看出:相较于LSTM和GRU,由于SRU消除了输出状态ht与ht-1的依赖性,具有并行处理的能力,SRU各层的参数能得到较快的训练,极大地降低了计算代价,所以仿真时间耗时最短。CNN预测模型仅考虑多风机之间的空间相关性,并没有考虑到时间相关性,所以 CNN预测模型效果没有时空集成预测模型佳。由于 ANN不能处理多维数据,其输出只能是一维向量形式,当将CNN和SRU集成预测模型输入维度 12×12×3映射至 ANN输入维度1×432的同时,也相应地损失了数据的时空相关性。相反,CNN和 SRU集成预测模型正是着眼于如何高效地提取风机数据时空特征,故CNN和SRU集成预测模型更优。
5.4 鲁棒性分析
在实际的工程应用中,会存在由于测量精度等原因造成的输入信息存在少许微小偏差的情况,故对CNN和SRU集成预测模型进行鲁棒性分析是有必要的。
将整个风机数据集的风速和风向累加以μ=0、σ= 0.5正太分布的随机误差,用来模拟存在少许微小偏差的输入数据信息。CNN和SRU集成模型的参数训练及预测输出均使用含有正太分布随机误差的噪声值进行训练,而测试集的RMSE和ME计算使用预测值和测量值计算,而不采用含有随机误差的噪声值。在使用风速和风向作为特征,预测时域h为1的条件下,表5给出了在多个不同预测时域下,分布使用测量值和噪声值的风速预测仿真结果。图22给出了 1号风机的风速预测值、含有随机误差的噪声值和测量值曲线。由图22可以看出,在输入风速和风向信息存在少许微小偏差的情况下,预测精度确实会变差,但是仍具有一定的参考价值。由于该时空集成预测模型会综合考量风电场内所有风机数据的空间相关性和时间相关性,若单台风机数据含有较大的误差值,但周围风机组没有误差值,或是误差值较小,考虑到风机数据在时空方面不能突变的特性,该时空集成预测模型可以较好地抑制单台风机的大扰动,仍然可以取得较佳的风速预测效果。
表5 数据扰动对预测性能的影响
Tab.5 The effect of data noise on forecast performance

images/BZ_28_1283_2673_1464_2738.png images/BZ_28_1464_2673_1659_2738.pngimages/BZ_28_1659_2673_1863_2738.png images/BZ_28_1863_2673_2074_2738.pngME/(m/s)images/BZ_28_1283_2740_1464_2870.png-0.026images/BZ_28_1464_2740_1659_2805.pngimages/BZ_28_1659_2740_1863_2805.pngimages/BZ_28_1863_2740_2074_2805.pngimages/BZ_28_1464_2805_1659_2870.pngimages/BZ_28_1659_2805_1863_2870.pngimages/BZ_28_1863_2805_2074_2870.png-0.108images/BZ_28_1283_2872_1464_3004.png0.157images/BZ_28_1464_2872_1659_2937.pngimages/BZ_28_1659_2872_1863_2937.pngimages/BZ_28_1863_2872_2074_2937.pngimages/BZ_28_1464_2939_1659_3004.pngimages/BZ_28_1659_2939_1863_3004.pngimages/BZ_28_1863_2939_2074_3004.png0.114images/BZ_28_1283_3006_1464_3138.png0.440images/BZ_28_1464_3006_1659_3071.pngimages/BZ_28_1659_3006_1863_3071.pngimages/BZ_28_1863_3006_2074_3071.pngimages/BZ_28_1464_3073_1659_3138.pngimages/BZ_28_1659_3073_1863_3138.pngimages/BZ_28_1863_3073_2074_3138.png0.778images/BZ_28_1283_3141_1464_3273.png0.506images/BZ_28_1464_3141_1659_3206.pngimages/BZ_28_1659_3141_1863_3206.pngimages/BZ_28_1863_3141_2074_3206.pngimages/BZ_28_1464_3208_1659_3273.pngimages/BZ_28_1659_3208_1863_3273.pngimages/BZ_28_1863_3208_2074_3273.png0.764
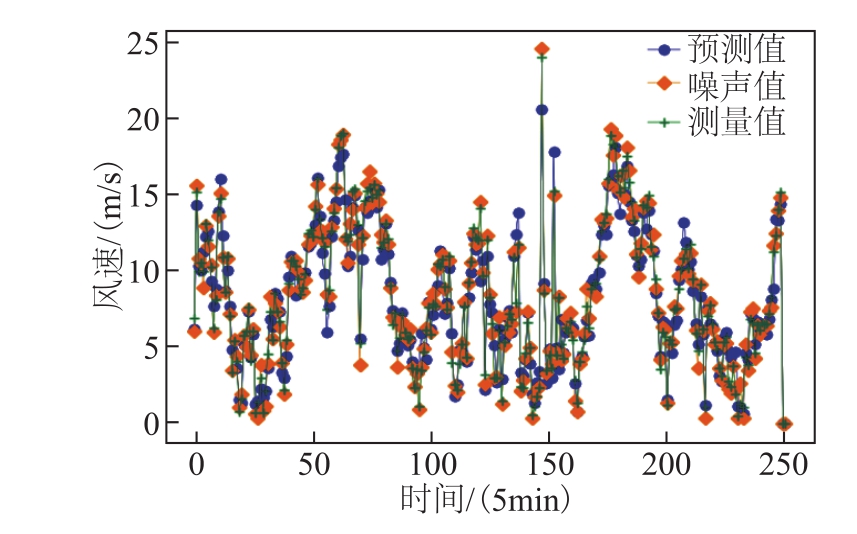
图22 1号风机基于含有随机误差噪声值的风速预测结果
Fig.22 Forecasted output of site ID 1 wind turbine based on noise values containing random error
6 结论
针对在同一风电场中不同地理位置分布的多风机风速预测问题,本文提出了一种基于CNN和SRU集成预测模型的预测方法。该方法通过 CNN提取多风机风速间空间特征和风向间空间特征,SRU提取多风机二维风速序列时间特征和二维风向序列时间特征,充分有效地利用风速和风向的内在关联性,进而提高了预测精度。本方法通过实际的风电场数据仿真分析,证明了该方法的有效性。通过仿真对比分析,可以得出以下结论:
1)与LSTM和GRU相比,SRU具有并行计算的能力,进而显著地减小了计算成本。在整个训练过程中,SRU一直保持着较大的梯度,可以有效地解决随着网络层次的增加带来的梯度消失问题。因此 SRU非常适用于处理具有十分丰富数据的深层深度学习问题。多个风速预测问题同样属于具有丰富数据的深层深度学习问题,故SRU非常适合应用于多风机风速预测。
2)CNN和SRU集成预测模型的输入仅是历史风特征(包括风速和风向),较只能针对特定环境和需要众多参数的物理建模预测模型,具有较好的适应性和鲁棒性。
3)通过学习风速和风向的时空相关性,首先提取空间特征,然后将蕴含空间特征的数据输入到多个SRU中提取时间特征,CNN和SRU的集成预测模型可以提取到十分丰富和有效的预测信息。相较于传统的深度学习方法,它最大限度地学习到类似于RGB图像结构输入数据的高维特征。
本文采用的集成预测模型在风电场内多风机风速预测方面取得较好效果。但输入预测模型中的历史特征序列长度等超参数如何进行科学优化、如何有效地对异常风机数据进行辨识等有待下一步的探索。
[1]World Wind Energy Association.Wind power capacity worldwide reaches 597 GW, 50.1 GW added in 2018 [EB/OL].[2019-07-04].http://wwindea.org/blog/2019/02/25/wind-power-capacity-worldwidereaches-600-gw-539-gw-added-in-2018.
[2]林旻威, 温步瀛.大规模风电接入对电力系统暂态稳定性影响研究综述[J].电气技术, 2017, 20(4): 1-8, 38.Lin Menwei, Wen Buying.The overview of influence of large scale wind generation on transient stability of power system[J].Electrical Engineering, 2017, 20(4):1-8, 38.
[3]唐程辉, 张凡, 张宁, 等.基于风电场总功率条件分布的电力系统经济调度二次规划方法[J].电工技术学报, 2019, 34(10): 2069-2078.Tang Chenghui, Zhang Fan, Zhang Ning, et al.Quadratic programming for power system economic dispatch based on the conditional probability distribution of wind farms sum power[J].Transactions of China Electrotechnical Society, 2019, 34(10):2069-2078.
[4]穆钢, 蔡婷婷, 严干贵, 等.双馈风电机组参与持续调频的双向功率约束及其影响[J].电工技术学报, 2019, 34(8): 1750-1759.Mu Gang, Cai Tingting, Yan Gangui, et al.Bidirectional power constraints and influence of doubly fed induction generator participating in continuous frequency regulation[J].Transactions of China Electrotechnical Society, 2019, 34(8): 1750-175.
[5]关中杰, 鲁效平, 李钢强, 等.基于风速模型的风电机组动态转矩前馈控制技术[J].电工技术学报,2018, 33(22): 5338-5345.Guan Zhongjie, Lu Xiaoping, Li Gangqiang, et al.Dynamic torque feed forward control technology of wind turbine based on wind speed model[J].Transactions of China Electrotechnical Society, 2018,33(22): 5338-5345.
[6]李军, 杜雪.稀疏高斯过程在短期风电功率概率预测中的应用[J].电机与控制学报, 2019, 23(8): 67-77.Li Jun, Du Xue.Application of sparse gaussian process in short-term wind power probability prediction[J].Electric Machines and Control, 2019,23(8): 67-77.
[7]Kou Peng, Liang Deliang, Yu Linbo, et al.Nonlinear model predictive control of wind farm for system frequency support[J].IEEE Transactions on Power Systems, 2019, 34(5): 3547-3561.
[8]沈小军, 付雪姣, 周冲成, 等.风电机组风速-功率异常运行数据特征及清洗方法[J].电工技术学报,2018, 33(14): 3353-3361.Shen Xiaojun, Fu Xuejiao, Zhou Chongcheng, et al.Characteristics of outliers in wind speed-power operation data of wind turbines and its cleaning method[J].Transactions of China Electrotechnical Society, 2018, 33(14): 3353-3361.
[9]杨正瓴, 刘阳, 张泽, 等.采用最近历史观测值和PLSR进行空间相关性超短期风速预测[J].电网技术, 2017, 41(6): 1816-1823.Yang Zhengling, Liu Yang, Zhang Ze, et al.Ultrashort-term wind speed prediction with spatial correlation using recent historical observations and PLSR[J].Power System Technology, 2017, 41(6):1816-1823.
[10]殷豪, 董朕, 陈云龙.基于 CEEMD 和膜计算优化支持向量机的风速预测[J].电力系统保护与控制,2017, 45(21): 27-34.Yin Hao, Dong Zhen, Chen Yunlong.Wind speed forecasting based on complementary ensemble empirical mode decomposition and support vector regression optimized by membrane computing optimization[J].Power System Protection and Control,2017, 45(21): 27-34.
[11]叶瑞丽, 郭志忠, 刘瑞叶, 等.基于小波包分解和改进 Elman神经网络的风电场风速和风电功率预测[J].电工技术学报, 2017, 32(21): 103-111.Ye Ruili, Guo Zhizhong, Liu Ruiye, et al.Wind speed and wind power forecasting method based on wavelet packet decomposition and improved Elman neural network[J].Transactions of China Electrotechnical Society, 2017, 32(21): 103-111.
[12]林洁, 吴布托, 陈伟.基于深层玻尔兹曼机的风电场异常风速值自适应检测预处理方法[J].电工技术学报, 2018, 33(增刊1): 205-212.Lin Jie, Wu Butuo, Chen Wei.Adaptive detection and preprocessing method for abnormal wind speed of wind farm based on deep Boltzmann machine[J].Transactions of China Electrotechnical Society, 2018,33(S1): 205-212.
[13]Wang Huaizhi, Li Gangqiang, Wang Guibing, et al.Deep learning based ensemble approach for probabilistic wind power forecasting[J].Applied Energy, 2017, 188(188): 56-70.
[14]鲁迪, 王星华, 贺小平.基于混合粒子群算法和多分位鲁棒极限学习机的短期风速预测方法[J].电力系统保护与控制, 2019, 47(5): 115-122.Lu Di, Wang Xinghua, He Xiaoping.Hybrid population particle algorithm and multi-quantile robust extreme learning machine based short-term wind speed forecasting[J].Power System Protection and Control, 2019, 47(5): 115-122.
[15]朱霄珣, 徐搏超, 焦宏超, 等.遗传算法对 SVR风速预测模型的多参数优化[J].电机与控制学报,2017, 21(2): 70-75.Zhu Xiaoxun, Xu Bochao, Jiao Hongchao, et al.Wind speed prediction method based on SVR and multiparameter optimization of GA[J].Electric Machines and Control, 2017, 21(2): 70-75.
[16]杨正瓴, 吴炳卫, 赵强, 等.我国冬季风路径上风速与其影响因子的优化延迟相关性分析[J].电力系统保护与控制, 2018, 46(19): 57-64.Yang Zhengling, Wu Bingwei, Zhao Qiang, et al.Analysis of the optimal lag time of wind speeds and their influence factors on the main path of China winter monsoon[J].Power System Protection and Control, 2018, 46(19): 57-64.
[17]Wang Huaizhi, Wang Guibing, Li Gangqiang, et al.Deep belief network based deterministic and probabilistic wind speed forecasting approach[J].Applied Energy, 2016, 182(8): 80-93.
[18]Khodayar M, Kaynak O, Khodayar M E.Rough deep neural architecture for short-term wind speed forecasting[J].IEEE Transactions on Industrial Informatics, 2017, 13(6): 2770-2779.
[19]杨茂, 周宜.计及风电场状态的风电功率超短期预测[J].中国电机工程学报, 2019, 39(5): 1259-1268.Yang Mao, Zhou Yi.Ultra-short-term prediction of wind power considering wind farm status[J].Proceedings of the CSEE, 2019, 39(5): 1259-1268.
[20]薛禹胜, 陈宁, 王树民, 等.关于利用空间相关性预测风速的评述[J].电力系统自动化, 2017, 41(10):161-169.Xue Yusheng, Chen Ning, Wang Shumin, et al.Review on wind speed prediction based on spatial correlation[J].Automation of Electric Power Systems,2017, 41(10): 161-169.
[21]陈宁, 薛禹胜, 丁杰, 等.利用空间相关性的超短期风速预测[J].电力系统自动化, 2017, 41(12): 124-130.Chen Ning, Xue Yusheng, Ding Jie, et al.Ultra-short term wind speed prediction using spatial correlation[J].Automation of Electric Power System, 2017, 41(12):124-130.
[22]Chen Niya, Qian Zheng, Nabney I T, et al.Wind power forecasts using gaussian processes and numerical weather prediction[J].IEEE Transactions on Power Systems, 2014, 29(2): 656-665.
[23]Wu Wenzu, Chen Kunjin, Qiao Ying, et al.Probabilistic short-term wind power forecasting based on deep neural networks[C]//2016 International Conference on Probabilistic Methods Applied to Power Systems, Beijing, China, 2016: 1-8.
[24]张文, 冯洋, 刘群.基于简单循环单元的深层神经网络机器翻译模型[J].中文信息学报, 2018, 32(10):36-44.Zhang Wen, Feng Yang, Liu Qun.Deep neural machine translation model based on simple recurrent units[J].Journal of Chinese Information Processing,2018, 32(10): 36-44.
[25]Tao Lei, Zhang Yu.Training RNNs as fast as CNNs[J].arXiv preprint, 2017.
[26]Lecun Y, Bottou L, Bengio Y, et al.Gradient-based learning applied to document recognition[J].Proceedings of the IEEE, 1998, 86(11): 2278-2324.
[27]Liu Tongtong, Wang Rubing, Chen Jikang, et al.Finegrained classification of product images based on convolutional neural networks[J].Advances in Molecular Imaging, 2018, 8: 69-87.
[28]He Kaiming, Zhang Xiangyu, Ren Shaoqing, et al.Spatial pyramid pooling in deep convolutional networks for visual recognition[J].IEEE Transactions on Pattern Analysis & Machine Intelligence, 2014,37(9): 1904-1916.
[29]Saratha S, Tajuddin W A W A.Logic learning in hopfield networks[J].Modern Applied Science, 2008,2(3): 57-63.
[30]Jin Hui, Yang Libin, Gan Jiatian, et al.Risk assessment of grid frequency deviation related to correlation considering wind speed and wind direction in a wind farm[C]//2018 2nd IEEE Conference on Energy Internet and Energy System Integration,Beijing, China, 2018: 1-5.