图1 局部放电特高频无线传感器结构
Fig.1 Prototype of UHF wireless sensor
摘要 局部放电（PD）是变电站电力设备绝缘劣化的主要表征之一。对局部放电的监测与定位是设备绝缘故障预警的重要手段。目前变电站设备局部放电定位主要是基于特高频（UHF）电磁波到达时间差法开展的。此方法需要极高采样率和时间同步精度，装置成本较高。因此，该文提出基于接收信号强度功率（RSSI）和最大似然（ML）估计的特高频局部放电测向（DOA）方法。首先，离线测试得到各特高频无线传感器的接收信号模型；然后，利用传感器阵列接收到的幅值和最大似然估计方法得到初步测向结果；最后，利用插值拟合、聚类分析等方法提高测向精度以得到最终的局部放电源方位角。实验测试结果表明，该方法的平均测向误差小于7°，且成本更低、现场使用更加便捷。
关键词：变电站 局部放电 接收信号强度 最大似然估计 到达角度
局部放电（Partial Discharge, PD）是造成电力设备电介质老化、绝缘性能下降的重要原因之 一[1-2]，因此对电力设备局部放电的检测和定位是电力设备状态检修和维护的重要组成部分[3-4]。现阶段对于局部放电的检测和定位，主要是运用特高频（Ultra-High Frequency, UHF）检测技术及特高频电磁波到达时间差法[5-7]。但是特高频到达时间差法要求检测装置具有非常高的采样率和时间同步精度，成本居高不下[8-10]。近年来，国内外学者提出了基于接收信号强度（Received Signal Strength Indicator, RSSI）的局部放电定位技术[11-12]。该方法具有成本低、环境适应好等优点[13-14]，但是已有研究需要预先建立RSSI指纹库[15-16]，才能对局部放电进行在线定位，现场实施工作量大，难以推广应用。
本文保留特高频检测和接收信号强度方法的优点，并针对以上问题，采用概率统计中最大似然估计方法[17-19]，提出了一种基于接收信号强度功率和最大似然估计的局部放电测向方法。其基本原理是通过特高频无线传感器阵列获取局部放电电磁波信号的功率强度数据，再根据特高频无线传感器自身的接收信号模型，结合最大似然估计方法来确定放电方向。最大似然估计是基于统计学中的概率模型，通过观察样本数值并利用系统的概率分布函数，来推断符合当前状态的最大概率的情况，从而得到测向结果。
本文首先介绍了特高频无线传感器阵列及测向流程；其次对最大似然估计的定向方法原理进行了理论推导；然后解释了测向结果的修正方法和误差分析；最后通过实验验证了该方法的有效性。测试结果表明，该方法的平均测向误差小于7°，且成本更低、现场使用更加便捷。
不同于传统变电站局部放电特高频定位方法，本文提出的基于特高频无线传感器阵列的测向方法只需同步采集特高频局部放电信号检波后的功率，无需对特高频信号时域波形进行高速采样。传感器结构如图1所示，其中传感器上层空间放置信号处理电路，下层空间放置印制电路板（Printed Circuit Board, PCB）特高频天线。传感器下层空间的天线外部用可透电磁波材料封装，其余所有结构均为金属以屏蔽电磁信号。具体地，本文将4个特高频无线传感器两两相背放置在一个平台上，将可透电磁波的一侧朝外，4个传感器的朝向分别间隔90°，形成如图2所示的传感器阵列。
图1 局部放电特高频无线传感器结构
Fig.1 Prototype of UHF wireless sensor
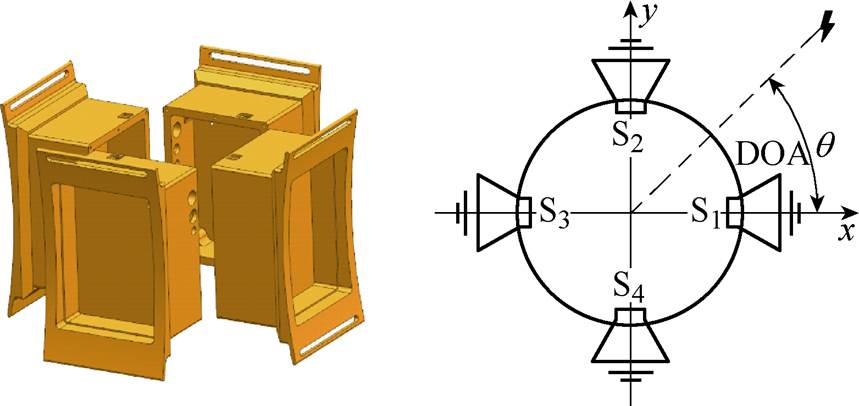
图2 传感器阵列示意图
Fig.2 Diagram of antenna array
在局部放电测向之前，需对特高频无线传感器阵列建立接收信号模型。以特高频传感器阵列为圆心，在传感器阵列外围一圈平均划分18等份，选取18个测试点，入射方位角q 设为10°～350°，每个点方位角相差20°。利用标准放电源在每个点上进行多次放电，对每个传感器在同一个点上接收到的多个接收信号强度功率数值取平均值，得到传感器阵列接收功率信号数组Y 为
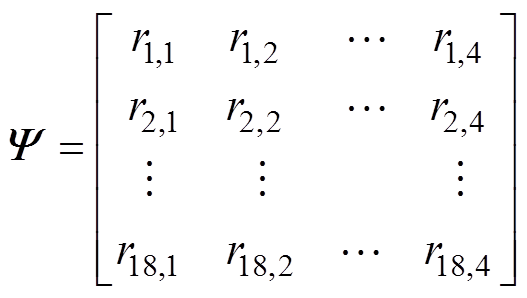（1）数组Y 中的每行表示每个点处4个传感器的数值，每列表示一共在18个点进行放电。对数组Y 进行归一化处理，有
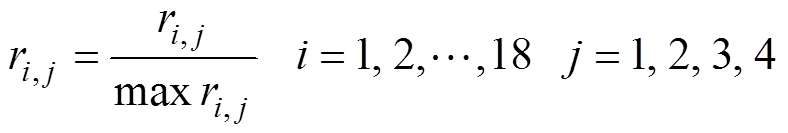（2）
最后得到该传感器阵列的天线接收信号模型，具体如图3所示。
整个局部放电定向过程如图4所示，测试现场对局部放电进行定向时，根据采集到的局部放电接收信号强度数值，利用最大似然估计和预先建立好的特高频天线接收信号模型来获得测向结果。
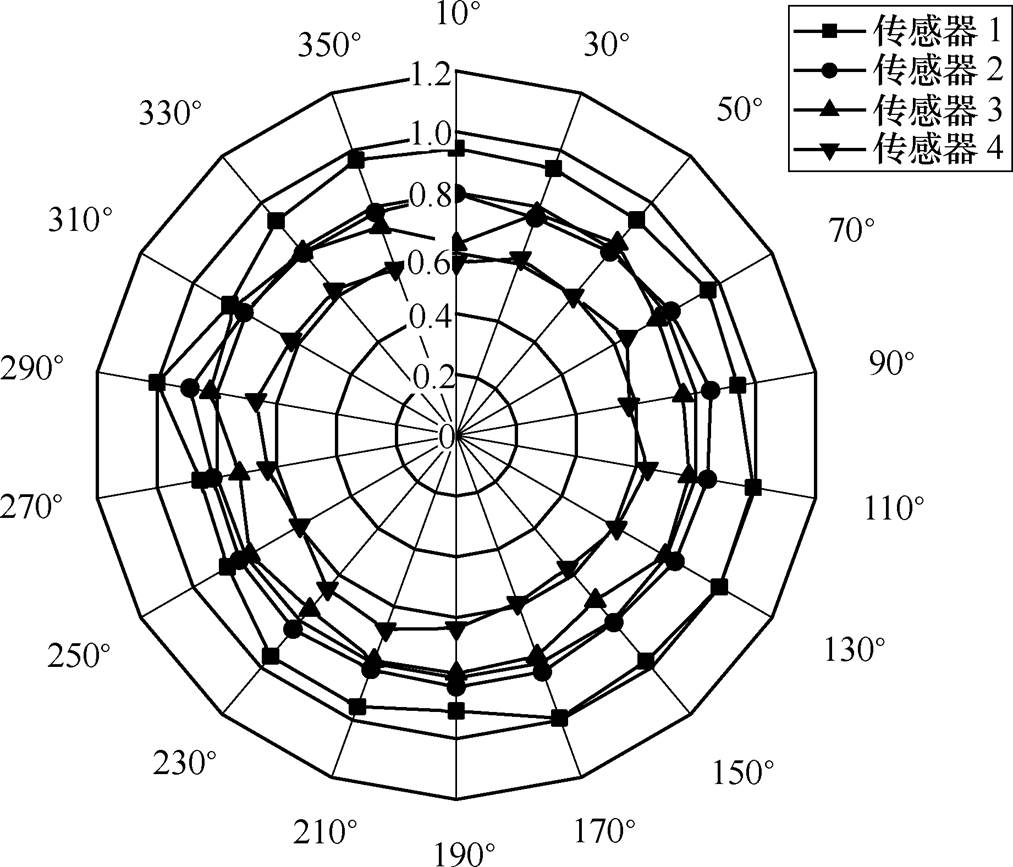
图3 无线传感器阵列的天线接收信号模型
Fig.3 UHF antenna power pattern in experiment
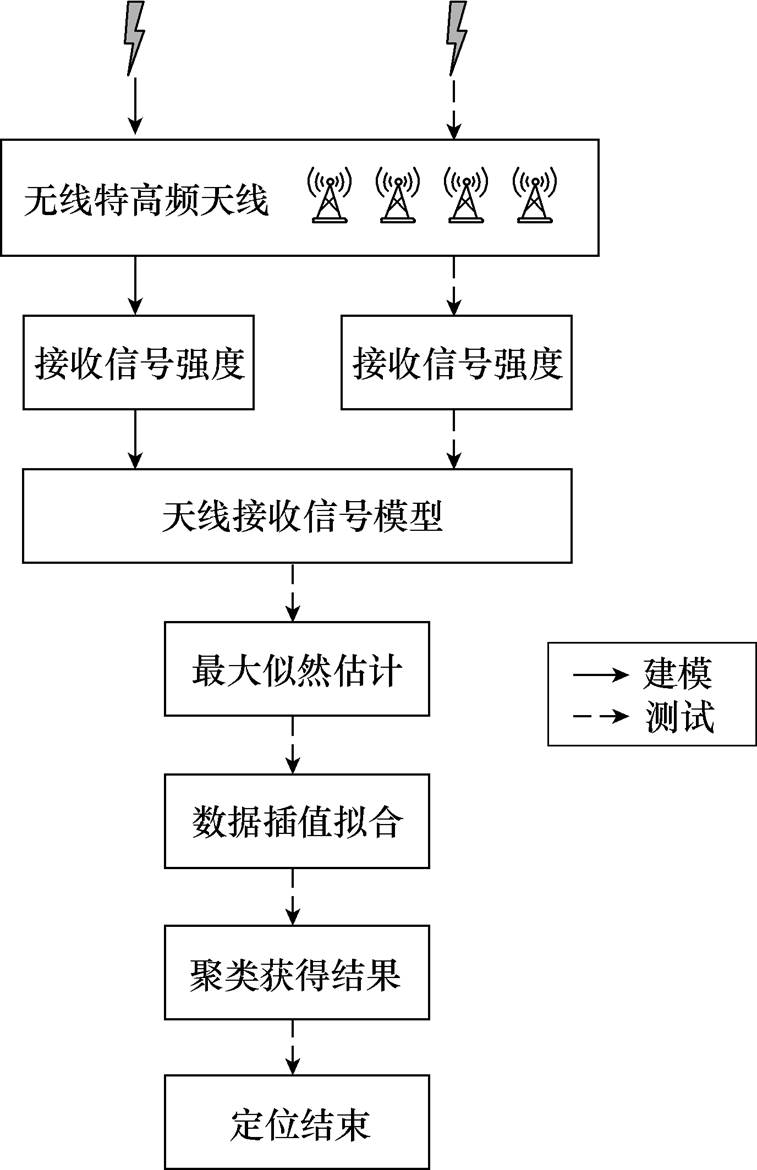
图4 局部放电测向流程
Fig.4 Flow chart of partial discharge direction of arrival estimation
局部放电测向中需计算每个传感器接收信号强度的功率的平均值。由于每个传感器每次接收的特高频信号强度功率数值相互独立，因此可认为接收信号强度的功率平均值服从卡方分布。本文将利用卡方分布的数学特性和最大似然估计法对接收信号强度功率进行分析，从而获得局部放电方向。
在测向过程中，假设第m个传感器对第k次局部放电的接收信号强度rm(k)可表示为
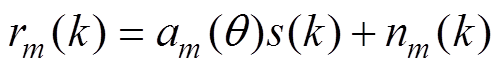（3）式中，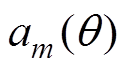
为天线增益；s(k)为局部放电信号传输到天线的信号强度；nm(k)为周围环境的高斯白噪声，并且服从均值为0，方差为
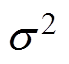的正态分布，记为nm(k)～N(0, 
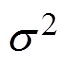)。假设噪声的功率谱密度在一定的频率范围内检测时近似为常数。经过一段放电时间，共采集了K次放电信号，一共有M个传感器，其中第m个传感器接收信号强度的功率平均值为Pr,m为
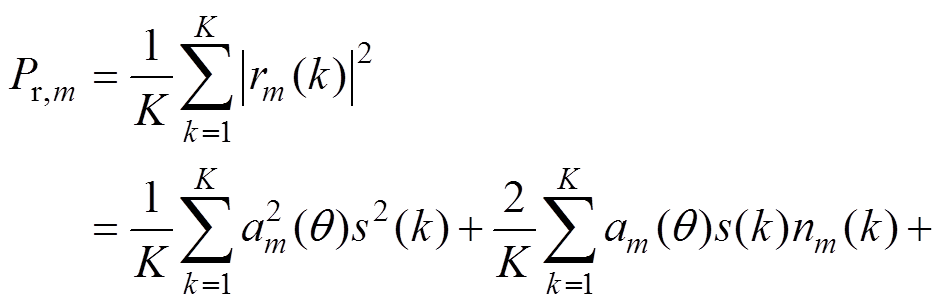
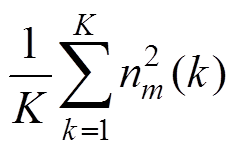（4）由于nm(k)均值为0，式（4）结果中第二项求和为0，并且到达天线的局部放电信号强度功率平均数值可表示为
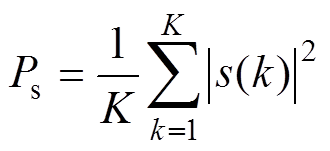（5）天线接收信号系数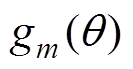
为
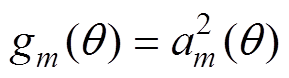（6）天线接收信号系数g(q)=[g1(q) g2(q) … gM (q)]需归一化，使得max g(q)=1。这样即可定义信噪比（Signal Noise Ratio, SNR）为
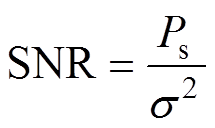（7）
将式（5）和式（6）代入式（4）得接收信号功率的平均值为
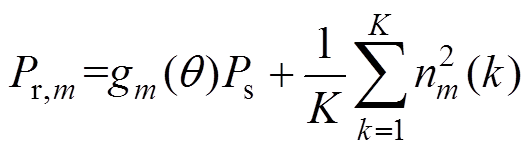（8）信号功率总和Sr,m定义为
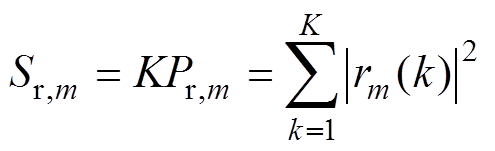（9）
Sr,m为服从自由度为K的非中心卡方分布，记为Sr,m～c2(K, lm, s2)，其中非中心参数lm可表达为
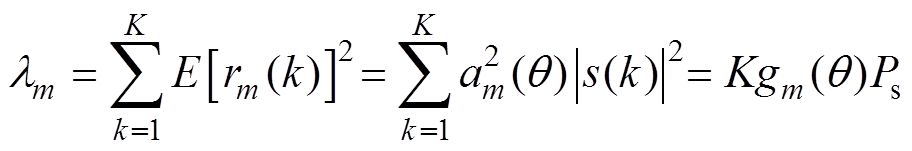（10）Sr,m的概率密度函数（Probability Density Function, PDF）为
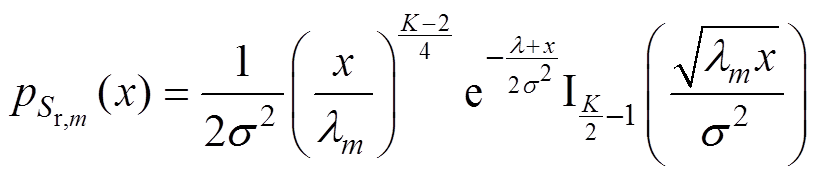（11）
式中，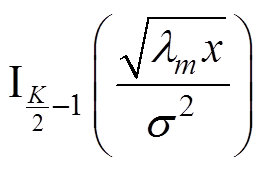
为第一类阶修正贝塞尔函数（modified Bessel function of the first kind）。
Pr,m的均值mm和方差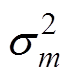
可通过信号功率总和Sr,m求得，有
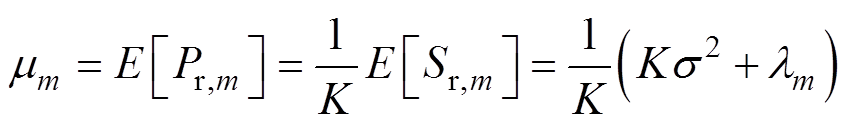
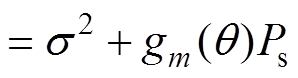（12）
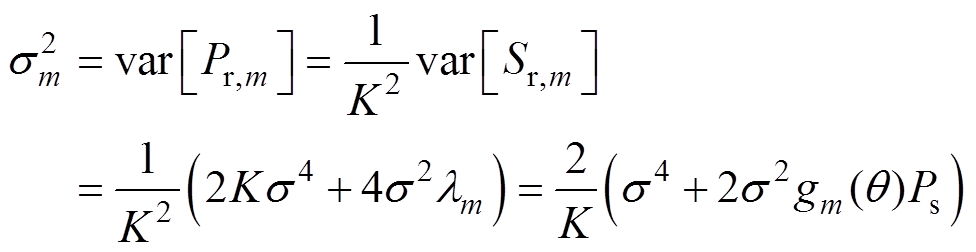（13）
当K或者lm很大时，Pr,m近似于正态分布Pr,m～N(mm, 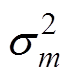)，其概率密度函数为
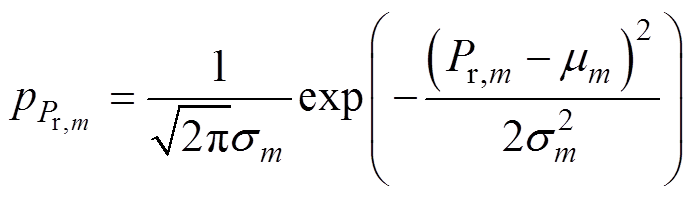（14）所有传感器接收信号功率记为Pr=[Pr,1Pr,2 … Pr,M]，概率估计参数为
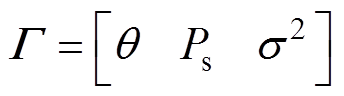（15）
可得似然函数为
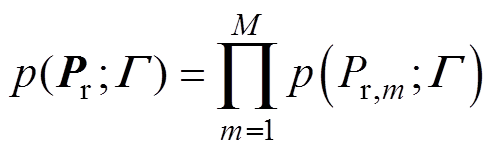（16）对式（16）两边取对数，可得
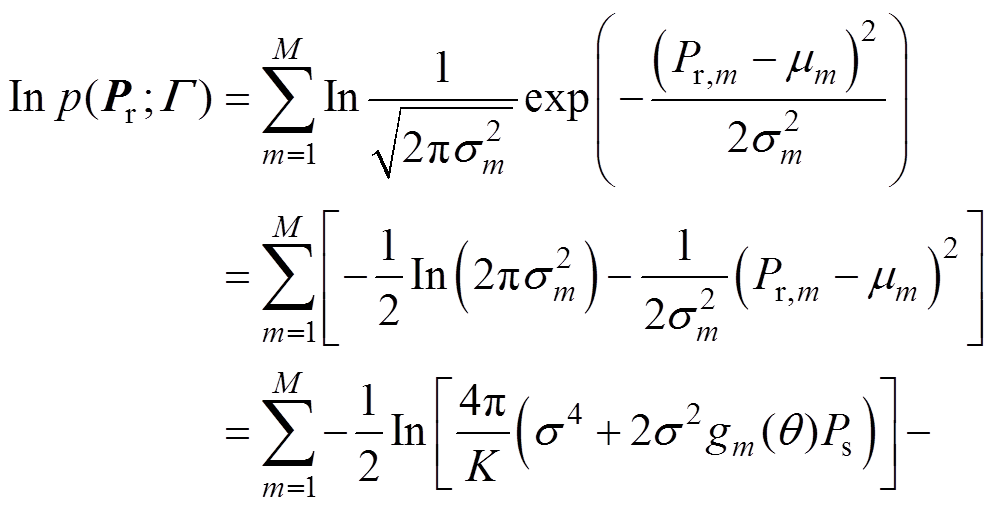
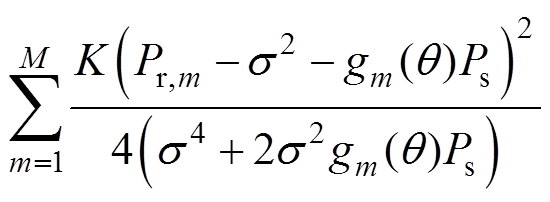（17）对式（17）结果中的两项提取公因子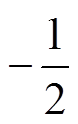
，之后进行最大似然估计（Maximum Likelihood Estimator, MLE）处理，可以表示为
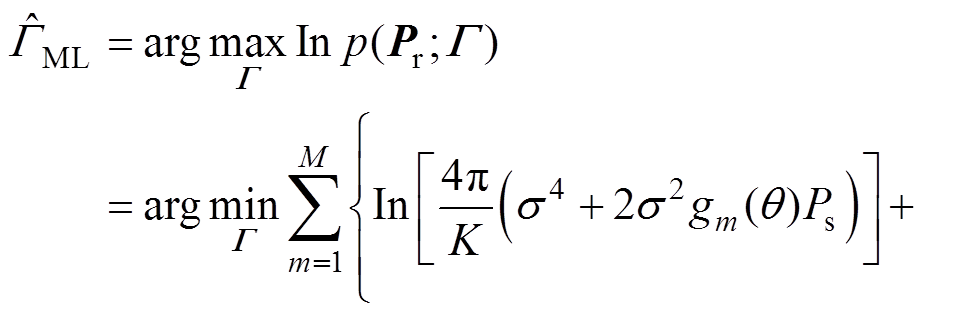
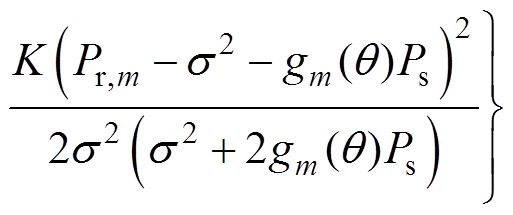（18）通过最大似然估计可求取使得式（18）最小时的角度，即为局部放电的测向结果。
从第2节的推导可看出，局部放电的定向精度取决于天线接收信号模型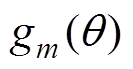的分辨率。因此，为获得更高精度的定向结果，需要对初步测向结果进行3次样条插值[20]。
根据式（18）计算每个角度上的似然函数值后，将天线衰减模型中18个角度值作为横坐标，对应的似然函数值作为纵坐标，在0°～360°区间上进行3次样条插值，有
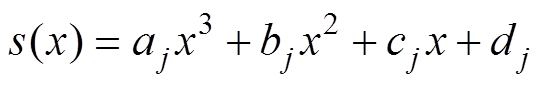（19）式中，aj、bj、cj、dj为待定系数，j为横坐标划分的第j个区间。在两个相邻的点之间利用三次函数平滑连接，寻找整段曲线上的最低点，将最低点的角度值作为每次放电的测向的结果。
进一步地，在同一位置进行多次放电实验，对于多次实验获取的结果，利用K-means聚类方法[21-24]对所有角度qj数据以最小化欧几里得距离为目标，将角度划分为h个聚类，取最大聚类的中心值作为最终测向结果，有
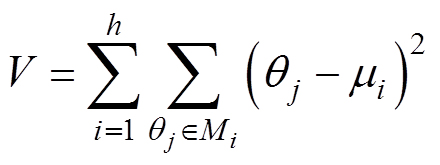（20）式中，mi为初始h个聚类的中心值；V为所有角度离各自中心值距离的和。
根据统计信号处理理论可知，无偏估计的方差存在理论下限，且其下界值可作为评价定位算法性能的重要指标之一。常用的克拉美罗下界（Cramer- Rao Lower Bound, CRLB）[25]表达为
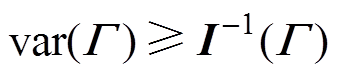（21）式中，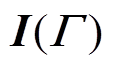
为费雪信息矩阵（Fisher Information Matrix, FIM）。对于
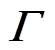中的q 的方差估计为
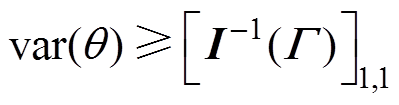（22）
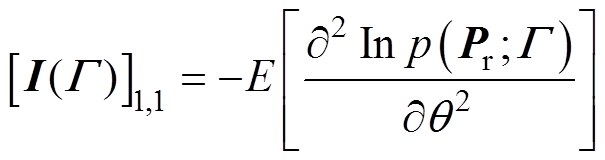（23）将式（16）代入式（23）进行计算，可得
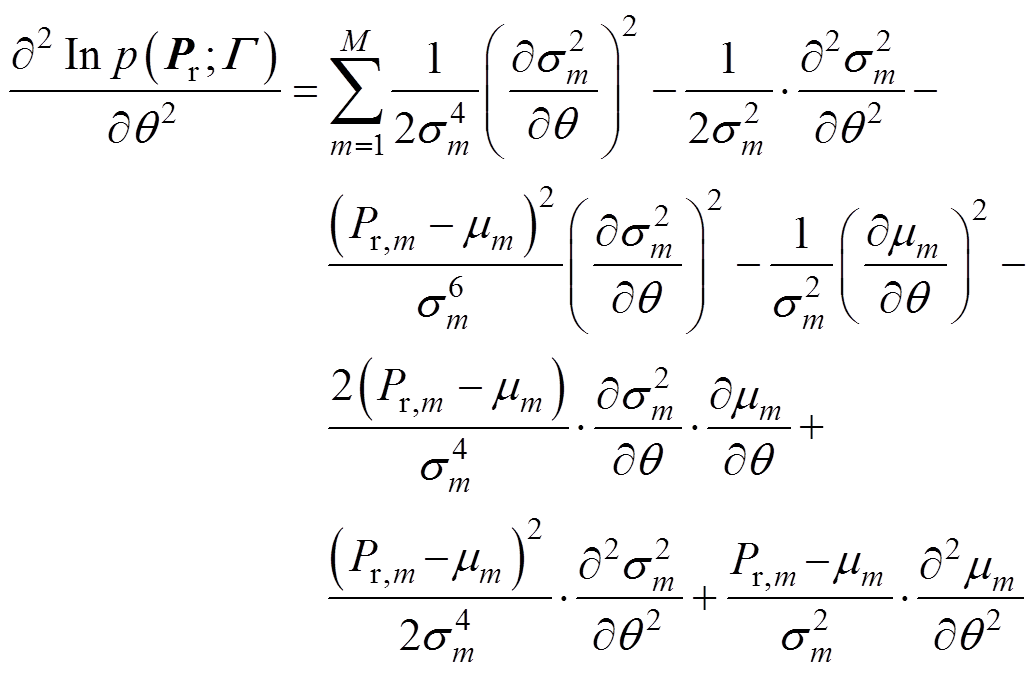（24）
将式（24）代入式（23），并化简可得
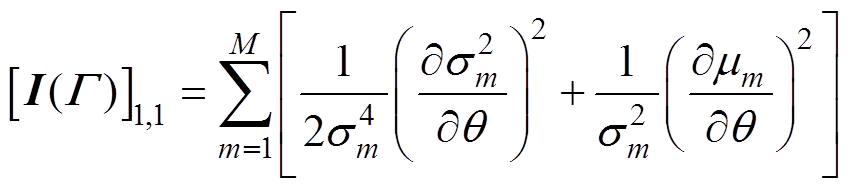（25）根据式（12）和式（13），mm和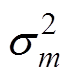均为gm(q )的函数关系式，而本文中的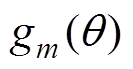为离散数据类型，本文将求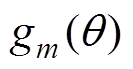对q 的导数转为求取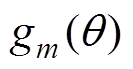在q 附近的变化率，并将结果代入式（25）可得
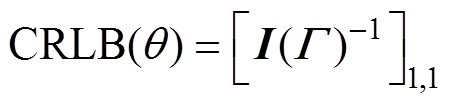（26）
为验证本文提出算法的正确性，在高压实验室进行了实验研究。其中特高频局部放电测向系统如图5所示，包括一个放电源、4个特高频无线传感器组成的无线传感器阵列、一个无线信号接收模块和接收终端（计算机）。
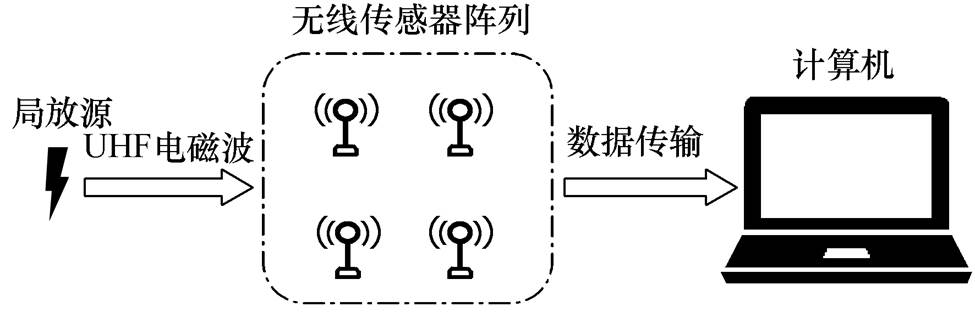
图5 特高频局部放电测向系统实验示意图
Fig.5 Diagram of UHF PD detection and orientation system
实验中将特高频无线传感器阵列放置在待测场地中，模拟局部放电源距离特高频无线传感器阵列6m，现场测试如图6所示。放电脉冲产生时，激发的电磁波信号将向四周辐射。当信号辐射至特高频无线传感器阵列时，4个传感器采集的电磁波接收信号强度功率数据，通过无线方式传输至后台，再利用本文提出的局部放电测向算法得到放电信号的方位角数值。
图6 现场实验
Fig.6 Field experiment diagram
选取局部放电信号的入射方位角q 分别为40°、80°、150°和340°进行测试。在每个方位角分别放电120次，并采集相应的局部放电功率信号。由于特高频无线传感器的放大、检波等电路特性，有些放电信号无法准确捕捉到。因此，每组120次的放电测试中，真正的有效放电脉冲不尽相同。对采集到放电数据通过最大似然估计及3次样条插值，分别获取对应曲线上最低点的横坐标作为测向结果。其中放电入射角为80°和340°时的局部放电测向结果如图7（有效放电脉冲数为108）和图8（有效放电脉冲数为117）所示。
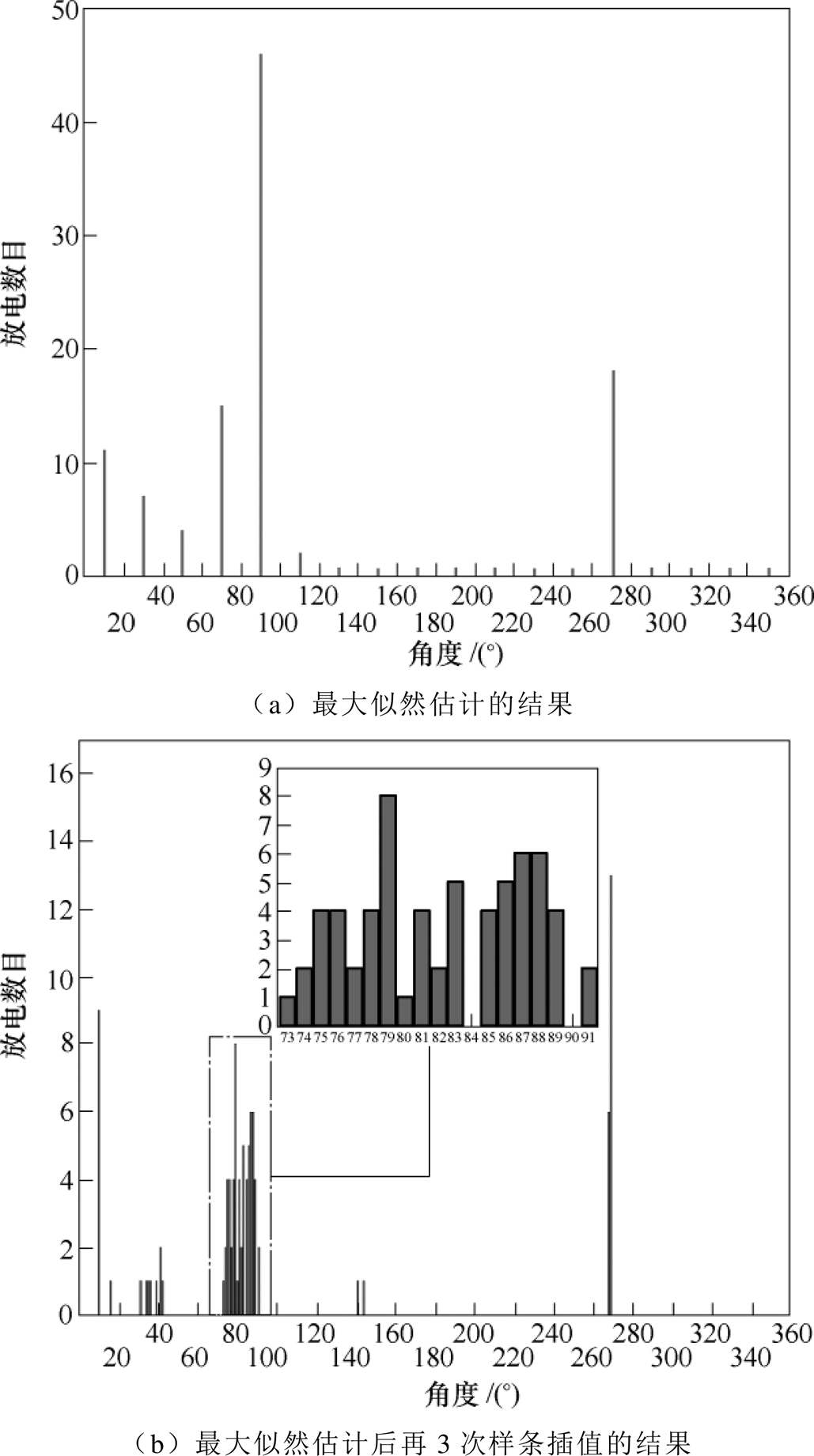
图7 入射角80°的局部放电测向结果方位
Fig.7 Azimuth diagram of PD DOA results at 80°
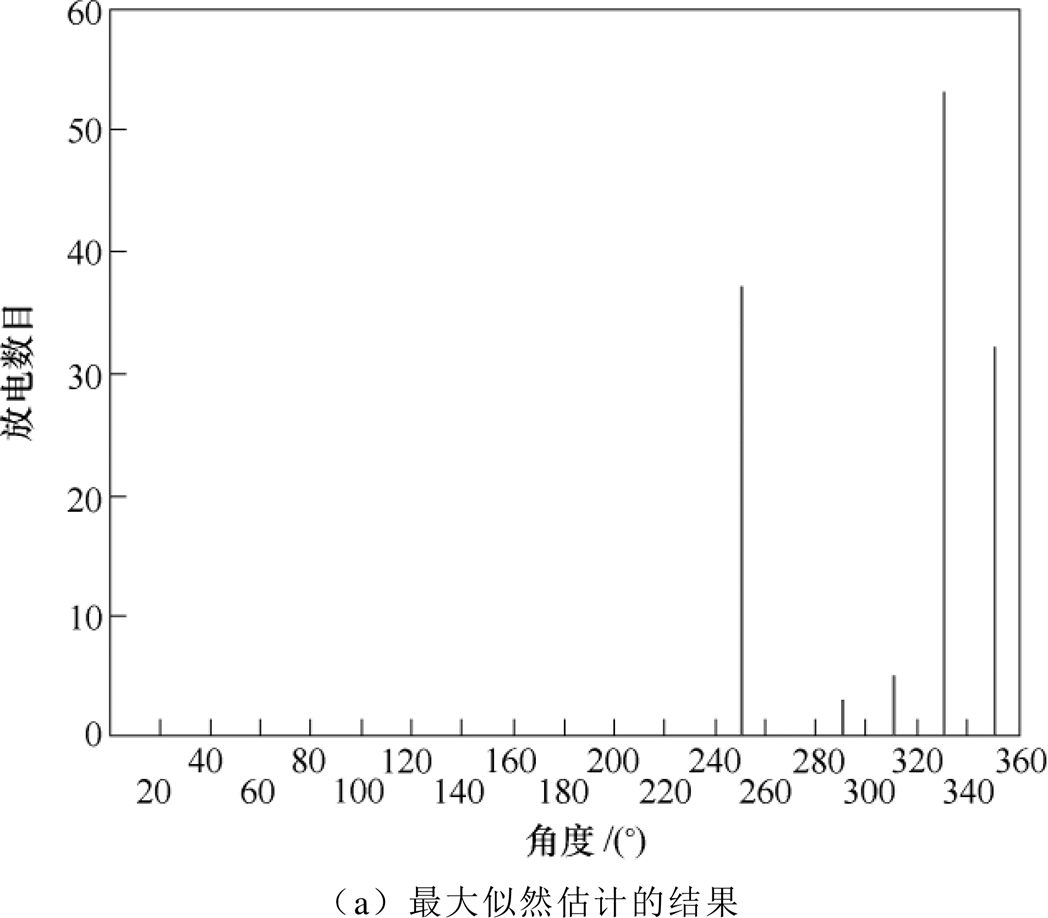
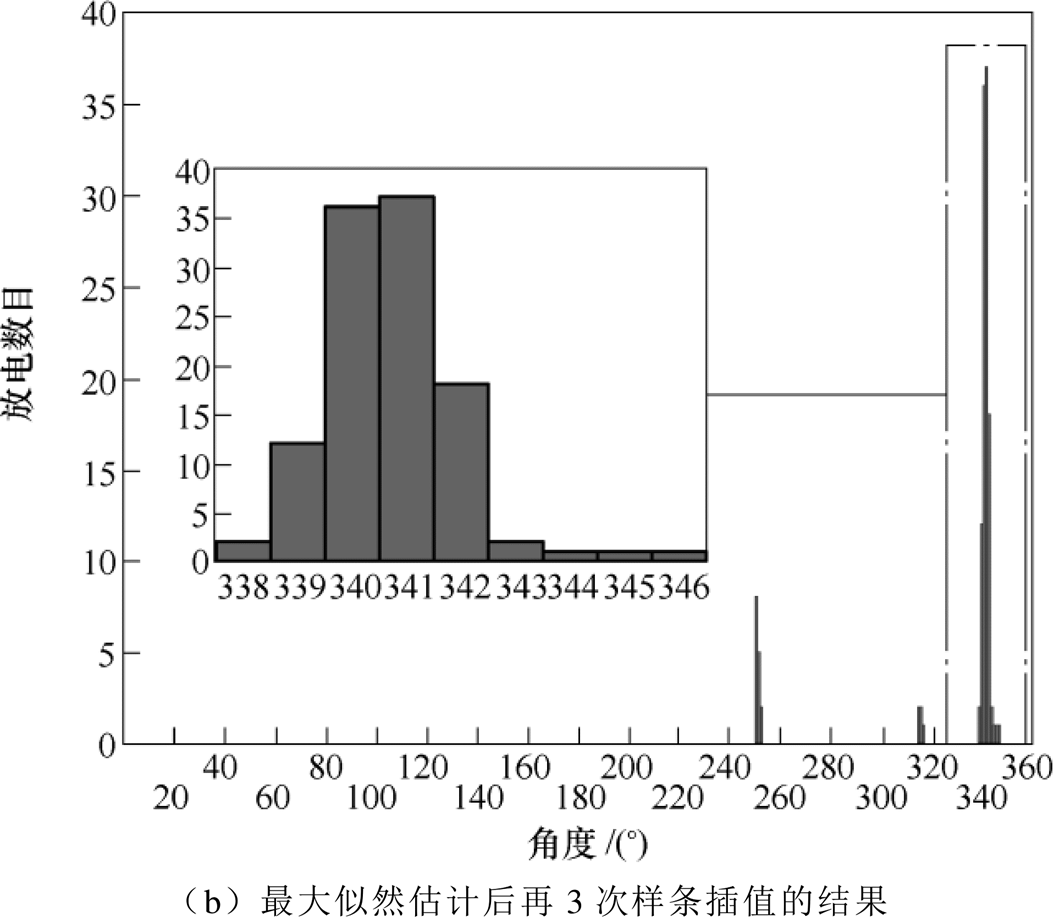
图8 入射角340°的局部放电测向结果方位
Fig.8 Azimuth diagram of PD DOA results at 340°
分别对每组测试所得到的初步测向结果运用K-means算法进行聚类，并将最大聚类的中心值作为最终的测向结果。根据插值与否得到的测向结果见表1。
表1 特高频阵列传感器测向结果
Tab.1 The results of DOA using UHF sensor array
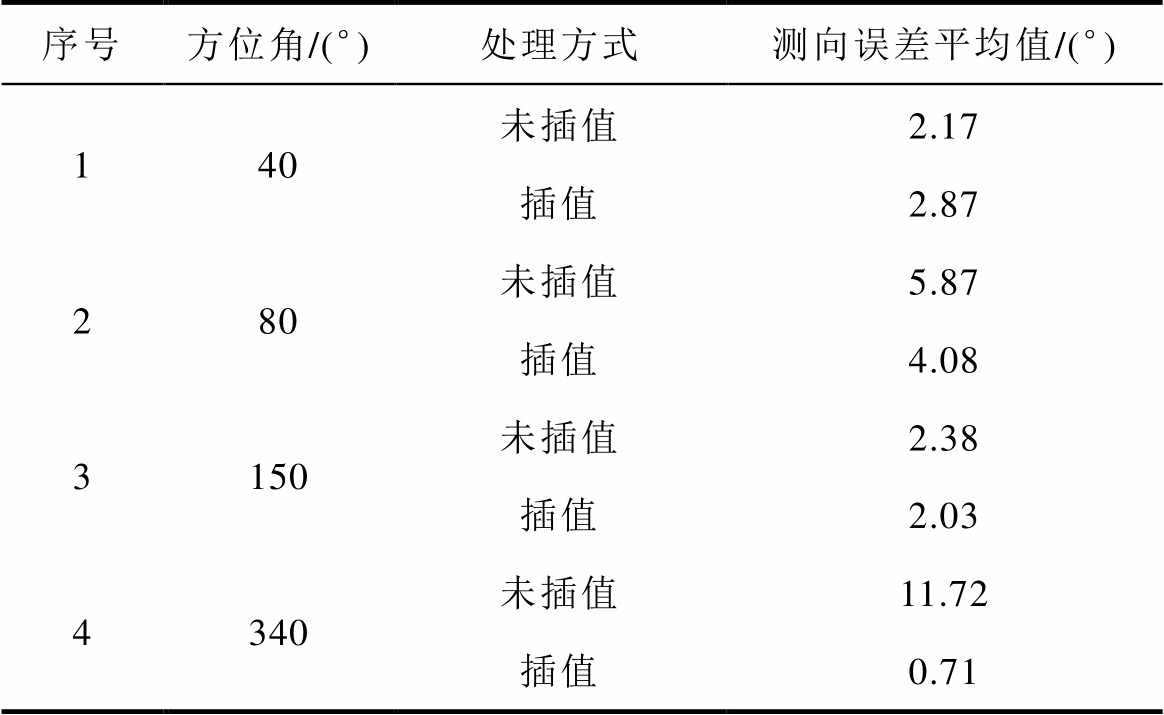
序号方位角/(°)处理方式测向误差平均值/(°) 140未插值2.17 插值2.87 280未插值5.87 插值4.08 3150未插值2.38 插值2.03 4340未插值11.72 插值0.71
从表1可知，未进行校正的测向结果具有较大的波动性，其中340°的平均测向误差近12°，而其余3个角度的平均测向误差均不超过6°。而进行插值校正后4个方位角的平均测向误差均小于5°。
实验中还测试了不同传感器个数对测向精度的影响。具体地，阵列中传感器由4个增加到8个，间隔45°放置于一个水平面上。分别在方位角10°、150°、270°和340°上进行放电测向实验。再将阵列恢复为4个传感器，在同样的角度进行相应的测向实验，两次测试对比结果见表2。可以看出，在放电方位角为10°时，8个传感器的测向误差大于4个传感器。而在放电方位角为150°和270°时，传感器个数对测向误差影响不大。即传感器数目的提高与测向精度的提高没有必然联系。
表2 不同传感器数目的测向结果
Tab.2 DOA results using UHF sensors of different numbers (单位: °)
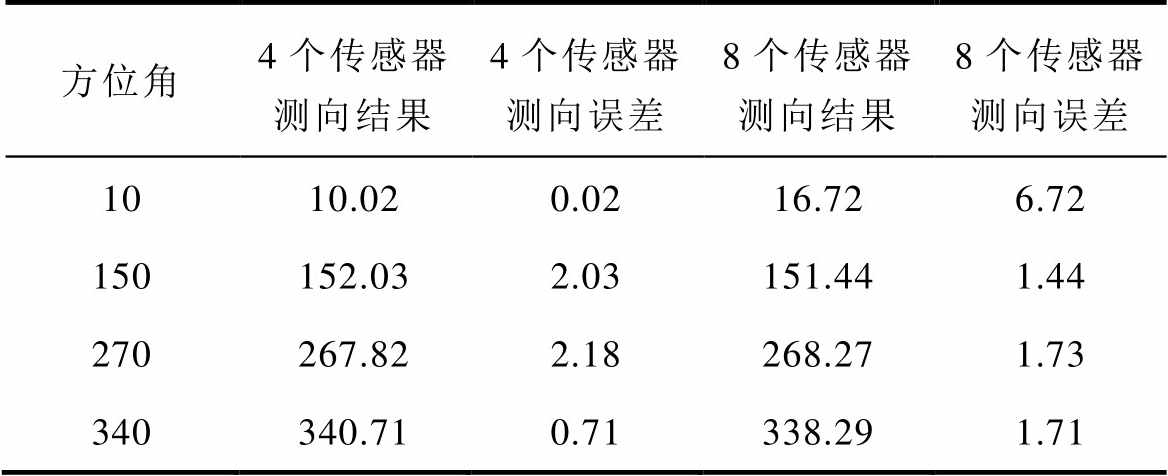
方位角4个传感器测向结果4个传感器测向误差8个传感器测向结果8个传感器测向误差 1010.020.0216.726.72 150152.032.03151.441.44 270267.822.18268.271.73 340340.710.71338.291.71
另外，对于本文提出的局部放电测向的方法，其测向方差与克拉美罗下界比较如图9所示，图中纵坐标为求取对数后的数值。从图9可以看出，本文方法在除30°和150°外的角度，其测向结果均优于无偏差估计的计算下界，从理论上也证明了本文测向方法具有较好的测向精度。
图9 计算方差和克拉美罗下界比较
Fig.9 Variance of ML and CRLB
综合不同角度及不同传感器数量的实验结果表明，本文提出方法的平均测向误差小于7°。作为对比，现有的基于特高频信号到达时间差法，文献给出的测向误差范围为2.4°～7.2°不等[26-27]；而基于接收信号强度指纹图谱定位法，距离20m内的定位误差为1.68m[15]（即测向精度小于5°）。因此，本文提出的定位方法无需高速同步采集装置，在取得与到达时间差法可比的测向精度下，具有成本低、易于使用等优点。
1）利用特高频无线传感器阵列接收信号强度功率和最大似然估计的局部放电测向方法可实现对局部放电源的测向，实验室环境测试表明其精度与传统时差法类似。
2）对局部放电特高频RSSI数据的最大似然估计分析充分利用了特高频监测数据的统计特性及累积效应，可有效地给出局部放电源的测向结果。而插值和聚类分析的应用进一步提高了测向精度。
3）后续工作中将重点开展该系统的现场测试及多源局部放电源定向功能等工作。
参考文献
[1] Portugues I E, Moore P J, Glover I A, et al. RF-based partial discharge early warning system for air- insulated substations[J]. IEEE Transactions on Power Delivery, 2008, 24(1): 20-29.
[2] 聂洪岩, 张潮海, 顾哲屹, 等. 局部放电条件下干式空心电抗器匝间绝缘的电老化特性研究[J]. 电工技术学报, 2018, 33(13): 3071-3079.
Nie Hongyan, Zhang Chaohai, Gu Zheyi, et al. The research on electrical aging characteristics of turn-to-turn insulation of dry-type air core reactor under partial discharge[J]. Transactions of China Electrotechnical Society, 2018, 33(13): 3071-3079.
[3] Moore P J, Portugues I E, Glover I A. Partial discharge investigation of a power transformer using wireless wideband radio-frequency measurements[J]. IEEE Transactions on Power Delivery, 2006, 21(1): 528-530.
[4] 李旭涛, 周凯, 万利, 等. 基于TEV法的电缆终端局部放电状态监测装置的研制[J]. 电力系统保护与控制, 2013, 41(12): 98-103.
Li Xutao, Zhou Kai, Wan Li, et al. Development of cable termination PD condition monitoring device based on TEV method[J]. Power System Protection and Control, 2013, 41(12): 98-103.
[5] 张晓星, 张戬, 肖淞. 大型变压器外置式特高频局部放电传感器设计[J]. 高电压技术, 2019, 45(2): 499-504.
Zhang Xiaoxing, Zhang Jian, Xiao Song. Design of external ultra-high frequency partial discharge sensor for large transformer[J]. High Voltage Engineering, 2019, 45(2): 499-504.
[6] 刘宇舜, 程登峰, 夏令志, 等. 基于单通道盲源分离算法的局部放电特高频信号去噪方法[J]. 电工技术学报, 2018, 33(23): 5625-5636.
Liu Yushun, Cheng Dengfeng, Xia Lingzhi, et al. Partial discharge ultra-high frequency signal de- noising method based on single-channel blind source separation algorithm[J] Transactions of China Electrotechnical Society, 2018, 33(23): 5625-5636.
[7] 侯慧娟, 盛戈皞, 孙岳, 等. 基于电磁波信号传播衰减模型的变电站局部放电定位方法[J]. 电工技术学报, 2014, 29(6): 326-332.
Hou Huijuan, Sheng Gehao, Sun Yue, et al. The localization method of partial discharge in substation based on propagation and attenuation model of electromagnetic signal[J]. Transactions of China Electrotechnical Society, 2014, 29(6): 326-332.
[8] Sinaga H H, Phung B T, Blackburn T R. Partial discharge localization in transformers using UHF detection method[J]. IEEE Transactions on Diele- ctrics and Electrical Insulation, 2012, 19(6): 1891- 1900.
[9] Zhang Yong, Upton D, Jaber A, et al. Radiometric wireless sensor network monitoring of partial discharge sources in electrical substations[J]. Inter- national Journal of Distributed Sensor Networks, 2015, 11(9): 1-9.
[10] 叶海峰, 钱勇, 刘宗杰, 等. 一种新型的放电源空间定位用特高频传感器[J]. 电工技术学报, 2015, 30(8): 333-340.
Ye Haifeng, Qian Yong, Liu Zongjie, et al. A new UHF sensor for spatial location of partial discharge sources[J]. Transactions of China Electrotechnical Society, 2015, 30(8): 333-340.
[11] 李臻, 罗林根, 盛戈皞, 等. 基于压缩感知的特高频局部放电定位法[J]. 电工技术学报, 2018, 33(1): 202-208.
Li Zhen, Luo Lingen, Sheng Gehao, et al. Ultrahigh frequency partial discharge localization methodology based on compressed sensing[J]. Transactions of China Electrotechnical Society, 2018, 33(1): 202-208.
[12] Gaouda A M. Adaptive partial discharge monitoring system for future smart grids[C]//IECON 2013 39th Annual Conference of the IEEE Industrial Electronics Society, Vienna, Austria, 2013: 4982-4987.
[13] 陶为戈, 朱昳华, 贾子彦. 基于RSSI混合滤波和最小二乘参数估计的测距算法[J]. 传感技术学报, 2012, 25(12): 1748-1753.
Tao Weige, Zhu Yihua, Jia Ziyan. A distance measurement algorithm based on rssi hybrid filter and least square estimation[J]. Chinese Journal of Sensors and Actuators, 2012, 25(12): 1748-1753.
[14] Zhang Yong, Upton D, Jaber A, et al. Multiple source localization for partial discharge monitoring in electrical substation[C]//2015 Loughborough Antennas & Propagation Conference (LAPC), Loughborough, UK, 2015: 1-4.
[15] Iorkyase E T, Tachtatzis C, Atkinson R C, et al. Localisation of partial discharge sources using radio fingerprinting technique[C]//2015 Loughborough Antennas & Propagation Conference (LAPC), Loughborough, UK, 2015: 1-5.
[16] 李臻, 罗林根, 陈敬德, 等. 基于特高频无线传感阵列的新型局部放电定位方法[J]. 高电压技术, 2019, 45(2): 418-425.
Li Zhen, Luo Lingen, Chen Jingde, et al. Novel localization method for partial discharge based on utral-high frequency wireless sensor array[J]. High Voltage Engineering, 2019, 45(2): 418-425.
[17] 翟国富, 王淑娟, 姜守旭, 等. 电器可靠性失效分析中极大似然估计方法的研究[J]. 中国电机工程学报, 2001, 21(3): 91-93.
Zhai Guofu, Wang Shujuan, Jiang Shouxu, et al. The research on method of maximum likelihood estimation for apparatus reliability failure analysis[J]. Proceedings of the CSEE, 2001, 21(3): 91-93.
[18] 程学珍, 陈强, 于永进, 等. 基于最大似然译码字的Petri网电网故障诊断方法[J]. 电工技术学报, 2015, 30(15): 46-52.
Cheng Xuezhen, Chen Qiang, Yu Yongjin, et al. A fault diagnosis approach of power networks based on maximum likelihood decoding Petri net models[J]. Transactions of China Electrotechnical Society, 2015, 30(15): 46-52.
[19] Mishra D K, Sarkar B, Koley C, et al. An unsuper- vised Gaussian mixer model for detection and localization of partial discharge sources using RF sensors[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2017, 24(4): 2589-2598.
[20] 蒋海峰, 张曼, 赵斌炎, 等. 基于改进Hilbert- Huang变换的电网故障诊断[J]. 电工技术学报, 2019, 34(增刊1): 336-342, 351.
Jiang Haifeng, Zhang Man, Zhao Binyan, et al. Fault diagnosis of power grid based on improved Hilbert- Huang transform[J]. Transactions of China Electro- technical Society, 2019, 34(S1): 336-342, 351.
[21] 张雨金, 杨凌帆, 葛双冶, 等. 基于Kmeans-SVM的短期光伏发电功率预测[J]. 电力系统保护与控制, 2018, 46(21): 118-124.
Zhang Yujin, Yang Lingfan, Ge Shuangye, et al. Short-term photovoltaic power forecasting based on Kmeans algorithm and support vector machine[J]. Power System Protection and Control, 2018, 46(21): 118-124.
[22] 陈敬德, 李峰, 孙源文, 等. 基于KNN和MSR的局部放电模式识别研究[J]. 电气技术, 2018, 19(1): 10-14.
Chen Jingde, Li Feng, Sun Yuanwen, et al. Research on pattern recognition of partial discharge based on KNN and MSR[J]. Electrical Engineering, 2018, 19(1): 10-14.
[23] 秦雪, 钱勇, 许永鹏, 等. 基于2D-LPEWT的特征提取方法在电缆局部放电分析中的应用[J]. 电工技术学报, 2019, 34(1): 170-177.
Qin Xue, Qian Yong, Xu Yongpeng, et al. Appli- cation of feature extraction method based on 2D-LPEWT in cable partial discharge analysis[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 170-177.
[24] Peng Xiaosheng, Zhou Chengke, Hepburn D M, et al. Application of K-means method to pattern recog- nition in on-line cable partial discharge monitoring[J]. IEEE Transactions on Dielectrics and Electrical Insulation, 2013, 20(3): 754-761.
[25] Kay S M. Fundamentals of statistical signal pro- cessing[M]. Upper Saddle River, NJ: Prentice Hall PTR, 1993.
[26] Moore P J, Portugues I E, Glover I A. Radiometric location of partial discharge sources on energized high-voltage plant[J]. IEEE Transactions on Power Delivery, 2005, 20(3): 2264-2272.
[27] Tian Ye, Kawada M. Simulation on locating partial discharge source occurring on distribution line by estimating the DOA of emitted EM waves[J]. IEEJ Transactions on Electrical and Electronic Engin- eering, 2012, 7(S1): S6-S13.
RSSI-Power-Based Direction of Arrival Estimation Using Maximum Likelihood Estimator and Antenna Array
Abstract Partial discharge is one of the main reasons of electrical equipment insulation deterioration in substations. The detection and localization of partial discharge (PD) using ultra-high frequency (UHF) antennas is an important means for equipment fault warning in substations. UHF PD localization system is usually based on time-difference of electromagnetic wave signal. However, this system requires high sampling rate and time synchronization accuracy, which has high cost. This paper studied the feasibility and accuracy of PD direction of arrival (DoA) using power of UHF received signal strength indicator (RSSI) and maximum likelihood (ML) estimation. First, the UHF antenna power pattern was achieved in the offline experiment. Then, a method using maximum likelihood estimator was proposed to handle PD direction of arrival estimation and obtain the preliminary orientation results. Last, in order to obtain the final results, interpolation and clustering were employed to improve the resolution. In a laboratory test, the experimental results show that the average error of direction of arrival is less than 7°, and the cost is lower and the use is more convenient.
keywords：Substation, partial discharge, received signal strength indicator, maximum likelihood estimator, direction of arrival
中图分类号：TM835
DOI: 10.19595/j.cnki.1000-6753.tces.190680
收稿日期 2019-06-04
改稿日期 2019-08-15
吴 凡 男，1994年生，硕士，研究方向为电力设备状态监测。E-mail: yzwufan@sjtu.edu.cn
罗林根 男，1982年生，博士，副研究员，研究方向为输变电设备状态评估、复杂电力系统脆弱性分析等。E-mail: llg523@sjtu.edu.cn（通信作者）
（编辑 崔文静）