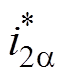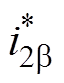、
为逆变器输出电流在a、b 坐标系下的给定值，Im为并网电流幅值；UPCC为PCC的电压，Ug为电网电压，Udc为直流母线电压，q 为PLL输出相位，wo为PLL输出角频率，G(s)为外环调节器，Kd为有源阻尼系数，KPWM为脉宽调制增益。wc为复数滤波器的截止频率，
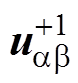与
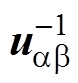分别为PCC电压在a、b 轴下的正、负序基波分量，Gp(s)为阻抗重塑控制策略的等效传递函数，GPLL(s)为考虑PLL影响的等效传递函数。摘要 针对传统的同步旋转坐标系锁相环结构的逆变器并网系统，结合复数滤波器基波正序电压提取特性，构建具有复数滤波器结构锁相环的逆变器并网系统（CFPLL-GIS）。在此基础上充分考虑锁相环影响，建立CFPLL-GIS的阻抗模型，并通过基于阻抗的稳定性判据分析，说明复数滤波器结构的引入可以提高逆变器并网系统等效输出阻抗在中频段内的相角，能够显著改善逆变器并网系统对弱电网的适应能力；同时结合CFPLL-GIS的结构特点并以逆变器并网系统的环路增益为设计指导，提出一种逆变器并网系统等效输出阻抗重塑控制策略，改善系统的阻抗特性，保证逆变器并网系统具有充足的稳定裕度，进一步拓宽CFPLL-GIS对电网阻抗的适应范围。最后，通过仿真和实验验证了本文理论分析的正确性以及所提控制策略的有效性。
关键词：弱电网 复数滤波器 锁相环 并网逆变器 阻抗判据 阻抗重塑 稳定裕度
随着新能源的持续发展和电力系统对于灵活可控的需求持续增长，变流器技术在电力系统中得到越来越多的应用[1]。大规模变流器的接入改变了电网的动态特性，当电力电子设备容量逐渐增大时，交流电网相对逐渐变弱，这种电网通常称之为弱电网[2-3]，而且电网运行方式的变化也导致电网阻抗呈宽范围变化的特点[4]。在弱电网下，电力电子设备的自身动态及其与交流电网的相互作用明显，容易引发复杂的振荡问题，给电力系统的安全稳定运行带来了新的挑战[5-7]。
针对弱电网下并网逆变器的稳定性控制研究，目前最受关注的问题是：①弱电网条件下逆变器并网系统的失稳机理；②如何提高弱电网条件下逆变器并网系统的稳定性。文献[8]分别对弱电网下并网逆变器采用有源阻尼控制、谐波谐振控制、重复控制以及电网电压前馈控制的工作性能进行了评估。文献[9]基于电网电流有源阻尼控制结构，提出了基波电压前馈与相位补偿控制策略，旨在提高并网逆变器对弱电网的适应性，但是该方法对参数设计要求高，设计难度大。文献[10-12]分析了电网阻抗与逆变器并网系统的交互作用机理，以及对逆变器并网系统控制环路的稳定性影响，研究表明随着电网变弱，电网阻抗不断增加，电流环截止频率会进一步降低，从而减小电流环控制器的相位裕度，降低了系统的稳定性。但是以上研究都没有考虑锁相环（Phase Locked Loop, PLL）对逆变器并网系统稳定性的影响。文献[13]虽基于状态空间模型分析PLL、短路比对系统稳定性的影响，但并未指出系统稳定性是否与其他控制环节相关，且状态空间模型只能提供参数变化对系统稳定性影响的量化结果，并不能揭示逆变器并网系统稳定性随短路比变化的机理。文献[14]分析了柔性直流输电接入弱电网时PLL和电流内环的控制交互作用以及交流电网强度、有功功率大小对二者交互作用影响的机理，但是并未详细说明该如何提高柔性直流输电接入弱电网系统的稳定性。文献[15]基于系统相位裕度动态补偿控制思路，提出一种并网逆变器的阻抗相位补偿控制策略，提高了弱电网下并网逆变器的稳定性。文献[16-18]考虑了弱电网下PLL对逆变器并网系统稳定性的影响，分析了PLL与电网阻抗的耦合关系以及不同电网阻抗和锁相环带宽与并网逆变器稳定性的内在联系，而且明确表示PLL带宽的减小将有助于系统的稳定。文献[19]指出弱交流系统下，逆变器的锁相环和无功功率控制环会对直流电压控制起滞后作用，引起负阻尼从而减弱直流电压的稳定性。但是以上分析研究都是基于传统的同步旋转坐标系锁相环（Synchronous Rotating Frame PLL, SRF-PLL）结构，并没有考虑具有其他PLL结构的逆变器并网系统对弱电网的适应性。文献[20-21]提出一种具有基波正序电压提取特性的复数滤波器结构PLL，并分析了该PLL结构在电网电压畸变/不平衡情况下的锁相特性，实验结果表明，基于该结构的锁相方法可以实现快速准确的电网同步锁相。但是，目前尚未有文献将这种PLL结构应用于弱电网下逆变器并网系统的同步，更没有对该种结构PLL对弱电网的适应性展开分析研究。为此本文将这种利用复数滤波器结构提取基波正序分量用于获取电网电压相位与频率信息的PLL应用于弱电网环境，研究其对弱电网下逆变器并网系统运行特性的影响及其交互作用机理。
通过上述分析，本文以采用传统SRF-PLL提供控制环路相位信息的电流双闭环三相LCL型并网逆变器为模型基础，综合考虑具有基波正序电压提取特性的复数滤波器的频率特性，将复数滤波器结构附加在SRF-PLL的前级，构成具有复数滤波器结构PLL的逆变器并网系统（Grid-Connected Inverter System with Complex Coefficient-Filter-Based Phase Locked Loop, CFPLL-GIS）：一方面从PLL自身的角度出发，复数滤波器作为前级结构获取公共并网点电压的基波分量，更加有利于后级SRF-PLL在电网阻抗扰动下对电网基波频率的提取，提高逆变器并网系统在弱电网下的稳定性；另一方面从逆变器等效输出阻抗的角度出发，复数滤波器结构的引入可以对逆变器的等效输出阻抗进行重塑，提高输出阻抗在中频段的相角，改善逆变器并网系统对弱电网的适应能力。同时，在以上分析的基础上，本文以逆变器并网系统的环路增益为设计指导，提出一种逆变器并网系统等效输出阻抗重塑控制策略，改善系统的阻抗特性，保证逆变器并网系统具有充足的稳定裕度，进一步拓宽CFPLL-GIS对电网阻抗的适应范围，使其对弱电网环境表现的更加友好。最后，通过仿真和实验验证了本文理论分析的正确性以及所提控制策略的有效性。
为了分析说明复数滤波器结构的引入可以显著提高逆变器并网系统对弱电网的适应能力，本文以电流双闭环三相LCL型并网逆变器为模型基础，构建系统在加入复数滤波器前后的等效输出阻抗模型。该逆变器并网系统的总体控制结构如图1所示，其控制系统数学框图模型如图2所示。
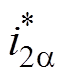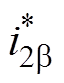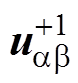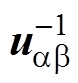在图1和图2中，L1、C和L2构成LCL滤波器；Zload为负载等效阻抗，Zg为电网阻抗；i1为逆变桥侧电感电流，iC为滤波电容电流，i2为逆变器输出电流，ig为并网电流，iCa、iCb 为电容电流在a、b 坐标系下的分量，i2a、i2b 为逆变器输出电流在a、b 坐标系下的分量，、为逆变器输出电流在a、b 坐标系下的给定值，Im为并网电流幅值；UPCC为PCC的电压，Ug为电网电压，Udc为直流母线电压，q 为PLL输出相位，wo为PLL输出角频率，G(s)为外环调节器，Kd为有源阻尼系数，KPWM为脉宽调制增益。wc为复数滤波器的截止频率，与分别为PCC电压在a、b 轴下的正、负序基波分量，Gp(s)为阻抗重塑控制策略的等效传递函数，GPLL(s)为考虑PLL影响的等效传递函数。
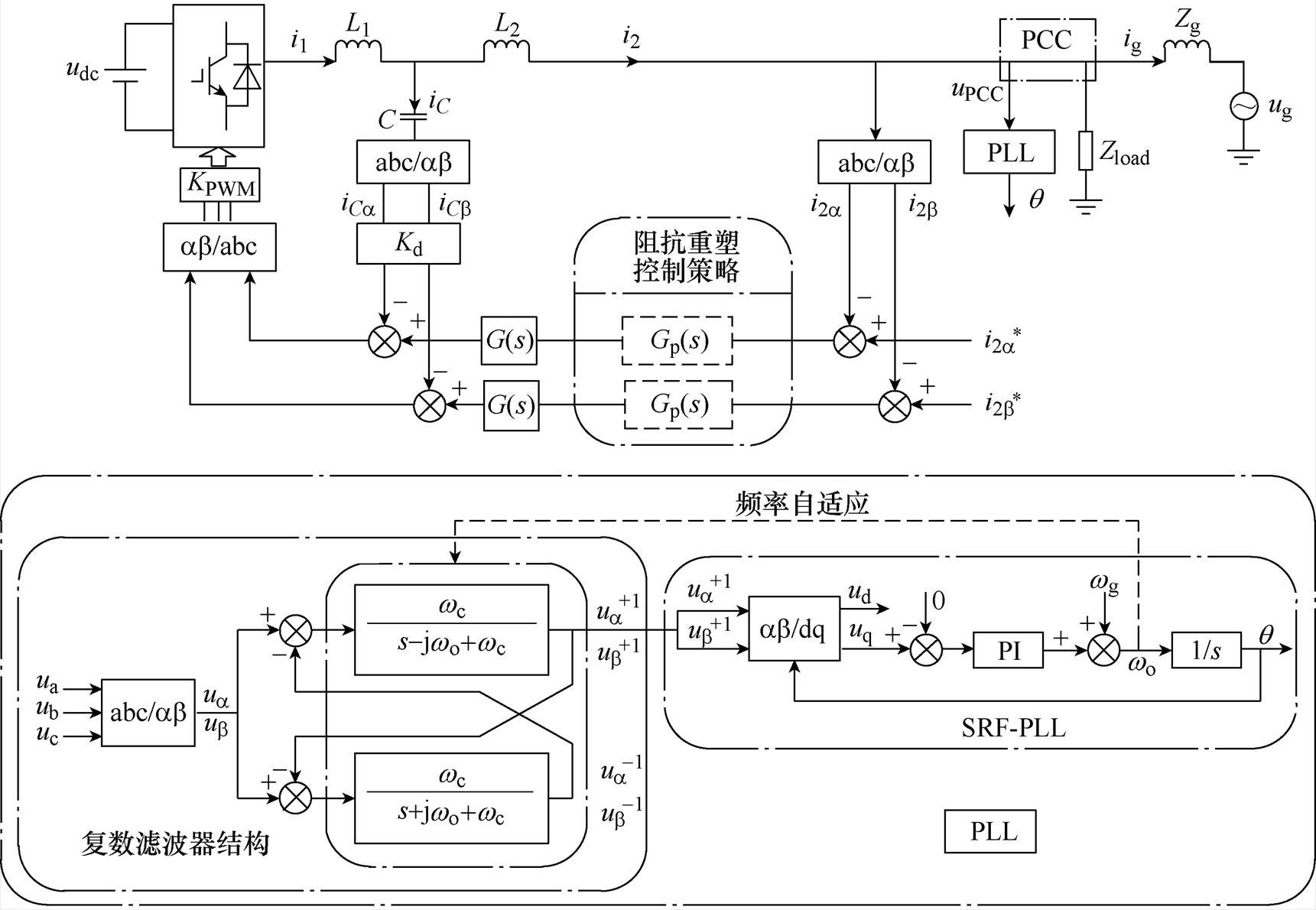
图1 LCL逆变器并网系统的总体控制结构
Fig.1 Overview of investigated configuration and control system for LCL inverter grid-connected system
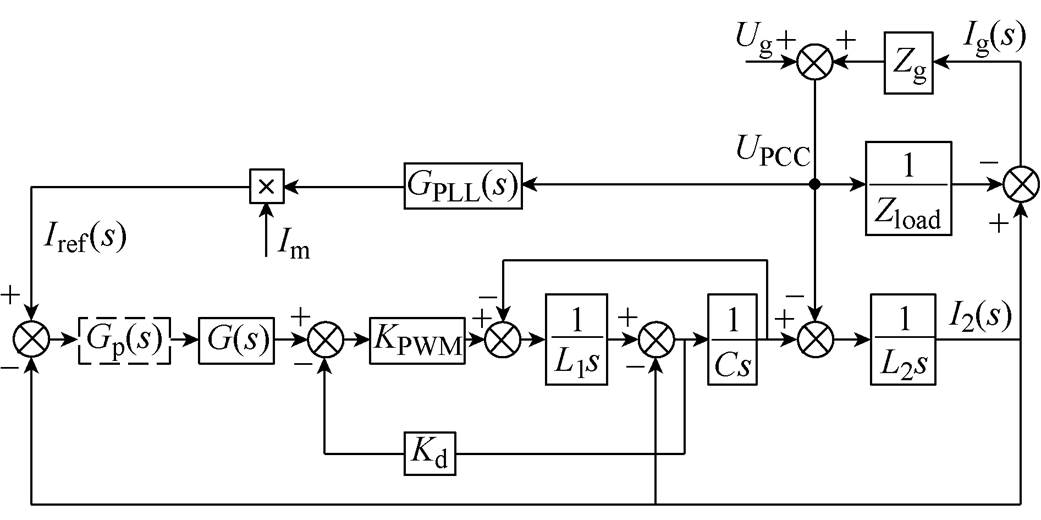
图2 并网逆变器控制系统数学框图模型
Fig.2 Mathematical model of grid-connected inverter control system
不考虑电网阻抗影响，在对逆变器并网系统进行阻抗重塑控制之前，根据控制框图等效变换可得等效控制框图如图3所示。其中，G1(s)、G2(s)以及系统环路增益TA1(s)的表达式分别为
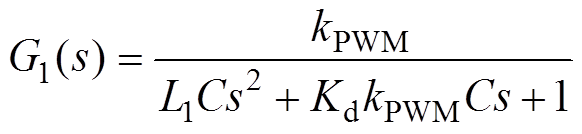（1）
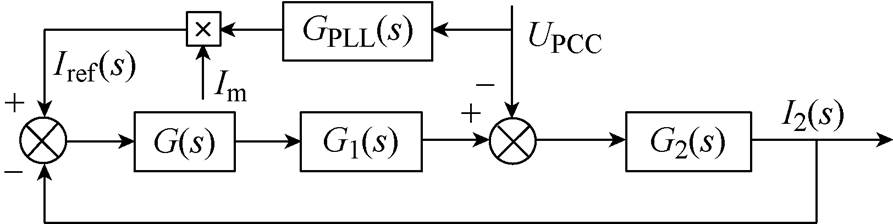
图3 等效控制框图
Fig.3 Equivalent control block diagram
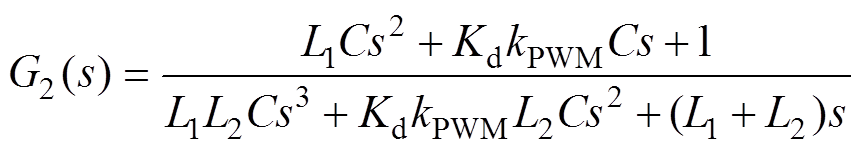（2）
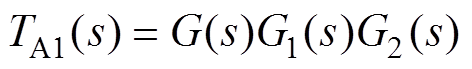（3）
根据图3的等效控制框图，可以求得考虑PLL影响的并网逆变器输出电流I2(s)的表达式为
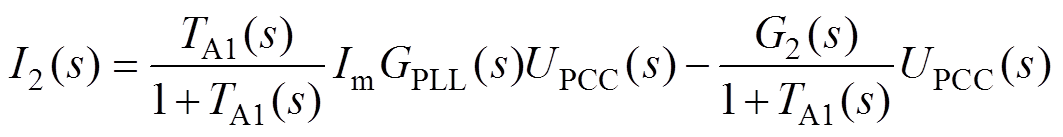（4）根据式（4）可以得到逆变器并网系统的诺顿等效阻抗模型如图4所示。
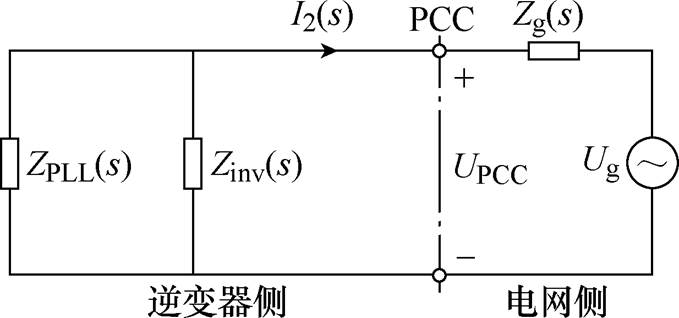
图4 逆变器并网系统的诺顿等效电路
Fig.4 The Norton equivalent circuit of grid-connected inverter system
图4中，ZPLL(s)、Zinv(s)的表达式分别为
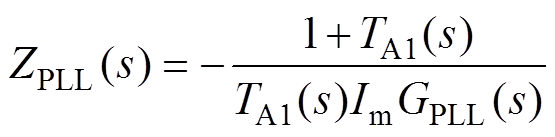（5）
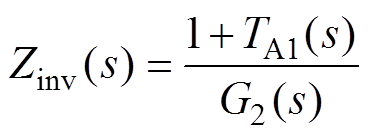（6）
当只考虑传统基于SRF-PLL结构的逆变器并网系统时，根据ab 到dq的坐标变换关系，可以得到uq的表达式为
（7）考虑到PCC电压扰动以及由此引起的SRF-PLL输出相位波动，通过分离扰动线性化处理，构建uq小信号模型的过程为
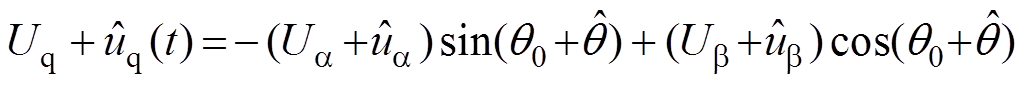（8）
根据式（8）消除稳态量以及高阶扰动项，可以得到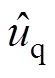
的表达式为
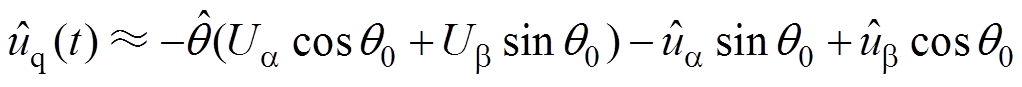
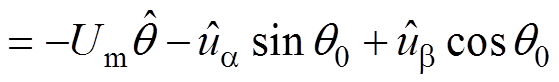（9）
式中，Um为公共并网点电压幅值。同时由图1中SRF-PLL的控制结构可以得到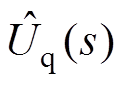
与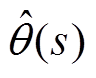
之间的关系为
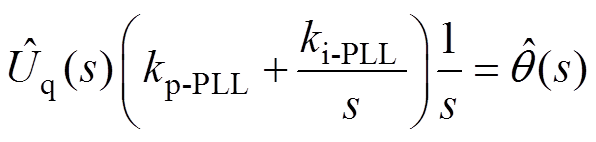（10）式中，kp-PLL为PLL模块中PI调节器的比例系数；ki-PLL为积分系数。又ub 滞后ua90°相位，即等式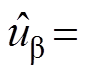
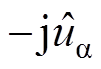成立，同时结合欧拉公式，sinq0=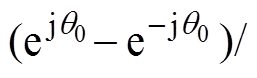
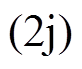，cosq0=
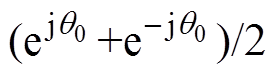，联立式（9）和式（10）可以求得
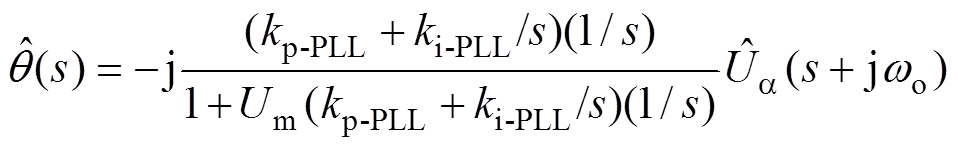（11）
同理，并网电流给定值I2ref (s)在分离扰动线性化处理后可以得到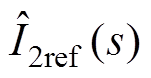
的表达式为
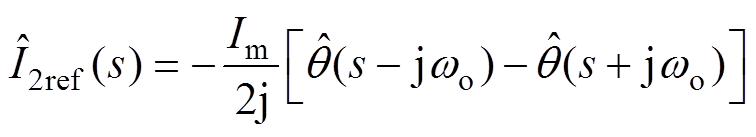（12）结合式（11）和式（12），可以求得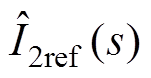与
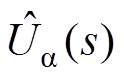之间的传递函数GPLL(s)的表达式为
（13）
根据式（5）和式（6）以及式（13），可以确定逆变器并网系统在考虑PLL影响后的等效输出阻抗表达式为
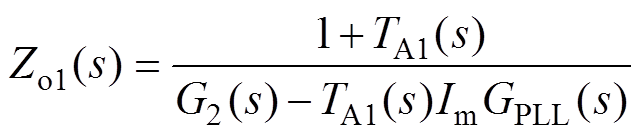（14）通过基于阻抗的稳定性判据可知：系统的稳定性可以通过Zg(s)/Zo1(s)是否满足Nyquist稳定性判据来进行判定。图5给出了Zg(s)与Zo1(s)的Bode图，相关参数与表1一致。
从图5可以看出：当电网阻抗分别为Lg=5mH与Lg=10mH时，用阻抗判据表征的系统相位裕度（Phase Margin, PM）分别为22.7°和10.4°。
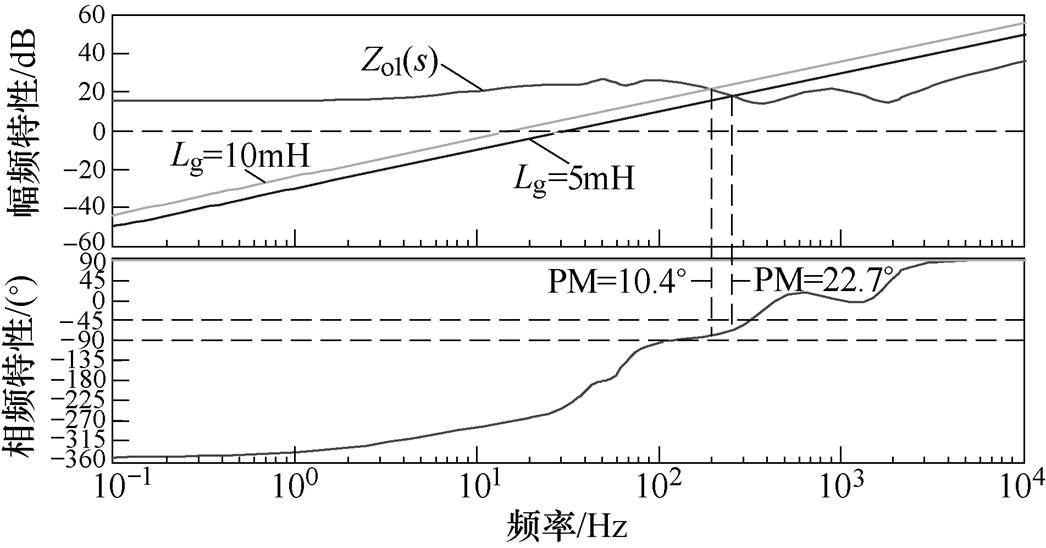
图5 并网逆变器等效输出阻抗Zo1(s)的Bode图
Fig.5 The Bode diagram of grid-connected inverter equivalent output impedance Zo1(s)
考虑到具有基波正序分量提取特性的复数滤波器结构可以很好地分离PCC电压的基波与谐波分量，为此将复数滤波器结构附加在SRF-PLL的前级，构成CFPLL-GIS。复数滤波器的结构如图1中PLL模块虚线框中所示，由此可以求得
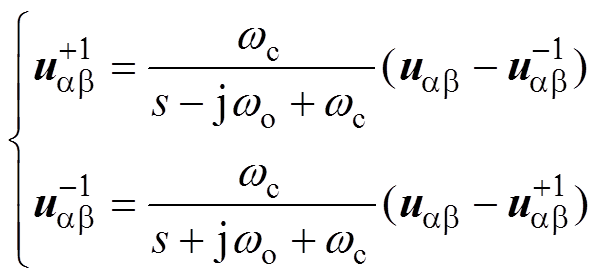（15）根据式（15）可以获取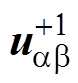
与
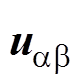之间的传递函数GCF(s)的表达式为
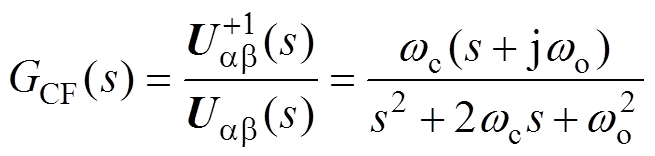（16）
为了避免复数滤波器结构与SRF-PLL之间发生交互影响，此处需要保证SRF-PLL的带宽要大于复数滤波器的带宽频率，为此本文选取wc的数值为222rad/s。此时考虑复数滤波器结构后的PLL等效阻抗ZPLL(s)与CFPLL-GIS的等效输出阻抗Zo2(s)的表达式分别为
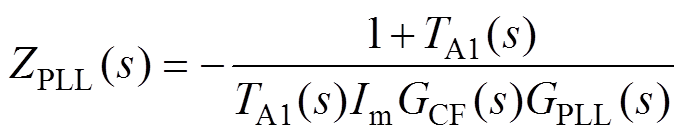（17）
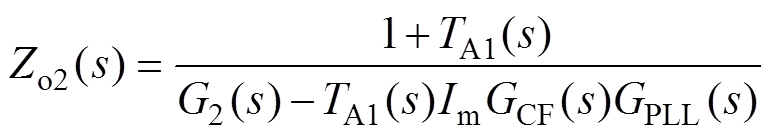（18）
引入复数滤波器前后的阻抗频率特性如图6所示。从图6可以看出：1/GCF(s)在大于50Hz的频段范围内具有0°～90°的正相移，相较于单一结构的SRF-PLL而言，复数滤波器结构的引入可以增加ZPLL(s)的相位，从而增加CFPLL-GIS等效输出阻抗Zo2(s)的相位，使系统的相位裕度增大、稳定性变好。此时，Zo1(s)与Zo2(s)的Bode图如图6所示，通过比较可以发现：复数滤波器结构的引入可以明显增加逆变器并网系统等效输出阻抗的相位，当电网阻抗分别为Lg= 5mH与Lg=10mH时，用阻抗判据表征的系统相位裕度（PM）分别为45°和30.3°。
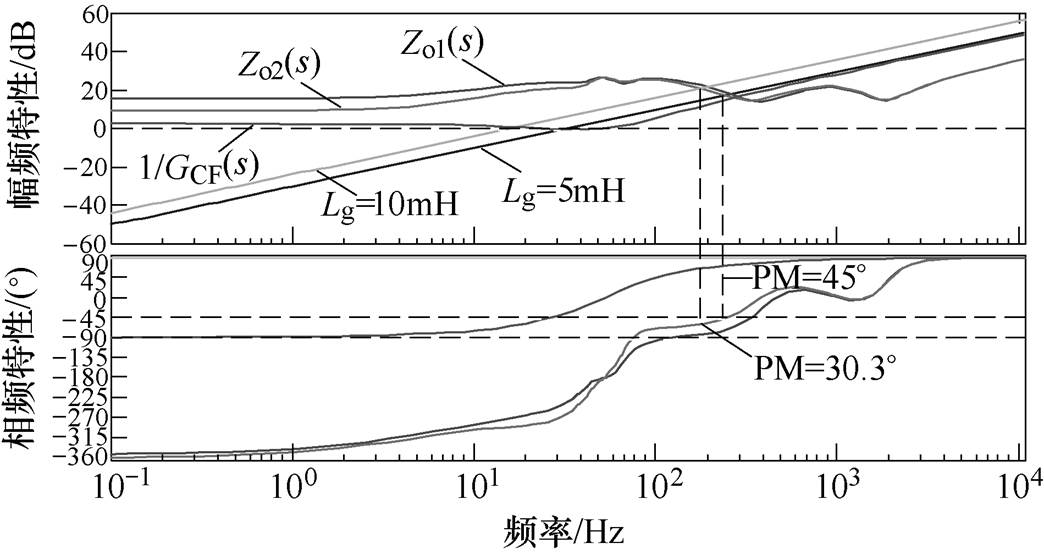
图6 引入复数滤波器前后的阻抗频率特性
Fig.6 The impedance frequency characteristics before and after introducing a complex coefficient-filter
不难理解：一方面从PLL自身的角度出发，复数滤波器作为前级结构获取PCC电压的基波分量，更加有利于后级SRF-PLL在电网阻抗扰动下对电网基波频率的提取，提高逆变器并网系统对弱电网的适应能力；另一方面从逆变器等效输出阻抗的角度出发，复数滤波器结构的引入可以对逆变器的等效输出阻抗进行重塑，增加输出阻抗在中频段的相角，改善逆变器并网系统在弱电网下的稳定性。
为了进一步拓宽CFPLL-GIS对电网阻抗的适应范围，提高逆变器并网系统应对弱电网的能力，本文以考虑电网阻抗影响的系统环路增益为设计指导，提出一种逆变器并网系统等效输出阻抗重塑控制策略，改善系统的阻抗特性，保证逆变器并网系统在电网阻抗宽范围变化时具有充足的稳定裕度。
考虑电网阻抗影响的系统环路增益TA2(s)的表达式为
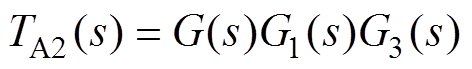（19）其中，G3(s)的表达式为
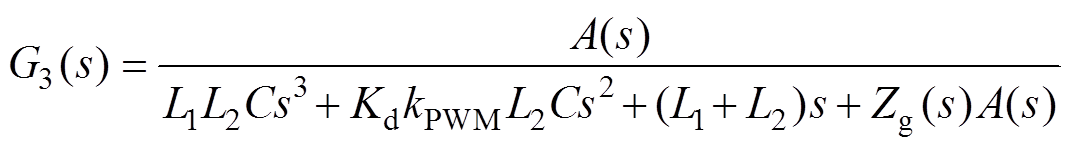（20）
式中，G(s)和G1(s)的表达式与上文一致，同时为了简化，令A(s)= L1Cs2+KdkPWMCs+1成立。
结合式（19）和式（20）以及表1中的参数取值，可以得到系统环路增益随电网阻抗Lg变化的幅频特性曲线如图7所示。
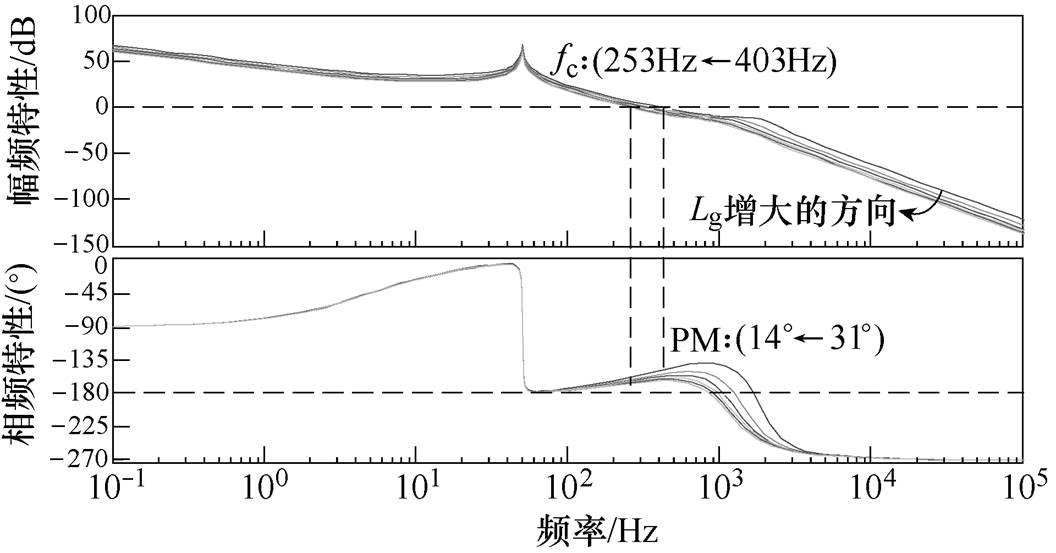
图7 TA2(s)随电网阻抗变化的Bode图
Fig.7 The Bode diagram of TA2(s) changing with Lg
从图7可以看出：当电网阻抗Lg从0mH变化到5mH时，系统的相位裕度（PM）从31°变化到14°，系统的截止频率fc从403Hz变化到253Hz。为了实现对相位裕度的补偿，可以在系统控制环路中增加相位补偿环节来弥补系统相位裕度不足的问题。为此，本文选择在电流外环调节器之后串联补偿环节Gp(s)，其具体表达式为
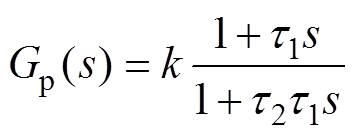（21）根据式（21）可以求得Gp(s)的补偿相位j (w)的表达式为
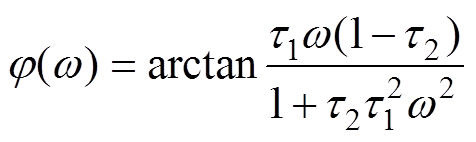（22）
假设补偿函数j (w)的最大补偿相位的角频率选在fcp处，则由此可得
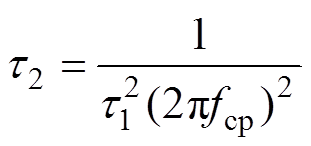（23）假设最大补偿相位为jideal，结合式（22）和式（23）可以求得t1的表达式为
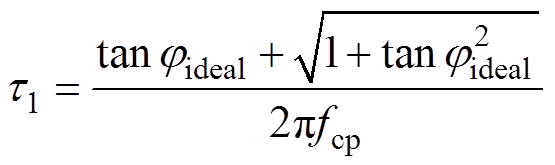（24）
在本文中选取fcp=100Hz，jideal=45°，从而可以求得t1=0.003 8，t2=0.171 6。同时为了抑制Gp(s)对高频谐波分量衰减程度减弱的问题，需要调节系数k进行幅值调整，在弱化高频谐波分量衰减程度减弱的同时还要保证系统环路增益在基波频率处具有足够的幅值，以尽可能减小并网电流的幅值误差。此时系统环路增益TA2(s)在补偿前后随调节系数k变化的Bode图如图8所示。从图8的分析结果可以看出：在加入补偿环节Gp(s)后，k取值过大会增加TA2(s)在大于基频段内的幅值，不利于高频谐波分量的衰减；k取值过小虽然更加有利于高频谐波分量的衰减，但是会导致系统在基波频率处的增益减小，增加了并网电流的幅值跟踪误差，因此k值需要折中选取。综合上述分析，本文取k=0.5。
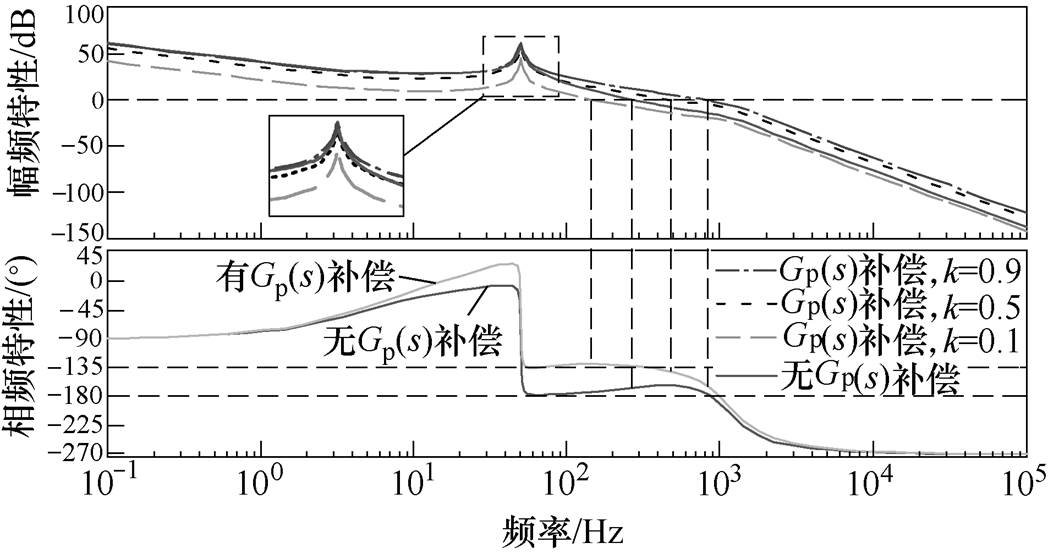
图8 Gp(s)补偿前后TA2(s)的Bode图
Fig.8 The Bode diagram of TA2(s) before and after Gp(s) compensation
同时Gp(s)环节的加入对于CFPLL-GIS的阻抗模型而言相当于是对其阻抗进行了重塑，此时系统等效阻抗与电网阻抗的频率特性曲线如图9所示。
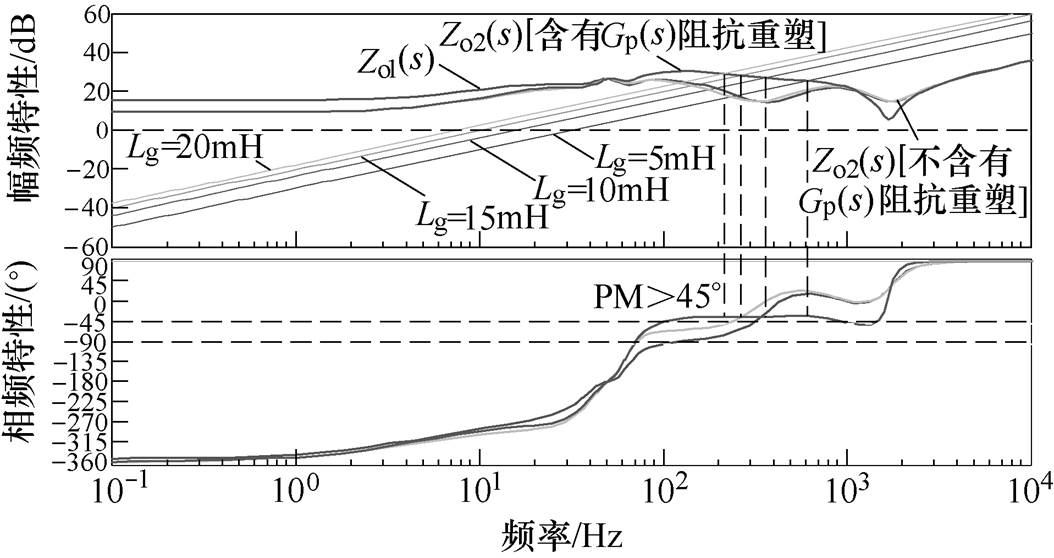
图9 引入Gp(s)阻抗重塑后的系统阻抗频率特性
Fig.9 The system impedance frequency characteristics after introduction of Gp(s) impedance remodeling
从图9可以看出：在加入Gp(s)对系统阻抗进行重塑之后，阻抗的幅相特性曲线与Zo1(s)以及不含Gp(s)阻抗重塑的Zo2(s)相比得到了明显改善，尤其是在中频段，不仅增加了阻抗的幅值，而且使阻抗的相位变得更加平稳且基本保持在-45°偏上，这使得CFPLL-GIS的等效输出阻抗在与电网阻抗匹配的过程中始终能够保持系统具有充足的相位裕度。而且上述的两种特性都更加有利于CFPLL-GIS应对弱电网环境，拓宽对电网阻抗的适应范围。
为了验证本文理论分析的正确性以及所提控制策略的合理性，利用Matlab/Simulink软件搭建了一套电压为220V、频率为50Hz、额定功率为14kW的LCL型并网逆变器模型并进行了仿真分析。主要仿真参数见表1。
表1 主要仿真参数
Tab.1 Main simulation parameters
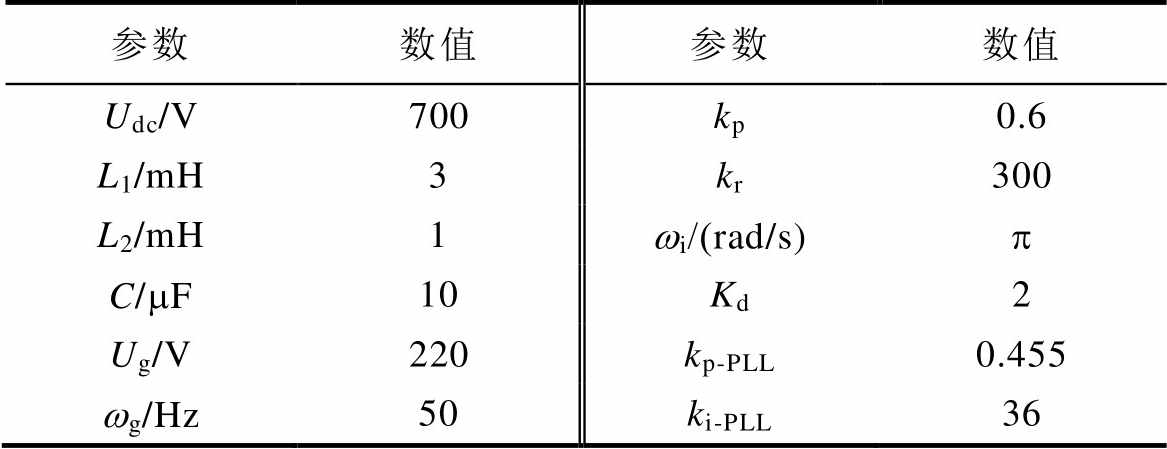
参数数值参数数值 Udc/V700kp0.6 L1/mH3kr300 L2/mH1wi/(rad/s)p C/mF10Kd2 Ug/V220kp-PLL0.455 wg/Hz50ki-PLL36
为了验证本文理论分析的正确性，将会通过以下四种情形进行对比说明：①只具有SRF-PLL结构；②复数滤波器+SRF-PLL结构；③SRF-PLL+阻抗重塑控制结构；④复数滤波器+SRF-PLL+阻抗重塑控制结构。
当考虑情形①时，在电网阻抗Lg=4.8mH时，系统的并网电流波形如图10a所示，此时并网电流i2已经开始出现明显的振荡，满载时i2a的总谐波畸变率（Total Harmonic Distortion, THD）为4.16%，半载时THD为2.27%；当电网阻抗进一步增大到Lg=5.1mH时，并网电流i2的波形如图10b所示，此时并网电流波形畸变严重，不再满足并网要求，系统稳定性差。由以上分析结果可以得出：在采用情形①的控制结构时，逆变器并网系统所能承受的最大电网阻抗值不会超过5.1mH。
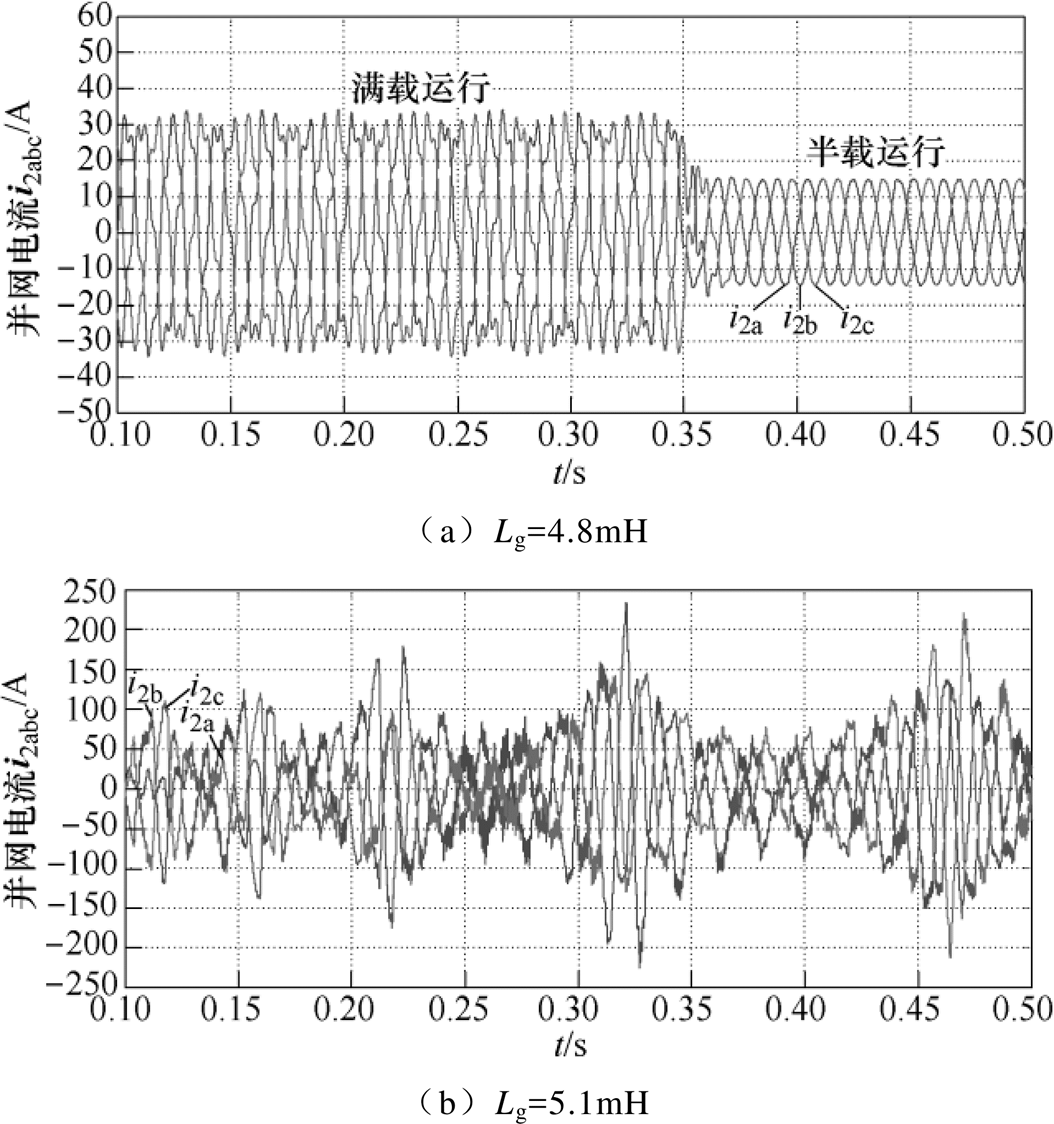
图10 情形①时的三相电流仿真波形
Fig.10 Simulation waveforms of three phase currentwith Case ①
当考虑情形②时，图11a给出了在电网阻抗Lg= 11mH时的并网电流波形，此时i2a满载时THD为0.55%，半载时THD为0.97%；图11b给出了在电网阻抗Lg=15mH时的并网电流波形。
图11 情形②时的三相电流仿真波形
Fig.11 Simulation waveforms of three phase currentwith Case ②
对比图10b和图11a的仿真结果可以看出：复数滤波器结构的引入可以明显提高逆变器并网系统对电网阻抗的适应范围，这与图6基于阻抗的稳定性判据所表征的阻抗相位提升特性分析结果是相符合的。
当考虑情形③时，图12a给出了在电网阻抗Lg= 8mH时的并网电流波形，此时i2a满载时THD为0.60%，半载时THD为0.85%；图12b给出了在电网阻抗Lg=11mH时的并网电流波形，此时i2a满载时THD为7.0%，半载时THD为0.71%。
对比图11a和图12b的仿真结果可以看出：相较于情形②的控制结构，采用情形③进行单一阻抗重塑控制结构时其所能适应的电网阻抗范围将有所下降；但是与采用情形①的控制结构相比，还是能够在一定程度上改善逆变器并网系统对弱电网的适应能力。
当考虑情形④时，图13a给出了在电网阻抗Lg=20mH时的并网电流波形，此时i2a满载时THD为0.25%，半载时THD为0.34%；图13b给出了系统在电网阻抗Lg=27mH时的并网电流波形，可以看出满载运行时波形振荡严重，系统不稳定，在半载运行达到稳态后并网电流i2a的THD为0.60%。
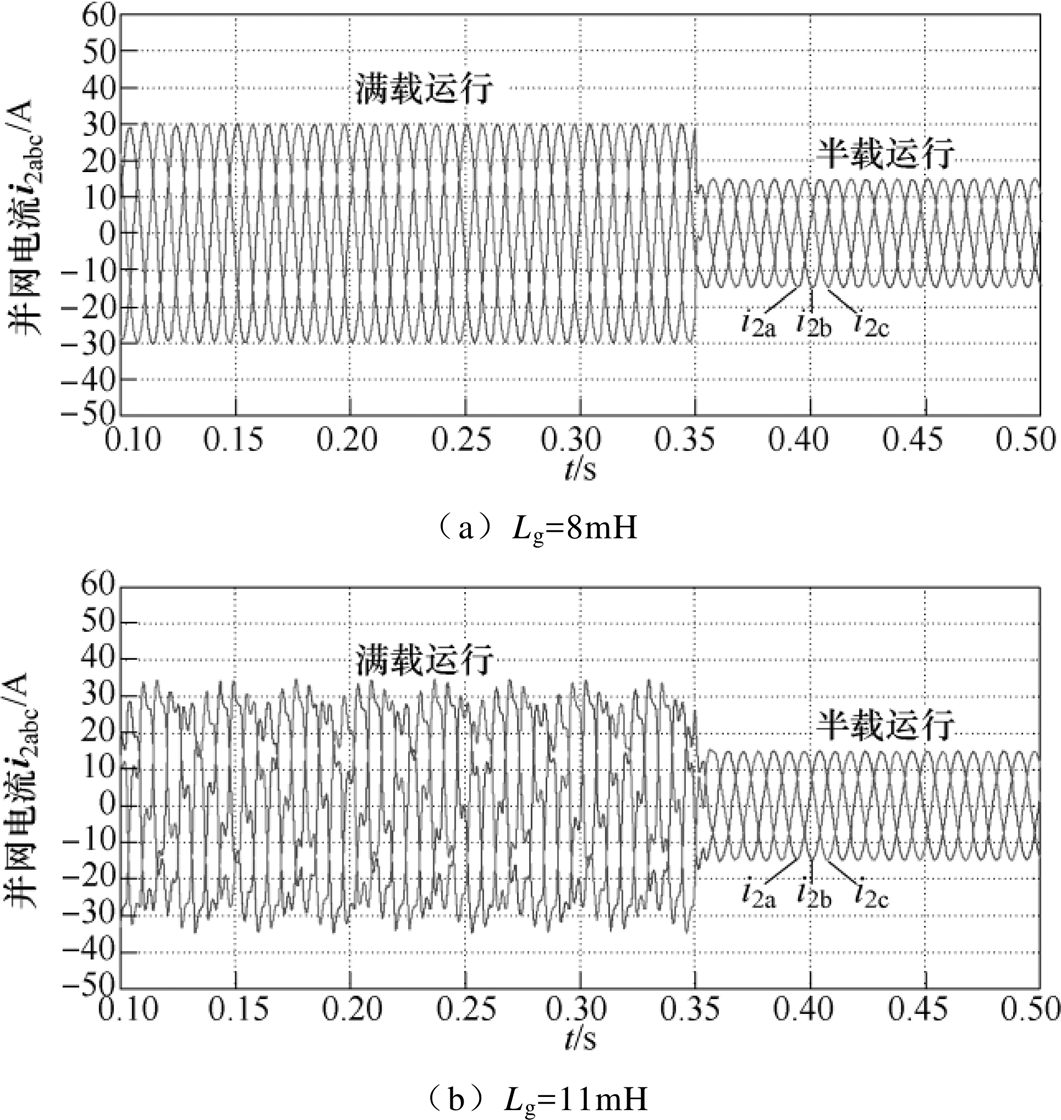
图12 情形③时的三相电流仿真波形
Fig.12 Simulation waveforms of three phase currentwith Case ③
图13 情形④时的三相电流仿真波形
Fig.13 Simulation waveforms of three phase currentwith Case ④
从图13的仿真结果可以看出：当Lg=20mH时三相并网电流依旧稳定，相较于前三种情形，采用情形④的控制结构时逆变器并网系统在弱电网下能够表现出更加优异的工作性能，说明复数滤波器结构与阻抗重塑控制策略的双重引入可以更进一步拓宽逆变器并网系统对电网阻抗的适应范围，显著提高并网逆变器应对弱电网的能力。
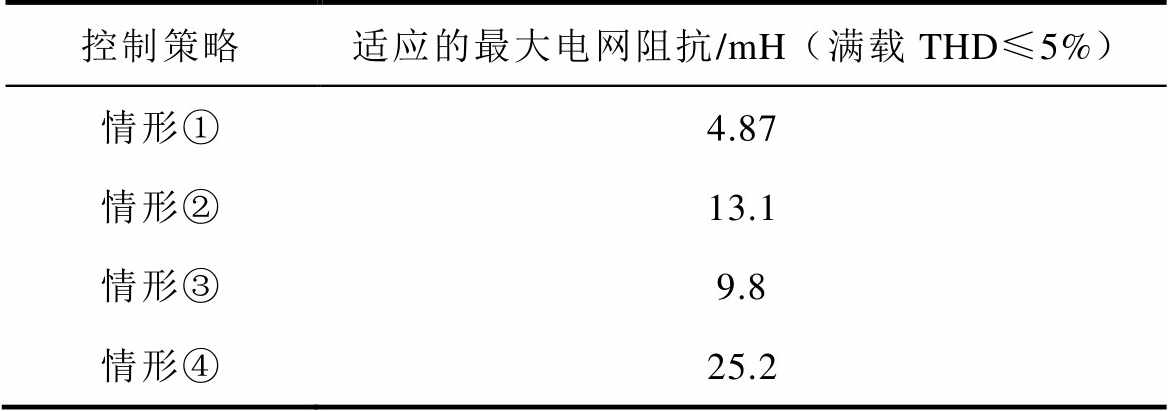
表2给出了逆变器并网系统分别采用以上四种不同控制结构时系统所能适应的最大电网阻抗范围，具体测试条件以及数值结果见表2。
表2 控制策略与适应电网阻抗仿真结果
Tab.2 The simulation results of control strategy and adaptive grid impedance
控制策略适应的最大电网阻抗/mH（满载THD≤5%） 情形①4.87 情形②13.1 情形③9.8 情形④25.2
为了验证本文所提CFPLL-GIS结构以及阻抗重塑控制策略的有效性，搭建了RT-LAB硬件在环实验平台，平台具体结构如图14所示。实验参数与仿真参数一致，控制器采用TI公司的TMS320F2812，系统开关频率fs=10kHz，采样频率fAD=10kHz。
图14 实验平台照片
Fig.14 Experimental platform
图15给出了逆变器并网系统采用情形①的控制结构时，系统分别在电网阻抗Lg=4.8mH与Lg= 5.1mH时的三相电流实验波形。可以看出：在Lg= 4.8mH时并网电流波形已经出现明显的振荡，系统的稳定性较差。
图16给出了逆变器并网系统采用情形②的控制结构时，系统分别在电网阻抗Lg=11mH与Lg= 15mH时的三相电流实验波形。
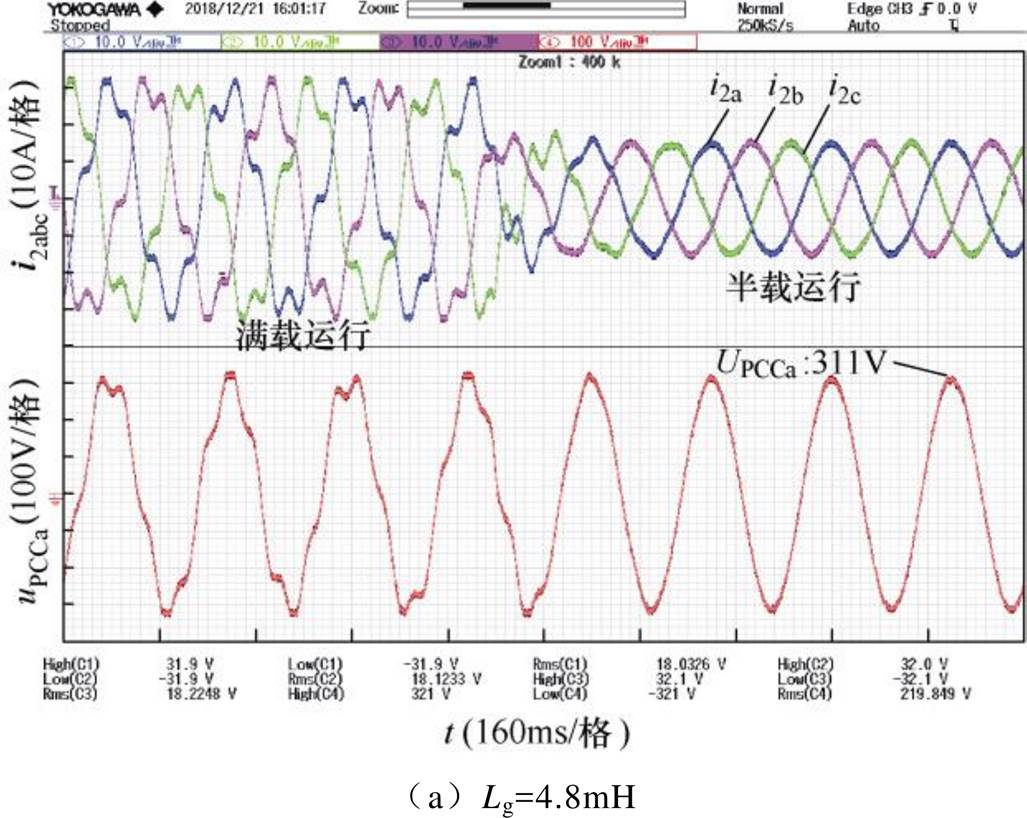
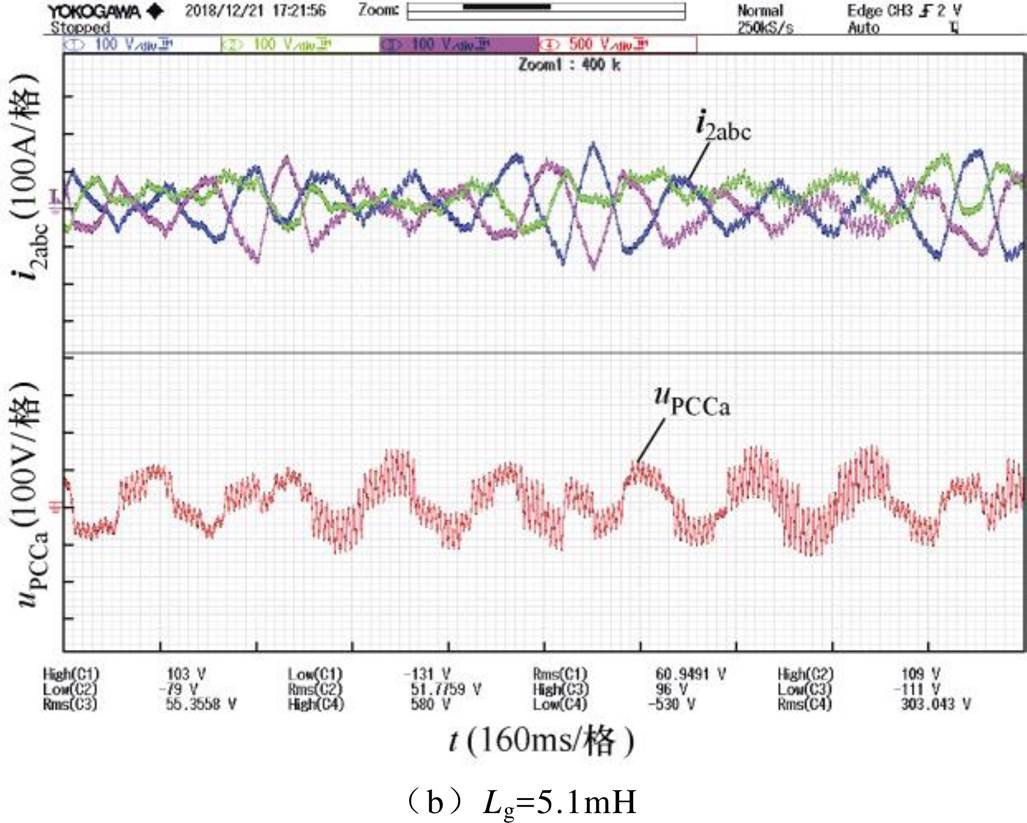
图15 采用情形①控制策略时三相电流实验波形
Fig.15 Experimental waveforms of three phase current with Case ① control strategy
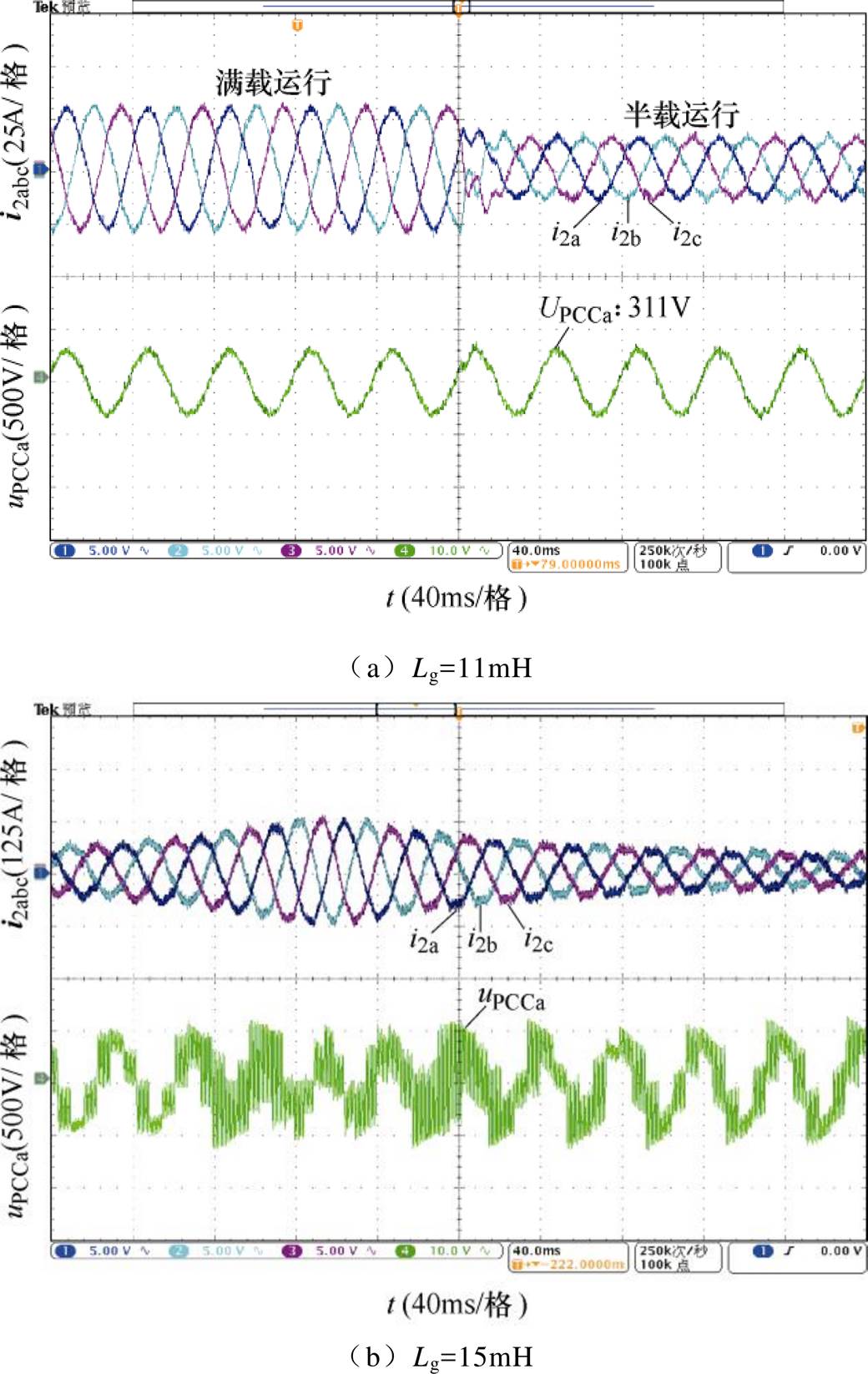
图16 采用情形②控制策略时三相电流实验波形
Fig.16 Experimental waveforms of three phase current with Case ② control strategy
图17给出了逆变器并网系统采用情形③的控制结构时，系统分别在电网阻抗Lg=8mH与Lg= 11mH时的三相电流实验波形。
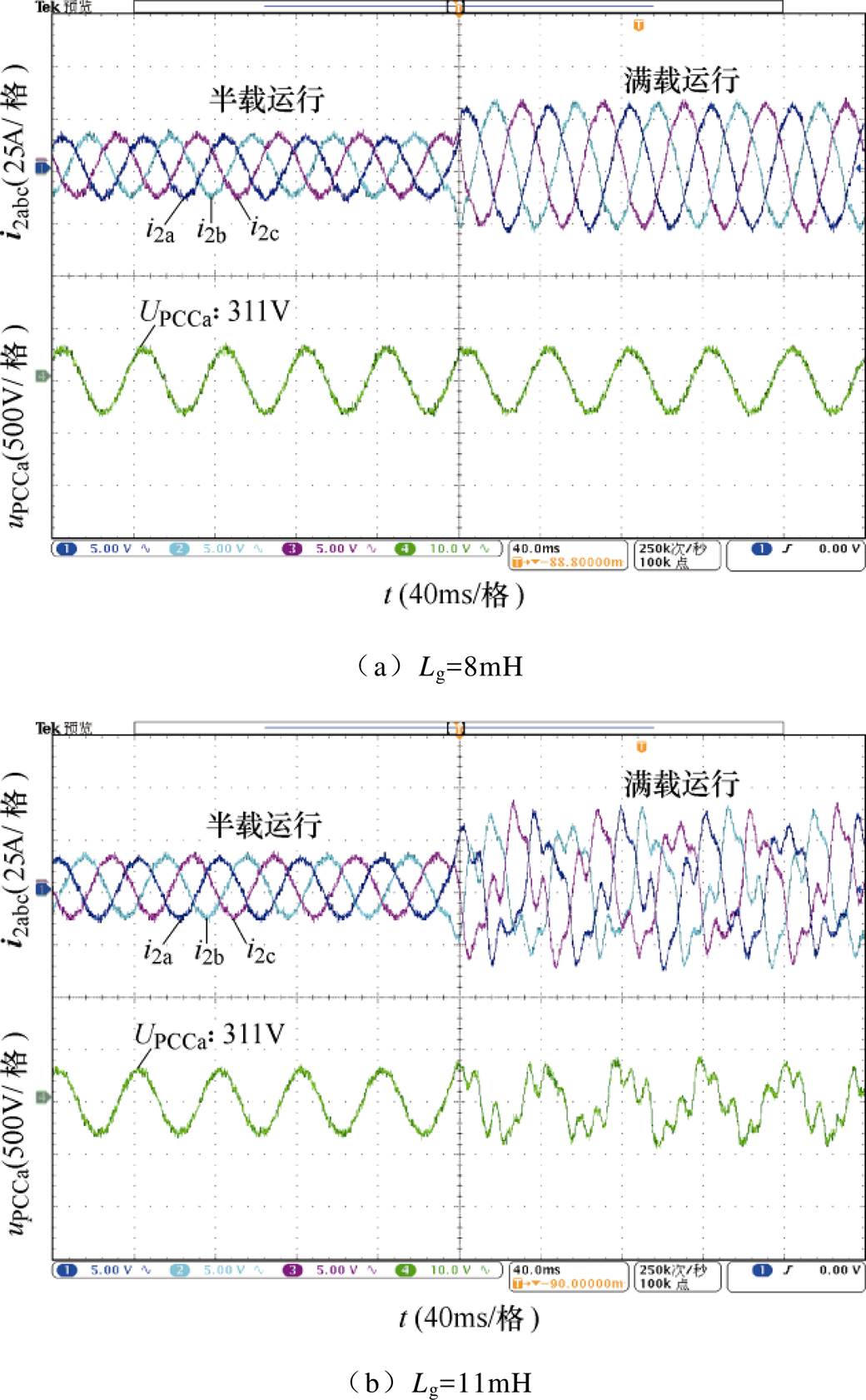
图17 采用情形③控制策略时三相电流实验波形
Fig.17 Experimental waveforms of three phase current with Case ③ control strategy
图18给出了逆变器并网系统采用情形④的控制结构时，系统分别在电网阻抗Lg=20mH与Lg= 27mH时的三相电流实验波形。
通过上述实验结果的对比分析可以进一步证明本文所提CFPLL-GIS控制结构以及阻抗重塑控制策略的合理性与有效性。
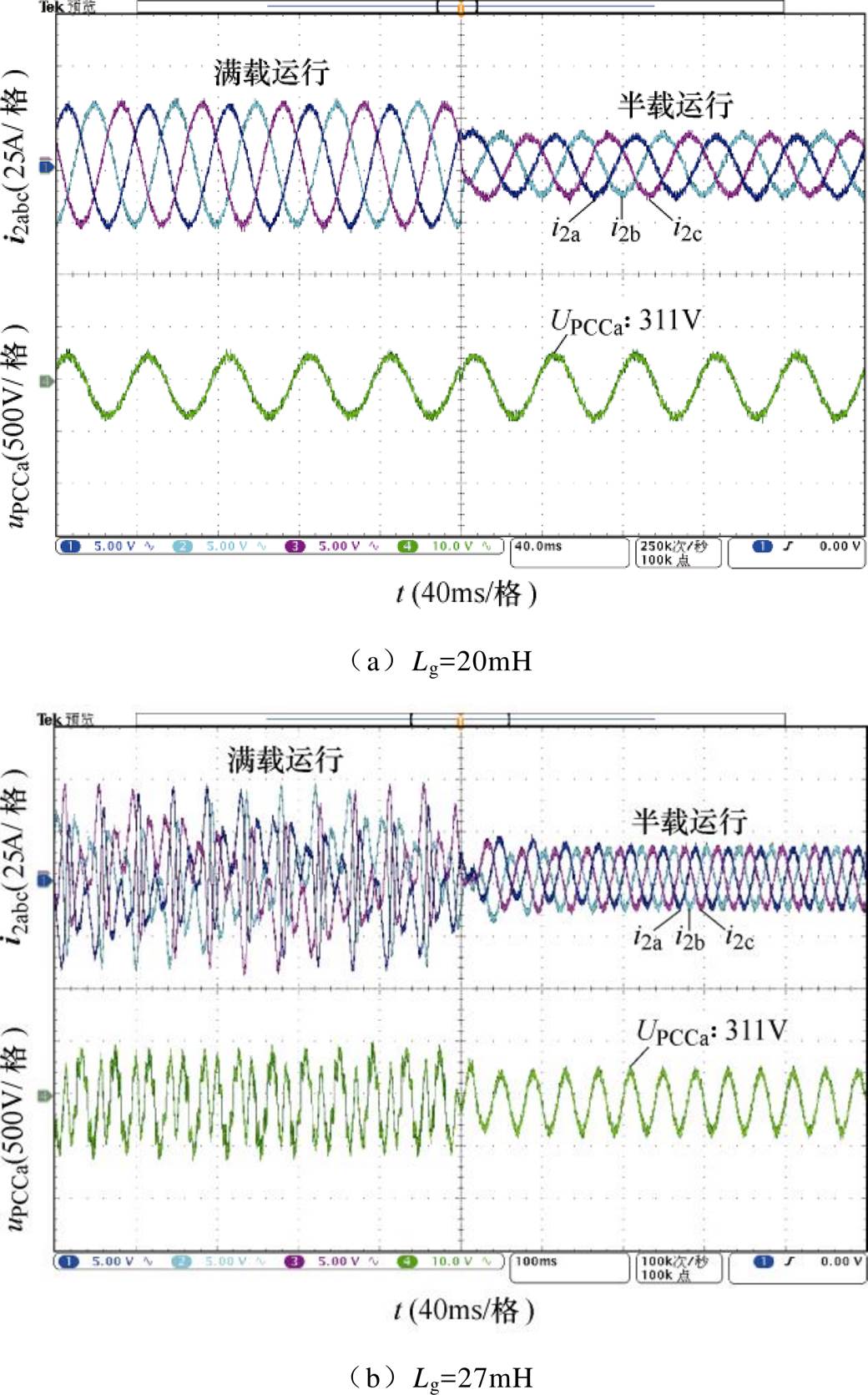
图18 采用情形④控制策略时三相电流实验波形
Fig.18 Experimental waveforms of three phase current with Case ④ control strategy
本文以采用传统SRF-PLL结构的电流双闭环三相LCL型逆变器并网模型为基础，综合考虑具有基波正序电压提取结构的复数滤波器的频率特性，将复数滤波器结构附加在SRF-PLL的前级，构成CFPLL-GIS系统，并利用基于阻抗的稳定性判据分析复数滤波器结构的引入可以对逆变器的等效输出阻抗进行重塑，提高输出阻抗在中频段的相角，改善逆变器并网系统对弱电网的适应能力。同时，在以上分析的基础上，本文以逆变器并网系统的环路增益为设计指导，提出一种逆变器并网系统等效输出阻抗重塑控制策略，显著改善了并网逆变器系统的阻抗特性，保证逆变器并网系统具有充足的稳定裕度，进一步拓宽CFPLL-GIS对电网阻抗的适应范围，增强逆变器在弱电网环境下的并网能力。最后，通过仿真和实验验证了本文理论分析的正确性以及所提控制策略的有效性。
参考文献
[1] Kothari D P, Singal K C, Ranjan R. Renewable energysources andemerging technologies[M]. Second Edition. New Delhi: PHI Learning Private Limited, 2012.
[2] Masoud Davari, Yasser Abdel-Rady I. Mohamed. Robust vector control of a very weak-grid- connected voltage-source converter considering the phase- locked loop dynamics[J]. IEEE Transactions on Power Electronics, 2017, 32(2): 977-994.
[3] 杨树德, 同向前, 尹军, 等. 增强并网逆变器对电网阻抗鲁棒稳定性的改进前馈控制方法[J]. 电工技术学报, 2017, 32(10): 222-231.
Yang Shude, Tong Xiangqian, Yi Jun, et al. An improved grid voltage feedforward strategy for grid-connected inverter to achieve high robust stability against grid-impedance variation[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(10): 222-231.
[4] Etxegarai A, Eguia P, Torres E, et al. Impact of wind power in isolated power systems[C]//2012 16th IEEE Mediterranean Electrotechnical Conference, Yasmine Hammamet, Tunisia, 2012: 63-66.
[5] 杜燕, 崔林波, 杨向真, 等. 并网逆变器的阻抗自适应控制方法[J]. 电力系统自动化, 2018, 42(6): 120-127.
Du Yan, Cui Linbo, Yang Xiangzhen, et al. Adaptive control method of impedance for grid-connected inverters[J]. Automation of Electric Power Systems, 2018, 42(6): 120-127.
[6] 谢小荣, 王路平, 贺静波, 等. 电力系统次同步谐振/振荡的形态分析[J]. 电网技术, 2017, 41(4): 1043-1049.
Xie Xiaorong, Wang Luping, He Jingbo, et al. Analysis of sub synchronous resonance/oscillation types in power systems[J]. Power System Technology, 2017, 41(4): 1043-1049.
[7] 徐路遥, 兰洲, 陈飞, 等. 弱电网下无功控制对并网变流器稳定性影响分析[J]. 电力系统自动化, 2019, 43(15): 56-63.
Xu Luyao, Lan Zhou, Chen Fei, et al. Analysis on impact of reactive power control on stability of grid-connected converter in weak grid[J]. Automation of Electric Power Systems, 2019, 43(15): 56-63.
[8] Xu Jinming, Xie Shaojun, Tang Ting. Evaluations of current control in weak grid case for grid-connected LCL-filtered inverter[J]. IET Power Electronics, 2013, 6(2): 227-234.
[9] Xu Jinming, Xie Shaojun, Zhuang Binfeng, et al. Robust grid current control with impedance-phase shaping for LCL-filtered inverters in weak and distorted grid[J]. IEEE Transactions on Power Electronics, 2018, 33(12): 10240-10250.
[10] 方天治, 黄淳, 陈乃铭, 等. 一种提高弱电网下LCL型并网逆变器鲁棒性的相位超前补偿策略[J].电工技术学报, 2018, 33(20): 4813-4822.
Fang Tianzhi, Huang Chun, Chen Naiming, et al. A phase-lead compensation strategy on enhancing robustness of LCL-type grid-tied inverters under weak grid conditions[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 4813-4822.
[11] 陈新, 王赟程, 华淼杰, 等. 采用混合阻尼自适应调整的并网逆变器控制方法[J]. 中国电机工程学报, 2016, 36(3): 765-774.
Chen Xin, Wang Yuncheng, Hua Miaojie, et al. Grid-connected inverters control schemes based on hybrid damping adaptive control[J]. Proceedings of the CSEE, 2016, 36(3): 765-774.
[12] 陈燕东, 王伊, 周乐明, 等. 弱电网下LCL逆变器阻尼谐振抑制与功率快速调节方法[J]. 电工技术学报, 2018, 33(11): 2565-2575.
Chen Yandong, Wang Yi, Zhou Yueming, et al. Damping resonance suppression and fast power regulation method for LCL-type inverter under weak grid[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2565-2575.
[13] Zhou Jenny Z, Ding Hui, Fan Shengtao, et al. Impact of short-circuit ratio and phase-locked-loop parameters on the small-signal behavior of a VSC-HVDC converter[J]. IEEE Transactions on Power Delivery, 2014, 29(5): 2287-2296.
[14] 吴广禄, 周孝信, 王姗姗, 等. 柔性直流输电接入弱交流电网时锁相环和电流内环交互作用机理解析研究[J]. 中国电机工程学报, 2018, 38(9): 2622-2634.
Wu Guanglu, Zhou Xiaoxin, Wang Shanshan, et al. Analytical research on the mechanism of the interaction between PLL and inner current loop when VSC-HVDC connected to weak grid[J]. Proceedings of the CSEE, 2018, 38(9): 2622-2634.
[15] 张旸, 陈新, 王昀, 等. 弱电网下并网逆变器的阻抗相角动态控制方法[J]. 电工技术学报, 2017, 32(1): 97-106.
Zhang Yang, Chen Xin, Wang Yun, et al. Impedance- phased dynamic control method of grid-connected inverters under weak grid condition[J]. Transactions of China Electrotechnical Society, 2017, 32(1): 97-106.
[16] Hu Jiabing, Huang Yunhui, Wang Dong, et al. Modeling of grid-connected DFIG-based wind turbines for DC-Link voltage stability analysis[J]. IEEE Transactions on Sustainable Energy, 2015, 6(4): 1325-1336.
[17] 张学广, 付志超, 陈文佳, 等. 弱电网下考虑锁相环影响的并网逆变器改进控制方法[J]. 电力系统自动化, 2018, 42(7): 139-145.
Zhang Xueguang, Fu Zhichao, Chen Wenjia, et al. An improved control method for grid-connected inverters considering impact of phase-locked loop under weak grid condition[J]. Automation of Electric Power Systems, 2018, 42(7): 139-145.
[18] 杨苓, 陈燕东, 周乐明, 等. 弱电网下锁相环对三相LCL型并网逆变器小扰动建模影响及稳定性分析[J]. 中国电机工程学报, 2018, 38(13): 3792-3805.
Yang Ling, Chen Yandong, Zhou Yueming, et al. Effect of phase locked loop on the small-signal perturbation modeling and stability analysis for three- phase LCL-type grid-connected inverter in weak grid[J]. Proceedings of the CSEE, 2018, 38(13): 3792-3805.
[19] Huang Yunhui, Yuan Xiaoming, Hu Jibing, et al. DC-bus voltage control stability affected by AC-bus voltage control in VSCs connected to weak AC grids[J]. IEEE Journal of Emerging and Selected Topics in Power Electronic, 2016, 4(2): 445-458.
[20] Guo Xiaoqiang, Wu Weiyang, Chen Zhe, et al. Multiple-complex coefficient-filter-based phase-locked loop and synchronization technique for three-phase grid-interfaced converters in distributed utility networks[J]. IEEE Transactions on Industrial Electro- nics, 2011, 58(4): 1194-1204.
[21] 唐轶, 沈佳, 刘齐齐, 等. 改进型解耦自适应复数滤波器的锁相环研究[J]. 电力系统保护与控制, 2017, 45(18): 120-127.
Tang Yi, Shen Jia, Liu Qiqi, et al. Study on improved crossing-decoupling frequency-adaptive complex filter PLL[J]. Power System Protection and Control, 2017, 45(18): 120-127.
Research on Adaptability of Grid-Connected Inverter with Complex Coefficient-Filter Structure Phase Locked Loop to Weak Grid
Abstract According to the traditional synchronous rotating frame PLL (SRF-PLL) grid- connected inverter system, combined with the fundamental positive sequence voltage extraction characteristics of complex coefficient-filter, an grid-connected inverter system with complex coefficient-filter-based PLL (CFPLL-GIS) is constructed. On this basis, considering the influence of PLL, the impedance model of CFPLL-GIS is established. The impedance-based stability criterion analysis shows that the introduction of complex coefficient-filter structure can improve the phase angle of equivalent output impedance of grid-connected inverter system in the middle frequency band, and can significantly improve the adaptability of grid-connected inverter system to weak grid. Meanwhile, taking the loop-gain of the grid-connected inverter system as the design guide, a remodeling control strategy of equivalent output impedance of the grid-connected inverter system is proposed to improve the impedance characteristics of the system, ensuring sufficient stability margin of the grid-connected inverter system and further broadening the adaptive range of the CFPLL-GIS to the grid impedance. Simulation and experimental measurements verify the proposed strategy.
keywords：Weak grid, complex coefficient-filter, phase locked loop, grid-connected inverter, impedance criterion, impedance remodeling, stability margin
中图分类号：TM464
DOI: 10.19595/j.cnki.1000-6753.tces.190619
国家自然科学基金（51577055）、国家自然科学基金青年基金（51707014）和湖南省自然科学基金青年基金（2018JJ3534）资助项目。
收稿日期 2019-05-22
改稿日期 2019-07-10
涂春鸣 男，1976年生，教授，博士生导师，研究方向为电力电子技术及其在电力系统中的应用。E-mail: chunming_tu@263.net
高家元 男，1991年生，博士研究生，研究方向为电力电子技术、分布式发电和逆变器控制技术。E-mail: Jiayuan_gao@163.com（通信作者）
（编辑 赵 鹏）