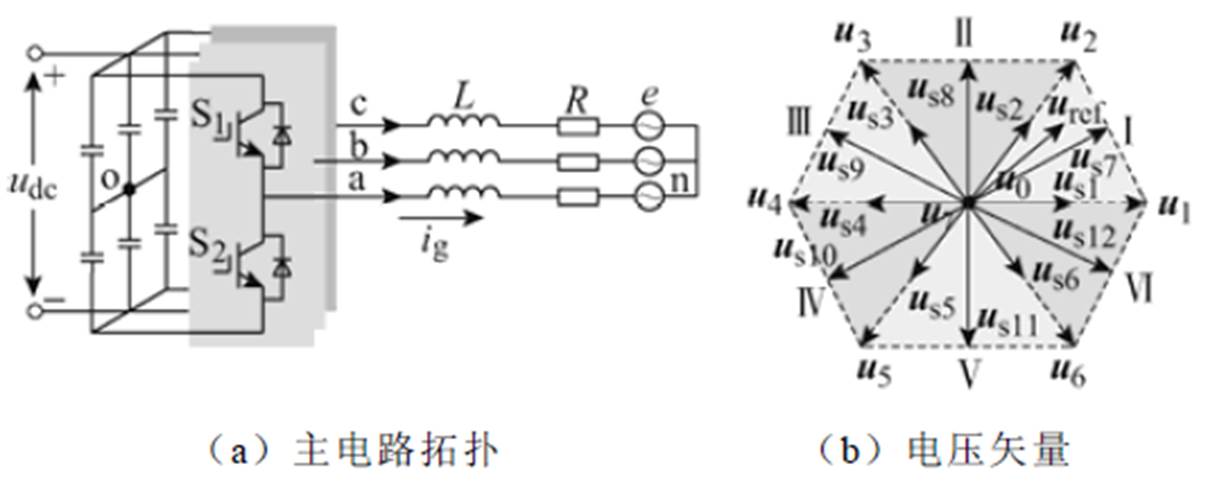
图1 并网逆变器的电路拓扑及电压矢量
Fig.1 Topology and voltage vectors of the grid-connected inverters
摘要 近年来,模型预测控制被广泛应用于并网逆变器的控制中。为进一步降低并网电流的谐波,提高系统的可靠性,该文提出一种并网逆变器无电网电压传感器双矢量模型预测控制方法。首先,提出一种基于改进型滑模观测器的电网电压在线观测方法,以实现无电网电压传感器控制。所提方法不需要电网的精确频率即可实现电网电压的频率自适应观测。同时,由于观测器中低通滤波器的使用,电网电压背景谐波对电流控制的影响得到一定程度的抑制。其次,为了进一步降低电流谐波,文中基于调制模型预测控制的原理提出一种双矢量模型预测控制方法,并从理论上证明了所提双矢量模型预测控制方法的有效性。详细的对比实验结果验证了所提方法的正确性。
关键词:并网逆变器 模型预测控制 滑模观测器 双矢量 无电网电压传感器
近年来,两电平并网逆变器在新能源并网发电系统中的应用越来越广,其安全稳定运行也直接影响着新能源并网发电系统的可靠性[1-2]。
常用的并网逆变器控制方法主要包括矢量控制和直接功率控制等。然而,矢量控制需要较多的坐标变换运算和较复杂的脉冲宽度调制模块,直接功率控制则存在开关频率不固定、功率纹波较大等问题。随着微处理器技术和先进控制理论的快速发展,近年来,模型预测控制等先进控制策略在并网逆变器控制中的应用也越来越广[3-4]。然而,无论是矢量控制、直接功率控制,还是模型预测控制,都常常需要至少5个传感器以采集电压、电流等反馈信号,包括两个电网电压传感器、两个并网电流传感器和一个直流电压传感器。传感器一旦发生故障,必然会导致控制系统失稳,进而会大大降低新能源并网发电系统的可靠性。
为了减少电流传感器的使用,文献[5-7]研究了基于单电流采样的三相交流电流重构方法。然而,电流重构的方法受采样噪声和死区的影响,其重构精度较低且存在一定的盲区,因此会降低电流的控制精度。
考虑到高精度的交流电流采样对实现电流闭环控制和系统过电流保护具有重要作用,不宜进行重构,文献[8-17]研究了并网逆变器的无电网电压传感器控制方法,以避免使用电网电压传感器,从而提高新能源并网发电系统的运行可靠性。无电网电压传感器的控制方法通常可分为虚拟磁链法[8-12]和电网电压观测法[13-17]两类。
文献[8]研究了基于虚拟磁链的并网逆变器控制方法。然而,观测虚拟磁链时需要进行纯积分运算,而这受积分初始值和直流偏置的影响较严重。针对该问题,文献[9]研究了采用一阶低通滤波器代替纯积分的虚拟磁链观测方法。然而,会引入相位和幅值偏移。文献[10]研究了一种带反馈补偿的虚拟磁链观测方法,克服了积分初始值的影响,但其反馈限幅器的设计对磁链观测精度的影响较大。为了实现虚拟磁链的准确观测,文献[11-12]进一步研究了基于二阶广义积分器的虚拟磁链观测方法。然而,这一类方法需要已知精确的电网频率信息。当电网频率出现不确定偏移时,上述方法的虚拟磁链观测精度会大大降低。
此外,文献[13-17]研究了电网电压观测方法,以实现并网逆变器的无电网电压传感器控制。其中,文献[13-14]研究了电网电压自适应神经网络观测器的设计方法,然而,这类方法需要同时在线调整多个观测器参数。文献[15-16]设计了状态观测器以实现电网电压观测。然而,观测器增益矩阵的设计较复杂。为了简化观测器设计,提高观测器的收敛性,文献[17]设计了一种基于滑模观测器的电网电压观测方法。文中详细分析了滑模观测器的设计方法。然而,该方法对电网频率偏移也较敏感。
此外,虽然文献[17]也研究了并网逆变器的无电网电压传感器模型预测控制方法,但由于每个控制周期仅采用一个电压矢量作用,其电流谐波较大。为了降低模型预测控制输出的电流谐波,多矢量模型预测控制在近年来也得到广泛关注[18-22]。在多个电压矢量共同作用时,需要采用合理的方法计算每个矢量的作用时间。这种方法主要包含两类,即基于无差拍思想的矢量作用时间计算方法[18-19]和基于调制模型预测控制思想的矢量作用时间计算方法[20-22]。前者理论上可以获得精确的矢量作用时间,但存在计算量大等缺点。后者则由于其实现简单、控制效果较好等优点而在诸多文献中得到研究。然而,虽然已有文献通过仿真和实验研究证明了调制模型预测控制的有效性,但关于其有效性的理论证明尚未见报道。
为了实现并网逆变器的无电网电压传感器模型预测控制,并降低电流谐波,本文提出了一种基于改进型滑模观测器的电网电压观测方法,并设计了一种双矢量模型预测控制方法,以进一步降低电流谐波。所提电网电压观测方法对电网频率偏移不敏感,因此,在电网频率闪变时可以获得更高的电网电压观测精度。所提双矢量模型预测控制方法采用调制模型预测控制的思想计算矢量作用时间,从而降低了算法复杂度。同时,文中还给出了详细的理论分析,证明了所提双矢量法的有效性。最后,实验结果进一步验证了本文所提方法的正确性。
常规两电平并网逆变器的电路拓扑和电压矢量如图1所示。其8个基本电压矢量分别为u0(0 0 0),u1(1 0 0),u2(1 1 0),u3(0 1 0),u4(0 1 1),u5(0 0 1),u6(1 0 1),u7(1 1 1),如图1b所示。
并网逆变器在静止ab 坐标系上的数学模型可表示为

图1 并网逆变器的电路拓扑及电压矢量
Fig.1 Topology and voltage vectors of the grid-connected inverters
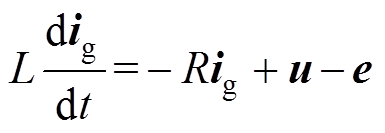 (1)
(1)式中,u为并网逆变器的输出电压矢量;e为电网电压矢量;ig为并网电流矢量;L为滤波电感;R为滤波电感上的杂散电阻;u=[uaub]T;e=[eaeb]T;ig= [ia ib]T。
对式(1)进行离散化,可得
 (2)
(2)式中,变量x(k)代表该变量在k时刻的值;Ts为控制周期。
为了实现模型预测控制,并进行延时补偿,可首先根据当前时刻并网逆变器输出的电压矢量u(k)和式(2)预测k+1时刻的并网电流ig(k+1),然后,将并网逆变器的8个电压矢量u(k+1)依次代入式(3)和式(4)进行电流预测和目标函数优化,并最终选出使目标函数最小的电压矢量作为最优矢量。考虑到电网电压变化较慢,预测时可近似认为e(k+1)=e(k)。
 (3)
(3)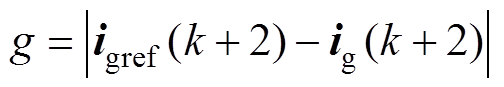 (4)
(4)
式中,igref(k+2)为电流指令,igref(k+2)=[igaref(k+2) igbref(k+2)]T。
并网逆变器常采用电网电压定向的矢量控制,以实现有功功率和无功功率的解耦。控制系统常常直接给定有功电流igdref和无功电流igqref,然后可根据式(5)计算得到电流指令igref(k+2)。
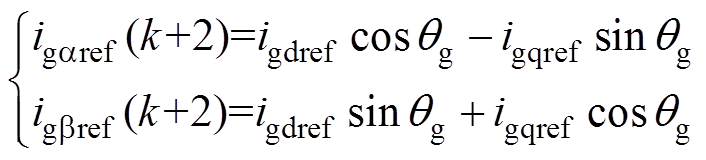 (5)
(5)式中,qg为电网电压矢量的角度。
由上述可见,为了实现并网逆变器的模型预测控制,一方面需要采样电网电压进行电流预测;另一方面还需要求取电网电压矢量的角度以进行电流解耦控制。因此,常规的控制方法常常需要至少两个交流电压传感器以采样电网电压。然而,一旦电压传感器出现故障,并网逆变器将无法稳定运行。
为了提高并网逆变器的运行可靠性,避免使用交流电压传感器,本文提出了一种改进的电网电压观测方法,以实现并网逆变器的无电网电压传感器控制。
首先,根据并网逆变器的数学模型,本文建立如下滑模观测器,满足
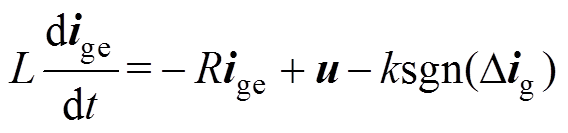 (6)
(6)式中,ige为估计的电网电流;sgn( )为符号函数;Dig为电流估计误差,满足Dig=ige-ig。
由式(1)和式(6)可得
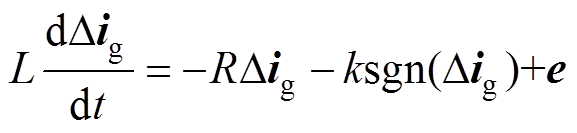 (7)
(7)为保证所设计的滑模观测器收敛,需要满足Dig(dDig/dt)<0[23-24],由此可得滑模观测器收敛的条件为
 (8)
(8)
当滑模观测器收敛时,Dig=dDig/dt =0,由此可得
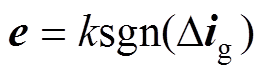 (9)
(9)然而,由于滑模项ksgn(Dig)含有大量高频噪声,因此,由式(9)无法直接得到电网电压信号,必须要对高频滑模信号进行滤波和补偿。
为了根据式(9)得到电网电压基波信号,可首先采用低通滤波器对滑模项ksgn(Dig)进行处理,以滤除高频滑模噪声,满足
 (10)
(10)式中,eLPF1=[eLPFa1 eLPFb1]T;GLPF为低通滤波器的传递函数,满足
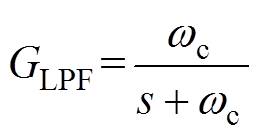 (11)
(11)
式中,wc为低通滤波器的截止频率。
虽然低通滤波器可以滤除高频滑模噪声,但电网电压基波也会受低通滤波器的影响。若电网电压的基波角频率为wg,则低通滤波器对电网电压基波产生的幅值衰减DE和相位偏移Dq 可表示为
 (12)
(12)为了获得准确的电网电压,必须根据式(12)对电网电压的幅值和相位分别进行补偿[25]。然而,式(12)所示的补偿方法需要精确的电网电压角频率信息。虽然采用锁相环可以估计得到电网电压的角频率,但其估计精度受控制器参数的影响。
为了获得准确的电网电压,且不使用电网电压角频率信息,本文提出了一种改进的滤波和补偿方法。该方法的基本思想是同一个低通滤波器对同一频率的信号产生的幅值衰减和相位偏移是相同的。
根据该原理,本文引入了第二个低通滤波器GLPF以对滤波后的信号eLPF1再次进行低通滤波,从而得到一个新的变量eLPF2,满足
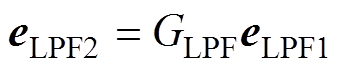 (13)
(13)式中,eLPF2=[eLPFa2eLPFb2]T。
由于eLPF1经过了低通滤波器GLPF的处理,基本不含高频滑模噪声,因此,其幅值E1和相位q1,满足
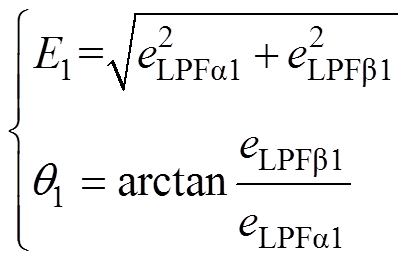 (14)
(14)同理,eLPF2的幅值E2和相位q2满足
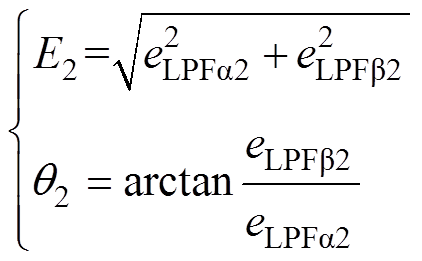 (15)
(15)
此时,结合式(13)~式(15)可知,低通滤波器GLPF产生的幅值衰减和相位偏移可表示为
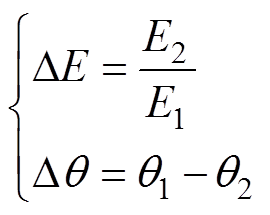 (16)
(16)对比式(12)和式(16)可知,本文所提改进的电网电压滤波和补偿方法不需要已知精确的电网电压角频率,即可对电网电压进行相位和幅值补偿。经过补偿后的电网电压可表示为
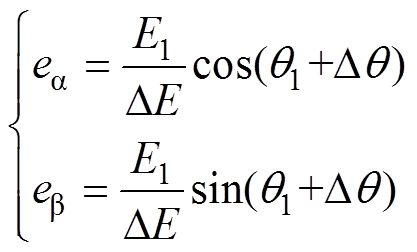 (17)
(17)
将式(17)所估计的电网电压代入模型预测控制系统,即可实现并网逆变器的无电网电压传感器控制。由于上述改进的电网电压观测方法无需精确的电网角频率,因此,即使在电网频率出现闪变时,本文所提方法依然可以获得较高的电网电压观测精度。同时,由于低通滤波器GLPF的使用,电网固有背景谐波也得到一定程度的抑制,从而有助于降低电网背景谐波对电流控制的影响,降低电流谐波。
为了实现并网逆变器的无电网电压传感器模型预测控制,并进一步降低电流谐波,本文进一步提出了一种双矢量模型预测控制方法,并给出了详细的理论分析证明。
首先,本文根据两电平并网逆变器的8个基本电压矢量,定义了12个虚拟矢量usi(i=1, 2,…,12)。这12个虚拟矢量分别由电压矢量(u0, u1),(u7, u2),(u0, u3),(u7, u4),(u0, u5),(u7, u6),(u1, u2),(u2, u3),(u3, u4),(u4, u5),(u5, u6),(u6, u1)合成,如图1b所示。
根据伏秒平衡原理,合成的虚拟电压矢量与基本电压矢量之间的关系可表示为
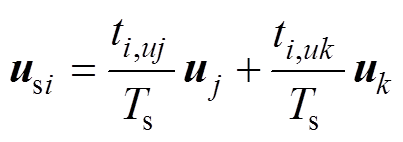 (18)
(18)式中,ti,uj和ti,uk分别为电压矢量uj和uk的作用时间,满足ti,uj+ti,uk=Ts。
为了降低计算复杂度,本文根据无差拍控制的思想直接计算目标电压矢量所在的扇区,然后选择3个虚拟矢量作为备选矢量,再进行优化运算。电压矢量平面可以平分为6个扇区,分别为Ⅰ、Ⅱ、Ⅲ、Ⅳ、Ⅴ、Ⅵ,如图1b所示。
根据无差拍控制思想可知,目标电压矢量uref (k+1) 满足
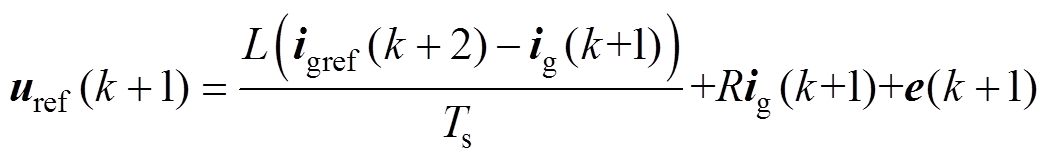 (19)
(19)然后由式(19)易知目标电压矢量所在的扇区。例如,若目标电压矢量位于扇区Ⅰ,则选择虚拟矢量us1, us2, us7来进行预测控制。这样,每个控制周期都只需要采用3个虚拟矢量进行预测优化,从而降低了计算复杂度。
在确定了3个备选虚拟矢量后,需要计算合成虚拟矢量的基本电压矢量作用时间。为了简化算法,本文采用调制模型预测控制的思想进行矢量作用时间的计算,其基本思想是相应矢量对应的目标函数越大,即意味着其控制误差越大,因此,其作用时间应该越短[20-22]越好。例如,虚拟矢量us7的作用时间分配满足
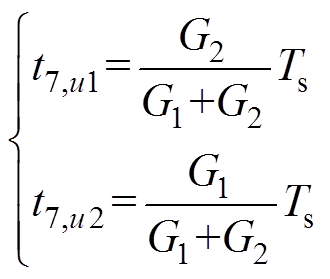 (20)
(20)式中,Gp(p =0, 1,…,7)表示并网逆变器8个基本电压矢量对应的目标函数,其定义为
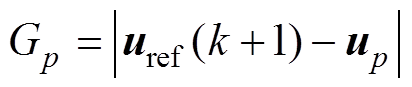 (21)
(21)
基于式(18)和式(20)可得具体的虚拟矢量值,然后将求解出的3个虚拟矢量依次代入式(21),并选择一个使式(21)最小的虚拟矢量作为最优输出,从而实现并网逆变器的双矢量模型预测控制。
虽然已有文献通过仿真和实验证明了调制模型预测控制的有效性,但到目前为止,关于调制模型预测控制有效性的理论证明尚未见报道。本文基于调制模型预测控制的思想设计了一种双矢量模型预测控制方法。为了证明其有效性,本文进行了详细的理论分析。
图2给出了目标电压矢量uref位于扇区I时的情况。图中,us7由u1和u2合成,满足
 (22)
(22)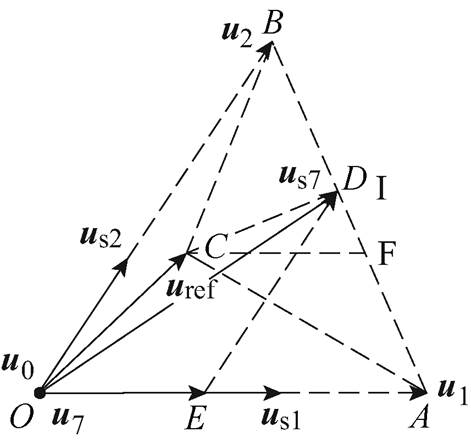
图2 电压矢量分布示意图
Fig.2 Voltage vector distribution diagram
由式(22)可知
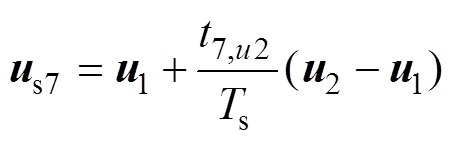 (23)
(23)结合图2可知,|AD|=t7,u2/Ts|(u2-u1)|,|BD|= t7,u1/Ts|u2-u1|。由式(20)可知,t7,u1/t7,u2=G2/G1,因此,|BD|/|AD|= G2/G1。此外,由式(21)和图2可知,G1=|AC|,G2=|BC|。因此,|BD|/|AD|=|BC|/|AC|。
假设线段AB上存在一点F,满足|BC|=|BF|。由于|BC|+|AC|>|AB|,且|AB|=|BF|+|AF|,因此,|AC|>|AF|,且
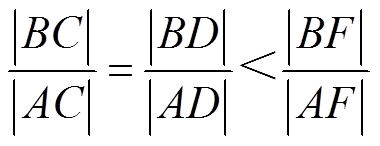 (24)
(24)由此可知,点F必然位于线段AD上。由于|BC|= |BF|,所以∠BCF=∠BFC。同时,由于∠CDB是△CDF的一个外角,因此满足∠CDB>∠BCF。由于∠CBD小于p/3,所以∠BCF和∠BFC必然大于p/3,∠CDB>∠BCF>p/3>∠CBD。根据正弦定理可知,|BC|>|CD|。由于|BC|代表电压矢量u2的控制误差,|CD|代表电压矢量us7的控制误差,因此,虚拟矢量us7作用时,其控制误差比矢量u2要小。同理,可以证明虚拟矢量us7作用时,其控制误差比矢量u1也小。由此可知,采用式(20)计算虚拟矢量作用时间,并合成虚拟矢量进行作用时,与单矢量法相比,有助于减小控制误差,提高控制精度。这就从理论上证明了调制模型预测控制思想的有效性。
为了验证本文所提并网逆变器无电网电压传感器双矢量模型预测控制方法的有效性,建立了如图3所示的实验平台,并进行了详细的对比实验研究。实验所用参数见表1。实验系统采用DSP28335芯片作为主控制器,采样频率设为15kHz,死区时间为2ms。
首先,为了验证本文所提方法的有效性,图4~图7给出了理想电网下常规有电网电压传感器单矢量法、无电网电压传感器单矢量法和无电网电压传感器双矢量法的动稳态电流波形及其快速傅里叶变换(Fast Fourier Transform, FFT)分析结果。为了方便起见,本文称常规有电网电压传感器单矢量法为方法1,称无电网电压传感器单矢量法为方法2,称无电网电压传感器双矢量法为所提方法。方法2采用2.2节所示传统的滤波和补偿方法进行电网电压观测,所提方法采用2.3节改进滤波和补偿方法进行电网电压观测。在该实验中,无功电流igqref设为0,有功电流igdref由3A突增为10A。
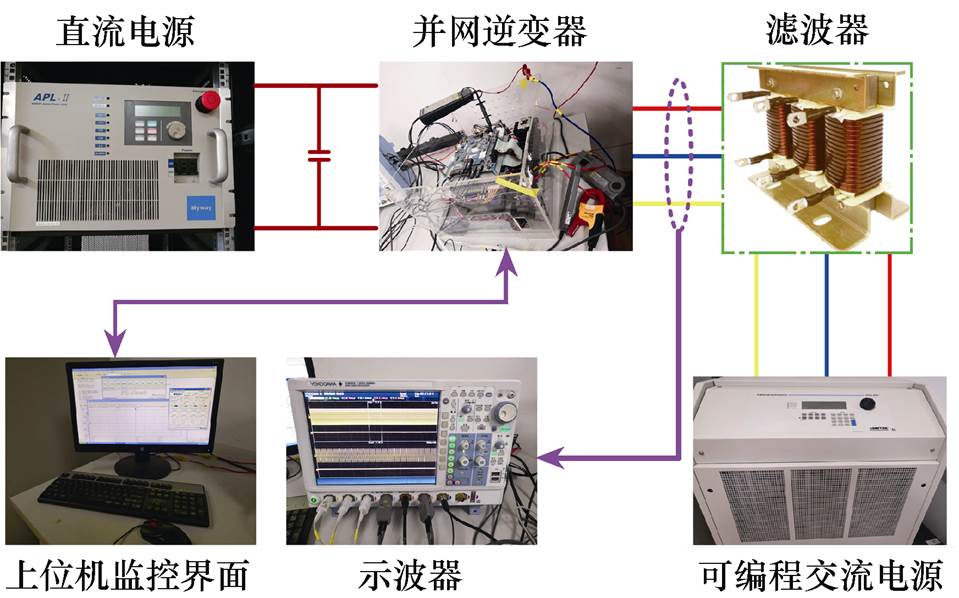
图3 实验平台
Fig.3 Photo of the experimental platform
表1 实验系统参数
Tab.1 Parameters of the experimental system
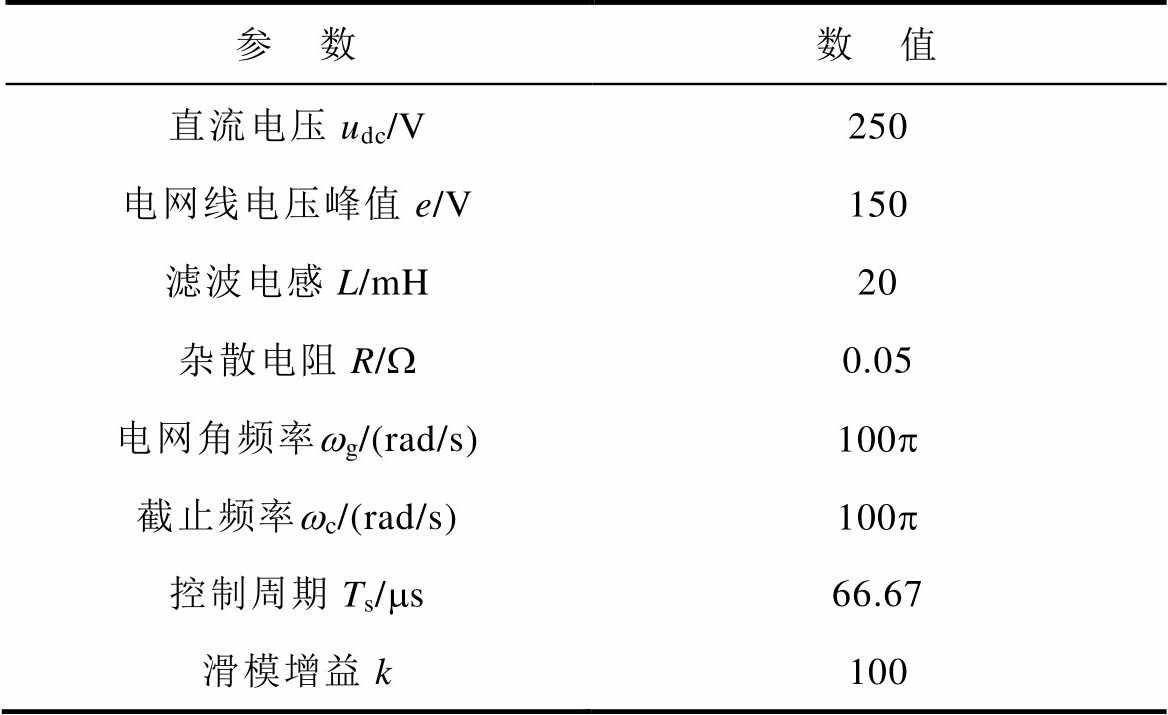
参 数数 值 直流电压udc/V250 电网线电压峰值e/V150 滤波电感L/mH20 杂散电阻R/W0.05 电网角频率wg/(rad/s)100p 截止频率wc/(rad/s)100p 控制周期Ts/ms66.67 滑模增益k100
理想电网下方法1和方法2的实验结果如图4和图5所示,可见,方法1和方法2可以获得类似的电流动稳态控制特性,这说明采用2.2节所示传统的滤波和补偿方法进行电网电压观测是有效的。理想电网下所提方法的实验结果如图6所示,对比图4~图6进一步可见,采用本文所提改进型电网电压观测方法和双矢量模型预测控制策略,可以明显减小电流稳态纹波,这证明了本文所提方法的有效性,也证明了3.2节理论分析的正确性。
图7给出了有功电流igdref =3A时三种方法的电流FFT分析结果,由此可见,与方法1、方法2相比,本文所提方法可明显降低电流总谐波畸变率(Total Hormonic Distortion, THD),再次证明了其优越性。
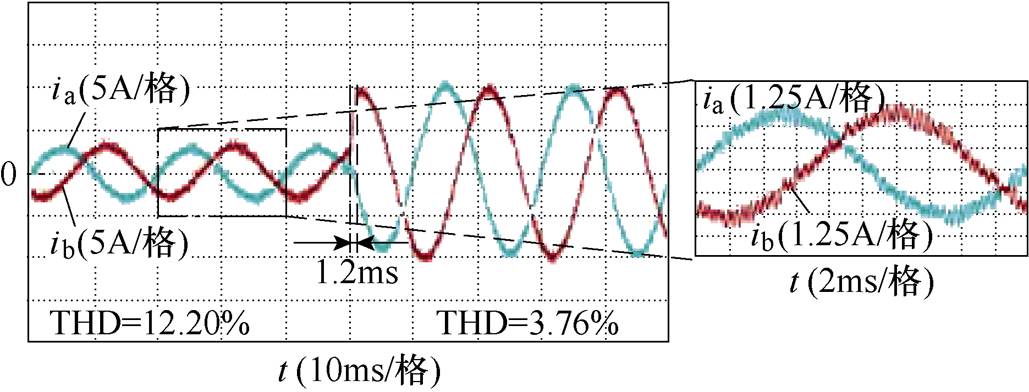
图4 理想电网下方法1的实验结果
Fig.4 Experimental results of method 1 under ideal grid voltage conditions

图5 理想电网下方法2的实验结果
Fig.5 Experimental results of method 2 under ideal grid voltage conditions
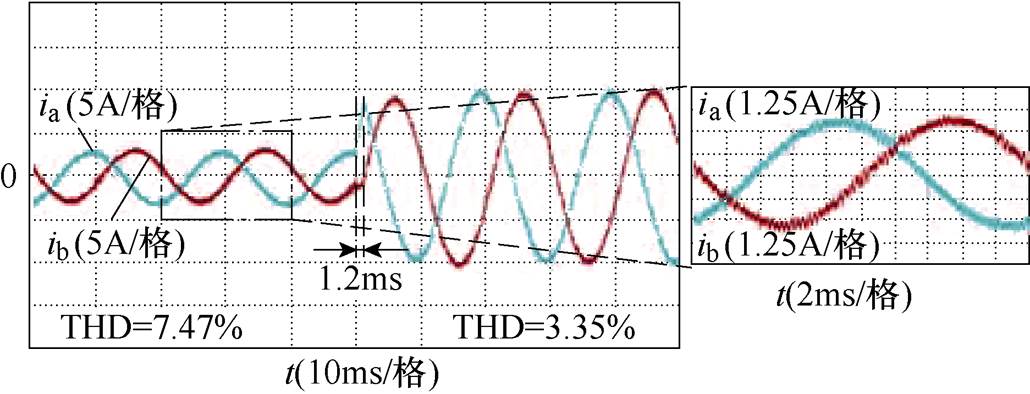
图6 理想电网下所提方法的实验结果
Fig.6 Experimental results of the proposed method under ideal grid voltage conditions
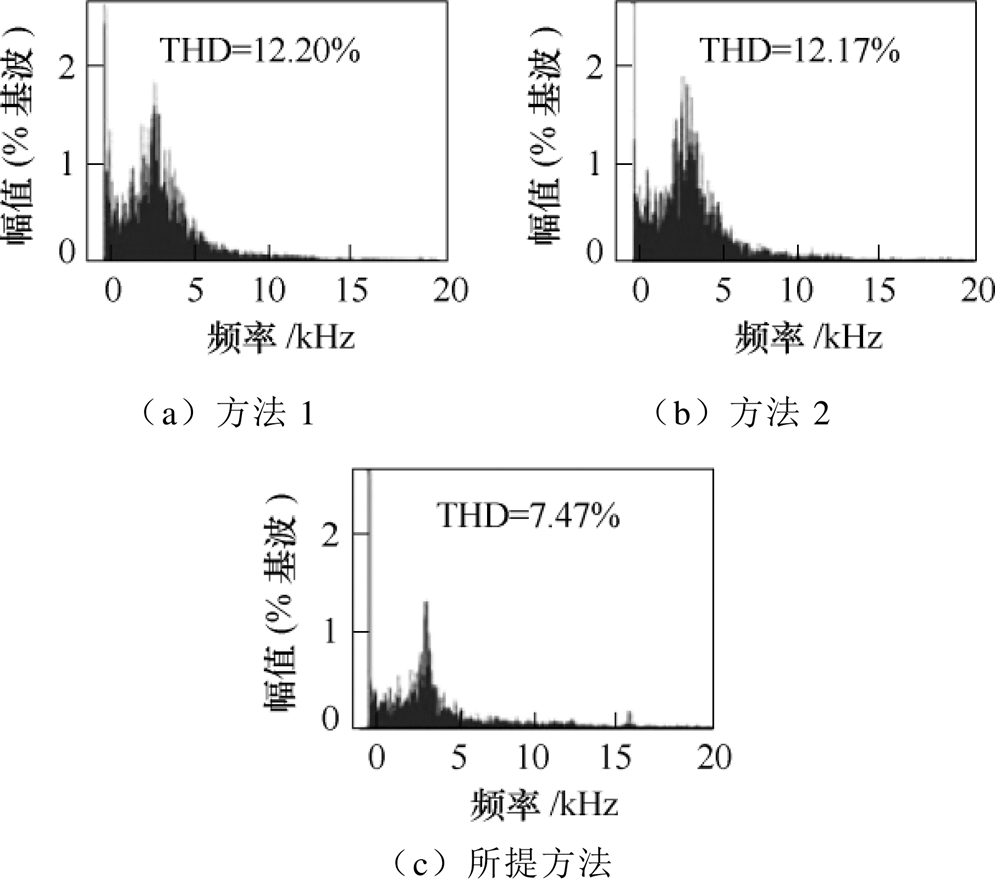
图7 理想电网下三种方法的电流FFT分析结果
Fig.7 The current FFT analysis results of the three methods under ideal grid voltage conditions
其次,为了进一步说明本文所提方法的有效性,在非理想电网下对比研究了方法1、方法2和所提方法的控制性能。在该实验中,通过电网模拟器向电网中注入了20%的三相7次谐波电压。无功电流igqref设为0,有功电流igdref设为10A。注入谐波后的三相电网电压波形如图8a所示,其FFT分析结果如图8b所示。三种方法的电流波形及电流FFT分析结果如图9~图12所示。
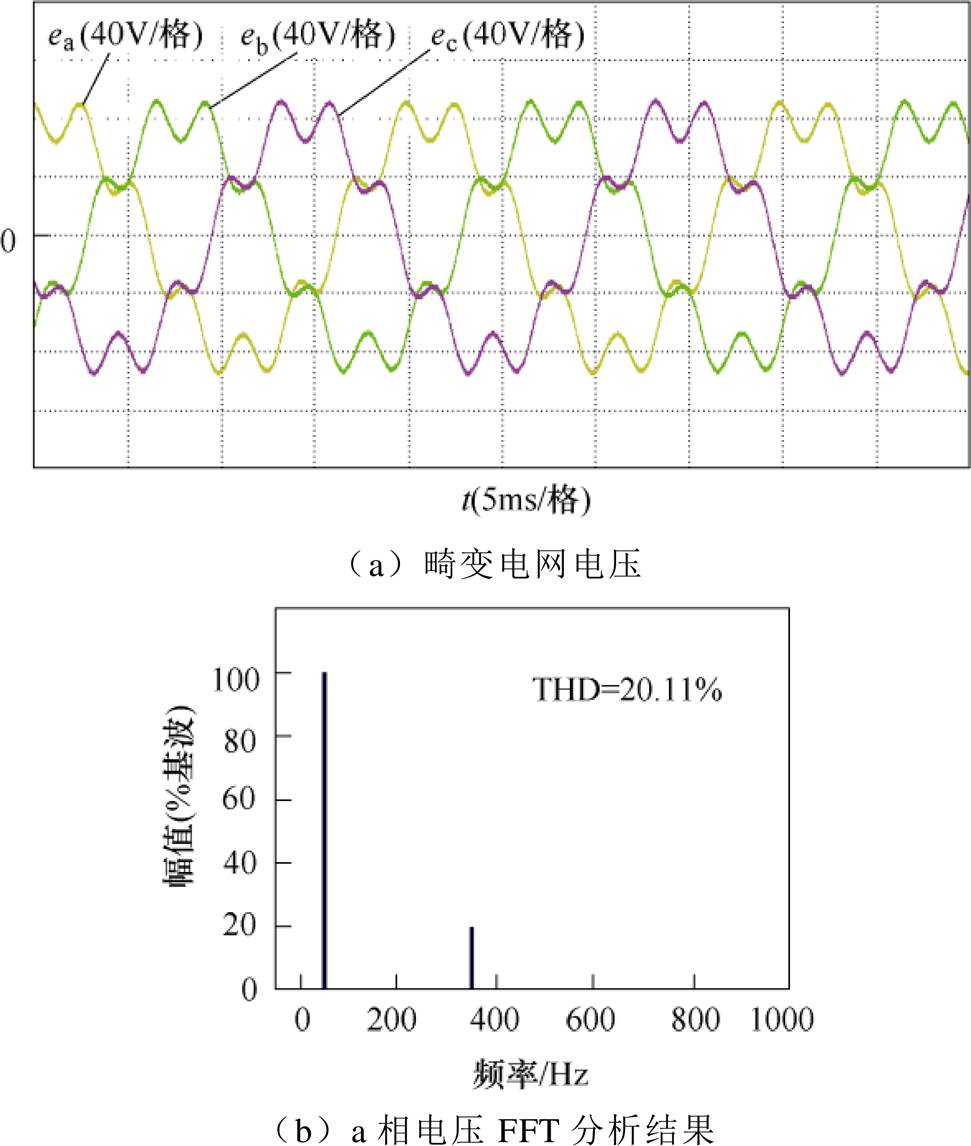
图8 畸变电网电压波形
Fig.8 Waveforms of the distorted grid voltages
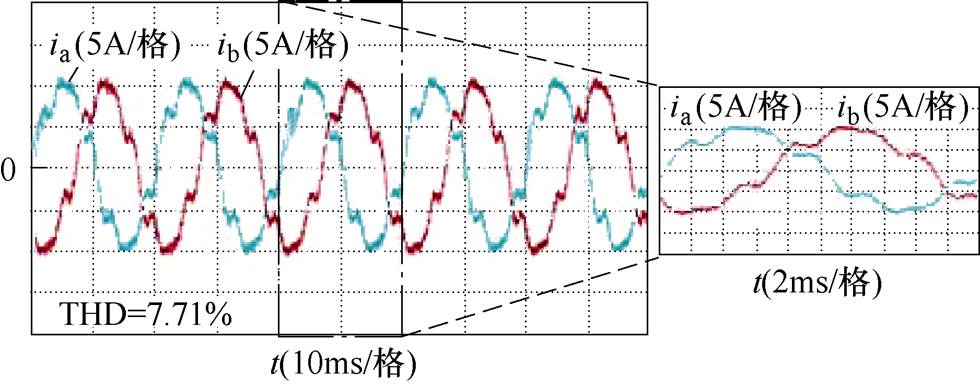
图9 畸变电网下方法1的实验结果
Fig.9 Experimental results of method 1 under distorted grid voltage conditions
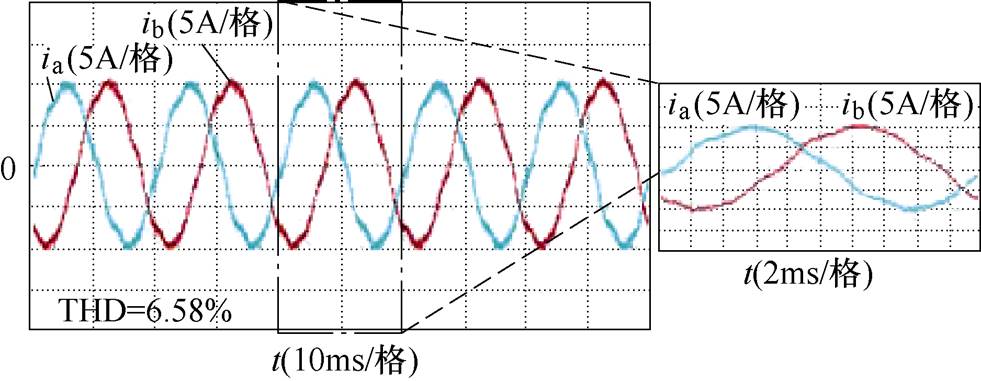
图10 畸变电网下方法2的实验结果
Fig.10 Experimental results of method 2 under distorted grid voltage conditions

图11 畸变电网下所提方法的实验结果
Fig.11 Experimental results of the proposed method under distorted grid voltage conditions

图12 畸变电网下三种方法的电流FFT分析结果
Fig.12 The current FFT analysis results of the three methods under distorted grid voltage conditions
畸变电网电压波形如图8所示,可以清晰地看到,注入谐波后,电网电压出现了明显的畸变。畸变电网下方法1的实验结果如图9所示,畸变的电网电压直接导致方法1的输出电流也出现了较大的畸变。畸变电网下方法2的实验结果如图10所示,与方法1相比,方法2输出电流的畸变明显得到减小。这是因为方法2在观测电网电压时使用了低通滤波器,而低通滤波器可以抑制电网的背景谐波,减小估计的电网电压中所含的谐波,从而减小了电流输出谐波。畸变电网下所提方法的实验结果如图11所示,本文所提方法可以进一步降低电流畸变,这是因为该方法每一个控制周期同时使用了两个电压矢量。
同时,图12给出了无功电流igqref =0,有功电流igdref =10A时三种方法的电流FFT分析结果。由此可见,本文所提方法由于在观测电网电压时使用了低通滤波器,且每个控制周期同时输出两个电压矢量作用,因此,其电流THD最小,这再次验证了本文所提方法的有效性。
如第2.3节所述,本文所提电网电压观测方法不仅可以通过低通滤波器抑制电网电压的背景谐波,而且可以通过采用改进的滤波和补偿方法,实现无需精确电网电压角频率的电网电压观测。这意味着,即使电网电压角频率发生了闪变,本文所提方法依然可以获得较高的电网电压观测精度和电流控制精度。
为了验证所提方法的有效性,图13和图14给出了电网频率变化时采用常规滤波和补偿方法得到的电网电压和采用本文所提方法得到的电网电压。图中,ea 和eb 代表实测的电网电压,eea 和eeb 代表观测的电网电压。在该实验中,常规方法所使用的电网角频率wg设为100p rad/s,并保持不变[26]。
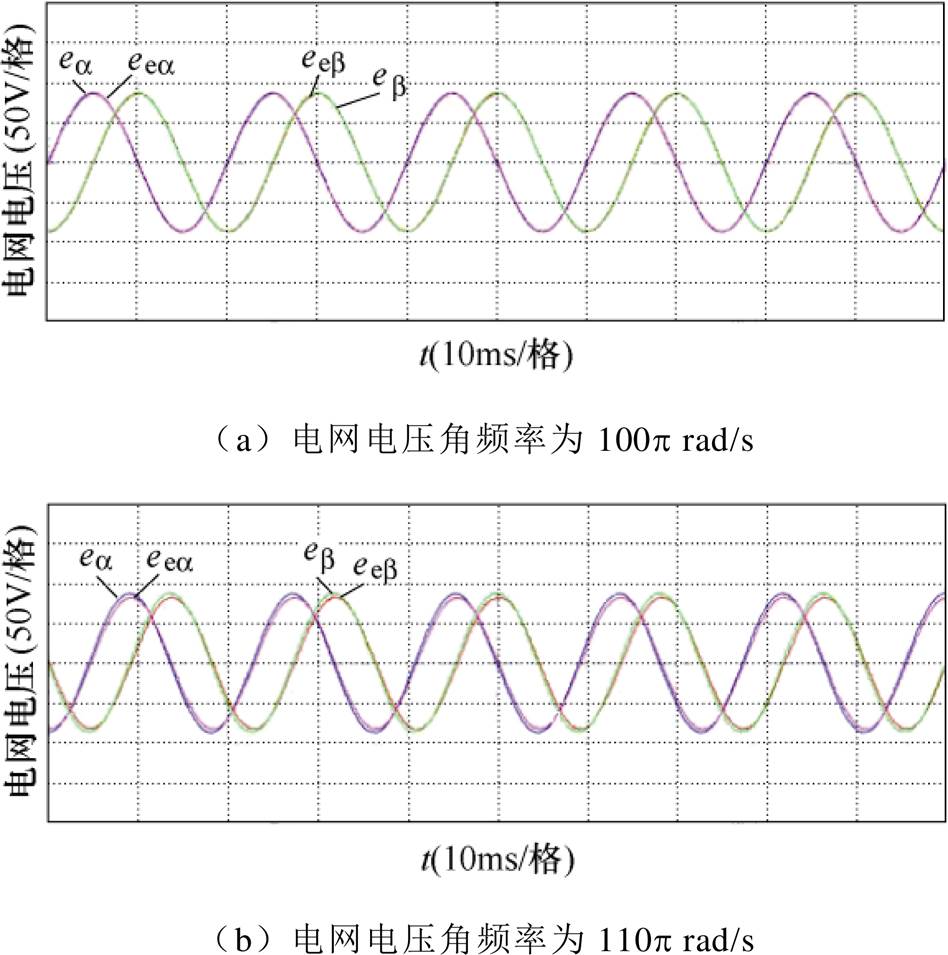
图13 常规方法观测的电网电压
Fig.13 The estimated grid voltage of the conventional method
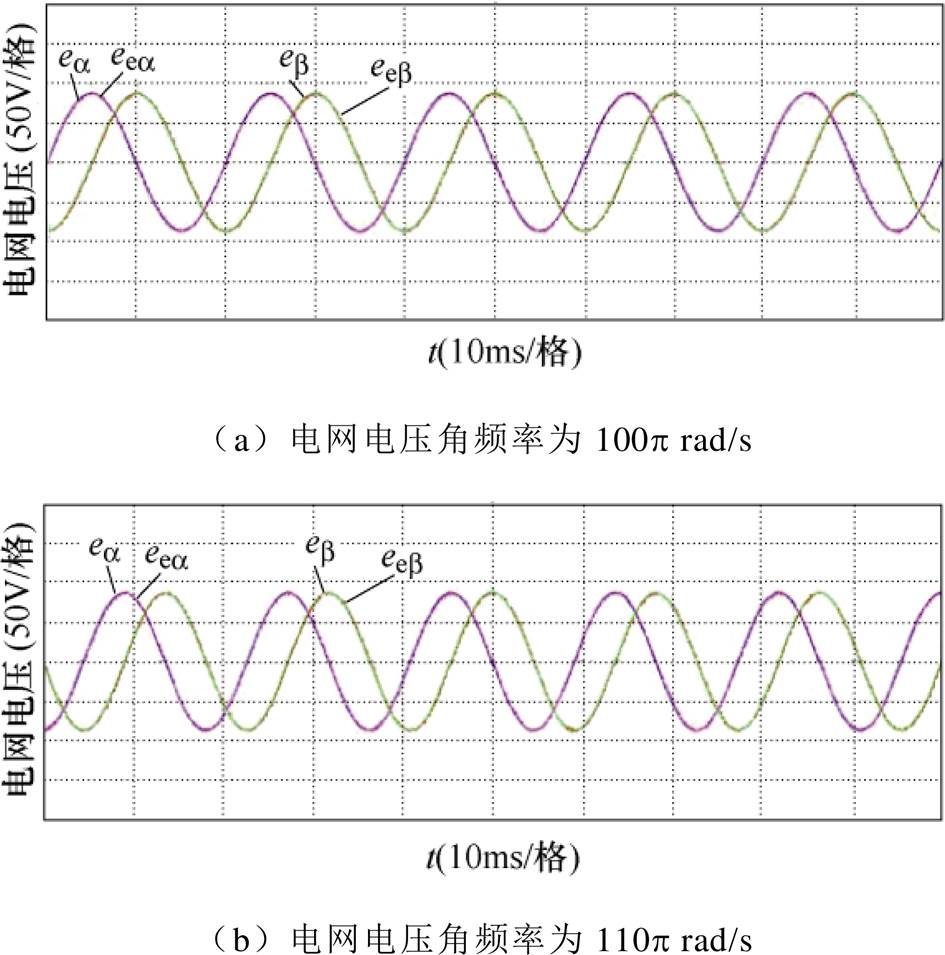
图14 所提方法观测的电网电压
Fig.14 The estimated grid voltage of the proposed method
图13a和图14a给出了电网电压实际角频率为100p rad/s时两种方法观测的电网电压波形。对比可见,在电网角频率已知时,两种方法均可以获得较好的电网电压观测效果。图13b和图14b给出了电网电压角频率为110p rad/s时两种方法的电网电压观测结果。对比可见,在电网电压频率闪变时,常规方法观测得到的电网电压出现了明显的相位和幅值偏差,这主要是因为常规滤波和补偿模块里需要已知电网的精确频率。而本文所提方法依然可以获得较准确的电网电压观测值,这是因为所提方法在对电网电压相位和幅值进行补偿时,不需要已知精确的电网频率。这就验证了所提方法的频率自适应性。
为了进一步对比这两种电网电压观测方法对电流控制的影响,进行了如下对比实验。该实验均采用本文所提双矢量法进行电流控制,电网电压观测方法则分别采用常规电网电压观测方法和所提电网电压观测方法。实验时,igqref设为0,igdref设为10A。实验结果如图15和图16所示。
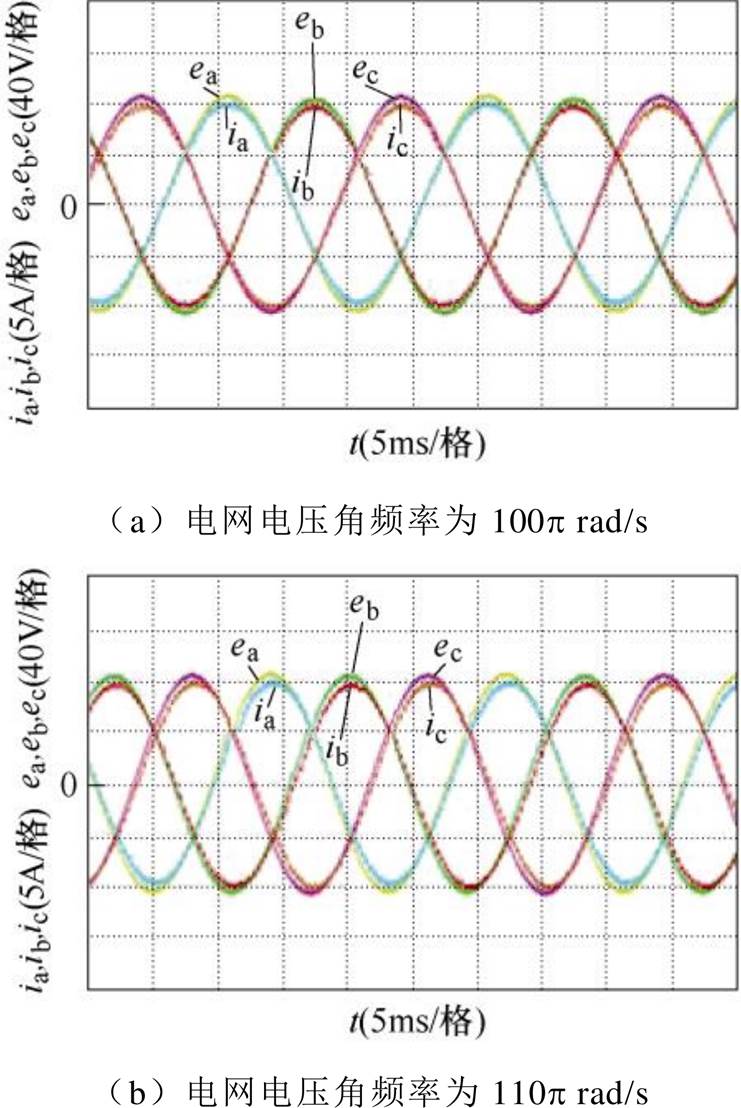
图15 频率变化时常规方法的电流实验结果
Fig.15 The current experimental results of the conventional method when frequency changes
图15a和图16a给出了电网电压实际角频率为100p rad/s时两种方法的电流控制效果。对比可见,这两种方法具有类似的电流控制性能。然而,当电网频率为110p rad/s时,由图15b可见,常规方法的电流明显出现了相位滞后,这主要是因为估计的电网电压存在相位滞后,如图13b所示。而本文所提方法即使在电网频率出现变化时,依然可以实现较准确的电流控制,如图16b所示。这就验证了本文所提方法的优越性。

图16 频率变化时所提方法的电流实验结果
Fig.16 The current experimental results of the proposed method when frequency changes
虽然采用锁相环可以获得较准确的电网电压角频率,从而有助于提高常规电网电压观测方法的观测精度,并提高电流控制精度。但锁相环控制器参数的失调也会增大电网角频率观测误差,进而会降低电网电压观测和并网电流控制精度。
为了提高并网逆变器的运行可靠性,避免使用电网电压传感器,并降低并网电流谐波,本文提出了一种并网逆变器无电网电压传感器双矢量模型预测控制方法。所提电网电压观测方法无需精确的电网角频率信息即可实现电网频率自适应。所提双矢量模型预测控制方法采用调制模型预测控制的原理进行电压矢量作用时间计算以降低计算量。同时,文中还通过详细的理论分析,首次从理论上证明了所提双矢量法的有效性。最后,详细的对比实验结果验证了所提方法的正确性。
此外,本文所提无电网电压传感器模型预测控制方法还可为实现永磁同步电机的无速度传感器模型预测控制提供一种新思路和新方法。
参考文献
[1] 李伟, 张勇军, 肖雄. 实时电感辨识的模型预测并网逆变器控制方法[J]. 电工技术学报, 2018, 33(15): 3450-3460.
Li Wei, Zhang Yongjun, Xiao Xiong. The model predictive grid-connected inverter control method based on real-time inductance identification[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3450-3460.
[2] 陈燕东, 王伊, 周乐明, 等. 弱电网下LCL逆变器阻尼谐振抑制与功率快速调节方法[J]. 电工技术学报, 2018, 33(11): 2564-2574.
Chen Yandong, Wang Yi, Zhou Leming, et al. Damping resonance suppression and fast power regulation method for LCL-type inverter under weak grid[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2564-2574.
[3] 陈卓易, 邱建琪, 金孟加. 内置式永磁同步电机无位置传感器自适应集总电动势模型预测控制[J]. 电工技术学报, 2018, 33(24): 5659-5669.
Chen Zhuoyi, Qiu Jianqi, Jin Mengjia. Sensorless adaptive lumped electromotive-force model predictive control of interior permanent magnet synchronous motors[J]. Transactions of China Electrotechnical Society, 2018, 33(24): 5659-5669.
[4] 姚骏, 刘瑞阔, 尹潇. 永磁同步电机三矢量低开关频率模型预测控制研究[J]. 电工技术学报, 2018, 33(13): 2937-2945.
Yao Jun, Liu Ruikuo, Yin Xiao. Research on 3-vector model predictive control with low switching frequency of permanent magnet synchronous motor[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(13): 2937-2945.
[5] 刘建华, 朱蓓蓓, 张亚健, 等. 有源电力滤波器相电流互感器容错控制[J]. 电力系统保护与控制, 2015, 43(20): 90-96.
Liu Jianhua, Zhu Beibei, Zhang Yajian, et al. Fault- tolerant control of phase current transformer for active power filter[J]. Power System Protection and Control, 2015, 43(20): 90-96.
[6] Gan Chun, Wu Jianhua, Yang Shiyou, et al. Phase current reconstruction of switched reluctance motors from DC-link current under double high-frequency pulses injection[J]. IEEE Transactions on Industrial Electronics, 2015, 62(5): 3265-3276.
[7] 程明, 姜云磊, 王伟, 等. 线电压调制的PWM逆变器相电流重构策略[J]. 电机与控制学报, 2018, 22(2): 9-16.
Cheng Ming, Jiang Yunlei, Wang Wei, et al. Phase current reconstr uction strategy for PWM inverter[J]. Electric Machines and Control, 2018, 22(2): 9-16.
[8] 杜少通, 伍小杰, 周娟, 等. 一种采用虚拟磁链模型预测的新型PWM算法[J]. 中国电机工程学报, 2015, 35(3): 688-694.
Du Shaotong, Wu Xiaojie, Zhou Juan, et al. A novel algorithm of PWM using virtual flux model prediction[J]. Proceedings of the CSEE, 2015, 35(3): 688-694.
[9] Tao Yukun, Wu Qinghua, Wang Lei, et al. Voltage sensorless predictive direct power control of three- phase PWM converters[J]. IET Power Electronics, 2016, 9(5): 1009-1018.
[10] 侯兆然. 基于虚拟磁链定向的PWM整流器控制方法研究[J]. 电力系统保护与控制, 2014, 42(21): 105-109.
Hou Zhaoran. Research on control method of PWM rectifier based on virtual flux orientation[J]. Power System Protection and Control, 2014, 42(21): 105-109.
[11] Bozorgi A M, Chayjani M S, Nejadm R M, et al. Improved grid voltage sensorless control strategy for railway power conditioners[J]. IET Power Electronics, 2015, 8(12): 2454-2461.
[12] Suul J A, Luna A, Rodrıguez P, et al. Voltage- sensor-less synchronization to unbalanced grids by frequency-adaptive virtual flux estimation[J]. IEEE Transactions on Industrial Electronics, 2012, 59(7): 2910-2923.
[13] Rahoui A, Bechouche A, Seddiki H, et al. Grid voltages estimation for three-phase PWM rectifiers control without AC voltage sensors[J]. IEEE Transa- ctions on Power Electronics, 2018, 33(1): 859-875.
[14] Yasser A R I M, Ehab F E S,Magdy M A S. Adaptive grid-voltage sensorless control scheme for inverter-based distributed generation[J]. IEEE Transa- ctions on Energy Conversion, 2009, 24(3): 683-694.
[15] Fantino R, Busada C A, Solsona J A. Observer-based grid-voltage sensorless synchronization and control of a VSI-LCL tied to an unbalanced grid[J]. IEEE Transactions on Industrial Electronics, 2019, 66(7): 4972-4981.
[16] Kukkola J, Hinkkanen M. State observer for grid- voltage sensorless control of a converter under unbalanced conditions[J]. IEEE Transactions on Industry Application, 2018, 54(1): 286-297.
[17] Yang Haitao, Zhang Yongchang, Liang Jiejunyi, et al. Sliding-mode observer based voltage-sensorless model predictive power control of PWM rectifier under unbalanced grid conditions[J]. IEEE Transa- ctions on Industrial Electronics, 2018, 65(7): 5550- 5560.
[18] 徐艳平, 李园园, 张保程, 等. 一种消除权重系数三矢量模型预测转矩控制[J]. 电工技术学报, 2018, 33(16): 3926-3934.
Xu Yanping, Li Yuanyuan, Zhang Baocheng, et al. Three-vector based model predictive torque control of eliminating weighting factor[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3926- 3934.
[19] 陈炜, 曾思坷, 张国政, 等. 永磁同步电机改进型三矢量模型预测转矩控制[J]. 电工技术学报, 2018, 33(增刊2): 420-426.
Chen Wei, Zeng Sike, Zhang Guozheng, et al. Improved three-vector model predictive torque control of permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 420-426.
[20] Tarisciotti L, Zanchetta P, Watson A, et al. Modulated model predictive control for a three-phase active rectifier[J]. IEEE Transactions on Industry Application, 2015, 51(2): 1610-1620.
[21] 吕恒志, 张涛, 章凯旋, 等. 三相四开关容错变换器调制模型预测控制策略[J]. 轻工学报, 2019, 34(3): 95-103.
Lü Hengzhi, Zhang Tao, Zhang Kaixuan, et al. Three- phase four-switch fault-tolerant converter modulation model predictive control strategy[J]. Journal of Light Industry, 2019, 34(3): 95-103.
[22] Shi Xiaolong, Zhu Jianguo, Li Li, et al. Model- predictive-based duty cycle control with simplified calculation and mutual influence elimination for AC/DC converter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 7(1): 504-514.
[23] 樊英, 张丽, 程明. 基于宽速滑模观测器的新型自减速永磁轮毂电机无传感器直接转矩控制[J]. 电工技术学报, 2014, 29(5): 141-148.
Fan Ying, Zhang Li, Cheng Ming. A wide-speed sliding mode observer for sensorless direct torque control of a new self-decelerating permanent magnet in-wheel motor[J]. Transactions of China Electro- technical Society, 2014, 29(5): 141-148.
[24] Qiao Zhaowei, Shi Tingna, Wang Yindong, et al. New sliding-mode observer for position sensorless control of permanent-magnet synchronous motor[J]. IEEE Transactions on Industrial Electronics, 2013, 60(2): 710-719.
[25] Yang Shuying, Guo Leilei, Chang Liuchen, et al. Closed-loop control on PMSG torque in direct-drive wind power generation system without speed sensor[C]//2015 IEEE Applied Power Electronics Conference & Exposition, Charlotte, NC, 2015: 2984-2987.
[26] Li Hui, Lin Mingyao, Yin Ming, et al. Three-vector- based low-complexity model predictive direct power control strategy for PWM rectifier without voltage sensors[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2019, 7(1): 240-251.
Grid Voltage Sensorless Model Predictive Control for Grid-Connected Inverters
Abstract In recent years, model predictive control methods have been widely used to control grid-connected inverters. To further reduce the harmonics of the grid current and improve the reliability of the system, a grid voltage sensorless double-vector model predictive control method for grid- connected inverters is proposed in this paper. Firstly, an improved sliding mode observer-based grid voltage online observation method is proposed to achieve grid voltage sensorless control. The proposed method can realize grid voltage observation without the precise frequency of the grid. Meanwhile, the influence of the grid voltage background harmonics on the current control is restrained to a certain extent due to the utilization of the low-pass filter in the observer. Secondly, to further reduce the current harmonics, a double-vector based-model predictive control method is proposed based on the principle of the modulated model predictive control, and its validity is proved theoretically. Detailed comparative experimental results verify the proposed method.
keywords:Grid-connected inverters, model predictive control, sliding mode observer, double- vector, grid voltage sensorless
中图分类号:TM464
DOI: 10.19595/j.cnki.1000-6753.tces.190684
国家自然科学基金项目(51607159,51707176)、新能源与储能运行控制国家重点实验室(中国电力科学研究院有限公司)开放基金和河南省高等学校重点科研项目(18A470020,20A470011)资助。
收稿日期2019-06-05
改稿日期 2019-07-22
郭磊磊 男,1987年生,博士,讲师,硕士生导师,主要研究方向为并网逆变器模型预测优化控制等。E-mail: 2006guoleilei@163.com(通信作者)
金 楠 男,1982年生,副教授,硕士生导师,主要研究方向为新能源变换技术等。E-mail: jinnan@zzuli.edu.cn
(编辑 崔文静)