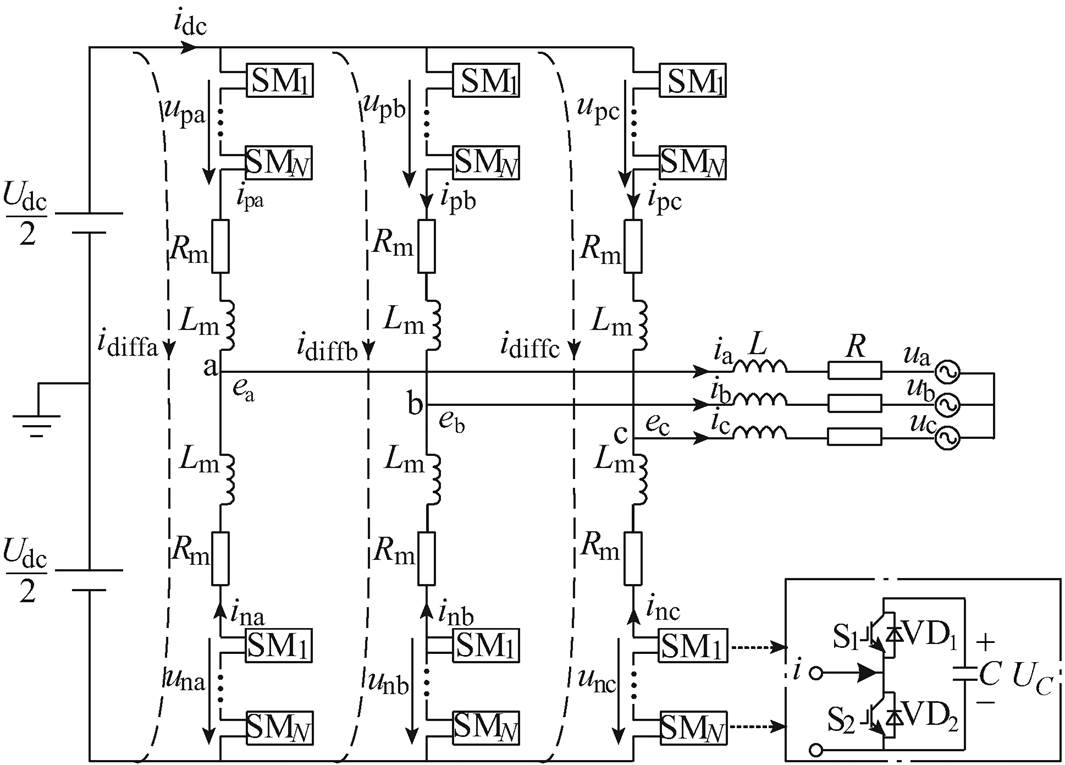
图1 三相MMC电路结构及子模块拓扑
Fig.1 Three-phase MMC circuit structure and submodule topology
摘要 模块化多电平变换器(MMC)应用于大功率可再生能源发电并网时,由于存在可再生能源的随机性波动、系统参数摄动和本身的非线性特性,采用传统矢量控制方法实现MMC环流抑制难以确保系统全局稳定运行和强鲁棒性能。针对这一问题,提出基于端口受控耗散哈密顿系统(PCHD)模型的MMC无源反步环流抑制方法。在构建基于PCHD模型的MMC全局能量函数基础上,设计无源性控制器,通过能量函数整形,修正闭环系统的能量耗散和能量流动方式,使系统能量在期望平衡点取最小值,以实现系统全局渐进稳定。结合反步控制方法,消除不确定扰动与MMC系统参数摄动引起的跟踪误差,从而实现系统内、外扰动情形下环流二倍频分量的快速平抑。基于Matlab/Simulink的仿真结果与基于dSPACE的实验结果表明:所提无源反步环流抑制方法具有形式简单、无奇异点、暂态性能好的特点,同时能够确保系统全局稳定与强鲁棒性。
关键词:模块化多电平变换器 环流抑制 端口受控耗散哈密顿系统模型 无源性控制 反步法
近年来,模块化多电平变换器(Modular Multi- level Converter, MMC)凭借其谐波含量少、开关损耗低、故障穿越能力强、便于模块化扩容与工程应用等优点,广泛应用于大规模可再生能源并网领 域[1-4]。但由于MMC主电路各个子模块的并联电容相互独立且子模块投入切出个数不同,使桥臂电压难以达到完全均衡,因而在MMC三相间形成内部环流,环流的存在使桥臂电流峰值与有效值增大,严重时会影响系统安全稳定运行[5]。
国内外众多学者针对MMC环流抑制展开了相关研究。传统矢量控制方法通过坐标变换使MMC数学模型得到降阶和简化,但并未改变其非线性系统的本质,局部线性化得到的小信号模型会带来建模误差,在可再生能源发电的随机性波动、MMC系统参数摄动的综合作用下,矢量控制器的抗扰性和鲁棒性面临严峻挑战[6-11]。不同于传统矢量控制,非线性控制方法以系统稳定性为出发点,设计鲁棒性强、抗扰性优的控制系统,通过设置系统性能目标,使控制器跟踪参考轨迹实现动、静态性能指标。2015年,宋平岗等通过寻找合适的输出量,使得非线性控制器的输入量和中间量能够由输出量及其整数阶微分形式表示,并提出基于微分平滑理论的MMC环流抑制策略[12]。2016年,Lazhar Ben-Brahim等通过MMC最小化负载电流总谐波失真和环流来选择加权因子,实现基于加权模型预测的MMC环流抑制策略[13]。2017年,Zhang Xiaotong等将反步法应用于MMC环流抑制,保留环流方程中非线性因素,通过设计非线性控制量,使得控制精准且暂态性能优异[14]。上述非线性控制方法在实现系统稳定的基础上,取得较好的MMC环流控制效果,但非线性控制器设计复杂、计算量大、工程应用存在难点,且由于控制器阻尼系数通常选择较大,则会引起系统内部损耗过大问题,在能量优化设计方面尚存不足。
无源性控制(Passivity Based Control, PBC)从电气角度对非线性系统能量入手,将系统视为能量变换装置,通过求取与被控量相关的能量函数,设计无源性控制律,可在保证系统稳定性的同时,优化整个控制系统的输入、输出能量,降低能量损耗、简化控制器结构、易于工程实际问题的解决[15-16]。2013年,蔡新红等提出一种基于欧拉-拉格朗日(Euler-Lagrange, EL)模型的MMC电流内环无源控制器,通过注入较小阻尼使得系统能量加速耗散,快速收敛到期望点[17]。2017年,祝贺等将EL模型应用于基于五电平MMC的统一电能质量调节器电流内环无源性控制上,进一步验证了无源性理论应用于MMC稳定控制的可行性和有效性[18]。但基于EL模型的无源性控制中无源映射能量函数不能确定是总能量函数,设计过程中需要沿着预设参考轨迹对系统进行求逆计算,这不仅改变了Lagrange结构,同时对系统稳定性证明提出了可逆性要求[19-20]。基于端口受控耗散哈密顿系统(Port-Controlled Hamiltonian with Dissipation, PCHD)模型的无源性控制,映射能量函数为闭环系统的总能量,通过选择闭环系统期望结构及与系统结构兼容的全局能量函数,设计阻尼注入与能量成形方法,可使系统实现在期望平衡点的全局渐进稳定。相比基于EL模型的无源性控制,基于PCHD模型的无源性控制方法避免了在非线性系统物理意义上的过多研究,将控制问题转化成偏微分方程求解,对外界波动的抗扰性能有所增强,稳定性更好,但基于PCHD模型的无源性控制器设计过程中由于牺牲了对系统能量平衡没有影响的“无功力”,在一定程度上影响了系统的暂态性能。如何在控制器设计尽量简洁的前提下,实现基于PCHD的无源性控制方法动、静态响应性能的提升,同时确保系统全局渐进稳定性和鲁棒性的进一步提升,是无源性控制方法实现MMC环流抑制工程应用必须解决的关键问题。
综上所述,针对大规模可再生能源发电MMC并网时功率波动、直流侧电压波动、内部参数扰动等问题,将基于PCHD模型的无源性控制方法与反步法有机结合,提出MMC无源反步环流抑制(Circulating Current Suppressing Controller, CCSC)方法。基于PCHD模型的无源性控制通过能量函数整形和控制修正系统性能,确保系统的全局稳定性,减小系统内部损耗,实现能量优化设计;反步法实现MMC在内、外扰动情形下环流二倍频分量的快速跟踪,所提出的控制律可在保证全局稳定性的同时实现系统控制目标的快速动态响应。基于Matlab/Simulink的仿真结果与基于dSPACE的实验结果表明,所提方法实现简单、稳定性好、鲁棒性强,能有效抑制由功率波动、直流侧电压扰动、系统内部参数扰动等引起的MMC环流二倍频分量跟踪误差,具有优良的静、动态响应特性。
MMC三相桥式电路结构原理与半桥式子模块拓扑结构如图1所示。MMC每相有上、下两个桥臂,每个桥臂由N个相同的单相半桥式子模块级联构成,每个桥臂均串联一个桥臂电感和桥臂电阻。单相半桥式子模块包括两个IGBT,两个反并联二极管VD1、VD2和一个电容C,通过脉冲信号控制S1、S2的关断,可实现子模块输出电压在UC和0之间的切换,UC为单个子模块电容电压,各个子模块投入切出引起桥臂间电压不均衡,从而在MMC三相间形成环流。

图1 三相MMC电路结构及子模块拓扑
Fig.1 Three-phase MMC circuit structure and submodule topology
考虑不同相桥臂之间的能量交换,MMC环流主要包括直流分量和偶数次谐波,其中2 次谐波分量占主导,影响最为显著[21]。MMC环流抑制目标是通过一定的控制策略使环流二倍频分量为零。
忽略环流高次谐波分量,MMC环流可表示为
 (1)
(1)式中,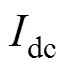 为直流侧电流幅值;
为直流侧电流幅值;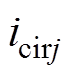 为j相二倍频环流分量(j =a, b, c)。
为j相二倍频环流分量(j =a, b, c)。
单相MMC等效电路如图2所示。图中,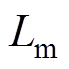 、
、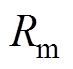 分别为桥臂电感、桥臂电阻,
分别为桥臂电感、桥臂电阻,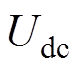 、
、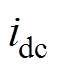 分别为直流侧总电压、总电流,
分别为直流侧总电压、总电流,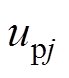 、
、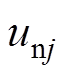 分别为第j相上桥臂与下桥臂子模块端口电压之和,j=a, b, c。
分别为第j相上桥臂与下桥臂子模块端口电压之和,j=a, b, c。
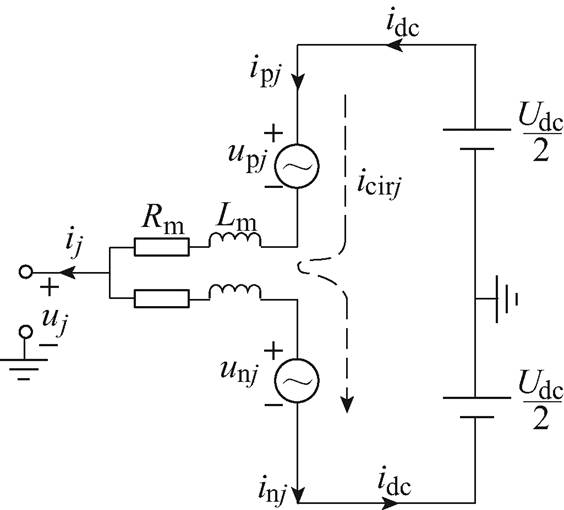
图2 单相MMC等效电路
Fig.2 The single equivalent circuit of MMC
由图2可知,上、下桥臂电流可表示为
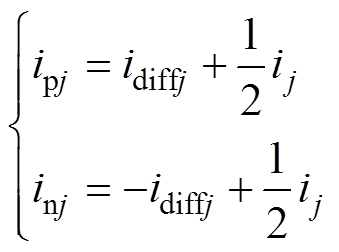 (2)
(2)则MMC环流表达式可由式(2)改写为
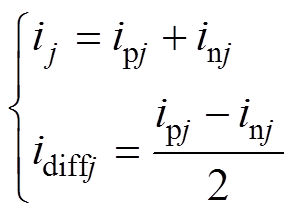 (3)
(3)
根据单相MMC等效电路[22],由基尔霍夫定律可得
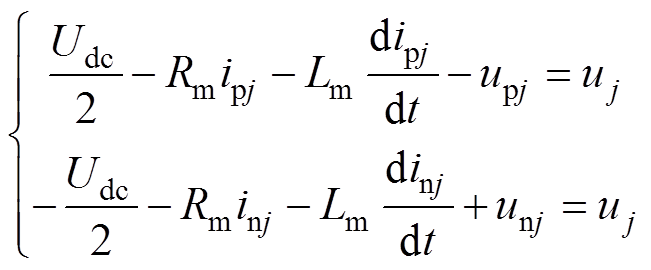 (4)
(4)联立式(3)、式(4),可得j相环流动态方程式为
 (5)
(5)
式中,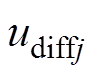 为环流经过桥臂产生的环流压降。
为环流经过桥臂产生的环流压降。
j相环流动态方程式(5)经坐标变换可得dq旋转坐标系下MMC环流动态方程式为
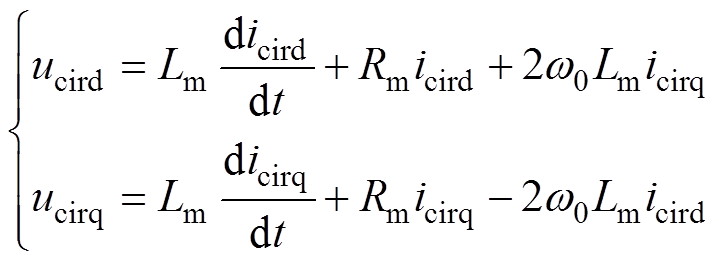 (6)
(6)式中,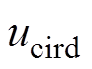 、
、 分别为MMC三相环流压降在dq旋转坐标系下的二倍频d轴、q轴分量;
分别为MMC三相环流压降在dq旋转坐标系下的二倍频d轴、q轴分量;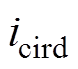 、
、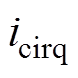 分别为三相环流在旋转dq坐标系下的二倍频d轴、q轴分量。
分别为三相环流在旋转dq坐标系下的二倍频d轴、q轴分量。
由MMC环流动态方程式(6)分析可知:在dq旋转坐标系下,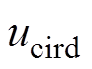 、
、 与
与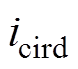 、
、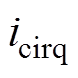 依然存在耦合,表现为非线性特性,矢量控制在平衡点附近采用线性控制方式,在系统的不确定性干扰、内部参数摄动情形下,会发生鲁棒性和抗扰性下降问题。
依然存在耦合,表现为非线性特性,矢量控制在平衡点附近采用线性控制方式,在系统的不确定性干扰、内部参数摄动情形下,会发生鲁棒性和抗扰性下降问题。
为提升系统稳定性与鲁棒性,从能量角度出发,采用PCHD模型定义MMC环流抑制系统,通过合理设置状态变量,定义全局能量函数,为实现全局渐进稳定的无源性控制方法设计准备条件。根据PCHD模型的控制特性,设置MMC环流抑制系统的状态变量、输入变量、输出变量分别为
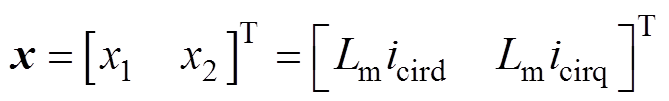 (7)
(7)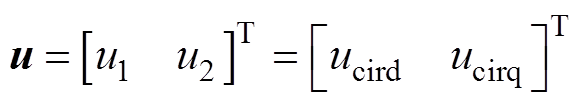 (8)
(8)
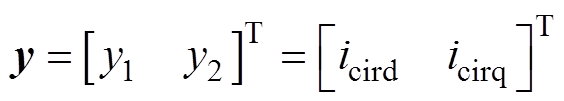 (9)
(9)
设计正定二次型全局能量函数为
 (10)
(10)对MMC环流动态方程式(6)进行等效变换,可得MMC环流系统PCHD模型方程式为
 (11)
(11)
式中,反对称矩阵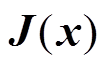 为
为

其反映系统能量平衡互联结构,且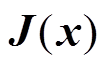 满足
满足
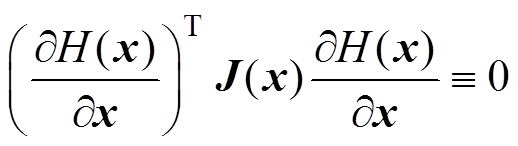
半正定对称矩阵为

其反映系统内部电阻结构,内外部交互结构矩阵为
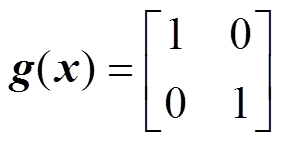
其反映系统端口特性。
由MMC全局能量函数式(10)和环流系统PCHD模型方程式(11)可得耗散不等式为
 (12)
(12)由分析耗散不等式(12)可知:左边是整个MMC环流系统的能量增量;右边是伴随着输入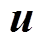 由外部注入到系统的能量供给量,系统增量总和总是小于等于外部注入的能量总和,则由无源性控制理 论[23],非线性映射
由外部注入到系统的能量供给量,系统增量总和总是小于等于外部注入的能量总和,则由无源性控制理 论[23],非线性映射 为输出严格无源,因此MMC环流系统具有无源性特性。
为输出严格无源,因此MMC环流系统具有无源性特性。
对于MMC环流系统PCHD模型方程式(11),若有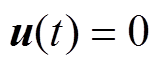 ,
,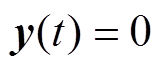 ,
,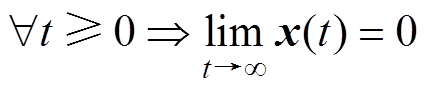 ,则满足非线性系统零状态可检测。在此条件下,由于MMC环流系统全局能量函数
,则满足非线性系统零状态可检测。在此条件下,由于MMC环流系统全局能量函数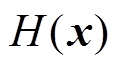 连续可微且正定,则可直接作为Lyapunov函数,且
连续可微且正定,则可直接作为Lyapunov函数,且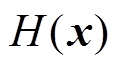 取值包含有界范围内所有取值。因此,根据无源性与Lyapunov稳定性的关系可知,MMC环流系统零平衡状态是全局渐进稳定的。
取值包含有界范围内所有取值。因此,根据无源性与Lyapunov稳定性的关系可知,MMC环流系统零平衡状态是全局渐进稳定的。
由MMC环流PCHD模型方程式(11)和耗散不等式(12)分析可知
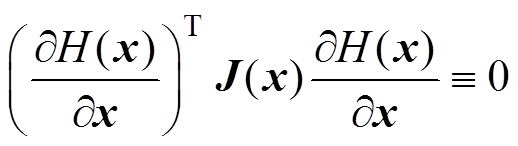
根据无源性定义, 即为MMC环流系统PCHD模型全局能量函数中可配置的“无功力”。由于“无功力”对能量平衡没有影响,且不影响系统稳定性,因此在进行无源性控制器状态反馈设计时无需被抵消,从而使系统无源性控制律的设计进一步得到简化。
即为MMC环流系统PCHD模型全局能量函数中可配置的“无功力”。由于“无功力”对能量平衡没有影响,且不影响系统稳定性,因此在进行无源性控制器状态反馈设计时无需被抵消,从而使系统无源性控制律的设计进一步得到简化。
基于MMC环流系统PCHD模型,设计无源性控制律,通过引入合理的状态反馈控制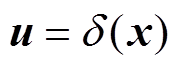 ,实现MMC环流系统全局能量函数的整形,使得系统在期望平衡点全局渐进稳定。
,实现MMC环流系统全局能量函数的整形,使得系统在期望平衡点全局渐进稳定。
设置MMC环流闭环控制系统期望能量函数为
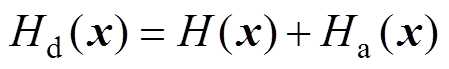 (13)
(13)式中,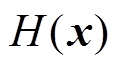 为MMC环流系统中原存储的能量;
为MMC环流系统中原存储的能量;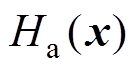 为通过引入状态反馈控制所注入系统的能量。
为通过引入状态反馈控制所注入系统的能量。
根据系统控制性能目标,设置MMC环流系统的期望平衡点为
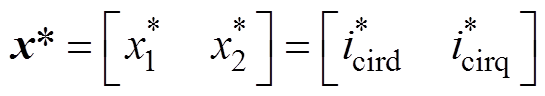 (14)
(14)由MMC环流系统PCHD模型方程式(11)和闭环系统期望能量函数式(13)推导可得MMC环流闭环系统的状态方程为
 (15)
(15)
式中,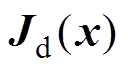 为系统期望的互联矩阵,
为系统期望的互联矩阵,
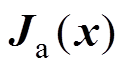 ;
;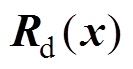 为系统期望的阻尼矩阵,
为系统期望的阻尼矩阵,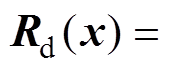
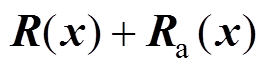 ;
;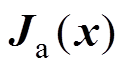 、
、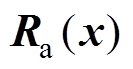 分别为注入的耗散矩阵、阻尼矩阵。
分别为注入的耗散矩阵、阻尼矩阵。
定义状态变量误差 ,引入状态反馈,则期望的能量函数为
,引入状态反馈,则期望的能量函数为
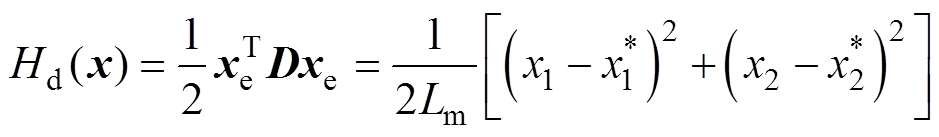 (16)
(16)式中,系数矩阵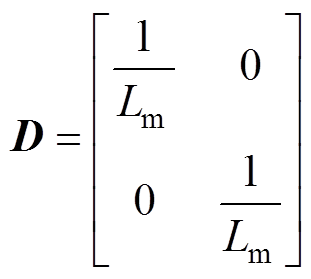 。
。
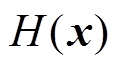 、
、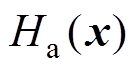 、
、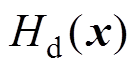 对x的导数分别为
对x的导数分别为
 (17)
(17)由全局能量函数式(10)和MMC环流闭环系统状态方程式(15)推导可得状态反馈控制律的偏微分方程形式为
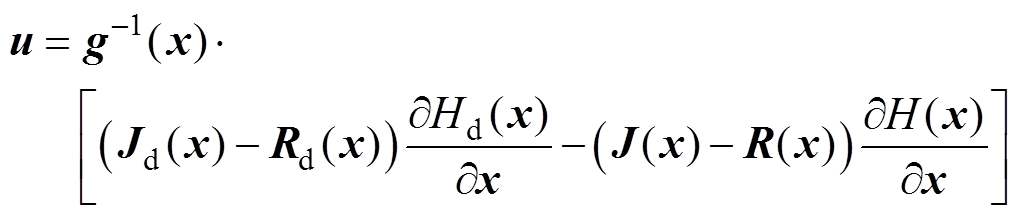 (18)
(18)
通过配置合理的注入耗散矩阵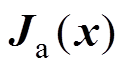 ,仅需较小阻尼矩阵
,仅需较小阻尼矩阵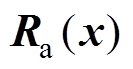 ,即可在保证闭环系统全局渐进稳定的前提下求得状态反馈控制率,即MMC环流无源性控制律。较小的阻尼矩阵
,即可在保证闭环系统全局渐进稳定的前提下求得状态反馈控制率,即MMC环流无源性控制律。较小的阻尼矩阵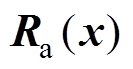 可实现内部耗散能量的有效控制,避免了能量在系统内部过多的消耗,实现了系统能量的优化设计与利用。
可实现内部耗散能量的有效控制,避免了能量在系统内部过多的消耗,实现了系统能量的优化设计与利用。
期望互联矩阵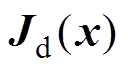 与期望阻尼矩阵
与期望阻尼矩阵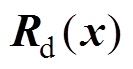 符合
符合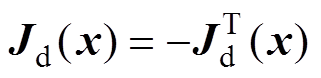 ,
, 。合理选取
。合理选取 ,
, ,使得无源性控制律简易可行且系统收敛速率可控。
,使得无源性控制律简易可行且系统收敛速率可控。
联立式(17)、式(18)可得
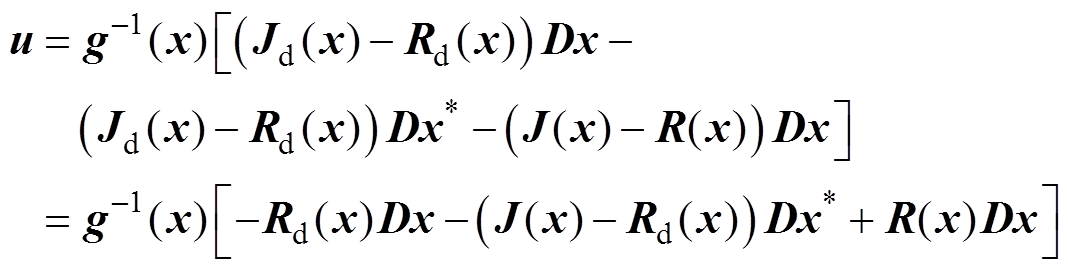
 (19)
(19)
由式(19)推导可得基于PCHD模型的MMC无源性CCSC控制律为
 (20)
(20)式中,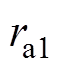 、
、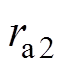 为注入的正阻尼参数,可用于降低控制系统对参数变化的敏感度,适当调节
为注入的正阻尼参数,可用于降低控制系统对参数变化的敏感度,适当调节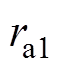 、
、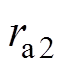 可使得环流二倍频实际值渐进跟随参考值。
可使得环流二倍频实际值渐进跟随参考值。
利用La Salle不变集定理[24-25]证明基于PCHD模型的无源性CCSC全局渐进稳定性。
选择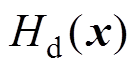 作为MMC环流系统的Lyapunov函数,即
作为MMC环流系统的Lyapunov函数,即
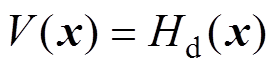 (21)
(21)对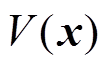 求导可得
求导可得
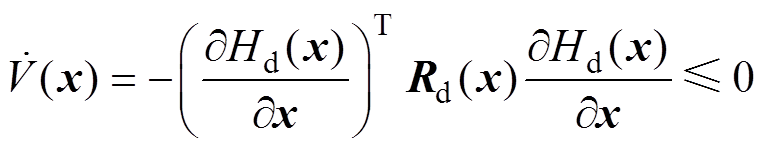 (22)
(22)
由式(17)和式(22)可得,当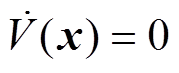 时,
时,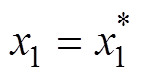 ,
,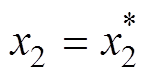 ,则系统在
,则系统在 内的解只有
内的解只有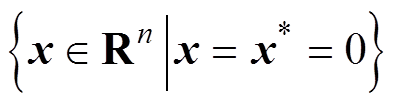 ,即系统的最大不变集只有
,即系统的最大不变集只有 。
。
因所选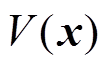 是半正定函数,
是半正定函数,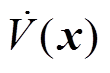 是半负定函数,且系统最大不变集只有
是半负定函数,且系统最大不变集只有 ,由La Salle不变集定理可得,MMC环流系统收敛于最大不变集,即在平衡点是渐进稳定的。
,由La Salle不变集定理可得,MMC环流系统收敛于最大不变集,即在平衡点是渐进稳定的。
由式(21)可得,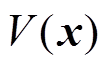 是径向无界的,即
是径向无界的,即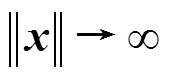 时,
时,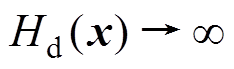 ,则系统在平衡点
,则系统在平衡点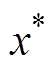 是全局渐进稳定的。
是全局渐进稳定的。
MMC无源性CCSC设计过程中牺牲了对系统能量平衡没有影响的“无功力”,在一定程度上影响了系统的暂态性能。针对这一问题,在基于PCHD模型的MMC无源性CCSC设计基础上,加入反步控制,控制策略中保留MMC环流系统的非线性项,来提升闭环系统的动态响应性能。
dq旋转坐标系下MMC环流动态方程式(6)可等效变换为
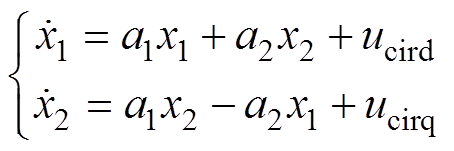 (23)
(23)式中,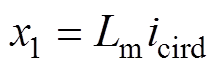 ;
;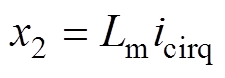 ;
;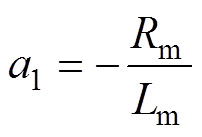 ;
; 。
。
定义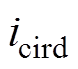 和
和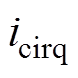 的渐进跟踪误差为
的渐进跟踪误差为
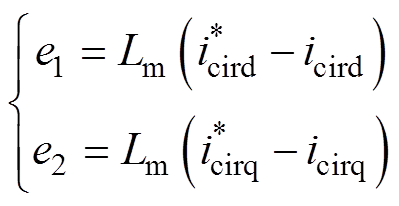 (24)
(24)则误差的导数可写为
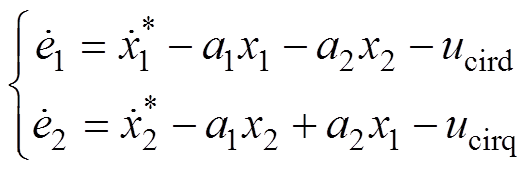 (25)
(25)
为实现系统控制目标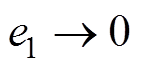 和
和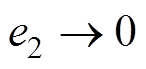 ,定义Lyapunov函数为
,定义Lyapunov函数为
 (26)
(26)联立渐进跟踪误差表达式(24)、误差导数表达式(25)、Lyapunov函数式(26),可得Lyapunov函数的一阶导数为
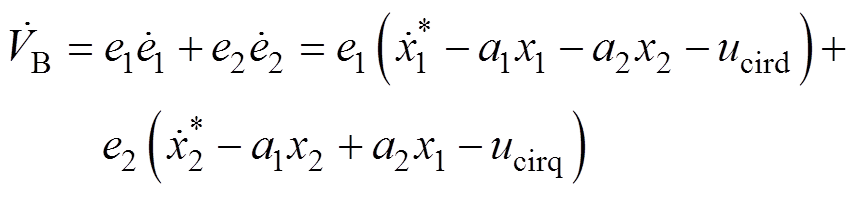 (27)
(27)
反步控制器通过保留非线性项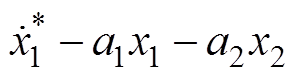 、
、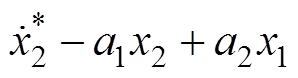 ,抵消Lyapunov函数一阶导数表达式(27)中的非线性项,使其满足Lyapunov稳定性定理;同时引入线性量
,抵消Lyapunov函数一阶导数表达式(27)中的非线性项,使其满足Lyapunov稳定性定理;同时引入线性量 、
、 ,改善闭环系统的暂态性能。由于MMC环流系统的期望平衡点为
,改善闭环系统的暂态性能。由于MMC环流系统的期望平衡点为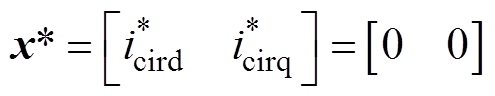 ,忽略状态变量参考值的微分项
,忽略状态变量参考值的微分项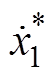 和
和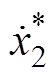 ,设计MMC反步环流抑制控制律为
,设计MMC反步环流抑制控制律为
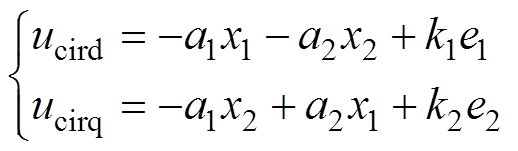 (28)
(28)式中,k1、k2为反馈增益。
分析式(28)可知,MMC反步环流抑制控制律保留了MMC环流系统的非线性特性,未对MMC环流系统的非线性做简化处理,使反步控制量含有完整的非线性控制项,具有良好的暂态特性。
当反馈增益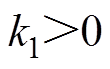 、
、 时,由式(27)、式(28)推导可得
时,由式(27)、式(28)推导可得
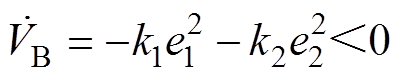 (29)
(29)实现误差函数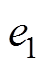 和
和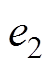 以指数速度趋近于零。
以指数速度趋近于零。
由式(29)分析可知,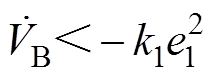 ,两边同时积分可得
,两边同时积分可得
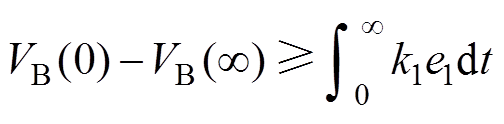 (30)
(30)分析式(30)可知,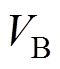 有界且
有界且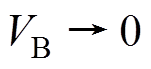 ,满足系统全局渐进稳定性。由于
,满足系统全局渐进稳定性。由于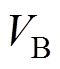 有界,可得
有界,可得 ,
,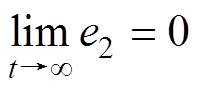 ,即跟踪误差
,即跟踪误差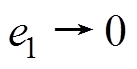 和
和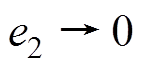 ,实现MMC环流二倍频分量的精确跟踪。
,实现MMC环流二倍频分量的精确跟踪。
联立式(20)、式(28),推导可得基于PCHD模型的MMC无源反步CCSC控制律为
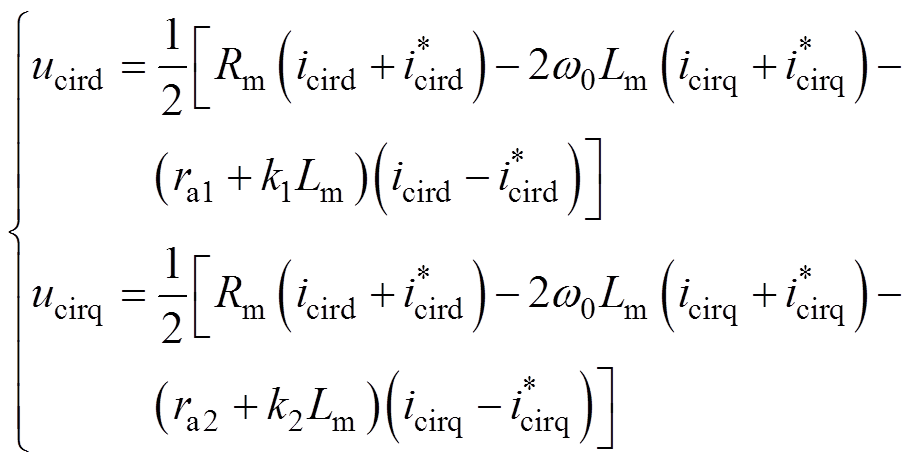 (31)
(31)由式(31)可得基于PCHD模型的MMC无源反步CCSC结构框图,如图3所示。
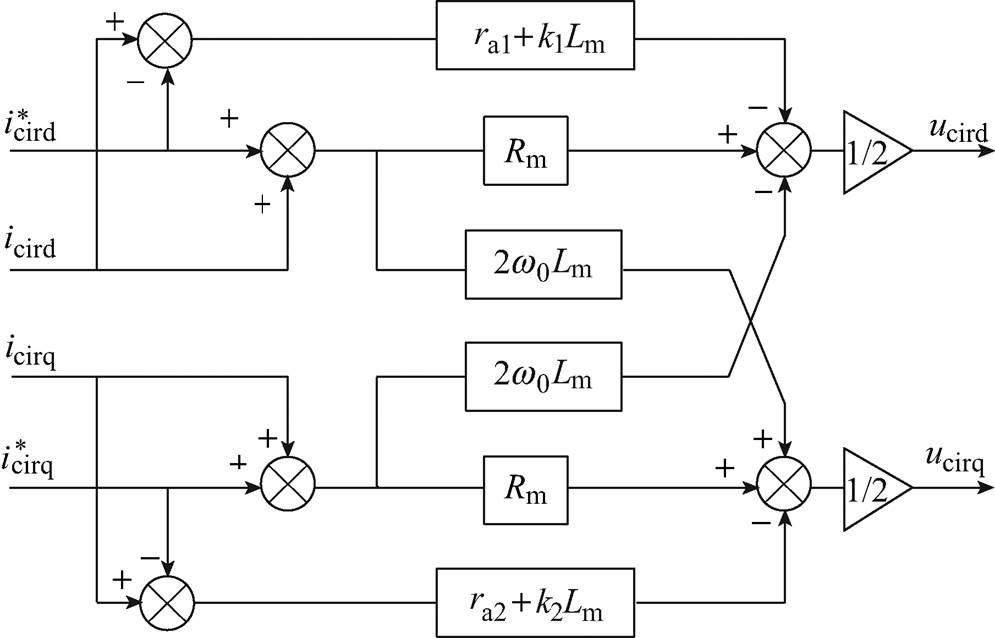
图3 无源反步环流抑制器结构框图
Fig.3 MMC block diagram of the passivity-based backstepping circulating current suppression
利用基于PCHD模型的无源性控制器和反步控制器定义的Lyapunov函数,证明所提方法闭环系统的全局渐进稳定性。
定义MMC无源反步环流控制系统的Lyapunov函数为
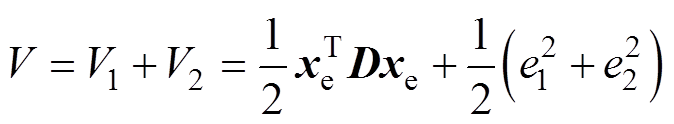 (32)
(32)式中, 和
和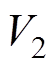 分别为基于PCHD模型的无源性控制器全局能量函数和反步控制器Lyapunov函数。无源性控制器设计已证明PCHD模型下MMC环流系统是全局渐进稳定的,满足
分别为基于PCHD模型的无源性控制器全局能量函数和反步控制器Lyapunov函数。无源性控制器设计已证明PCHD模型下MMC环流系统是全局渐进稳定的,满足 且
且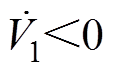 ;由式(27)和式(28)可知,选择合理的
;由式(27)和式(28)可知,选择合理的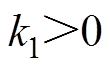 ,
,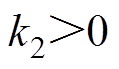 可使
可使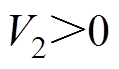 且
且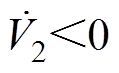 。
。
对式(32)求导可得
 (33)
(33)由Lyapunov稳定性判据可得,设计的MMC环流无源反步CCSC满足全局渐进稳定性要求。
综上所述,基于PCHD模型的MMC无源反步CCSC整体框图如图4所示,由并网控制回路和环流抑制回路构成。MMC并网控制回路由外环功率控制和内环电流控制组成,外环功率控制为内环电流控制提供MMC并网交流侧d、q轴电流参考值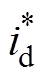 、
、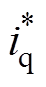 ;内环电流控制通过无源性控制实现电流
;内环电流控制通过无源性控制实现电流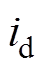 、
、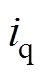 渐进跟踪其参考值,同时给出环流抑制回路采用如式(29)所示的无源反步环流抑制器,环流抑制输出信号
渐进跟踪其参考值,同时给出环流抑制回路采用如式(29)所示的无源反步环流抑制器,环流抑制输出信号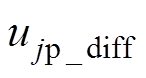 、
、 经坐标变换后可求得MMC上、下臂基准电压;调制环节采用载波移相调制和子模块电容电压均衡控制。并网控制回路和环流抑制回路的输出通过和、差运算产生上、下桥臂调制信号
经坐标变换后可求得MMC上、下臂基准电压;调制环节采用载波移相调制和子模块电容电压均衡控制。并网控制回路和环流抑制回路的输出通过和、差运算产生上、下桥臂调制信号 、
、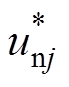 ,通过调制环节输出触发脉冲,控制MMC各相桥臂子模块中半桥变换器的开关状态,实现MMC环流有效抑制与并网稳定控制。
,通过调制环节输出触发脉冲,控制MMC各相桥臂子模块中半桥变换器的开关状态,实现MMC环流有效抑制与并网稳定控制。
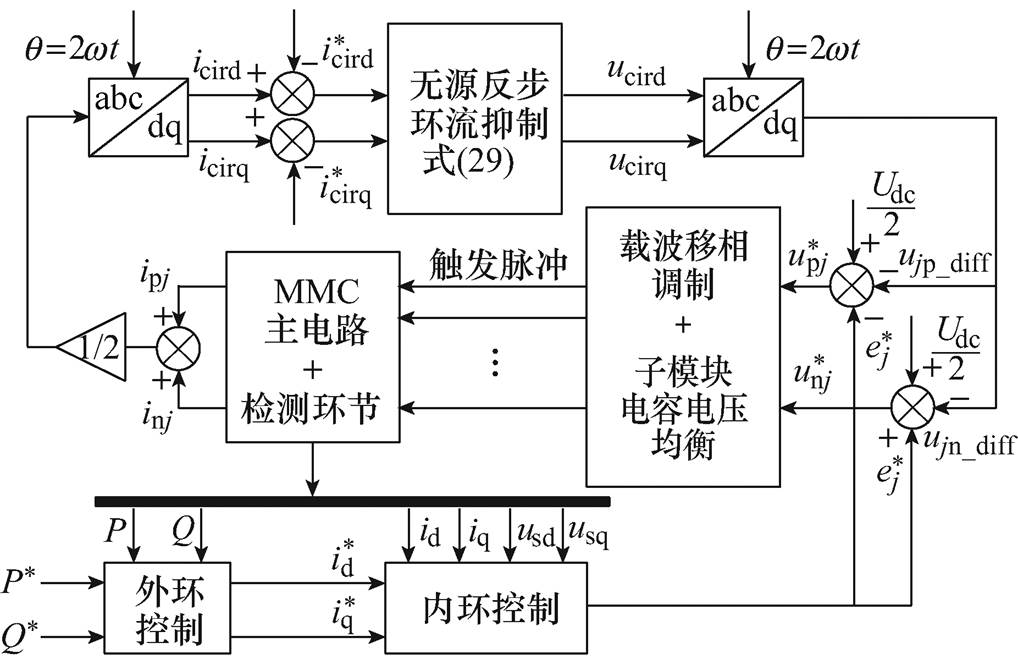
图4 MMC整体控制框图
Fig.4 Overall block diagram of MMC
为验证基于PCHD模型的MMC无源反步CCSC的可行性与有效性,在Matlab/Simulink环境下搭建五电平MMC仿真模型,将所提方法与传统矢量CCSC、反步CCSC、基于EL模型的无源CCSC进行仿真对比研究。MMC系统仿真参数见表1,各MMC环流抑制方法的仿真参数见表2,表2中各MMC CCSC仿真参数均在最优动、静态控制效果下取得。
表1 MMC系统仿真参数
Tab.1 Parameters of the MMC system

参 数数 值 单桥臂子模块数量n4 子模块电容C/mF2 桥臂电感Lm/mH5 桥臂电阻Rm/W5 交流侧额定电压uj/V220 交流系统频率f/Hz50 直流侧电压Udc/V650 交流侧电感L/mH1 交流侧电阻R/mW100
表2 各MMC CCSC仿真参数
Tab.2 Parameters of the MMC CCSCs

控制策略参 数 传统矢量CCSCkp1=kp2=35ki1=ki2=100 反步CCSCk1=k2=1 000 基于EL模型的无源CCSCra1=ra2=100 基于PCHD模型的无源反步CCSCra1=ra2=50J1=J2=0k1=k2=1 000
在MMC系统稳态运行下采用基于PCHD模型的MMC无源反步CCSC进行仿真测试。当t =0.4s时启动环流抑制,稳态下基于PCHD模型的MMC无源反步CCSC仿真波形如图5所示。
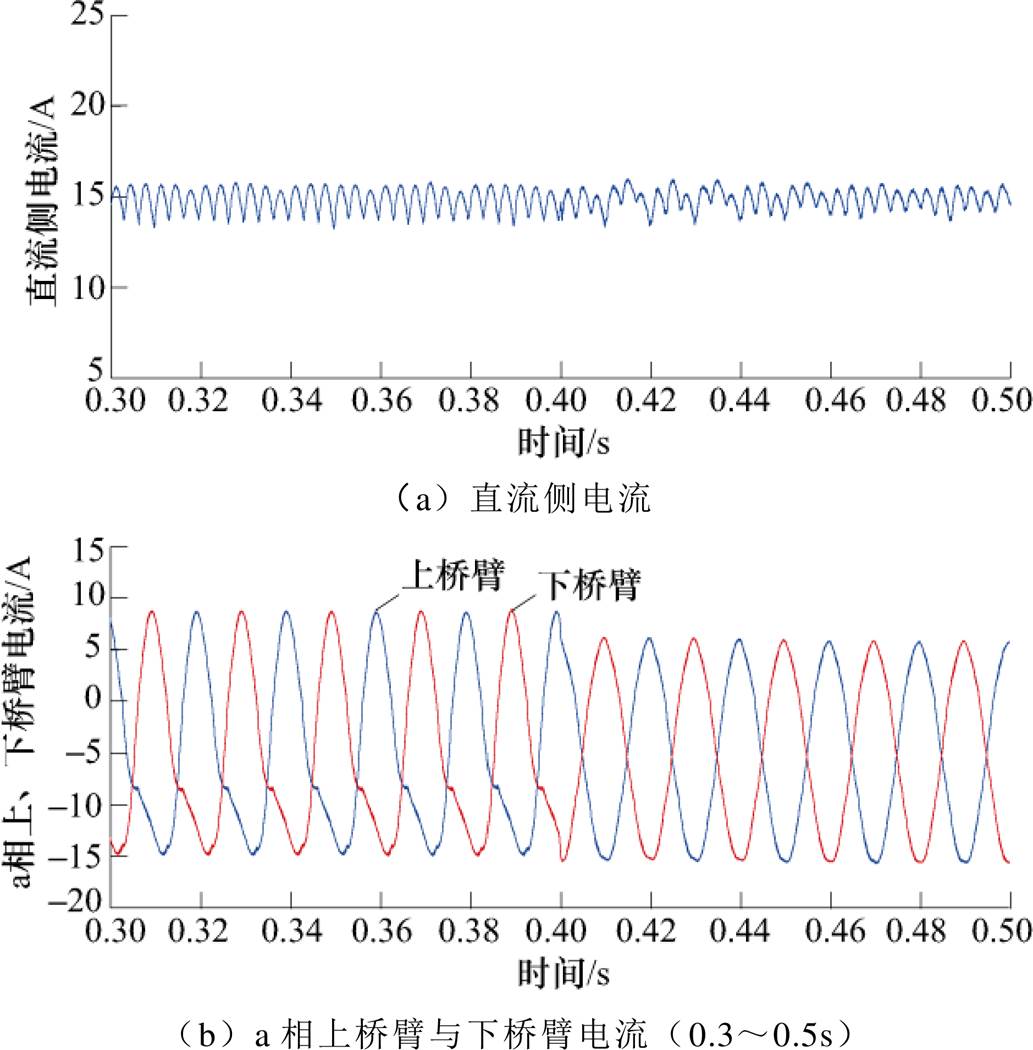
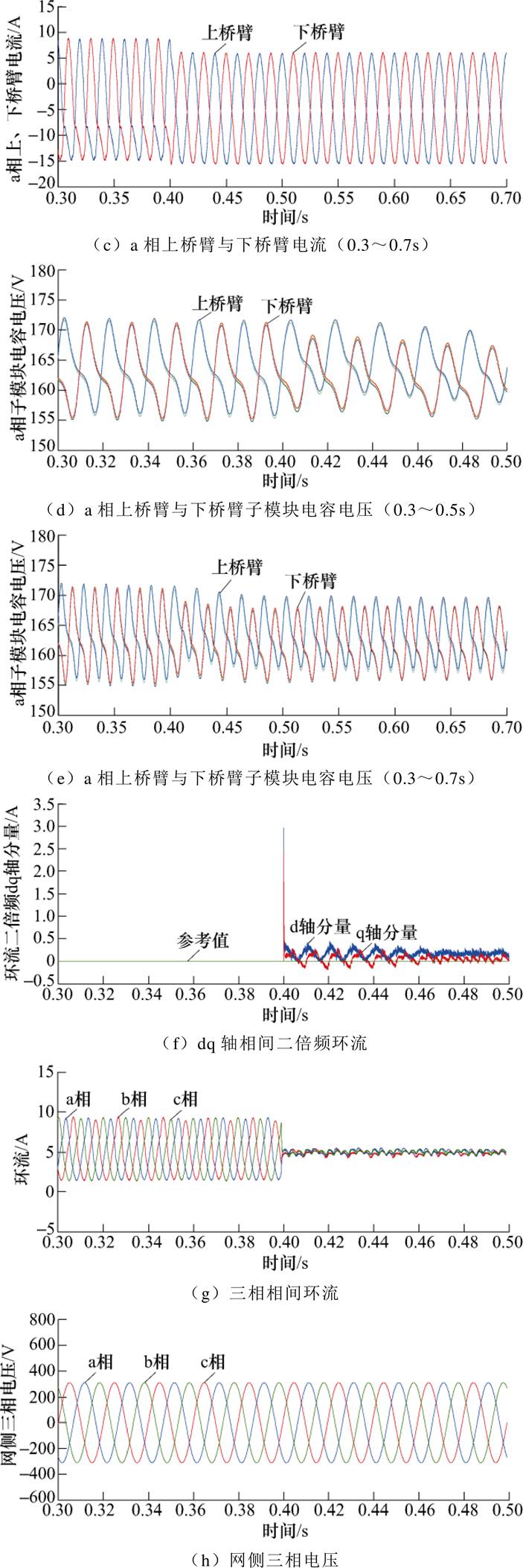

图5 稳态下基于PCHD模型的MMC无源反步CCSC仿真波形
Fig.5 Simulation waveforms of passivity-based backstepping circulating current suppression under steady state
分析图5a可知,无源反步CCSC有效地降低了直流侧电流脉动,提升系统稳定性;由图5b可知,未采用环流抑制时,由于存在二倍频负序环流分量,导致a相上桥臂电流存在畸变,t =0.4s后,实施基于PCHD模型的无源反步CCSC,MMC桥臂电流主要为直流分量和基频分量,接近于理想正弦波,波形质量得到改善;由图5c可知,实施环流抑制后a相上、下桥臂电流快速跟踪期望轨迹,进入新的稳定运行状态;由图5d可知,二倍频负序分量的抑制使得直流电容量和子模块电容电压波动明显减小;由图5e可知,实施环流抑制后,子模块电容电压能够保持平稳,无明显衰减;由图5f可知,二倍频负序dq轴分量 、
、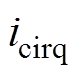 均能够快速地跟踪给定环流二倍频分量
均能够快速地跟踪给定环流二倍频分量 、
、 ;由图5g可知,t =0.4s前三相环流波形具有明显的二倍频特性,启动环流抑制后,三相环流均在
;由图5g可知,t =0.4s前三相环流波形具有明显的二倍频特性,启动环流抑制后,三相环流均在 处波动,与理论分析结果一致,采用基于PCHD模型的无源反步CCSC二倍频环流分量抑制,环流抑制效果明显;由图5h和图5i可得,MMC环流不影响交流侧输出外特性,系统运行平稳。
处波动,与理论分析结果一致,采用基于PCHD模型的无源反步CCSC二倍频环流分量抑制,环流抑制效果明显;由图5h和图5i可得,MMC环流不影响交流侧输出外特性,系统运行平稳。
MMC稳态运行条件下传统矢量控制、反步控制、基于EL模型的无源控制、基于PCHD模型的无源反步控制四种CCSC a相环流仿真波形如图6所示。分析图6可知,在MMC稳态运行条件下,四种CCSC均起到较好的环流抑制效果,二倍频分量抑制效果明显。为定量比较四种CCSC抑制环流二倍频分量性能优劣,进一步对MMC a相环流进行5个周期的快速傅里叶变换(Fast Fourier Trans- form, FFT)谐波分析。
在t =0.4s时启动环流抑制,未采用CCSC与采用传统矢量CCSC、反步CCSC、基于EL模型的无源CCSC、基于PCHD模型的MMC无源反步CCSC 五种情形下MMC a相环流谐波成分柱状如图7所示,四种CCSC谐波分析见表3。由图7和表3可知,四种CCSC均能较好地控制MMC环流二倍频分量,量化比较结果表明,基于PCHD模型的MMC无源反步CCSC二倍频占比最小,环流抑制效果最优,直流量损耗最小,能量传输最优。
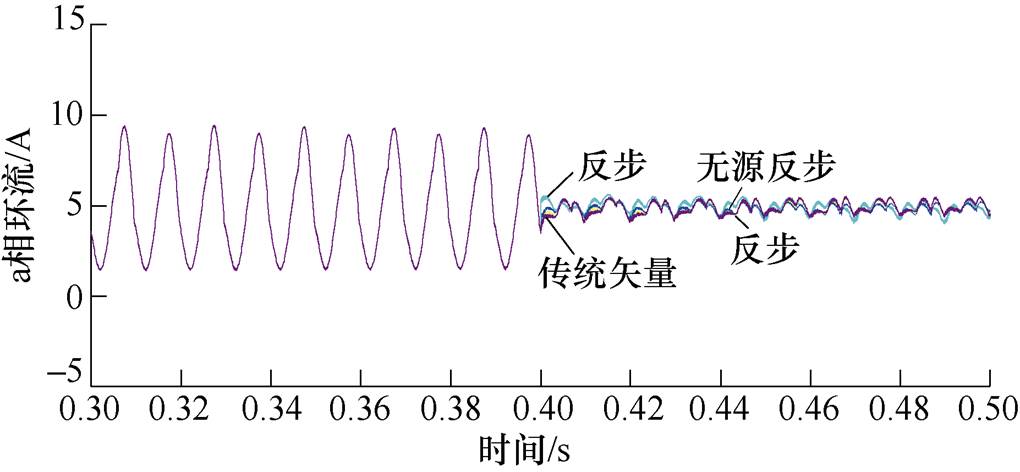
图6 稳态下四种CCSC a相环流仿真波形
Fig.6 Simulation waveforms of phase-a circulating currents under steady state
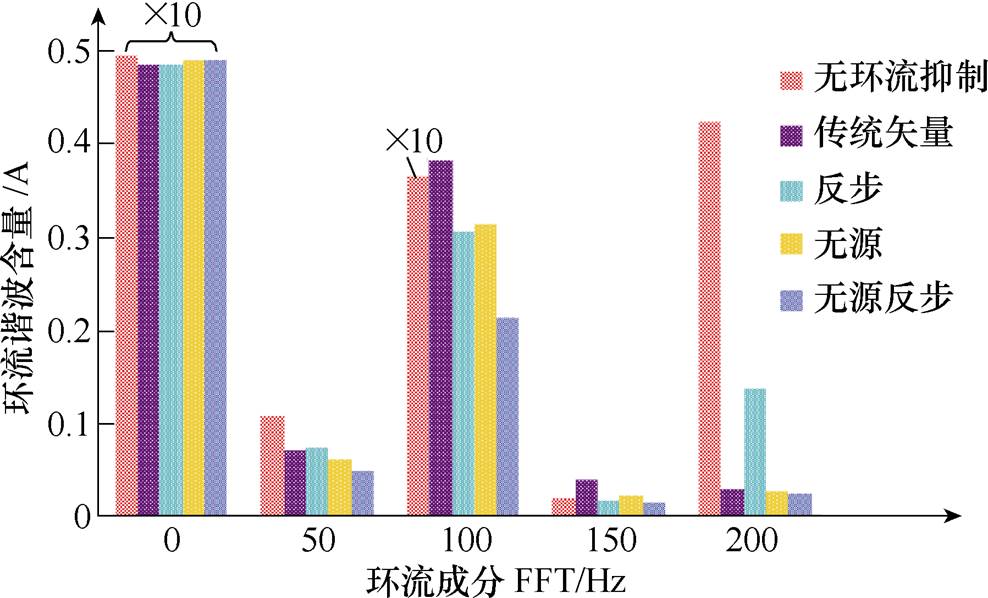
图7 五种情形下MMC a相环流FFT分析
Fig.7 FFT analysis of phase-a circulating current under five different conditions of MMC
表3 五种CCSC谐波分析
Tab.3 Harmonic analysis under five CCSE
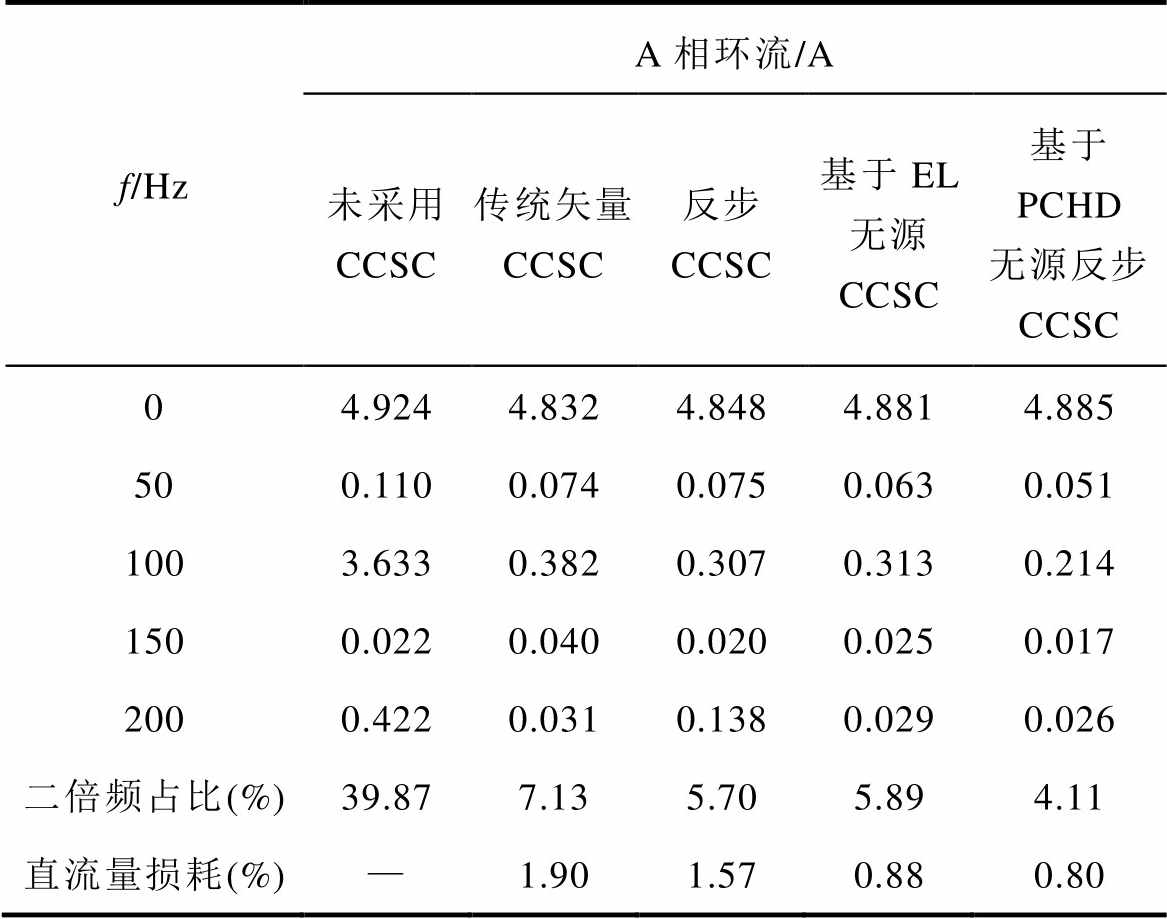
f/HzA相环流/A 未采用 CCSC传统矢量 CCSC反步 CCSC基于EL无源 CCSC基于 PCHD无源反步 CCSC 04.9244.8324.8484.8814.885 500.1100.0740.0750.0630.051 1003.6330.3820.3070.3130.214 1500.0220.0400.0200.0250.017 2000.4220.0310.1380.0290.026 二倍频占比(%)39.877.135.705.894.11 直流量损耗(%)—1.901.570.880.80
在MMC系统功率突变、直流侧电压突变和桥臂阻感突变条件下采用传统矢量CCSC、基于EL模型无源CCSC、反步CCSC和基于PCHD模型的无源反步CCSC的仿真结果进行对比测试。
3.2.1 功率突变情形
初始设置MMC并网控制回路有功功率参考值为10kW,无功功率参考值为0kvar;t =0.35s时启动MMC环流抑制;t =0.4s时MMC有功功率参考值由10kW阶跃上升至15kW,无功功率参考值保持不变;t =0.45s时有功功率参考值阶跃下降至10kW,无功功率参考值保持不变。功率突变时MMC各CCSC仿真结果如图8所示,分析在有功功率突变时各方法对MMC环流和dq相间二倍频分量的抑制情况。
分析图8可知:MMC并网控制回路外环有功功率发生突变时,环流二倍频环流分量实际值 、
、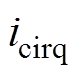 均未发生明显突变,四种CCSC均能响应功率突变并实现环流抑制。传统矢量CCSC依赖于PI反馈环节得到控制量
均未发生明显突变,四种CCSC均能响应功率突变并实现环流抑制。传统矢量CCSC依赖于PI反馈环节得到控制量 、
、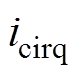 ,响应速度取决于PI控制器参数的设计,通常PI控制器参数设计为MMC系统稳态运行下的最优性能参数。当MMC系统发生功率突变时,PI控制器参数并未调整,因此采用传统矢量CCSC的环流二倍频分量实际值波动较大。三种非线性控制方法从能量角度出发,设计系统渐进稳定的控制律,针对外部不确定性波动的发生,其抗干扰能力优于传统矢量CCSC。比较三种非线性控制方法可知,反步CCSC上升时间短、动态响应速度快,但在功率波动发生期间环流及二倍频分量出现明显波动;基于EL模型的无源CCSC动态响应速度慢于反步CCSC,但在有功功率波动期间环流及二倍频分量波动幅度较小,抗干扰能力较好;基于PCHD模型的无源反步CCSC响应速度快、超调小、环流及二倍频分量波动幅度小、抗干扰能力强、稳定性好以及综合性能最优。
,响应速度取决于PI控制器参数的设计,通常PI控制器参数设计为MMC系统稳态运行下的最优性能参数。当MMC系统发生功率突变时,PI控制器参数并未调整,因此采用传统矢量CCSC的环流二倍频分量实际值波动较大。三种非线性控制方法从能量角度出发,设计系统渐进稳定的控制律,针对外部不确定性波动的发生,其抗干扰能力优于传统矢量CCSC。比较三种非线性控制方法可知,反步CCSC上升时间短、动态响应速度快,但在功率波动发生期间环流及二倍频分量出现明显波动;基于EL模型的无源CCSC动态响应速度慢于反步CCSC,但在有功功率波动期间环流及二倍频分量波动幅度较小,抗干扰能力较好;基于PCHD模型的无源反步CCSC响应速度快、超调小、环流及二倍频分量波动幅度小、抗干扰能力强、稳定性好以及综合性能最优。
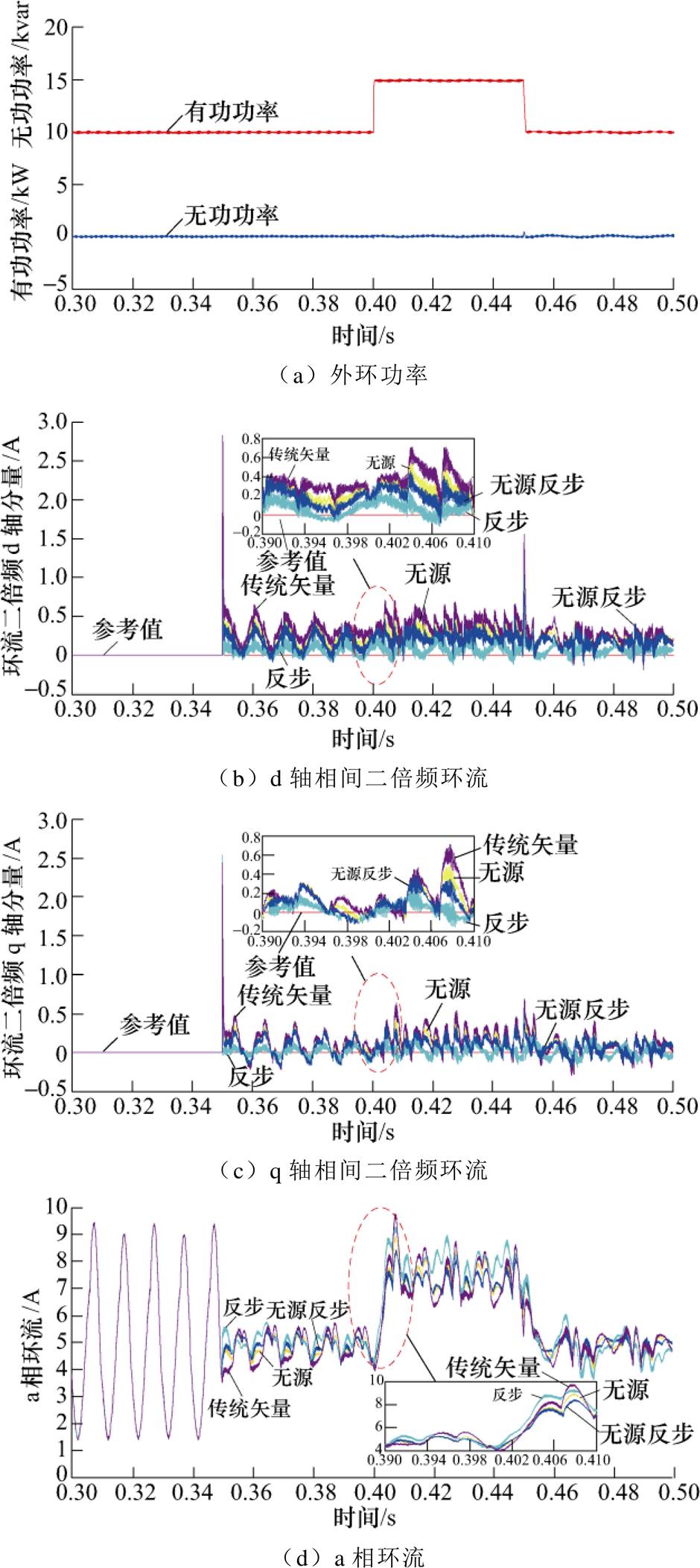
图8 功率突变时四种CCSC仿真波形
Fig.8 Simulation waveforms of four CCSCs with load mutation
3.2.2 直流侧电压突变情形
初始设置MMC直流侧电压为650V,t =0.35s时启动MMC环流抑制;t =0.4s时直流侧电压阶跃上升5%,为682.5V;t =0.45s时直流侧电压跌落至650V。直流侧电压突变时四种CCSC仿真波形如图9所示,分析在直流侧电压突变时四种CCSC对MMC环流和dq相间二倍频分量的抑制情况。
分析图9可知:直流侧电压发生突变时,四种CCSC均能跟踪环流二倍频期望值,实现环流抑制。但传统矢量CCSC在跟踪过程中存在较大的稳态误差且波动幅值较大;反步CCSC动态响应较好,但存在较大的超调;基于EL模型无源CCSC超调小,能够实现环流二倍频分量的渐进跟踪;基于PCHD模型的无源反步CCSC响应速度快、超调小、环流及二倍频分量波动幅度小、抗干扰能力强以及系统全局稳定性好。
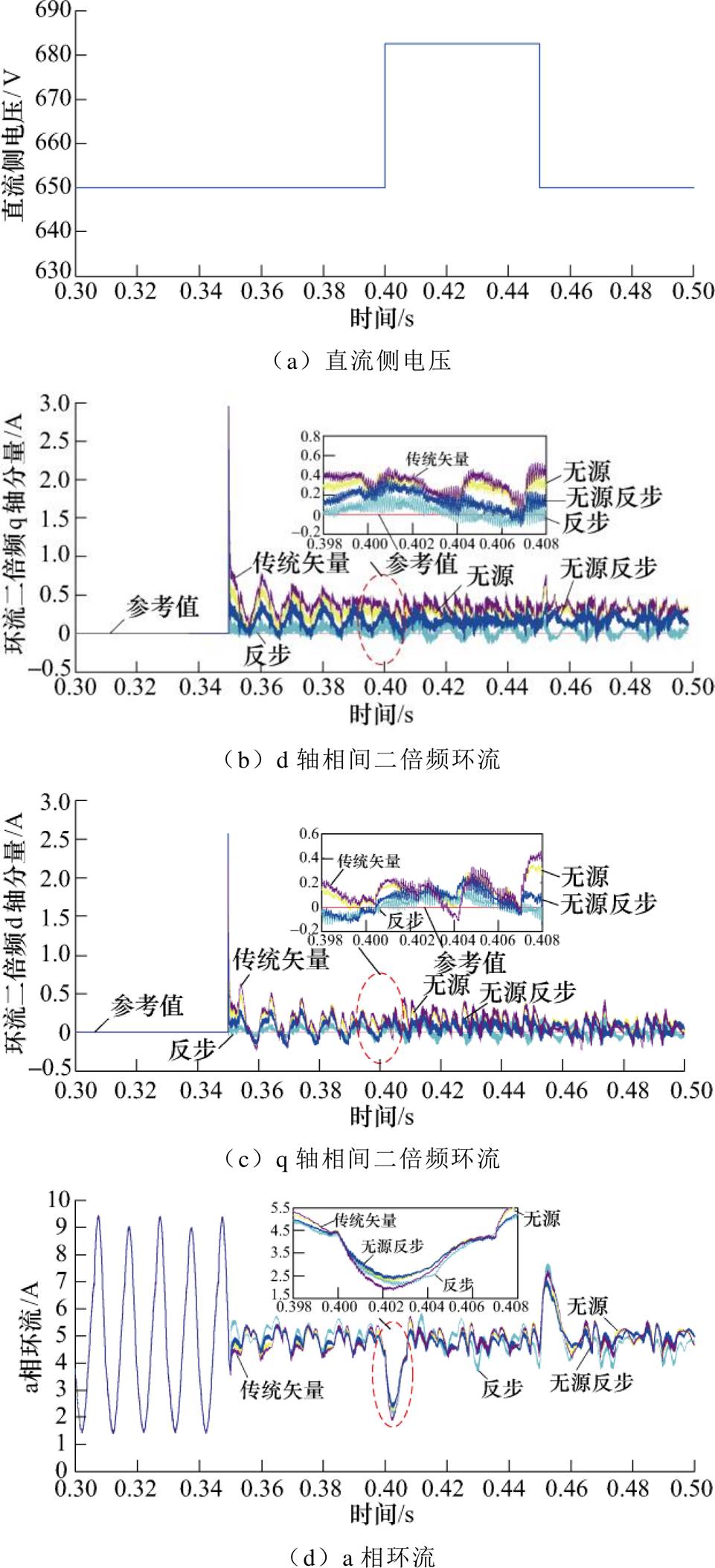
图9 直流侧电压突变时四种CCSC仿真波形
Fig.9 Simulation waveforms of four CCSCs with DC side voltage mutation
3.2.3 系统桥臂阻感参数突变情形
初始设置桥臂电阻为0.5W、电感为5mH,t = 0.35s时启动MMC环流抑制;t =0.4s时a相桥臂阻感阶跃上升20%,分别为0.6W、6mH;t =0.45s时恢复至初始值。MMC桥臂阻感参数突变时四种CCSC仿真波形如图10所示,分析在内部桥臂阻感参数突变时四种CCSC对MMC环流和dq相间二倍频分量的抑制情况。
由图10分析可知:当系统内部模型参数发生摄动时,PI控制器参数并未调整,传统矢量CCSC只能在平衡点附近达到稳定,无法适应新的平衡点,因而环流波动幅值较大、鲁棒性欠佳。反步CCSC虽能保持系统渐进稳定,具有较快的响应速度,但环流二倍频分量跟踪时波动程度较无源性CCSC显著。分析比较桥臂阻感参数突变对应的a相环流过冲幅度可知,基于EL模型的无源CCSC与基于PCHD模型的无源反步CCSC均具有较好的鲁棒性,当系统内部参数发生摄动时能较快达到新平衡点,环流变化尖峰相对较小,稳态后谐波抑制能力较好,具有较好的抗扰性能。两种无源性控制方法中,基于PCHD模型的无源反步CCSC由于反步环节的加入具有动态响应好、跟踪性能优的特点,在MMC桥臂阻感发生突变期间,环流波动幅度较小,说明所提出的方法对于系统参数摄动具有较好的鲁棒性。

图10 MMC桥臂阻感参数突变时四种CCSC仿真波形
Fig.10 Simulation waveforms of four CCSCs with internal bridge arm resistance parameter mutation
为评估系统在功率突变、直流侧电压突变、系统桥臂阻感参数突变三种情况下MMC环流的波动程度,引入环流波动幅度评价指标为
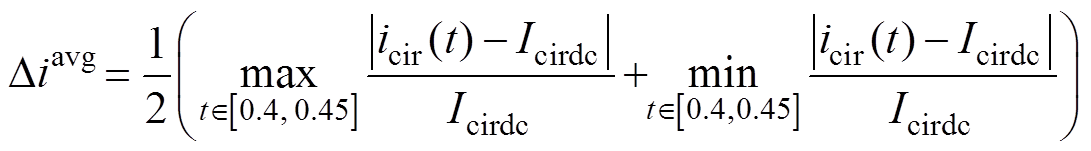 (32)
(32)式中,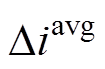 为波动幅度;
为波动幅度;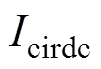 为突变时环流直流分量有效值。
为突变时环流直流分量有效值。
结合功率突变、直流侧电压突变、系统桥臂阻感参数突变三种情形下传统矢量控制、反步控制、基于EL模型的无源控制、基于PCHD模型的无源反步控制四种CCSC的环流动态响应波形,四种环流抑制方法动态响应性能指标量化计算结果见表4。分析表4可知,基于PCHD模型的无源反步CCSC在系统运行条件变化时动态响应超调小、调节时间短;环流波动幅度小,在系统运行条件发生外部或内部变化而控制器参数未做调整情况下,依然能够保持优良的环流抑制性能,综合性能优。
表4 四种CCSC动态性能指标量化计算结果
Tab.4 Quantitative calculation results of four CCSC dynamic performance indicators

情形控制方法响应时间/ms超调(%)调节时间/ms波动幅度(%) 1传统矢量4.3023.429.6015.19 反步4.1020.2516.5013.29 基于EL无源4.4011.259.106.39 基于PCHD无源反步4.405.386.405.76 2传统矢量13.2048.8213.6012.97 反步7.6053.7019.3020.76 基于EL无源7.3041.0313.305.82 基于PCHD无源反步7.6041.0513.305.25 3传统矢量3.8022.3125.3016.32 反步1.5011.4410.9012.24 基于EL无源3.703.0010.906.61 基于PCHD无源反步3.802.4010.704.61
注:情形1、2、3分别指功率突变情形、直流侧电压突变情形和系统桥臂阻感参数突变情形。
借助dSPACE系统的软硬件快速联调功能,建立如图11所示的122V/750W MMC硬件安装设备实验平台,来验证基于PCHD模型的无源反步CCSC的正确性与可行性。

图11 MMC硬件安装设备
Fig.11 MMC hardware setup devices
MMC控制系统的dSPACE集成化结构如图12所示。MMC系统每相桥臂串联3个子模块,主电路开关选择SKM50GB123D功率模块,采用SKHI21A驱动模块,由dSPACE系统DS2201生成MMC功率模块的PWM触发信号;控制器以dSPACE系统DS1005的DSP TMS320F28335高速处理器为核心,控制方法在Matlab/Simulink环境下建模实现,通过RTI实时接口完成dSPACE系统与Simulink模型的连接,利用RTW进行扩展,实现两者间硬件代码的自动下载;由dSPACE系统的Control Desk软件对调试过程进行综合管理,实时监测控制效果。基于dSPACE的MMC实验系统参数见表5。
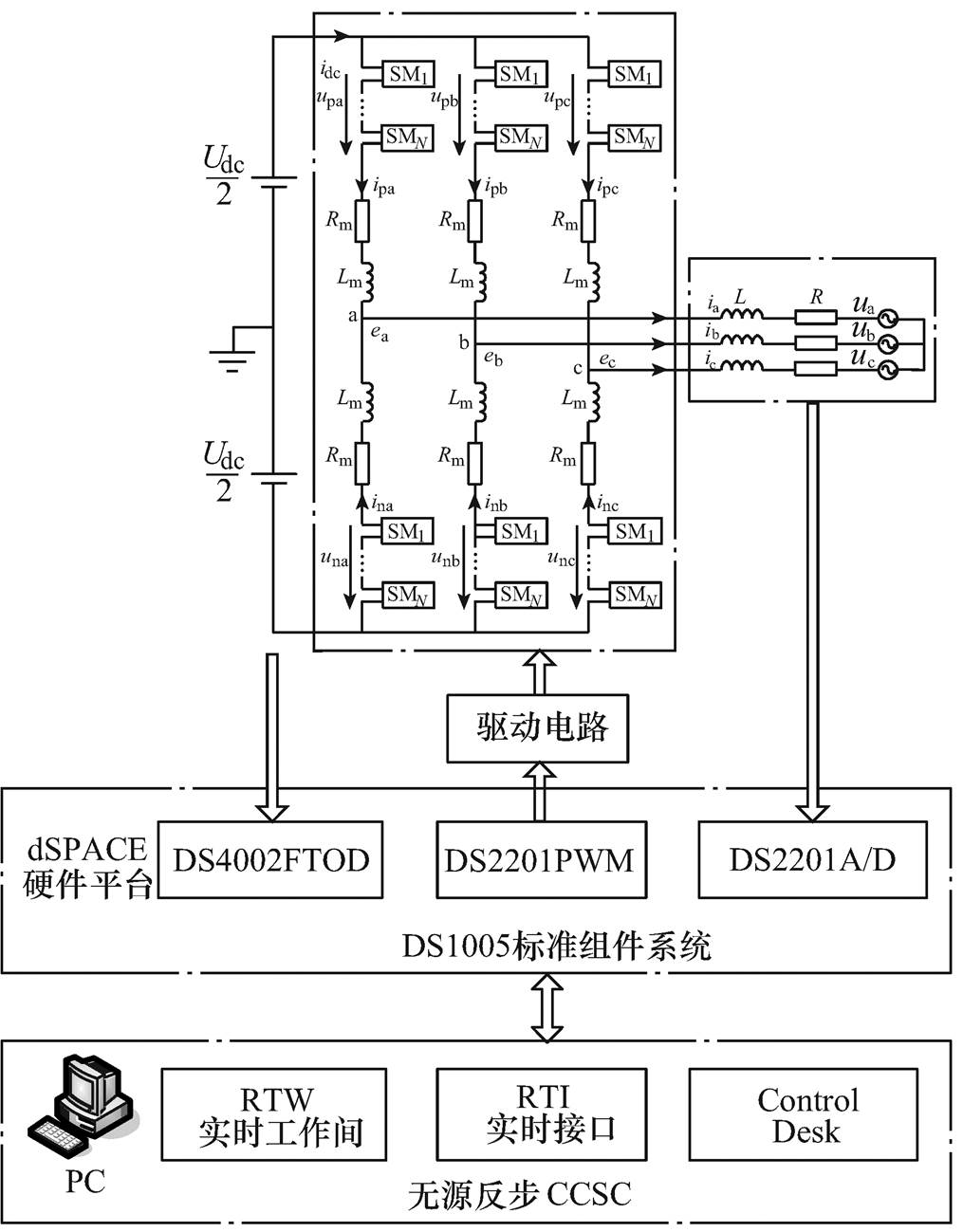
图12 MMC控制系统的dSPACE集成化结构
Fig.12 Integrated architecture of MMC experimental system based on dSPACE
表5 基于dSPACE的MMC实验系统参数
Tab.5 Parameters of MMC for experiment baced on dSPACE

参 数数 值 单桥臂子模块数量n3 子模块电容C/mF2.2 桥臂电感Lm/mH2 桥臂电阻Rm/W0.025 交流侧额定电压uj/V122 交流系统频率f/Hz50 直流侧电压Udc/V150 交流侧电感L/mH0.5 交流侧电阻R/W5 控制器参数ra1=ra2=50J1=J2=0k1=k2=400
图13为基于PCHD模型的无源反步CCSC在MMC系统稳态运行条件下网侧电压、网侧电流、a相上、下桥臂电流和a相环流的实验波形。分析图13可知,MMC系统额定参数下,采用基于PCHD模型的无源反步CCSC可实现系统稳定运行,网侧电压呈现较好的正弦性;网侧电流为近似50Hz正弦波形,较为平滑,且与电压相位一致;a相上、下桥臂电流因含较少谐波,桥臂电流畸变得到有效控制;环流幅度较小、抑制效果好。
图14为直流侧电压由150V降至140V、桥臂电阻由0.025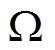 变至0.05
变至0.05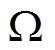 时MMC系统网侧电压、网侧电流、a相上、下桥臂电流和a相环流的实验波形。分析图14可知,在MMC系统外部与内部运行条件改变情形下,基于PCHD模型的无源反步CCSC依然可实现系统稳定运行,网侧电压与电流维持平稳;a相上、下桥臂电流与MMC系统额定参数运行条件下的结果比较,虽然出现稍明显的波形畸变,但依然能够保持较优的运行特性;因直流侧电压下降,环流幅度变小,抑制效果保持较好。
时MMC系统网侧电压、网侧电流、a相上、下桥臂电流和a相环流的实验波形。分析图14可知,在MMC系统外部与内部运行条件改变情形下,基于PCHD模型的无源反步CCSC依然可实现系统稳定运行,网侧电压与电流维持平稳;a相上、下桥臂电流与MMC系统额定参数运行条件下的结果比较,虽然出现稍明显的波形畸变,但依然能够保持较优的运行特性;因直流侧电压下降,环流幅度变小,抑制效果保持较好。

图13 平稳运行条件下实验波形
Fig.13 Experimental waveforms under balanced condition

图14 系统运行条件变化下实验波形
Fig.14 Experimental waveforms under MMC with MMC operation condition changed
图15为系统额定参数与系统参数变化条件下MMC a相环流FFT谐波分析结果。由图15分析可知,在系统额定参数与系统参数变化情形下,基于PCHD模型的无源反步CCSC的环流THD分别为7.43%和6.98%,环流二倍频分量分别为5.95%和5.67%,环流抑制效果明显,同理论分析与仿真结论一致。
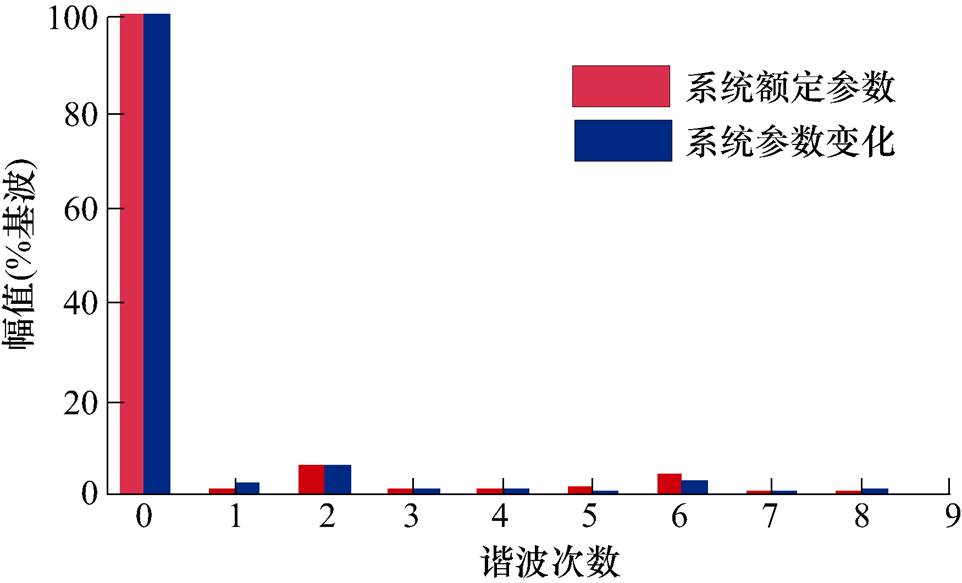
图15 系统不同运行条件下MMC a相环流FFT谐波分析
Fig.15 FFT analysis of MMC phase-a circulating currents under different operation conditions
由基于dSPACE的实验结果分析可知:基于PCHD模型的无源反步CCSC能够实现MMC系统平稳运行,并网电压、电流稳态运行静差小,环流抑制作用好,电能质量高;在MMC直流侧电压和参数同时发生变化情况下依然能够实现MMC系统的稳定控制与环流抑制。基于dSPACE的实验结果证明了基于PCHD模型的无源反步CCSC的正确性和有效性。
针对MMC自身非线性特性和大功率可再生能源并网不确定性扰动带来的环流抑制稳定性与鲁棒性问题,提出基于PCHD模型的无源反步CCSC。通过能量函数整形和控制修正系统性能,确保系统的全局稳定性;通过设置较小的阻尼矩阵,实现内部耗散能量得到有效控制,优化系统内部能量;通过保留非线性项,抵消Lyapunov函数一阶导数中的非线性项,使MMC环流系统在满足Lyapunov稳定性定理的前提下实现环流二倍频分量渐进跟踪,具有良好的暂态性能。
将所提方法与传统矢量CCSC、反步CCSC、基于EL模型的无源CCSC进行稳态控制效果MMC a相环流FFT分析,并在系统有功功率波动、直流侧电压扰动、桥臂参数摄动情形下测试各MMC CCSC环流抑制效果,对比分析仿真和实验结果表明基于PCHD模型的MMC无源反步CCSC可实现:
1)环流二倍频抑制效果优,直流量损耗小,内部能量损耗少。
2)通过设计全局能量函数,实现MMC环流闭环控制系统的全局渐进稳定,具有稳定域宽、鲁棒性强的特点,克服了传统控制方法基于稳定运行点简单线性化的缺点。
3)新型构造方式便于设计动态性能响应快速的扰动抑制算法,摆脱现有干扰抑制方法的约束要求,如测量输出的可微性,消除不稳定零极点、需采集干扰的峰值信息等。
4)具有结构简单、无源性控制器与反步控制器满足分离原理,具有两个自由度的特点,与现有非线性控制方法相比,更易于工程实现。
参考文献
[1] Debnath S, Qin Jiangchao, Bahrani B, et al. Oper- ation, control, and applications of the modular multilevel converter: a review[J]. IEEE Transactions on Power Electronics, 2015, 30(1): 37-53.
[2] Zhang Lei, Zou Yuntao, Yu Jicheng, et al. Modeling, control, and protection of modular multilevel converter-based multi-terminal HVDC systems: a review[J]. CSEE Journal of Power and Energy Systems, 2017, 3(4): 340-352.
[3] 关维德, 黄守道, 黄小庆. 一种基于改进模块化多电平换流器的中压风电系统及其控制方法[J]. 电工技术学报, 2018, 33(16): 3782-3791.
Guan Weide, Huang Shoudao, Huang Xiaoqing. A medium-voltage wind power generation system based on improved modular multilevel converter and its control scheme[J]. Transactions of China Electro- technical Society, 2018, 33(16): 3782-3791.
[4] 王一凡, 赵成勇, 郭春义, 等. 双馈风电场孤岛经模块化多电平换流器直流输电并网系统小信号稳定性分析与振荡抑制方法[J]. 电工技术学报, 2019, 34(10): 2116-2129.
Wang Yifan, Zhao Chengyong, Guo Chunyi, et al. Small signal stability and oscillation suppression method for islanded double fed induction generator- based wind farm integrated by modular multilevel converter based HVDC system[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2116- 2129.
[5] Li Yalong, Edward A J, Wang Fei. Circulating current suppressing control’s impact on arm indu- ctance selection for modular multilevel converter[J]. IEEE Journal of Emerging and Selected Topics in Power Electronics, 2017, 5(1): 182-188.
[6] Behrooz B, Suman D, Maryam S. Circulating current suppression of the modular multilevel converter in a double-frequency rotating reference frame[J]. IEEE Transactions on Power Electronics, 2016, 31(1): 783-792.
[7] 李金科, 金新民, 吴学智, 等. 不平衡交流电网模块化多电平变流器特性分析及环流抑制方法[J]. 中国电机工程学报, 2017, 37(12): 3535-3544, 3682.
Li Jinke, Jin Xinmin, Wu Xuezhi, et al. Characteristic analysis and a circulating current control method in modular multilevel converters under unbalanced grid conditions[J]. Proceedings of the CSEE, 2017, 37(12): 3535-3544, 3682.
[8] Wang Jinyu, Liang Jun, Wang Chengfu, et al. Circulating current suppression for MMC-HVDC under unbalanced grid conditions[J]. IEEE Transa- ctions on Industry Applications, 2017, 53(4): 3250- 3259.
[9] 施恩泽, 吴学智, 荆龙, 等. 网压不平衡下环流注入对模块化多电平换流器的影响分析[J]. 电工技术学报, 2018, 33(16): 3719-3731.
Shi Enze, Wu Xuezhi, Jing Long, et al. Analysis of the impact on modular multilevel converter with circulating current injection under unbalanced grid voltage[J]. Transactions of China Electrotechnical Society, 2018, 33(16): 3719-3731.
[10] Yang Shunfeng, Wang Peng, Tang Yi, et al. Cir- culating current suppression in modular multilevel converters with even-harmonic repetitive control[J]. IEEE Transactions on Industry Applications, 2018, 54(1): 298-309.
[11] 张臣, 叶华, 韦凌霄, 等. 不平衡状态下MMC双回路环流抑制策略[J]. 电工技术学报, 2019, 37(9): 1924-1933.
Zhang Chen, Ye Hua, Wei Lingxiao, et al. Double- loop circulating current suppressing strategy for modular multilevel converter under unbalanced conditions[J]. Transactions of China Electrotechnical Society, 2019, 37(9): 1924-1933.
[12] 宋平岗, 何峰. 基于微分平坦理论模块化多电平换流器环流抑制控制方法[J]. 电力系统保护与控制, 2015, 43(19): 43-48.
Song Pinggang, He Feng. Differential flatness based method of circulating current suppressing control for modular multilevel converter[J]. Power System Protection and Control, 2015, 43(19): 43-48.
[13] Lazhar B, Adel G, Mohamed T, et al. Modular multilevel converter circulating current reduction using model predictive control[J]. IEEE Transactions on Industrial Electronics, 2016, 63(6): 3857-3866.
[14] Zhang Xiaotong, Huang Jingjing, Zhang Xin, et al. Backstepping based nonlinear control strategy for MMC topology[C]//IECON 2017-43rd Annual Con- ference of the IEEE Industrial Electronics Society, Beijing, 2017: 1-7.
[15] Romeo O, Arjan V S, Fernando C, et al. Control by interconnection and standard passivity-based control of port-Hamiltonian systems[J]. IEEE Transactions Automatic Control, 2008, 53(11): 2527-2542.
[16] Seung-Ju L, kWang-Kyo O, Hyo-Sung A. Passivity- based output synchronisation of port-controlled Hamiltonian and general linear interconnected systems[J]. IET Control Theory & Applications, 2013, 7(2): 234-245.
[17] 蔡新红, 赵成勇. 基于欧拉-拉格朗日模型的模块化多电平换流器的无源控制[J]. 电工技术学报, 2013, 28(10): 224-232.
Cai Xinhong, Zhao Chengyong. Euler-Lagrange model based passive control for modular multilevel converter[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 224-232.
[18] 祝贺, 王久和, 郑成才, 等. 五电平MMC-UPQC的无源控制[J]. 电工技术学报, 2017, 32(增刊2): 172-178.
Zhu He, Wang Jiuhe, Zheng Chengcai, et al. Passivity based control of five-level MMC-UPQC[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(S2): 172-178.
[19] Romeo O, Arjan V S, Bernhard M, et al. Inter- connection and damping assignment passivity-based control of port-controlled Hamiltonian systems[J]. Automatica, 2002, 38(4): 585-596.
[20] Zhang Qi, Liu Guangjun.Precise control of elastic joint robot using an interconnection and damping assignment passivity-based approach[J]. IEEE/ASME Transactions on Mechatronics, 2016, 21(6): 2728- 2736.
[21] 杨晓峰, 李泽杰, 郑琼林. 基于虚拟阻抗滑模控制的MMC环流抑制策略[J]. 中国电机工程学报, 2018, 38(23): 6893-6904, 7123.
Yang Xiaofeng, Li Zejie, Zheng Qionglin. A novel MMC circulating current suppressing strategy based on virtual impedance sliding mode control[J]. Pro- ceedings of the CSEE, 2018, 38(23): 6893-6904, 7123.
[22] 范志华, 苗世洪, 刘子文, 等. 模块化多电平换流器子模块故障特性分析与解耦控制策略[J]. 电工技术学报, 2018, 33(16): 3707-3718.
Fan Zhihua, Miao Shihong, Liu Ziwen, et al. Modular multilevel converter sub-module fault characteristics analysis and decoupling control strategy[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(16): 3707-3718.
[23] 薛花, 姜建国. 基于无源性的同步电动机自适应控制[J]. 电工技术学报, 2009, 24(10): 33-39.
Xue Hua, Jiang Jianguo. Adaptive passivity-based control of synchronous motors[J]. Transactions of China Electrotechnical Society, 2009, 24(10): 33-39.
[24] Jean-Jacques E, Slotine. Applied nonlinear control[M]. Englewood: Prentice Hall, 1991.
[25] Richard M M, Li Zexiang, Shankar S. A mathe- matical introduction to robotic manipulation[M]. Florida: Chemical Rubber Company, 1994.
MMC Passivity-Based and Backstepping Circulating Current Suppressing Method Based on Port-Controlled Hamiltonian with Dissipation Model
Abstract Modular multilevel converter (MMC) is widely used in renewable energy power grid connection. However, due to the random fluctuations, system parameter perturbation and its nonlinear characteristics, it is difficult to ensure the global asymptotic stability and strong robustness of MMC circulation suppression using traditional vector control methods. To solve this problem, a novel passivity-based and backstepping circulating current suppressing method based on port-controlled Hamiltonian with dissipation (PCHD) model was proposed. Based on the MMC global energy function of the PCHD model, the passivity-based controller was designed to correct the energy dissipation and flow of the closed-loop system through energy function shaping, so that the system energy could obtain the minimum value at the desired equilibrium point. The global asymptotic stability of the system was realized. The backstepping control method was adopted to eliminate the tracking error caused by uncertain disturbance and MMC parameter perturbation, thereby realizing the fast tracking of circulating double frequency components. The results of Matlab/Simulink and dSPACE show that the proposed passivity-based and backstepping circulating current suppressing method of MMC has the advantages of simplicity, no singularity and good transient performance, which can ensure the global stability and robustness of the system.
keywords:Modular multilevel converter, circulating current suppressing, port-controlled Hamiltonian with dissipation (PCHD) model, passivity-based control, backstepping
中图分类号:TM46
DOI: 10.19595/j.cnki.1000-6753.tces.190850
国家自然科学基金(51407114)、上海市科技创新行动计划(19DZ2204700)和上海工程技术研究中心(13DZ2251900)资助项目。
收稿日期 2019-07-17
改稿日期 2019-08-19
薛 花 女,1979年生,博士,副教授,研究方向为大功率新能源并网逆变器技术、非线性理论与控制方法。E-mail: distributepower@163.com(通信作者)
潘哲晓 男,1994年生,硕士研究生,研究方向为模块化多电平技术、非线性控制。E-mail: pzxdyx@foxmail.com
(编辑 陈 诚)