图1 SIDO Buck变换器电路拓扑
Fig.1 SIDO Buck converter
摘要 由于后级开关的存在，使得单电感双输出（SIDO）Buck变换器的供能模式变得复杂化，为给SIDO Buck变换器的分析设计提供正确的理论指导，该文对SIDO Buck变换器的供能模式进行深入分析。发现变换器工作在连续导电模式（CCM）时存在完全电感供能模式（CISM）和不完全电感供能模式（IISM）两种供能模式，同时变换器工作在断续导电模式（DCM）时也存在两种供能模式：双支路供能模式（DSM）和单支路供能模式（SSM）。该文得到各供能模式的临界电感，推导各供能模式的输出纹波电压解析式，总结出供能模式和输出纹波电压与电感之间的关系，并指出变换器工作在CCM时两条支路输出纹波电压间存在交叉影响。仿真和实验结果验证了理论分析的正确性。
关键词：单电感双输出 供能模式 临界电感 输出纹波电压 交叉影响
随着电力电子技术的快速发展，人们对电源的成本、体积和效率提出了更高的要求[1-4]，单电感双输出（Single-Inductor Dual-Output, SIDO）DC-DC开关变换器仅使用一个电感实现双路输出，节约了成本，减小了体积，同时提高了电源的转换效率，成为近年来国内外研究的热点[5-8]。
SIDO Buck变换器两条支路输出端存在交叉影响，为了提高SIDO Buck变换器的性能，国内外学者已经做了许多研究。文献[9]提出了一种恒流控制方法，所提出的恒流调节器采用电容和输出端的电流作为辅助反馈控制变量，通过抑制变换器的交叉影响，显著改善了负载瞬态响应。文献[10]提出了一种多变量控制器，得到了期望的开环传递函数矩阵，所提出的控制器最大限度地减少了变换器输出之间的耦合，提高了变换器的动态性能。文献[11]建立了电压控制SIDO Buck变换器的状态空间平均模型，分析了控制参数变化时变换器的稳定性及稳定边界，研究结果表明，电压控制参数具有稳定的上界或下界。以上研究均显著提高了SIDO Buck变换器的动态性能，但国内外关于SIDO Buck变换器的稳态分析，如变换器的供能模式和输出纹波电压研究还未见报道。
SIDO Buck变换器由于后级开关的存在，使得其供能模式较传统Buck变换器复杂得多，文献[12]对SIDO Buck变换器工作在连续导电模式（Continuous Conduction Mode, CCM）和断续导电模式（Dis- continuous Conduction Mode, DCM）的工作情况分别进行了讨论和归纳总结，但还不够完整和深入。再者，国内外关于SIDO Buck变换器的输出纹波电压研究仍缺少理论参考，而输出纹波电压是衡量变换器性能的重要指标，同时也是变换器参数设计的重要依据[13]，应用于煤矿、化工等危险环境下的开关变换器必须满足本质安全要求，因此这类变换器应尽量减小储能元件（电感和电容）的取值。而变换器储能元件的取值直接影响到输出纹波电压的大小，如何选取储能元件，使得变换器能同时满足本质安全和输出纹波电压要求成为一个重要问题。因此明确变换器工作在各供能模式的输出纹波电压情况是这类变换器设计的关键[13-16]。
鉴于以上两方面研究的不足，为给SIDO Buck变换器的分析设计提供理论指导，本文对其供能模式进行深入分析，推导出各供能模式的临界电感和输出纹波电压解析式，总结出供能模式和输出纹波电压与电感的关系，并讨论了两条支路输出纹波电压间的交叉影响情况。研究结果对于SIDO Buck变换器的分析设计具有指导意义。
SIDO Buck变换器电路拓扑如图1所示，其主要由开关管Qi、Qa和Qb，续流二极管VD，储能电感L，输出滤波电容Ca和Cb以及负载电阻Ra和Rb组成。变换器将一路输入电压转换为两路输出电压，其中Qi控制能量的输入，Qa、Qb和VD控制能量的输出及能量的分配。Di、Da和Db分别为Qi、Qa和Qb的占空比，且满足Da+Db=1。
图1 SIDO Buck变换器电路拓扑
Fig.1 SIDO Buck converter
SIDO Buck变换器的开关管占空比存在Di＞Db、Di=Db和Di＜Db三种情况，对应有三种工作方式[12]，由于三种工作方式的分析方法类似，限于篇幅，本文以Di＜Db的工作方式为例对SIDO Buck变换器的供能模式和输出纹波电压进行讨论。
当SIDO Buck变换器工作在CCM时，根据最小电感电流ILV与两路负载电流Ioa和Iob之间的大小关系，可将CCM再分为完全电感供能模式（Complete Inductor Supply Mode, CISM）和不完全电感供能模式（Incomplete Inductor Supply Mode, IISM），下面对这两种情况进行详细分析。
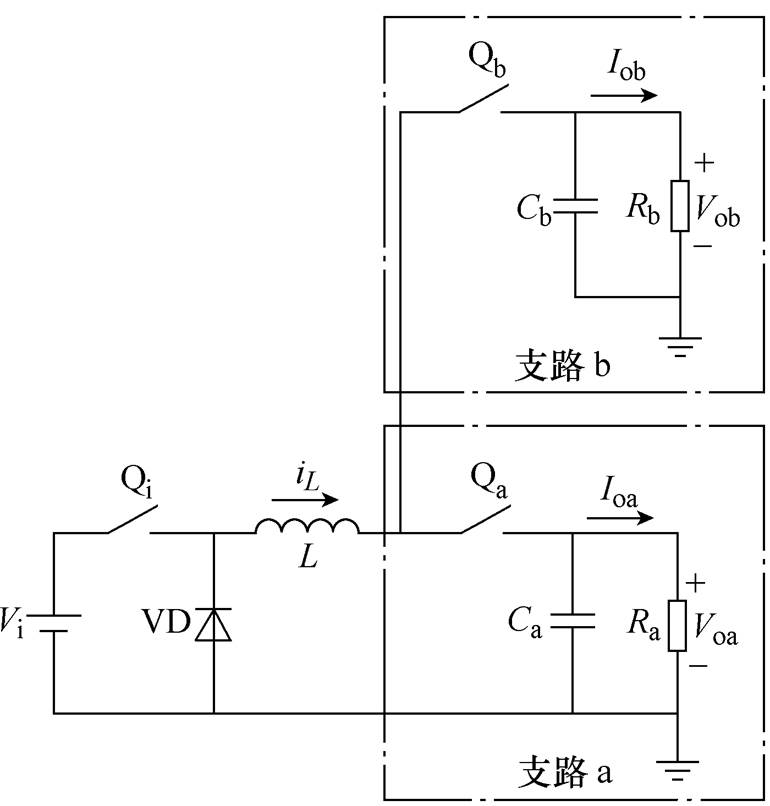
SIDO Buck变换器工作在CCM-CISM时的工作波形如图2所示，图中，ILP为最大电感电流，ILT为电路换路（即开关管Qb关断，Qa开通，电感电流通路切换到支路a）时的转折电感电流，ILV为最小电感电流。此时两条支路的负载电流与最小电感电流ILV之间满足ILV＞Ioa、ILV＞Iob。在0～t2时间段，电感L同时向负载Rb和电容Cb供能；在t2～t3时间段，电感L同时向负载Ra和电容Ca供能。
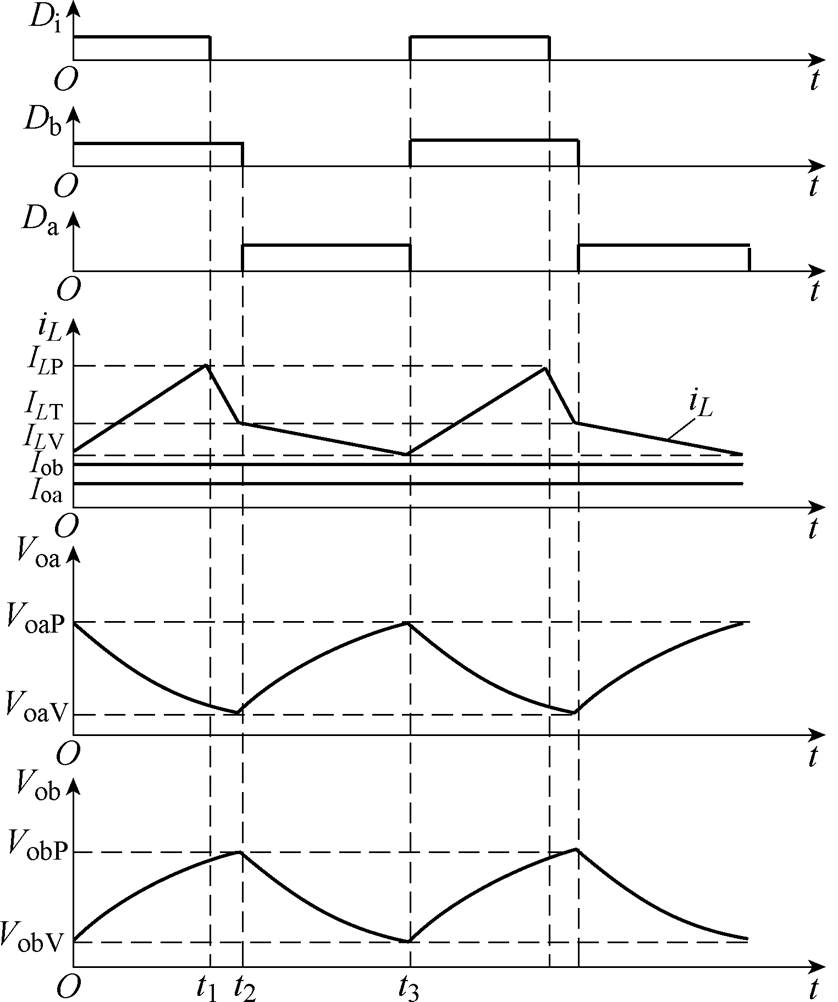
图2 CCM-CISM工作波形
Fig.2 Working waveforms of CCM-CISM
SIDO Buck变换器工作在CCM-IISM时，两条支路的负载电流与最小电感电流之间满足：ILV＜Ioa、ILV＜Iob，工作波形如图3所示。在0～t2时间段，当iL＜Iob时，电感L和电容Cb共同为负载Rb供能，直到iL＞Iob，电感L同时向负载Rb和电容Cb供能；在t2～t3时间段，当iL＞Ioa时，电感L同时向负载Ra和电容Ca供能，直到iL＜Ioa，电感L和电容Ca共同向负载Ra供能。
当SIDO Buck变换器工作在DCM时，根据电感电流下降到零的时刻所在开关区间的不同，可将DCM再分为双支路供能模式（Dual-Branch Supply Mode, DSM）和单支路供能模式（Single-Branch Supply Mode, SSM），下面对这两种情况进行详细分析。
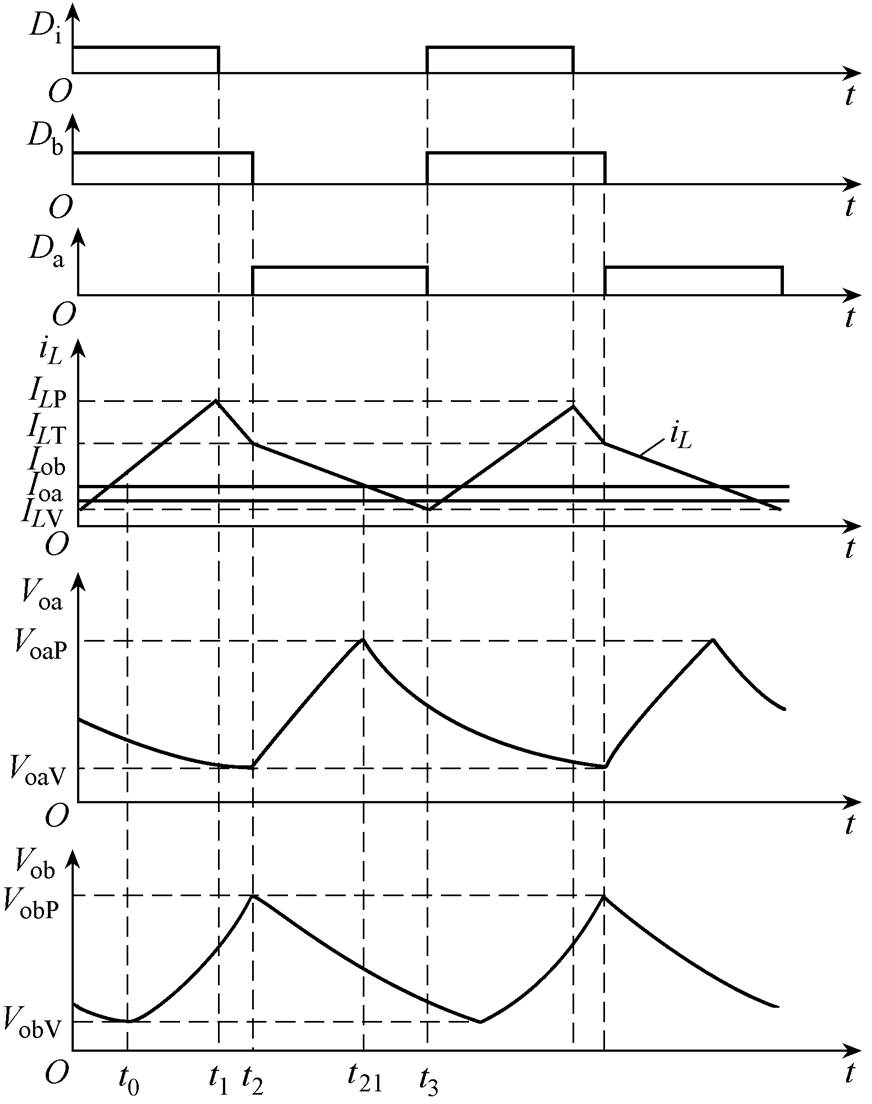
图3 CCM-IISM工作波形
Fig.3 Working waveforms of CCM-IISM
SIDO Buck变换器工作在DCM-DSM时，电感电流iL在t2～t3时间段降为零，工作波形如图4所示。图4中，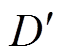
为变换器工作于DCM时支路a的实际占空比。在0～t2时间段，当iL＜Iob时，电感L和电容Cb共同为负载Rb供能，直到iL＞Iob，电感L同时向负载Rb和电容Cb供能；在t2～t22时间段，当iL＞Ioa时，电感L同时向负载Ra和电容Ca供能，直到iL＜Ioa，电感L和电容Ca共同向负载Ra供能；在t22～t3时间段，电感电流为零，负载由电容供能。
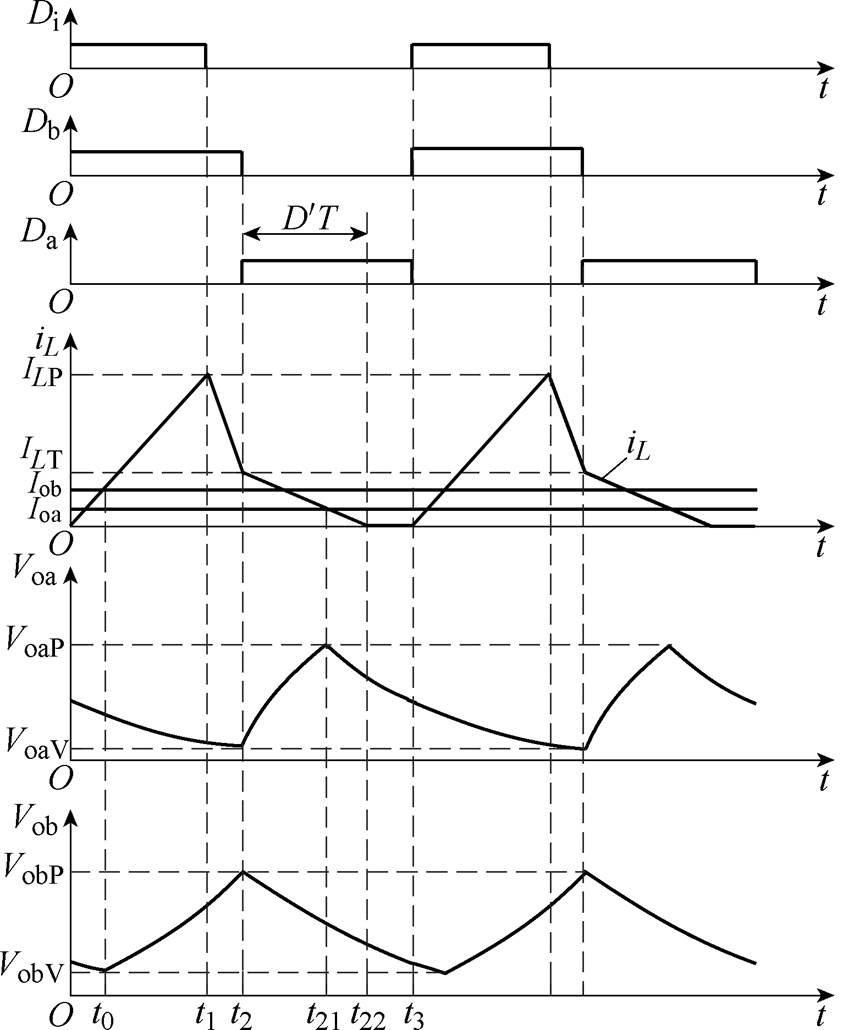
图4 DCM-DSM工作波形
Fig.4 Working waveforms of DCM-DSM
SIDO Buck变换器工作在DCM-SSM时，电感电流iL在t1～t2时间段降为零，工作波形如图5所示。在此模式下，由于电感电流在支路a开关管Sa开通前就已经下降到零，故支路a获得的能量为零，因此工作在DCM-SSM的SIDO Buck变换器与工作在DCM的Buck变换器工况完全相同。在0～t12时间段，当iL＜Iob时，电感L和电容Cb共同为负载Rb供能，当iL＞Iob时，电感L同时向负载Rb和电容Cb供能；在t12～t3时间段，电感电流为零，电容Cb为负载Rb供能。
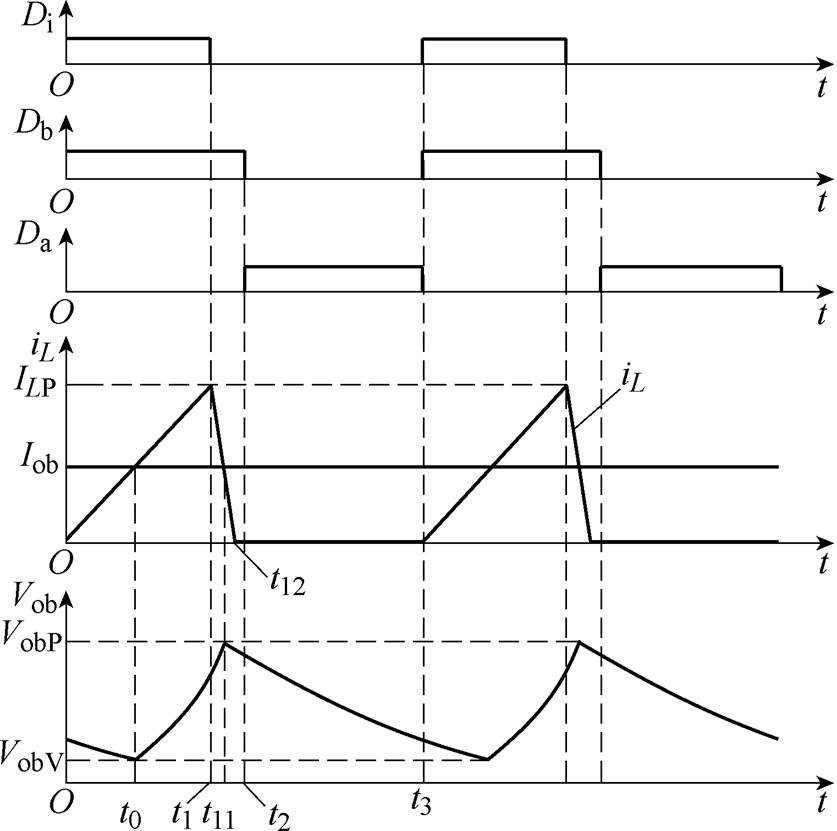
图5 DCM-SSM工作波形
Fig.5 Working waveforms of DCM-SSM
由图2和图3可知
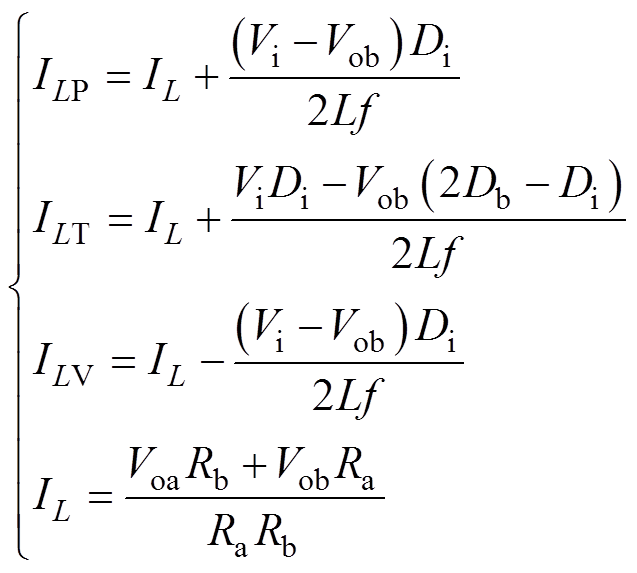（1）式中，IL为平均电感电流；f为开关频率；Vi为输入电压；Voa和Vob分别为变换器两条支路的输出电压。
根据时间平均等效电路方法[17]，求得CCM SIDO Buck变换器两条支路的输出电压分别为
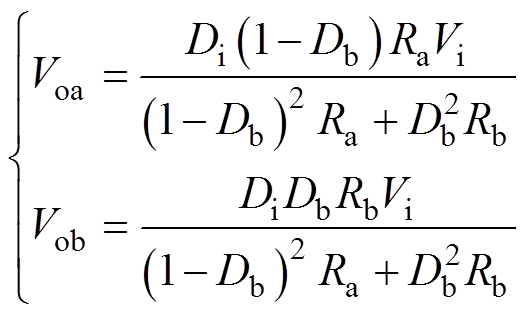（2）2.2.1 DCM-DSM稳态关系式
由图4可知
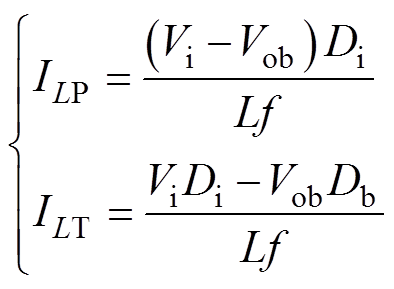（3）同理，根据时间平均等效电路方法[17]，可以求得DCM-DSM SIDO Buck变换器两条支路的输出电压分别为
（4）
式中，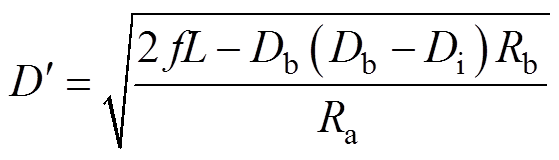
。
2.2.2 DCM-SSM稳态关系式
由图5可知，工作在DCM-SSM的SIDO Buck变换器与工作在DCM的Buck变换器工况完全相同。根据文献[16]可知，最大电感电流ILP为
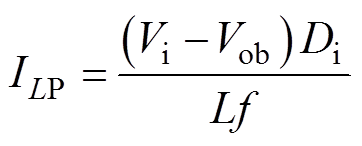（5）输出电压为
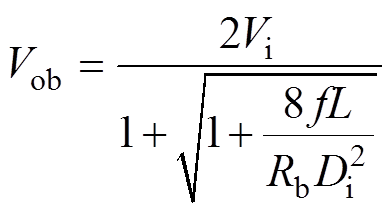（6）
当变换器工作在CCM与DCM的临界状态时，满足ILV=0，即令式（1）中ILV=0，可得CCM与DCM的临界电感LC为
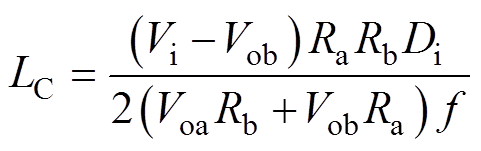（7）分析式（7）可知，当L＞LC时，变换器工作在CCM；当L＜LC时，变换器工作在DCM。
当变换器两支路分别工作在CCM-CISM与CCM-IISM的临界状态时，最小电感电流与负载电流的关系满足ILV=Ioa且ILV=Iob（当且仅当Ioa=Iob时才可能出现两支路同时工作于临界状态），即
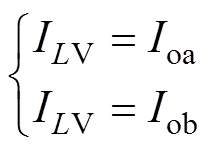（8）将式（8）代入式（1）中可得CCM-CISM与CCM-IISM的临界电感LKa和LKb分别为
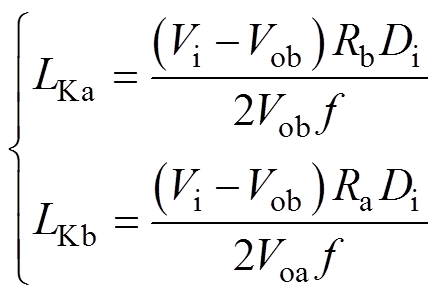（9）
设LK=max(LKa, LKb)，分析式（9）可知，当L＞LK时，变换器工作在CCM-CISM；当LC＜L＜LK时，变换器工作在CCM-IISM。由于LC＜LK，因此，当SIDO Buck变换器工作在CCM时，既可能工作在CISM，也可能工作在IISM；而变换器工作在DCM时，必工作在IISM。
当变换器工作在DCM-DSM与DCM-SSM的临界状态时，满足ILT=0，即令式（1）中ILT=0，可得DCM-DSM与DCM-SSM的临界电感LDC为
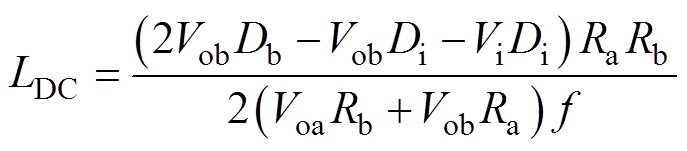（10）分析式（10）可知，当LDC＜L＜LC时，变换器工作在DCM-DSM；当L＜LDC时，变换器工作在DCM-SSM。根据以上分析，可以得到SIDO Buck变换器供能模式与电感取值的关系如图6所示。
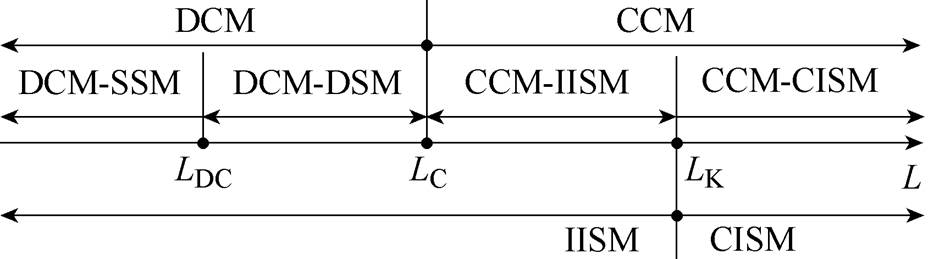
图6 供能模式与电感取值的关系
Fig.6 The relationship between supply modes and inductance
如图2所示，变换器两条支路的输出纹波电压为
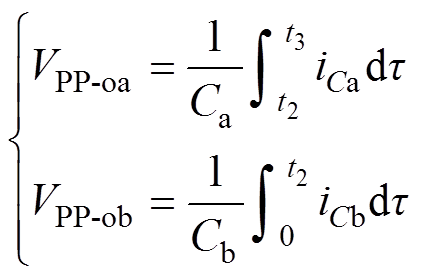（11）式中，iCa、iCb分别为变换器两条支路输出滤波电容处于充电状态时的电流，其表达式为
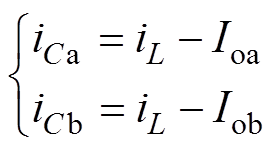（12）
将式（1）和式（12）代入式（11）中可得变换器工作在CCM-CISM时支路a、支路b的输出纹波电压解析式分别为
（13）
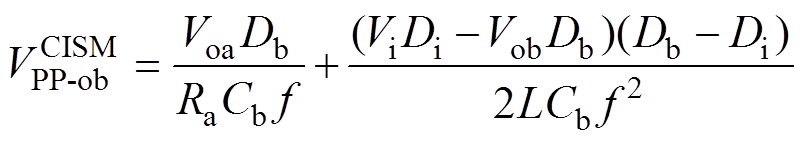（14）
将式（13）分别对电感L和负载Rb求偏导可得
（15）分析式（15）可知，变换器工作在CCM-CISM时，支路a的输出纹波电压随着电感L的增大而增大，随着负载Rb的增大而减小。
同理，将式（14）分别对电感L和负载Ra求偏导可得
（16）分析式（16）可知，变换器工作在CCM-CISM时，支路b的输出纹波电压随着电感L和负载Ra的增大而减小。
如图3所示，变换器两条支路的输出纹波电压为
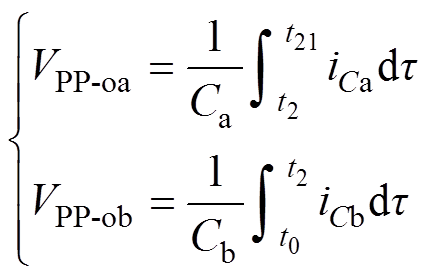（17）在t21时刻，电感电流满足iL=Ioa，即
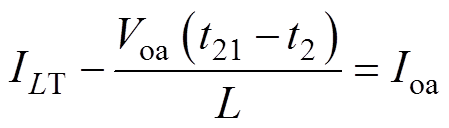（18）
已知t2=DbT（T为开关周期），求解式（18）可得t21为
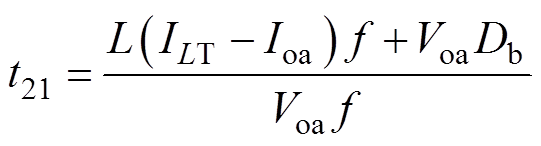（19）将式（1）、式（12）和式（19）代入式（17）中可得，变换器工作在CCM-IISM时支路a的输出纹波电压解析式为
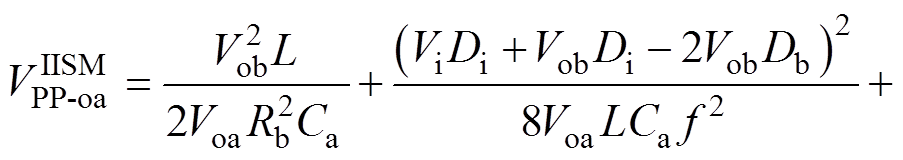
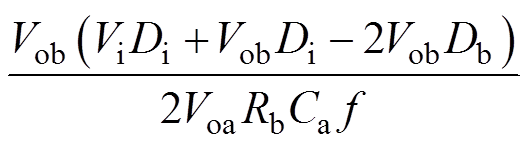（20）将式（20）分别对电感L和负载Rb求偏导可得
（21）
分析式（21）可知，变换器工作在CCM-IISM时，支路a的输出纹波电压随着电感L的增大而增大，随着负载Rb的增大而减小。
t0时刻，电感电流满足iL=Iob，即
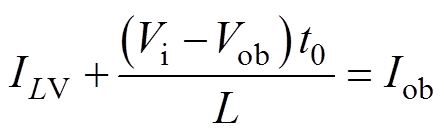（22）求解式（22）可得t0为
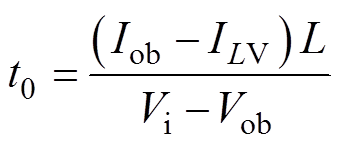（23）
将式（1）、式（12）和式（23）代入式（17）中可得变换器工作在CCM-IISM时支路b的输出纹波电压解析式为
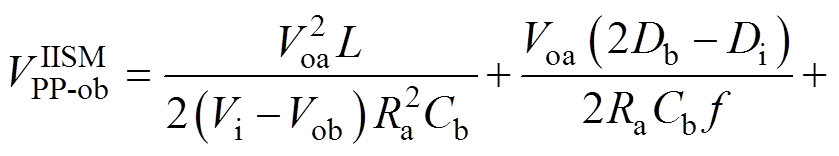
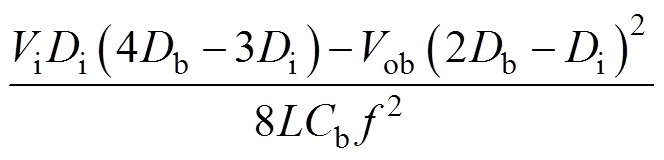（24）
将式（24）分别对电感L和负载Ra求偏导可得
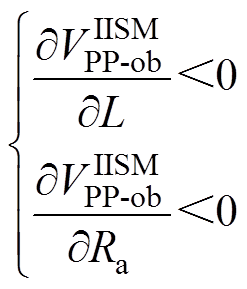（25）分析式（25）可知，变换器工作在CCM-IISM时，支路b的输出纹波电压随着电感L和负载Ra的增大而减小。
由以上分析可知，SIDO Buck变换器工作在CCM时，支路a的输出纹波电压随着电感的增大而增大，支路b的输出纹波电压随着电感的增大而减小。并且变换器两支路的输出纹波电压与本支路的负载无关，但与另一支路的负载有关，即两条支路输出纹波电压间存在交叉影响，表现为本支路的输出纹波电压随着另一支路负载阻值的增大而减小。
DCM-DSM的输出纹波电压计算方法与CCM- IISM相同，为了节约篇幅，这里仅给出推导结果。支路a、支路b的输出纹波电压解析式分别为
（26）
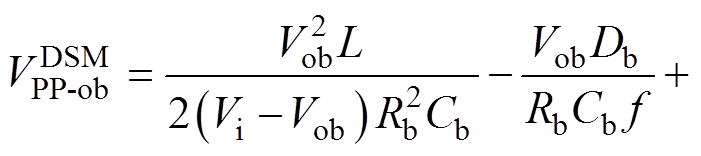
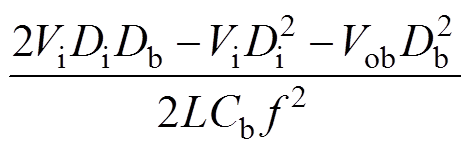（27）
将式（26）和式（27）对负载Ra和Rb求偏导可得
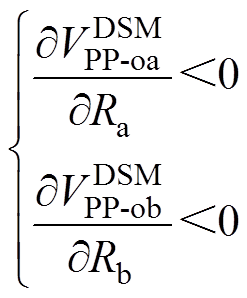（28）分析式（28）可知，变换器工作在DCM-DSM时，输出纹波电压随着本支路负载阻值的增大而 减小。
将式（26）和式（27）分别对电感L求偏导可得
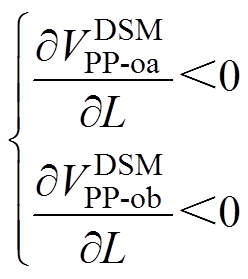（29）分析式（29）可知，变换器工作在DCM-DSM时，变换器两条支路的输出纹波电压随着电感L的增大而减小。
由于工作在DCM-SSM的SIDO Buck变换器与工作在DCM的Buck变换器工况完全相同，由文献[16]可知，变换器工作在DCM-SSM时输出纹波电压解析式为
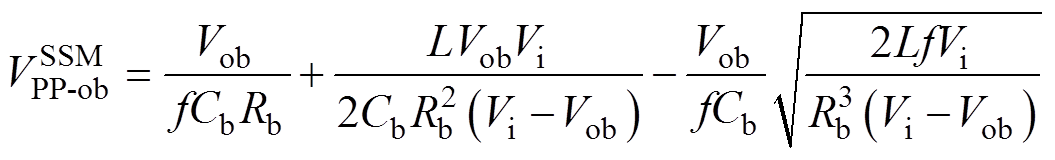（30）将式（30）分别对电感L和负载Rb求偏导可得
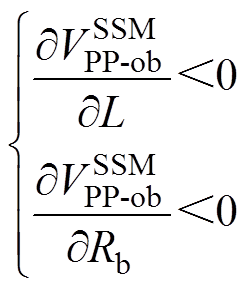（31）
由上面的分析可知，SIDO Buck变换器工作在DCM时，变换器两条支路的输出纹波电压均随着电感的增大而减小。并且此时两条支路输出纹波电压间不存在交叉影响，但输出纹波电压与本支路的负载有关，且随着本支路负载阻值的增大而减小。
根据以上分析，可以得到SIDO Buck变换器输出纹波电压与电感的关系如图7所示。
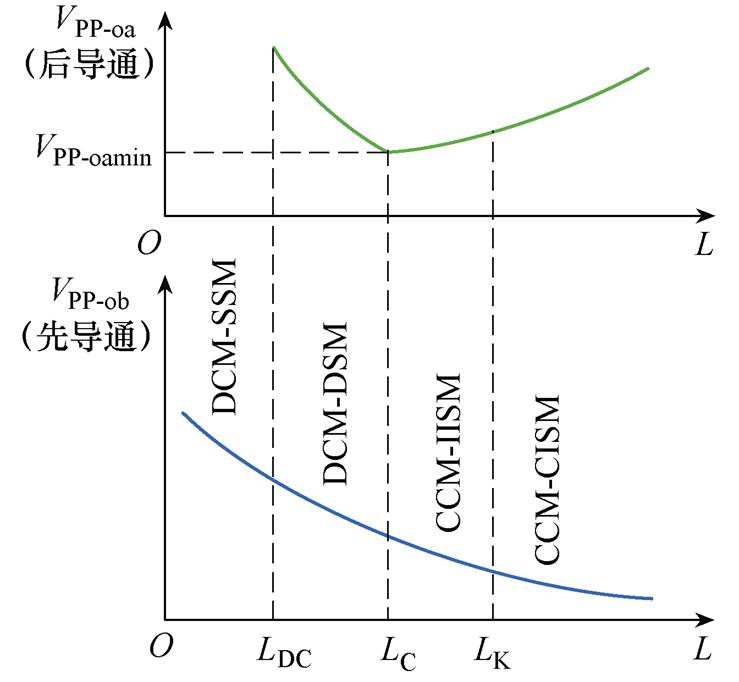
图7 输出纹波电压与电感的关系
Fig.7 The relationship between ORV and inductance
由图7可知，当L＞LC时，支路a（后导通支路）的输出纹波电压随着电感的增大而增大，当L＜LC时，支路a的输出纹波电压随着电感的增大而减小，因而支路a的输出纹波电压在LC处取得极小值。而支路b（先导通支路）的输出纹波电压始终随着电感的增大而减小。
当变换器工作在CCM时，SIDO Buck变换器两条支路输出纹波电压间存在交叉影响，因此图8给出了在一定负载范围内变换器的交叉影响情况。
图8 SIDO Buck变换器的交叉影响情况
Fig.8 The cross-regulation of SIDO Buck Converter
由图8可以看出，对于恒压输出的SIDO Buck变换器，在整个负载动态范围内（曲线VPP1～VPP4表示支路a或支路b的输出纹波电压），存在A、B、C、D四个特殊工作点。当变换器工作在A点时，输出纹波电压间的交叉影响最严重（此时变换器工作在CCM且负载最重）。当变换器工作在B点时，支路b对支路a的交叉影响最轻微，支路a对支路b的交叉影响最严重。当变换器工作在C点时，支路b对支路a的交叉影响最严重，支路a对支路b的交叉影响最轻微。当变换器工作在D点时，变换器输出纹波电压间不存在交叉影响（此时变换器工作在DCM且负载最轻）。
为了验证理论分析的正确性，对SIDO Buck变换器进行了仿真，仿真参数见表1。
表1 SIDO Buck变换器电路参数
Tab.1 Circuit parameters of SIDO Buck converter
参 数数 值 输入电压Vi/V20 开关频率f/kHz20 输出电压Voa/V5 输出电压Vob/V9 负载电阻Ra/W20 负载电阻Rb/W20 滤波电容Ca/mF30 滤波电容Cb/mF30 滤波电感L/mH根据供能模式待定
将表1中的参数代入式（7）、式（9）和式（10）中可得临界电感LKa=232mH、LKb=417mH、LC= 150mH。因此变换器电感分别取500mH、180mH和100mH，各供能模式的仿真波形如图9所示。
从图9a～图9c可以看出，当电感取500mH时，ILV＞0且ILV＞Ioa、ILV＞Iob，变换器工作在CCM- CISM；当电感取180mH时，ILV＞0且ILV＜Ioa、ILV＜Iob，变换器工作在CCM-IISM；当电感取100mH时，ILV=0且电感电流在支路a导通后才下降到零，变换器工作在DCM-DSM，仿真与理论分析一致，仿真得到的输出纹波电压数据见表2和表3。
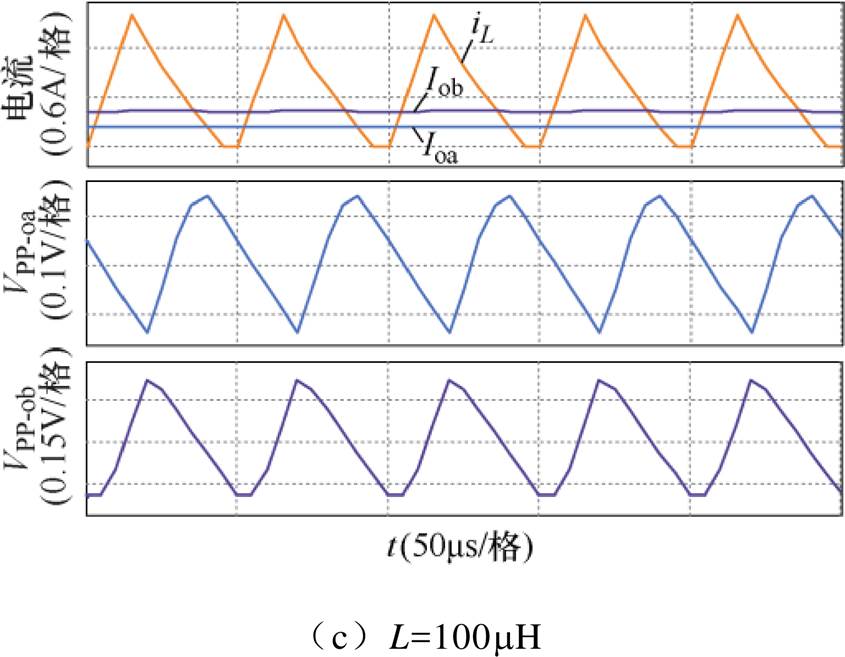
图9 各供能模式的仿真波形
Fig. 9 Simulation waveforms for each supply mode
表2 VPP-oa与L的关系
Tab.2 Relationship between VPP-oa and L
L/mH供能模式VPP-oa/mV 理论仿真实验 500CCM-CISM230240286 180CCM-IISM195202248 100DCM-DSM233238288
表3 VPP-ob与L的关系
Tab.3 Relationship between VPP-ob and L
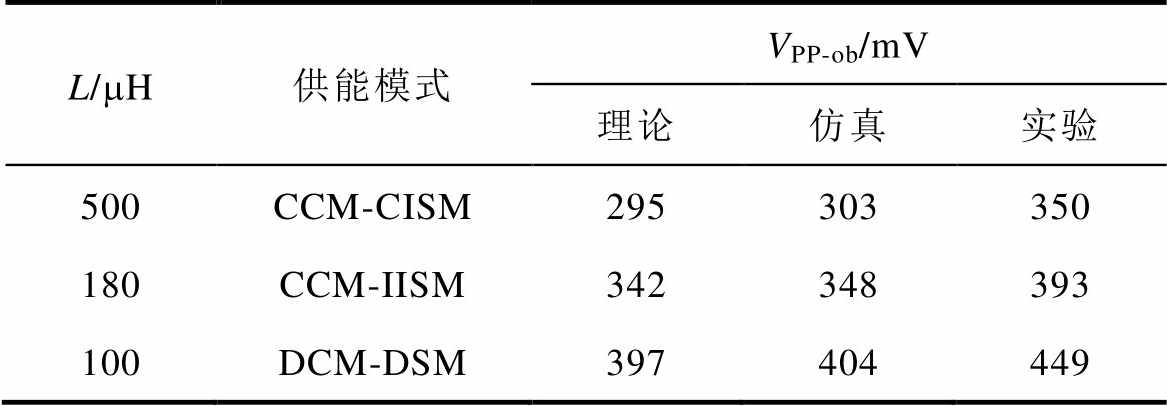
L/mH供能模式VPP-ob/mV 理论仿真实验 500CCM-CISM295303350 180CCM-IISM342348393 100DCM-DSM397404449
为进一步验证理论分析的正确性，搭建了实验平台，实验参数与仿真一致。
5.2.1 供能模式与输出纹波电压实验分析
实验电感分别取500mH、180mH和100mH，各供能模式的实验波形如图10所示，实验所得输出纹波电压数据见表2和表3。
由图10a～图10c可以看出，当电感取500mH时，ILV＞0且ILV＞Ioa、ILV＞Iob，变换器工作在CCM- CISM；当电感取180mH时，ILV＞0且ILV＜Ioa、ILV＜Iob，变换器工作在CCM-IISM；当电感取100mH时，ILV=0且电感电流在支路a导通后才下降到零，变换器工作在DCM-DSM，实验结果与理论分析结果一致。根据表2和表3可知，随着变换器电感取值的增大，变换器支路a（后导通支路）的输出纹波电压先减小再增大，而支路b（先导通支路）的输出纹波电压单调减小，即对于给定输入电压、开关频率、负载、输出电压和滤波电容的SIDO Buck变换器，先导通支路的输出纹波电压随着电感的增大而减小，后导通支路的输出纹波电压随着电感的增大表现为先减小后增大（指的是随着电感的增大，变换器的工作模式由DCM变为CCM的过程）。理论计算和实验得到的输出纹波电压数据十分接近，说明了本文对SIDO Buck变换器输出纹波电压分析的正确性。受元器件寄生参数等影响，实验所得输出纹波电压略大于理论值，在实际计算电感和电容值时，可在本文理论分析的基础上，加入相应的裕度即可满足供能模式和输出纹波电压要求。
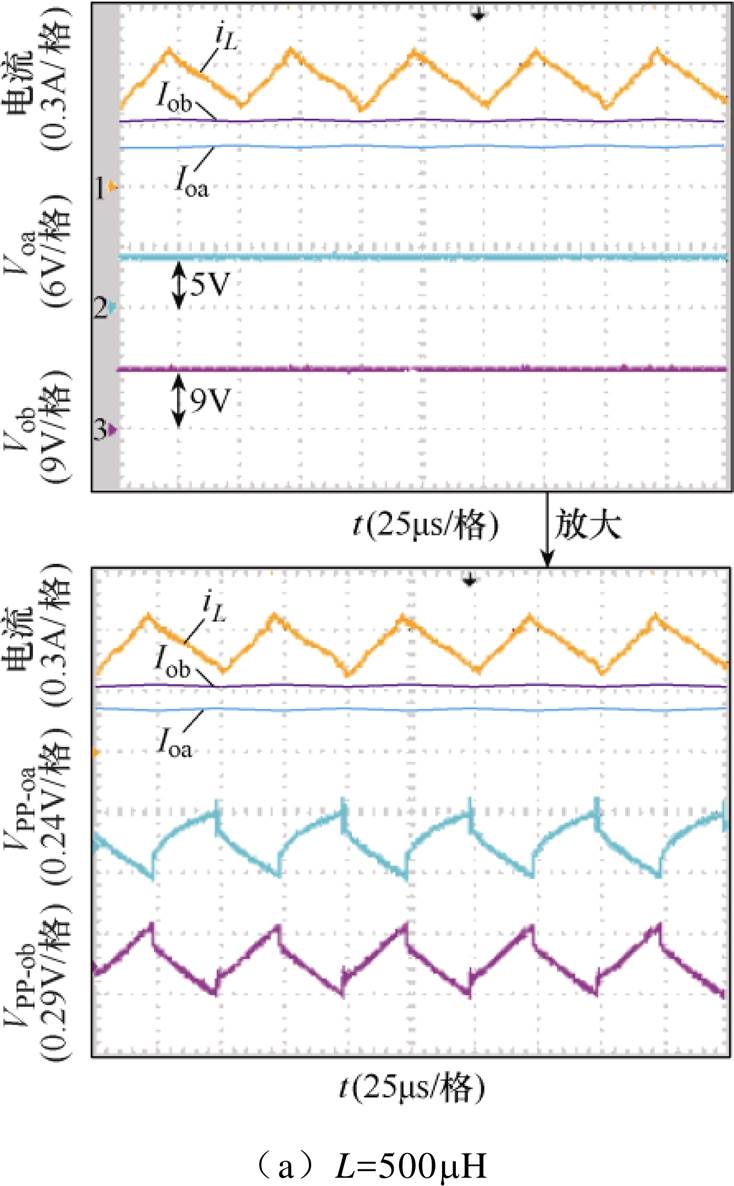
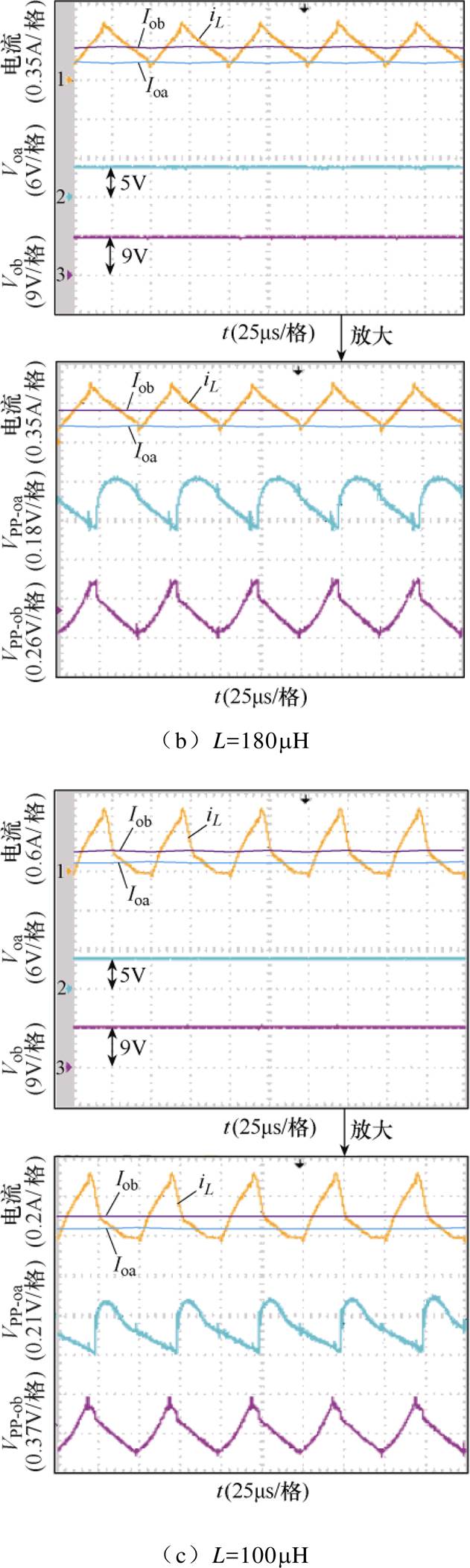
图10 各供能模式的实验波形
Fig.10 Experimental waveforms for each supply mode
5.2.2 交叉影响实验分析
为了验证SIDO Buck变换器工作在CCM时输出纹波电压间的交叉影响关系，给定变换器的负载Ra和Rb的范围为10～40W。为保证变换器工作于CCM，电感取500mH。
先保持Ra=20W不变，Rb分别取10W、20W、30W 和40W，观察支路a输出纹波电压VPP-oa的变化情况。再保持Rb=20W不变，Ra分别取10W、20W、30W 和40W，观察支路b输出纹波电压VPP-ob的变化情况，理论计算和实验所得输出纹波电压数据见表4。
表4 VPP与R的关系
Tab.4 Relationship between VPP and R
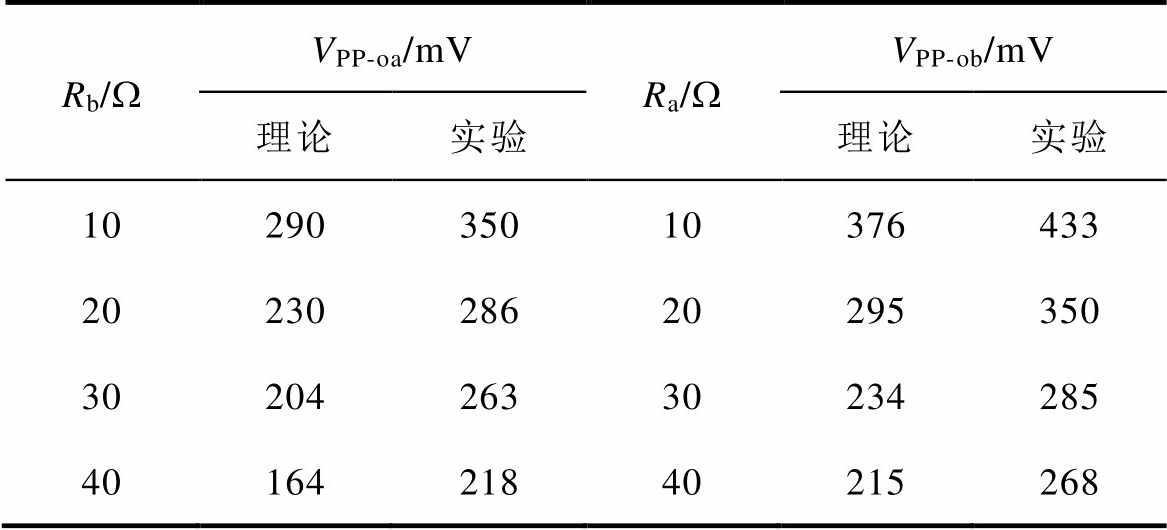
Rb/WVPP-oa/mVRa/WVPP-ob/mV 理论实验理论实验 1029035010376433 2023028620295350 3020426330234285 4016421840215268
由表4可知，在支路b负载阻值增大的过程中，支路a的输出纹波电压逐渐减小，并且当支路b的负载阻值取最大时，支路a的输出纹波电压最小。在支路a负载阻值增大的过程中，支路b的输出纹波电压逐渐减小，并且当支路a的负载阻值取最大时，支路b的输出纹波电压最小。即对于给定输入电压、开关频率、输出电压、滤波电感和滤波电容的SIDO Buck变换器，其本支路的输出纹波电压随着另一支路负载阻值的增大而减小，实验结果与理论分析结果一致，验证了交叉影响分析的正确性。
在不同的负载条件下，测得了SIDO Buck变换器的效率，并在相同输出规格下与传统并联Buck变换器进行了对比，效率对比如图11所示，传统并联Buck变换器如图12所示。
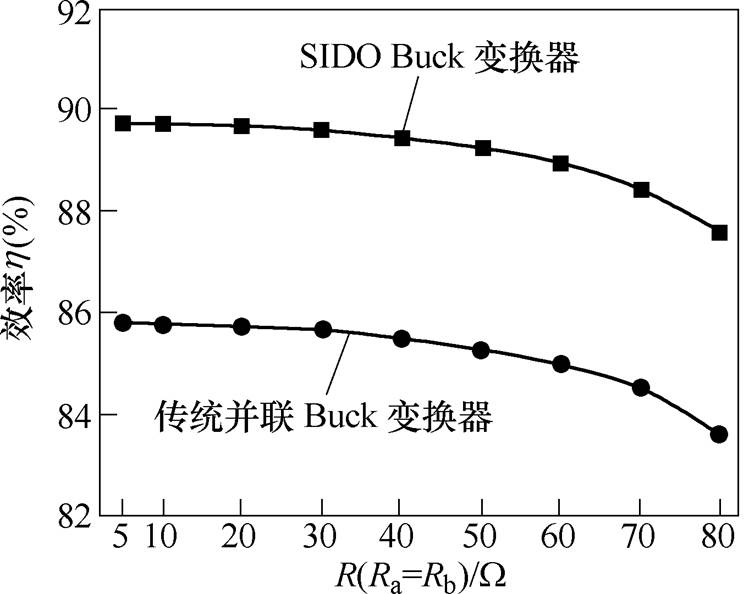
图11 两种Buck变换器的效率对比
Fig.11 Efficiency comparison of two Buck converters
当负载Ra和Rb的取值为5～40W时，SIDO Buck变换器工作在CCM。当负载Ra和Rb的取值为40～80W 时，变换器工作在DCM。分析图11可知，由于SIDO Buck变换器结构简单且元器件数量少，因此其效率明显高于传统并联Buck变换器。SIDO Buck变换器的整体工作效率较高，但在不同供能模式时效率有一定差异，总体趋势为变换器工作在CCM（重载）时效率较高，工作在DCM（轻载）时效率略低。这是由于在DCM时，变换器的杂散损耗比重较大；而在CCM时，杂散损耗比重很小，因此变换器的效率较高。
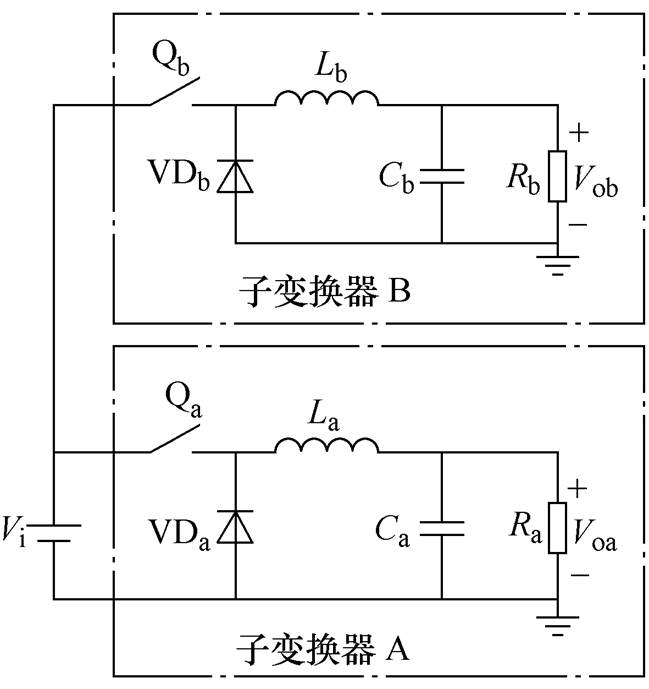
图12 传统并联Buck变换器
Fig.12 Traditional parallel Buck converter
本文深入分析了SIDO Buck变换器的供能模式和输出纹波电压，得到了如下结论：
1）变换器的供能模式与电感的大小密切相关，存在一个临界电感LC，当L＞LC时，变换器工作在CCM；当L＜LC时，变换器工作在DCM。存在一个临界电感LK，当L＞LK时，变换器工作在CCM- CISM；当LC＜L＜LK时，变换器工作在CCM-IISM。存在一个临界电感LDC，当LC＞L＞LDC时，变换器工作在DCM-DSM；当L＜LDC时，变换器工作在DCM-SSM。
2）先导通支路的输出纹波电压始终随着电感的增大而减小。对于后导通支路，当变换器工作于CCM时，其输出纹波电压随着电感的增大而增大；当变换器工作于DCM时，其输出纹波电压随着电感的增大而减小，因此后导通支路的输出纹波电压在临界电感LC处取得极小值。
3）变换器工作在CCM时，输出纹波电压与本支路负载无关，但两条支路输出纹波电压间存在交叉影响，即本支路的输出纹波电压随着另一支路负载阻值的增大而减小。变换器工作在DCM时，两条支路输出纹波电压间不存在交叉影响，但输出纹波电压与本支路负载有关，且随着本支路负载阻值的增大而减小。本文研究所得结论对应用于煤矿、化工等危险环境的本质安全型SIDO Buck变换器(这类变换器要求尽量减小储能元件的取值)的分析设计具有指导意义。
参考文献
[1] 肖龙, 伍梁, 李新, 等. 高频LLC变换器平面磁集成矩阵变压器的优化设计[J]. 电工技术学报, 2020, 35(4): 758-766.
Xiao Long, Wu Liang, Li Xin, et al. Optimal design of planar magnetic integrated matrix transformer for high frequency LLC converter[J]. Transaction of China Electrotechnical Society, 2020, 35(4): 758- 766.
[2] Mojtaba Forouzesh, Shen Yanfeng, Keyvan Yari, et al. High-efficiency high step-up DC-DC converter with dual coupled inductors for grid-connected photovoltaic systems[J]. IEEE Transactions on Power Electronics, 2018, 33(7): 5967-5982.
[3] 王萍, 陈博, 王议锋, 等. 一种多谐振隔离双向DC-DC变换器[J]. 电工技术学报, 2019, 34(8): 1667- 1676.
Wang Ping, Chen Bo, Wang Yifeng, et al. A multi resonant bidirectional DC-DC converter[J]. Transa- ction of China Electrotechnical Society, 2019, 34(8): 1667-1676.
[4] Tian Jie, Mao Chengxiong, Wang Dan, et al. A short- time transition and cost saving redundancy scheme for medium-voltage three-phase cascaded h-bridge electronic power transformer[J]. IEEE Transactions on Power Electronics, 2018, 33(11): 9242-9252.
[5] 冉祥, 周国华, 周述晗. 共模-差模电压型控制连续导电模式单电感双输出Boost变换器交叉影响特性分析[J]. 电工技术学报, 2019, 34(12): 2519-2528.
Ran Xiang, Zhou Guohua, Zhou Shuhan. Cross- regulation characteristic of continuous conduction mode single-inductor dual-output Boost converter with common-mode voltage and differential-mode voltage control[J]. Transaction of China Electro- technical Society, 2019, 34(12): 2519-2528.
[6] 刘雪山, 许建平, 王楠, 等. 断续模式单电感双输出Buck功率因数校正变换器[J]. 电工技术学报, 2015, 30(22): 62-70.
Liu Xueshan, Xu Jianping, Wang Nan, et al. Single- inductor dual output Buck power factor correction converter operating in discontinuous conduction mode[J]. Transaction of China Electrotechnical Society, 2015, 30(22): 62-70.
[7] Jing Xiaocheng, Philip K T Mok, Ming Chak Lee. A wide-load-range constant-charge-auto-hopping control single-inductor-dual-output Boost regulator with minimized cross-regulation[J]. IEEE Journal of Solid- State Circuits, 2011, 46(10): 2350-2362.
[8] Zheng Yanqi, Ho Marco, Guo Jianping, et al. A single-inductor multiple-output auto-Buck-Boost DC- DC converter with tail-current control[J]. IEEE Transa- ctions on Power Electronics, 2016, 31(11): 7857- 7875.
[9] Wang Yao, Xu Jianping, Yin Gang. Cross-regulation suppression and stability analysis of capacitor current ripple controlled SIDO CCM Buck converter[J]. IEEE Transactions on Industrial Electronics, 2019, 66(3): 1770-1780.
[10] Jaya Deepti Dasika, Behrooz Bahrani, Maryam Saeedifard, et al. Multivariable control of single- inductor dual-output Buck converters[J]. IEEE Transa-ctions on Power Electronics, 2014, 29(4): 2061- 2070.
[11] 王瑶. 基于状态空间平均模型的电压控制SIDO Buck变换器稳定性分析[J]. 中国电机工程学报, 2018, 38(6): 1810-1817.
Wang Yao. Stability analysis for voltage controlled single-inductor dual-output Buck converter based on state space average model[J]. Proceedings of the CSEE, 2018, 38(6): 1810-1817.
[12] Chun-Shih Huang, Dan Chen, Ching-Jan Chen, et al. Mix-voltage conversion for single-inductor dual- output Buck converters[J]. IEEE Transactions on Power Electronics, 2010, 25(8): 2106-2114.
[13] 杨玉岗, 祁鳞, 吴建鸿. 三相交错并联磁集成Boost变换器的内部本质安全特性[J]. 电工技术学报, 2014, 29(4): 54-62.
Yang Yugang, Qi Lin, Wu Jianhong. Analysis of inner-intrinsic safety for three-phase interleaving magnetic integrated Boost converter[J]. Transaction of China Electrotechnical Society, 2014, 29(4): 54-62.
[14] 刘树林, 曹剑, 胡传义, 等. 正-反激组合变换器的能量传输模式及输出纹波电压分析[J]. 电工技术学报, 2019, 34(8): 1647-1656.
Liu Shulin, Cao Jian, Hu Chuanyi, et al. Energy transmission modes and output ripple voltage of forward-flyback converter[J]. Transaction of China Electrotechnical Society, 2019, 34(8): 1647-1656.
[15] Liu Shulin, Liu Jian, Mao Hong, et al. Analysis of operating modes and output voltage ripple of Boost DC-DC converters and its design considerations[J]. IEEE Transactions on Power Electronics, 2008, 23(4): 1813-1821.
[16] 刘树林, 刘健. 开关变换器分析与设计[M]. 北京: 机械工业出版社, 2010.
[17] 曾绍桓, 周国华, 周述晗, 等. 电流型控制三态Boost变换器的小信号建模与负载瞬态特性分析[J]. 电工技术学报, 2019, 34(7): 1468-1477.
Zeng Shaohuan, Zhou Guohua, Zhou Shuhan, et al. Small-signal modeling and load transient characteri- stic analysis of current mode controlled Tri-State Boost converter[J]. Transaction of China Electro- technical Society, 2019, 34 (7): 1468-1477.
Supply Modes and Output Ripple Voltage of Single-Inductor Dual-Output Buck Converter
Abstract The supply mode of the single-inductor dual-output (SIDO) Buck converter becomes complicates due to thepresence of post-stage switch. In order to provide correct theoretical guidance for the analysis and design of SIDO Buck converter, this paper deeply analyzes the supply mode of SIDO Buck converter. It is found that there are two supply modes when the converter works in continuous conduction mode (CCM): complete inductor supply mode (CISM) and incomplete inductor supply mode (IISM). Moreover, when the converter works in discontinuous conduction mode (DCM), there are also two supply modes: dual-branch supply mode (DSM) and single-branch supply mode (SSM). The critical inductance of each supply mode is obtained, and the output ripple voltage (ORV) expression of each supply mode is derived. The relations of inductance with supply mode and ORV are summarized. It is pointed that there is a cross-regulation between the ORV of the two branches when the converter works in CCM. The correctness of theoretical is verified by simulation and experimental results.
keywords：Single-inductor dual-output (SIDO), supply modes, critical inductance, output ripple voltage (ORV), cross-regulation
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.191183
国家自然科学基金项目（51777167）、陕西省教育厅重点实验室计划研究项目（18JS021）、陕西省工业自动化重点实验室开放课题（SLGPT2019KF01-14）和陕西理工大学人才启动基金项目（SLGQD1808）资助。
收稿日期 2019-09-17
改稿日期 2020-01-11
谢 锋 男，1994年生，硕士研究生，研究方向为开关变换器的分析与设计。E-mail: xiefeng5335@163.com
皇金锋 男，1978年生，博士，副教授，硕士生导师，研究方向为开关变换器的分析与设计。E-mail: jfhuang2000@163.com（通信作者）
（编辑 陈 诚）