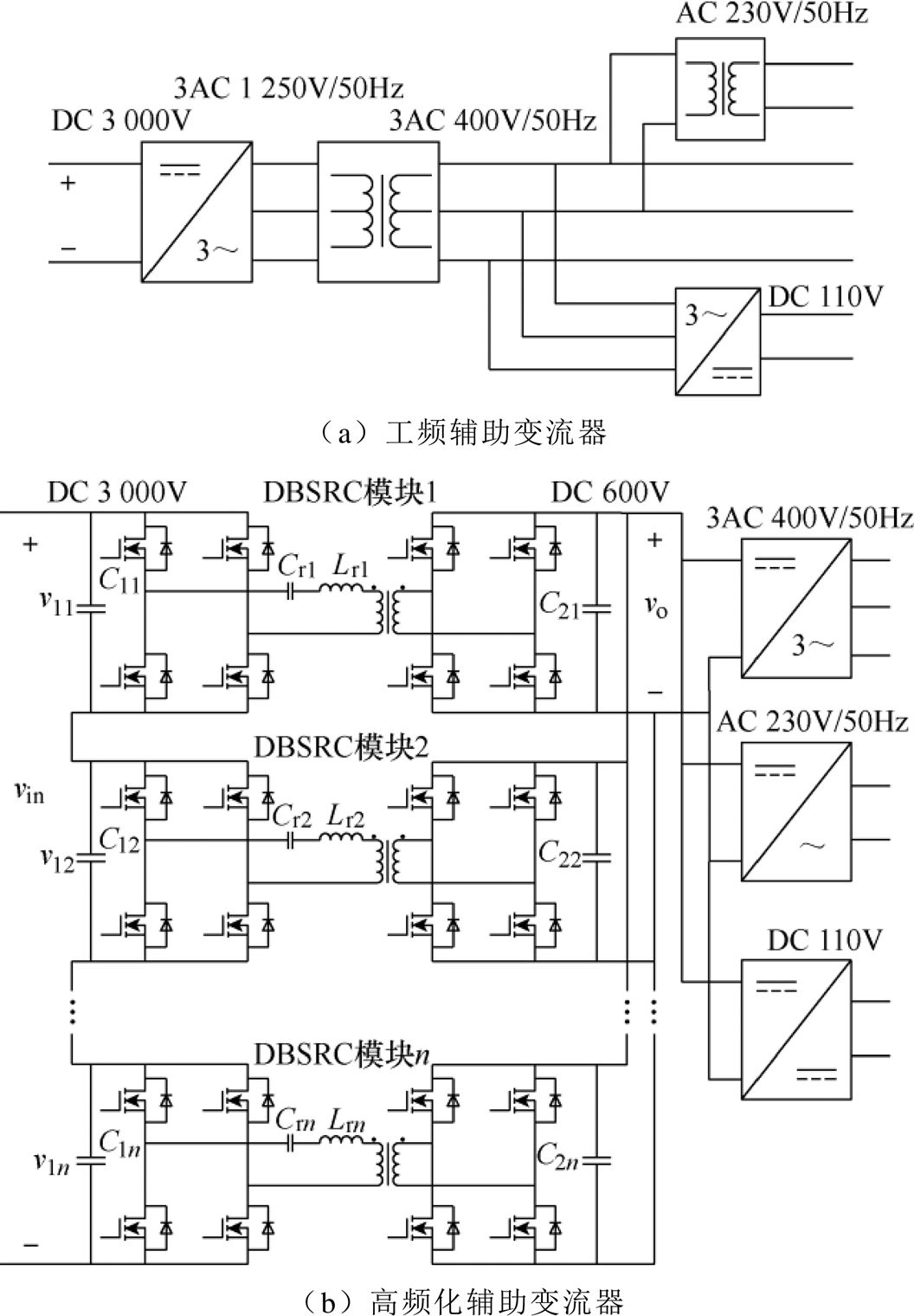
图1 工频辅助变流器与高频化辅助变流器拓扑对比
Fig.1 Topology comparison of line-frequency and high-frequncy auxiliary converter
摘要 对基于输入串联输出并联（ISOP）的双向全桥串联谐振DC-DC变换器（DBSRC）系统的控制策略进行研究。采用周期平均法构建DBSRC及其ISOP级联系统的小信号模型及对应传递函数，其中各DBSRC子模块输入电压均受其他模块移相角影响。为了实现子模块输入电压的均衡，提出一种差分输入电压均压（DIVS）控制策略，该策略实现了系统控制框图中输出电压环和输入均压环的解耦控制。相比传统输入均压控制策略，该策略所需的通信数据量较少，具有较高的动态响应性能。最后，通过仿真和12kW样机的实验结果验证了DBSRC小信号模型的准确性及DIVS控制策略的有效性和优越性。
关键词：输入串联输出并联 双向全桥串联谐振DC-DC变换器 小信号模型 差分输入电压
传统高铁辅助变流器多采用工频变压器进行电压等级变换，具有体积大、质量大等缺陷，不利于列车内部空间优化和运力的提升。近年来，受益于电力电子器件和技术的发展，高频化的电力电子变压器（Power Electronic Transformer, PET）具有替代现有工频变压器的优势[1]。CRH3型高铁的工频辅助变流器拓扑如图1a所示[2]，输入从主牵引变流器的直流母线取电，经逆变并工频降压后得到三相400V交流电及其他制式电源；而高频化辅助变流器采用输入串联输出并联（Input Series Output Parallel, ISOP）模块化结构，将高压直流母线变换为低压直流母线，进而通过逆变或DC-DC得到各个制式的电源，如图1b所示。由于去掉了工频降压变压器，高频化辅助变流器的体积和质量均大幅下降。
图1 工频辅助变流器与高频化辅助变流器拓扑对比
Fig.1 Topology comparison of line-frequency and high-frequncy auxiliary converter
目前，应用于高铁变流器ISOP结构的DC-DC变换器主要有双有源桥（Dual Active Bridge, DAB）DC-DC变换器[3-4]和双向谐振变换器[5]等。DAB采用移相控制，具有控制简便、易于进行模块并联等特点，但其关断损耗大，限制了高频化发展[6]。双向谐振变换器采用变频控制，具有输出调压范围广、效率高等优点，但变换器的电流不受控制，运行点受硬件参数的影响较大，不利于模块并联控制[7]。针对以上两种变换器的优势，文献[8]提出了双向全桥串联谐振DC-DC变换器（Dual Bridge Series Resonant DC-DC Converter, DBSRC）。该拓扑在DAB的基础上加入串联谐振电容，并采用移相控制，同时具有开关损耗低且易于级联控制的特点，适合在高铁牵引、辅助变流器大功率等场合应用。目前，关于DBSRC的文献主要基于稳态模型对其电流应力[9-10]、软开关特性[11-12]等特性进行研究，鲜有文献关注其动态模型。
ISOP级联控制的目标是实现DC-DC变换器模块之间输入均压（Input Voltage Sharing, IVS）和输出均流（Output Current Sharing, OCS）。文献[13-14]分析表明，以上两个控制目标是等价的，即实现其中任一目标，另一目标可以自然实现。若同时考虑控制的准确性和简便性，ISOP的主要控制策略可以分为以OCS为目标的控制策略、以IVS为目标的控制策略和无互联控制策略三类。由于传统基于子模块输出电流反馈控制会造成系统不稳定[15]，文献[15-16]分别以差分电流、交叉电流作为电流环反馈量，均实现了较好的均流效果。但以OCS为目标的控制策略对于母线阶跃的动态响应较快，而对负载阶跃的动态响应较慢[17]，因此并不适合在高铁变流器场合应用；相反，以IVS为目标的控制策略对于负载阶跃响应较快，文献[4, 14, 18]均以输出电压环输出为前馈量，分别提出直接功率控制、解耦控制和共用占空比控制，实现了较好的均压效果。文献[19]在共用占空比的基础上，加入不同模块之间的交错控制，使输出电流纹波进一步降低。以上两类控制策略均属于主从控制，模块间需要大量通信数据，从而影响系统动态特性。无互联控制策略[20-21]无需模块间通信，采用输出电压上翘特性实现模块间的均压控制，便于模块化冗余，提高了系统的稳定性，但其控制精度较低。
本文以DBSRC为DC-DC变换器ISOP级联的高频化辅助变流器的直流环节为研究对象，对其控制策略进行研究。建立了DBSRC动态小信号模型及其ISOP级联系统模型，提出了一种基于IVS目标的差分输入电压均压（Differential Input Voltage Sharing, DIVS）控制策略，该控制策略所需的通信数据量较小，控制更为简便。采用DIVS控制策略后，系统模型中的输出电压控制环和输入均压控制环相互解耦，进而可分别对控制器进行设计。首先，仿真结果验证了DBSRC小信号模型在低频段的准确性；其次，验证了DIVS控制策略可以实现DBSRC子模块的输入电压均衡，并表现出优于现有控制策略的动态响应性能；最后，构建了一个12kW的实验样机进行实验，结果验证了DIVS均压控制的有效性和快速的动态恢复性能。
DBSRC原理如图2所示，主要由两个H桥和谐振回路组成。其中，C1和C2分别为输入、输出侧支撑电容，Cr和Lr分别为谐振电容和谐振电感，高频变压器电压比为1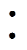
Nt。输入为直流电源v1，输出接电阻负载R，输出电压为v2。i1为DBSRC输入电流，iac1为输入一次侧H桥的输入电流，iac2为二次侧H桥的输出电流，i2为DBSRC输出电流，ip、isec分别为变压器一、二次侧交流电流。
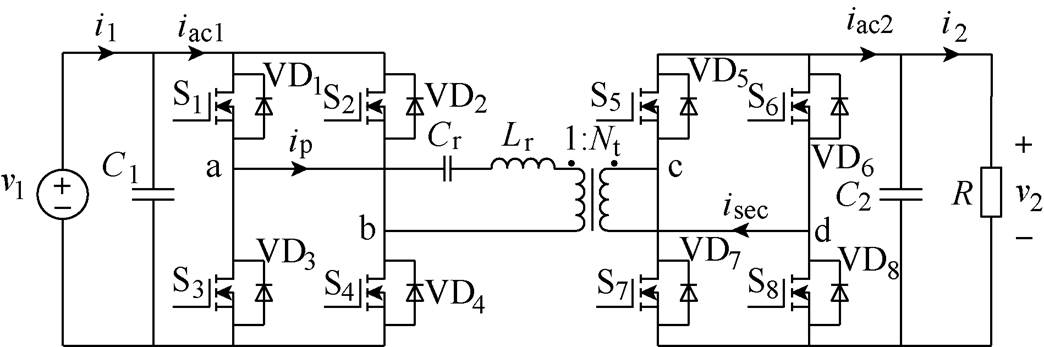
图2 DBSRC原理
Fig.2 The topology of DBSRC
DBSRC的换相过程及稳态模型已经在文献[22]中分析和建立，其中电流ip在半个周期内表达式为
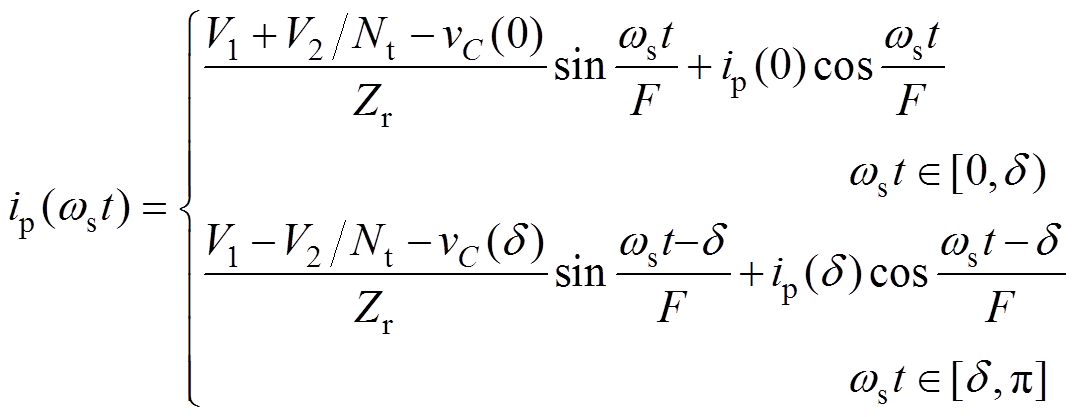（1）式中，ws为开关角频率；V1为输入直流母线电压；V2为输出直流母线电压；d 为移相角；vC为谐振电容电压；F为开关频率与谐振频率之比；
为谐振回路特性阻抗，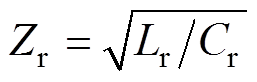
；ip(0)、ip(d)、vC(0)、vC(d)均在文献[22]中给出；输出功率Po表达式为
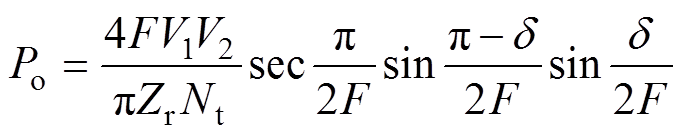（2）假设忽略开关器件的压降，根据DBSRC的换相过程，当wstÎ[0, d]时，iac1=ip，iac2=-ip/Nt；当wstÎ[d, p]时，iac1=ip，iac2=ip/Nt，因此iac1和iac2的周期平均值分别为
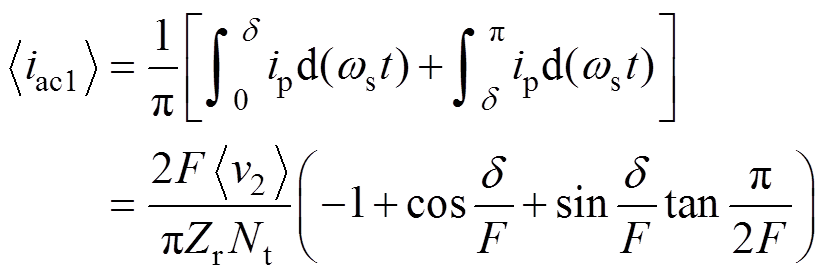（3）
（4）对于DBSRC输入部分和输出部分，可通过基尔霍夫电流定律得到
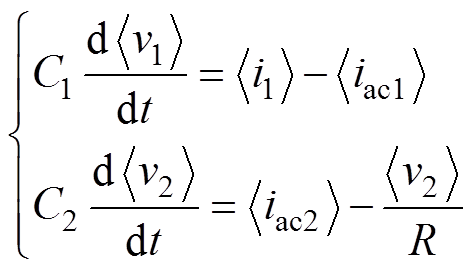（5）
因此，DBSRC的平均值模型如图3所示。
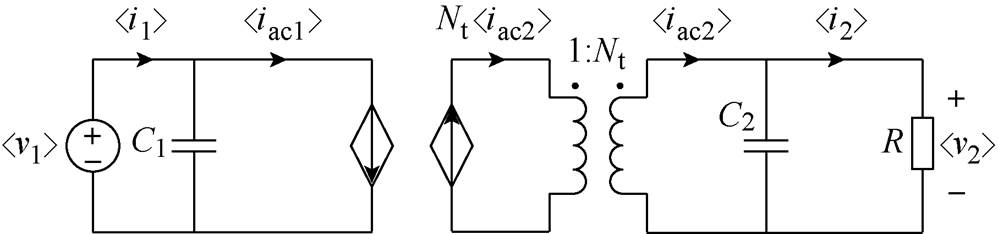
图3 DBSRC平均值模型
Fig.3 The average model of DBSRC
对以上周期平均值施加扰动，令
（6）式中，V1、V2、D、I1、Iac1、Iac2均为稳态量；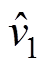
、
、
、
、
、
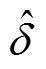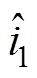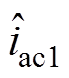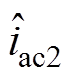均为扰动量。将式（6）代入式（3）～>式（5），并进行线性化处理，可得
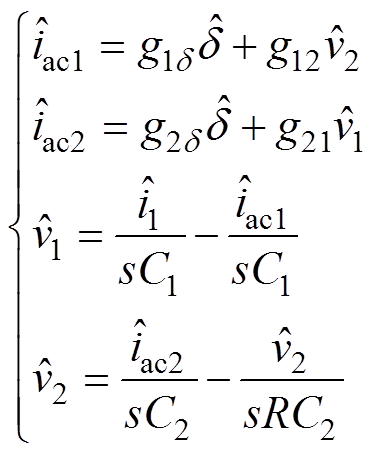（7）其中
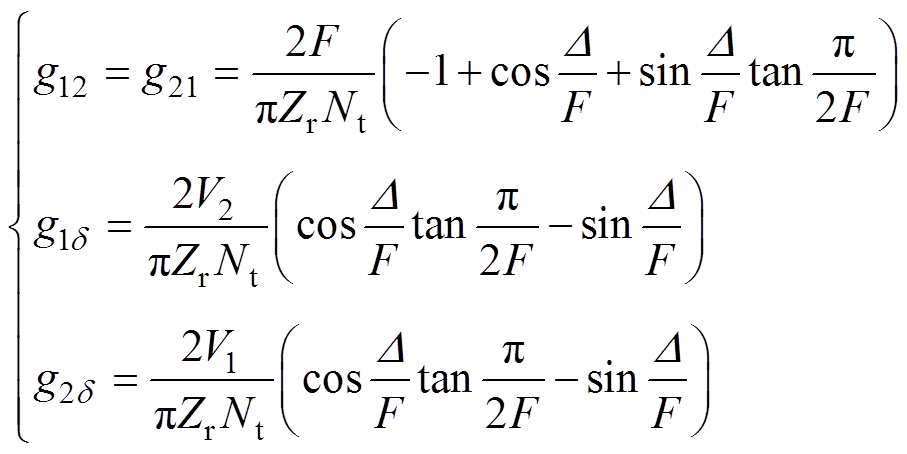
于是，DBSRC的小信号模型如图4所示。
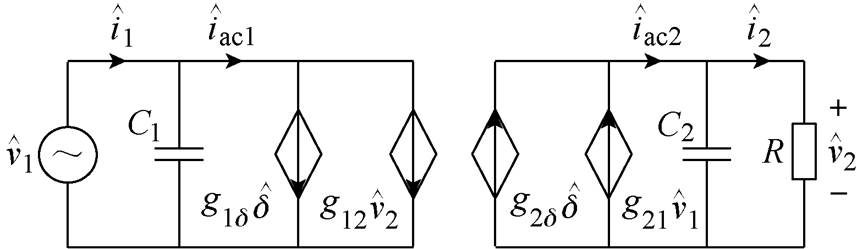
图4 DBSRC小信号模型
Fig.4 The small-signal model of DBSRC
因此，DBSRC控制-输出和输入-输出传递函数分别为
（8）
（9）
对于n个子模块的DBSRC级联系统，根据ISOP拓扑结构，系统小信号模型如图5所示。
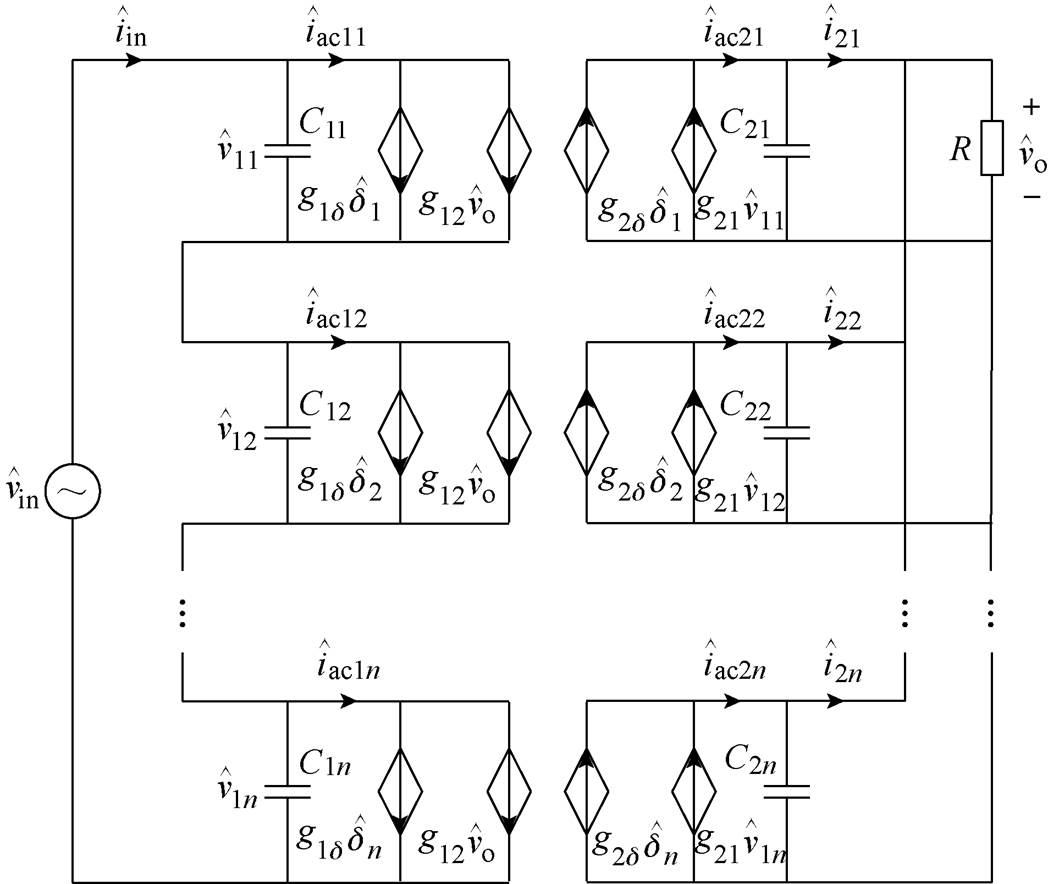
图5 基于ISOP的DBSRC系统小信号模型
Fig.5 The small-signal model of DBSRC system based on ISOP connection
系统输入侧根据基尔霍夫电流、电压定律可得
（10）
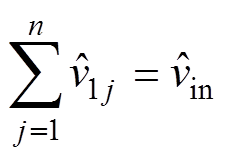（11）
式中，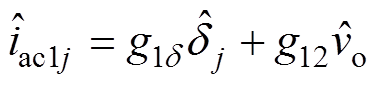
，j=1, 2,…, n；
、
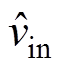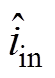分别为系统电压、电流输入扰动；
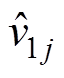为子模块输入电压扰动；
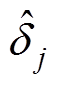为子模块移相角扰动；C1j为子模块输入支撑电容。
系统输出侧根据基尔霍夫电流定律可得
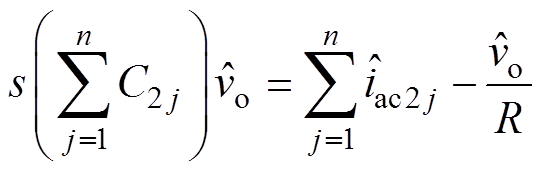（12）式中，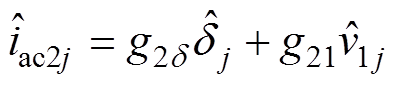
；C2j为子模块输出支撑 电容。
假设ISOP级联系统内，各子模块的硬件参数一致，即输入支撑电容C11=C12=…=C1n=C1，输出支撑电容C21=C22=…=C2n =C2，变压器电压比Nt1=Nt2=…= Ntn=Nt，特性阻抗Zr1=Zr2=…=Zrn=Zr，开关频率谐振频率比F1=F2=…=Fn=F，那么稳态时，各子模块的移相角相同，即D1=D2=…=Dn=D，同时各子模块可实现输入均压和输出均流。那么，子模块控制-输出电压和系统输入电压-输出电压的传递函数分别为
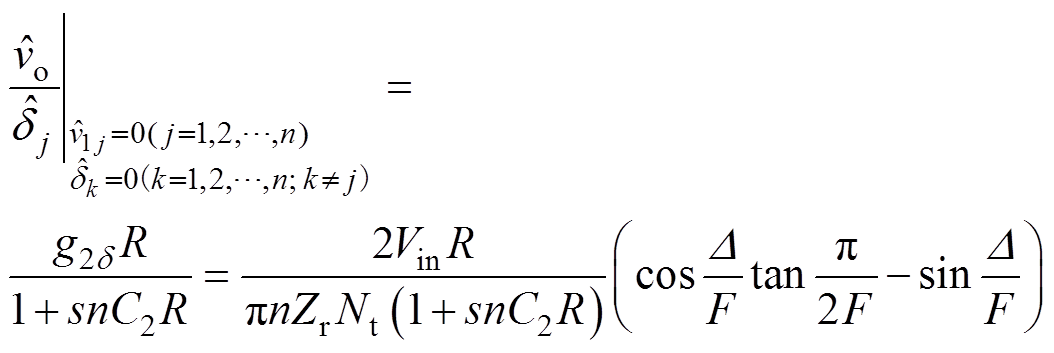（13）
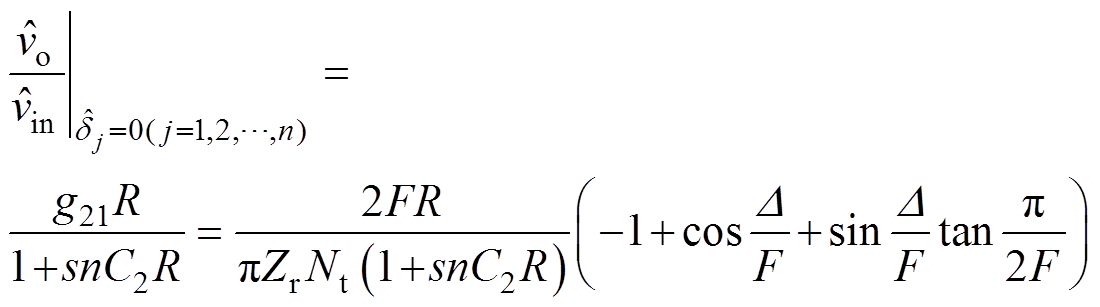（14）
若系统处于稳定状态，输入扰动为零，即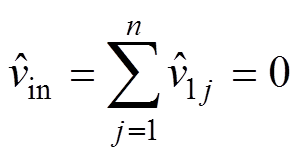
，那么式（10）中各式两两相减可得
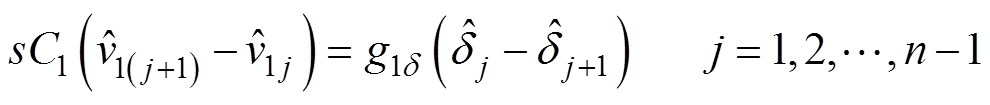（15）改写得
（16）
由式（16）可解得控制-子模块输入电压数学模型为
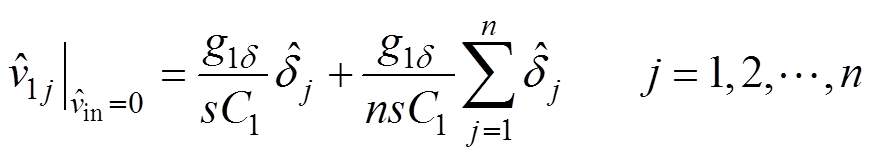（17）由式（17）可知，各子模块的输入电压同时受该模块移相角及其他模块移相角影响，各子模块的控制相互耦合。以上分别得到了基于ISOP的DBSRC系统的控制-输出电压、系统输入电压-输出电压和控制-子模块输入电压的传递函数。
对于高频化高铁辅助变流器，电压较为稳定，而负载范围变化范围较大，因此本文基于IVS目标提出一种差分输入电压均压（DIVS）控制策略，如图6所示。该控制策略采用主从控制，包含一个输出电压环和n-1个输入均压环。Gvo为输出电压环控制器，Gvin为输入均压环控制器。输出电压环的反馈量为vo，用来保持输出电压的稳定。输出电压环输出作为第n个DBSRC模块（主机）的控制量和前n-1个DBSRC模块（从机）的前馈量。输入均压环的参考值为第n个DBSRC模块的输入电压，反馈量为对应DBSRC模块的输入电压。
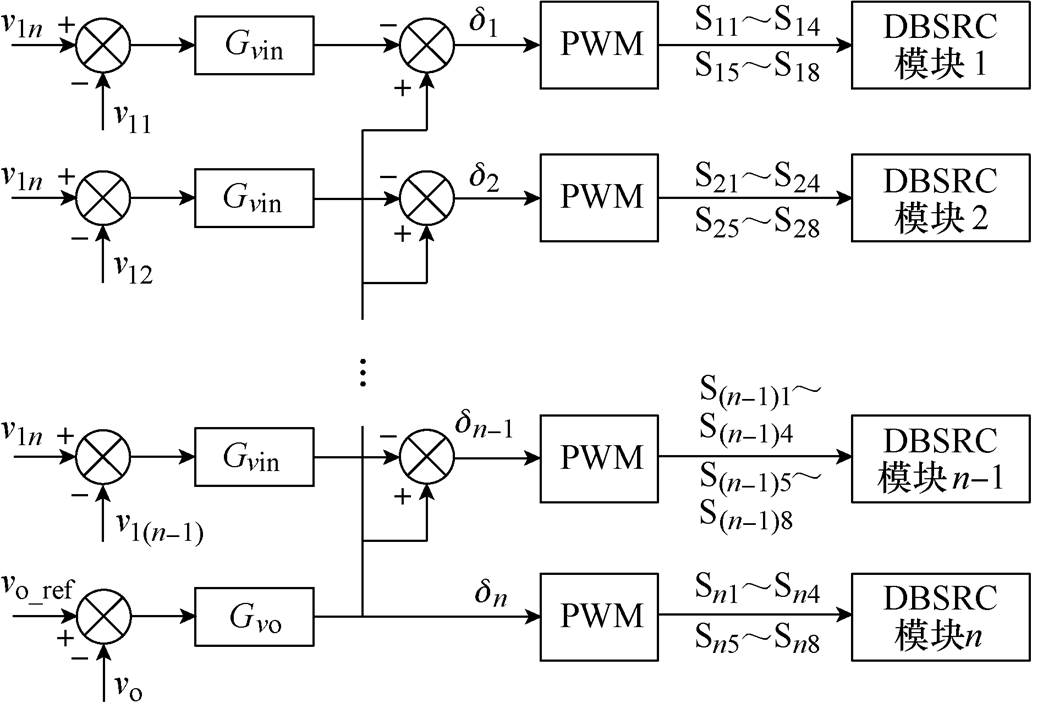
图6 基于ISOP的DBSRC系统差分输入均压控制策略
Fig.6 The proposed DIVS control strategy of DBSRC system based on ISOP connection
若前n-1个模块的输入电压低于第n个模块，对应输入均压环输出移相角将降低，输入电流和输出电流降低，那么对应模块的输入支撑电容将开始储能直到等于第n个模块的输入电压；反之亦然。若第n个模块的输入电压降低，前n-1个模块的输入电压将高于第n个模块，对应输入支撑电容开始放电，而第n个模块的输入支撑电容充电，从而保证输入均压的稳定。综上，该控制策略稳态时可以保证系统稳定工作。
在一个控制周期内，第n个模块仅需将输出电压环的输出以及该模块输入电压采样值下发给前n-1个模块，此过程包含一次通信（下发）及2(n-1)的通信数据量。而文献[4, 14, 18]提出的均压控制策略均采用系统输入电压的平均值作为反馈量，需将前n-1个模块的输入电压值上传至主机，经计算后，再下发回前n-1个模块，此过程增加了一次通信过程（上传）及n-1的通信数据量。而文献[4, 14]需将前n-1个模块输入均压环的输出再上传至第n个模块，又增加了一次通信过程及n-1的通信数据量。具体通信次数及通信数据量见表1。DIVS控制策略所需的通信过程及数据量更少，因此控制延迟更低，系统动态性能更好。
表1 各个IVS控制策略通信次数及数据量对比
Tab.1 The communication comparison of different IVS control strategies
控制策略上传/下发次数通信数据量 DIVS12(n-1) 文献[18]23(n-1) 文献[14]34(n-1)
对于基于ISOP的DBSRC系统的任意子模块，由式（17）给出的传递函数，其输入电压不仅受到本模块移相角的影响，其他模块移相角的变化也对其造成影响，故需考虑解耦控制。将式（10）中各式与最后一式相减可得
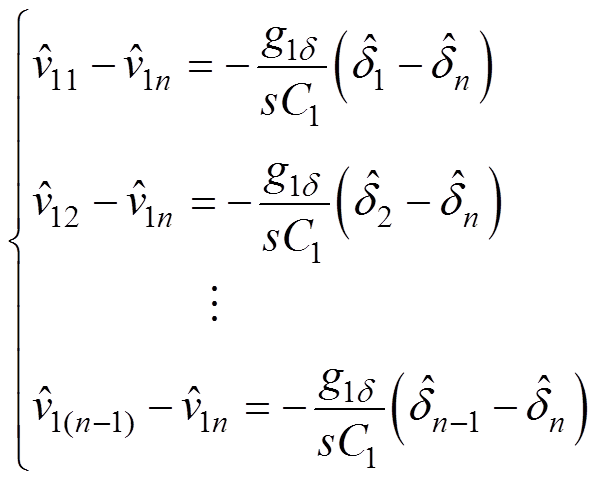（18）令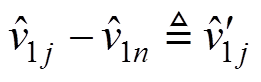
，
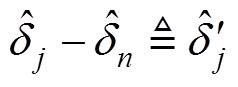（j=1, 2,…, n-1），那么式（18）改写为矩阵形式为
（19）
由式（19）可以看出，虽然子模块移相角不能独立确定对应子模块输入电压，但差分移相角可以独立确定差分输入电压。结合DIVS控制策略，系统框图如图7所示。根据式（13）、式（14）和式（19）传递函数，被控系统可用点画线框内模型表示，点画线框外是DIVS的模型。
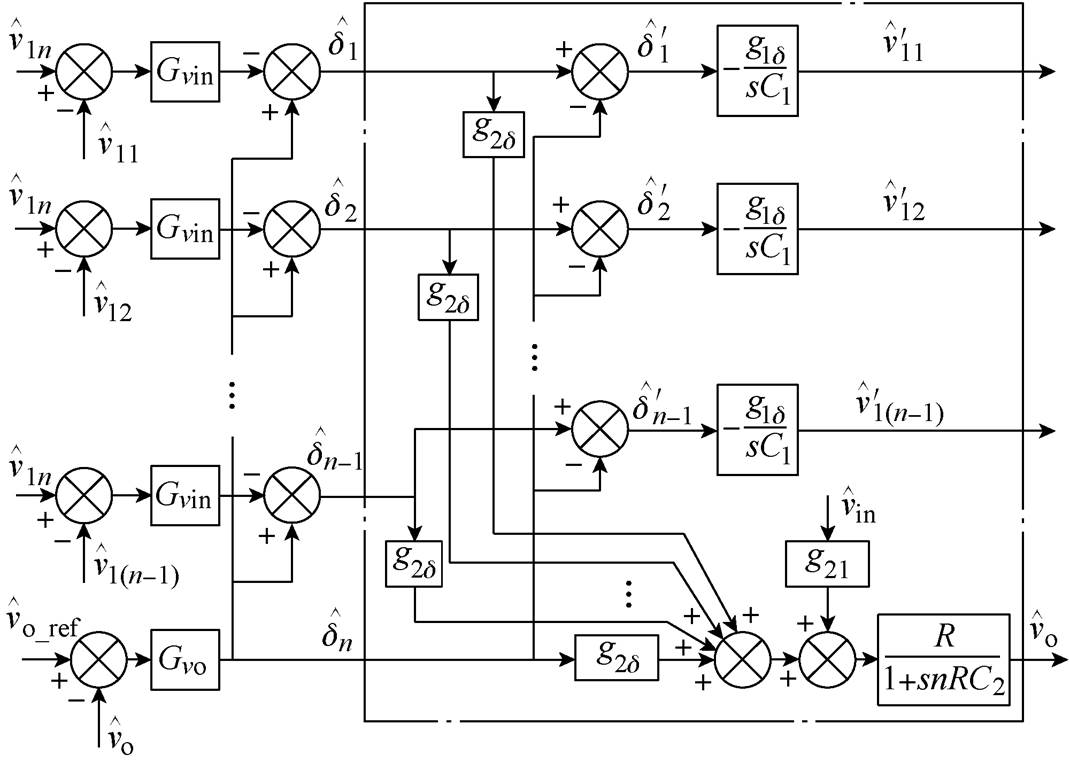
图7 考虑DIVS控制策略的系统框图
Fig.7 The system block diagram considering the proposed DIVS control strategy
对于每个输入均压环，其输入误差量为
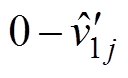，等效于以0为参考量，以
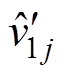为反馈量的形式，而第n个模块的移相角
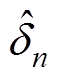作为输入均压环的前馈量，抵消了系统模型中其对输入均压环的影响。同理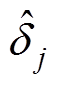，对于输出电压环的影响，可通过控制理论及式（11）化简，并将前馈量归算为与
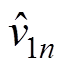和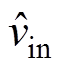相关的前馈量。化简后的系统框图如图8所示，各个输入均压环与输出电压环实现相互解耦，因此各个控制环均可独立设计控制器。
DBSRC小信号模型是ISOP级联系统模型及其控制策略提出的基础，因此本文首先针对DBSRC小信号模型在PSIM软件平台进行仿真验证。按照图2搭建仿真电路，其中输入电压为650V，输入、输出支撑电容均为1.5mF，高频变压器匝数比为1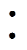1，其漏感为18mH，谐振电容为1.1mF，因此谐振频率约为36kHz，设置开关频率为43kHz。输出接负载电阻，功率为35kW，所需的移相角通过式（2）计算得到。当DBSRC达到稳定时，交流电压、电流波形如图9所示。由于移相作用，输出电压可以保持与输入电压相等。
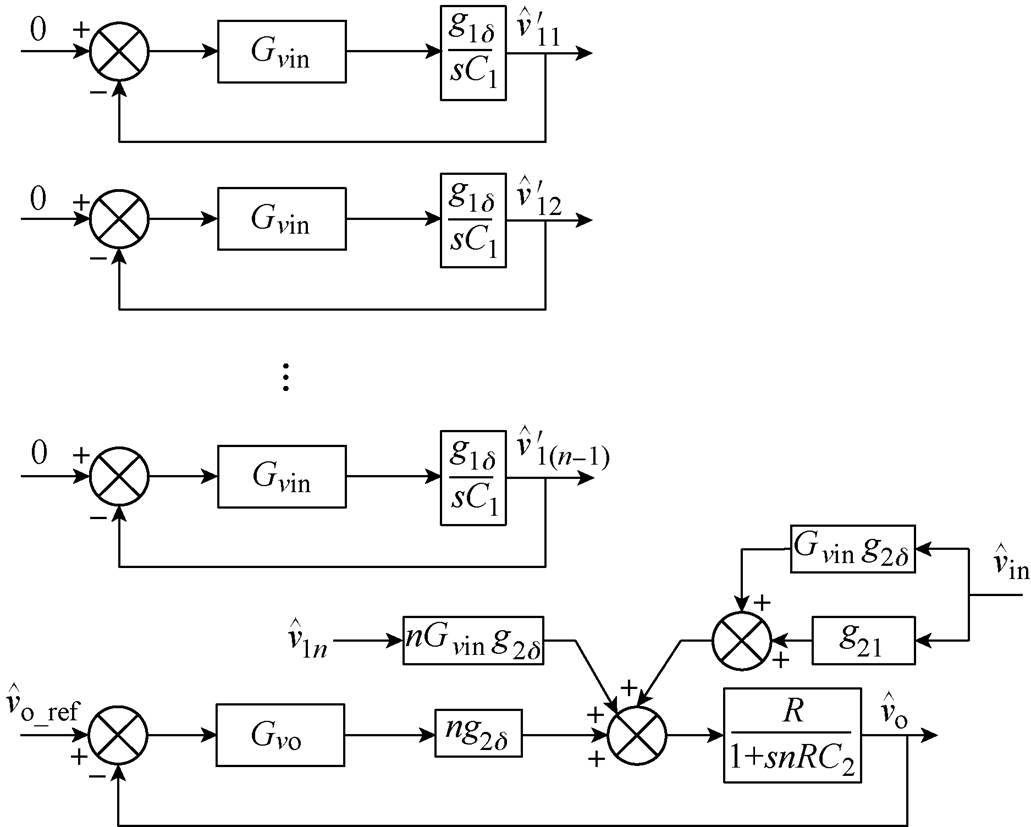
图8 化简后的系统框图
Fig.8 The simplified system block diagram
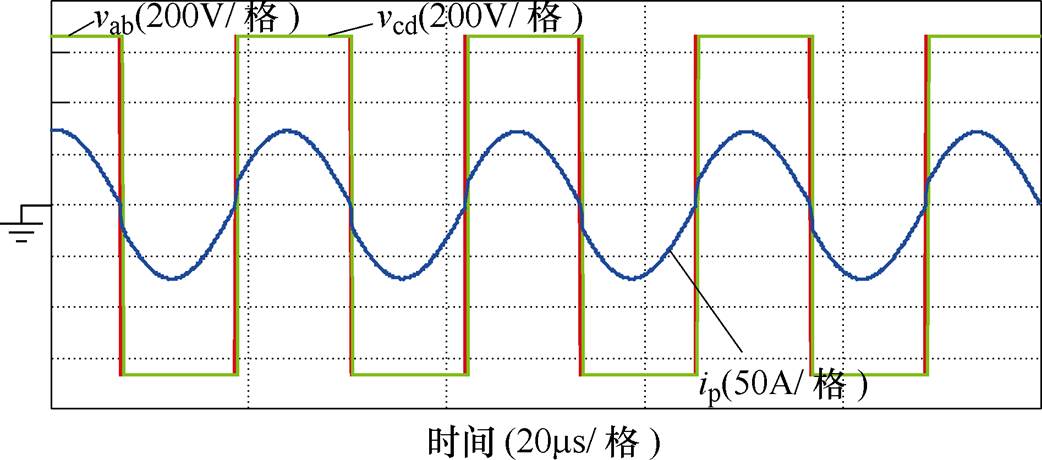
图9 DBSRC稳态交流电压、电流波形
Fig.9 The AC voltage and current waveforms of DBSRC at steady state
为了验证DBSRC控制-输出传递函数的正确性，在稳态时，对移相角施加低频扰动，观测输出电压的波动。移相角扰动为正弦量，频率变化范围为1～3kHz。100Hz移相角d 扰动与输出电压v2响应如图10所示，幅值响应为输出电压响应峰峰值与移相角扰动峰峰值之比，相位响应为两者相位差。
DBSRC控制-输出传递函数伯德图如图11所示。图11表明仿真结果与所提的DBSRC小信号模型匹配较好，特别是在低频段，即1kHz以下。在高频段幅值响应与仿真结果有一定差异，这是因为在建立小信号模型过程中，DBSRC高频谐振电流采用了周期平均值替代，忽略了高频成分对模型的影响。然而，ISOP级联系统的电压变化在ms级，该小信号模型在低频段的准确性足以用来反映ISOP级联系统的动态性能。
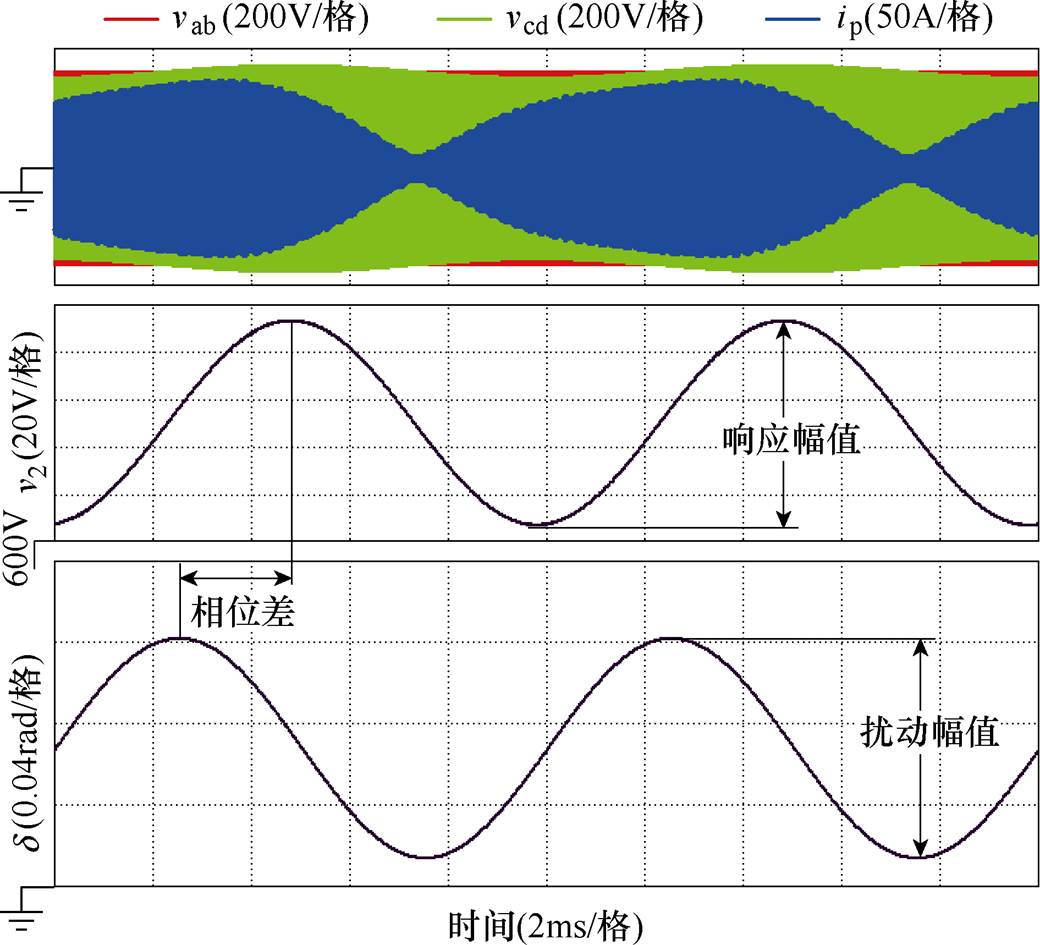
图10 100Hz移相角d 扰动与输出电压v2响应
Fig.10 The 100Hz perturbation of phase-shift angle d and the response of output voltage v2
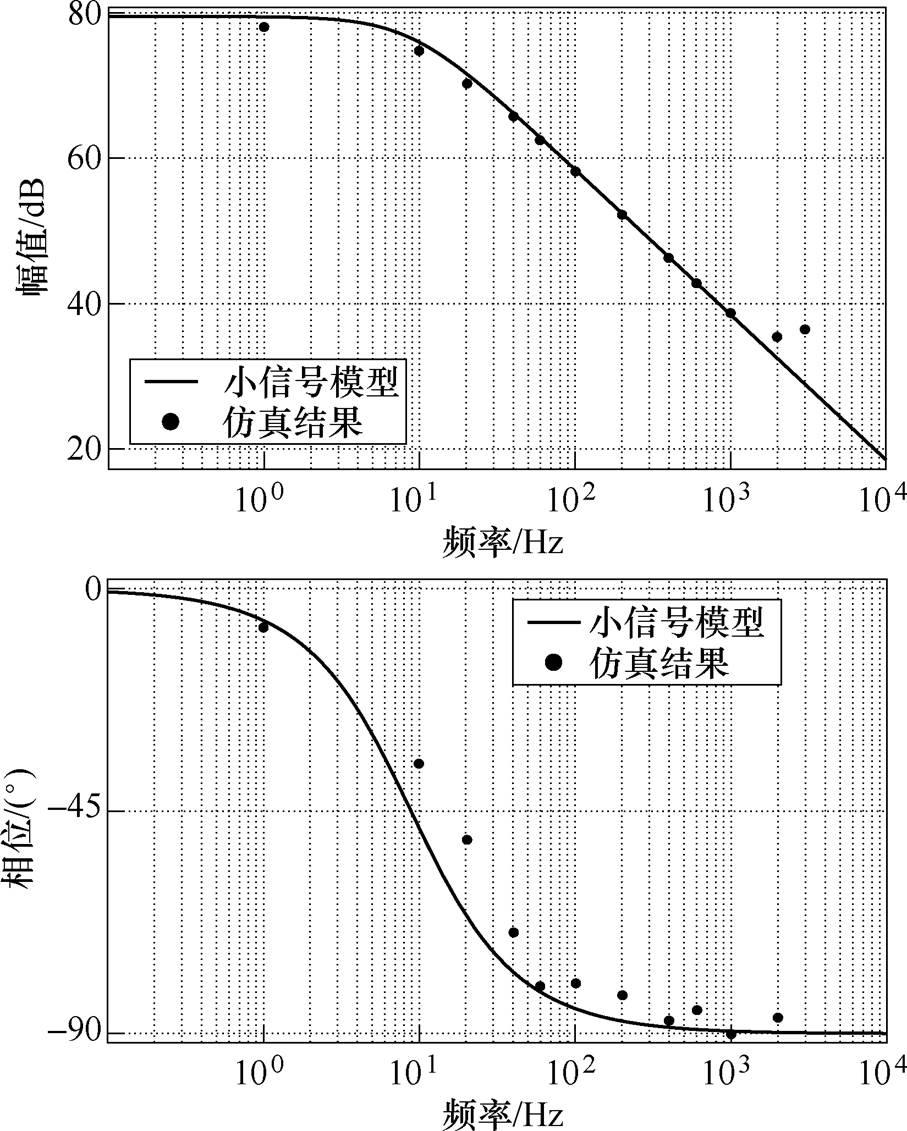
图11 DBSRC控制-输出传递函数伯德图
Fig.11 Bode plots of control-to-output transfer function of DBSRC
本文按照图1b所示高频化辅助变流器的DC- DC变换部分搭建三个DBSRC模块的ISOP级联系统。系统仿真参数见表2，各子模块的谐振电感、谐振电容略有差异，用来模拟实际中谐振参数的不一致性。
表2 ISOP级联DBSRC系统仿真参数
Tab.2 Simulation parameters of ISOP DBSRC system
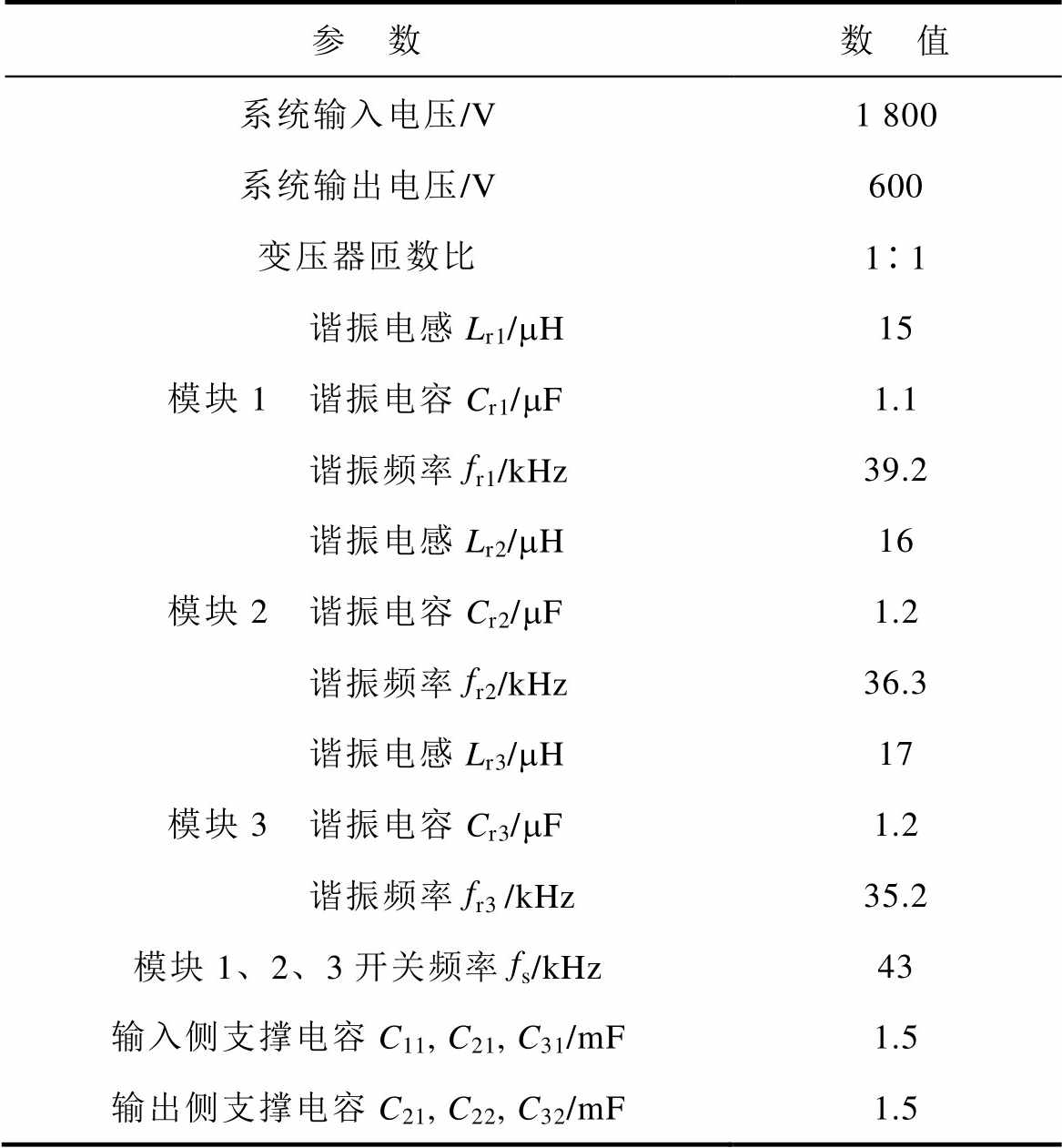
参 数数 值 系统输入电压/V1 800 系统输出电压/V600 变压器匝数比11 谐振电感Lr1/mH15 模块1 谐振电容Cr1/mF1.1 谐振频率fr1/kHz39.2 谐振电感Lr2/mH16 模块2 谐振电容Cr2/mF1.2 谐振频率fr2/kHz36.3 谐振电感Lr3/mH17 模块3 谐振电容Cr3/mF1.2 谐振频率fr3 /kHz35.2 模块1、2、3开关频率fs/kHz43 输入侧支撑电容C11, C21, C31/mF1.5 输出侧支撑电容C21, C22, C32/mF1.5
为了验证本文提出的DIVS控制策略的有效性和优越性，仿真对比了文献[14, 18]中的均压控制策略。三种控制策略均由输出电压环和输入均压环构成，本文采用相同的PI控制器，IVS控制策略控制器参数见表3。
表3 IVS控制策略控制器参数
Tab.3 Controller parameters of IVS control strategies
参数输出电压环Gvo输入均压环Gvin Kp1.35×10-25.40×10-3 Ki27.02.70
5.2.1 输入均压有效性
系统的输出功率设置为180kW，各控制策略下子模块输入电压、输出电压波形如图12所示。图12a给出了DIVS控制策略的各子模块输入电压、输出电压波形。系统启动后，各子模块输入电压和系统输出电压均稳定在600V，然后停止控制策略的执行，以输出电压环的输出作为各子模块的移相角。由于各子模块谐振参数的差异，输入电压出现偏差，谐振频率相对较低的模块输入电压较高。当电压偏差稳定后，重新启动IVS控制策略，系统快速恢复输入电压的均衡，且输出电压并未产生较大的波动，从而验证了DIVS控制策略的有效性。相比文献[14, 18]的控制策略，在输入电压恢复均衡的过程中，输入电压最大过冲（模块3电压过冲）更小，体现出更好的电压阶跃时的动态特性。
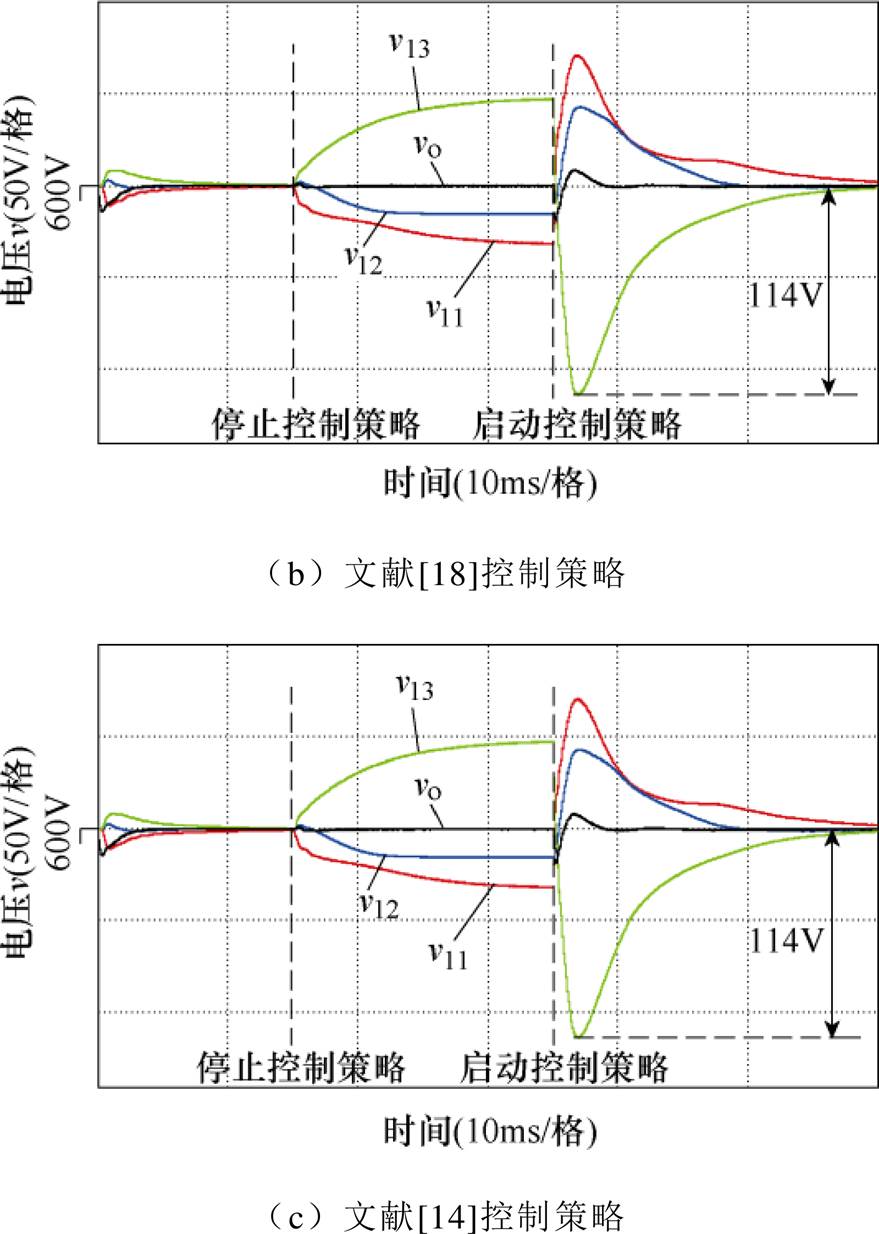
图12 各控制策略下子模块输入电压、输出电压波形
Fig.12 Simulation waveforms of module input voltage and system output voltage under different strategies
5.2.2 负载阶跃动态响应
系统的初始功率设置为90kW，然后负载阶跃至180kW，当系统稳定后，再切除负载至90kW。在不考虑通信延时情况下，图13给出了各控制策略下负载阶跃时模块输入电压、系统输出电压波形。无论突加还是突减负载，DIVS控制策略均能保证各模块输入电压、系统输出电压稳定在600V。即使各模块谐振参数不同，也可通过控制各模块移相角大小实现各子模块的功率均衡。在突加、突减负载过程中，对不同控制策略，每个模块输入电压的恢复过程相差不大，但DIVS输出电压的响应时间分别为3.7ms和3.1ms，低于文献[14, 18]控制策略，展现出更好的动态性能。
实际应用中，模块间需要通信传递控制前馈量，如第3节中所述，不同控制策略的通信数据量和时间是不同的。假设一次通信过程所产生的延时为0.1ms，图14给出了不同控制策略下负载阶跃波形。由于通信延时的作用，过渡过程中输入电压和输出电压均出现波动，但DIVS控制策略波动更小，输出电压恢复时间均为3.6ms，低于文献[14, 18]的控制策略，这是因其通信数据量最小。若通信延迟时间增大，DIVS控制策略动态响应优势将更加明显。
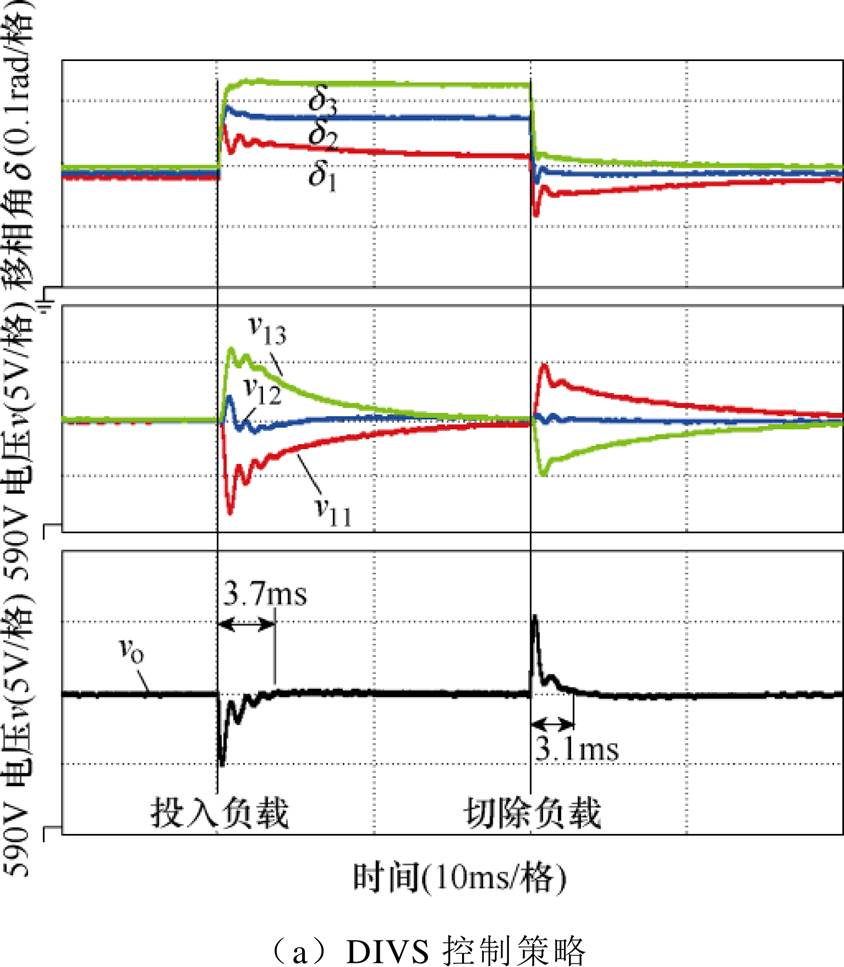
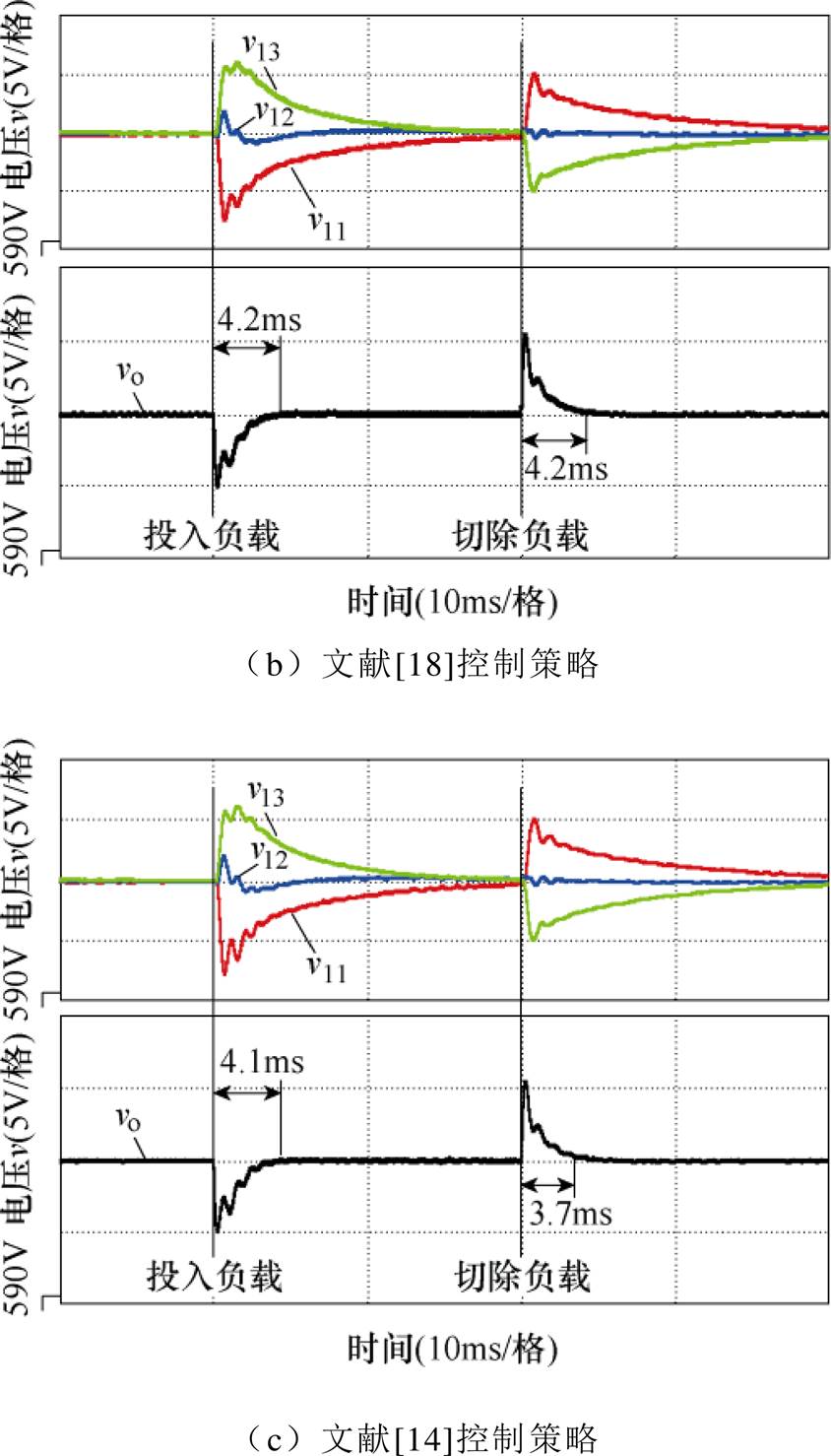
图13 未考虑通信延时，各控制策略下负载阶跃时模块输入电压、系统输出电压波形
Fig.13 Simulation waveforms of module input voltage and system output voltage with load step under different strategies without considering communication delay
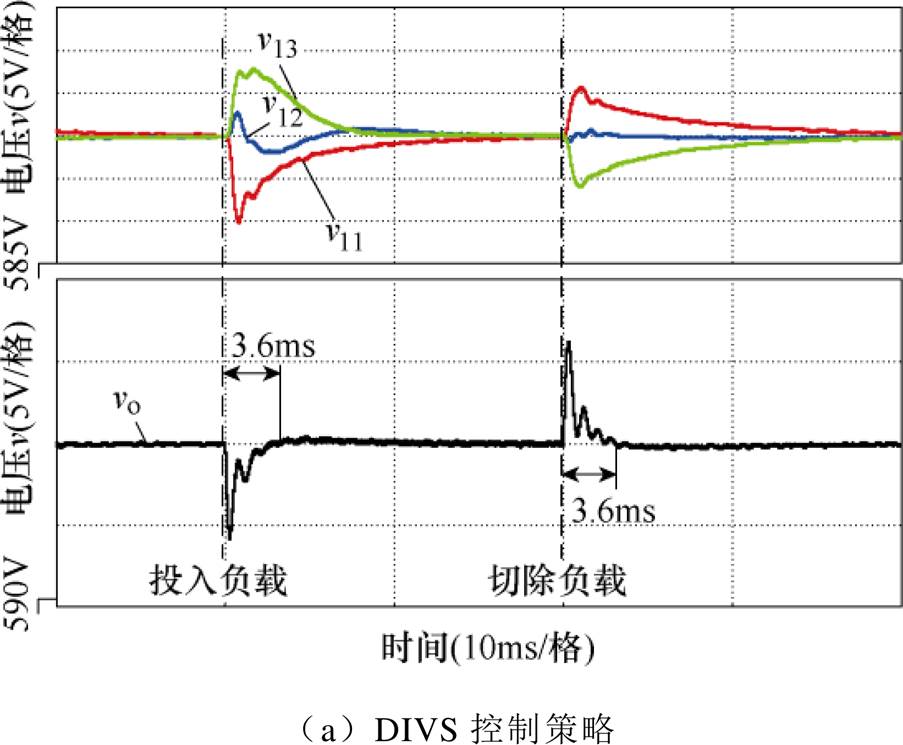
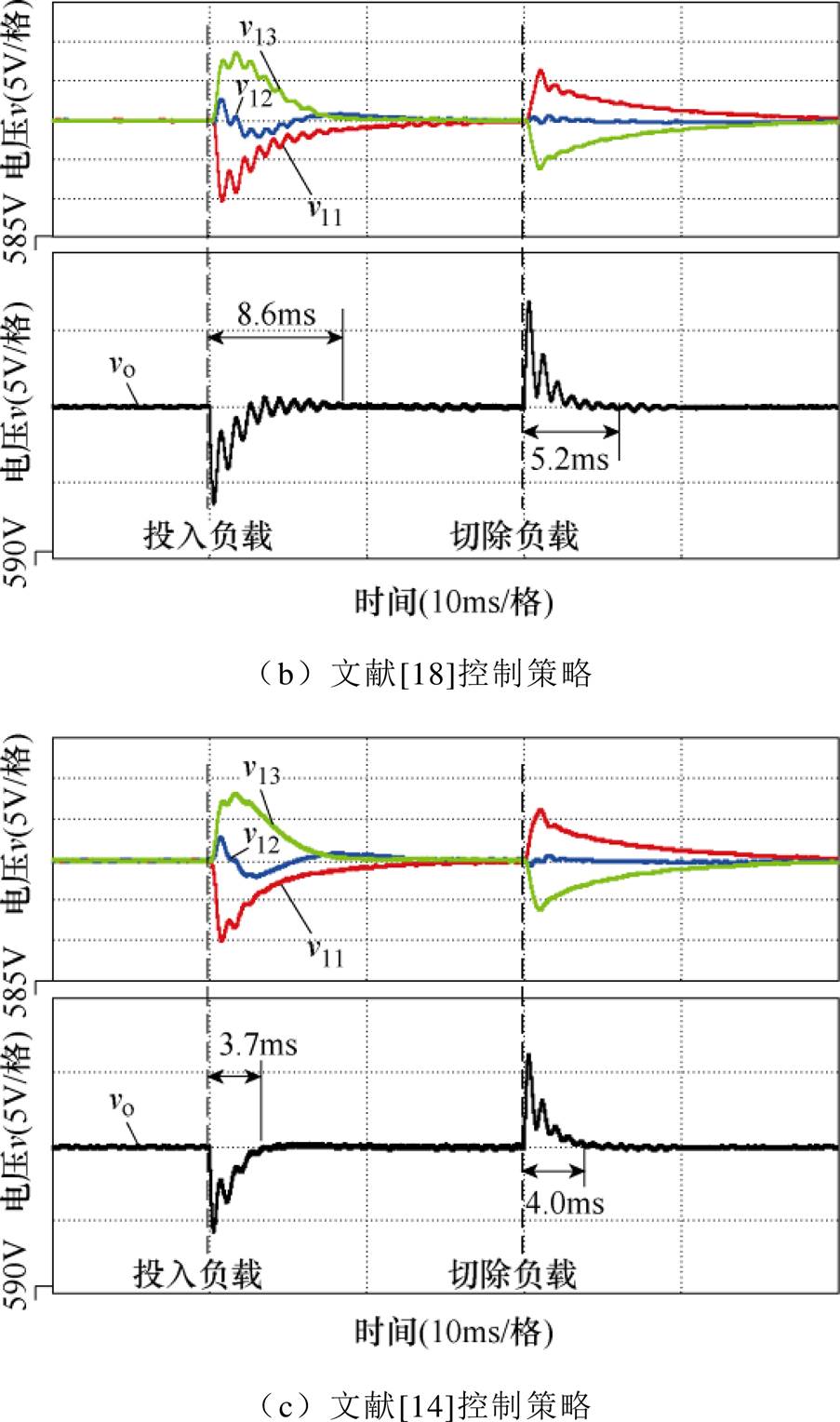
图14 当通信延时为0.1ms时，各控制策略下负载阶跃时模块输入电压、系统输出电压波形
Fig.14 Simulation waveforms of module input voltage and system output voltage with load step under different strategies when communication delay is 0.1ms
为了验证DIVS控制策略的有效性，本文搭建了三个DBSRC模块ISOP级联实验样机，如图15所示。三个模块的硬件参数保持一致，输入、输出支撑电容均为2.3mF，高频变压器匝数比为1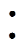
1，谐振电感为18mH，谐振电容为1.1mF。模块1作为主机，向模块2和模块3提供控制信号。开关管采用IGBT，型号为FF300R12KS4，设置开关频率为40kHz。系统直流输入母线由PWM整流提供，输入母线电压固定为650V，分别采用三种均压控制策略，控制输出电压为输入母线电压的1/3。负载为电阻负载，最大为12kW。当系统稳定运行时，模块2的高频交流电压、电流波形如图16所示。
图15 三个DBSRC模块ISOP级联实验样机
Fig.15 The prototype of three DBSRC modules based on ISOP connection
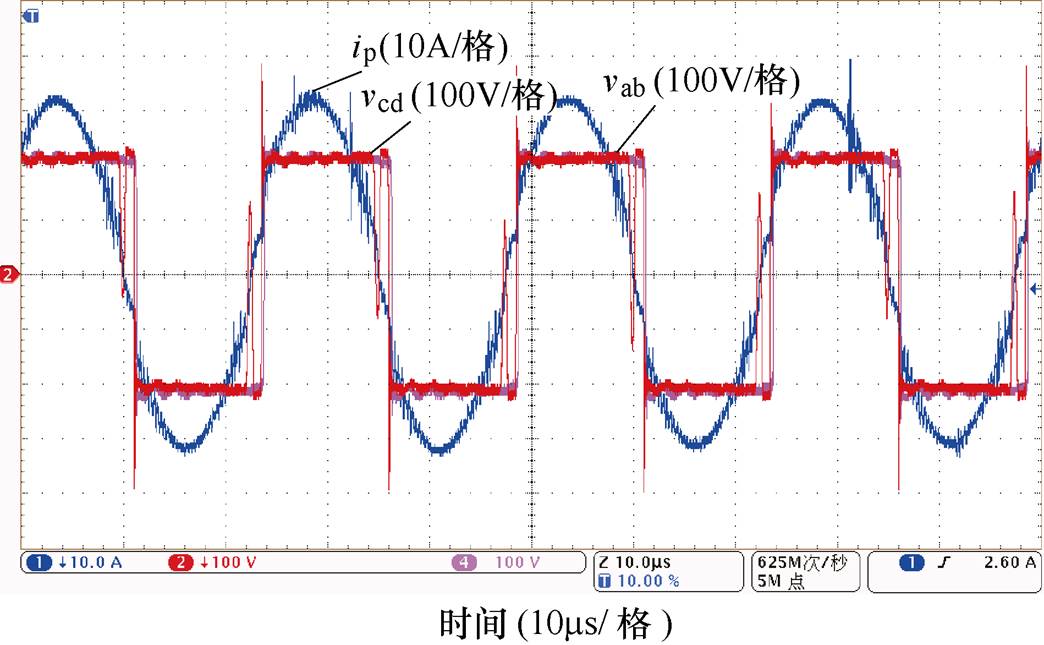
图16 稳态时模块2高频交流电压、电流波形
Fig.16 The waveforms of AC voltage and current of DBSRC module 2 at steady state
图17给出了不同控制策略下，系统从空载到12kW切换的过渡过程。图17a显示，DIVS控制策略在空载和带载情况下，均能实现模块输入电压的均衡。由于在负载切换时，PWM整流控制的输入母线电压产生了一定的波动，所以输入、输出电压的过渡过程时间相比仿真结果有所增长，但其相对时长可以反映不同控制策略下系统的动态性能。图17中的v13电压波形显示，DIVS策略输入电压过渡过程恢复时间明显小于文献[14, 18]的控制策略，展现出更好的动态性能。
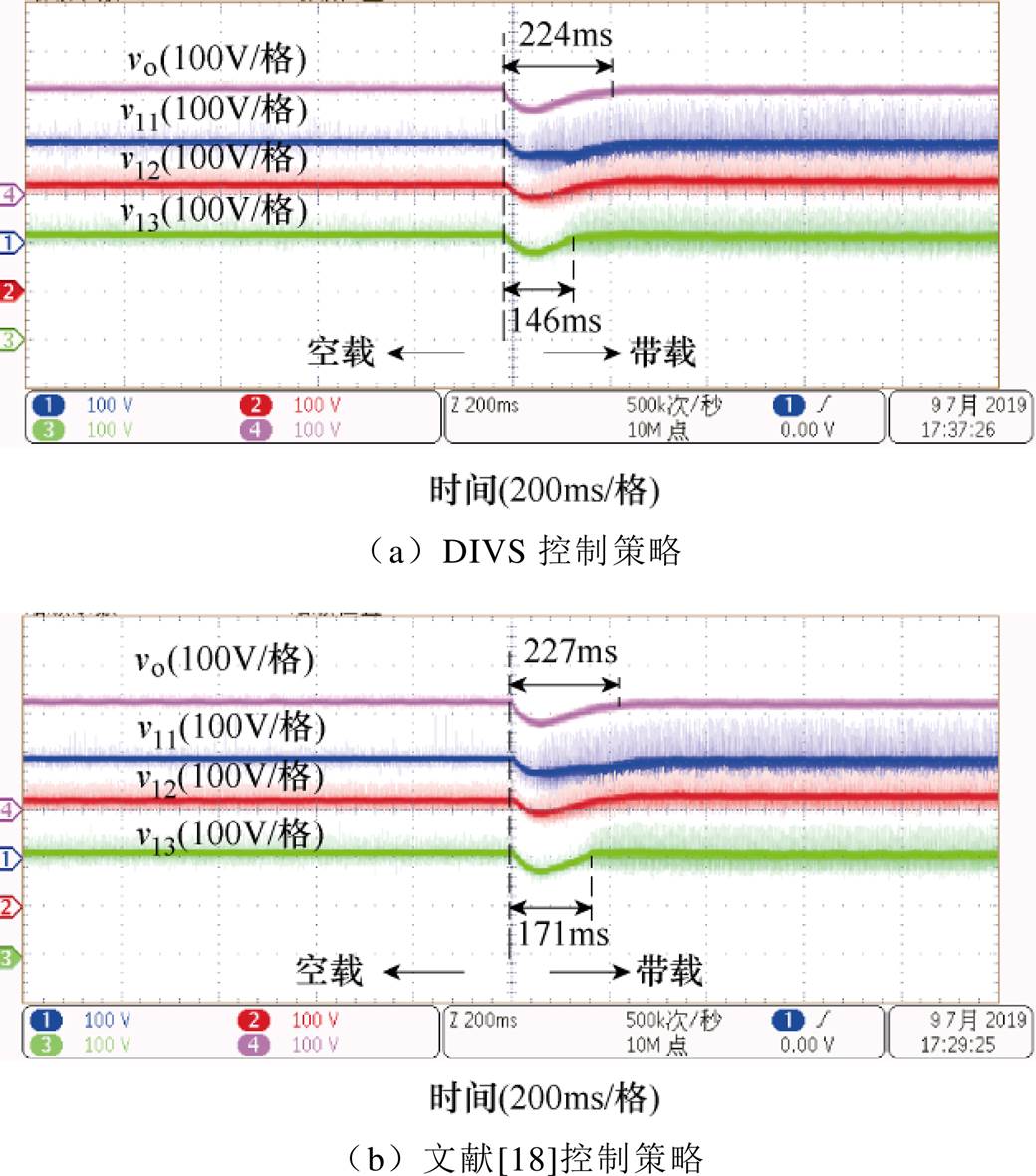
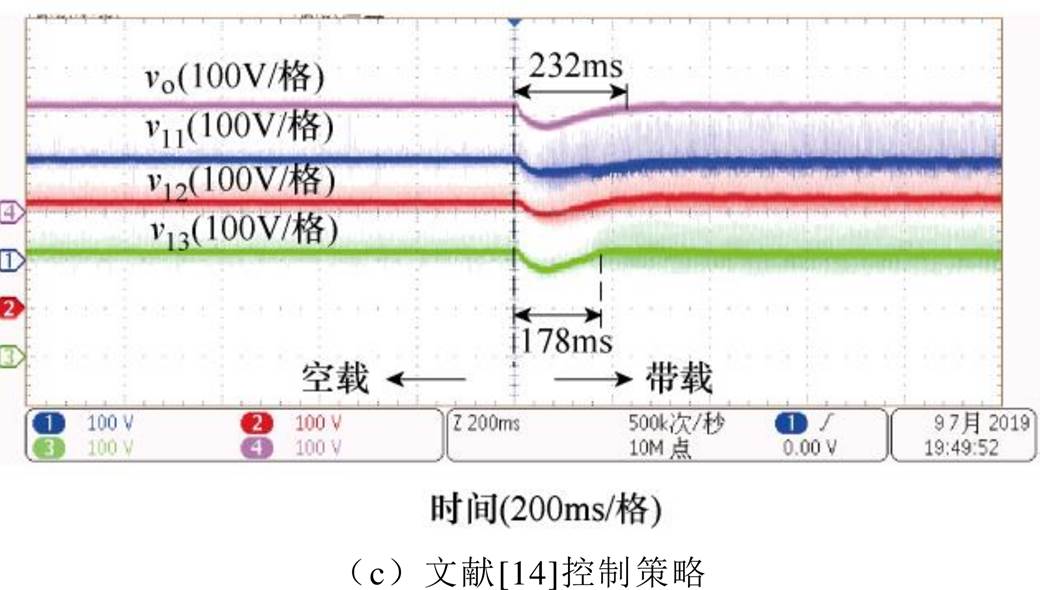
图17 各控制策略下负载阶跃时模块输入电压、系统输出电压实验波形
Fig.17 Experimental waveforms of module input voltage and system output voltage under different strategies
本文建立了输入串联输出并联的双向全桥串联谐振DC-DC变换器系统的小信号模型，提出一种基于差分输入电压的均压控制策略，该策略可实现各个控制环路的解耦控制，并且所需的通信数据量少。仿真结果首先验证了DBSRC小信号模型在低频段的准确性，在谐振参数不一致的三个DBSRC模块系统中，本文所提的均压控制策略能实现各子模块功率均衡。突加、突减负载的仿真结果显示，无论是否考虑通信延时，该均压控制策略均有优于传统均压控制策略的动态响应性能。在12kW的实验样机上，证明了DIVS策略均压的有效性以及其优越的动态性能。
参考文献
[1] Ronanki D, Singh S A, Williamson S S. Com- prehensive topological overview of rolling stock architectures and recent trends in electric railway traction systems[J]. IEEE Transactions on Trans- portation Electrification, 2017, 3(3): 724-738.
[2] 郑华熙, 高吉磊, 郑琼林. 我国高速动车组辅助供电系统的比较与分析[J]. 电气传动, 2010, 40(3): 53-59.
Zheng Huaxi, Gao Jilei, Zheng Qionglin. Comparison and analysis of auxiliary power supply systems of China railway high-speed[J]. Electric Drive, 2010, 40(3): 53-59.
[3] 杨景熙, 刘建强, 张捷频, 等. 基于双有源桥式DC-DC变换器的电力电子牵引变压器的电压平衡控制[J]. 电工技术学报, 2016, 31(增刊1): 119-127.
Yang Jingxi, Liu Jianqiang, Zhang Jiepin, et al. Voltage balance control of a power electronic traction transformer based on dual active bridge DC-DC converters[J]. Transactions of China Electrotechnical Society, 2016, 31(S1): 119-127.
[4] 安峰, 王嵩, 杨柯欣. 输入串联输出并联双有源全桥DC-DC变换器多模块优化功率平衡控制方法[J]. 电工技术学报, 2018, 33(16): 3732-3742.
An Feng, Wang Song, Yang Kexin. Multi-module optimized power balance control scheme of the input- series-output-parallel operated dual-active-bridge DC-DC converters[J]. Transactions of China Electro- technical Society, 2018, 33(16): 3732-3742.
[5] 张捷频, 刘建强, 杨景熙, 等. 输入串联输出并联变换器的控制器设计及稳定性分析方法[J]. 电工技术学报, 2017, 32(17): 180-188.
Zhang Jiepin, Liu Jianqiang, Yang Jingxi, et al. Con- troller design and stability analysis method for input- series-output-parallel converters[J]. Transactions of China Electrotechnical Society, 2017, 32(17): 180-188.
[6] 武琳, 刘志刚, 洪祥. 隔离式双向全桥DC-DC变换器的功率控制特性比较与分析[J]. 电工技术学报, 2013, 28(10): 179-187.
Wu Lin, Liu Zhigang, Hong Xiang. Comparison and analysis of power control characteristic for isolated bidirectional full-bridge DC-DC converter[J]. Transa- ctions of China Electrotechnical Society, 2013, 28(10): 179-187.
[7] 顾春阳. 用于电力牵引的电力电子变压器拓扑及控制研究[D]. 北京: 清华大学, 2015.
[8] Li Xiaodong, Bhat A K S. Analysis and design of high-frequency isolated dual-bridge series resonant DC/DC converter[J]. IEEE Transactions on Power Electronics, 2010, 25(4): 850-862.
[9] Corradini L, Seltzer D, Bloomquist D, et al. Minimum current operation of bidirectional dual-bridge series resonant DC/DC converters[J]. IEEE Transactions on Power Electronics, 2012, 27(7): 3266-3276.
[10] Hu Song, Li Xiaodong, Bhat A K S. Operation of a bidire-ctional series-resonant converter with mini- mized tank current and wide ZVS range[J]. IEEE Transa- ctions on Power Electronics, 2019, 34(1): 904-915.
[11] 王世恩, 郑泽东, 李永东. 串联谐振双有源桥DC- DC变换器的频域分析[J]. 大功率变流技术, 2017(4): 26-30.
Wang Shien, Zheng Zedong, Li Yongdong. Frequency domain analysis of dual active bridge DC-DC converter with series resonant[J]. High Power Converter Technology, 2017(4): 26-30.
[12] 武琳, 张燕枝, 李子欣, 等. 一种隔离式双向全桥DC/DC变换器的控制策略[J]. 电机与控制学报, 2012, 16(12): 21-27, 35.
Wu Lin, Zhang Yanzhi, Li Zixin, et al. A control strategy of isolated bidirectional full bridge DC/DC converter[J]. Electric Machines & Control, 2012, 16(12): 21-27, 35.
[13] 赵彪, 宋强, 刘文华, 等. 用于柔性直流配电的高频链直流固态变压器[J]. 中国电机工程学报, 2014, 34(25): 4295-4303.
Zhao Biao, Song Qiang, Liu Wenhua, et al. High- frequency-link DC solid state transformers for flexible DC distribution[J]. Proceedings of the CSEE, 2014, 34(25): 4295-4303.
[14] Ruan Xinbo, Chen Wu, Cheng Lulu, et al. Control strategy for input-series-output-parallel converters[J]. IEEE Transactions on Industrial Electronics, 2009, 56(4): 1174-1185.
[15] Qu Lu, Zhang Donglai, Bao Zhiyun. Output current- differential control scheme for input-series-output- parallel-connected modular DC-DC converters[J]. IEEE Transactions on Power Electronics, 2017, 32(7): 5699-5711.
[16] Sha Deshang, Guo Zhiqiang, Liao Xiaozhong. Cross- feedback output-current-sharing control for input- series-output-parallel modular DC-DC converters[J]. IEEE Transactions on Power Electronics, 2010, 25(11): 2762- 2771.
[17] 曲璐. 输入串联型组合变换器控制策略关键技术研究[D]. 哈尔滨: 哈尔滨工业大学, 2018.
[18] Siri K, Willhoff M, Conner K. Uniform voltage distribution control for series connected DC-DC converters[J]. IEEE Transactions on Power Elec- tronics, 2007, 22(4): 1269-1279.
[19] 黄先进, 赵鹃. 一种基于输入串联输出并联移相全桥变换器的改进型交错控制方法[J]. 电工技术学报, 2020, 35(增刊1): 70-80.
Huang Xianjin, Zhao Juan. An improved interleaved control method based on input-series output-parallel phase-shifted full-bridge converter[J]. Transactions ofChina Electrotechnical Society, 2020, 35(S1): 70-80.
[20] Chen Wu, Wang Guangjiang, Ruan Xinbo, et al. Wireless input-voltage-sharing control strategy for input-series output-parallel (ISOP) system based on positive output-voltage gradient method[J]. IEEE Transactions on Industrial Electronics, 2014, 61(11): 6022-6030.
[21] 陈武, 王广江, 阮新波. 基于输出电压上翘特性的串-并型组合变换器无互联均压控制策略[J]. 电工技术学报, 2013, 28(10): 188-194.
Chen Wu, Wang Guangjiang, Ruan Xinbo. Input voltage sharing control strategy for ISOP converter without interconnection based on positive output voltage gradient method[J]. Transactions of China Electrotechnical Society, 2013, 28(10): 188-194.
[22] Yang Bo, Ge Qiongxuan, Zhao Lu, et al. Study on reducing switching current in dual bridge series resonant DC/DC converter[C]//2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonic, USA, 2018: 808-813.
Control Strategy of Dual Bridge Series Resonant DC-DC Converter System Based on Input Series Output Parallel Connection
Abstract The control strategy of dual bridge series resonant DC/DC converter (DBSRC) system based on the input series output parallel (ISOP) connection is studied in this paper. The small-signal models and the corresponding transfer function of DBSRC and its ISOP system are constructed through the periodic averaging method, where the input voltage of one DBSRC sub-module is influenced by all phase-shift angles of other sub-modules. In order to achieve the input voltage balance of different sub-modules, a differential input voltage sharing (DIVS) control strategy is proposed. This strategy realizes the decoupling control of the output voltage regulation loop and the input voltage sharing regulation loop in the system block diagram. Compared with the traditional input voltage sharing control strategy, this strategy requires less communication data and has higher dynamic response performance. Finally, the simulation and experiments on a 12kW prototype show the correctness of DBSRC small-signal model as well as the effectiveness and superiority of DIVS control strategy.
keywords：Input series output parallel, dual bridge series resonant DC-DC converter, small-signal model, differential input voltage
中图分类号：TM46
DOI: 10.19595/j.cnki.1000-6753.tces.190570
国家重点研发计划资助项目（2016YFB1200602-20，2017YFB1200901）。
收稿日期 2019-05-14
改稿日期 2019-07-10
杨 博 男，1993年生，博士研究生，研究方向为大功率DC-DC变换器。E-mail: yangbo@mail.iee.ac.cn
葛琼璇 女，1967年生，研究员，博士生导师，研究方向为大功率电力电子变流技术、直线电机分析与控制等。E-mail: gqx@mail.iee.ac.cn（通信作者）
（编辑 陈 诚）