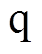 轴超前
轴超前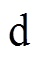 轴90°电角度,则电磁推力
轴90°电角度,则电磁推力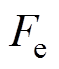 表示为
表示为摘要 为解决永磁直线同步电机(PMLSM)伺服系统位置跟踪精度易受参数变化、负载扰动、摩擦力等不确定性因素影响的问题,该文提出一种基于径向基函数(RBF)神经网络反推终端滑模控制方法。首先,建立含有不确定性的PMLSM动态数学模型。然后,采用反推终端滑模控制将系统状态在有限时间内收敛到平衡点,提高系统的响应速度;为了进一步削弱抖振现象,利用双曲正切函数与边界层厚度相结合来设计饱和函数,以取代符号函数;并且利用RBF神经网络去逼近系统中存在的不确定性,进而获得快速的跟踪性能和较强的抗扰能力。最后,实验结果表明,所提出的控制方法不仅改善了系统的跟踪性和鲁棒性,而且明显削弱了抖振问题。
关键词:永磁直线同步电机 反推终端滑模控制 径向基函数神经网络 抖振 鲁棒性
永磁直线同步电机(Permanent Magnet Linear Synchronous Motor, PMLSM)具有效率高、磨损小、精度高等优点,广泛用于机器人、数控机床和XY平台等设备,是高速度高精度设备的首选[1-3]。PMLSM省略了中间传动机械环节,负载和电机动子直接连接,进而大大地提高了机械传动的效率。然而,由于中间缓冲传动机构的简化,使机械结构间的各种摩擦力、负载扰动和参数变化等不确定因素直接作用于PMLSM动子上,这导致了控制难度的增加[4]。因此,设计强鲁棒控制器来抑制这些不确定性因素,对实现系统高速度高精度的控制性能具有十分重要的意义。
滑模控制具有强鲁棒性、收敛速度快、设计简单等优点。但在滑模控制中,通常选择一个线性滑模面,这会导致系统状态的收敛性是渐近收敛的。虽然可以通过调整滑模控制参数以使收敛速度更快,但是这种收敛只能在无限时间内实现[5]。对于高精度控制系统,快速的收敛速度是优先考虑的问题,但只有在控制输入较大时才能实现,这会导致执行器饱和。而终端滑模控制采用的是动态非线性滑模面,使系统状态能够迅速收敛,而不需要额外的控制操作[6]。然而,终端滑模控制的最大缺点是抖振现象,为解决抖振问题,国内外相关学者进行研究并取得一些成果。文献[7]采用积分终端滑模控制方法,降低抖振现象且提高了系统的收敛速度,但滑模控制律中符号函数的引入仍会影响系统的稳定性。文献[8]提出了基于反推的滑模控制方法,降低了抖振且保证了系统的鲁棒性,但当系统的切换增益过大时,系统的跟踪性能被破坏,系统稳定性得不到保证。文献[9]将自适应控制和反推滑模控制相结合,对系统的切换增益参数进行估计,抖振现象明显改善,系统跟踪性得到提高,但系统的收敛性比较慢。文献[10]采用径向基神经网络和非奇异终端滑模控制相结合的方法,来逼近系统的不确定性,避免了奇异性,但系统存在较大的扰动时,系统的稳定性被破坏。文献[11]提出了自适应非奇异快速终端滑模控制方法,利用径向基函数神经网络方法,解决了系统中复合扰动上界难以估计的问题,有效地削弱了抖振,但当系统切换增益过大时,系统的稳定性还是难以得到保证。
为此,本文设计了基于径向基函数(Radial Basis Function, RBF)神经网络反推终端滑模控制(Back- stepping Terminal Sliding Mode Control, BTSMC)方法。利用反推控制将复杂的非线性系统分解成低阶子系统,使系统对参数不确定性和外部扰动具有强鲁棒性;采用终端滑模改善系统的动态响应,使系统状态更快地收敛到平衡点;RBF神经网络用于逼近系统中的不确定性,来提高系统的跟踪精度。实验结果证实,该方法能够提高系统的控制性能。
表贴式PMLSM采用dq轴电流控制,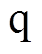 轴超前
轴超前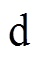 轴90°电角度,则电磁推力
轴90°电角度,则电磁推力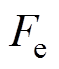 表示为
表示为
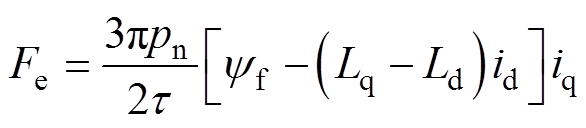 (1)
(1)式中,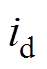 、
、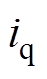 、
、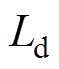 、
、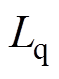 分别为
分别为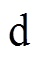 、
、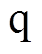 轴电流和电感;
轴电流和电感;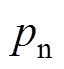 为极对数;
为极对数;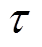 为极矩;
为极矩;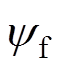 为基波磁链。
为基波磁链。
根据磁场定向原理,取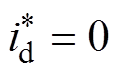 ,为了设计方便,假设电机的电感、电阻在稳态时是不变的,
,为了设计方便,假设电机的电感、电阻在稳态时是不变的,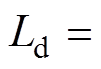
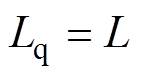 ,
,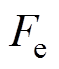 可简化为
可简化为
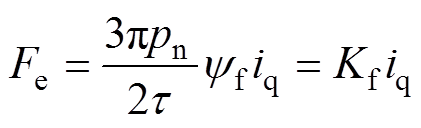 (2)
(2)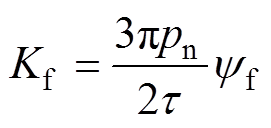 (3)
(3)
式中,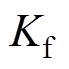 为电磁推力系数。
为电磁推力系数。
PMLSM的机械运动方程为
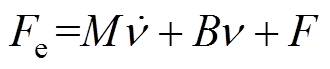 (4)
(4)式中,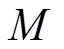 为PMLSM的动子总质量;
为PMLSM的动子总质量;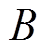 为黏滞摩擦因数;
为黏滞摩擦因数; 为动子速度;
为动子速度;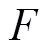 为非线性扰动,包括系统外部扰动、非线性摩擦力和电机参数变化等。
为非线性扰动,包括系统外部扰动、非线性摩擦力和电机参数变化等。
不考虑扰动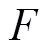 时,动态方程为
时,动态方程为
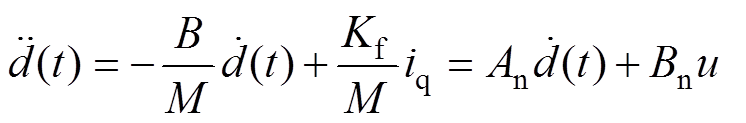 (5)
(5)式中,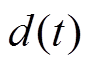 为动子位置;
为动子位置;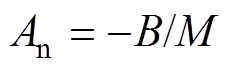 ;
;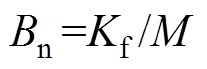 ;
;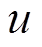 为控制器输出,
为控制器输出,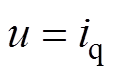 ,即推力电流。
,即推力电流。
考虑扰动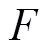 时,动态方程为
时,动态方程为
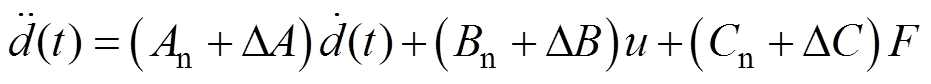
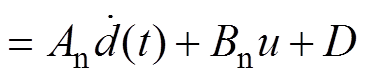 (6)
(6)
式中,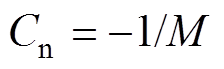 ;
;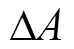 、
、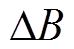 和
和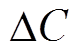 分别为系统参数
分别为系统参数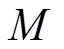 和
和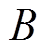 所引起的不确定量。
所引起的不确定量。
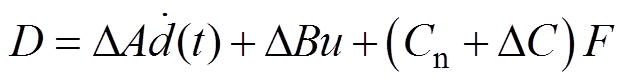 (7)
(7)这里,假设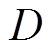 有界,即
有界,即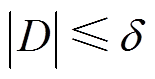 ,
,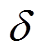 为不确定性总和
为不确定性总和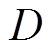 的上界,为一正常数。
的上界,为一正常数。
基于RBF神经网络的PMLSM反推终端滑模控制系统框图如图1所示,采用BTSMC和RBF神经网络相结合的方法设计PMLSM伺服控制系统。
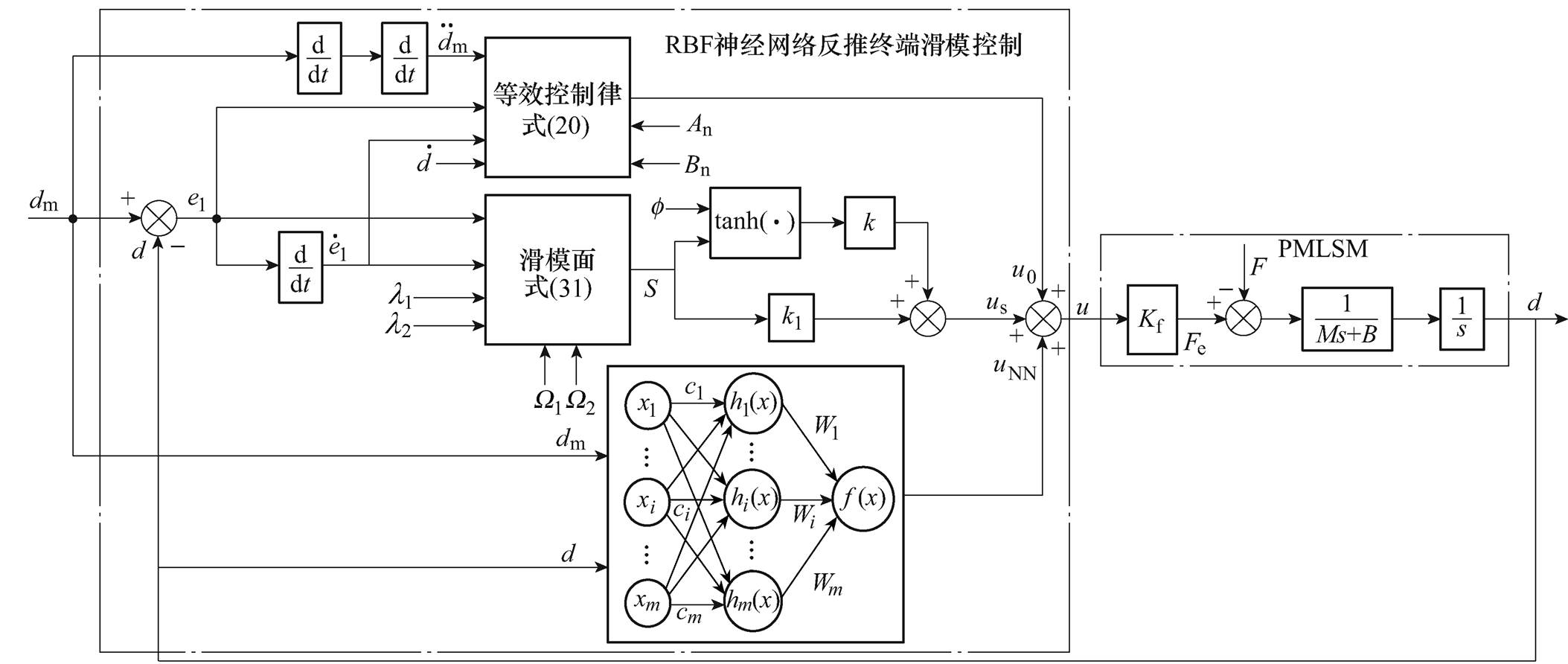
图1 基于RBF神经网络的PMLSM反推终端滑模控制系统框图
Fig.1 Block diagram of backstepping terminal sliding mode control system based on RBF neural network for PMLSM
定义位置跟踪误差为
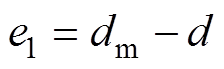 (8)
(8)式中,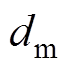 、
、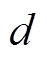 分别为参考位置输入和实际位置输出。
分别为参考位置输入和实际位置输出。
定义稳定函数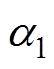 为
为
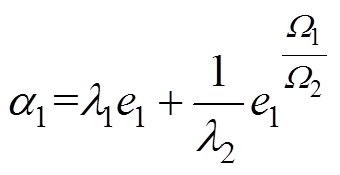 (9)
(9)式中, 、
、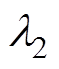 、
、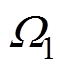 、
、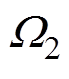 (
(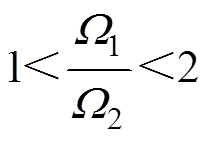 )都是正奇数。
)都是正奇数。
定义速度误差为
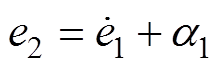 (10)
(10)式中,速度的跟踪误差随稳定函数的增大而增大。
第一个李雅普诺夫函数为
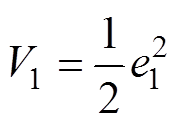 (11)
(11)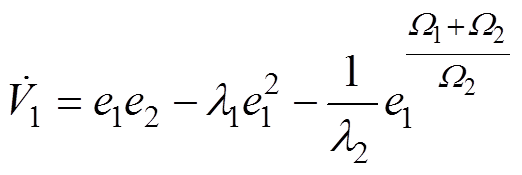 (12)
(12)
由式(6)和式(10)得
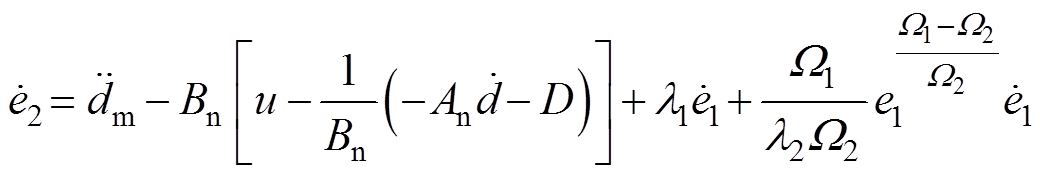 (13)
(13)第二个李雅普诺夫函数为
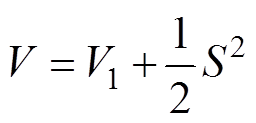 (14)
(14)
下面给出了跟踪误差从到达阶段到滑动阶段的满足条件,即可达条件。
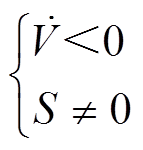 (15)
(15)滑模面为
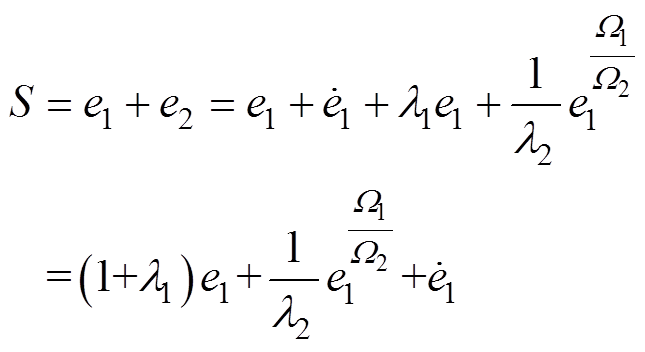 (16)
(16)
对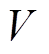 求导得
求导得
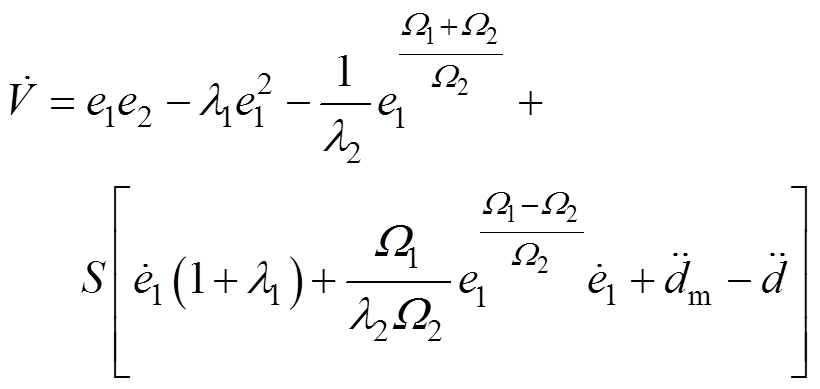 (17)
(17)总控制律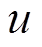 为
为
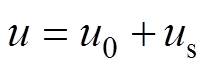 (18)
(18)
将式(18)代入式(17)得
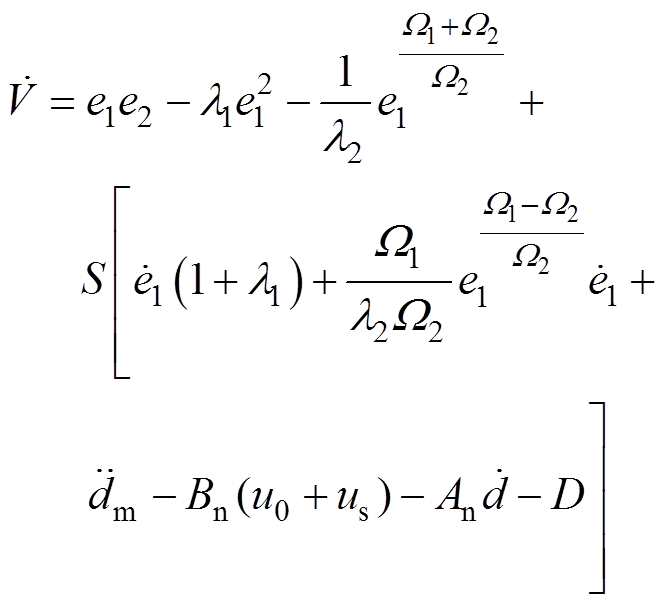 (19)
(19)在不考虑扰动和不确定因素的情况下,结合式(5)对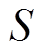 求导并令
求导并令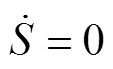 时,得到等效控制律
时,得到等效控制律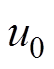 为
为
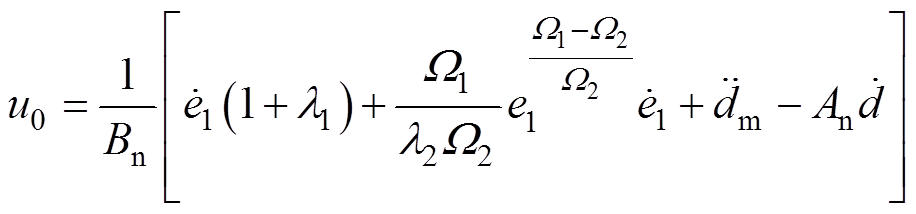 (20)
(20)
当等效控制律不能提供理想的跟踪性能时,需要一个额外的控制去消除不可预测的扰动和不确定性,直到跟踪误差逐渐消失,意味着滑模面变得稳定。
为了证明所设计控制器的稳定性,采用李雅普诺夫定理。由式(19)和式(20)得
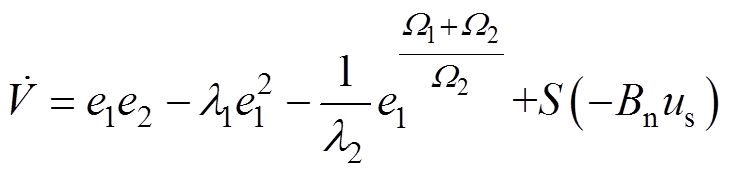 (21)
(21)为了满足李雅普诺夫稳定性条件,切换控制律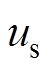 为
为
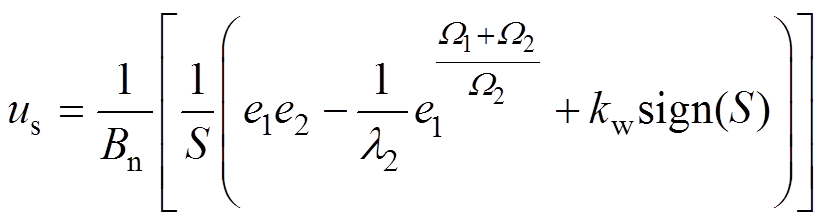 (22)
(22)
将式(22)代入式(19)得
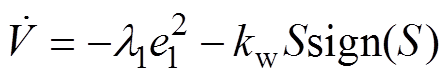 (23)
(23)式中,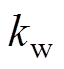 为切换增益。
为切换增益。
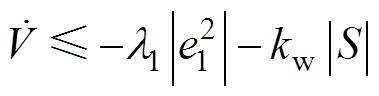 (24)
(24)
式中,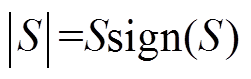 。由于符号函数
。由于符号函数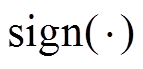 的不连续性会对控制输入信号产生抖振影响,因此选用双曲正切函数
的不连续性会对控制输入信号产生抖振影响,因此选用双曲正切函数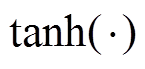 。
。
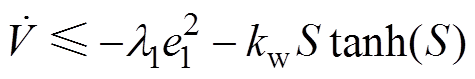 (25)
(25)式中,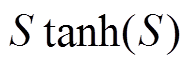 这一项总是正数(不管
这一项总是正数(不管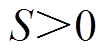 或
或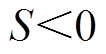 ,则
,则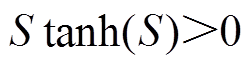 总成立)。
总成立)。
改进后的切换控制律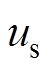 为
为
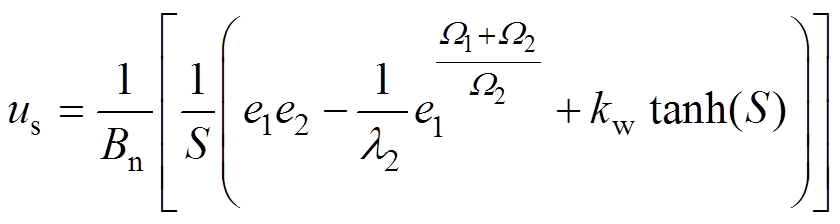 (26)
(26)为了消除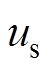 中的不连续部分,设计了带有边界层的饱和函数为
中的不连续部分,设计了带有边界层的饱和函数为
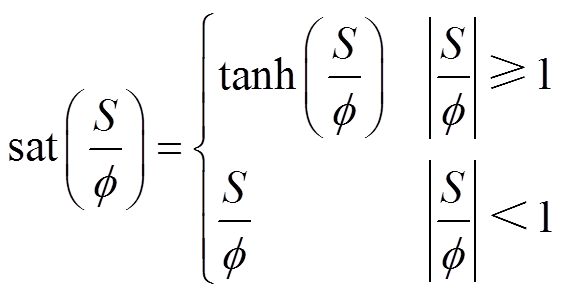 (27)
(27)
式中,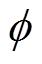 为边界层厚度。
为边界层厚度。
因此,切换控制律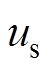 为
为
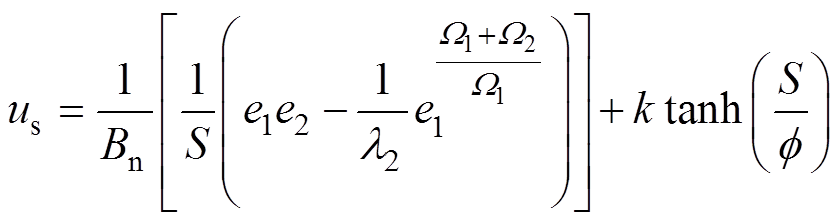 (28)
(28)式中,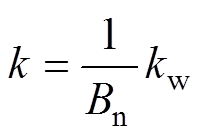 。
。
PMLSM的数学模型已知,故采用反推终端滑模控制使系统的状态输出直接跟踪期望轨迹。但由于存在较大建模不确定性,需要较大的切换增益,这就造成了抖振。为此,采用RBF神经网络来估计系统中的不确定性,进而消除不确定性对系统的影响。
定义逼近函数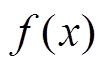 为
为
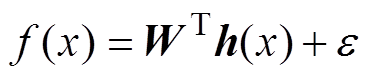 (29)
(29)式中,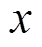 为网络的输入;
为网络的输入;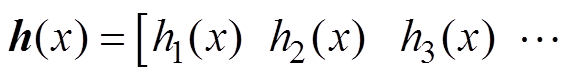
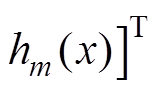 为网络的高斯径向基函数输出;
为网络的高斯径向基函数输出;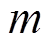 为网络隐含层第
为网络隐含层第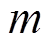 个节点;
个节点;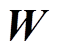 为理想权值;
为理想权值;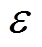 为逼近误差。
为逼近误差。
RBF函数定义为
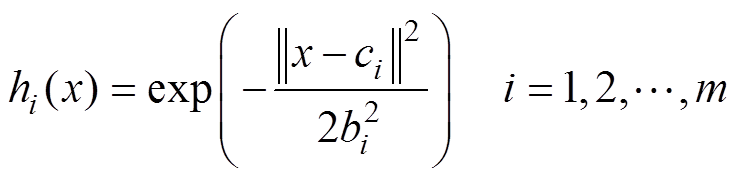 (30)
(30)式中,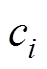 为中心;
为中心;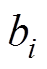 为第
为第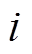 个神经元的宽度。
个神经元的宽度。
将式(16)改写为
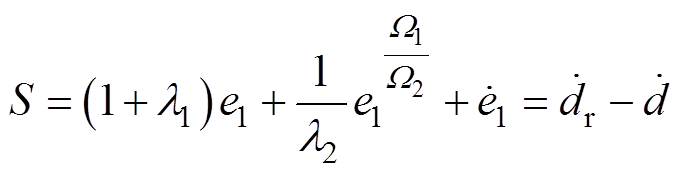 (31)
(31)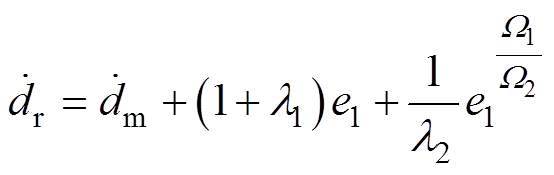 (32)
(32)
由式(6)和式(31)得
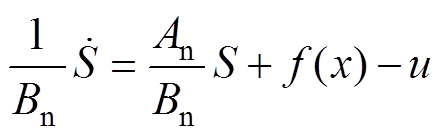 (33)
(33)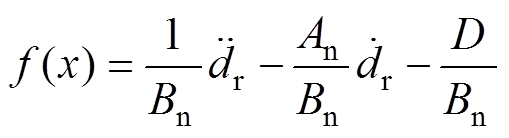 (34)
(34)
网络输入取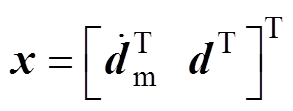 ,则网络输出为
,则网络输出为
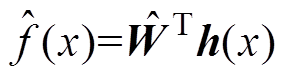 (35)
(35)式中,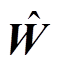 为神经网络调整律。
为神经网络调整律。
将式(33)变为
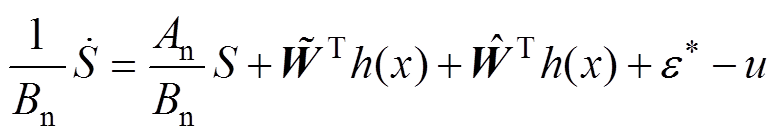 (36)
(36)式中,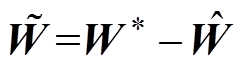 。
。
设计总控制律为
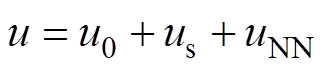 (37)
(37)其中
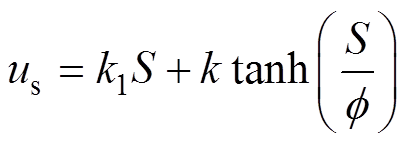 (38)
(38)
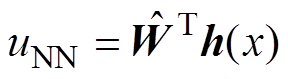 (39)
(39)神经网络参数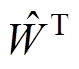 的自适应律为
的自适应律为
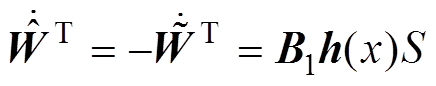 (40)
(40)
式中,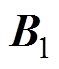 为正定矩阵。
为正定矩阵。
建立李雅普诺夫函数,有
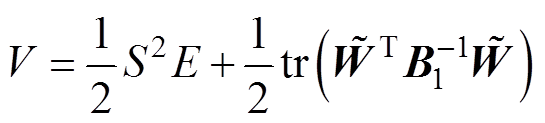 (41)
(41)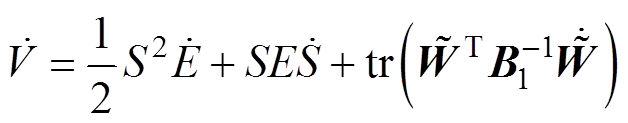 (42)
(42)
式中,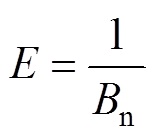 。
。
将式(36)代入式(42)得
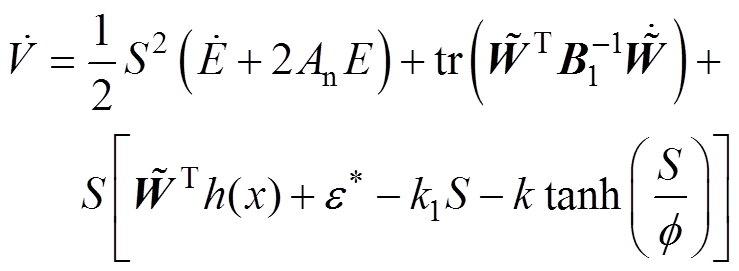 (43)
(43)由于式(43)中的第一项变为0,即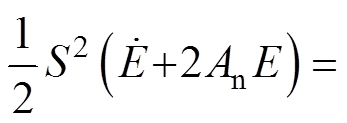 0。通过式(25)和式(35)得
0。通过式(25)和式(35)得
 (44)
(44)
式中,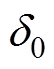 为
为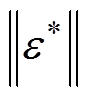 的上界。
的上界。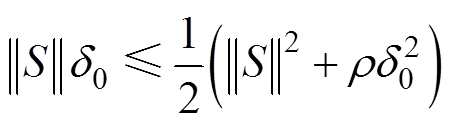 ,在这里
,在这里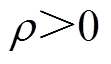 ,因此
,因此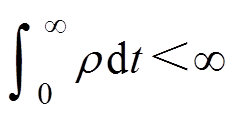 。由此得
。由此得
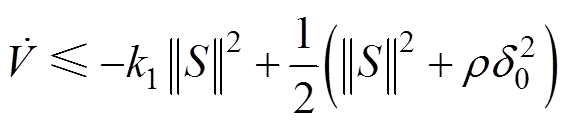 (45)
(45)从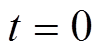 到
到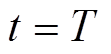 对式(45)两边同时积分,得
对式(45)两边同时积分,得
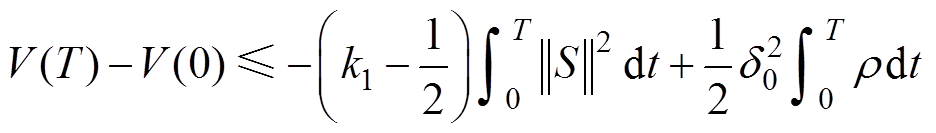 (46)
(46)
由于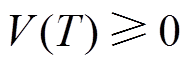 和
和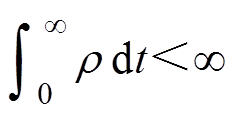 成立,则
成立,则
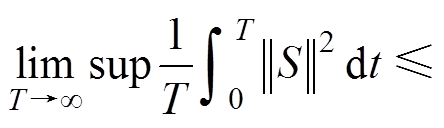
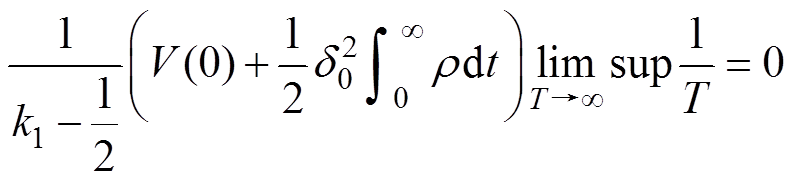 (47)
(47)
从式(46)和式(47)可知,当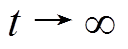 时,得到
时,得到 ,表明系统状态已运动到滑模面上。由此从式(31)得出,当
,表明系统状态已运动到滑模面上。由此从式(31)得出,当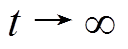 时,位置和速度的跟踪误差渐近收敛到零。因此,RBF神经网络BTSMC方法满足稳定性判据。
时,位置和速度的跟踪误差渐近收敛到零。因此,RBF神经网络BTSMC方法满足稳定性判据。
基于DSP的PMLSM控制系统结构如图2所示。PMLSM型号为美国Kollmorgen公司生产的IC11- 050A1,最大行程260mm,选用TMS320F2812A的DSP作为核心控制单元,整流器和IPM组成的主电路作为PMLSM的供电电路。电流传感器和直线光栅尺(SR-1-75-2020J3-5F05E型号的直线光栅尺,其长度为750mm,分辨率为1mm)作为检测电路,将检测到的信号传送给DSP进行实时监测处理。一旦系统发生故障,DSP就会立即产生故障保护信号进行处理。基于DSP的PMLSM控制系统实验装置如图3所示。
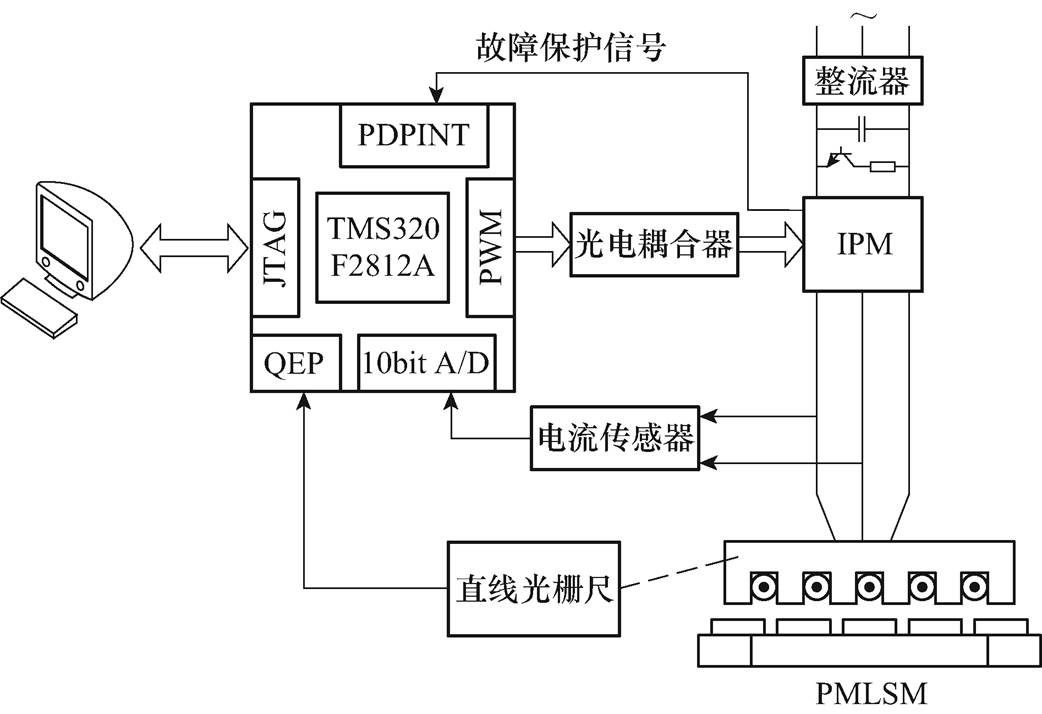
图2 基于DSP的PMLSM控制系统结构
Fig.2 Structure diagram of PMLSM control system based on DSP

图3 基于DSP的PMLSM控制系统实验装置
Fig.3 Experimental device diagram of PMLSM control system based on DSP
实验中所用PMLSM的参数为: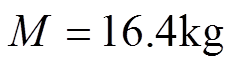 ,
,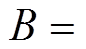
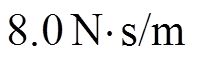 ,
,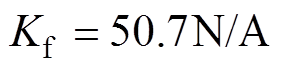 ,
,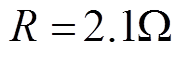 ,
,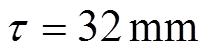 ,
,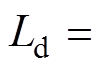
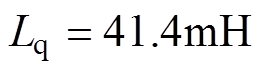 ,
,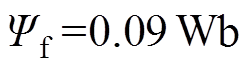 。实验中对系统参数进行多次调试以获得最优的系统性能。BTSMC的参数为:
。实验中对系统参数进行多次调试以获得最优的系统性能。BTSMC的参数为: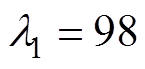 ,
,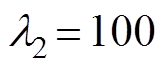 ,
,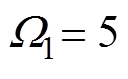 ,
,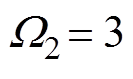 ,
,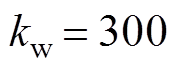 ,
,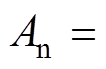
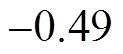 ,
, ,
,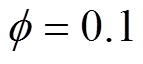 。RBF神经网络BTSMC的参数为:
。RBF神经网络BTSMC的参数为: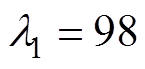 ,
,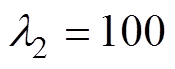 ,
,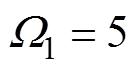 ,
,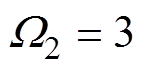 ,
,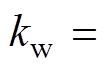
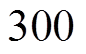 ,
,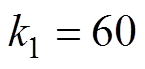 ,
,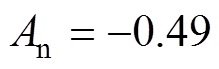 ,
, ,
,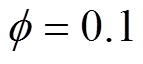 。
。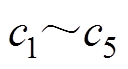 取值为
取值为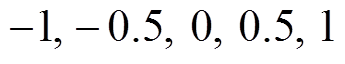 。
。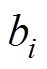 取值为0.5。三层神经元数量分别为2、5和1。
取值为0.5。三层神经元数量分别为2、5和1。
分别对采用BTSMC和RBF神经网络BTSMC的PMLSM控制系统进行实验研究,来验证所提出的控制方案的有效性。首先,给系统输入两种不同的信号和进行三组实验:①幅值为1mm的阶跃信号,在0.5s给系统突加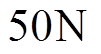 的恒定负载扰动(负载扰动占负载比例为40%);②幅值为1mm的阶跃信号,在0.5s给系统突加非周期性变化扰动;③幅值为1mm,频率为0.16Hz的正弦信号;④幅值为1mm,频率为100Hz的正弦信号。然后,通过实验验证系统的跟踪性和鲁棒性。
的恒定负载扰动(负载扰动占负载比例为40%);②幅值为1mm的阶跃信号,在0.5s给系统突加非周期性变化扰动;③幅值为1mm,频率为0.16Hz的正弦信号;④幅值为1mm,频率为100Hz的正弦信号。然后,通过实验验证系统的跟踪性和鲁棒性。
实验一:在情况①下,两种控制方法的系统位置跟踪曲线如图4a所示。由图可知,虽然RBF神经网络BTSMC有一定的超调量,但是它比BTSMC先到达平衡点,然后在0.07s时使系统稳定在平衡状态。在0.5s系统突加外部扰动,其中RBF神经网络BTSMC偏离平衡状态的幅度小。系统位置误差曲线如图4b所示,RBF神经网络BTSMC的位置误差更小,响应速度更快。在0.5s突加扰动后,采用RBF神经网络BTSMC方法的位置跟踪误差变化小,表明其抗干扰能力更强。两种控制方法的推力曲线和动子速度曲线分别如图4c和图4d、图4e和图4f所示,电机起动瞬间,两种控制方法的电磁推力都比较大,很快就恢复到稳定状态。在0.5s突加扰动情况下,电磁推力也迅速增加,此时BTSMC方法的速度曲线出现了短时间的波动,而RBF神经网络BTSMC方法的速度曲线依然保持稳定状态。
实验二:在情况②下,系统突加的变负载扰动曲线如图4g所示,所加扰动是非周期性扰动,更贴近于工程实际状况。图4h是系统位置跟踪曲线,随着负载变化,系统的位置跟踪曲线也在时刻变化,两种控制方法下位置跟踪曲线偏离期望位置轨迹的程度不同。采用RBF神经网络BTSMC方法的跟踪性能更好,鲁棒性更强。系统的位置误差曲线如图4i所示,RBF神经网络BTSMC的跟踪误差小,且随着负载扰动变化,跟踪误差趋近零的响应速度比BTSMC更快。
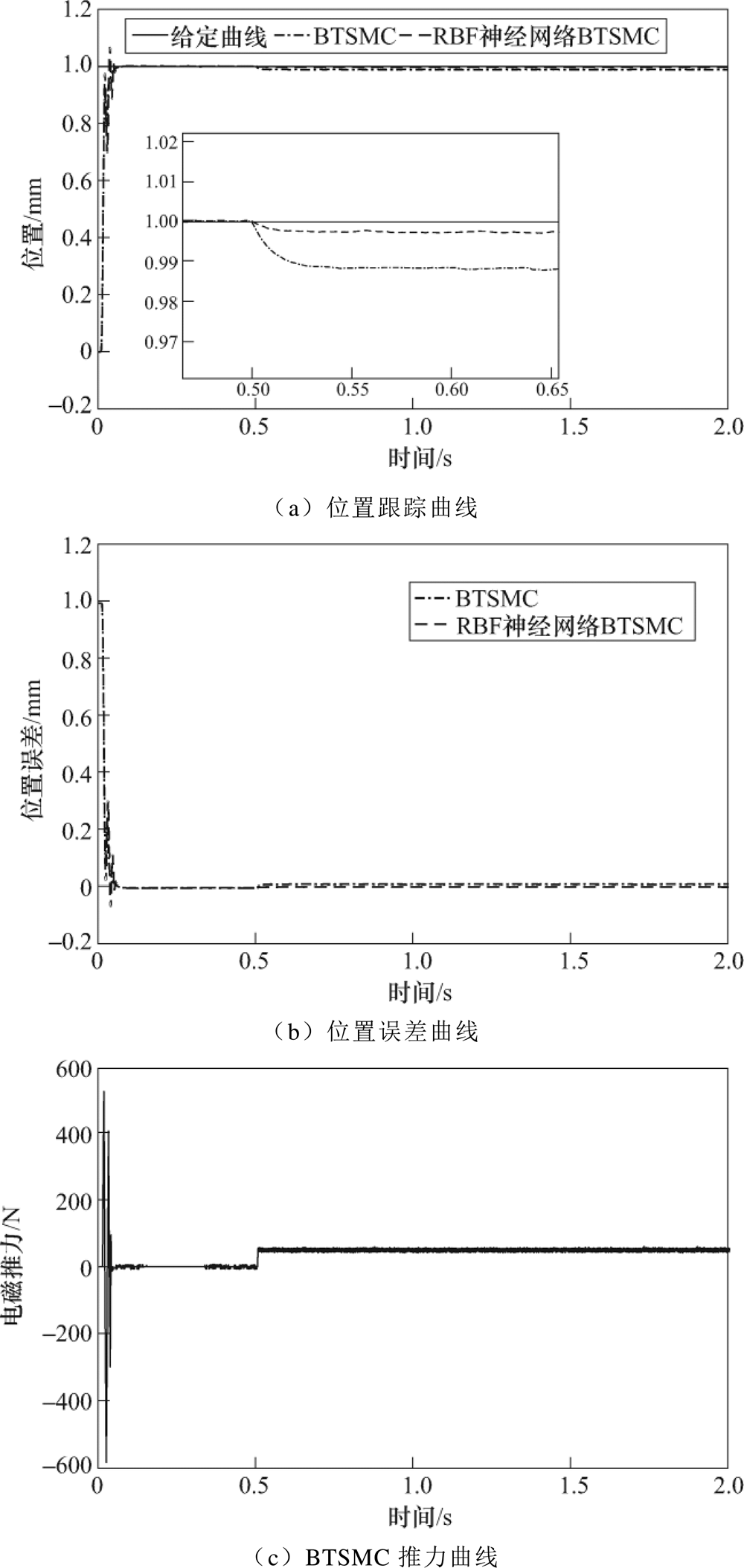
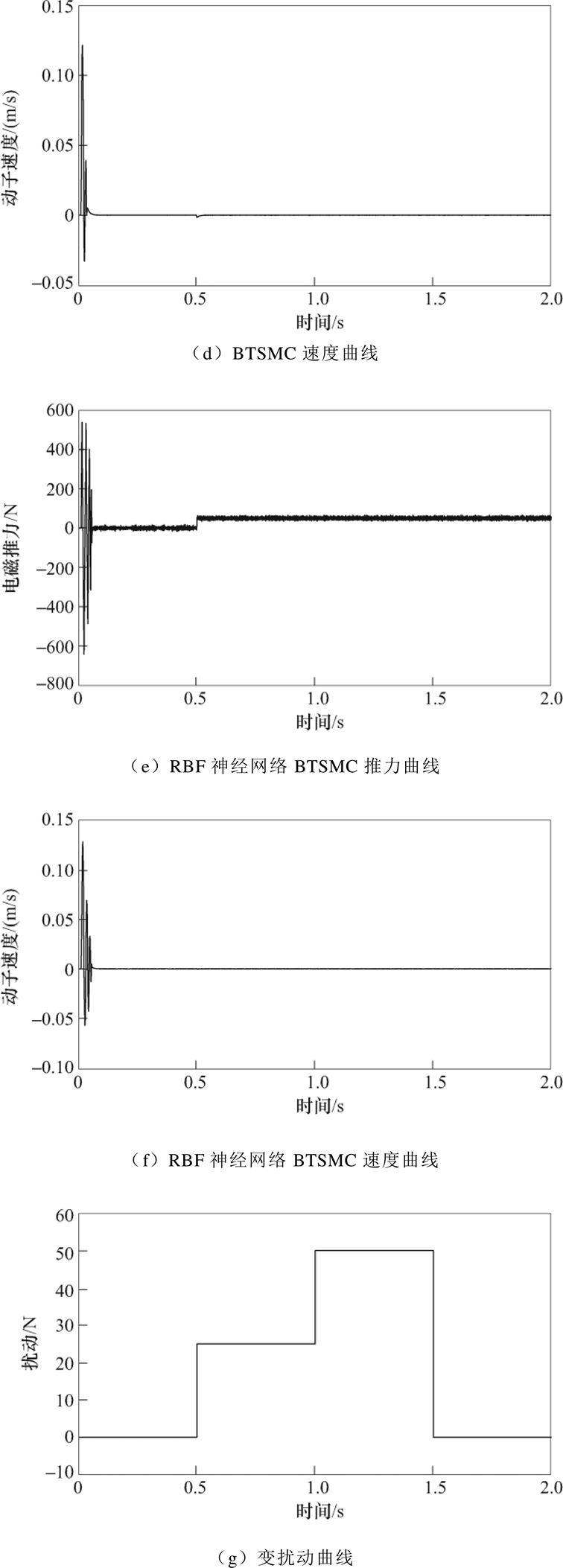
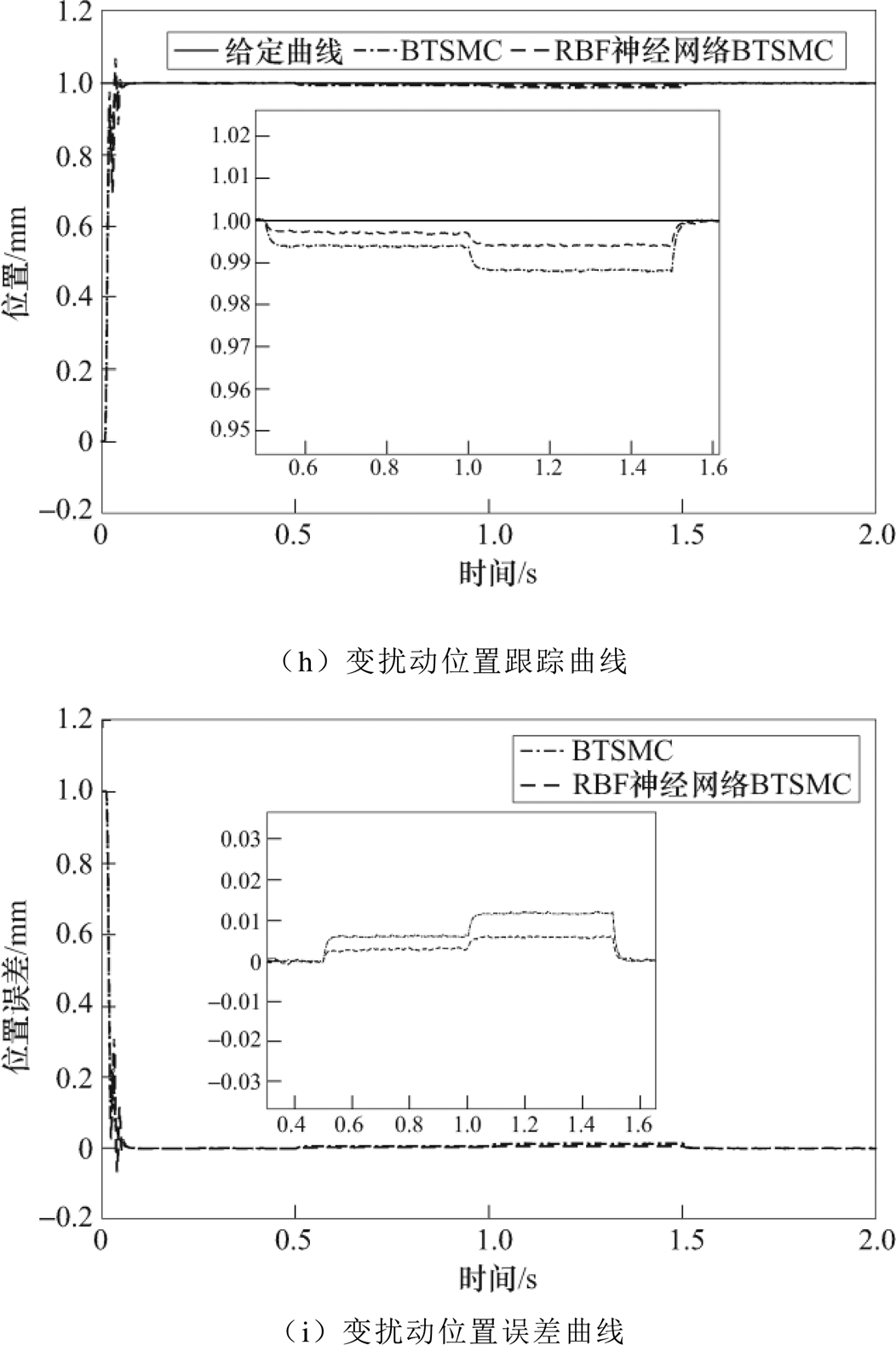
图4 阶跃输入的BTSMC和RBF神经网络BTSMC系统位置曲线
Fig.4 Position curves of BTSMC and RBF neural network BTSMC system for step input
实验三:在情况③下,系统位置跟踪曲线如图5a所示,从第一个波峰的局部放大图可以看出,采用RBF神经网络BTSMC方法的位置跟踪曲线基本上和给定信号曲线重合,而BTSMC的位置跟踪曲线在给定信号曲线上下浮动。图5b和图5c是其系统位置跟踪误差曲线,BTSMC的位置跟踪误差在电机刚起动运行那一瞬间幅值达到了将近30mm,在之后的动态稳定过程中最大位置跟踪误差约为9mm左右,最终稳定在5mm左右,且抖振现象明显。而RBF神经网络BTSMC的跟踪误差在电机刚起动运行一瞬间幅值约25mm,在之后的动态稳定过程中最大跟踪误差约为4mm,最终稳定在2mm,且抖振现象明显得到改善。与BTSMC相比,RBF神经网络BTSMC能更精确地逼近系统中的不确定性,提高系统的跟踪精度。
实验四:在情况④下,两种控制方法的位置跟踪曲线如图5d所示。图5e是其位置跟踪误差曲线,与实验三相比,随着给定正弦信号频率的增加,两种控制方法下的跟踪误差也在相应的增加,BTSMC的误差稳定在9mm左右,RBF神经网络BTSMC的误差稳定在5mm附近,具有更高的跟踪精度。

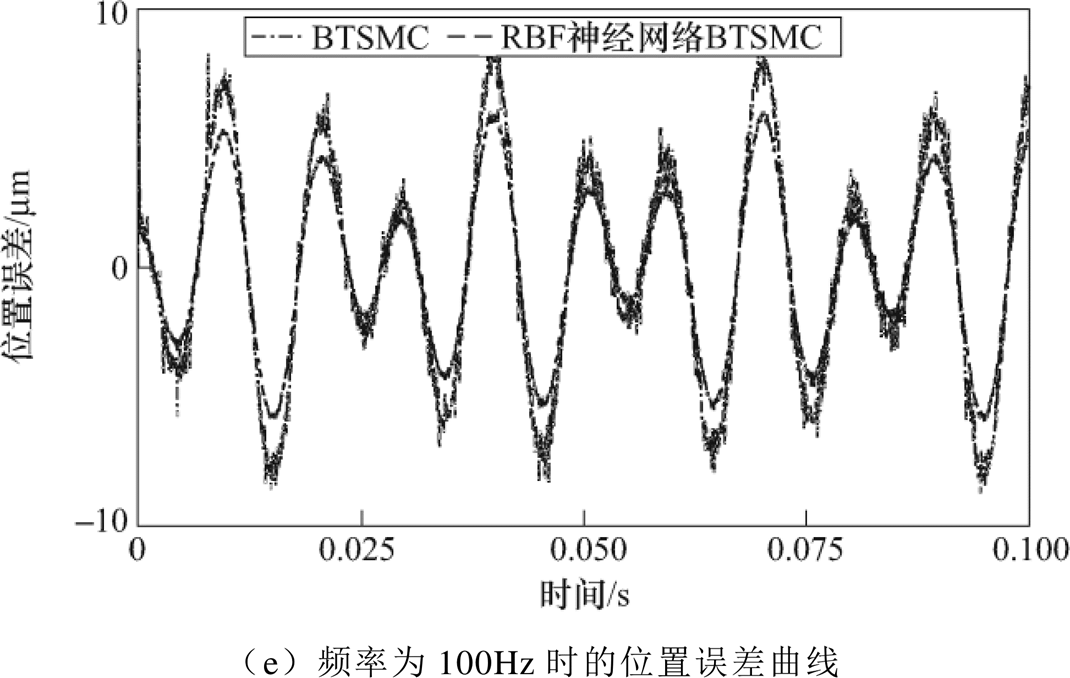
图5 正弦波输入的BTSMC和RBF神经网络BTSMC系统位置曲线
Fig.5 Position curves of BTSMC and RBF neural network BTSMC system for sinusoidal input
通过分析PMLSM伺服系统存在参数变化和负载扰动等不确定性因素的问题,设计了BTSMC和RBF神经网络BTSMC两种控制方案。在BTSMC控制方案的基础上引入了RBF神经网络,进一步提高了系统的跟踪精度。考虑了两种不同输入和外部扰动的情况,研究了所设计的控制器的控制性能。实验结果表明,与BTSMC相比,RBF神经网络BTSMC明显提高了系统的位置跟踪精度并保证了系统鲁棒性。
参考文献
[1] Yang Xiaojun, Lu Dun, Zhang Jun, et al. Dynamic electromechanical coupling resulting from the air-gap fluctuation of the linear motor in machine tools[J]. International Journal of Machine Tools & Manu- facture, 2015, 94: 100-108.
[2] 智淑亚, 吴洪兵. 数控进给伺服系统摩擦补偿控制仿真[J]. 沈阳工业大学学报, 2019, 41(4): 361-365.
Zhi Shuya, Wu Hongbing. Simulation of friction compensation control of NC feed servo system[J]. Journal of Shenyang University of Technology, 2019, 41(4): 361-365.
[3] 朱国昕, 雷鸣凯, 赵希梅. 永磁同步电机伺服系统自适应迭代学习控制[J]. 沈阳工业大学学报, 2018, 40(1): 6-11.
Zhu Guoxin, Lei Mingkai, Zhao Ximei. Adaptive iterative learning control for permanent magnet synchronous motor servo system[J]. Journal of Shenyang University of Technology, 2018, 40(1): 6-11.
[4] 赵希梅, 原浩, 朱文彬. 基于小波神经网络和非线性扰动观测器的直线伺服系统控制[J]. 电工技术学报, 2019, 34(19): 3989-3996.
Zhao Ximei, Yuan Hao, Zhu Wenbin. Control of linear servo system based on wavelet neural network and nonlinear disturbance observer[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 3989-3996.
[5] 原浩, 赵希梅. 基于积分滑模的永磁直线同步电动机直接推力控制[J]. 电工技术学报, 2019, 34(3): 483-488.
Yuan Hao, Zhao Ximei. Direct thrust force control based on integral sliding mode for permanent magnet linear synchronous motor[J]. Transactions of China Electrotechnical Society, 2019, 34(3): 483-488.
[6] 张博, 齐蓉, 林辉. 激光切割永磁直线伺服系统的反演滑模控制[J]. 电工技术学报, 2018, 33(3): 642- 651.
Zhang Bo, Qi Rong, Lin Hui. Back-stepping sliding mode control of laser cutting permanent magnet linear servo control system[J]. Transactions of China Electrotechnical Society, 2018, 33(3): 642-651.
[7] Gao Jianguo, Liu Yuchao, Zhou Jun. Integral termi- nal sliding mode control for nonlinear systems[J]. Journal of Systems Engineering and Electronics, 2018, 29(3): 571-579.
[8] Nadda S, Swarup A. Development of backstepping based sliding mode control for a quadrotor[C]//IEEE 10th International Colloquium on Signal Processing & ITS Applications, Kuala Lumpur, Malaysia, 2014: 10-13.
[9] Guan Lirong, Gong Min, Sun Shengbing. Adaptive backstepping sliding mode robust tracking control for permanent magnet linear synchronous motor[J]. Electric Drive, 2009, 15(2): 124-133.
[10] Tran M D, Kang H J. A novel adaptive finite-time tracking control for robotic manipulators using nonsingular terminal sliding mode and RBF neural networks[J]. International Journal of Precision Engineering and Manufacturing, 2016, 17(7): 863- 870.
[11] Liang Bo, Zhu Yuqing, Li Yuren, et al. Adaptive nonsingular fast terminal sliding mode control for braking systems with electro-mechanical actuators based on radial basis function[J]. Energies, 2017, 10(10): 1637-1651.
Backstepping Terminal Sliding Mode Control Based on Radial Basis Function Neural Network for Permanent Magnet Linear Synchronous Motor
Abstract The position tracking accuracy of permanent magnet linear synchronous motor (PMLSM) servo system is susceptible to parameter variation, load disturbance, friction and other uncertain factors. Therefore, a backstepping terminal sliding mode control method based on radial basis function (RBF) neural network is proposed. Firstly, the PMLSM dynamic mathematical model with uncertainty is established. Then, the state of the system converges to the equilibrium point in a finite time and the response speed of the system is improved by using the backstepping terminal sliding mode control. In order to further weaken chattering phenomenon, the saturation function is designed combined the hyperbolic tangent function with boundary layer thickness to replace the signum function. Moreover, RBF neural network is used to approximate the uncertainties in the system, and then fast-tracking performance and strong immunity ability are obtained. Finally, the experimental results show that the proposed control method not only improves the tracking and robustness of the system, but also significantly weakens the chattering problem.
keywords:Permanent magnet linear synchronous motor, backstepping terminal sliding mode control, radial basis function (RBF) neural network, chattering, robustness
中图分类号:TP273; TM351
DOI: 10.19595/j.cnki.1000-6753.tces.190308
辽宁省自然科学基金计划重点项目(20170540677)和辽宁省教育厅科学技术研究项目(LQGD2017025)资助。
收稿日期2019-03-25
改稿日期 2019-09-10
付东学 男,1992年生,博士研究生,研究方向为电机控制、智能控制。E-mail: 18629974521@163.com
赵希梅 女,1979年生,教授,博士生导师,研究方向为电机控制、机器人控制、智能控制等。E-mail: zhaoxm_sut@163.com(通信作者)
(编辑 赵 鹏)