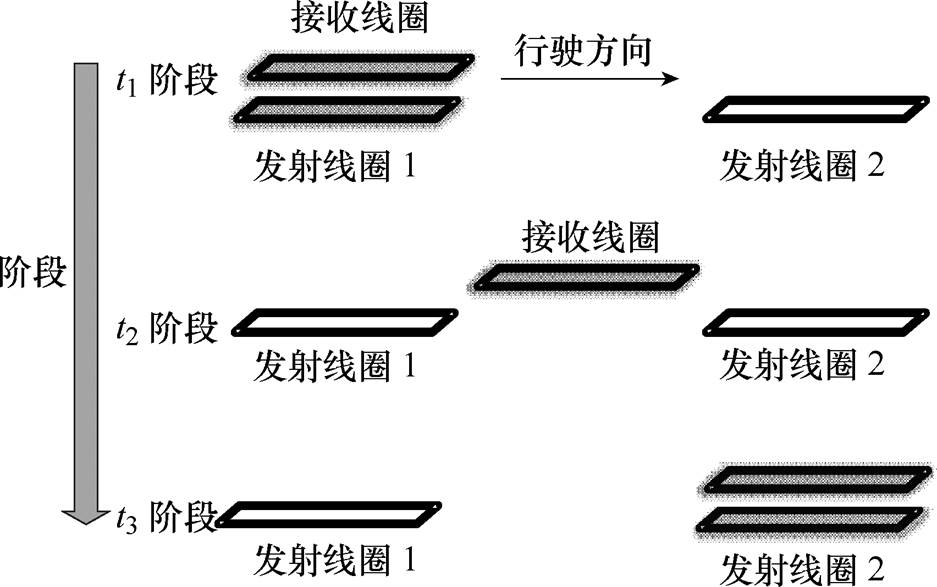
图1 最小动态耦合模型
Fig.1 Minimum dynamic coupling model
摘要 在动态无线供电系统中,多发射线圈交替工作是提高电动汽车动态无线充电系统效率的有效途径。该文首先推导动态耦合过程的互感表达式,得到互感随位移而变化,进而影响传输功率的结论。其次,为提高输电系统的稳定性,减小由于发射端切换而导致的传输功率降低,对最小动态耦合单元的工作全周期进行分析,并通过有限元仿真软件设计了三组仿真进行对比,证明了双线圈同时供电方案相比轮流交替供电在提高互感和接收功率方面的有效性,并且提出了在0.1~0.3m这一最佳区间内实行双线圈同时供电,而在最佳区间范围之外实行单线圈供电的供电模式。最后,基于所提出的供电方案搭建实验平台进行了测试。结果表明,在最佳区间内实现第一、二发射线圈同时供电可以显著提高无线电力系统的稳定性,减小接收功率的降低。
关键词:电动汽车 动态无线充电 供电模式 最佳区间
电动汽车静态无线充电技术存在停车后充电、单次充电时间长、充电频繁以及续航里程短等问题,导致用户体验性和便利性较差[1-5]。为此,一种基于多初级绕组并联方式的动态无线充电(Dynamic Wireless Charging, DWC)方法被提出,采用发射单元单独交替供电方式,工作过程中只有距离移动受电体最近的线圈单元开启。该方法不但可以降低系统损耗,还极大程度地减小了漏磁[6-10]。
然而,受电体采用DWC技术供电,电能收发端相对位置实时变化,实际工况环境具有不可控性,能量传输稳定性下降[11-15]。文献[6-9]通过建立磁耦合谐振式无线电能传输系统的互感模型,指出收发线圈间相对位置变化所引起功效波动的本质原因是互感发生变化。为提高切换前后供电系统的稳定性,文献[7]提出基于Buck变换器和二次侧半控整流器的双边控制策略,但此方案需要给电动汽车配备超级电容,超级电容会占据车内大量空间,使得电动汽车重量增加,成本提高。文献[10]提出一种基于能量自由振荡模式的电动汽车无线供电导轨切换方法,实现了供电导轨的软切换,但并未明确切换时刻。文献[11]提出一种新型的初级线圈可切换的三相无线供电平台系统,可有效地根据负载位置选择开通合适的初级线圈为负载供电,但其设计方式过于繁琐,使得操作复杂。除此之外,文献[12]从控制算法的角度提出一种在满足负载功率需求条件下的系统效率最优的功率分配策略。文献[16-17]则从耦合结构角度分析影响功率和效率的扰动因素。
本文针对移动受电体动态供电中,由于发射线圈切换导致功率降低的问题展开研究。首先,利用电路理论得到接收功率降低的本质原因是由于收发线圈位置变化而导致的互感下降,并推导出了互感关于受电体位移距离的解析表达式。其次,为了减小由于发射端切换而导致的接收功率波动,提高输电系统的稳定性,分三个阶段对动态磁场耦合全周期进行供电模式分析,提出了接收端运行至两发射线圈中点处双线圈同时供电模式,并通过三组仿真分别验证了理论推导的正确性以及与其他供电模式进行对比分析确定第二个发射线圈的导通时间。最后,通过实验验证了所提供电模式的有效性。
在动态无线充电系统中,分段导轨供电模式具有提高能量传输效率、降低电磁辐射、成本低等优点,成为目前各个科研机构的研究热点[18]。分段导轨供电模式下,双发射-单接收系统可反映动态磁耦合过程中每个时间点的耦合状态,因而可作为最小动态耦合模型进行问题研究,如图1所示。

图1 最小动态耦合模型
Fig.1 Minimum dynamic coupling model
t1阶段,受电体刚进入无线充电区域,高频电源接收到开启信号,双发射系统开始工作,此时受电体主要依靠第一个发射单元的电磁能量工作。t2阶段,受电体在两发射单元之间运行,此时有两种供电模式:双发射系统的两个发射单元同时为受电体提供能量和轮流交替为受电体供给能量。t3阶段,受电体离开双发射系统,此时主要由第二个发射单元供给能量,电源收到关闭信号,停止工作。
本文以t1~t3三个阶段为动态耦合全周期进行分析,建立如图2所示的双发射-单接收系统电路模型。

图2 双发射-单接收电路模型
Fig.2 Dual transmit-single receive circuit model
图2中,V0、Rs为工频电源电压与内阻;Us为高频逆变电源的电压;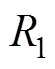 、
、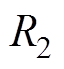 和
和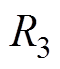 ,
,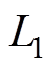 、
、 和
和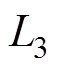 ,
,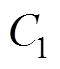 、
、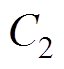 和
和 ,分别为发射端与接收端线圈等效电阻、电感和电容;M3为发射线圈间互感,M1和M2分别为发射线圈与接收线圈间的互感;ZL为接收侧等效阻抗;I1、I2和IL分别假设为流过发射端与接收端的电流,且为顺时针方向。
,分别为发射端与接收端线圈等效电阻、电感和电容;M3为发射线圈间互感,M1和M2分别为发射线圈与接收线圈间的互感;ZL为接收侧等效阻抗;I1、I2和IL分别假设为流过发射端与接收端的电流,且为顺时针方向。
根据基尔霍夫电压定律和欧姆定律,可列出相量形式的状态变量方程为
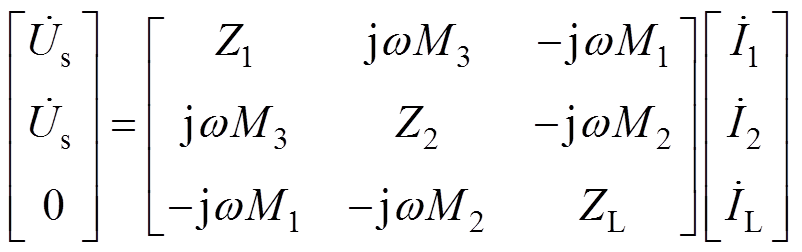 (1)
(1)式中,Z1和Z2为能量发射端两回路的等效阻抗。
由于两发射线圈处于同一水平面且相距较远,导致两者耦合程度极低,因此,忽略M3。系统发生谐振时,Z1=R1,Z2=R2,ZL=RL,得到负载接收功率表达式为
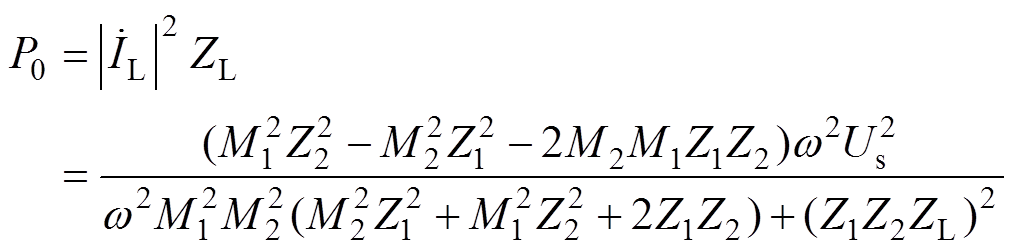 (2)
(2)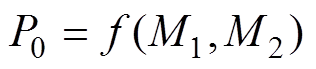 (3)
(3)
在特定工作频率和特定负载下,系统输出功率解析式中除了变量M1和M2实时变化外,角频率和等效电阻等参数均为恒定值。因此,传输功率只与收发端间互感有关,见式(3)。因而,要探究动态耦合全周期内接收功率变化规律,则需对动态耦合全周期三个阶段的互感进行分析。
首先推导任意空间位置线圈间互感表达式。由于动态耦合系统收发端均采用平面矩形线圈结构,因此可先计算出每条边之间的互感,然后求和即可得到两平面矩形线圈之间的互感。根据针对互感计算的聂以曼公式,有


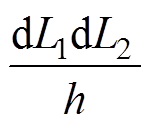 (4)
(4)式中,M为收发线圈之间互感;m0为真空磁导率;h为收发线圈之间距离;dL1dL2为所对应收发线圈之间无限小的单元,可展开为
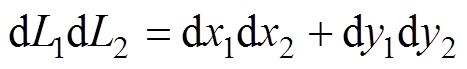 (5)
(5)
假设dL1单元中任一点的坐标为(x1, y1, 0),dL2单元中任一点的坐标为(x2, y2, z2),则收发线圈之间距离h为
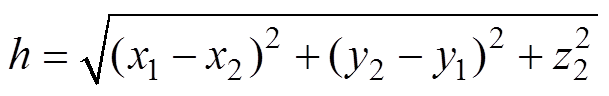 (6)
(6)设发射线圈第i条边两端点为(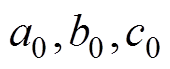 )和(
)和(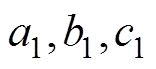 ),接收线圈第j条边两端点为(
),接收线圈第j条边两端点为(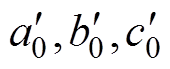 )和(
)和(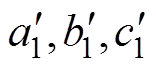 )。此时发射线圈第i条边与接收线圈第j条边之间的互感Mij表达式为
)。此时发射线圈第i条边与接收线圈第j条边之间的互感Mij表达式为
 (7)
(7)
收发线圈之间总互感M1即为任意两边互感之和,有
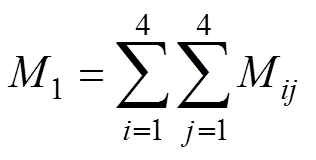 (8)
(8)由法拉第电磁感应定律可知,相互垂直的两通电导线互感为0,即
M12=M14=M21=M23=M32=M34=M41=M43=0 (9)
因此,收发线圈间互感值M1为
M1=M11+M13+M22+M24+M31+M33+M42+M44(10)
下面对双发射-单接收动态耦合系统进行建模分析,如图3所示。a为矩形线圈边长,h为传输距离,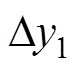 为接收线圈相对于发射线圈1的移动距离。
为接收线圈相对于发射线圈1的移动距离。
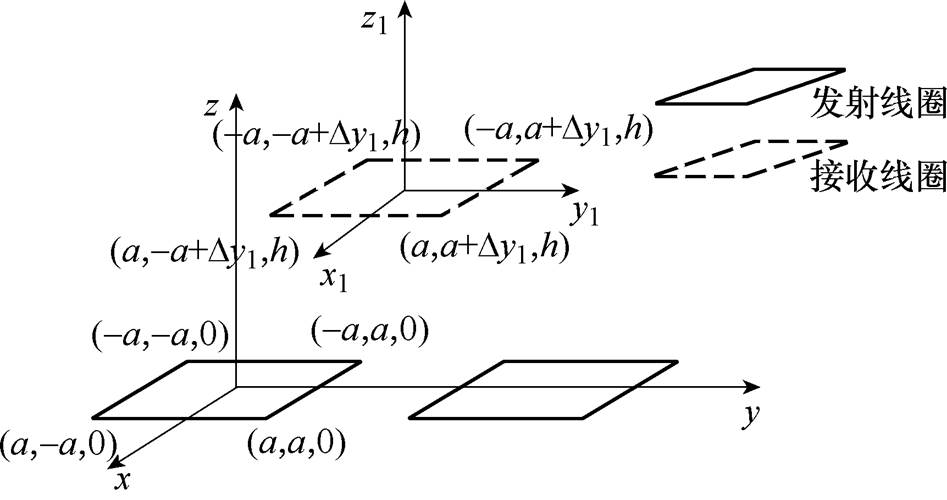
图3 耦合系统数学模型
Fig.3 Mathematical model of coupling system
根据上述推导的式(7)和式(8)可计算图3数学模型中发射线圈1与接收线圈互感值,利用Matlab进行计算得
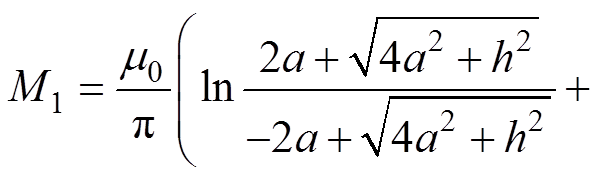
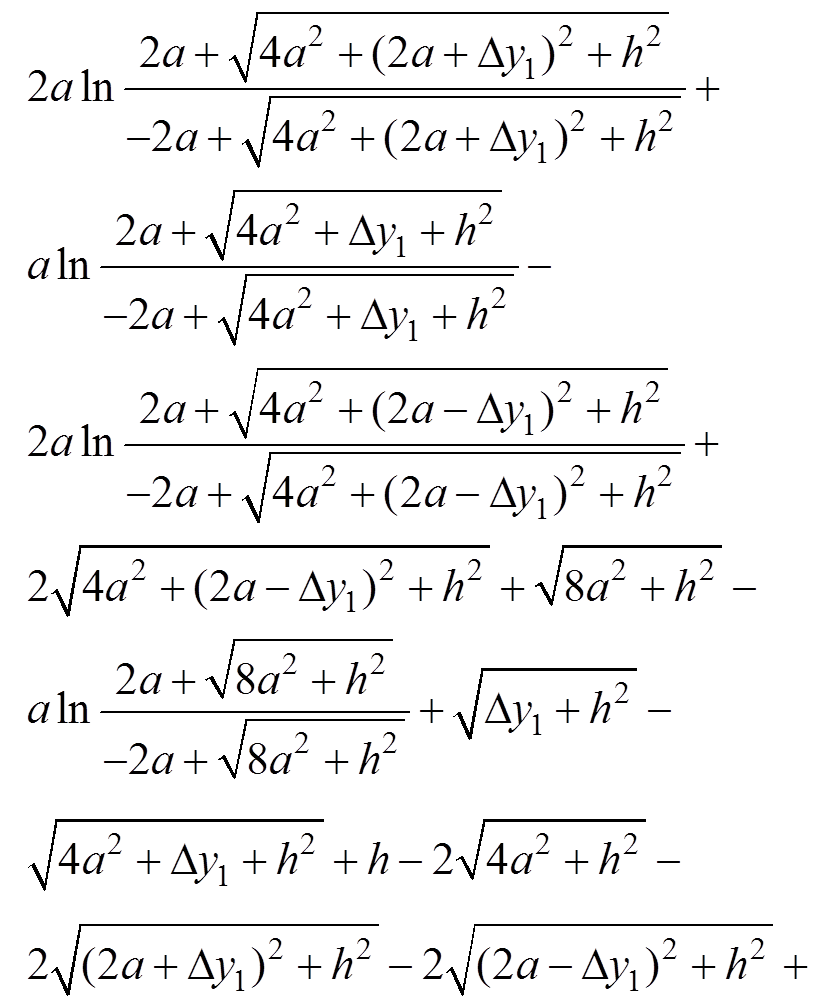
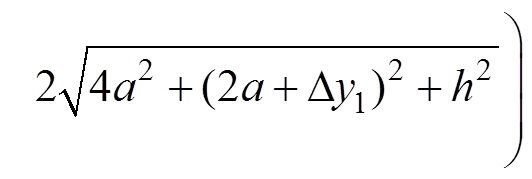 (11)
(11)
由于在实际工作中,动态无线供电系统的a和h为定量,所以发射线圈1与接收线圈互感M1关于位移距离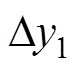 的函数关系式为
的函数关系式为
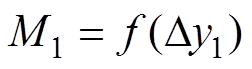 (12)
(12)同理,以发射线圈2为基准建立坐标系可得
 (13)
(13)
式中,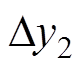 为接收线圈相对于发射线圈2的移动距离。
为接收线圈相对于发射线圈2的移动距离。
由此可以得到动态耦合全周期内三个阶段的互感。t1阶段接收线圈能量来源主要为第一个发射线圈,收发端之间互感为M1;t2阶段由于存在两种供电模式,需要分别对两种模式下的互感进行计算,若两发射线圈同时对接收线圈供电,则总互感为M1与M2之和;若两发射线圈轮流交替供电,则在切换时刻之前接收线圈仅由发射线圈1供电,发射线圈2关闭,收发端互感为M1,切换之后接收线圈变为仅由发射线圈2供电,发射线圈1关闭,收发端互感为M2;t3阶段接收线圈能量来源主要为第二个发射线圈,收发端之间互感为M2。
接下来用Matlab对耦合全周期下互感进行计算,电动汽车实际底盘大小和高度参考当前市场上常见尺寸,采用边长a=0.2m,传输距离h =0.25m的平面方形线圈,收发线圈各参数完全相同且假设两发射线圈中心相距0.4m,为简化计算过程,假设线圈无漏感且每匝线圈之间无介质损耗,比较t2阶段两种供电模式下的互感,如图4所示。
由图4可知,当接收线圈位于发射线圈正上方时互感最大,说明此时收发线圈之间耦合程度最高;当接收线圈向相邻发射线圈运动,由于收发端耦合面积减小导致互感降低,而互感会进一步使得接收功率下降,且发射线圈同时供电,互感稳定性要明显强于轮流交替供电,即输电系统稳定性更高。因此t2阶段应采用双线圈同时供电方案。为验证该结论及进一步分析动态过程的功率变化,接下来用有限元仿真软件对动态耦合磁场全周期进行仿真分析。
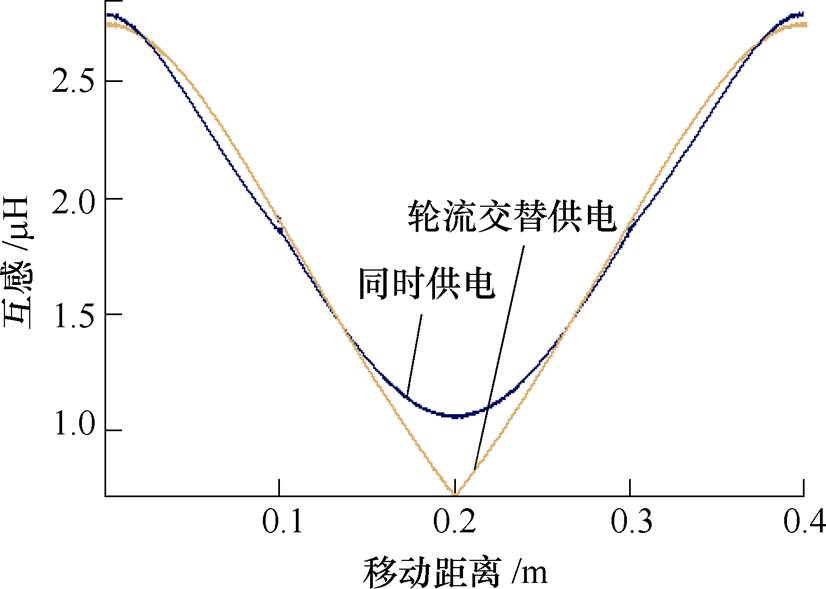
图4 移动过程互感波动
Fig.4 Mutual inductance fluctuations in motion
通过理论推导可知,受电体移动导致收发线圈间互感降低,从而使得接收功率波动,影响移动受电体受电稳定性。为进一步详细阐述动态过程下系统电磁场耦合特性,本文应用COMSOL多物理场耦合分析软件,在85kHz的工作频率下建立动态传输系统仿真模型,如图5所示。
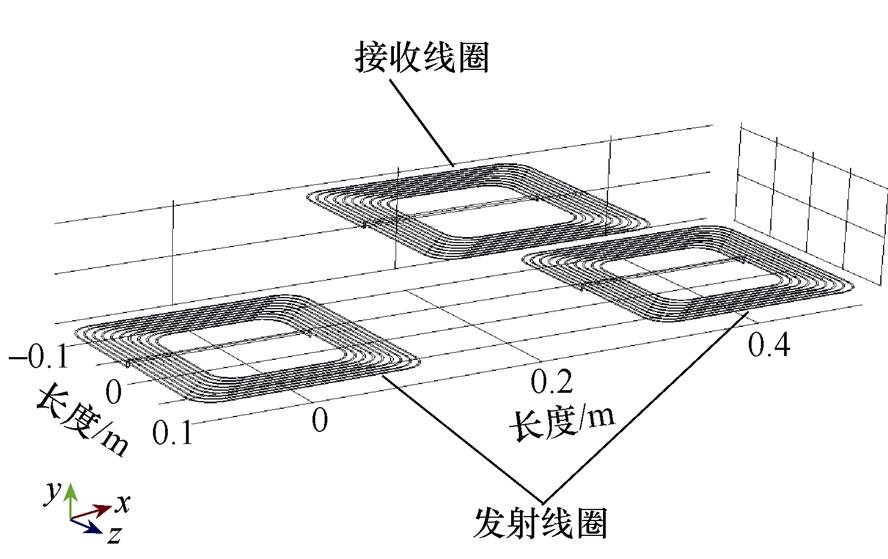
图5 DWC仿真模型
Fig.5 DWC simulation model
本文设计三组仿真,第一组从互感稳定性和发射线圈铺设的经济成本角度考虑,确定在线圈宽度为0.2m下两发射线圈最佳中心间距,并依据此最佳间距建立双发射-单接收最小动态耦合单元仿真模型;第二组目的是对t2阶段两种供电模式磁场强度和磁感线分布进行分析,确定两种供电模式在稳定接收功率方面的优劣;第三组目的是进一步确定双线圈同时供电的最佳区间。
考虑到在85kHz工作频率下的趋肤深度为0.2mm,为尽可能减小高频下线圈产生的电阻损耗与涡流损耗,应使线圈厚度高于趋肤深度。因此,仿真与实验均采用线径为1mm,匝数为10匝的平面方形线圈,其余参数与理论部分完全一致,即线圈边长为0.2m,收发线圈传输距离为0.25m。设置边界条件为完美电导体并对线圈施加阻抗边界条件,用以计算在85kHz工作频率下由于趋肤效应而产生的电阻损耗。在频域的研究中,两发射单元分别采用幅值为Us=100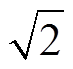 V,内阻为20W的交流电源,对无线电能传输系统激励,收发两侧均采用串联-串联(Series-Series, SS)补偿网络。根据法拉第电磁感应定律,在电流同相时,相邻交界处的磁场强度会相互抵消,磁场减弱;在电流反相时,相邻交界处的磁场强度相互叠加,磁场得以加强,所以设置两发射线圈相位差为180°。
V,内阻为20W的交流电源,对无线电能传输系统激励,收发两侧均采用串联-串联(Series-Series, SS)补偿网络。根据法拉第电磁感应定律,在电流同相时,相邻交界处的磁场强度会相互抵消,磁场减弱;在电流反相时,相邻交界处的磁场强度相互叠加,磁场得以加强,所以设置两发射线圈相位差为180°。
第一组仿真统一采用双线圈同时供电方式,由于互感系数可以表征线圈间耦合程度,而动态耦合过程中最小互感值越高说明耦合程度波动越小,因此,描绘出发射线圈在间距为0.3~0.6m区间范围内,动态耦合过程中的最小互感值曲线,如图6 所示。
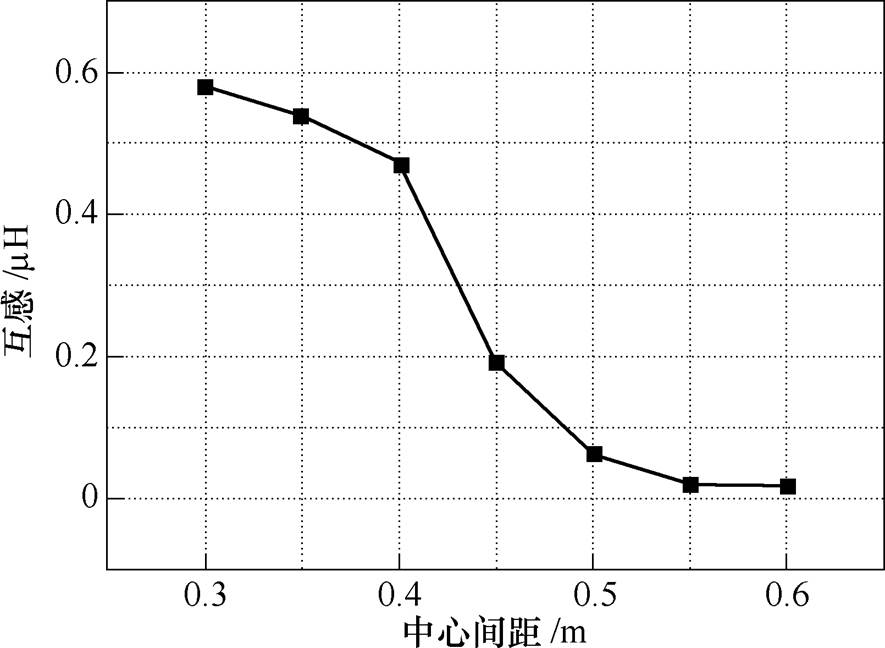
图6 最小互感值曲线
Fig.6 Minimum mutual inductance curve
由图6可看出,最小互感值随发射线圈中心间距扩大而减小,即输电系统稳定性随中心间距增大而降低,并且在0.4~0.45m之间最小互感值出现骤降,0.5m之后最小互感值趋近于0,说明若间距大于0.45m,接收端与发射端会出现无耦合情况。考虑到线圈长度为0.2m,采用分段式导轨供电,中心间距应大于0.2m。此外,在0.3~0.4m区间内最小互感值差值仅为0.1mH,从经济成本角度考虑,若中心间距过小会增加发射线圈数量,使得导轨铺设成本增加,因此,本文选用发射线圈的中心间距为0.4m。
参照上述中心间距建立最小动态单元耦合模型,进行第二组仿真,得到双线圈同时供电和单独供电下的磁场分布,并绘制出互感曲线,如图7、图8所示。
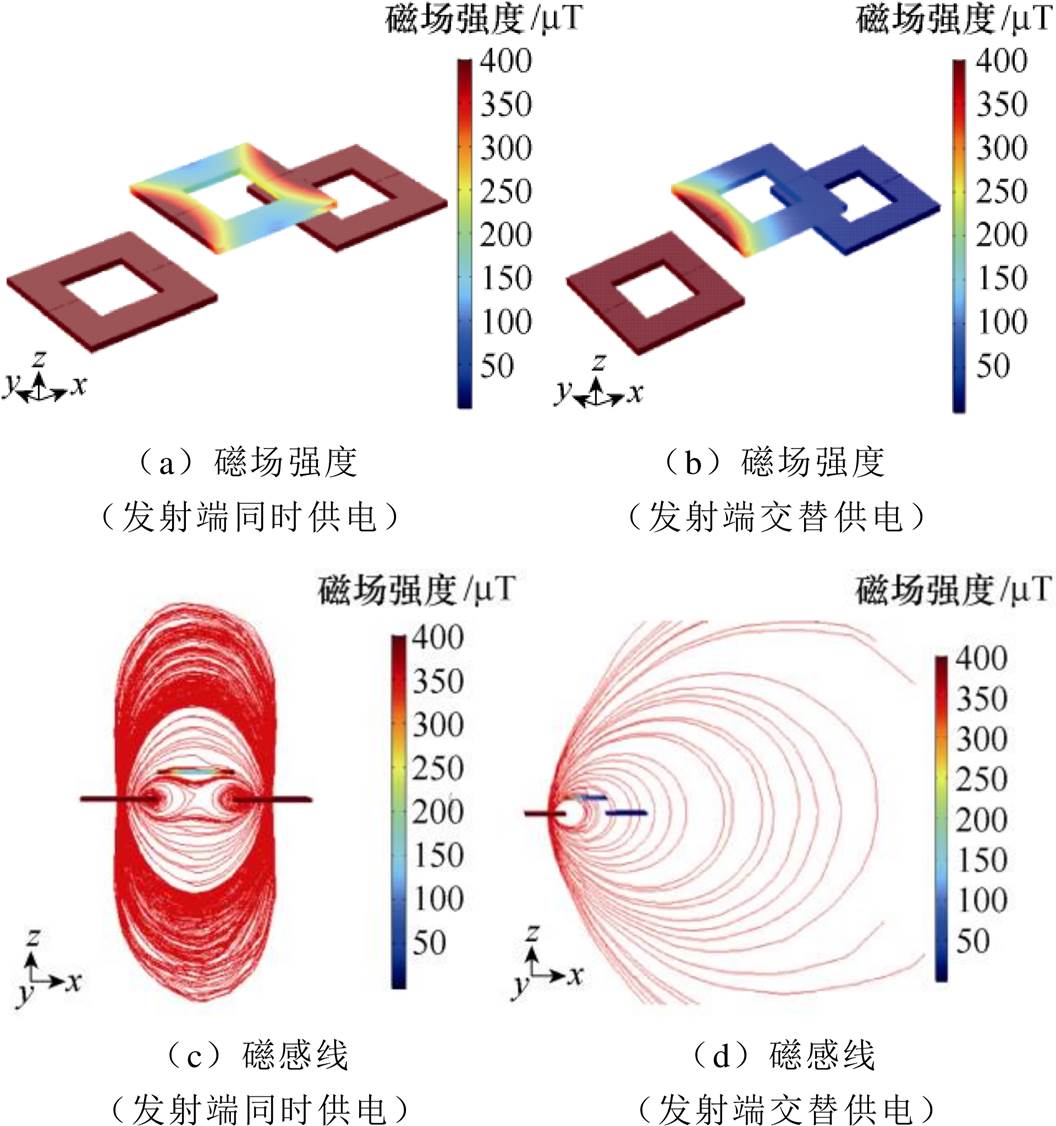
图7 供电模式磁场分布
Fig.7 Charging mode magnetic field distribution
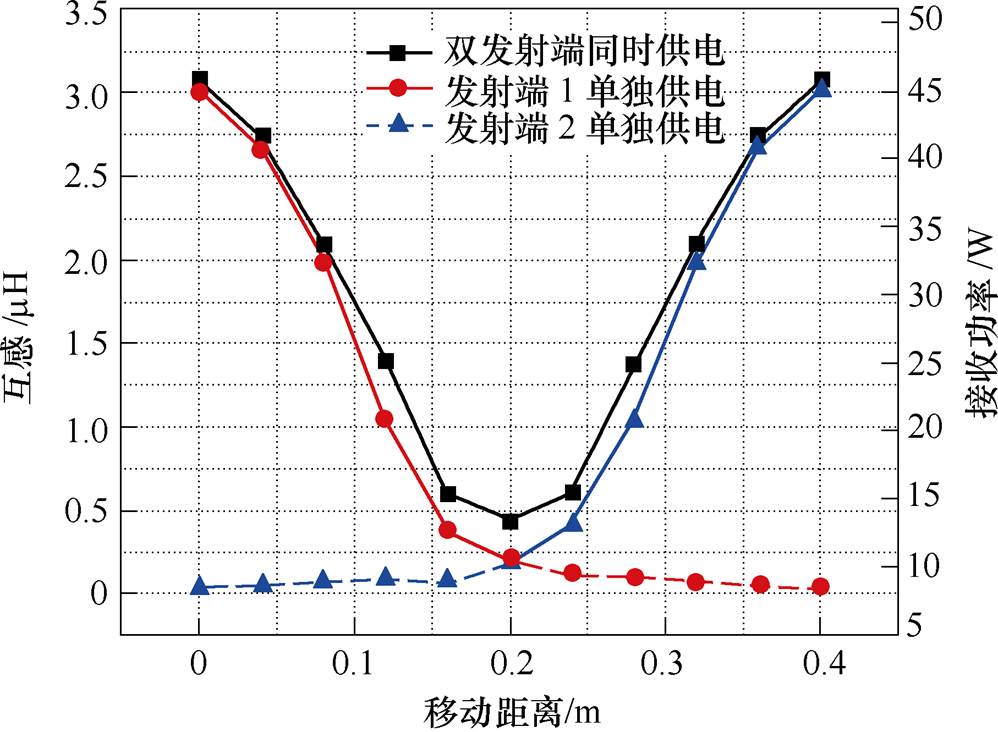
图8 互感与功率变化曲线
Fig.8 Mutual inductance and power change curves
图7a和图7b为两种模式磁场强度对比,图7c和图7d为磁感线对比,可知,双发射端同时对接收线圈供电时,接收线圈的磁场耦合程度更高。图8为不同供电模式下互感与功率变化曲线,可以看出,互感与接收功率具有明显的一致性,且受电体位于发射端正上方时互感和接收功率最大,随着受电体逐渐偏离发射端,互感和功率开始下降。其中,发射端1、2单独供电组合可看作在中点处发射端轮流交替供电模式下的互感曲线,对比可知,同时供电模式下互感与功率波动小,并且图8互感变化趋势与理论推导中的图4趋势一致,验证了理论的正确性。因此,t2阶段发射端同时供电方案要优于轮流交替供电。
另外,观察图8发现,虽然同时供电相比于轮流交替供电互感和接收功率会有提高,但接收端在发射端附近运动时两种供电模式的互感与接收功率却差别不大,原因是最初接收端在发射线圈1附近时,发射线圈2与接收端相距较远,此时接收线圈只与发射线圈1产生磁场耦合,而发射线圈2与接收线圈的磁场耦合程度极小,近似为0。从节省成本以及电磁安全角度考虑,应当避免发射线圈与接收线圈在无磁场耦合情况下导通。因此,同时供电模式应当存在最佳供电区间,即在此区间内双线圈同时供电可以有效提高互感和接收功率,在区间外接收端只需依靠与其相对位置近的发射线圈供电。为此设置第三组仿真探究最佳区间。
第三组仿真:在发射线圈1导通基础上,探究发射线圈2在接收端运行至不同位置时导通,以确定双线圈同时供电的最佳区间。测量接收端移动至1/4处(0.1m)、1/3处(0.15m)以及中点处(0.2m)3个位置的互感及接收功率,绘制成不同位置处互感与功率变化曲线如图9所示。
图9a~图9c对比可知,发射线圈2在接收端运行至1/4处导通与全程导通的效果基本一致,如图9a所示;而在运行至1/3处和中点处导通时相比在全程范围导通会出现互感与接收功率下降的情况,如图9b和图9c所示。这说明当受电体未到达1/4位置时,接收线圈只与发射线圈1产生磁场耦合,能量主要来源于发射线圈1,直到运行至1/4处时,发射线圈2才开始与接收线圈产生磁场耦合。由于最小动态耦合模型具有对称性,在接收端运行至3/4处时,接收线圈只与发射线圈2产生磁场耦合,此时能量主要来源于发射线圈2,因此,双线圈同时供电模式的最佳区间范围应为1/4~3/4处,即0.1~0.3m。

图9 不同位置处互感与功率变化曲线
Fig.9 Variation curves of mutual inductance and power at different positions
综上,在t2阶段供电模式应为:受电体由起始点出发移动至0.1m前,发射线圈1导通,发射线圈2关闭,受电体仅由发射线圈1提供能量;受电体运行至1/4处时发射线圈2导通,此时发射线圈1、2同时对受电体提供能量,实现双线圈同时供电,直至运行至3/4处,即0.3m,此时发射线圈1关断,受电体仅由发射线圈2提供能量。
为了验证理论及仿真分析的正确性,本文搭建了12m长动态无线供电平台,接收端通过外电路控制可模拟移动负载在0~2m/s不同速度下系统接收功率的波动规律,该实验平台如图10所示。

图10 动态无线供电系统
Fig.10 Dynamic wireless power transmission system
发射端由高频逆变电源、双发射线圈以及谐振电容组成。高频逆变电源内包括整流逆变电路模块和频率跟踪模块,且电源输出功率调节范围为0~5kW,实验选用60W灯泡作为负载。接收端由接收线圈、谐振电容、整流滤波模块和纯阻性负载组成。接收线圈接收的高频交流电通过整流模块转化为负载所需直流电,同时配置滤波电容确保输出稳定的直流电压。发射和接收线圈参数见表1。
高频电源输入电压幅值为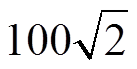 V,工作频率为85kHz。测得受电体移动过程中在几种供电模式下的接收功率与互感值见表2。
V,工作频率为85kHz。测得受电体移动过程中在几种供电模式下的接收功率与互感值见表2。
表1 发射线圈和接收线圈参数
Tab.1 The parameters of transmitting and receiving coil
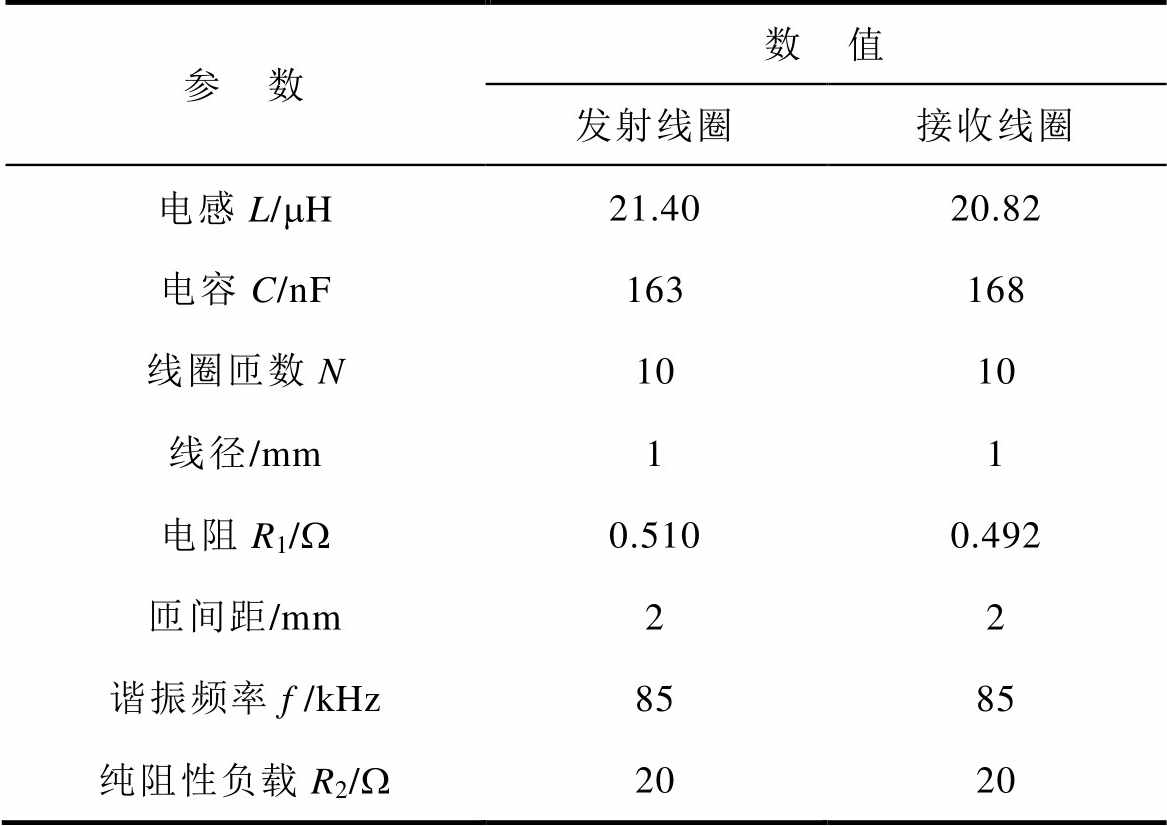
参 数数 值 发射线圈接收线圈 电感L/mH21.4020.82 电容C/nF163168 线圈匝数N1010 线径/mm11 电阻R1/W0.5100.492 匝间距/mm22 谐振频率f /kHz8585 纯阻性负载R2/W2020
将表2中实测功率与互感值绘制成曲线,如图11a所示。其中实线代表仿真值,虚线代表实验值,实验表明,互感与接收功率的变化趋势与仿真一致,当接收线圈与发射线圈完全对中时,受电体接收功率最大,随着受电体逐渐驶离发射线圈,互感与功率均开始下降,且双线圈同时供电模式能在一定程度上提高接收功率,使受电体持续稳定接收能量。接下来对最佳区间进行验证,对发射线圈2全程导通、1/4处导通以及在中点处导通三种情形进行实验验证,绘出图11b和图11c。
表2 几种供电模式下实测接收功率与互感值
Tab.2 The measured received power and mutual in several power supply modes

移动距离/m同时供电线圈1供电线圈2供电 接收功率/W互感/mH接收功率/W互感/mH接收功率/W互感/mH 045.912.5745.572.50.010.04 0.0435.322.2335.252.160.010.009 0.0828.431.5928.091.490.030.008 0.129.650.895.050.690.040.011 0.165.520.312.790.12.020.001 0.24.020.152.040.0612.010.061 0.245.570.311.040.0012.940.1 0.289.470.890.050.0115.650.69 0.3228.431.590.030.00828.091.49 0.3635.322.230.020.00935.252.16 0.445.912.570.010.0445.572.5

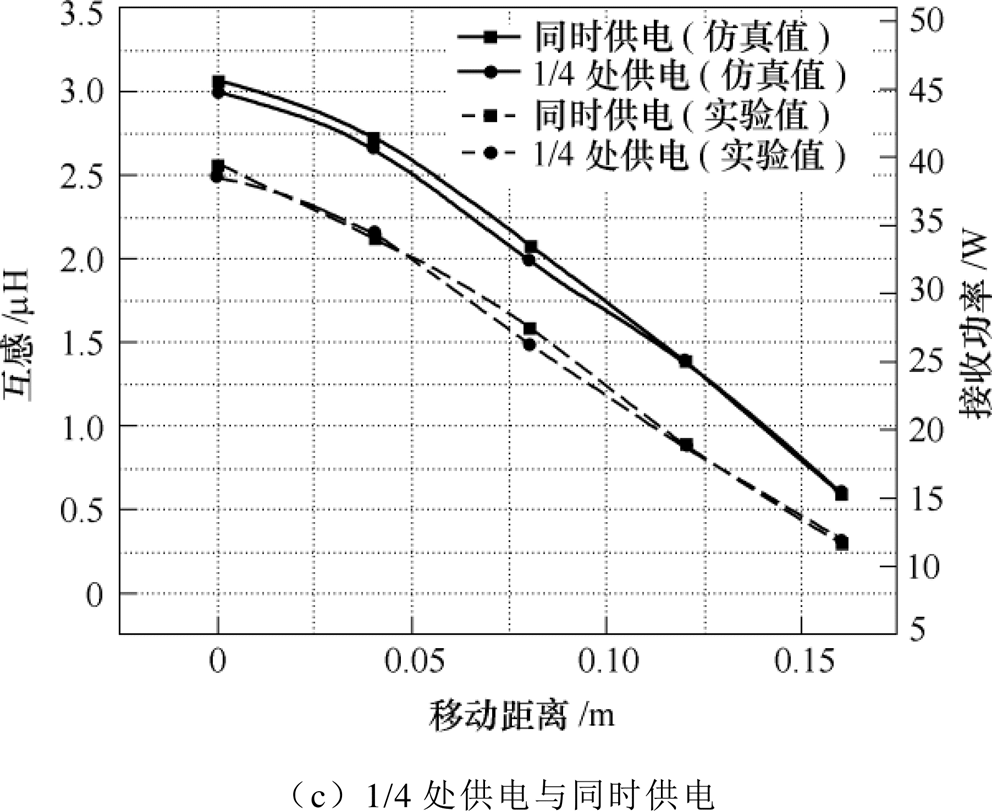
图11 实测互感与接收功率
Fig.11 The measured received power and mutual
由图11b和图11c可知,实验结果与仿真结果具有一致性,在接收端运行至1/4处,即0.1m时导通发射线圈2,可以有效减小接收功率与互感的波动,验证了所得最佳区间的有效性。实验中实际测得的接收功率比仿真值偏低,原因在于实验中高频逆变电源以及整流电路中的半导体元件在工作频率较高时会产生较大的开关损耗。
综上,双线圈同时供电相比于轮流交替供电可以有效提高互感与接收功率,且同时供电模式存在最佳区间,即接收端运行范围在1/4~3/4处,即0.1~0.3m内。另外,值得注意的是,双发射端同时供电模式下的最佳区间长度,与线圈的尺寸、相对位置以及施加的激励有关,本文所得的最佳区间适用于幅值为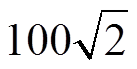 V的高频电源,为激励以及线圈边长为0.2m的情况。因此,可以进一步深入研究双线圈同时供电模式下最佳区间长度与线圈尺寸、相对位置以及电压电流等电气参数之间的关系。
V的高频电源,为激励以及线圈边长为0.2m的情况。因此,可以进一步深入研究双线圈同时供电模式下最佳区间长度与线圈尺寸、相对位置以及电压电流等电气参数之间的关系。
本文对动态无线电能传输系统在受电体实际动态运行过程下的发射单元切换模式及时刻分析,进行了数学建模、仿真分析和实验研究。研究结果如下:
1)应用电路耦合模型推导了耦合系统在动态过程下,互感关于位移的解析表达式,并得到位移变化影响互感进而使得功率降低的结论。
2)对实况下全周期内的动态耦合系统应用多物理场耦合软件进行仿真研究。确定了所设置线圈尺寸下的发射线圈最佳间距,并验证了双线圈同时供电相比于轮流交替供电在提高互感与接受功率方面的有效性。
3)在双线圈同时供电基础上,进一步确定双线圈同时供电的最佳区间,并通过实验加以验证。
对实际工况下的动态无线供电系统切换模式展开研究,不仅具有工程应用价值,而且能加快动态无线电能传输技术在交通领域的应用化进程,因此本研究具有深远意义。
参考文献
[1] 杨庆新, 章鹏程, 祝丽花, 等. 无线电能传输技术的关键基础与技术瓶颈问题[J]. 电工技术学报, 2015, 30(5): 1-8.
Yang Qingxin, Zhang Pengcheng, Zhu Lihua, et al. Key fundamental problems and technical bottlenecks of the wireless power transmission technology[J]. Transactions of China Electrotechnical Society, 2015, 30(5): 1-8.
[2] 张波, 疏许健, 黄润鸿. 感应和谐振无线电能传输技术的发展[J]. 电工技术学报, 2017, 32(18): 3-17.
Zhang Bo, Shu Xujian, Huang Runhong. The development of inductive and resonant wireless power transfer technology[J]. Transactions of China Electrotechnical Society, 2017, 32(18): 3-17.
[3] 赵争鸣, 张艺明, 陈凯楠. 磁耦合谐振式无线电能传输技术新进展[J]. 中国电机工程报, 2013, 33(3): 1-13, 21.
Zhao Zhengming, Zhang Yiming, Chen Kainan. New progress of magnetically-coupled resonant wireless power transfer technology[J]. Proceedings of the CSEE, 2013, 33(3): 1-13, 21.
[4] 黄学良, 王维, 谭林林. 磁耦合谐振式无线电能传输技术研究动态与应用展望[J]. 电力系统自动化, 2017, 41(2): 2-14, 141.
Huang Xueliang, Wang Wei, Tan Linlin. Technical progress and application development of magnetic coupling resonant wireless power[J]. Automation of Electric Power Systems, 2017, 41(2): 2-14, 141.
[5] 宋凯, 朱春波, 李阳, 等. 用于电动汽车动态供电的多初级绕组并联无线电能传输技术[J]. 中国电机工程学报, 2015, 35(17): 4445-4453.
Song Kai, Zhu Chunbo, Li Yang, et al. Wireless power transfer technology for electric vehicle dynamic charging using multi-parallel primary coils[J]. Pro- ceedings of the CSEE, 2015, 35(17): 4445-4453.
[6] 张望, 伍小杰, 夏晨阳, 等. 串/串补偿型无线电能传输系统的建模分析[J]. 电力系统自动化, 2017, 41(10): 135-140.
Zhang Wang, Wu Xiaojie, Xia Chenyang, et al. Model analysis of series/series compensated wireless power transfer system[J]. Automation of Electric Power Systems, 2017, 41(10): 135-140.
[7] 程岩松, 胡宏民, 叶方圆, 等. 磁耦合谐振式无线电能传输系统建模与仿真[J]. 电工技术, 2018(16): 135-136, 140.
Cheng Yansong, Hu Hongmin, Ye Fangyuan, et al. Modeling and simulation of magnetically coupled resonant wireless power transmission system[J]. Electric Engineering, 2018(16): 135-136, 140.
[8] 吴德会, 何天府, 王晓红, 等. 感应电能传输中矩形螺线线圈互感耦合的解析建模与分析[J]. 电工技术学报, 2018, 33(3): 680-688.
Wu Dehui, He Tianfu, Wang Xiaohong, et al. Analytical modeling and analysis of mutual inductance coupling of rectangular spiral coils in inductive power transfer[J]. Transactions of China Electrotechnical Society, 2018, 33(3): 680-688.
[9] 刘洋, 何圣民. 任意空间位置两多边形多匝线圈的互感计算[J]. 价值工程, 2013, 32(31): 235-237.
Liu Yang, He Shengmin. The calculation of mutual inductance of two polygons with multiturn coils at arbitrarily position[J]. Value Engineering, 2013, 32(31): 235-237.
[10] 蒋成, 孙跃, 王智慧, 等. 电动汽车无线供电导轨切换模式分析[J]. 电力系统自动化, 2017, 41(12): 188-193.
Jiang Cheng, Sun Yue, Wang Zhihui, et al. Switching mode analysis of wireless supplying rail for electric vehicles[J]. Automation of Electric Power Systems, 2017, 41(12): 188-193.
[11] 朱运晓, 段平平. 基于初级线圈切换的三相无线供电平台设计[J]. 电气传动, 2018, 48(9): 93-96.
Zhu Yunxiao, Duan Pingping. Design of three-phase wireless power supply platform based on primary coil switching[J]. Electric Drive, 2018, 48(9): 93-96.
[12] 陈国东, 吴剑青, 孙跃, 等. 基于互感差异的双拾取无线电能传输系统功率分配控制策略[J]. 电力系统自动化, 2018, 42(21): 154-163.
Chen Guodong, Wu Jianqing, Sun Yue, et al. Power distribution control strategy of wireless power transfer system with dual-pick up coils based on mutual inductance[J]. Automation of Electric Power Systems, 2018, 42(21): 154-163.
[13] Zhou Shijie, Mi Chunting. Multi-paralleled LCC reactive power compensation networks and its tuning method for electric vehicle dynamic wireless charging[J]. IEEE Transactions on Industrial Elec- tronics, 2016, 63(10): 6546-6556.
[14] Limb B J, Zane R, Quinn J C, et al. Infrastructure optimization and economic feasibility of in-motion wireless power transfer[C]//2016 IEEE Trans- portation Electrification Conference and Expo (ITEC), Dearborn, MI, 2016: 1-4.
[15] Jaehee Kim, Byung-Song Lee, Jun-Ho Lee, et al. Development of 1MW inductive power transfer system for a high speed train[J]. IEEE Transactions on Industrial Electronics, 2015, 62(10): 6242-6250.
[16] 孙跃, 张路, 王智慧, 等. 包络调制无线电能传输系统边界条件研究[J]. 电工技术学报, 2017, 32(18): 26-35.
Sun Yue, Zhang Lu, Wang Zhihui, et al. Study on boundary conditions of envelope modulated radio transmission system[J]. Transactions of China Elec- trotechnical Society, 2017, 32(18): 26-35.
[17] 张献, 王杰, 杨庆新, 等. 电动汽车动态无线供电系统电能耦合机构与切换控制研究[J]. 电工技术学报, 2019, 34(15): 3093-3101.
Zhang Xian, Wang Jie, Yang Qingxin, et al. The power coupling mechanism and switching control for dynamic wireless power supply system of electric vehicle[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3093-3101.
[18] 苑朝阳, 张献, 杨庆新, 等. 无线供电高铁列车非对称耦合机构[J]. 电工技术学报, 2017, 32(18): 18-25.
Yuan Chaoyang, Zhang Xian, Yang Qingxin, et al. Asymmetric coupling mechanism of wireless power transmission system for high-speed train[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(18): 18-25.
Analysis of Transmitter Unit Switching Mode in Dynamic Wireless Charging for Electric Vehicles
Abstract In dynamic wireless charging (DWC) system, the alternate work of multi-transmitters is an effective way to improve the efficiency. Firstly, the paper inferred the mutual inductance expression, and then obtained the conclusion that mutual inductance changes with movement and then affects the transmission power. Secondly, in order to reduce the power fluctuation caused by transmitter switching and improve the stability of DWC system, the working cycle of the minimum dynamic coupling unit was analyzed. Three groups of simulation were designed and compared using the finite element software, which proved the dual coil supply scheme is more effective than alternate power supply scheme in improving mutual inductance and receiving power compared. In addition, a power supply mode with dual coil supply in the optimal range of 0.1m to 0.3m and single coil supply outside the optimal range was proposed. Finally, an experimental platform was built based on the proposed power supply scheme, which shows that the simultaneous power supply of the first and second transmitters in the optimal interval improves the stability of the DWC system and reduces the reduction of receiving power.
keywords:Electric vehicle, dynamic wireless charging, power supply mode, optimal interval
中图分类号:TM72
DOI: 10.19595/j.cnki.1000-6753.tces.190636
国家自然科学基金项目(51607121,51877151)、国家重点研发计划(2018YFB0106300)和天津市自然科学基金项目(18JCQNJC70500)资助。
收稿日期 2019-05-25
改稿日期 2019-08-30
薛 明 男,1987年生,博士,研究方向为无线电能传输技术。E-mail: xueming@tjpu.edu.cn(通信作者)
王嘉浩 男,1994年生,硕士,研究方向为工程电磁场与磁技术。E-mail: xueshuowang123@163.com
(编辑 崔文静)