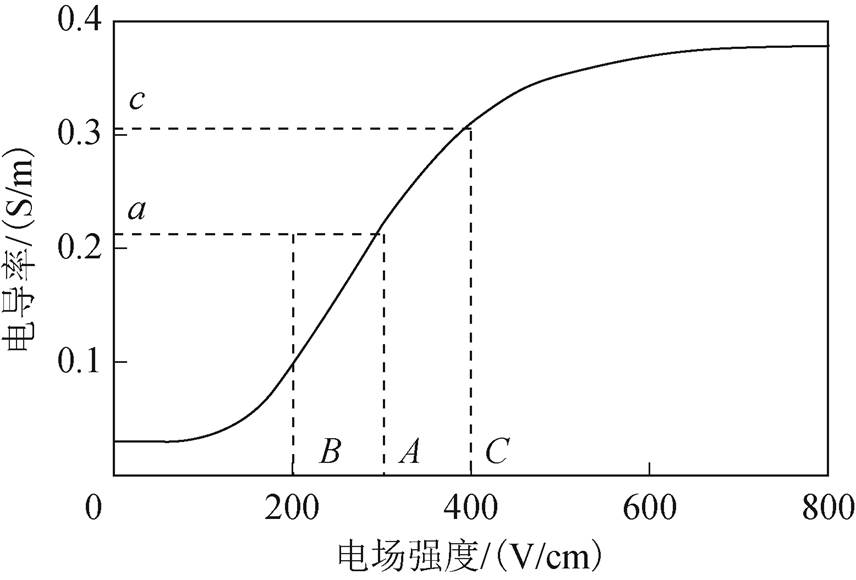
图1 叠加模型电导率曲线
Fig.1 Superimposed model conductivity curve
摘要 在不可逆电穿孔肿瘤治疗临床应用中，由于电场脉冲产生的消融区域较小，因此对于肿瘤尺寸较大的病患，需采用多电极治疗以实现肿瘤组织的完全消融。然而，目前多针治疗仍延用两针治疗效果的叠加进行预测，不利于制定精确的治疗计划。针对此问题，该文基于多电极作用下不可逆电穿孔肿瘤消融的电场分布与消融效果，建立适用于多电极治疗方式的数值模型。基于电导率模型分析，建立考虑多针治疗情况下累积效应的量效关系模型，并通过电压为500V、600V、700V、800V及1 000V的脉冲作用下马铃薯组织消融实验，比较不考虑多针累积效应的传统模型、叠加模型及量效关系模型的预测结果。结果表明量效关系模型的准确性和可行性（平均误差低于5.04%），能够用于多针治疗方式的术前治疗方案指导，为不可逆电穿孔临床应用中治疗方案的制定提供理论与数据支撑。
关键词：累积效应 量效关系模型 治疗计划 不可逆电穿孔 消融效果
不可逆电穿孔（Irreversible Electroporation, IRE）以其治疗时间短，对靶区内重要血管、胆管等正常组织影响小等优势成为一种新兴肿瘤消融的物理治疗手段[1-8]，已被用于前列腺肿瘤[9-10]、胰腺癌[11-12]、肾癌[13-15]、皮肤癌[16-17]、头颈癌[17-18]、肝癌[20-22]等多种肿瘤治疗中，并取得良好效果。
在以不可逆电穿孔肿瘤消融技术为背景的临床治疗中，病灶的杀伤主要依靠超声[23]、CT[24]（computed tomography）及MRI[25]（magnetic resonance imaging）等引导将两根相对的电极针插入靶区，施加特定的不可逆电穿孔脉冲，以实现两对电极间及周围组织的消融。其术前治疗方案（包括术前的脉冲参数、电极参数设置及预期治疗疗效等）的确定主要依赖数值模型的仿真模拟，通过患者CT或MRI切片重建三维真实组织模型，运用最优解算法寻求最佳的脉冲参数及电极配置。目前，针对形态复杂、体积较大的肿瘤组织，简单的单对电极已不能通过调节脉冲参数的方式来满足治疗需实现病灶区域有效电场全覆盖的要求，多针电极循环治疗已成为必要的治疗方式。例如C. G. Martin等报道，在临床胰腺癌的治疗中，对于最大半径在2.5~3cm之间的肿瘤组织治疗中，采用了4针电极分别对电极对4-1、1-3、2-3、1-2、2-4及3-4施加治疗脉冲[26]，方能确保肿瘤病灶区的完全覆盖。2017年，S. Campel等在前列腺肿瘤的治疗中，使用纳米刀以及4根治疗用针电极，通过对4-1、1-3、2-3、1-2、2-4及3-4循坏施加脉宽为70μs脉冲，每两针间施加电场强度保持为1 500V/cm的方式，来实现体积大于15cm3的肿瘤组织消融[27]。目前在不可逆电穿孔大尺寸肿瘤治疗中，多针电极的应用能够很好地满足临床需求，推进不可逆电穿孔技术的发展进程，但是仍有问题亟需解决。目前针对多针电极不可逆电穿孔肿瘤治疗计划制定，通常采用将多对电极产生的消融范围进行叠加，且电极对之间作用效果相互独立无影响的简化模型。以四针电极（两对电极）为例，传统的不可逆电穿孔治疗计划是基于电导率模型进行制定，将两对电极产生的消融区域进行叠加，从而得到整体的消融区域。但是第一对电极作用后，电极周围组织的电特性由于不可逆电穿孔效应发生了显著的改变，因此会影响下一对电极作用时的电场分布，从而影响治疗计划的制定。所以，传统的数值模型在多针电极治疗方式下是不能进行直接叠加，否则会导致预测与实际治疗效果的不匹配，不能满足临床治疗需求。因此，多针不可逆电穿孔肿瘤消融治疗方案中的数值模型需要进一步修正。基于此，本文在多电极单独作用模型的基础上，进一步考虑电极对作用前后的累积效应，建立量效关系模型，通过马铃薯块茎实验比较了传统数值模型、多针叠加模型和量效关系模型的效果预测情况，证实量效关系模型用于多针治疗方式的术前治疗方案指导的有效性（平均误差低于5.04%），为临床多针电极治疗方案提供理论参考与数据支撑。
在一对电极作用结束后，周围组织电导率发生了显著的变化，该对电极对后续治疗的影响可通过电导率间接体现。多针叠加模型在传统模型基础上，考虑了前一对电极作用影响，以电导率形式进行叠加考虑。具体变化过程如图1所示。
图1 叠加模型电导率曲线
Fig.1 Superimposed model conductivity curve
若组织内存在某一点X，在第1对电极作用时承受的电场强度为A，根据电导率曲线，此时电导率值为a。在第2对极作用时，将存在两种可能：①若此时X位置承受电场强度为B，B小于或等于第一次作用时承受的电场强度A，则认为在第二对极作用时电导率保持不变，仍取第1对极作用后电导率值a；②若此时X位置承受的电场强度为C大于A，则此时电导率仍按照电导率曲线变化达到c值。该过程可描述为
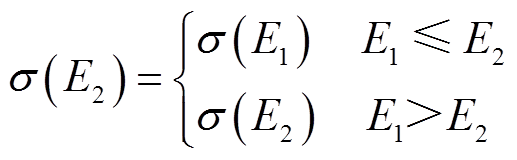（1）式中，E1为电极对1-3作用时电场强度；E2为电极对2-4作用时电场强度；s(E1)与s(E2)分别为第一对与第二对电极作用时随电场强度变化的电导率。此种叠加电导率模型将第1对电极作用后的影响以电导率的形式保留，在此基础上进行第2对极作用，充分考虑前一对电极对后续治疗的影响，符合理论分析。
多针叠加模型考虑了先作用脉冲对后作用脉冲的影响，同样，在后作用脉冲作用期间，也会对先作用脉冲区域产生影响，因此需考虑先作用脉冲与后作用脉冲的相互影响，即考虑总体脉冲对组织的影响，本文提出量效关系模型。针对本文采用的对角线脉冲施加方式，电极对1-3和2-4分别施加90个脉冲，传统数值模型采用的消融面积判据为[27]
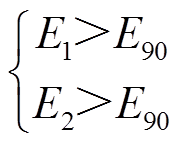（2）
式中，E90为施加90个脉冲的阈值电场强度。
但实际对组织而言，总共承受脉冲数量为180个，传统判据使用90个脉冲阈值存在一定的不合理性。同时由于两对电极作用时电场强度并非恒定分布，采用180个脉冲阈值E180同样存在问题。E180对应于持续承受180个相同脉冲作用后的消融判据，但针对本文所采用的电极1-3作用90个脉冲，再对电极2-4作用90个脉冲的施加方式，组织所承受电场强度已发生变化，且可知道第二对电极作用时，第一对电极作用区域所承受电场强度减小，同理可得，第二对电极作用区域在第一对电极作用时所承受电场强度同样减小，因此取180个脉冲对应阈值电场强度将产生更大预测消融面积，将可能导致最终治疗为欠量治疗。基于以上问题，本文提出量效关系模型，采用剂量学模型作为组织坏死的判据。传统的脉冲剂量定义为脉冲施加的剂量[28]。
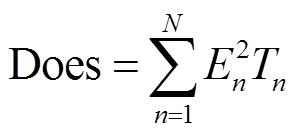（3）
式中，Does为脉冲剂量，kV2ms/cm2；En为第n个脉冲的电场强度，kV/cm；Tn为第n个脉冲的脉宽；N为施加的脉冲总数。
根据脉冲剂量模型，本文定义量效关系模型为
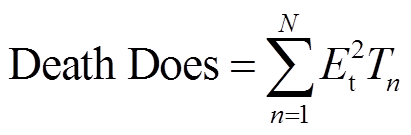（4）式中，Et为施加N个脉冲的阈值电场强度，该阈值是组织坏死的临界值，因此该剂量认为是坏死的临界剂量，组织承受脉冲剂量高于此坏死剂量，则可认为组织坏死。由此，对于本文脉冲参数而言，量效关系剂量模型主要分为以下三个部分：
（5）
式中，E1为电极对1-3作用时电场强度；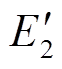
为考虑第一对电极作用后电极2-4作用时的电场强度；E180为施加180个脉冲的阈值电场强度。在量效关系模型中，以上三个判据满足其中一个，则可认为组织坏死。
马铃薯属于茄类植物组织，虽然没有概括肿瘤的所有特性，但它是评估趋势的合理模型。对于马铃薯切片，脉冲作用后细胞膜损伤，细胞内多酚氧化酶得以释放并发生氧化，因此产生暗区。此外，已有文章显示马铃薯组织反映了体内观察到的电穿孔的影响，并且通过治疗区域明显变暗可以很容易地确定坏死区域[29]。因此，众多学者采用马铃薯组织作为一种体外模型研究脉冲作用下的电穿孔效应[30]。本文所有马铃薯均处理为直径37mm，厚度5mm的圆柱体，实验系统与电极布置如图2所示。在传统IRE脉冲处理后放置于阴凉处静置24h，24h后水平剖开，脉冲处理的区域变黑。由于土豆组织内经络明显，导致消融边界不规则，因此消融面积的计算采用图像处理软件image J选取消融边界[31]，进行面积的计算。
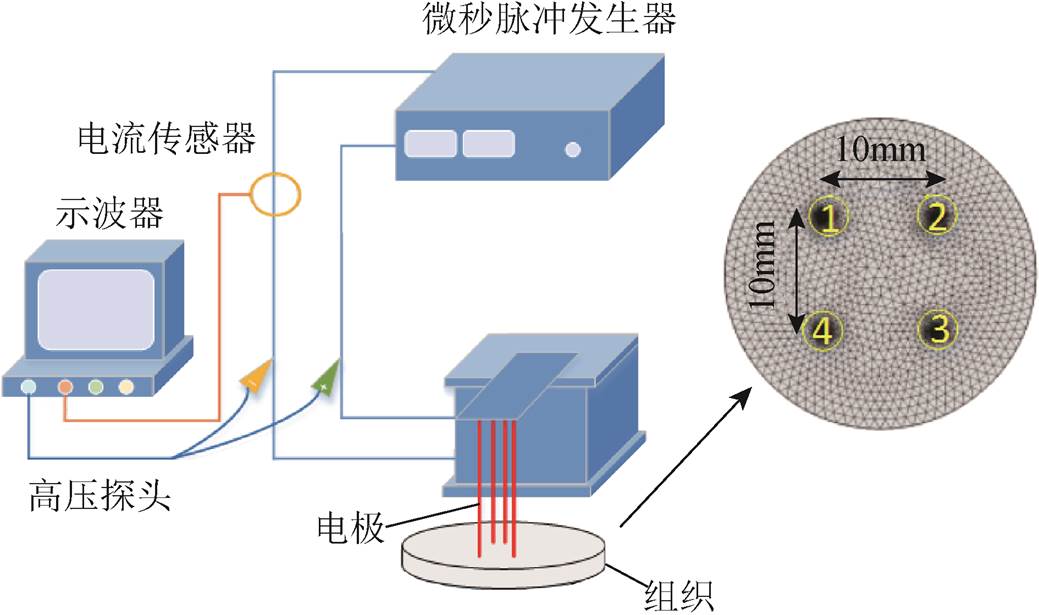
图2 实验系统示意
Fig.2 Experimental system schematic
马铃薯组织消融面积示意图如图3所示。图3a为电压600V时针电极1-3施加后消融效果图。图3b为电压600V时针电极1-3与2-4均施加完后消融图。由于单独电极1-3施加与单独电极2-4施加效果相同，因此将施加1-3后的消融图旋转90°后即可代表单独施加2-4后消融图。将施加1-3后坏死区域与施加2-4后坏死区域重叠作为单独作用模型所对应的实验消融面积（标记为灰色区域），从图3c可见，累积作用后的坏死区域相较于两次单独作用的叠加面积更大，且主要增加区域在两针之间，因此，通过该实验，直观验证多针电极施加情况下存在累积效应，若采用传统单独作用模型进行仿真模拟，将不能体现多电极的累积作用。
图3 马铃薯组织消融示意图
Fig.3 Schematic diagram of potato tissue ablation
马铃薯仿真模型采用有限元分析软件COMSOL Multiphysics建立了二维模型，数值模型中针电极采用铜电极，电极如图2所示，直径0.5mm，间距10mm，呈正方形分布。仿真模型采用动态电导率，根据文献[28]，马铃薯随电场强度E变化的动态电导率为
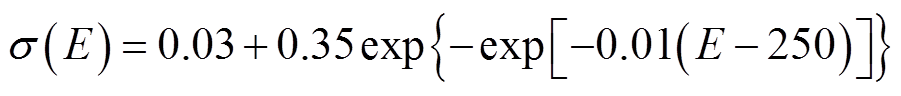（6）组织内的电场分布可通过Laplace方程得到，即
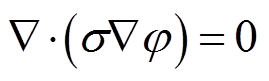（7）
式中，σ为组织电导率；φ为电位。
两电极电势分别为
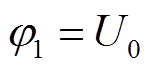（8）
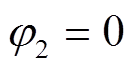（9）
设组织的外部边界条件为电绝缘。由于仿真中设有判断语句，因此对模型精度要求较高，网格剖分选取较细化，模型剖分单元为6 170域单元。
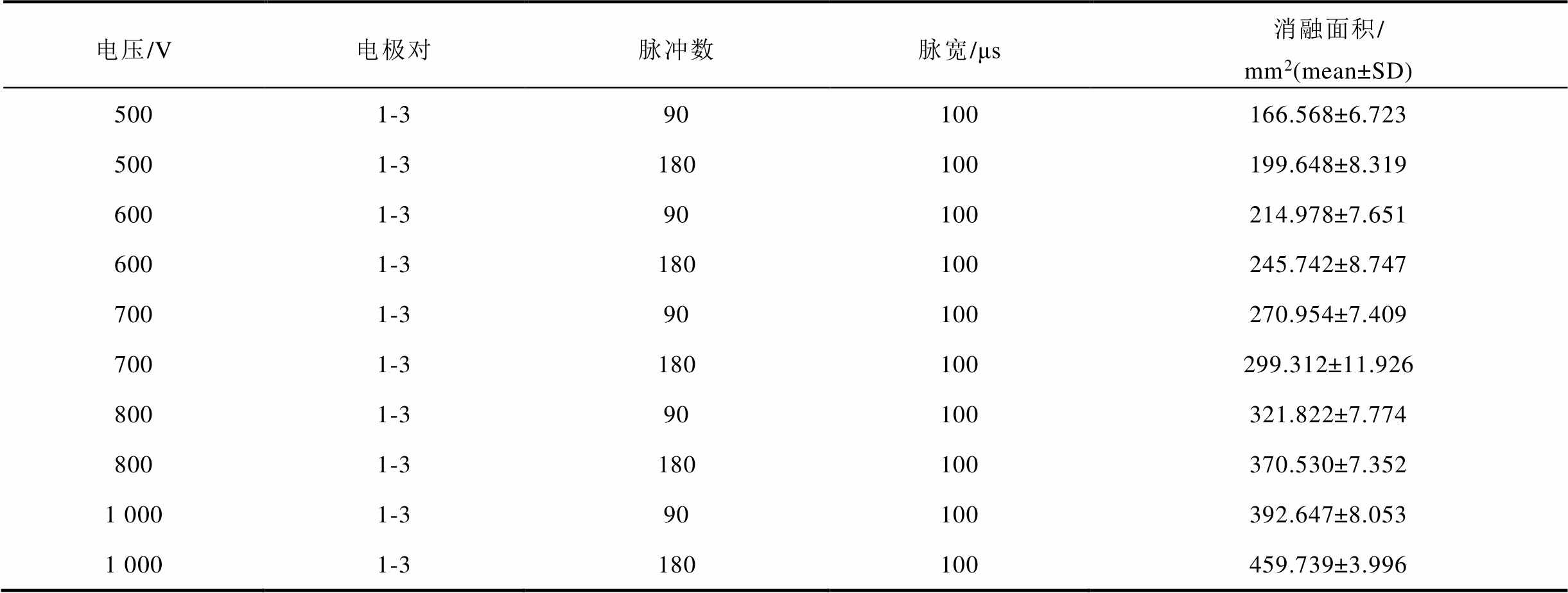
实验脉冲刺激后，使用图像处理软件image J对马铃薯消融面积进行选取，在电极电压为500V、600V、700V、800V及1 000V时，电极1-3分别施加90个脉冲及180个脉冲情况下的消融面积见表1。
表1 马铃薯实验消融面积
Tab.1 Potato experimental ablation area
电压/V电极对脉冲数脉宽/μs消融面积/ mm2(mean±SD) 5001-390100166.568±6.723 5001-3180100199.648±8.319 6001-390100214.978±7.651 6001-3180100245.742±8.747 7001-390100270.954±7.409 7001-3180100299.312±11.926 8001-390100321.822±7.774 8001-3180100370.530±7.352 1 0001-390100392.647±8.053 1 0001-3180100459.739±3.996
由于马铃薯组织消融面积较为不规则，因此难以通过边界拟合的方式判断阈值电场强度，故本文采用面积拟合的方式，仿真不同电压等级下电极1-3作用时的电场强度分布，将实验消融面积与不同电场强度范围内面积相比较，取最为接近的电场强度值为阈值电场强度。
图4为不同电极电压时不同电场强度对应的面积。将仿真面积与实验面积相比较，确定马铃薯组织90个脉冲作用下阈值电场强度为(193±2.449)V/cm，180个脉冲作用下阈值电场强度为(174±2.000)V/cm。
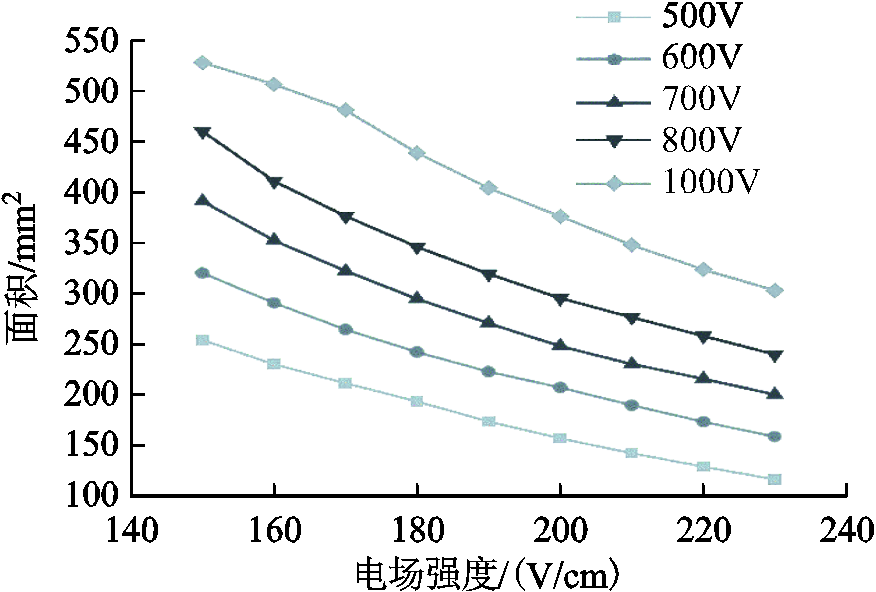
图4 仿真模型中不同电压下不同电场强度对应面积
Fig.4 Corresponding area of different field strengths at different voltages in the simulation model
根据电场强度阈值及判据要求，传统的单独作用模型、叠加模型与量效关系模型的仿真数据与实验数据见表2。
表2 两对极作用实验与仿真数据
Tab.2 Two pairs of pole action experiments and simulation data
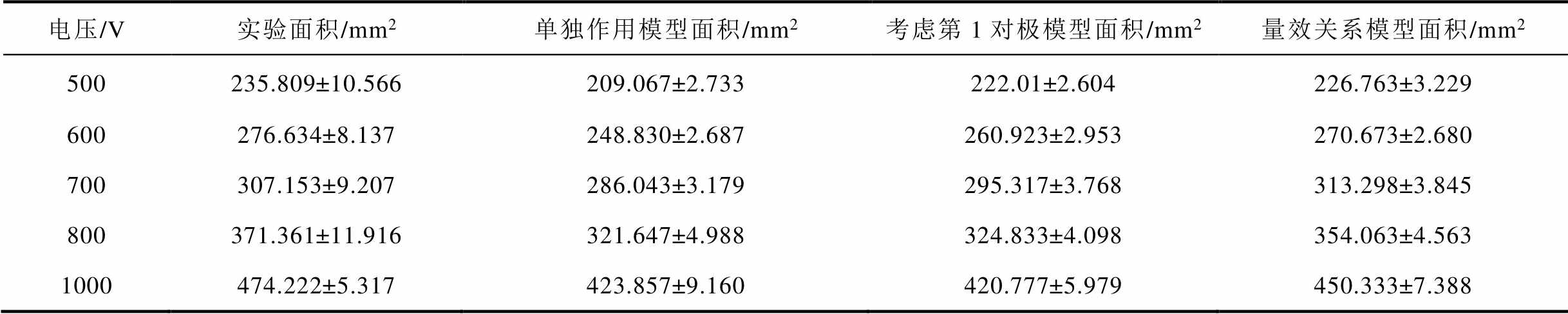
电压/V实验面积/mm2单独作用模型面积/mm2考虑第1对极模型面积/mm2量效关系模型面积/mm2 500235.809±10.566209.067±2.733222.01±2.604226.763±3.229 600276.634±8.137248.830±2.687260.923±2.953270.673±2.680 700307.153±9.207286.043±3.179295.317±3.768313.298±3.845 800371.361±11.916321.647±4.988324.833±4.098354.063±4.563 1000474.222±5.317423.857±9.160420.777±5.979450.333±7.388
通过实验消融数据与不同判据消融面积比较，三种模型与实验数据的误差比如图5所示。
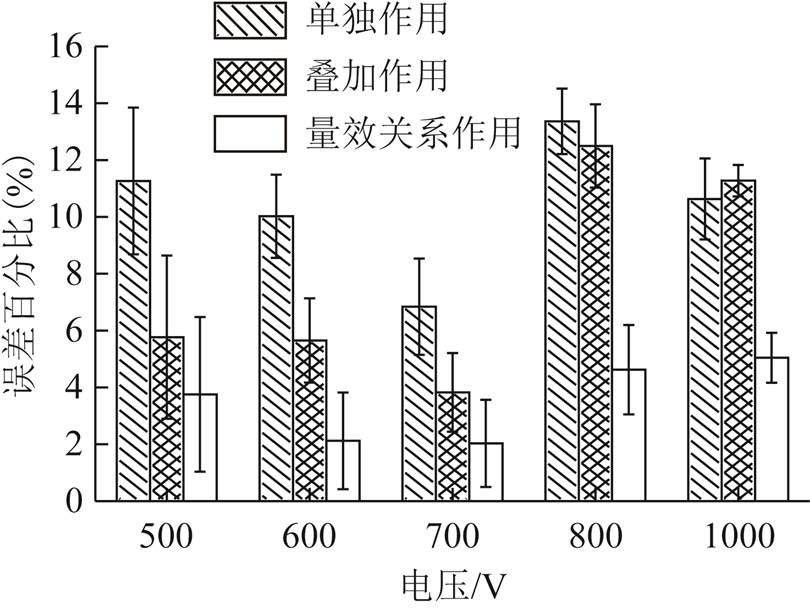
图5 三种模型与实验误差对比
Fig.5 Comparison of three models and experimental errors
由图5可直观看出，在任一电压等级作用下，量效关系模型仿真数据均更接近于实验数据。从实验数据可以看出，传统单独作用模型在500V、600V、700V、800V及1 000V电压作用下仿真与实验消融面积的误差分别为(11.26±2.11)%、(10.02±1.19)%、(6.84±1.38)%、(13.36±0.94)%及(10.63±1.16)%，平均误差在10.42%左右；叠加作用模型在各电压等级下的误差分别为(5.76±2.34)%、(5.65±1.21)%、(3.82±1.13)%、(12.49±1.19)%及(11.27±0.45)%，平均误差在7.82%左右；而量效关系模型各电压等级误差分别为(3.76±2.22)%、(2.12±1.38)%、(2.03±1.25)%、(4.62±1.28)%及(5.04±0.71)%，平均误差在3.51%左右。从三种模型的比较可知，量效关系模型的误差最小，远小于传统单独作用模型，与实验数据最为接近。由此可以认为量效关系模型相对于单独作用模型而言，更符合客观规律，满足预测要求。
众所周知，脉冲作用后电导率分布发生改变[32]，电场强度越大所引起的电导率变化越大。因此第二对极作用时忽略第一对电极影响将产生极大误差，必须将第二对极的作用建立在第一对极电导率分布基础上。取电压为500V时等值线进行分析，如图6所示，考虑第一对极作用的影响，第二对电极作用后的消融面积呈现针电极附近面积增大、中间叠加区域面积减小的形式。这是由于第一对电极作用后，中间叠加区域电导率增大，阻抗减小，在第二对电极作用时，叠加区域由于阻抗的减小所承受的压降减小，针电极附近所承受压降增大，因此消融面积增大，仿真与实际理论相符合。
图6 单独作用模型（灰色）与叠加模型（白色）消融面积
Fig.6 Separate action model and superposition model ablation area
单独作用模型与叠加模型电导率分布如图7所示，由此同样可以看出传统的单独作用模型在电极2-4作用后仅对电极2-4之间的区域产生影响，但叠加模型已经将前一对针电极的作用考虑在内，在电极2-4作用时，保留电极1-3作用后电导率，在此基础上，进行电极2-4脉冲作用。从理论上分析，第一对电极作用后组织电导率必然出现重新分布，因此考虑第一对电极的叠加模型更接近多针理论分析。
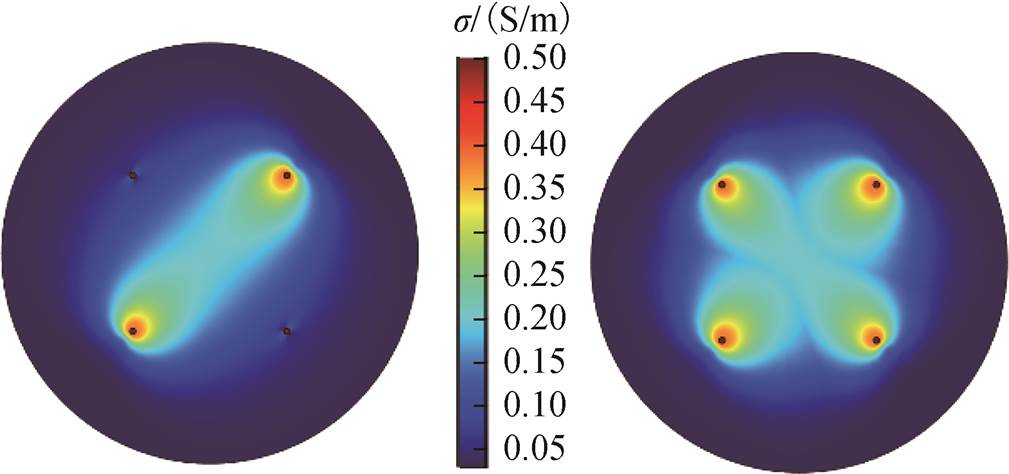
图7 单独作用模型与叠加模型电导率分布
Fig.7 Conductivity distribution of the single acting model and the superimposed model
量效关系模型建立在叠加模型基础之上，即考虑先作用脉冲对后续作用脉冲的影响，同时也考虑了后作用脉冲对先作用脉冲的影响，包含整个脉冲过程带来的影响。如图8a所示，灰色区域表示在电压为500V时，考虑叠加作用的两对电极的消融面积，白色线内表示考虑叠加作用的量效关系模型的消融面积。可以看出量效关系模型在叠加模型消融区域上主要作用于两电极之间的区域，该区域在两次脉冲作用期间电场强度较大，且脉冲作用有效时间较长，易于达到坏死剂量。对于以上三个判别条件，既考虑了单对极作用时造成的坏死，同时也考虑了多对电极共同对组织的作用，考虑因素更为全面，更贴近实际情况。
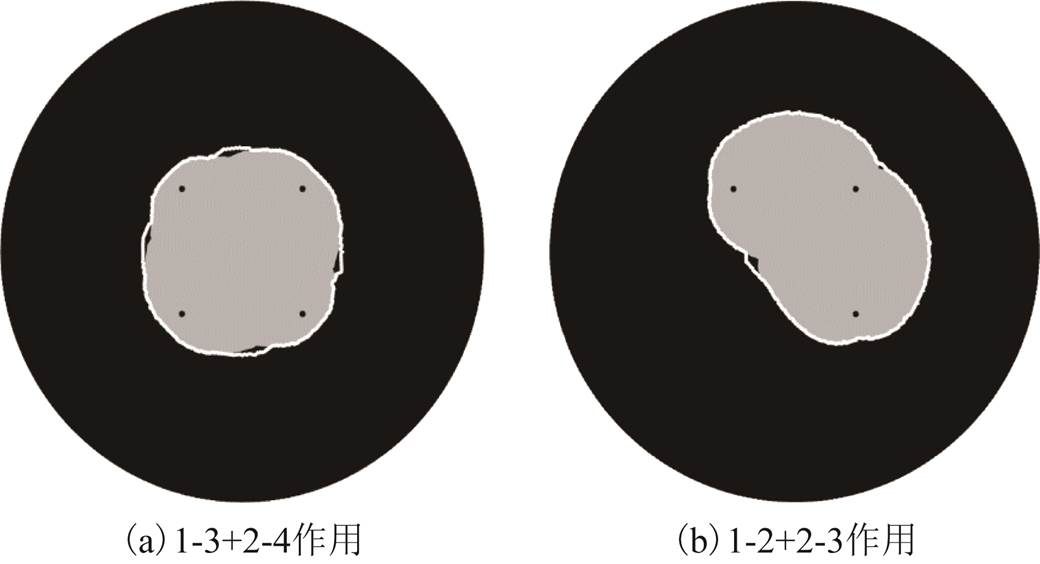
图8 叠加模型与坏死剂量模型消融面积
Fig.8 Superimposed model and ablation dose model ablation area
量效关系模型不仅与脉冲数量、电场强度相关，还与脉冲施加方式联系紧密。对于以上本文分析的对角线施加方式，两对电极作用的重叠区域较大，因此量效关系作用明显，但对于连续施加方式，即1-2+2-3施加方式，两次脉冲作用重叠区域较小，所能达到量效关系的区域相对更小。如图8b所示，白色线条内代表的量效关系模型消融面积仅在中心区域较叠加模型有所区别，整体而言，两者效果相近。由此可知，量效关系模型所代表的累积效应随脉冲施加方式的不同效果差异很大。在多对电极作用区域重叠较大时，累积效应明显；相反，重叠区域较小时，累积效应程度较小。
本文从组织层面观测到多电极作用下的累积效应，分析该种累积作用，主要有两个方面产生原因：
1）电极之间相互作用，先作用脉冲刺激后，组织电导率发生变化，进而引起电场的重新分布，因此后续脉冲作用时，电场强度分布发生变化；而同样，后续脉冲作用时所引起的电场强度分布也将对先作用区域产生进一步影响，因此认为脉冲作用的相互影响是引起多电极累积作用的主要原因。
2）C. Muratori等在文献[33]中提出，将一串脉冲等分为两部分，每一部分之间间隔一定时间施加，细胞杀伤效果比一次性全部施加成倍增加。由此，前一部分脉冲的施加，增加细胞对脉冲的敏感程度，使后续脉冲施加时的杀伤阈值有所降低，造成更多的细胞坏死。根据该文献，对于本文提到的多针治疗而言，有可能第一对电极作用后引起细胞对脉冲的敏感度增加，组织杀伤阈值有所减小，造成更大面积的坏死。
因此，造成累积效应的原因可能是剂量作用和敏感度变化共同作用的结果，所以难以检测单个因素作用时对累积效应的贡献。一对电极作用后组织对电场敏感度的增加及其增加程度均无法验证，还需要进一步的研究分析。
本文基于临床多针模型需求，建立符合多针规律的量效关系模型，并通过实验验证其合理性。该模型在传统电导率模型基础上，考虑了先作用脉冲与后作用脉冲的相互影响，与实际更为贴近。但本文对脉冲作用后的电导率恢复过程进行了简化，存在一定误差，因此，在后续研究过程中，将考虑脉冲作用后的恢复过程，使多电极脉冲施加过程与实际更为贴近，为临床多电极治疗提供更精准的仿真计算模型。
为满足不可逆电穿孔临床多针治疗计划的需求，本文在已有单对电极作用电导率模型的基础上，考虑先施加脉冲对后续脉冲作用的影响，建立多针叠加模型。在此基础上，进一步考虑后作用脉冲对先作用脉冲区域的影响，建立量效关系模型，并通过实验与仿真验证该模型与实验误差在5.04%以下，极大地降低了传统模型与实验数据间误差。量效关系模型的建立有助于多针电极术前治疗计划的精确性，为多针电极的临床应用提供理论基础与数据支持。
参考文献
[1] Weaver J C. Electroporation of cells and tissues[J]. IEEE Transactions on Plasma Science, 2000, 28(1): 24-33.
[2] Lü Yanpeng, Yao Chenguo, Rubinsky B. A conceivable mechanism responsible for the synergy of high and low voltage irreversible electroporation pulses[J]. Annals of Biomedical Engineering, 2019, 47(7): 1552-1563.
[3] Domenge C, Orlowski S, Luboinski B, et al. Antitumor electrochemotherapy: new advances in the clinical protocol [J]. Cancer, 2015, 77(5): 956-963.
[4] Heller R, Jaroszeski M J, Reintgen D S, et al. Treatment of cutaneous and subcutaneous tumors with electrochemotherapy using intralesional bleomycin[J]. Cancer, 2015, 83(1): 148-157.
[5] 米彦, 徐进, 刘宏亮, 等. 基于网格传输网络模型的高频纳秒脉冲串作用下单细胞穿孔特性仿真[J]. 电工技术学报, 2018, 33(18): 41-54. Mi Yan, Xu Jin, Liu Hongliang, et al. Simulation on perforation features in a single-cell system exposed to high-frequency nanosecond pulse bursts based on mesh transport network model[J]. Transactions of China Electrotechnical Society, 2018, 33(18): 41-54.
[6] Bos W V D, Scheltema M J, Siriwardana A R, et al. Focal irreversible electroporation as primary treatment for localized prostate cancer[J]. BJU International, 2017, 119(2): 37-38.
[7] 米彦, 孙才新, 姚陈果, 等. 基于等效电路模型的细胞内外膜跨膜电位频率响应[J]. 电工技术学报, 2007, 22(6): 6-11. Mi Yan, Sun Caixin, Yao Chenguo, et al. Frequency response of transmembrane potential on cell inner and outer membrane based on equivalent circuit model[J]. Transactions of China Electrotechnical Society, 2007, 22(6): 6-11.
[8] 姚陈果, 吕彦鹏, 赵亚军, 等. 基于能量概率与微孔力模型的脉冲电场对细胞电穿孔动态过程的仿真分析[J]. 电工技术学报, 2016, 31(23): 141-149. Yao Chenguo, Lu Yanpeng, Zhao Yajun, et al. Simulation analysis of dynamic process of cell electroporation based on energy probability and microporous force model[J]. Transactions of China Electrotechnical Society, 2016, 31(23): 141-149.
[9] Onik G, Mikus P, Rubinsky B. Irreversible electroporation: implications for prostate ablation[J]. Technology in Cancer Research & Treatment, 2007, 6(4): 295-300.
[10] Rubinsky J, Onik G, Mikus P, et al. Optimal parameters for the destruction of prostate cancer using irreversible electroporation[J]. The Journal of Urology, 2008, 180(6): 2668-2674.
[11] Martin R C G, Mcfarland K, Ellis S, et al. Irreversible electroporation in locally advanced pancreatic cancer: potential improved overall survival[J]. Annals of Surgical Oncology, 2013, 20(3): 443-449.
[12] Charpentier K P, Wolf F, Noble L, et al. Irreversible electroporation of the pancreas in swine: a pilot study[J]. International Hepato-Pancreato-Biliary Association, 2010, 12(5): 348-351.
[13] Wendler J J, Pech M. Urinary tract effects after multifocal nonthermal irreversible electroporation of the kidney: acute and chronic monitoring by magnetic resonance imaging, intravenous urography and urinary cytology[J]. Cardiovascular & Interventional Radiology, 2012, 35(4): 921-926.
[14] Olweny E O, Kapur P, Tan Y K, et al. Comparison of nonthermal irreversible electroporation (NT-IRE) to thermal irreversible electroporation (T-IRE) for kidney ablation in a porcine model[J]. Journal of Endourology, 2011, 25(1): A4-A4.
[15] Tracy C R, Kabbani W, Cadeddu J A . Irreversible electroporation (IRE): a novel method for renal tissue ablation[J]. Journal of Urology, 2011, 183(4): 286-287.
[16] Calmels L, Al-Sakere B, Ruaud J P, et al. In vivo MRI follow-up of murine tumors treated by electrochemotherapy and other electroporation-based treatments[J]. Technology in Cancer Research & Treatment, 2012, 11(6): 561-570.
[17] 米彦, 彭文成, 芮少琴, 等. 高频纳秒脉冲串作用下皮肤肿瘤热效应的多参数有限元仿真与实验[J]. 电工技术学报, 2017, 32(22): 264-274. Mi Yan, Peng Wencheng, Rui Shaoqin, et al. Thermal effects in skin tumor exposed to high-frequency nanosecond pulse bursts: multi-parametric finite element simulation and experiment[J]. Transactions of China Electrotechnical Society, 2017, 32(22): 264-274.
[18] Wong D, Lee E W, Kee S T. Translational research on irreversible electroporation: VX2 rabbit head and neck[M]. Clinical Aspects of Electroporation, 2011.
[19] 郭飞, 李成祥, 唐贤伦, 等. 冲激辐射天线实现皮秒脉冲电场在人体大脑模型中聚焦的研究[J]. 电工技术学报, 2016, 31(3): 195-202. Guo Feng, Li Chengxiang, Tang Xianlun, et al. Focusing of picosecond pulsed electric field in human brain model with impulse radiating antenna[J]. Transactions of China Electrotechnical Society, 2016, 31(3): 195-202.
[20] Lee E W, Chen C, Prieto V E, et al. Advanced hepatic ablation technique for creating complete cell death: irreversible electroporation[J]. Radiology, 2010, 255(2): 426-433.
[21] Xiong Zhengai. Percutaneous ultrasound-guided irreversible electroporation: a goat liver study[J]. Oncology Letters, 2012, 4(3): 450-454.
[22] Appelbaum L, Bendavid E, Sosna J, et al. US findings after irreversible electroporation ablation: radiologic-pathologic correlation[J]. Radiology, 2012, 262(1): 117-125.
[23] Hsiao C Y, Huang K W. Irreversible electroporation: a novel ultrasound-guided modality for non-thermal tumor ablation[J]. Journal of Medical Ultrasound, 2017, 25(4): 195-200.
[24] Sommer C M, Fritz S, Vollherbst D, et al. CT-guided irreversible electroporation in an acute porcine liver model: effect of previous transarterial iodized oil tissue marking on technical parameters, 3D computed tomographic rendering of the electroporation zone, and histopathology[J]. Cardio Vascular and Interventional Radiology, 2015, 38(1): 191-200.
[25] Figini M, Wang Xifu, Lyu T, et al. Preclinical and clinical evaluation of the liver tumor irreversible electroporation by magnetic resonance imaging[J]. American Journal of Translational Research, 2017, 9(2): 580-590.
[26] Martin R C. Irreversible electroporation of locally advanced pancreatic head adenocarcinoma[J]. Journal of Gastrointestinal Surgery, 2013, 17(10): 1850-1856.
[27] Campelo S, Valerio M, Ahmed H U, et al. An evaluation of irreversible electroporation thresholds in human prostate cancer and potential correlations to physiological measurements[J]. APL Bioengineering, 2017, 1(1): 1-10.
[28] Ivorra A, Mir L M, Rubinsky B. Electric field redistribution due to conductivity changes during tissue electroporation: experiments with a simple vegetal model[J]. Ifmbe Proceedings, 2009, 25(13): 59-62.
[29] Yao Chenguo, Lü Yanpeng, Dong Shoulong, et al. Irreversible electroporation ablation area enhanced by synergistic high- and low-voltage pulses[J]. Plos One, 2017, 12(3): 1-19.
[30] Hjouj M, Rubinsky B. Magnetic resonance imaging characteristics of nonthermal irreversible electroporation in vegetable tissue[J]. Journal of Membrane Biology, 2010, 236(1): 137-146.
[31] Bhonsle S P, Arena C B, Daniel C S. Mitigation of impedance changes due to electroporation therapy using bursts of high-frequency bipolar pulses[J]. BioMedical Engineering OnLine, 2015, 14(S3): 1-14.
[32] Zupanic A, Kos B, Miklavcic D . Treatment planning of electroporation-based medical interventions: electrochemotherapy, gene electrotransfer and irreversible electroporation[J]. Physics in Medicine and Biology, 2012, 57(17): 5425-5440.
[33] Muratori C, Pakhomov A G, Shu X, et al. Electrosensitization assists cell ablation by nanosecond pulsed electric field in 3D cultures[J]. Scientific Reports, 2016, 6(1): 1-9.
Model of Irreversible Electroporation Dose-Effect Relationship for Clinical Multi-Needle Ablation Tumors
Abstract In the clinical application of irreversible electroporation tumor therapy, because the ablation area generated by the electric field pulse is small, multi-electrode treatment need to achieve complete ablation of tumor tissue for patients with large tumor size. However, at present, multi-needle treatment is still predicted by the superposition of two treatment effects, which is not conducive to the development of an accurate treatment-planning. Aiming at this problem, based on the electric field distribution and ablation effect of irreversible electroporation tumor ablation with multi-electrode, a numerical model suitable for multi-electrode treatment is established. Based on analysis of the conductivity model, a dose-effect relationship model considering the cumulative effect under multi-needle treatment was established. The potato tissue ablation experiment was performed under the voltage of 500V, 600V, 700V, 800V and 1 000V, and compared the prediction results of the traditional model, the superposition model and the dose-response model. The results show that the accuracy and feasibility of the dose-response model (mean error is less than 5.04%), and it can be used for pre-treatment of multi-needle treatment guidance, providing theoretical and data support for the development of treatment options for clinical applications of irreversible electroporation.
keywords：Cumulative effect, dose-effect relationship model, treatment plan, irreversible electroporation, ablation effect
中图分类号：TM11; TM836; Q64
DOI： 10.19595/j.cnki.1000-6753.tces.190470
国家自然科学基金项目（51877022）、重庆市研究生科研创新项目（CYB17011）和中央高校基本科研业务费（106112017CDJQJ158835）资助。
收稿日期 2019-04-22
改稿日期 2019-06-02
姚陈果 男，1975年生，教授，博士生导师，研究方向为电气设备在线监测与故障诊断技术、生物医学中的电工新技术及高电压新技术研究。E-mail：yaochenguo@cqu.edu.cn
董守龙 男，1989年生，讲师，博士，研究方向为高电压新技术在生物医学及其治疗装置中的应用等。E-mail：dsl@cqu.edu.cn（通信作者）
（编辑 赫蕾）