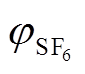 下的扩散过程进行计算,并结合理论分析及多元非线性拟合,得到八种主要特征分解气体浓度的时域和空间预测模型。结果表明,分解气体的扩散主要与扩散系数DG有关,T、p以及
下的扩散过程进行计算,并结合理论分析及多元非线性拟合,得到八种主要特征分解气体浓度的时域和空间预测模型。结果表明,分解气体的扩散主要与扩散系数DG有关,T、p以及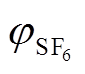 对于扩散过程的影响也主要体现在扩散系数上,且温度对扩散系数的影响要小于压力p和SF6混合比
对于扩散过程的影响也主要体现在扩散系数上,且温度对扩散系数的影响要小于压力p和SF6混合比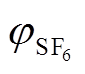 。各分解气体浓度cG随距离的增加呈指数衰减,随时间的增加呈指数增长。扩散过程会使检测处和缺陷源头处间的cG产生差异,从而影响化学检测法的准确性。此外,在扩散作用下,各类特征气体在绝缘诊断中的权重也会发生改变。
。各分解气体浓度cG随距离的增加呈指数衰减,随时间的增加呈指数增长。扩散过程会使检测处和缺陷源头处间的cG产生差异,从而影响化学检测法的准确性。此外,在扩散作用下,各类特征气体在绝缘诊断中的权重也会发生改变。摘要 为明确气体绝缘传输线或称气体绝缘输电管道(GIL)内分解气体的扩散过程及其对化学检测法的影响,基于Fick定律和Fuller-Schettler-Giddings(FSG)方程建立GIL内分解气体在SF6及SF6/N2中的扩散模型。利用密度泛函理论(DFT)和范德华表面分析,得到了分子扩散体积Vd的预测方法。通过有限元法(FEM)对不同温度T、压力p及SF6混合比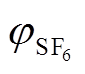 下的扩散过程进行计算,并结合理论分析及多元非线性拟合,得到八种主要特征分解气体浓度的时域和空间预测模型。结果表明,分解气体的扩散主要与扩散系数DG有关,T、p以及
下的扩散过程进行计算,并结合理论分析及多元非线性拟合,得到八种主要特征分解气体浓度的时域和空间预测模型。结果表明,分解气体的扩散主要与扩散系数DG有关,T、p以及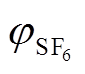 对于扩散过程的影响也主要体现在扩散系数上,且温度对扩散系数的影响要小于压力p和SF6混合比
对于扩散过程的影响也主要体现在扩散系数上,且温度对扩散系数的影响要小于压力p和SF6混合比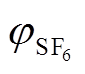 。各分解气体浓度cG随距离的增加呈指数衰减,随时间的增加呈指数增长。扩散过程会使检测处和缺陷源头处间的cG产生差异,从而影响化学检测法的准确性。此外,在扩散作用下,各类特征气体在绝缘诊断中的权重也会发生改变。
。各分解气体浓度cG随距离的增加呈指数衰减,随时间的增加呈指数增长。扩散过程会使检测处和缺陷源头处间的cG产生差异,从而影响化学检测法的准确性。此外,在扩散作用下,各类特征气体在绝缘诊断中的权重也会发生改变。
关键词:化学检测法 气体绝缘传输线 分解气体扩散 扩散系数 分子扩散体积 传质模型
目前,气体绝缘输电线或称气体绝缘输电管道(Gas Insulated transmission Lines, GIL)在电力系统中的推广应用已受到重视,现有GIL多采用SF6作为绝缘介质,而由于SF6温室效应潜能值(Global Warming Potential, GWP)较高,且在高气压下SF6的液化温度很难满足极寒运行条件的要求,因此已有部分GIL采用SF6/N2混合气体来解决上述问题[1]。而化学检测法作为较成熟的绝缘诊断方法,已在SF6气体绝缘设备的运行维护方面得到广泛应用[2]。该方法是通过测定气室内特征分解气体种类及浓度的方式来判断设备内的绝缘缺陷水平。分解气体在密闭气室内从产生到进入化学检测装置的过程主要分为三个阶段:①在绝缘缺陷处的SF6在局部放电作用下发生分解,并生成特征分解气体;②特征分解气体通过扩散在腔体内传播;③特征分解气体扩散到采样口附近,随SF6或SF6/N2送入SF6组分检测装置。相较于其他气体绝缘设备,GIL体积大,距离长,特征分解气体在气室内的轴向扩散过程对其浓度分布的影响更明显。扩散过程中,特征分解气体浓度cG会随距离L和时间t的变化而发生改变,从而影响绝缘诊断的准确性。因此,需要对GIL内特征分解气体在SF6及SF6/N2中的扩散过程及分布特征进行研究[3]。
对于SF6或SF6/N2中的气体扩散问题,文献[3]对H2O和H2S在GIL中的扩散过程进行了仿真分析,得到了H2O和H2S的浓度在GIL内的径向和轴向分布特征,并依此优化了GIL内气体传感器的布置方案。但由于部分扩散参数未知,文献[3]并未对其他特征气体的扩散过程进行计算。日本东芝公司通过扩散试验和Fuller公式对SF6在N2中的扩散系数进行了测定[4]。美国辛辛那提大学的W. L. Taylor等对稀有气体在SF6中的热扩散因子和分子作用势进行了测定[5]。墨西哥国立自治大学的J. D. Urquijo-Carmona及马来西亚珀坦尼亚大学的Z. A. Talib等对SF+、SF2+、SF3+和SF5+在SF6中的传递系数进行了实验测定[6-7]。此外,文献[8]利用流体力学计算技术(Computational Fluid Dynamics, CFD)中的传质模型对气体绝缘全封闭组合电器(Gas Insulated Swithgear, GIS)内H2O的扩散过程进行了仿真分析,结果表明在封闭静置的GIS内,H2O仅通过分子热运动扩散的速度很慢,而在流动体系中,扩散速度则会大幅度提高。因此在设备内出现局部高湿度时,采气口处的湿度很难准确表征设备内的真实湿度。同样,该方法也适用于SF6中其他的微量气体扩散问题(如特征分解气体及泄漏示踪气体He[9])。此外,西安交通大学的Zhang J. L.[10]和Zhong L.[11]等通过A. B. Murphy[12]提出的组合扩散系数对C2F4、铜蒸气、电子、离子和自由基在SF6断路器中的扩散特性进行了计算分析。由于断路器在灭弧时具有高温、高压和高电场强度的特点,因此组合扩散系数中的一般扩散系数、温度扩散系数、压力扩散系数和场强扩散系数都会对扩散过程产生影响。该方法适用于描述高温等离子体内的分解和扩散过程,但对于GIL内的扩散问题,由于分解气体含量较少,腔体内的温度梯度和压力梯度较小,且一般呈电中性,电场对于气体扩散的影响不明显,因此该问题主要与浓度梯度和一般扩散系数有关。各分解气体之间的扩散影响较小,各分解气体的扩散可视为独立扩散,可通过传质模型和二元扩散系数对GIL内的分解气体扩散过程进行计算。
通过上述分析可知,目前对于特征分解气体在SF6及SF6/N2中的扩散过程研究仍存在不足,而且相关气体扩散参数的缺失是限制其研究进展的主要障碍之一。因此,为明确分解气体在GIL内的扩散过程及影响其扩散速度的条件因素,本文首先结合分子表面分析技术及相关传质扩散理论,建立气体扩散系数的预测模型,并根据扩散模型及扩散系数对不同温度T、压力p及SF6混合比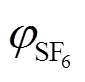 下分解气体在SF6及SF6/N2中的扩散过程及气体浓度变化规律进行了研究分析,讨论了扩散问题对化学检测法的影响。
下分解气体在SF6及SF6/N2中的扩散过程及气体浓度变化规律进行了研究分析,讨论了扩散问题对化学检测法的影响。
因分子运动而形成的物质传递现象称为分子传质,也称分子扩散。分子扩散可在气相、液相和固相中进行。本文研究的各特征分解气体在SF6及SF6/N2中的扩散过程属于两组分气体扩散,根据Fick定律
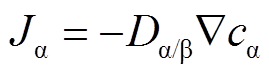 (1)
(1)
式中,Jα为气体α在气体β中的扩散传质通量,kg/(m2∙s);Dα/β为气体α在气体β中的扩散系数,m2/s;Ñ为哈密顿算子;cα为气体α的浓度,kmol/m3;Ñca为气体α的浓度梯度,kmol/m4。可知扩散传质通量Jα的大小与扩散系数Dα/β和浓度梯度Ñca成正比。对于瞬态扩散问题,气体α在气体β中的扩散浓度cα随时间变化关系可表示为
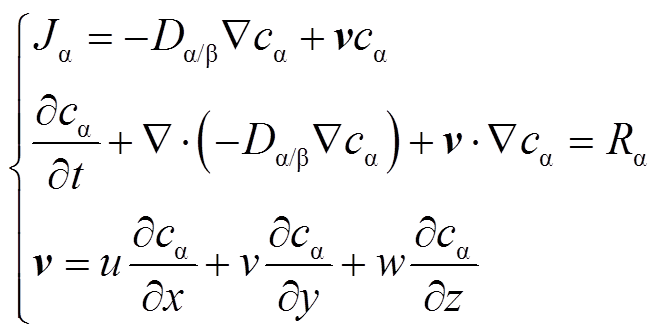 (2)
(2)式中,v为流速矢量,m/s;u、v、w分别为v在x、y、z轴上的速度分量,m/s;Rα为化学反应引起的气体α浓度增加速率,kg/(m3∙s)。对于无流速和化学反应的单纯扩散传质,即有v=0;Rα=0,式(2)可简化为
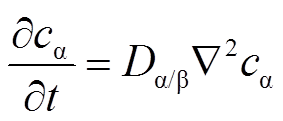 (3)
(3)
此外,对于两组分扩散系统,有
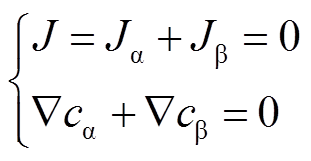 (4)
(4)则
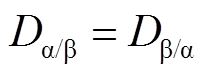 (5)
(5)
式中,Dβ/α为气体β在气体α中的扩散系数,m2/s,它与气体α在气体β中的扩散系数Dα/β相等。
由于GIL的轴向长度远大于径向,相较于轴向扩散,径向扩散对分解物浓度分布影响较小。此外,径向对流会使特征气体在径向快速扩散,这使得径向扩散时间远小于轴向扩散时间,因此本文忽略了径向扩散。而根据文献[3]中的对比结果也可知,径向对流并不会对分解气体的轴向扩散造成较大的影响。各特征气体的产量主要参考现有的试验结果[13-14],但文献中的检测结果只能够表征试验腔体内的平均浓度cva。为了使参考数据能够作为输入量代入到模型中计算,需要对仿真模型参数进行调整。而考虑到cva与GIL径向截面的平均浓度csa之间存在一定映射关系,本文忽略了GIL径向截面内部的浓度分布,而是将截面内的整体浓度水平作为研究对象,并用其面平均浓度csa来表征。参考文献中测得的cva可作为csa代入到计算模型中。此外,由于GIL内壁一般会进行特殊处理(如涂氟、涂漆等),可以抑制其对SF6及分解气体的吸附。根据上述分析,本文对GIL仿真模型做出如下假设:①主要考虑腔体内的轴向扩散;②忽略径向对流对分解气体轴向扩散的影响;③腔体、固体绝缘件及SF6不与分解气体发生二次反应,且各气固交界面无通量。
结合上述假设,本文根据国内某厂商的110kV GIL设备进行了数值化建模,并设立了相应边界条件,如图1所示。整个模型长5m,GIL外壳内径约为270mm,内设有中心导体,导体外径约为50mm。由于局部放电一般发生在中心导体外壁、盆式绝缘子表面及外壳内壁,且各部件间有密封措施,因此分解气体一般只在中心导体与外壳间的区域扩散,即图1中的阴影处。
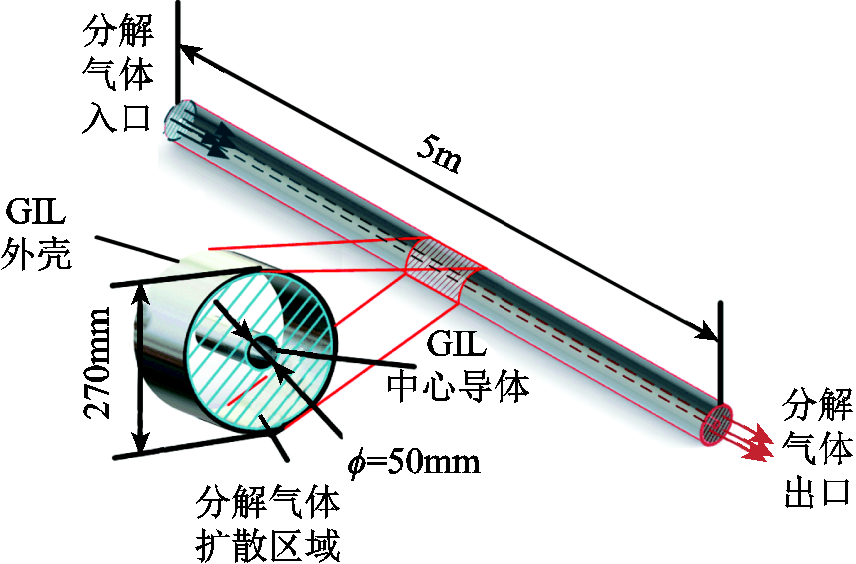
图1 GIL分解气体扩散模型
Fig.1 Decomposition gas diffusion model in GIL
气体从GIL模型一端流入,通过扩散从另一端流出,腔体中的特征分解气体初始浓度为0kmol/m3,t为时间;以入口为参考点,L为距离参考点的距离。导体外壁及壳体内壁边界的特征分解气体通量JG为0kg/(m2∙s)。入口处分解气体浓度为cG0(t),由于出口距离入口较远,出口处的浓度梯度较小,可设为0kmol/m4。将式(3)与上述条件联立,求解特征气体浓度。
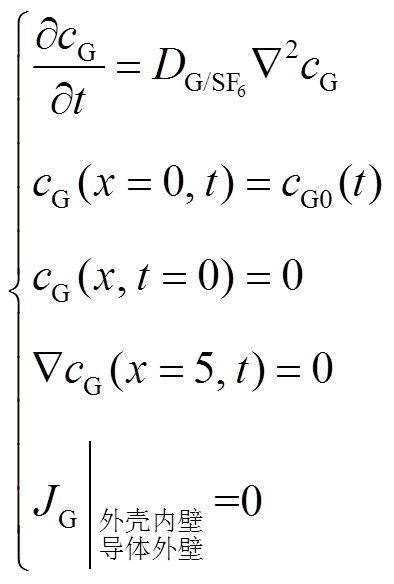 (6)
(6)式中,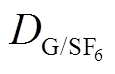 为特征分解气体在SF6中的扩散系数,m2/s。
为特征分解气体在SF6中的扩散系数,m2/s。
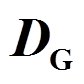 计算方法
计算方法通过式(3)可以看出,影响气体扩散速度和组分通量的主要因素为扩散系数D。而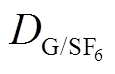 与体系压力p、温度T及相对分子质量M和分子扩散体积Vd性质有关,可由Fuller-Schettler-Giddings (FSG)公式得到[15]。
与体系压力p、温度T及相对分子质量M和分子扩散体积Vd性质有关,可由Fuller-Schettler-Giddings (FSG)公式得到[15]。
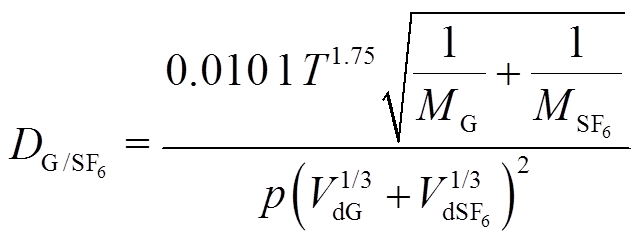 (7)
(7)式中,T为体系温度,K;p为体系压力,Pa;MG和 分别为分解气体及SF6的相对分子质量,g/mol;VdG和
分别为分解气体及SF6的相对分子质量,g/mol;VdG和 分别为特征分解气体及SF6的分子扩散体积,cm3/mol。该方法的相对准确度大于90%,若
分别为特征分解气体及SF6的分子扩散体积,cm3/mol。该方法的相对准确度大于90%,若
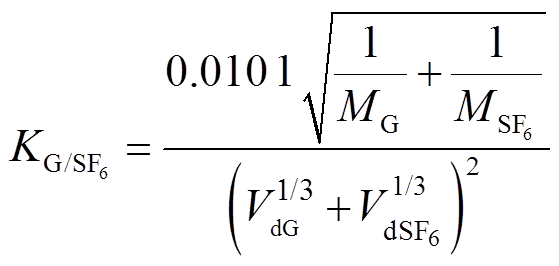 (8)
(8)
则式(7)可简化为
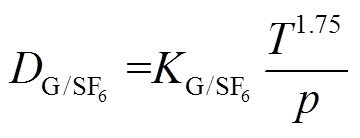 (9)
(9)式中, 为分解气体在SF6中的扩散特性常数,仅与分子性质有关,不随p和T变化。相同条件下,
为分解气体在SF6中的扩散特性常数,仅与分子性质有关,不随p和T变化。相同条件下, 越大,分解气体的扩散越快。对于在SF6/N2混合气体中的分解气体扩散系数
越大,分解气体的扩散越快。对于在SF6/N2混合气体中的分解气体扩散系数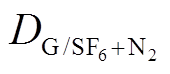 ,可根据
,可根据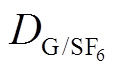 和
和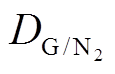 按体积分数加权求和得到[16]
按体积分数加权求和得到[16]
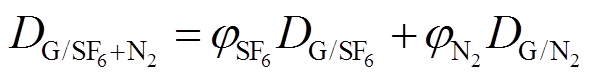 (10)
(10)
式中,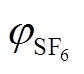 和
和 分别为SF6/N2混合气体中SF6及N2的体积分数。类似地,式(10)可改写成为
分别为SF6/N2混合气体中SF6及N2的体积分数。类似地,式(10)可改写成为

式中,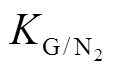 为分解气体在N2中的扩散常数;
为分解气体在N2中的扩散常数;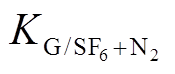 为分解气体在SF6/N2混合气中的扩散常数。对于本文研究的扩散体系,式(6)及式(11)中的
为分解气体在SF6/N2混合气中的扩散常数。对于本文研究的扩散体系,式(6)及式(11)中的 、
、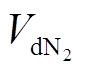 、
、 及
及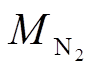 已知,见表1。
已知,见表1。
表1 FSG经验公式中参数取值
Tab.1 Parameters of FSG formula in this paper

参数数值 SF6的分子扩散体积/(cm3/mol)71.3 SF6的相对分子质量/(kg/kmol)146.05 N2的分子扩散体积/(cm3/mol)18.5 N2的相对分子质量/(kg/mol)28.01
而对于VdG,目前尚未有完整的实验数据,需进一步研究。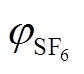 和
和 可根据实际气体混合比进行设置。
可根据实际气体混合比进行设置。
2.2.1 计算参数的选择
分子扩散体积Vd是指1mol气体在正常沸点时的自由扩散体积,单位为cm3/mol。由于气体的性质及分子间相互作用的不同,各气体的分子扩散体积会有所差异。目前通过实验测得的原子扩散体积Vda及分子扩散体积Vdm见表2[17]。
表2 原子扩散体积Vda及分子扩散体积Vdm
Tab.2 The atomic diffusion volume Vda and molecular diffusion volume Vdm

原子原子扩散体积Vda/ (cm3/mol)分子分子扩散体积Vdm/ (cm3/mol) C15.9H26.12 H2.31CO18 O6.11CO226.9 S22.9N2O35.9 N4.54SF671.3 F14.7H2O13.1 Cl21SO241.8 Cl238.4 NH320.7
对于无相关实验数据的气体,一般根据其分子式将所包含原子的Vda按原子数相加,从而得到气体的叠加分子扩散体积Vds,即
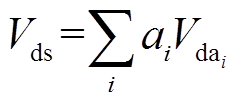 (12)
(12)
式中,i为气体分子所含原子种类,i=1,2,3…;ai为分子所含i原子的个数;Vdai为i原子的扩散体积,cm3/mol。本文根据各分子的Vda对表3中给出分子的Vds进行了计算,所得Vds与Vdm的拟合结果如图2所示。
表3 部分分子的分子体积Vm
Tab.3 The molecular volume Vm of some molecules

分子分子体积Vm/bohr3分子分子体积Vm/bohr3 H2122.35SF6594.14 CO249.00H2O180.53 CO2270.18SO2381.83 Cl2439.45N2O313.50 NH3233.59
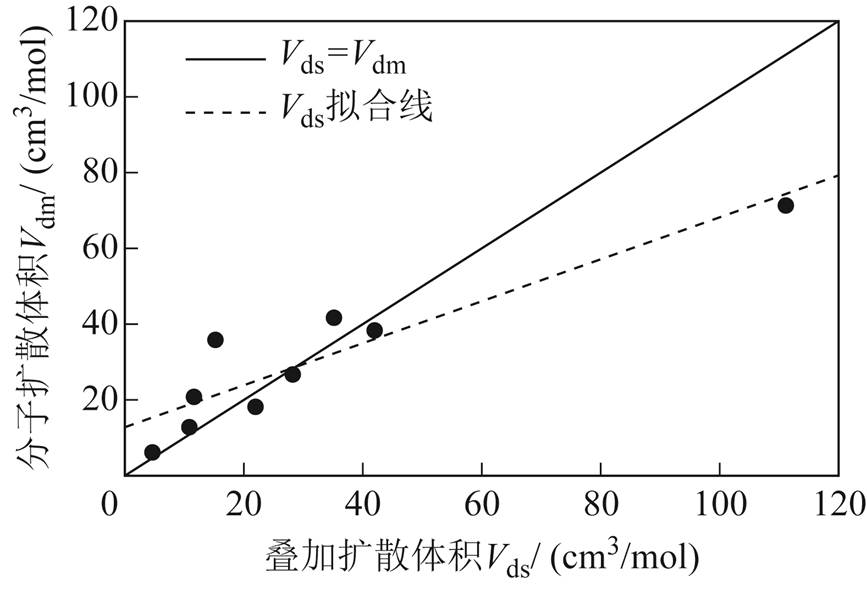
图2 叠加扩散体积与扩散体积对比拟合
Fig.2 Comparison and regression between superimposed diffusion volume and diffusion volume
图2中,实线为Vds=Vdm的标准线,虚线为Vds对Vdm的线性拟合线,拟合结果为
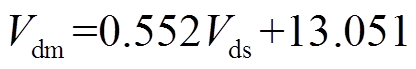 (13)
(13)其可决系数R2为0.84。可以看出,Vds与Vdm偏差较大,即使通过式(13)矫正,准确度仍较低,这主要与两者的定义有关。以图3中的CO2为例,Vds是组成分子的原子(C和O)独立扩散得到的体积,而Vdm是分子(CO2)扩散出的体积,因此很难采用Vds来准确表征Vdm。
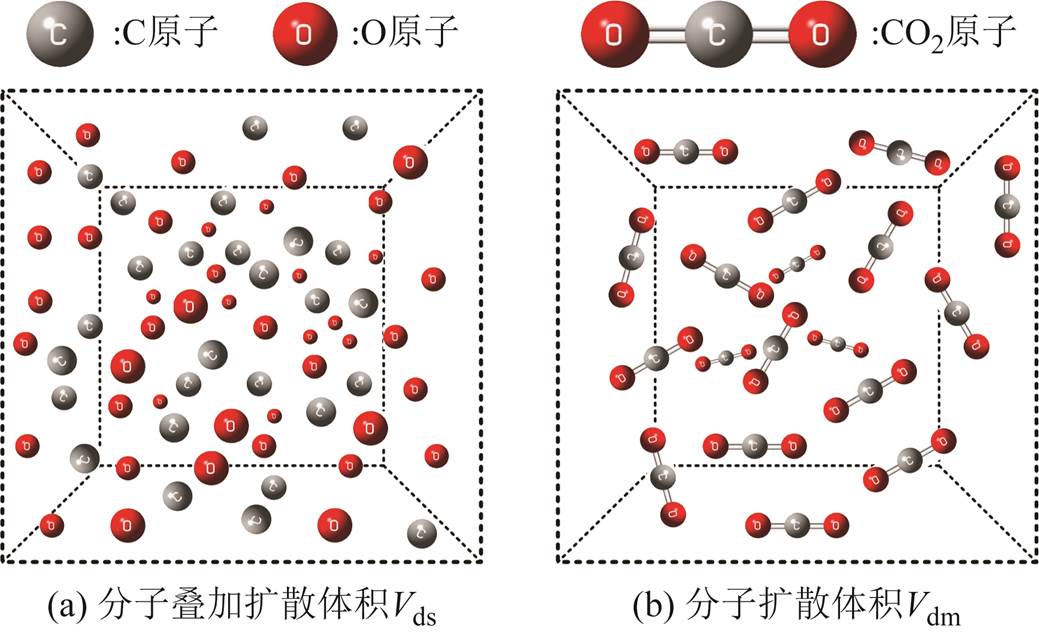
图3 分子叠加扩散体积Vds和分子扩散体积Vdm示意图
Fig.3 Schematic diagram of molecular superimposed diffusion volumeVds and molecular diffusion volume Vdm
为解决上述问题,本文采用其他参数和方法对Vdm进行预测。结合实际气体的范德华公式
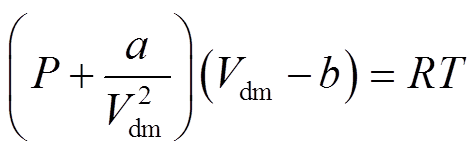 (14)
(14)式中,a和b为范德华参量,与分子间作用(如范德华力)和分子体积Vm有关;R为普适气体常数,约为8.31J/(mol∙K)。气体的Vdm会受其Vm的影响,此外,分子体积Vm可通过范德华表面进行计算,而范德华表面与分子间作用有着较强的相关性。综合考虑,本文通过范德华表面计算Vm,并用其预测气体分子的Vdm。
2.2.2 分子扩散体积Vdm的拟合及预测
根据Barder的定义,原子或分子体电荷密度为1.08×109C/m3(0.001au)的等值面为范德华表面,其所围成的几何体积为原子体积Va或分子体积Vm[18]。本文通过密度泛函理论(Density Function Theory, DFT)中的B3LYP方法[19]和6-311G**基组[20]对表2中九种分子的几何结构进行优化,并利用Multiwfn软件[21]的MT(Marching Tetrahedra)方法[22]对各分子原子进行表面静电势分析,得到了其分子体积Vm,单位为bohr3,1bohr3≈1.48×10-31m3,结果见表3(分子范德华表面如附图1所示)。
为得到Vdm的预测公式,对表2及表3中的Vm和Vdm进行了相关性分析,并利用线性拟合分别得到了Vm与Vdm的关系函数,结果如图4和式(15)所示。图4中实线为Vm与Vdm的拟合线,表达式为
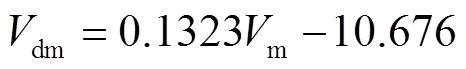 (15)
(15)其可决系数R2为0.95,优于叠加扩散体积Vds。因此,本文最终选用Vm和式(15)对Vdm进行预测。
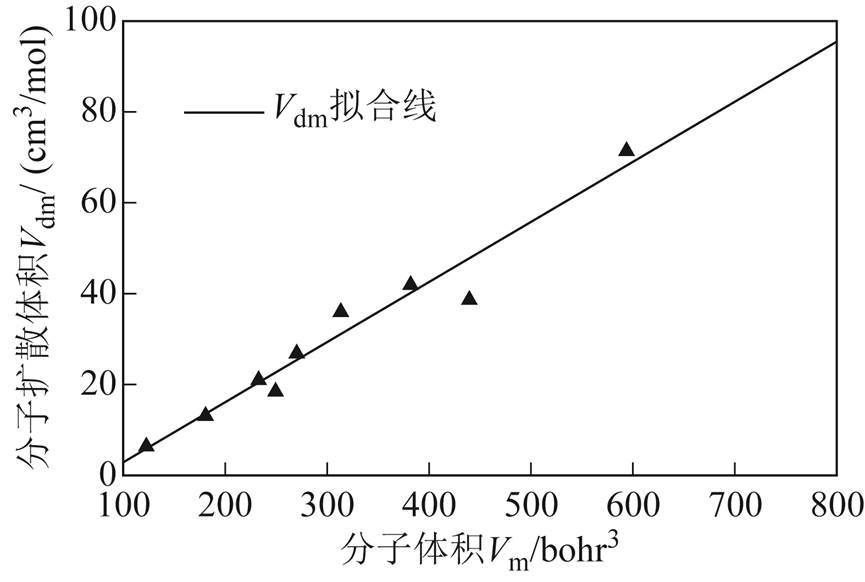
图4 Vm与Vdm的对比及拟合
Fig.4 Comparison between Vm and Vdm and its linear fitting
通过B3LYP方法和6-311G**基组,本文对八种SF6主要特征分解气体(HF、H2S、SO2、SOF2、SO2F2、S2OF10、CS2及COS[13])的分子几何结构进行了优化,并通过Multiwfn对其波函数进行分析,得到分子范德华表面及分子体积。结合式(7)、式(8)和式(10),本文对各分子的Vm、Vdm、 及
及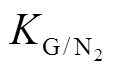 进行了计算,结果见表4(各分子的范德华表面如附图2所示)。通过计算结果可知分解气体在N2中的
进行了计算,结果见表4(各分子的范德华表面如附图2所示)。通过计算结果可知分解气体在N2中的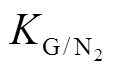 大于SF6中的
大于SF6中的 ,这主要是因为SF6的Vm及Vdm约为N2的3.9倍,在扩散过程中分解气体分子与SF6的碰撞概率要大于N2,扩散受到的阻力也会强于N2。而在SF6中混入N2后,可能有助于分解气体的均匀扩散,便于对GIL内的气体组分检测和诊断分析。
,这主要是因为SF6的Vm及Vdm约为N2的3.9倍,在扩散过程中分解气体分子与SF6的碰撞概率要大于N2,扩散受到的阻力也会强于N2。而在SF6中混入N2后,可能有助于分解气体的均匀扩散,便于对GIL内的气体组分检测和诊断分析。
表4 分解气体的扩散特性参数计算结果
Tab.4 The calculation results of diffusion parameters of characteristic decomposition gases
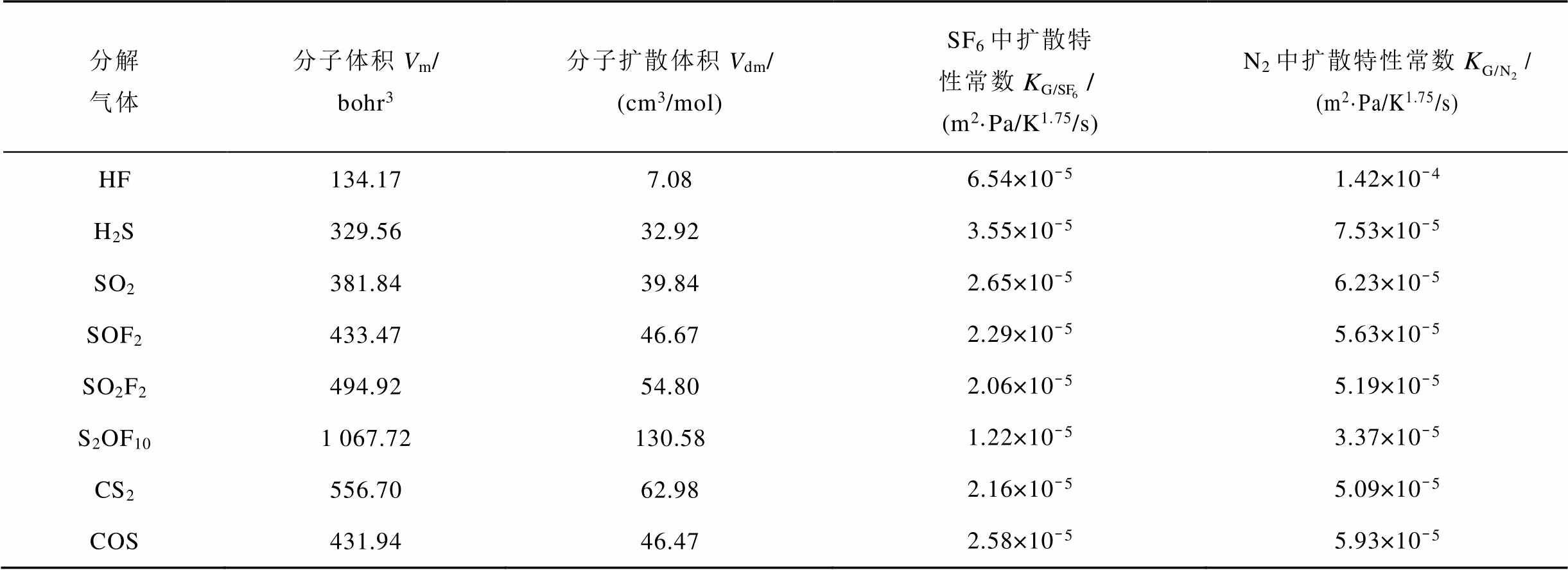
分解气体分子体积Vm/ bohr3分子扩散体积Vdm/ (cm3/mol)SF6中扩散特性常数 (m2·Pa/K1.75/s)N2中扩散特性常数/ (m2·Pa/K1.75/s) HF134.177.086.54×10-51.42×10-4 H2S329.5632.923.55×10-57.53×10-5 SO2381.8439.842.65×10-56.23×10-5 SOF2433.4746.672.29×10-55.63×10-5 SO2F2494.9254.802.06×10-55.19×10-5 S2OF101067.72130.581.22×10-53.37×10-5 CS2556.7062.982.16×10-55.09×10-5 COS431.9446.472.58×10-55.93×10-5
此外,HF的 及
及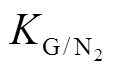 约为其他气体的2倍,这与HF的分子体积Vm较小有关,在扩散过程中HF与SF6及N2的碰撞概率较低,因此其扩散速度要大于其他气体。而较低的碰撞概率使得HF与其他分子接触的机会较小,所以HF虽易与其他物质反应,但凭借较高的扩散系数,HF在腔体内浓度仍可持续增长。在扩散均匀后HF便会参与反应消失。从图5也可以看出在放电期间HF浓度连续增长,在放电结束后才开始缓慢下降(图5实验条件如下:SF6绝对压力为0.4MPa,含水率为128.3μL/L,电压约为50kV,放电量约为12 000pC,5h后停止放电并静置72h)。
约为其他气体的2倍,这与HF的分子体积Vm较小有关,在扩散过程中HF与SF6及N2的碰撞概率较低,因此其扩散速度要大于其他气体。而较低的碰撞概率使得HF与其他分子接触的机会较小,所以HF虽易与其他物质反应,但凭借较高的扩散系数,HF在腔体内浓度仍可持续增长。在扩散均匀后HF便会参与反应消失。从图5也可以看出在放电期间HF浓度连续增长,在放电结束后才开始缓慢下降(图5实验条件如下:SF6绝对压力为0.4MPa,含水率为128.3μL/L,电压约为50kV,放电量约为12 000pC,5h后停止放电并静置72h)。
而对于H2S,其化学性质也较为活泼,但由于 较小,与其他分子的碰撞概率较高,这导致H2S在扩散时就会参与反应,并在放电过程中含量就有先升高后下降的现象[23]。S2OF10的Vm最大,
较小,与其他分子的碰撞概率较高,这导致H2S在扩散时就会参与反应,并在放电过程中含量就有先升高后下降的现象[23]。S2OF10的Vm最大, 及生成速率较低,因此S2OF10含量增长较其他分解气体更为缓慢[14]。其他五种分解气体的
及生成速率较低,因此S2OF10含量增长较其他分解气体更为缓慢[14]。其他五种分解气体的 及
及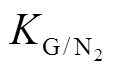 都比较接近。
都比较接近。
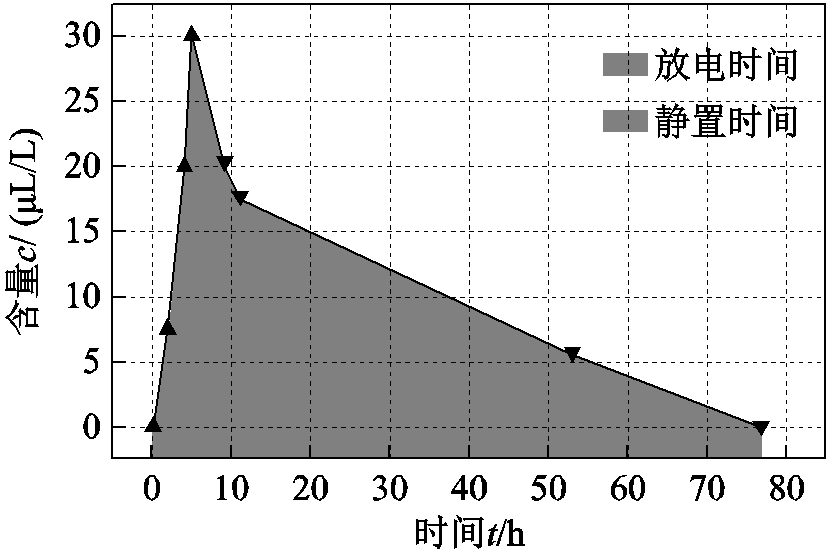
图5 HF在放电时和放电后的含量变化
Fig.5 The change in concentration of HF during and after discharge
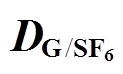
本文分别对八种分解气体的不同气压p和温度T下的特征分解气体扩散系数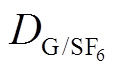 进行了计算,结果如图6所示。
进行了计算,结果如图6所示。

图6 不同温度T及压力p下的扩散系数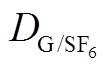
Fig.6 Diffusion coefficient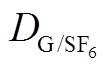 at different temperatures T and pressures p
at different temperatures T and pressures p
由式(9)可知,其他p及T下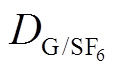 的变化趋势分别与图6a和图6b相似,仅需在各分解气体
的变化趋势分别与图6a和图6b相似,仅需在各分解气体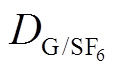 上乘以温度系数kT和压力系数kP比例系数即可,即
上乘以温度系数kT和压力系数kP比例系数即可,即
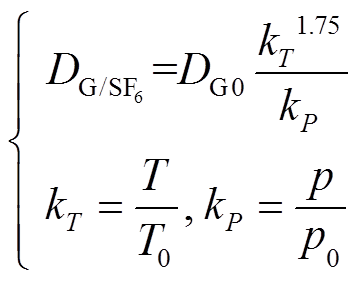 (16)
(16)式中,DG0为温度T0和压力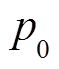 下的分解气体扩散系数。通过图6a与图6b的对比可以看出,随着温度T的增加,扩散系数
下的分解气体扩散系数。通过图6a与图6b的对比可以看出,随着温度T的增加,扩散系数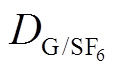 平稳上升,且变化幅度较小;而
平稳上升,且变化幅度较小;而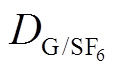 对于压力p敏感度更高,整体呈负指数关系,在300kPa以下时
对于压力p敏感度更高,整体呈负指数关系,在300kPa以下时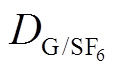 变化较为明显,在600kPa后开始趋于平稳。此外,考虑到GIL等高电压设备通常为刚性腔体,即体积V为常数,当设备存在温升时,腔体内压力可能会升高,因此在实际工况下,温度对扩散的影响是一个压力p和温度T的复合模型。将气态方程代入到式(9)中,可得
变化较为明显,在600kPa后开始趋于平稳。此外,考虑到GIL等高电压设备通常为刚性腔体,即体积V为常数,当设备存在温升时,腔体内压力可能会升高,因此在实际工况下,温度对扩散的影响是一个压力p和温度T的复合模型。将气态方程代入到式(9)中,可得
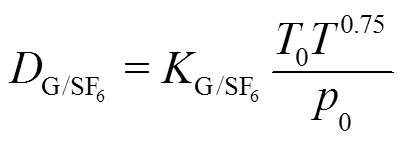 (17)
(17)
式中,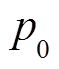 为初始气压,Pa;T0为初始温度,K。以分解气体在初始条件为
为初始气压,Pa;T0为初始温度,K。以分解气体在初始条件为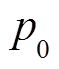 =600kPa、T0=298K的SF6中的扩散为例,
=600kPa、T0=298K的SF6中的扩散为例,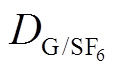 随T变化趋势如图7所示(T变化范围为298~393K)。
随T变化趋势如图7所示(T变化范围为298~393K)。
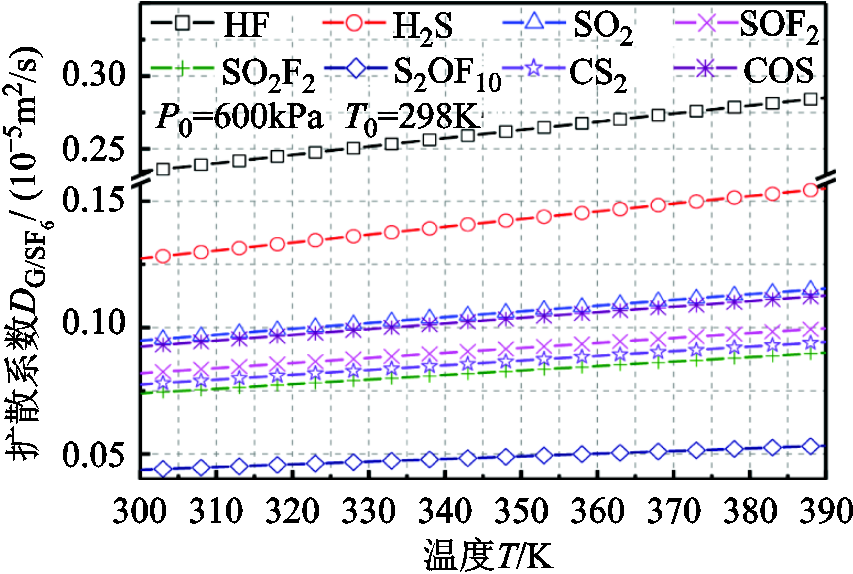
图7 实际工况下扩散系数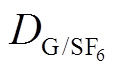 随温度T变化趋势
随温度T变化趋势
Fig.7 Variation trend of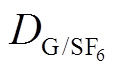 with T under the actual working conditions
with T under the actual working conditions
与图6a对比可以看出,在质量和体积一定的条件下,由于T升高而引起的p上升会使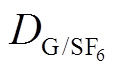 的增加速率减慢,约为理想状况下的85%,因此在实际GIL刚性密闭空间中温度对气体轴向扩散的影响较小。此外,根据文献[3]中的环境条件,本文计算的H2S的扩散系数
的增加速率减慢,约为理想状况下的85%,因此在实际GIL刚性密闭空间中温度对气体轴向扩散的影响较小。此外,根据文献[3]中的环境条件,本文计算的H2S的扩散系数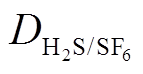 为2.12×10-6m2/s,与文献[3]给出的2.27×10-6m2/s接近,证明该模型具有较高的准确性。
为2.12×10-6m2/s,与文献[3]给出的2.27×10-6m2/s接近,证明该模型具有较高的准确性。
 计算结果分析
计算结果分析根据美国国家标准技术研究所NIST 的L. G. Christophorou等对不同比例下SF6/N2绝缘性能的分析总结可知,混合气体中的SF6含量一般不超过60%,最小占比为20%[24]。因此,本文分别对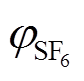 为20%、30%、40%、50%和60%的SF6/N2混合气体的扩散特性常数
为20%、30%、40%、50%和60%的SF6/N2混合气体的扩散特性常数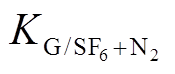 进行了计算,结果见表5。随着SF6含量的增加,分解气体的
进行了计算,结果见表5。随着SF6含量的增加,分解气体的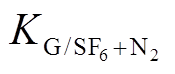 逐渐减小,即N2的加入会加速分解气体的扩散,从而起到优化GIL内分解气体均匀度的作用。而对于不同p和T下的
逐渐减小,即N2的加入会加速分解气体的扩散,从而起到优化GIL内分解气体均匀度的作用。而对于不同p和T下的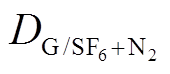 ,其变化趋势与纯气一致,仅需在
,其变化趋势与纯气一致,仅需在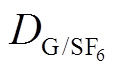 上乘以与
上乘以与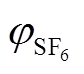 有关的比例系数
有关的比例系数 即可。根据式(9)和式(11),可得
即可。根据式(9)和式(11),可得 表达式为
表达式为
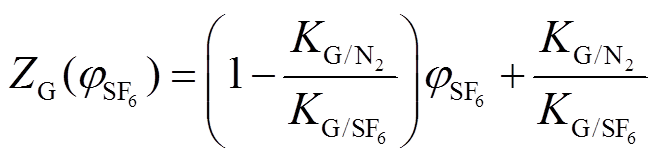 (18)
(18)表5 不同比例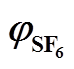 下的扩散特性常数
下的扩散特性常数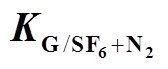 计算结果
计算结果
Tab.5 Calculation results of diffusion characteristic constant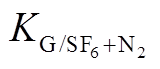 with different mixingratio
with different mixingratio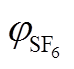
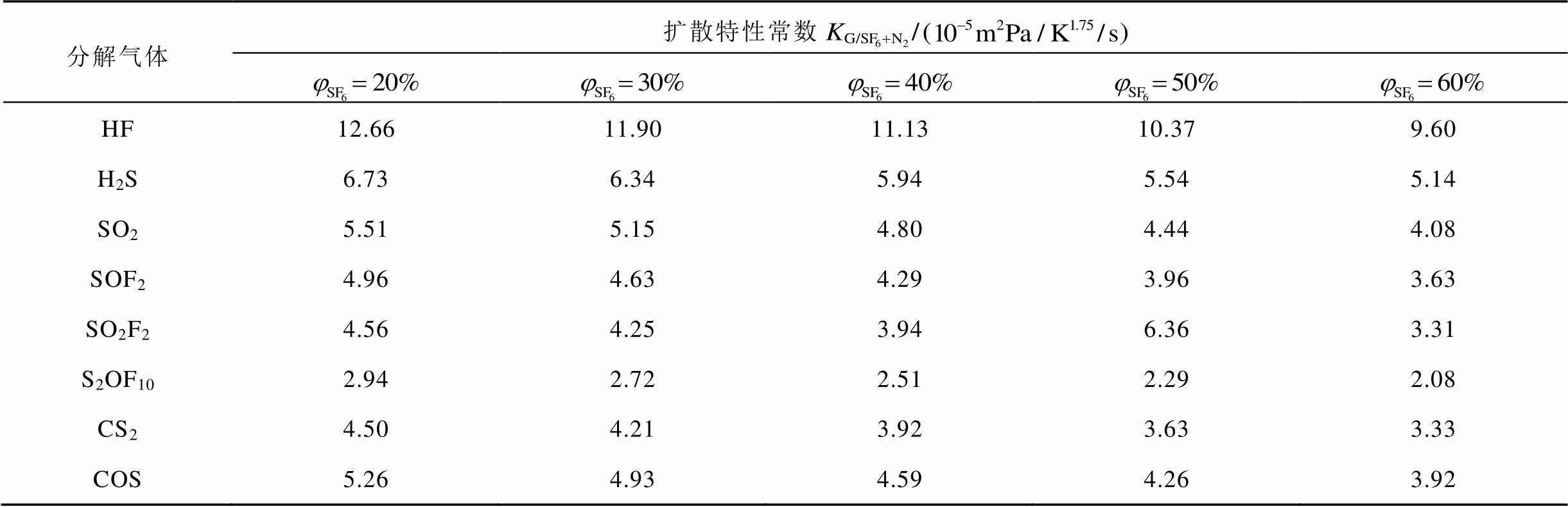
分解气体扩散特性常数 HF12.6611.9011.1310.379.60 H2S6.736.345.945.545.14 SO25.515.154.804.444.08 SOF24.964.634.293.963.63 SO2F24.564.253.946.363.31 S2OF102.942.722.512.292.08 CS24.504.213.923.633.33 COS5.264.934.594.263.92
通过式(18)和表5可计算不同分解气体的 ,见附表1。
,见附表1。
3.4.1 分解气体生成速率
为分析GIL内不同距离、不同时间下分解气体的浓度变化趋势,本文对GIL模型内的扩散过程进行了仿真分析。根据文献[13]和文献[14]中的实验结果,在相近电压(25kV左右)、放电量(200pC左右)、放电模型(沿面放电)和气体压力(0.3~ 0.4MPa)下各分解气体浓度的平均增长速率WG见表6。
由于上述实验结果是在小腔体内完成的,可忽略扩散过程对分解气体浓度检测的影响,WG可用来表示各分解气体的生成速率。通过对比可知,HF具有最高的生成速率,COS的生成速率最低。虽然该组WG仅是特定条件下的实验结果,但不同条件下分解产物的生成难度接近,且本文主要研究的内容为分解气体在扩散过程中的浓度分布特性,具体浓度的取值并不影响分布形式。因此,本文以COS气体的浓度平均增长率WCOS为基准,将各特征气体的WG转换为相对增长速率WRG/COS,并用其来表征气体产生的难易程度。WRG/COSt可表示不同时间t时的入口处特征气体浓度。
表6 相近条件下分解气体生成速率
Tab.6 Decomposition rate under similar condition

分解气体浓度生成速率WG/(μL/L/h)相对增长速率WRG/COS HF4.90490 H2S0.066 SO20.9090 SOF20.3030 SO2F20.5757 S2OF100.022 CS20.022 COS0.011
3.4.2 相对浓度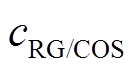 随时间t和距离L的变化规律
随时间t和距离L的变化规律
结合GIL的实际工作情况[25],本文选择p为0.5MPa,T为298K的SF6进行扩散仿真。由于T、p及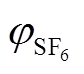 在扩散模型中仅对扩散系数
在扩散模型中仅对扩散系数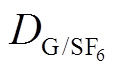 和
和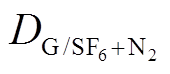 有影响,对于其他条件下的扩散过程,仅需要改变DG即可。此外根据文献[23],SF6/N2的最佳
有影响,对于其他条件下的扩散过程,仅需要改变DG即可。此外根据文献[23],SF6/N2的最佳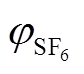 在20%~30%之间,而该范围内的
在20%~30%之间,而该范围内的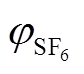 对GIL温度影响较小[26],因此对SF6及SF6/N2混合气均采用同一温度进行计算。为分析时间t对浓度分布的影响,本文记录了扩散30天内不同t下距离入口1m、2.5m和5m处的以COS气体浓度为参考的分解物相对浓度cRG/COS计算结果,如图8所示。
对GIL温度影响较小[26],因此对SF6及SF6/N2混合气均采用同一温度进行计算。为分析时间t对浓度分布的影响,本文记录了扩散30天内不同t下距离入口1m、2.5m和5m处的以COS气体浓度为参考的分解物相对浓度cRG/COS计算结果,如图8所示。
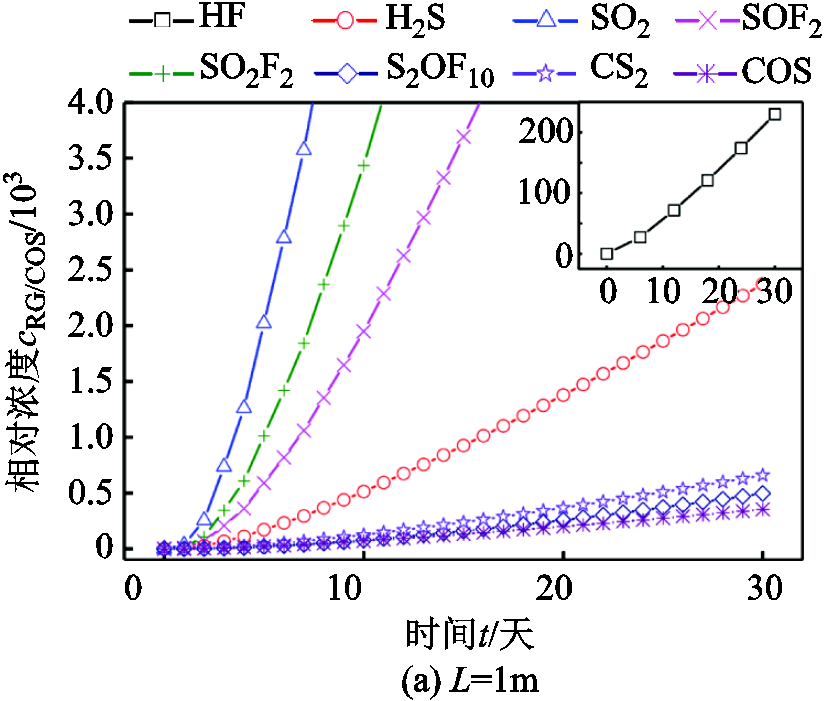

图8 不同距离下分解气体浓度随时间变化趋势
Fig.8 The variation trend of decomposition gas concentration with time at different distances
由图8可以看出分解气体cRG/COS随着t呈指数增长趋势,且由于WRG/COS和DG较小,除HF外的其他七种气体cRG/COS的变化较慢。此外,随着L的增加,分解气体浓度呈减小趋势,而各分解气体的浓度差逐渐增大。为明确L对cRG/COS的影响,本文计算了9天、19天和29天时不同距离L处的cRG/COS,结果如图9所示。
随着L的增加,分解气体浓度呈指数衰减,且扩散时间t越长,各气体间的浓度差距越大;扩散距离L越大,浓度差越小。为得到cRG/COS与t和L的函数关系,本文对式(6)和数值仿真结果进行了分析拟合。由于式(6)中方程的形式与一维热传导方程一致[27],可通过类似的Fourier变换得到通解[28],将数值模型各变量代入可得
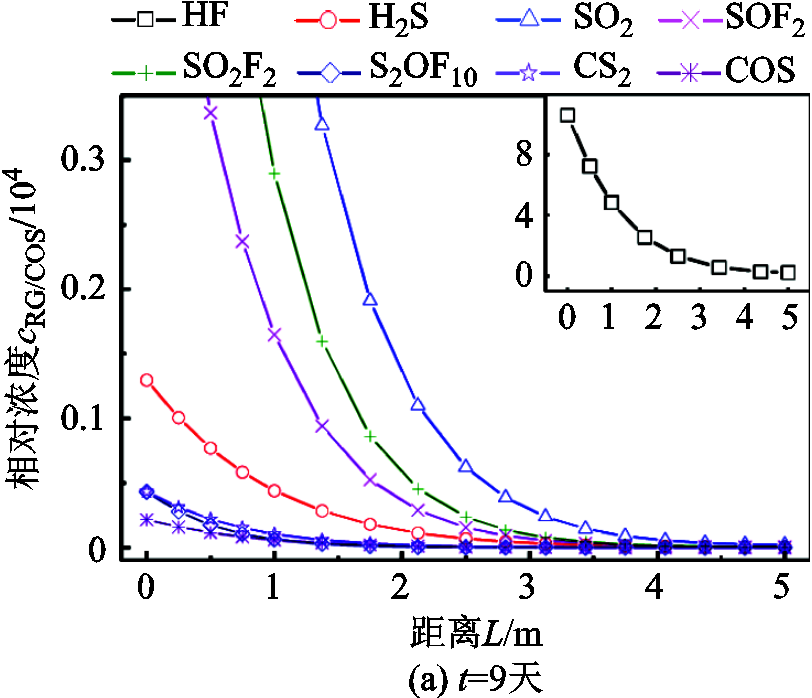
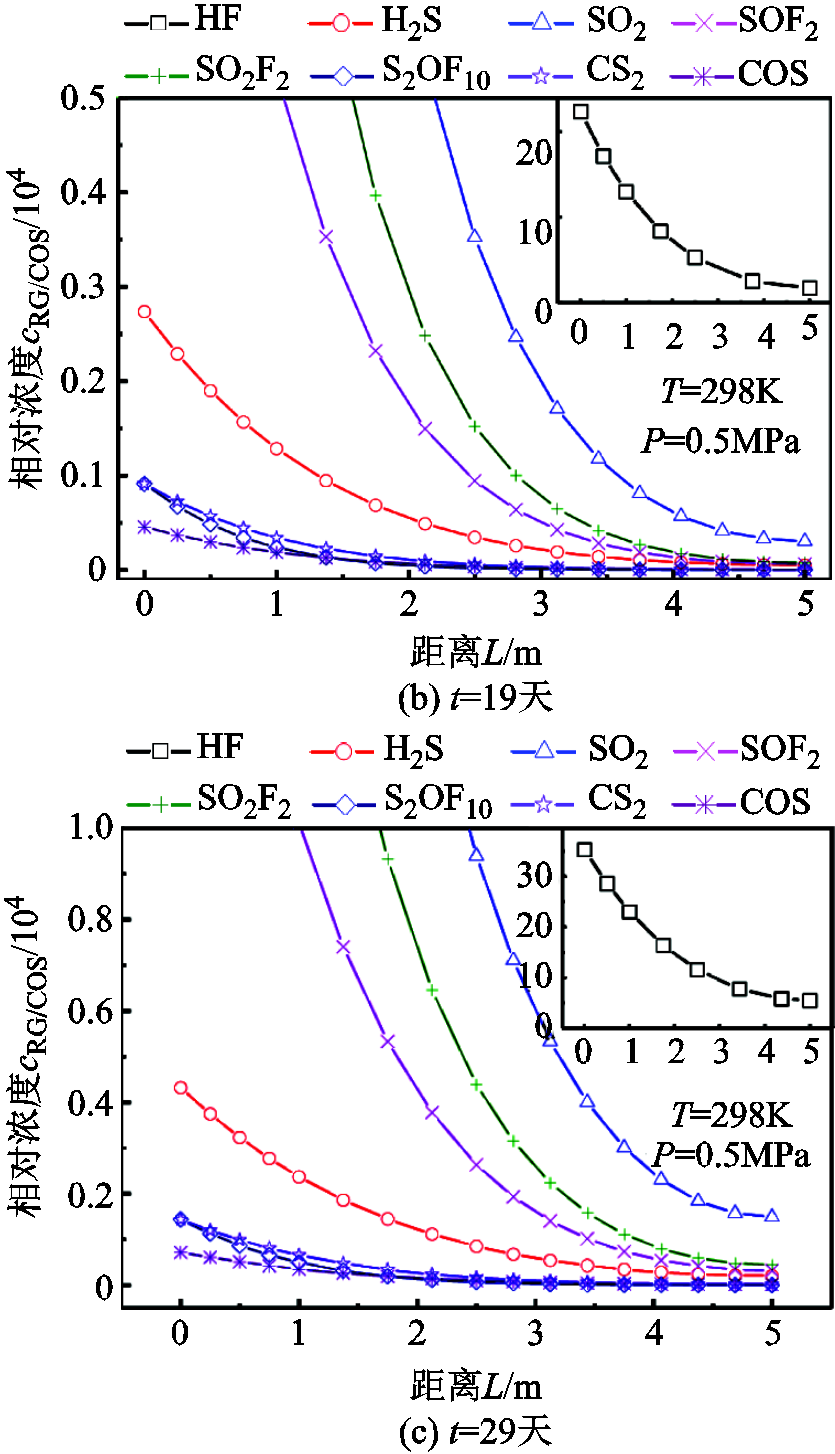
图9 不同时间t下相对浓度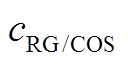 随距离L的变化趋势
随距离L的变化趋势
Fig.9 The variation trend of of decomposition gas concentration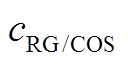 with distance L at different time t
with distance L at different time t
 (19)
(19)式中,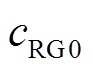 (t)为入口处分解气体浓度随时间变化函数,在本模型中cRG0(t)=WRG/COSt;
(t)为入口处分解气体浓度随时间变化函数,在本模型中cRG0(t)=WRG/COSt;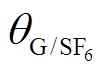 为约化扩散系数。但式(19)中的f比较复杂,很难直观地描述变化趋势,此外,由于
为约化扩散系数。但式(19)中的f比较复杂,很难直观地描述变化趋势,此外,由于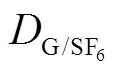 的数量级一般在10-6~10-7,即使混入N2也不高于10-5,则f中的
的数量级一般在10-6~10-7,即使混入N2也不高于10-5,则f中的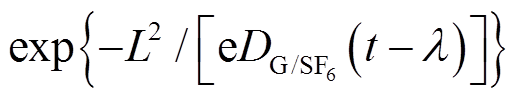 部分数值很小,因此cRG/COS主要与
部分数值很小,因此cRG/COS主要与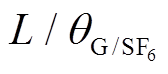 有关。本文对t=216h(9天)时不同L下的各分解气体的cRG/COS和
有关。本文对t=216h(9天)时不同L下的各分解气体的cRG/COS和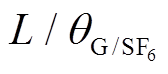 进行对比分析,如图10所示。可以看出,各分解气体的cRG/COS与
进行对比分析,如图10所示。可以看出,各分解气体的cRG/COS与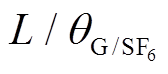 之间具有指数衰减关系,通过式(20)分别对t=216h(9天),t=456h(19天)和t=696h(29天)时的变化趋势进行分析拟合,结果见表7。
之间具有指数衰减关系,通过式(20)分别对t=216h(9天),t=456h(19天)和t=696h(29天)时的变化趋势进行分析拟合,结果见表7。
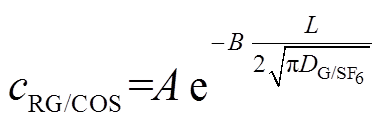 (20)
(20)

图10 t=216h时分解气体浓度随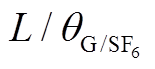 变化趋势
变化趋势
Fig.10 The variation trend of decomposition gas concentration with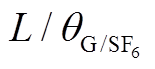 at t = 216h
at t = 216h
表7 不同时间下各分解气体的A、B及相对入口浓度cRG0
Tab.7 The values of A and B of each decomposition gas and Relative inlet concentration cRG0 at different time

分解气体AB相对入口处浓度cRG0 t =216h(9天)HF104 9800.005105 840 H2S1 3770.0051 296 SO221 5320.00519440 SOF27 3410.0056 480 SO2F214 1800.00512312 S2OF105480.005432 CS24940.005432 CSO2400.005216 t =456h(19天)HF218 2000.004223440 H2S2 8920.0042 736 SO245 8110.00441 040 SOF215 7550.00413 680 SO2F230 6530.00425 992 S2OF101 0640.004912 CS24940.004912 CSO5120.004456
(续)

分解气体AB相对入口处浓度cRG0 t= 696h(29天)HF336 5600.003341 040 H2S43900.0034 176 SO269 1890.00362 640 SOF223 7590.00320 880 SO2F246 1950.00339 672 S2OF101 8870.0031 392 CS21 6040.0031 392 CSO7720.003696
拟合结果的可决系数R2≥0.99,拟合度较高。可以看出不同气体的A约等于WGt,即
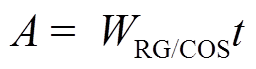 (21)
(21)
这主要是因为当L=0时,cRG/COS为入口处的分解物浓度WGt。而根据式(21),当L=0时,cRG/COS=A,所以A=WRG/COSt。而对于参数B,通过表8可以看出其只与时间t有关,为分析B与t的具体函数关系,本文将L=1m处不同时间t(0~720h)下的cRG/COS数值计算结果代入式(20)中进行非线性拟合,并对参数B和t进行对比分析,结果如图11所示。
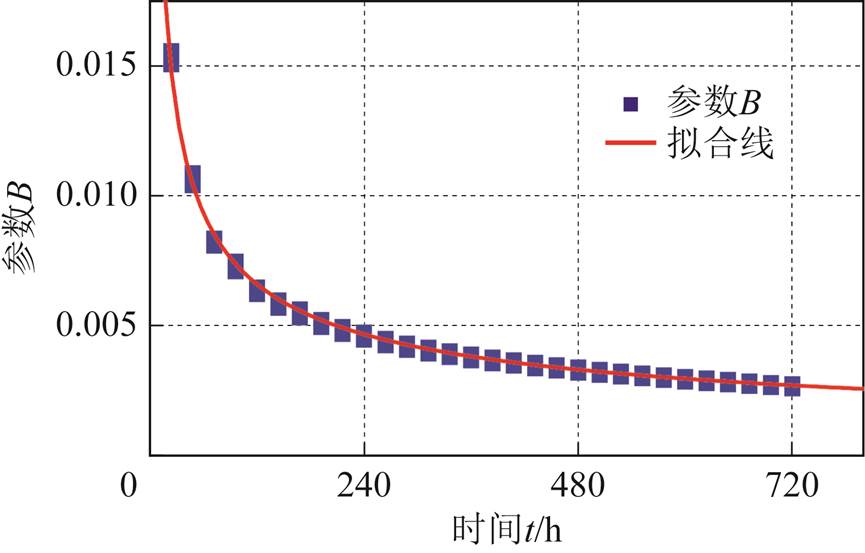
图11 距离L=1m时参数B随时间t变化趋势
Fig.11 The variation trend of the parameter B withtime t at distance L=1m
通过非线性拟合,得到B与t的关系式为
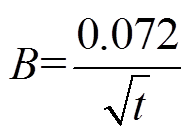 (22)
(22)
拟合可决系数R2为0.996。将式(21)和式(22)代入到式(20)中,可得到不同时间t和距离L下各分解气体的浓度cRG/COS预测公式为
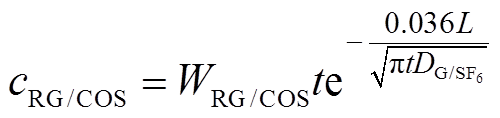 (23)
(23)式中,WRG/COSt可近似为绝缘缺陷源头附近的浓度水平,则不同L处cRG/COS相对源头的衰减比ηG为
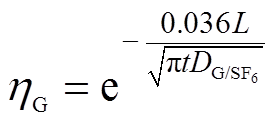 (24)
(24)
由于各特征气体的产量不同,其对化学检测法判断的贡献和权重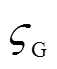 也不同,ηG的存在可能会引起
也不同,ηG的存在可能会引起 发生改变。若在原化学检测法中各气体的权重为
发生改变。若在原化学检测法中各气体的权重为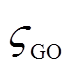 ,则针对GIL的化学诊断权重系数
,则针对GIL的化学诊断权重系数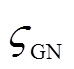 可表示为
可表示为
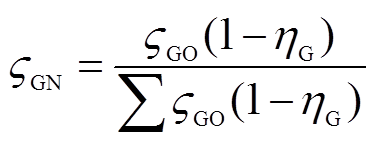 (25)
(25)但式(25)具有一定的局限性,例如当COS和CS2气体出现时,无论含量大小,都能够说明腔体内存在较为严重的固体绝缘缺陷。因此,在任何化学检测方案中,其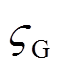 都是1。则此类气体的判断依据及ηG对判断准确度的影响主要与检测设备的最低检出限有关。当COS和CS2气体在缺陷处出现且浓度已经超过设备检出限时,由于扩散过程会导致气体浓度随距离衰减,采样口处的气体浓度可能会低于检出限,从而导致检测设备无法对其有效检出。这一问题在改进检测方案时是需要考虑的。为验证预测模型准确性,分别对t=360h(15天)时不同L处的cRG/COS及L=4m处不同t时的cRG/COS进行了数值计算和预测,计算结果cn与预测结果cp对比如图12所示。
都是1。则此类气体的判断依据及ηG对判断准确度的影响主要与检测设备的最低检出限有关。当COS和CS2气体在缺陷处出现且浓度已经超过设备检出限时,由于扩散过程会导致气体浓度随距离衰减,采样口处的气体浓度可能会低于检出限,从而导致检测设备无法对其有效检出。这一问题在改进检测方案时是需要考虑的。为验证预测模型准确性,分别对t=360h(15天)时不同L处的cRG/COS及L=4m处不同t时的cRG/COS进行了数值计算和预测,计算结果cn与预测结果cp对比如图12所示。
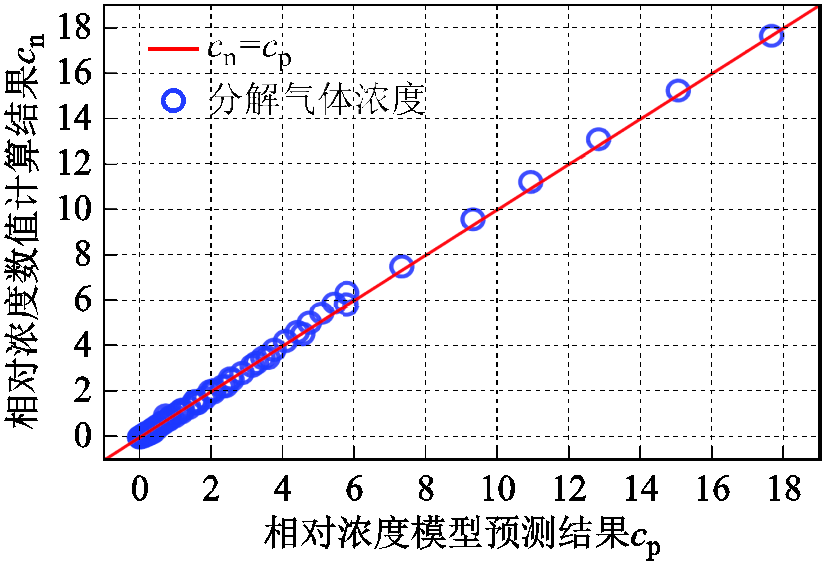
图12 浓度计算结果cn与预测结果cp对比
Fig.12 The comparison between the calculated result cn and the predicted result cp
可以看出,cn与cp比较接近,证明预测模型具有一定的准确性。因此,对于GIL内的分解气体扩散过程,若已知分解气体的生成速率WG和扩散系数DG,便可将式(23)中的相应参数进行替换,并对特征分解气体浓度cG进行预测。根据式(9)和式(23)可知,温度T、压力p以及SF6比例 对于扩散过程分解物浓度的影响主要体现在DG上。因此,根据式(17)和式(18),可将式(23)整理为
对于扩散过程分解物浓度的影响主要体现在DG上。因此,根据式(17)和式(18),可将式(23)整理为
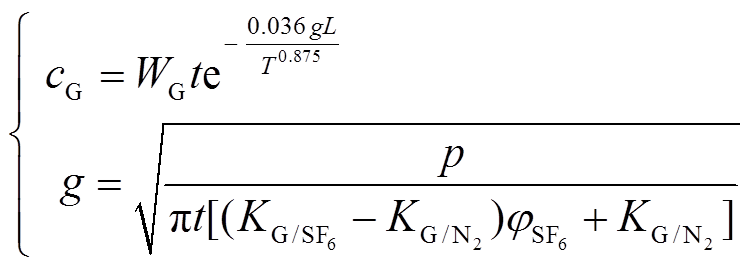 (26)
(26)对于不同T、p及 下的分解气体扩散过程及浓度变化问题,可通过式(24)或式(26)进行预测。由于本文采用的计算模型忽略了GIL内的部分条件,因此仍具有一定的改善空间,例如考虑GIL内的自然对流、轴向温差、采样口流速以及缺陷位置对浓度分布的影响。此外,若能将反应过程和扩散过程同时加入计算模型中,分析放电强度和缺陷位置等因素对扩散过程的影响,并实现相关试验的验证,则模型的实用价值和理论深度将会进一步提高,所得结果也可以为GIL化学检测法改进方案提供参考和依据。
下的分解气体扩散过程及浓度变化问题,可通过式(24)或式(26)进行预测。由于本文采用的计算模型忽略了GIL内的部分条件,因此仍具有一定的改善空间,例如考虑GIL内的自然对流、轴向温差、采样口流速以及缺陷位置对浓度分布的影响。此外,若能将反应过程和扩散过程同时加入计算模型中,分析放电强度和缺陷位置等因素对扩散过程的影响,并实现相关试验的验证,则模型的实用价值和理论深度将会进一步提高,所得结果也可以为GIL化学检测法改进方案提供参考和依据。
本文通过Fick定律和FSG公式建立了分解气体在GIL内的扩散模型,并利用量子化学计算方法和范德华表面参数对气体的扩散体积及扩散系数进行了预测和计算。根据计算结果分析了扩散系数随压力p、温度T及SF6混合比 的变化规律,采用非线性拟合,得到了分解气体浓度的简化预测模型。主要结论为:
的变化规律,采用非线性拟合,得到了分解气体浓度的简化预测模型。主要结论为:
1)分解气体的扩散能力主要与扩散系数DG有关,影响气体DG的主要参数为分子扩散体积Vdm,温度T、压力p及SF6比例 。Vdm可通过分子体积Vm进行简单预测。温度T、压力p及SF6比例
。Vdm可通过分子体积Vm进行简单预测。温度T、压力p及SF6比例 对于扩散过程及分解物浓度cG的影响主要体现在DG上。
对于扩散过程及分解物浓度cG的影响主要体现在DG上。
2)压力p对DG的影响较为明显,而温度T对DG的影响较弱。此外,在实际密闭的GIL内,T升高会使p升高,这就导致在实际工况下T对DG和扩散过程的影响被进一步削弱,温度对于实际GIL的扩散影响较小。
3)各分解气体浓度cG随距离L的增加呈指数衰减,随时间t的增加呈指数上升。通过多元非线性拟合建立的cG与t和L之间的简化指数关系模型,其预测结果与FEM计算结果的一致性较高,可实现不同温度T、压力p及SF6比例 条件下各时间t及距离L处的分解气体浓度cG预测,并为GIL内气体检测策略及分解强度反演等问题提供前期的理论支持和技术探索。
条件下各时间t及距离L处的分解气体浓度cG预测,并为GIL内气体检测策略及分解强度反演等问题提供前期的理论支持和技术探索。
用于拟合分子扩散体积预测模型的气体分子范德华表面及SF6特征放电分解气体分子的范德华表面分别如附图1和附图2所示。

附图1 分子范德华表面
App.Fig.1 The van der Waals surface of molecules
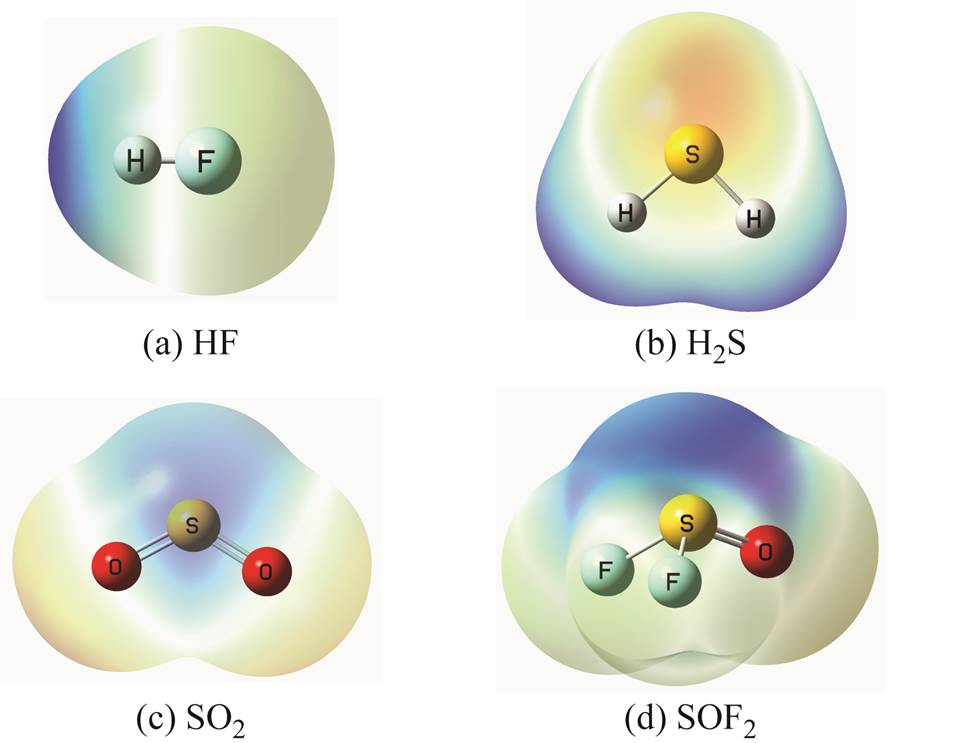
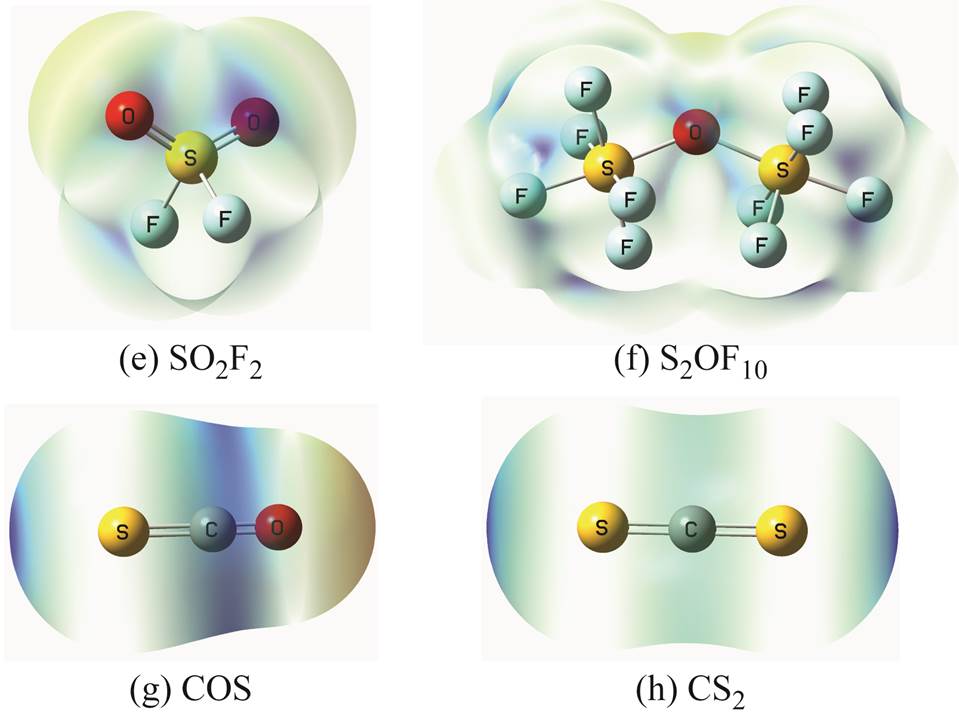
附图2 分解气体分子范德华表面
App.Fig.2 The van der Waals surfaces of decomposition gas molecules
各分解气体在不同混合比下的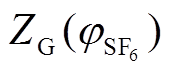 计算公式见附表1。
计算公式见附表1。
附表1 不同比例下分解气体的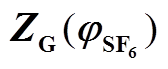
App.Tab.1 The 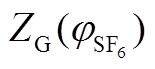 of decomposition gases with different mixingratio
of decomposition gases with different mixingratio

分解气体 HF H2S SO2 SOF2 SO2F2 S2OF10 CS2 COS
参考文献
[1] 李鑫涛, 林莘, 徐建源, 等. SF6/N2混合气体电击穿特性仿真及实验[J]. 电工技术学报, 2017(20): 48-58.Li Xintao, Lin Xin, Xu Jianyuan, et al. Simulations and experiments of dielectric breakdown characteristics in SF6/N2 gas mixtures[J]. Transactions of China Electrotechnical Society, 2017, 32(20): 48-58.
[2] 赵明月, 林涛, 颜湘莲, 等. 基于氧同位素示踪法的电晕放电中H2O和O2对SF6分解气体形成的影响[J]. 电工技术学报, 2018, 33(20): 4722-4728. Zhao Mingyue, Lin Tao, Yan Xianglian, et al. Influence of trace H2O and O2 on SF6 decomposition characteristics under corona discharge based on oxygen isotope tracer[J]. Transactions of China Electrotechnical Society, 2018, 33(20): 4722-4728.
[3] 刘栋财. GIL故障气体在线监测技术研究与系统开发[D]. 成都: 西南交通大学, 2017.
[4] Suzuki T. The determination of the diffusion rate of SF6 into nitrogen[J]. IEEE Transactions on Electrical Insulation, 1982, 17(1): 34-38.
[5] Taylor W L, Hurly J J. Thermal diffusion factors and intermolecular potentials for noble gas-SF6 systems[J]. The Journal of Chemical Physics, 1993, 98(3): 2291-2297.
[6] Talib Z A, Saporoschenko M. Transport coefficients of SF3+ and SF5+ ions in SF6 gas[J]. Journal of Physics D: Applied Physics, 1994, 27(11): 2307-2311.
[7] Urquijo-Carmona J D, Cisneros C, Martinez H, et al. Transport coefficients of SF+ and SF2+ in SF6[J]. Journal of Physics D: Applied Physics, 1992, 25(8): 1277-1279.
[8] 周舟, 万涛, 龚尚昆, 等. 基于CFD技术的六氟化硫电气设备中气体湿度测量方法研究[J]. 电工技术学报, 2014, 29(增刊1): 29-35. Zhou Zhou, Wan Tao, Gong Shangkun, et al. Investigation on measurement method of gas humidity in sulfur hexafluoride electric equipment based on CFD technique[J]. Transactions of China Electrotechnical Society, 2014, 29(S1): 29-35.
[9] 张驰, 蔡萱, 张莹, 等. 基于流体计算力学模拟技术研究氦示踪气体分子在六氟化硫绝缘气体中的扩散情况[J]. 湖北电力, 2018, 44(1): 35-42. Zhang Chi, Cai Xuan, Zhang Ying, et al. Study on the diffusion of helium tracer gas molecules in sulfur hexafluoride insulating gas based on fluid computational mechanics simulation technology[J]. Hubei Electric Power, 2018, 44(1): 35-42.
[10] Zhang Jinliang, Yan Jiudun, Murphy A B, et al. Computational investigation of arc behavior in an auto-expansion circuit breaker contaminated by ablated nozzle vapor[J]. IEEE Transactions on Plasma Science, 2002, 30(2): 706-719.
[11] Zhong Linlin, Wang Xiaohua, Rong Mingzhe, et al. Calculation of combined diffusion coefficients in SF6-Cu mixtures[J]. Physics of Plasmas, 2014, 21(10): 103506.
[12] Murphy A B. Diffusion in equilibrium mixtures of ionized gases[J]. Physical Review E, 1993, 48(5): 3594-3603.
[13] 乔胜亚, 周文俊, 唐念, 等. 不同吸附剂对GIS局部放电特征气体变化规律的影响[J]. 电工技术学报, 2016, 31(3): 113-120. Qiao Shengya, Zhou Wenjun, Tang Nian, et al. Effects of different adsorbents on gas variation characteristics of partial discharge in GIS[J]. Transactions of China Electrotechnical Society, 2016, 31(3): 113-120.
[14] 周永言, 乔胜亚, 李丽, 等.GIS中S2OF10作为局部放电特征气体的有效性分析[J]. 中国电机工程学报, 2016, 36(3): 871-878. Zhou Yongyan, Qiao Shengya, Li Li, et al. Validity analysis of S2OF10 as a target gas of partial discharge in GIS[J]. Journal of Chinese Electrical Engineering Science, 2016, 36(3): 871-878.
[15] Greenkorn R. Momentum, heat, and mass transfer fundamentals[M]. New York: McGraw-Hill, 1999.
[16] Atta K R, Gavril D, Karaiskakis G. New methodology for the measurement of diffusion coefficients of pure gases into gas mixtures[J]. Instrumentation Science & Technology, 2002, 30(1): 67-78.
[17] 诸林, 刘瑾, 王兵, 等. 化工原理[M]. 北京: 石油工业出版社, 2007.
[18] 陈庆国, 邱睿, 林林,等. 基于密度泛函理论的SF6潜在替代气体筛选[J]. 高电压技术, 2019, 45(4): 1026-1039. Chen Qingguo, Qiu Rui, Lin Lin, et al. Screening of SF6 potential alternative gas based on density functional theory[J]. High Voltage Technology, 2019, 45(4): 1026-1039.
[19] Stephens P J D, Devlin F J C, Chabalowski C F N, et al. Ab initio calculation of vibrational absorption and circular dichroism spectra using density functional force fields[J]. Journal of Physical Chemistry, 1994, 98(45): 11623-11627.
[20] Krishnan R, Binkley J S, Seeger R, et al. Self-consistent molecular-orbital methods. XX. A basis set for correlated wave-functions[J]. Journal of Chemical Physics, 1980, 72(1): 650-654.
[21] Lu Tian, Chen Feiwu. Multiwfn: a multifunctional wavefunction analyzer[J]. Journal of Computational Chemistry, 2012, 33(5): 580-592.
[22] Lu Tian, Chen Feiwu. Quantitative analysis of molecular surface based on improved marching tetrahedra algorithm[J]. Journal of Molecular Graphics & Modelling, 2012, 38(9): 314-323.
[23] 唐念, 乔胜亚, 李丽, 等. HF和H2S作为气体绝缘组合电器绝缘缺陷诊断特征气体的有效性[J].电工技术学报, 2017, 32(19): 206-215. Tang Nian, Qiao Shengya, Li Li, et al. Validity of HF and H2S as target gases of insulation monitoring in gas insulated switchgear[J]. Transactions of China Electrotechnical Society, 2017, 32(19): 206-215.
[24] Christophorou L G, Olthoff J K, Green D S. Gases for electrical insulation and arc interruption: possible present and future alternatives to pure SF6[R]. NIST Technical Note, 1997, 8(3): 12-15.
[25] 周安春, 高理迎, 冀肖彤, 等. SF6/N2混合气体用于GIS母线的研究与应用[J].电网技术, 2018, 42(10):3429-3435. Zhou Anchun, Gao Liying, Yi Xiaotong, et al. Research and application of SF6/N2 mixed gas used in GIS bus[J]. Power System Technology, 2018, 42(10): 3429-3435.
[26] 李冰, 肖登明, 赵谡, 等. 第二代气体绝缘输电线路的温升数值计算[J]. 电工技术学报, 2017, 32(13):271-276. Li Bing, Xiao Dengming, Zhao Su, et al. Temperature rise numerical calculation of the second generation gas insulated transmission line[J]. Transactions of China Electrotechnical Society, 2017, 32(13): 271-276.
[27] 杨世铭, 陶文铨. 传热学[M]. 4版. 北京: 高等教育出版社, 2006.
[28] 金启胜. 利用Fourier变换求解热传导方程的定解问题[J]. 上饶师范学院学报, 2011, 31(3): 54-55. Jin Qisheng. Using Fourier transform to solve fixed solution problems of heat conduction equations[J]. Journal of Shangrao Normal University, 2011, 31(3): 54-55.
The Computation of Diffusion Characteristics of Decomposition Gases in SF6 and SF6/N2 within Gas Insulated Transmission Lines
Abstract In order to obtain the impact of diffusion process on chemical detections for gas insulated transmission lines (GIL), the diffusion model of decomposition gases in SF6 and SF6/N2 was done based on Fick's law and Fuller-Schettler-Giddings (FSG) equation. The prediction method of molecular diffusion volume Vd was built by density functional theory (DFT) and van der Waals surface analysis. The diffusion processes under different temperature T, pressure p and mixed ratio of SF6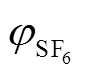 were calculated by finite element method (FEM). The prediction models for concentrations cG of 8 main decomposition gases at different time and position were built by multivariate nonlinear regressions. The results shew that the diffusion of decomposition gases were mainly related to their diffusion coefficient DG. The influences of T, p and
were calculated by finite element method (FEM). The prediction models for concentrations cG of 8 main decomposition gases at different time and position were built by multivariate nonlinear regressions. The results shew that the diffusion of decomposition gases were mainly related to their diffusion coefficient DG. The influences of T, p and 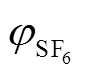 were mainly reflected on DG. The effect of T was smaller than that of p and
were mainly reflected on DG. The effect of T was smaller than that of p and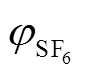 . The cG decayed exponentially with distance and increased exponentially with time. Diffusions could cause difference in cG between sites of detection and defection. That would affect the accuracy of chemical detection methods. In addition, the diffusion may change the weights of decomposition gases in insulation diagnoses.
. The cG decayed exponentially with distance and increased exponentially with time. Diffusions could cause difference in cG between sites of detection and defection. That would affect the accuracy of chemical detection methods. In addition, the diffusion may change the weights of decomposition gases in insulation diagnoses.
keywords:Chemical detection method, gas insulted transmission lines(GIL), diffusions of decomposition gases, diffusion coefficient, molecular diffusion volume, mass transfer model
中图分类号:TM835
DOI:10.19595/j.cnki.1000-6753.tces.190544
国家电网公司科技项目(SGHZ0000AJJS1800199)和国家重点研发计划(2017YFB0902500)资助。
收稿日期2019-05-07
改稿日期2019-06-18
刘 溟 男,1975年生,博士,高级工程师,从事电网安全监督和输变电设备运维检修管理工作。E-mail:lium1212@ cc.sgcc.com.cn
邱 睿 男,1992年生,博士研究生,研究方向为SF6替代技术。E-mail:rui_qiu@whu.edu.cn(通信作者)
(编辑 郭丽军)