
图1 灵活性改造涉及子系统示意图
Fig.1 Schematic diagram of the subsystem involved in the flexibility retrofits
摘要 对于以煤炭为主要能源的国家而言,实施火电机组灵活性改造是提升电力系统灵活性最为现实可行的选择。基于此,提出一种考虑多投资主体博弈的灵活性改造两阶段规划方法。首先,概述灵活性改造涉及的范围及相关技术,提出机组间的改造方案及投资成本具有多样性和差异性的特点;其次,在系统规划阶段,构建发电企业在电量和调峰市场的收益模型,对不同投资主体的博弈行为进行分析,提出一种解决改造博弈问题的快速求解方法;再次,在企业规划阶段,以发电企业运行与投资成本最小化为目标,以系统规划阶段的改造效果和灵活性约束等为边界条件,建立发电企业多技术改造混合整数规划模型;最后,对所提出的模型和方法的合理性及有效性通过算例进行验证,结果表明,所提方法能够统筹兼顾所有投资主体的利益,有效保证了市场活力,可以为规划部门和发电企业提供帮助。
关键词:灵活性改造 多主体博弈 调峰市场 混合整数规划
以风电、光伏为代表的大规模间歇性可再生能源(Intermittent Renewable Energy Sources, IRES)正在加速能源结构的低碳化转变。但是,大规模IRES并网发电,需要电力系统中有足够的灵活性资源实时响应IRES的变化[1-2]。现有的灵活性资源主要有四个来源[3]:可调度发电厂的灵活运行[4]、储能设施[5-6]、跨省跨区交易[7]和需求侧资源[8-10]。相比于其他三类灵活性资源,可调度发电厂的灵活运行是目前为电力系统提供灵活性最主要的方式。对于含有极高份额不灵活火电厂(尤其是燃煤电厂)的电力系统(如中国、波兰)而言,实施灵活性改造是提升电力系统灵活性最为现实可行的选择[11]。
近年来,各区域纷纷建立调峰服务市场[12],以期通过调峰补偿或惩罚的方式激励火电机组进行改造。文献[13]以东北调峰辅助服务市场为背景,建立了改造投资经济性评价模型,并分析了某台350MW机组改造的经济性及其影响因素。文献[14]采用实物期权法对德国某座褐煤电厂应该采取怎样的改造技术以及何时实施进行了研究,认为在获得有效补贴的支持下,灵活性改造是盈利的。而文献[15]则从系统统一规划角度,构建了系统灵活性改造规划(Flexibility Retrofits Planning, FRP)模型,利用Benders分解算法实现了投资决策问题的高效求解。
然而,上述两个角度的研究均忽略了不同机组的博弈特性及其不同投资主体的博弈关系。机组单独规划在改造初期可能收益可观,但系统大规模进行灵活性改造后,电厂的长期收益存在较大不确定性,存在由市场竞争带来的投资风险。而系统统一规划方法使用统一目标函数进行投资决策,难以描述改造投资主体间的博弈现象,不能兼顾发电企业的改造投资意愿。
博弈理论目前在电力系统领域研究广泛,主要应用于定价决策、收益分配和调度规划等问题[16-17]。文献[16]针对主动配电网多利益主体参与下的调度问题,提出了多利益主体参与下主动配电网完全信息动态博弈策略。文献[17]对不同投资主体的博弈进行了分析,提出了一种面向电力-天然气综合能源系统联合规划的动态博弈模型,兼顾了所有市场参与者的利益。虽然博弈理论已在电力系统的多类规划问题中得到了应用,但是将其应用于FRP问题的研究鲜见报道。
FRP问题考虑的时间周期较短,是对既有的发电扩展规划方案进行合理的修缮和补充[18]。另外,为了更快速地响应系统调度指令,机组经过改造后,其调峰能力、爬坡速度和起动时间等多种运行参数都可能会发生改变。但是,这些运行细节(灵活性约束)通常会被传统发电规划模型忽略[19],仅在较短时间尺度的机组组合模型中才能被捕捉。因此,在考虑FRP问题时,需采用基于机组组合的时序模拟方法。但是,这种做法却引入了大量的二进制变量,在解决规划模拟问题时计算量巨大。为此,文献[15]提出采用多个典型日的方法模拟系统长时间的变化情况,实现了对具有多时间维度的FRP问题的高效求解。文献[20-22]提出了集群机组组合模型并将其嵌入发电扩展规划模型中,将机组聚类后用整数决策变量替代机组组合中的二进制决策变量,从而降低了规划模型的计算量。但是,上述两种方法并没有改变混合整数规划问题的本质,仅适用于统一规划角度,在考虑多投资主体动态博弈的背景下,多次机组组合迭代运算依旧需要巨大的计算量。
基于此,本文考虑引入快速机组组合(Fast Unit Commitment, FUC)模型[23]模拟系统多投资主体的动态博弈。FUC模型的决策变量都是连续的,在IEEE测试系统和我国某实际系统环境下与传统机组组合模型相比,FUC计算速度快2万倍,且仿真结果只存在不到1%的误差。但是,FUC模型以机群为单位进行优化,忽略了机组间可行改造方案及投资成本的差异性和多样性,因此,本文提出一种考虑多投资主体博弈的两阶段FRP模型。首先,在系统博弈规划阶段,通过引入FUC模型,提出发电企业在电量和调峰市场的收益模型,在此基础上,基于不同投资主体的博弈机理分析,提出一种解决改造博弈问题的快速求解方法;其次,在企业规划阶段,考虑机组多方案改造和多参数变化,建立发电企业多技术改造规划模型;最后,基于我国东北某电网数据进行算例分析,并与统一规划方法进行对比,证明本文所提方法的有效性与合理性。
灵活性改造涉及电厂内部多个子系统的变化,可能需对机组设备的本体进行改造,也可能新建其他辅助设备。研究表明[24-25],对图1所示的几个子系统进行改造是提高火电机组灵活性最有效的手段,除控制和通信系统外,热电机组和纯凝机组的改造范围存在差异。

图1 灵活性改造涉及子系统示意图
Fig.1 Schematic diagram of the subsystem involved in the flexibility retrofits
针对纯凝机组,主要涉及图1左侧的3个子系统:燃料供应、锅炉和烟气化学处理系统。一方面,锅炉的最低负荷取决于其燃烧稳定性。低负荷时火焰稳定性差,容易发生灭火事故,降低了机组运行安全性,改造路线主要从燃料供应和锅炉侧入手,包括富氧燃烧、等离子稳燃技术和煤粉分离器改造等技术[24];另一方面,节能及环保指标也是制约锅炉低负荷运行的关键因素,必须要保证低负荷运行时脱硝、除尘器和脱硫等系统[26]的正常投运,考虑因低负荷脱销投运可能造成的空预器低温腐蚀、空预器堵塞等烟气化学处理系统问题的相关技术措施。
针对供热机组,一般较少涉及锅炉低负荷运行问题,主要矛盾集中在热电解耦的问题,涉及图1右侧的两个子系统:汽轮机系统,蒸汽、水循环及储热系统。改造技术包括两类[27-28]:一类是汽轮机本体改造,包括高背压技术、光轴改造技术和低压缸零出力技术;另一类是增加电锅炉、储热罐等热电解耦设备,增加热电机组的调峰能力。
因此,由于功能定位、技术要求和现场条件不同,一台机组可能有多种可行性改造方案,且方案间的投资成本和改造效果存在差异[29-30]。机组i的改造投资成本Cr i为
 (1)
(1) 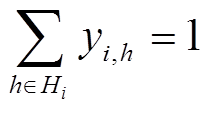 (2)
(2)
式中, 为机组i的铭牌容量;Cr i,h为机组i采用h方案改造的单位容量投资成本;yi,h为二进制投资决策变量;Hi为机组i的可行改造方案集合,其中,h=1为不进行改造方案,其相应投资成本Cr i,1=0。
为机组i的铭牌容量;Cr i,h为机组i采用h方案改造的单位容量投资成本;yi,h为二进制投资决策变量;Hi为机组i的可行改造方案集合,其中,h=1为不进行改造方案,其相应投资成本Cr i,1=0。
由于考虑发电企业间改造博弈行为需要巨大的计算量,本节通过引入FUC模型,提高了博弈模拟效率,并建立了发电企业在电量和调峰市场的收益模型。
为提高电力系统时序模拟的效率,文献[23]在集群机组组合模型的基础上提出了FUC模型,在提高计算速度的同时,误差不足1%。该模型主要通过两个步骤来提升模拟速度:①将多台相似机组聚类为一个机群,在模型中优化整体机群运行而非单台机组;②引入如图2所示的三个连续变量来近似模拟机组组合决策。
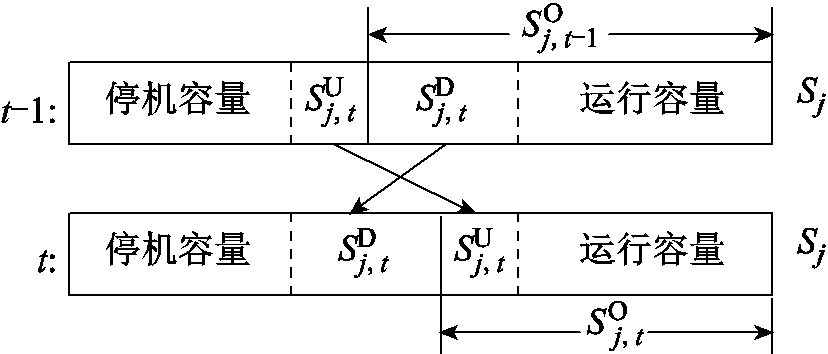
图2 机群运行状态的时序关系
Fig.2 The temporal relationship of the operational status of a group of units
图2中,SO j,t为机群j在t时刻的运行容量;SU j,t为机群j在t时刻新增加的运行容量;SD j,t为机群j在t时刻计划的关停容量。三类变量的逻辑及变化范围为
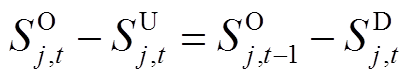 (3)
(3)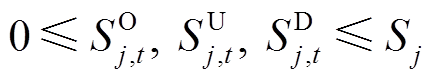 (4)
(4)
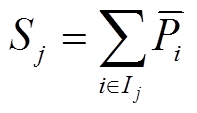 (5)
(5)
式中,Sj为机群j中所有机组的铭牌容量之和;Ij为机群j中机组的集合。机群输出功率约束为
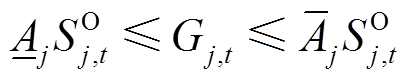 (6)
(6)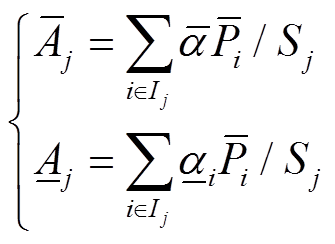 (7)
(7)
式中,Gj,t为机群j在时刻t的输出功率;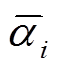 和
和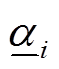 分别为机组出力上、下限系数;相应的
分别为机组出力上、下限系数;相应的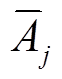 和
和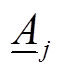 为机群出力的上、下限系数,为机群j中所有机组的加权平均值。FUC模型的爬坡限制和最小开关机时间等其他运行约束详见文献[23]中说明。
为机群出力的上、下限系数,为机群j中所有机组的加权平均值。FUC模型的爬坡限制和最小开关机时间等其他运行约束详见文献[23]中说明。
发电企业X在电量市场和调峰市场的收入主要来自于售电收入IE X和调峰补偿收入IR X,主要成本包括机群的运行成本CE X、调峰惩罚成本CR X和改造年投资成本Cret X,其收益函数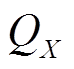 为
为
 (8)
(8)1)售电收入,包括火电、IRES的电量收入
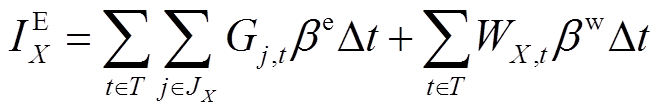 (9)
(9)
式中,T为时序集合;JX为发电企业X的机群集合;WX,t为t时刻发电企业X的IRES实际上网功率;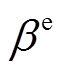 和
和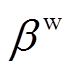 分别为火电和IRES的单位上网电价;
分别为火电和IRES的单位上网电价;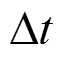 为调度间隔,取1h。
为调度间隔,取1h。
2)调峰补偿收益
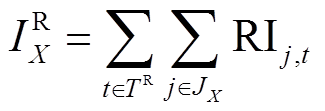 (10)
(10)式中,TR为调峰市场的触发时段集合,由调峰市场机制所确定;RIj,t为机群j在t时刻的调峰收益,为
 (11)
(11)
式中,θ为深度调峰标准;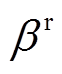 为深度调峰补偿价格。
为深度调峰补偿价格。
3)运行成本,主要包括运行能耗成本以及开停机成本
 (12)
(12)式中,Cn j为当机群j处于出力下限时的单位煤耗成本;Cm j为线性增量成本;Cu j为单位容量启动成本;Cd j为单位容量关机成本。
4)调峰分摊成本
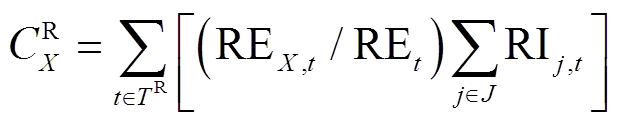 (13)
(13)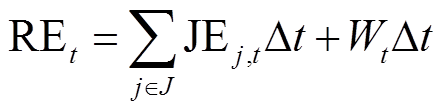 (14)
(14)
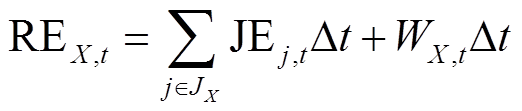 (15)
(15)
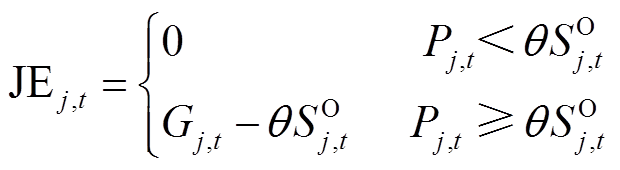 (16)
(16)式中,J为系统中机群集合;REt为系统时刻t需分摊的总电量;Wt为系统IRES的总上网电量;REX,t为发电企业X时刻t需分摊电量;JEj,t为机群j时刻t需分摊的电量。
5)改造投资成本。为了便于同时序模拟中的运行成本等相比较,本文采用等额年金法,考虑灵活性改造的年化投资成本。
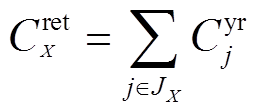 (17)
(17)
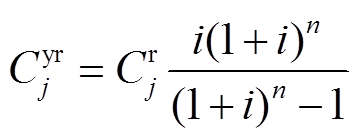 (18)
(18)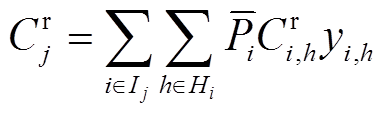 (19)
(19)
式中,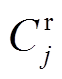 为机群j的改造投资成本;
为机群j的改造投资成本;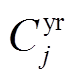 为机群j的年化投资成本;i为利率;n为摊销年限。
为机群j的年化投资成本;i为利率;n为摊销年限。
需要说明的是,收益模型中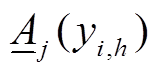 、
、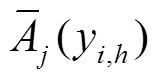 和Cd j(yi,h)等机群参数是yi,h的函数。当机组的改造决策确定时,机群的运行参数才通过式(7)的加权平均法求得。当机组的改造决策改变时,机群的运行参数也会发生变化。因此,收益
和Cd j(yi,h)等机群参数是yi,h的函数。当机组的改造决策确定时,机群的运行参数才通过式(7)的加权平均法求得。当机组的改造决策改变时,机群的运行参数也会发生变化。因此,收益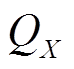 也是yi,h的函数。
也是yi,h的函数。
在电力系统灵活性改造中,投资主体为各个发电企业,投资决策为企业的机组采取何种方案进行改造,本节考虑发电企业间的博弈行为,提出了一种两阶段火电机组灵活性改造规划方法。
由于各个发电企业处于同一电量和调峰市场下,发电企业间的独立改造决策彼此互相影响,形成动态博弈格局,如图3所示。
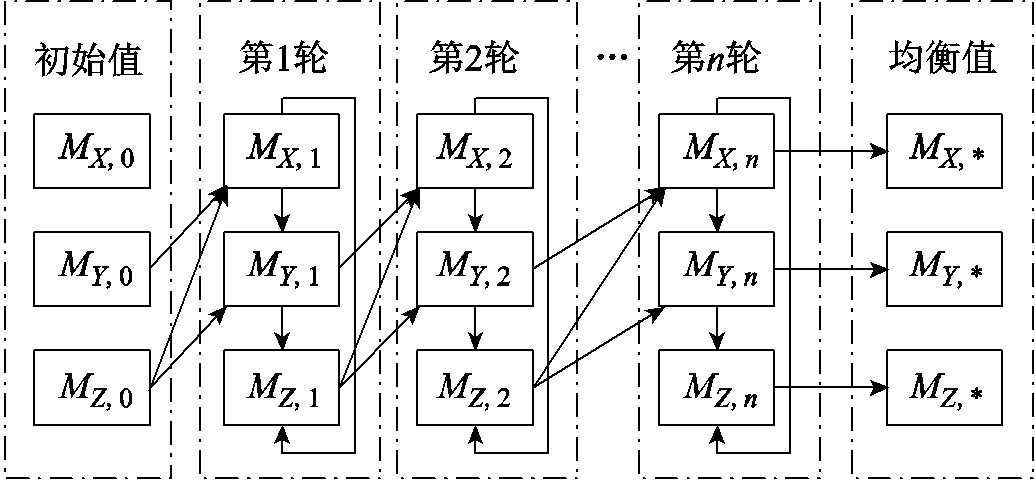
图3 发电企业间博弈行为示意图
Fig.3 Schematic diagram of game behavior among power generation enterprises
图3中以三个发电企业X、Y、Z为例,描述了发电企业间的博弈过程。首先,最大规模企业X参考上一轮其他企业的决策值后,做出本轮的决策;其次,中等规模Y参考本轮X和上轮Z的决策值后,做出本轮决策;最后,较小规模Z参考本轮其他企业决策值后,做出本轮决策。经过n轮博弈后,博弈各方都无法实现更大收益时,博弈达到相对静止、均衡的状态,此时发电企业的决策为
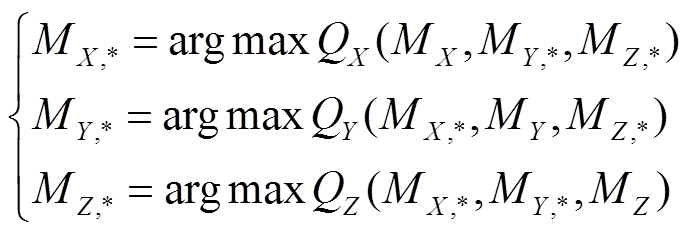 (20)
(20)
式中,MX,*、MY,*、MZ,*为企业各自认为的最大收益时的改造决策。
如果系统中的机组数量或改造方案较多,例如系统中含16台机组,每台机组有三种可行方案,系统中共有约4.3×107种决策,即使采用FUC模型也存在巨大的计算量,在实际工程中很难对式(19)中的变量yi,h进行博弈决策。基于此,本文提出了一种灵活性改造两阶段规划方法。
3.2.1 系统博弈规划阶段
由于考虑博弈时计算量较大,本文提出一种解决改造博弈问题的快速求解方法。该方法的步骤如下:
1)初始化数据。载入博弈模型所需数据,包括负荷时序数据、IRES时序数据、机组不同改造方案下的运行参数与投资成本等,将发电企业中的相似机组进行聚类,构造FUC模型中的机群。
2)生成机群的决策集合及运行参数。枚举每台机组的改造决策,生成机群的改造决策J(yi,h)及相应的机群参数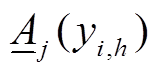 ,
,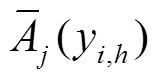 和Cd j(yi,h)等。
和Cd j(yi,h)等。
3)更新机群的决策集合及运行参数。将步骤2)中机群所有决策下的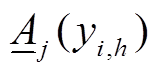 进行聚类,实现机群决策数量的削减。例如,第j机群中含350MW、330MW和300MW共三台机组,改造后机组最小出力系数
进行聚类,实现机群决策数量的削减。例如,第j机群中含350MW、330MW和300MW共三台机组,改造后机组最小出力系数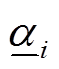 都可能为{0.5,0.42,0.35}。所有决策下的
都可能为{0.5,0.42,0.35}。所有决策下的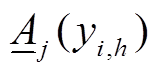 的聚类过程如图4所示。图中δj为机群j由聚类带来的最大误差。
的聚类过程如图4所示。图中δj为机群j由聚类带来的最大误差。
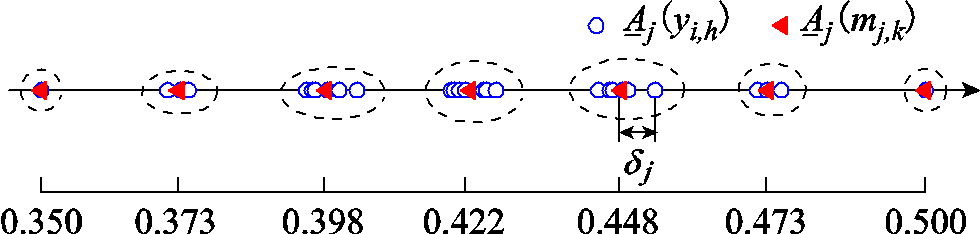
图4 机群最小出力系数聚类过程示意图
Fig.4 Schematic diagram of clustering a group of units’ minimum output coefficient
由图4可知,第j机群27种决策下的所有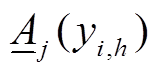 分为了7类,第k类的中心为
分为了7类,第k类的中心为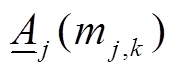 ,如图4中三角形标记所示。由于最小出力系数(调峰能力)是灵活性改造中的最关键参数,可以近似认为上述聚类过程也实现了对机群改造决策数量的削减。因此,机群的改造决策由J(yi,h)变为了J(mj,k),mj,k为机群j采用k策略改造的二进制决策变量,同时也得到了机群其他参数Cd j(mj,k),Cu j(mj,k)等。其中,发电企业的改造投资成本由式(17)变为
,如图4中三角形标记所示。由于最小出力系数(调峰能力)是灵活性改造中的最关键参数,可以近似认为上述聚类过程也实现了对机群改造决策数量的削减。因此,机群的改造决策由J(yi,h)变为了J(mj,k),mj,k为机群j采用k策略改造的二进制决策变量,同时也得到了机群其他参数Cd j(mj,k),Cu j(mj,k)等。其中,发电企业的改造投资成本由式(17)变为
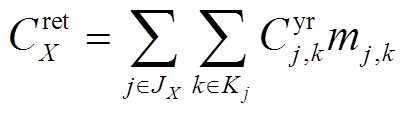 (21)
(21)式中,Cyr j,k为机群j采用k策略下的年化投资成本;Kj为机群j的改造策略集合。
4)生成各个发电公司的改造策略集合。发电公司X、Y、Z根据步骤3)中各个机群的改造策略,生成公司的策略集MX ={(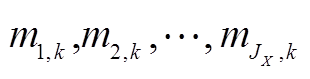 )|k
)|k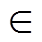 Kj},MY,MZ。
Kj},MY,MZ。
5)动态博弈。如图3所示,每一个参与者进行多轮方案优化,直至达到均衡状态,输出各公司内部各个机群改造决策MX,*、MY,*和MZ,*。
该方法通过步骤3)的聚类过程,降低了各发电公司改造决策集合的维度,加速了博弈均衡状态的实现。但是,这种方法是以机群为单位,忽略了机组层面的多方案改造决策问题,需要发电企业进一步规划。
3.2.2 企业多技术改造决策阶段
在考虑系统动态博弈规划后,确定了发电企业X内部各个机群的改造决策,即确定了机群的最小出力系数的改造效果。并且,发电企业X也能通过FUC模型推测出其在整个发电市场的地位及收益。因此,发电企业需要在考虑经济性的基础上,完成系统博弈规划阶段的改造效果,对机组层面多技术改造的选择问题做出决策。
为此,本文提出了一种发电企业多技术改造规划模型。该模型以最小化企业的运行和改造投资成本为目标,即
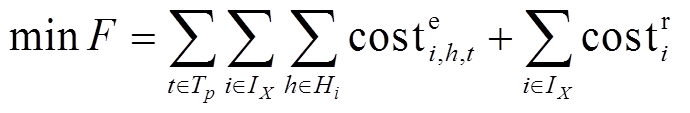 (22)
(22)式中,Tp为第p时段的时序集合;IX为企业X所有火电机组的集合;Hi为机组i的可行改造方案集合;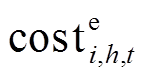 为机组i经过h方案改造后的运行成本,包含机组的发电能耗成本、启动成本、停机成本,即
为机组i经过h方案改造后的运行成本,包含机组的发电能耗成本、启动成本、停机成本,即
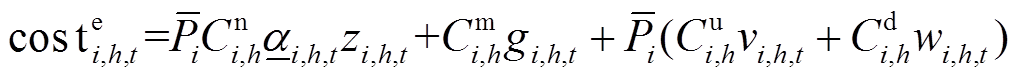 (23)
(23)
式中,zi,h,t、vi,h,t和wi,h,t分别为机组i经过h方案改造后的开关机、启机和停机二进制变量;gi,h,t为机组i经过h方案改造后在最小技术出力之上的出力变量;Cn i,h为机组处于出力下限时的单位煤耗成本;Cm i,h、Cu i,h和Cd i,h分别为机组i采用h方案改造后的线性增量成本、单位容量启动成本和关机成本。
模型同样采用等额年金法,考虑灵活性改造的年化投资成本。
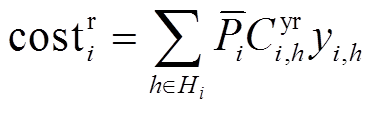 (24)
(24)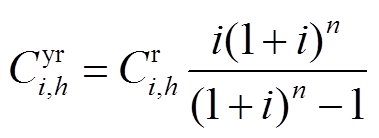 (25)
(25)
式中,Cyr i,h为机组i采用h方案改造的年化投资成本。模型同时也受式(2)约束,模型中的其他约束主要包括灵活性约束、功率平衡约束、变量逻辑约束和改造效果约束。
1)灵活性约束,包含机组出力上下限,爬坡速率和启停机时间等约束。
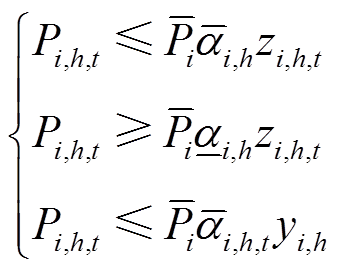 (26)
(26)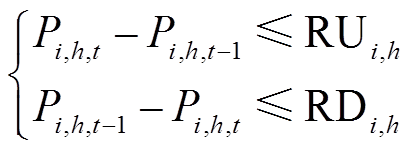 (27)
(27)
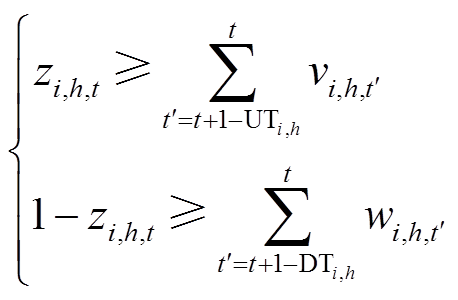 (28)
(28)
式中,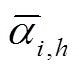 、
、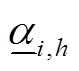 、RUi,h、RDi,h、UTi,h和DTi,h分别为机组i采用h方案改造后的出力上限和下限系数、向上和向下爬坡速率限制、最小持续开机和停机时间约束。
、RUi,h、RDi,h、UTi,h和DTi,h分别为机组i采用h方案改造后的出力上限和下限系数、向上和向下爬坡速率限制、最小持续开机和停机时间约束。
2)功率平衡约束
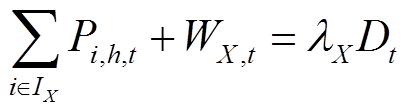 (29)
(29)式中,λX为发电企业X在考虑博弈均衡状态下在整个发电市场的占比。
3)变量逻辑约束
 (30)
(30)式中,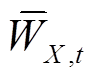 为发电企业X的IRES时刻t的可用发电功率。
为发电企业X的IRES时刻t的可用发电功率。
4)改造效果约束。在考虑系统博弈均衡状态时,每个机群的最小出力系统的改造效果基本确定。
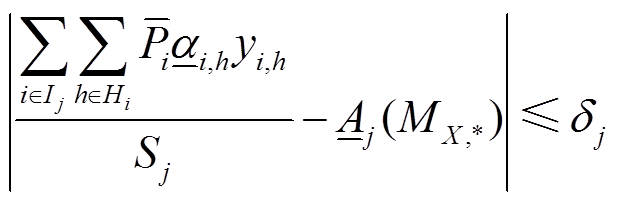 (31)
(31)式中, 为系统博弈均衡状态下,发电企业第j机群最小出力系数的改造效果。
为系统博弈均衡状态下,发电企业第j机群最小出力系数的改造效果。
综上所述,本文所提出的灵活性改造两阶段规划方法的结构与流程如图5所示。
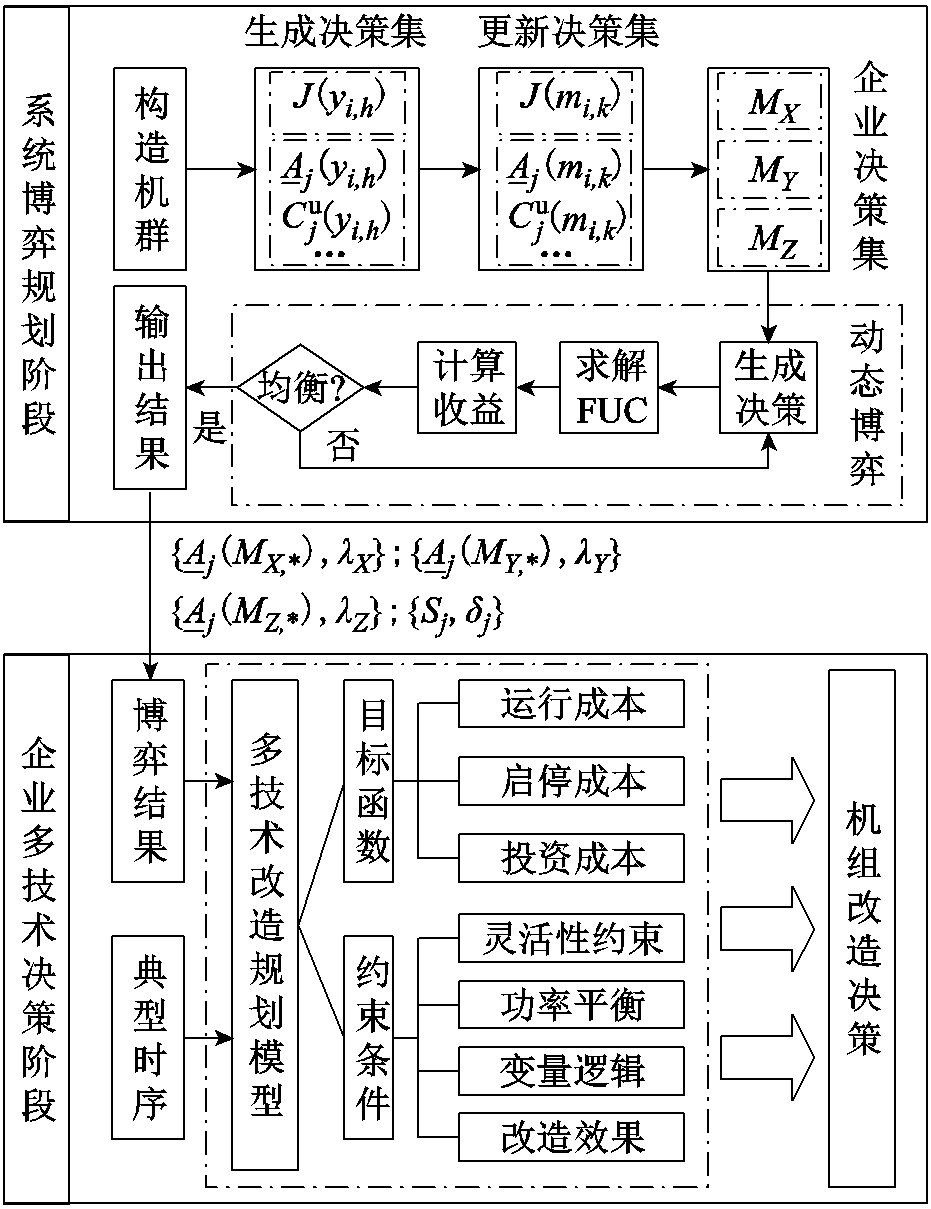
图5 火电机组灵活性改造两阶段规划方法
Fig.5 Two-stage planning method for flexibility retrofit of thermal power units
本节对所提出的考虑博弈的灵活性改造规划方法进行验证。
算例中包含火电装机容量5 750MW,风电装机容量3 400MW,分别隶属于三个发电企业,见表1。其中,不同火电机组的可行改造方案的年化投资成本及其详细运行参数见附表1~附表3。系统年负荷峰值为5 300MW,风电发电量占比约为20%。负荷和风电的时序数据来源于东北某省2018年相应数据的等比缩放。火电和风电的上网电价分别为0.37元/(kW∙h)和0.55元/(kW∙h)。深度调峰标准为50%,调峰补偿价格为0.5元/(kW∙h)。本文考虑了两种改造规划方法:一种是本文提出的考虑多主体博弈的两阶段规划方法(博弈规划);另一种是文献[15]提出的统一规划方法(统一规划)。
表1 不同发电企业的装机容量
Tab.1 Installed capacity of different companies

发电企业纯凝/MW热电/MW风电/MW合计/MW C11 2001 0609003 160 C26001 2001 2003 000 C37009901 3002 990
然而,文献[15]中忽略了机组多方案改造的选择性,以及由改造带来的多参数变化等问题。因此,本文通过扩展和修改3.2.2节提出的发电企业多技术规划模型,对上述统一规划模型进行了完善。扩展应用后,模型的目标函数修改为以最小化整个系统的运行成本和投资成本为目标,以系统的功率平衡为约束,如式(32)和式(33)所示。
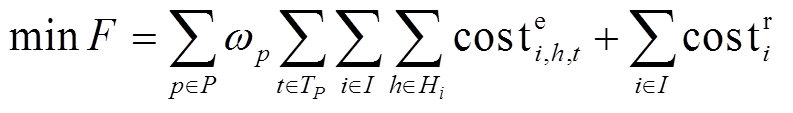 (32)
(32)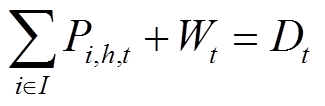 (33)
(33)
式中,P为典型时段集合;ωp为典型时序p的权重;I为系统中所有机组的集合。另外,模型还受式(23)~式(28)以及式(2)、式(30)约束。
本文对比了两种改造方法的改造成本及改造效果,博弈规划与统一规划的改造决策见表2。
表2 两种方法的改造决策
Tab.2 The retrofit decision of two methods

机组编号博弈规划统一规划 U133 U213 U313 U413 U521 U611 U722 U811 U911 U1022 U1111 U1233 U1312 U1413 U1513 U1611
表2中方案为“1”表示该机组保持原样不进行改造,为其他数字表示该机组进行改造。两种方法中,U1、U16和U6~U12的机组改造决策相同。其中,博弈规划涉及火电机组改造总容量较小,为2 050MW,改造比例约为36%。统一规划方法涉及改造总容量较大,为4 120MW,改造比例约为71%。改造后系统的风电消纳情况如图6所示。

图6 两种方法的弃风率对比
Fig.6 Comparison of wind curtailment rate between two methods
两种方法都降低了系统的弃风率,分别降低了约10%和15%,呈现出灵活性改造规模越大,弃风率越低的趋势。以系统中机组都不改造为基准,两种改造方法下的系统运行与投资成本如图7所示。

图7 两种方法的运行与投资成本对比
Fig.7 Comparison of system operation and investment cost of two methods
改造后,两种改造方法的系统运行成本都有所下降,其原因是灵活性改造增加了风电的上网空间,减少了火电的发电量。虽然统一规划与博弈规划相比,具有较高的改造投资成本,但系统总的运行与投资成本却更低,这是由于统一规划方法是以最小化系统总运行与投资成本为目标进行决策的。从系统整体角度而言,博弈规划是统一规划模型的一个次优解。
两种规划方法下,发电企业间的改造投资成本存在差异,如图8所示。
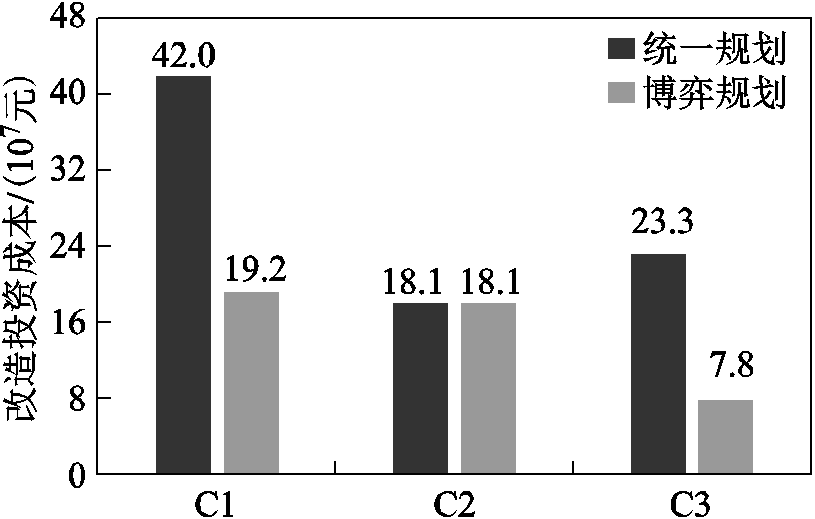
图8 企业的改造投资成本对比
Fig.8 Comparison of retrofit investment costs of enterprise
从图8中可以看出,两种方法下C2的投资成本相同,其他两个企业存在较大差异。博弈规划方法下C1的改造投资变化最大,其原因可能是C1火电装机容量最大,在火电市场占据较大份额,C1大规模改造会大幅度降低其火电的发电量,而其风电的装机容量最小,风电收益增长有限,投资意愿相对较低。采用两种方法改造前后,发电企业在电量市场和调峰市场中的各项收益见表3。表3中调峰收益为负表示该企业在调峰市场中是分摊者,存在调峰分摊成本。
表3 各项收益指标对比
Tab.3 Comparison of various income indicators

企业火电收益/元风电收益/元调峰收益/元 不改造C11.88×1098.42×108-4.03×106 C21.60×1091.12×1098.74×106 C31.20×1091.22×109-4.71×106 博弈规划C11.84×1099.25×1082.43×107 C21.61×1091.23×109-1.37×107 C31.14×1091.34×109-1.07×107 统一规划C11.69×1099.95×1086.03×107 C21.79×1091.33×109-4.81×107 C31.08×1091.44×109-1.22×107
在统一规划方法下,C1的调峰收益约为6 030万元,高于其改造投资成本4 200万元,仅考虑调峰市场C1的净收益是增长的。然而,在电量市场中,C1的火电收益却下降了约19 200万元,虽然C1的风电收益增长了约15 300万元,但其远弥补不了火电收益的损失。相反,C2的调峰分摊成本为4 810万元,在调峰市场处于不利地位。但该企业在电量市场中,火电和风电的收益分别增长了19 000万元和20 400万元,不仅能够弥补其在调峰市场中的损失,还能增加企业的利润。
而在博弈规划方法下,C1在调峰市场中由分摊者变为了受益者,在调峰市场中增加收益约2 840万元,且在电量市场中其风电电量收益增加了8 310万元,大大弥补了火电电量的亏损和改造投资成本。C1企业总的净收益(火电收益+风电收益+调峰收益-投资成本)是增长的。不同发电企业在两类方法下较不改造方案的净收益增长率如图9所示。
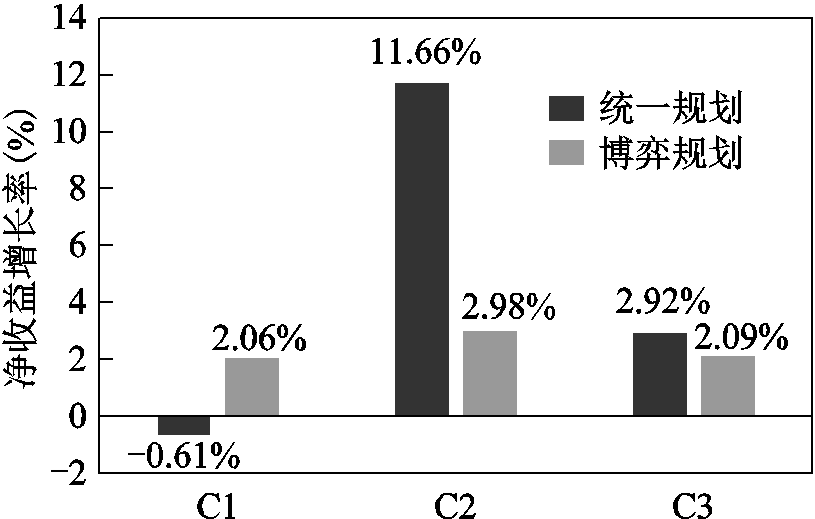
图9 净收益增长率对比
Fig.9 Comparison of net income growth rate
结合图8、图9可以看出,统一规划决策中,C2的灵活性改造投资成本最低,但其净收益增加了约11.66%,是灵活性改造最大的受益者。相反,C1虽然灵活性改造投资成本最高,但其净收益却减少了0.61%。高投入不仅没有获得高收益,反而出现了亏损,企业改造的能动性较差。统一规划方法忽视了发电企业的改造意愿,不能平衡各方的利益,改造规划决策难以推行。反观博弈规划方法下,各个企业的净收益都能增长大约2%~3%,各发电企业的利益都能得到平衡,各个企业的改造能动性都较强。
此外,虽然博弈规划方法能够平衡各个发电企业的利益,但发电企业需要做好内部利润的合理分配。例如,C3在电量市场中收益增加了6 400万元,但其火电收益减少了5 610万元,风电收益增长了12 000万元,企业/集团内部存在竞争问题,需要在未来工作中继续展开研究。
对火电机组进行灵活性改造是提高电力系统灵活性、降低IRES削减的一种重要手段。由于功能定位、技术要求和现场条件不同,机组间的改造方案与投资成本存在多样性和差异性。并且,灵活性改造涉及不同运营商在电量和调峰市场的博弈关系。基于此,本文建立了一个考虑多主体博弈的两阶段规划方法。首先,通过引入FUC模型,建立了发电企业在电量和调峰市场的收益模型。其次,提出了一种考虑多主体动态博弈和发电企业多技术改造的两阶段规划方法。最后,通过算例分析验证了所提模型和方法的准确性。得到以下结论:
1)本文提出两阶段改造方法,能够兼顾各个发电企业的主体利益。虽然该方法与统一规划方法相比改造规模较小,但其更加贴近实际市场运行机制,有效保证了市场活力。
2)发电企业做改造决策时,不仅需要考虑调峰市场收益,还需综合考虑其在电量和调峰市场的两方面收益。
在未来的研究中,将会进一步考虑企业或集团内部的利润分配及灵活性改造的工程周期等问题,为规划部门、发电企业等部门提供帮助。
附表1 纯凝机组采用不同技术改造参数
APP.Tab.1 The parameters of power units with different retrofits technologies

发电企业机组编号/ MW方案编号RU,RD/(MW/h)Cn/[元/(MW∙h)]Cm/(元/MW)UT, DT/hCu/(元/MW)Cd/(元/MW)Cyr/(元/MW) C11600110.630023616182 0106700 210.436024516382 01067026 300 310.3542026116182 01067027 962 2600110.5530024116882 0006670 210.436025618082 00066725 984 310.342027318982 00066727 120 C27600110.5536023614782 0106700 210.3548025215582 01067025 864 C315350110.5521025417041 6505500 210.4824526117541 64054719 500 310.428027018041 65055022 400 16350110.5521025216841 6405470 210.45262.527518341 64054720 000
附表2 热电机组非供暖期运行参数
App.Tab.2 The parameters of CHP units during nonheating period

发电企业机组编号/ MWRU,RD/(MW/h)Cn/[元/(MW∙h)]Cm/(元/MW)UT, DT/hCu/(元/MW)Cd/(元/MW) C1333010.65198262 173 51 890 630 433010.65198264 174 51 870 623 520010.65120275 157 41 695 565 620010.65120280 160 41 680 560 C2830010.65165270 174 51 700 567 930010.65165265 170 51 710 570 1030010.6180270 169 51 820 607 1130010.6180270 169 51 790 597 C31233010.6198257 171 51 760 587 1333010.6198259 173 51 750 583 1433010.6198261 174 51 740 580
附表3 热电机组供暖期运行参数
APP.Tab.3 The parameters of CHP units during heating period

发电企业机组编号方案编号Cn/[元/(MW∙h)]Cm/(元/MW)Cyr/(元/MW) C1310.640.61401400 20.640.51271888 600 30.640.4411120413 520 410.650.591411410 20.650.481231929 000 30.650.4311219813 560 510.680.61471470 20.680.513817312 000 610.660.581501500 20.660.514815712 650 C2810.640.61451450 20.640.51351778 000 30.640.4511322112 000 910.650.591421420 20.650.51281877 500 30.650.4311519511 500 1010.590.551451450 20.590.481262258 600 1110.60.581421420 C31210.660.581381380 20.660.51241798 400 30.660.4210918713 200 1310.670.571391390 20.670.51231849 500 30.670.4111218112 302 1410.420.421111880
参考文献
[1] 鲁宗相, 李海波, 乔颖. 高比例可再生能源并网的电力系统灵活性评价与平衡机理[J]. 中国电机工程学报, 2017, 37(1): 13-24. Lu Zongxiang, Li Haibo, Qiao Ying. Flexibility evaluation and supply/demand balance principle of power system with high-penetration renewable electricity[J]. Proceedings of the CSEE, 2017, 37(1): 13-24.
[2] 施涛, 朱凌志, 于若英. 电力系统灵活性评价研究综述[J]. 电力系统保护与控制, 2016, 44(5): 146-154. Shi Tao, Zhu Lingzhi, Yu Ruoying. Overview on power system flexibility evaluation [J]. Power System Protection and Control, 2016, 44(5): 146-154.
[3] International Energy Agency. Harnessing variable renewables[R]. Paris: International Energy Agency, 2011: 43-50.
[4] 侯文庭, 韦化. 考虑核电可调度性的风-光-核-水-火多源协调短期优化调度[J]. 电工技术学报, 2018, 33(12): 227-236. Hou Wenting, Wei Hua. A multi-source coordinated short-term dispatch model considering the dispatchability of nuclear power plants[J]. Transactions of China Electrotechnical Society, 2018, 33(12): 227-236.
[5] 严毅, 张承慧, 李珂, 等. 含压缩空气的微网复合储能系统主动控制策略[J]. 电工技术学报, 2017, 32(20): 232-240. Yan Yi, Zhang Chenghui, Li Ke, et al. An active control strategy for composited energy storage with compressed air energy storage in micro-grid[J]. Transactions of China Electrotechnical Society, 2017, 32(20): 232-240.
[6] 张利, 杨建, 菅学辉, 等. 考虑次小时尺度运行灵活性的含储能机组组合[J]. 电力系统自动化, 2018, 42(16): 48-55. Zhang Li, Yang Jian, Jian Xuehui, et al. unit commitment with energy storage considering operation flexibility at sub-hourly time-scales[J]. Automation of Electric Power System, 2018, 42(16): 48-55.
[7] 侯依昕, 丁坚勇, 杨东俊. 基于最大受电公平性指标的跨区直流消纳模型[J]. 电力系统保护与控制, 2017, 45(9): 80-87. Hou Yixin, Ding Jianyong, Yang Dongjun. Model for cross-region DC power consumption based on the index of fairness for maximum receiving electric power[J]. Power System Protection and Control, 2017, 45(9): 80-87.
[8] 易文飞, 张艺伟, 曾博, 等. 多形态激励型需求侧响应协同平衡可再生能源波动的鲁棒优化配置[J]. 电工技术学报, 2018, 33(23): 155-168. Yi Wenfei, Zhang Yiwei, Zeng Bo, et al. Robust optimization allocation for multi-type incentive-based demand response collaboration to balance renewable energy fluctuations[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 155-168.
[9] 邓婷婷, 娄素华, 田旭, 等. 计及需求响应与火电深度调峰的含风电系统优化调度[J]. 电力系统自动化, 2019, 45(15): 34-40. Deng Tingting, Lou Suhua, Tian Xu, et al. optimal dispatch of power system integrated with wind power considering demand response and deep peak regulation of thermal power units[J]. Automation of Electric Power System, 2019, 45(15): 34-40.
[10] 贾雨龙, 米增强, 余洋, 等. 计及不确定性的柔性负荷聚合商随机-鲁棒投标决策模型[J]. 电工技术学报, 2019, 34(19): 4096-4105. Jia Yulong, Mi Zengqiang, Yu Yang, et al. Stochastic-robust decision-making model for flexible load aggregator considering uncertainties[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4096-4105.
[11] International Energy Agency. The power of transformation: wind, sun and the economics of flexible power systems[R]. Paris: International Energy Agency, 2014: 115-160.
[12] 国家能源局东北监管局. 东北电力辅助服务市场运营规则[R]. 沈阳: 国家能源局东北监管局, 2016.
[13] 吕泉, 杜思瑶, 刘乐, 等. 东北辅助服务市场下热电厂配置电锅炉调峰的经济性分析[J]. 电力系统自动化, 2019, 43(20): 49-56. Lü Quan, Du Siyao, Liu Le, et al. Economic analysis of peak shaving of combine heat and power plant with electric boilers in auxiliary service market of northeast China[J]. Automation of Electric Power System, 2019, 43(20): 49-56.
[14] Barbara G, Reinhard M. Evaluating the enhanced flexibility of lignite-fired power plants: a real options analysis[J]. Energy Conversion and Management. 2018, 177: 737-749.
[15] 李星梅, 钟志鸣, 阎洁. 大规模风电接入下的火电机组灵活性改造规划[J]. 电力系统自动化, 2019, 43(3): 69-76. Li Xingmei, Zhong Zhiming, Yan Jie. Comprehensive evaluation of transmission network planning for integeration of high-penetration renewable energy[J]. Automation of Electric Power System, 2019, 43(3): 69-76.
[16] 李力行, 苗世洪, 孙丹丹, 等. 多利益主体参与下主动配电网完全信息动态博弈行为[J]. 电工技术学报, 2018, 33(15): 3499-3509. Li Lixing, Miao Shihong, Sun Dandan, et al. Dynamic games of complete information in active distribution network with multi-stakeholder participation[J]. Transactions of China Electrotechnical Society, 2018, 33(15): 3499-3509.
[17] 杨楠, 黄禹, 董邦天, 等. 基于多主体博弈的电力-天热气综合能源系统联合规划方法研究[J]. 中国电机工程学报, 2019, 39(22): 6521-6532. Yang Nan, Huang Yu, Dong Bangtian, et al. Research on the joint planning method of electricity-gas integrated energy system based on multi-agent game[J]. Proceedings of the CSEE, 2019, 39(22): 6521-6532.
[18] International Energy Agency. Status of power system transformation 2018[R]. Paris: International Energy Agency, 2018: 31-62.
[19] Steven Stoft. Power system economics: designing markets for electricity[M]. New York: Wiley, 2002: 30-39.
[20] Belderbos A , Delarue E . Accounting for flexibility in power system planning with renewables[J]. International Journal of Electrical Power & Energy Systems, 2015, 71: 33-41.
[21] Palmintier B S, Webster M D. Heterogeneous unit clustering for efficient operational flexibility modeling[J]. IEEE Transactions on Power Systems, 2014, 29(3): 1089-1098.
[22] Meus J, Poncelet K, Delarue E. Applicability of a clustered unit commitment model in power system modeling[J]. IEEE Transactions on Power Systems, 2017, 33(2): 2195-2204.
[23] He Xingning, Chen Xinyu, Michael B M, et al. Modeling formulation and validation for accelerated simulation and flexibility assessment on large scale power systems under higher renewable penetrations[J]. Applied Energy, 2019, 237: 145-154.
[24] Agora Energiewende. Flexibility in thermal power plants—with a focus on existing coal-fired power plants[M]. Berlin: Agora Energiewende, 2017: 57-80.
[25] IEA Clean Coal Centre. Increasing the flexibility of coal-fired power plants[R]. London: IEA Clean Coal Centre, 2014.
[26] 陈秀芳, 阎寒冰. 低温烟气脱硝技术在火电机组灵活性改造中的应用[J]. 应用化工, 2019, 49(12): 3027-3031. Chen Xiufang, Yan Hanbing. Application of low temperature flue gas denitration technology in flexibility reconstruction of thermal power units[J]. Applied Chemical Industry, 2019, 49(12): 3027-3031.
[27] 章艳, 吕泉, 李扬, 等. 四种热电厂电热解耦改造方案的运行灵活性剖析[J]. 电力系统自动化, 2020,44(2): 164-172. Zhang Yan, Lü Quan, Li Yang, et al. Analysis on operation flexibility of conbined heat and power plant with four improved power-heat decoupling schemes[J]. Automation of Electric Power System, 2020, 44(2): 164-172.
[28] 胡康, 陈群. 电-热综合能源系统整体能效及灵活性改造方案分析[J]. 热力发电, 2018, 47(5): 14-21. Hu Kang, Chen Qun. Overall energy efficiency and flexibility retrofit scheme analysis of heat-power integrated energy system[J]. Thermal Power Generation, 2018, 47(5): 14-21.
[29] NREL. Cost-benefit analysis of flexibility retrofits for coal and gas-fueled power plants [R]. Golden, Colorado: National Renewable Energy Laboratory, 2013.
[30] 张勇, 马斌. 干货|火电厂灵活性改造技术对比分析[EB/OL]. (2019-08-18)[2019-09-06]. http://news. bjx. com.cn/html/20190117/957375.shtml.
Planning of Flexibility Retrofits of Thermal Power Units Considering Multi-Agent Game
Abstract For countries with coal as their main energy source, implementing the flexibility retrofit of thermal power units is the most realistic and feasible option to improve the power system flexibility. This paper proposes a two-stage planning method for the retrofit planning based on multi-agent game. First, the different subsystems and diverse technologies involved in the flexibility retrofitting had been overviewed. Second, in the system planning stage, the profit model for power generation companies in the down-regulation and energy market was constructed, considering the game behavior of different investment entities. Then, a fast solution method was proposed to solve the large-scale game iterative operation problem. Third, in the company planning stage, a mixed-integer planning model for multi-technology retrofit of power generation companies was established. The model aims to minimize the company’s operation and investment cost, constrained by flexibility constraints and the results of the system planning stage. Finally, the rationality and effectiveness of the proposed model and method were verified by a case study. The results show that the proposed method can balance the interests of all investment entities, effectively ensure market vitality, and provide assistance to planning departments and power generation companies.
keywords:Flexibility retrofit, multi-agent game, down-regulation market, mixed integer programming
中图分类号:TM73
DOI:10.19595/j.cnki.1000-6753.tces.191153
国家自然科学基金资助项目(51607068)。
收稿日期 2019-09-11
改稿日期 2020-03-16
郭 通 男,1993年生,博士研究生,研究方向为高比例可再生能源电力系统规划与运行。E-mail:ncepugt@163.com
李永刚 男,1967年生,教授,博士生导师,研究方向为大型电气设备故障检测与诊断、电力系统规划与运行。E-mail:lygzxm0@163.com(通信作者)
(编辑 赫蕾)