图1 固态电制热储热系统结构示意图
Fig.1 Structure of solid-state electric heating thermal storage system
摘要 固态电制热储热系统是一种新兴电力系统大容量调峰技术，研究电热元件与储热体间的传热匹配特性和热控制方法，对提升电储热系统的可靠性和强化传热具有重要意义。该文通过建立传热速率平衡方程，利用数值模拟的方法对电储热系统各设计参数与传热匹配的交互特性进行分析，并利用级贡献率、毕渥数和傅里叶数等传热匹配性能评价指标对传热匹配效果进行量化比较。结果表明，储热单元温度与加热功率线性正相关，与孔占比和循环风速指数型负相关，降低加热功率、提高孔占比和循环风速能改善储热体均热性，提高孔占比能，增加储热深度。经实验证明，通过多参数协同优化设计和前馈补偿控制，可以实现较好的传热匹配效果，为固态电制热储热系统的优化和热控制提供了方法。
关键词：固态电制热储热 传热匹配 性能评价指标 热控制
固态电制热储热技术是最近几年兴起的一项新型大容量调峰技术，具有良好的柔性特性和热电解耦能力，已经成为大容量储能技术的研究热点之一。固态电制热储热技术应用于热电机组灵活性改造，既可降低热电耦合程度[1]，增加电网调峰裕度[2-3]，有效解决清洁能源消纳问题[4-5]，又能满足清洁供暖的民生需求。根据国家电网统计数据，截至2018年末，固态电制热储热装置已推广至我国北方14个省（市、区），总功率2 077.69MW（单台最大功率90MW）。经过近4年应用，辽宁、吉林电网弃风率分别从最高的14.6%（2015年）和42.14%（2016年）下降至2018年0.97 %和6.85 %。
近年来，随着各类储热技术的发展，储热传热特性的研究也逐渐受到了重视。例如：杨小平等通过对高温填充床储热过程进行数值计算，研究了蓄热材料参数对填充床的熵产值的影响，分析了填充床的传热温度差变化规律[6-7]；杨勇平等对以导热油与沙砾为填料的斜温层单罐显热蓄热罐进行实验，研究了换热流体流速对罐体蓄热性能的影响[8]；M. Belusko分析了一种通过空气进行传热的相变储热结构的传热特性，研究了空气传热过程中的泵送损失[9]；M. Hänchen对岩石填料床进行分析和实验，提出一种联合传热能量方程[10]；A. Andreozzi对平行方槽储热结构和平行板式储热结构的瞬态传热进行数值模拟，提出了一种储热传热模型[11-12]。
笔者在对储热系统传热特性的研究中发现，以往的研究均未涉及传热速率对产热元件和储热材料的影响，也很少对传热性能确立明确的评价指标。电热元件向储热体传热时，传热速率受储热结构的限制[13]，容易出现电热元件与储热体间的传热不匹配。一方面使热量积累在电热元件中，电热元件温度过高，造成电热元件寿命缩减甚至熔断[14-15]。另一方面使储热体传热不均衡，储热体内部各点温度差过大，造成储热体的变形或破裂。因此在固态电制热储热系统设计和运行过程中，需要进行传热匹配优化设计以及传热速率及温度的热控制。
为解决固态电制热储热系统电热元件与储热体间传热匹配设计及热控制的难题，本文将采用数值模拟方法对电制热储热系统的储热单元进行有限体积法分析，开展传热匹配特性研究。通过研究电热元件和储热体间的传热速率平衡关系，分析影响储热装置传热匹配的关键设计参数，建立传热匹配目标与电储热系统设计参数的关联方程及传热匹配性能评价指标。运用Fluent数值模拟分析软件建立储热单元传热模型，分析传热匹配目标与储热设计参数的传热规律，实现固态电制热储热装置传热匹配的多参数协同优化设计和前馈补偿控制。
固态电制热储热系统采用氧化镁非金属类单体储热模块构造储热体[16]，将螺旋形铁铬铝合金电热元件嵌入储热体内进行辐射强化传热，控制系统利用变频风机进行储热体内负压气流循环，并经由换热器对外供热，实现电加热和热能释放相对独立。固态电制热储热系统结构示意图和传热原理如图1和图2所示。
图1 固态电制热储热系统结构示意图
Fig.1 Structure of solid-state electric heating thermal storage system
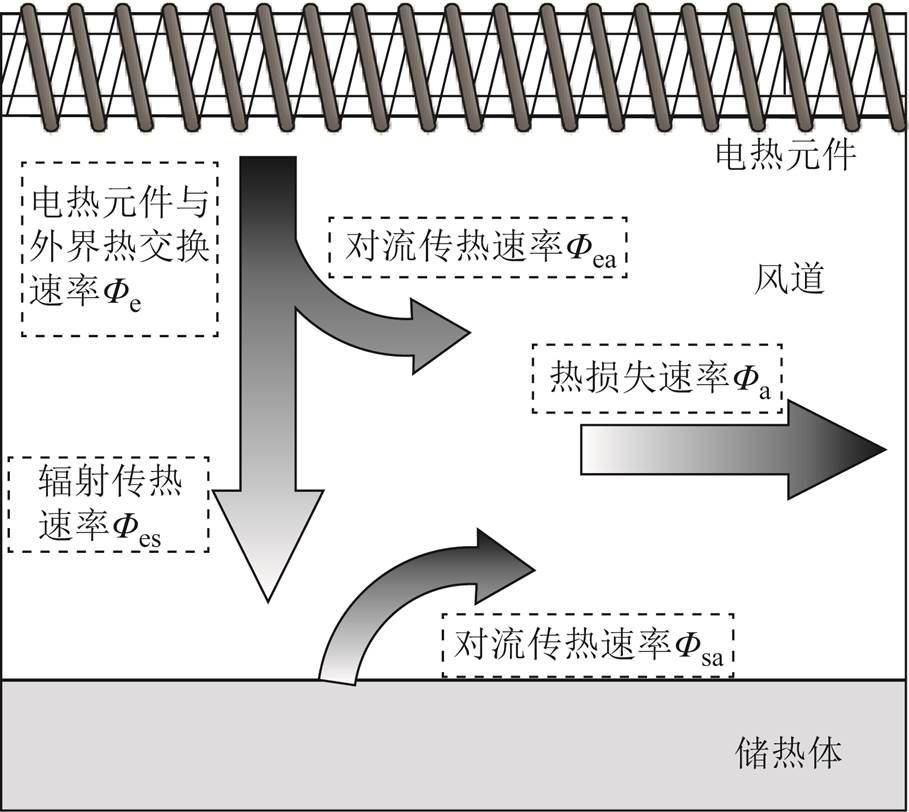
图2 固态电制热储热系统传热原理
Fig.2 Schematic diagram of heat transfer in solid-state thermal storage system
根据传热原理，固态电制热储热系统的电热元件、空气及储热体三部分之间的传热速率表示为[17]
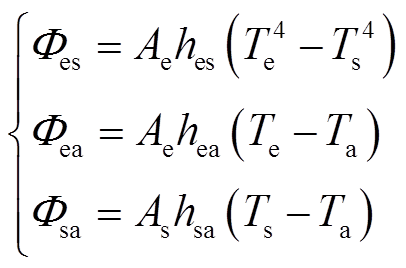（1）式中，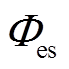
为辐射传热速率；
、
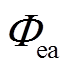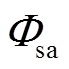分别为电热元件和储热体对空气的对流传热速率；
、
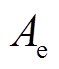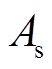分别为电热元件表面积和风道表面积；
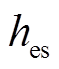为辐射传热系数；
、
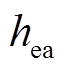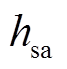分别为电热元件和风道表面的对流传热系数；
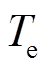为电热元件温度；
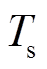为风道表面温度；
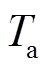为空气温度。
电热元件与外界热交换的速率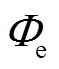
为
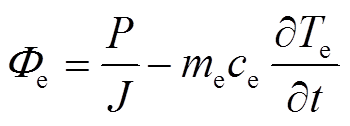（2）式中，P为电热元件加热功率；J为热功当量；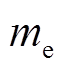
为电热元件质量；
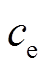为电热元件比热容；t为时间。
空气在换热器中的热损失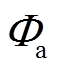
可表示为
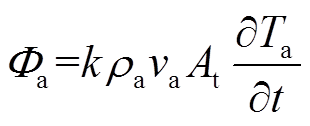（3）式中，k为换热器换热系数；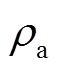
为空气密度；
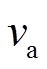为循环风速；
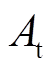为换热器截面积。
根据图2所示热量传递方向，可得
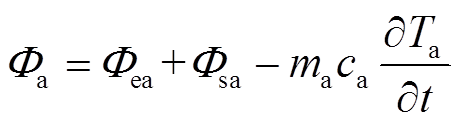（4） 
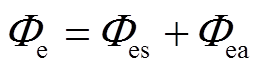（5）
式中，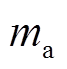
为空气的质量；
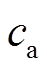为空气的比热容。
将式（2）、式（4）代入式（5）中，则有
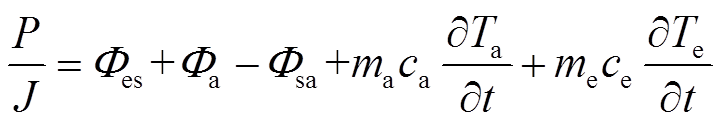（6）将式（1）、式（3）代入式（6）整理得
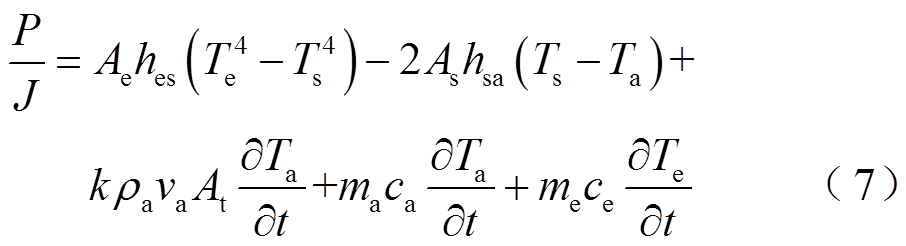
式（7）即为固态电制热储热系统的传热速率平衡方程，可以看出，与电热元件和储热体温度相关的参数有系统几何结构参数、电热元件功率、材料热物性参数及系统运行条件。由于固态电制热储热系统设计过程中，材料热物性参数及电热元件结构参数较难改变，不适合参与传热匹配设计。因此，选择电热元件功率P、风道表面积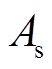和循环风速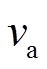为变量进行传热匹配设计。
式（7）中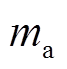、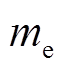的值很小，即空气和电热元件吸收的热量相对于电储热系统总热量可以忽略不记，因此式（7）可变为
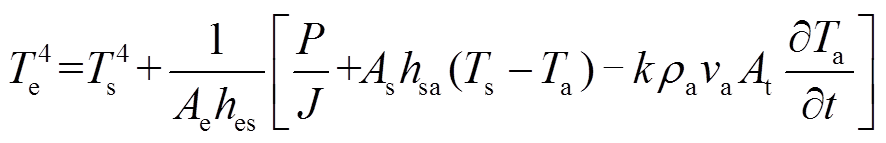（8）在实际工程设计中，电储热装置受场地及换热效率限制，风道长度设计较难修改。因此，可以将风道表面积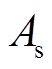换算为工程标准量——孔占比
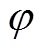，设定风道长度为不变量。
（9）
铁铬铝电热元件温度在1 173 K以上时，会出现脆性[18]。为延长电热元件寿命，电储热系统设计时，要求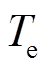尽可能低。以加热结束时电热元件的温度Teend为传热匹配优化目标，可得设计方程为
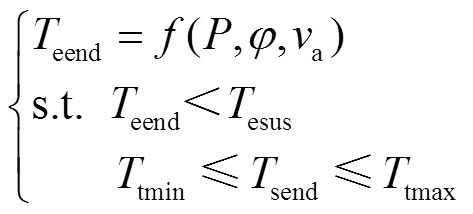（10）式中，Teend是关于电热元件功率P、孔占比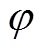和循环风速va的方程，Teend不能超过电热元件最高耐受温度Tesus [19]。Tsend是加热结束时储热体的温度，要求其值在[
,
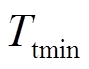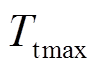]范围内。由式（8）可知，f(P,j,va)中包含Ts、Ta两个时变量，很难通过简单的解析法进行求解，因此，本文将通过数值模拟的方法研究储热装置的传热规律。
受储热体结构影响，传热匹配优化设计及热控制时，加热功率、孔占比、循环风速等参数只能分级调节。为判断各参数的可优化度，本文引入级贡献度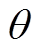
来表征参数对储热体温度的影响程度，级贡献度为
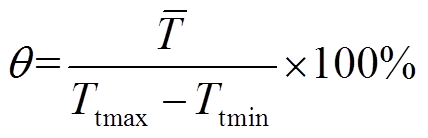（11）式中，
为设计参数分级调节时，储热体温度的单级平均变化量。级贡献度约为50 %时，参数可优化性更好。
为判断加热结束时储热体的储热程度，本文引入毕渥数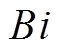
[20]和傅里叶数
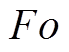[21]，分别来表征储热体的均热性和储热深度（即某一时刻，热扰动在储热体内的传播深度）。由于储热体由内表面向四周传热，不能简单地用平板模型进行计算。因此，本文采用特征长度
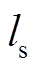表征储热体热传导距离进行计算，则毕渥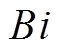数和傅里叶数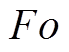计算公式为
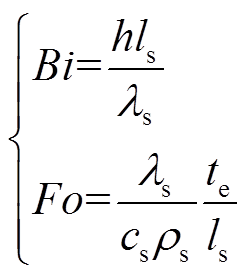（12）
式中，
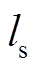为储热体内表面总传热系数；为特征长度，
，
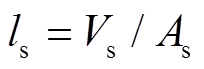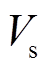为储热体体积；
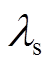为储热体的导热系数；
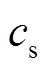为储热体比热容；
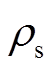为储热体密度；
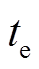为加热时长。当
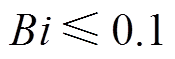时，可以忽略储热体内阻，认为储热体内各点温度接近均匀。当
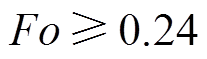时，储热体温度场分布仅受边界条件和物性的影响，与时间无关。
本文通过Fluent软件对固态电制热储热系统进行仿真。由于储热体内电热元件均匀分布，各电热元件周围传热特性相同，本文将电热元件及周围的空气和储热体视作储热单元。由于电热元件螺距远小于风道长度，为简化网格，本文将螺旋状电热元件假设为圆管。图3为储热单元结构及网格划分，表1、表2为储热单元的关键参数。由于本文主要目的为探索固态电制热储热传热匹配设计方法，为简化分析，对高温固态系统储热单元进行如下假设：①风道内气体流动为非稳态、不可压缩流动；②气体黏性扩散忽略不计；③材料热物性参数恒定，不随温度发生变化。
图3 储热单元结构及网格划分
Fig.3 Thermal storage unit structure and mesh generation
表1 储热单元关键几何参数
Tab.1 Thermal storage unit geometrical parameter
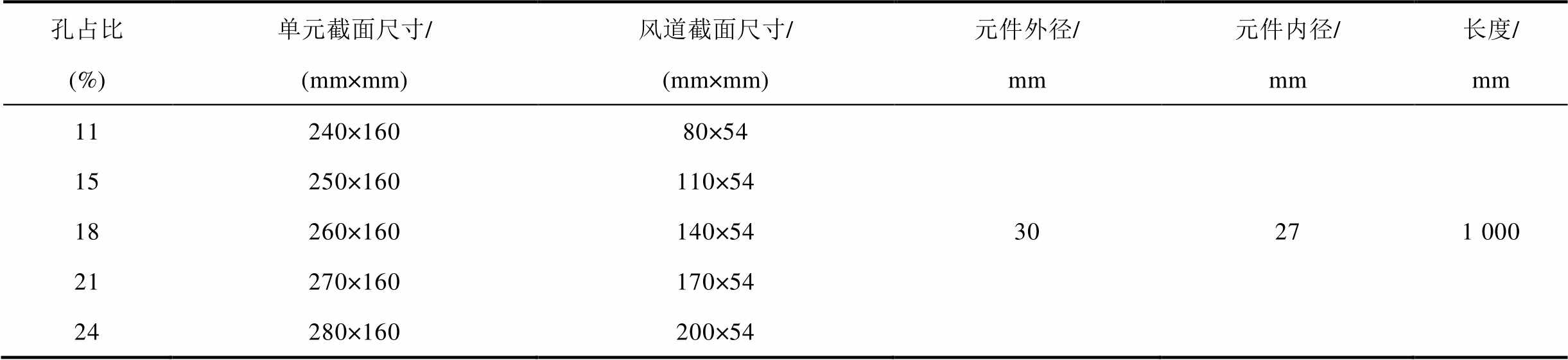
孔占比 (%)单元截面尺寸/ (mm×mm)风道截面尺寸/ (mm×mm)元件外径/ mm元件内径/ mm长度/ mm 11240×16080×54 15250×160110×54 18260×160140×5430271 000 21270×160170×54 24280×160200×54
表2 储热单元关键热物性参数
Tab.2 Thermal storage unit thermophysical parameter
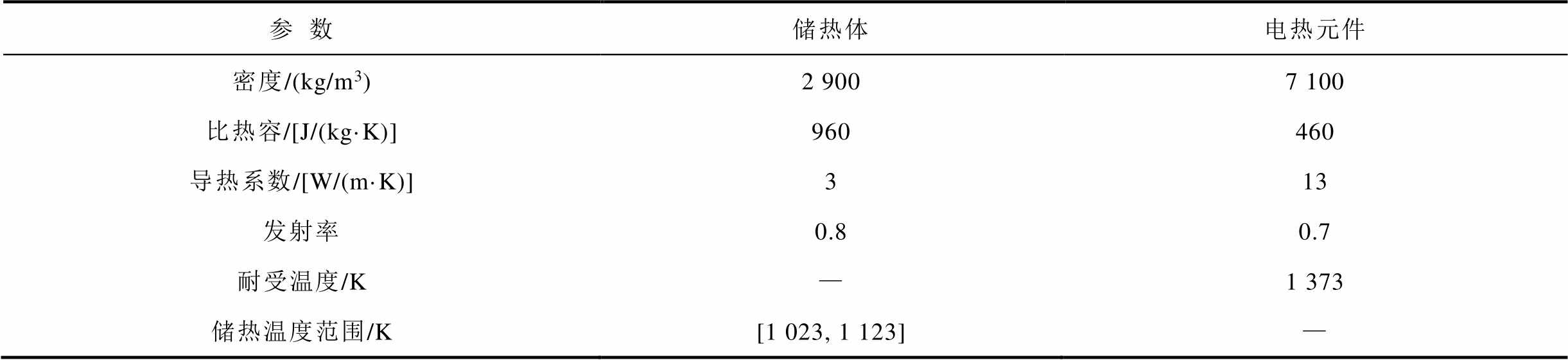
参数储热体电热元件 密度/(kg/m3)2 9007 100 比热容/[J/(kg·K)]960460 导热系数/[W/(m·K)]313 发射率0.80.7 耐受温度/K—1 373 储热温度范围/K[1 023, 1 123]—
根据质量守恒、动量守恒、能量守恒定理，风道内流动与传热过程三维非稳态数学模型控制方程如下[22]。
连续性方程为
（13）动量传输方程为
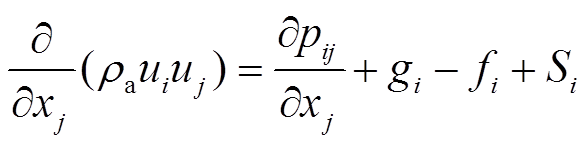（14）
固相区域控制方程为
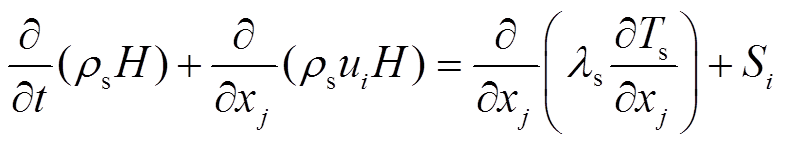（15）式中，ui、uj分别为在i和j方向的速度分量；xj在j方向的位移分量；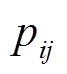
为表面静压；
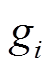为流体在i方向的体积作用力；
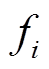为作用在流体上的反方向阻力；Si为源项；H为显焓。
初始条件：储热单元和空气起始温度为573 K。
边界条件：入口边界采用速度入口边界条件，出口采用自由出流边界条件，储热单元四周壁面采用第二类传热边界条件。
在储热单元孔占比为11%，循环风速为0 m/s的条件下，电热元件与储热体温度在不同加热功率下的升温曲线如图4和图5所示。可以看出，随着加热功率增加，电热元件温度和储热体温度值基本呈线性变化趋势增长，其线性函数斜率分别为248.6 K/kW和260.2 K/kW，储热体温度变化量更大。加热功率为1 667W和1 923W时，符合式（10）约束。经计算，加热功率对储热体温度的级贡献度为148.99 %。
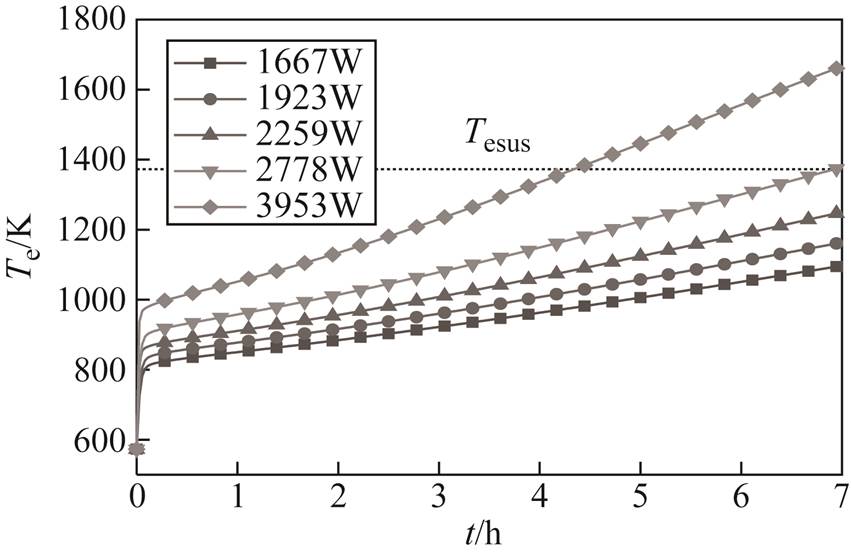
图4 不同加热功率下电热元件温度曲线
Fig.4 Electric heating wire temperature curve at different electric heating powers
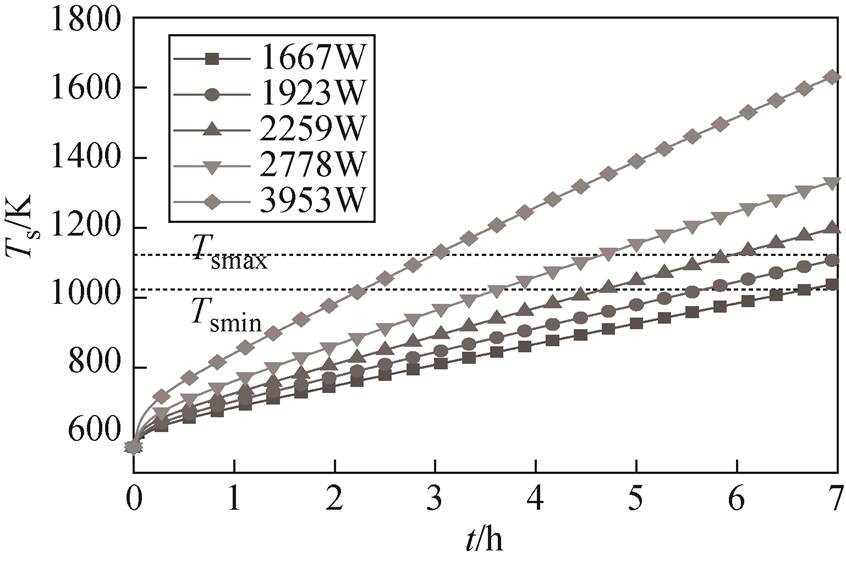
图5 不同加热功率下储热体温度曲线
Fig.5 Thermal storage masonry temperature curve at different electric heating powers
经计算，功率为1 677W、2 778W和3 953W的储热单元加热7h时，毕渥数分别为0.31、0.35和0.36，而傅里叶数均为0.21，表明加热功率越低，储热体均热性越好，而对储热深度没有影响。
在电热元件功率为2 259W，循环风速为0 m/s的条件下，储热单元电热元件与储热体温度在不同孔占比下的升温曲线如图6和图7所示。可以看出，随着孔占比增加，由于电热元件与储热体的间距增大，辐射热量减少，电热元件和储热体温度变化量基本呈指数变化趋势减小，其指数型函数系数分别为5.14和7.09，储热体温度变化量更大。孔占比为21 %和24 %时，符合式（10）约束。经计算孔占比对储热体温度的级贡献度为23.41 %。
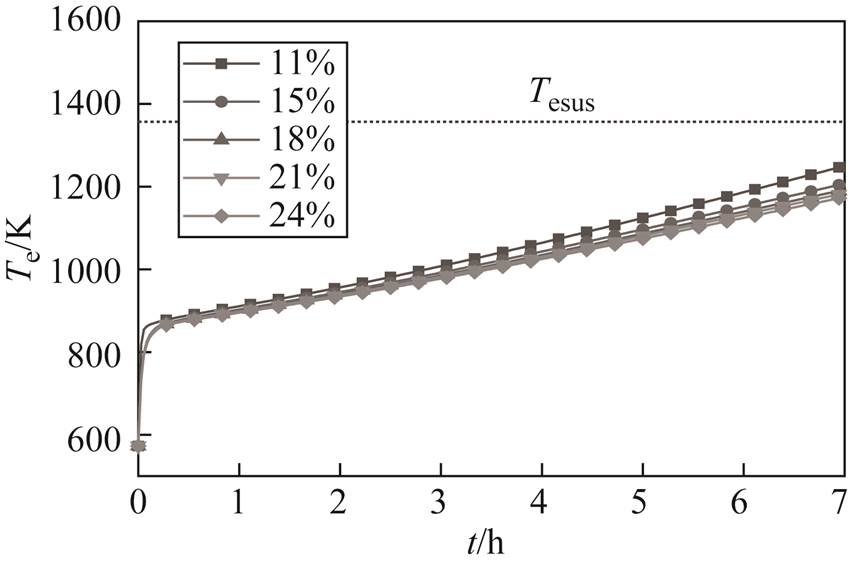
图6 不同孔占比下电热元件温度曲线
Fig.6 Electric heating wire temperature curve at different hole ratios
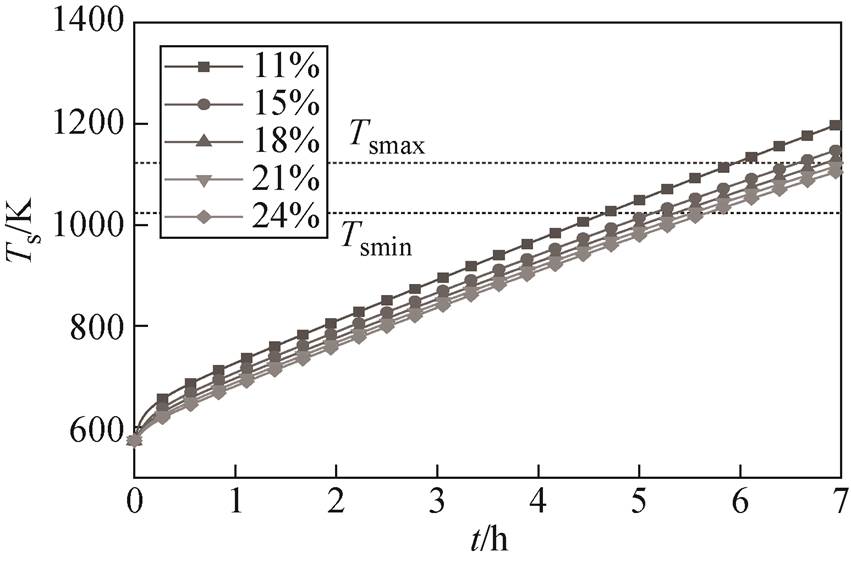
图7 不同孔占比下储热体温度曲线
Fig.7 Thermal storage masonry temperature curve at different hole ratios
经计算，孔占比为11 %、15 %和24 %的储热单元加热7 h时，毕渥数分别为0.33、0.14和0.04，傅里叶数分别为0.21、0.26和0.41，表明孔占比越大，储热体均热性越好，储热深度更深。
在储热单元电热元件功率为2 259 W，孔占比为11 %的条件下，储热单元电热元件与储热体温度在不同循环风速下的升温曲线如图8和图9所示。可以看出，随着循环风速增加，由于换热器换热速率的增大，电热元件和储热体温度变化量基本呈指数变化趋势减小，其指数型函数系数分别为9.23和11.93，储热体温度变化量更大。不存在方案符合式（10）约束。经计算循环风速对储热体温度的级贡献度为109.81 %。
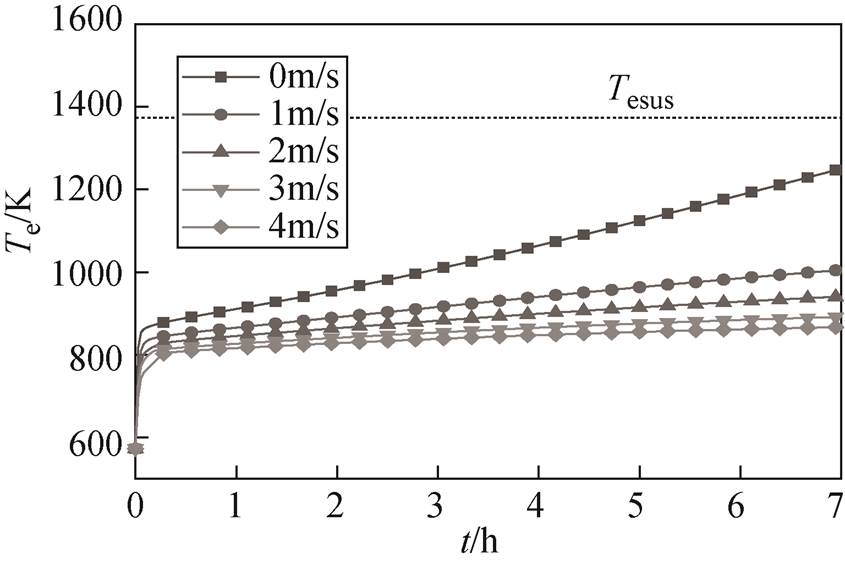
图8 不同循环风速下电热元件温度曲线
Fig.8 Electric heating wire temperature curve at different circulating wind speeds
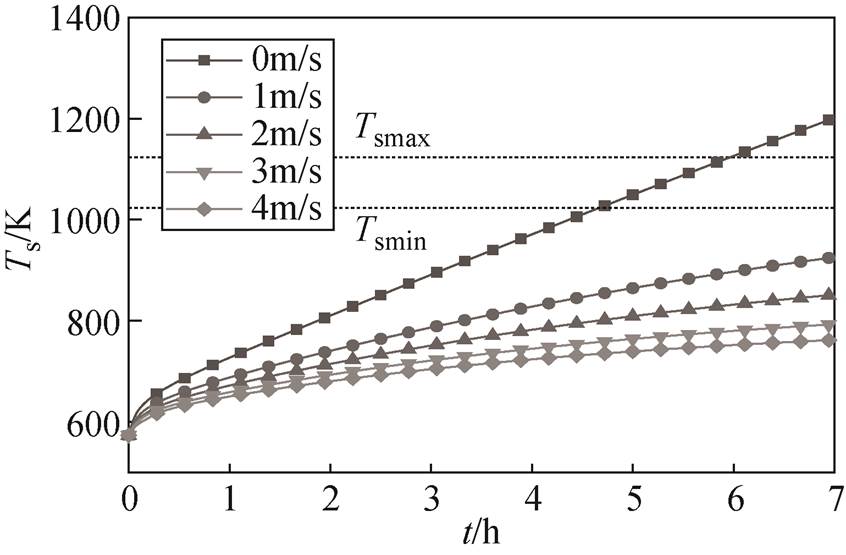
图9 不同循环风速下储热体温度曲线
Fig.9 Thermal storage masonry temperature curve at different circulating wind speeds
经计算，循环风速为0 m/s、1 m/s和4 m/s的储热单元加热7 h时，毕渥数分别为0.33、0.19和0.096，而傅里叶数均为0.21，证明循环风速越大，储热体均热性越好，而对储热深度没有影响。
由于循环风速在固态电制热储热系统设计完成后依然为可调参数，可以对加热过程进行控制，因此有必要对循环风速在不同时间对储热单元温度的影响进行研究。图10和图11分别为不同时段下循环风速对电热元件和储热体的影响曲线。
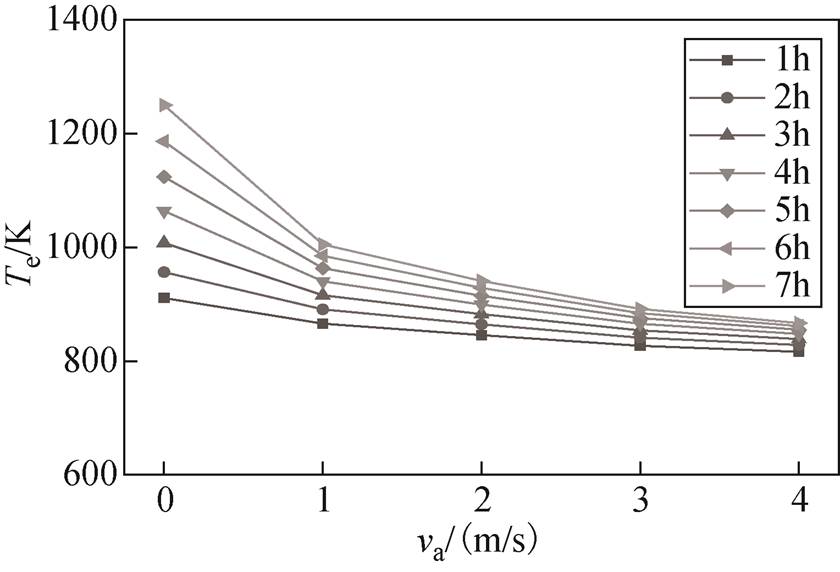
图10 循环风速对电热元件温度的影响曲线
Fig.10 Effect of circulating wind speed on electric heating wire temperature
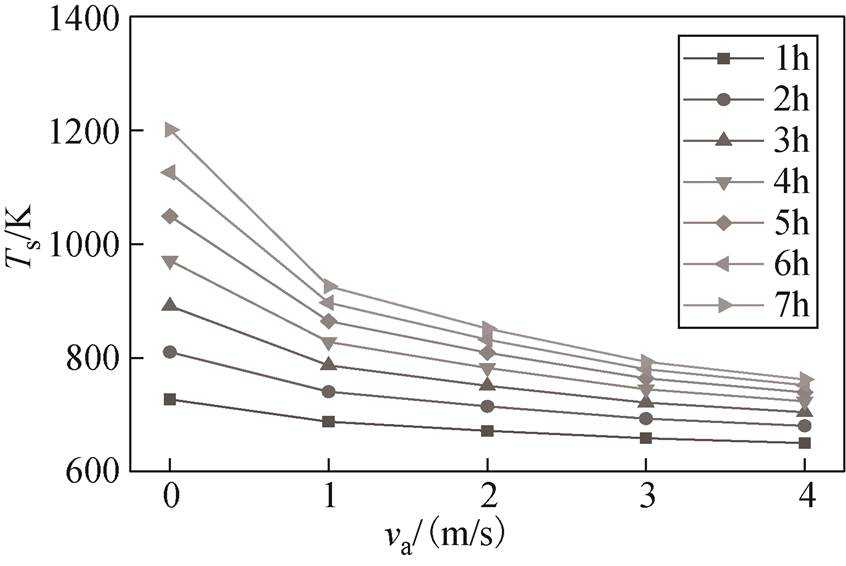
图11 循环风速对储热体温度的影响曲线
Fig.11 Effect of circulating wind speed on temperature of thermal storage masonry
在不同时间点，循环风速对电热元件和储热体温度的影响均呈指数型变化趋势，加热1 h、5 h和7 h时，电热元件温度指数型函数系数分别为7.02、8.28和9.23，储热体温度指数型函数系数分别为5.01、10.97和11.93。说明加热时间越长，循环风速的影响越大，且加热5 h后，储热体温度受到的影响大于电热元件。经计算，在加热1 h、3 h和7 h时，循环风速对储热体温度的级贡献度分别为19.19 %、46.74 %和109.81 %，表明在加热3~5 h时适合进行风速调节。
为研究固态电制热储热系统的热控制方法，本文对固态电制热储热装置进行实验。首先对电储热系统初步设计，得到初始参数。通过本文所提供模型，求取功率、孔占比和风速等参数对应线性函数斜率和指数型函数系数，再进行多参数协同优化，使其满足式（10）和式（12）条件。
实验装置如图12所示，设计功率为100kW，电压为400V，选用HM-92型镁砖和Kanthal A-1型电热元件，一、二级投切功率下单根电热元件功率分别为1 667W和3 953W，储热体孔占比为15 %。实验装置的控制系统采用基于时变负荷的二级可调加热功率投切控制[23]和自适应前馈补偿控制[24]两层控制方法。实验装置具有一级和二级两级投切功率，以风速和投切功率为控制量，通过基于本文所提供的传热匹配规律及评价指标建立的数值模拟修正模型和基于遗忘因子的最小二乘（Forgotten Factor Recursive Least Square Method, FFRLS）在线辨识系统模型对实验装置进行前馈补偿控制。实验装置控制结构和策略如图13和图14所示。
图12 实验装置
Fig.12 Experimental facility
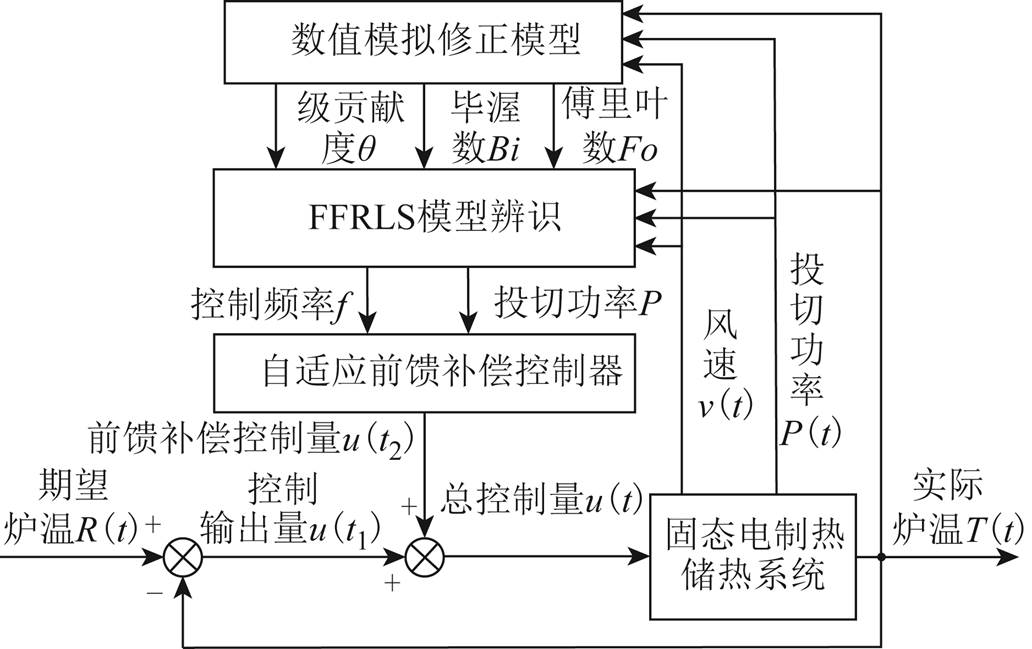
图13 实验装置控制结构图
Fig.13 Experimental facility control structure diagram
为验证所提出传热匹配优化设计方法及炉温控制系统的有效性，本文利用固态电制热储热装置进行炉温控制实验，分别于2.7 h和5.5 h时，将循环风速增加至2 m/s和3 m/s。根据储热系统全模型仿真结果和实践经验，储热体高的2/3处更容易发生传热不匹配，测量风道宜选择为该处。电热元件温度通过红外测温仪测量，储热体温度通过热电偶测量，测点位置如图12所示，热电偶工作端插入深度为0.5 m，一级、二级投切功率下储热体各测点的温度曲线如图15和图16所示。图17和图18为电热元件和储热体温度优化的验证曲线，图中，设计值为二级投切功率下，固态电制热储热装置全模型仿数值模拟结果。优化值为循环风速控制下，固态电制热储热装置全模型仿数值模拟结果。实际值1为循环风速控制下，实验装置各测点测量温度平均值。实际值2为一级投切功率下，实验装置各测点测量温度平均值。
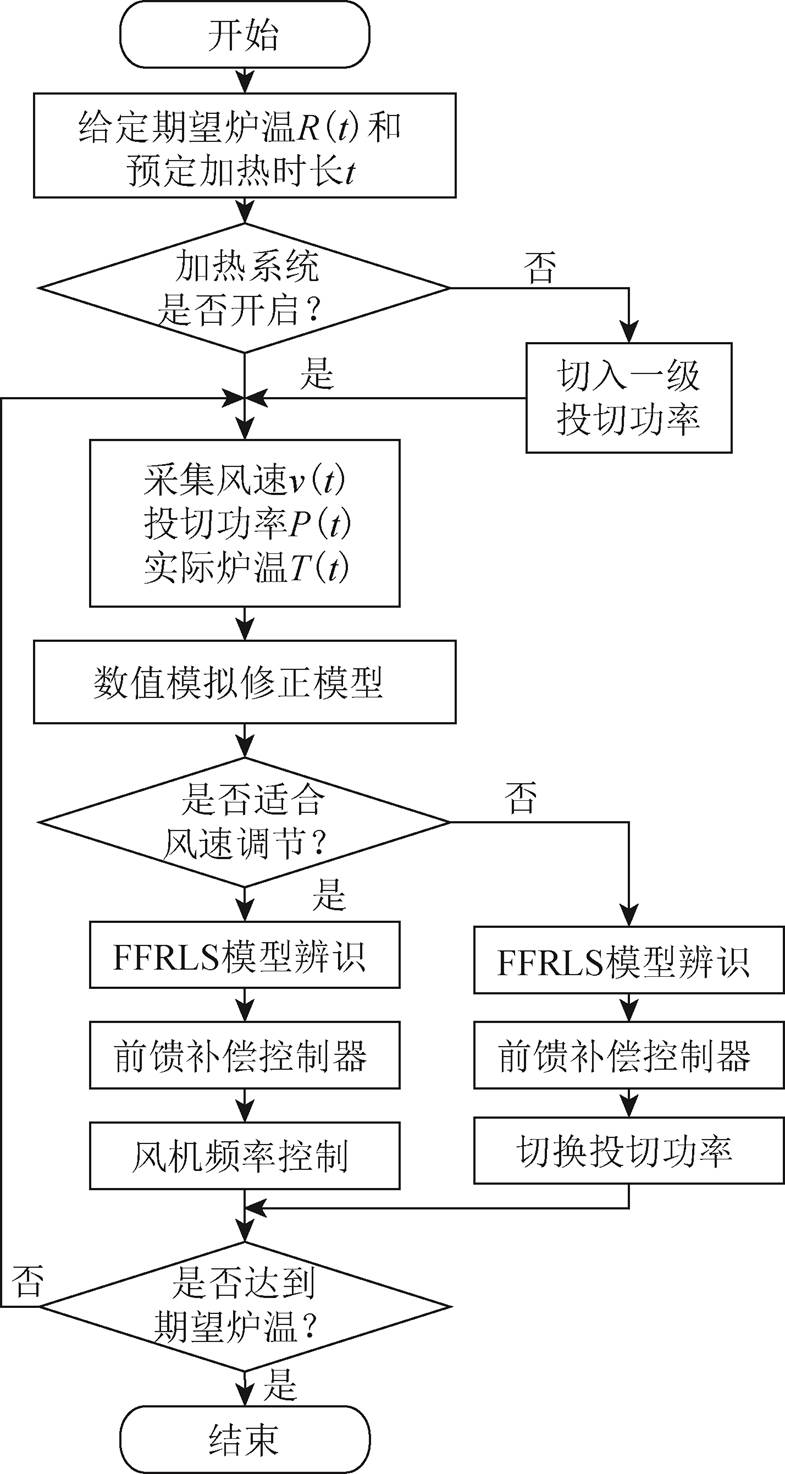
图14 实验装置控制策略
Fig.14 Experimental facility control strategy diagram
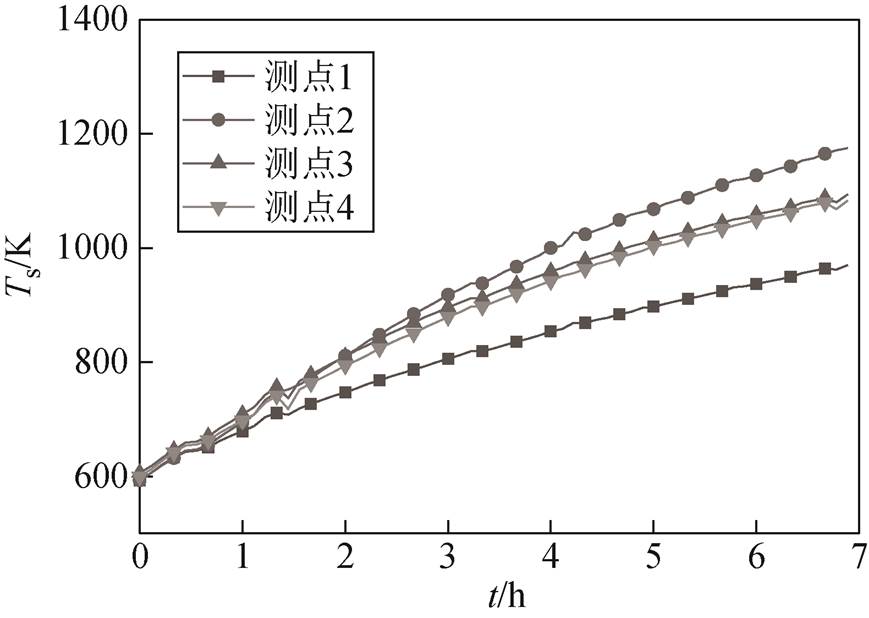
图15 一级投切功率储热体各测点温度
Fig.15 Temperature of measuring points of the heat storage masonry under the first-stage switching power
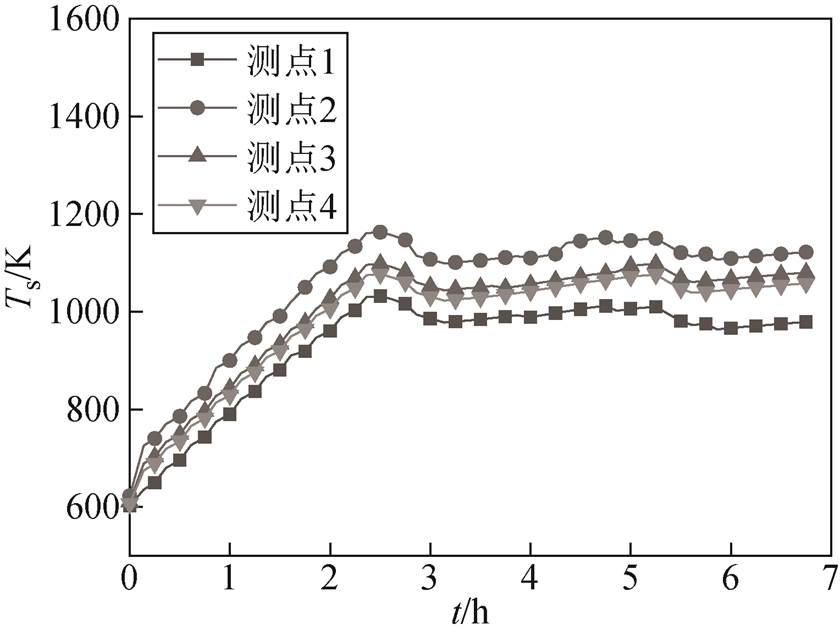
图16 二级投切功率储热体各测点温度
Fig.16 Temperature of measuring points of the heat storage masonry under the second-stage switching power
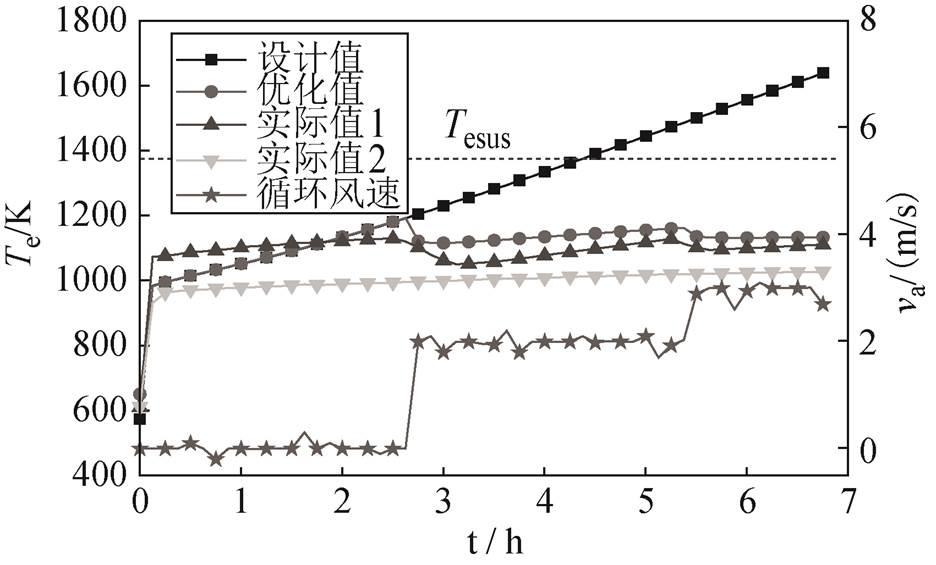
图17 电热元件温度的优化验证曲线
Fig.17 Verification curve of temperature optimization of electric heating element
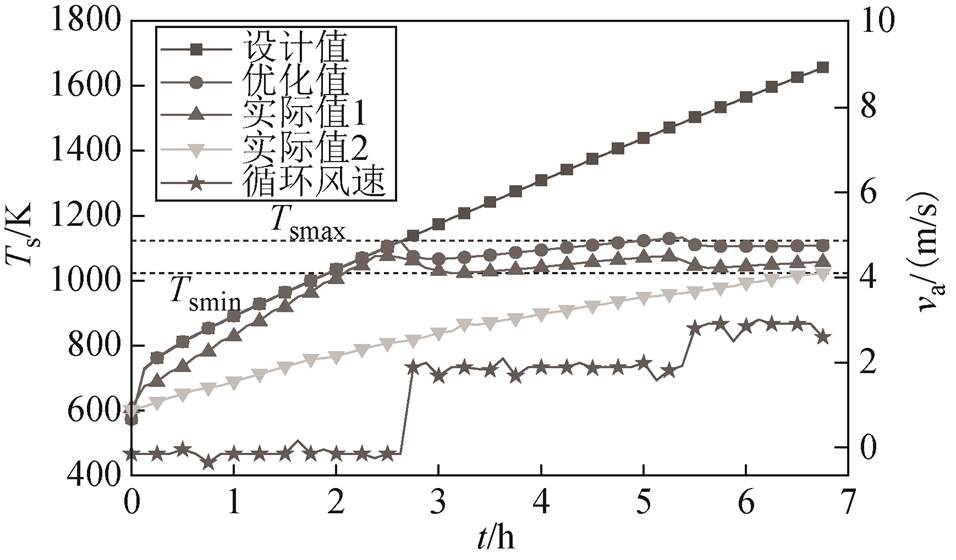
图18 储热体温度的优化验证曲线
Fig.18 Verification curve of temperature optimization of thermal storage masonry
根据图15和图16所示一级、二级投切功率下储热体各测点的温度曲线，测点1与测点2的最大温差分别为205 K和143 K，证明在增加循环风速后，储热体温度分布更均匀，可以实现储热体的储热效果控制。由图17和图18可知，实际值1与优化值基本吻合，电热元件和储热体温度最大误差分别为90 K和77 K。实际值1与优化值变化趋势一致，证明可以实现电热元件和储热体的温度控制，3h时，储热体毕渥数降至0.1以下。
本文通过数值模拟方法对固态电制热储热系统的传热匹配特性和热控制方法进行研究，得出如下结论：
1）建立传热速率平衡方程，分析得出加热功率、孔占比和循环风速是传热匹配设计的主要影响参数。提出级贡献度、毕渥数和傅里叶数作为传热匹配优化程度的评价指标。
2）加热元件和储热体的温度随加热功率的增加线性升高，随孔占比或循环风速的增加呈指数型降低。根据级贡献度，储热系统适合通过控制循环风速进行热控制，且适合在加热3~5 h时进行风速调节。储热体在加热结束时的毕渥数与加热功率正相关，与孔占比或循环风速负相关。当孔占比增大至15 %，且循环风速增大至1 m/s时，储热体的毕渥数可以降至0.1以下，储热体的傅里叶数提高至0.24以上。
3）将数值模拟结果应用到多参数协同优化设计和前馈补偿控制中，并通过实验进行有效性验证。实验结果表明，数值模拟结果与实验数值基本吻合，且通过投切功率和循环风速控制，可以实现储热体的温度和储热效果的控制。
参考文献
[1] 章艳, 吕泉, 李杨, 等. 四种热电厂“电热解耦”改造方案的运行灵活性剖析[J]. 电力系统自动化, 2020, 44(2):163-171. Zhang Yan, Lv Quan, Li Yang, et al. Analysis on operation flexibility of combined heat and power plant with four improved power-heat decoupling schemes[J]. Automation of Electric Power Systems, 2020, 44(2):163-171.
[2] 车泉辉, 娄素华, 吴耀武, 等. 计及条件风险价值的含储热光热电站与风电电力系统经济调度[J]. 电工技术学报, 2019, 34(10): 2047-2055. Che Quanhui, Lou Suhua, Wu Yaowu, et al. Economic dispatching for power system of concentrated solar power plant with thermal energy storage and wind power considering conditional value-at-risk[J]. Transactions of China Electrotechnical Society, 2019, 34(10): 2047-2055.
[3] 葛维春, 张艳军, 高超, 等. 基于风电消纳能力态势划分的源荷储系统分阶段优化策略[J]. 电力系统自动化, 2019, 43(15): 26-33. Ge Weichun, Zhang Yanjun, Gao Chao, et al. Phased optimal strategy of source-load-storage system based on state partition of accommodation capacity of wind power[J]. Automation of Eectric Power Systems, 2019, 43(15): 26-33.
[4] 程中林, 杨莉, 江全元, 等. 储热消纳弃风的市场竞价策略算法[J]. 电力系统保护与控制, 2018, 46(10): 31-38. Cheng Zhonglin, Yang Li, Jiang Quanyuan, et al. Research on bidding algorithm for wind accommodation by thermal storage market[J]. Transactions of China Electrotechnical Society, 2018, 46(10): 31-38.
[5] 陈柏翰, 冯伟, 孙凯, 等. 冷热电联供系统多元储能及孤岛运行优化调度方法[J]. 电工技术学报, 2019, 34(15): 3231-3243. Chen Bohan, Feng Wei, Sun Kai, et al. Multi-energy storage system and islanded optimal dispatch method of CCHP[J]. Transactions of China Electrotechnical Society, 2019, 34(15): 3231-3243.
[6] 杨小平, 杨晓西, 徐勇军, 等. 太阳能热发电系统蓄热过程熵产分析[J]. 工程热物理学报, 2014, 35(5): 854-857. Yang Xiaoping, Yang Xiaoxi, Xu Yongjun, et al. The analysis of entropy generation during thermal charging process in solar thermal power system[J]. Journal of Engineering Thermophysics, 2014, 35(5): 854-857.
[7] 杨小平, 杨晓西, 左远志, 等. 高温填充床蓄热过程中流固传热温差分析[J]. 工程热物理学报, 2015, 36(4): 825-828. Yang Xiaoping, Yang Xiaoxi, Zuo Yuanzhi, et al. The transfer temperature difference study between fluid and solid during the charging process of a high temperature packed bed storage system[J]. Journal of Engineering Thermophysics, 2015, 36(4): 825-828.
[8] 杨勇平, 汉京晓, 李沛文, 等. 导热油与沙砾混合物斜温层单罐蓄热特性[J]. 中国电机工程学报, 2015, 35(3): 631-637. Yang Yongping, Han Jingxiao, Li Peiwen, et al. Thermal energy storage characteristics of synthetic oil and sand mixture for thermocline single tank[J]. Proceedings of the CSEE, 2015, 35(3): 631-637.
[9] Belusko M, Sheoran S, Bruno F. Effectiveness of direct contact PCM thermal storage with a gas as the heat transfer fluid[J]. Applied Energy, 2015, 137: 748-757.
[10] Hänchen M, Brückner S, Steinfeld A. High-temperature thermal storage using a packed bed of rocks–heat transfer analysis and experimental validation[J]. Applied Thermal Engineering, 2011, 31(10): 1798-1806.
[11] Andreozzi A, Buonomo B, Manca O, et al. Transient analysis of heat transfer in parallel squared channels for high temperature thermal storage[J]. Computational Thermal Sciences, 2015, 7(5-6): 477-489.
[12] Andreozzi A, Buonomo B, Pasqua A D, et al. Heat transfer behaviors of parallel plate systems in sensible thermal energy storage[J]. Energy Procedia, 2017, 126: 107-114.
[13] 胡志培, 孙志高, 李安桂. 蓄热单元尺寸对融化传热增强作用的数值研究[J]. 工程热物理学报, 2018, 39(7): 1532-1537. Hu Zhipei, Sun Zhigao, Li Angui. Numerical investigation of melting heat transfer enhancement of enclosure geometry[J]. Journal of Engineering Thermophysics, 2018, 39(7): 1532-1537.
[14] 张新彤, 张成明, 李立毅, 等. 基于绕组温度约束的永磁同步电机裂比优化方法（英文）[J]. 电工技术学报, 2019, 34(9): 1886-1899. Zhang Xintong, Zhang Chengming, Li Liyi, et al. Split ration optimization for permanent magnet synchronousmachines considering winding temperature limitation[J]. Journal of Engineering Thermophysics, 2019, 34(9): 1886-1899.
[15] Lim S H, Oh J S, Kong Y M, et al. High temperature oxidation behaviors of Fe-Cr-Al based powder porous metal and a strip[J]. Journal of Korean Institute of Metals & Materials, 2013, 51(10): 743-751.
[16] Khare S, Dell'Amico M, Knight C, et al. Selection of materials for high temperature sensible energy storage[J]. Solar Energy Materials and Solar Cells, 2013, 115: 114-122.
[17] 杨世铭, 陶文铨. 传热学 [M]. 4版. 北京: 高等教育出版社, 2006.
[18] Capdevila C, Miller M K, Pimentel G, et al. Influence of recrystallization on phase separation kinetics of oxide dispersion strengthened Fe-Cr-Al alloy[J]. Scripta Materialia, 2012, 66(5): 254-257.
[19] 王振东, 宫元生. 电热合金应用手册[M]. 北京: 冶金工业出版社, 1997.
[20] 李明飞, 李雪英, 任静, 等. 综合冷却效率多参数影响分析[J]. 工程热物理学报, 2017(12): 2720-2724. Li Mingfei, Li Xueying, Ren Jing, et al. Multi-parameters influence analysis of overall cooling effectiveness[J]. Journal of Engineering Thermophysics, 2017(12): 2720-2724.
[21] 赵镇南, 时雨荃. 相变乳状液的储冷模型与参数分析[J]. 工程热物理学报, 2003(4): 658-660. Zhao Zhennan, Shi Yuquan. The cold-storage model and parameters analyses for a phase change emulsion[J]. Journal of Engineering Thermophysics, 2003(4): 658-660.
[22] 佟文明, 孙静阳, 舒圣浪, 等. 不同数值方法在自扇冷永磁同步电机三维热分析中的应用[J]. 电工技术学报, 2017, 32(增刊1): 151-159. Tong Wenming, Sun Jingyang, Shu Shenglang, et al. Application of different numerical methods in 3D thermal analysis for fan-ventilated permanent magnet synchronous machines[J]. Transactions of China Electrotechnical Society, 2017, 32(S1): 151-159.
[23] 邢作霞. 基于时变负荷的三级可调加热功率投切控制方法: 中国, 201610053611.1[P]. 2016-05-25.
[24] 于洪霞. 分工况PID+自适应前馈补偿的相变电蓄热供暖系统及方法: 中国, 201811197010.3[P]. 2018-10-15.
Heat Transfer Matching Characteristic and Heat Control Method of Solid-State Electric Heating Thermal Storage System
Abstract The solid-state electric heating thermal storage system is an emerging large-capacity peak shaving technology in power system. Studying its heat transfer matching characteristic and heat control method is of great significance for improving reliability and heat transfer. In this paper, by establishing the heat transfer rate balance equation and using numerical simulation method, the correlation between the design parameters of heat storage system and heat transfer matching is analyzed. And through the heat transfer matching performance evaluation criteria such as the step contribution degree, the Biot number and the Fourier number, the heat transfer matching optimization design effect is quantified and compared. The results show that the temperature of the thermal storage unit increases linearly with the increase of electric heating power, decreases exponentially with the increase of hole ratio and circulating wind speed. Reducing the electric heating power, increasing the hole ratio and circulating wind speed can enhanced the soaking heat, and increasing the hole ratio can improve the thermal storage degree. The experimental verification proves that through the multi-parameter collaborative optimization and the feedforward compensation control, better heat transfer matching can be achieved.
keywords：Solid-state electric heating thermal storage, heat transfer matching, performance evaluation criteria, heat control
中图分类号：TM924
DOI：10.19595/j.cnki.1000-6753.tces.190442
国家科技支撑计划（2015BAA01B00）和国家电网公司科技项目（2018YF-14）资助。
收稿日期2019-04-16
改稿日期 2019-10-18
邢作霞 女，1976年生，教授，博士生导师，研究方向为风力发电并网控制与新能源消纳。E-mail：xingzuox@163.com（通信作者）
樊金鹏 男，1995年生，硕士研究生，研究方向为新能源技术及应用。E-mail：fjp5555@163.com
（编辑 郭丽军）