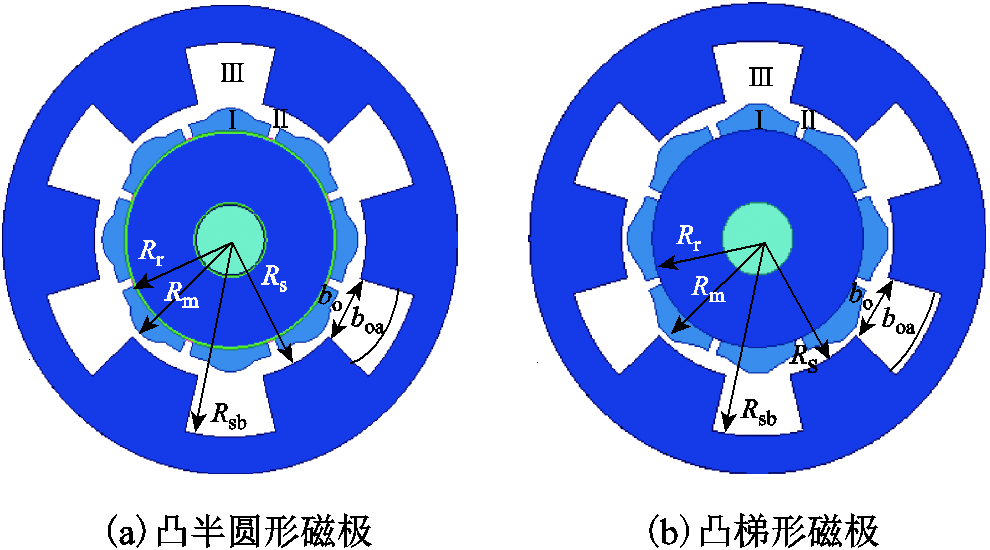
图1 凸形不等厚磁极永磁电机结构
Fig.1 Structure of PM machines with salient shape unequal thickness magnets
摘要 在永磁电机设计中,转子磁极形状对永磁电机的电磁性能产生较大的影响。该文提出两种凸形不等厚磁极的永磁电机,分别为凸半圆形和凸梯形。对这两种凸形不等厚磁极的永磁电机进行建模,采用精确的子域模型方法,通过边界条件求解每个子域中的拉普拉斯方程和准泊松方程,从而得到气隙磁场的解析式,并得到空载感应电动势、电磁转矩以及齿槽转矩等电磁性能参数的解析式。与永磁用量相同的传统表贴式永磁电机相比,结果表明:两种凸形不等厚磁极的永磁电机不仅空载感应电动势基波幅值较高,谐波含量较低,而且电磁转矩较大、齿槽转矩较小。此外,还分析了两种凸形不等厚永磁结构参数对永磁电机电磁性能的影响。最后,利用有限元法对解析模型的正确性进行了验证。
关键词:凸形不等厚磁极 永磁电机 解析法 子域模型法 电磁性能
随着对永磁材料研究的不断深入和电机设计与制造工艺的持续进步,永磁电机的电磁性能得到了快速的提升。因此永磁电机广泛应用在各种领域中。
正确建立永磁电机的模型是分析电机电磁性能的重要基础。文献[1]建立了定子为扇形槽的表贴式永磁电机的线性子域模型,计算精度很高。文献[2]建立了具有任意分段数的磁极均匀分段表贴式永磁电机的解析模型。文献[3]利用子域模型和磁路的混合方法建立了表贴式永磁电机的非线性模型。文献[4]利用谐波建模法提出一种永磁轮毂电机的解析模型。文献[5]建立了一种考虑永磁体分段斜极和磁性槽楔的解析模型。文献[6]分析了低温对材料特性及电磁参数的影响,建立多物理耦合的模型。通过各种方法优化永磁电机的电磁性能,一直是国内外的研究热点。文献[7]对车用永磁同步电机的拓扑结构进行了优化分析。文献[8]建立了偏心磁极永磁电机气隙磁场的正弦优化模型。文献[2]对磁极进行分段,能够减小永磁电机的齿槽转矩。一种改变磁极形状的方法是,通过设计磁极的不同厚度,改变磁极边缘形状,实现减小齿槽转矩[9]。通过定子齿的偏心,同样可以减小齿槽转矩[10]。文献[11]提出基于多目标优化方法设计的非对称V型内置式永磁同步电机,不仅能够减小转矩脉动,而且能够提高转矩密度。文献[12]提出一种双层组合磁极电机,通过改变上下层磁极的厚度比、极弧系数以及磁化角等参数,优化气隙磁通密度。
有限元法虽然能够高精度地计算永磁电机的磁场,但是在对电机优化时,会非常耗时而且效率很低。因此,通过用满足工程精度的解析法来求解,可以快速得到电机最优的设计方案。
本文提出两种凸形不等厚永磁结构的永磁电机模型,分别为凸半圆形和凸梯形。对这两种凸形不等厚的永磁体进行分块叠加建模,采用精确的子域模型方法,求解获得气隙磁通密度解析式,然后计算电机的感应电动势、电磁转矩以及齿槽转矩,并利用有限元法验证了解析模型的正确性。
提出两种凸形不等厚永磁结构的永磁电机,如图1所示。为了便于求解子域模型,定子槽型均为扇形槽。

图1 凸形不等厚磁极永磁电机结构
Fig.1 Structure of PM machines with salient shape unequal thickness magnets
传统的表贴式永磁电机转子外表面是光滑的圆周曲线。而对于凸半圆形和凸梯形永磁体而言,由于二者的永磁体外表面不光滑,使其边界条件很难用一个简单的函数表示。为解决该问题,由于假定材料是线性的,可对两个凸形永磁体沿圆周方向进行分块与分段,然后进行叠加。为便于分析,这里取一个极的分块区域图形,如图2所示。

图2 凸形永磁分区域叠加原理
Fig.2 Superposition principle of salient magnets
为得到两种凸形不等厚永磁电机的解析模型,需要获得永磁半径与转子角度的关系。两种凸形永磁区域A永磁半径都为常量,而区域B分割的每块永磁半径都随角度变化而变化,则需要建立两种凸形永磁区域B的每块永磁半径与角度的函数关系。图3为凸半圆形永磁几何模型。图中,O为模型的几何中心,O1为凸半圆形的圆心;r1为凸半圆形的半径;Rmj为区域B中的第j块永磁的外半径;Rm为区域A永磁的外半径,Rr为永磁体区域A、B的内半径,L1与L2为区域B第j块磁极对应以Rmj为斜边的直角三角形的直角边长度,d为几何中心O与圆心O1的距离;θ1为区域B所占的角度;θ0j为区域B第j块磁极与磁极中心的角度。
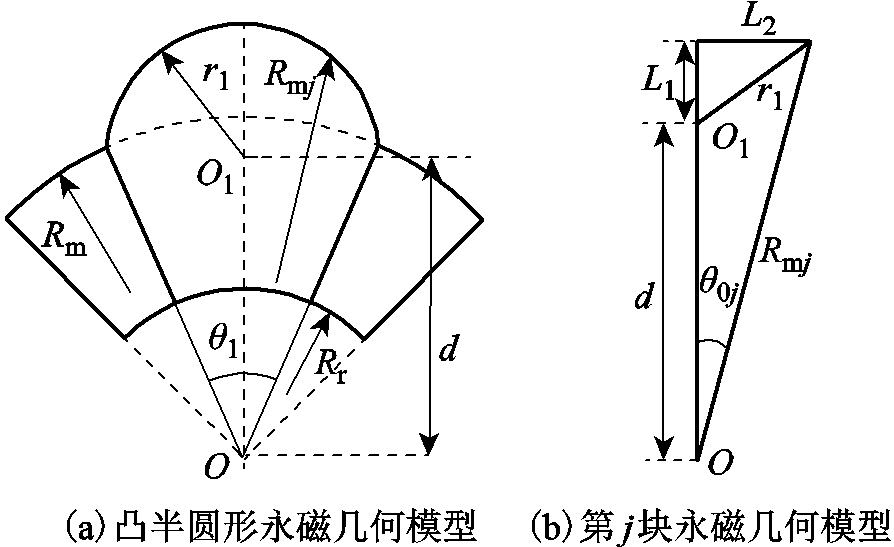
图3 凸半圆形永磁几何模型
Fig.3 Geometry model of salient semi-circular magnet
从图3可得到,对于凸半圆B区域,Rmj、θ1、r1和d之间的数量关系为
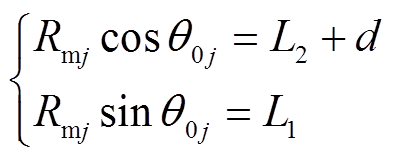 (1)
(1) 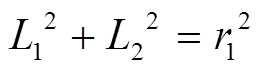 (2)
(2)
联立式(1)和式(2)解得
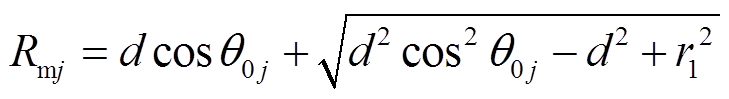 (3)
(3)将凸半圆形区域B分割成n1小段,由于区域B所占的角度为θ1,从而每小段的角度为θ1/n1。当n1足够大时,分割的每块永磁体可以近似为传统的扇形小磁块,且第j小段永磁体所占的区间为
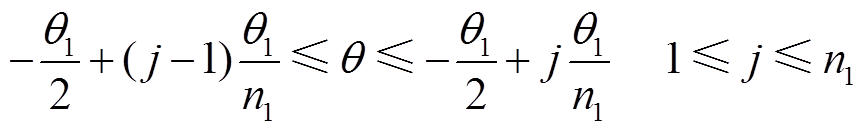 (4)
(4)
图4为凸梯形永磁几何模型。图中,θ1为梯形永磁的一条边界距离磁极中心的角度;O1为三角形的顶点,其距离圆心O为S;以半径为r1的圆弧与三角形相截,得到区域B凸梯形部分。
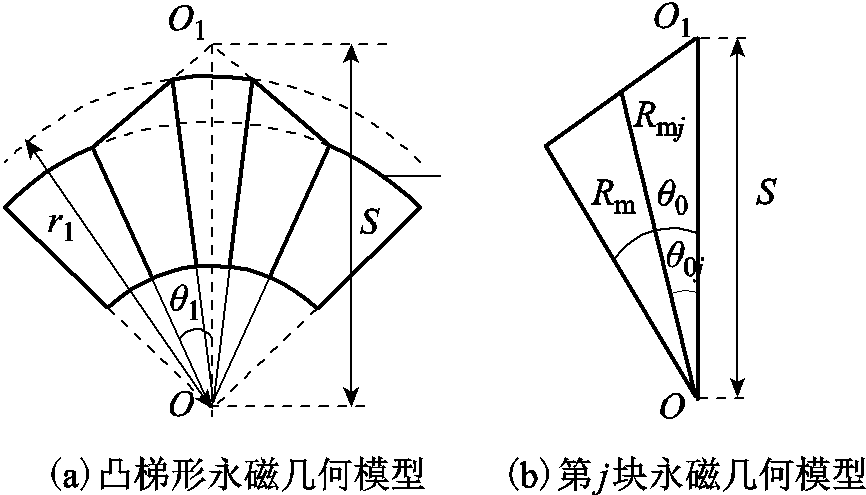
图4 凸梯形永磁几何模型
Fig.4 Geometry model of salient trapezoid magnet
从图4可以得到Rmj与θj的几何关系为
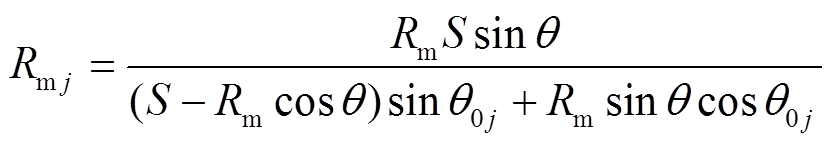 (5)
(5)式中,Rmj的取值范围是Rm≤Rmj≤r1;θ1的取值范围是0≤θ1≤αpπ/(2p),αp为磁极的极弧系数,p为磁极的磁对数。
将凸梯形区域B分为n1段,区域B的两块永磁区域各占的角度均为θ1,从而每小段的角度为2θ1/n1,且第j小段永磁所占的区间为
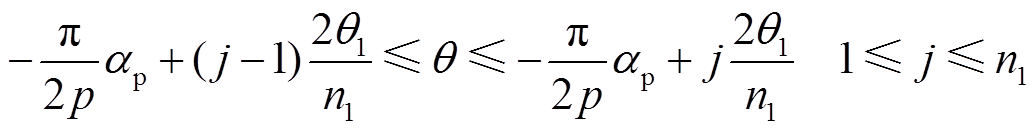 (6)
(6)为简化问题分析,对电机模型需作如下假设:①定子槽为理想的扇形槽如图1所示;②定转子铁心的磁导率为无穷大;③永磁为线性退磁,且完全磁化;④忽略端部的作用,只考虑二维场。
由图2,两种凸形永磁区域A的永磁边界都十分规则,可利用边界条件求得气隙磁通密度函数,这里不进行论述。而永磁区域B的永磁边界与传统瓦片形永磁边界不一致且十分复杂,不能用一般的边界条件来求解。这里采用“微元”方法,把区域B的永磁体沿圆周方向分成尽可能多的段,认为每段的永磁厚度相同,每小段就可以用边界条件得到气隙磁通密度函数,然后对每块运用叠加法得到区域B永磁体产生的气隙磁通密度,再与区域A永磁体产生的气隙磁通密度进行叠加,得到整个模型的气隙磁通密度函数。
利用精确的子域模型得到凸形不等厚磁极的永磁电机气隙磁通密度解析式。限于篇幅,只论述两种凸形电机模型的永磁区域B的第j块永磁体存在时产生的槽气隙磁通密度函数。
要得到该永磁电机的解析模型,需要将该电机模型划分为三个子域,永磁区域(子域Ⅰ),气隙区域(子域Ⅱ),槽区域(子域Ⅲ),如图1所示。三个子域中标量磁位的通解分别为
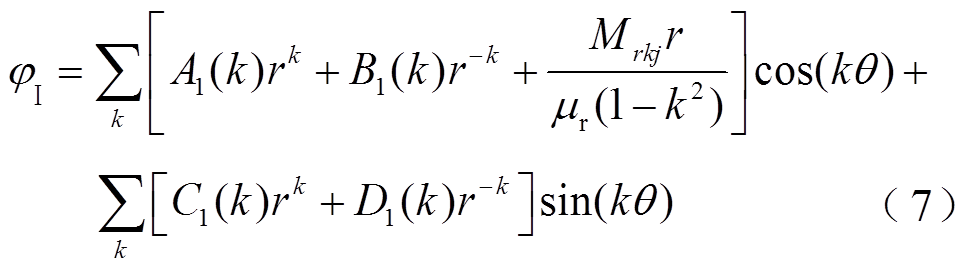
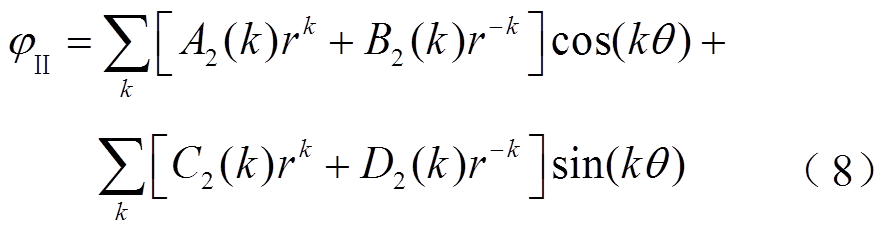
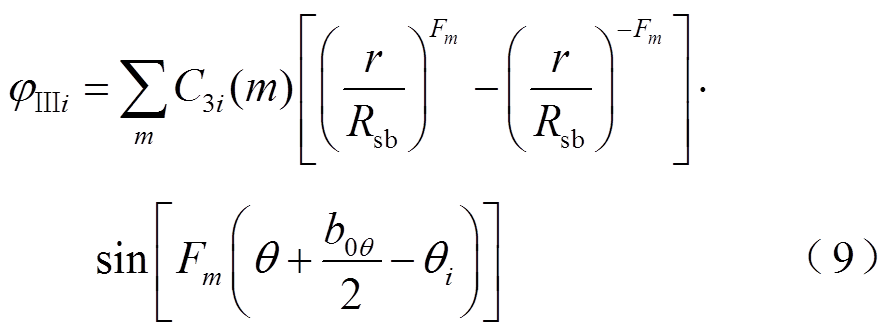
式中,i表示第i个槽;Rsb为槽底的半径;A1(k)~D1(k)、A2(k)~D2(k)和C3i(m)为系数,这些系数通过边界条件来确定;θi为第i个槽的角度;b0θ为定子槽口的角度,其对应的宽度为b0, b0θ=b0/Rs, Rs为定子内半径;且Fm=mπ/b0θ;Mrkj为j段永磁磁化强度径向分量傅里叶分解系数;r为磁极半径;mr为相对磁导率;θ为永磁电机旋转的电角度。
图5为两种凸形永磁区域B的永磁分段磁化强度矢量图。图中θk为永磁的任意磁化方向,当θk=0时,表示磁极为径向充磁。
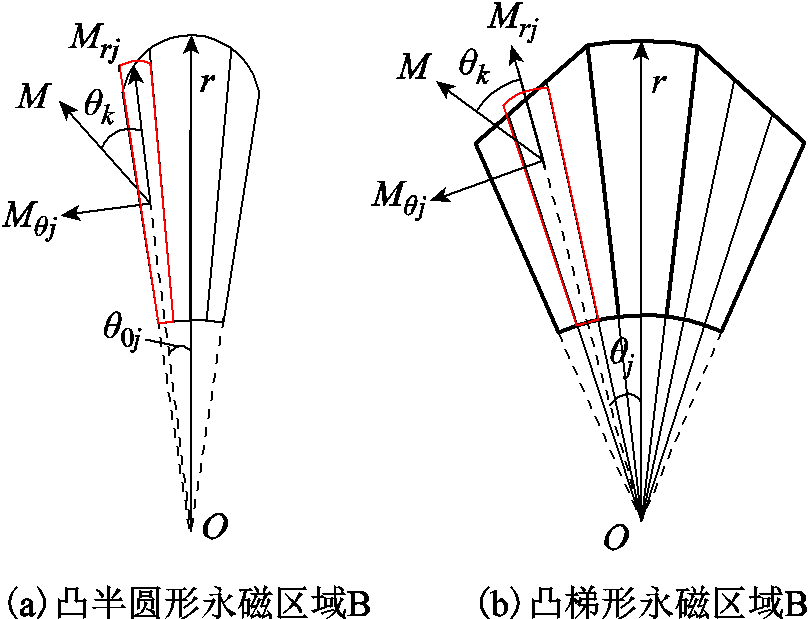
图5 凸形永磁区域B分段建模
Fig.5 Segmented modeling of salient magnet region B
两种凸形不等厚永磁电机的磁化强度为M时,径向充磁,则第j段小磁块,对其分解成径向磁化强度分量Mrj和切向磁化强度分量Mθj,分别为
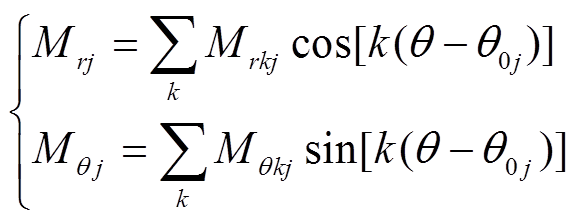 (10)
(10)式中
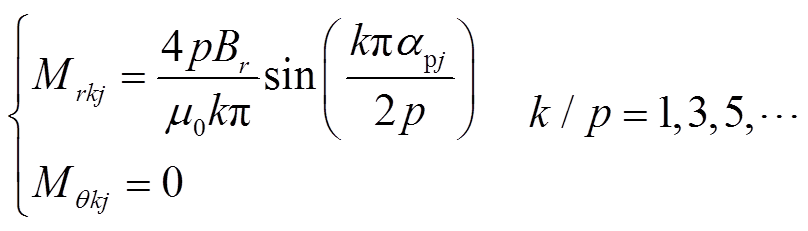 (11)
(11)
式中,Br为径向气隙磁通密度;m0为空气磁导率;apj为区域B第j段永磁极弧系数。
根据电磁场的连续条件可得,气隙子域Ⅱ槽子域区域Ⅲ在定子内径处标量磁位相等,即将r=Rs分别代入式(8)和式(9),得
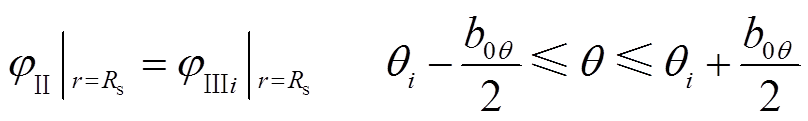 (12)
(12)从式(12)可以看出,气隙子域Ⅱ的标量磁位通解中的积分常数与槽子域Ⅲ的标量磁位通解中的积分常数有关系,这就是子域模型法的本质。
利用下列边界条件
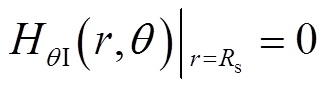 (13)
(13)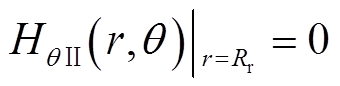 (14)
(14)
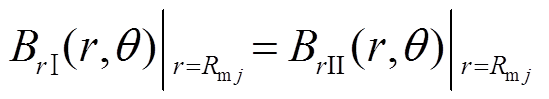 (15)
(15)
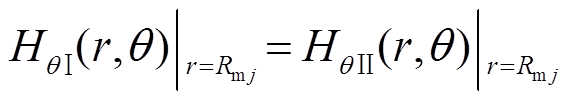 (16)
(16) (17)
(17)
式中,B、H的下角标分别表示在不同子域下径向和切向的气隙磁通密度和磁场强度。
利用标量磁位与磁场强度之间关系,再结合磁密与磁场强度的关系,可以得到第j段永磁体的径向和切向气隙磁通密度函数分别为
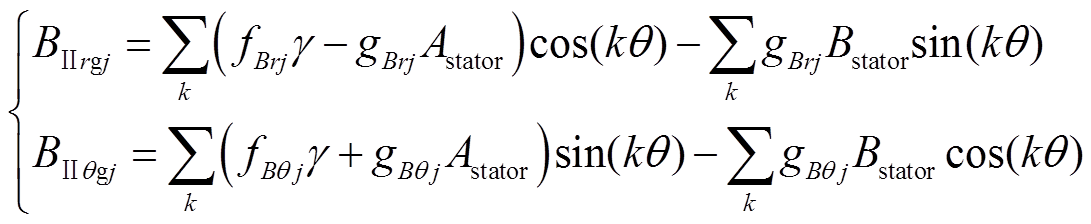 (18)
(18)式中,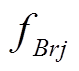 、
、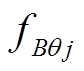 、
、 、
、 、Astator和Bstator的具体表达式在文献[1]给出。
、Astator和Bstator的具体表达式在文献[1]给出。
通过前述可知,凸形不等厚永磁结构的整个永磁区域B产生的气隙磁通密度,可以由分割为各段的小永磁块单独产生,然后进行叠加得到
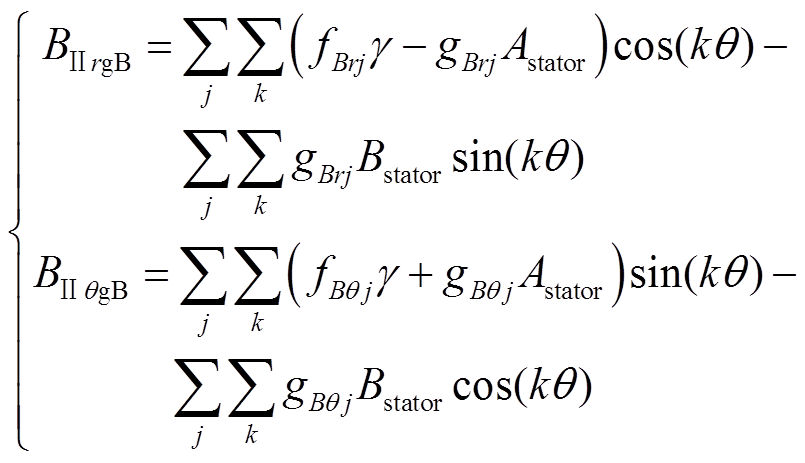 (19)
(19)凸形不等厚永磁结构的永磁由区域A永磁与区域B永磁构成。前述为不规则区域B永磁产生的气隙磁通密度。而对于区域A永磁产生的气隙磁通密度,由于其是传统的瓦片形,永磁厚度相等,于是将式(18)中的Rmj改成Rm,得到区域A永磁产生的气隙磁通密度。
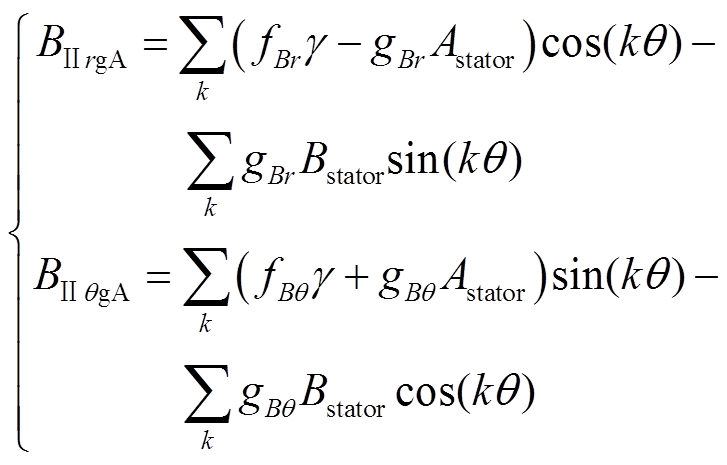 (20)
(20)
最后将式(19)与式(20)叠加,即区域A永磁与区域B永磁分别产生的气隙磁通密度进行叠加,从而得到凸形不等厚磁极永磁电机的气隙磁通密度函数为
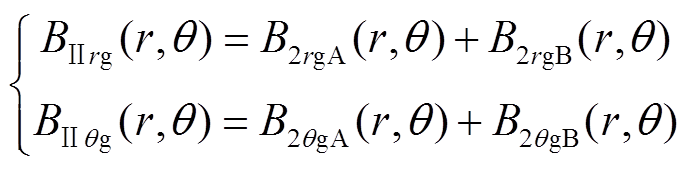 (21)
(21)永磁电机的转子在转动过程中,定子绕组会被永磁体产生的主磁场切割。根据Faraday定律可知,将会在线圈中感应电动势,因此感应电动势与定子内径、每相串联匝数、转速和轴向长度等参数相关。每个线圈内的磁通为
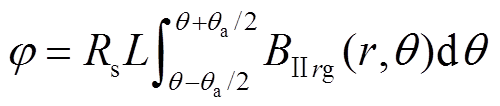 (22)
(22)式中,θ为转子的位置角,θ=ωrt,ωr为转子旋转的机械角速度;L为定子的轴向长度;θa为一个线圈的节距角。
每相绕组的感应电动势为
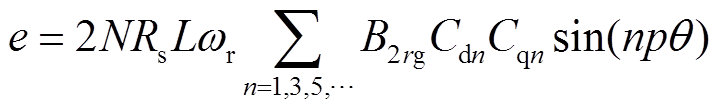 (23)
(23)式中,Cdn为定子绕组的节距因数;Cqn为定子绕组的分布系数;N为线圈匝数。
由电机学理论可知,当对称三相电压加载在电机的定子绕组中,三相绕组会产生旋转的合成磁场。而永磁电机的转子为自励磁的永磁体,两者相互作用,从而使转子发生旋转。因此电磁转矩是电机实现电能与机械能转换的物理量。电机的电磁转矩为
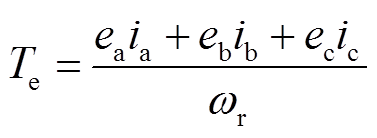 (24)
(24)式中,ea为A相的感应电动势;eb和ec分别滞后ea 120°和240°电角度;ia、ib、ic分别为三相绕组a、b、c的电流,其表达式为
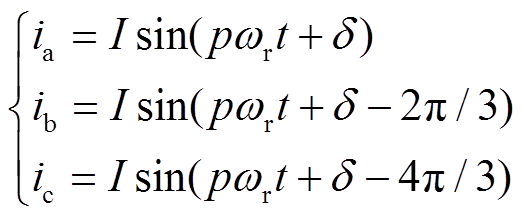 (25)
(25)
式中,I为相绕组电流的峰值;δ为相位。
在电机设计过程中,为了固定绕组,需要在定子上开槽。这些齿槽使得磁通路径的磁阻发生变化,从而产生了齿槽转矩。齿槽转矩是永磁电机固有的结构特性造成的,会造成机械振动和电磁噪声等问题,是研究的重要内容之一。
利用麦克斯韦应力张量法求取齿槽转矩,即
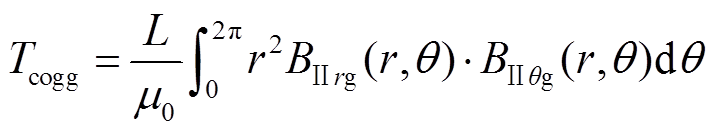 (26)
(26)为验证两种凸形不等厚永磁结构的永磁电机解析模型的正确性,并结合图1的两种凸形不等厚磁极的永磁电机结构。这里给出两台6槽8极凸形不等厚磁极的永磁电机。电机的额定转速为3 000 r/min。两台电机的主要参数见表1。为了体现凸形不等厚磁极永磁电机的优越性,需要与传统表贴式永磁电机的电磁性能进行比较。比较的前提是:三种电机的永磁使用量相等,即磁体体积和质量相等。这里取三种电机的极弧系数都相等,均为0.9。
表1 永磁电机参数
Tab.1 Parameters of PM machines
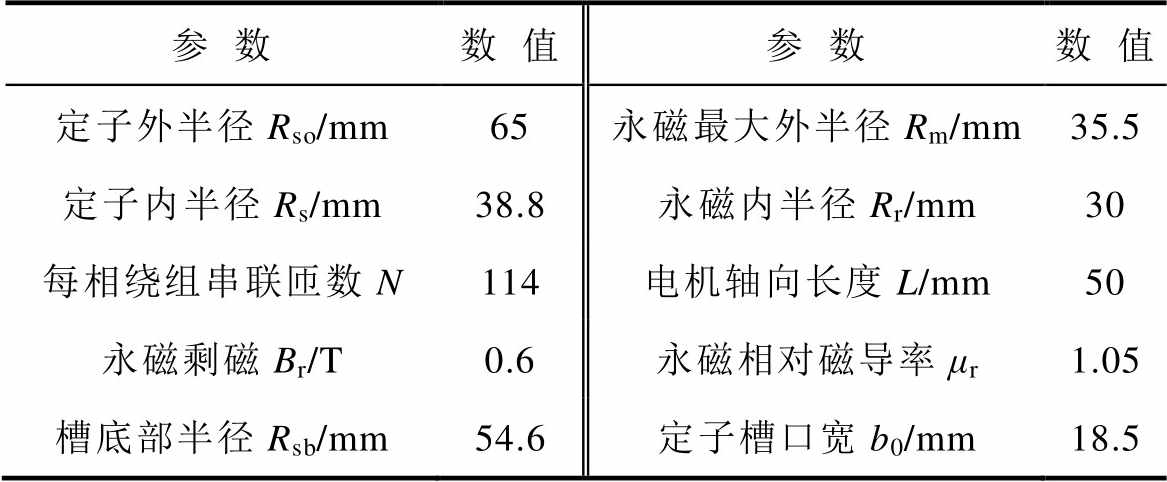
参数数 值参数数 值 定子外半径Rso/mm65永磁最大外半径Rm/mm35.5 定子内半径Rs/mm38.8永磁内半径Rr/mm30 每相绕组串联匝数N114电机轴向长度L/mm50 永磁剩磁Br/T0.6永磁相对磁导率μr1.05 槽底部半径Rsb/mm54.6定子槽口宽b0/mm18.5
凸半圆形不等厚永磁结构中,不规则永磁区域B中的凸半圆形尺寸与半圆形半径r1及两圆心距离d相关;凸梯形不等厚永磁结构中,不规则永磁区域B中的梯形尺寸与梯形边界角度θ1、圆弧半径r1以及三角形的顶点高度S相关。对于凸半圆形,选取半圆形半径r1为16.5 mm,两圆心距离d为20.7 mm。对于凸梯形,选取边界角度θ1为37.11°,圆弧半径r1为16.25 mm,三角形的顶点在定子内径处。传统的表贴式永磁电机的永磁厚度为6.334 mm。
磁力线的分布反映了电机内部的磁场强弱。不同的转子结构导致电机的磁力线分布也不同。图6为两种凸形永磁结构与传统瓦片形永磁结构的空载场磁力线分布图。
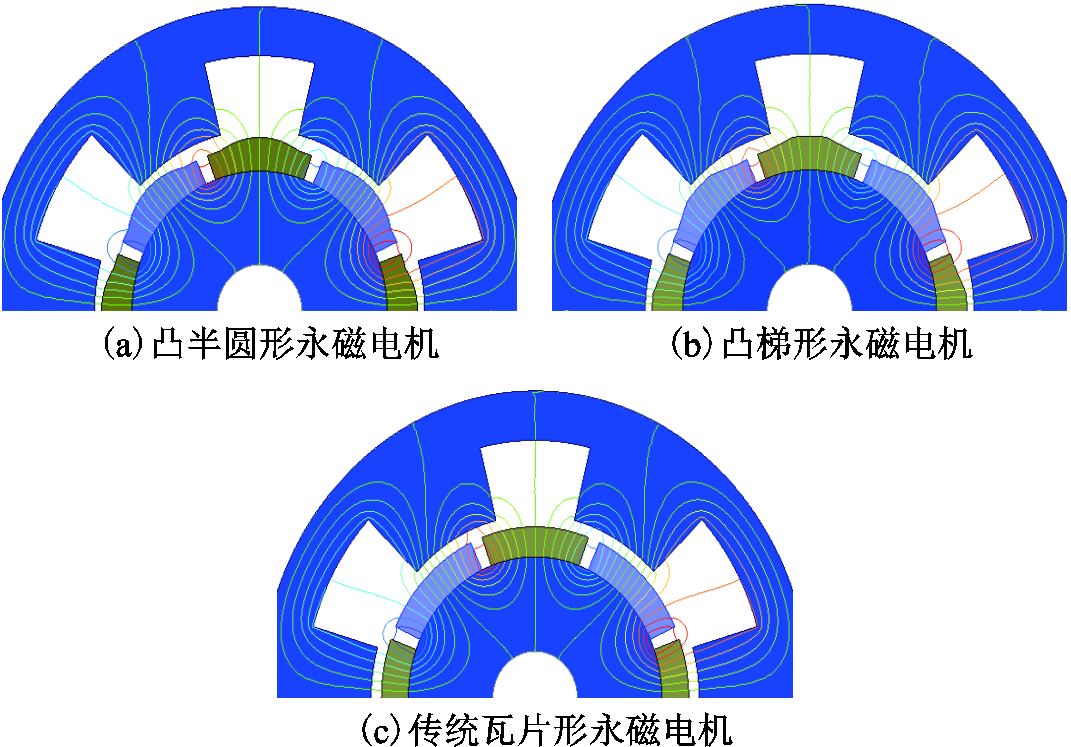
图6 三种磁极的永磁电机磁力线分布
Fig.6 Flux line distributions for three PM machines
通过对凸极不等厚永磁结构采用分段叠加的方法,得到电机的径向气隙磁通密度解析式。将凸半圆形磁极与凸梯形磁极的电机参数代入解析式中,得到两种电机的径向气隙磁通密度波形,如图7a和图7b所示。可以看出,利用两种电机的解析模型得到的波形与有限元法得到的波形吻合度很好,从而验证了采用叠加法获得的两种凸形不等厚磁极电机解析模型的正确性。图7c为两种凸形不等厚磁极永磁电机与用磁量相等的传统瓦片形永磁电机的径向气隙磁通密度波形。对其傅里叶分解可以得到,凸半圆形、凸梯形和瓦片形三种电机气隙磁通密度的基波幅值分别为0.474T、0.468T和0.452T。显然,两种凸形磁极永磁电机的气隙磁通密度基波幅值明显大于传统瓦形磁极的永磁电机。
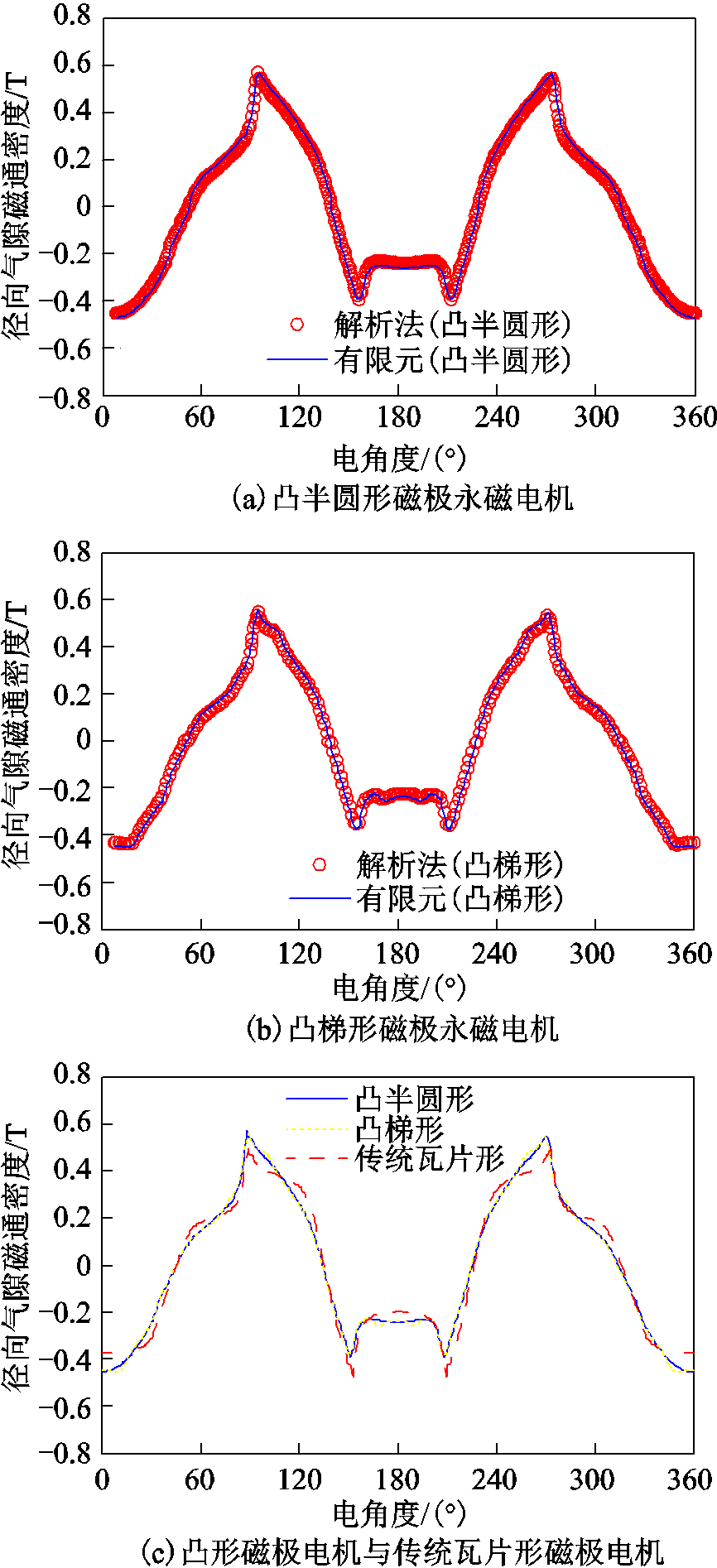
图7 三种永磁电机径向气隙磁通密度波形
Fig 7 Comparison of the radial air-gap flux density waveforms for three machines
空载感应电动势是永磁电机电磁性能中的一个重要参数。图8为用解析法与有限元法得到两种凸形不等厚永磁电机空载感应电动势的波形,验证了感应电动势解析模型的正确性。表2比较了永磁量相等的、三种磁极永磁电机的空载感应电动势。从表中可以看出,两种凸形不等厚磁极永磁电机空载感应电动势的基波幅值和THD均优于传统的瓦片形磁极。
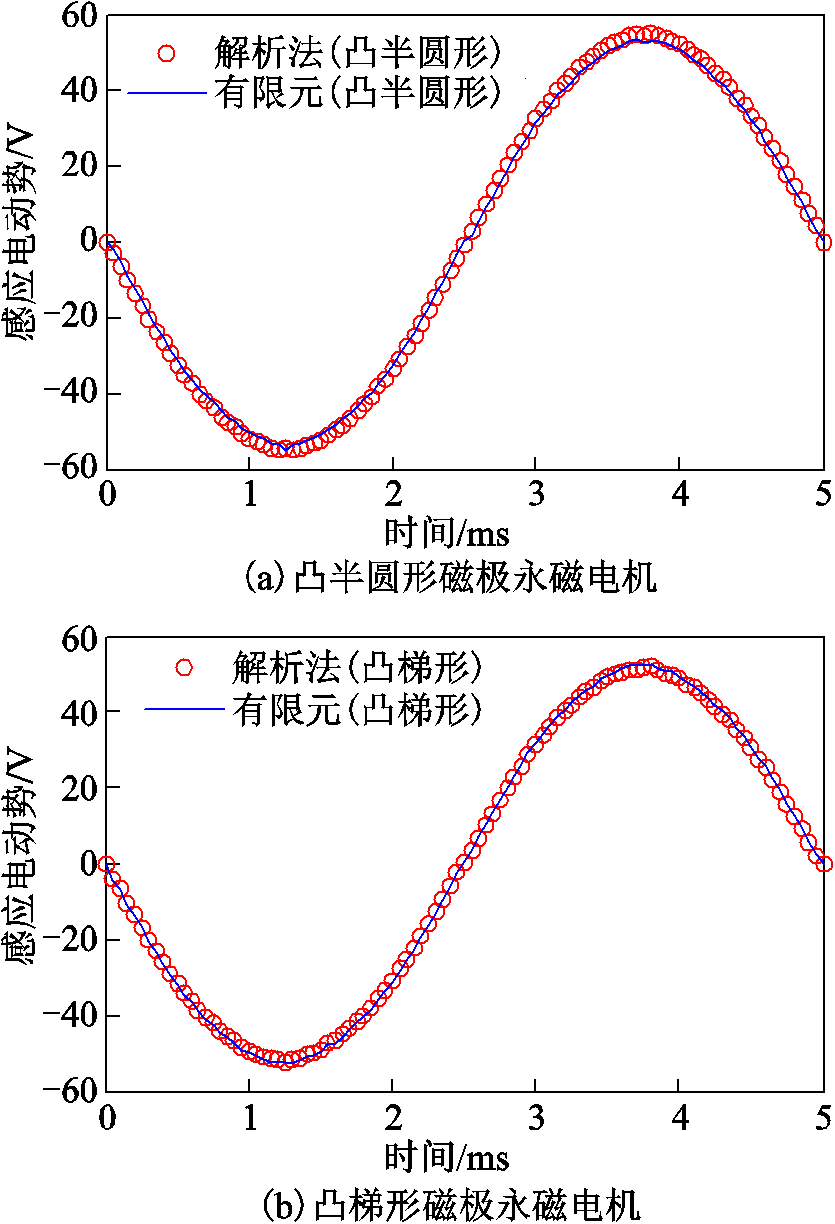
图8 两种电机感应电动势波形
Fig.8 Back EMF waveforms of two PM machines with salient shape unequal thickness magnets
表2 三种磁极永磁电机的感应电动势比较
Tab.2 Back EMF comparison for three PM machines

永磁形状感应电动势基波幅值/V感应电动势THD (%) 凸半圆形54.971.07 凸梯形52.521.05 传统瓦片形51.443.23
电磁转矩表示电机的输出能力,而齿槽转矩是电机产生振动和噪声的主要原因。对这两个重要参数的分析,有助于对电机设计和优化。图9a和图9b为分别利用解析法与有限元法得到的两种凸形不等厚磁极永磁电机的电磁转矩波形。图9c为永磁用量相等的三种永磁电机的电磁转矩波形。可以看出,解析法和有限元法得到的电磁转矩波形基本一致,证明解析模型的有效性。同时也可以看出,凸半圆形电机与凸梯形电机电磁转矩的平均值分别为2.079N·m和2.224N·m,而传统瓦片形电机的电磁转矩的平均值为2.027N·m。显然,两种凸形磁极永磁电机的电磁转矩优于传统瓦形磁极的永磁电机。
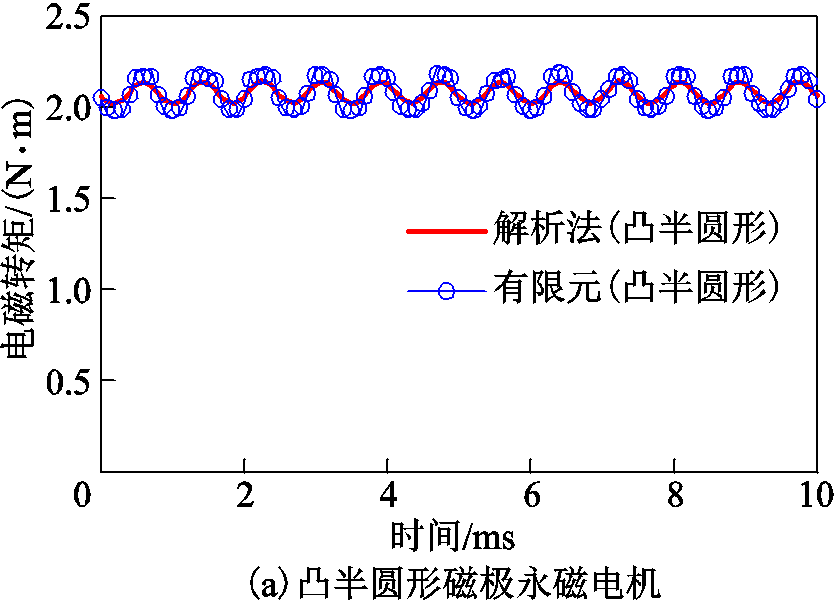
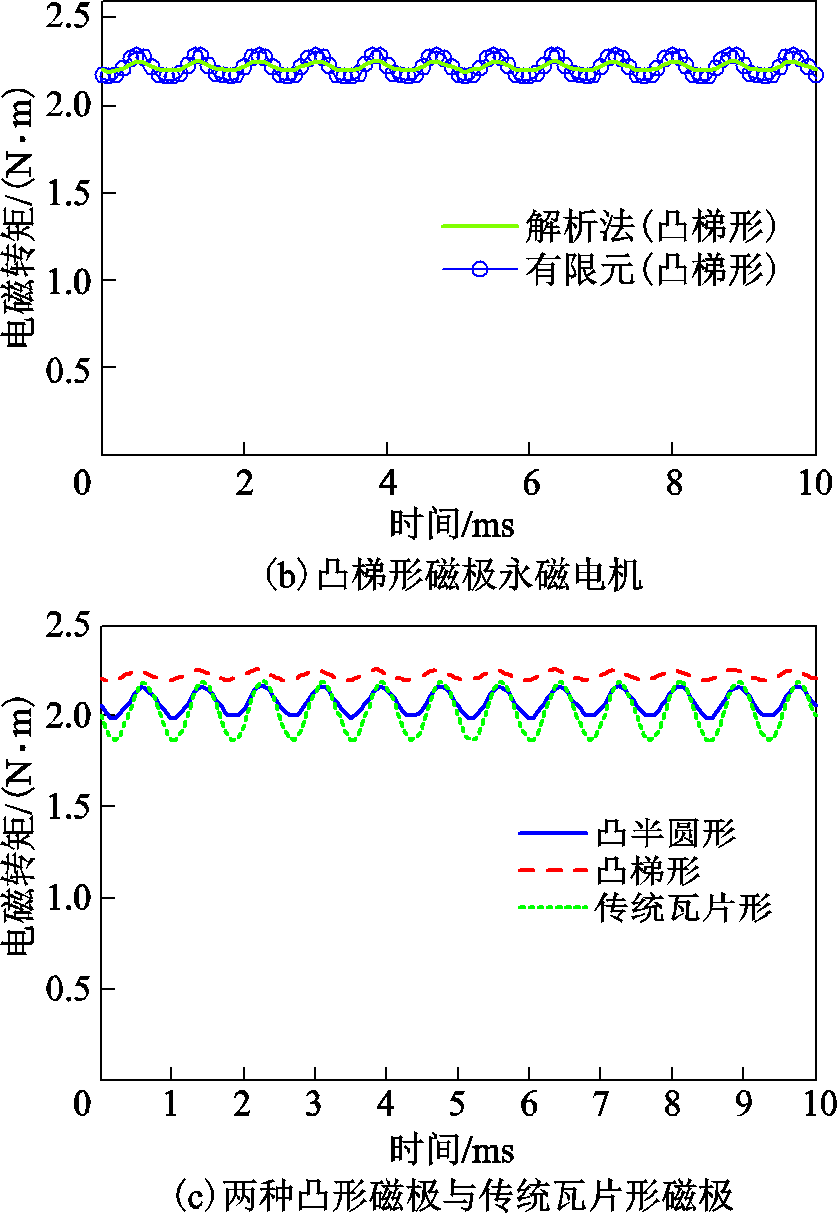
图9 三种永磁电机电磁转矩波形比较
Fig.9 Comparison of electromagnetic torque waveforms for three PM machines
图10为分别利用解析法与有限元法得到两种凸形不等厚磁极电机的齿槽转矩波形以及与永磁量相等的传统瓦片形永磁电机的电磁转矩比较图。从图中可以看出,凸半圆形电机和凸梯形电机的齿槽转矩的峰值分别为69.35mN·m和28.29mN·m,而传统瓦片形电机的齿槽转矩峰值为164.28mN·m。因此,这两种凸形磁极永磁电机的齿槽转矩明显优于传统瓦形磁极的永磁电机。
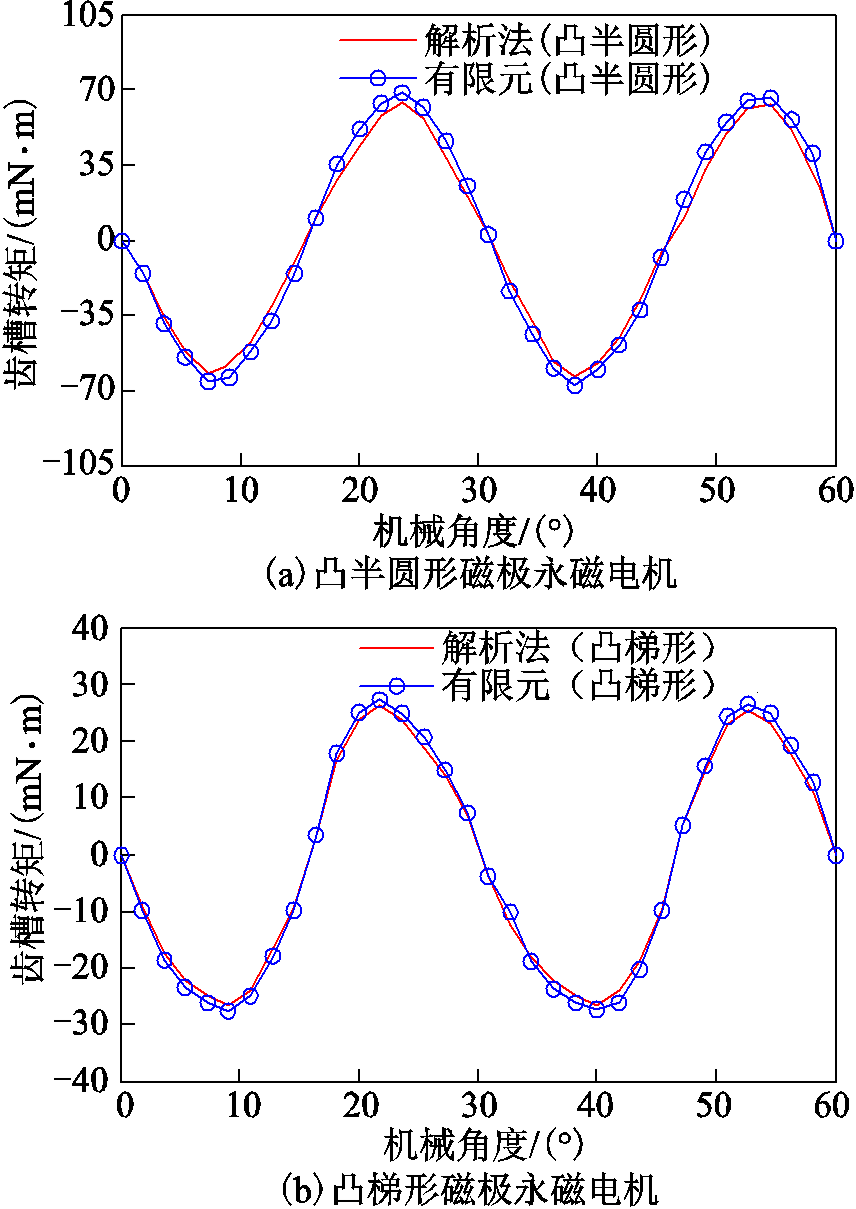

图10 三种永磁电机的齿槽转矩波形
Fig.10 Comparison of cogging torque waveforms for three PM machines
凸形不规则永磁区域B的尺寸对电机的电磁性能会产生较大的影响。凸半圆形尺寸与半圆形的半径r1及两圆心距离d的选择直接相关。这里首先对两圆心距离d取一个定值,然后改变半径r1,分析其对电机的感应电动势基波幅值和总谐波畸变率(Total Harmonic Distortion, THD)、电磁转矩及齿槽转矩等电磁性能的影响。同时再改变两圆心距离d和选择对应的半径r1,得到对电磁性能的影响,见表3。
表3 凸半圆形尺寸对永磁电机电磁性能的影响
Tab.3 Influence of salient semicircle size on the electromagnetic performance of PM machines
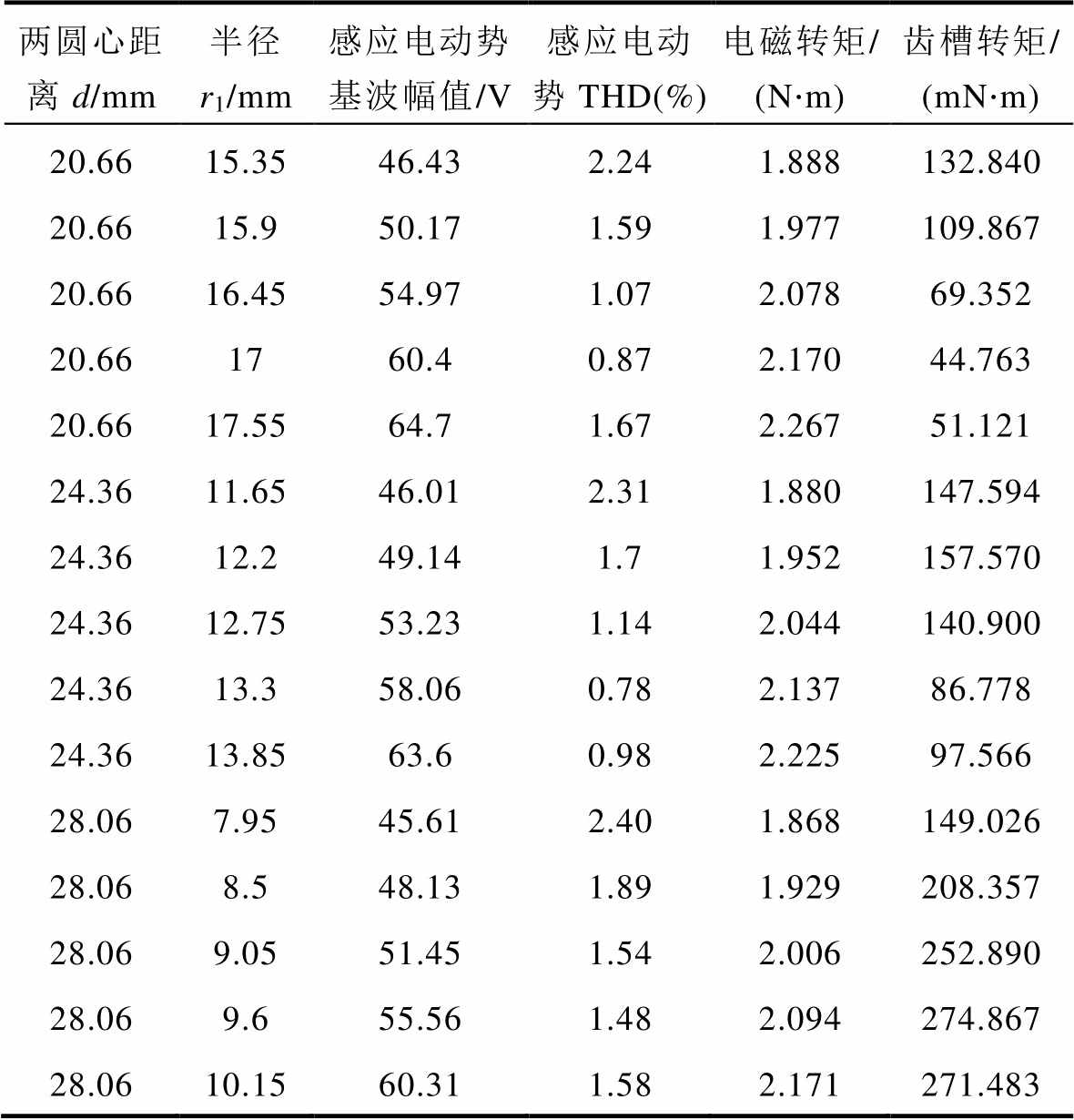
两圆心距离d/mm半径r1/mm感应电动势基波幅值/V感应电动势THD(%)电磁转矩/(N×m)齿槽转矩/(mN×m) 20.6615.3546.432.241.888132.840 20.6615.950.171.591.977109.867 20.6616.4554.971.072.07869.352 20.661760.40.872.17044.763 20.6617.5564.71.672.26751.121 24.3611.6546.012.311.880147.594 24.3612.249.141.71.952157.570 24.3612.7553.231.142.044140.900 24.3613.358.060.782.13786.778 24.3613.8563.60.982.22597.566 28.067.9545.612.401.868149.026 28.068.548.131.891.929208.357 28.069.0551.451.542.006252.890 28.069.655.561.482.094274.867 28.0610.1560.311.582.171271.483
从表3中可以得到,当两圆心距离d一定时,凸半圆形的半径r1越大,即永磁量越大,感应电动势的基波幅值与电磁转矩越大,而感应电动势的THD与齿槽转矩大多情况会先减小后增大,而有时会一直增大,这取决于距离d。原因是,当两圆心距离d很大时,对应的凸半圆形半径r1很小,使得永磁体不规则区域不光滑,变化率很大,从而得到的气隙磁通密度波形不够理想,使得齿槽转矩变大。当两圆心距离d变大时,对应半径的气隙磁通密度基波幅值与电磁转矩变小。从表中可看出,当两圆心距离d为20.66mm,且半径r1为17mm时,凸半圆形磁极永磁电机的电磁性能最好。
凸梯形不等厚永磁结构中,不规则永磁区域B的尺寸与梯形边界角度θ1及圆弧半径r1和三角形的顶点高度S选择相关。这里固定三角形的顶点高度S为定子内半径的长度,通过改变梯形边界角度θ1与圆弧半径r1来分析其对电机电磁性能的影响。具体参数列于表4中。从表中可以得到,圆弧半径r1为定值时,梯形边界角度θ1越小,感应电动势的基波幅值与电磁转矩越小。因为梯形边界角度θ1越小,永磁量就越小。而当圆弧半径r1很大时,削掉的三角形很小,于是永磁体不规则区域不光滑,突变率较大,使得气隙磁通密度的THD增加,齿槽转矩也增加。从表中可以看出,当圆弧半径r1为37.11 mm,且梯形边界角度θ1为18.25°时,凸梯形磁极永磁电机的电磁性能最好。
表4 凸梯形尺寸对永磁电机电磁性能的影响
Tab.4 Influence of salient trapezoid size on the electromagnetic performance of PM machines
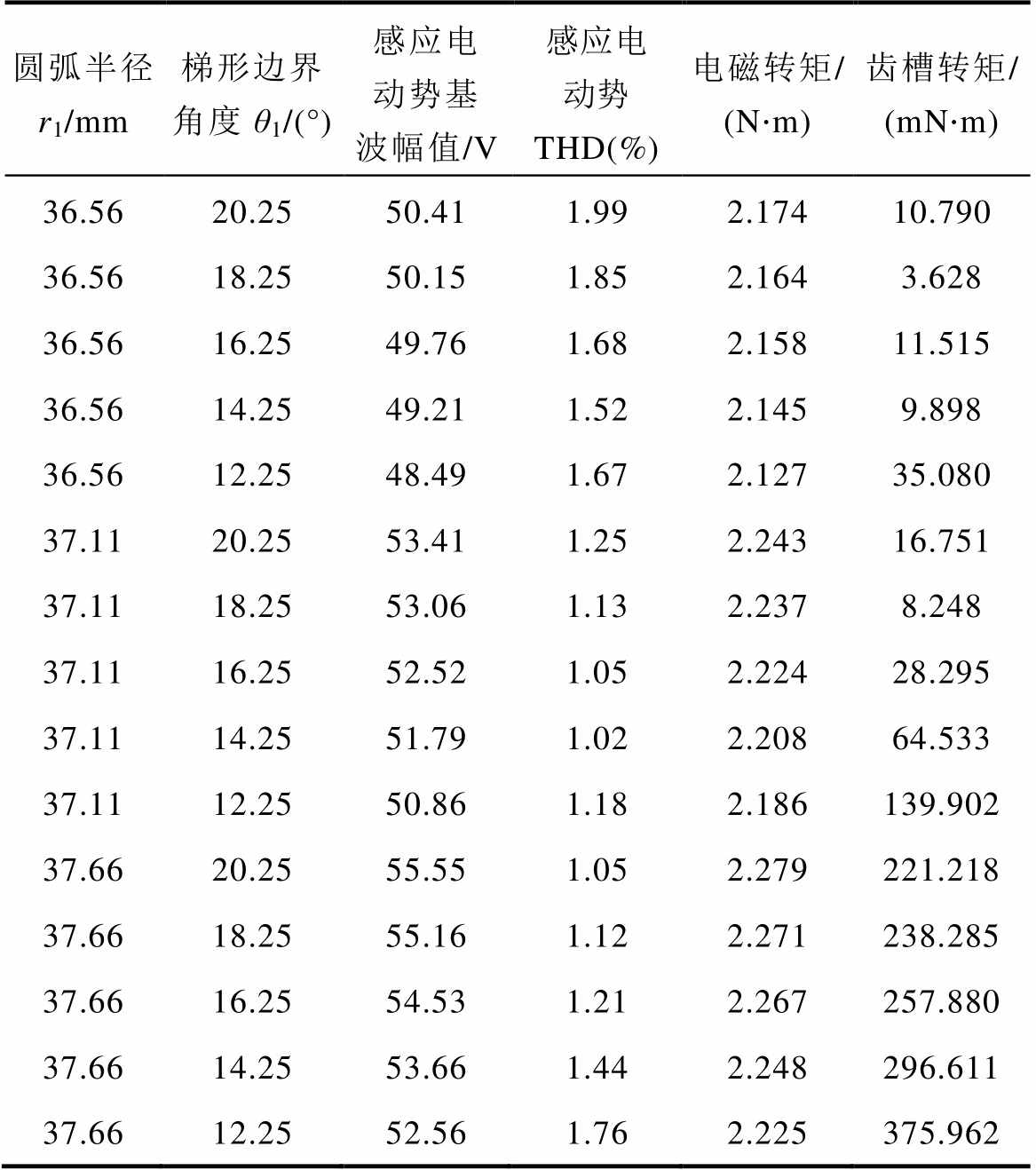
圆弧半径r1/mm梯形边界角度θ1/(°)感应电动势基波幅值/V感应电动势THD(%)电磁转矩/ (N×m)齿槽转矩/ (mN×m) 36.5620.2550.411.992.17410.790 36.5618.2550.151.852.1643.628 36.5616.2549.761.682.15811.515 36.5614.2549.211.522.1459.898 36.5612.2548.491.672.12735.080 37.1120.2553.411.252.24316.751 37.1118.2553.061.132.2378.248 37.1116.2552.521.052.22428.295 37.1114.2551.791.022.20864.533 37.1112.2550.861.182.186139.902 37.6620.2555.551.052.279221.218 37.6618.2555.161.122.271238.285 37.6616.2554.531.212.267257.880 37.6614.2553.661.442.248296.611 37.6612.2552.561.762.225375.962
通过改变磁极结构,提出了凸半圆形和凸梯形两种凸形不等厚磁极的永磁电机。对不规则区域采用分块叠加法,再通过子域模型方法分别求解得到凸形不等厚、扇形槽永磁电机的气隙磁通密度、空载感应电动势、电磁转矩、齿槽转矩等电磁性能的解析表达式。与用磁质量相等的传统表贴瓦片形永磁电机比较结果表明,提出的两种凸形不等厚永磁结构的永磁电机不仅气隙磁通密度的基波幅值较大,THD较低,而且电磁转矩较大、齿槽转矩较小。最后在Maxwell电磁仿真软件中建立这两种电机模型,得到了有限元计算结果,验证了解析模型的正确性。考虑扇形齿是为了便于用子域模型的方法求解。对于实际常用的平行齿,可以采用卡特系数获得解析表达式,结论是一致的:与传统表贴瓦片形永磁电机相比,两种凸形不等厚永磁结构的永磁电机具有较好的电磁性能。
参考文献
[1] Zhu Z Q, Wu L J, Xia Z P. An accurate subdomain model for magnetic field computation in slotted surface-mounted permanent-magnet machines[J]. IEEE Transactions on Magnetics, 2010, 46(4): 1100-1115.
[2] 杨思雨, 夏长亮, 王慧敏.磁极分段型表贴式永磁电机建模与分析[J]. 电工技术学报, 2015, 30(增刊2): 49-55.Yang Siyu, Xia Changliang, Wang Huimin. Modeling and analyzing for surface mounted permanent magnet machine with segmented pole[J]. Transactions of China Electrotechnical Society, 2015, 30(S2): 49-55.
[3] Wu Lijian, Yin Hao, Dong Wang, et al. A nonlinear subdomain and magnetic circuit hybrid model for open-circuit field prediction in surface-mounted PM machines[J]. IEEE Transactions on Energy Conversion, 2019, 34(2): 1485-1495.
[4] 杨定伟, 邓兆祥, 张河山, 等. 永磁轮毂电机磁场解析建模[J]. 电工技术学报, 2019, 34(7): 1423-1433. Yang Dingwei, Deng Zhaoxiang, Zhang Heshan, et al. Exact analytical solution of magnetic field in permanent magnet in-wheel motor[J]. Transactions of China Electrotechnical Society, 2019, 34(7): 1423-1433.
[5] 张守首, 郭思源. 考虑分段斜极和磁性槽楔的永磁同步电机磁场解析方法[J]. 电工技术学报, 2019, 34(1): 11-22. Zhang Shoushou, Guo Siyuan. Analytical magnetic field method of permanent magnet synchronous machine considering step-skewed magnets and magnetic slot wedge[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 11-22.
[6] 郭超, 黄守道, 王家堡, 等. 潜液式低温永磁同步电机的设计与特性研究[J]. 电工技术学报, 2019, 34(18): 3769-3777.Guo Chao, Huang Shoudao, Wang Jiabao, et al. Design and characteristic research of submerged cryogenic permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3769-3777.
[7] 宋腾飞, 刘慧娟, 张振洋, 等. 车用永磁同步电机拓扑结构优化与实验研究[J]. 电机与控制学报, 2019, 23(6): 44-53. Song Tengfei, Liu Huijuan, Zhang Zhenyang, et al. Topology optimization and experimental research of the interior permanent magnet synchronous motor for EVs[J]. Electric Machines and Control, 2019, 23(6): 44-53.
[8] 胡鹏飞, 王东, 靳栓宝, 等. 偏心磁极永磁电机气隙磁场正弦优化模型[J]. 电工技术学报, 2019, 34(18): 3759-3768. Hu Pengfei, Wang Dong, Jin Shuanbao, et al. Sinusoidal optimization model for air gap magnetic field of eccentric magnetic pole permanent magnet motor[J]. Transactions of China Electrotechnical Society, 2019, 34(18): 3759-3768.
[9] Zhao Jing, Hu Hengzai, Liu Xiangdong. Influence of edge permanent-magnet shape on the performance of an arc-linear permanent-magnet synchronous machine[J]. IEEE Transactions on Magnetics, 2015, 51(11): 2804-2809.
[10] Wang Kai, Liang Yanping, Wang Dongmei, et al. Cogging torque reduction by eccentric structure of teeth in external rotor permanent magnet synchronous motors[J]. IET Electric Power Applications, 2019, 13(1): 57-63.
[11] 刘国海, 王艳阳, 陈前, 等. 非对称V型内置式永磁同步电机的多目标优化设计[J]. 电工技术学报, 2018, 33(增刊2): 385-393. Liu Guohai, Wang Yanyang, Chen Qian, et al. Multi-objective optimization of an asymmetric V-shaped interior permanent magnet synchronous motor[J]. Transactions of China Electrotechnical Society, 2018, 33(S2): 385-393.
[12] 倪有源, 刘跃斌, 王群京. 组合磁极结构的永磁电机解析法建模与分析[J]. 电机与控制学报, 2019, 23(1): 52-62. Ni Youyuan, Liu Yuebin, Wang Qunjing. Analytical modeling and analysis of a permanent magnet machine with combined magnetic poles[J]. Electric Machines and Control, 2019, 23(1): 52-62.
Modeling and Analysis of Permanent Magnet Machines with Salient Shape Unequal Thickness Magnets
Abstract The shape of magnets directly influences the electromagnetic performance of permanent magnet (PM) machines significantly. Two kinds of novel PM machines with salient shape unequal thickness magnets were presented. Two salient shape unequal thickness magnets were modeled. The air-gap magnetic field in the machines was analytically obtained by a subdomain model method with solving the Laplacian and quasi-Poissonian equations in each subdomain and applying the boundary conditions. Besides, the back electromotive force (EMF), electromagnetic torque and cogging torque were analytically obtained. Compared with the conventional structure with equal thickness magnets, the machines with salient shape unequal thickness magnets can improve the electromagnetic performance with the equal magnet usage. In addition, the influences of the parameters of salient shapes on the electromagnetic performance were also investigated. Finally, the correctness of the analytical models was verified by a finite element method (FEM).
keywords:Salient shape unequal thickness magnetic pole, permanent magnet machine, analytical method, subdomain model method, electromagnetic performance
中图分类号:TM351
DOI:10.19595/j.cnki.1000-6753.tces.190074
国家自然科学基金资助项目(51637001)。
收稿日期 2019-01-17
改稿日期 2019-08-03
倪有源 男,1976年生,博士,副教授,研究方向为特种电机设计。E-mail:nyy76@163.com (通信作者)
王 磊 男,1992年生,硕士研究生,研究方向为永磁电机设计。E-mail:1715583862@qq.com
(编辑 郭丽军)