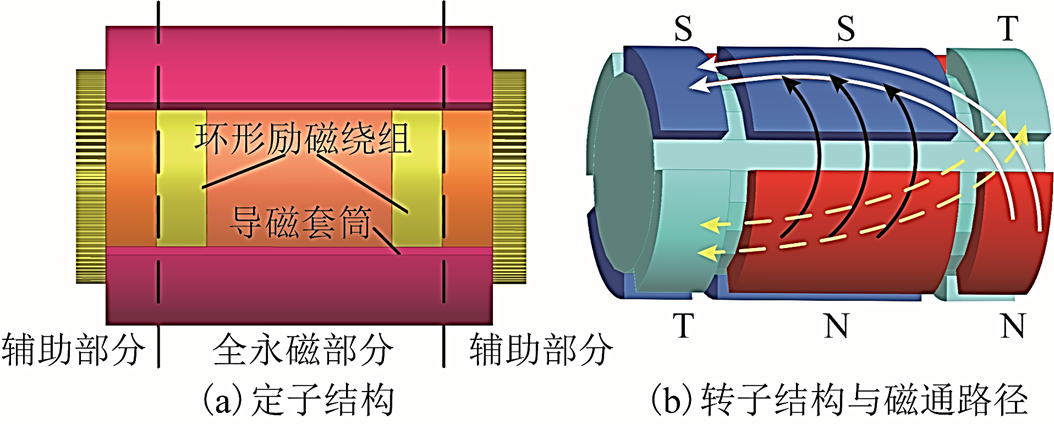
图1 混合励磁电机结构与磁通路径示意图
Fig.1 Schematic diagram of structure and flux path of the proposed hybrid excitation machine
摘要 为提高高速交错磁极混合励磁同步发电机直流侧短路电流的计算精度，通过在dq轴上设立阻尼回路的方法，建立电机动态数学模型。该模型能够同时考虑定子导磁套筒、实心转轴、永磁体和铁心极在短路过程中涡流效应对电枢绕组电流的影响，在此基础上推导出电机瞬态、超瞬态电感以及短路电流的表达式。通过与某型高速交错磁极混合励磁电机短路电流试验结果进行对比，验证了模型的有效性，并对存在误差的原因进行分析，指出该类电机在短路过程中由于交错磁极结构导致的动态饱和现象是造成误差的主要原因之一。
关键词：环形励磁绕组 交错磁极 实心转轴 直流侧短路
舰船综合电力系统将机械推进系统和电力系统以电能的形式合二为一，实现了全舰能源综合利用，具有传统机械推进动力无法比拟的优势[1]。
发电模块是舰船综合电力系统中的核心模块，高功率密度是其追求的目标。而提高发电机的转速是提高发电机功率密度最直接的方法之一，但是受到传统交流负载频率的限制，发电机转速得不到大幅度提高[2]。
随着大功率电力电子技术的不断发展，采用交-直-交供电模式的舰船综合电力系统解除了对发电机供电频率的限制[3-5]，从而可以通过提高转速的方法实现电机高功率密度。
目前高速发电机主要有电励磁同步发电机、感应发电机和永磁同步发电机[6]。电励磁同步发电机存在转子结构复杂的问题，难以满足高速运行时对机械强度的要求；感应发电机转子结构简单，但是交流励磁绕组的无功功率相对较大，加大了定子热负荷[7-8]；永磁同步发电机结构简单、效率高[9]，但是传统永磁电机存在气隙磁场调节困难的问题，成为制约其作为发电机进一步发展的重要原因。
为了能够找到一种适用于高速大功率场合的发电机，本课题组在永磁电机、电励磁同步电机的基础上，提出了一种具有定子导磁套筒、环形励磁绕组、交错磁极、实心转轴结构的新型高速混合励磁发电机[10]。目前对于该类电机的理论研究主要集中在稳态性能方面[10-20]，对其结构特征与调压原理有了较为清晰的认识，但目前对其暂态性能方面的研究较少。
发电机直流侧突然短路是整流发电机典型的暂态行为。在发生突然短路时，短路电流的冲击时间很短，但却会对电机产生巨大的影响，存在严重的安全隐患[21]；同时短路电流的计算是断路器设计的关键因素，通过准确地计算短路电流可以为电力系统保护整定提供依据。为此有必要对该类电机的短路特性进行研究。
高速交错磁极混合励磁电机发生直流侧突然短路时，其暂态过程与常规永磁同步电机、感应电机、电励磁同步电机都有所不同。与常规永磁同步电机、感应电机[22]相比，在短路过程中它不仅存在由定子导磁套筒、实心转轴、永磁体和铁心极引起的超瞬态过程，同时还存在由环形励磁绕组结构引起的瞬态过程；与电励磁同步电机相比，虽然两者同时具有超瞬态、瞬态过程，但是由于高速交错磁极混合励磁电机三维磁路的特点，其在定子导磁套筒、实心转轴上的涡流效应更为复杂，不仅有因电枢绕组电流引起的径向磁场变化而在实心转轴感应的涡流，同时有因环形励磁绕组电流引起的轴向磁场变化而在定子导磁套筒、实心转轴感应的涡流。利用三维有限元对电机直流侧突然短路工况进行仿真分析，发现如果不考虑在暂态过程的涡流效应将会对短路电流的计算带来较大影响。
本文针对高速交错磁极混合励磁同步发电机（Hybrid Excitation Synchronous Generator, HESG）直流侧突然短路工况，为计及定子导磁套筒、实心转轴、永磁体和铁心极在暂态过程中涡流效应对电枢绕组电流的影响，用dq轴上两个阻尼回路对其进行等效模拟，建立电机在暂态过程中考虑涡流效应的动态数学模型，在此基础上推导出电机瞬态、超瞬态电感的表达式以及短路电流表达式，为该类电机电磁优化设计和电力系统保护提供了理论依据。
高速交错磁极混合励磁电机结构与磁通路径示意图如图1所示，其中T表示铁心极。
图1 混合励磁电机结构与磁通路径示意图
Fig.1 Schematic diagram of structure and flux path of the proposed hybrid excitation machine
电机在轴向上分段，中间为全永磁部分，两端为辅助部分。定子铁心叠片被两套串联环形励磁绕组分为三段，定子铁心外圆套有导磁套筒，为环形励磁绕组产生的电励磁磁场提供轴向磁路；转子全永磁部分的结构与常规表贴式永磁电机类似，转子两端辅助部分永磁极与铁心极交错排布。
该类电机利用永磁极与铁心极的磁阻不同，通过调节励磁电流的大小和方向，实现对铁心极气隙磁场的调节，在负载和转速变化时可以维持输出电压恒定。环形励磁绕组产生的电励磁磁通路径如图1b虚线所示，其路径为：转子铁心极→气隙→定子铁心→导磁套筒→定子铁心→气隙→转子铁心极→转子轭部→转子铁心极。当由环形励磁绕组产生的磁场进入气隙时的方向与处在同一端由永磁极产生磁场进入气隙时的方向一致时属于弱磁工况；反之属于增磁工况[10]。
在短路过程中定子导磁套筒、实心转轴、永磁体和铁心极的涡流效应用dq轴上两套阻尼绕组Lkd、Lkq进行等效模拟；电机环形励磁绕组在交错磁极结构的作用下仅产生直轴磁场，用d轴方向一套励磁绕组进行等效；除十二相电枢绕组之间的相互交链，以及环形励磁绕组与电枢绕组之间的交链，还有d轴阻尼绕组与电枢绕组、励磁绕组之间的相互交链，以及q轴阻尼绕组与电枢绕组之间的交链。为便于分析，可作如下假设：
（1）忽略铁心材料的饱和、磁滞效应，忽略定子铁心材料涡流，不计导线的趋肤效应。
（2）定子两套环形励磁绕组产生的电励磁磁场对电机的全永磁部分的影响忽略不计。
（3）气隙磁场按正弦分布，定子和转子表面光滑，齿槽效应通过卡氏系数计入。
正方向选定：
（1）定子电枢绕组电压、电流采用发电机惯例；励磁绕组及转子阻尼回路电压、电流采用电动机惯例。
（2）正的励磁、阻尼绕组电流产生正的磁链，正的电枢绕组电流产生负的磁链。
（3）转子旋转正方向为逆时针方向，q轴正方向领先d轴正方向90°电角度。
（4）由转子外表面进入定子内表面的径向方向为气隙磁场正方向。
由于十二相定子电枢绕组结构为4Y互移15°电角度，各个Y中点独立且不引出，故无需考虑零轴分量。
dq坐标系下的磁链、电压方程为
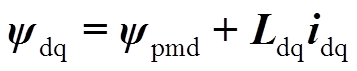（1）
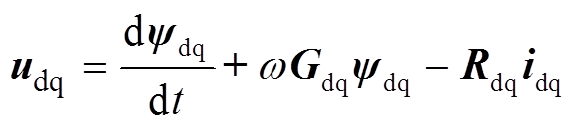（2）
其中
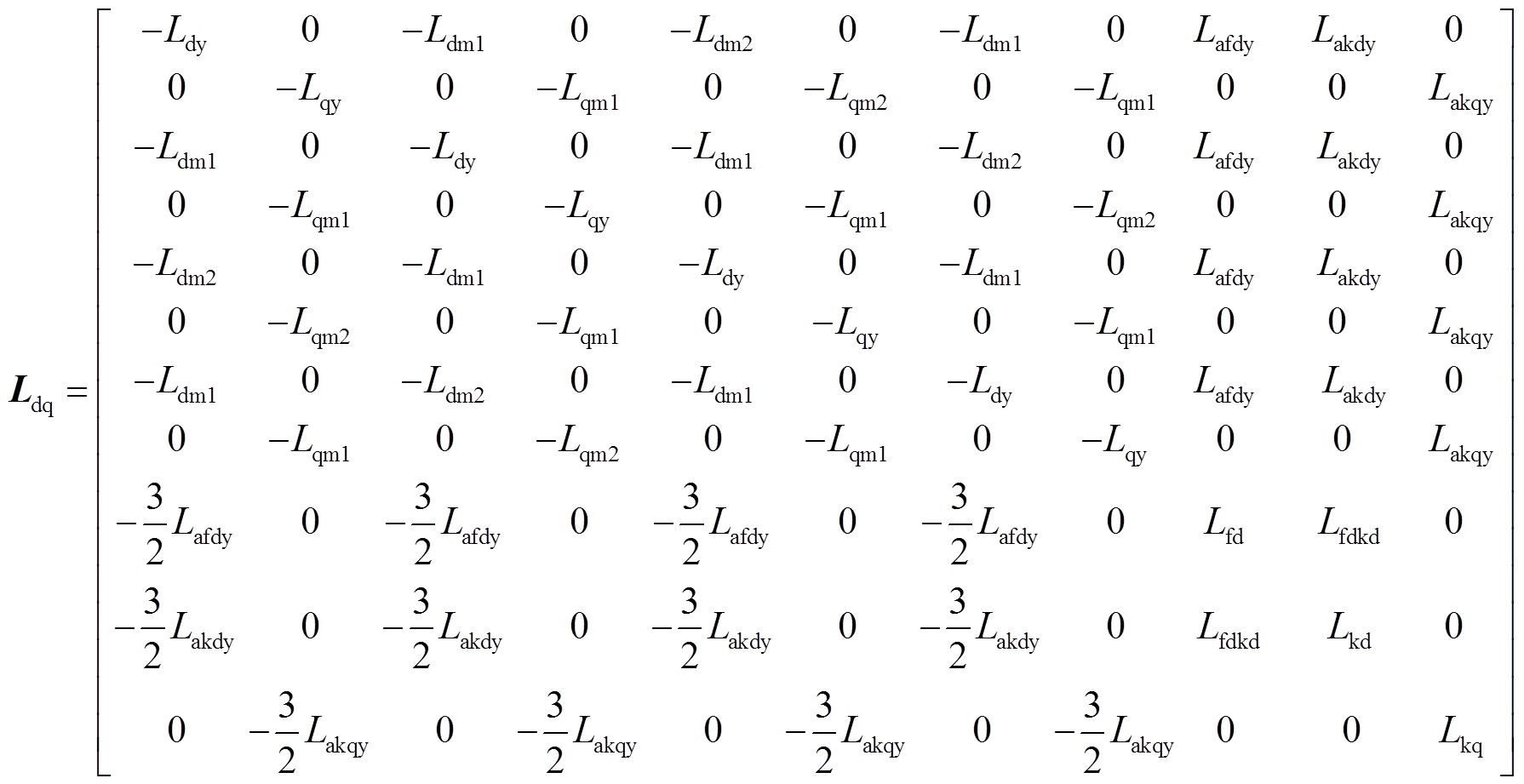
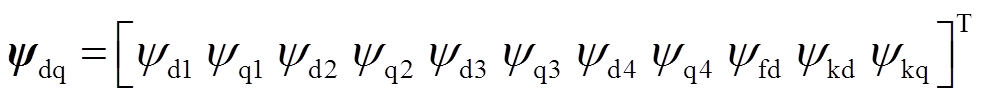
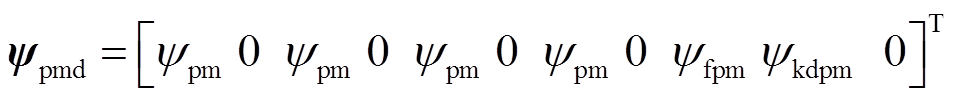
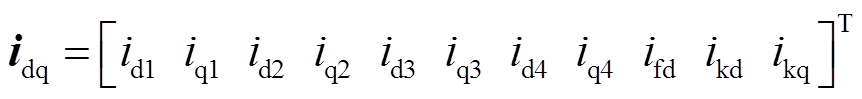
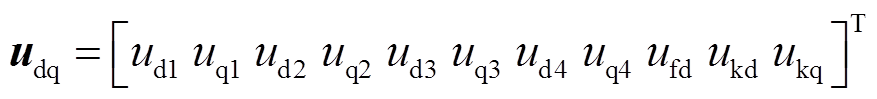
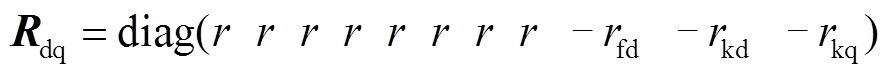
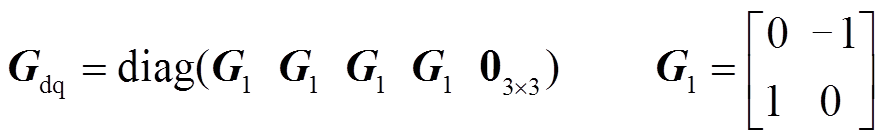
式中，ufd、ukd、ukq和ifd、ikd、ikq分别为励磁绕组、dq轴阻尼绕组的电压和电流；udi、uqi和idi、iqi（i=1~4）分别为各Y形绕组dq轴电压和电流；r、rfd、rkd、rkq分别为电枢绕组、环形励磁绕组、dq轴阻尼绕组电阻；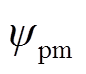
为转子永磁体产生的磁场与电枢绕组交链的磁链幅值；
、
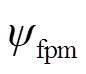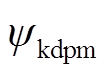分别为永磁体在励磁绕组、d轴阻尼绕组产生的磁链；Ldy、Lqy分别为单Y相绕组d、q轴同步电感；Ldm1、Lqm1、Ldm2、Lqm2分别为相差15°、30°电角度两Y绕组间d、q轴互感；Lfd、Lkd、Lkq、Lafdy、Lakdy、Lakqy分别为环形励磁绕组、dq轴阻尼绕组自感以及与电枢绕组互感幅值；Lfdkd为励磁绕组与d轴阻尼绕组互感。
交错磁极混合励磁同步发电机整流系统结构如图2所示。
当发电机发生直流侧突然短路时，可认为电机发生十二相对称短路[23]。由十二相电枢绕组结构可知，在正常运行以及对称短路的时候满足
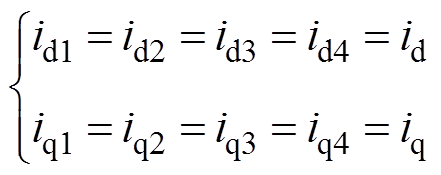（3）
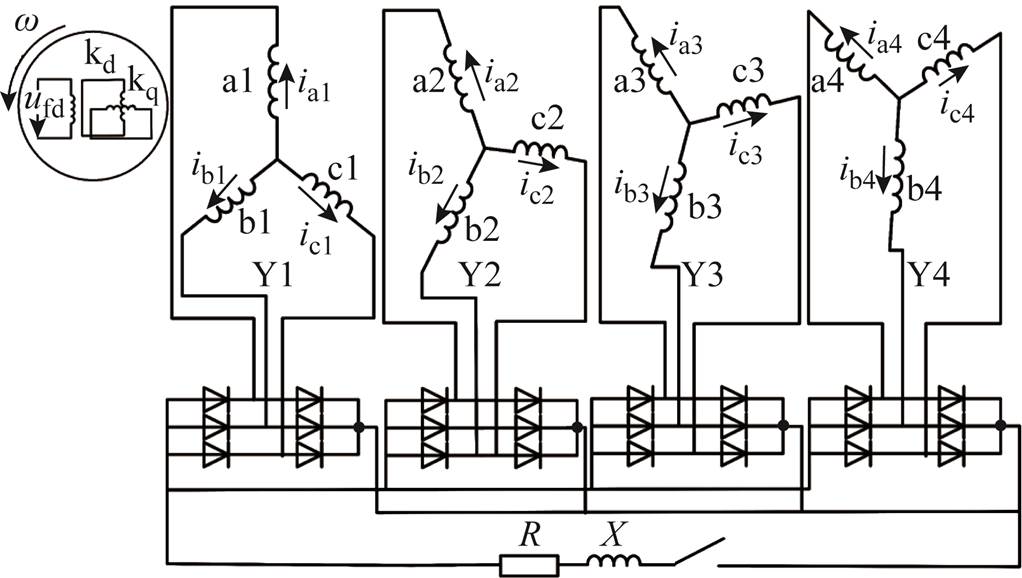
图2 混合励磁同步发电机整流系统结构示意图
Fig.2 Structural diagram of rectifier system of HESG
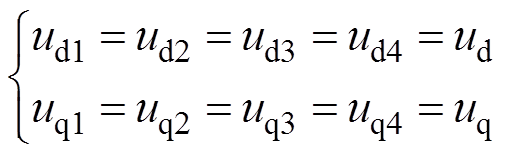（4）
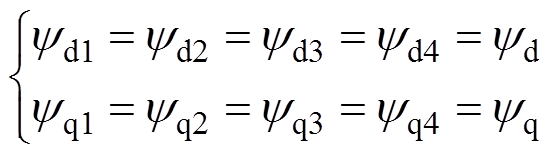（5）
因此，式（1）和式（2）得到化简之后磁链、电压方程为
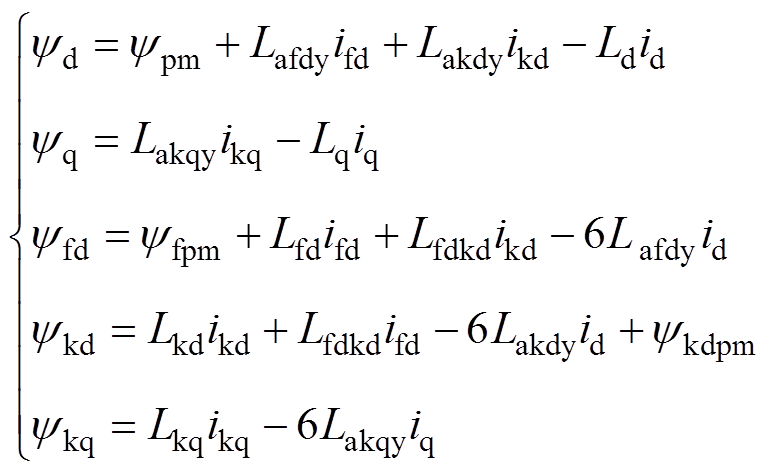（6）
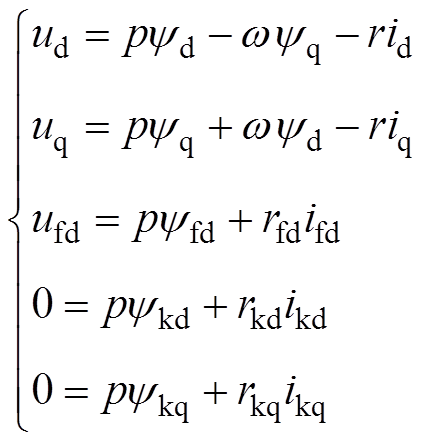（7）
式中，p为对时间求导的算子。
不考虑电机机械过渡过程，利用叠加原理对其进行求解，短路工况可以分解为短路前的正常分量和短路后的故障分量[21]。
电机正常分量为
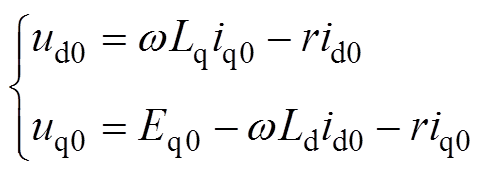（8）式中，Eq0为短路前永磁体和励磁绕组共同产生的磁场在电枢绕组中的感应电动势幅值q轴分量；uq0、ud0分别为电机短路前端电压幅值d、q轴的分量；iq0、id0分别为电机短路前电流d、q轴的分量。
由于中大功率高速电机电枢绕组电阻相对于电抗来说一般很小，可以忽略不计，式（8）化简得到
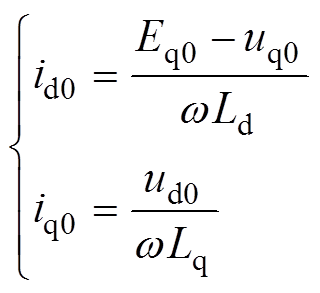（9）在式（6）和式（7）的基础上可得故障分量为
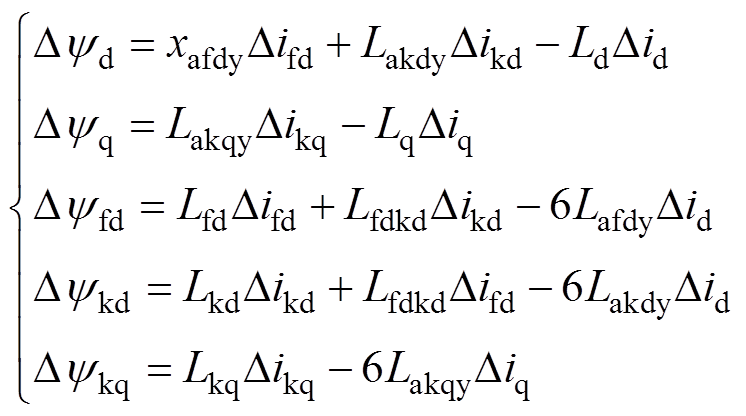（10）
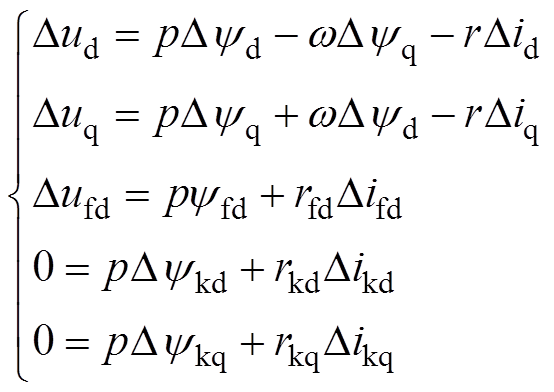（11）式中，变量用增量的形式来表示；Δufd=0为不考虑励磁装置的调节作用；dq轴电压的变化量是一个阶跃信号。
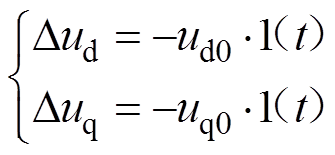（12）
式中，1(t)表示阶跃信号。联立式（10）~式（12）可以得到
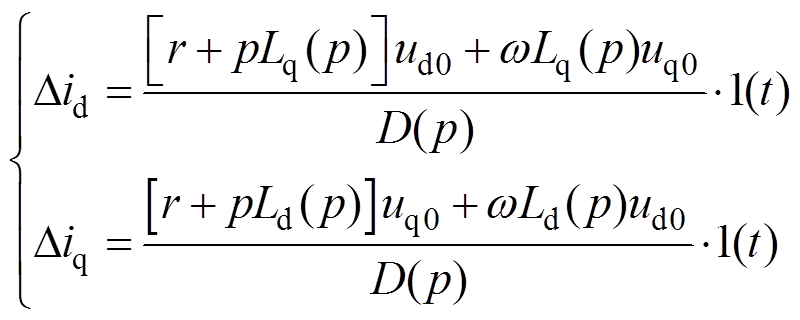（13）
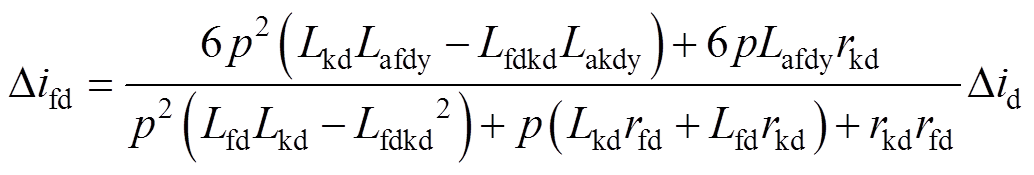（14）
其中
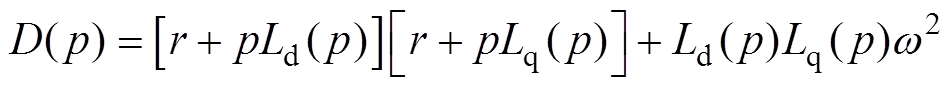
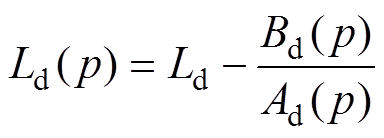
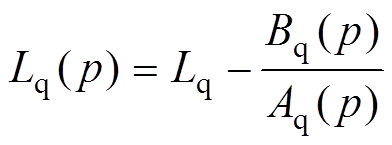
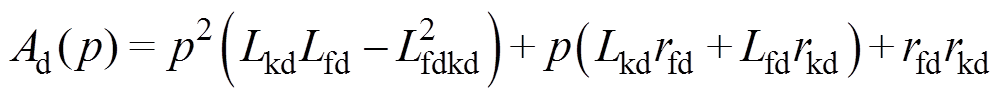
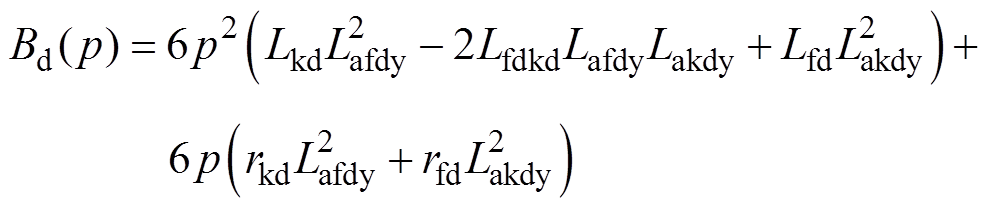
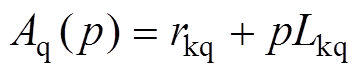
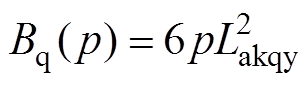
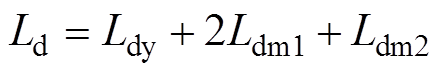
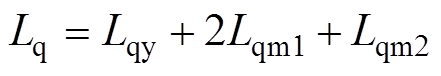
在忽略定子、转子高阶小量的情况下，将正常分量、故障分量叠加可得直轴、交轴、励磁电流表达式为
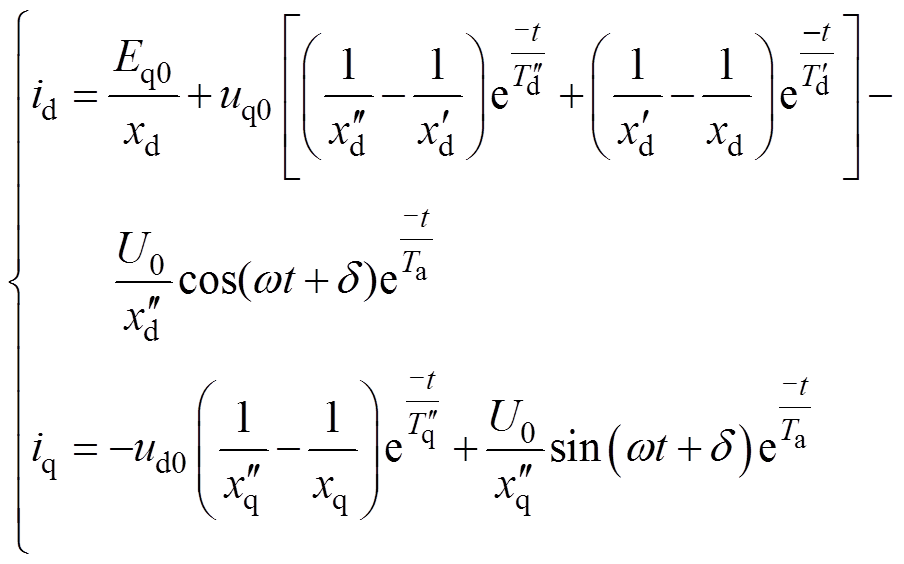（15）
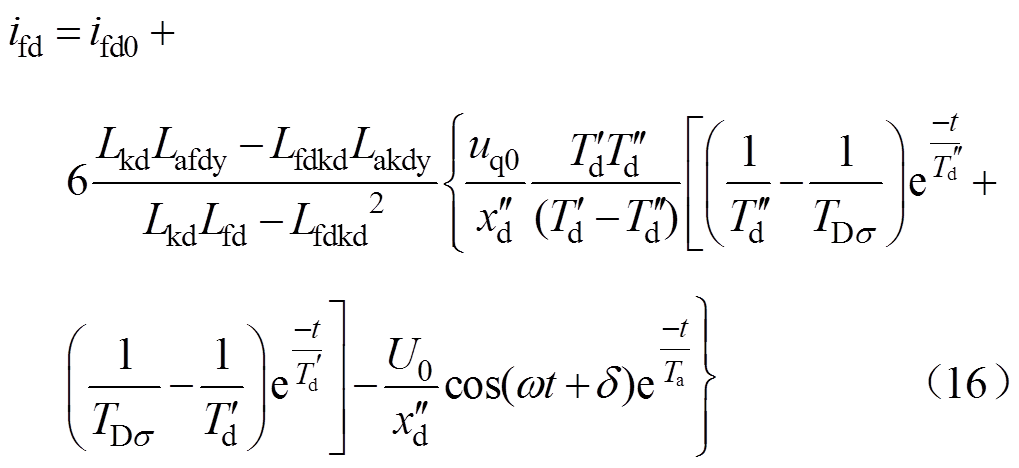
式中，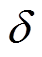
为功率角；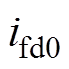
为短路前环形励磁绕组电流。
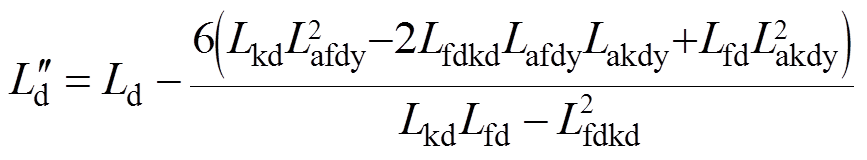
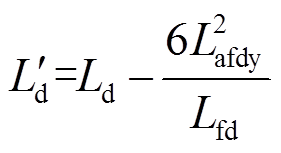
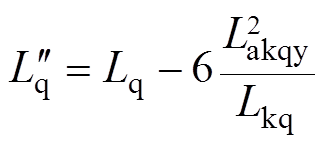
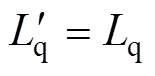
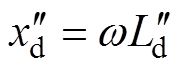
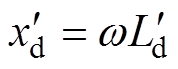
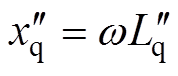
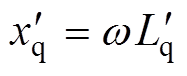
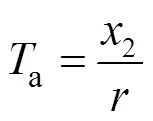
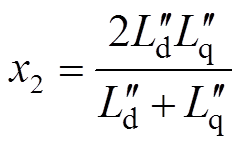
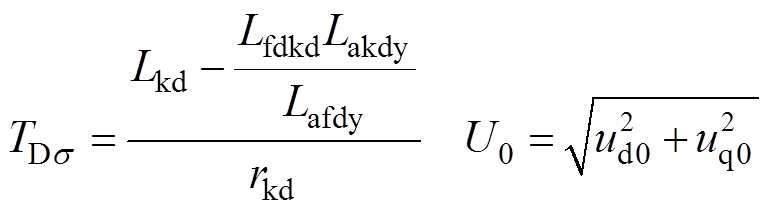
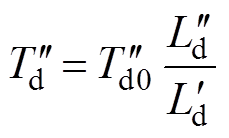
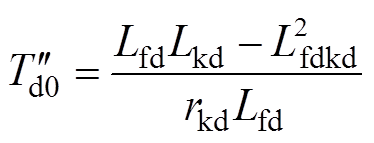
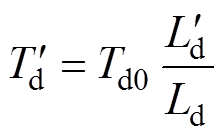
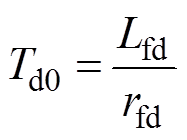
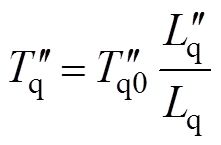
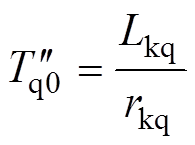
通过Park反变换可得，十二相电枢绕组短路电流表达式为
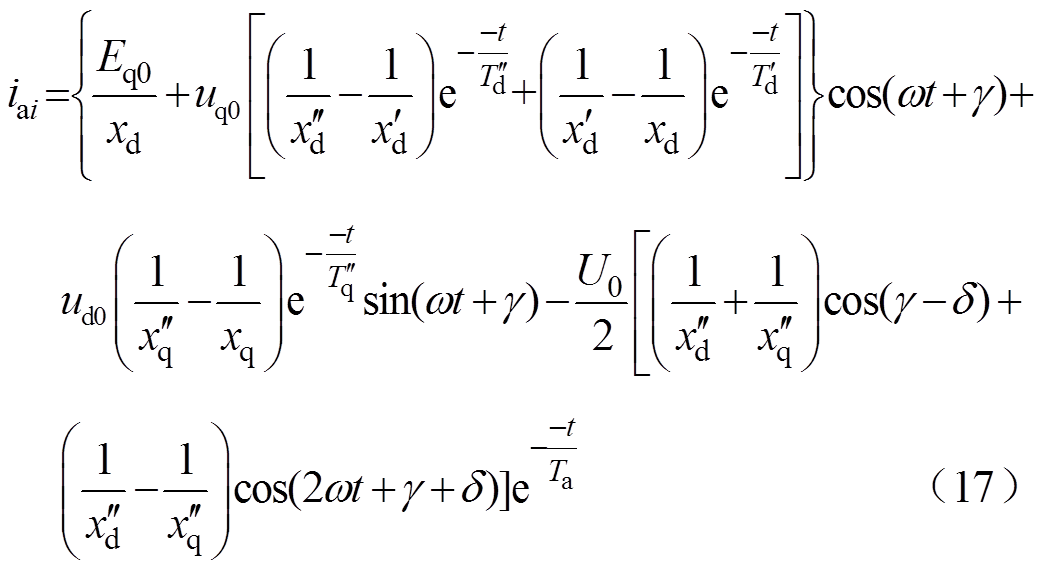
式中，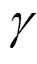
为转子初始位置角，将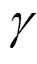替换为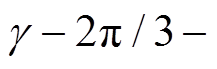
、
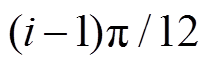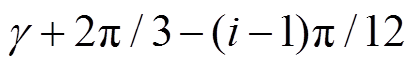（i=1~4）即可得到各相电流表达式。由于在空载时有
、
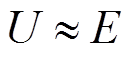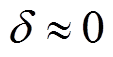可得空载突然短路相电流表达式为
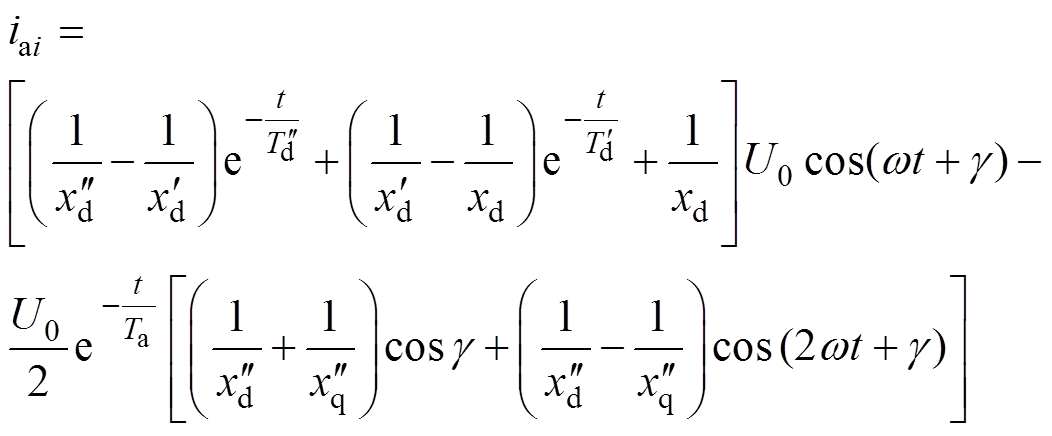（18）由式（18）可知，电枢绕组电流随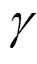及时间的变化而变化，当
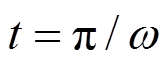且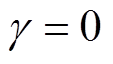
时电流绝对值取最大值为
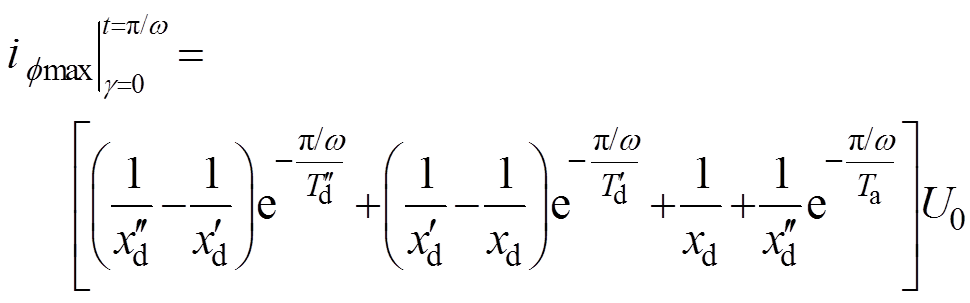（19）
在不考虑电流衰减的情况下，可以得到空载直流侧突然短路相电流峰值为
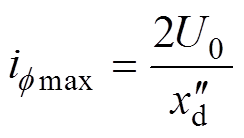（20）
综上所述，电机发生空载直流侧突然短路，相电流需经半个周期左右时间到达峰值，相电流最大值可由式（19）表示，当不考虑电流衰减时，可简化为式（20）；由于直流侧短路电流峰值是相电流峰值的3.831[23]倍，所以可以求出空载突然短路直流侧电流峰值。
为求取混合励磁电机暂态参数，采用三维有限元数值计算方法获取电机运算电抗频率特性，利用电机运算电抗表达式[24]进行复数拟合求取电机参数。
在三维涡流场中，励磁绕组短接，A1相绕组轴线对准d轴并给定脉振电流为
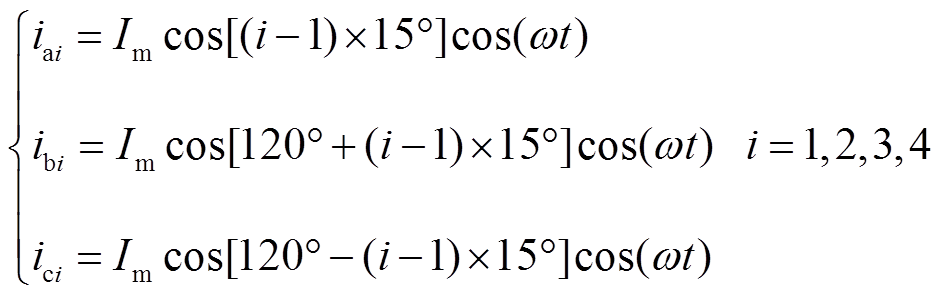（21）由此获得d轴磁链为
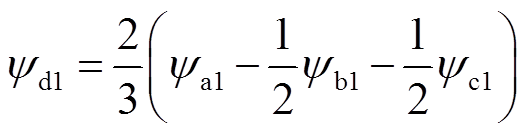（22）
进而可获得d轴运算电抗为
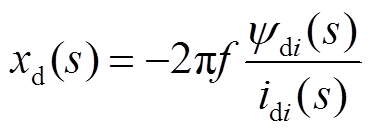（23）q轴运算电抗计算与d轴类似。
交错磁极混合励磁电机的运算电抗式[25]为
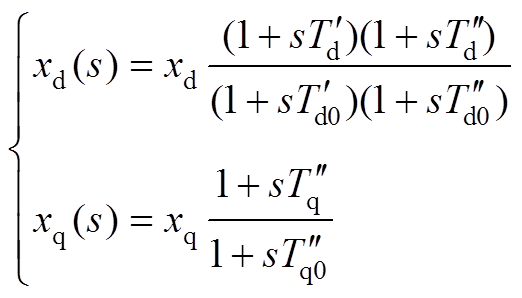（24）
瞬态电抗通常利用被表示为标准形式的运算电抗的倒数进行最小二乘法的拟合。
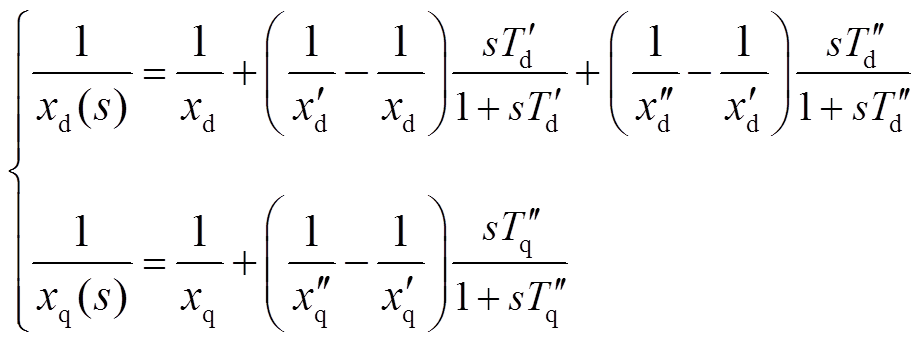（25）令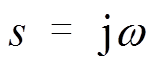
，即可得频率特性的拟合方程，通过频率特性的复数拟合，便可确定稳态电抗（s→0）、初（超）瞬态电抗（s→∞）、瞬态电抗与各时间常数[25]。
对某型高速交错磁极混合励磁同步发电机在空载工况下进行直流侧突然短路的试验；同时基于Matlab/Simulink软件建立高速交错磁极混合励磁同步发电机系统仿真模型，其结构如图3所示。电机主要电磁参数见表1。
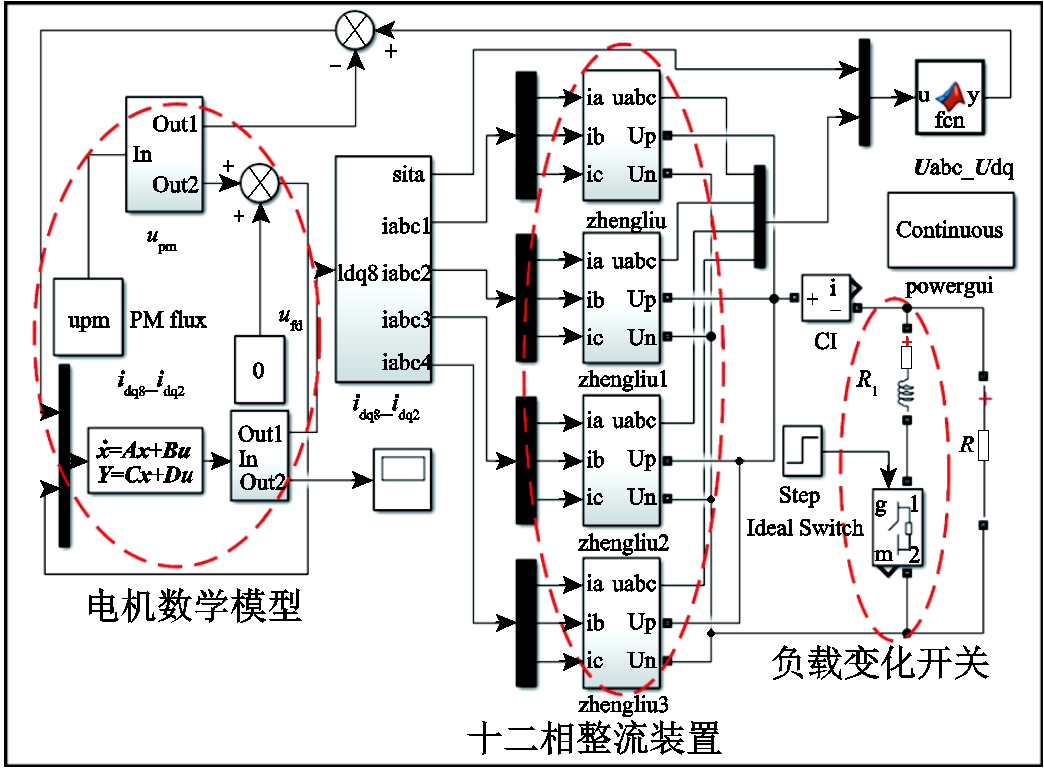
图3 混合励磁同步发电机系统仿真模型
Fig.3 Simulation model of HESG system
表1 电机主要电磁参数
Tab.1 Main electromagnetic parameters of the machine
参数数值 rs/Ω0.004 67 rfd/Ω3.469 Lfd/H2 Lafdy/mH2.7 0.023 Ta/s0.071 0.55 318.2 447.5 Ld/μH469.3
试验以及Simulink仿真空载直流侧突然短路电流波形如图4所示，励磁电流波形如图5所示，短路电流峰值计算结果见表2。
由图4、表2计算结果可知，在短路过程中，如不考虑定子导磁套筒、实心转轴、永磁体和铁心极的涡流效应对电枢绕组电流的影响，将会给短路电流峰值计算结果带来较大误差，而考虑涡流效应的短路电流峰值计算结果与试验值误差在10%以内，满足工程要求。
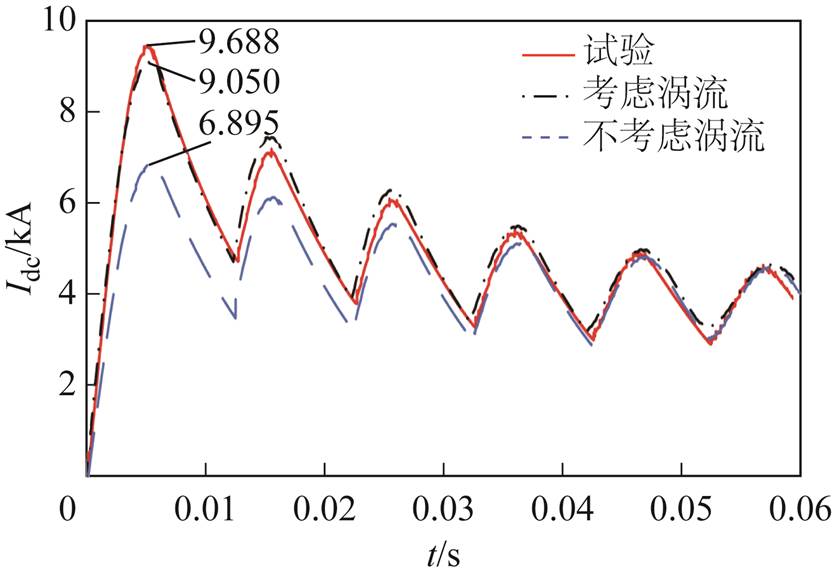
图4 试验、Simulink仿真直流侧短路电流波形
Fig.4 Test, Simulink simulation DC-side short-circuit current waveforms
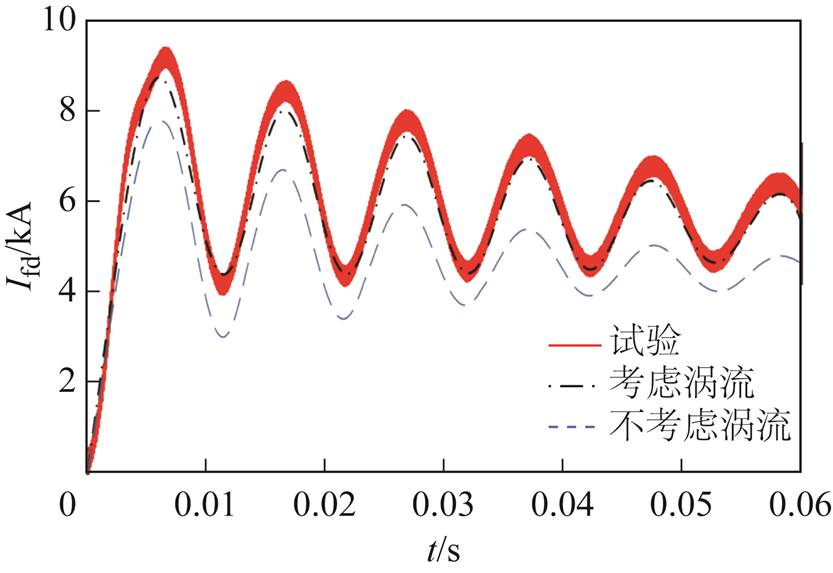
图5 试验以及Simulink仿真励磁电流波形
Fig.5 Test, Simulink simulation DC-side short-circuit current waveform
表2 直流侧短路电流峰值计算结果
Tab.2 DC-side short-circuit current peak calculation results
试验Simulink考虑涡流解析计算考虑涡流Simulink不考虑涡流 短路电流峰值/A9 6889 0509 2296 895 误差（%）—-6.59-4.74-28.83
对产生误差的原因进行分析。电机从空载工况到短路稳态过程中电流的轨迹如图6所示。x轴正方向表示d轴方向、y轴正方向表示q轴方向；坐标原点与每个点的连线表示当前时刻电枢绕组合成磁动势的大小和方向。由图6可以发现，在短路过程当中，直轴电流始终在-d方向，因此在短路过程中电机全永磁部分一直处于去磁状态[26-27]。电机短路过程磁场分布示意图如图7所示。
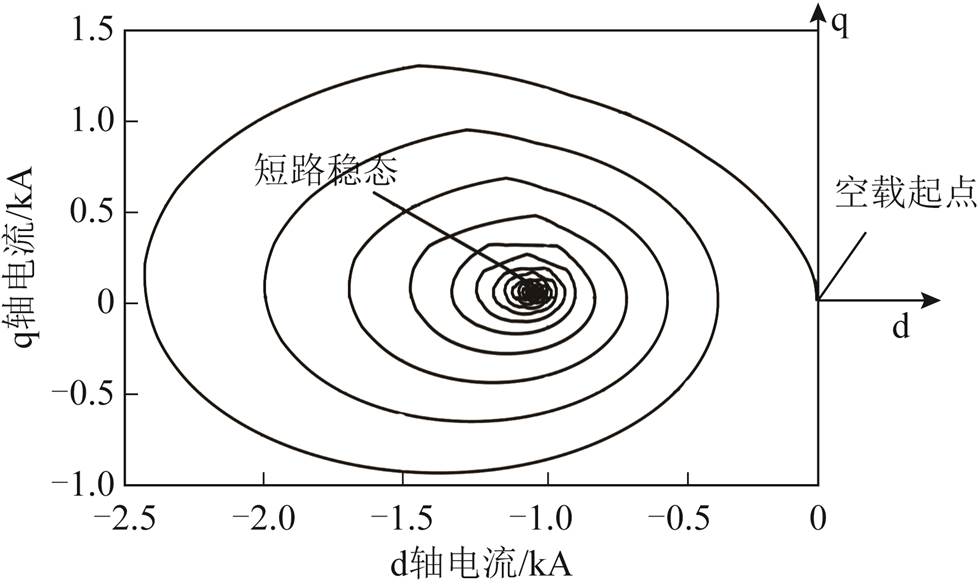
图6 空载到短路稳态过程中电流轨迹
Fig.6 Current trajectory from no load to short-circuit steady-state process
与全永磁部分不同，辅助部分由于采用交错磁极结构，辅助部分永磁极产生的磁通不经过铁心极，而是从一侧永磁极经过气隙进入辅助部分定子铁心，再由轴向通过定子导磁套筒进入另一侧永磁极，然后进入转子轭部形成闭合回路[10]，原本对于全永磁部分去磁性质的电枢绕组电流，在辅助部分会使得定子铁心齿部磁路饱和。
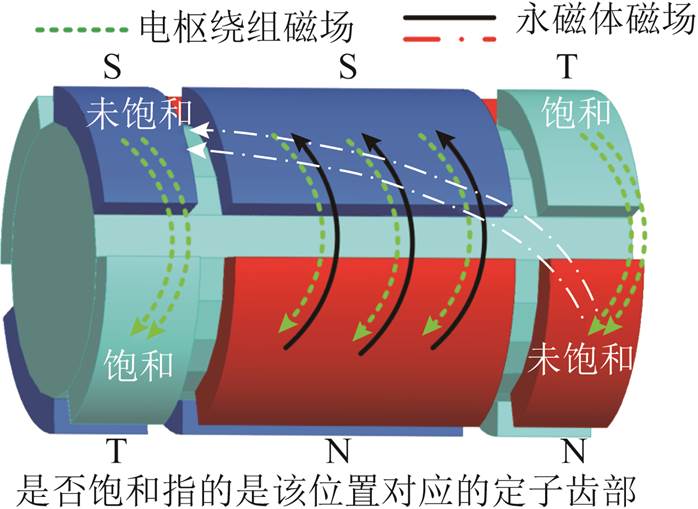
图7 短路过程磁场分布示意图
Fig.7 Schematic diagram of magnetic field distribution in short circuit process
电机辅助部分空载时刻、短路峰值时刻的径向气隙磁通密度波形如图8所示。在短路峰值时刻，辅助部分铁心极处径向气隙磁通密度与处在同一侧永磁极产生的磁场方向一致，并且磁通密度数值在1.1T左右，铁心极对应定子齿部磁路饱和。
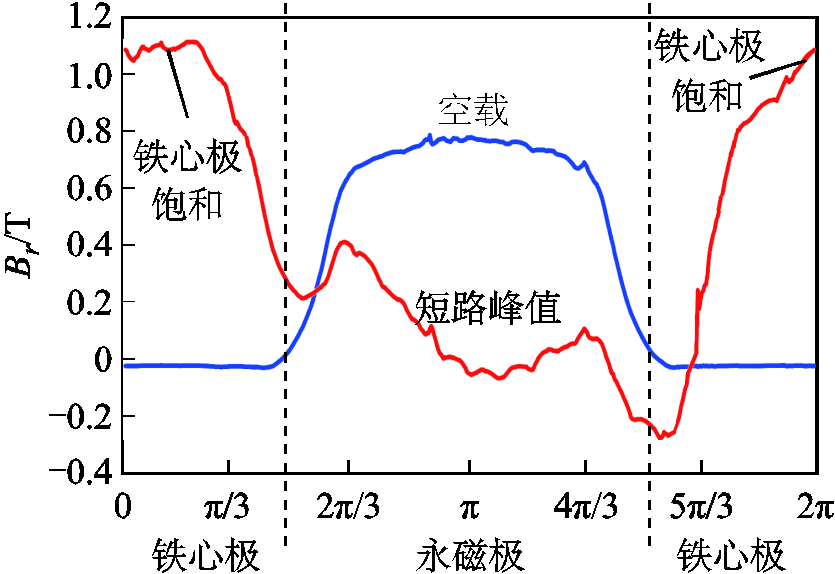
图8 辅助部分径向气隙磁通密度波形
Fig.8 Radial air gap magnetic density waveform of the auxiliary part
利用三维有限元模型分别对辅助部分定子齿部铁心线性以及非线性情况下的短路电流峰值进行计算，计算结果见表3。
表3 三维有限元短路峰值计算结果
Tab.3 Three dimensional finite element short circuit peak calculation results
模型短路电流峰值/A误差（%） 齿部非线性9 631.6-5.0 齿部线性9 150.2
在短路过程中，电机辅助部分定子齿部磁路将发生饱和，在不考虑磁路饱和的情况下，将会导致电机电感参数比实际的大，进而使得动态模型计算的电机短路电流峰值变小。表3计算结果验证了理论分析的正确性。
本文针对高速交错磁极混合励磁同步发电机直流侧突然短路工况进行分析，可以得到如下结论：
1）高速交错磁极混合励磁电机直流侧短路电流计算如果不考虑实心转轴等导电体涡流效应对暂态性能的影响，将会给计算结果带来较大误差；通过在dq轴上设立阻尼绕组回路来等效模拟涡流效应建立电机动态数学模型能够同时考虑定子导磁套筒、实心转轴、永磁体和铁心极的涡流效应，提高了短路电流的计算精度。
2）高速交错磁极混合励磁电机短路电流的表达式与常规电机具有相同的形式，但参数代表的物理含义有所不同，超瞬态电抗参数体现的是定子导磁套筒、实心转轴、永磁体和铁心极在暂态过程中的阻尼作用。
3）由于具有交错磁极结构，该类电机在短路过程中，原本对于全永磁部分去磁性质的电枢绕组电流，在辅助部分会使得定子齿部磁路饱和；在不考虑磁路饱和情况下计算得到的短路电流会比实际值偏小。
参考文献
[1] 马伟明. 舰船动力发展的方向－综合电力系统[J]. 海军工程大学学报, 2002, 14(6): 1-5, 9. Ma Weiming. Integrated power systems-trend of ship power development[J]. Journal of Naval University of Engineering, 2002, 14(6): 1-5, 9.
[2] Ma Weiming, Wang Dong, Zhang Botao, et al. A high speed induction generator based on power integration techniques[C]//Proceedings of the 40th Annul Conference on Industry Applications, Hong Kong, China, 2005: 2272-2279.
[3] 赵争鸣, 施博辰, 朱义诚. 对电力电子学的再认识——历史, 现状及发展[J]. 电工技术学报, 2017, 32(12): 5-15. Zhao Zhengming, Shi Bochen, Zhu Yicheng. Reconsideration on power electronics: the past, present and future[J]. Transactions of China Electrotechnical Society, 2017, 32(12): 5-15.
[4] 李响, 郭希铮, 游小杰, 等. 一种改进的级联H桥整流器直流电压平衡策略[J]. 电工技术学报, 2017, 32(4): 66-75. Li Xiang, Guo Xizheng, You Xiaojie, et al. An advanced DC voltage balance strategy for cascaded H-bridge rectifier[J]. Transactions of China Electrotechnical Society, 2017, 32(4): 66-75.
[5] 孟凡刚, 骆霁嵘, 高蕾, 等. 基于直流侧有源谐波抑制方法的高功率密度多脉波整流器[J]. 电工技术学报, 2017, 32(19): 134-140. Meng Fangang, Luo Jirong, Gao Lei, et al. A high power density multi-pulse rectifier based on harmonic reduction technology at DC link[J]. Transactions of China Electrotechnical Society, 2017, 32 (19): 134-140.
[6] Jacek F G. Multi-megawatt synchronous generators for airborne applications: a review[C]//Electric Machines & Drives Conference (IEMDC), Chicago, IL, USA, 2013: 626-633.
[7] 张宸菥, 陈立芳, 王维民, 等. 高速电动机损耗分析及温度场计算[J]. 电气技术, 2017, 18 (5): 44-50. Zhang Chenxi, Chen Lifang, Wang Weimin, et al. High speed motor loss analysis and temperature field calculation[J]. Electrical Engineering, 2017, 18 (5): 44-50.
[8] Wang Dong, Ma Weiming, Xiao Fei, et al. A novel stand-alone dual stator-winding induction generator with static excitation regulation[J]. IEEE Transactions on Energy Conversion, 2005, 20(4): 826-835.
[9] 王秀和. 永磁电机[M]. 北京: 中国电力出版社, 2007.
[10] 林楠, 王东, 魏锟, 等. 高速混合励磁发电机的结构及调压性能[J]. 电工技术学报, 2016, 31(07): 19-25. Lin Nan, Wang Dong, Wei Kun, et al. Structure and voltage regulation performance of a high speed hybrid excitation synchronous generator[J]. Transactions of China Electrotechnical Society, 2016, 31(7): 19-25.
[11] 林楠, 王东, 魏锟, 等. 新型混合励磁同步电机的数学模型与等效分析[J]. 电工技术学报, 2017, 32(3): 149-156. Lin Nan, Wang Dong, Wei Kun, et al. Mathematical model and equivalent analysis of a novel hybrid excitation synchronous machine[J]. Transactions of China Electrotechnical Society, 2017, 32(3): 149-156.
[12] 徐敦煌, 王东, 林楠, 等. 失磁故障下交错磁极混合励磁发电机的等效二维解析磁场模型[J]. 电工技术学报, 2017, 32(21): 87-93. Xu Dunhuang, Wang Dong, Lin Nan, et al. An equivalent two-dimensional analytical model for the consequent-pole hybrid-excitation generator with demagnetization fault[J]. Transactions of China Electrotechnical Society, 2017, 32(21): 87-93.
[13] 武洁, 王一丁, 闫浩, 等. 交流调磁双交错混合励磁电机的等效磁路模型[J]. 微电机, 2018, 51(6): 16-21, 49. Wu Jie, Wang Yiding, Yan Hao, et al. Equivalent magnetic circuit model for DCHES machine[J]. Micromotors, 2018, 51(6): 16-21, 49.
[14] 杨成峰, 林鹤云, 刘细平. 新型非对称交错混合励磁同步电机电磁设计[J]. 中国电机工程学报, 2008, 28(24): 82-87. Yang Chengfeng, Lin Heyun, Liu Xiping. Electromagnetic design of a novel asymmetrically stagger hybrid excitation synchronous machine[J]. Proceedings of the CSEE, 2008, 28(24): 82-87.
[15] 杨成峰, 林鹤云. 非对称交错混合励磁爪极同步电机调磁性能三维有限元分析[J]. 东南大学学报(自然科学版), 2007, 37(4): 614-617. Yang Chengfeng, Lin Heyun. 3D finite element analysis for field-control capability of asymmetrically stagger hybrid excitation claw-pole synchronous machine[J]. Journal of Southeast University (Natural Science Edition), 2007, 37(4): 614-617.
[16] 张晓祥, 张卓然, 刘业, 等. 双端励磁内置转子磁分路混合励磁电机设计与转子强度分析[J]. 电工技术学报, 2018, 33(2): 245-254. Zhang Xiaoxiang, Zhang Zhuoran, Liu Ye, et al. Design and rotor strength analysis of a hybrid excitation synchronous machine with dual-direction built-in field windings[J]. Transactions of China Electrotechnical Society, 2018, 33(2): 245-254.
[17] 戴冀, 张卓然, 沐杨, 等. 转子磁分路混合励磁同步电机电枢反应磁场与电感特性研究[J]. 电工技术学报, 2015, 30(12): 276-283. Dai Ji, Zhang Zhuoran, Mu Yang, et al. Armature reaction field and inductance feature analysis of a hybrid excitation synchronous machine with magnetic shunting rotor[J]. Transactions of China Electrotechnical Society, 2015, 30(12): 276-283.
[18] 樊英, 谭超. 内置式交替极永磁同步电机性能及机理研究[J]. 电工技术学报, 2018, 33(11): 2414-2422. Fan Ying, Tan Chao. Analysis of electromagnetic performance and principles in inserted consequent-pole permanent magnet synchronous machines[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 2414-2422.
[19] 杨晨, 白保东, 陈德志, 等. 可变磁通永磁辅助同步磁阻电机设计与性能分析[J]. 电工技术学报, 2019, 34(3): 489-496. Yang Chen, Bai Baodong, Chen Dezhi, et al. Design and analysis of a variable flux permanent magnet assisted synchronous motor[J]. Transactions of China Electro technical Society, 2019, 34(3): 489-496.
[20] 孙玉坤, 于丰源, 袁野, 等. 一种混合双定子磁悬浮开关磁阻电机[J]. 电工技术学报, 2019, 34(1): 1-10. Sun Yukun, Yu Fengyuan, Yuan Ye, et al. A hybrid double stator bearingless switched reluctance motor[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 1-10.
[21] 高景德, 张麟征. 交流电机及其系统的分析[M]. 北京: 清华大学出版社, 2007.
[22] 海世芳, 孙士云, 范小红, 等. 计及频率特性的感应电动机参数变化对负荷特性的影响[J].电力系统保护与控制, 2019, 47(8): 17-25. Hai Shifang, Sun Shiyun, Fan Xiaohong, et al. Influence of induction motor parameter change considering frequency charact eristics on load characteristics[J]. Power System Protection and Control, 2019, 47(8): 17-25.
[23] 马伟明, 胡安, 袁立军. 十二相同步发电机整流系统直流侧突然短路的研究[J]. 中国电机工程学报, 1999, 19(3): 32-37. Ma Weiming, Hu An, Yuan Lijun. Sudden DC-side short circuit of a 12-phase synchronous generator-rectifier system[J]. Proceedings of the CSEE, 1999, 19(3): 32-37.
[24] 汤蕴璆, 梁艳萍. 汽轮发电机的三阶模型和超–超瞬态电抗[J]. 电工技术学报, 2000, 15(1): 7-11. Tang Yunqiu, Liang Yanping. The 3rd order model and sub-subtransient reactances of turbogenerator[J]. Transactions of China Electrotechnical Society, 2000, 15(1): 7-11.
[25] 戈宝军, 林鹏, 陶大军, 等. 多Y绕组同步电机瞬态参数的频域法数值计算[J]. 中国电机工程学报, 2013, 33(6): 120-127, 17. Ge Baojun, Lin Peng, Tao Dajun, et al. Frequency-domain numerical calculation of transient parameters for synchronous alternators with multiple Y-connected windings[J]. Proceedings of the CSEE, 2013, 33(6): 120-127, 17.
[26] 潘超, 米俭, 蔡国伟, 等. 交直流混杂环境下变压器漏电感参数分析方法[J].电机与控制学报, 2019, 23(5): 25-33. Pan Chao, Mi Jian, Cai Guowei, et al. Analysis method of leakage inductance parameters under AC/DC hybrid environment in transformer[J]. Electric Machines and Control, 2019, 23(5): 25-33.
[27] 梁艳萍, 李伟, 王泽宇, 等. 高速感应电机转子涡流损耗的计算方法及影响因素[J].电机与控制学报, 2019, 23(5): 42-50. Liang Yanping, Li Wei, Wang Zeyu, et al. Calculation method and effect factors of eddy current losses in rotor of high speed induction motor[J]. Electric Machines and Control, 2019, 23(5): 42-50.
Analysis and Calculation of DC Side Short-Circuit Current of High-Speed Staggered Pole Hybrid Excitation Generator
Abstract In order to improve the calculation accuracy of the short-circuit current on the DC side of the high-speed staggered pole hybrid excitation synchronous generator (HESG), a dynamic mathematical model of the generator was established by setting up damped winding loops on dq-axis respectively, which could take into account the eddy current effect of stator magnetic sleeve, solid shaft, permanent magnet and iron core pole at the same time. Based on this, the expressions of transient, subtransient inductance and short-circuit current were derived. By comparing with the short-circuit current test results of a high-speed staggered pole HESG, the validity of the model was verified, and the causes of the error were analyzed. It is pointed out that the dynamic saturation phenomenon caused by the staggered-pole structure during the short-circuit process of the generator is one of the main reasons of the error.
keywords：Circular excitation winding, staggered pole, solid shaft, DC side short circuit
中图分类号：TM351
DOI：10.19595/j.cnki.1000-6753.tces.190546
国家自然科学基金资助项目（51690181, 51807202, 51677092, 51707201）。
收稿日期2019-05-17
改稿日期 2019-07-15
吕智勇 男，1994年生，硕士研究生，研究方向为集成化发电技术。E-mail：1564738140@qq.com
王 东 男，1978年生，教授，博士生导师，研究方向为集成化发电技术、电力推进、独立电源系统等方面的研究。E-mail：wangdongl@vip. sina.com（通信作者）
（编辑 郭丽军）