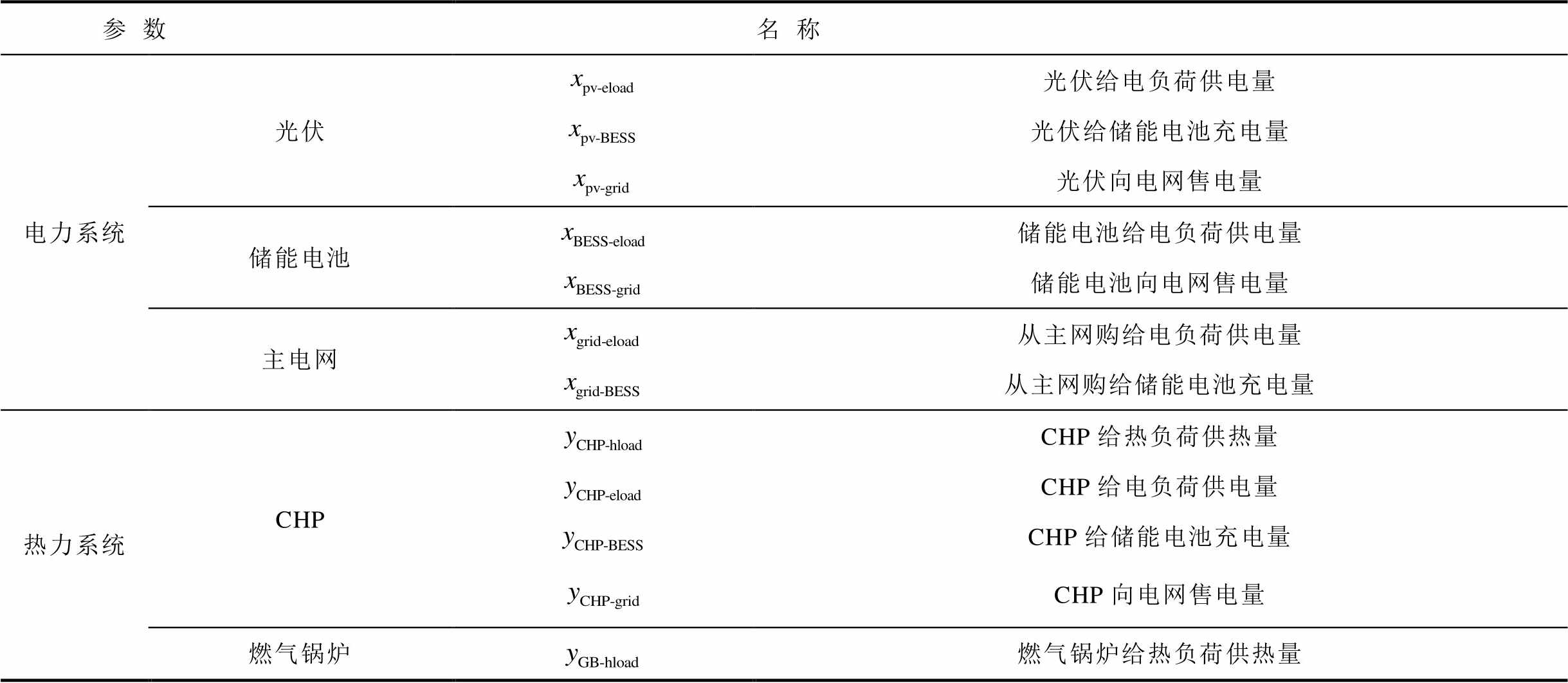
Tab.1 The output variable of each device
参数名称 电力系统光伏光伏给电负荷供电量 光伏给储能电池充电量 光伏向电网售电量 储能电池储能电池给电负荷供电量 储能电池向电网售电量 主电网从主网购给电负荷供电量 从主网购给储能电池充电量 热力系统CHPCHP给热负荷供热量 CHP给电负荷供电量 CHP给储能电池充电量 CHP向电网售电量 燃气锅炉燃气锅炉给热负荷供热量
摘要 为了实现综合能源系统电热网在各自信息隐私保护情况下达到全局最优,该文研究了光伏-储能-热电联产(CHP)综合能源系统的协调优化运行,探讨了在隐私保护前提下运用分解协调优化方法求解的可行性。该文首先建立电热耦合系统的分解优化运行模型。其次,利用Benders分解方法对模型进行求解,将模型分解为热力系统主问题和电力系统子问题,通过两个系统之间迭代计算,得出各系统设备的最优出力分配;然后,研究了基于Benders分解法的系统间交互模式,在尽可能保证主、子问题各自信息有效保护隔离的前提下,两个系统之间只需要交换隐私化后的参数及Benders约束,最大程度地保护了电/热系统的信息隐私。最后,利用三个典型场景下的算例对比分析验证了该文方法的合理性。
关键词:综合能源系统 Benders分解 信息隐私保护 协调优化运行
随着可再生能源的迅速发展带来的能源市场的变革,多能互补分布式能源系统成为研究的重要方向[1-3]。最典型的综合能源系统(Integrated Energy System,IES)优化运行即是通过热电联产机组和热泵等能源转换设备,将热力系统和电力系统耦合起来,从而提高综合能源利用率[4]。近年来兴起的能源互联网是在多能互补系统的基础上,结合互联网等技术,实现信息与物理系统间的深度融合[5],是一种典型的信息物理融合系统(Cyber-Physical System, CPS)。
在能源互联网分布式运行体系下,电网调度中心的主导地位将逐渐弱化,能源互联网面临着去中心化的发展趋势。然而目前综合能源系统去中心化的交易模式面临诸多挑战[6],其中很大原因是由于目前综合能源系统的运行中存在信息安全的问题。
由于综合能源系统包含设备多,覆盖的各能源网络广泛,在引入互联后将产生很大的安全风险。综合能源系统中,电网和热网之间的信息保护和隐私安全就受到了广泛关注。文献[7]提出综合能源各系统将由不同能源供应商负责,从而不愿向其他系统传递自身信息。文献[8]分析提出目前尚未形成成熟的多能流信息安全风险控制方法,但未提出具体的解决方案。文献[9]对系统的信息-能量流进行量化计算,但是其只针对电力系统,未考虑多能源系统。针对现有的综合能源系统优化运行的信息安全性研究,还存在一些问题和不足:①若一个能源网络遭到信息攻击导致信息泄漏,其他能源网络甚至整个系统的信息都会泄露;②各能源网络希望尽可能地保护自己系统和设备的信息隐私[8]。
综合以上问题,综合能源系统互联化的发展使得存在多个区域综合能源系统和大电网相连的情况,由于用户隐私、数量规模等原因,不适宜将热力系统内详细数据上传到电力系统调控中心。因此,在区域综合能源系统中,电力系统与热力系统有一定相互关联,但又保持各自的独立性,在这样的情况下,两者之间的信息是无法充分且透明地实现交互化的,系统信息的隐私保障是必要的。由此,如何对电热独立的系统进行优化,达到整体的效益最大化,是一个具有挑战性的问题。为解决电热隐私保护情况下综合能源系统优化运行问题,通常采用Benders分解方法。Benders分解方法所要求的协调只需要一些隐私加密化的信息,能够将优化问题分解,独立优化求解并通过反复迭代达到整体效益的最优。
对于Benders分解方法在综合能源系统运行优化的研究,文献[10]建立的电气集成能源系统的统一规划运行模型利用了Benders分解解耦,但其重点只考虑了电网;文献[11-12]考虑了综合电热网的区域能源供给系统,但实现的是投资决策问题和运行优化问题的解耦,而不是各能源主体之间的解耦;文献[13]将多能系统分解为热力系统主问题和电力系统子问题,但其只是将Benders分解方法作为求解方法,未展开其对两个系统间信息隔离的具体探讨;文献[14]利用Benders分解方法将大量的网络潮流约束与其他约束条件解耦,重点关注的是Benders分解方法降低求解维度以减少计算量的优势;文献[15]将空调暖通系统(Heating,Ventilation,Air-Conditioning and Cooling, HAVC)开关状态和储能电池充放电状态分解计算,但是其Benders分解主要用于处理光伏输出的不确定性与HAVC系统的交互影响。
因此,本文总结了对电热系统在信息隐私保护的情况下进行各自独立的优化,两者的迭代信息遵循一定的机制准则,能够实现总体效益最大化。这是可以由Benders分解优化原理所保证的。本文基于Benders分解法,在调度中心信息加密化的情况下,在实现各系统优化运行的同时,能够保护综合能源系统中不同能源网络或不同设备主体之间的信息隐私,减少信息共享,保护信息安全。
本文首先对综合能源系统的电热系统优化运行模型分别进行建模;然后基于Benders分解方法求解模型并研究系统信息交互机制;最后针对曼彻斯特大学春季某典型日的数据进行了算例分析,验证了本文方法的有效性。
本文研究的并网综合能源系统,考虑设备包括电力系统的光伏(Photovoltaic, PV)、储能电池(Battery Energy Storage System, BESS)和热力系统的燃气锅炉(Gas Boiler, GB)和热电联供机组(Combined Heat and Power, CHP),其中CHP作为电热耦合元件通常归入热力系统中考虑[16],针对各设备出力的具体变量设置见表1,各设备之间的能量流动关系如图1所示。
表1 各设备出力变量表
Tab.1 The output variable of each device

参数名称 电力系统光伏光伏给电负荷供电量 光伏给储能电池充电量 光伏向电网售电量 储能电池储能电池给电负荷供电量 储能电池向电网售电量 主电网从主网购给电负荷供电量 从主网购给储能电池充电量 热力系统CHPCHP给热负荷供热量 CHP给电负荷供电量 CHP给储能电池充电量 CHP向电网售电量 燃气锅炉燃气锅炉给热负荷供热量
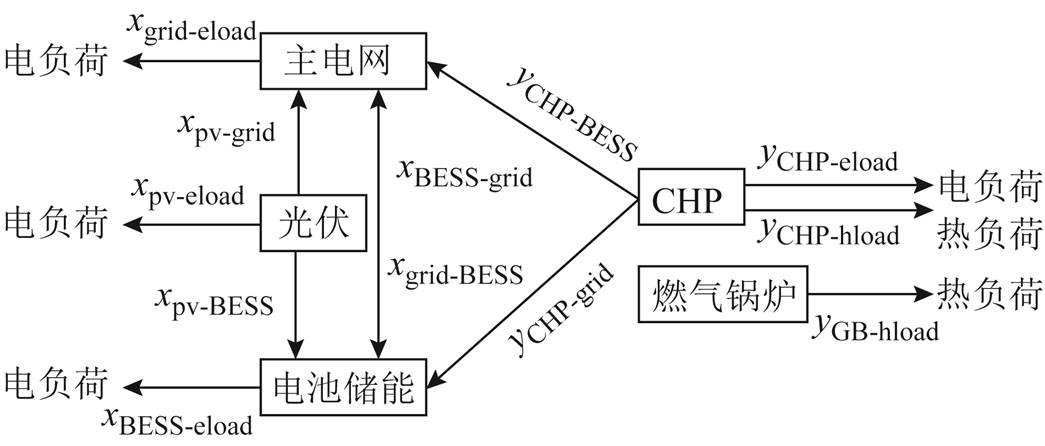
图1 设备能量流动关系
Fig.1 Energy flows between devices
为了实现电热解耦,本文利用Benders分解方法将IES模型分解为热力系统主问题和电力系统子问题,由于热力系统和电力系统各自优化平等独立,不同系统作为主问题只是使得迭代第一步求解方产生改变,初始化步骤的不同不影响主、子问题迭代的最终收敛,因此将热力系统还是电力系统作为主问题不影响最终结果,本文采用热力系统为主问题。Benders分解方法的原理将在第2节详细阐述。模型具体分解优化架构如图2所示。对于电力系统子问题,固定热能单元各设备的出力,影响电力净负荷曲线,从而影响电能各设备运行。对于热力系统主问题,回代电能单元各设备出力和Benders约束,影响CHP、燃气锅炉出力[17]。
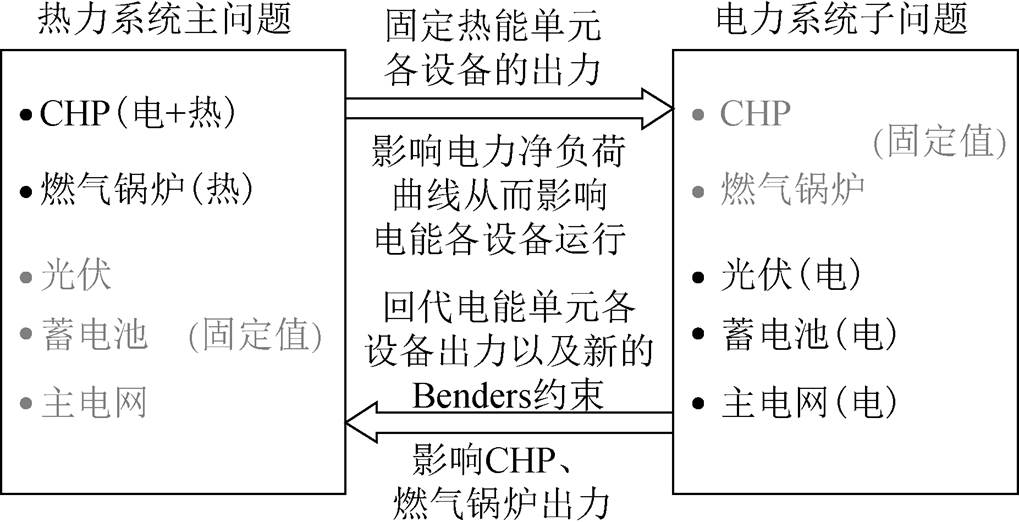
图2 基于Benders分解的优化架构
Fig.2 The optimization architecture diagram based on Benders decomposition
基于图1设置的电热综合能源系统变量类型变量,将变量划分至主问题和子问题,即热力系统设备出力的变量y为主问题变量,电力系统设备出力的变量x为子问题变量。具体变量划分原则如图3所示。这样的划分原则使两个系统只需要交互系统最优出力及Benders 割约束,两个系统之间有效保护的信息和共享的信息在2.3节和2.4节中将会具体分析。因此,该方法能够在优化运行的同时,保证两个系统的隐私性。
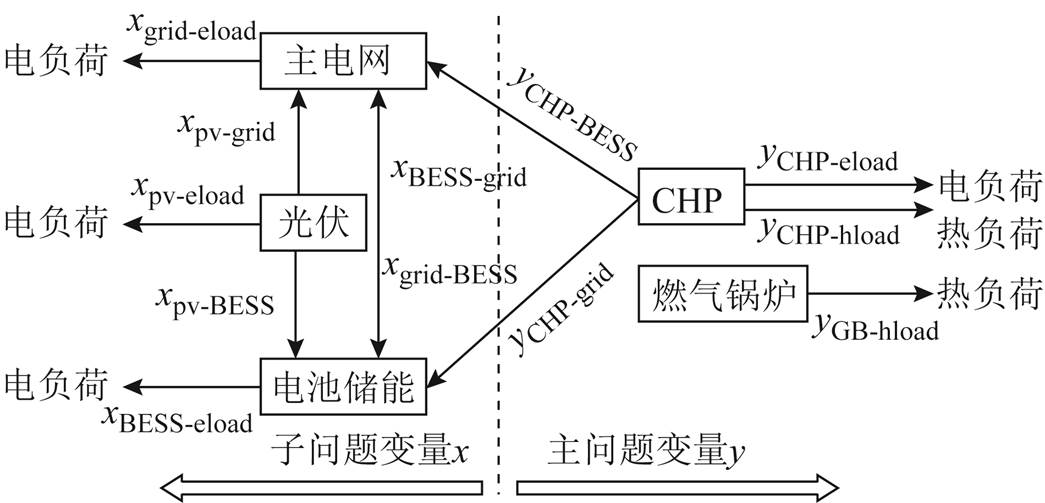
图3 Benders主子问题变量划分
Fig.3 Division of variables of master problem and subproblem in Benders decomposition
1.3.1 目标函数
本文以最小化经济运行成本为目标,由于热力系统和电力系统需要在各自优化的基础上迭代传递耦合信息,因此在模型建立时,分为热力系统和电力系统两个部分建立[18]。
1)热力系统目标函数
对于热力系统,其目标函数fy包括燃料成本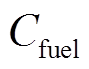 、主电网交互收益
、主电网交互收益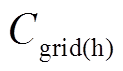 和维护成本
和维护成本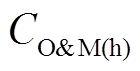 。
。
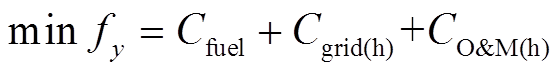 (1)
(1)(1)燃料成本
对于CHP和燃气锅炉,均通过消耗天然气产生电能和热能,所产生的相应的燃料成本计算公式为
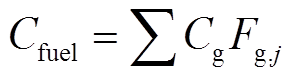 (2)
(2)
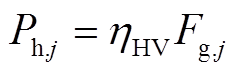 (3)
(3)
式中,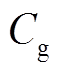 为燃气价格;
为燃气价格;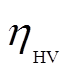 为天然气热值;
为天然气热值;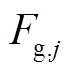 为燃气消耗总量;
为燃气消耗总量;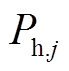 为生成热量;j的取值代表不同设备,1代表CHP,2代表燃气锅炉。由此可得CHP和燃气锅炉的燃气消耗量分别为
为生成热量;j的取值代表不同设备,1代表CHP,2代表燃气锅炉。由此可得CHP和燃气锅炉的燃气消耗量分别为
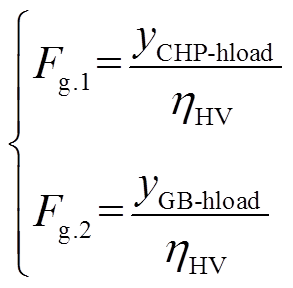 (4)
(4)
(2)主电网交互收益
热力系统中CHP发电可以向主电网售电获得收益,其交互收益计算公式为
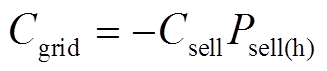 (5)
(5)式中,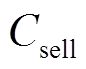 为售电价;
为售电价;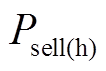 为热力系统向主电网售电功率,其具体表达式为
为热力系统向主电网售电功率,其具体表达式为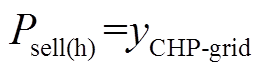 。
。
(3)维护成本
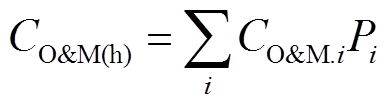 (6)
(6)式中,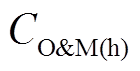 为单位出力的维护成本;
为单位出力的维护成本;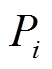 为设备在各时段的总出力值,其中i的取值代表不同设备,1代表CHP,2代表燃气锅炉。对应变量表列出
为设备在各时段的总出力值,其中i的取值代表不同设备,1代表CHP,2代表燃气锅炉。对应变量表列出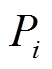 具体函数形式为
具体函数形式为
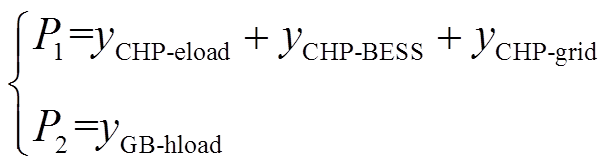 (7)
(7)
2)电力系统目标函数
对于电力系统,其目标函数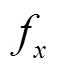 包括主电网交互收益Cgrid(e)和维护成本
包括主电网交互收益Cgrid(e)和维护成本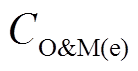 。
。
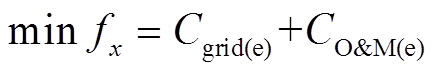 (8)
(8)(1)主电网交互收益
系统可以由从主电网购电和向主电网售电的差价中获得收益,其交互收益计算公式为
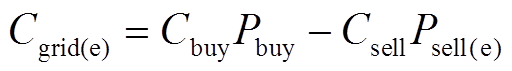 (9)
(9)式中,Cbuy为购电价;Pbuy和Psell(e)分别为电力系统从主电网购电功率和向主电网售电功率,其具体表达式为
 (10)
(10)
(2)维护成本
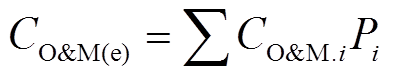 (11)
(11)式中,i的取值为3时代表光伏,为4时代表储能电池[19]。对应变量表列出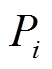 具体函数形式为
具体函数形式为
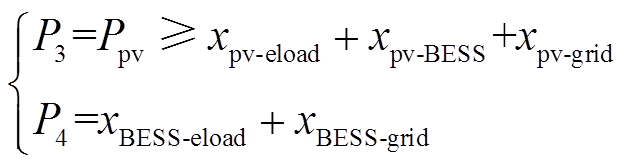 (12)
(12)
式中,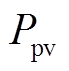 为光伏发电量。
为光伏发电量。
1.3.2 约束条件
1)电力系统约束
电力系统约束不含热力系统变量的电力系统内部约束,其表达式为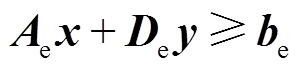 ,其中De为零。
,其中De为零。
(1)光伏功率约束
光伏总出力值受光伏发电功率约束为
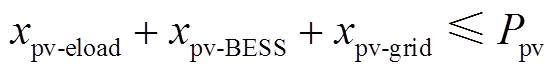 (13)
(13)(2)主电网购电功率约束
系统自发电量上网或从电网购电时,线路存在交互功率约束。
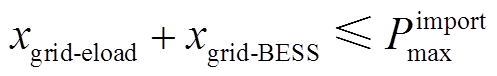 (14)
(14)式中,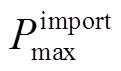 为从电网购入的最大功率。
为从电网购入的最大功率。
(3)储能电池最大放电功率约束
储能电池需满足功率平衡约束,放电功率由供给电负荷和售给主电网供电量构成。
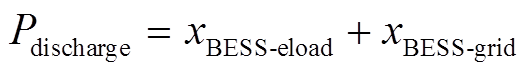 (15)
(15)储能电池在每个时段的放电功率也存在最大值,即最大充放电功率。
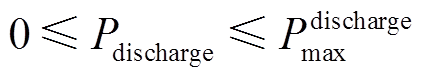 (16)
(16)
式中,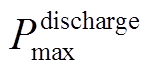 为最大放电功率。
为最大放电功率。
2)热力系统约束
热力系统约束不含任何电力系统变量的热力系统内部约束,其表达式为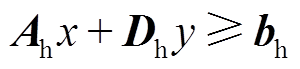 ,其中
,其中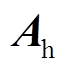 为零[20]。
为零[20]。
(1)热功率平衡约束
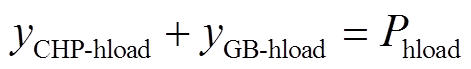 (17)
(17)式中,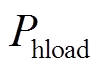 为热负荷。
为热负荷。
(2)CHP运行约束
CHP燃气轮机的发热功率和发电功率之比为定值,此定值即热电比,即热功率和电功率存在固定的函数关系。
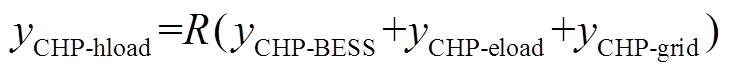 (18)
(18)式中,R为热电比。
同时,CHP存在出力上限,受额定功率影响。
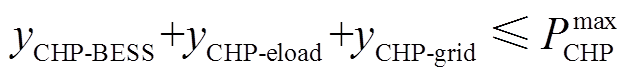 (19)
(19)式中,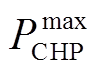 为CHP出力上限。
为CHP出力上限。
其次,燃气轮机运行时会受到爬坡约束的限制,即燃气轮机的发电功率要满足向上和向下爬坡速率。
 (20)
(20)式中,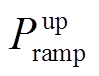 和
和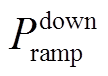 分别为最大增幅和最大降幅(向上/下爬坡速率);t为运行时刻。
分别为最大增幅和最大降幅(向上/下爬坡速率);t为运行时刻。
3)电热耦合约束
电热耦合约束即关联热力系统变量和电力系统变量的约束条件。其表达式为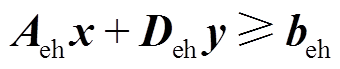 [21]。
[21]。
(1)电功率平衡约束
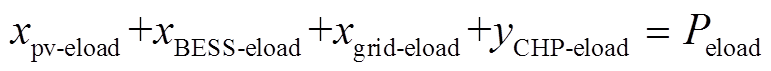 (21)
(21)式中,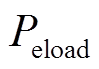 为电负荷。
为电负荷。
(2)主电网售电功率约束
系统自发电量上网或从电网购电时,线路存在交互功率约束。
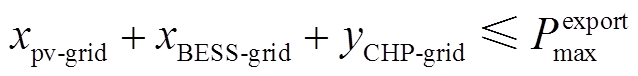 (22)
(22)式中,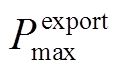 为向主电网售出的最大功率。
为向主电网售出的最大功率。
(3)储能电池最大充电功率约束
储能电池需满足功率平衡约束,充电功率由光伏、主电网和CHP构成。
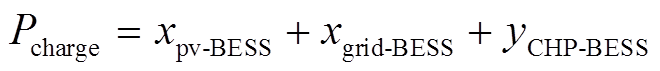 (23)
(23)储能电池在每个时段的充电功率也存在最大值,即最大充电功率,即
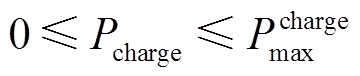 (24)
(24)
式中,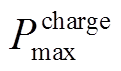 为最大充电功率。
为最大充电功率。
(4)储能电池电量约束
此外,储能电池还存在电量约束,S(t)表示t时刻荷电状态(State of Charge, SOC),即反映储能电池剩余电量。
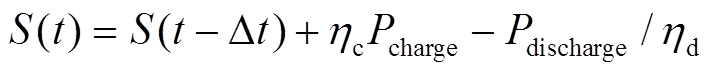 (25)
(25)式中,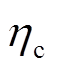 和
和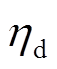 分别表示充、放电效率。
分别表示充、放电效率。
储能电池在每个时段荷电状态存在上下限,即
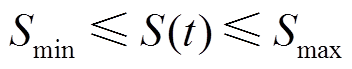 (26)
(26)式中,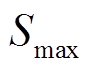 和
和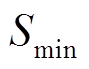 分别为荷电量最大值和最小值。
分别为荷电量最大值和最小值。
在总运行周期内也需要满足首末状态一致,即
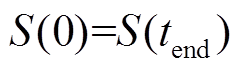 (27)
(27)
在综合能源系统中电热松散耦合的情况下,综合能源系统的优化可以由Bender分解法作为技术、理论支撑。本文由Benders分解法证明推论获得电热联合运行的准则,电热系统在遵循准则的前提下,各自优化,传递加密后的变量,以实现隐性保护下的整体社会效益最大。
Benders分解方法是求解大规模线性优化问题的典型方法,其一般求解原理如图4所示。对于整体优化原问题,将其分解为主问题和子问题,通过主子问题各自优化、传递信息、反复迭代的过程进行整体优化,迭代后的最终解即为原整体问题的最优解[22]。特别地,子问题要转化为其对偶形式求解,图中u为子问题变量x的对称变量,主、子问题之间传递的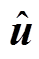 、
、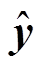 、
、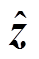 分别为变量u、y、z求解后的定值。
分别为变量u、y、z求解后的定值。
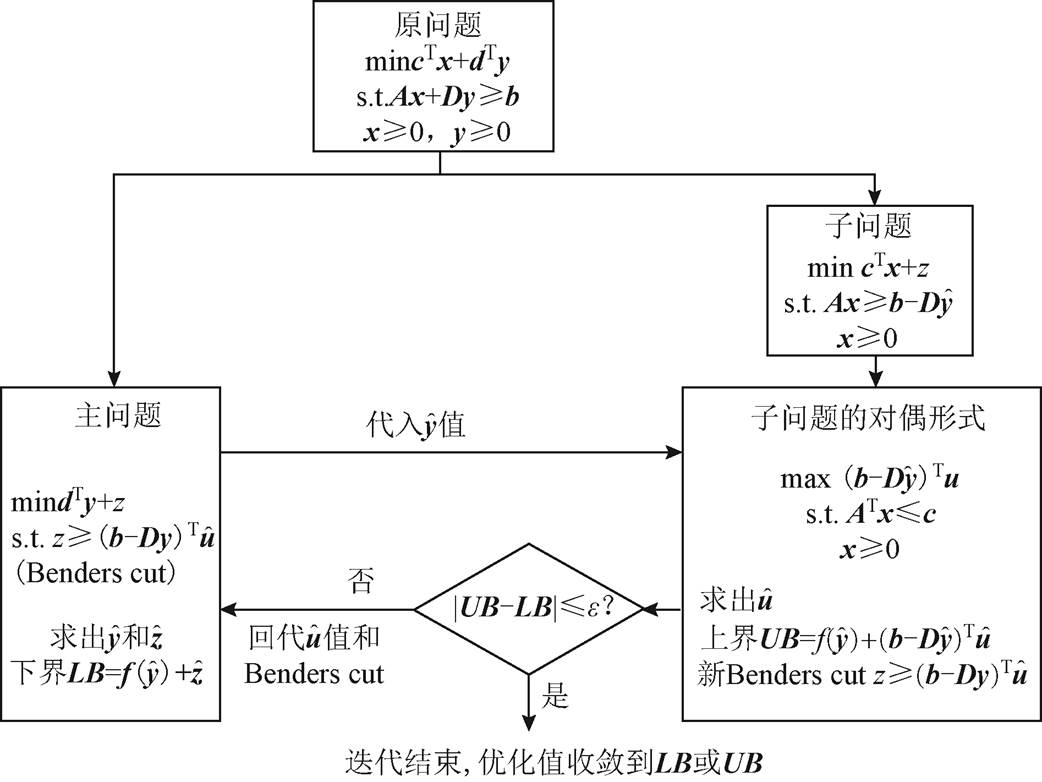
图4 Benders分解算法的模型求解原理
Fig.4 The resolution principles of Benders decomposition method
对应图4,由第1节模型可知,电力系统目标函数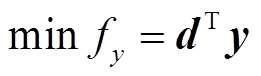 、热力系统目标函数
、热力系统目标函数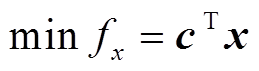 、电力系统约束
、电力系统约束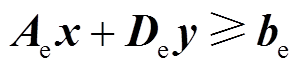 、热力系统约束
、热力系统约束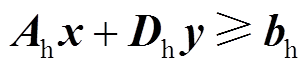 和电热耦合约束
和电热耦合约束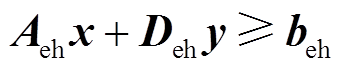 中,电力系统子问题内部信息为d、
中,电力系统子问题内部信息为d、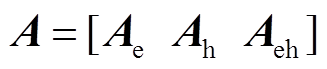 和be,热力系统主问题内部信息为c、
和be,热力系统主问题内部信息为c、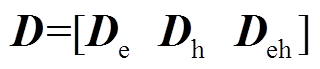 和bh。beh可成为任意一方内部信息,本文将其作为电力系统内部信息。
和bh。beh可成为任意一方内部信息,本文将其作为电力系统内部信息。
利用Benders分解法中主问题和子问题各自优化的特性,基于图4将原Benders分解法进行改进,通过加密的方式实现信息隐私化,将子问题中包含的主问题信息保护隔离,主问题中包含的子问题信息保护隔离。改进方法如下。
1)子问题参数处理
由图4可知,主问题中不含子问题参数,而子问题中含有主问题参数D和bh,因此首先处理子问题参数。
将子问题中的约束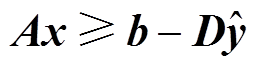 按热力系统内部约束、电力系统内部约束和电热耦合约束拆解为三部分,即
按热力系统内部约束、电力系统内部约束和电热耦合约束拆解为三部分,即
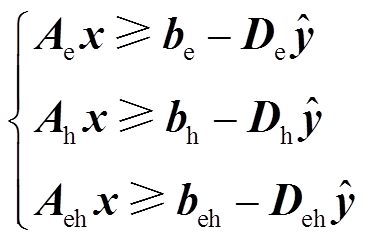
式中,令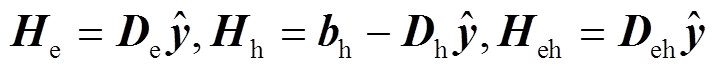 。上式可改写为
。上式可改写为
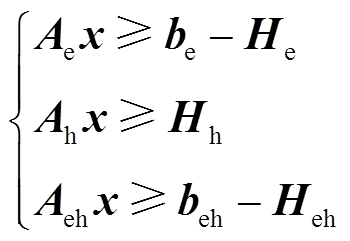
进而,子问题约束可以改写为
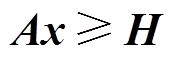
式中,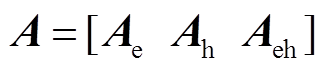 ,
,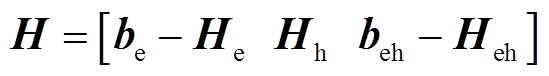 。特别地,
。特别地,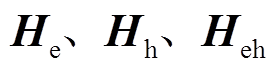 是在热力系统主问题中先生成后再传递给子问题的封闭变量,是为了保护热力系统内部的bh和D信息。
是在热力系统主问题中先生成后再传递给子问题的封闭变量,是为了保护热力系统内部的bh和D信息。
由此形成的子问题中不含bh,仅含be和beh。
2)Benders约束处理
在子问题中生成新的Benders约束时,由于电力系统子问题中无bh信息,因此子问题内仅生成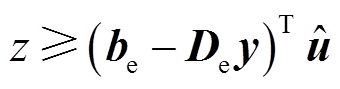 和
和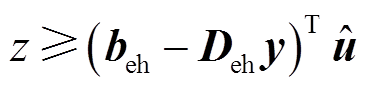 两类Benders割,令这两类Benders割为子问题Benders割。剩下的
两类Benders割,令这两类Benders割为子问题Benders割。剩下的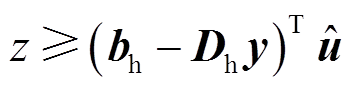 在热力系统主问题中生成,令其为主问题Benders割。
在热力系统主问题中生成,令其为主问题Benders割。
由此,生成完整Benders约束步骤部分在子问题中完成,部分在主问题中完成。
3)原问题虚拟化
由于本文系统没有能够完全地获得两个系统完整信息的统一管理机构,对应到数学形式中即无原问题。因此改进后的Benders分解法首先建立主问题和子问题,主、子问题各自优化,反复迭代相关变量或参数,迭代过程趋近于一个虚拟原问题。而此虚拟原问题即代表综合主问题和子问题的整体效益的最大化。虚拟原问题的最小值即主问题和子问题各自优化趋近的最小值。
由此,信息隐私化后的Benders分解法可以描述如图5所示。
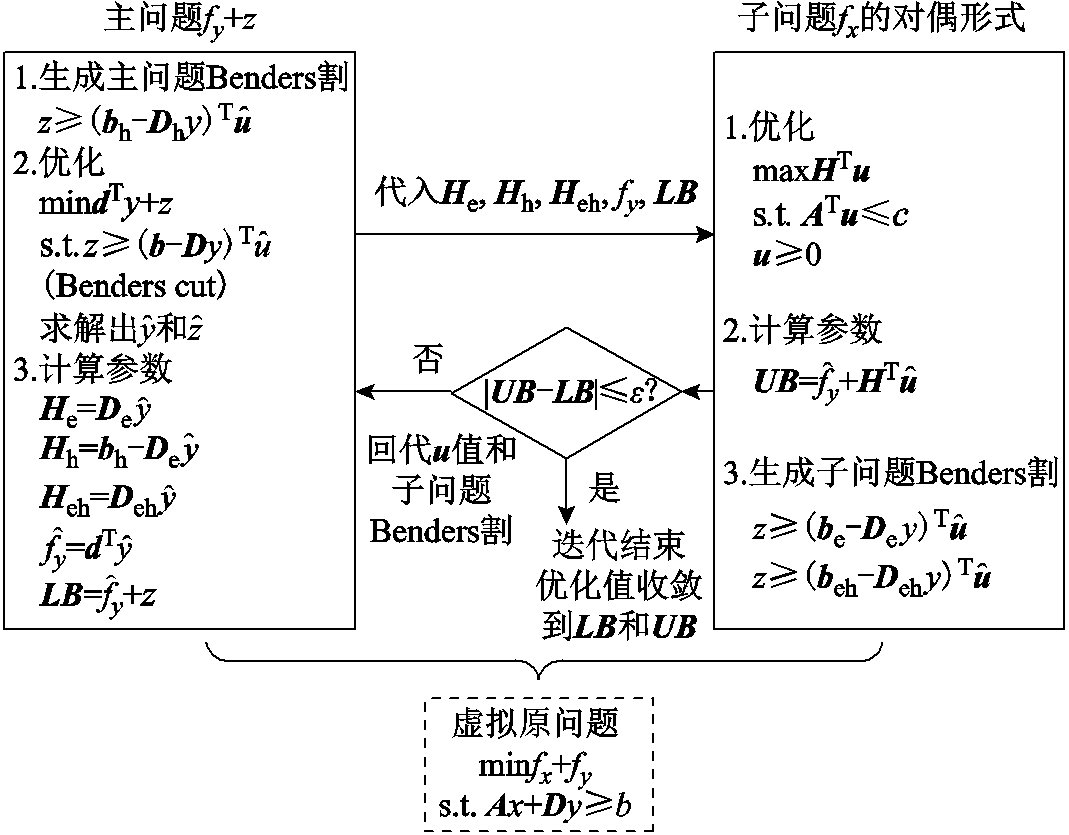
图5 信息隐私化后的Benders分解算法的模型求解原理
Fig.5 The resolution principles of the privatized Benders decomposition method
对于电力系统,将其设置为子问题(28),子问题再形成其对偶问题(29)。
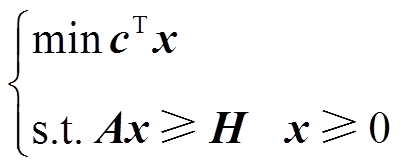 (28)
(28)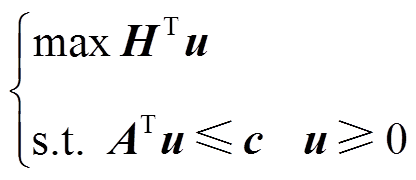 (29)
(29)
式中,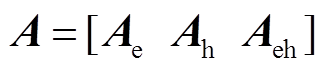 ,
, 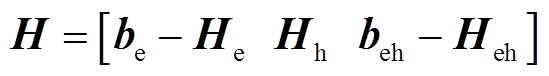 。而
。而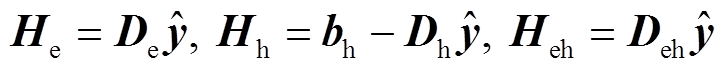 。
。
特别地,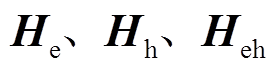 是在主问题中生成后再传递给子问题的封闭变量,是为了保护热力系统主问题内部的
是在主问题中生成后再传递给子问题的封闭变量,是为了保护热力系统主问题内部的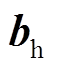 和D信息。
和D信息。
对于热力系统,将其设置为
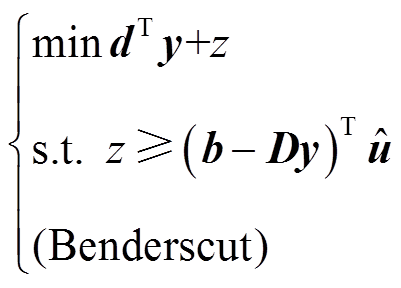 (30)
(30)式中,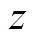 为两个系统间的影响系数,代表电力系统对热力系统的影响及约束。
为两个系统间的影响系数,代表电力系统对热力系统的影响及约束。
在图5的信息隐私化的迭代交互模式下,系统有效保护的信息总结见表2。
对于迭代的收敛判定,为了完成个体优化同时达到整体社会效益最优,在各自优化的进行过程中,各自的优化值要趋向于一个整体优化值,此时可以构建一个虚拟原问题,即综合主子问题整体的原问题,此原问题为
表2 信息隐私化交互模式下的有效保护信息
Tab.2 Protected information in the interaction mode
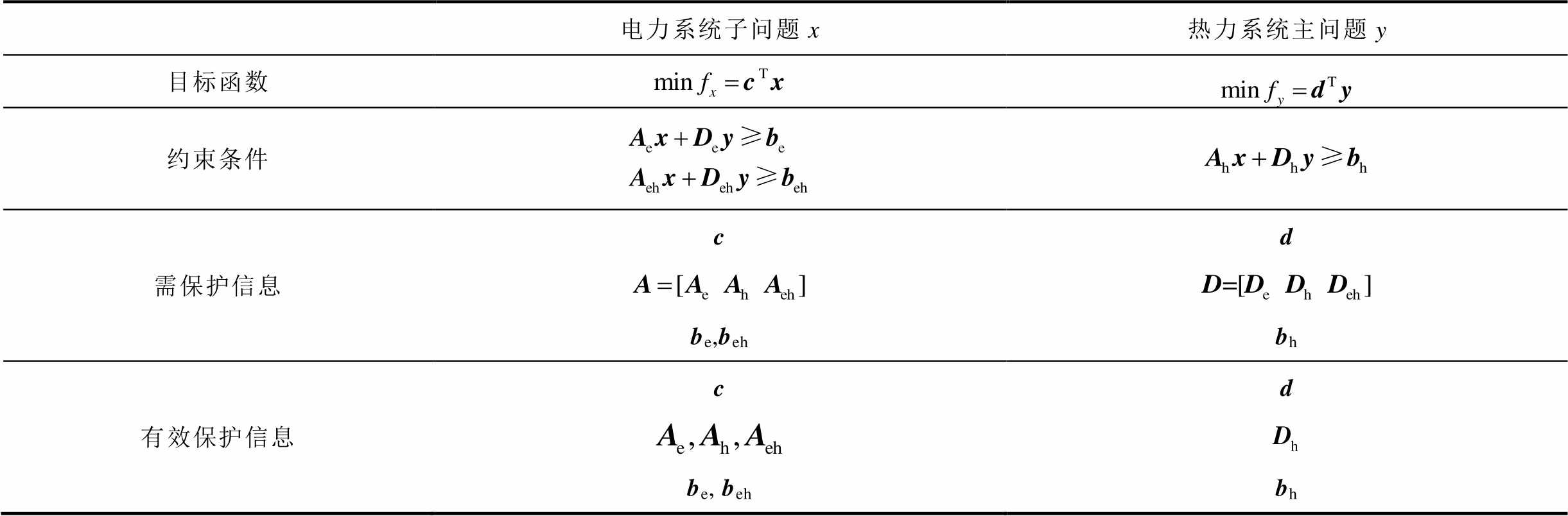
电力系统子问题x热力系统主问题y 目标函数 约束条件 需保护信息cbe,behdbh 有效保护信息cbe, behdbh
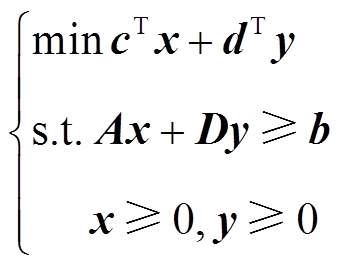 (31)
(31)式中,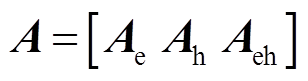 ,
,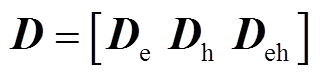 ,
,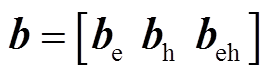 。该原问题综合了主问题目标函数
。该原问题综合了主问题目标函数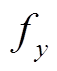 和子问题目标函数
和子问题目标函数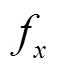 ,同时也综合了主子问题约束条件。将原问题目标函数作为主问题和子问题最终收敛值的目标,即设置主问题中
,同时也综合了主子问题约束条件。将原问题目标函数作为主问题和子问题最终收敛值的目标,即设置主问题中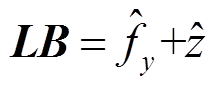 ,子问题中
,子问题中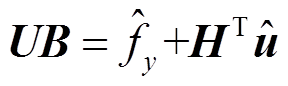 ,收敛条件为
,收敛条件为
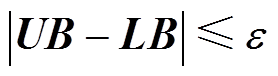 (32)
(32)
由此形成的Benders分解迭代求解流程框图如图6所示。
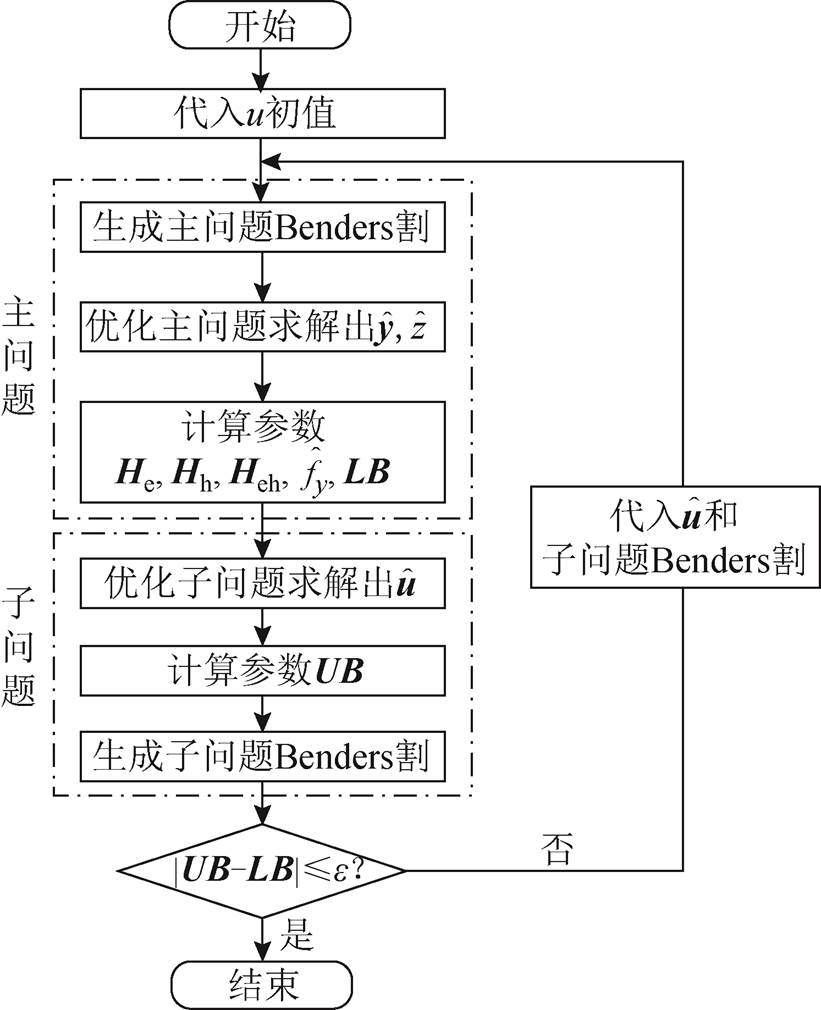
图6 Benders分解迭代求解流程
Fig.6 The flow chart of the improved Benders decomposition method
由表2中总结的信息隐私化交互模式下的有效保护信息,需研究其物理意义,从模型的目标函数和约束条件来分别进行分析。
2.3.1 目标函数分析
对于目标函数,由于Benders分解中主、子问题目标函数分别为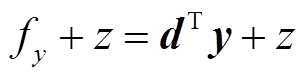 和
和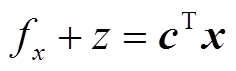 ,所以首先将两个系统目标函数的
,所以首先将两个系统目标函数的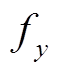 和
和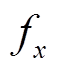 按变量形式写为
按变量形式写为
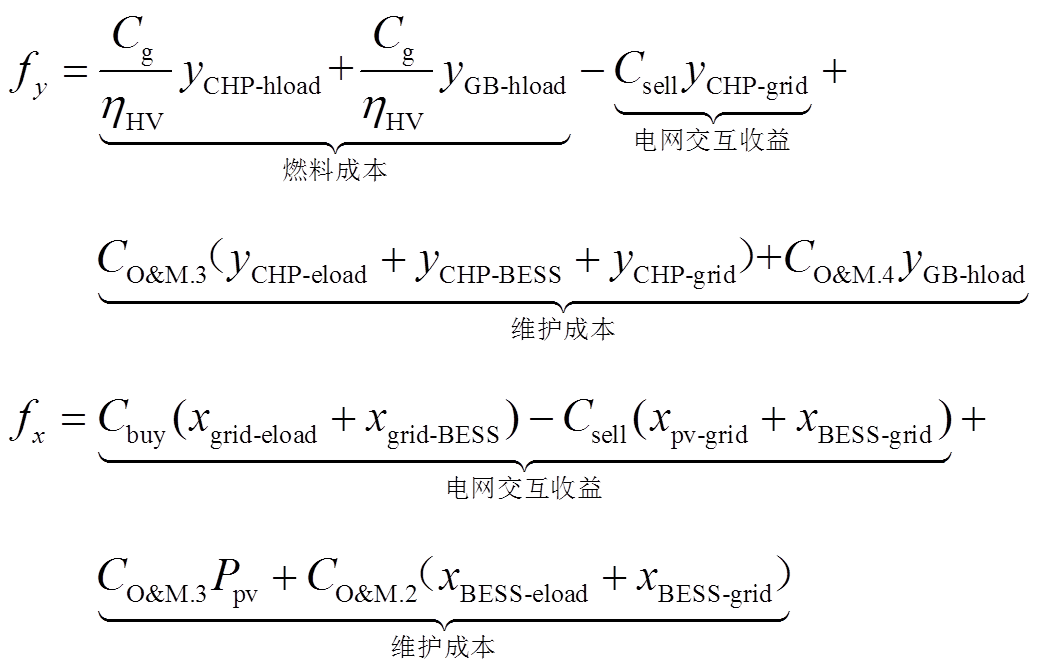 (33)
(33)整理可得,y变量的系数矩阵dT为
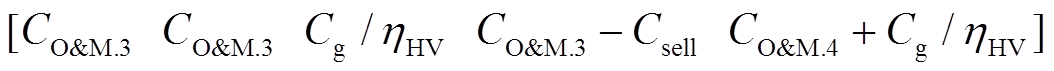 (34)
(34)
x变量的系数矩阵cT为
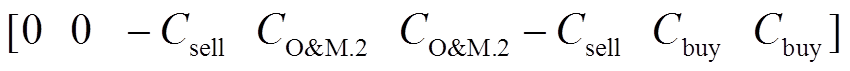 (35)
(35)由系数矩阵可以看出,对于有效保护信息:①dT中不含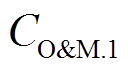 、
、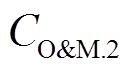 和
和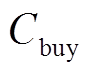 ,即电力系统的光伏和储能电池的维护成本信息以及购电价被有效隔离;②cT中不含
,即电力系统的光伏和储能电池的维护成本信息以及购电价被有效隔离;②cT中不含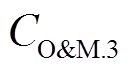 、
、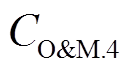 、
、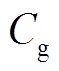 和
和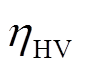 ,即热力系统的CHP和燃气锅炉的维护成本信息、燃气价格和热值信息也被有效隔离。
,即热力系统的CHP和燃气锅炉的维护成本信息、燃气价格和热值信息也被有效隔离。
对于必须共享的信息dT和cT,均包含的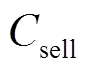 ,为无法隔离的共享信息。
,为无法隔离的共享信息。
2.3.2 约束条件分析
对于约束条件方程式(13)~式(27),将约束条件中x变量和y变量分离开,以探讨A、D、b中所包含的系统信息的物理意义。各个约束条件的热电变量分离见表3。
从表中可以看出,对于有效保护信息:①A中隐藏信息有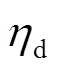 ,因此电力系统的储能电池放电效率信息被有效隔离;②Dh中隐藏信息有
,因此电力系统的储能电池放电效率信息被有效隔离;②Dh中隐藏信息有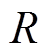 ,因此热力系统中热电比信息被有效隔离;③b中隐藏信息包括电力系统隐藏的be和beh与热力系统隐藏的bh。从表3可以看出
,因此热力系统中热电比信息被有效隔离;③b中隐藏信息包括电力系统隐藏的be和beh与热力系统隐藏的bh。从表3可以看出
表3 电热变量分离处理的约束条件
Tab.3 Constraints after the separation of electrical and thermal variables

式号约束名称电力系统变量热力系统变量等式/不等式常数b 电力系统约束(13)光伏发电功率约束— (14)从主网购电约束— (16)储能电池最大放电功率约束— 热力系统约束(17)热功率平衡约束— (18)CHP热电比约束— (19)CHP出力上限约束— (20)CHP爬坡约束— (20)CHP爬坡约束— 电热耦合约束(21)电功率平衡约束 (22)向主网售电约束 (24)储能电池最大充电功率约束 (26)储能电池电量约束
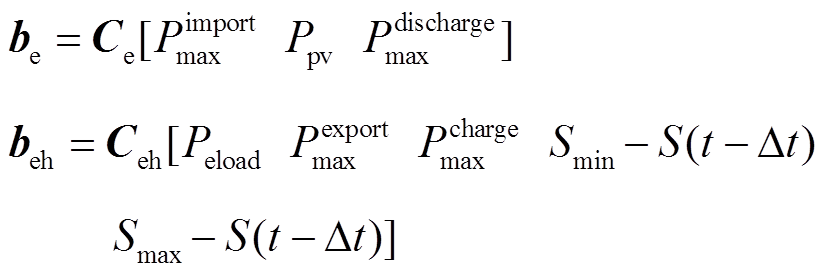
式中,Ceh、Ce为常数向量,因此电力系统的主网最大购售电功率、光伏发电量、电负荷数据、储能电池最大充放电功率、荷电量上下限被有效隔离。
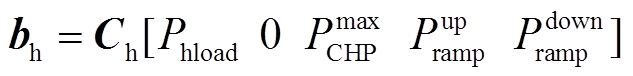
式中,Ch为常数向量。则电力系统的热电比、燃气锅炉组发电功率最大增幅和最大降幅、CHP出力上限被有效隔离。
对于必须共享信息:①De中不包含任何系统参数,无共享信息;②Deh中包含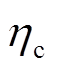 ,即电力系统的储能电池充电效率信息为必须共享的信息。
,即电力系统的储能电池充电效率信息为必须共享的信息。
2.3.3 有效保护信息物理意义总结
综合对目标函数和约束条件的分析,将电网和热网各自有效保护信息和共享信息总结见表4。特别地,共享信息中热力系统的设备出力和数据参数是在被加密化之后再传递给电力系统的,是加密化的信息共享。
在2.2节描述的主、子问题交互迭代模式下,总结得出电力系统和热力系统必须遵循以下准则:
表4 信息隐私化交互模式下的有效保护信息物理意义
Tab.4 The physical meaning of Protected information in the interaction mode
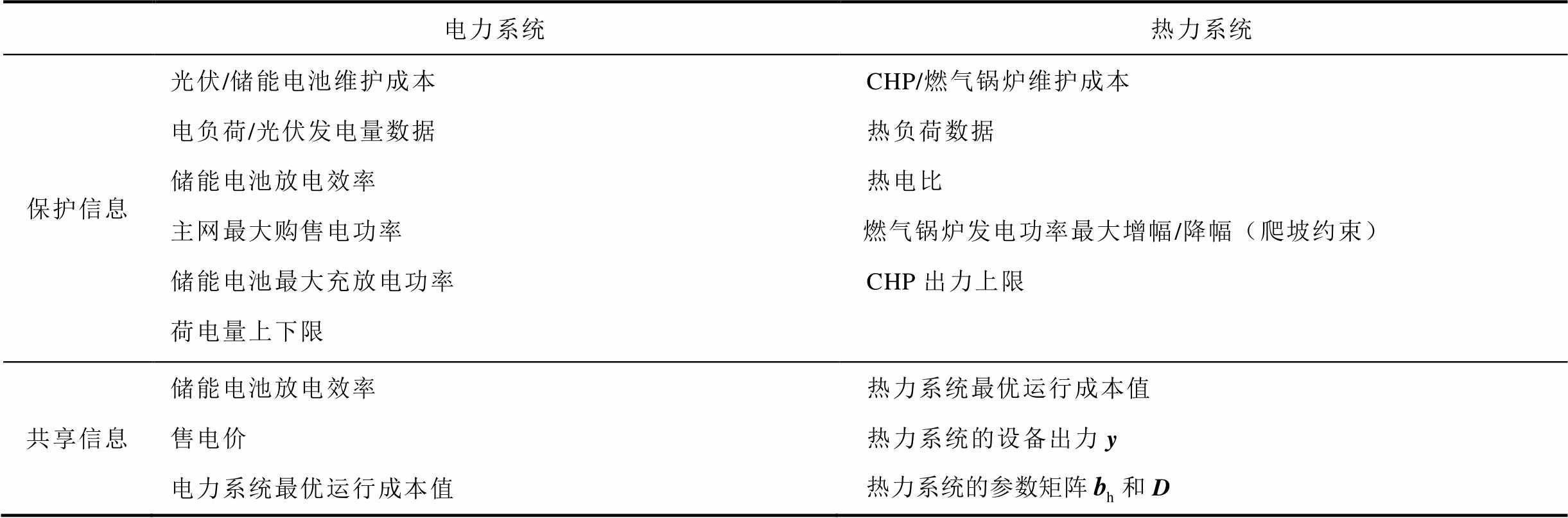
电力系统热力系统 保护信息光伏/储能电池维护成本电负荷/光伏发电量数据储能电池放电效率主网最大购售电功率储能电池最大充放电功率荷电量上下限CHP/燃气锅炉维护成本热负荷数据热电比燃气锅炉发电功率最大增幅/降幅(爬坡约束)CHP出力上限 共享信息储能电池放电效率售电价电力系统最优运行成本值热力系统最优运行成本值热力系统的设备出力y热力系统的参数矩阵和D
(1)对于热力系统,在Benders分解过程中每次迭代时,向电力系统送出信息为:本设备优化后计算得出的H参数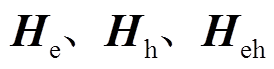 热力系统局部最优解(上界UB)。
热力系统局部最优解(上界UB)。
(2)对于电力系统,在Benders分解过程中每次迭代时,向热力系统返回信息为:电网出力分配对偶化后的变量u、电力系统局部最优解(下界LB)、新形成的子问题Benders割。
在这样的交互模式下,能够有效保护2.3节所描述的信息,仅需要共享H参数和本系统最优成本值。在这里,H参数由He=Dey, Hh=bh-Dhy, Heh=Dehy计算得出,其是由热力系统的设备出力y和热力系统的参数矩阵bh和D综合形成的。因此H参数可以理解为系统出力和系统参数信息加密后形成的综合参数。而热力系统和电力系统局部最优解即为该系统自身的最优运行成本值。
于是,在这样形成信息隐私加密化的信息交互模式的前提下,完成整个系统的优化。两个系统之间迭代信息交互全过程如图7所示,包括信息的传递和返回过程。
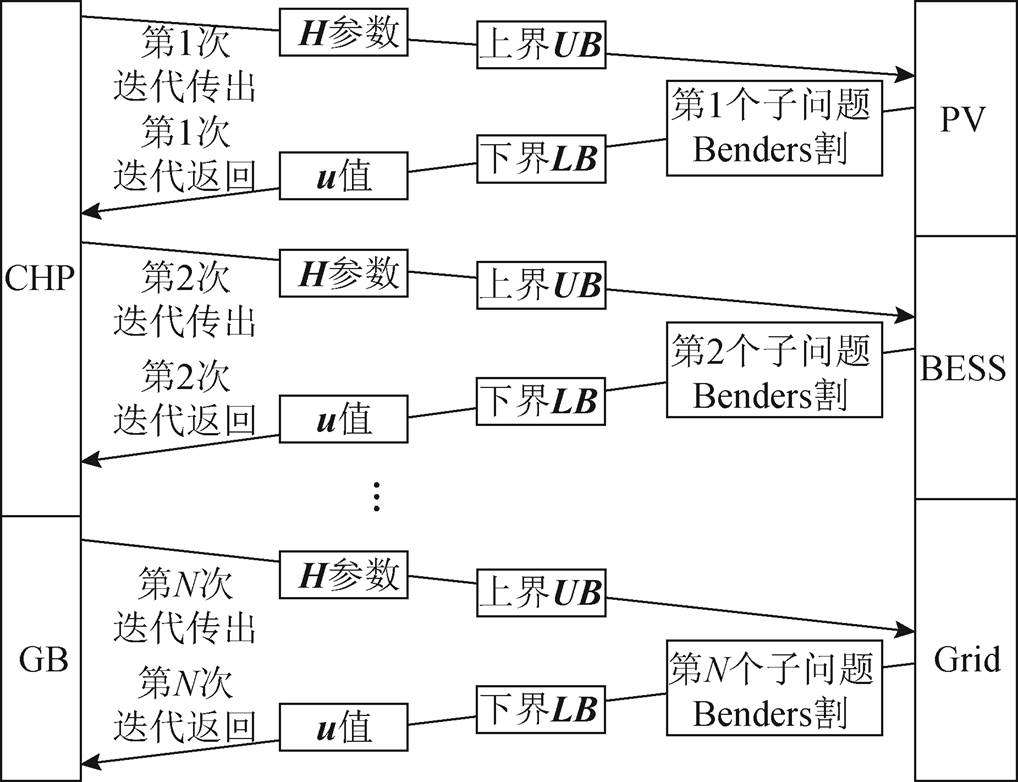
图7 主子问题迭代信息交互全过程
Fig.7 Iterative information interaction process between the main problem and the sub-problem
光伏、储能电池、CHP、燃气锅炉各设备单位出力的维护成本分别为0.015元/kW、0.018元/kW、0.025元/kW、0.02元/kW。光伏额定容量450kW。CHP出力上限300kW,热电比300%,最大增幅(向上爬坡速率)180kW/h,最大降幅(向下爬坡速率)180kW/h。储能电池容量500kW×h,充电效率0.97,放电效率0.92;最大充电功率125kW,最大放电功率125kW。SOC最大值0.8,最小值0.1,初值50kW·h。
燃气价格为3.3元/m3;天然气热值为9.7kW×h/m3。购电价采用分时电价如图8所示[24],有谷价(L)、平价(M)、峰价(H)三个等级,L时段包含每天0:00~8:00,M时段包含每天8:00~14:00、17:00~19:00、22:00~24:00,H时段包含每天14:00~17:00、19:00~ 22:00。L时段电价为0.4元/(kW×h),M时段电价为0.8元/(kW×h), H时段电价为1.2元/(kW×h);售电价统一0.35元/(kW×h)。
电热负荷和光伏发电量数据选取曼彻斯特大学春季某典型日的数据,30min为一个时段,一天分为48个时段下电负荷、热负荷和光伏发电量(kW×h)如图9所示。
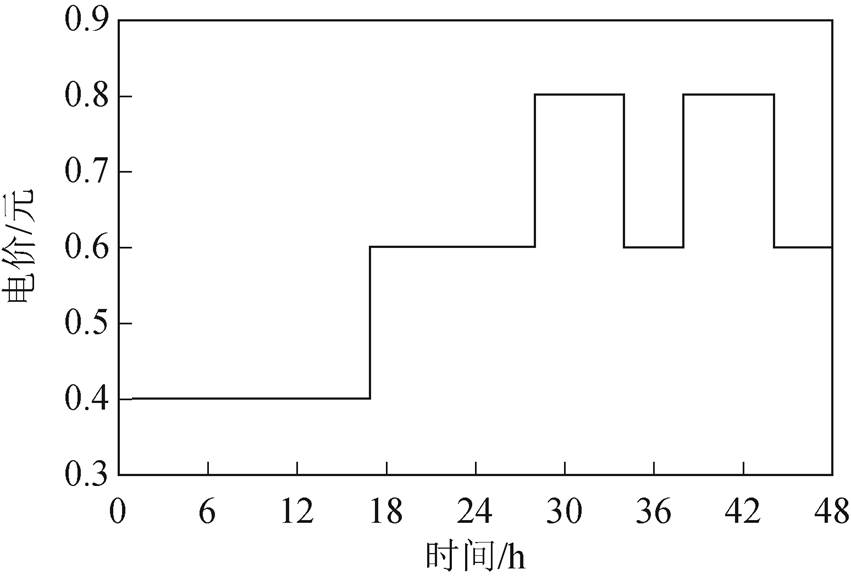
图8 分时电价曲线
Fig.8 TOU curve
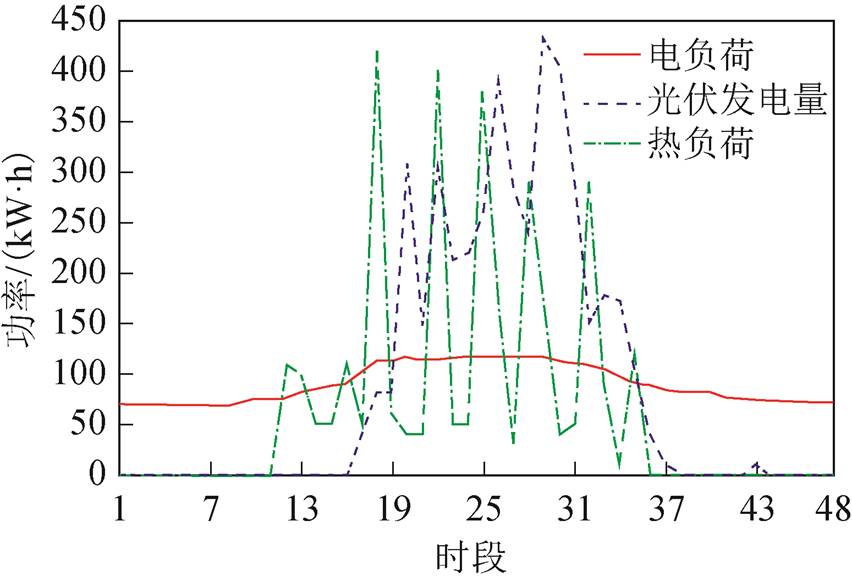
图9 电热负荷和光伏发电量数据
Fig.9 The data of the heat/electrical load and PV generation
设置三个场景进行分析:
Case 1:此场景下系统不含燃气锅炉,只由CHP供热。以此探讨CHP的电热并发特性,和此场景下的热力系统灵活性。
Case 2:此场景下系统不含CHP,只由燃气锅炉供热。此时电热完全解耦,电力系统和热力系统分解计算。
Case 3:此场景即本文讨论的优化模型,含有CHP和燃气锅炉。电力系统和热力系统之间通过CHP协调运行,分解计算,达到整体优化。
3.2.1 负荷构成
电热负荷供给来源出力分解如图10a和图10b所示。
对于图10a中Case 3的电负荷在每个时刻的供给来源进行分析如下,可以得出结论:电负荷构成情况可以反映电价、热负荷和光伏发电信息。
(1)主电网供电:6:00以前及22:00以后电负荷全部由主电网提供,这是因为此时没有光伏发电且电价处于低电价。
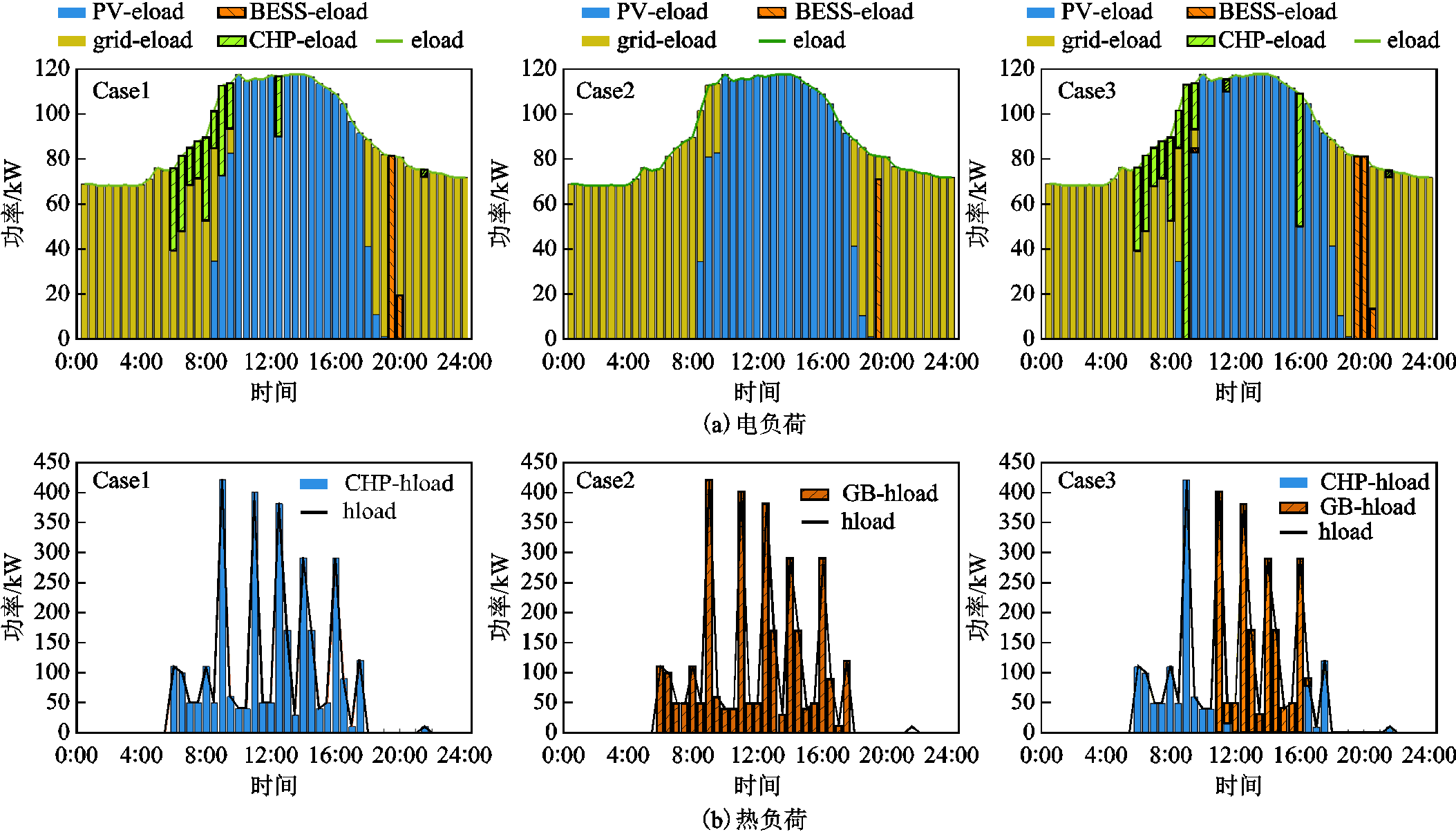
图10 电热负荷供给来源分解图
Fig.10 Electrical and heat load supply source
(2)CHP供电:6:00开始出现CHP供电,这是因为此时出现热负荷,CHP供给热负荷的同时生成的电能会供给电负荷。可以看到9:00时全部由CHP供给,这是因为此时热负荷激增,CHP供应热负荷同时生成的电能随之剧增,因此全部供给电负荷。
(3)光伏供电:在8:30~18:30,电负荷大部分由光伏构成,因为此时间段出现了光伏发电,光伏发电优先供给电负荷。
(4)储能电池供电:可以看出电负荷大部分是由主电网、光伏和CHP构成,而在8:30、9:30、10:30和11:30,光伏发电和CHP发电不足以满足电负荷,且这些时段均处于高电价,因此需要储能电池供给电负荷。
对于图10a中Case 1和Case 2进行分析:Case 1与Case 3差别较小,即不含燃气锅炉对电负荷的供给来源分配影响较小,这是因为燃气锅炉只与热负荷有关,与电负荷只能通过CHP产生间接联系。通过Case 2与Case 3对比,可明显看出,由于不存在CHP,由电网购电和光伏发电共同补充供给电负荷。
而对于图10b 中Case 3热负荷进行分析,可以得出如下结论:燃气锅炉在一定程度上能够提高供热灵活性,弥补CHP因为电热并发可能造成的能源损失。
燃气锅炉在9:30以前和16:00以后大部分由CHP构成,而9:30~16:00期间由GB构成。这是因为CHP具有同时发电发热的特性,白天电负荷主要由PV提供,所以不需要CHP电能,此时若CHP供热,随之产生的电能可能会造成能源浪费,因此白天电负荷主要由燃气锅炉提供。
3.2.2 各设备出力分配
针对各个设备元件,储能电池充放电功率分配、主电网购售电功率分配、CHP发电功率分配和光伏发电功率分配[25-26],如图11a~图11d所示。
对图11a进行分析:对于储能电池,正值表示充电,负值表示放电。可以得出结论:储能电池充放电信息可以反映电价信息,同时储能电池通过其存储能力提供了电力系统灵活性,减小运行成本。
(1)充电时段:三个场景下的充电大部分由光伏充电组成是由于此时光伏发电量极大而电负荷已经全部满足,所以多余电量存入储能电池。其中Case 1由于CHP发电量大,所以在11:00时存在多余的CHP发电存入储能电池。
(2)放电时段:三个场景下的放电时段也集中在19:30~20:30,因为此时段无光伏发电和CHP发电,且购电价处于峰电价,因此用储能电池供给电负荷。
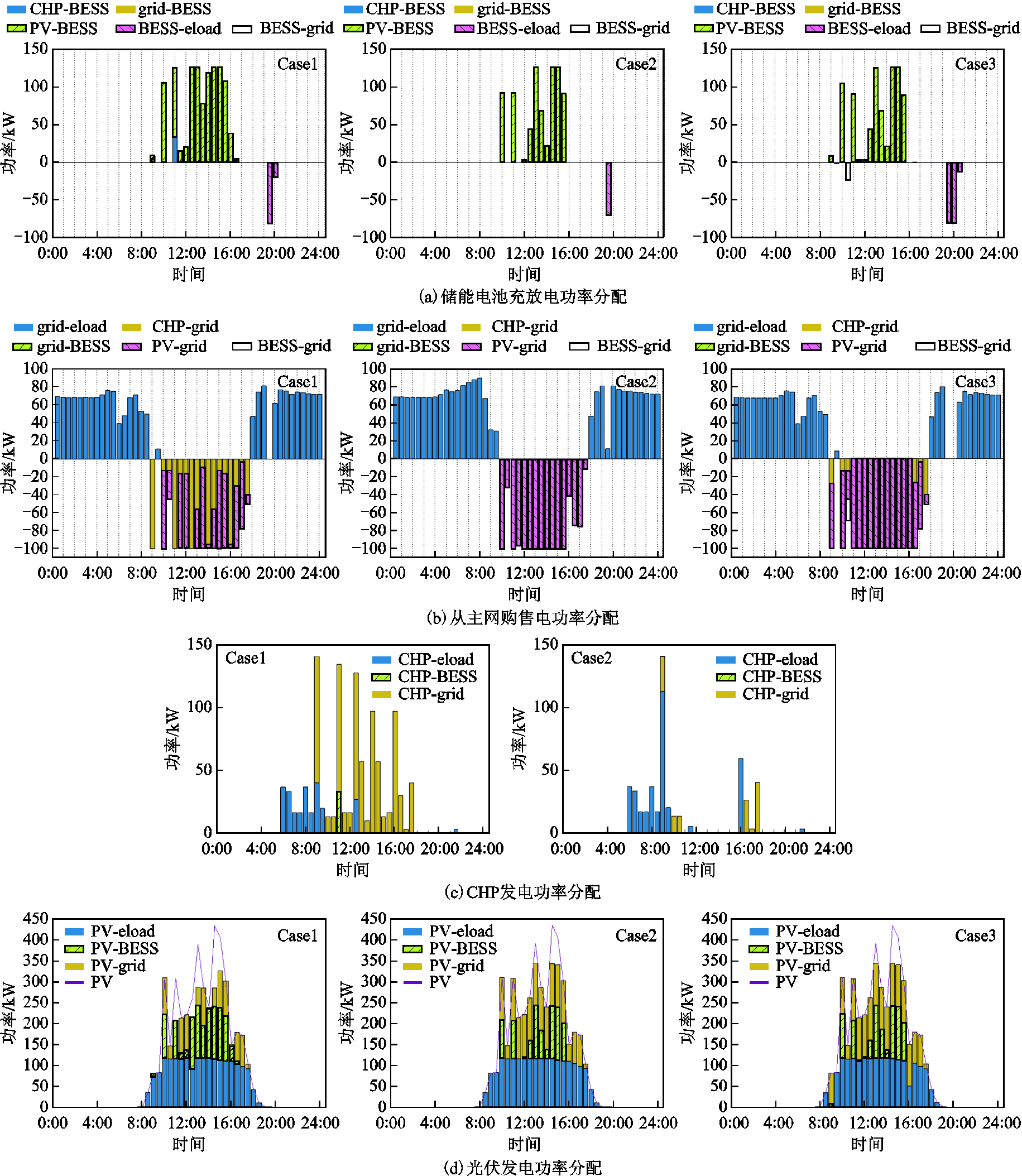
图11 各设备出力分配
Fig.11 The output distribution of devices
对图11b进行分析如下,对于主电网,正值表示从主电网购电,负值表示向主电网售电。可以得出结论:CHP的发电会影响光伏发电售电量,即燃气锅炉的存在与否。
(1)购电时段:三个场景的购电情况基本一致,第一个购电时段由于谷电价,购电给电负荷;第二个购电时段由于没有光伏发电和有CHP发电,因此在平电价时期购电给负荷(19:30~20:30的峰电价时期则利用储能电池供电)。
(2)售电时段:将多余光伏发电和CHP发电售出,可看出部分时间达到售电功率上限100kW。对于Case 1,出现大量CHP售电,因为此场景不含燃气锅炉,只能由CHP供热,随之出现了大量CHP发电量,多余的CHP发电售给电网,这使得Case 1与Case 3相比光伏售给电网的空间减少,这也将造成更多的弃光。对于Case 2,不含CHP,因此全部为光伏发电售电。
对于图11c进行分析,由于CHP供给热负荷为CHP发电量的3倍,因此图中未画出热功率,仅展示CHP发电功率的分配。可看出CHP发电量优先满足电负荷,多余部分售给电网或储能电池存储。而Case 1中,由于此场景不含燃气锅炉,只能由CHP供热,随之出现了大量CHP发电量,多余的CHP发电售给电网或者存入储能电池中。9:00时刻,Case 1中CHP发电少量供给负荷而大量售给主网,Case 3中CHP 发电少量售给主网而大量供给负荷。这是由于Case 1不含燃气锅炉,因此为了满足热负荷,CHP的发电功率固定,同时光伏发电量也是固定值。在这种CHP发电和光伏发电固定的情况下,由于CHP发电量和光伏发电量对于负荷的供给在本文的优化计算中优先等级是一样的(只以总成本最小为唯一优化目标),因此可能存在多解情况,即Case 1中,CHP供给负荷和CHP售给主网对于总成本的影响是一样的。
对图11d 进行分析,可以看出均存在一定程度的弃光现象,这是因为此时电负荷供给完成,且达到电网售电功率和储能电池充电功率上限,不得不弃光。Case 2的光伏出力分配与Case 3一致,而Case 1的弃光率更大,这是因为燃气锅炉的缺失导致的CHP发电量剧增,CHP售给电网使得售电功率达到上限,此时光伏发电无法售给电网,造成了弃光。
能源互联网的发展使得多个区域综合能源系统和大电网相联,由于用户隐私、数量规模等原因,不适宜将热力系统和电力系统的详细数据与设备参数完全共享。由此产生了在各系统信息隐私保护前提下的整体优化求解问题,本文提出了Benders分解方法进行求解,在对光伏-储能-CHP综合能源系统进行优化运行建模和Benders方法求解分析后,本文证明其可行性并得到了以下结论:
1)Benders分解方法将电热综合优化问题分解为热力系统主问题和电力系统子问题,在本文所总结的主问题和子问题交互模式下,电力系统和热力系统必须遵循以下准则:每次迭代时,热力系统向电力系统传递热网优化后热网各设备出力和热网数据参数被加密化之后的综合参数H和热网最优运行成本值(上界UB),而电力系统返回信息为电网设备出力对偶化后的变量、电网最优运行成本值(下界LB)、子问题Benders割。
2)由于Benders分解法的引入,将电力系统和热力系统解耦,两个系统间只需要传递共享必要的加密化信息,各个系统自身的部分参数被保护起来。由此形成的信息隐私化的交互模式实现了系统间部分信息的有效保护,保证了信息隐私安全。
3)Benders分解法下的优化求解结果分析,可以总结得出:电负荷供给分配情况可以反映电价信息、热负荷信息和光伏发电信息;而储能电池充放电信息可以反映电价信息,同时储能电池通过其存储能力提供了电力系统灵活性,减小运行成本。燃气锅炉能够弥补CHP因为电热并发可能造成的电能损失,从而提高热力系统供热灵活性;同时,由于CHP担任发电和发热的共同职责,因此通过电热负荷情况和光伏发电情况可以判断CHP和燃气锅炉对热负荷的供给分配。
4)本文所总结的交互模式,是在默认双方交互准确真实信息的前提下进行的,即默认遵循诚信准则。而后续的研究需要利用博弈论对此进行数学证明,即证明得出:违反信用的一方优化结果受损,以保证系统遵循诚信准则。因此,在之后的研究中,要对于Benders分解法中数学语言进行更多分析研究,系统化地总结出两个系统应遵循的准则或机制,为实际运行提供参价值。
5)本文探讨了在隐私保护前提下,分解协调来优化求解的可行性,证明了能用分布式求解实现全局最优。在后续的研究中,将考虑建立更详细的模型,例如考虑热电网的网络计算的模型[27-28]和包含混合整数规划的模型等。
参考文献
[1] Liu X, Jenkins N, Wu J, et al. Combined analysis of electricity and heat networks[J]. Applied Energy, 2016, 162: 1238-1250.
[2] Liu Xuezhi, Pierluigi Mancarella. Modelling, assessment and sankey diagrams of integrated electricity-heat-gas networks in multi-vector district energy systems[J]. Applied Energy, 2016, 167: 336-352.
[3] Liu Xuezhi, Yan Zheng, Wu Jianzhong. Optimal coordinated operation of a multi-energy community considering interactions between energy storage and conversion devices[J]. Applied Energy, 2019, 248: 256-273.
[4] Liu Xuezhi, Zhang Peichao, Andrew Pimm, et al. Optimal design and operation of PV-battery systems considering the interdependency of heat pumps[J]. Journal of Energy Storage, 2019, 23: 526-536.
[5] 余晓丹, 徐宪东, 陈硕翼, 等. 综合能源系统与能源互联网简述[J]. 电工技术学报, 2016, 31(1): 1-13.
Yu Xiaodan, Xu Xiandong, Chen Shuoyi, et al. A brief review to integrated energy system and energy internet[J]. Transactions of China Electrotechnical Society, 2016, 31(1): 1-13.
[6] 殷爽睿, 艾芊, 曾顺奇, 等. 能源互联网多能分布式优化研究挑战与展望[J]. 电网技术, 2018, 42(5): 1359-1369.
Yin Shuangrui, Ai Qian, Zeng Shunqi, et al. Challenges and prospects of multi-energy distributed optimization for energy internet [J]. Power System Technology, 2018, 42(5): 1359-1369.
[7] 瞿凯平, 黄琳妮, 余涛, 等. 碳交易机制下多区域综合能源系统的分散调度[J]. 中国电机工程学报, 2018, 38(3): 697-707.
Qu Kaiping, Huang Linni, Yu Tao, et al. Decentralized dispatch of multi-area integrated energy systems with carbon trading[J]. Proceedings of the CSEE, 2018, 38(3): 697-707.
[8] 艾芊, 郝然. 多能互补、集成优化能源系统关键技术及挑战[J]. 电力系统自动化, 2018, 42(4): 2-10, 46.
Ai Qian, Hao Ran. Key technologies and challenges for multi-energy complementarity and optimization of integrated energy system[J]. Automation of Electric Power Systems, 2018, 42(4): 2-10, 46.
[9] 郭庆来, 辛蜀骏, 孙宏斌, 等. 电力系统信息物理融合建模与综合安全评估: 驱动力与研究构想[J]. 中国电机工程学报, 2016, 36(6): 1481-1489.
Guo Qinglai, Xin Shujun, Sun Hongbin, et al. Power system cyber-physical modeling and security assessment: motivation and ideas[J]. Proceedings of the CSEE, 2016, 36(6): 1481-1489.
[10] 张睿, 黄国日, 文福拴, 等. 电力-天然气集成能源系统的统一规划模型与Benders解耦方法[J]. 电力建设, 2017, 38(7): 67-76.
Zhang Rui, Huang Guori, Wen Fushuan, et al. Unified planning model of integrated electric power and natural gas energy systems based on Benders decomposition[J]. Electric Power Construction, 2017, 38(7): 67-76.
[11] 曾鸣, 白学祥, 李源非, 等. 基于Benders分解优化算法的区域能源供给服务网络系统规划方法研究[J]. 华北电力大学学报(自然科学版), 2017, 44(1): 89-96. Zeng Ming, Bai Xuexiang, Li Yuanfei, et al. Study on system planning solution for regional energy supply service network based on Benders decomposition optimization method[J]. Journal of North China Electric Power University: Natural Science Edition, 2017, 44(1): 89-96.
[12] 杨艳红, 裴玮, 屈慧, 等. 基于广义Benders分解的分布式热电联供机组规划方法[J]. 电力系统自动化, 2014, 38(12): 27-33.
Yang Yanhong, Pei Wei, Qu Hui, et al. A planning method of distributed combined heat and power generator based on generalized Benders decomposition [J]. Automation of Electric Power Systems, 2014, 38(12): 27-33.
[13] 卢志刚, 杨宇, 耿丽君, 等. 基于Benders分解法的电热综合能源系统低碳经济调度[J]. 中国电机工程学报, 2018, 38(7): 1922-1934, 2208.
Lu Zhigang, Yang Yu, Geng Lijun, et al. Low-carbon economic dispatch of the integrated electrical and heating systems based on Benders decomposition[J]. Proceedings of the CSEE, 2018, 38(7): 1922-1934, 2208.
[14] 丁强, 李锴, 朱泽磊, 等. 基于变量降维的大电网经济调度优化方法[J]. 电力系统自动化, 2017, 41(18): 130-136.
Ding Qiang, Li Kai, Zhu Zelei, et al. Economic dispatch optimization method for large-scale power grid based on variable dimension reduction[J]. Automation of Electric Power Systems, 2017, 41(18): 130-136.
[15] Alhaider M, Fan Lingling, Miao Zhixin. Benders decomposition for stochastic programming-based PV/battery/HVAC planning[C]// 2016 IEEE Power and Energy Society General Meeting (PESGM). IEEE, Boston, MA, USA, 2016, DOI: 10. 1109/PESGM. 2016. 7741775.
[16] 车泉辉, 娄素华, 吴耀武, 等. 计及条件风险价值的含储热光热电站与风电电力系统经济调度[J]. 电工技术学报, 2019, 34 (10): 2047-2055.
Che Quanhui, Lou Suhua, Wu Yaowu, et al. Economic dispatching for power system of concentrated solar power plant with thermal energy storage and wind power considering conditional value-at-risk[J]. Transactions of China Electrotechnical Society, 2019, 34 (10): 2047-2055.
[17] Liu Xuezhi, Yan Zheng, Wu Jianzhong. Optimal coordinated operation of a multi-energy community considering interactions between energy storage and conversion devices[J]. Applied Energy, 2019, 248: 256-273.
[18] 韩佶, 苗世洪, 李超, 等. 计及相关性的电-气-热综合能源系统概率最优能量流[J]. 电工技术学报, 2019, 34(5): 1055-1067.
Han Ji, Miao Shihong, Li Chao, et al. Probabilistic optimal energy flow of electricity-gas-heat integrated[J]. Transactions of China Electrotechnical Society, 2019, 34(5): 1055-1067.
[19] 朱翰超, 马蕊. 考虑需求侧管理的冷热电联供微电网优化配置方法[J]. 电力系统保护与控制, 2019, 47(2): 139-146.
Zhu Hanchao, Ma Rui. Optimal configuration method of CCHP microgrid considering demand side management [J]. Power System Protection and Control, 2019, 47(2): 139-146.
[20] 张义志, 王小君, 和敬涵, 等. 考虑供热系统建模的综合能源系统最优能流计算方法[J]. 电工技术学报, 2019, 34 (3): 562-570.
Zhang Yizhi, Wang Xiaojun, He Jinghan, et al. Optimal energy flow calculation method of integrated energy system considering thermal system modeling [J]. Transactions of China Electrotechnical Society, 2019, 34 (3): 562-570.
[21] 邵世圻, 戴赛, 胡林献, 等. 计及热网特性的电热联合系统调度方法[J]. 电力系统保护与控制, 2018, 46(10): 24-30.
Shao Shiqi, Dai Sai, Hu Linxian, et al. Research on heat-electricity combined scheduling method considering the characteristics of the heating network[J]. Power System Protection and Control, 2018, 46(10): 24-30.
[22] 李本新, 韩学山. 发输电检修与机组组合联合决策的Benders分解方法[J]. 电工技术学报, 2015, 30(3): 224-231.
Li Benxin, Han Xueshan. Benders decomposition algorithm to coordination of generation and transmission maintenance scheduling with unit commitment[J]. Transactions of China Electrotechnical Society, 2015, 30(3): 224-231.
[23] 吴志, 刘亚斐, 顾伟, 等. 基于改进Benders分解的储能、分布式电源与配电网多阶段规划[J]. 中国电机工程学报, 2019, 39(16): 4705-4715, 4973.
Wu Zhi, Liu Yafei, Gu Wei, et al. A modified decomposition method for multistage planning of energy storage, distributed generation and distribution network [J]. Proceedings of the CSEE, 2019, 9(16): 4705-4715, 4973.
[24] 倪驰昊, 刘学智. 光伏储能系统的电池容量配置及经济性分析[J]. 浙江电力, 2019, 38(1) : 1-10.
Ni Chihao, Liu Xuezhi. Battery capacity configuration and economic analysis of photovoltaic energy storage system[J]. Zhejiang Electric Power, 2019, 38(1): 1-10.
[25] 陈柏翰, 冯伟, 孙凯, 等. 冷热电联供系统多元储能及孤岛运行优化调度方法[J]. 电工技术学报, 2019, 34 (15): 3231-3243.
Chen Pohan, Feng Wei, Sun Kai, et al. Multi-energy storage system and islanded optimal dispatch method of CCHP[J]. Transactions of China Electrotechnical Society, 2019, 34 (15): 3231-3243.
[26] 郑国太, 李昊, 赵宝国, 等. 基于供需能量平衡的用户侧综合能源系统电/热储能设备综合优化配置[J]. 电力系统保护与控制, 2018, 46(16): 8-18.
Zheng Guotai, Li Hao, Zhao Baoguo, et al. Comprehensive optimization of electrical/thermal energy storage equipments for integrated energy system near user side based on energy supply and demand balance[J]. Power System Protection and Control, 2018, 46(16): 8-18
[27] 赵霞, 杨仑, 瞿小斌, 等. 电-气综合能源系统能流计算的改进方法[J]. 电工技术学报, 2018, 33 (3): 464-477.
Zhao Xia, Yang Lun, Qu Xiaobin, et al. An improved energy flow calculation method for integrated electricity and natural gas system [J]. Transactions of China Electrotechnical Society, 2018, 33 (3): 464-477.
[28] 李晓露, 单福州, 宋燕敏, 等. 考虑热网约束和碳交易的多区域综合能源系统优化调度[J]. 电力系统自动化, 2019, 43(19): 52-59.
Li Xiaolu, Shan Fuzhou, Song Yanmin, et al. Optimal dispatch of multi-region integrated energy systems considering heating network constraints and carbon trading[J]. Automation of Electric Power Systems, 2019, 43(19): 52-59.
Decomposition-Coordination Based Optimizaation for PV-BESS-CHP Integrated Energy Systems
Abstract To realize the global optimization of the electricity and heat networks in the integrated energy system in the case of information privacy protection, this paper conducted the optimal coordinated operation of the photovoltaic (PV)-battery energy storage system (BESS)-combined heat and power (CHP) integrated energy system,and studied the feasibility of using decomposition and coordination to optimize the solution under the premise of privacy protection. Firstly, an overall optimal operation model of the coupled electricity-heat energy system was established. Secondly, Benders decomposition method was proposed to solve this model. The model was decomposed into the main problem of the thermal system and the sub-problem of the electrical system, the optimal power distribution of each system was obtained through the iterative calculation between two systems. Besides, the interactive mode of systems based on Benders decomposition method was studied. On the premise of ensuring the effective protection and isolation of the information of master problem and sub-problem as much as possible, two systems only exchange the privacy parameters and Benders cuts, to maximize the protection of the electrical/thermal system privacy. Finally, comparative analysis of three typical scenarios was used to validate this method.
keywords:Integrated energy system, Benders decomposition, information privacy protection, optimal coordinated operation
中图分类号:TM732
DOI: 10.19595/j.cnki.1000-6753.tces.191468
国家重点研发计划(2018YFB0905000)、上海交通大学—英国利兹大学学术交流基金项目和上海市浦江人才计划(17PJ1404800)资助项目。
收稿日期 2019-11-13
改稿日期 2020-01-22
张雨曼 女,1996年生,硕士研究生,研究方向为综合能源系统运行优化等。E-mail:zyuman0610@sjtu.edu.cn
刘学智 男,1985年生,博士,讲师,研究方向为综合能源系统分析规划与运行等。E-mail:liuxz@sjtu.edu.cn(通信作者)
(编辑 郭丽军)