图1 DERC系统通信架构图
Fig.1 Communication architecture of DERC system
摘要 随着分布式能源的大量接入并网运行，通信延时的可确定性和网络控制成为保证系统稳定运行的关键。该文基于以太网通信的分布式能源系统，采用随机网络演算理论提出传输时延边界计算方法。其通过建立自相似业务流量模型，在网络节点处采用延时保证服务和加权公平排队机制调度算法将随机服务曲线具体化，推导出分布式能源通信业务端到端传输延时边界，有效克服了传统基于排队论仅能计算平均延时而遗漏长延时，造成网络控制失效的问题。最后，通过OPNET仿真软件构建的计及分布式能源物理设备与通信网络紧耦合分析模型的实验，验证了该文提出的随机网络演算时延边界数值计算结果的准确性。研究对精确分析不同通信体系架构的传输特性和分布式能源网络化控制提供了通信层面的理论支撑。
关键词：分布式能源 随机网络演算 服务曲线 端到端传输 时延边界
分布式可再生能源由于具备分散性、灵活性、环保性等良好特性，在能源消费结构中占比越来越重[1-2]。分布式能源的大规模渗透是智能电网与传统电力系统的主要区别之一，但分布式能源特有的间歇性和波动性不能保证完全地自发自用，而公共电网的集中式调控过于粗粒化，无法直接用于分布式能源系统[3-4]。因此，实时、精准的调控对分布式能源系统的优化运行十分重要。随着“互联网+”智慧能源和现代通信技术的发展，通信网络俨然已经成为电力系统的“中枢神经”，有助于分布式能源系统调控尺度的精细化。文献[5]通过分析通信延时对分布式系统控制灵敏度和稳定性的影响，提出了利用稀疏通信网络实现分布式协同控制方案。文献[6]提出了一种考虑通信时延的分布式调度算法，有效提升了微电网中分布式能源的最优配比。
然而，在通用以太网环境下的分布式能源调控（Distributed Energy Resource Coordinated-control, DERC）系统中，存在传输时延不确定、不可预测的问题，无法满足多主体双向实时通信的需求，直接影响网络化DERC控制器设计性能。文献[7-8]实验表明，通信延时上界估计不足会造成乐观设计，导致执行器无法及时获取控制指令而影响调控性能，甚至波及系统稳定性。相反，延时上界设置过大则会导致保守设计，损失系统的动态性能。因此，DERC系统亟需一种完备可靠的通信时延计算方法作为保证。
针对系统通信延时计算问题，传统方法多采用排队论。文献[9-10]基于排队论推导了电网高级计量系统的数据包传输延迟表达式，但其建立的M|M|1|∞|FCFS排队系统计算出的是系统稳态下的平均等待延时，而非延时上界。另外，排队论只适用于具有特定分布的数据流和“先进先服务”等简单调度的网络，对于有多个分布式设备协调运行和多种业务流聚合参与通信的DERC系统而言，排队论无法直接对DERC系统通信网络进行精准的实时性分析。与此同时，信息中心型的分布式能源电力系统所带来的分散、多径传输和网络缓存的特点也使得传统的排队论难以分析因缓存引起的数据包无序的情况。
与排队论不同，网络演算（Network Calculus, NC）理论是一种基于最小加代数的分析网络性能边界的有力工具，其主要思想是将复杂网络转换为便于分析处理的系统，即使用包络或者曲线来约束系统的流量到达和服务过程，并运用最小加卷积等运算得到通信网络的端到端传输时延边界等性能指标[11]。近年来，部分学者采用确定网络演算（Deterministic Network Calculus, DNC）理论研究智能电网通信系统[12]。然而，DNC得到的结果是基于保证服务最坏情况下的性能边界，以此进行的网络控制器设计必然会造成系统动态性能下降。
本文针对该问题，基于随机网络演算（Stochastic Network Calculus, SNC）理论研究分布式能源调控系统时延上界计算问题。SNC理论考虑了由实际环境以及多流聚合带来的随机性因素，同时，基于统计概率下的通信延时边界与DERC系统中实时突发业务流的时间敏感特性相契合，补偿了通信延时的随机性为分布式能源系统协调控制带来的不利影响。本文首先分析了DERC系统的通信网络特性，然后利用SNC理论推导出DERC通信传输时延边界，为DERC系统的精细化控制提供通信网络分析依据。
与通信网络紧耦合的DERC系统是典型的物理信息融合系统，如图1所示[13-14]。DERC通信系统按照功能可以划分为传感层、接入层、骨干层以及调控中心。
传感层主要由分布式光伏、分布式风机、分布式储能等分布式能源设备和以电动汽车、家庭用电为代表的负荷，以及与之相连的实现本地控制和通信功能的智能终端设备（Intelligent Terminal Device, ITD）组成。其中，ITD又分为智能监测装置、智能控制器和智能保护装置。各ITD的功能表述见表1[15]。
接入层主要由边缘路由器、汇聚路由器以及网关等通信设备组成，负责所管辖区域内传感层终端数据的汇集、处理与转发，接入层设备兼容多种通信规约，并对各业务数据进行分类标记和流量监管，同时具备自检维护、故障报警和异常自复位等修护功能。
图1 DERC系统通信架构图
Fig.1 Communication architecture of DERC system
骨干层承载着DERC系统的通信骨干网络，通过光纤以太网通信技术与调度自动化系统、数据采集与监控系统互联，实现分布式能源设备模拟量、状态量等数据和遥控、遥调、同期并网等控制操作信息的实时交互。
表1 传感层智能终端设备（ITD）及功能[15]
Tab.1 Sensing layer intelligent terminal device (ITD) and its functions[15]
设备名称功能 智能监测装置本地数据采集，孤岛监测、电能质量监测和分析 智能控制器响应调控中心的控制指令，电压无功功率自动控制，同期并网 智能保护装置过电流保护、过/欠电压保护、过/欠频率保护
调控中心实现多点分布式能源与外部电网的协调控制、分布式能源发电功率分配与控制、分布式能源与储能系统的协调控制等调度自动化管理，以及事件记录、故障隔离、人机交互等高级应用管理。
调控中心通过通信网络与各个分布式能源设备的双向实时信息交互是影响DERC系统安全稳定运行的关键，因此交互过程的传输时延势必成为制约DERC系统稳定的重要因素。然而由于以太网CSMA/CD协议自身的局限性，使得DERC系统的传输时延呈现不确定性和不可预测性。DERC系统的通信时延分布如图2所示，由图2可知，DERC系统时延由多个部分组成。
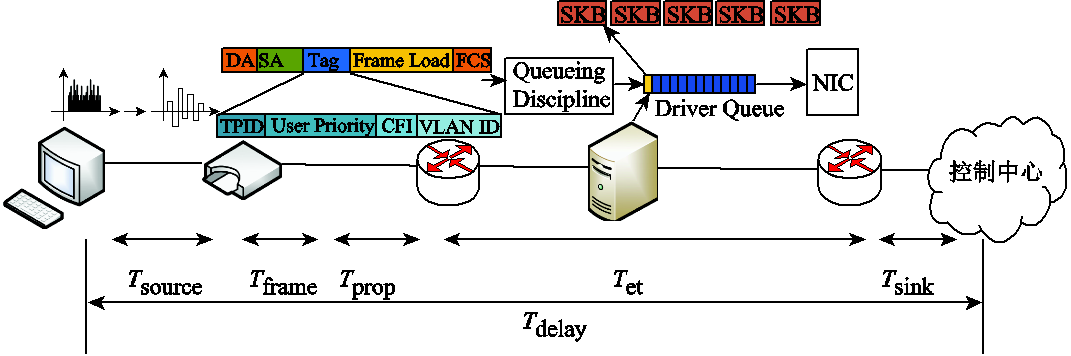
图2 DERC系统的通信时延分布图
Fig.2 Communication delay distribution of DERC system
图2中的Tdelay代表整个DERC系统业务流的端到端通信时延，其包含多个部分的延时，即
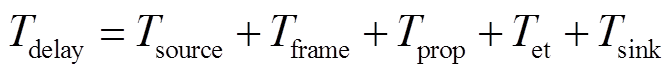（1）式中，Tsource为数据帧在源节点的预处理时间；Tframe为数据帧的打包封装处理时延；Tprop为电信号在物理媒介上的传播时延；Tsink为数据帧在宿节点的处理时间，以上时延在整个传输过程中可视为确定值；Tet为数据帧通过统一规约转换等节点路由设备转发带来的时延，包括服务时延、设备存储转发时延和排队时延。其中，服务时延和存储转发时延依赖报文的转发类型、设备的CPU处理性能；排队时延依赖流量类型以及节点设备的调度策略，如果网络中流量过大，则会出现拥塞，致使排队时间无法预测，成为传输时延不确定性的主要因素。由以上分析可知，通信时延Tet是影响DERC系统的主要时延。
随着电力物联，DERC系统业务流量的类型和数量急剧增加，从应用角度分析，涵盖了从电气设备实时监控数据、继电保护数据、变压器配置数据到智能计量、事件驱动信息、日志文件等多种应用数据；从数据类型的角度分析，大致可分为周期性数据、随机性数据和突发性数据[16-17]。表2列出了DERC系统业务流量的类型和时延要求[18]。
表2 分布式能源通信网业务类型及特点
Tab.2 Business types and characteristics of distributed energy communication network
时延要求/ms数据流类型应用举例 5~10突发型故障、控制类 10~500周期型采样、测量类 ＞1 000随机型文件传输、事件记录类
在实际传输过程中，常常是三种数据流并存，而聚合数据流的实时突发性往往会导致系统时延抖动，使得DERC系统产生较大的时延冗余，传输时间难以确定以及预测，甚至有可能阻塞网络，影响DERC系统的稳定性和调控任务的正常进行。因此，突发型数据是影响整个系统时延的关键流量。
突发型数据流的统计概率分布不再符合传统的泊松分布，而是表现出重尾化的特征，这使得DERC流量数据样本的方差趋于无穷[19]，其概率分布函数（Probability Distribution Function, PDF）不再对称，累积分布函数（Cumulative Distribution Function, CDF）的形式也不满足高斯情况，如图3所示。因此传统的高斯分布模型并不能完全正确地反映DERC系统中通信数据的真实状态。
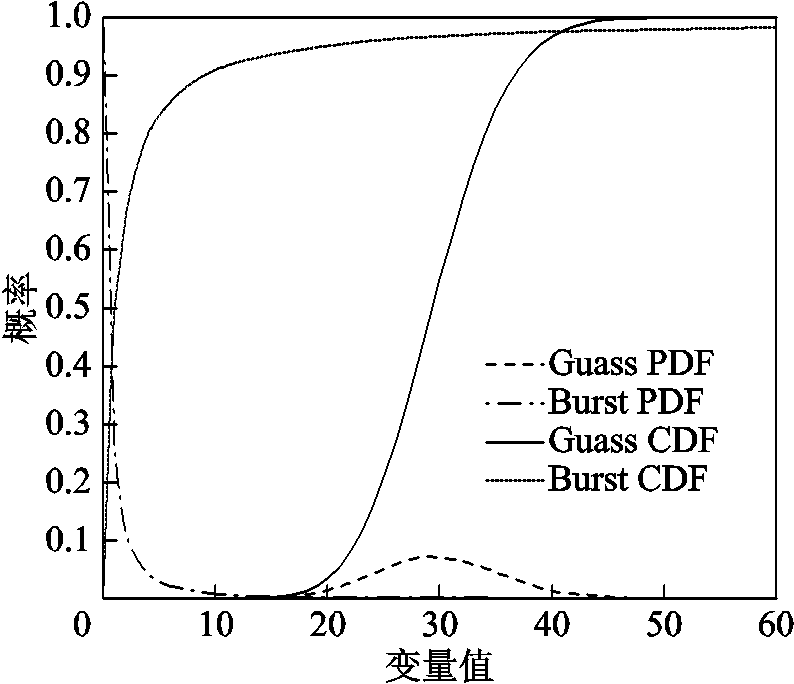
图3 突发型数据流的概率分布函数和累积分布函数
Fig.3 Probability distribution function and cumulative distribution function of burst data flow
大量研究表明，大量突发型流量在聚合后呈现出自相似性，且不会随时间尺度的放大而平滑[20]。典型的自相似突发流量模型有M|G|∞排队模型、分形布朗运动（Fractal Brown Motion, FBM）模型、分数差分自回归滑动平均（Fractional Autoregressive Integration Moving Average, FARIMA）模型[21]、线性分形稳定噪声（Linear Fractional Stable Noise, LFSN）模型和小波模型等基于数据统计特征的流量模型。不同的流量模型有不同的参数表述、边缘分布、稳定性以及复杂度，具体的自相似流量模型对比见表3。
表3 自相似流量模型对比
Tab.3 Comparison of self-similar traffic models
流量模型边缘分布分形性稳定性复杂度 M|G|∞高斯单形否O(n) FBM高斯单形是O(n) FARIMA高斯单形是O(n2) LFSN非高斯多形是O(n) 小波对数正态多形是O(n)
由表3可知，只有LFSN模型的边缘分布是非高斯的，由文献[22]可知，该流量模型可以有效地拟合具有突发特性的聚合数据流，能够较为准确地刻画DERC系统业务流量的统计特性，且该模型参数较少，相对于其他自相似流量模型更为简洁，更适合用于DERC系统通信流量建模和分析。
SNC作为NC理论的一个重要分支，不仅弥补了排队论在到达和服务过程建模单一的局限性，而且突破了DNC过于保守的计算方式，近年来在无线传感网络等复杂场景得到了较为广泛的应用。
在SNC理论中，随机到达曲线是对系统到达流量的约束，也是建立DERC系统实时业务模型的关键，其定义如下。
定义1：随机到达曲线[23]：当某一累积输入数据流A(t)对于任意的t≥0和x≥0满足
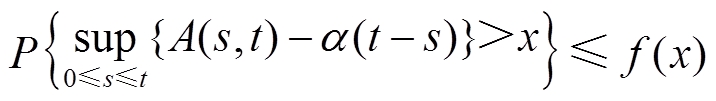
其中，到达累积量A(s, t) =A(t)-A(s)，称α(t)为A(t)的随机到达曲线，f(x)称作随机到达曲线的边界函数，是统计概率思想的体现。上式可简化为
A(t)~<f, α>
建立合适的流量到达模型是分析DERC系统延时性能的首要条件，文献[23]总结了SNC中的几种流量到达模型，包括流量中心型、虚拟积压中心型、最大虚拟积压中心型。考虑到DERC系统实时业务的突发型和非高斯分布，本文将选用虚拟积压中心型流量模型，也就是用于描述非高斯情况下的广义随机突发边界（generalized Stochastically Bounded Burstiness, gSBB）模型[24]，再结合从流量统计特性角度出发的LFSN模型，建立基于SNC的DERC系统实时业务到达模型为
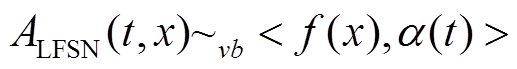（2）式中，随机到达曲线为α(t) = ρt + σ，ρ为实时业务数据传输的上限速率，σ为数据突发量。
根据文献[23]的LFSN模型参数可知，式（2）中边界函数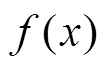
应满足
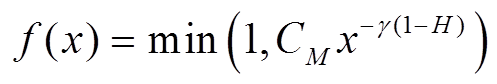（3）其中
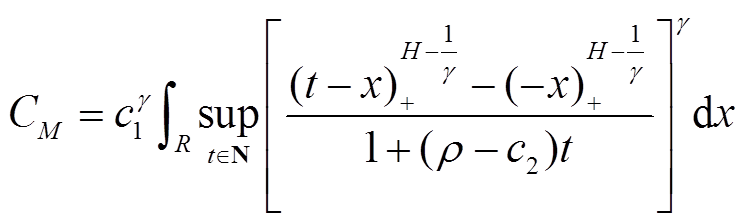
式中，γ为特征指数，表示DERC系统通信数据量的突发程度，当γ＜2时，业务流量的随机变量不存在二阶原点矩，即满足无穷方差，故有0＜γ＜2；H为Hurst参数，用来衡量突发数据流的自相似性强弱，取值范围为1/g＜H＜1；c1为尺度参数，用于描述DERC业务量统计分布的偏差程度；c2为流量均值，这两个参数由实际流量的形状特征决定，其中尺度参数c1的估计值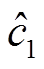
通过分位数估计法得到，即尺度参数c1的估计值满足
式中，K为分位间隔；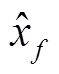
为f-分位数的估计值，其由经验分布函数定义
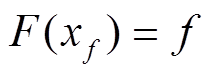，即
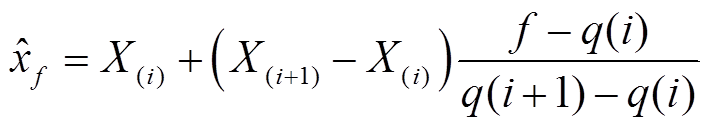
式中，q(i)=(2i-1)/(2N)，N为数据样本个数；X(i)为i阶数据样本，且0≤i≤N，(2i-1)/(2N)≤f≤ (2i+1)/(2N)。对于典型的α稳定分布LFSN模型，采用标准化分位数f1=0.72，f2=0.28，分位间隔K= 1.654±0.006。
服务模型是DERC系统中通信节点调度的体现，SNC理论引入随机服务曲线这一概念对复杂网络节点进行约束，其定义如下。
定义2：随机服务曲线[23]：当累积输出数据流A*(t)对于任意的t≥0和x≥0满足
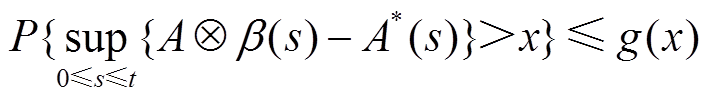
式中，β(t)为随机服务曲线；g(x)称作随机服务曲线的边界函数。上式可简化为S(t)~<g, β>。
实际的DERC系统或因电磁环境干扰而造成信道质量不佳引起通信网络的随机传输错误，或因多流融合竞争服务，使得提供给实时业务流的服务呈现随机的特点。于是引入能体现随机性本质的损失过程就显得十分有必要。
假设DERC通信网络的随机损失过程I(t)对于任意的t≥0和x≥0满足
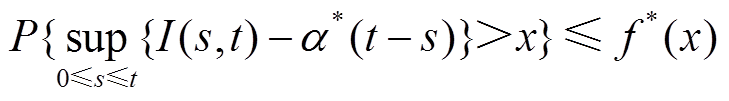（4）其中，DERC系统通信网络的损失累积量为I(s,t)=I(t)-I(s)，称α*(t)=ρ*t为随机损失过程I(t)的随机损失曲线，可以理解为DERC系统实时业务传输过程中的干扰，ρ*表示错误数据传输的速率，称f*(x)=pe-q x为随机损失曲线的边界函数，p和q为任意正参数。式（4）可简化为I(t)~<f*, α*>。
文献[23]将引入损失过程的随机服务曲线称作严格随机服务曲线，对于任意的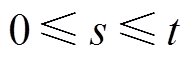
及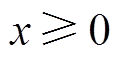
，严格随机服务模型满足
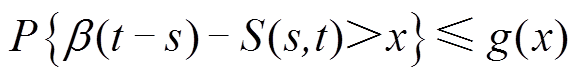（5）式中，S(s,t)为DERC系统服务累积量，S(s, t) = S(t)-S(s)；β(t)为随机严格服务曲线；g(x)为随机严格服务曲线的边界函数，式（5）可简化为S(t)~ssc<g(x), β(t)>。严格随机服务模型还有一个好处就是将系统的服务过程与到达过程解耦，研究证明在独立情况下延时边界的运算复杂度由原本的Ο(nlogn)降为Ο(n)，且能够提升边界的紧密度，更好地保证业务时延性能[23]。
为保证在DERC系统多业务融合场景中时间敏感型业务的实时传输，节点服务模型采用加权公平排队（Weighted Fair Queuing，WFQ）调度机制，将DERC系统中的多业务按照各自的时延要求划分成特定的业务等级，并将关键流量设为高优先级，以便时延敏感型数据得到可靠的服务保证。于是，节点提供给第t条实时数据流的服务速率Rt满足
（6）
式中，W为DERC系统的通信链路带宽；φt为第t条数据流的服务权重系数。
因此，DERC系统中第t条实时数据流的严格随机服务模型为
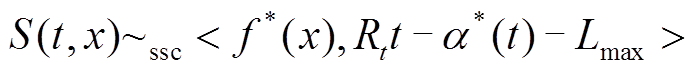（7）式中，Lmax为被服务数据包的最大报文长度。
SNC理论在分析单服务器系统时的模型如图4所示，其含义是一条流量到达模型满足A(t)~<f, α>的数据流进入了一个随机服务模型满足S(t)~<g, β>的系统，系统的输出数据流为A*(t)。
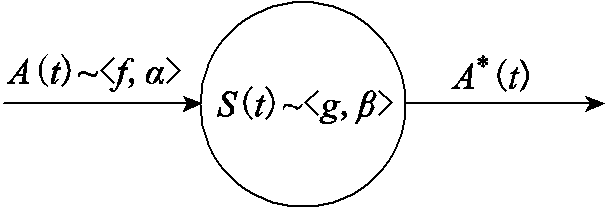
图4 基于SNC的系统模型
Fig.4 Network model based on SNC
不仅如此，任何端到端的通路都可以看成是由不同网络元素串联而成的系统，无论多复杂的网络都可被抽象为提供某种服务曲线的系统。为便于分析，本文假设DERC系统中不存在环状网络（若存在环网则需要保证在任意一时刻都为单向通路通信，而无路由环路），在基于SNC分析DERC系统的端到端链路时，可以将各个通信环节模块化，抽象为由若干个服务节点串联而成的分层级联网络，如图5所示。
图5 DERC系统的端到端传输链路模型
Fig.5 End-to-end transmission link model
假设DERC系统通信网络中的某条实时业务流At(t, x)~vb<f(x), α(t)>经过包含k个服务节点的端到端链路到达目的节点时，在每个节点处有m条来自其他分布式能源设备的竞争数据流（可视为背景流量）与该数据流一同竞争节点提供的服务。于是问题就变成了在关键流量和背景流量共享服务的基础上确保时间敏感型业务的可靠性传输。由于在DERC系统中的竞争数据流主要为周期型和随机型业务流，因此流量到达模型满足泊松分布，故基于SNC随机到达过程的流量模型为
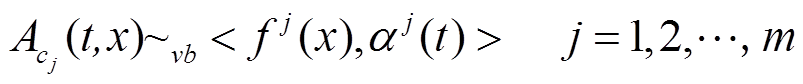（8）式中，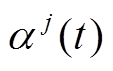
为随机到达曲线，αj(t)= rt + b，r为到达曲线的数据传输速率，b为数据突发量。由文献[23]可知边界函数为
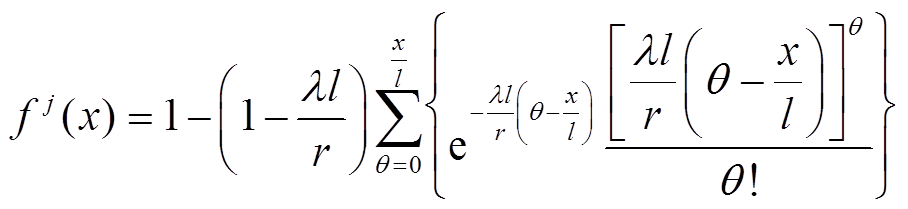
式中，λ为背景数据流的平均到达速率；l为数据包大小。
根据SNC理论数据流叠加定理[23]，得到第i个节点处的m条竞争数据流聚合后的流量模型满足
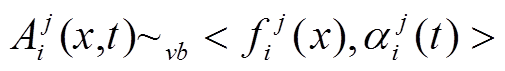（9）其中
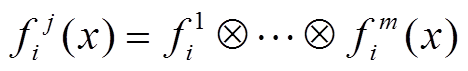
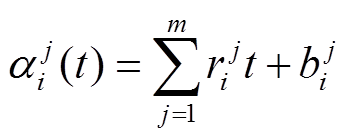
式中，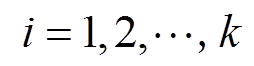
；
。
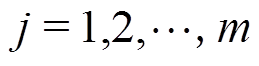对于单节点来说，第i个节点提供的严格随机服务模型为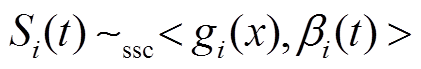
, i = 1,2,…,k 。则该节点提供给传输的实时业务流At的剩余服务应满足
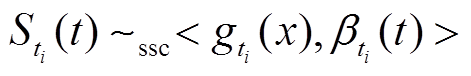（10）式中，边界函数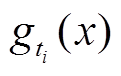
和服务曲线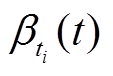
分别为
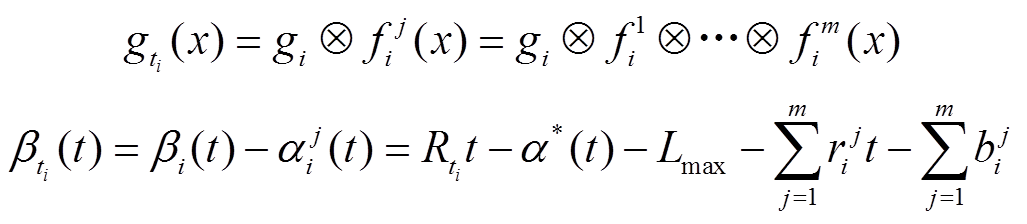
而对于多节点的DERC系统来说，需要将实时业务流经过的所有节点服务进行加合。因此，DERC系统端到端链路中对特定数据流At提供的随机服务模型满足
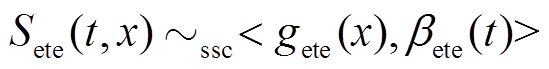（11）其中，边界函数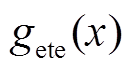
和服务曲线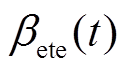
分别表示为
在计算DERC系统的端到端时延之前，基于最小加代数引入SNC理论中几个基本概念。
定义3：最小加卷积[23]：对于任意函数f(x)和g(x)的最小加卷积运算
规则为
定义4：最大水平距离[23]：在t时刻到达曲线α(t)和服务曲线β(t)的最大水平距离为
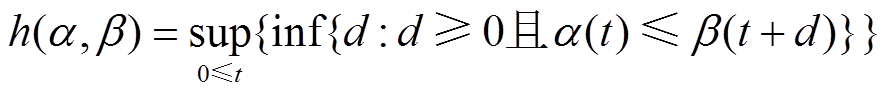
定义5：随机延迟边界[23]：当到达过程和服务过程分别满足A(t)~<f, α>和S(t)~<g, β>时，对于任意的t≥0和x≥0，t时刻的延时D(t)满足
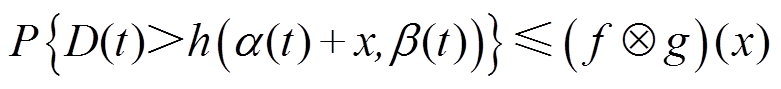
上式表明，只要已知系统的随机到达曲线及其边界函数和随机服务曲线及其边界函数，即可求得该系统的延时边界以及超出该边界的违背概率。因而DERC系统的时间敏感型业务流At的随机时延边界与概率分布的关系为
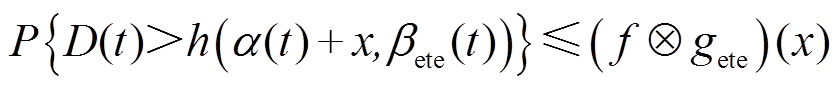（12）
将随机到达曲线及其边界函数和随机服务曲线及其边界函数代入式（12）后，得到
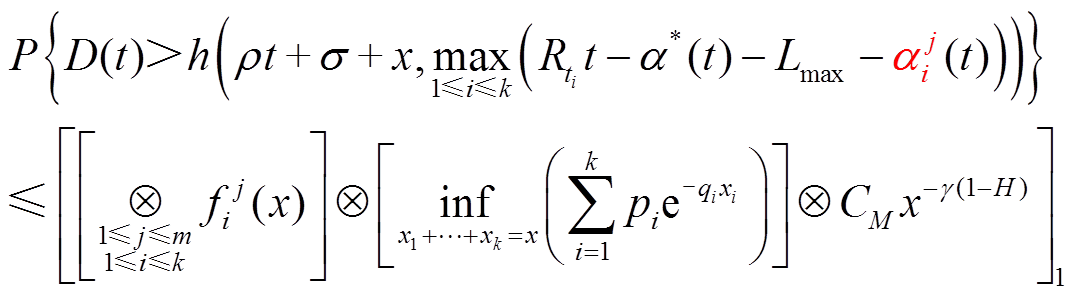（13）式中，
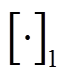为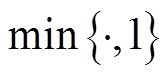
。
基于SNC的DERC通信系统实时业务的传输时延边界就可利用式（13）计算出来，得出不超过[·]1延迟边界的概率分布。当得到延迟边界的概率分布后，就可基于该分布设计DERC系统最优控制器，保证系统动态性能和稳定运行。
本文使用的数据集来自于欧洲可再生能源电力系统数据集（RE-Europe_Set）[25]，其涵盖了电力通信传输网络流量数据子集，包括常规发电机以及可再生能源发电设备的状态量数据库以及业务生成和电力需求信号数据集等，各数据子集间存在电气耦合关系。本文提取了与分布式能源系统通信流量相关的连续3年共26 304条流量记录，共7.3GB流量。仿真实验将RE-Europe_Set数据集通过转换和标准化数据进行预处理以消除冗余记录和消除数据分布中的偏差。首先采用R/S方法计算了RE-Europe_Set流量的Hurst参数H = 0.803＞0.5，即从工程计算的角度表明分布式能源系统通信网络中实时数据流具有明显的自相似特性。进而通过统计参数估计得到基于SNC流量模型参数，见表4。
表4 基于SNC的流量模型参数
Tab.4 Parameters of traffic model based on SNC
参数数值 特征指数γ1.5 自相似参数H0.8 尺度参数c160 流量均值c245 上限传输速率ρ/(kbit/s)10 突发量σ/kbit2.5
同时，将RE-Europe_Set流量映射到图6所示的计及物理信息耦合DERC系统，通信网络与整个分布式能源电力网络相耦合，双向实时交互的通信机制实现对分布式电源的监控与用户侧的需求管理，保证DERC系统正常运行。
基于RE-Europe_Set流量特性和映射的DERC系统模型，本文采用OPNET搭建DERC系统的通信网络，拓扑如图7所示，以分析不同场景下的通信延时分布。通过仿真实验结果与基于SNC计算结果的对比，验证本文所提出的时延边界计算方法的有效性和准确性。同时，本文在此基础上分别探究了接入网信道带宽和服务节点个数对DERC系统的端到端传输延时边界的影响程度，为优化DERC系统实时性和提升调控性能提供理论依据。
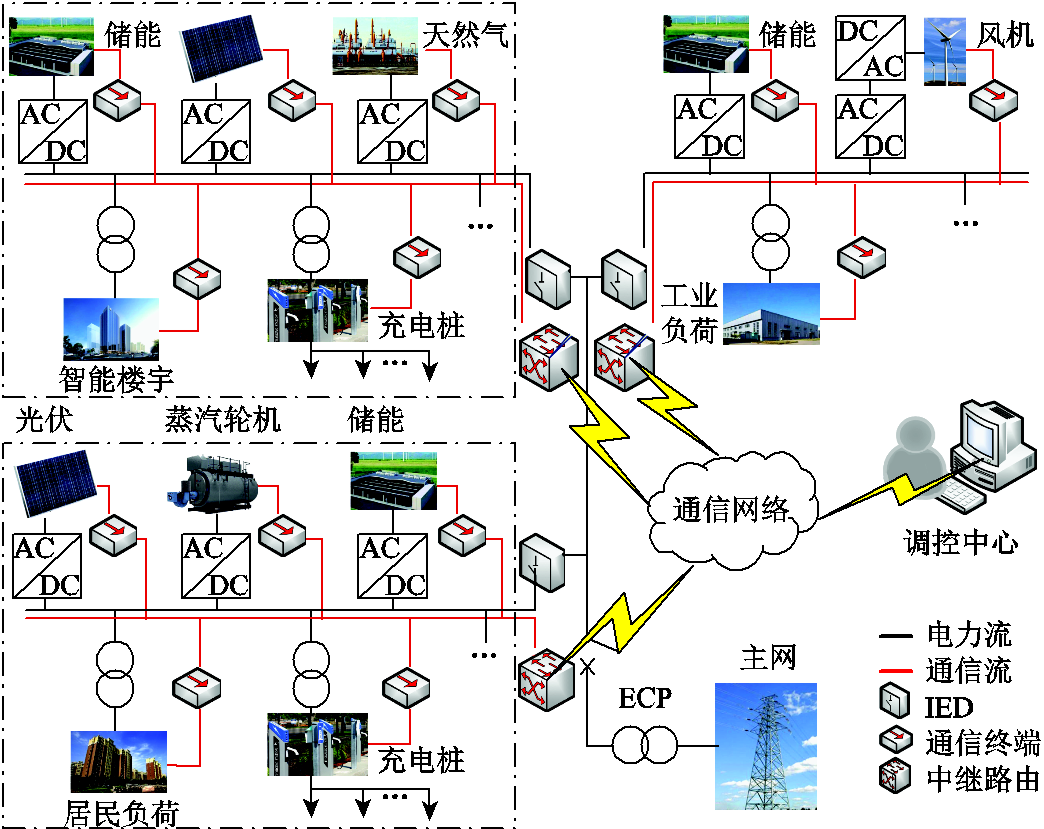
图6 计及物理信息耦合的DERC系统模型
Fig.6 DERC system model considering physical information coupling
图7 基于OPNET的DERC网络拓扑
Fig.7 DERC network topology based on OPNET
在图7中，IED代表与DERC系统物理层连接的智能终端，为实时业务流信号源，包括光伏监控系统、风机监控系统以及微机测控保护装置等；交换机“Switch_0”为分布式能源设备提供接口并与各个工作站代表的分布式能源设备组成分布式能源微网子系统，图中圈出Local部分为子网Area_3；系统中还包括另外两个子网“Area_1”和子网“Area_2”。图8分别给出了子网“Area_1”和子网“Area_2”的内部结构；路由器“E_Router_0”是子系统“Local”的边缘路由器，负责接入流量的业务标记和监管配置；路由器“S_Router_1”~“S_Router_6”是汇聚路由器，将DERC系统中的聚合业务流接入以太网；IP云“CN”代表DERC系统的通信网络，进行统一规约转换、服务映射等通信环节，并通过路由器“Router”与调度中心相连；工作站“DES”和服务器“CC_Server”组成DERC系统的调度中心，并通过通信网络将控制指令传输至各底层子系统完成双向实时信息的交互以及分布式能源系统的调控。
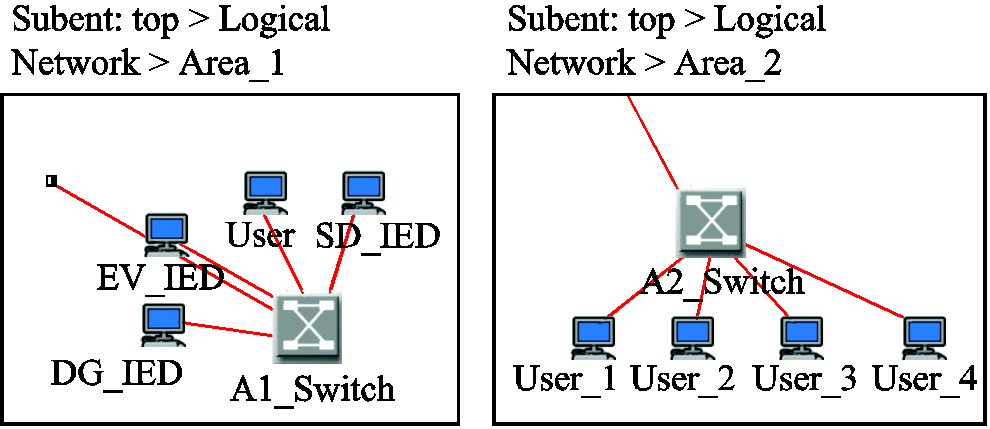
图8 左“Area_1”和右“Area_2”的网络模型
Fig.8 Network model for area 1 (left) and area 2 (right)
考虑DERC系统中存在大量“即插即用”的分布式设备、各分布式能源底层子系统组网和网络拓扑的多样化，以及突发的自然灾害或者网络安全攻击引起的电力系统故障在很大的程度上影响了系统的调控性能，建立四种不同的场景进行验证。各场景描述见表5。
表5 基于OPNET下的不同场景特点
Tab.5 Different scene characteristics based on OPNET
场景特点 场景1无背景流量 场景2背景流量20% 场景3背景流量40% 场景4链路故障
为了分析并验证本文提出的LFSN流量模型与DERC系统业务数据流的相似度以及流量模型的准确性，在此采用评价指标方均误差（MSE）和方均根误差（RMSE）衡量，计算公式分别为
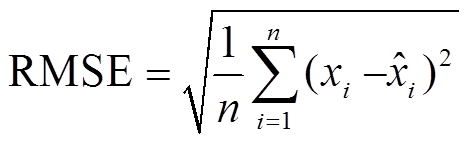
式中，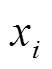
为第i个数据真实值；
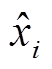为第i个数据模拟值。分析对比生成的模拟流量和仿真流量的均值和标准方差，见表6。
表6 模拟流量与仿真流量统计特性参数
Tab.6 Generated flow and simulation flow statistical characteristic parameters
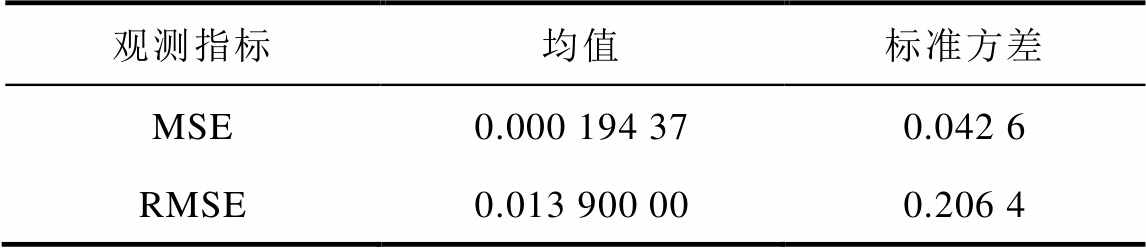
观测指标均值标准方差 MSE0.000 194 370.042 6 RMSE0.013 900 000.206 4
图9a为基于SNC的LFSN模型生成的模拟流量和仿真场景流量的统计分布直方对比图，可以看出二者的流量统计分布基本呈正态分布且大致相同。图9b为两流量的经验累积分布函数对比图，该函数用于反映流量的边缘分布特性，可以看出两条曲线形式基本相同。
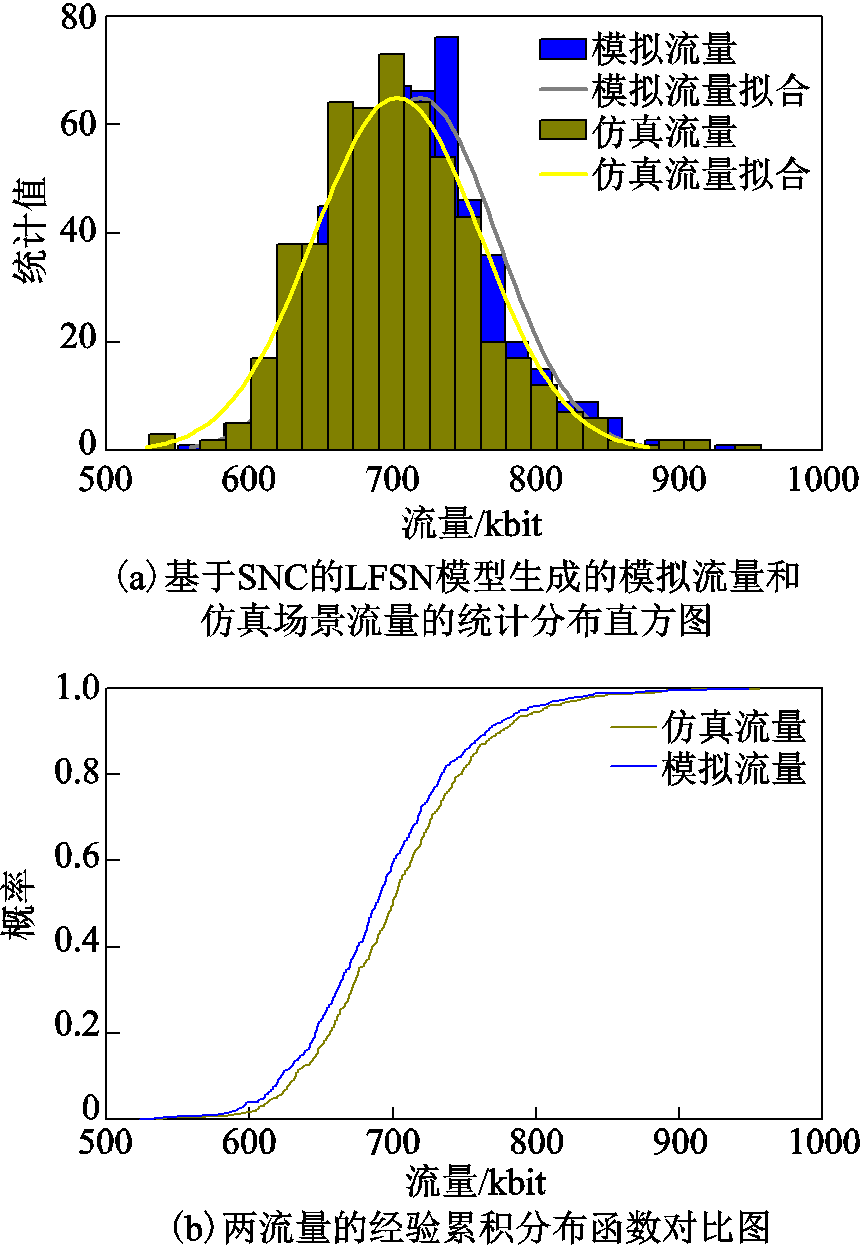
图9 模拟流量与仿真流量特性的对比
Fig.9 Comparison between generated flow and simulation flow characteristics
无论是从统计分布还是边缘分布都可以看出，LFSN流量模型对于DERC聚合数据流具有较好拟合特性，通过以上分析进一步验证了本文流量模型的有效性。
图10a~图10d分别对比了DERC系统四种不同场景下基于SNC理论推导的通信传输时延边界与OPNET搭建的DERC通信网络运行仿真时延对比结果。
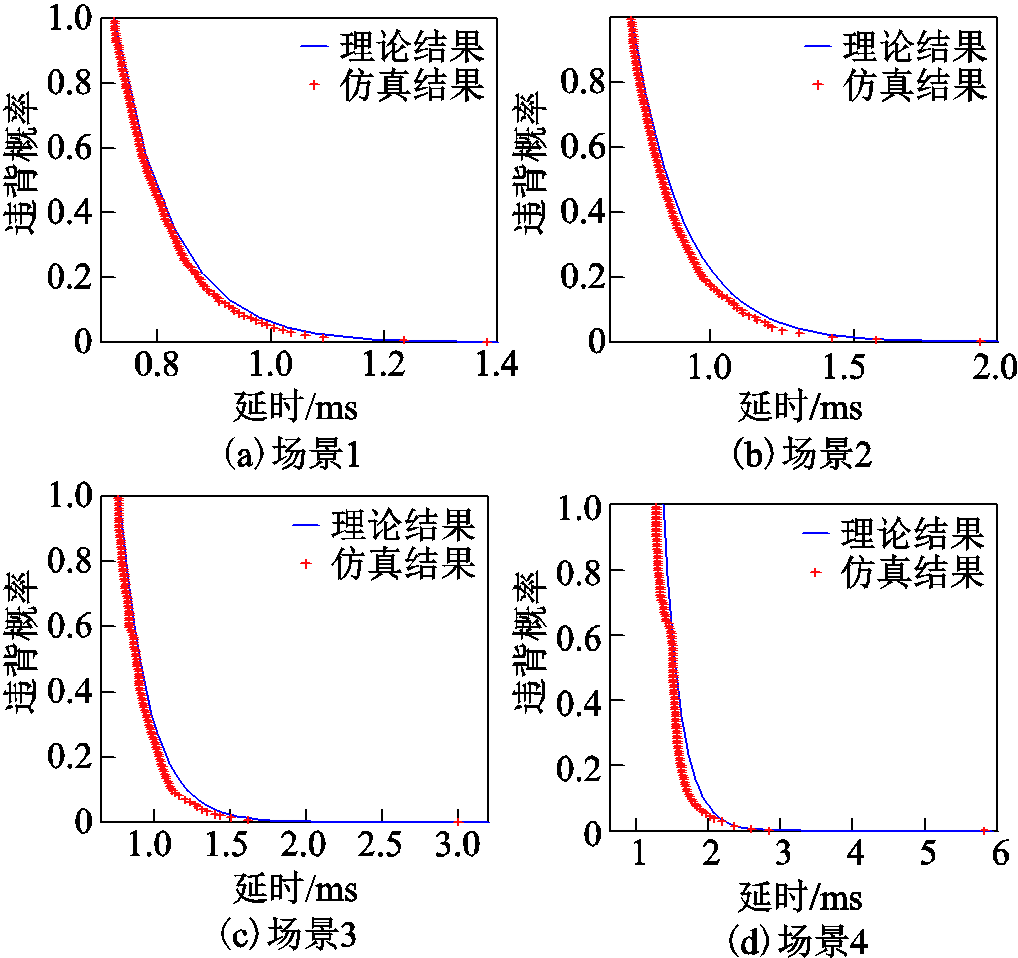
图10 理论推导的时延边界与仿真结果的对比
Fig.10 Comparison between theoretical delay boundary and simulation results
由图10a~图10d的对比结果可以看出在四种不同场景下基于SNC理论推导的时延概率分布均为仿真结果的紧致上边界，并随着不同场景下仿真结果的时延分布趋势的改变而自适应地改变。
为了说明SNC算法时延计算准确性，本文与传统的排队论（Queuing Theory, QT）以及确定网络演算（DNC）方法进行了对比，图11a~图11d为QT法得到的平均时延以及DNC得到的最大时延与真实时延数据的概率分布图。可以看出由QT法得到的基于系统稳态下的平均延时存在遗漏大延时的现象，在正常状态下有39.55%的报文传输延时超过平均延时，而在故障场景中，则有66.42%的超过平均延时。因此会造成DERC系统的控制偏差，甚至导致控制策略失稳；而由DNC方法得到的基于系统“最坏情况”下的延时估计过于保守，一定程度上浪费了系统资源，降低了DERC系统的即时控制响应效率。
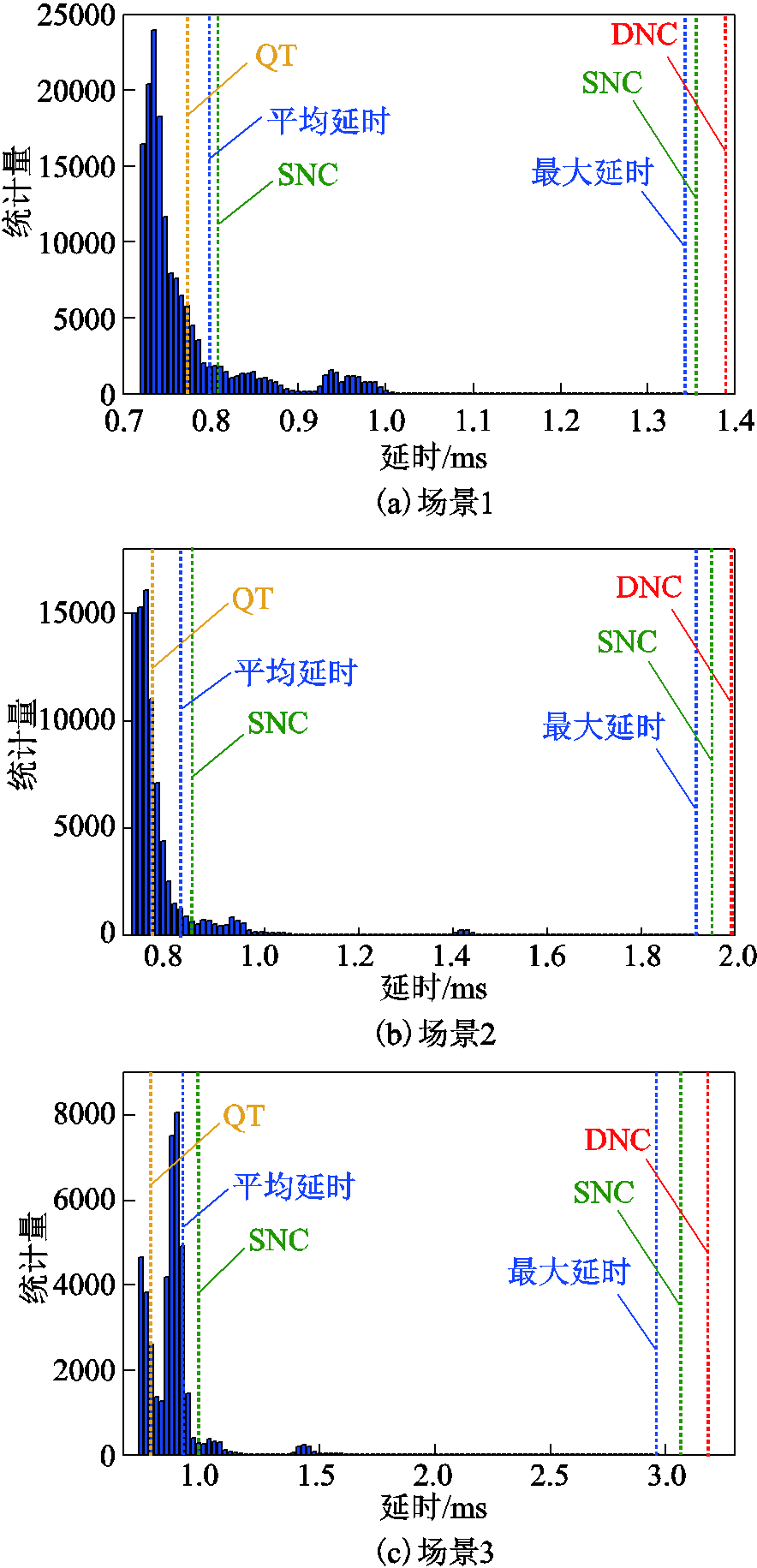
图11 由QT法和DNC法得到的时延与仿真结果对比
Fig.11 Comparison between the time delay obtained by QT method and DNC method and the simulation results
图12对比了SNC、QT、DNC三种网络性能评估方法在DERC四种不同场景下的时延结果。其中，SNC算法的平均时延为时延概率边界曲线的拐点，最大时延为违背概率为0时的时延取值。可以明显看出，无论是平均延时还是最大延时，SNC计算的准确性都是最高的，而且随着场景复杂程度的不断增加，这种优势愈发明显。
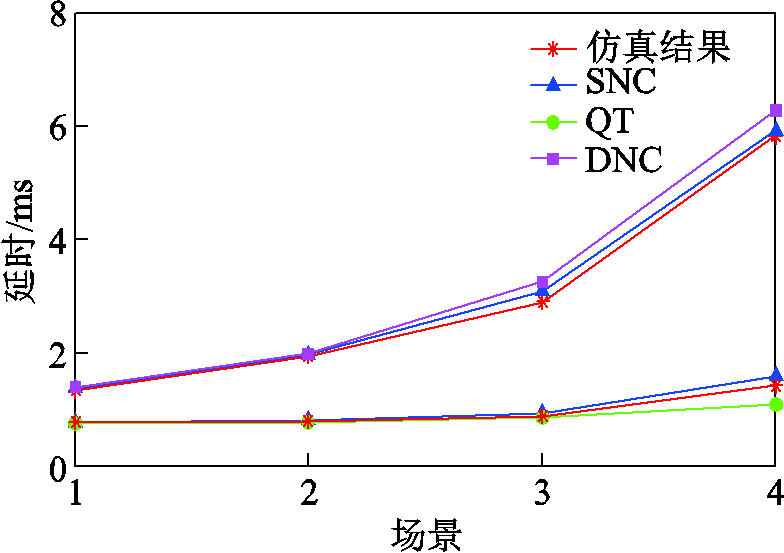
图12 三种算法的性能对比
Fig.12 Performance comparison of three algorithms
通过以上分析可知，基于SNC的时延边界有效地约束了仿真结果，说明本文所建立的时间敏感型业务流量模型以及DERC系统服务模型适用于DERC系统，同时也说明该方法有效地解决了分布式能源系统中传输时延的不确定性和不可预测性，可准确地估计DERC系统通信网络的传输时延上界。
本节通过两组对比实验进一步分析影响DERC系统端到端时延的网络参数及其影响程度。
4.4.1 链路带宽的影响探究实验
随着分布式能源多业务接入点的增多，DERC系统的通信接入网络的带宽也会相应地进行扩展，这里将DERC系统的通信接入网络带宽W范围取为100k~100Mbit/s，其余参数不变，测试不同带宽对DERC系统的通信网络端到端传输时延性能影响，结果如图13所示。
图13 不同带宽对延迟边界的影响
Fig.13 Influence of different bandwidth on delay boundary
图13表明，随着系统中链路传输带宽的增加，同一延时的违背概率也随之减小，同样地，同一违背概率下的系统可容忍的传输时延也随着带宽的增加而减小。虽然链路容量的增加确实可以极大地优化分布式能源系统的实时性，但是带宽增加至一定程度后链路容量增加的趋势明显减缓，时延和违背概率趋于饱和，因此实际中并非一味增加链路带宽资源就能实现对通信性能的提升。这是由于DERC系统的时延特性还与分布式智能电子设备（Intelligent Electronic Devices, IEDs）微流汇聚有关。
4.4.2 节点个数的影响探究实验
将DERC系统中通信服务节点个数设为k=5, 10, 15, 30，其余参数不变，研究系统中包括不同数量的子网对DERC系统的通信网络端到端传输时延性能影响，结果如图14所示。
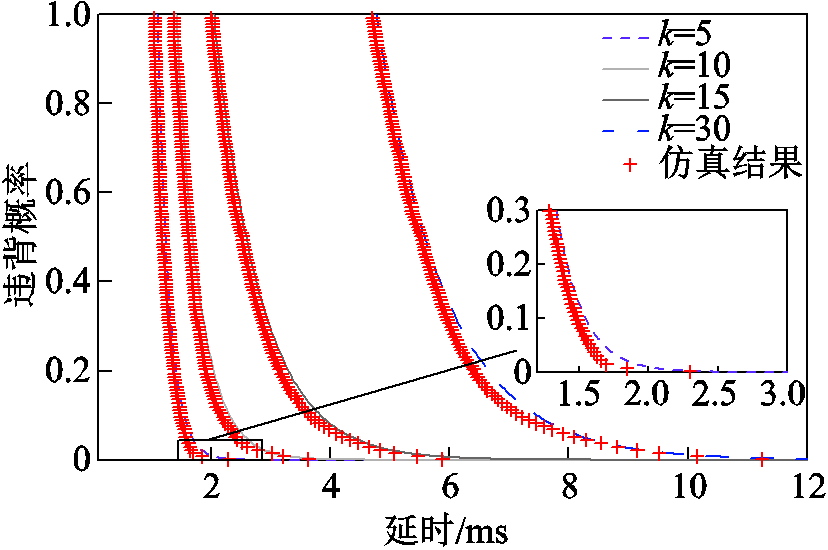
图14 不同节点数量对随机延迟边界的影响
Fig.14 Influence of different number of nodes on random delay boundary
图14表明，随着系统中服务节点个数的增加，同一延时的违背概率也随之增加，同样地，同一违背概率下的系统可容忍的传输时延也随着系统节点个数的增加而增大。因此在DERC系统中，网络规格和接入点多少是影响通信延时的关键因素。这是因为各子网间以及各IEDs间的微流将互相影响，导致积压增加、延时增长。因此，合理规划网络架构将更有效提升分布式能源调控系统的通信性能。
为了进一步说明基于SNC方法计算DERC系统通信时延上界对系统控制性能的提升效果，以图6所示的DERC系统负荷频率控制（Load Frequency Control, LFC）为研究对象进行仿真分析。其频率信息等状态量由IED终端连接接入层上传至骨干层，调控中心根据系统感知的状态信息生成控制命令反馈给各区域分布式能源以维持系统频率稳定，控制算法采用文献[26]提出的LFC-H∞控制算法，依照QT、DNC及SNC三种方法计算的通信延时预设控制器参数，对比DERC系统频率控制效果。其他参数设置见表7。
表7 DERC系统的LFC参数
Tab.7 Parameters of DERC system with LFC
参数含义参数取值 QT延时上界TQT/ms1.10 DNC延时上界TDNC/ms6.29 SNC延时上界TSNC/ms5.93 发电机转动惯量M/(s2×pu)12 发电机阻尼系数/(pu/Hz)1.0 涡轮机时间常数Tch /s0.30 调速器时间常数Tg /s0.37 频率偏差系数β/(pu/Hz)0.425
图15给出DERC系统在由QT、DNC和SNC三种方法计算的延时上界设定下的频率控制偏差。
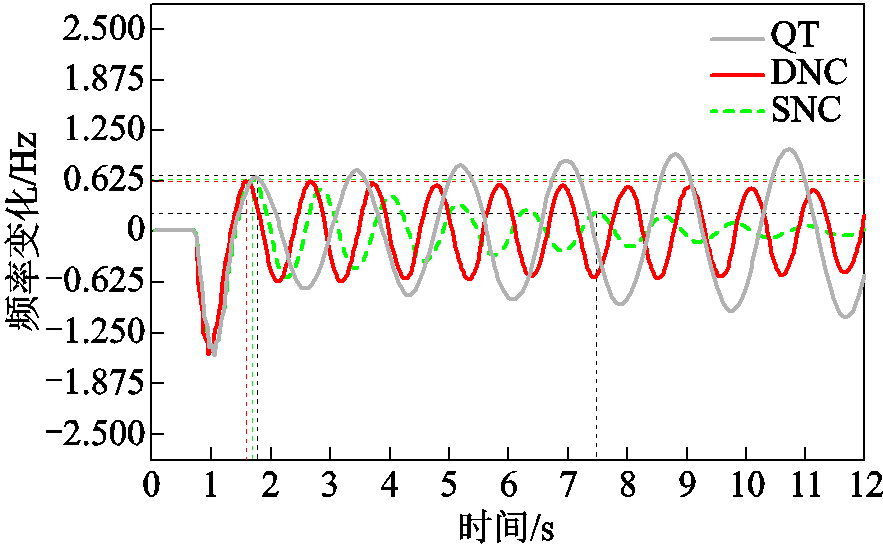
图15 不同时延下DERC系统的频率控制偏差
Fig.15 Frequency control deviation of DERC system under different delays
由实验可知，依据QT法计算延时的控制器设计有使系统失稳的风险，这是因为基于QT法计算的延时上界为平均延时，因此存在大于该上界的情况，致使网络化LFC控制失稳。而DNC和SNC计算延时上界都能够保证系统频率稳定。但SNC方法在7.536s即收敛，表现出比DNC更好的动态性能。
本文研究基于以太网通信的DERC系统，采用SNC理论给出了一种传输时延边界计算方法。其通过建立线性分形稳定噪声（LFSN）自相似业务流量模型，在网络节点处采用延时保证服务和加权公平排队机制调度算法将随机服务曲线具体化，推导出分布式能源通信业务端到端传输延时边界。相较于以往的传统方法，本文所提方法不仅考虑了实际环境干扰因素和聚合数据流竞争服务带来的随机性，而且有效克服了基于QT仅能计算平均延时而遗漏长延时造成网络控制失效的问题，及DNC仅能计算最大延时而易损失系统动态性能且造成网络资源浪费的问题，同时本文在分布式能源系统通信网络框架以及延时模型的研究对DERC系统的优化调度具有指导性意义。通过计及分布式能源物理设备与通信网络紧耦合分析模型的实验，验证了本文提出的SNC时延边界数值计算结果的准确性。并探究了带宽和DERC系统中节点数量对通信端到端时延边界的影响，这为构建满足低时延高可靠性的分布式能源通信网络设计提供了理论支撑。
参考文献
[1] 范士雄, 蒲天骄, 刘广一, 等. 主动配电网中分布式发电系统接入技术及其进展[J]. 电工技术学报, 2016, 31(增刊2): 92-101. Fan Shixiong, Pu Tianjiao, Liu Guangyi, et al. Technologies and its trends of grid integration of distributed generation in active distribution network[J]. Transactions of China Electrotechnical Society, 2016, 31(S2): 92-101.
[2] 丛鹏伟, 唐巍, 娄铖伟, 等. 含高渗透率可再生能源的主动配电网两阶段柔性软开关与联络开关协调优化控制[J]. 电工技术学报, 2019, 34(6): 1263-1272. Cong Pengwei, Tang Wei, Lou Chengwei, et al. Two-stage coordination optimization control of soft open point and tie switch in active distribution network with high penetration renewable energy generation[J]. Transactions of China Electrotechnical Society, 2019, 34(6): 1263-1272.
[3] 李宇泽, 周念成, 侯健生, 等. 计及光伏发电低电压穿越不确定性的主动配电网短路电流概率评估[J]. 电工技术学报, 2020, 35(3): 564-576. Li Yuze, Zhou Niancheng, Hou Jiansheng, et al. Probabilistic evaluation of short-circuit currents in active distribution grids considering low voltage ride-through uncertainty of photovoltaic[J]. Transactions of China Electrotechnical Society, 2020, 35(3): 564-576.
[4] 易文飞, 张艺伟, 曾博, 等. 多形态激励型需求侧响应协同平衡可再生能源波动的鲁棒优化配置[J]. 电工技术学报, 2018, 33(23): 5541-5554. Yi Wenfei, Zhang Yiwei, Zeng Bo, et al. Robust optimization allocation for multi-type incentive-based demand response collaboration to balance renewable energy fluctuations[J]. Transactions of China Electrotechnical Society, 2018, 33(23): 5541-5554.
[5] Lai Jingang, Lu Xiaoqing, Tang Ruoli, et al. Delay-tolerant distributed voltage control for multiple smart loads in AC microgrids[J]. ISA Transactions, 2019, 86: 181-191.
[6] Chen Gang, Zhao Zhongyuan. Delay effects on consensus-based distributed economic dispatch algorithm in microgrid[J]. IEEE Transactions on Power Systems, 2018, 33(1): 602-612.
[7] Xiong Linyun, Li Hao, Wang Jie. LMI based robust load frequency control for time delayed power system via delay margin estimation[J]. International Journal of Electrical Power & Energy Systems, 2018, 100: 91-103.
[8] Singh V P, Kishor N, Samuel P. Load frequency control with communication topology changes in smart grid[J]. IEEE Transactions on Industrial Informatics, 2016, 12(5): 1943-1952.
[9] Ghasempour A. Optimum packet service and arrival rates in advanced metering infrastructure architecture of smart grid[C]//IEEE Green Technologies Conference (Green Tech), Kansas City, MO, USA, 2016:1-5.
[10] Ghasempour A, Moon T K. Optimizing the number of collectors in machine-to-machine advanced metering infrastructure architecture for internet of things-based smart grid[C]//IEEE Green Technologies Conference (Green Tech), Kansas City, MO, USA, 2016: 51-55.
[11] Fidler M. A survey of deterministic and stochastic service curve models in the network calculus[J]. IEEE Communications Surveys & Tutorials, 2010, 12(1): 59-86.
[12] Muller C, Putzke M, Wietfeld C. Traffic engineering analysis of smart grid services in cellular networks[C]//IEEE Third International Conference on Smart Grid Communications, National Cheng Kung University, Taiwan, China, 2012: 252-257.
[13] 高昆仑, 王宇飞, 赵婷. 电网信息物理系统运行中信息-物理交互机理探索[J]. 电网技术, 2018, 42(10): 3101-3109. Gao Kunlun, Wang Yufei, Zhao Ting. Exploration of cyber-physical interaction mechanism in power grid cyber-physical systems operation[J]. Power System Technology, 2018, 42(10): 3101-3109.
[14] 杨挺, 翟峰, 赵英杰, 等. 泛在电力物联网释义与研究展望[J]. 电力系统自动化, 2019, 43(13): 9-20, 53. Yang Ting, Zhai Feng, Zhao Yingjie, et al. Explanation and prospect of ubiquitous electric power internet of things[J]. Automation of Electric Power Systems, 2019, 43(13): 9-20, 53.
[15] IEC 61850—90—7 Communication networks and systems for power utility automation-object models for power converters in distributed energy resources (DER) system[S].
[16] Yang Ting, Zhao Rui, Zhang Weixin, et al. On the modeling and analysis of communication traffic in intelligent electric power substations[J]. IEEE Transactions on Power Delivery, 2017, 32(3): 1329-1338.
[17] 李昌超, 康忠健, 于洪国, 等. 考虑电力业务重要性的电力通信网关键节点识别[J]. 电工技术学报, 2019, 34(11): 2384-2394. Li Changchao, Kang Zhongjian, Yu Hongguo, et al. Identification of key nodes in power communication network[J]. Transactions of China Electrotechnical Society, 2019, 34(11): 2384-2394.
[18] Budka K C, Deshpande J G, Doumi T L, et al. Communication network architecture and design principles for smart grids[J]. Bell Labs Technical Journal, 2010, 15(2): 205-227.
[19] Wang P, Akyildiz I F. Improving network connectivity in the presence of heavy-tailed interference[J]. IEEE Transactions on Wireless Communications, 2014, 13(10): 5427-5439.
[20] Iftikhar M, Mathkour H, Imran M, et al. A novel framework for G/M/1 queuing system based on scheduling-cum-polling mechanism to analyze multiple classes of self-similar and LRD traffic[J]. Wireless Networks, 2016, 22(4): 1269-1284.
[21] 郝唯杰, 杨强, 李炜. 基于FARIMA模型的智能变电站通信流量异常分析[J]. 电力系统自动化, 2019, 43(1): 158-169. Hao Weijie, Yang Qiang, Li Wei. FARIMA model based analysis of communication traffic anomaly in smart substation[J]. Automation of Electric Power Systems, 2019, 43(1): 158-169.
[22] Karasaridis A, Hatzinakos D. Network heavy traffic modeling using α-stable self-similar processes[J]. IEEE Transactions on Communications, 2001, 49(7): 1203-1214.
[23] Jiang Yuming, Liu Yong. Stochastic network calculus[M]. London U K: Springer-Verlag, 2008.
[24] Jiang Yuming, Yin Qinghe, Liu Yong, et al. Fundamental calculus on generalized stochastically bounded bursty traffic for communication networks[J]. Computer Networks, 2009, 53(12): 2011-2021.
[25] Jensen Tue V, de Sevin Hugo, Greiner Martin, et al. The RE-Europe data set[DB/OL]. Zenodo, 2017, http://doi.org/10.5281/zenodo.999150
[26] Peng Chen, Li Jicai, Fei Minrui. Resilient event-triggered H-infinity load frequency control for networked power systems with energy-limited DoS attacks[J]. IEEE Transactions on Power Systems, 2017, 32(5): 4110-4118.
Upper Bound Calculation of Delay of Distributed Energy Resource Coordinated-Control System Based on Stochastic Network Calculus
Abstract As a large number of distributed energy resources are connected to the grid for operation, the determinability of communication delay and network control become the keys to ensure the stable operation of the system. This paper studied the distributed energy system based on Ethernet communication and proposed a calculation method of transmission delay boundary using stochastic network calculus theory. With the establishment of self-similar traffic model, we use delay guarantee services and weighted fair queuing mechanism scheduling algorithms at the network nodes to concretize the random service curve and derive the end-to-end transmission delay boundary of distributed energy communication network, which could effectively overcome traditional queuing theory that can cause the problem of network control failure due to calculating the average delay only and omitting the long delay. Finally, the accuracy of the numerical calculation results of the delay boundary of the stochastic network algorithm proposed in this paper is verified by experiments that take into account the tightly coupled analysis model of distributed energy physical equipment and communication networks constructed by OPNET simulation software. The research provides an accurate analysis of the transmission characteristics of different communication architectures and provides theoretical support at the communication level for distributed energy networked control.
keywords：Distributed energy resource, stochastic network calculus, service curve, end-to-end transmission, delay bound
中图分类号：TM734
DOI：10.19595/j.cnki.1000-6753.tces.191802
国家电网公司总部科技项目（5400-202024116A-0-0-00）、国家自然科学基金（61971305）、国家重点研发计划（2017YFE0132100）、天津市自然科学基金（19JCQNJC06000）资助。
收稿日期 2019-12-23
改稿日期 2020-02-24
孟广雨 女，1995年生，硕士研究生，研究方向为电力系统通信。E-mail：mengguangyu@tju.edu.cn
杨 挺 男，1979年生，教授，博士生导师，研究方向为电力信息物理系统。E-mail：yangting@tju.edu.cn（通信作者）
（编辑 郭丽军）