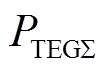 与MPPT换流器端电压
与MPPT换流器端电压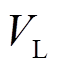 的特性曲线(
的特性曲线(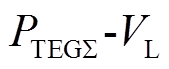 )是一条含多个局部最大功率点(Local Maximum Power Point, LMPP)和唯一全局最大功率点(Global Maximum Power Point, GMPP)的非线性曲线[11]。系统的非线性特性往往给系统的运行、控制和优化带来巨大的挑战[12]。文献[4-9]所提MPPT算法还存在因无法识别LMPP和GMPP,导致系统发电效率较低的问题。
)是一条含多个局部最大功率点(Local Maximum Power Point, LMPP)和唯一全局最大功率点(Global Maximum Power Point, GMPP)的非线性曲线[11]。系统的非线性特性往往给系统的运行、控制和优化带来巨大的挑战[12]。文献[4-9]所提MPPT算法还存在因无法识别LMPP和GMPP,导致系统发电效率较低的问题。摘要 该文提出一种基于贪婪搜索的神经网络(GSNN)算法,以实现非均匀温差分布下集中式温差发电系统的最大功率跟踪(MPPT)。首先,以DC-DC升压变换器占空比为输入,系统输出功率为输出,建立双层前馈神经网络模型。然后,采用Levenberg-Marquardt法训练神经网络,得到系统的输入-输出(I/O)拟合曲线,以准确区分局部最大功率点(LMPP)和全局最大功率点(GMPP)。同时,基于拟合的曲线,设计压缩范围的贪婪策略快速逼近GMPP。恒定温度、阶跃温度和灵敏度分析三种算例下的仿真结果表明,与扰动观测法、粒子群算法和灰狼算法相比,GSNN能在非均匀温差分布下快速、稳定地输出最大功率。最后,基于dSpace的硬件在环(HIL)实验验证了所提算法的硬件可行性。
关键词:集中式温差发电系统 非均匀温差分布 最大功率跟踪 神经网络
温差发电(Thermoelectric Generation,TEG)的原理是利用热电材料的Seebeck效应将热能转换为电能,其不仅能有效利用自然界中的地热能、海洋热能和太阳能等清洁能源,还可回收工业及生活中产生的大量余热废热,提高能源利用率[1]。因此,在能源危机和环境污染的时代背景下,TEG被认为是一种具有广阔前景的绿色发电技术[2]。
通常,TEG系统工作在具有时变温差的动态环境中。因此,需设计有效的最大功率跟踪(Maximum Power Point Tracking, MPPT)算法,以在各种复杂工况下最大限度地获得系统输出功率[3]。目前,增量电导法(Incremental Conductance,INC)[4]和扰动观测法(Perturb and Observe,P&O)[5]是TEG系统中两种常用的MPPT方法,具有结构简单、可靠性高的优点。但是,上述两种方法在收敛到最大功率点(Maximum Power Point,MPP)附近时振荡明显。开路电压法(Open-Circuit Voltage,OCV)[6]和短路电流法(Short-Circuit Current,SCC)[7]是基于TEG模块固有特性提出的MPPT方法,其仅需测量电压或电流一个物理量,但电压、电流的测量需周期性地断开TEG负载,易导致功率损失。同时,文献[8]结合P&O和OCV的优点,设计了一种混合算法,能快速实现MPPT,且无需额外电路。但由于P&O的固有缺陷,该方法仍然存在稳态振荡的问题。文献[9]提出了一种基于线性外推原理的MPPT算法,仅需两个工作点即可快速计算出最大功率点的位置,但该方法需要精确的TEG系统模型。
此外,上述MPPT算法多针对组串式TEG系统和模块式TEG系统开发。这两类TEG系统为实现精确的MPPT,包含了大量MPPT换流器,极大地增加了系统的运行成本[10]。相比之下,集中式TEG系统仅需一个MPPT换流器,可极大地降低系统成本。但是,在TEG系统实际运行中,每个TEG模块的温度不尽相同,即处于非均匀温差分布(Non-Uniform Temperature Distribution, NTD)条件。NTD下,集中式TEG系统总输出功率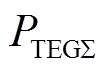 与MPPT换流器端电压
与MPPT换流器端电压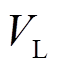 的特性曲线(
的特性曲线(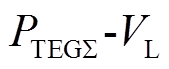 )是一条含多个局部最大功率点(Local Maximum Power Point, LMPP)和唯一全局最大功率点(Global Maximum Power Point, GMPP)的非线性曲线[11]。系统的非线性特性往往给系统的运行、控制和优化带来巨大的挑战[12]。文献[4-9]所提MPPT算法还存在因无法识别LMPP和GMPP,导致系统发电效率较低的问题。
)是一条含多个局部最大功率点(Local Maximum Power Point, LMPP)和唯一全局最大功率点(Global Maximum Power Point, GMPP)的非线性曲线[11]。系统的非线性特性往往给系统的运行、控制和优化带来巨大的挑战[12]。文献[4-9]所提MPPT算法还存在因无法识别LMPP和GMPP,导致系统发电效率较低的问题。
启发式算法具有无模型、搜索能力强以及能避免局部最优的特点,为解决上述难题提供了新的思路。目前,粒子群优化算法(Particle Swarm Optimization, PSO)[13]、灰狼优化算法(Grey Wolf Optimizer, GWO)[14]和细菌觅食算法(Bacteria Foraging Algorithm, BFA)[15]等启发式算法已在与本文研究领域类似的阴影条件下光伏系统MPPT上得到了成功应用。然而,这类算法为找到高质量的MPP通常需要较长的计算时间,难以满足TEG系统实现快速MPPT的要求[16]。
近年来,神经网络成为了人工智能领域的研究热点,其通过模拟大脑处理信息的过程,可实现非线性关系的良好映射。目前,神经网络已成功应用于电力负荷识别[17]、短期负荷预测[18]和锂离子电池健康状态预测[19]等工程问题。因此,基于神经网络的思想,可以不考虑TEG系统的详细数学模型,将NTD下集中式TEG系统的MPPT等效为一个黑箱问题,从该“黑箱”的实际输入数据和输出数据中挖掘两者的非线性关系。
基于上述讨论,本文针对NTD下集中式TEG系统的MPPT,提出了一种基于贪婪搜索的神经网络(Greedy Search Based Neural Network, GSNN)算法。该方法采用前馈神经网络,基于系统实时运行数据拟合系统控制输入与功率输出的非线性关系,以准确区分LMPP和GMPP。其中,神经网络训练的样本数据通过贪婪搜索获得。最后,通过恒定温度、阶跃温度、灵敏度分析三种算例,对所提方法的MPPT效果与P&O、PSO和GWO的效果进行对比,仿真结果证明了GSNN的有效性与优势。同时,基于dSpace的硬件在环(Hardware-In-Loop, HIL)实验验证了GSNN的硬件可行性。
图1为TEG系统的示意图和等效电路。如图所示,如果将N型和P型半导体连接起来,并将其一端置于热端(温度为Th),另一端置于冷端(温度为Tc),则会产生一个温差电动势Voc,这种现象称为Seebeck效应。其中,Voc的表达式为[8]
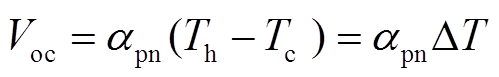 (1)
(1)式中,apn为Seebeck系数;Th和Tc分别为热端和冷端的温度;DT为热端和冷端之间的温差。
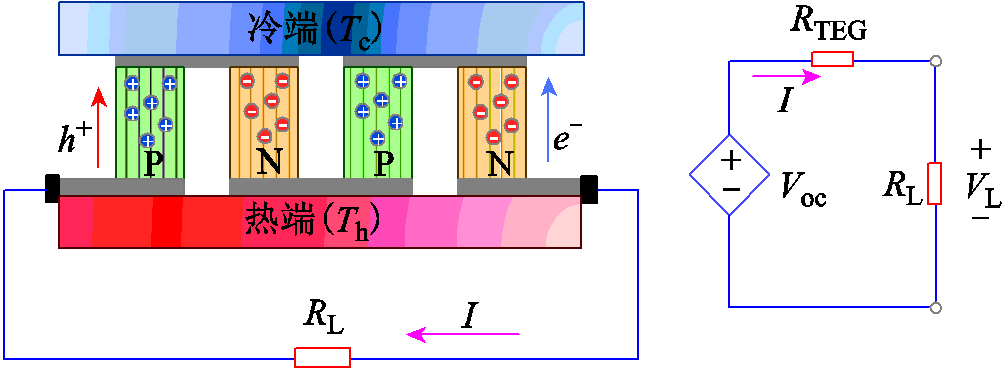
图1 TEG模块示意图及等效电路
Fig.1 Diagrammatic drawing and equivalent circuit of a TEG module
此外,在温度梯度的均匀导体中通有电流时,导体除产生和电阻有关的焦耳热外,还要吸收或放出热量,这一现象称为Thomson效应。Thomson系数τ可表示为
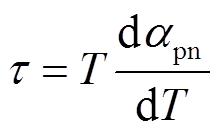 (2)
(2)
式中,T为平均温度。
实际上,对于确定的TEG模块,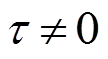 。因此,Seebeck系数将随着平均温度的变化而变化,具体数学关系可描述为
。因此,Seebeck系数将随着平均温度的变化而变化,具体数学关系可描述为
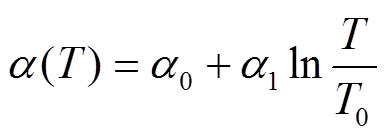 (3)
(3)式中,a0为Seebeck系数的初始变化率;a1为Seebeck系数的变化率;T0为参考温度。
最后,根据基本电路理论,TEG模块的输出功率PTEG可表示为
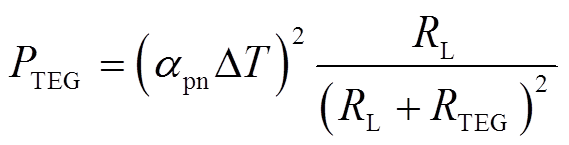 (4)
(4)式中,RTEG和RL分别为TEG模块的内阻和负载电阻。
在集中式TEG系统中,为获得期望的输出电压和功率,通常将若干TEG模块通过串、并联方式组合在一起,其输出电流和电压间的关系可表示为[9]
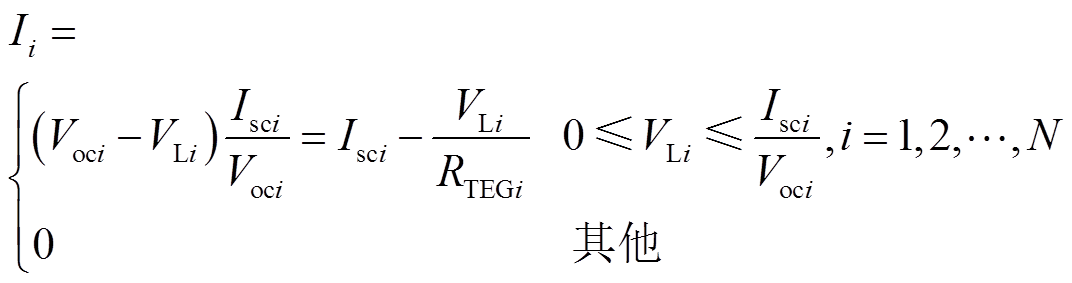 (5)
(5)式中,Voci和Isci分别为第i个TEG模块的开路电压和短路电流;VLi和RTEGi分别为第i个TEG模块的端电压和内阻。
第i个TEG模块的输出功率PTEG可表示为
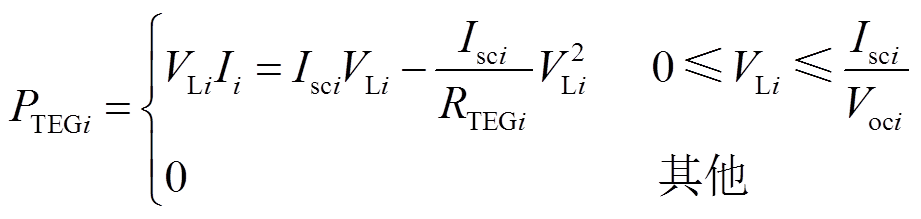 (6)
(6)集中式TEG系统的总输出功率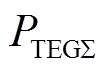 可表示为
可表示为
 (7)
(7)
在NTD条件下,各TEG模块的温度不尽相同,因此集中式TEG系统的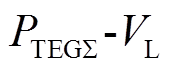 的特性曲线是呈多峰特性的非线性曲线,如图2所示。MPPT设计的目的即为快速稳定地寻找GMPP。
的特性曲线是呈多峰特性的非线性曲线,如图2所示。MPPT设计的目的即为快速稳定地寻找GMPP。
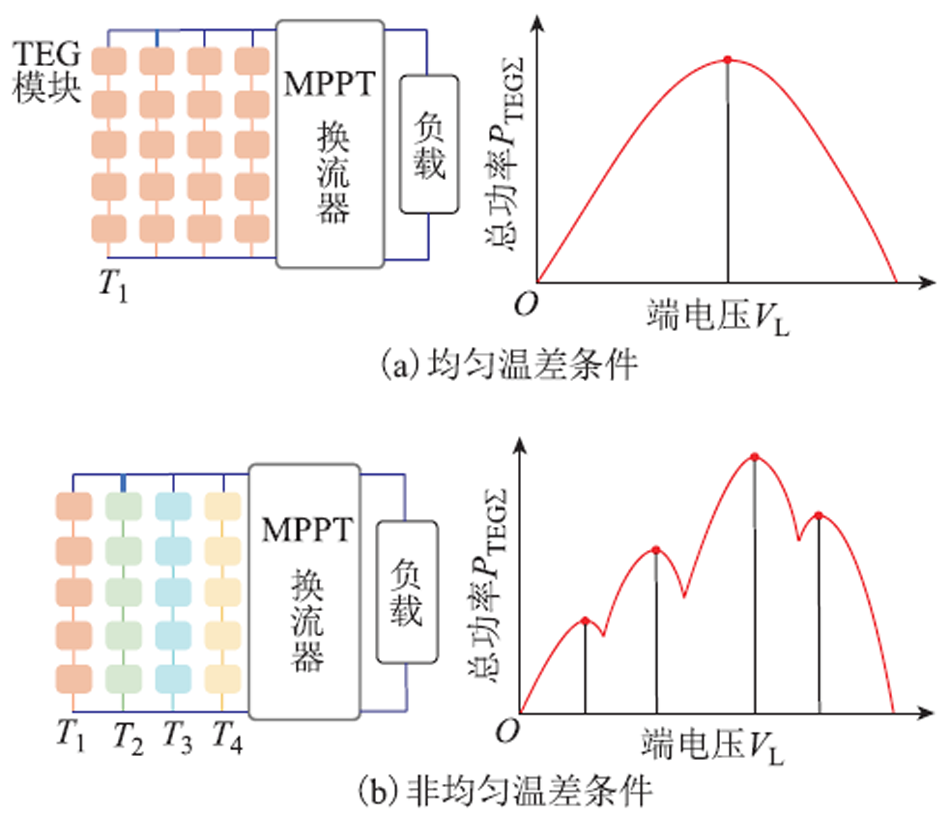
图2 不同工况下集中式TEG系统运行图及其特性曲线
Fig.2 Operation diagram and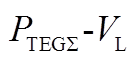 curve of centralized TEG systems under different circumstances
curve of centralized TEG systems under different circumstances
目前,TEG系统的MPPT一般基于DC-DC升压变换器实现,具体控制结构如图3所示。由图可见,MPPT控制器输出的占空比指令经脉冲宽度调制(Pulse Width Modulation, PWM)后进入绝缘栅双极型晶体管(Insulated Gate Bipolar Transistor, IGBT),TEG系统的输出电压因此动态变化并反馈至MPPT控制器中。DC-DC升压变换器的输入电压和输出电压的关系可表示为[20]
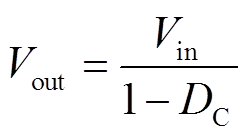 (8)
(8)
式中,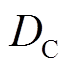 为DC-DC升压变换器的占空比,
为DC-DC升压变换器的占空比,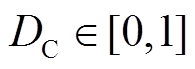 ;Vin和Vout分别为DC-DC升压变换器的输入和输出电压,其中Vin也是集中式TEG系统的输出电压。
;Vin和Vout分别为DC-DC升压变换器的输入和输出电压,其中Vin也是集中式TEG系统的输出电压。
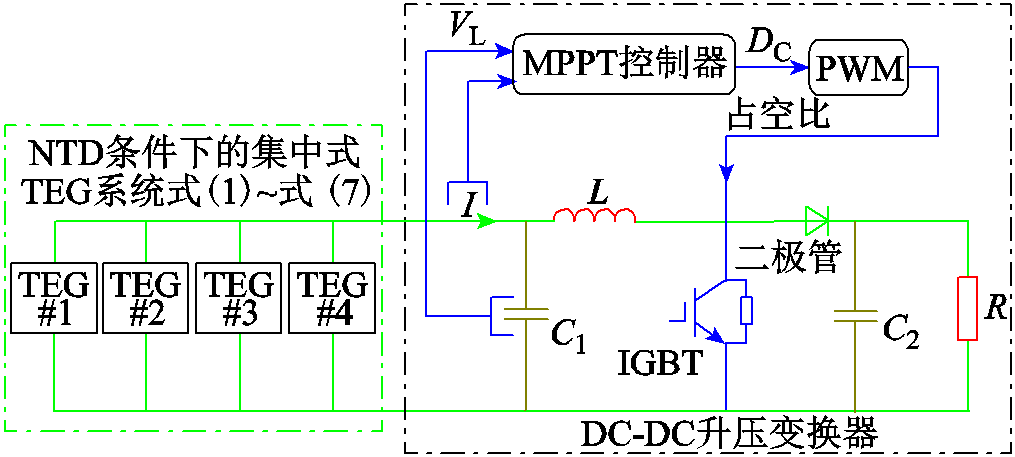
图3 NTD下TEG系统的MPPT控制结构
Fig.3 Overall MPPT framework of centralized TEG system under NTD condition
GSNN实现MPPT的控制框架包括训练神经网络和贪婪搜索两部分,如图4所示。首先,将前馈神经网络的输入和输出分别设置为DC-DC升压变换器的占空比和对应的TEG系统输出功率,进行神经网络训练。然后,基于神经网络训练拟合的输入-输出(I/O)曲线,执行贪婪搜索,得到新的训练样本,并重新训练神经网络。上述过程将反复执行,直至满足算法迭代终止条件。
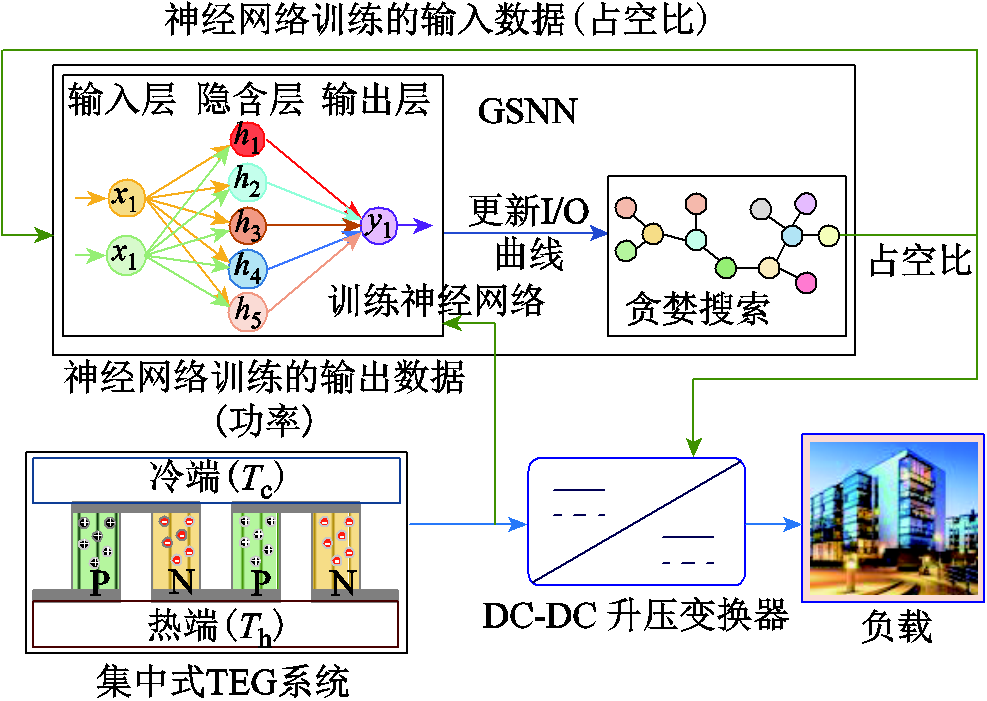
图4 DSNN整体控制框架
Fig.4 Overall control framework of DSNN
由MPPT控制结构可知,集中式TEG系统总输出功率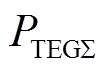 与DC-DC升压变换器占空比的特性曲线和
与DC-DC升压变换器占空比的特性曲线和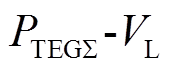 特性曲线一样,是一条具有多个局部极值的单输入-单输出非线性曲线。因此,采用简单的双层前馈神经网络即可实现上述单输入-单输出非线性曲线的良好拟合。双层前馈神经网络的结构如图4所示,其由输入层、隐含层和输出层组成[21]。
特性曲线一样,是一条具有多个局部极值的单输入-单输出非线性曲线。因此,采用简单的双层前馈神经网络即可实现上述单输入-单输出非线性曲线的良好拟合。双层前馈神经网络的结构如图4所示,其由输入层、隐含层和输出层组成[21]。
为实现集中式TEG系统的MPPT,分别将前馈神经网络的输入、输出矢量设置为DC-DC升压变换器占空比和对应的TEG系统输出功率,分别为
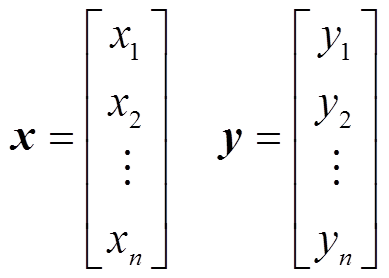 (9)
(9)式中,x为占空比矢量,即输入层输入矢量;y为系统输出功率矢量,即输出层输出矢量;n为训练样本数。
隐含层和输出层的输出分别为
 (10)
(10)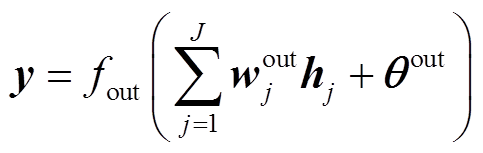 (11)
(11)
式中,hj为第j个隐含层神经元的输出矢量;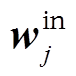 为输入层和第j个隐含层神经元之间的权值;
为输入层和第j个隐含层神经元之间的权值;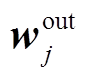 为输出层和第j个隐含层神经元之间的权值;qj为第j个隐含层神经元的阈值;
为输出层和第j个隐含层神经元之间的权值;qj为第j个隐含层神经元的阈值;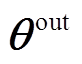 为输出层的阈值;J为隐含层神经元总数;fh和fout分别为隐藏层神经元和输出层神经元的激活函数,本文分别设计Sigmoid函数和线性函数为
为输出层的阈值;J为隐含层神经元总数;fh和fout分别为隐藏层神经元和输出层神经元的激活函数,本文分别设计Sigmoid函数和线性函数为
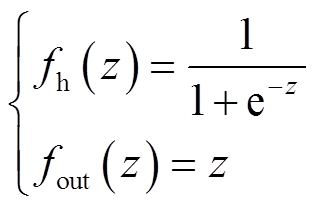 (12)
(12)基于神经网络训练拟合的I/O曲线,GSNN采用贪婪搜索来逼近真实的功率全局最优点。为提高收敛速度,贪婪搜索范围设计为随迭代次数的增加而逐渐压缩,即
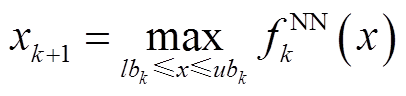 (13)
(13)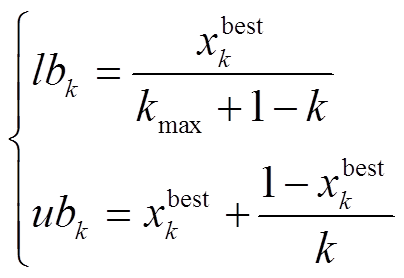 (14)
(14)
式中,k为迭代次数;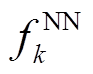 为神经网络在第k次迭代的映射函数;xk+1为第k+1次迭代的占空比;
为神经网络在第k次迭代的映射函数;xk+1为第k+1次迭代的占空比;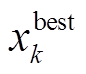 为第k次迭代的当前最优解;lbk和ubk为搜索范围的上、下边界,即占空比的取值范围;kmax为最大迭代次数。
为第k次迭代的当前最优解;lbk和ubk为搜索范围的上、下边界,即占空比的取值范围;kmax为最大迭代次数。
通常,神经网络的初始训练样本对算法的搜索性能有重要影响。为增加初始样本的代表性及多样性,GSNN在搜索范围内均匀选择初始样本,即
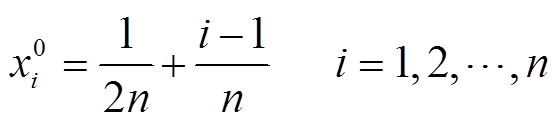 (15)
(15)式中,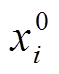 为第i个训练样本的初始占空比。
为第i个训练样本的初始占空比。
对于实际系统来说,只要温差发电系统连接的DC-DC变换器占空比能进行控制,则完全有条件得到多个训练样本进行多次寻优。占空比进入DC-DC升压变换器后,即可获得对应的集中式TEG系统输出功率,即第i个训练样本的实际输出值,即
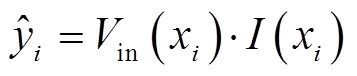 (16)
(16)式中,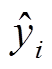 为第i个训练样本期望的输出功率,即实际值;Vin(xi)和I(xi)分别为执行占空比xi后集中式TEG系统的输出电压和电流。
为第i个训练样本期望的输出功率,即实际值;Vin(xi)和I(xi)分别为执行占空比xi后集中式TEG系统的输出电压和电流。
目前,常用的神经网络训练方法有Momentum法、Adagrad法和Levenberg-Marquardt法等[22]。其中,Levenberg-Marquardt法具有稳定性高、收敛速度快的优点,适合全局寻优[23]。因此,本文选择其训练神经网络,以满足集中式TEG系统MPPT实时计算的需求。
将训练样本预测值与期望值的方均误差作为神经网络训练的目标函数,以最小化两者间的差异,其表达式为
 (17)
(17)式中,yi为第i个训练样本预测的输出功率。
基于上述设计,将初始训练样本数设置为10,进行神经网络预训练,结果如图5所示。由图可见,由初始样本获得的I/O曲线与实际曲线已十分接近。而随着样本数的增加,实际曲线与拟合曲线间的拟合误差将逐渐减小。
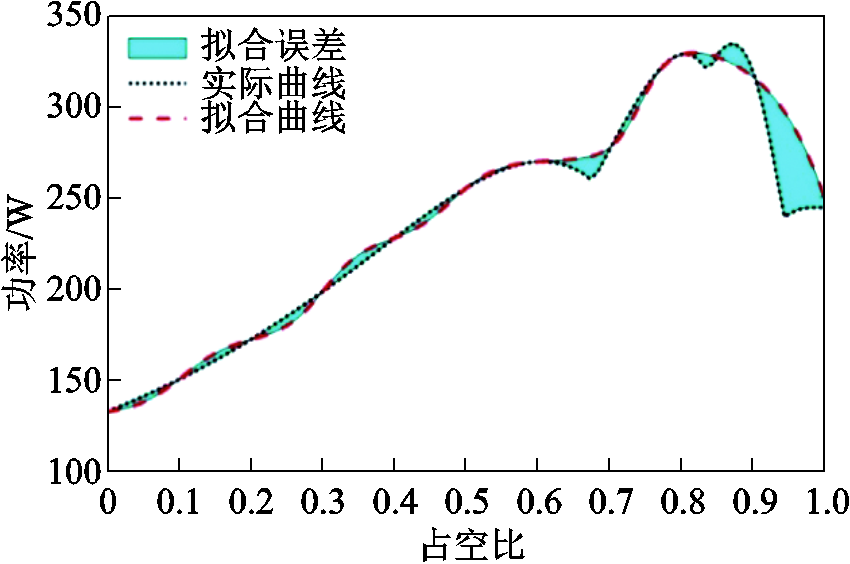
图5 初始样本拟合的I/O曲线
Fig.5 I/O curve fitting of initial samples
至此,NTD下基于GSNN的集中式TEG系统MPPT总体流程见表1。本质上来说,在通过初始训练样本训练之后,GSNN算法是同时获取新样本更新网络参数,同时进行寻优的。对于不同的集中式温差发电系统,本文所提算法主要通过寻找DC-DC直流变换器的最优占空比来实现最大功率运行点的跟踪。因此,对于更大规模的集中式温差发电系统来说,算法的控制变量及复杂程度并没有发生较大改变,算法只需在较短时间内逼近最优占空比即可,总的收敛计算时间为(n0+kmax)×MPPT控制周期。
表1 NTD下基于GSNN的集中式TEG系统MPPT总体流程
Tab.1 The overall execution procedure of GSNN based MPPT of centralized TEG under NTD

1. 初始化训练样本(式(15))2. 初始化前馈神经网络的激活函数(式(17))3. 设置k=14. FORi=1 to n05. 将第i个训练样本的占空比输入DC-DC升压变换器6. 采集集中式TEG系统的实时电流、电压信号7. 计算第i个训练样本的输出功率期望值(式(16))8. END FOR9. 确定当前最优解10. WHILE k
为验证所设计GSNN的有效性,本节以P&O[5]、PSO[13]和GWO[14]为参照对象,在恒定温度、阶跃温度和灵敏度分析三种算例下进行仿真比较。其中,P&O的固定步长设置为0.005s,启发式算法的种群大小和最大迭代次数均设置为5,而所有算法的控制周期均为0.01s。由于PSO和GWO算法寻优迭代需要耗费时间为5×5×MPPT控制周期,加上初始化种群5个个体的探索所需时间,总的收敛计算时间为5×(5+1)×0.01=0.3s。与之相比,GSNN计算所需耗费时间为(10+10)×0.01=0.2s。GSNN集中式TEG系统和DC-DC升压变换器参数见表2。仿真在1.8GHz IntelR CoreTMi7 CPU和16GBRAM配置的个人计算机上运行,模型利用Matlab/ Simulink2017b搭建。
表2 集中式TEG系统和DC-DC升压变换器参数表
Tab.2 The main parameters of centralized TEG system and the connected DC-DC boost converter
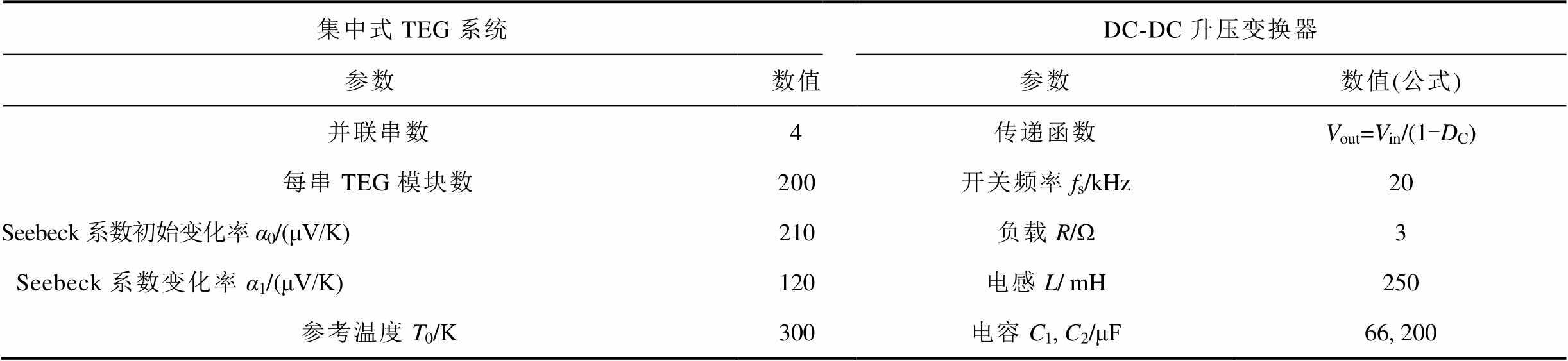
集中式TEG系统DC-DC升压变换器 参数数值参数数值(公式) 并联串数4传递函数Vout=Vin/(1-DC) 每串TEG模块数200开关频率fs/kHz20 Seebeck系数初始变化率α0/(μV/K)210负载R/Ω3 Seebeck系数变化率α1/(μV/K)120电感L/ mH250 参考温度T0/K300电容C1, C2/μF66, 200
在GSNN中,有五个主要参数对算法性能有重要影响,包括:初始训练样本数n0、Levenberg-Marquardt法最大迭代次数Imax、隐含层神经元数目J、贪婪搜索的控制精度σ和GSNN的最大迭代次数kmax。以主要参数n0及kmax为例,分别取值为5、10、15和20,总共4×4=16个组合。图6给出了不同参数组合下的收敛输出功率和计算时间分布图,其中四个TEG模块串的冷端温度分别设置为47℃、31℃、18℃和13℃;热端温度分别设置为247℃、123℃、76℃和41℃。从图6a可以看出:随着n0和kmax的增加,算法可以收敛到更大的功率运行点;当n0>10且kmax>10之后,输出功率增加幅度较小。另外,如图6b所示,算法的计算时间随着n0和kmax的增加而明显增加。为有效平衡计算时间和收敛功率点质量两者的权重,本文将其分别取n0=10和kmax=10。同理,其他参数也通过多次仿真结果对比进行选定,参数见表3。
表3 GSNN主要参数
Tab.3 The main parameters of GSNN

参数范围取值 n010 Imax300 J5 σ0.001 kmax10
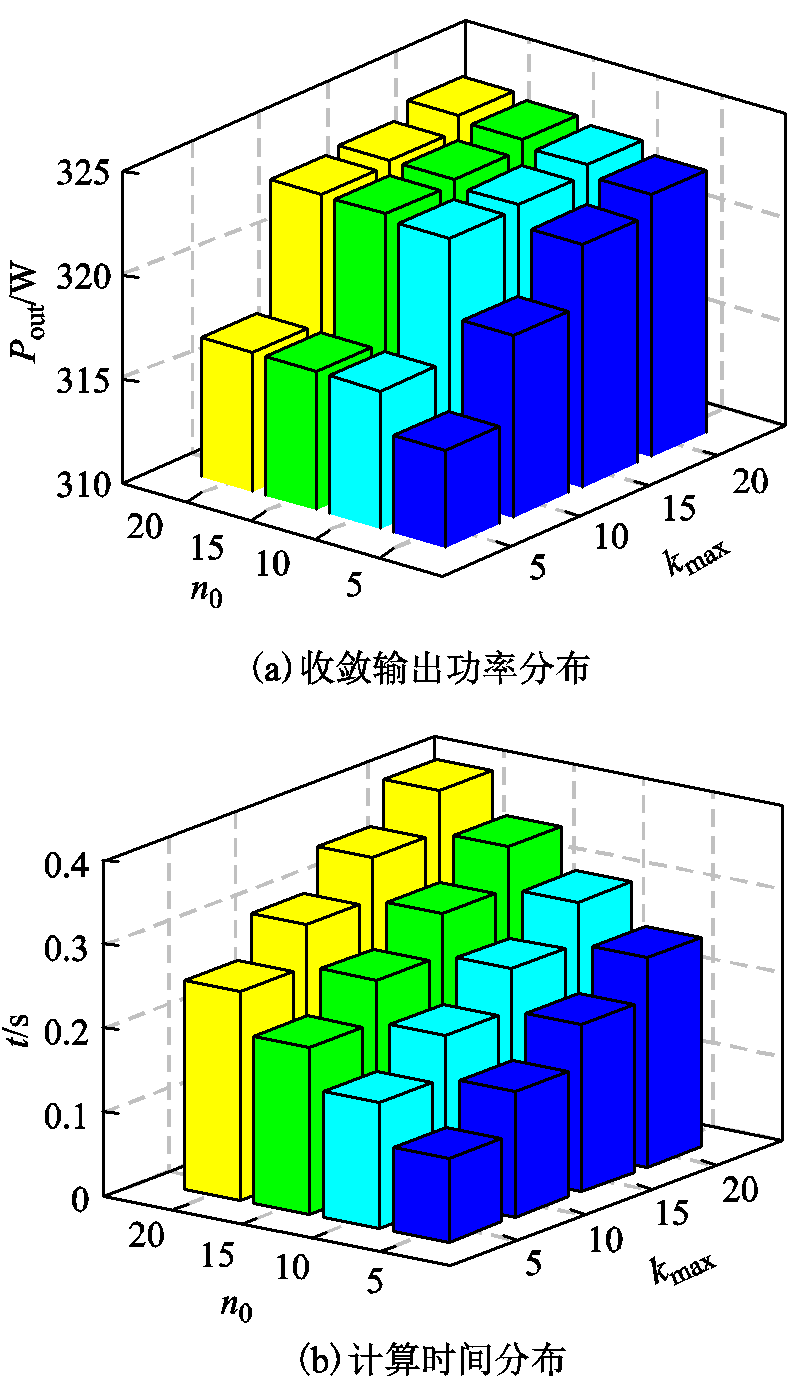
图6 不同参数(n0和kmax)下MPPT结果分布
Fig.6 Distributions of MPPT results obtained under different parameters (n0 and kmax)
通过仿真多次对比选择的方法得到最优参数,本质上也会增加算法的计算时间,但这部分计算时间属于实际应用前的算法参数调试过程或离线仿真测试选定过程。当算法投入到实际系统应用后,不会增加多余的计算时间。同样地,对于本文的对比算法,例如PSO和GWO,其参数也是经过多次仿真结果对比选定的结果。具体来说,这两种算法的共性参数是种群大小和最大迭代步数,这也是最重要的两个参数。同样地,这两个参数取值越大,算法则以更高概率收敛到更高质量的功率运行点,但也会增加总的计算时间。因此,与本文所提算法参数设置原则一样,需要根据优化结果平衡计算时间和功率运行点二者的权重,进而选定最优的参数。为了对比算法公平性,对于不同的群智能算法,这些共性参数也应设置为一样。对于算法的特有参数,例如PSO算法的惯性权重系数,则可以根据自身的寻优结果对比各自设定。
将四个TEG模块串的冷端温度分别设置为47℃、31℃、18℃和13℃;热端温度分别设置为247℃、123℃、76℃和41℃。上述工况下,不同算法的MPPT结果如图7所示。显然,P&O由于不能区分LMPP和GMPP,输出的功率最小。相比之下,PSO和所设计GSNN具有较强的搜索能力,能够收敛到高质量的MPP。但是,与PSO相比,GSNN收敛更加稳定。特别地,GSNN的功率超调量分别仅为PSO和GWO的4.85%、11.53%。这表明基于拟合曲线的高效引导,GSNN可避免盲目的随机搜索。
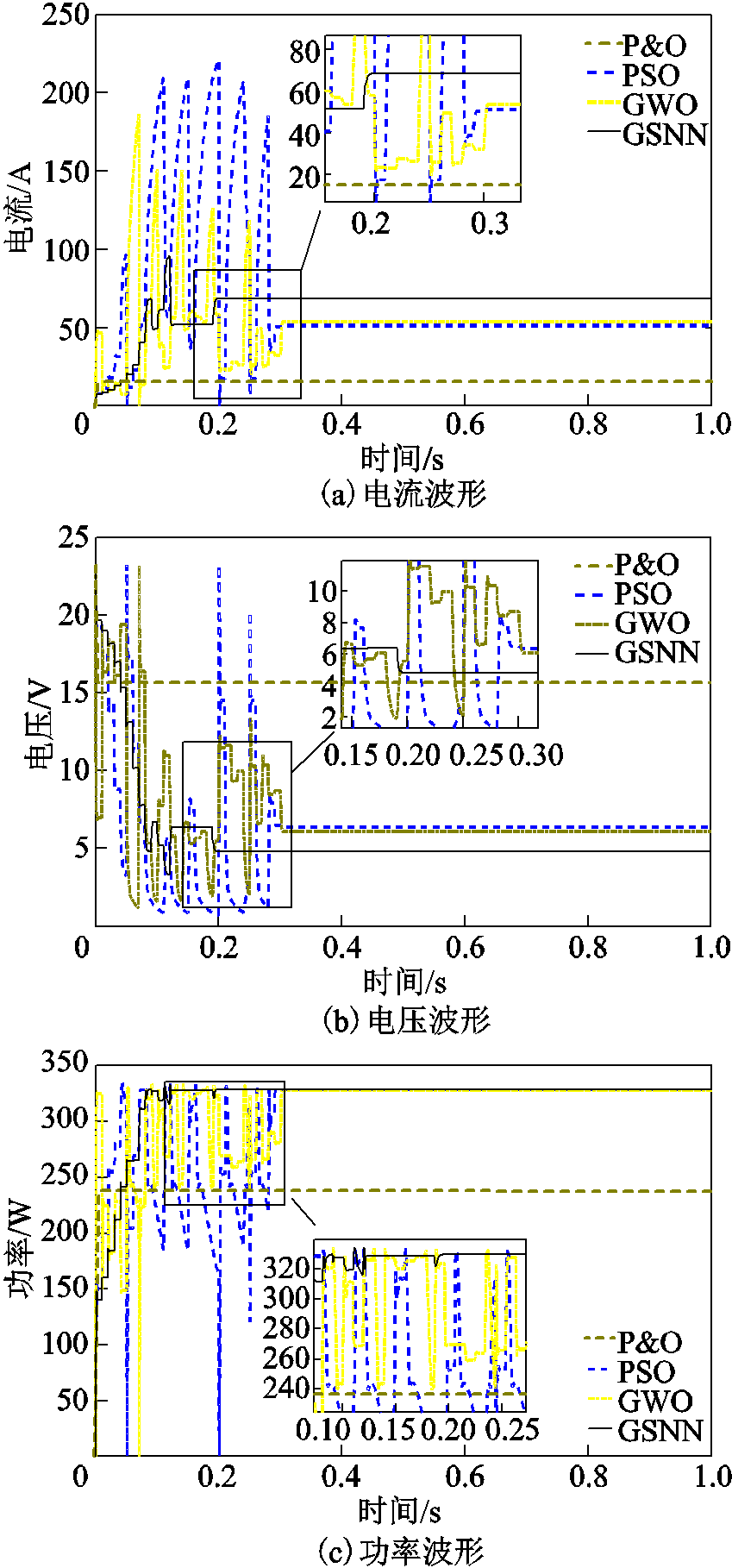
图7 恒定温度下不同算法的MPPT结果
Fig.7 MPPT results of different algorithms obtained under constant temperature
TEG模块的冷端和热端温度阶跃变化曲线分别如图8a和图8b所示。图9给出了上述工况下四种算法的MPPT结果。由图可见,P&O再次陷入了低质量的LMPP。由于群体智能算法的寻优机制一般会加入一定权重的随机搜索,导致其在MPPT寻优过程中输出功率容易出现较大波动,最后才逐渐收敛到最优功率点。另一方面,为了使算法收敛到较高质量的功率运行点,群体智能算法需经历更多的试探迭代,容易导致较长的收敛计算时间。相比之下,GSNN基于实时更新的神经网络映射关系,并采用高效的贪婪搜索策略,能以更快的速度和更小的功率波动收敛到高质量的MPP。特别地,在第二次温度阶跃变化时,PSO、GWO和GSNN的功率超调量分别为94.07%、90.37%、55.56%。
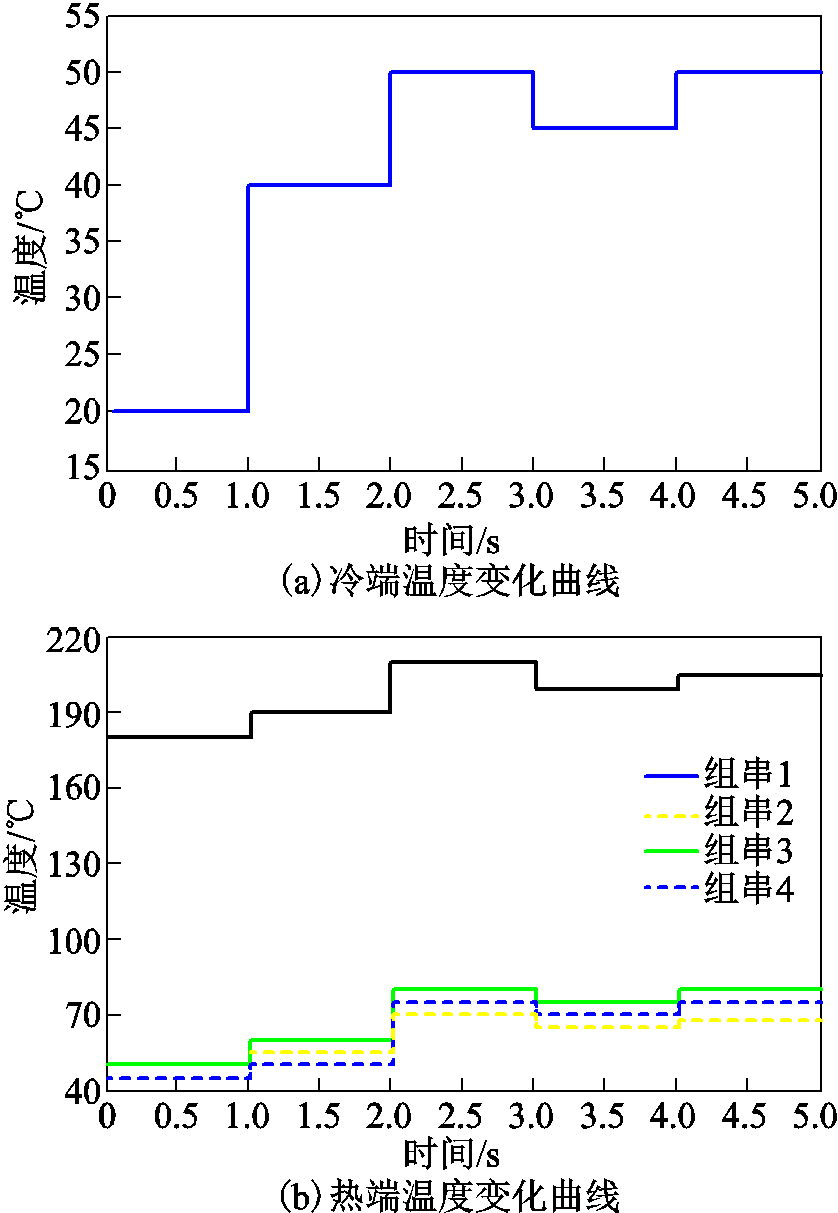
图8 温度阶跃变化曲线
Fig.8 Step change of temperature curve
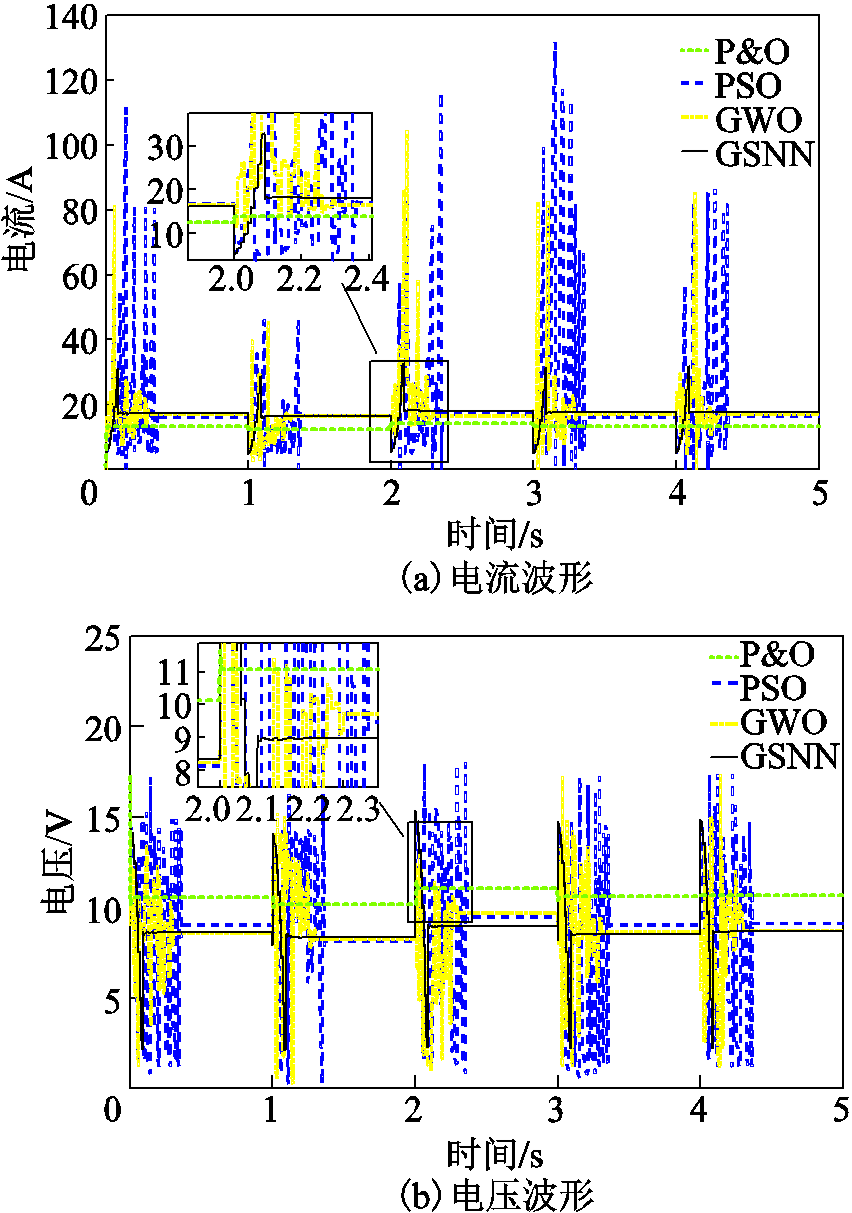
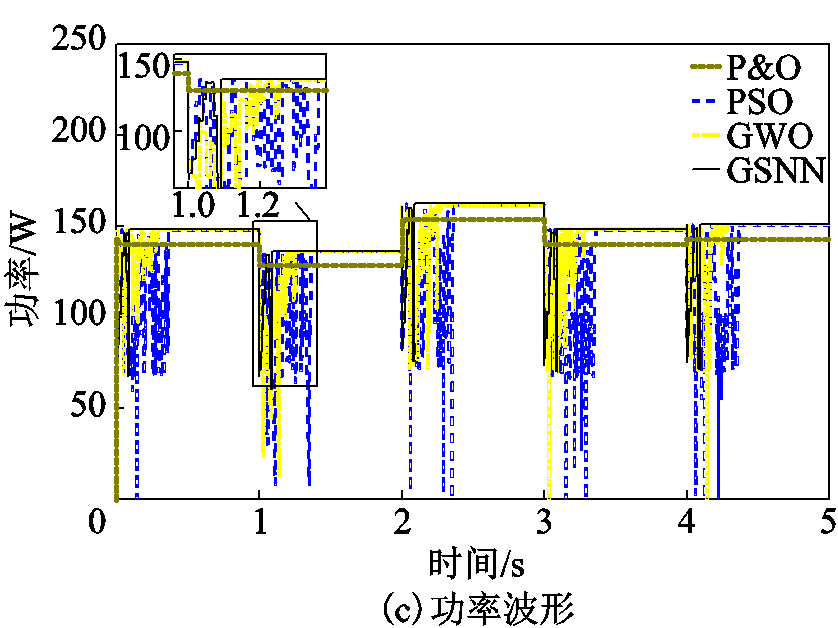
图9 阶跃温度下不同算法的MPPT结果
Fig.9 MPPT results of different algorithms obtained under step change of temperature
对系统施加从0%~100%的一系列不同温度比进行温度和系统输出功率间的灵敏度分析,其中温度比变化间隔设置为5%,冷端和热端的100%参考温度与恒定温度算例相同。
此外,为定量评估集中式TEG系统的功率振荡幅度,引入平均振荡指标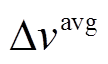 和最大振荡指标
和最大振荡指标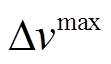 [24]为
[24]为
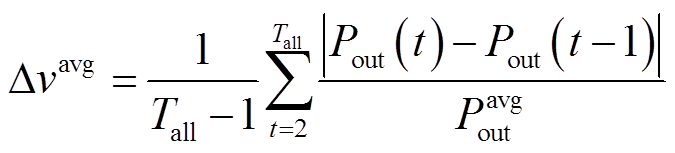 (18)
(18)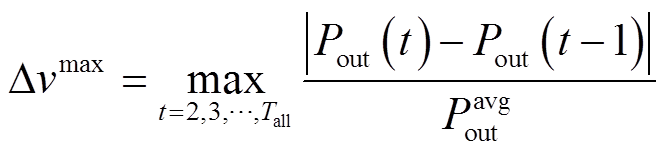 (19)
(19)
式中,t为时间;Tall为总运行时间;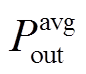 为在总迭代次数内集中式TEG系统输出功率的平均值。
为在总迭代次数内集中式TEG系统输出功率的平均值。
四种算法的平均功率、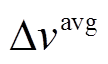 和
和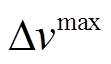 仿真结果如图10所示。由图可见,随着温度比的增加,输出功率也随之增加;而
仿真结果如图10所示。由图可见,随着温度比的增加,输出功率也随之增加;而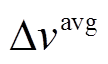 和
和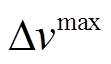 变化无明显规律,说明温度对功率波动的影响有限。此外,与启发式算法相比,GSNN的
变化无明显规律,说明温度对功率波动的影响有限。此外,与启发式算法相比,GSNN的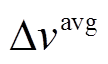 和
和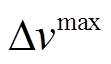 最小,因而收敛稳定性更好。
最小,因而收敛稳定性更好。
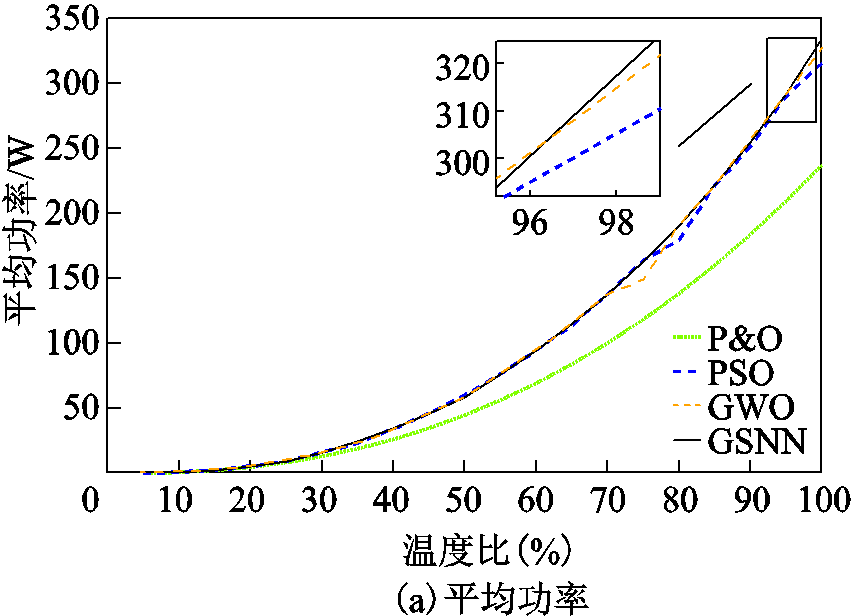
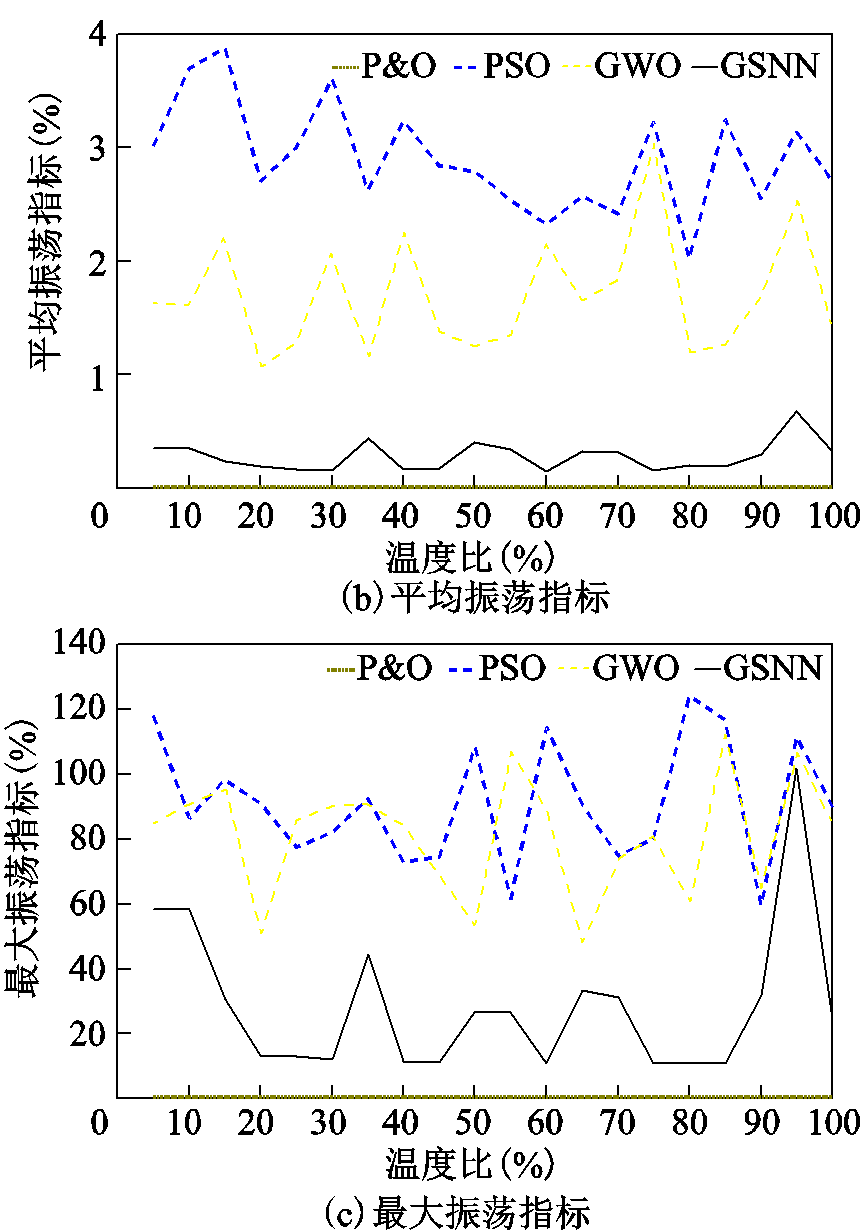
图10 灵敏性测试结果
Fig.10 Sensitivity test results
表4给出了两种算例下四种算法的输出能量、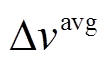 和
和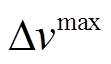 统计结果(最优值加粗表示)。由表4可见,虽然P&O的
统计结果(最优值加粗表示)。由表4可见,虽然P&O的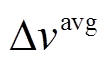 和
和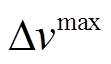 最小,但其陷入了局部最优,获得的能量也最小。而在所有算例中,GSNN产生的能量均最大。特别地,在恒定温度下,P&O、PSO和GWO产生的能量分别为GSNN的73.91%、94.95%、97.38%。此外,GSNN的
最小,但其陷入了局部最优,获得的能量也最小。而在所有算例中,GSNN产生的能量均最大。特别地,在恒定温度下,P&O、PSO和GWO产生的能量分别为GSNN的73.91%、94.95%、97.38%。此外,GSNN的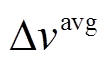 和
和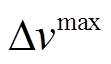 均小于启发式算法。
均小于启发式算法。
表4 两种算例下各算法的统计结果
Tab.4 Statistical results obtained by different methods under two cases

算例指标P&OPSOGWOGSNN 恒定温度能量/(W·s)237.024 4304.467 9312.280 3320.655 7 0.497 1102.440 169.631 810.371 1 0.010 61.073 00.799 70.103 0 阶跃温度能量/(W·s)706.256 8666.389 2712.966 8729.083 0 13.622 9106.667 590.342 059.342 3 0.008 21.549 20.669 50.218 4
本节基于dSpace进行HIL实验以验证GSNN的硬件可行性。HIL系统框架如图11所示。其中,式(8)~式(17)置于DS1104平台,其采样频率fc=10kHz;集中式TEG系统式(1)~式(7)和温度模拟器则置于DS1006平台,其采样频率fs=100kHz。特别地,DS1006平台实时模拟温度,并将数据传输到DS1104平台,以实时计算输出电压VL。
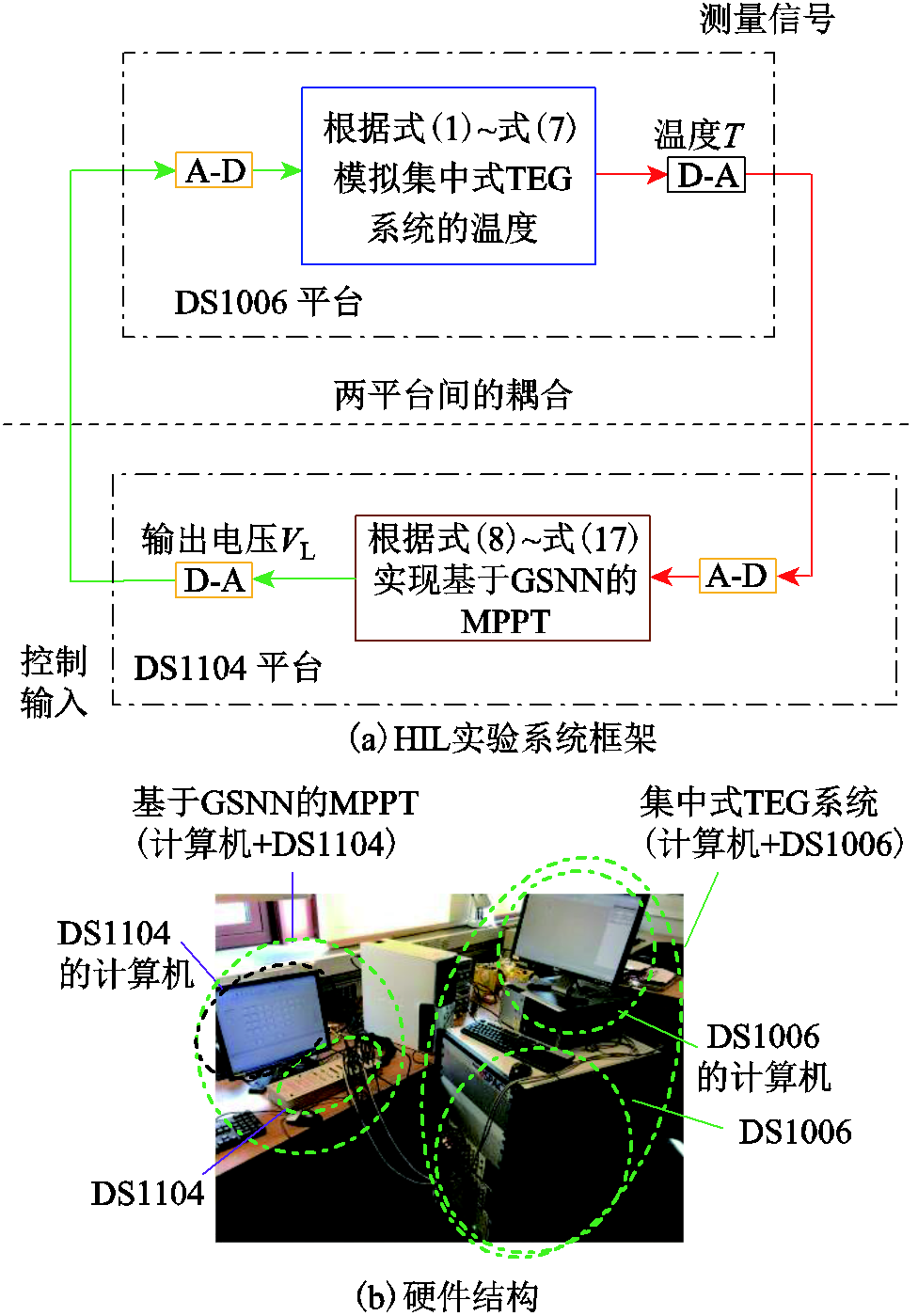
图11 HIL实验系统框架和硬件结构
Fig.11 The configuration of HIL test and hardware structure
将恒定温度的仿真结果与HIL实验结果进行比较,结果如图12所示。显然,HIL实验能实现与仿真几乎相同的优化性能。
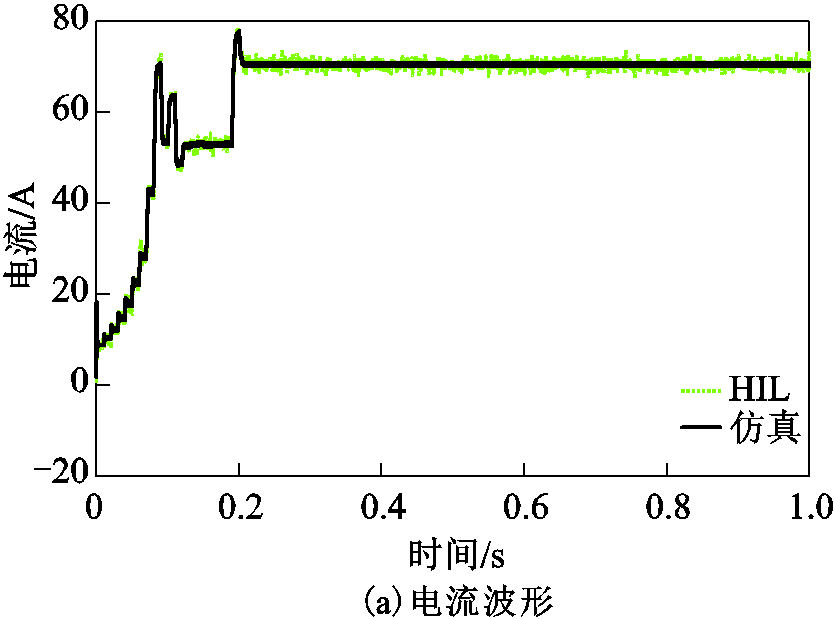
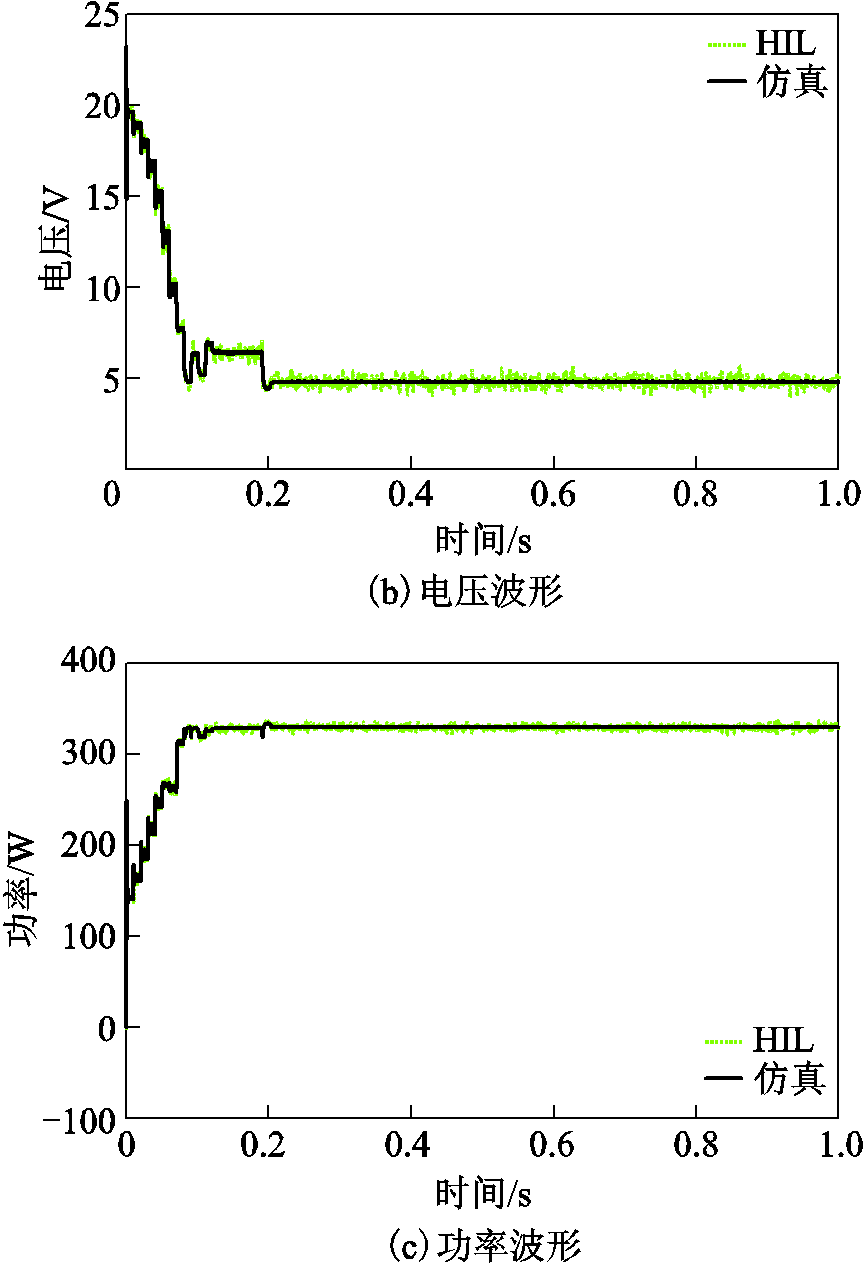
图12 恒定温度下仿真和HIL实验结果对比
Fig.12 Comparison of simulation and HIL test acquired under constant temperature
阶跃温度算例得到的仿真结果和HIL实验结果如图13所示。由图可见,HIL实验结果与仿真结果非常接近。
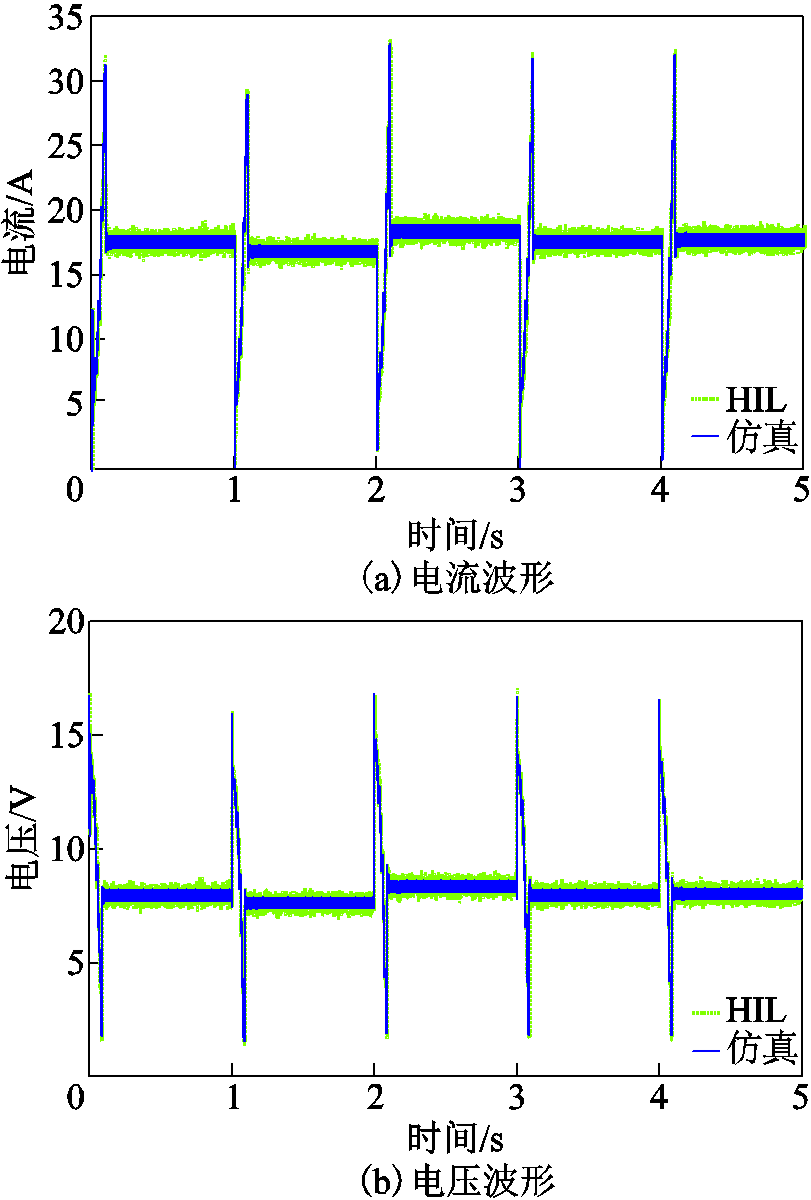
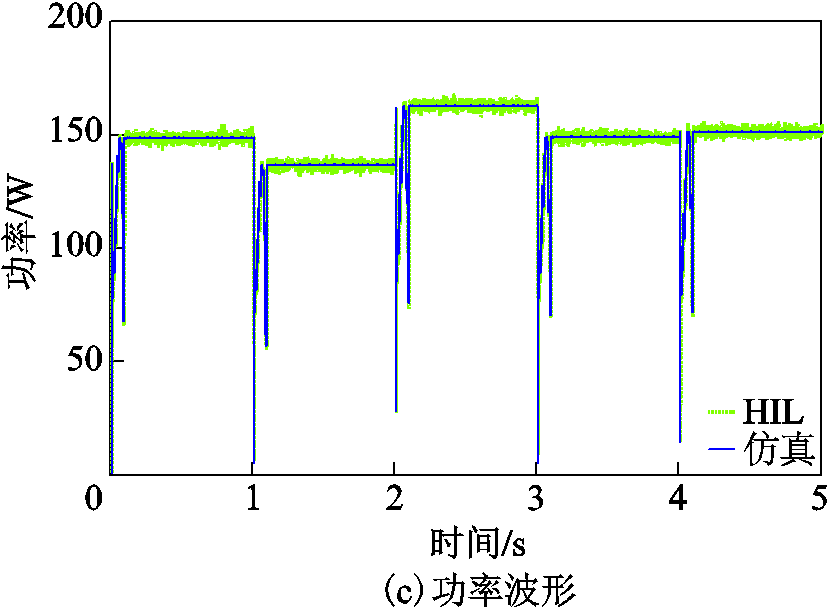
图13 阶跃温度下仿真和HIL实验结果对比
Fig.13 Comparison of simulation and HIL test acquired under step change of temperature
本文设计了一种新型GSNN算法以实现NTD下集中式TEG系统的MPPT,其主要贡献和创新点可总结如下:
1)GSNN利用神经网络拟合出NTD下集中式TEG系统的控制输入-功率输出多极值曲线,将MPPT等效为一个黑箱问题,无需精确系统模型,就可实现快速稳定的全局MPPT,符合MPPT实时控制的要求。
2)与传统启发式算法相比,GSNN通过拟合的I/O曲线引导贪婪搜索,可有效避免盲目的随机搜索,从而提高收敛速度及稳定性。
3)三种算例的仿真结果表明,GSNN能在NTD下快速稳定地产生最大能量。特别地,在阶跃温度下,GSNN产生的能量分别为P&O、PSO和GWO的103.23%、109.40%、102.26%。此外,基于dSpace的HIL实验验证了所提算法的硬件可行性。
参考文献
[1] 晏维, 邱国跃, 袁旭峰. 半导体温差发电技术应用及研究综述[J]. 电源技术, 2016, 40(8): 1737-1740. Yan Wei, Qiu Guoyue, Yuan Xufeng. Application and research of semiconductor thermoelectric power generation technology[J]. Chinese Journal of Power Sources, 2016, 40(8): 1737-1740.
[2] Uchida K, Adachi H, Kikkawa T, et al. Thermoelectric generation based on spin Seebeck effects[J]. Proceedings of the IEEE, 2016, 104(10): 1946-1973.
[3] He Wei, Zhang Gan, Zhang Xingxing, et al. Recent development and application of thermoelectric generator and cooler[J]. Applied Energy, 2015, 143: 1-25.
[4] Twaha S, Zhu J, Yan Y, et al. Performance analysis of thermoelectric generator using DC-DC converter with incremental conductance based maximum power point tracking[J]. Energy for Sustainable Development, 2017, 37: 86-98.
[5] Yu C, Chau K T. Thermoelectric automotive waste heat energy recovery using maximum power point tracking[J]. Energy Conversion and Management, 2009, 50(6): 1506-1512.
[6] Montecucco A, Knox A R. Maximum power point tracking converter based on the open-circuit voltage method for thermoelectric generators[J]. IEEE Transactions on Power Electronics, 2014, 30(2): 828-839.
[7] Laird I, Lu D D C. High step-up DC/DC topology and MPPT algorithm for use with a thermoelectric generator[J]. IEEE Transactions on Power Electronics, 2012, 28(7): 3147-3157.
[8] Liu, Yihua, Chiu Y H, Huang Jiawei, et al. A novel maximum power point tracker for thermoelectric generation system[J]. Renewable Energy, 2016, 97: 306-318.
[9] Bijukumar B, Raam A G K, Ganesan S I, et al. A linear extrapolation-based MPPT algorithm for thermoelectric generators under dynamically varying temperature conditions[J]. IEEE Transactions on Energy Conversion, 2018, 33(4): 1641-1649.
[10] Champier D. Thermoelectric generators: a review of applications[J]. Energy Conversion and Management, 2017, 140: 167-181.
[11] Sun Kai, Qiu Zhaoxin, Wu Hongfei, et al. Evaluation on high-efficiency thermoelectric generation systems based on differential power processing[J]. IEEE Transactions on Industrial Electronics, 2017, 65(1): 699-708.
[12] 杨博, 束洪春, 邱大林, 等. 变风速下双馈感应发电机非线性鲁棒状态估计反馈控制[J]. 电力系统自动化, 2019, 43(4): 60-76. Yang Bo, Shu Hongchun, Qiu Dalin, et al. Nonlinear robust state estimation feedback control of doubly-fed induction generator under variable wind speeds[J]. Automation of Electric Power Systems, 2019, 43(4): 60-76.
[13] Koad R B A, Zobaa A F, El-Shahat A. A novel MPPT algorithm based on particle swarm optimization for photovoltaic systems[J]. IEEE Transactions on Sustainable Energy, 2016, 8(2): 468-476.
[14] Mohanty S, Subudhi B, Ray P K. A new MPPT design using grey wolf optimization technique for photovoltaic system under partial shading conditions[J]. IEEE Transactions on Sustainable Energy, 2015, 7(1): 181-188.
[15] 商立群, 朱伟伟. 基于全局学习自适应细菌觅食算法的光伏系统全局最大功率点跟踪方法[J]. 电工技术学报, 2019, 34(12): 2606-2614. Shang Liqun, Zhu Weiwei. Photovoltaic system global maximum power point tracking method based on the global learning adaptive bacteria foraging algorithm[J]. Transactions of China Electrotechnical Society, 2019, 34(12): 2606-2614.
[16] Mohapatra A, Nayak B, Das P, et al. A review on MPPT techniques of PV system under partial shading condition[J]. Renewable and Sustainable Energy Reviews, 2017, 80: 854-867.
[17] 徐春华, 陈克绪, 马建, 等. 基于深度置信网络的电力负荷识别[J]. 电工技术学报, 2019, 34(19): 4135-4142. Xu Chunhua, Chen Kexu, Ma Jian, et al. Recognition of power loads based on deep belief network[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 4135-4142.
[18] 陆继翔, 张琪培, 杨志宏, 等. 基于CNN-LSTM混合神经网络模型的短期负荷预测方法[J]. 电力系统自动化, 2019, 43(8): 131-137 Lu Jixiang, Zhang Qipei, Yang Zhihong, et al. Short-term load forecasting method based on CNN-LSTM hybrid neural network model[J]. Automation of Electric Power Systems, 2019, 43(8): 131-137.
[19] 郭永芳, 黄凯, 李志刚. 基于短时搁置端电压压降的快速锂离子电池健康状态预测[J]. 电工技术学报, 2019, 34(19): 3968-3978. Guo Yangfang, Huang Kai, Li Zhigang. Fast state of health prediction of lithium-ion battery based on terminal voltage drop during rest for short time[J]. Transactions of China Electrotechnical Society, 2019, 34(19): 3968-3978.
[20] Molina M G, Juanico L E, Rinalde G F, et al. Design of improved controller for thermoelectric generator used in distributed generation[J]. International Journal of Hydrogen Energy, 2010, 35: 5968-5973.
[21] 孙祥晟, 陈芳芳, 贾鉴, 等. 基于经验模态分解的神经网络光伏发电预测方法研究[J]. 电气技术, 2019, 20(8): 54-58. Sun Xiangsheng, Chen Fangfang, Jia Jian, et al. Neural network based photovoltaic power generation prediction method based on empirical mode decomposition[J]. Electrical Engineering, 2019, 20(8): 54-58.
[22] Wang Xizhao, Cao Weipeng. Non-iterative approaches in training feed-forward neural networks and their applications[J]. Soft Computing, 2018, 22(11), 3473-3476.
[23] Kayri M. Predictive abilities of Bayesian regularization and Levenberg-Marquardt algorithms in artificial neural networks: a comparative empirical study on social data[J]. Mathematical and Computational Applications, 2016, 21(2): 20.
[24] 杨博, 钟林恩, 朱德娜, 等. 部分遮蔽下改进樽海鞘群算法的光伏系统最大功率跟踪[J]. 控制理论与应用, 2019, 36(3): 339-352. Yang Bo, Zhong Linen, Zhu Dena, et al. Modified salp swarm algorithm based maximum power point tracking of PV system under partial shading condition[J]. Control Theory & Applications, 2019, 36(3): 339-352.
Maximum Power Point Tracking of Centralized Thermoelectric Generation System using Greedy Neural Network
Abstract A novel greedy search based neural network (GSNN) for centralized thermoelectric generation (TEG) system under non-uniform temperature distribution (NTD) condition is designed to achieve maximum power point tracking (MPPT) in this paper. Firstly, a two-layer feed-forward neural network model is established, where input is defined as duty cycle of DC-DC boost converter while output as power output of TEG system. Then, Levenberg-Marquardt method is adopted to train neural network, accordingly the I/O curve that draws an evident distinction between local maximum power point (LMPP) and global maximum power point (GMPP) is fitted. Meanwhile, a greedy search is well performed to explore GMPP over a compressed search range. Lastly, three case studies are carried out, i.e., constant temperature, step temperature and sensitivity analysis. Simulation results demonstrate that GSNN could achieve maximum power output with speediness and stability under NTD compared to perturb and observe (P&O), particle swarm optimization (PSO) and grey wolf optimizer (GWO). Furthermore, a dSpace based hardware-in-the-loop (HIL) experiment is undertaken to validate implementation feasibility of the proposed algorithm.
keywords:Centralized thermoelectric generation system, non-uniform temperature distribution, maximum power point tracking (MPPT), neural network
中图分类号:TM76; TP183
DOI:10.19595/j.cnki.1000-6753.tces.191769
国家自然科学基金资助项目(61963020、51977102、51777078)。
收稿日期2019-12-17
改稿日期 2020-03-02
杨 博 男,1988年生,博士,副教授,硕士生导师,研究方向为新能源发电/储能系统优化与控制,以及人工智能在智能电网中的应用。E-mail:yangbo_ac@outlook.com
张孝顺 男,1990年生,博士,副教授,硕士生导师,研究方向为电力系统优化控制与启发式算法。E-mail:xszhang1990@sina.cn(通信作者)
(编辑 郭丽军)