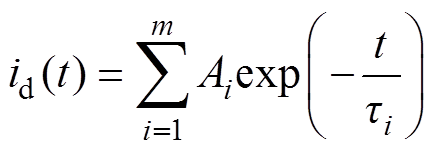（1）摘要 交联聚乙烯（XLPE）电力电缆绝缘等效电路模型的参数辨识是评估其绝缘老化状态的关键。针对现有等效电路参数辨识方法的局限性，该文提出了一种基于稳定图和状态空间模型（SSM）算法的扩展Debye等效电路模型参数计算方法。首先，利用去极化电流数据通过SSM算法生成稳定图；然后，由稳定图中稳定轴的数量确定弛豫支路数；最后，利用SSM准确地计算出等效电路的唯一参数。仿真结果表明，该方法抗噪声能力强、精度高，克服了传统方法存在的问题。实例验证了该方法的可行性和有效性。
关键词：去极化电流 扩展Debye模型 稳定图 状态空间模型 参数计算
近年来随着城市建设的快速发展，交联聚乙烯（Cross-Linked Polyethylene, XLPE）电力电缆开始被广泛应用。但是由于电力电缆长期铺设于地下，不良的散热条件、密集的铺设以及环境潮湿等诸多不利因素会造成XLPE电力电缆绝缘发生老化，导致绝缘失效，因此有效全面地评价电缆的绝缘性能有着重大的意义[1-2]。目前，介质响应测量技术由于拥有测试速度快、对被测样本绝缘损伤小等优点，被广泛应用于XLPE电力电缆绝缘诊断中。极化去极化电流法（Polarization and Depolarization Current, PDC）是其中一种重要的方法，该方法通过准确地反映绝缘材料的弛豫过程进而诊断设备的绝缘老化状态[3]。
目前，国内外学者主要通过建立XLPE电力电缆绝缘的扩展Debye等效电路模型来提取相应的特征量进而完成绝缘性能评估。但是现有的扩展Debye等效电路模型参数辨识方法存在以下问题：文献[4-6]提前假设好弛豫支路数，然后用智能算法求解等效电路参数，虽然可以在一定精度上得到参数辨识结果，但是由于没有考虑弛豫支路数，降低了绝缘等效电路模型的可信度；文献[7-8]选取每次剩余谱线的末端任意两点对谱线参数求解，虽然考虑了弛豫支路数的问题，但是选点存在一定的人为随机性，导致求解结果不唯一；文献[9-11]根据时域介电谱原理提出了微分法，该方法通过微分谱线峰值的个数来确定弛豫支路数，虽然简化了弛豫支路数的判断问题，但是该方法的精度受到弛豫支路时间常数分布的影响，对于时间常数分布较近和时间常数较大的支路存在辨识盲区。
针对上述方法的不足，本文引入稳定图和状态空间模型（State Space Model, SSM）算法相结合的方法用于扩展Debye模型的参数辨识。首先使用稳定图法确定扩展Debye模型的弛豫支路数，然后通过SSM求解各支路极化电阻和极化电容，进而构建出唯一的XLPE电力电缆的扩展Debye等效电路模型。仿真和实例的参数辨识结果表明，相比于传统的方法，本文所提方法更具优越性。
目前研究学者们普遍采用图1所示的XLPE电缆绝缘扩展Debye模型来表征电力电缆中的复合绝缘介质。该模型主要包括几何等效电路和极化等效电路，几何等效电路中的Rg和Cg分别表示绝缘设备的绝缘电阻和几何电容，其具体参数可以通过常规方法测量得到，本文将不予讨论。极化等效电路采用不同的一阶RiCi串联支路来表征不同的松弛极化，Ri表示支路电阻，Ci表示支路电容，i=1, 2,…, m，通过电路基本理论知识很容易得到基于扩展Debye模型的去极化电流为
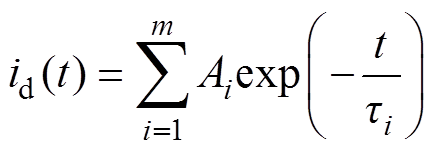（1）式中，m为弛豫支路数；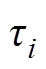
为第i条支路的时间常数；Ai为第i条支路的弛豫贡献系数。进而计算得到Ri和Ci分别为
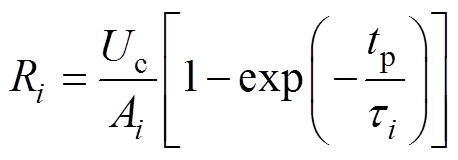（2）
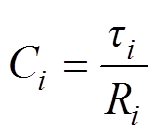（3） 式中，Uc为极化时的直流电压；tp为极化时间。
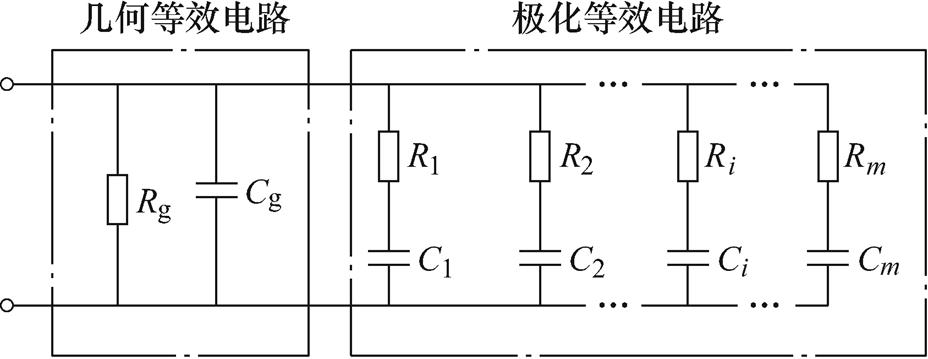
图1 XLPE电缆绝缘扩展Debye等效电路
Fig.1 Extended Debye equivalent circuit of XLPE cable insulation
综上所述，极化等效电路参数辨识的难点在于根据去极化电流数据准确求解出弛豫支路数m、时间常数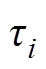、弛豫贡献系数Ai的值。
分析常用模态参数辨识方法发现，随机子空间方法[12]在处理单通道数据时辨识效果欠佳，不适用于弛豫支路参数辨识；矩阵束方法[13]存在高维数据矩阵的特征值分解，计算复杂；TLS-ESPRIT方法[14]虽然避免了高维数据矩阵的特征值分解问题，但是存在两次奇异值分解，计算同样较为复杂。
SSM的参数估计方法[15-16]作为一种改进的模态参数辨识方法，避免了上述方法的缺点，同时该方法还可以抑制噪声的影响，因此其在辨识极化等效电路模型参数方面具有独特的优势。
通过测试得到电缆样本的去极化电流数据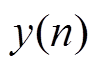
，
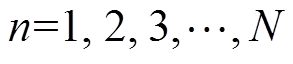，采用状态空间模型把式（1）描述为
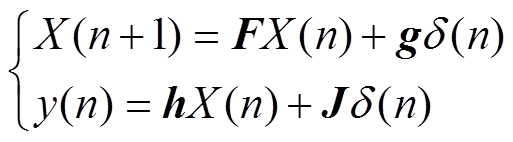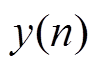（4）式中，为输出；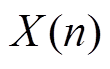
为状态变量；
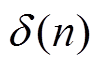为脉冲函数；F为系统状态矩阵；g、h、J为相应的常数矩阵。
由状态空间理论可知
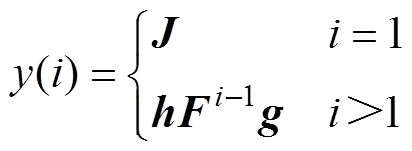（5）构造数据矩阵H为
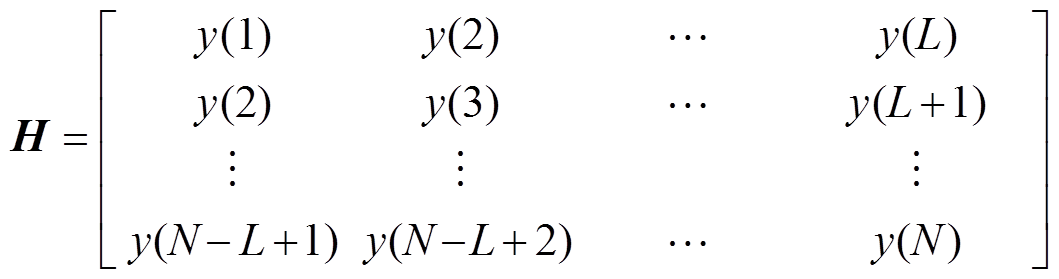（6）
式中，L为窗长度，一般选为N/3。将式（5）代入式（6）得
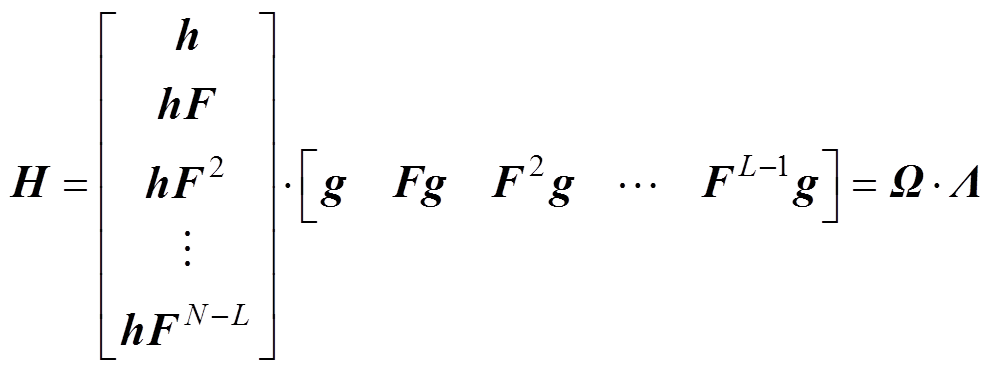（7）式中，定义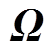
、
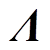分别为
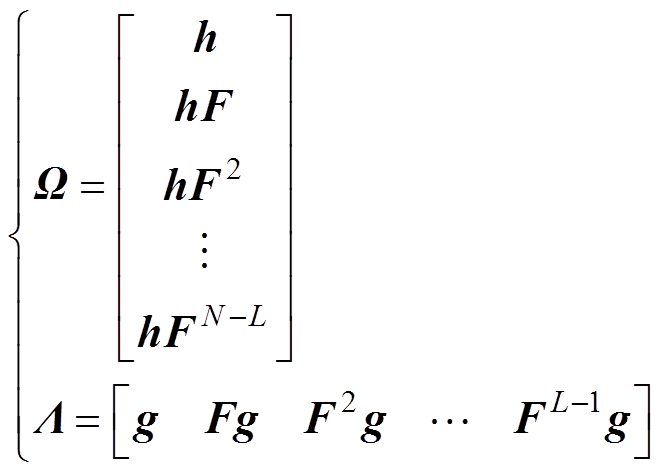（8）
同时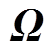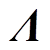，、分别有以下性质
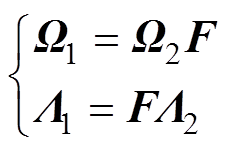（9）式中，下标1和2分别表示删除相应矩阵的第一行（列）以及最后一行（列）。将H进行奇异值分解得到
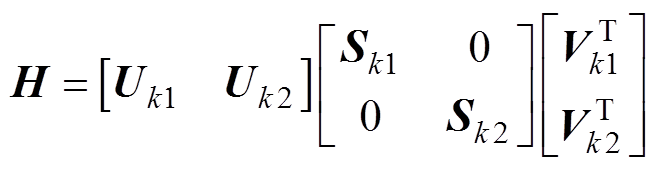（10）
式中，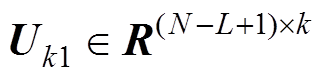
、
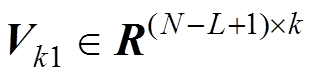分别为k个主奇异值对应的左、右奇异矢量矩阵；
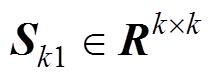为主奇异值对角阵，k为模型阶数。因此得到k阶近似逼近估计为
（11）将式（11）代入式（9）得到状态转移矩阵F的近似估计为
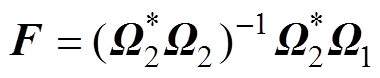（12）
式中，“*”表示共轭转置。计算F的特征值为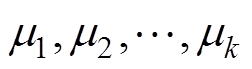
，得到
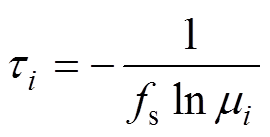（13）式中，fs为采样频率。
再通过求解式（14）得到Ai。
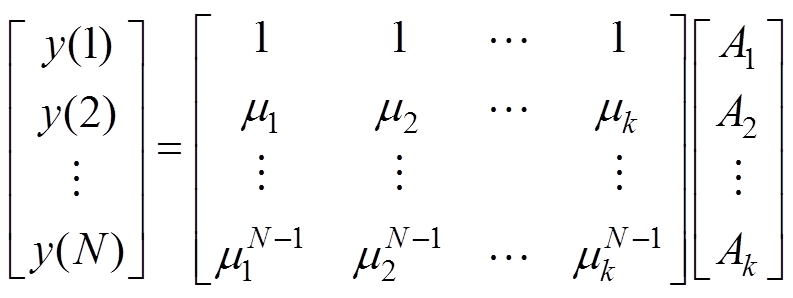（14）稳定图[17]是状态空间理论中一种非常重要的工具，其在信号的定阶和鉴别真假模态方面有着广泛的运用。在稳定图中，随着系统阶次的增加，代表真实模态的值和代表虚假模态的值会同时出现在稳定图中，其中真实模态的值代表真实的计算结果，虚假模态的值代表噪声造成的计算结果。因此真实模态的值通常是稳定的，会逐渐形成稳定轴，而虚假模态的值则一般不稳定，会呈现随机分布。稳定图正是根据这一原则，将虚假模态的值进行剔除，以真实模态的数量来确定系统解的个数。由于SSM算法的计算结果也会受到噪声的影响，所以本文引入稳定图法用于判断真实解的个数，即弛豫支路数，以辅助SSM辨识弛豫支路元件参数。
稳定图法首先假设系统具有不同的阶次，即式（10）中不同的k值，本文分别取k=1, 2,…, 20。通过SSM辨识得到不同阶次下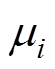
的值，注意，这里由于虚数的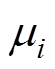一定是虚假模态，所以不予统计。将统计的实数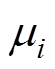代入式（13）得到不同阶次下
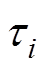的值，将其绘制到二维坐标图中来直观地得到模型的真实阶数，横坐标为k值，纵坐标为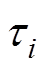值。对应真实模态的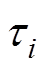会排列形成一条稳定轴，而虚假模态的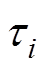会分散不稳定，即通过观察稳定图中稳定轴的数量便可以得到弛豫支路数。
由于实际测试中的去极化电流往往会存在量测噪声，而这种噪声会导致SSM算法计算得到错误的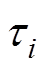，因此需要对计算结果进行有效地甄别。稳定图法是一种有效的结果甄别方法，在稳定图中，正确的计算结果会随着计算阶次的增加而逐渐稳定，进而形成稳定轴，同时每个稳定轴都代表着一个真实正确的计算结果，因此可以通过观察稳定图中稳定轴的数量确定SSM算法计算得到的真实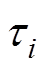值的个数，即弛豫支路数。只有在成功确定弛豫支路数之后才可以用SSM算法得到真实的弛豫支路元件的参数。
在介绍了算法的基本原理和相关技术之后，本小节将给出实际应用中的实施流程，具体步骤如下：
（1）测量去极化电流数据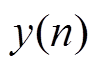，确定采样频率和极化电压大小。
（2）构建数据矩阵H。
（3）分别取k=1, 2,…, 20（如果量测噪声过大，可以适当地增加k的取值范围），求解不同k值条件下状态矩阵F的特征值。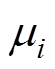
（4）剔除虚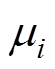数的，以实数的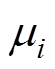求解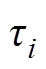，从而构建稳定图，确定弛豫支路数m。
（5）以k=m的SSM辨识结果计算得到弛豫支路元件参数。
本节通过对去极化电流的仿真数据进行分析来体现本文方法的正确性和优越性。借助式（1）仿真一组4条弛豫支路的去极化电流数据，其仿真参数设置见表1，设置去极化的时间为180s，采样频率为10Hz。仿真去极化电流曲线如图2所示。
表1 仿真参数
Tab.1 Parameters of simulation
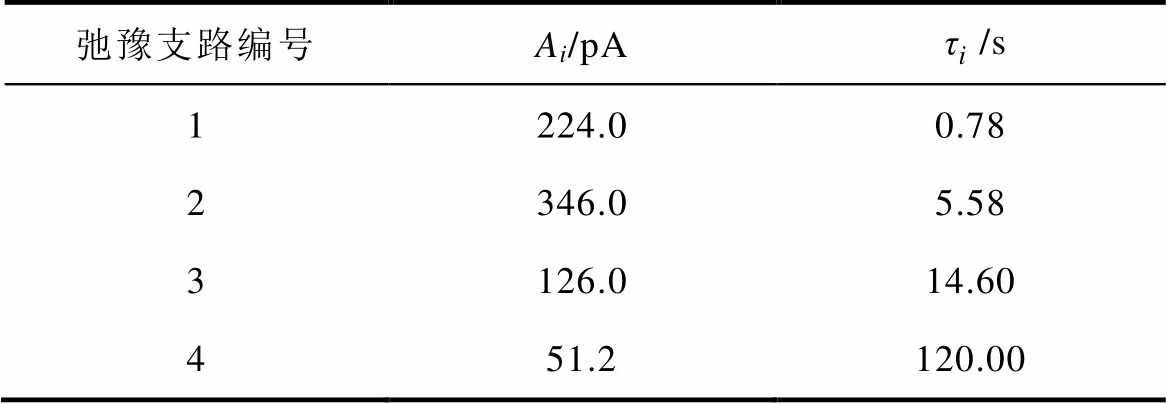
弛豫支路编号Ai/pA/s 1224.00.78 2346.05.58 3126.014.60 451.2120.00
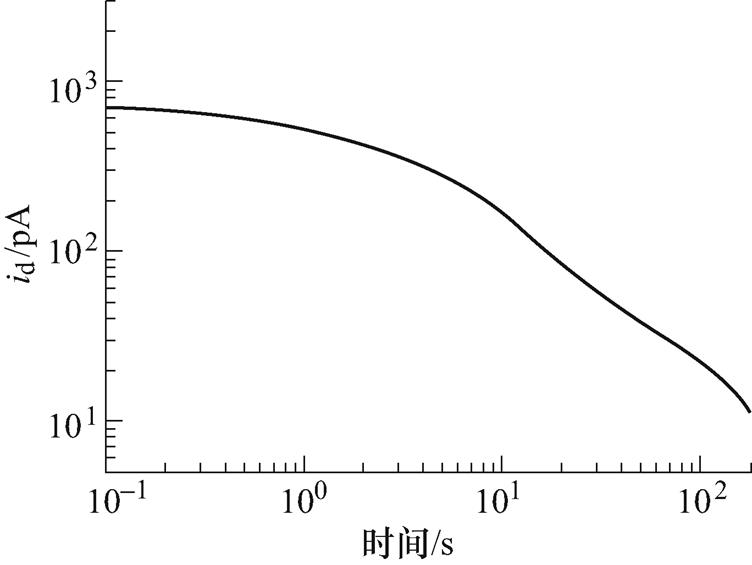
图2 仿真去极化电流曲线
Fig.2 Depolarization current curve of simulation
理想情况指不考虑量测噪声的干扰。本文直接将仿真得到的去极化电流数据作为输入信号，得到其稳定图如图3所示，从图中可以清楚地看出，弛豫支路数为4，与仿真设置的数据一致，证明了稳定图法确定弛豫支路数的可行性。
为了说明本文使用的稳定图法定阶的优越性，计算其数据矩阵的奇异值如图4所示，可以看出，由于各有效奇异值间的数量级差距太大，难以根据有效奇异值的个数来确定弛豫支路数。通过进一步分析发现，仅使用H矩阵的奇异值来判断弛豫支路数可能会由于噪声而判断产生虚假的弛豫支路数，而本文的稳定图法在构建稳定图前进行了虚假模式的剔除（如2.4节中的步骤（4）所述），从而避免了这个问题。
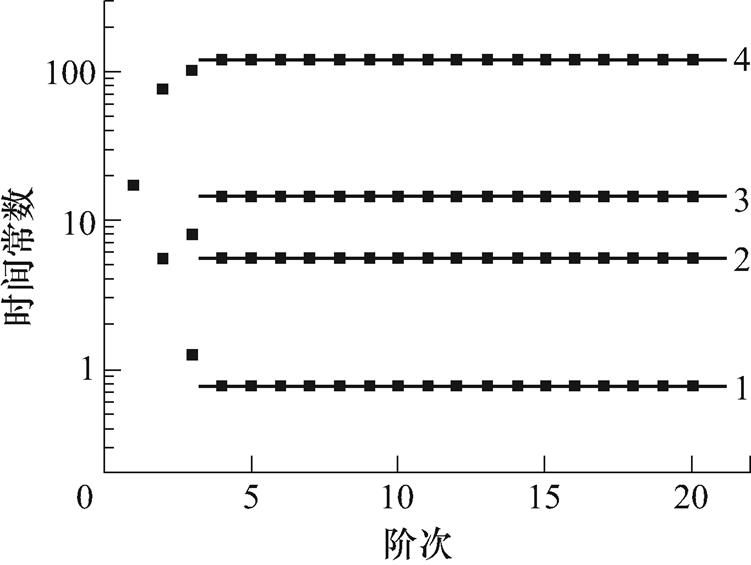
图3 仿真数据的稳定图
Fig.3 Stabilization diagram of simulation data
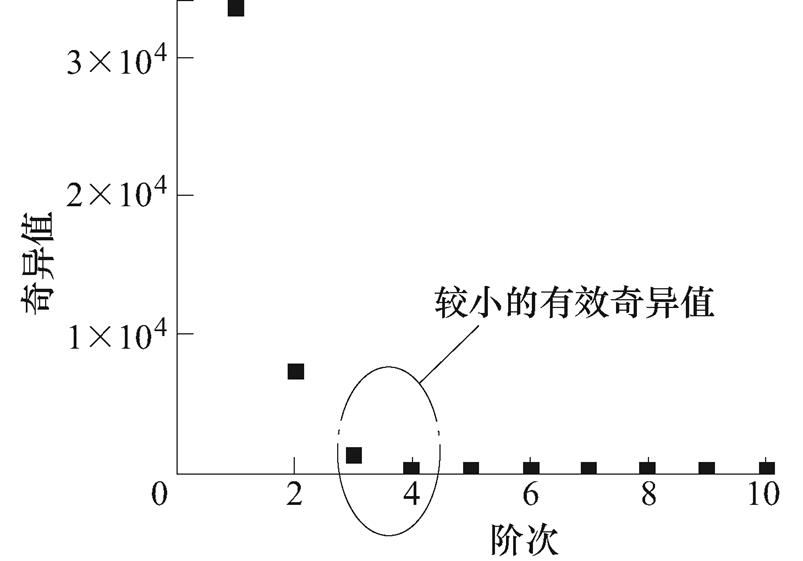
图4 仿真数据的奇异值
Fig.4 Singular value of simulation data
为了进一步验证在判断弛豫支路数方面稳定图法的优越性，在相同的仿真条件下，将本文方法和传统微分法的辨识结果进行了对比。将原始无噪声去极化电流信号分别进行相应的一、二、三次微分，得到其微分谱线如图5所示。从图中可以看出，3条微分谱线均只能识别到2条弛豫支路，无法识别到第3条和第4条弛豫支路，辨识结果和仿真的4条支路数存在明显的差异，辨识出现错误。通过进一步分析表明，一方面微分法存在峰值点覆盖现象，无法辨识到时间常数分布较近的支路（表1中的第3条支路）；另一方面微分法对于时间常数较大的支路（表1中的第4条支路）存在辨识盲区。对比图3可以看出，稳定图法不存在微分法的辨识盲区。
在确定弛豫支路数之后，通过SSM得到其参数辨识结果见表2。对比表2和表1可以看出，在理想情况下，SSM可以很准确地辨识得到极化等效电路模型参数。
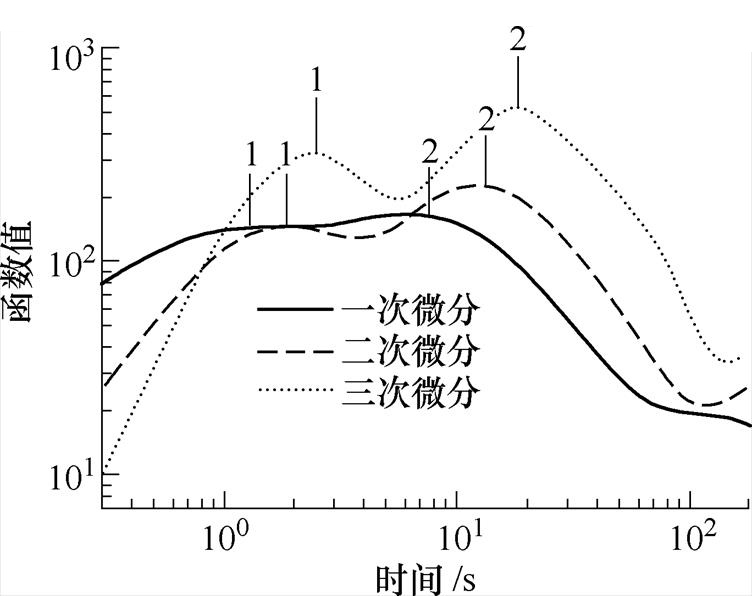
图5 仿真的一、二、三次时域微分曲线
Fig.5 First, second and cubic time domain differential curves of simulation
表2 参数辨识结果
Tab.2 Identification results of parameters
支路编号Ai/pA/s 1224.00.78 2346.05.58 3126.014.60 451.2120.00
在实测得到的去极化电流数据中，往往会存在量测噪声，本文通过向仿真数据中叠加不同分贝高斯白噪声的方式来验证本文算法的性能。为了排除偶然因素的影响，在各种噪声水平下采用蒙特卡洛思路，进行100次试验并把辨识结果记录下来。
图6给出了不同噪声水平下，任意一次仿真中稳定图对于弛豫支路数的判断结果以及100次蒙特卡洛仿真中SSM对于仿真去极化电流的参数辨识值和真实值的对比结果。在弛豫支路数的判断方面，即使在噪声处于较高水平（信噪比SNR=-5dB）时，稳定图法仍旧可以准确地判断弛豫支路数。在弛豫支路参数辨识方面，当信噪比为20dB和5dB时，SSM法仍旧可以准确判断得到4条弛豫支路的参数。在噪声水平较高时（信噪比SNR=-5dB），SSM法对于时间常数最小的支路1和时间常数最大的支路4的参数辨识结果依旧较为准确，对于时间常数分布在中间的支路2和支路3的辨识结果存在较小的误差。对于含有噪声的去极化电流数据，传统的微分法需要引入微分器，微分器的参数选择要考虑多方面影响，使得微分法难以准确地辨识等效电路参数[18]。综上所述，本文所提方法具有良好的抗噪性能。
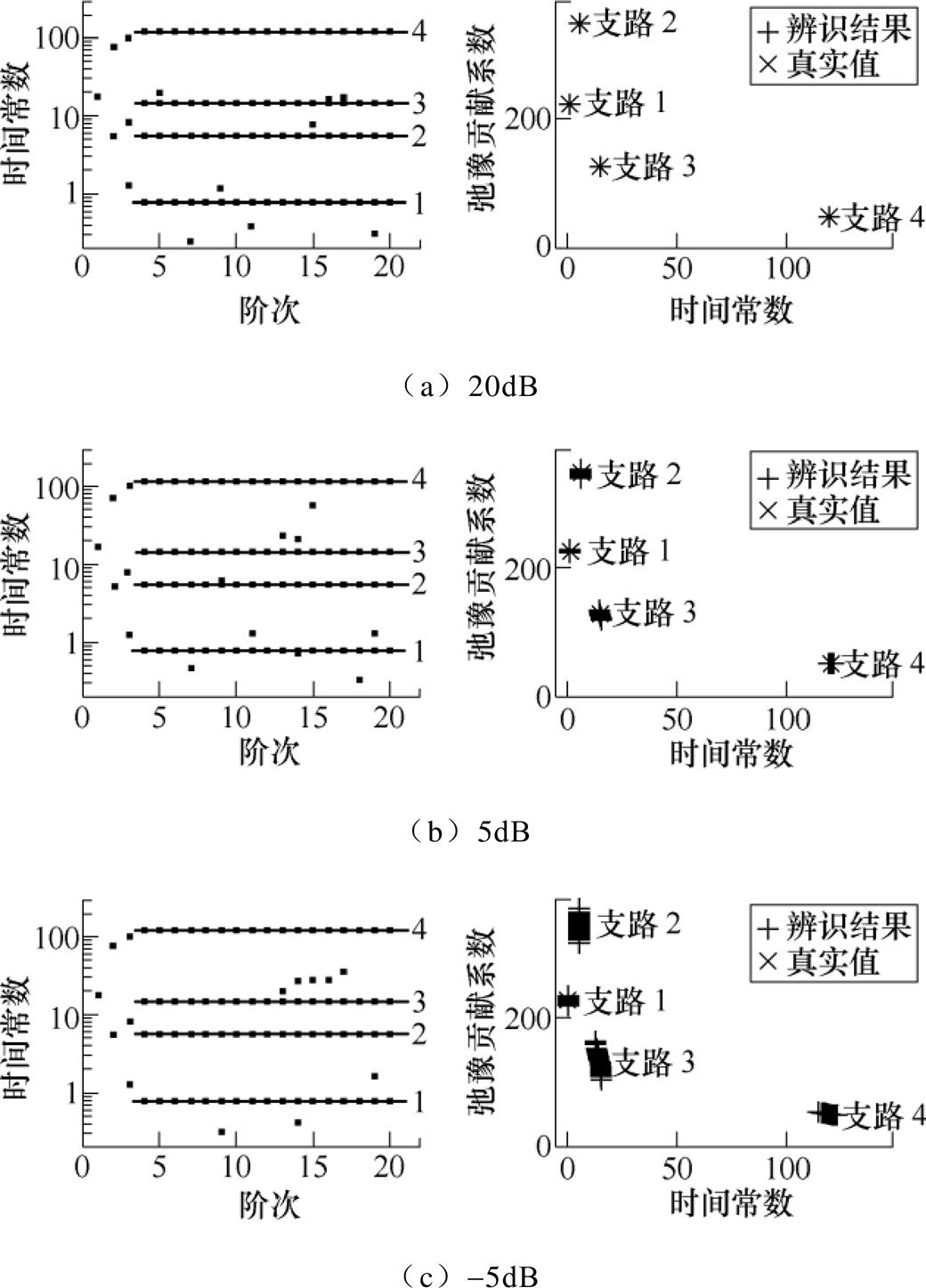
图6 噪声下的参数辨识结果
Fig.6 Identification results with noise
为了研究采样长度和采样频率对本文算法的影响，首先对本文算法不同采样长度下的性能进行比较，设置表1中参数的去极化时间分别为90s和360s，采样频率均为10Hz，得到其稳定图如图7所示。接着对本文算法进行不同采样频率下的性能比较，设置表1仿真参数的去极化频率分别为5Hz和20Hz，采样时间均为180s，得到其稳定图如图8所示。
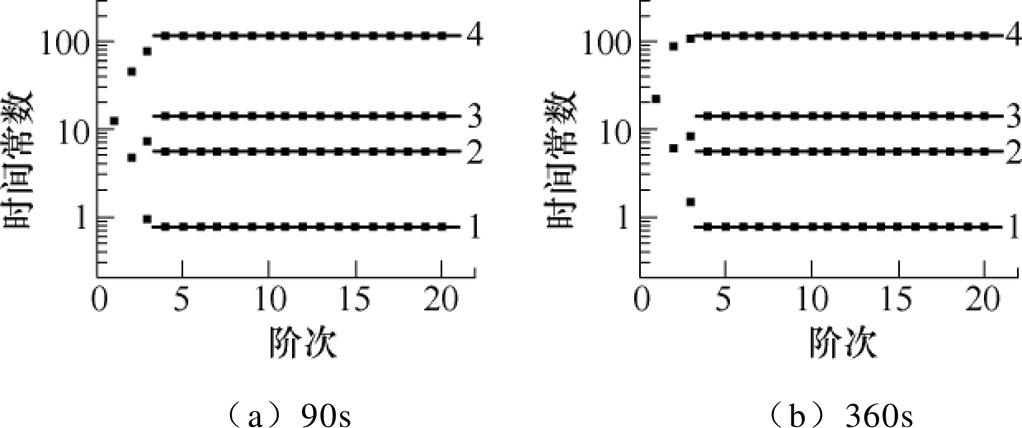
图7 不同采样长度下的稳定图
Fig.7 Stabilization diagram under different sampling length
由图7和图8可知，在上述不同采样长度和采样频率的条件下，稳定图法均可以很好地辨识得到弛豫支路数为4，和仿真数据一致。在已经得到弛豫支路数之后，利用SSM辨识得到不同采样长度和采样频率条件下的极化等效电路模型参数，其结果均与表2一致，不再赘述。
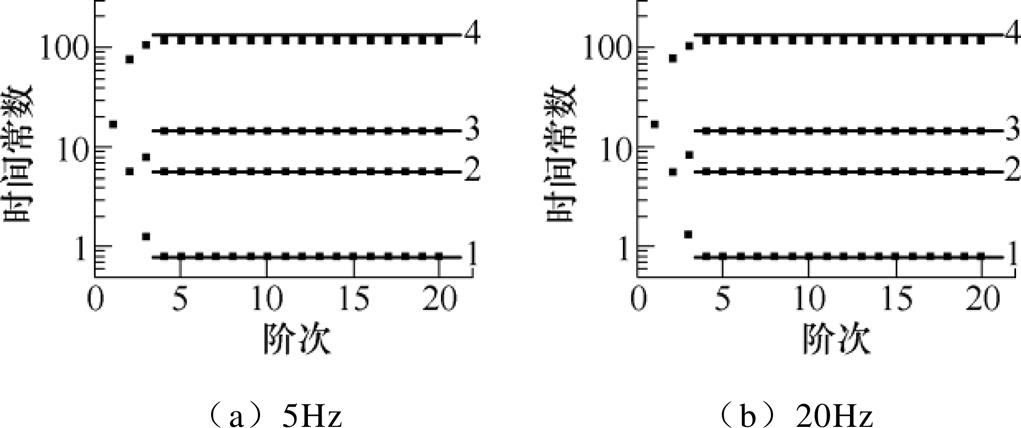
图8 不同采样频率下的稳定图
Fig.8 Stabilization diagram under different sampling frequency
因此，可以说明采样长度和采样频率对本文算法的影响不大，使用本文算法进行PDC数据分析时，一方面可以有效地缩短工程现场的测试时间，提高测试效率，解决PDC测试时间长的问题；另一方面可以适度降低设备的采样频率，减少测试设备成本。
本节以水树老化不同程度的电缆的去极化电流数据为例，验证本文算法在XLPE电力电缆等效极化电路的参数辨识效果。将多根长度为50cm的国产10kV短电缆进行老化，使用水针电极法制备水树缺陷[19]。将钢针在电缆样本的外半导电层上等间距（3～5mm）扎深度为1.5mm的小孔，随后套上热缩管并向热缩管空腔中注入1.7mol/L氯化钠（NaCl）溶液，最后插入铜电极接地。施加的老化电压选择为Urms=6kV，频率f =400Hz。分别将加速水树老化一个月和三个月的典型样本取出进行PDC测试，极化测试电压选择为1kV，极化以及去极化时间均选择为90s。在测试得到其去极化电流数据之后，做出两组样本的稳定图如图9所示。借助图9的稳定图确定老化一个月样本的弛豫支路数为4，老化三个月样本的弛豫支路数为5。接着通过SSM算法得到不同样本的极化等效电路参数见表3和表4。
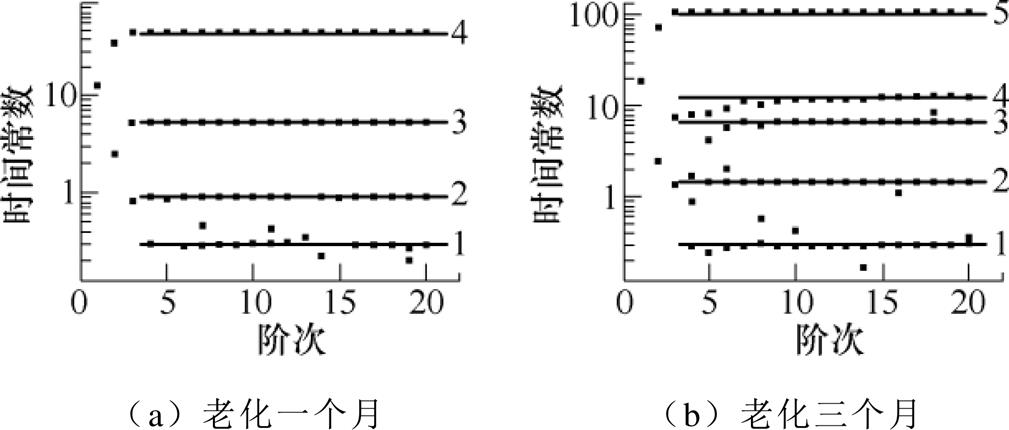
图9 测试数据的稳定图
Fig.9 Stabilization diagram of test data
表3 加速老化一个月后样本参数辨识结果
Tab.3 Identification results of sample after one month of accelerated aging
支路编号Ai/pA/s 177.71710.2904 2582.22530.8996 3430.62975.3150 4126.527944.2766
表4 加速老化三个月后样本参数辨识结果
Tab.4 Identification results of sample after three months of accelerated aging
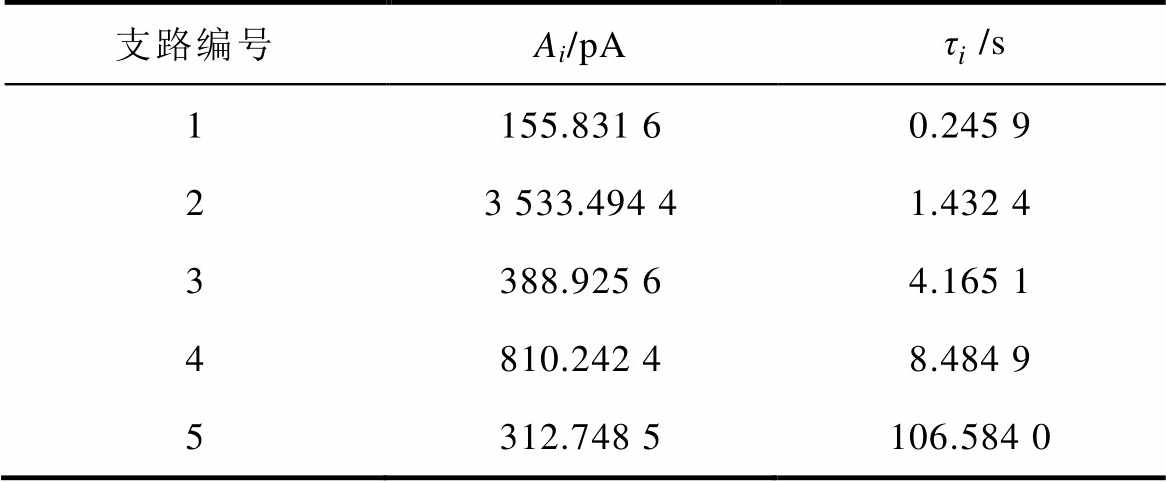
支路编号Ai/pA/s 1155.83160.2459 23533.49441.4324 3388.92564.1651 4810.24248.4849 5312.7485106.5840
为了验证辨识结果的正确性和有效性，将辨识得到的仿真电流曲线和实测电流曲线进行对比，如图10所示，计算得到拟合度分别为99.49%、99.61%。对比结果证实了本文所提方法的准确性。
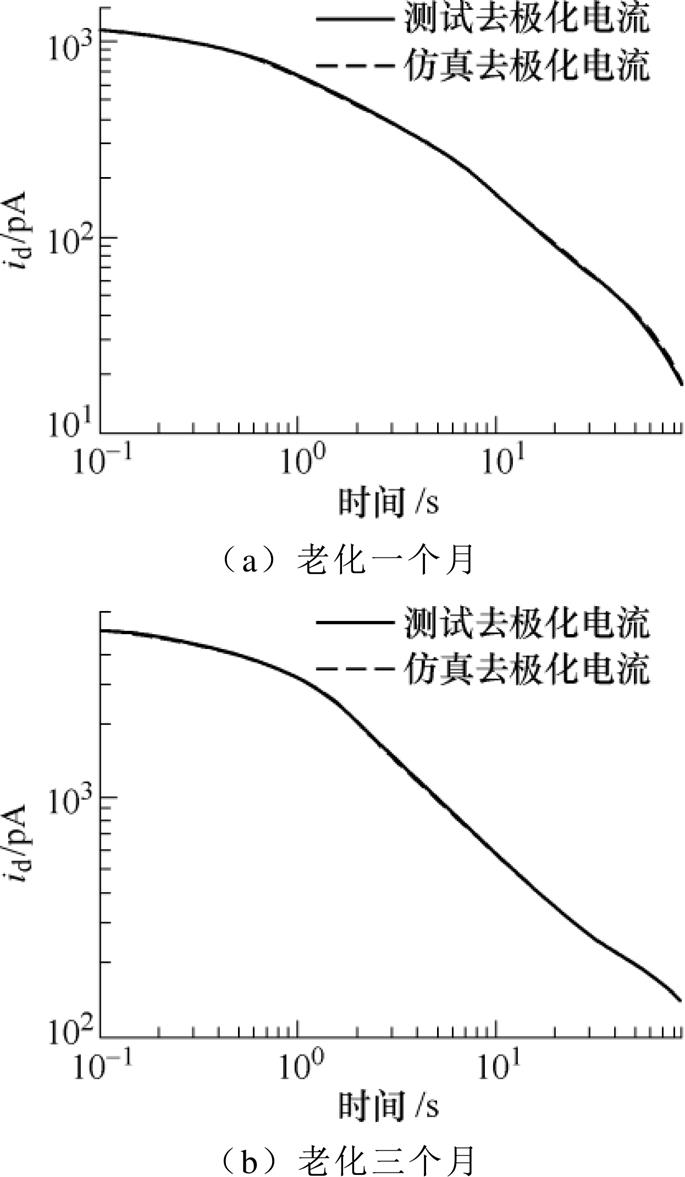
图10 去极化电流测试与仿真值对比
Fig.10 Comparison of simulated and measured depolarization current
为了进一步表现本文算法的优越性，采用仿真电流曲线构造数据矩阵的奇异值如图11所示，同时构造其微分谱线如图12所示。图11中可以看出，由于各有效奇异值之间数量级悬殊太大，难以根据奇异值的大小来确定弛豫支路数；图12中可以看出，微分法中性能最优越的三次微分[11]仍旧对两个样本的弛豫支路数辨识出现了错误，进而导致无法完成极化等效电路的参数辨识，因此实际中运用奇异值法和微分法往往存在很大的局限性。
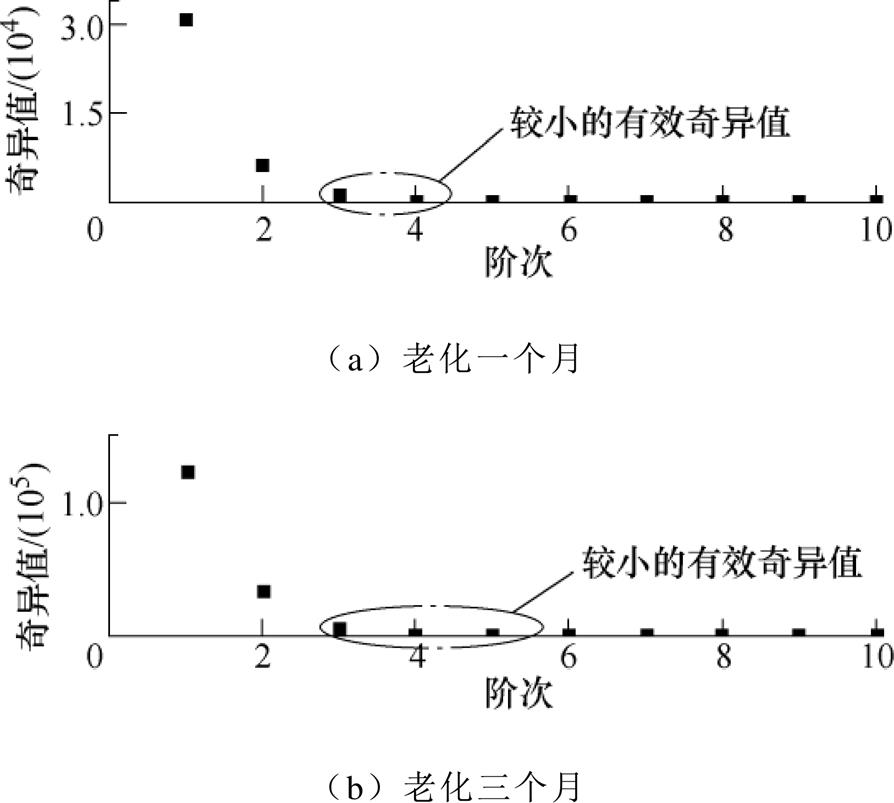
图11 测试数据的奇异值
Fig.11 Singular value of test data
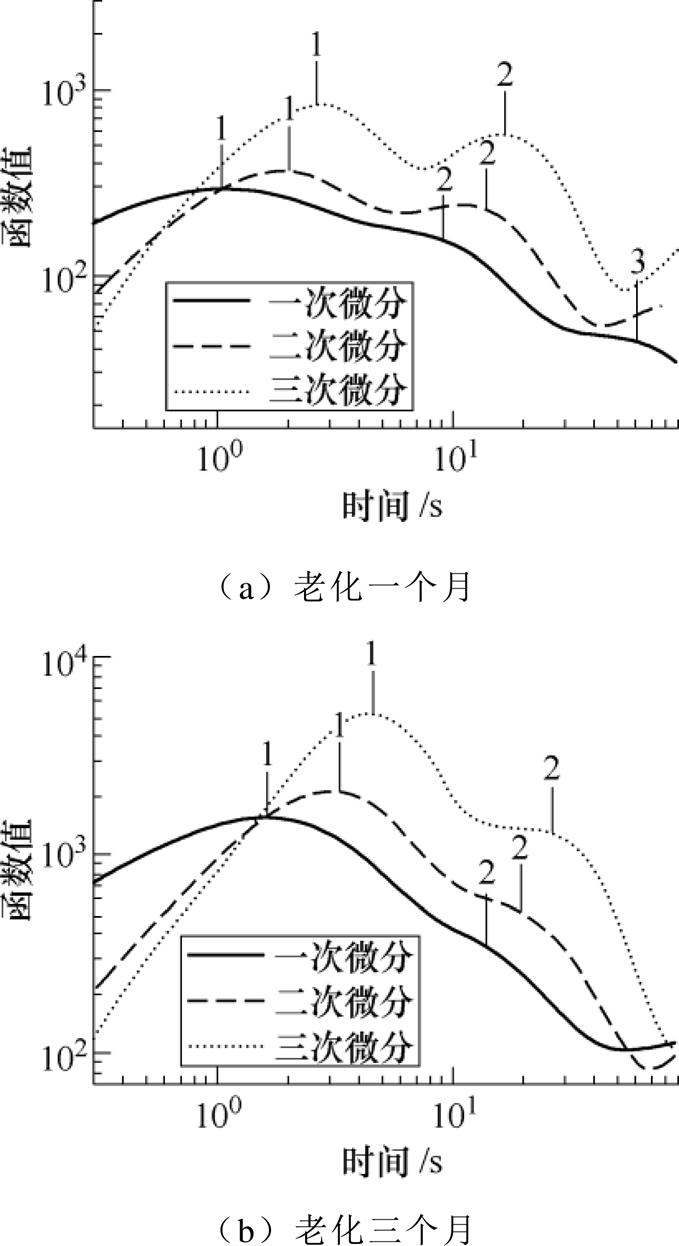
图12 样本的一、二、三次时域微分曲线
Fig.12 First, second and cubic time domain differential curves of samples
对比表3和表4可以看出，随着电缆水树缺陷的加深，SSM辨识得到的最小时间常数变化不大，而最大时间常数出现了明显的增大。最小时间常数直接反映电缆绝缘材料的中体极化，其值变化小说明了电缆主体结构相同，老化过程中没有发生较大的改变[20-21]。最大时间常数的弛豫支路表征绝缘材料中水树等绝缘缺陷造成的松弛极化，随着水树老化程度的增加，电缆中缺陷不断增多，陷阱深度增大，这些陷阱中的电荷难以逸出，导致去极化过程时间变大，进而使得最大时间常数增加[21]。
综上所述，由于电缆水树老化过程中存在最小时间常数变化不大，而最大时间常数变化较大的现象，因此将最小时间常数作为基准，以最大时间常数来反映电缆老化程度，即定义时间常数比K来反映电缆相对老化状态，有
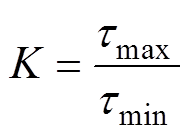（15）分别计算上述老化一个月和老化三个月样本的K值分别为152.467 6，433.444 5。随着老化程度的加重，K值发生了明显的增大，即K值很好地表征了电缆的相对老化程度。
本文针对传统弛豫支路参数辨识方法中的问题，提出了一种新的稳定图和SSM算法相结合的方法进行分析，该方法使用稳定图确定弛豫支路数，并且借助SSM求解各支路元件参数。通过对仿真和实测去极化电流数据进行参数辨识分析，得到以下结论：
1）稳定图可以清晰地得到弛豫支路数，并且不存在传统微分法的辨识盲区问题。
2）SSM可以唯一确定地得到极化等效电路参数，并且具有很强的抗噪能力。
3）SSM辨识得到的最大时间常数和最小时间常数的比值可以用来表征电缆的相对老化程度，其值越大，电缆老化相对严重。
参考文献
[1] 李露露, 雍静, 曾礼强, 等. 基于系统电力扰动的交叉互联电缆绝缘整体老化在线监测[J]. 电工技术学报, 2018, 33(14): 3396-3405.
Li Lulu, Yong Jing, Zeng Liqiang, et al. On-line monitoring of insulation overall aging for cross- bonded cables based on system power disturbances[J]. Transactions of China Electrotechnical Society, 2018, 33(14): 3396-3405.
[2] 秦雪, 钱勇, 许永鹏, 等. 基于2D-LPEWT的特征提取方法在电缆局部放电分析中的应用[J]. 电工技术学报, 2019, 34(1): 170-178.
Qin Xue, Qian Yong, Xu Yongpeng, et al. Appli- cation of feature extraction method based on 2D- LPEWT in cable partial discharge analysis[J]. Transactions of China Electrotechnical Society, 2019, 34(1): 170- 178.
[3] 张宁, 蔡金锭. 基于模糊物元-逼近理想点法的油纸绝缘状态评估[J]. 电工技术学报, 2018, 33(22): 5381-5389.
Zhang Ning, Cai Jinding. Evaluation of oil-paper insulation condition based on fuzzy matter element- technique for order preference by similarity to ideal solution method[J]. Transactions of China Electro- technical Society, 2018, 33(22): 5381-5389.
[4] 袁佳波, 徐鹏程, 李磊, 等. 基于鸡群算法的变压器油纸绝缘扩展Debye等效电路参数识别[J]. 电气自动化, 2018, 40(3): 67-70.
Yuan Jiabo, Xu Pengcheng, Li Lei, et al. Parameter identification for transformer oil-paper insulation extended Debye equivalent circuit based on chicken swarm optimization algorithm[J]. Electrical Auto- mation, 2018, 40(3): 67-70.
[5] 江修波, 黄彦婕, 赖祥生. 改进蚁群算法及其在变压器绝缘介质响应电路参数辨识中的应用[J]. 高电压技术, 2011, 37(8): 1982-1988.
Jiang Xiubo, Huang Yanjie, Lai Xiangsheng. Improved ant colony algorithm and its application in parameter identification for dielectric response equivalent circuit of transformer[J]. High Voltage Engineering, 2011, 37(8): 1982-1988.
[6] 郑君亮, 江修波, 蔡金锭. 变压器油纸绝缘等效电路参数辨识及绝缘状态对参数的影响分析[J]. 电力自动化设备, 2015, 35(8): 168-172.
Zheng Junliang, Jiang Xiubo, Cai Jinding. Parameter identification for equivalent circuit of transformer oil-paper insulation and effect of insulation condition on parameters[J]. Electric Power Automation Equi- pment, 2015, 35(8): 168-172.
[7] 蔡金锭, 刘永清, 蔡嘉. 油纸绝缘变压器极化等效电路分析及其老化评估[J]. 电工技术学报, 2016, 31(15): 204-212.
Cai Jinding, Liu Yongqing, Cai Jia. Analysis of equivalent circuit of oil-paper insulation transformer relaxation response and aging evaluation[J]. Transa- ctions of China Electrotechnical Society, 2016, 31(15): 204-212.
[8] 贺德华, 蔡金锭, 蔡嘉. 基于时域谱线特征量的变压器油纸绝缘诊断[J]. 电力自动化设备, 2017, 37(4): 122-127.
He Dehua, Cai Jinding, Cai Jia. Transformer oil- paper insulation diagnosis based on time-domain spectral curve characteristic parameters[J]. Electric Power Automation Equipment, 2017, 37(4): 122-127.
[9] 林朝明, 蔡金锭. 基于时域介电谱法分析油纸绝缘变压器极化等效电路弛豫支路数[J]. 电气技术, 2016, 17(4): 20-24.
Lin Chaoming, Cai Jinding. Analyzing relaxation branches of oil-paper insulation polarization equi- valent circuit of transformer based on time domain dielectric spectrum[J]. Electrical Engineering, 2016, 17(4): 20-24.
[10] 蔡金锭, 曾静岚. 基于二次时域微分解析法的油纸绝缘介质响应参数辨识[J]. 高电压技术, 2017, 43(6): 1937-1943.
Cai Jinding, Zeng Jinglan. Parameter identification for dielectric response of oil-paper insulation based on second time-differential analysis[J]. High Voltage Engineering, 2017, 43(6): 1937-1943.
[11] 叶荣, 蔡金锭. 油纸绝缘极化等效电路的时域介电谱三次微分解析法[J]. 仪器仪表学报, 2018, 39(6): 112-119.
Ye Rong, Cai Jinding. Analytic method of cubic differential in time domain dielectric spectroscopy for oil-paper insulation polarization equivalent cir- cuit[J]. Chinese Journal of Scientific Instrument, 2018, 39(6): 112-119.
[12] 高洁, 李群湛, 汪佳, 等. 基于NExT-ERA与SSI- DATA环境激励下的低频振荡辨识方法比较[J]. 电力自动化设备, 2016, 36(1): 89-96.
Gao Jie, Li Qunzhan, Wang Jia, et al. Comparison of low-frequency oscillation identification between NExT-ERA and SSI-DATA ambient excitation methods[J]. Electric Power Automation Equipment, 2016, 36(1): 89-96.
[13] 刘君, 肖辉, 曾林俊, 等. 基于RSSD和ICA算法的低频振荡模态参数辨识[J]. 电工技术学报, 2018, 33(21): 5051-5058.
Liu Jun, Xiao Hui, Zeng Linjun, et al. Parameter identification of low frequency oscillation based on RSSD and ICA algorithm[J]. Transactions of China Electrotechnical Society, 2018, 33(21): 5051-5058.
[14] 徐遐龄, 林涛, 张帆, 等. 基于TLS-ESPRIT的低频振荡负荷参与程度量化分析[J]. 电网技术, 2012, 36(11): 109-113.
Xu Xialing, Lin Tao, Zhang Fan, et al. TLS-ESPRIT based quantitative analysis on participating degree of load in low-frequency oscillation[J]. Power System Technology, 2012, 36(11): 109-113.
[15] 曾跃, 袁仕继. 状态空间模型(SSM)算法和矩阵束(MP)算法分析比较[J]. 电脑知识与技术, 2009, 5(36): 10263-10266.
Zeng Yue, Yuan Shiji. Analysis and comparison of state-spacemodel (SSM) algorithm and matrix pencil (MP) algorithm[J]. Computer Knowledge and Tech- nology, 2009, 5(36): 10263-10266.
[16] 袁仕继, 陈明明, 张家伟. 基于四阶累积量状态空间模型的间谐波参数估计[J]. 数据采集与处理, 2012, 27(增刊1): 14-17.
Yuan Shiji, Chen Mingming, Zhang Jiawei. Parameter estimation of inter-harmonics based on fourth-order cumulant state space model[J]. Journal of Data Acquisition & Processing, 2012, 27(S1): 14-17.
[17] 李洪伟, 周云龙, 刘旭, 等. 基于随机子空间结合稳定图的气液两相流型分析[J]. 物理学报, 2012, 61(3): 102-110.
Li Hongwei, Zhou Yunlong, Liu Xu, et al. Stochastic subspsace parameter identification and stability diagram of gas-liquid two-phase flow patterns[J]. Acta Physica Sinica, 2012, 61(3): 102-110.
[18] 李功新, 江修波, 蔡金锭, 等. 采用微分去极化电流法解析变压器油纸绝缘的介质响应函数[J]. 高电压技术, 2012, 38(8): 1930-1936.
Li Gongxin, Jiang Xiubo, Cai Jinding, et al. Dielectric response function for transformer oil-paper insulation solved by the method of differential depolarization current[J]. High Voltage Engineering, 2012, 38(8): 1930-1936.
[19] 周凯, 杨明亮, 黄明, 等. 有机硅修复后水树电缆在电热老化下的电气性能和微观结构变化[J]. 高电压技术, 2017, 43(5): 1656-1663.
Zhou Kai, Yang Mingliang, Huang Ming, et al. Changes of electrical properties and micro structures of water-tree cables rejuvenated by siloxane during the process of electrical-thermal aging[J]. High Voltage Engineering, 2017, 43(5): 1656-1663.
[20] 杨帆, 沈煜, 王彦博, 等. 基于极化/去极化电流法的交联聚乙烯电缆热老化程度判定[J]. 高电压技术, 2016, 42(2): 496-503.
Yang Fan, Shen Yu, Wang Yanbo, et al. Thermal aging status diagnosis of XLPE cable using polarization/depolarization current method[J]. High Voltage Engineering, 2016, 42(2): 496-503.
[21] 叶刚, 姚星辰, 李涛, 等. XLPE电缆绝缘老化的时频域介电特性[J]. 高电压技术, 2018, 44(11): 3713- 3719.
Ye Gang, Yao Xingchen, Li Tao, et al. Time/ frequency domain dielectric characteristics of XLPE cable insulation aging[J]. High Voltage Engineering, 2018, 44(11): 3713-3719.
Application of Stabilization Diagram Method for Solving Polarization Equivalent Circuit Parameters
Abstract The parameter identification of equivalent circuit model for XLPE power cable insulation is critical to evaluate the aging status of XLPE insulation. To avoid the limitations of the existing methods, this paper presents a new approach based on stabilization diagram and SSM algorithm to calculate the parameters of extended Debye equivalent circuit model. Firstly, the stabilization diagram is created by the depolarization current data through SSM algorithm. Then, the number of relaxation branches is determined by the number of stability axis. Finally, the unique parameters of the equivalent circuit can be accurately calculated by SSM. The results of simulation show that the method has strong anti-noise ability and high accuracy, and overcomes the problems of traditional methods. Case study verifies the feasibility and effectiveness of the proposed method.
keywords：Depolarization current, extended Debye model, stabilization diagram, state space model (SSM), parameter calculation
中图分类号：TM854
DOI: 10.19595/j.cnki.1000-6753.tces.190581
饶显杰 男，1996年生，硕士研究生，研究方向为电力设备状态监测。E-mail: 1953520244@qq.com
周 凯 男，1975年生，教授，博士生导师，研究方向为电缆绝缘状态检测与修复等。E-mail: zhoukai_scu@163.com（通信作者）
收稿日期2019-05-14
改稿日期 2019-06-28
国家自然科学基金资助项目（51477106）。
（编辑 崔文静）