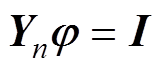 (1)
(1)摘要 杆塔冲击接地阻抗是输电线路雷击跳闸的主要影响因素之一,在我国的山地、丘陵地区,杆塔冲击接地电阻往往较高,使得线路跳闸事故频发。该文基于有限元与电路理论结合的方法,通过试验探究了广东地区典型土壤的冲击特性,建立了精确的输电线路接地暂态模型,基于该模型探究了地表下存在岩层区的输电杆塔冲击降阻优化方法。研究结果表明,对于地表下存在岩层区的接地装置,使用外引射线配合针刺短导体以及外引射线配合垂直接地极有着较好的优化效果。其中,外引射线配合针刺短导体时,针刺长度为射线的3%~6%、针刺间距为射线的10%~14%时降阻效果最好;外引射线配合垂直接地极时,垂直接地极布置于射线最外端时降阻效果最好。研究结果可为山区杆塔接地改造和优化提供参考和理论支持。
关键词:接地暂态模型 岩石层 降阻方法 针刺短导体 垂直接地极
杆塔冲击接地电阻是衡量架空线路防雷性能的重要指标,冲击下杆塔接地电阻过高会在塔顶产生很大的过电压,易造成绝缘子闪络,最终导致线路跳闸事故[1-2]。在我国西北和南方的诸多山区,地表以下存在电阻率极高的岩层,此类区域的输电杆塔往往接地电阻高,线路雷击跳闸事故频繁发生。为了有效降低输电线路雷击跳闸率,在保障实际工程可行性与经济性的前提下,需建立精确的输电线路接地暂态模型,并实现岩石地区的杆塔接地装置合理设计与优化改造。
现阶段,接地系统的暂态模型研究主要有传输线理论、电路理论、电磁场理论等。其中,传输线理论是将雷电冲击响应等效为分布参数在传输线上的波过程[3-5],此方法有着较快的计算速率,但假设了导体为无限长,不具有普适性;电路理论则将导体分段等效为p 型等效电路来模拟其暂态特性[6-8],此方法可模拟土壤非线性过程,但未考虑各导体间的耦合影响,高频电流下计算误差较大;现如今,基于Maxwell方程组的电磁场方法是分析接地暂态特性的有效方法之一[9-12]。重庆大学司马文霞团队利用COMSOL等电磁场软件模拟了土壤火花效应,通过将媒质的单元电阻率设置为该单元的电场强度关系函数以表征土壤火花效应[13],此方法考虑了火花效应的局部不均匀性,计算结果更加贴近实际。此外,冲击下输电杆塔的接地降阻方法也是国内外的研究重点之一。马来西亚科技大学Yunns等对不同接地极形式进行了冲击测试比较,试验结果显示接地电阻相近时,Y型射线配合垂直接地极所用的材料仅为田字型接地网所用材料的3/10[14];重庆大学黄勇等对长垂直接地极的利用系数和降阻效果进行研究,结果表明在低土壤电阻率地区增设长垂直接地极有较好的降低接地电阻效果[15];武汉大学研究人员对方框带射线型接地体进行过冲击特性探究,试验结果发现射线存在有效长度,且冲击下导体间的屏蔽作用不容忽略[16];司马文霞等对水平直线和并联垂直型两种常见形状接地极的电流分布进行研究,结果表明过长的水平接地极以及过多的并联垂直接地极都会降低接地极的利用率[17];重庆大学袁涛等研究发现,在长导体上施加“针刺”短导体可有效扩大火花面积,一定程度增强降阻效果[18]。武汉大学肖微等探究了柔性石墨复合接地材料的相关特性,研究发现石墨复合接地材料的冲击接地阻抗小于钢接地材料[19]。然而,现有的研究大多直接探究不同接地形式结构及材料的冲击特性,较少考虑对现有的典型接地装置进行优化改进,且大多未考虑接地极周边具体环境,未对接地装置下方存在岩石这一典型的工况进行探究,也未提出岩层地带的输电杆塔接地装置有效优化方法。
本文基于有限元与电路理论结合的方法,通过实测获取了广东地区不同土壤的非线性关系函数,由此建立了精确的输电线路接地暂态模型,基于该模型探究了含岩层地带的输电杆塔降阻方法,研究结果可为杆塔接地优化和改造提供参考和理论支持。
高频雷电流注入接地装置时,将接地装置有效分为k段,分段后含n个节点,运用节点电压法,节点电位电流满足
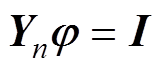 (1)
(1)式中,j=(j1, j2,…, jn)T为各节点电位;I=(I1, I2,…, In)T为注入节点的电流;Yn为节点导纳矩阵。
由于注入源为高频雷电流,本文在电路中只考虑接地导体的自感和互感,忽略导体内阻,则有
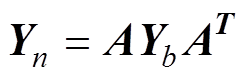 (2)
(2)式中,A为n×k阶的关联矩阵;Yb为支路导纳矩阵;互感可看作电流控制电压源,则有
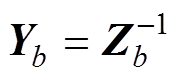 (3)
(3)
式中,Zb为支路阻抗矩阵,对于分段后的接地装置,有
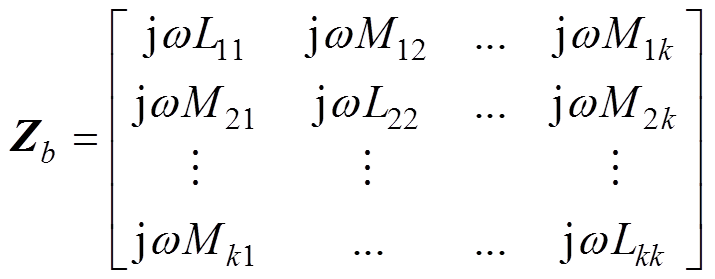 (4)
(4)式中,Lii(i=1,2,…, k)为第i段导体自感;Mij(i=1, 2,…, k;j=1,2,…, i-1, i+1,…, k)为第j段导体对第i段导体的互感。
当雷电流由接地装置注入土壤,冲击电流入地时接地系统的动态物理过程可由准静态Maxwell方程组表示
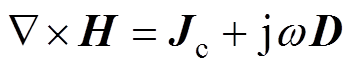 (5)
(5)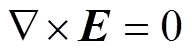 (6)
(6)
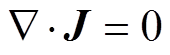 (7)
(7)
式中,Jc为土壤中的电流密度;D为电位移矢量;E为电场强度;J为由传导电流和位移电流构成的全电流密度。对于标量电位j,有E=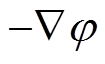 ,联立本构方程和麦克斯方程组,得到散流电位控制方程[20]为
,联立本构方程和麦克斯方程组,得到散流电位控制方程[20]为
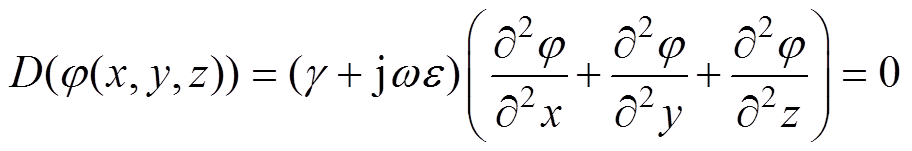 (8)
(8)式中,g、e 分别为煤质的电导率和介电常数。式(8)的边界条件需满足
无穷远处电位为0,有
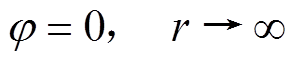
 (9)
(9)地表处,法向电流密度为0,有
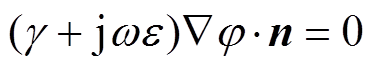 (10)
(10)
在电流注入处导体截面上满足
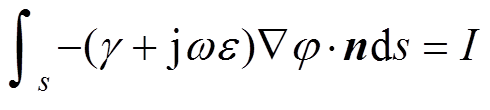 (11)
(11)式中,n为分界面处的法向量;I为注入电流幅值;S为注入处导体截面。联立式(1)和式(11),以实现电路和电磁场的耦合求解。
对此边值问题进行直接求解,易出现病态系数矩阵,易出现难以收敛甚至不收敛的情况,本文考虑将此泛函问题转化为多元函数的极值问题进行处理。在土壤区域,散流物理过程边值问题可转化为对应的变分问题,即
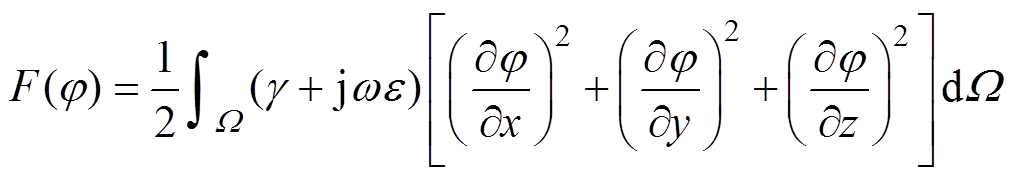
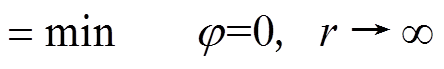 (12)
(12)
式中,W 为媒质所在域。对于接地装置,对应的变分问题为
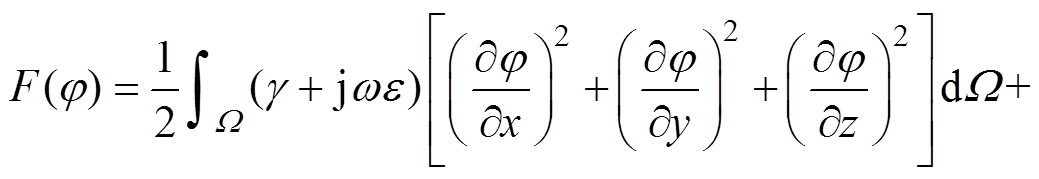
 (13)
(13)
式中,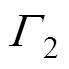 为导体分段区域。
为导体分段区域。
对于式(12),将其在区域W 上表示成各四面体单元积分和,有
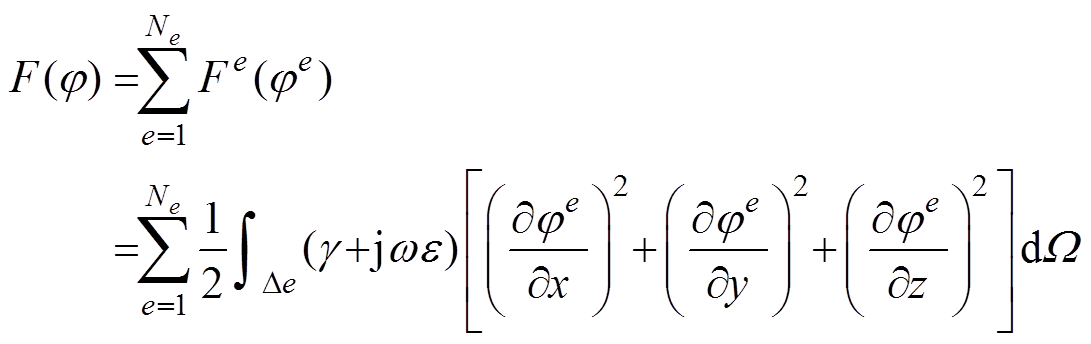 (14)
(14)式中,De为单元体积;Ne为求解区域的单元总数。
式(14)中,F(j)是求解区域中以所有节点电位为变量的多元函数,泛函的变分问题转化为多元函数的极值问题,即
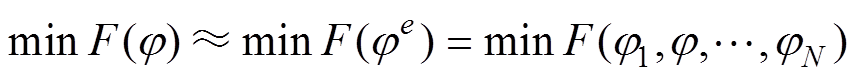 (15)
(15)式中,N为土壤区域节点总数,问题转化为求解电位向量j =(j1 j2 j3 … jN)T,该电位向量可使多元函数F(j)取得极值,由极值定理有
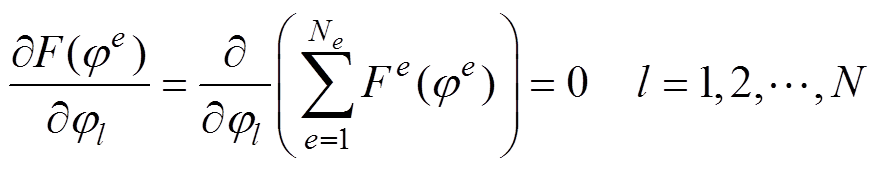 (16)
(16)
同样地,令M为接地装置上节点总数,可由式(13)获取相应代数方程。
由此构成以N+M个节点电位为未知数的代数方程组,即
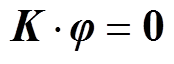 (17)
(17)进行单元拆分和整体合成后,最终形成(N+M)× (N+M)阶矩阵方程,求解该矩阵方程可得各单元节点电势。
雷电流从接地装置向土壤散流的过程中,满足
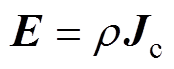 (18)
(18)
式中,r为土壤电阻率。为了更好地体现土壤非线性特性,土壤击穿前,通过现场试验获取土壤电阻率随电场强度变化的关系函数,即r =f (E),对于击穿后的电阻率则设为初始电阻率的7%[21]。
本文选取了广东地区典型的五种土壤进行冲击特性探究,如图1所示。
对不同土壤进行冲击特性试验,在平行板电极间填充典型土壤进行多次冲击试验,试验平台如图2所示。

图1 广东地区典型土壤
Fig.1 Typical soil in Guangdong
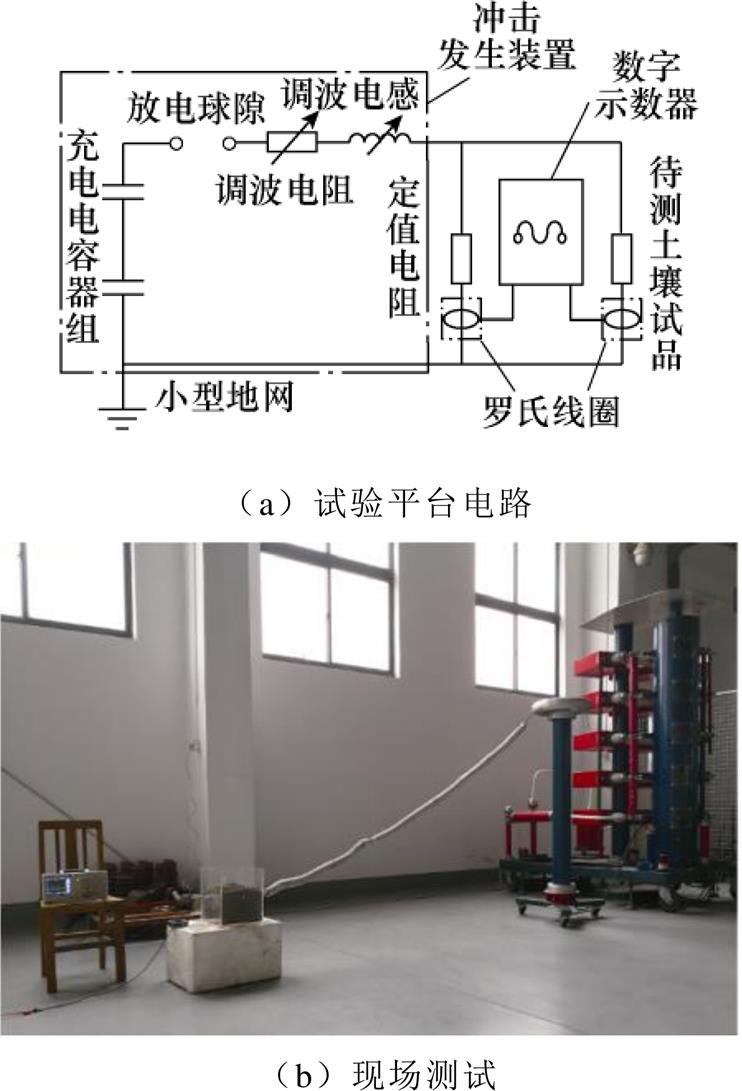
图2 模拟雷电流试验平台
Fig.2 Simulated lightning current test platform
选取广东地区土壤含水量7.5%,通过多次重复冲击试验获取不同土壤的冲击特性曲线,如图3 所示。
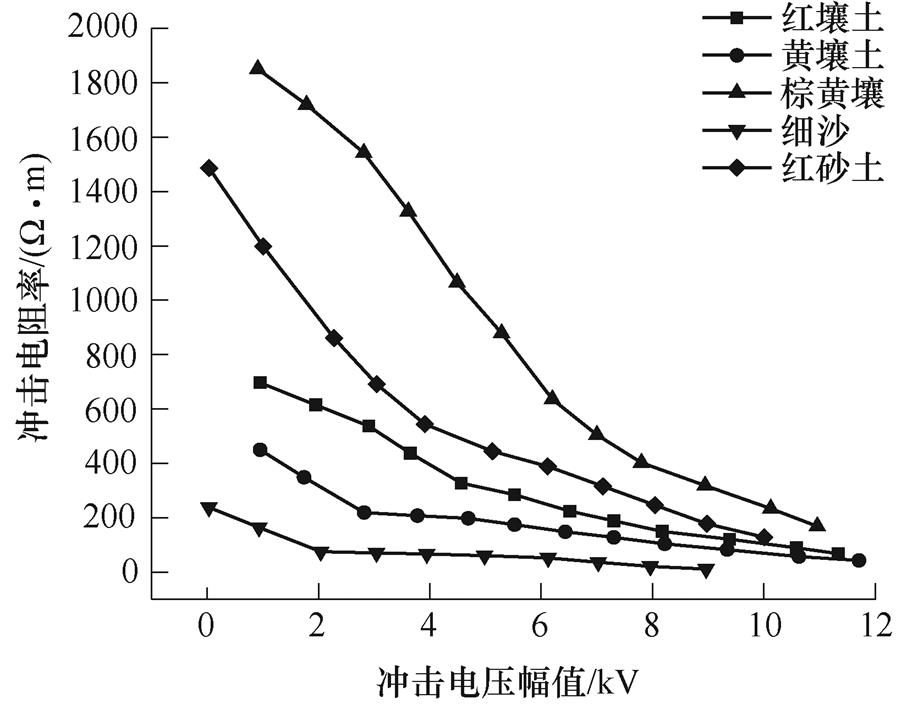
图3 不同土壤冲击特性
Fig.3 Impact characteristics of different soil
试验结果表明,不同类型土壤非线性特性差异较大,红壤土和红砂土电阻率非线性变化程度明显,细沙和黄壤土非线性变化程度较小。通过试验结果可获取广东地区典型的电阻率与电场强度关系函数,带入有限元软件可实现土壤非线性特性的准确表征。
雷电流可傅里叶分解为多个高频正余弦波,高频电流下的接地导体自身和导体之间的电感效应不容忽略。基于电路理论搭建典型的p 型等效电路,对导体进行分段,每段长度为DL,在保障结果准确性前提下考虑到计算的工作量,进行多次仿真后发现,选取Dl=8cm时结果较为精确。
对水平接地极和垂直接地极,其自感取值[22]分别为
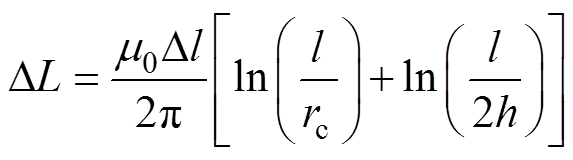 (19)
(19)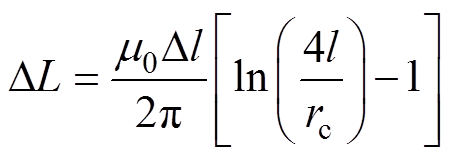 (20)
(20)
式中,m0为煤质相对磁导率;l为导体长度;h为水平导体埋深;rc为导体半径。
接地极的数量与布置方式会使得导体间存在互感作用,由电磁感应相关理论可知,互感作用存在于不垂直的导体间。根据黎曼公式[23],任意两段导体间的互感可表示为
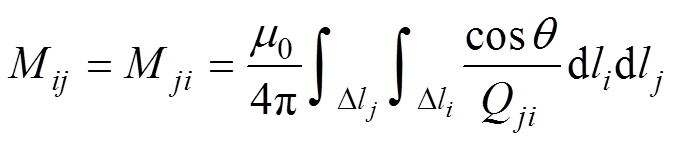 (21)
(21)式中,q 为dli和dlj之间的夹角;Qij为dli和dlj之间的距离,如图4所示。
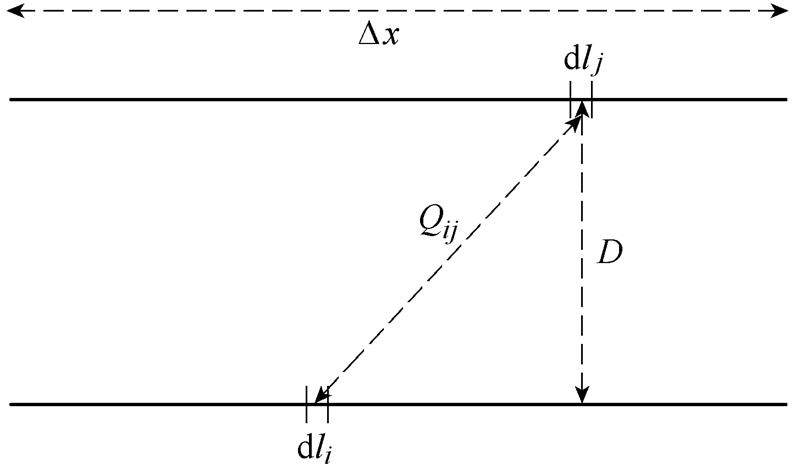
图4 平行导体间的互感
Fig.4 Mutual inductance between parallel conductors
当两导体间相互平行时,其互感可表示为
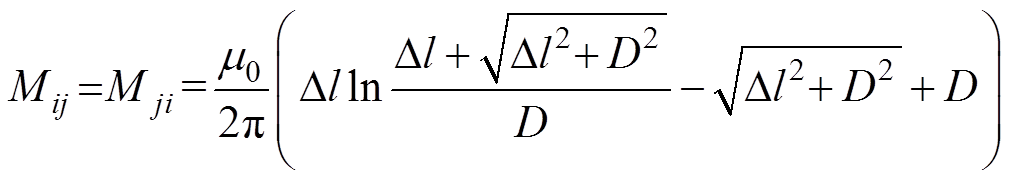 (22)
(22)式中,D为两平行导体间的距离。
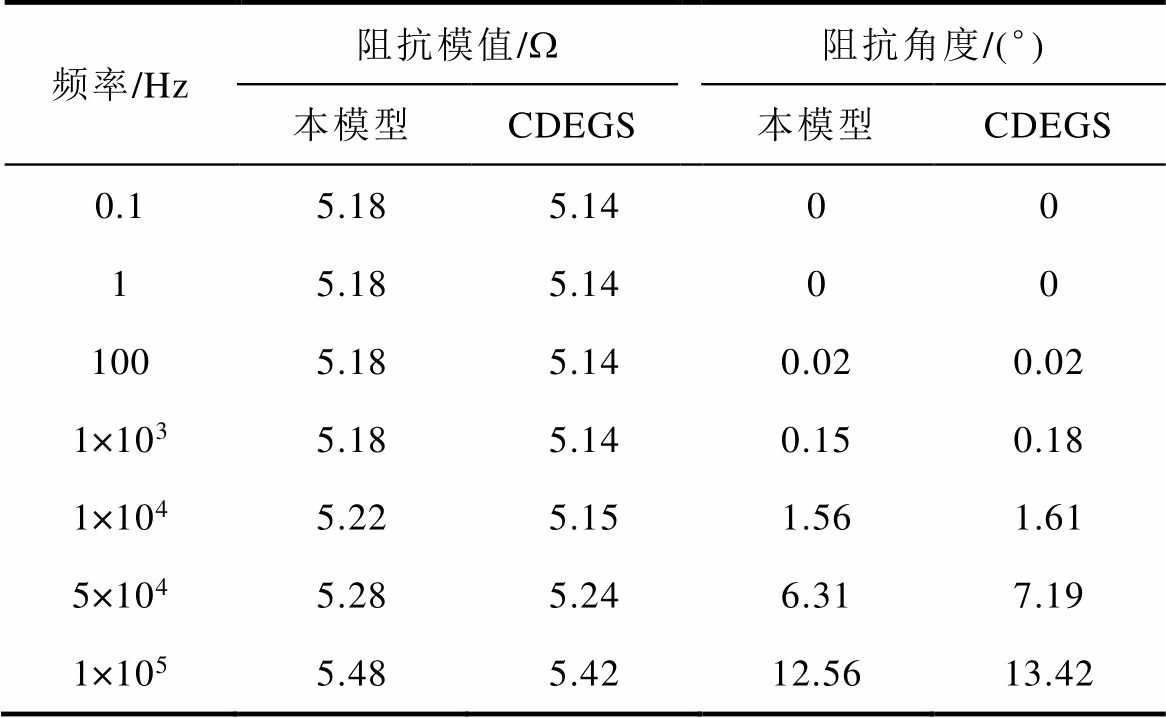
建立方框型的接地装置,边长设为10m×10m,导体材料为镀锌铜,半径7mm,接地装置埋深0.8m,埋设在电阻率为100W·m的均匀土壤中,将本文模型和国际权威的电磁仿真软件CDEGS进行接地阻抗计算值对比,见表1。
表1 不同频率下的接地阻抗对比
Tab.1 Comparison of ground impedance at different frequencies
频率/Hz阻抗模值/W阻抗角度/(°) 本模型CDEGS本模型CDEGS 0.15.185.1400 15.185.1400 1005.185.140.020.02 1×1035.185.140.150.18 1×1045.225.151.561.61 5×1045.285.246.317.19 1×1055.485.4212.5613.42
由表1可知,本模型在不同频率下所测的阻抗模值和阻抗角度与CDEGS误差均在5%以内。
在广东电网公司接地技术与工程实验室开展了冲击模拟实验,实验原理如图5所示。实验现场连线和测试如图6所示。
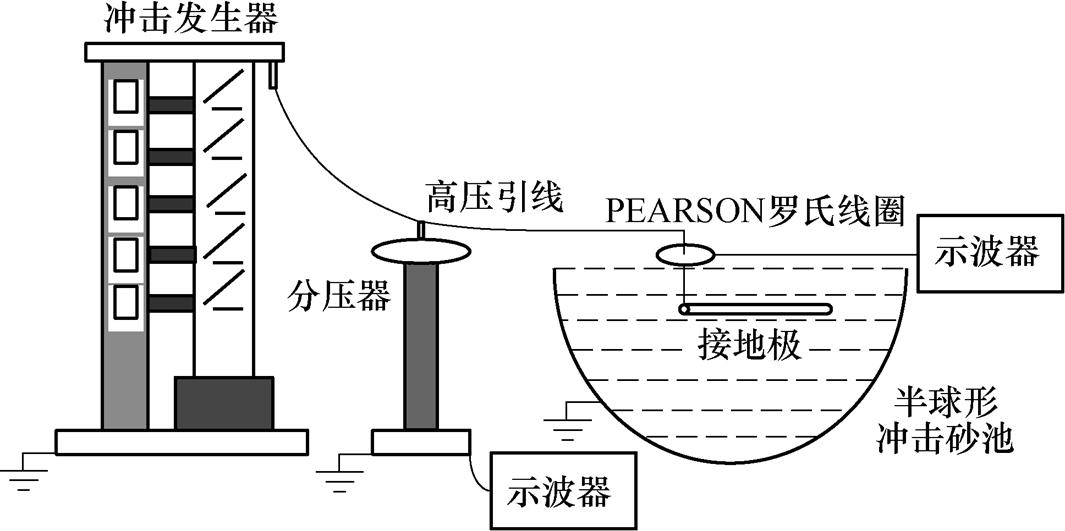
图5 实验原理
Fig.5 Experimental schematic

图6 现场测试
Fig.6 Field test
冲击模拟实验中,接地材料使用单根圆钢,长1.2m,半径3mm,圆钢埋深10cm,砂池为直径5m、深3m的半球形铜质砂池,土壤电阻率为290W·m。图7为实测值与模型计算值结果对比。
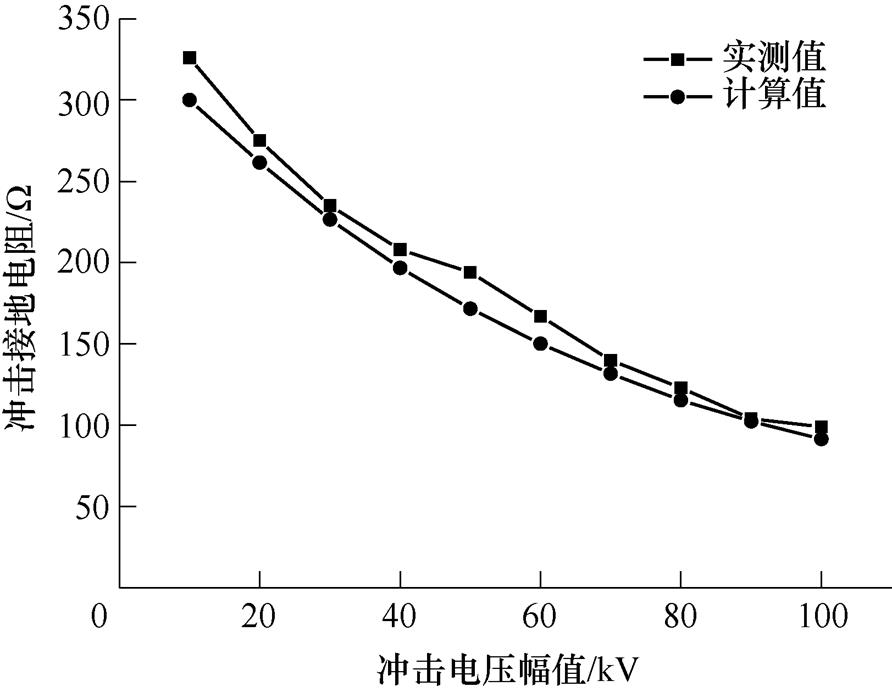
图7 实测值与计算值结果对比
Fig.7 Comparison of measured and calculated values
与CDEGS软件的对比以及与现场实验结果的对比,共同验证了本模型的正确性。
在我国,大量的输电杆塔搭建在山地之上,而山区杆塔周边地况环境恶劣,施工困难。我国几乎所有山地地表下均分布有岩石层,岩石层密度大,电阻率往往超过5 000W·m,将很大程度地影响接地装置的雷击散流效果,使接地电阻过大。岩石层存在于地表的几米到几十米以下,不同深度的岩层雷电散流效果差异较大,本文将岩层分布考虑为接地装置下方2m为岩层和下方10m为岩层两种情况。
现有研究表明,相同材料时,在原接地装置四角处分别焊接4根与原边呈135°的射线时降阻效果最好。因为导体之间存在屏蔽效应,电流越大,导体距离越近,屏蔽效应越明显。山区杆塔周边开阔地小,施工面积有限,因此可针对性地使用树状型外引射线来合理利用周围面积,如图8所示。
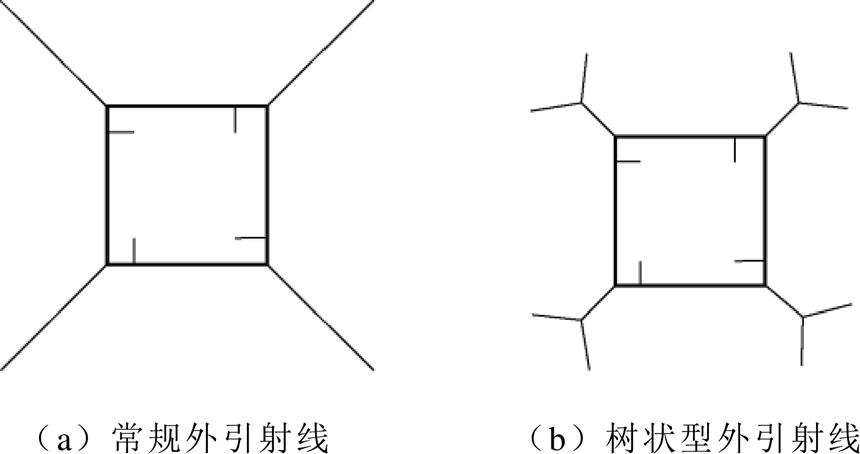
图8 外引水平接地极
Fig.8 External horizontal grounding pole
山地一般电阻率高,达到降阻效果需足够长的外引射线,而山区环境使得长外引射线很难实现。在外引射线上施加“针刺”类金属短导体,如图9所示,可在有限的施工空间内实现较好的降阻效果。
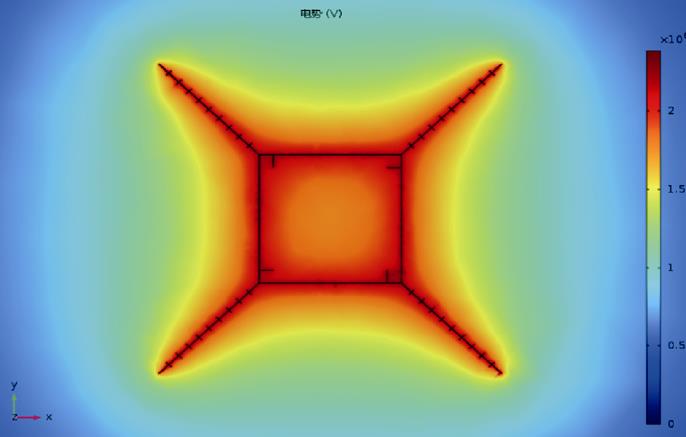
图9 外引射线加装金属短导体
Fig.9 External horizontal grounding electrodes with metal short conductors
由于接地极屏蔽效应和端部效应的影响,金属短导体的数量、长度和布置方式都会对整体降阻效果产生影响。定义单位材料降阻效果为
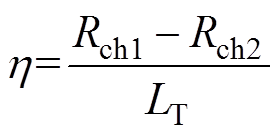 (23)
(23) 式中,Rch1为优化前的冲击接地电阻;Rch2为优化后的冲击接地电阻;LT为所采用的降阻材料总长度。在10m×10m方框形接地装置四角装配10m长外引射线,在外引射线上等距焊接针刺导体,单位长度针刺导体降阻效果如图10所示。
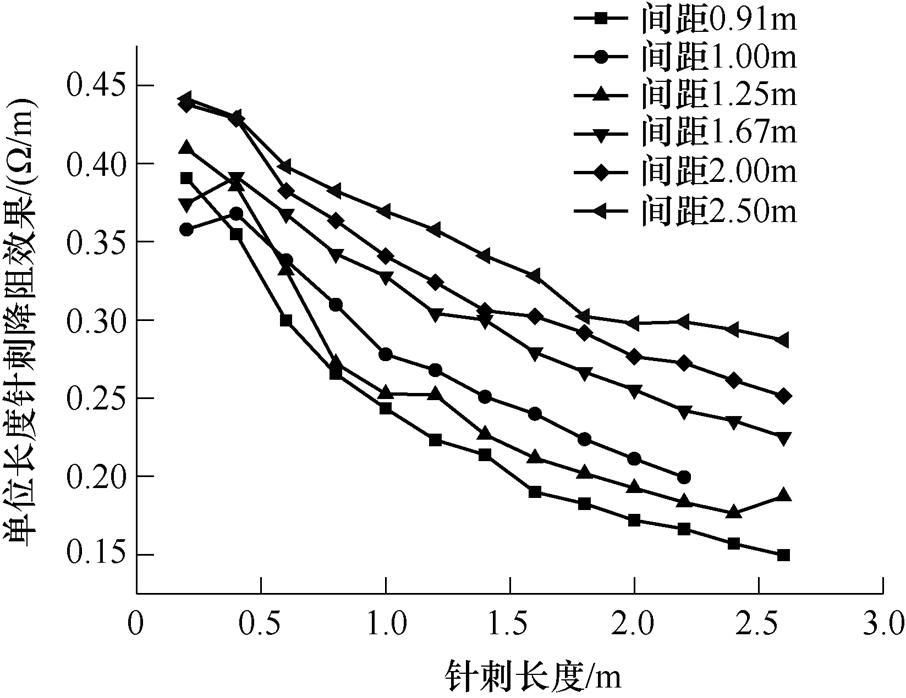
图10 短导体长度对单位材料降阻效果的影响
Fig.10 Effect of short conductor length on resistance reduction of unit material
冲击散流时导体间屏蔽效应越强,散流的难度就越大。由图10可知,随着针刺长度的增加,单位长度针刺的降阻效果整体呈下降趋势。但长度为0.5m左右时,单位长度针刺的降阻效果达到最大,即对10m的外引射线,针刺材料总量相同时,针刺长0.5m降阻效果最优。改变针刺导体在外引射线上的间距,单位长度短导体的降阻效果如图11所示。
由图11可知,随着针刺间距的增加,单位长度针刺的降阻效果整体呈现上升趋势,然而针刺间距过大必然使得针刺数量减少,整个接地装置难以降到适宜的冲击接地电阻。因此,当针刺间距为1m左右,数量足够时,接地装置整体冲击接地电阻较小,且单位长度材料降阻效果良好,因此10m外引射线下,针刺间距保持1m左右为最佳的间距布置。
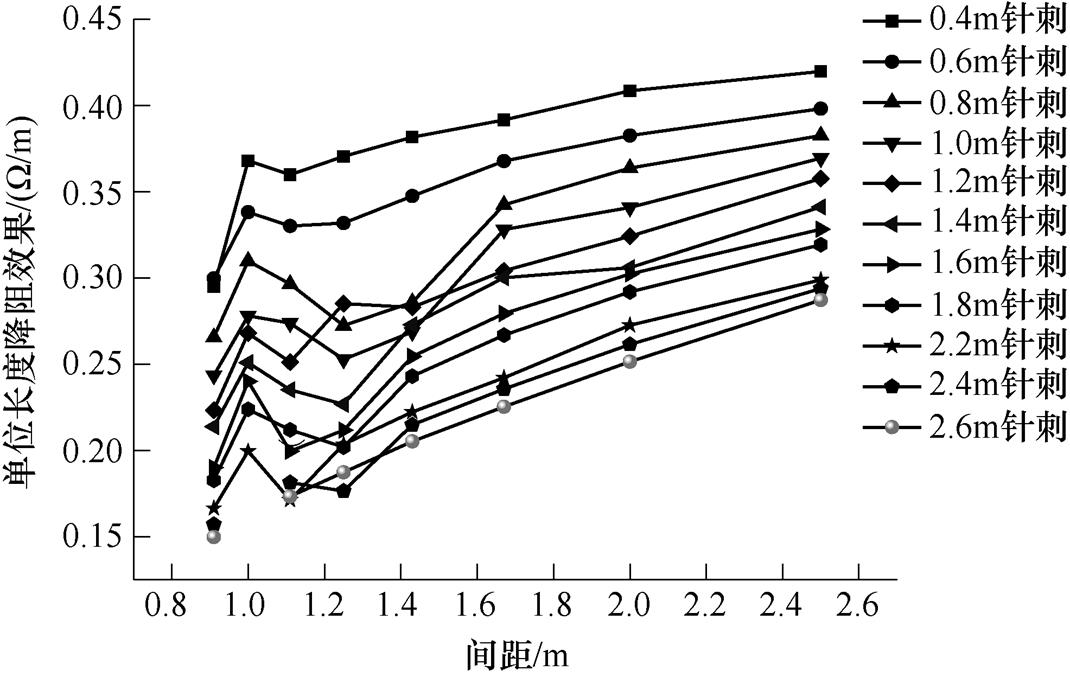
图11 短导体间距对单位材料降阻效果的影响
Fig.11 Effect of short conductor spacing on resistance reduction of unit material
类似地,对不同长度外引射线在不同土壤电阻率下进行上述探究,结果发现,对于地表下方2m存在岩石的地区,若接地材料恒定,控制针刺长度为射线长度的4%~6%、针刺间距为射线长度的10%~12%时,接地装置有最好的降阻效果。
下方2m存在岩层区域,当外加接地材料总长度均为64m时,不同方式的降阻效果见表2。
表2 降阻效果比较
Tab.2 Comparison of resistance reduction

土壤电阻率/(W·m)冲击接地电阻/W 常规射线树状射线配备针刺 60018.5819.3720.17 1 00026.1026.9428.21 1 50034.1135.0236.68 2 00041.4942.2944.16
对比可知,在相同材料长度下,三种方法效果差异不大,其中常规射线和树状型射线的降阻效果相对较好,但考虑到此类区域可延展面积受限,射线配合针刺更适宜下方2m存在岩层地区。
3.2.1 外引射线加装金属短导体
同样,使用外延长射线是降低冲击接地电阻的有效方法。若环境受限,考虑使用外引射线配合针刺短导体进行优化。
在10m×10m方框形接地装置四角装配10m外引射线,外引射线上等距焊接针刺导体,针刺长度和间距对降阻效果的影响分别如图12和图13所示。
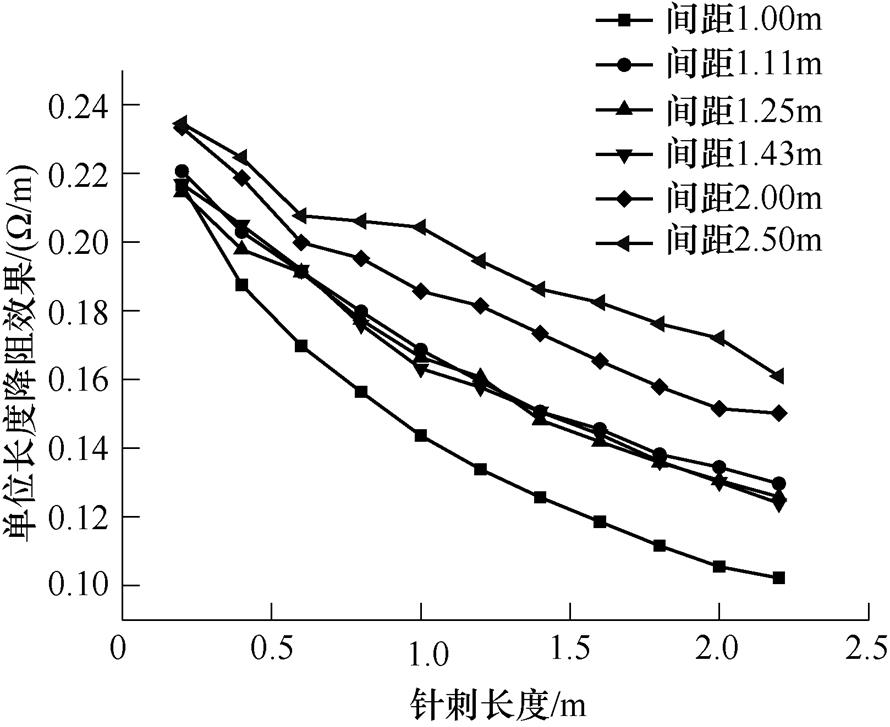
图12 针刺长度对到降阻效率的影响
Fig.12 Effect of short conductor length on resistance reduction of unit material
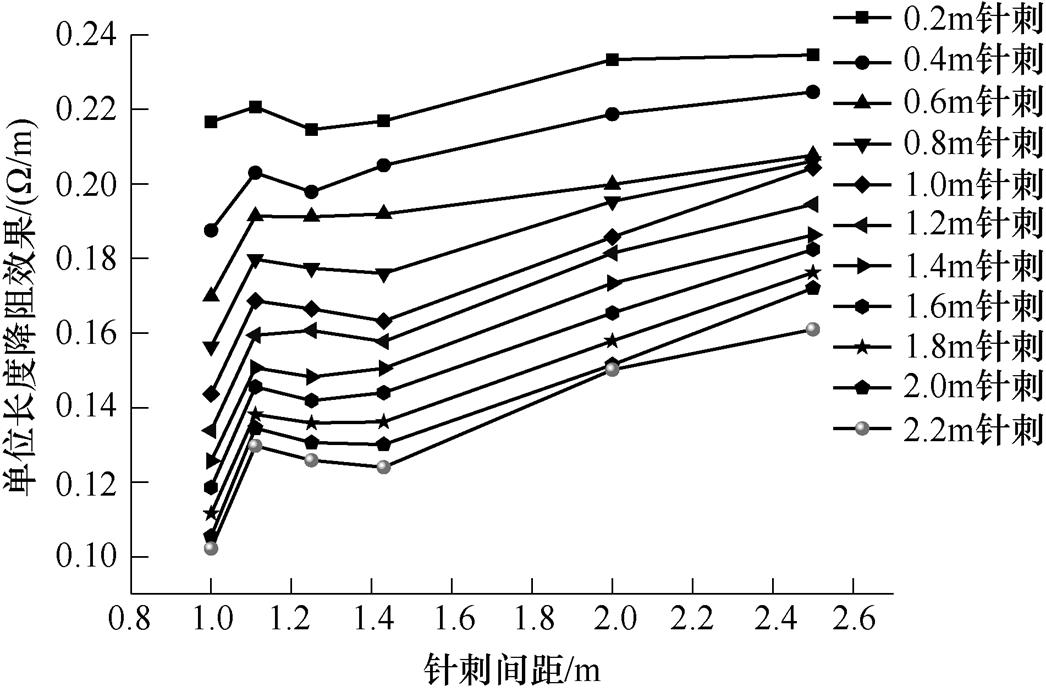
图13 针刺间距对到降阻效率的影响
Fig.13 Effect of short conductor length on resistance reduction of unit materials
由图12可知,随着针刺短导体长度的增加,单位长度针刺的降阻效果整体趋于下降,当材料总量相同时,针刺长0.3m有最优的降阻效果。
由图13及3.1节分析可知,在下方10m存在岩石的区域,当接地装置外引射线为10m时,针刺间距保持1.1m左右时为最佳的间距布置。
类似地,对不同长度外引射线在不同土壤电阻率下进行大量仿真分析,结果发现,对于地表下方10m存在岩石的地区,若接地材料恒定,控制针刺长度为射线长度的3%~5%、针刺间距为射线长度的10%~14%时,接地装置有最好的降阻效果。
3.2.2 外引射线配合垂直接地极
使用多根垂直接地极时,由于各垂直接地极两两平行,其相互之间的屏蔽效应往往较大,为了对垂直接地极进行有效利用,将四根垂直接地极首先布置于射线和框体的连接处,然后依次沿着射线方向等距向外布置,如图14所示,垂直接地极布置在不同位置时的冲击接地电阻见表3。
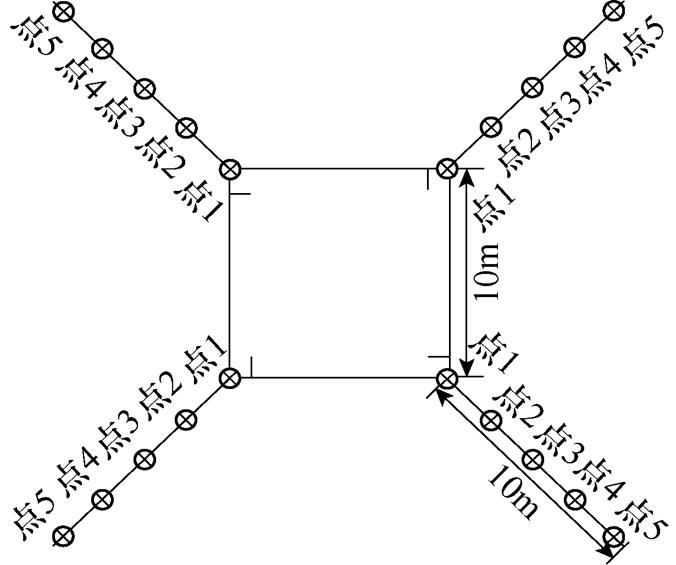
图14 在不同位置布置垂直接地极
Fig.14 Arranging vertical grounding electrodes at different locations
表3 不同位置垂直接地极的接地电阻比较
Tab.3 Comparison of grounding resistance of vertical grounding electrodes in different positions
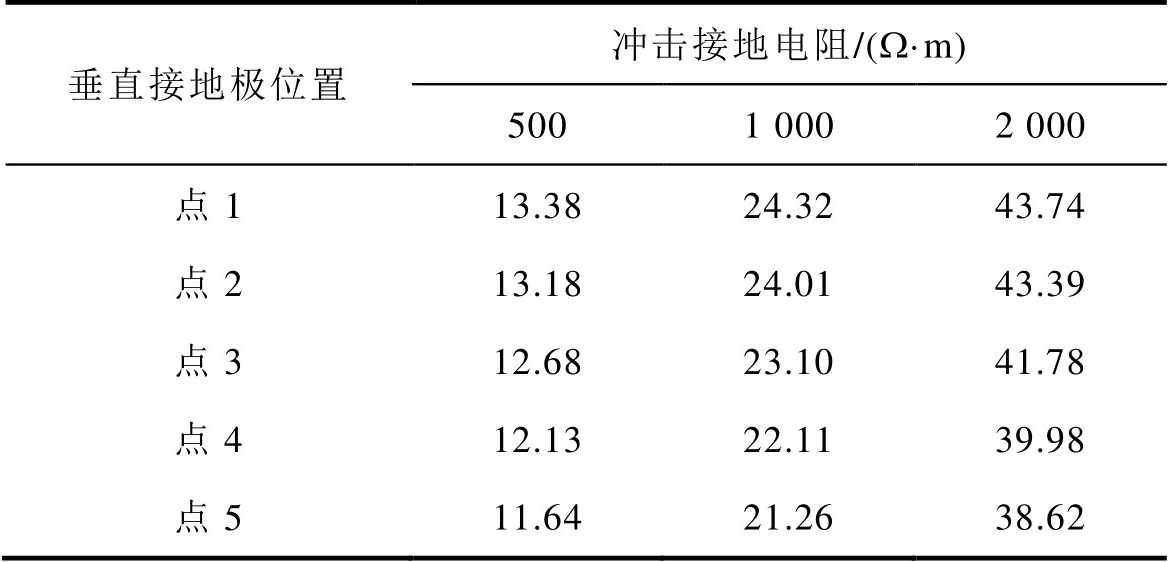
垂直接地极位置冲击接地电阻/(W·m) 5001 0002 000 点113.3824.3243.74 点213.1824.0143.39 点312.6823.1041.78 点412.1322.1139.98 点511.6421.2638.62
由图14和表3可知,随着垂直接地极布置位置的外移,冲击接地电阻整体趋于下降,即当垂直接地极布置在外引射线末端时,接地装置整体降阻效果最优。
对此规律进一步探究,保持接地材料总长度不变,分别在外引射线末端和射线框体连接处同时施加垂直接地极,并在外引射线末端和射线中部同时施加垂直接地极,垂直接地极长度变化时的接地电阻见表4。
表4 垂直接地极长度变化时的接地电阻
Tab.4 Grounding resistance when the length of the vertical grounding electrodes change at different positions
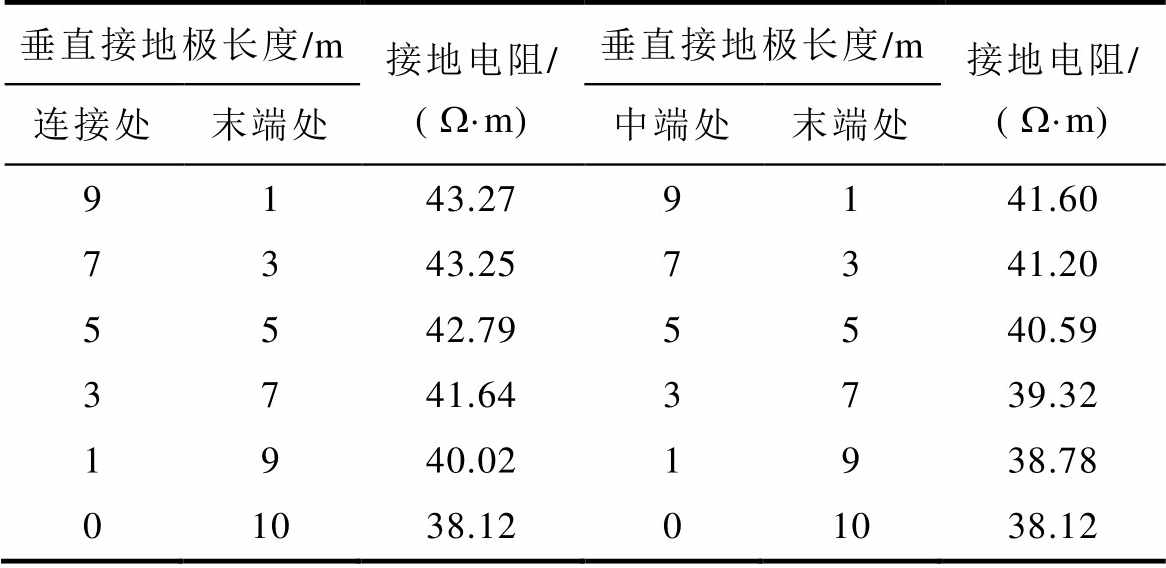
垂直接地极长度/m接地电阻/ ( W·m)垂直接地极长度/m接地电阻/ ( W·m) 连接处末端处中端处末端处 9143.279141.60 7343.257341.20 5542.795540.59 3741.643739.32 1940.021938.78 01038.1201038.12
由表4可知,垂直接地极总长度恒定时,只在四条射线末端布置四条垂直接地极有最好的降阻优化效果。对不同雷电流幅值及土壤电阻率进行仿真探究,所得规律与本结论一致。
3.2.3 各种优化方法降阻效果的比较
对于现研究的各种优化方法,基于典型尺寸结构接地装置,当外加材料总用量相同时各种优化措施的降阻效果比较如图15所示。
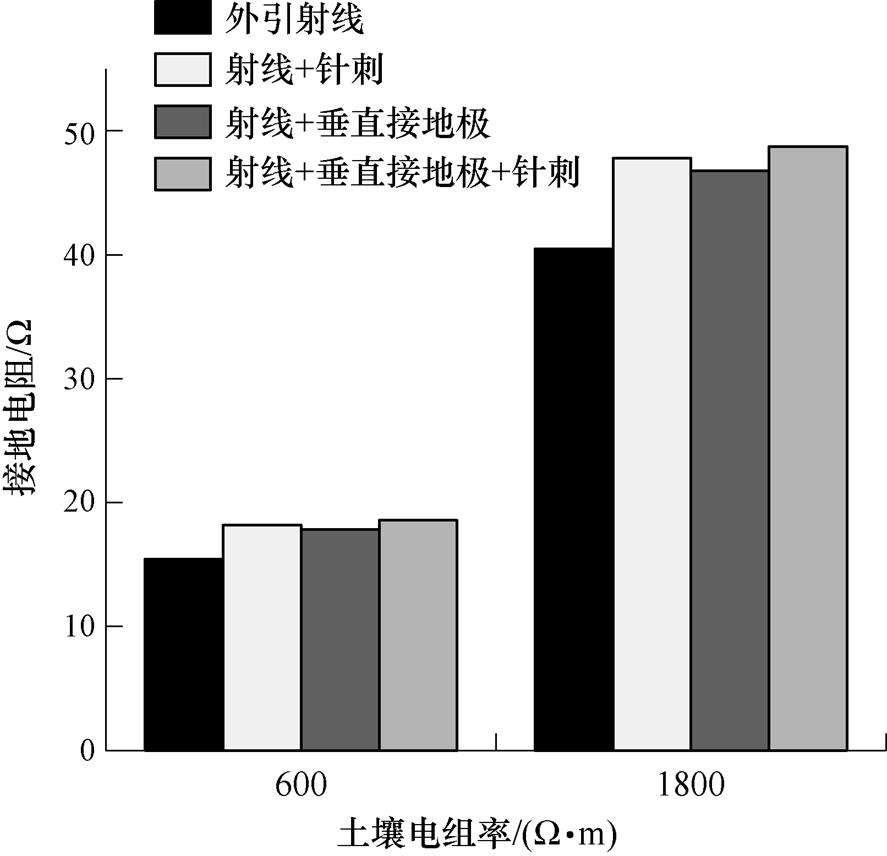
图15 材料总用量相同时的降阻效果比较
Fig.15 Comparison of the effect of reducing the resistance when the total amount of materials are constant
其中,口字型接地装置尺寸为10m×10m,埋深0.8m,下方10m存在岩石,外加接地材料总长度为58m。由图15可知,对于接地装置下方10m存在岩石的区域,外加材料相同时,相对降阻效果由强到弱依次为外引射线、射线配合垂直接地极、射线配合针刺、射线同时配合针刺和垂直接地极。考虑到山区地形的复杂及可施工区域的限制,此类区域接地装置安装外引射线并在连接处和射线末端焊接适宜比例的垂直接地极为较为适宜的降阻优化方法。
本文采用有限元和电路理论结合的方法,基于实测的广东地区典型土壤冲击特性,精确搭建了杆塔接地暂态模型,并由此对含岩层地带的输电杆塔接地装置进行了降阻优化分析。所得结论如下:
1)接地装置下方2m存在岩石层地区,设置针刺长度为外引射线的3%~5%、针刺间距为外引射线的10%~12%时降阻效果最好;接地装置下方10m存在岩石地区,设置针刺长度为外引射线的4%~6%、针刺间距为外引射线的10%~14%时降阻效果最好。
2)可使用垂直接地极时,将垂直接地极设置在外引射线的外部末端时降阻效果最好。
3)接地装置下方2m存在岩石层时,各种降阻方法效果相近;接地装置下方10m存在岩石层时,外引射线以及射线配合垂直接地极有更好的降阻效果。
参考文献
[1] 何金良,曾嵘. 电力系统接地技术[M]. 北京: 科学出版社, 2007.
[2] 张刘春. ±1100kV特高压直流输电线路防雷保护[J]. 电工技术学报, 2018, 33(19): 197-203.
Zhang Liuchun. Lightning protection of ±1100kV UHVDC transmission lines[J]. Transactions of China Electrotechnical Society, 2018, 33(19): 197-203.
[3] Grcev L D, Heimbach M. Frequency dependent and transient characteristics of substation grounding systems[J]. IEEE Transactions on Power Delivery, 1997, 12(1): 172-178.
[4] He Jinlian, Gao Yanqing, Zeng Rong, et al. Effective length of counterpoise wire under lightning current[J]. IEEE Transactions on Power Delivery, 2005, 20(2): 1585-1591.
[5] 文刚, 齐世举, 姜勤波, 等. 大地水平分层电导率对架空线缆HEMP响应的影响[J]. 电工技术学报, 2016, 31(1): 91-95.
Wen Gang, Qi Shiju, Jiang Qinbo, et al. Effect of horizontal layered earth conductivity on HEMP response of overhead cables[J]. Transactions of China Electrotechnical Society, 2016, 31(1): 91-95.
[6] 张丽萍, 袁建生, 李中新. 变电站接地网不等电位模型数值计算[J]. 中国电机工程学报, 2000, 20(1): 1-3.
Zhang Liping, Yuan Jiansheng, Li Zhongxin. Nume- rical calculation of unequal potential model of substation grounding grid[J]. Proceedings of the CSEE, 2000, 20(1): 1-3.
[7] Otero A F, Cidras J, Del Alamo J L. Frequency- dependent grounding system calculation by means of a conventional nodal analysis technique[J]. IEEE Transactions on Power Delivery, 1999, 14(3): 873- 878.
[8] Grecv L. Modeling of grounding electrodes under lightning currents[J]. IEEE Transactions on Electro- magnetic Compatibility, 2009, 51(3): 559-571.
[9] 李景丽, 袁涛, 杨庆, 等. 考虑土壤电离动态过程的接地体有限元模型[J]. 中国电机工程学报, 2011, 31(22): 149-157.
Li Jingli, Yuan Tao, Yang Qing, et al. Finite element model of grounding body considering soil ionization dynamic process[J]. Proceedings of the CSEE, 2011, 31(22): 149-157.
[10] Grcev L. Impulse efficiency of ground electrodes[J]. IEEE Transactions on Power Delivery, 2009, 24(1): 441-451.
[11] Visacro S, Alipio R. Frequency dependence of soil parameters: experimental results, predicting formula and influence on the lightning response of grounding electrodes[J]. IEEE Transactions on Power Delivery, 2012, 27(2): 927-935.
[12] Xiong Wei, Dawalibi F. Transient performance of substation grounding systems subjected to lightning and similar surge currents[J]. IEEE Transactions on Power Delivery, 1994, 9(3): 1412-1420.
[13] 李景丽, 袁涛, 杨庆, 等. 考虑土壤非线性的接地网有限元分析[J]. 高电压技术, 2011, 37(1): 249-256.
Li Jingli, Yuan Tao, Yang Qing, et al. Finite element analysis of grounding grid considering soil non- linearity[J]. High Voltage Engineering, 2011, 37(1): 249-256.
[14] Yunus M, Nor N, Etobi N, et al. Performance of earthing systems for different earth electrode configurations[J]. IEEE Transactions on Industry Applications, 2015, 51(6): 5335-5342.
[15] 黄勇, 陈先禄. 长垂直接地极的利用系数和降阻效果研究[J]. 高电压技术, 1995, 21(4): 17-19.
Huang Yong, Chen Xianlu. Research on utilization coefficient and resistance reduction effect of long vertical grounding electrode[J]. High Voltage Engin- eering, 1995, 21(4): 17-19.
[16] 杨帅, 李超英, 谭波, 等. 方框带射线型接地体冲击特性影响因素[J]. 高电压技术, 2016, 42(5): 1548- 1555.
Yang Shuai, Li Chaoying, Tan Bo, et al. Factors affecting the impact characteristics of framed beam type grounding body[J]. High Voltage Engineering, 2016, 42(5): 1548-1555.
[17] 司马文霞, 袁涛. 两种常见接地极电流分布的探讨[C]//中国电机工程学会高电压专委会学术年会, 深圳, 2007: 1021-1024.
[18] 袁涛, 雷超平, 司马文霞, 等. 提高接地极散流效率的冲击接地降阻分析[J]. 电工技术学报, 2012, 27(11): 278-284.
Yuan Tao, Lei Chaoping, Sima Wenxia, et al. Analysis of impulse earthing resistance reduction for grounding extreme diffusion efficiency[J]. Transa- ctions of China Electrotechnical Society, 2012, 27(11): 278-284.
[19] 肖微, 胡元潮, 阮江军, 等. 柔性石墨复合接地材料及其接地特性[J]. 电工技术学报, 2017, 32(2): 85-94.
Xiao Wei, Hu Yuanchao, Ruan Jiangjun, et al. Flexible graphite composite grounding material and its grounding characteristics[J]. Transactions of China Electrotechnical Society, 2017, 32(2): 85-94.
[20] 李景丽, 张宇, 郭丽莹, 等. 复杂土壤结构对水电站接地装置散流机理影响分析[J]. 电工技术学报, 2017, 32(23): 167-175.
Li Jingli, Zhang Yu, Guo Liying, et al. Influence of complex soil structure on the scattering mechanism of grounding device in hydropower station[J]. Transa- ctions of China Electrotechnical Society, 2017, 32(23): 167-175.
[21] Kherif O, Chiheb S, Teguar M, et al. Time-domain modeling of grounding systems’ impulse response incorporating nonlinear and frequency-dependent aspects[J]. IEEE Transactions on Electromagnetic Compatibility, 2018, 60(4): 907-916.
[22] 倪光正. 工程电磁场原理[M]. 北京: 高等教育出版社, 2002.
[23] Liu Yaqing, Theethayi N, Gonzalez R M, et al. The residual resistivity in soil ionization region around grounding system for different experimental results[C]// IEEE 2003 International Symposium on Electro- magnetic Compatibility, Boston, 2003: 794-799.
Impulse Impedance Modeling and Application of Tower Grounding Device
Abstract Tower grounding impedance is one of the main influencing factors of lightning trip accidents on transmission lines. In the mountainous and hilly areas of China, the tower usually has a large impulse grounding resistance, which causes frequent line trip accidents. Based on the combination of finite element method and circuit theory, this paper explored the impulse characteristics of typical soils in Guangdong and established a precise grounding transient model of transmission lines. Based on this model, an optimization method for the impulse resistance reduction of transmission towers in rock zones was studied. The results show that for grounding devices with rock formations below the earth surface, the application of external grounding electrodes with short conductors and external grounding electrodes with vertical grounding electrodes has a better optimization effect. If the short conductors are used to match external grounding electrodes, the effect of reducing the resistance is the best when the length of the short conductor is 3%~6% of the external grounding conductor and the spacing of the short conductors is 10%~14% of the external grounding conductor. If the vertical grounding electrodes are used to match external grounding electrodes, the effect of reducing the resistance is the best when the vertical grounding electrodes are placed at the outermost ends of the external grounding conductors. The results can provide reference and theoretical support for grounding transformation and optimization of mountain towers.
keywords:Grounding transient model, rock layer, resistance reduction method, metal short conductor, vertical grounding electrode
中图分类号:TM862
DOI: 10.19595/j.cnki.1000-6753.tces.190542
郭 蕾 女,1981年生,副教授,硕士生导师,研究方向为牵引供电系统、电力系统建模和电能质量分析。E-mail: guolei_mail@swjtu.cn(通信作者)
古维富 男,1994年生,硕士研究生,研究方向为电力系统过电压及其防护。E-mail: weifu_gu@163.com
中国南方电网有限责任公司科技项目(GDKJXM20182401)资助。
收稿日期2019-05-06
改稿日期 2019-09-03
(编辑 崔文静)