
图1 双向交直流变换器容错结构
Fig.1 Fault-tolerant structure of bidirectional AC-DC converter
摘要 双向交直流变换器运行过程中的浪涌、尖峰等瞬态冲击会导致桥臂器件故障,进而威胁双向交直流变换器工作的可靠性。常规模型预测容错控制每个开关周期选取单个矢量作用于双向交直流容错变换器,所以开关频率不固定,难以准确跟踪目标矢量,电流谐波含量和功率脉动较大。为抑制常规模型预测容错控制下双向交直流变换器桥臂故障后的电流谐波和功率脉动,提出一种多矢量恒频模型预测容错控制方法。首先,重构桥臂故障后的双向交直流变换器系统结构,阐明故障容错运行机理及电压矢量变化。其次,建立容错运行模式的预测模型,在每个开关周期采用多个电压矢量的合成矢量跟踪目标矢量,并固定各矢量切换顺序,形成恒定开关频率。最后,仿真及实验结果表明,在所提控制策略下,双向交直流变换器发生桥臂故障后能够容错运行,且输出电流谐波减小,功率脉动下降,具有较好的稳态及动态性能。
关键词:双向交直流变换器 桥臂故障 多矢量恒频 模型预测容错控制 容错运行
双向交直流变换器广泛应用于交直流微电网及电能转换系统中[1],但运行过程中浪涌、尖峰等瞬态冲击会导致变换器桥臂故障,变换器一旦出现故障,原本的控制策略就会失效,导致变换器无法正常工作,进而威胁整个电能转换系统的稳定与安全运行。
为了确保变换器在桥臂故障下能够容错运行,文献[2]对电力电子功率变换器故障诊断方法进行了研究。文献[3]对变频器故障诊断及容错控制进行了分析。目前,主流的容错结构有两种,文献[4]采用器件冗余的方法,即当功率器件发生故障时立即让冗余器件投入运行,此种方法虽无需改变控制策略,但硬件成本较高。此外,文献[5-8]是在某一桥臂或某一器件发生故障后,将变换器由三相六开关重构为三相四开关(Three Phases Four Switches, TPFS),即在直流侧串联两组电容,将故障相连接至两组电容的中点,通过相应的控制策略实现容错运行。然而,TPFS变换器虽然实现了变换器的容错运行,但在四开关变换器中只有长度不等的四个电压矢量,且没有零矢量,对于变换器常规矢量控制策略来讲,较少的电压矢量将导致变换器控制自由度降低,进而引起输出电流谐波增大、输出功率脉动明显等问题[9-10]。
传统的并网变换器控制方法有旋转坐标系下的矢量控制、电流滞环控制、无差拍控制等[11-13]。矢量控制中比例积分参数的选择影响较大,同时还需要锁相环进行并网同步控制[14]。电流滞环控制相对简单,但采样频率要求高,变换器输出电压、电流频谱比较分散,不利于输出滤波器的设计。无差拍控制对系统的参数准确性要求较高,鲁棒性较差。近年来,模型预测控制(Model Predictive Control, MPC)具有良好的自适应性、灵活性和鲁棒性,且不需要内环电流控制,控制方案容易实现等优点受到广大学者青睐[15-17]。然而,常规模型预测控制在每个开关周期只选取单个矢量作用于变换器[18],应用于双向交直流容错变换器时,不可避免地由于矢量减少导致控制精度下降,难以准确跟踪实际最优矢量,电流谐波含量和功率脉动较大。
为此,针对双向交直流变换器桥臂故障后输出电流谐波与功率脉动较大的问题,提出一种多矢量恒频模型预测容错控制策略。在每个开关周期使用多个电压矢量共同作用,利用合成矢量准确跟踪目标矢量,并固定各矢量切换顺序,形成恒定开关频率,提高变换器桥臂故障后容错运行能力,抑制并网电流谐波及功率脉动,最后通过仿真与实验验证所提控制策略的有效性。
双向交直流变换器容错结构如图1所示,3个双向晶闸管作为连接开关,连接直流侧电容中点与a、b、c三相,每一个输出桥臂中串联1个快速熔断器。当变换器正常工作时,双向晶闸管断开。当某一桥臂(如a相桥臂)发生开路或者短路故障时,熔断对应桥臂上的快速熔断器(Fa),同时对应相的双向晶闸管(VTra)导通,重构为三相四开关结构,如图1b所示,实现变换器故障容错运行。

图1 双向交直流变换器容错结构
Fig.1 Fault-tolerant structure of bidirectional AC-DC converter
双向交直流变换器重构为三相四开关容错变换器结构,故障相直接连接直流侧两电容中点,非故障相的四个开关器件依然正常工作,交流侧通过滤波电感L、线电阻R与电网相连。
开关信号Si(i=b, c)控制变换器的开关状态
 (1)
(1)开关信号决定输出电压,即
 (2)
(2)
式中,Van、Vbn、Vcn为逆变器输出三相电压值;Vdc为直流母线电压。
变换器输出电压矢量定义为

 (3)
(3)式中,a =ej2p/3。
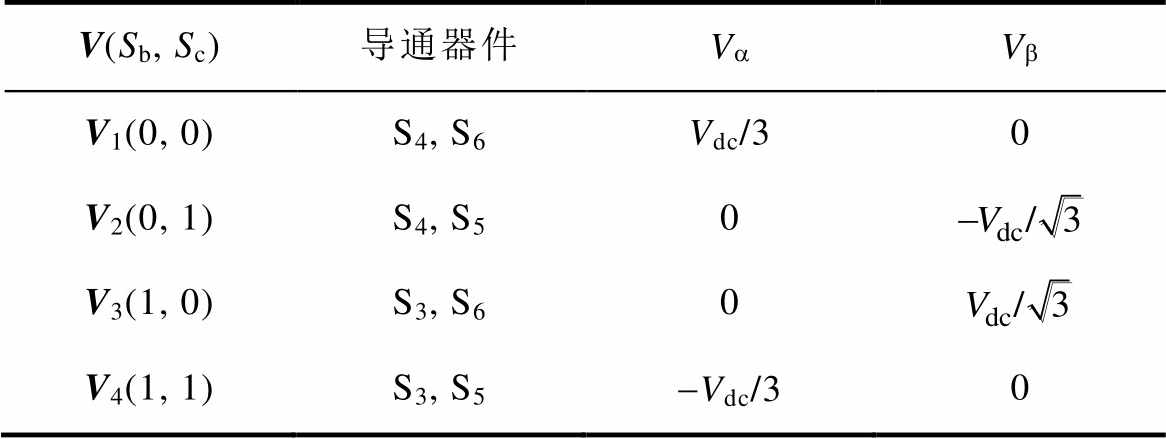
通过坐标变换得到两相静止坐标系下的电压矢量分量Va 和Vb 见表1。交直流变换器在不同桥臂故障下的电压矢量如图2所示。
表1 三相四开关变换器电压矢量
Tab.1 Three-phase four-switch converter voltage vector
V(Sb, Sc)导通器件VaVb V1(0, 0)S4, S6Vdc/30 V2(0, 1)S4, S50 V3(1, 0)S3, S60 V4(1, 1)S3, S5-Vdc/30

图2 桥臂故障下电压矢量
Fig.2 Voltage vector under bridge arm fault
重构三相四开关变换器如图1b所示,根据基尔霍夫定律,得到系统在三相静止坐标系下的状态方程为
 (4)
(4)式中,ea、eb、ec为三相电网电压;ia、ib、ic为三相电流。
将式(4)变换到两相静止坐标系下,得到ab静止坐标系下的状态方程为
 (5)
(5)式中,ia、ib、Va、Vb、ea、eb 分别为变换器输出电流、电压以及电网电压的ab 分量。
对式(5)进行欧拉前向公式离散化,得到
 (6)
(6)式中,Ts为信号采样周期;ia(k)、ib(k)、Va(k)、Vb(k)、ea(k)、eb(k)分别为tk时刻变换器输出电流、电压以及电网电压的ab 分量;ia(k+1)、ib(k+1)为tk+1时刻的预测电流值的ab 分量。
化简式(6),得到tk+1时刻的预测电流为
 (7)
(7)根据瞬时功率理论,变换器输出有功功率P和无功功率Q分别为
 (8)
(8)
对于三相平衡电网,当采样频率远高于电网频率时,有以下假设
 (9)
(9)式中,ea (k+1)、eb(k+1)分别为tk+1时刻变换器输出电网电压的ab 分量。
将式(7)、式(9)代入式(8),得到tk+1时刻的功率预测模型为
 (10)
(10)常规模型预测控制在每一个开关周期只使用一个电压矢量,无法准确跟踪实际矢量,导致输出电流与功率脉动较大。同时,由于矢量切换顺序不固定,导致其功率器件开关频率不固定,这就使得其输出电压和电流的谐波频率不固定。恒定开关频率的模型预测容错控制的每个开关周期采用三个电压矢量,计算各电压矢量的作用时间后,合成新的电压矢量,通过价值函数择优,选定最优合成电压矢量产生控制信号。多个矢量共同作用可以更好地跟踪实际目标矢量。为实现对给定功率快速精确的跟踪,根据给定功率与预测功率建立关于功率的代价函数为
 (11)
(11)式中,Pref、Qref为参考有功和无功功率;Pi(k+1)、Qi(k+1)为预测有功和无功功率,i=1, 2, 3, 4。
以a相故障下模型预测容错控制为例,假定此时给定电压矢量在图2a的第Ⅰ扇区,定义等效电压零矢量V0的代价函数为g0,作用时间为t0;电压矢量V1的代价函数为g1,作用时间为t1;电压矢量V3的代价函数为g3,作用时间为t3。根据前文建立的代价函数式(11),可得电压矢量V0、V1、V3的代价函数分别为
 (12)
(12)各电压矢量的作用时间与代价函数呈反比,即
 (13)
(13)
四开关结构中没有零矢量,使用V1和V4各作用一半时间代替零矢量V0。图3所示为a相故障下各矢量在各扇区下的作用时间和顺序。

图3 a相故障下各矢量在各扇区下的作用时间和顺序
Fig.3 The time and sequence of each vector in the sector under phase a fault
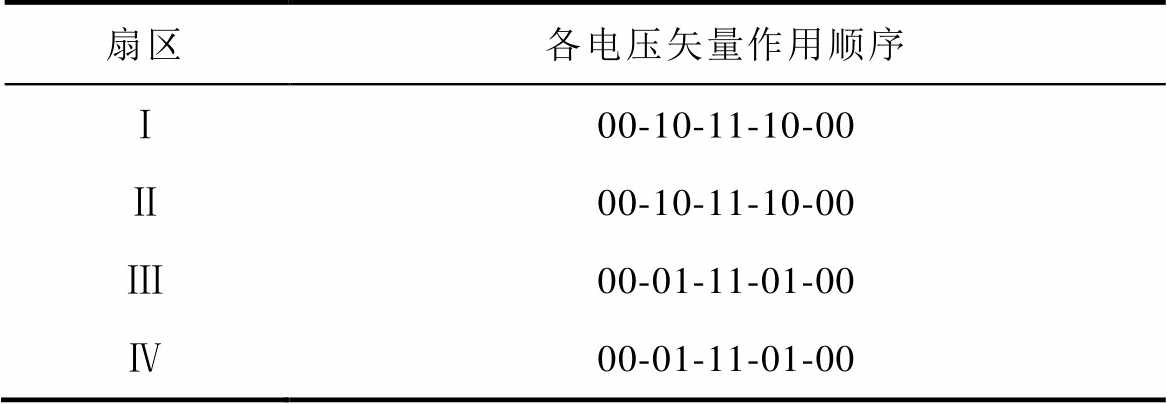
变换器a相故障下各扇区电压矢量的作用顺序见表2。
表2 a相故障下各扇区电压矢量作用顺序
Tab.2 Sequence of voltage vectors under phase a fault
扇区各电压矢量作用顺序 Ⅰ00-10-11-10-00 Ⅱ00-10-11-10-00 Ⅲ00-01-11-01-00 Ⅳ00-01-11-01-00
每个扇区各电压矢量的作用时间确定以后,计算此时矢量组共同作用后的等效矢量,以第Ⅰ扇区为例,得
 (14)
(14)式中,Vaj与Vbj分别为合成等效矢量的ab 分量,j=Ⅰ, Ⅱ, Ⅲ, Ⅳ。
将Vaj与Vbj代入预测函数式(10)可得到新的预测功率Pj(k+1)与Qj(k+1),此时代入代价函数为
 (15)
(15)式中,j =Ⅰ, Ⅱ, Ⅲ, Ⅳ。
求出代价函数最小值,对应开关状态的三个矢量应用于下一周期。双向交直流容错变换器控制框图如图4所示。

图4 双向交直流容错变换器控制框图
Fig.4 Bidirectional AC-DC fault-tolerant converter control block diagram
在Matlab/Simulink环境下搭建双向交直流容错变换器仿真模型,为验证所提多矢量恒频模型预测容错控制方法的有效性,采用常规模型预测容错控制作为对比策略。系统仿真和实验模型参数见表3。
表3 仿真与实验模型参数
Tab.3 Simulation and experiment parameters

参 数数 值 直流母线电压Vdc/V400 滤波电感L/mH10 电网相电压e/V110 采样频率fs /kHz10 电网频率f/Hz50
1)变换器处于逆变模式时,仿真结果如图5所示。假设a相桥臂发生故障,给定参考有功功率为1 000W,参考无功功率为0var。常规模型预测容错控制下,三相输出并网电流、有功功率与无功功率波形如图5a所示,并网电流总谐波畸变率(Total Harmonics Distortion, THD)(谐波含有量)为4.05%;在多矢量恒频模型预测容错控制下,三相输出并网电流、有功功率与无功功率如图5b所示,并网电流THD=1.93%。在逆变模式下,相比于常规模型预测容错控制,多矢量恒频模型预测容错控制输出功率脉动减小,输出电流THD降低了2.12%,谐波分量主要集中在10kHz、20kHz、30kHz,低频谐波含量减小,电能质量明显提升。

图5 逆变模式下仿真结果
Fig.5 Simulation results in inverter mode
2)变换器处于整流模式时,整流模式下仿真结果如图6所示。a相桥臂发生故障,给定参考有功功率为-1 000W,参考无功功率为0var。常规模型预测容错控制下,三相输出并网电流、有功功率与无功功率如图6a所示,并网电流THD=4.24%;在多矢量恒频模型预测容错控制下,三相输出并网电流、有功功率与无功功率如图6b所示,输出功率脉动下降,并网电流THD=2.04%,相比于常规模型预测容错控制下降了2.2%。仿真结果验证了在逆变与整流模式下,所提控制策略具有较好的稳态性能,控制效果优于常规模型预测容错控制。
3)为验证动态控制效果,双向交直流容错变换器处于逆变模式到整流模式的切换状态,给定参考有功功率在0.1~0.15s为1 000W,0.15~0.2s为-1 000W。在多矢量恒频模型预测容错控制下,逆变与整流动态切换下三相并网电流、有功功率与无功功率如图7所示。仿真结果表明,当参考有功功率给定值发生突变时,双向交直流容错变换器迅速调整到新的功率输出,没有出现电流浪涌和功率脉动等瞬态过程,输出电流谐波含量减小,输出功率平稳。该结果验证了多矢量恒频模型预测容错控制具有良好的动态性能。

图6 整流模式下仿真结果
Fig.6 Simulation results in rectification mode

图7 逆变与整流动态切换仿真结果
Fig.7 Dynamic simulation results from inverter mode to rectifier mode
4)为了验证不同输出功率下的控制效果,双向交直流变换器处于不同功率值切换状态,给定参考有功功率在0~0.1s为1 000W,0.1~0.2s为1 500W,0.2~0.3s为2 000W,无功功率为0。不同输出功率仿真结果如图8所示。在多矢量恒频模型预测控制下,三相并网电流、有功功率和无功功率如图8b所示,并网电流THD在三种输出功率下分别为1.93%、1.52%、1.28%,相对于图8a所示的常规模型预测容错控制下的结果,并网电流THD分别为4.05%、3.72%、2.83%,电流THD明显降低且功率脉动下降。仿真结果验证了在不同输出功率仿真中,所提控制策略能够稳定运行,功率切换过程中没有明显波动,控制效果优于常规模型预测容错控制。

图8 不同输出功率仿真结果
Fig.8 Simulation results for different output power levels
为进一步验证所提控制策略的有效性,搭建了一套基于PE-PRO双向交直流变换器的容错控制实验平台如图9所示。

图9 双向交直流容错变换器实验平台
Fig.9 Bidirectional AC-DC fault-tolerant converter experimental platform
实验中a相桥臂故障,重构为三相四开关变换器结构如图1b所示,系统参数见表3。为测试稳态工作效果,将常规模型预测容错控制和所提多矢量恒频模型预测容错控制策略的实验结果进行对比分析。当变换器处于逆变模式时,给定参考有功功率为1 000W,参考无功功率为0var,逆变模式下实验结果如图10所示。当变换器处于整流模式时,给定参考有功功率为-1 000W,参考无功功率为0var,整流模式下实验结果如图11所示。

图10 逆变模式下实验结果
Fig.10 Experimental results in inverter mode

图11 整流模式下实验结果
Fig.11 Experimental results in rectifier mode
采用常规模型预测容错控制策略的实验结果如图10a、图11a所示,虽然能够保证容错状态下设备的连续运行,但在逆变模式和整流模式下THD分别为4.16%、4.37%,输出功率脉动较大。采用所提多矢量恒频模型预测容错控制实验结果如图10b、图11b所示,相对于常规模型预测容错控制,在逆变模式和整流模式下THD分别下降到了2.02%、2.10%,且谐波畸变集中在开关频率的整数倍,输出功率更加平稳,脉动减小。
为进一步分析所提多矢量恒频模型预测容错控制的动态性能,进行了容错变换器的动态实验。给定参考有功功率从1 000W跳变至-1 000W,参考无功功率为0var,工作模式由逆变转为整流,逆变模式与整流模式动态切换实验结果如图12所示。实验结果表明,在所提多矢量恒频模型预测容错控制策略下,双向交直流变换器在桥臂故障后依然具有良好的动态性能,输出功率能够快速稳定跟踪参考值,电流波形良好,无冲击过电流现象,验证了所提控制策略的有效性。

图12 逆变模式与整流模式动态切换实验结果
Fig.12 Dynamic experimental results from inverter mode to rectifier mode
本文分析了双向交直流变换器桥臂故障后的结构及电压矢量变化,针对双向交直流变换器容错结构,提出了一种多矢量恒频模型预测容错控制方法。该方法在每个开关周期采用三个电压矢量,各电压矢量的作用时间与目标函数呈反比,再固定各矢量的开关顺序,以形成固定开关频率,通过合成矢量更加精确的跟踪目标矢量,从而降低并网电流的谐波含量,减小容错变换器的输出功率脉动。最后,将所提多矢量恒频模型预测容错控制与常规模型预测容错控制进行了仿真和实验的对比。结果表明,在所提多矢量恒频模型预测容错控制下,双向交直流变换器在桥臂故障后能够稳定容错运行,控制效果优于常规模型容错预测控制,且低频谐波降低,电流谐波与功率脉动进一步减小,具有良好的稳态与动态性能,为双向交直流变换器的容错控制提供了一种有效的控制方法。
参考文献
[1] 杨新法, 苏剑, 吕志鹏, 等. 微电网技术综述[J]. 中国电机工程学报, 2014, 34(1): 57-70.
Yang Xinfa, Su Jian, Lü Zhipeng, et al. Overview on micro-grid technology[J]. Proceedings of the CSEE, 2014, 34(1): 57-70.
[2] 吴娟, 沈艳霞. 电力电子功率变换器故障诊断方法综述[J]. 电工电能新技术, 2015, 34(11): 48-54.
Wu Juan, Shen Yanxia, Review of fault diagnosis technology for power electronic converters[J]. Advanced Technology of Electrical Engineering and Energy, 2015, 34(11): 48-54.
[3] 徐殿国, 刘晓峰, 于泳. 变频器故障诊断及容错控制研究综述[J]. 电工技术学报, 2015, 30(21): 1-12.
Xu Dianguo, Liu Xiaofeng, Yu Yong. A survey on fault diagnosis and tolerant control of inverters[J]. Transactions of China Electrotechnical Society, 2015, 30(21): 1-12.
[4] 杨国润, 肖飞, 范学鑫, 等. 中压大容量三重化三电平直流变换器冗余容错控制[J]. 电工技术学报, 2017, 32(增刊1): 186-195.
Yang Guorun, Xiao Fei, Fan Xuexin, et al. Redundant and fault tolerant control of a medium-voltage high- power three-phase three-level DC-DC converter[J]. Transactions of China Electrotechnical Society, 2017, 32(S1): 186-195.
[5] 袁庆伟, 赵荣祥. 三相四开关逆变器供电的IPMSM直接转矩控制系统建模与分析[J]. 电工技术学报, 2017, 32(15): 76-88.
Yuan Qingwei, Zhao Rongxiang. Modeling and analysis of the direct torque control system for IPMSM fed by three-phase four-switch inverter[J]. Transactions of China Electrotechnical Society, 2017, 32(15): 76-88.
[6] 郭小强, 贺冉, 菅佳敏, 等. 非隔离型三相四桥臂光伏逆变器漏电流抑制研究[J]. 电工技术学报, 2016, 31(19): 66-73.
Guo Xiaoqiang, He Ran, Jian Jiamin, et al. Leakage current reduction for three-phase four-leg photo- voltaic inverter[J]. Transactions of China Electro- technical Society, 2016, 31(19): 66-73.
[7] 郑玮仪, 曾志勇, 赵荣祥. 容错型三相并网变换器的建模分析与矢量调制[J]. 中国电机工程学报, 2016, 36(8): 2202-2212.
Zheng Weiyi, Zeng Zhiyong, Zhao Rongxiang. Modeling and modulation of the fault-tolerant grid- connected three-phase PWM converters[J]. Pro- ceedings of the CSEE, 2016, 36(8): 2202-2212.
[8] 刘宏超, 吕胜民, 张春晖. 三相四开关并联型有源电力滤波器的SVPWM调制算法[J]. 电工技术学报, 2011, 26(4): 128-134.
Liu Hongchao, Lü Shengmin, Zhang Chunhui. Space vector pulse width modulation of three-phase four-switch shunt active power filter[J]. Transactions of China Electrotechnical Society, 2011, 26(4): 128- 134.
[9] 王文, 罗安, 黎燕. 三相四开关并联有源电力滤波器的控制方法[J]. 电工技术学报, 2014, 29(10): 183-190.
Wang Wen, Luo An, Li Yan. Control method of three-phase four-switch shunt active power filter[J]. Transactions of China Electrotechnical Society, 2014, 29(10): 183-190.
[10] Jin Nan, Guo Leilei, Zhao C, et al. Finite states model predictive direct power control for phase leg faults tolerant operation of bidirectional AC/DC con- verter[C]//2018 IEEE Applied Power Electronics Conference and Exposition (APEC), San Antonio, TX, 2018: 2330-2336.
[11] 吉宇, 梅军, 杜晓舟, 等. 基于模块化多电平变换器的电流滞环跟踪型并网控制策略[J]. 电工技术学报, 2015, 30(4): 26-34.
Ji Yu, Mei Jun, Du Xiaozhou, et al. Hysteresis-band current tracking control strategy to connect modular multilevel converter with power grid[J]. Transactions of China Electrotechnical Society, 2015, 30(4): 26-34.
[12] 冯腾, 康龙云, 胡毕华, 等. 基于无差拍控制的T型三电平逆变器中点电位平衡策略[J]. 电工技术学报, 2018, 33(8): 1827-1834.
Feng Teng, Kang Longyun, Hu Bihua, et al. A neutral point potential balancing strategy for three-level T-type inverter based on deadbeat control[J]. Transa- ctions of China Electrotechnical Society, 2018, 33(8): 1827-1834.
[13] Jin Nan, Hu S, Gan C, et al. Finite states model predictive control for fault-tolerant operation of a three-phase bidirectional AC/DC converter under unbalanced grid voltages[J]. IEEE Transactions on Industrial Electronics, 2018, 65(1): 819-829.
[14] 赵克, 安群涛, 孙力, 等. 容错逆变器PMSM无位置传感控制系统[J]. 电机与控制学报, 2010, 14(4): 25-30.
Zhao Ke, An Quntao, Sun Li, et al. Fault-tolerant inverter permanent magnet synchronous motor position sensorless control system[J]. Electric Machines and Control, 2010, 14(4): 25-30.
[15] 郭磊磊, 金楠, 申永鹏. 一种基于优化电压矢量选择的电压源逆变器模型预测共模电压抑制方法[J]. 电工技术学报, 2018, 33(6): 1347-1355.
Guo Leilei, Jin Nan, Shen Yongpeng. A model predictive common-mode voltage suppression method for voltage source inverter based on optimum voltage vector selection[J]. Transactions of China Electro- technical Society, 2018, 33(6): 1347-1355.
[16] 金涛, 沈学宇, 苏泰新, 等. 不平衡电网下并网逆变器的模型预测电流限幅灵活控制[J]. 电工技术学报, 2018, 33(11): 1-13.
Jin Tao, Shen Xueyu, Su Taixin, et al. Flexible model predictive control with peak current limitation for grid-connected inverter under unbalanced grid voltage[J]. Transactions of China Electrotechnical Society, 2018, 33(11): 1-13.
[17] 薛花, 张芮嘉, 胡英俊. PV-FC-BS混合系统全状态模型预测能量管理优化策略[J]. 电力系统保护与控制, 2017, 45(11): 49-58.
Xue Hua, Zhang Ruijia, Hu Yingjun. Full-state model predictive energy management optimization for PV- fuel cell-battery hybrid system[J]. Power System Protection and Control, 2017, 45(11): 49-58.
[18] 杨勇, 赵方平, 阮毅, 等. 三相并网逆变器模型电流预测控制技术[J]. 电工技术学报, 2011, 26(6): 153-159.
Yang Yong, Zhao Fangping, Ruan Yi, et al. Model current predictive control for three-phase grid- connected inverters[J]. Transactions of China Electro- technical Society, 2011, 26(6): 153-159.
Multi-Vector Constant Frequency Model Predictive Fault-Tolerant Control of Bidirectional AC-DC Converter with Leg Fault
Abstract Due to the transient impact of surge and spike during operation, the leg switch device fault of AC-DC converter will occur and threaten the reliable operation of converter. In the conventional model predictive fault-tolerant control method, only a single vector is selected to act on the bidirectional AC-DC converter with leg fault in each switching cycle, so the frequency is not fixed. It is difficult to track the target vector accurately, and the current harmonic content and power ripple are large as well. In order to reduce the current harmonics and power ripple in AC-DC converter after bridge arm fault under conventional model predictive fault-tolerant control, a multi-vector model constant frequency predictive fault-tolerant control strategy is proposed in this paper. Firstly, the system topology of bidirectional AC-DC converter with leg fault is reconstructed. Then the operation mechanism of fault-tolerant structure and the relationship of voltage vectors are clarified. Secondly, the power prediction model under fault-tolerant operation mode is established. Multiple voltage vectors are used in each switching cycle. The synthetic vector is used to track the target vector. The switching order of each vector is fixed to form constant switching frequency. Finally, the simulation model and experimental platform are built. The results show that under the proposed control strategy, the bidirectional AC-DC converter can operate fault-tolerant operation after the bridge arm fault, and the output current harmonics and power ripples are reduced. The system has good steady-state and dynamic performance.
keywords:Bidirectional AC-DC converter, bridge arm fault, multi-vector constant frequency, model predictive fault-tolerant control, fault-tolerant operation
中图分类号:TM464
李琰琰 女,1987年生,博士,讲师,主要研究方向为新能源逆变器的模型预测控制。E-mail: lyy0825@zzuli.edu.cn
金 楠 男,1982年生,博士,副教授,硕士生导师,主要研究方向为电能变换可靠性、模型预测控制。E-mail: Jinnan@zzuli.edu.cn(通信作者)
DOI: 10.19595/j.cnki.1000-6753.tces.190526
国家自然科学基金(51607159,51707176),河南省高等学校创新人才资助计划(18HASTIT025)和河南省高等学校重点科研(18A470020,20A470011)资助项目。
收稿日期 2019-05-06
改稿日期 2019-07-31
(编辑 陈 诚)