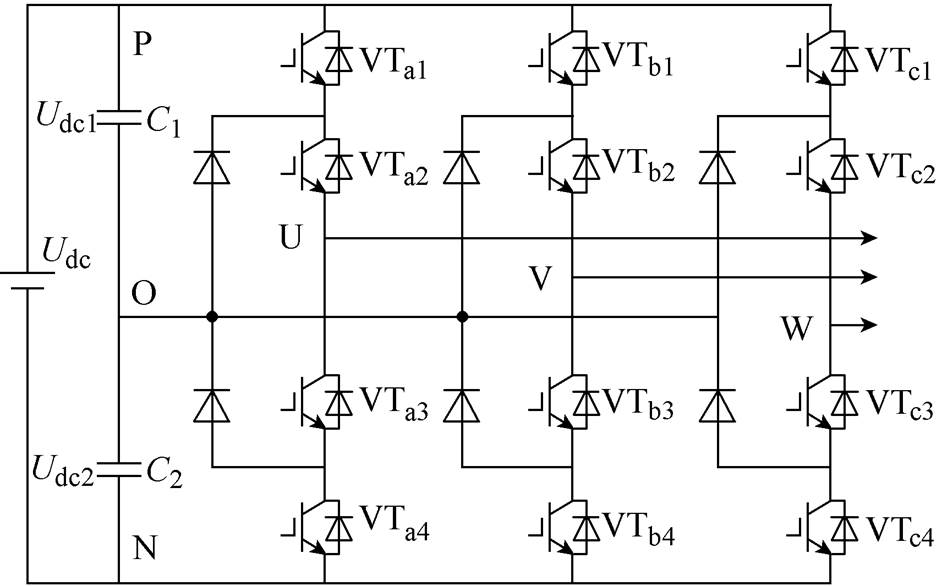
图1 三电平NPC变流器主电路拓扑结构
Fig.1 Three-level NPC converter topology diagram
摘要 三电平变流器零矢量首发SVPWM（SVPWM-BWZ）策略在低调制比下具有能满足最小脉宽限制、可产生任意小线电压值的优点，故适用于变频调速系统的起动和低速轻载状态，但其实现方式较为复杂。针对这一问题，该文首先介绍了SVPWM-BWZ策略的基本原理，分析了SVPWM-BWZ策略与载波脉宽调制策略之间的调制波等效关系。在此基础上提出基于载波实现的SVPWM-BWZ（CBSVPWM-BWZ）方法及相应的中点平衡控制策略，并推导CBSVPWM-BWZ作用下三电平变流器输出相电压的频谱、脉宽特性和功率器件的开关频率。最后利用仿真和实验对CBSVPWM-BWZ的有效性进行了验证，结果表明CBSVPWM-BWZ可完全等效传统SVPWM- BWZ策略，其在低调制比下具备较好的调制效果且无需计算各空间矢量作用时间，实现更为方便。
关键词：三电平 空间矢量脉宽调制 零电压矢量 载波脉宽调制 中点平衡控制
三电平中点箝位（Neutral Point Clamped, NPC）变流器的主电路拓扑结构如图1所示。相比传统的两电平变流器，三电平NPC变流器具有输出功率大、器件电压应力低等优点[1]；相比于级联H 桥多电平拓扑，其具有电路结构简单、便于背靠背运行等优点[2]。基于以上优点，三电平NPC变流器在中高压变频调速领域得到了广泛的应用[3]。
图1 三电平NPC变流器主电路拓扑结构
Fig.1 Three-level NPC converter topology diagram
当三电平NPC变流器应用于大功率变频调速系统时，为保证大功率开关器件的顺利开通与关断，输出相电压必须满足最小脉宽（Minimum Pulse width, MinP）限制[4]。对于脉冲宽度小于MinP的窄脉冲，需将其持续时间延长至MinP，但这会导致线电压有效值产生畸变[5]。当变频调速系统处于起动和低速轻载状态时，对应的调制比较低，此时MinP对线电压的畸变影响尤其显著[6]，需选择合适的脉宽调制策略来降低MinP产生的不良影响。
空间矢量脉宽调制（Space Vector PWM, SVPWM）是三电平变流器常用的一种脉宽调制策略[7]，其可根据每个采样周期内首发/结尾的矢量类型分类为小矢量首发的SVPWM（SVPWM Begins With the Small voltage vector, SVPWM-BWS）和零矢量首发的SVPWM（SVPWM Begins With the Zero voltage vector, SVPWM-BWZ）[8]。对比SVPWM-BWZ和SVPWM-BWS在低调制比下的性能，文献[4]计算了两种方法的谐波畸变因数，结果表明当调制比低于0.3时，采用SVPWM-BWZ可以获得更好的谐波性能；文献[9]通过分析两种方法的脉宽特性，指出SVPWM-BWZ的相电压在低调制比下不会产生窄脉冲，天然满足MinP限制。因此在变频调速系统的起动和低速轻载状态下，SVPWM-BWZ是一种更适用的SVPWM方法。
SVPWM-BWZ和SVPWM-BWS通过计算各空间矢量的作用时间来实现调制，运算量较大且不可避免存在计算误差[10]。利用载波脉宽调制（Carrier- Based PWM, CBPWM）来等效SVPWM，可在保持调制效果不变的基础上减少计算量，从而使得调制更易实现。对于SVPWM和CBPWM的统一理论，目前已有很多研究成果[11-17]：
针对传统七段式SVPWM和CBPWM的统一理论，文献[11]指出SVPWM和CBPWM的本质联系在于二者是同一控制方程在不同附加条件下的两个不同的特解。文献[12]从广义零序分量的角度出发，推导出了CBPWM和SVPWM在特定区域的零序分量表达式。文献[13]通过两种方法推导了过调制区域内SVPWM与CBPWM之间的等效关系，从而将三电平SVPWM与CBPWM的等效关系从线性调制区扩展到了过调制区I和过调制区II。
针对传统七段式外的SVPWM和CBPWM的统一理论，文献[14]通过调制波分解原理对统一理论进行了完善，使之在单采样周期内10、12、14 段输出下可实现统一。文献[15]利用双调制波与单载波比较，推导了虚拟空间矢量脉宽调制对应的双调制波表达式，从而基于载波实现了虚拟空间矢量脉宽调制。
目前针对SVPWM和CBPWM的统一理论，其研究对象多为SVPWM-BWS，而对SVPWM-BWZ与CBPWM的等效研究较少。本文基于调制波等效，具体分析了SVPWM-BWZ与CBPWM的内在联系并提出了基于载波实现的SVPWM-BWZ（Carrier- Based SVPWM-BWZ, CBSVPWM-BWZ）方法及其中点平衡控制策略。仿真和实验结果证明，本文所提方法可完全等效传统SVPWM-BWZ，其在低调制比下天然满足MinP限制并具备良好谐波性能，从而更适用于变频调速系统的起动和低速轻载阶段，且无需计算空间矢量的作用时间，实现非常方便。
如图1所示，定义三电平NPC变流器直流侧母线电压为Udc，每相由上到下四个可控功率器件分别为VT1、VT2、VT3、VT4，则每相输出电平状态与各功率器件的导通关系见表1，对应的三电平变流器空间矢量分布如图2所示。各空间矢量根据其幅值大小可分为零矢量、小矢量、中矢量和大矢量，各空间矢量的具体类型见表2。
表1 三电平变流器电平状态与功率器件导通关系
Tab.1 Relationship between the output voltage level of the three-level converter and conducted device
电平状态功率器件状态 PVT1、VT2导通，VT3、VT4关断 OVT2、VT3导通，VT1、VT4关断 NVT3、VT4导通，VT1、VT2关断
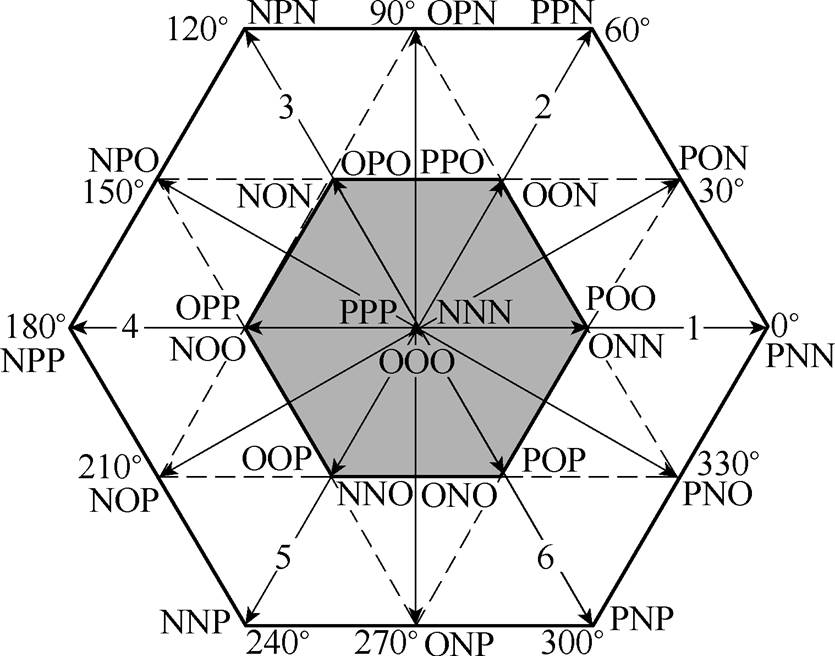
图2 三电平变流器空间矢量
Fig.2 Space vector of the three-level converter
表2 三电平变流器各空间矢量分类
Tab.2 Classification of space vectors for three-level converter
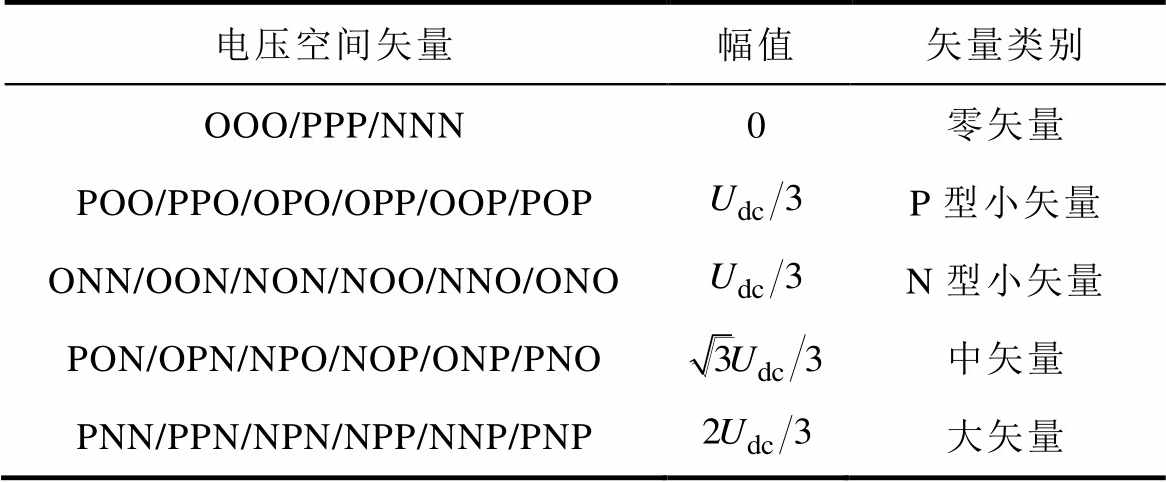
电压空间矢量幅值矢量类别 OOO/PPP/NNN0零矢量 POO/PPO/OPO/OPP/OOP/POPP型小矢量 ONN/OON/NON/NOO/NNO/ONON型小矢量 PON/OPN/NPO/NOP/ONP/PNO中矢量 PNN/PPN/NPN/NPP/NNP/PNP大矢量
传统SVPWM策略基于伏秒原理，即将参考电压与采样周期的乘积分解为最近的3个空间矢量与各自作用时间的乘积，通过在相应作用时间内控制各功率器件的开关状态来分别输出3个空间矢量，从而实现调制。为实现SVPWM策略，需判断参考电压位置并计算各空间矢量的作用时间。图2中各空间矢量作用时间[18]需满足
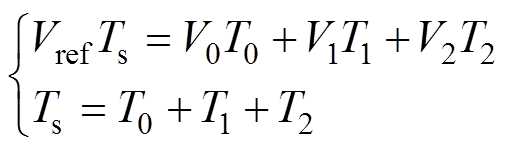（1）式中，Vref为参考电压；Ts为采样周期；V0、V1、V2和T0、T1、T2分别为最近三矢量及各自的作用时间。
SVPWM策略根据每个采样周期内首发的矢量类型可分类为SVPWM-BWS和SVPWM-BWZ。其中，SVPWM-BWS以小矢量作为每个采样周期的起始状态和结尾状态，而SVPWM-BWZ以零矢量作为每个采样周期的起始状态和结尾状态。
当参考电压Vref位于图2中的内六边形区域时，两类SVPWM方法的Vref可以分解为作用时间完全相同的3个空间矢量，区别只在于3个空间矢量的作用顺序和使用的冗余状态不同。假定Vref位于0°～30°的内六边形区域，SVPWM-BWZ和SVPWM- BWS在连续4个采样周期内的开关序列分别如图3a和图3b所示。
图3 SVPWM-BWZ和SVPWM-BWS的开关序列
Fig.3 Switching sequences of SVPWM-BWZ and SVPWM-BWS
图3中，Uao、Ubo、Uco分别代表A相、B相、C相对应的相电压。对比图3a和图3b，两种SVPWM方法在每个Ts内三相电平状态均只改变一次，但在连续4个Ts内，SVPWM-BWZ三相电平状态以N- O-P-O-N的顺序循环变化，而SVPWM-BWS电平状态则以P-O-P-O-P或O-N-O-N-O的顺序循环变化，故SVPWM-BWS为单极性调制而SVPWM- BWZ为双极性调制。
相比于SVPWM-BWS，SVPWM-BWZ在低调制比下具备更好的脉宽特性和谐波性能[4,8]，故其更适用于电机的起动和低速轻载状态。但现有方法实现SVPWM-BWZ需判断参考电压所处扇区位置并需求解各空间矢量的作用时间，运算量较大且不可避免存在计算误差，实现较为复杂。
为更简单实现SVPWM-BWZ，首先基于调制波等效分析SVPWM-BWZ和CBPWM的内在联系。SVPWM-BWZ在连续4个Ts内三相电平状态以N- O-P-O-N的顺序循环变化，针对电平状态O-N-O和O-P-O，对应等效调制波并不相同，需分别分析。
CBPWM的三相原始调制波定义为
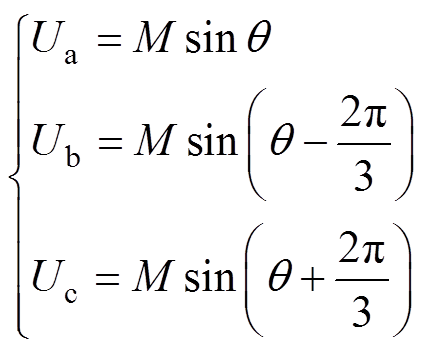（2）式中，θ为相位；M为调制比。通过三相原始调制波叠加零序分量U0_n来得到三相电平状态O-N-O对应的等效调制波Ua_n、Ub_n和Uc_n，即
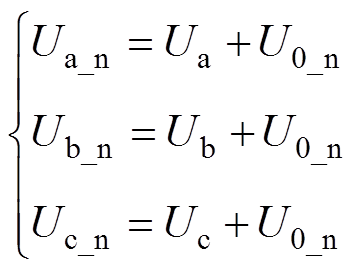（3）
假定Vref位于图2中0°～30°的内六边形区域，则三相电平状态O-N具体为OOO-OON-ONN-NNN。设OOO在一个Ts内作用时间为kT0，NNN为(1-k)T0，OON为T1，ONN为T2，有
（4） 等效调制波的采样值在一个Ts内保持不变， 则通过Ua_n、Ub_n和Uc_n与上升方向起始的三角载波比较得到三相电平状态O-N-O的示意图如图4 所示。
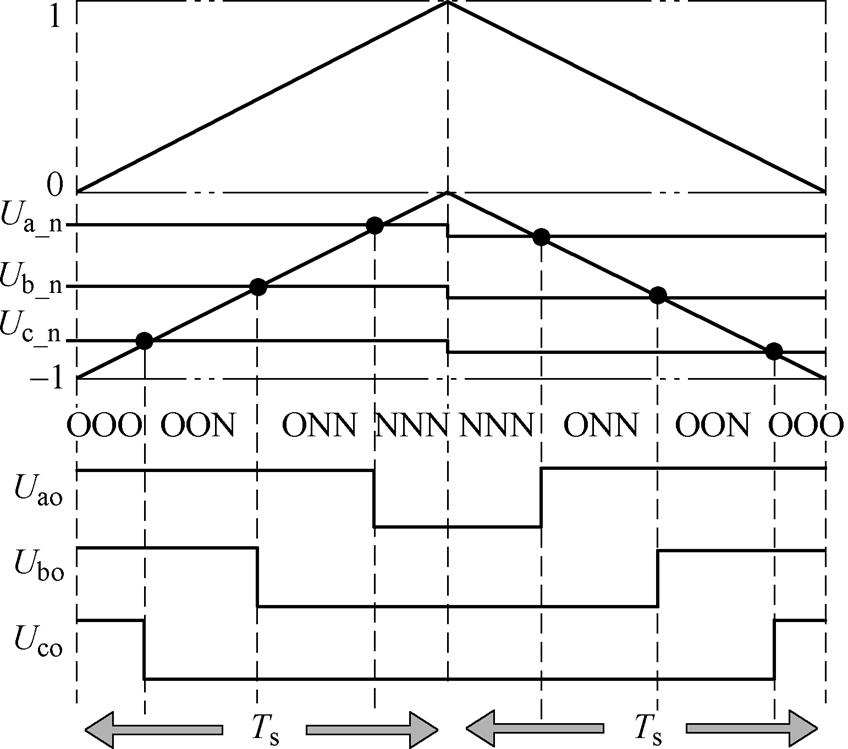
图4 等效调制波与三角载波比较得到O-N-O
Fig.4 The level state of O-N-O is obtained by comparing the equivalent modulation wave with the triangular carrier
由图4可得
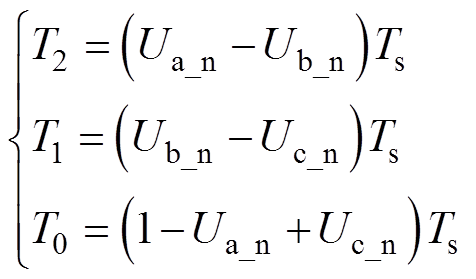（5）将式（5）和式（3）代入式（4），并令k=0.5，可得到空间角0°～30°区域O-N-O对应等效调制波的零序分量表达式为
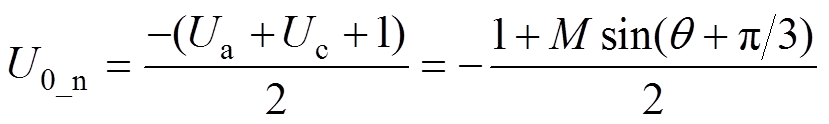（6）
同样思路可得到内六边形其余区域内电平状态O-N-O对应等效调制波零序分量表达式，具体有
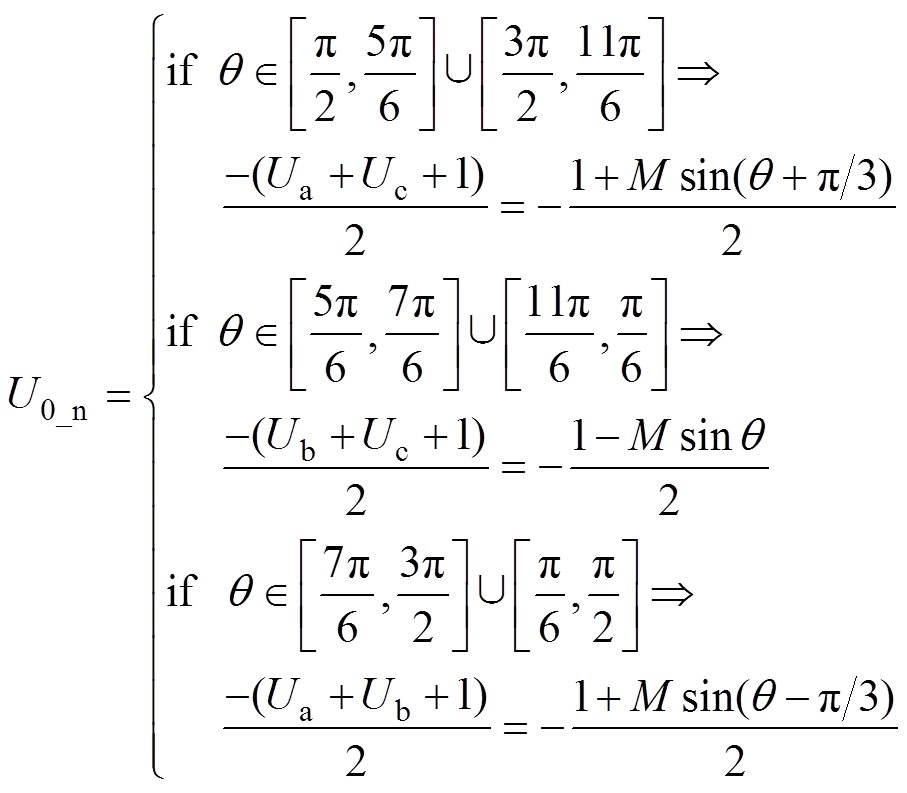（7）对式（7）进一步化简，可得
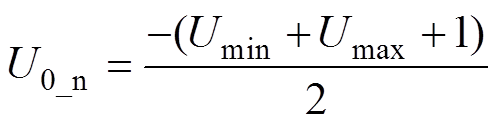（8）
式中，Umin和Umax分别为三相原始调制波的最小值和最大值。式（8）即为电平状态O-N-O对应等效调制波的零序分量表达式。
三相原始调制波叠加零序分量U0_p可得到电平状态O-P-O对应等效调制波Ua_p、Ub_p和Uc_p，即
（9） 假定Vref位于图2中0°～30°的内六边形区域，三相电平状态O-P具体为OOO-POO-PPO-PPP。通过Ua_p、Ub_p和Uc_p与下降方向起始的三角载波比较得到三相电平状态O-P-O的示意图如图5所示。
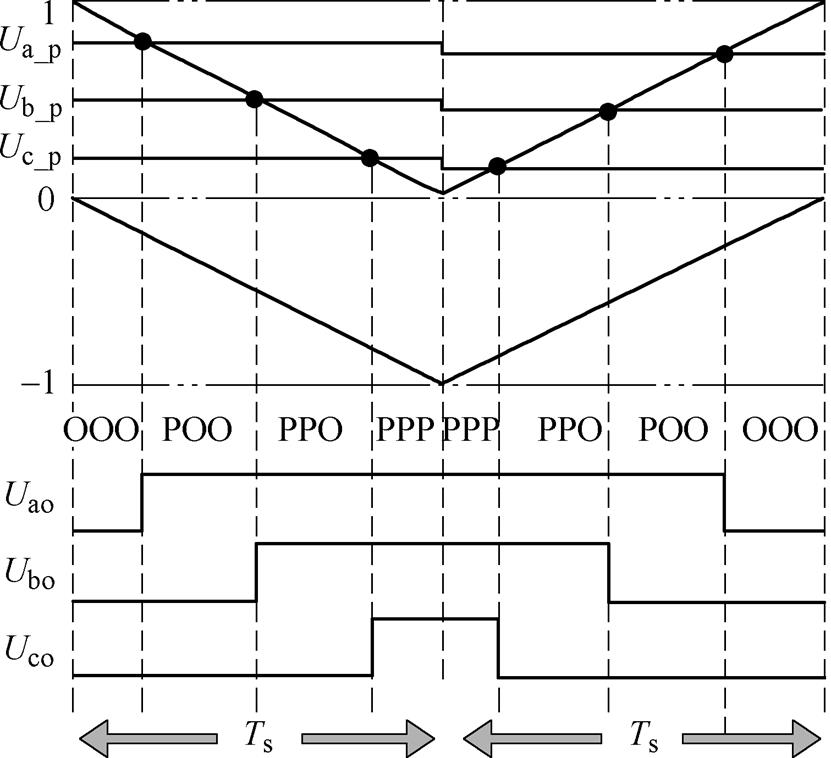
图5 等效调制波与三角载波比较得到O-P-O
Fig.5 The level state of O-P-O is obtained by comparing the equivalent modulation wave with the triangular carrier
由图5可得到空间角0°～30°区域O-P-O对应的零序分量表达式为
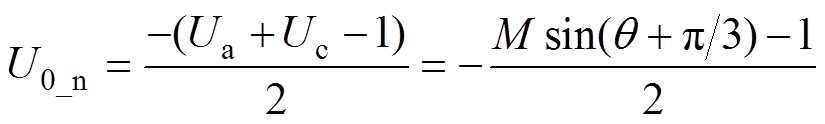（10）同样思路可得到内六边形其余角度区域内电平状态O-P-O对应等效调制波的零序分量表达式，具体为
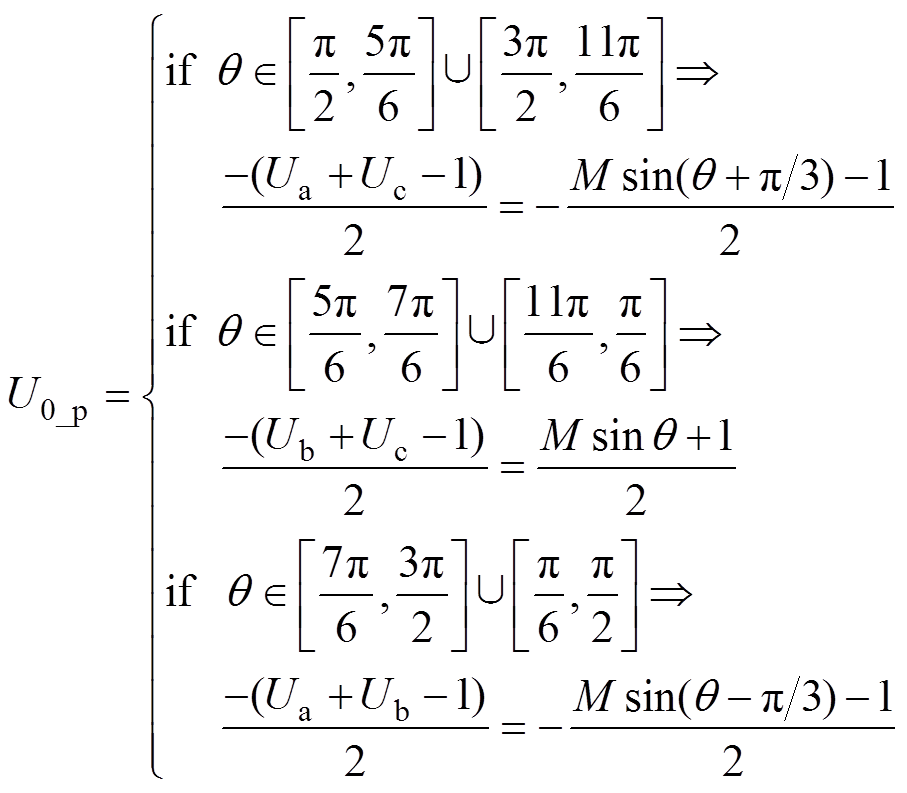（11）
对式（11）进一步化简，可得
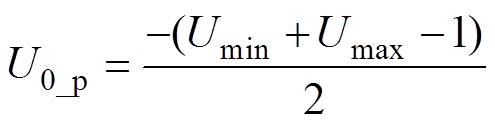（12）式（12）即为三相电平状态O-P-O对应等效调制波的零序分量表达式。
三相原始调制波叠加零序分量U0_n可得到等效调制波Ua_n、Ub_n和Uc_n，对应电平状态O-N-O；叠加零序分量U0_p可得到等效调制波Ua_p、Ub_p和Uc_p，对应电平状态O-P-O。SVPWM-BWZ的相电压电平状态以O-N-O-P-O的顺序循环变化，则通过轮换利用三相原始调制波叠加U0_n和U0_p，可得到CBSVPWM-BWZ对应的等效调制波Ua_m、Ub_m和Uc_m，有
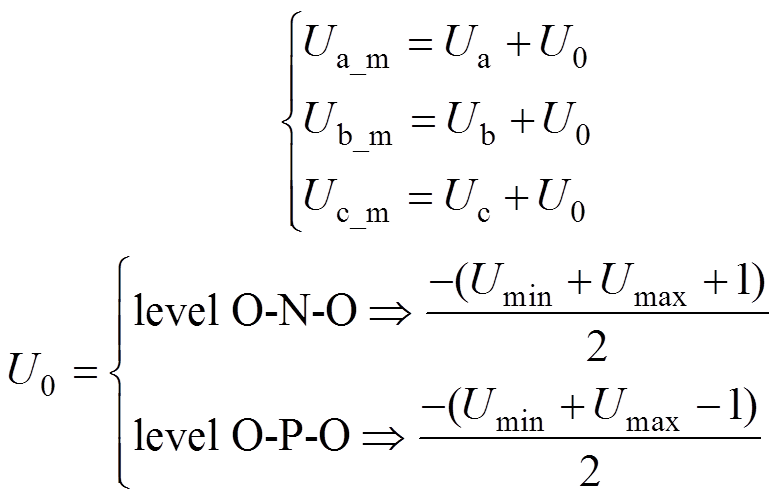（13）CBSVPWM-BWZ通过等效调制波与载波比较实现调制，在得到等效调制波的基础上，进一步分析CBSVPWM-BWZ所使用的调制载波。
三相等效调制波Ua_m、Ub_m和Uc_m与上升方向起始的三角载波比较可得到电平状态O-N-O，与下降方向起始的三角载波比较可得到电平状态O-P- O。定义三角载波周期为Tcarr，则以Tcarr作为时间单位，通过轮换使用上升方向起始的三角载波和下降方向起始的三角载波，可得到CBSVPWM- BWZ对应的调制载波。
利用等效调制波与调制载波进行比较，并根据比较的结果直接控制各开关器件的动作状态，可得到循环变化的三相电平状态O-N-O-P-O，从而基于载波实现了SVPWM-BWZ，其具体实现流程和原理分别如图6a和图6b所示。
中点平衡控制是三电平变流器的关键问题，只有小矢量和中矢量会对三电平变流器中点电位产生影响且同一空间角处的两个冗余小矢量对中点电位的影响相反[19]。对比图3，SVPWM-BWS在每个Ts内首发和结尾为两个冗余小矢量，而SVPWM-BWZ首发和结尾为两个冗余零矢量。故不同于SVPWM- BWS，在SVPWM-BWZ作用下无法利用重新分配冗余小矢量作用时间的方式来控制中点电位平衡。
图6 CBSVPWM-BWZ的实现流程和原理
Fig.6 Flowchart and schematic of the CBSVPWM-BWZ
SVPWM-BWZ在每个采样周期内分布有两个非冗余小矢量，作用时间不同且各自作用时间内中点电流对应的负载相不同。定义两非冗余小矢量中作用时间较长的为主小矢量，则在每个采样周期内对中点电位产生影响的主要为主小矢量。在SVPWM- BWZ作用下，可通过控制主小矢量的作用时间来维持中点电位平衡。
CBSVPWM-BWZ利用调制波与载波比较等效得到各空间矢量，为对CBSVPWM-BWZ方法添加中点平衡控制策略，首先分析中点电位不平衡时各扇区内主小矢量作用时间变化原则。定义DU为中点电位偏差，ix为流过中点的负载电流，Ux_m为对应负载相的调制波，↑/↓分别代表应增加/减小主小矢量作用时间，则图2各60°扇区内主小矢量在中点不平衡时作用时间变化原则见表3。
表3 中点不平衡时各主小矢量作用时间变化原则
Tab.3 The principle of duration variation of each principal small vector when the neutral is unbalanced
扇区主小矢量DUixUx_m ＞0＜0 1POO/ONN↑↓ 2PPO/OON↓↑ 3OPO/NON↑↓ 4OPP/NOO↓↑ 5OOP/NNO↑↓ 6POP/ONO↓↑
进一步分析在不同扇区内移动调制波对主小矢量作用时间的影响。针对扇区1、3、5，将调制波上移对应增加主小矢量作用时间，下移对应减小主小矢量作用时间；针对扇区2、4、6，将调制波上移对应减小主小矢量作用时间，下移对应增加主小矢量作用时间。以扇区1、4为例，主小矢量作用时间变化示意图如图7所示。结合表3，可得出CBSVPWM- BWZ中点平衡控制策略。
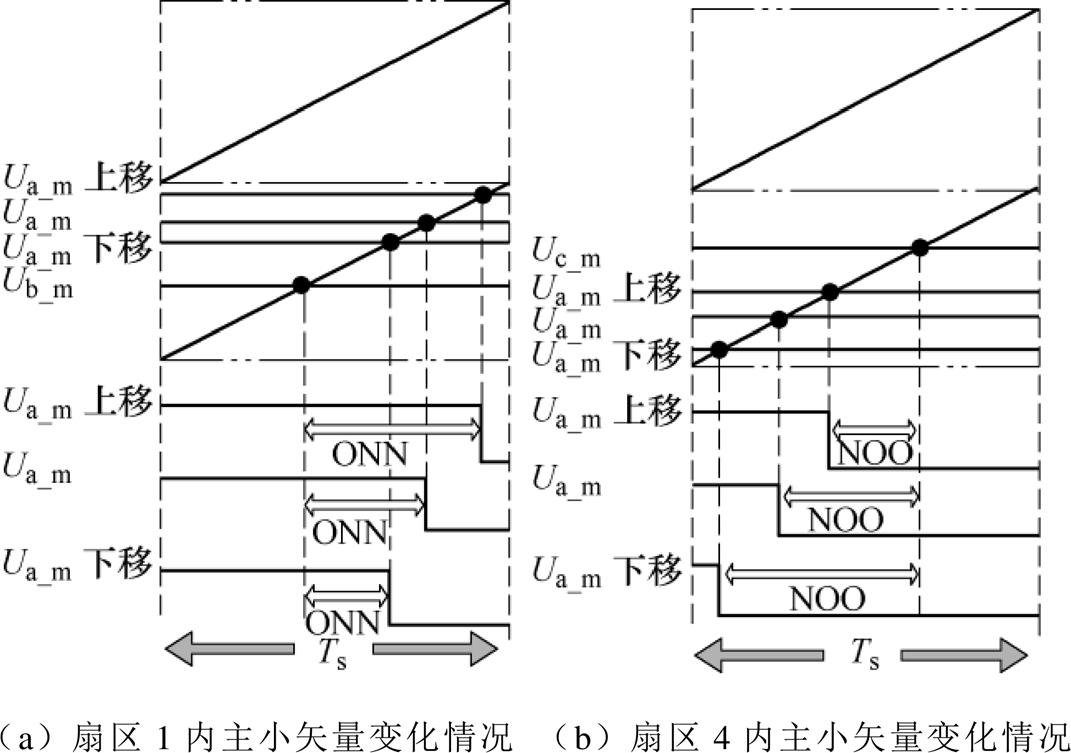
图7 上移/下移调制波对主小矢量影响示意图
Fig.7 Schematic diagram of the effect of up/down modulation waves on principal small vectors
对于扇区1、4，ix=ia，Ux_m=Ua_m；对于扇区2、5，ix=ic，Ux_m=Uc_m；对于扇区3、6，ix=ib，Ux_m=Ub_m。判断DUixUx_m的方向并将其叠加到Ux_m上，当其为正时，使得Ux_m上移；当其为负时，使得Ux_m下移。通过移动Ux_m来控制主小矢量的作用时间，从而实现中点电位平衡，其具体控制框图如图8所示。其中，sign代表取符号，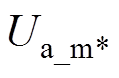
、
、
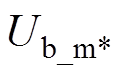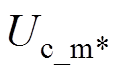代表修正后的三相调制波。
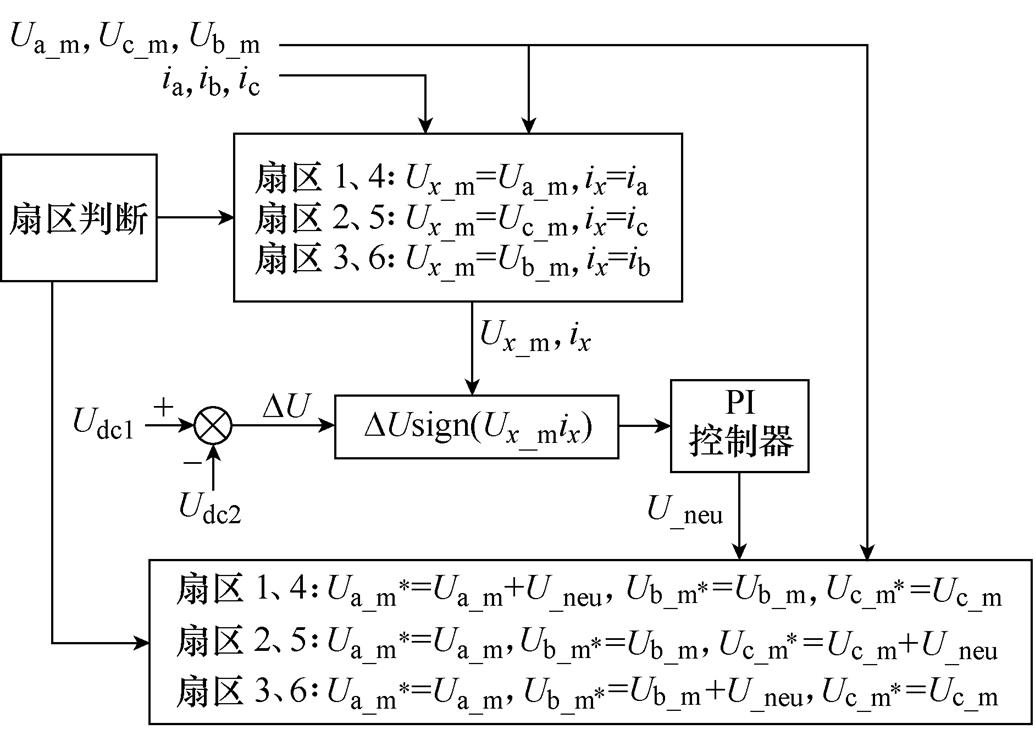
图8 CBSVPWM-BWZ中点平衡控制框图
Fig.8 Block of neutral control for CBSVPWM-BWZ
CBPWM可借助双重傅里叶级数较为方便地分析频谱特性。利用双重傅里叶级数，对CBSVPWM- BWZ方法作用下的相电压谐波特性进行分析。
任意一种周期性开关波形，均可以对其进行双重傅里叶分解[8]为
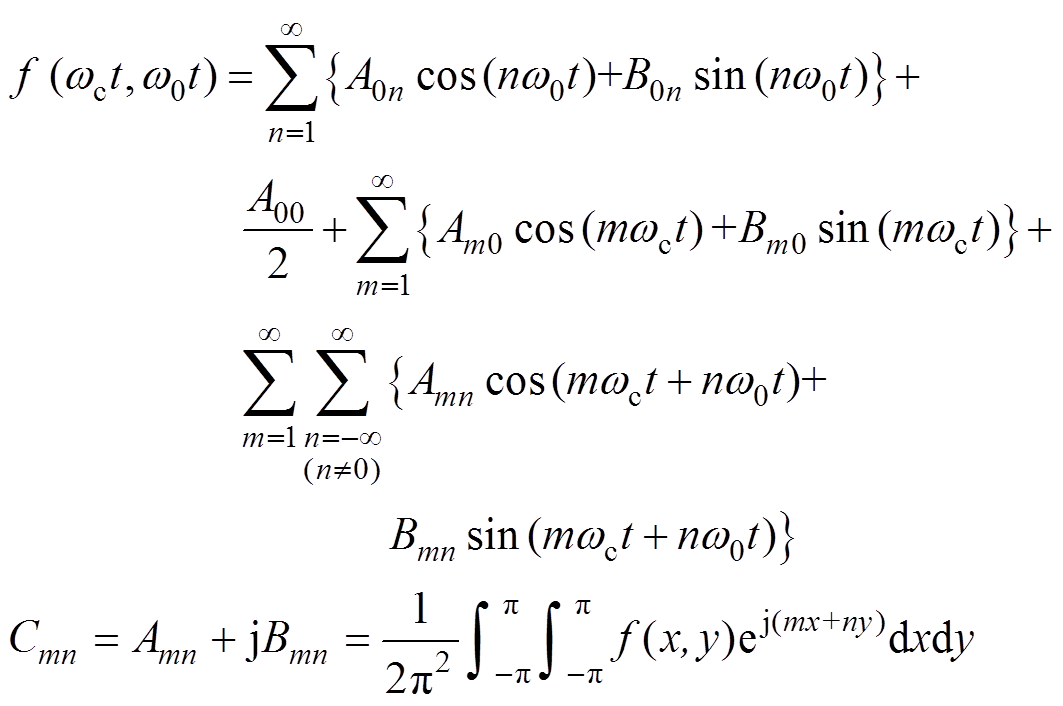（14）式中，w0和wc分别为调制波基波频率和载波频率；n和m分别为基波倍频次数和载波倍频次数；Amn和Bmn分别为边带谐波余弦、正弦项系数。
对开关波形进行双重傅里叶分解的关键在于求解边带谐波系数Amn和Bmn，在求解过程中需对包含有另一正弦变量的余弦或正弦函数进行处理。此时可利用式（15）的雅可比-安格尔展开将表达式展开为贝塞尔级数形式，以化简运算。
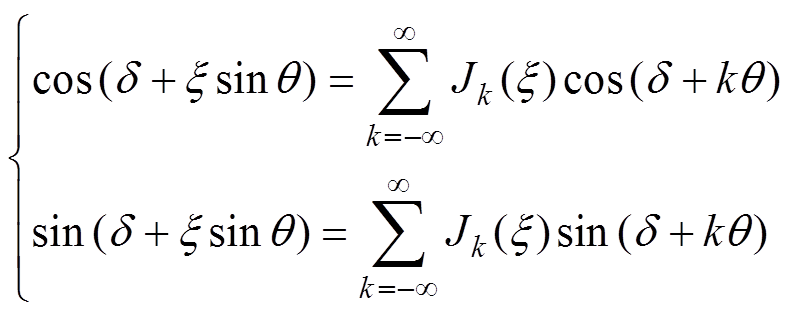（15）由式（14）、式（15）推导出CBSVPWM-BWZ的双重傅里叶级数，总结于式（16）。其中，M为调制比，E为三电平变流器直流侧母线电压值的1/2，即E=Udc/2。Amn和正弦项系数Bmn的表达式比较复杂，单独总结于式（17）。
由式（16）、式（17）分析CBSVPWM-BWZ作用下相电压的频谱，结论如下：
1）对于直流偏置，A00=0，故输出相电压不含直流偏置。
2）对于基波分量，C01=jEM，故输出相电压基波幅值为EM。
3）对于基带谐波，输出相电压只含有为基波3的奇数倍频的基带谐波。
4）对于载波谐波，输出相电压只含有为载波奇数倍频的载波谐波。
5）对于边带谐波，输出相电压只在n±k为偶数时在载波倍频附件存在边带谐波。
为保证大功率开关器件顺利开通和关断，三电平变流器的脉宽调制策略必须要满足MinP限制[4]。CBSVPWM-BWZ利用调制波与载波比较得到各开关器件的开关信号，载波幅值在-1～1，则当调制波的幅值绝对值在0.1～0.9时，O、P、N三种电平状态的作用时间均能够得到保证，不会出现持续时间不满足MinP的窄脉冲。
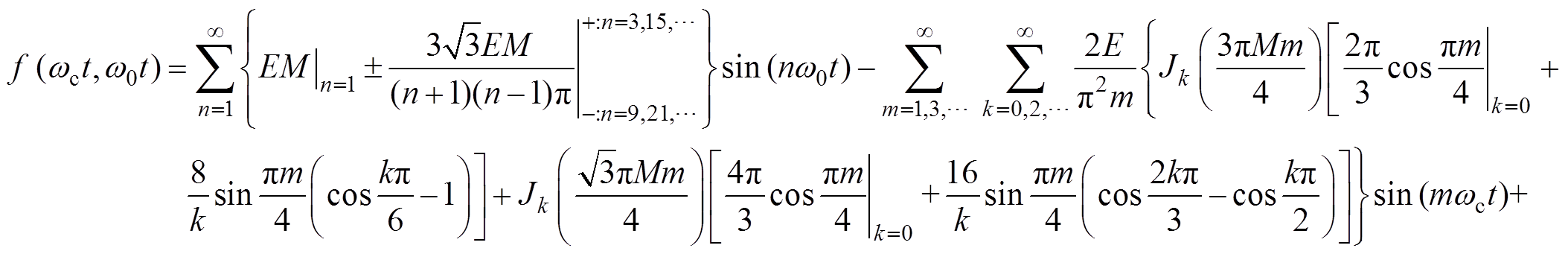
（16）
（17）
由式（2）和式（13）计算CBSVPWM-BWZ在调制比0～0.35时调制波幅值的分布情况，如图9所示。
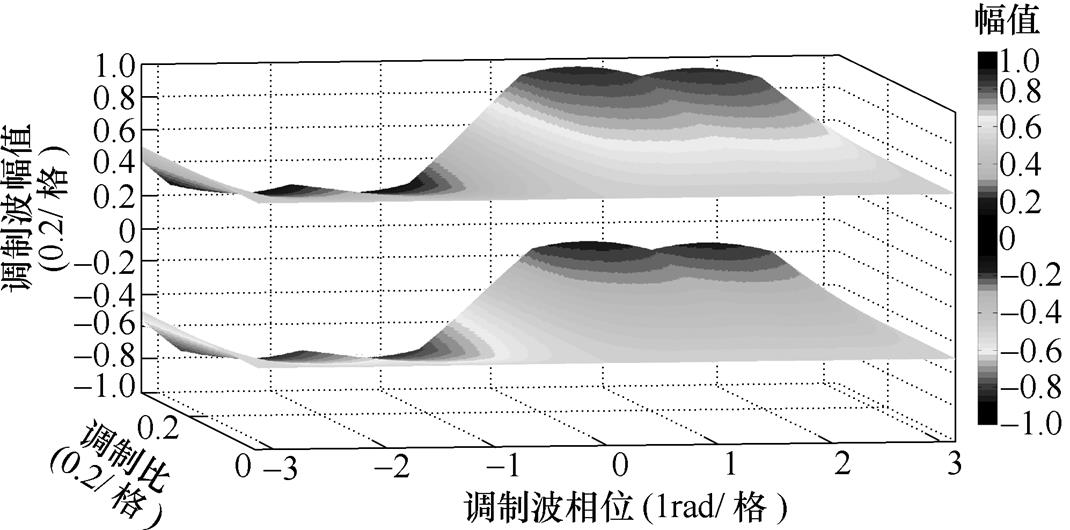
图9 CBSVPWM-BWZ调制波幅值
Fig.9 Modulation wave amplitude of the CBSVPWM-BWZ
由图9可得出CBSVPWM-BWZ的脉宽特性：
1）调制比低于0.35时，CBSVPWM-BWZ调制波幅值绝对值在0.2～0.8，故CBSVPWM-BWZ在低调制比下天然满足MinP限制。
2）随着调制比增加，CBSVPWM-BWZ调制波幅值绝对值由0.5向1或0变化。故若调制比增加至0.35以上时，可能出现不满足MinP的窄脉冲。
在CBSVPWM-BWZ作用下，三相输出电平状态在一个载波周期内以O-N-O-P-O的顺序循环变化，对应一个载波周期内每相由上到下4个功率器件各开通、关断一次。故在CBSVPWM-BWZ作用下，三电平变流器各功率器件的开关频率一致，均等于调制载波频率，而与基波频率无关。定义fswitch为功率器件的开关频率，fc为等效载波频率，则有
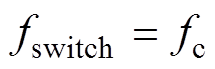（18）为验证本文所提CBSVPWM-BWZ方法的有效性，利用PSIM软件搭建三电平NPC逆变器模型，其中，直流侧母线电压200V，等效载波频率300Hz，采样频率1 200Hz，基波频率15Hz，调制比0.087。仿真结果如图10所示。
图10a为本文所提CBSVPWM-BWZ和传统SVPWM-BWZ、SVPWM-BWS的相电压波形。对比可知，本文所提CBSVPWM-BWZ和SVPWM-BWZ的相电压波形基本一致，且其相比于SVPWM- BWS，在低调制比下相电压脉冲宽度可以得到保证。若设计MinP为60ms，则CBSVPWM-BWZ在低调制比下天然满足MinP限制。
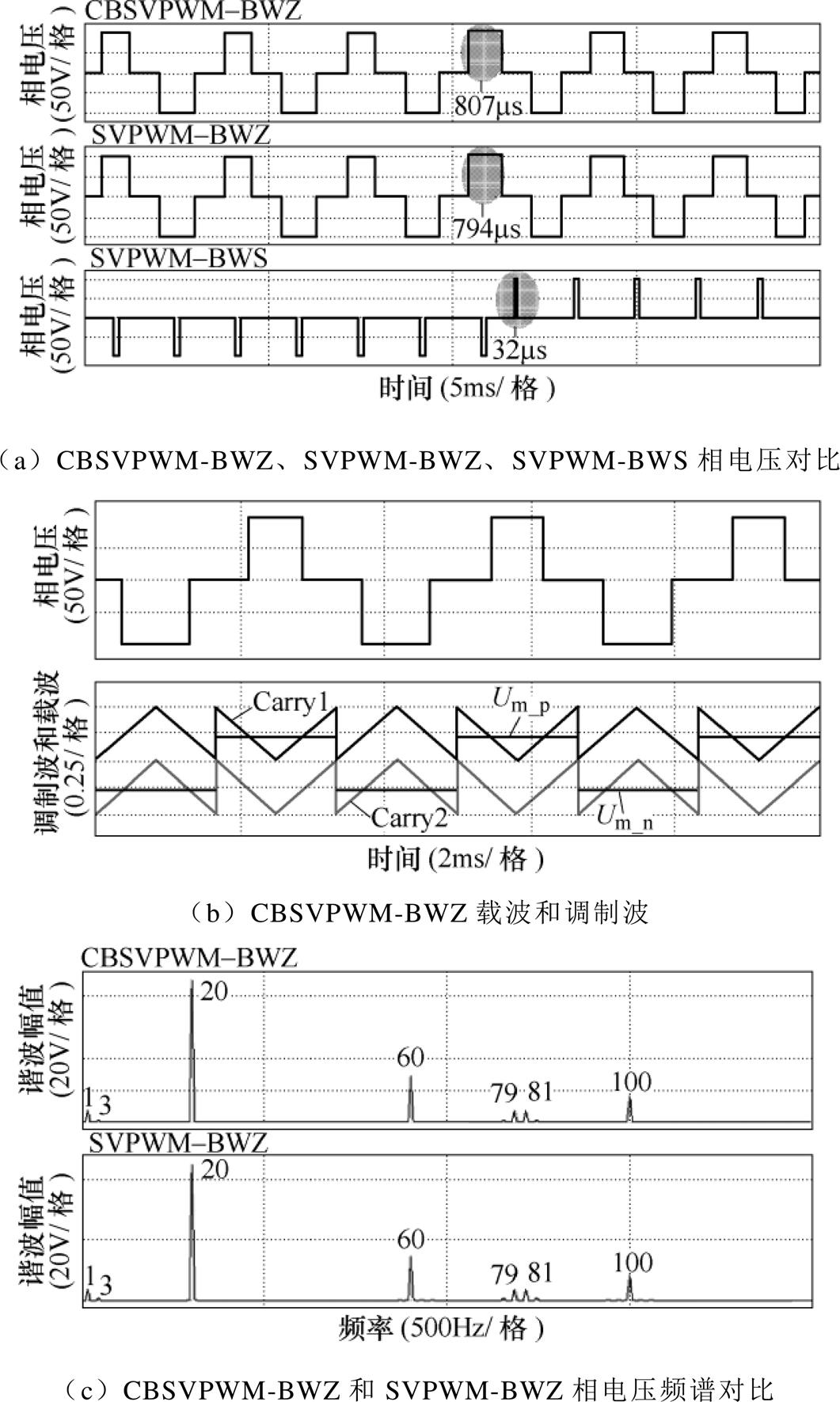
图10 CBSVPWM-BWZ仿真结果
Fig.10 Simulation results of the CBSVPWM-BWZ
图10b为CBSVPWM-BWZ的载波和调制波波形，其中，Carry1、Carry2代表上下同相层叠的三角载波，Um_p、Um_n为调制波。通过轮换使用调制波与上升方向起始/下降方向起始的三角载波比较，可得到循环变化的三相电平状态O-N-O-P-O。每个载波周期内各功率器件各动作一次，开关频率为300Hz。
图10c为CBSVPWM-BWZ和SVPWM-BWZ相电压频谱对比。两种方法作用下主要谐波的幅值情况见表4。表中，15Hz基波分量幅值为8.695V，对应理论计算值EM=8.7V，两者基本一致。
表4 CBSVPWM-BWZ和SVPWM-BWZ的谐波分布
Tab.4 Harmonic distribution of CBSVPWM-BWZ and SVPWM-BWZ
谐波次数谐波幅值/V CBSVPWM-BWZSVPWM-BWZ 18.6958.696 31.7991.799 2089.59389.668 6028.70928.631 798.4208.452 818.4058.371 10015.87015.931
由图10a、图10c和表4可知，本文所提CBSVPWM- BWZ和传统SVPWM-BWZ的相电压波形及相电压谐波分布基本相同，证明本文所提方法可取得和传统SVPWM-BWZ一致的控制效果。
为验证本文所提CBSVPWM-BWZ中点平衡控制策略的有效性，设置上母线电容电压Udc1初值为120V，下母线电容电压Udc2初值为80V，Udc1和Udc2的仿真变化情况如图11所示。相比不添加中点平衡控制的情况，在添加了本文所提的中点平衡控制策略后，Udc1和Udc2可以迅速趋于平衡，从而证明了本文所提中点平衡控制策略的有效性。
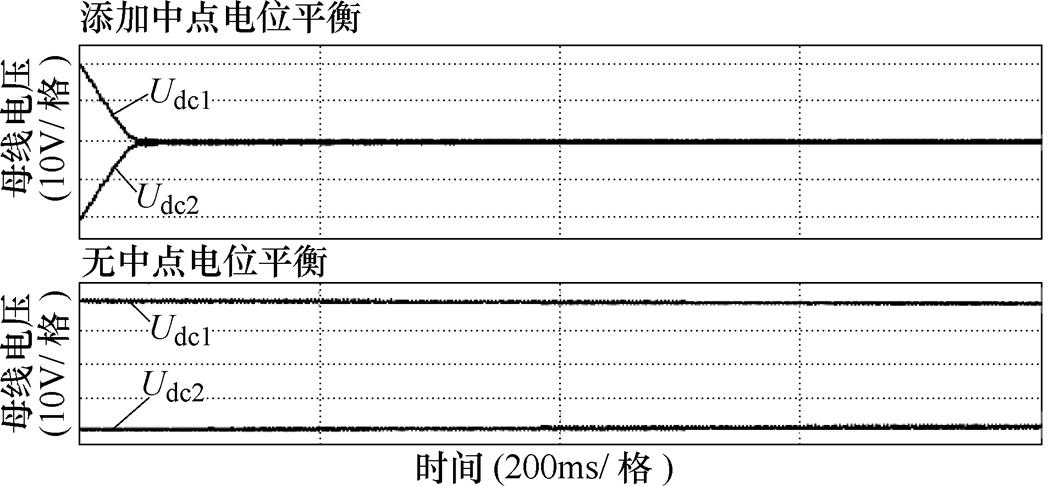
图11 CBSVPWM-BWZ中点平衡控制策略仿真结果
Fig.11 Simulation results of neutral balance control strategy of the CBSVPWM-BWZ
为验证仿真的正确性，搭建了如图12所示的75kV·A基于IGBT的三电平NPC变流器实验平台。该实验平台通过VME机箱进行控制。实验平台的功率器件选用英飞凌公司的FZ300R12KE3G。
图12 三电平NPC变流器样机
Fig.12 Three-level NPC converter prototype
实验条件如下：直流侧电压200V，基波频率15Hz，等效载波频率300Hz，采样频率1 200Hz。MinP限制为60ms，当脉冲持续时间少于60ms时自动延长至60ms。死区设置为10ms。实验数据分别如图13～图15所示。
图13为CBSVPWM-BWZ在不同调制比下的线电压、相电压和相电压频谱，从中可得出以下结论：
图13 不同调制比下CBSVPWM-BWZ实验结果
Fig.13 Experimental results of the CBSVPWM-BWZ under different modulation indexs
1）在CBSVPWM-BWZ作用下，相电压电平状态以O-N-O-P-O的顺序循环变化，证明CBSVPWM- BWZ为双极性调制。
2）CBSVPWM-BWZ只适用于图2内六边形的低调制比区域，故在其作用下线电压为三电平状态。
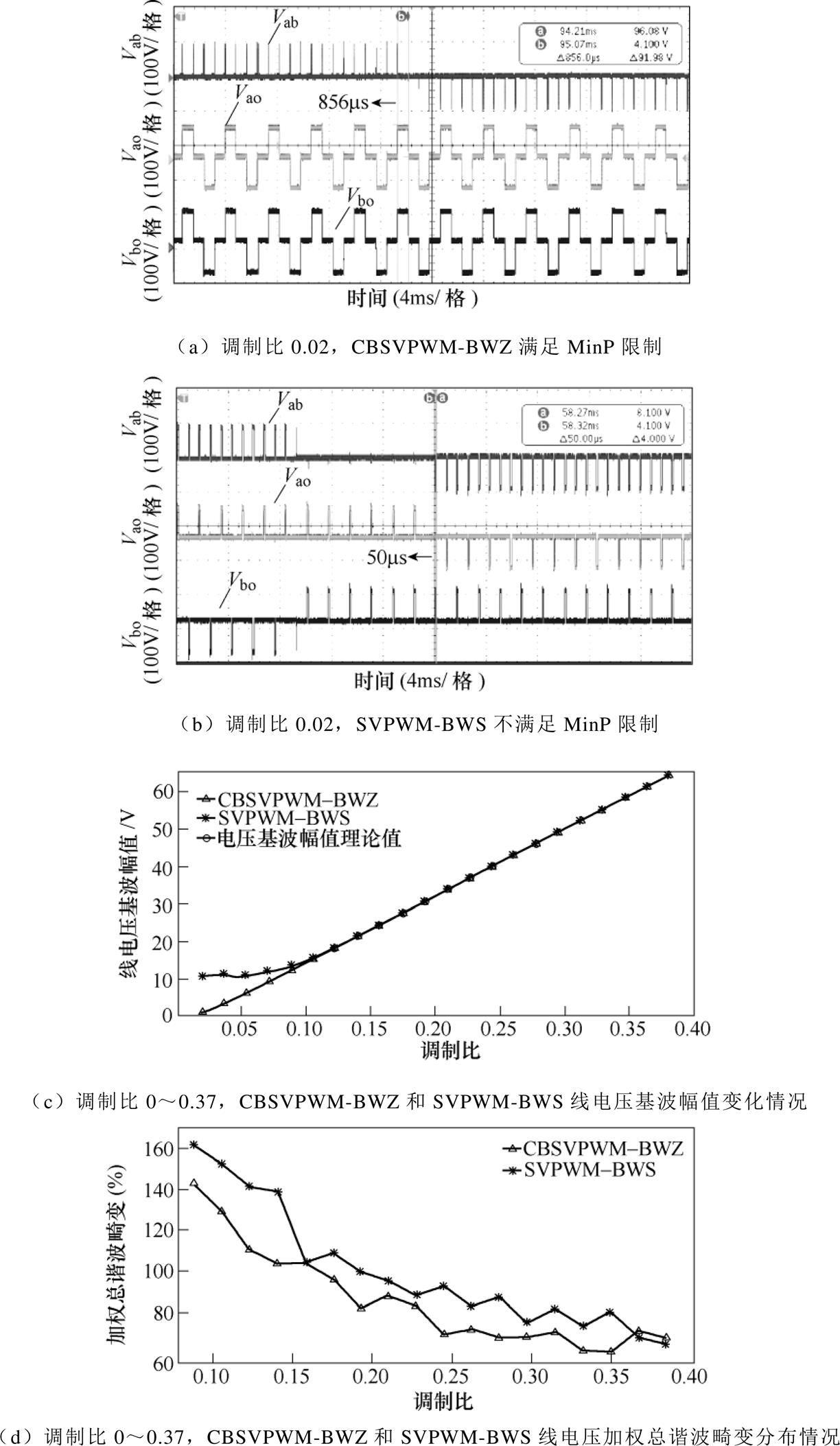
图14 CBSVPWM-BWZ和SVPWM-BWS对比实验结果
Fig.14 Comparison experiment results of the CBSVPWM-BWZ and SVPWM-BWS
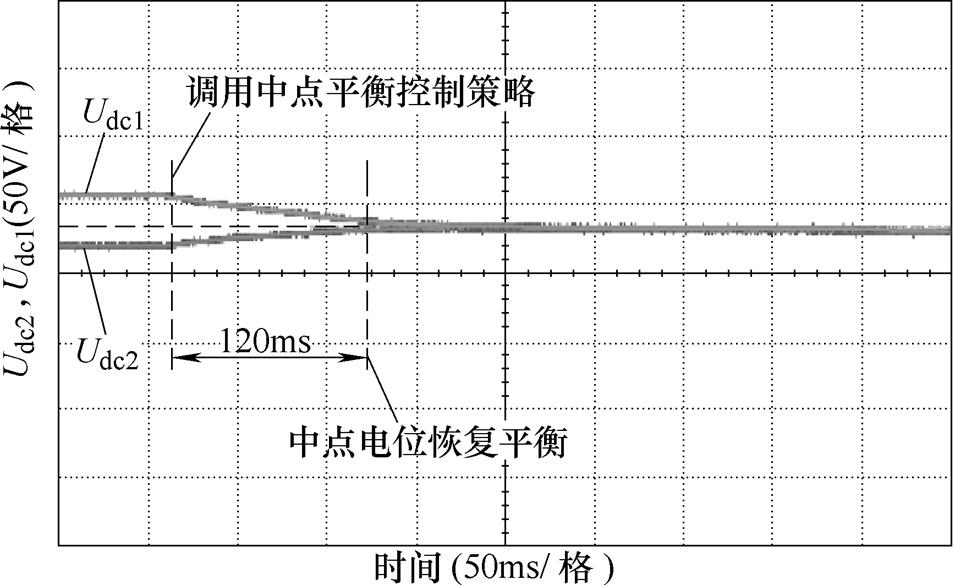
图15 CBSVPWM-BWZ中点平衡控制实验结果
Fig.15 Experimental results of neutral balance control strategy of the CBSVPWM-BWZ
3）在CBSVPWM-BWZ作用下，最大谐波出现在300Hz，即载波频率处。其余较大谐波分布在900Hz、1 500Hz处，对应载波奇数倍频的载波谐波，以及1 185Hz、1 215Hz处，对应边带谐波和45Hz处，对应基波3的奇数倍频的基带谐波。以上谐波分布特性和理论分析结果一致。
4）相电压电平状态在10ms内以O-N-O-P-O的顺序循环变化3次，对应各功率器件开关频率均为300Hz。证明了在CBSVPWM-BWZ作用下，各功率器件开关频率等于载波频率。
图14为调制比0～0.37变化下，CBSVPWM- BWZ与SVPWM-BWS的实验结果对比图。由图14的对比结果可知：
1）在调制比为0.02时，对应变频调速系统的起动阶段，此时SVPWM-BWS输出相电压中存在持续时间为50ms的脉冲，其等于MinP减去死区时间，为不满足MinP限制的窄脉冲。作为对比，CBSVPWM-BWZ输出相电压脉宽在800ms以上，证明了CBSVPWM-BWZ在低调制比下天然满足MinP限制，其在低调制比下具备更好的脉宽特性。
2）在调制比低于0.1时，CBSVPWM-BWZ的线电压基波幅值可以有效跟踪理论值，而SVPWM- BWS因为MinP限制导致输出线电压的基波幅值产生了畸变，证明了CBSVPWM-BWZ在低调制比下可产生任意小的线电压值，其在低调制比下具备更好的线电压输出能力。
3）在调制比低于0.35时，对应变频调速系统的低速轻载状态，CBSVPWM-BWZ的整体线电压加权总谐波畸变值要优于SVPWM-BWS，证明了CBSVPWM-BWZ在低调制比下谐波性能更优。
图15为中点不平衡时，调用CBSVPWM-BWZ中点平衡控制策略后直流母线上端电压Udc1和下端电压Udc2的变化情况。在中点平衡控制策略下，经过120ms时间，Udc1和Udc2重新恢复平衡，证明了本文所提CBSVPWM-BWZ中点平衡控制策略的有效性。
图13～图15的实验结果和理论分析结果一致，证明了本文所提CBSVPWM-BWZ方法及其中点平衡控制策略的有效性。本文所提方法具备在低调制比下天然满足MinP限制并产生任意小线电压值的能力，故其能在低调制比下取得较好的控制效果，且其实现简单，更便于工程应用。
本文在分析SVPWM-BWZ与CBPWM等效关系基础上推导了CBSVPWM-BWZ的等效调制波和调制载波，利用等效调制波与调制载波进行比较，基于载波实现了SVPWM-BWZ。通过分析中点电位不平衡时主小矢量作用时间的变化原则，提出了CBSVPWM-BWZ的中点平衡控制策略。在此基础上，对CBSVPWM-BWZ作用下的相电压谐波特性、脉宽特性和功率器件的开关频率进行了分析。最后，仿真和实验结果验证了本文所提CBSVPWM-BWZ方法的有效性，其可以完全等效传统SVPWM- BWZ，在变频调速系统的起动和低速轻载状态下取得较好的控制效果。本文所提方法相比于传统SVPWM-BWZ，无需进行坐标变化和计算空间矢量的作用时间，实现更为方便。
参考文献
[1] Shen Jie, Schröder S, Rösner R, et al. A comprehensive study of neutral-point self-balancing effect in neutral- point-clamped three-level inverters[J]. IEEE Transa- ctions on Power Electronics, 2011, 26(11): 3084- 3095.
[2] 罗锐, 何英杰, 陈晖, 等. 三电平变流器中点电位平衡及低开关损耗SVPWM调制策略[J]. 电工技术学报, 2018, 33(8): 1-10.
Luo Rui, He Yingjie, Chen Hui, et al. SVPWM scheme for three-level converters with neutral point potential balancing and switching loss reduction[J]. Transactions of China Electrotechnical Society, 2018, 33(8): 1-10.
[3] Kouro S, Rodriguez J, Wu Bin, et al. Powering the future of industry: high-power adjustable speed drive topologies[J]. IEEE Industry Applications Magazine, 2012, 18(4): 26-39.
[4] 殷正刚. 大功率三电平逆变器脉宽调制及磁场定向控制的研究[D]. 北京: 中国科学院大学, 2012.
[5] Tan Longcheng, Liu Congwei, Li Yaohua, et al. The effect of minimum pulse width limitation on neutral point voltage control and their cooperation in high power three-level NPC converters[C]//IEEE Inter- national Conference on Electrical Machines & Systems, Incheon, 2010: 215-218.
[6] 白华, 赵争鸣, 张永昌, 等. 最小脉宽特性对高压三电平变频器的影响[J]. 电工技术学报, 2006, 21(12): 60-65.
Bai Hua, Zhao Zhengming, Zhang Yongchang, et al. Effect of minimum pulse width on high voltage three-level inverters[J]. Transactions of China Elec- trotechnical Society, 2006, 21(12): 60-65.
[7] Beig A R. Synchronized SVPWM algorithm for the overmodulation region of a low switching frequency medium-voltage three-level VSI[J]. IEEE Transa- ctions on Industrial Electronics, 2012, 59(12): 4545- 4554.
[8] Holmes D G, Lipo T A. Pulse width modulation for power converters: principles and practice[M]. New York: IEEE Press, 2003.
[9] Koyama M, Fujii T, Uchida R, et al. Space voltage vector based new PWM method for large capacity three-level GTO inverter[C]//IEEE International Con- ference on Industrial Electronics, San Diego, 1992: 271-276.
[10] Bowes S R, Lai Y S. The relationship between space- vector modulation and regular-sampled PWM[J]. IEEE Transactions on Industrial Electronics, 1997, 44(5): 670-679.
[11] 周卫平, 吴正国, 唐劲松, 等. SVPWM的等效算法及SVPWM与SPWM的本质联系[J]. 中国电机工程学报, 2006, 26(2): 133-137.
Zhou Weiping, Wu Zhengguo, Tang Jinsong, et al. A novel algorithm of SVPWM and the study on the essential relationship between SVPWM and SPWM[J]. Proceedings of the Chinese Society for Electrical Engineering, 2006, 26(2): 133-137.
[12] Zhou Keliang, Wang Danwei. Relationship between space-vector modulation and three-phase carrier- based PWM a comprehensive analysis three-phase inverters[J]. IEEE Transactions on Industry Appli- cations, 2002, 49(1): 186-196.
[13] 方辉, 吴瑕杰, 宋文胜, 等. 过调制区内三电平SVPWM与CBPWM算法的统一性研究[J]. 电工技术学报, 2015, 35(8): 1993-2001.
Fang Hui, Wu Xiajie, Song Wenshen, et al. Unity studies between three-level SVPWM and CBPWM in the over-modulation region[J]. Transactions of China Electrotechnical Society, 2015, 35(8): 1993-2001.
[14] 陈娟, 何英杰, 王新宇, 等. 三电平空间矢量与载波调制策略统一理论的研究[J]. 中国电机工程学报, 2013, 33(9): 71-78.
Chen Juan, He Yingjie, Wang Xinyu, et al. Research of the unity theory between three-level space vector and carrier-based PWM modulation strategy[J]. Proceedings of the CSEE, 2013, 33(9): 71-78.
[15] 姜卫东, 赵德勇, 胡杨, 等. 基于载波实现的二极管钳位型三电平逆变器虚拟空间矢量脉宽调制方法[J]. 电工技术学报, 2016, 31(12): 153-160.
Jiang Weidong, Zhao Deyong, Hu Yang, et al. Carrier- based virtual space vector pulse width modulation for diode clamped three-level inverter[J]. Transactions of China Electrotechnical Society, 2016, 31(12): 153- 160.
[16] 方辉, 宋文胜, 冯晓云, 等. 三电平SVPWM与CBPWM算法的内在联系研究[J]. 电工技术学报, 2014, 29(10): 19-26.
Fang Hui, Song Wenshen, Feng Xiaoyun, et al. Relationship between three-level SVPWM and CBPWM[J]. Transactions of China Electrotechnical Society, 2014, 29(10): 19-26.
[17] Zhang Zhe, Thomsen O C, Andersen M A E, et al. Discontinuous PWM modulation strategy with circuit- level decoupling concept of three-level neutral- point-clamped (NPC) inverter[J]. IEEE Transactions on Industrial Electronics, 2013, 60(5): 1897-1906.
[18] 陆原, 胡丙辉, 张军伟, 等. 基于SVPWM调制的三段式算法研究[J]. 电力系统保护与控制, 2016, 44(6): 68-75.
Lu Yuan, Hu Binghui, Zhang Junwei, et al. A three- segment algorithm research based on SVPWM modulation[J].Power System Protection and Control, 2016, 44(6):68-75.
[19] Pou J, Pindado R, Boroyevich D, et al. Limits of the neutral-point balance in back-to-back connected three- level converters[J]. IEEE Transactions on Power Electronics, 2004, 19(3): 722-731.
A Carrier-Based SVPWM Begins with the Zero Voltage Vector for Three-Level Neutral Point Clamped Converter
Abstract The space vector PWM begins with the zero voltage vector (SVPWM-BWZ) for the three-level converter has the advantages of satisfying the minimum pulse width limitation and generating arbitrarily small line voltage at a low modulation index. It is suitable for start-up and low-speed status of variable frequency speed regulation system, but its implementation is complex. To solve this problem, the basic principle of SVPWM-BWZ is introduced in this paper firstly, then the equivalent relationship between SVPWM-BWZ and carrier-based PWM is analyzed. Accordingly, a carrier-based SVPWM-BWZ (CBSVPWM-BWZ) method and the corresponding neutral point balancing control strategy are proposed. The output phase voltage spectrum and pulse width characteristics of three-level converter and the switching frequency of power devices under CBSVPWM-BWZ are derived. Finally, the effectiveness of the proposed method is verified by simulation and experiments. The results show that the proposed method is completely equivalent to the traditional SVPWM-BWZ strategy. It has better modulation effect at low modulation ratio and does not need to calculate the duration of the space vector, which is more convenient to implement.
keywords：Three-level, space vector PWM, zero voltage vector, carrier-based PWM, neutral point balance control
中图分类号：TM464
DOI: 10.19595/j.cnki.1000-6753.tces.190550
高 瞻 男，1993年生，博士研究生, 研究方向为大功率电力电子变流器控制技术。E-mail: gz1993@mail.iee.ac.cn
赵 鲁 男，1984年生，副研究员, 硕士生导师, 研究方向为大功率变流器及高性能电机牵引控制技术。E-mail: zhaolu@mail.iee.ac.cn（通信作者）
收稿日期2019-05-07
改稿日期 2019-07-27
国家重点研发计划高速磁浮交通系统关键技术研究课题资助项目（2016YFB1200602-20）。
（编辑 崔文静）